平面凸七邊形內臨近周邊兩相鄰交叉對角線 長度乘積方程式

平面凸七邊形內臨近周邊兩相鄰交叉對角線

長度乘積方程式

李輝濱

壹、前言

自 探 索 推 證 出 平 面 凸 四 邉 形、五 邉 形、六 邉 形 等 圖 形 內 臨 近 周 邊 兩 相 鄰 交 叉 對 角 線 長 度 乘 積 方 程 式 後，作 者 實 際 詳 細 逐 一 觀 察 並 對 照 比 較 這 些 方 程 式 型 態 內 容 裡 的 各 項 組 合 結 構，隱 約 發 現 此 三 個 圖 形 裡 毎 一 方 程 式 的 獨 自 組 合 關 係 式 都 呈 現 出 各 對 應 多 邉 形 餘 弦 公 式 型 態 的 微 妙 契 合 ！ 為 了 要 確 定 如 此 的 歸 納 思 考 是 否 真 能 有 效 地 推 理 出 類 似 的 餘 弦 公 式，於 是 進 行 規 劃 作 圖 深 入 鑽 研 ； 試 看 下 圖a.的一 平 面 凸 四邉 形 ， 透 過幾 何 作 圖 法在 此 圖 形 邉長

A

₁

A

₄內 部 作 一 個 三 角 形



A

₁

A

₄

T

， 使 得



A

₁

A

₄

T





A

₂

A

₄

A

₃(互 為 相 似 形 ) 且



A

₄

TA

₁





A

₄

A

₃

A

₂。 並 繼 續 連 接 T 與

A

₃兩 點 ， 使 形 成 線 段

TA

₃， 再 連 接 對 角 線 長

A

₁

A

₃， 得 一 新 的



TA

₁

A

₃如 圖 b.。這新



TA

₁

A

₃的 兩 邉 長

TA

₁與

TA

₃的 長 度 恰 能 分 別 由 原 凸 四 邉 形 的 四 個 邉 長 以 比 例 關 係 式 構 成 ， 而 此



TA

₁

A

₃的 三 邉 長 與 內 角 所 形 成 的 餘 弦 公 式 也 恰 能 推 導 出 凸 四 邉 形 的 兩 交 叉 對 角 線 長 度 乘 積 方 程 式 ！ 像 這 樣 能 將 四 邉 形 的 各 邉 長 以 幾 何 作 圖 法 縮 減 成 一 新 三 角 形 的 概 念 肯 定 是 一 項 指 標 思 維 的 創 新 ！ 根 據 這 預 想 的 觀 念 及 規 劃 初 以 選 定 平 面 凸 五 邉 形 5 4 3 2 1

A

A

A

A

A

其 兩 相 鄰 交 叉 對 角 線 長 度 乘 積 公 式 的 構 圖 軌 跡 概 念，以 其 圖 形 最 前 緣 四 個 頂 點 所 形 成 的 四 邊 形

A

₁

A

₂

A

₃

A

₄為 基 底 先 作 出 一 個 如 上 述 的 輔 助 三 角 形 ， 再 將 五 邉 形 最 後 兩 個 邉 長 所 屬 的 三 角 形 依 循 著 相 似 形 型 式 另 作 一 相 似 圖 形 並 使 其 附 著 於 輔 助 三 角 形 的

TA

₁

對 應 邉 上，如 此 即 構 作 出 一 輔 助 四 邉 形，這 新 造 輔 助 四 邉 形 的 所 有 邉 長 與 內 角 所 形 成 的 餘 弦 公 式 就 是 提 供 輔 助 解 題 的 重 要 關 鍵，將 此 等 特 殊 解 題 要 領 適 度 推 廣 至 六 邉 形，以 至 於 七 邉 形 等 圖 形 結 構，竟 然 皆 能 絕 妙 完 整 的 求 證 出 各 圖 形 方 程 式 來，而 且 這 三 個 圖 形 的 解 題 驗 證 計 劃 都 是 遵 循 著 完 全 一 致 的 基 礎 理 念 。 正 弦 定 理 僅 能 應 用 在 圓 內 接 多 邉 形 圖 形，而 相 對 地 餘 弦 定 理 及 其 推 廣 公 式 更 能 廣 泛 有 效 地 應 用 到 所 有 平 面 多 邉 形 圖 形，其 效 能 更 為 強 大 ！ 下 列 正 文 基 於 大 膽 假 設、小 新 求 證 意 念 將 詳 盡 敘 述 標 題 內 容 的 理 論 推 導 思 路 歷 程 及 解 題 分 析 的 特 定 理 念，以 新 穎 獨 自 開 發 的 策 略 來 完 成 方 程 式 的 論 證 ！

貳、本文

在 研 析 推 導 廣 義 的 平 面 凸 七 邊 形 內 臨 近 周 邊 兩 相 鄰 交 叉 對 角 線 長 度 乘 積 一 般 化 方 程 式 之 前，為 了 要 完 整 且 有 條 理 地 導 證 出 應 得 的 型 態 關 係 式，則 必 在 下 列 撰 文 推 理 演 繹 的 運 算 過 程 中 ， 需 應 用 或 對 照 到 下 述 已 知 的 幾 個 數 學 應 用 性 質 ；

一、數學應用性質─引理

引 理1. 平面 四邉 形 餘 弦 定理 : 在 平 面上 給 定 一 個凸 四 邊 形

A

₁

A

₂

A

₃

A

₄， 如 圖1. 圖 1 圖 2 令 線 段

A

₁

A

₂ =

V

₁，

A

₂

A

₃=

V

₂，

A

₃

A

₄ =

V

₃，

A

₄

A

₁=

V

₄， 則 此 凸 四 邊 形 的 面 積 型 餘 弦 公 式 為

V

₄2=

V

₁2+

V

₂2+

V

32－ 2

V

1

V

2

cos A

2－2

V

2

V

3

cos A

3+ 2

V

1

V

3

cos



A

2



A

3



··· (1) 因 上 列 公 式 中 各 項 的 量 綱 都 是 邊 長 的 平 方 ， 故 稱 為 面 積 型 餘 弦 公 式 。

證 明 ： 幾 何 作 圖 ； 連 接 圖 1.的 兩 個 頂 點

A

₁與

A

₃形 成 一 對 角 線

A

₃

A

₁。

形 餘 弦 定 理 ；

d

2=

V

₁2+

V

₂2－ 2

V

₁

V

₂

cos A

₂， 又 對



A

₁

A

₃

A

₄言 ， 可 得 餘 弦 公 式 為 2

4

V

=

d

2+

V

₃2－ 2

V cos

₃

d

m



V

₄2=

V

₁2+

V

₂2+

V

₃2－ 2

V

₁

V

₂

cos A

₂－2

V cos

₃

d

m

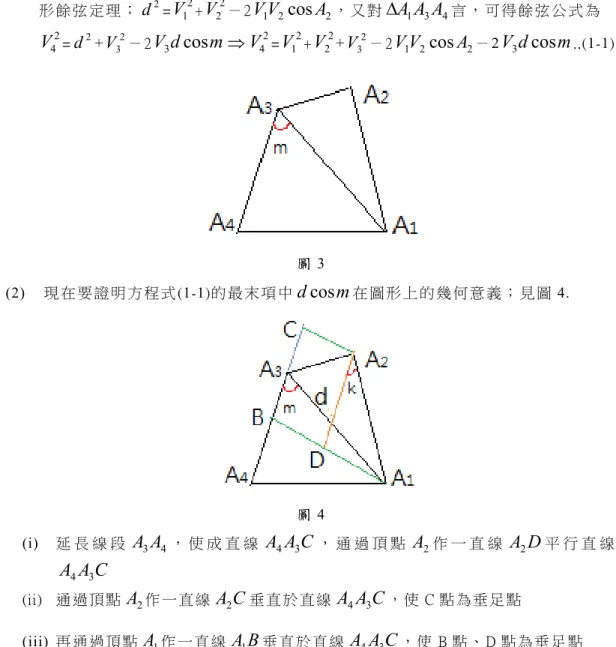
..(1-1)

圖 3 (2) 現 在要 證 明 方 程式 (1-1)的 最末 項 中

d cos

m

在 圖 形 上 的 幾 何 意 義 ； 見 圖4. 圖 4 (i) 延 長 線 段

A

₃

A

₄， 使 成 直 線

A

₄

A

₃

C

， 通 過 頂 點

A

₂作 一 直 線

A

₂

D

平 行 直 線

C

A

A

_{4 3} (ii) 通 過 頂 點

A

₂作 一 直 線

A

₂

C

垂 直 於 直 線

A

₄

A

₃

C

， 使 C 點 為 垂 足 點 (iii) 再 通過 頂 點

A

₁作 一 直 線

A

₁

B

垂 直 於 直 線

A

₄

A

₃

C

， 使 B 點 、 D 點 為 垂 足 點 (iv) 由 直 角



A

₁

A

₃

B

性 質 知

d cos

m

的 值 恰 為 投 影 線 段 長

A

₃

B

， 同 理

V

₂在 直 線

C

A

A

_{4 3} 上 的 投 影 線 段 長 為

A

₃

C

， 而 線 段 長

A

₃

C

恰 等 於

V

₂

cos(





A

₃

)

= 3 2

cos

A

V



(v)

V

₁在 直 線

A

₄

A

₃

C

上 的 投 影 線 段 長 為

A

₂

D



CB

線 段 ； 因

A

₂

D

平 行

CB

， 令

k

D

A

A





_{1 2} ，則 頂 角

A

₃與

A

₂的 關 係 為

A

₃+ (

A

₂-k) =





A

₃+

A

₂=



+ k，而 線 段 長

A

₂

D

恰 等 於

V cos

₁

k

，但 由

V

₁

cos



A

₂



A

₃



=

V

₁

cos







k



=



V cos

₁

k

，

得 線 段 長

A

₂

D

=

V cos

₁

k

=



V

₁

cos



A

₂



A

₃



。

(vi) 因 此 ， 由

A

₃

B

+

A

₃

C

=

CB

=

A

₂

D

， 得

d cos

m

=

V

₂

cos

A

₃



V

₁

cos



A

₂



A

₃



(3) 最 後將 此

d cos

m

的 值 代 入 方 程 式 (1-1)， 即 得 證出 方 程 式 (1) 。 事 實 上 ， 方 程 式 (1)不 僅 適 用於 圖 1.凸 四邉 形 ， 也 適用 於 如 圖 2.的 凹 四 邉 形； 只 要 仿 效 上 述 構 圖 要 領 即 可 完 整 證 明 出 平 面 凹 四 邉 形 餘 弦 定 理 為 方 程 式 (1)。 引 理2. 平 面 五 邉 形 餘 弦 定 理 ： 先 參 考 下 圖 5.的 平 面 凹 五 邊 形 。 圖 5 圖 6 任 給 一 個 平 面 凹 五 邊 形

A

₁

A

₂

A

₃

A

₄

A

₅， 假 設 選 取

A

₄頂 角 為 優 角 ， 優 角 意 指 其 角 度 是 大 於



但 小 於

2



，令 線 段

A

₁

A

₂ =

V

₁，

A

₂

A

₃ =

V

₂，

A

₃

A

₄ =

V

₃，

A

₄

A

₅ =

V

₄，

A

₅

A

₁=

V

₅， 則 此 五 邊 形 的 面 積 型 餘 弦 公 式 為

V

₅2=

V

₁2+

V

₂2+

V

32+ 2 4

V

－2

V

₁

V

₂

cos A

₂－2

V

₂

V

₃

cos

A

₃－2

V

₃

V

₄

cos

A

₄

+2

V

₁

V

₃

cos



A

₂



A

₃



+2

V

₂

V

₄

cos



A

₃



A

₄



－2

V

₁

V

₄

cos(

A

₂



A

₃



A

₄

)

···· (2) 證 明 ： 下 圖7. 連 接兩 頂 點

A

₁與

A

₄形 成 對 角 線 長

A

₁

A

₄



d

， 令



A

₁

A

₄

A

₅



m

，

(1) 圖 7.中 的 部 份 四邉 形

A

1

A

2

A

3

A

4言 ， 由 引 理1.有 平面 四 邉 形 餘弦 公 式 為 2

d

=

V

₁2+

V

₂2+

V

₃2－2

V

₁

V

₂

cos A

₂－2

V

₂

V

₃

cos

A

₃+2

V

₁

V

₃

cos



A

₂



A

₃



又 對



A

₁

A

₄

A

₅言 ， 可 得 三 角 形 餘 弦 公 式 為

V

₅2=

d

2+

V

₄2－2

V cos

₄

d

m



V

52= 2 1

V

+

V

₂2+

V

32+ 2 4

V

－2

V

₁

V

₂

cos A

₂－2

V

₂

V

₃

cos

A

₃+ 2

V

₁

V

₃

cos



A

₂



A

₃



－2

V cos

₄

d

m

··· (2-1) 圖 7 (2) 仿 效引 理 1.的 幾何 作 圖 法 ，作 出 圖 8.， 即 延 長 線 段

A

₄

A

₅使 形 成 一 直 線

CA

₄

A

₅， 另 作 三 綠 色 直 線

A

₃

E

、

A

₂

B

與

A

₁

D

相 互 平 行 且 皆 與 直 線

CA

₄

A

₅相 垂 直。使 得

B

、

D

、

E

三 點 都 是 垂 足 點。再 通 過 頂 點

A

₂作 一 直 線

A

₂

G

平 行 直 線

CA

₄

A

₅，使

G

點 為 垂 足 點 。 (3) 圖 8.中 ， 由 直 角



A

₁

A

₄

D

性 質 知

d cos

m

的 值 恰 為 投 影 線 段 長

A

₄

D

， 同 理

V

₃ 在 直 線

CA

₄

A

₅上 的 投 影 線 段 長 為

A

₄

E

， 恰 等 於

V

₃

cos(

A

₄





)

=



V

₃

cos

A

₄。 圖 8 (4)

V

₂ 在 直 線

CA

₄

A

₅ 上 的 投 影 線 段 長 為

BE

， 恰 等 於 [π ]=

)

cos(

3 4 2

A

A

V



。 (5)

V

₁在 直 線

CA

₄

A

₅上 的 投 影 線 段 長 為

BD

=

A

₂

G

線 段 長 ， 因

BD

平 行

A

₂

G

， 令

t

G

A

A





_{1 2} ，由 圖8.中 知 x=

A

₃+ (

A

₄





)

且 x+ (

A

₂

 )

t





，則

A

₂+

A

₃+

A

₄ =

2





t



V

₁

cos



A

₂



A

₃



A

₄



=

V

₁

cos



2





t



=

V cos

₁

t

=

A

₂

G

=

BD

。 (6) 在 直 線

CA

4

A

5上 ， 線 段 長

BD

=線 段 長

A

4

D

+

A

4

E

+

BE

， 故 得

A

4

D

=

BD

－

A

4

E

－

BE



d cos

m

=

V

₁

cos



A

₂



A

₃



A

₄





V

₂

cos(

A

₃



A

₄

)

+

V

₃

cos

A

₄。 (7) 將 此

d cos

m

關 係 式 直 接 代 入 方 程 式 (2-1)中 ， 即得 證 出 方 程式 (2)。 事 實 上，方 程 式 (2)不 僅 適 用於 凹 五 邉 形，也適 用 於凸 五 邉 形；只 要仿 效 上述 引 理 1.與 引 理2.構 圖 要 領即 可 完 整 證明 出 平 面 凸五 邉 形 餘 弦定 理 為 方 程式 (2) 。若 換成 選 取 頂 角

A

₃ 為 優 角 如 圖6.， 則同 樣 可 推證 得 方 程 式(2) 。 引 理 3. 平 面 六 邉 形 餘 弦 定 理 ： 在 平 面 上 給 定 一 個 凸 六 邊 形

A

1

A

2

A

3

A

4

A

5

A

6， 令 線 段 長 2 1

A

A

=

V

₁，

A

₂

A

₃ =

V

₂，

A

₃

A

₄ =

V

₃，

A

₄

A

₅ =

V

₄，

A

₅

A

₆ =

V

₅，

A

₆

A

₁=

V

₆，則 此 六 邊 形 的 面 積 型 餘 弦 公 式 為 ： 2 6

V

=

V

₁2+

V

₂2+

V

32+ 2 4

V

+

V

52－2

V

1

V

2

cos A

2－2

V

2

V

3

cos

A

3－2

V

3

V

4

cos

A

4

－2

V

₄

V

₅

cos

A

₅+2

V

₁

V

₃

cos



A

₂



A

₃



+2

V

₂

V

₄

cos



A

₃



A

₄



+2

V

₃

V

₅

cos



A

₄



A

₅



－2

V

₁

V

₄

cos(

A

₂



A

₃



A

₄

)

－2

V

₂

V

₅

cos(

A

₃



A

₄



A

₅

)

+2

V

₁

V

₅

cos(

A

₂



A

₃



A

₄



A

₅

)

··· (3) 證 明 ： 方 程 式 (3)也 適 用 於 凹 六 邉 形 ， 以 頂 角

A

₃為 優 角 的 凹 六 邉 形 來 推 證 之 ； 參 見 下 圖 9. 連 接 兩 頂 點

A

₁與

A

₅形 成 一 對 角 線 ， 使 對 角 線 長 度

A

₁

A

₅



d

， (1) 令



A

₁

A

₅

A

₆



m

， 對 圖9.中 的 部份 凹 五 邉形

A

₁

A

₂

A

₃

A

₄

A

₅言 ， 有 餘 弦 公 式 為 2

d

=

V

₁2+

V

₂2+

V

32+ 2 4

+2

V

₁

V

₃

cos



A

₂



A

₃



+2

V

₂

V

₄

cos



A

₃



A

₄



－2

V

₁

V

₄

cos(

A

₂



A

₃



A

₄

)

又 對



A

₁

A

₅

A

₆言 ， 可 得 三 角 形 餘 弦 公 式 為

V

₆2=

d

2+

V

52－2

V cos

5

d

m



2 6

V

=

V

₁2+

V

₂2+

V

₃2+

V

₄2+

V

₅2－2

V

₁

V

₂

cos A

₂－2

V

₂

V

₃

cos

A

₃－2

V

₃

V

₄

cos

A

₄

－2

V cos

₅

d

m

+2

V

₁

V

₃

cos



A

₂



A

₃



+2

V

₂

V

₄

cos



A

₃



A

₄



－2

V

₁

V

₄

cos(

A

₂



A

₃



A

₄

)

··· (3-1) 圖 9 (2) 仿 效引 理 1.與 2.的 幾 何 作 圖法，作 出 圖 10.，其 中 四直 線

A

₂

H

、

A

₃

GL

、

A

₄

F

與

B

A

CA

_{5 6} 相 互 平 行 ， 另 四 綠 色 直 線

A

₄

C

、

A

₃

D

、

A

₂

GE

與

HA

₁

FB

相 互 平 行 且 皆 與 直 線

A

₂

H

、

A

₃

GL

、

A

₄

F

與

CA

₅

A

₆

B

相 垂 直 。 而

B

、

C

、

D

、

E

、

F

、

G

、

H

七 點 都 是 垂 足 點 。 故 四 邉 形

A

₄

CBF

、

A

₃

DEG

、

A

₂

EFH

皆 為 長 方 形 。 圖 10

(3) 對 直角



A

₁

A

₅

B

言，

d cos

m

的 值 恰 為 投 影 線 段 長

A

₅

B

，同 理

V

₄在 直 線

CA

₅

A

₆

B

上 的 投 影 線 段 長 為

A

₅

C

， 恰 等 於

V

₄

cos(





A

₅

)

=



V

₄

cos

A

₅=

A

₅

C

。 (4) 由

A

₄

F

平 行

CA

₅

A

₆

B

， 令



A

₃

A

₄

D



x

， 得

A

₄+

A

₅=





x

， 而

V

₃在 直 線

A

₄

F

上 的 投 影 線 段 長 為

A

₄

D

， 恰 等 於

V

₃

cos

x





V

₃

cos(

A

₄



A

₅

)

=

A

₄

D

。 (5) 由

A

₄

F

平 行

A

₃

GL

， 令



A

₂

A

₃

G



t

， 得

x

+

A

₃



t

=



， 故

A

₃+

A

₄+

A

₅=

t





2

， 而

V

₂在 直 線

A

₃

GL

上 的 投 影 線 段 長 為

A

₃

G

=

DE

， 恰 等 於

V cos

₂

t

=

)

cos(

_{3 4 5} 2

A

A

A

V





=

A

₃

G

=

DE

。 (6) 由

A

₂

H

平 行

A

₃

GL

， 令



A

₁

A

₂

H



z

， 得

z

+

A

₂



t

=



， 故

z

=

3





(

A

₂



A

₃+

A

₄+

A

₅) ，而 邉 長

V

₁在 直 線

A

₂

H

上 的 投 影 線 段 長 為

A

₂

H

。再 由 圖10. 知

A

₂

H

=

EF

=

V cos

₁

z

=



V

₁

cos



A

₂



A

₃



A

₄



A

₅



。 (7) 因 四邉 形

A

₄

CBF

為 長 方 形 ， 得

A

₅

C

+

A

₅

B

=

CB

=

A

₄

F

=

A

₄

D

+

DE

+

EF

， 故

B

A

₅ =

d

cos

m

=

A

₄

D

+

DE

+

EF



A

₅

C

=



V

₃

cos(

A

₄



A

₅

)

+

V

₂

cos(

A

₃



A

₄



A

₅

)



V

₁

cos



A

₂



A

₃



A

₄



A

₅





V

₄

cos

A

₅。 至 此 找 到

d

cos

m

的 完 整 值 。

(8). 將 此

d

cos

m

的 完 整 值 直 接 代 入 方 程 式 (3-1)中 ， 即 得 證出 方 程 式 (3) 。

方 程 式 (3)不 僅 適用 於 凹 六 邉形 ， 也 適 用於 凸 六 邉 形； 只 要 仿 效上 述 引 理 1.與 引 理 2. 及 引 理3.構 圖 要領 即 可 完 整證 明 出 平 面凸 六 邉 形 餘弦 定 理 為 方程 式 (3) 。凹 六邉 形 有 各樣 不 同 型 態 ； 如 另 有 頂 角

A

₂是 單 一 優 角 情 形 ， 頂 角

A

₄是 單 一 優 角 情 形 ，

A

₂與

A

₄同 為 優 角

情 形 (其 餘 頂 角 為 劣 角 )，… 等。只 需 仿 效 上 述 作 圖 要 領，這 所 有 型 態 的 凹 六 邉 形 其 具 有 的 餘 弦 定 裡 皆 為 方 程 式 (3)。

二、平面凸七邊形內臨近周邊兩相鄰交叉對角線長度乘積一般化方程式

平 面 上 給 定 一 個 凸 七 邊 形

A

₁

A

₂

A

₃

A

₄

A

₅

A

₆

A

₇， 令 線 段 長

A

₁

A

₂ =

V

₁，

A

₂

A

₃ =

V

₂， 4 3

A

A

=

V

₃，

A

₄

A

₅ =

V

₄，

A

₅

A

₆ =

V

₅，

A

₆

A

₇ =

V

₆，

A

₇

A

₁=

V

₇， 對 角 線 長

A

₁

A

₃



d

₁， 2 4 2

A

d

A



， 見 下 圖 11. 的平 面 凸 七 邉 形； 此 凸 七 邊形 內 臨 近 周邊 的 兩 相 鄰交 叉 圖 11 對 角 線 長 度 乘 積 一 般 化 方 程 式 為 ： 下 述 方 程 式 (4)； 2 2 2 1

d

d

=

( V

V

_{1 3}

)

2+

(

V

₂

V

₄

)

2+

( V

V

_{2 5}

)

2+

( V

V

_{2 6}

)

2+

( V

V

_{2 7}

)

2－2

V

₁

V

₂

V

₃

V

₄

cos(

A

₂



A

₄

)

－2

V

₂2

V

₄

V

₅

cos A

₅－2

V

₂2

V

₅

V

₆

cos A

₆－2

V

₂2

V

₆

V

₇

cos A

₇ +

2

V

₁

V

₂

V

₃

V

₅

cos



A

₂



A

₄



A

₅



+ 2

V

₂2

V

₄

V

₆

cos



A

₅



A

₆



+ 2

V

₂2

V

₅

V

₇

cos



A

₆



A

₇



－2

V

₁

V

₂

V

₃

V

₆

cos(

A

₂



A

₄



A

₅



A

₆

)

－

證 明：連 接 兩 頂 點

A

₁與

A

₄形 成 對 角 線 長

A

₁

A

₄



d

，並 依 循 前 言 指 引 的 思 考 方 向 先 將 此 七 邉 形 最 前 緣 四 個 頂 點 所 形 成 的 四 邊 形

A

₁

A

₂

A

₃

A

₄為 基 底 作 出 一 個 如 前 言 所 述 的 輔 助 三 角 形



TA

₁

A

₃， 如 圖12.， 此 處



A

₁

A

₄

T





A

₂

A

₄

A

₃(互 為 相 似 形 )。 圖 12 (1) 由 兩 相 似 三 角 形 對 應 邊 長 必 成 正 比 例 關 係 ， 得

d

:

d

₂



A

₁

T

:

V

₂



A

₄

T

:

V

₃



可 得

d

:

A

₄

T



d

₂

:

V

₃，再 由



A

₁

A

₄

A

₂=



TA

₄

A

₃ 及 兩 對 應 邉 長 成 正 比 例 與 其 夾 角 相 等 的 相 似 形 性 質 ， 可 得 知 另 兩 相 似 形 關 係



A

₁

A

₄

A

₂





TA

₄

A

₃， 因 此 可 得 2 1 4

A

A

A



=



A

₄

TA

₃， 且 有 另 ㄧ 組 正 比 例 關 係 為

d

:

A

₄

T



d

₂

:

V

₃



V

₁

:

A

₃

T

。 (2) 在 上述(1).的 兩 組正 比 例 關 係式 中 可 求 得輔 助 三 角 形



TA

₁

A

₃的 兩 個 邉 長 ； 由 3 4 2 1 2

:

:

:

d

A

T

V

A

T

V

d







A

₁

T



(

V

₂

d

)

/

d

₂ (4-1) 及

d

:

A

₄

T



d

₂

:

V

₃



V

₁

:

A

₃

T



A

₃

T



(

V

₁

V

₃

)

/

d

₂ (4-2) ， 而 另 外 在 頂 點 T 處 四 周 圍 的 角 度 關 係 可 知 ；



A

₁

TA

₃=

2







A

₄

TA

₃





A

₁

TA

₄ =

2







A

₄

A

₁

A

₂





A

₂

A

₃

A

₄ =

A

₂(頂 角 )+



A

₁

A

₄

A

₃





A

₁

TA

₃ =

A

₂(頂 角 )+



A

₁

A

₄

A

₃ ··· (4-3) ， 此 處 對 四 邊 形

A

₁

A

₂

A

₃

A

₄言 ， 其 四 個 頂 角 總 和 為

2



， (3) 接 下 來 要 將 七 邉 形 (圖 12.)中 另 外 部 份 五 邉 形

A

₁

A

₄

A

₅

A

₆

A

₇以 相 似 形 結 構 黏 附 在 3 1

A

TA



的 邉 長

TA

₁上 ； 此 需 藉 由 下 列 幾 何 作 圖 法 來 完 成 輔 助 相 似 形 的 製 作 ；

(i) 連 接 圖 12.中 的對 角 線

A

₄

A

₇及

A

₄

A

₆， 將 五 邉 形 分 割 成 三 個 三 角 形 如 下 圖13. 圖 13 (ii) 作 相似 形 應 自 三角 形 做 起，此 處 先 從



A

₇

A

₁

A

₄開 始；見 圖 13.，對



TA

₁

A

₃的 一 邊 長

TA

₁自 頂 點

A

₁向 外 側 作 一 射 線

A

₁

B

，使



TA

₁

B

=



A

₄

A

₁

A

₇，又 在 頂 點

T

處 對 圖 形 外 側 作 另 一 射 線

TB

，使



A

₁

TB





A

₁

A

₄

A

₇，此 兩 射 線 交 在

B

點；見 圖 14.則



A

₁

BT





A

₁

A

₇

A

₄(互 為 相 似 形 ) 且



TBA

₁





A

₄

A

₇

A

₁。 由 對 應 邉 長 成 正 比 例 關 係 得 7 4 1 7 1

B

:

V

A

T

:

d

BT

:

A

A

A







A

₁

B



(

V

₇



A

₁

T

)

/

d

··· (4-1a) 再 將 (4-1)式 的 邉長

TA

₁代 入 (4-1a)式 ，即 得

A

₁

B



(

V

₇

V

₂

)

/

d

₂ ··· (4-4) 圖 14

(iii) 同 理， 在 圖 14.裡 自 線 段

TB

外 側 再 作 出 第 二 個 三 角 形



TCB

； 見 下 圖 15.； 自 頂 點

B

向 外 側 作 一 射 線

BC

，使



TBC

=



A

₄

A

₇

A

₆，又 在 頂 點

T

處 對 圖 形 外 側 作 另 一 射 線

TC

，使



BTC





A

₇

A

₄

A

₆，此 兩 射 線 交 在

C

點；則 可 得



TCB

與



A

₄

A

₆

A

₇兩 者 呈 相 似 形，且



TCB





A

₄

A

₆

A

₇。再 由 對 應 邉 長 成 正 比 例 關 圖 15 係 得

BC

:

V

₆



BT

:

A

₇

A

₄



CT

:

A

₆

A

₄ ， 又 因 為

BT

:

A

₇

A

₄



A

₁

T

:

d

， 故 聯 立 得 出 ；

BC

:

V

₆



BT

:

A

₇

A

₄



CT

:

A

₆

A

₄ =

A :

₁

T

d

··· (4-1b) 對 (4-1b)作 運 算得 出



BC



(

V

₆



A

₁

T

)

/

d

··· (4-1c) 再 將 (4-1)式 的 邉長

TA

₁代 入 (4-1c)式 ，即 得 出；

BC



(

V

₆

V

₂

)

/

d

₂··· (4-5) (iv) 繼 續 仿 效 (iii).的 作 圖 分 析 過 程 ， 在 圖 15.裡 自 線 段

TC

外 側 再 作 出 第 三 個 三 角 形



TCD

；見 下 圖16.；自 頂 點

C

向 外 側 作 一 射 線

CD

，使



TCD

=



A

₄

A

₆

A

₅， 圖 16

又 在 頂 點

T

處 對 圖 形 外 側 作 另 一 射 線

TD

， 使



CTD





A

₆

A

₄

A

₅， 而 此 兩 射 線 相 交 在

D

點；則 得



TCD





A

₄

A

₆

A

₅(互 為 相 似 形 )。且



TDC





A

₄

A

₅

A

₆。 再 由 對 應 邉 長 成 正 比 例 關 係 得

CD

:

V

₅



DT

:

V

₄



CT

:

A

₆

A

₄ ， 又 由 (4-1b) 式，得

CD

:

V

₅



DT

:

V

₄



CT

:

A

₆

A

₄=

BT

:

A

₇

A

₄



A

₁

T

:

d

，故 演 算 後 分 別 得 出 ； 邉 長

CD

的 長 度 值 為 ；

CD



(

V

₅



A

₁

T

)

/

d

··· (4-1d) 邉 長

DT

的 長 度 值 為 ；

DT



(

V

₄



A

₁

T

)

/

d

··· (4-1e) 再 將 (4-1)式 的 邉長

TA

₁代 入 (4-1d)式 ， 即 得 出；

CD



(

V

₅

V

₂

)

/

d

₂ ··· (4-6) 又 將 (4-1)式 的 邉長

TA

₁代 入 (4-1e)式 ，即 得 出；

DT



(

V

₄

V

₂

)

/

d

₂ ··· (4-7) (4) 由 步 驟 (3). 推 導 出 的 所 有 比 例 關 係 式 可 聯 結 成 下 列 各 對 應 邉 長 成 正 比 例 式 ；





A

T

d

V

B

A

₁

:

_{7 1}

:

BC

:V

₆



CD

:

V

₅



DT

:

V

₄ ， 則 平 面 五 邉 形

TA

₁

BCD

必 與 另 一 個 平 面 五 邉 形

A

₄

A

₁

A

₇

A

₆

A

₅兩 者 呈 相 似 形 關 係，見 上 圖 16. 。可 看 到 平面 五 邉 形

TA

₁

BCD

相 似 形 結 構 確 實 黏 附 在



TA

₁

A

₃的 邉 長

TA

₁外 側 上 。 到 這 裡，相 似 五 邉 形

TA

₁

BCD

的 四 個 邉 長

A

₁

B

、

BC

、

CD

、

DT

都 尋 獲 了。它 們 的 數 值 確 實 分 別 由 原 凸 七 邉 形 的 邉 長 以 比 例 式 關 係 構 成 ！ (5) 經 由以 上 幾 何 作圖 推 證，已 成 功 地 將 原凸 七 邉 形 的七 個 邉 長 以比 例 式 關 係縮 減 成 圖 16.中 的 平 面 凹 六 邊 形

A

₁

A

₃

TDCB

裡 六 個 邉 長 的 新 構 圖 ！ 這 新 構 的 凹 六 邊 形 有 一 個 頂 角



A

₃

TD

為 單 一 優 角 ， 由 圖 16.知 這優 角 的 值 為； 優 角



A

₃

TD

=



A

₃

TA

₁+



A

₁

TD

， 而 (4-3)式 ；



A

₁

TA

₃ =

A

₂(頂 角 )+



A

₁

A

₄

A

₃， 再 由 五 邉 形

TA

₁

BCD

與 五 邉 形

A

₄

A

₁

A

₇

A

₆

A

₅的 相 似 關 係，得



A

₁

TD

=



A

₁

A

₄

A

₅， 故 優 角



A

₃

TD

=

A

₂(頂 角 )+



A

₁

A

₄

A

₃+



A

₁

A

₄

A

₅ =

A

₂(頂 角 )+

A

₄(頂 角 )。 (6) 另 外由 五 邉 形 相似 形 性 質 知；兩 個 五 邉形 的 各 對 應角 必 完 全 相等，所 以 得下 列 關 係 ； 頂 角

A

₅=頂 角

D

， 頂 角

A

₆=頂 角

C

， 頂 角

A

₇=頂 角

B

， (7) 再 參考 新 構 的 圖 16. 如 下；新 構 的 平 面凹 六 邊 形

A

₁

A

₃

TDCB

裡，各 邉 長 與 所 需 的 各 頂 角 都 推 求 到 了 ， 應 用 引 理 3.平 面 凹 六 邊 形 的 餘 弦 定 理 方 程 式 (3)， 可 完 整 敘

述 出 新 構 的 平 面 凹 六 邊 形

A

₁

A

₃

TDCB

所 屬 的 餘 弦 定 理 公 式 ， 得 圖 16 2 3 1

A

A

=

TA

₃2+

TD

2+

DC

2+

CB

2+

BA

₁2－2

TA

₃



TD

cos(



A

₃

TD

)

－2

TD



DC

cos

D

－2

DC



CB

cos

C

－2

CB



BA

1

cos

B

+2

TA

3



DC

cos





A

3

TD



D



+

2

TD



CB

cos



D



C



+2

DC



BA

1

cos



C



B



－2

TA

3



CB

cos(



A

3

TD



D



C

)

－ 2

TD



BA

1

cos(

D



C



B

)

+2

TA

3



BA

1

cos(



A

3

TD



D



C



B

)

··· (3-2) 現 在 將 凹 六 邊 形 各 邉 長 的 比 例 數 值 及 各 角 角 度 值 代 入 方 程 式 (3-2)， 得 下 式； 2 1

d

=

[(

V

₁

V

₃

)

/

d

₂

]

2+

[(

V

₄

V

₂

)

/

d

₂

]

2+

[(

V

₅

V

₂

)

/

d

₂

]

2+

[(

V

₆

V

₂

)

/

d

₂

]

2+

[(

V

₇

V

₂

)

/

d

₂

]

2 －2

[(

V

₁

V

₃

)

/

d

₂

]

[(

V

₄

V

₂

)

/

d

₂

]

cos(

A

₂



A

₄

)

－2

[(

V

₄

V

₂

)

/

d

₂

]

[(

V

₅

V

₂

)

/

d

₂

]

cos A

₅ －2

[(

V

₅

V

₂

)

/

d

₂

]

[(

V

₆

V

₂

)

/

d

₂

]

cos A

₆－2

[(

V

₆

V

₂

)

/

d

₂

]

[(

V

₇

V

₂

)

/

d

₂

]

cos A

₇ + 2

[(

V

₁

V

₃

)

/

d

₂

]

[(

V

₅

V

₂

)

/

d

₂

]

cos



A

₂



A

₄



A

₅



+ 2

[(

V

₄

V

₆

V

₂2

)

/

d

₂2

]

cos



A

₅



A

₆



+ 2

[(

V

₅

V

₇

V

₂2

)

/

d

₂2

]

cos



A

₆



A

₇



－2

[(

V

₆

V

₁

V

₂

V

₃

)

/

d

₂2

]

cos(

A

₂



A

₄



A

₅



A

₆

)

－ 2

[(

V

₄

V

₇

V

₂2

)

/

d

₂2

]

cos(

A

₅



A

₆



A

₇

)

+ 2

[(

V

₇

V

₁

V

₂

V

₃

)

/

d

₂2

]

cos(

A

₂



A

₄



A

₅



A

₆



A

₇

)



將 上 式 運 算 展 開 後 ， 在 等 號 兩 側 同 乘 以

d

₂2， 再 化 簡 ， 整 裡 ， 最 後 得 下 式 ； 2 2 2 1

d

d

=

( V

V

_{1 3}

)

2+

(

V

₂

V

₄

)

2+

( V

V

_{2 5}

)

2+

( V

V

_{2 6}

)

2+

( V

V

_{2 7}

)

2－2

V

₁

V

₂

V

₃

V

₄

cos(

A

₂



A

₄

)

－2

V

₂2

V

₄

V

₅

cos A

₅－2

V

22

V

5

V

6

cos A

6－2 2 2

V

V

₆

V

₇

cos A

₇ + 2

V

₁

V

₂

V

₃

V

₅

cos



A

₂



A

₄



A

₅



+ 2

V

₂2

V

₄

V

₆

cos



A

₅



A

₆



+ 2

V

₂2

V

₅

V

₇

cos



A

₆



A

₇



－2

V

₁

V

₂

V

₃

V

₆

cos(

A

₂



A

₄



A

₅



A

₆

)

－ 2

V

₂2

V

₄

V

₇

cos(

A

₅



A

₆



A

₇

)

+2

V

₁

V

₂

V

₃

V

₇

cos(

A

₂



A

₄



A

₅



A

₆



A

₇

)

··· (4) 方 程 式 (4)即 為 得 證 出 的 平 面 凸 七 邊 形 內 臨 近 周 邊 的 兩 相 鄰 交 叉 對 角 線 長 度 乘 積 一 般 化 方 程 式 。 此 方 程 式 真 的 由 應 用 平 面 六 邊 形 的 餘 弦 公 式 推 證 而 來 。

三、檢驗

方 程 式 (4)的 結 構 型 態 中 毎 一 項 式 內 涵 裡 表 徵 的 邉 長 與 頂 角 排 列 型 式 都 呈 現 出 秩 序 、 規 律 、 條 理 。 縱 然 如 此 ， 仍 須 透 過 下 列 詳 盡 的 檢 驗 以 強 化 其 正 確 性 。 1. 若 令

V

₇



0

，使 頂 點

A

₇趨 近 於 頂 點

A

₁，頂 角

A

₇= 0 ，則 平 面 凸 七 邊形 退 化 成 平 面 凸 六 邊 形 ， 方 程 式 (4)隨 即縮 減 退 化 成下 式 ； 2 2 2 1

d

d

=

( V

V

_{1 3}

)

2+

(

V

₂

V

₄

)

2+

( V

V

_{2 5}

)

2+

( V

V

_{2 6}

)

2－2

V

₁

V

₂

V

₃

V

₄

cos(

A

₂



A

₄

)

－2

V

₂2

V

₄

V

₅

cos A

₅－2

V

₂2

V

₅

V

₆

cos A

₆ +2

V

₁

V

₂

V

₃

V

₅

cos



A

₂



A

₄



A

₅



+ 2

V

₂2

V

₄

V

₆

cos



A

₅



A

₆



－2

V

₁

V

₂

V

₃

V

₆

cos(

A

₂



A

₄



A

₅



A

₆

)

··· (5)

方 程 式 (5)最 末 一項 的 角 度 組合 有 四 個 頂角 相 加，再做 一 個 轉 換，使 其 變 換成 凸 六

2 2 2 1

d

d

=

( V

V

_{1 3}

)

2+

(

V

₂

V

₄

)

2+

( V

V

_{2 5}

)

2+

( V

V

_{2 6}

)

2－2

V

₁

V

₂

V

₃

V

₄

cos(

A

₂



A

₄

)

－2

V

₂2

V

₄

V

₅

cos A

₅－2

V

₂2

V

5

V

6

cos A

6 +2

V

1

V

2

V

3

V

5

cos



A

2



A

4



A

5



+ 2

V

₂2

V

₄

V

₆

cos



A

₅



A

₆



－2

V

₁

V

₂

V

₃

V

₆

cos(

A

₁



A

₃

)

··· (6) 方 程 式 (6)就 是 正 確 的 平 面 凸 六 邊 形 內 臨 近 周 邊 的 兩 相 鄰 交 叉 對 角 線 長 度 乘 積 一 般 化 方 程 式 。 此 方 程 式 也 能 仿 效 上 述 七 邉 形 的 幾 何 作 圖 要 領 直 接 證 明 出 來 。 2. 若 令

V

₇

 V

₆



0

， 使 頂 點

A

₇與

A

₆皆 趨 近 於 頂 點

A

₁， 頂 角

A

₇



A

₆= 0 ，則 平 面 凸 七 邊 形 退 化 成 平 面 凸 五 邊 形 ， 方 程 式 (4)立 即 縮 減退 化 成 下 式； 2 2 2 1

d

d

=

( V

V

_{1 3}

)

2+

(

V

₂

V

₄

)

2+

( V

V

_{2 5}

)

2－2

V

₁

V

₂

V

₃

V

₄

cos(

A

₂



A

₄

)

－2

V

₂2

V

₄

V

₅

cos A

₅ +2

V

₁

V

₂

V

₃

V

₅

cos



A

₂



A

₄



A

₅



··· (7) 同 理，將 方 程 式 (7)最 末 一 項的 角 度 組 合做 一 個 轉 換，使 其 變 換成 凸 五 邊 形的 另 外 兩 頂 角 ， 由

A

₂



A

₄



A

₅=

3





A

₁



A

₃ ， 代 入 (7)式中 ， 再 化 簡 得下 式 ； 2 2 2 1

d

d

=

( V

V

_{1 3}

)

2+

(

V

₂

V

₄

)

2+

( V

V

_{2 5}

)

2－2

V

₁

V

₂

V

₃

V

₄

cos(

A

₂



A

₄

)

－2

V

₂2

V

₄

V

₅

cos A

₅ －2

V

₁

V

₂

V

₃

V

₅

cos



A

₁



A

₃



··· (8) 方 程 式 (8)就 是 正 確 的 平 面 凸 五 邊 形 內 臨 近 周 邊 的 兩 相 鄰 交 叉 對 角 線 長 度 乘 積 一 般 化 方 程 式 。 此 方 程 式 也 能 仿 效 上 述 七 邉 形 的 幾 何 作 圖 要 領 直 接 證 明 出 來 。 3. 若 令

V

₇



V

₆



V

₅



0

，使 頂 點

A

₇與

A

₆、

A

₅皆 趨 近 於 頂 點

A

₁，則 此 平 面 凸 七 邊 形 必 退 化 成 平 面 凸 四 邊 形 ， 方 程 式 (4)立 即 縮 減 退 化成 下 式 ； 2 2 2 1

d

d

=

( V

V

_{1 3}

)

2+

(

V

₂

V

₄

)

2－2

V

₁

V

₂

V

₃

V

₄

cos(

A

₂



A

₄

)

··· (9) 方 程 式 (9)就 是 正確 的 平 面 凸四 邊 形 內 兩交 叉 對 角 線長 度 乘 積 一般 化 方 程 式。 4. 若 再 令 平 面 凸 四 邊 形 內 接 於 一 圓 ， 由 兩 頂 角

A

₂與

A

₄互 補 性 質 ， 得

d₁d₂=

V

₁

V

₃+

V

₂

V

₄ ··· (10) 方 程 式 (10)就 是著 名 圓 內 接四 邊 形 的 托勒 密 定 理 (Ptolemy theorem)。 5. 探 究 圓 內 接 七 邊 形 的 情 況 ： 下 圖 17.的 圓 內接 七 邊 形； 對 角 線 長

A

₁

A

₄



d

， 圖 17 (a) 對 圖 17.中 的 圓內 接 四 邊 形

A

₁

A

₂

A

₃

A

₄有 托 勒 密 定 理 關 係 式 如 下 ；

d

V

V

V

d

d

_{1 2}



_{1 3}



₂ ， 現在 將 其 完 全平 方 ， 得 下式 ；

d

V

V

V

d

V

V

V

d

d

1 2 3 2 2 2 3 1 2 2 1

)

(

)

(

)

2

(







··· (11) (b) 應 用引 理 2. 對五 邊 形

A

₁

A

₄

A

₅

A

₆

A

₇可 得 下 列 餘 弦 定 理 關 係 式 ； 2

d

=

V

₄2+

V

₅2+

V

₆2+

V

₇2－ 2

V

₄

V

₅

cos A

₅－2

V

₅

V

₆

cos A

₆－2

V

₆

V

₇

cos A

₇+

2

V

₄

V

₆

cos



A

₅



A

₆



+ 2

V

₅

V

₇

cos



A

₆



A

₇



－ 2

V

₄

V

₇

cos



A

₅



A

₆



A

₇



··· (12) (c) 另 外五 邊 形

A

₁

A

₄

A

₅

A

₆

A

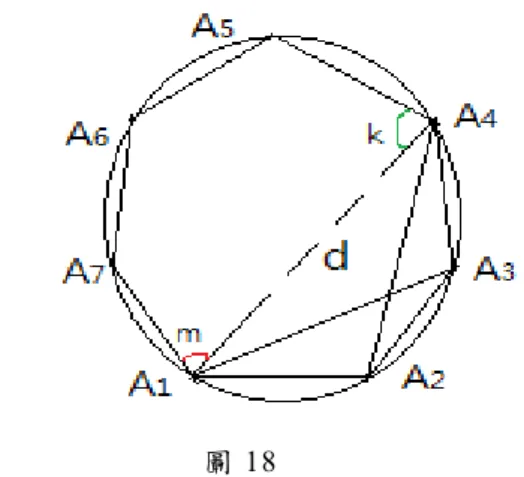
₇也 有 邉 長 與 頂 角 角 度 關 係 式 如 下 ； 見 下 圖 18.，

令 角 度

m





A

₇

A

₁

A

₄，角 度

k





A

₁

A

₄

A

₅，對 五 邊 形

A

₁

A

₄

A

₅

A

₆

A

₇言 可 得；

d

=

V cos

₄

k

+

V

₅

cos[

k



(





A

₅

)]

+

V

₆

cos[

k



(





A

₅

)



(





A

₆

)]

+

V cos

₇

m

=

V cos

₄

k



V

₅

cos(

k



A

₅

)

+

V

₆

cos(

k



A

₅



A

₆

)

+

V cos

₇

m

由 圖18. 知 ， 角度



























A

₇

A

₁

A

₄

A

₁

A

₂

A

₁

A

₄

A

₁

(

A

₃

)

A

₁

A

₃

m

， 同 理 ， 角 度 5 4 1

A

A

A

k





=

A

₂



A

₄





，現 將 此 兩 角度 代 入

d

的 等 式 中 ， 得 ；

d

=



V

₄

cos(

A

₂



A

₄

)

+

V

₅

cos(

A

₂



A

₄



A

₅

)



V

₆

cos(

A

₂



A

₄



A

₅



A

₆

)



V

₇

cos(

A

₁



A

₃

)

··· (13)