而表中左邊欄位為 Fractal 的規則，右邊欄位為所繪出的圖形

(1)

第三章碎形呈現演算法

本章中提出 Fractal 的概念與 SVG 呈現方式之比較，並且實做了將 Fractal 圖形以 SVG 來呈現的演算法。3.1 節介紹 Fractal 與 SVG 的概念以及兩者之間的相關性；3.2 節介紹 Fractal 與 SVG 的轉換模型（Transformation meta model）；3.3 節介紹一維細分法則的範例—Cantor Set；3.4 節介紹二維線段細分法則的範例—Koch Snowflake；3.5 節介紹二維區域細分法則的範例—Sierpinski gasket。

3.1 Fractal 與 SVG 之比較

第二章詳細介紹了 Fractal 與 SVG。由於這是兩種對於圖形完全不同的描述方法，

因此必須用轉換模型與演算法將 Fractal 的概念轉換成 SVG 的方式來繪出圖形。

本節將對 Fractal 的特性作說明描述。Fractal 運用了重複自我模仿的特性，使得一個幾何物件在越來越細微的尺度上，不斷重複自我模仿，以固定的方式重複製造細節。

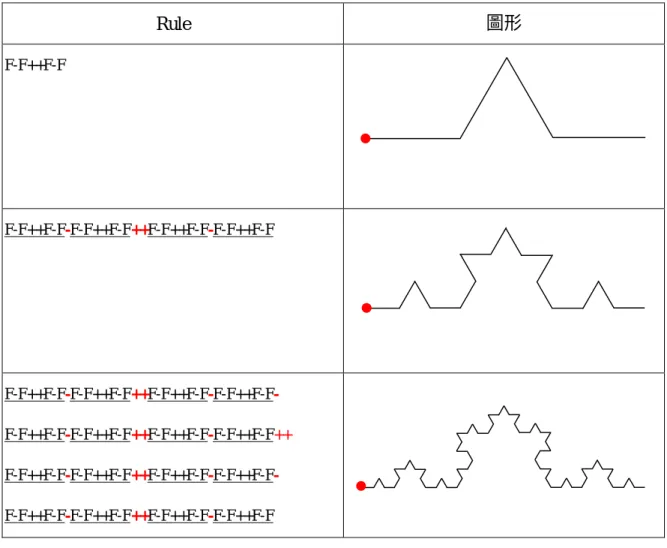
如果以高倍顯微鏡放大，則局部圖形與全體相同。表 3-1 使用了形成 Koch Snowflake 的其中一邊為例，起點為圖中紅色的圓點。而表中左邊欄位為 Fractal 的規則，右邊欄位為所繪出的圖形。

(2)

Rule 圖形

F-F++F-F

F-F++F-F-F-F++F-F++F-F++F-F-F-F++F-F

F-F++F-F-F-F++F-F++F-F++F-F-F-F++F-F- F-F++F-F-F-F++F-F++F-F++F-F-F-F++F-F++

F-F++F-F-F-F++F-F++F-F++F-F-F-F++F-F- F-F++F-F-F-F++F-F++F-F++F-F-F-F++F-F

表 3-1 Koch Snowflake 其中一邊的 Rule 與圖形

然而只有繪製的主體為「線段」的 Fractal 圖形才能利用規則寫出字串，如表 3-1。

有些 Fractal 的規則並沒有辦法用語言模型來表示，例如第二章提過的 Sierpinski gasket，這一類的 Fractal 圖形只能用文字敘述來幫助使用者瞭解。而且就算可以寫成字串的 Fractal 也不是一般的瀏覽器或是軟體就能看得懂、讀的出來的，使用者必須在電腦中安裝可以編譯 Fractal 字串的應用程式才能打開它，對於使用者來說相當不方便。

因此，本論文將 Fractal 與 SVG 相結合，藉由 SVG 的各種優勢將 Fractal 呈現在網頁上，

使得使用者在各個環境之下都可以瀏覽 Fractal。

第二章已經介紹過 SVG，本節將再描述 SVG 的編寫方式。SVG 是一種 2D 的可縮放式圖形語言，由於 SVG 是以 XML 為基礎，所以也是一種標籤式語言。SVG 最主要提供了幾項基本的標籤：向量圖形（圓形、直線或是曲線）、影像（image）以及文字

(3)

SVG 圖形

<?xml version="1.0" standalone="no"?>

</svg>

<?xml version="1.0" standalone="no"?>

</svg>

表 3-2 Koch Snowflake 其中一邊用 SVG 來繪製的原始碼與圖形

由表 3-2 可知，Fractal 的圖形即使再複雜也可以用簡單的規則再配合遞迴的次數控制顯示出來。如表 3-1 中，遞迴第二次時，Fractal 將每一條遞迴一次時的「線段」（F）

用遞迴一次時的「全圖」（F-F++F-F）來表示。而 SVG 則不同，他使用簡單的標籤來表示圖形，所以我們可以靜態或是動態的將要顯現出來的物件、點或是文字加入到 SVG document 當中繪出所需要的圖形。

另外，也可以藉由 JavaScript 來達成使用者能控制繪製 Fractal 圖形中各項變數的

(4)

態的方式跟隨著使用者的操作來增加或減少 SVG 的標籤數量，以及給予標籤中各個屬性的值。如表 3-2，遞回一次時需要畫出四個線段，所以演算法需藉由 L-system 的特性，

運用數學計算來找到這些座標點，並且用線段將座標點連起來，遞回 n 次的方式也相同。

綜合 Fractal 與 SVG 的概念可以做出以下的比較：

物件的數目方面：若是 Fractal 用圖檔的方式來呈現，就沒有物件多少的限制；在 SVG 呈現的部分，遞迴的次數越多，物件的個數也越多，並且成指數倍成長。

描述內容的方面：Fractal 是採用自我描述的方式，SVG 方面是使用迴圈的遞迴來呈現。除此之外，並不是所有的 Fractal 都可以用規則來表示出來，但若是使用 SVG 便可以清楚的看出繪製的遞迴方式以及繪製的順序。

圖形呈現的方面：現在 Fractal 多半是以圖檔來表現，而 SVG 是以 XML based 的 SVG 純文字檔。從此點看來，SVG 的檔案在物件數目不是太龐大時檔案會比較小。

若是 Fractal 以其他應用程式來呈現，使用者就需要安裝適合的應用程式，而 SVG 可以直接在裝有 SVG plug-in 的瀏覽器開啟，較其他應用程式方便。

檢視內容的部分：Fractal 的呈現方式很多種，但是無法看出檔案內容的製作方式；

另一方面，SVG 可以直接給使用者開啟，檢視程式內容。

(5)

3.2 轉換模型（Transformation meta model）

3.1 節中已介紹過了 Fractal 與 SVG 的差異性，在本節中將提出實際的轉換模型來解釋如何將 Fractal 轉換成 SVG。

要將一個 Fractal 圖形轉換為 SVG 的語法時需要經過以下的步驟與流程圖如下：

圖 3-1 轉換模型流程圖

1. 觀察圖形：Fractal 的基本概念是運用重複自我描述的特性，所以 Fractal 是由一個起始圖形開始，再將自己分為幾個小圖形；而這些小圖形在下一次的遞迴當中，每一個又將依照同樣的規則再分裂為更小的部分，一直持續的做下去。所以在本論文中稱其為細分法則（subdivision method）。在觀察圖形的這個步驟中，首先必須觀察出這個 Fractal 圖形是由什麼樣的規則在重複自我描述。在 0∼1 維的 Fractal 圖形當中，

本論文稱其為 1D subdivision method，例如 Cantor Set。在 1∼2 維的 Fractal 圖形中，

可以分為兩部分：一種是雖然圖形的座標有兩個維度，如（x,y），但圖形的是由線段來構成，本論文稱其為 2D line subdivision method，例如 Koch Snowflake ；另為一種座標有兩個維度，但圖形是由區域來構成的，本論文稱其為 2D area subdivision method，例如 Sierpinski gasket。

觀察圖形

幾何圖形分析

數學函式推導

細分法則演算法

(6)

2. 幾何圖形分析：在觀察出重複自我描述的規則之後，接著要由 SVG 的觀點來探討。

前面一節中提到 SVG 的圖形是由絕對或相對座標點來決定圖形的位置，所以在這一階段當中必須分析出這個 Fractal 要用 SVG 來表示時需要知道的座標點和物件類型。例如在前面介紹過的 Koch curve 的部分，我們就必須分析出當一條直線分為三個部分，切掉中間段之後，以此段為底邊向外做一正三角形，此為遞迴一次的製作步驟。所以需要知道的變數從「一個起始點與一條線段長」變為「四個起始點與原線段的¹

3的長度」。

3. 數學函式推導：在分析完了幾何圖形之後，接著必須討論這些座標點之間有何關連性。舉一個 Koch curve 的例子來說，當瞭解一個長為 L 的線段如何變成 Koch curve，

就必須分析這些線段與座標點間的關係，如下圖所示：

在步驟 2 已經分析出需要知道圖中的四個紅點座標與線段的長度，在步驟三中，則可以推論出若是點 1 的座標為（a1,b1），點 2 座標即為（a1+¹

3L,b1）＝（a2,b2），點 3 座標為（a2+¹

3L cos60^o,b2－¹

3L sin60^o），點 4 座標則為（a2＋¹

3L,b2）。

4. 細分法則演算法：經過精密的分析之後，可以將導出來的三角函數與遞迴概念套入演算法當中，實際由程式去執行，就可以用 SVG 來呈現 Fractal 圖形。本論文提出了轉換模型的架構以及 1D subdivision method、2D line subdivision method、2D area subdivision method 的概念，並且實做了具體的演算法，在 3.3、3.4 及 3.5 節有詳盡的描述。

1 2

3

4

(7)

3.3 一維細分法則（1D subdivision method）

依照上一節的轉換模型步驟，本節將探討一個屬於 1D subdivision method 的例子：

Cantor Set，並探討將其轉換為 SVG 的方法。

1. 觀察圖形：

Cantor Set 在拓樸學中是一個非常有名的例子，其繪製的方式如圖 3-2 所示。首先給定[0,1] 閉區間，挖掉其三分之一等份的中間段開區間(¹

3,²

3)，再將現有的兩個閉區間[0,¹

3]、[²

3,1]，各挖掉其三分之一等份的中間段開區間(¹

9,²

9)、(⁷

9,⁸

9)，無窮的依此步驟將現有的每一線段的三分之一等份的中間段開區間挖掉，最後所成的集合即為 Cantor Set。

Cantor Set 擁有一些很有趣的性質，以 Cantor Set 的原理來說，在製作的過程中，

每次都挖掉原有的¹

3，而剩下現有的²

3，所以當做了 n 個步驟後，剩下的長度為 ²

3

 n

   ，接著下一步驟將挖掉 ² ¹

3 3

  ⋅n

   。因此完成 Cantor Set 共挖掉

2 3

1 2 1 2 1 2 1

3 3 3 3 3 3 3

   

+ ⋅ +   ⋅ +   ⋅ + ⋅⋅⋅⋅⋅⋅，這是一個無窮等比級數，其和為 1。另外一個 Cantor Set 的特性就是它的元素與整條數線的點的個數一樣多，而證明的方式如下：首先我們可以觀察出，在挖除中間三分之一開區間 n 次後，產生了 2n 個小線段，而這些線段的端點並不會被挖除，所以 Cantor Set 至少有lim_n_→∞2ⁿ⁺¹= ∞ 個點。

k＝1 k＝2 k＝3 k＝4

圖 3-2 遞迴一到四次的 Cantor Set

(8)

根據觀察圖形的結果，Cantor Set 是在 0∼1 維之中的 Fractal 圖形（維度的計算請參考 2.2 節），所以本論文將其歸類為 1D subdivision method。

2. 幾何圖形分析：

藉由觀察圖形的結果可知，每遞迴一次需要知道的座標點為前一次的 2 倍（因為將每條線段切割成 3 部分，取左邊及右邊的部分），而我們所要知道的線段長度也為上一次遞迴時的¹

3。

3. 數學函式推導：

同樣的，在這個步驟當中必須分析出如何找到需要的座標點的方法。假設第一條線的起始點座標為 a，線段長度為 L，可以得到遞迴一到四次的結果，如圖 3-3。

k＝1

k＝2

k＝3

k＝4

圖 3-3 遞迴一到四次的 Cantor Set（含座標點）

而此圖中的始點個數與座標、線段長度的分析如表 3-3。

遞回次數始點個數始點座標線段長度

k＝1 2⁰（a1） a1＝a L1＝L

k＝2 2¹（a₁、a₂） a1同上

a2＝a₁＋2L₂ L2＝¹ 3L1

k＝3 2²（a₁、a₂、a₃、a₄） a₁、a₂同上 a₃＝a₁＋2L₃ a＝a＋2L

L3＝¹ 3L2

a1

a1 a3

a2

a4

a2

a3 a4

a5 a7 a2 a6 a8

(9)

k＝4 2³（a1、a2、a3、a4、a5、a6、a7、a8） a1、a2、a3、a4同上 a5＝a1＋2L4

a6＝a2＋2L4

a7＝a3＋2L4

a8＝a4＋2L4

L4＝¹ 3L3

表 3-3 遞迴一到四次的概念

4. 細分法則演算法：

經過了上面三個階段，接著把這些分析與架構套入演算法當中。

1. 宣告一個二維陣列存放始點及終點的 x 軸坐標

2. 當 k＝1 時，以始點的 x 軸座標 a、終點的 x 座標 a+L 繪出第一條線

3. 當 k＝2 到 n 時，

將線段長設為原長的三分之一（

3 L=L），

並且把上一次遞迴的每一始點依下列方式處理：

a. 以原來這一點為起點，起點加 L 為終點畫出左邊線段

b. 以原來此點加 2L 為起點，起點加 L 為終點畫出右邊線段

3.4 二維線段細分法則（2D line subdivision method）

根據 3.2 節的概念，我們就以寇茲雪花圖（Koch Snowflake）作為 2D line subdivision method 的代表，以下是根據轉換模型將 Koch Snowflake 轉換為 SVG 的方法。

(10)

1. 觀察圖形：

寇茲雪花圖（Koch Snowflake）是應用 Fractal 的自我描述性概念所形成的。首先給定一正三角形，切掉每邊的三等份的中間段，並以此段為底邊向外做一正三角形，此為遞迴一次的製作步驟。對現有的圖形的每一邊做一次製作步驟的處理，且無窮的重複下去，最後得到的圖形即為有名的 Koch Snowflake。

此碎形有其特別的性質，如周長為無限大時，所圍面積卻為有限的。周長無限大的性質可以很快的看出來，因為對正三角形每邊所做的步驟均相同，故只須考慮其中一邊的情況即可。若此正三角形的邊長為 1，則經過一個製作步驟後，此邊的邊長變成⁴

3，且原來的線段變成四段小線段，再對現有的四個小線段重複一次製作步驟，則每一個新的邊皆為原來邊的⁴

3倍長，其總長為

4 2

3

  

 。持續不斷的重複下去，

可推出當做了 n 個步驟後，其邊長為 ⁴

3

 n

   ，(詳細的證明可很簡單的利用數學歸納法來證得)，當 n 趨近到無窮大時，邊長也會趨近於無窮大。

對於其所圍面積的值，可以先假設一開始的三角形邊長為 1，則在完成第一次製作步驟後，增加了一個正三角形，其邊長為¹

3，面積為

3 1 2

4 3

  

  。完成第二次製作步驟後，增加了四個正三角形，每個邊長為

1 2

3

  

  ，總面積為

2 2

2 3 1

4 . .

4 3

  

   

 

  。完成第三次製作步驟後，增加了4 個正三角形，每個邊長為²

1 3

3

  

  ，總面積為

3 2

2 3 1

4 . .

4 3

  

   

 

  。依

此利用數學歸納法可簡單的得證：當完成第 n 次製作步驟後，可再增加的三角形面積為

2

1 3 1

4 . .

4 3

n

n−   

   

 

  。因此可得 Koch Snowflake 圖形所圍的面積為

2

2 1

1

3 3 1 2 3

1 3 4

4 4 3 5

n n

n

∞ −

−

  

⋅ + ⋅∑ ⋅     = ，這是一個有限值，而且為原三角形面積的⁸

5倍。

所以不管一開始的正三角形有多小，所做出的 Koch Snowflake 的周長皆為無窮大，而所圍面積都是原三角形的⁸

5倍，換句話說，我們可造出一個所圍面積任意小

(11)

而周長無窮大的封閉圖形。現在若有一個 Koch Snowflake 在面前，拿個剪刀將其任意邊剪斷，開始把它拉直後發現，永遠都不可能把圖形完全拉直；反之，也可將一個無窮長的直線圍成一個任意小的區域。圖 3-4 為遞回一次到四次的圖形：

k＝1 k＝2 k＝3 k＝4

圖 3-4 Koch Snowflake 遞回一到四次的情形

藉由上面的敘述可知，Koch Snowflake 是介於 1∼2 維之間（維度的計算請參考 2.2 節），並且圖形是由線段所構成，所以本論文將其分類為 2D line subdivision method。

藉由觀察圖形可以知道，Koch Snowflake 的三個邊都是依照 Koch Curve 的概念而來的。由此分析可以推論，Koch Snowflake 的原始圖形有三個頂點，並且必須把三個頂點連起來。遞迴第二次時每邊會變成需要四個頂點，所以整個圖形需要十二個頂點，線段長度為原來的¹

3，遞迴 n 次的結果以此類推。所以每遞迴一次的頂點數都是上一次的四倍，而所需要的線段長度也為上一次遞迴時的¹

3。

3.數學函式推導：

根據上面的分析，將遞迴一到三次的頂點存放方式以圖 3-5 表示。由於連線方式是以頂點的編號依序連結，所以必須將最後一點座標設為與原點相同，才能順利

(12)

（a）n=1

0

1 2

0

2 1

3

4 5

6

7 8

9 11 10 12

24 0 1 3 2 5 4 6 7 8

9 10 11

13 12 14

15 16 17

18 19 20

21

22 23 25 26 27

28 29 30

31 32 33 35 34 3637 38

39 41 40 42 43 4544 47 46 48

（b）n=2

（c）n=3

3

(13)

而在每次遞迴的過程當中，要從某點找尋到相關的四個頂點，可以按照以下的方法來求得。

首先將頂點分為三組：

a.由已知端點加上原線段長的¹

3向量即可求出的點，如圖 3-6 中的編號 1.5.9

b.由已知端點加上原線段長的²

3向量即可求出的點，如圖 3-6 中的編號 3.7.11 c.由已知端點兩兩求出中點，再加上中間向量才能求出的點，如圖 3-6 中的編號 2.6.10，方法如下：

以點 2 為例，由點 1 與點 3 可求出中間向量 a，a 與 b 垂直可求出向量 b，由點 1 與點 3 也可求出中點 P，而 P+b 向量可得到點 2 之座標，同理可求出 6.10 的座標。

若遞回更多次座標點求法相同，最後依照編號的順序用線段連起來。

圖 3-6 Koch Snowflake 頂點求法 0

2 1 3

4 5

6

7 8

9 11 10 12

b a P

(14)

根據上面的分析與架構所延伸出的演算法如下：

1. 宣告三個陣列 B 存放頂點坐標（x, y）、X 暫存中點與 Y 暫存中間向量 2. k=1 時，

定位上頂點（a，b）、左頂點（

2

a−L， ³

2

b+ L）、右頂點（

2

a+L， ³

2 b+ L）

並且將最後一點（第四點）設為與第一點座標相同，連成第一個三角形。

3. k=2 到 n 時，

將最後一點（B3 * 4^k⁻1+1）設為與第一點（B0）座標相同，線段長設為原線段的三分之一（

3

L=L），並將點分為三組，遞迴求出：

a. 由已知端點加上原線段長的¹

3向量即可求出的點，如導出圖 3-5 中的編號 1.5.9。

BX4*i+1=(BX4*i*2)/3+BX4*(i+1) /3;

BY4*i+1=(BY4*i*2)/3+BY4*(i+1) /3;

b. 由已知端點加上原線段長的²

3向量即可求出的點，如導出圖 3-5 中的編號 3.7.11。

BX4*i+3 =BX4*i/3+(BX4*(i+1) *2)/3;

BY4*i+3=BY4*i/3+(BY4*(i+1) *2)/3;

c. 由已知端點兩兩求出中點，再加上中間向量才能求出的點，如導出圖 3-5 中 2.6.10。

XX4*i+2=(BX4*i+1+BX4*i+3)/2;

XY4*i+2=(BY4*i+1+BY4*i+3)/2;

YX4*i+2=BX4*i+3-BX4*i+1;

YY4*i+2 =BY4*i+3-BY4*i+1;

BX4*i+2=XX4*i+2-(YY4*i+2*0.866);

BY4*i+2=XY4*i+2+(YX4*i+2*0.866);

最後依照編號的順序用線段連起來。

(15)

3.5 二維區域細分法則（2D area subdivision method）

根據 3.2 節的概念，我們就以 Sierpinski gasket 作為 2D area subdivision method 的代表，以下是根據轉換模型將 Sierpinski gasket 轉換為 SVG 的方法。

1. 觀察圖形：

Sierpinski gasket 這個有名的 Fractal 圖形製作的方式如圖 3-7。首先，給定一正三角形，取各邊中點，挖掉中間那塊正三角形（其邊界需留下），剩下三個相同的正三角形，接下來對剩下的每個三角形做同樣的步驟，挖掉其各邊中點連線所成正三角形，重複此步驟無窮次，即形成 Sierpinski Triangle。更詳盡一點的敘述為，當遞迴一次時，繪出一個三角形，如圖 3-7（a）；當遞迴二次時，以原三角形的三頂點兩兩取中點，連成如圖 3-7（b）的四個邊長為原三角形一半的小三角形，而留下 A、B、C 的三塊三角形（在此稱其為上、左、右方三角形）；而當遞迴三次時，圖二的上、左、右的三塊三角形又各自依照圖 3-7（a）到圖 3-7（b）的遞迴方式分為四個小三角形，如圖 3-7（c）所示；當遞迴第四次時，依此方法繪出如圖 3-7（d）

的圖形。

（a）n＝1 （b）n＝2

（c）n＝3 （d）n＝4 A

B C

(16)

藉由上面的敘述可知，Sierpinski gasket 是介於 1∼2 維之間（維度的計算請參考 2.2 節），並且圖形是由三角形的面所構成，所以本論文將其分類為 2D area subdivision method。

藉由觀察圖形的結果，Sierpinski gasket 的起始圖形為一正三角形，所以若以三角形為一個物件單位，則需要知道的頂點只有一個。遞迴一次時，取各邊中點，

挖掉中間那塊正三角形（其邊界需留下），剩下三個相同的正三角形。所以需要的頂點個數為三個，並畫出三個小三角形，邊長為原來的一半，若遞迴 n 次則以此類推。其中每遞迴一次的頂點數都是上一次的三倍，而所需要知道的線段長度也為上一次遞迴時的一半。

3.數學函式推導：

根據上述討論，假設初始的正三角形頂點座標為（a, b），而三角形物件的左頂點以及右頂點可由上面三項使用者輸入的變數得出：左頂點座標為（ a-

2 1 L,

b+ 2

3L）、右頂點座標為（a+

2 1L, b+

2

3L）。因為在 Sierpinski gasket 中所繪製的三角形為正三角形，所以只要知道三角形的上頂點，便可以計算出左頂點及右頂點，所以在演算法的基本概念中，只需找出三角形的上頂點。表 3-4 為 Sierpinski gasket 遞迴一到四次的基本概念，其餘遞迴次數以此類推：

遞回次數始點個數始點座標線段長度

n＝1 3⁰（a1, b1） a1＝a、b1＝b L1＝L n＝2 3¹（a1, b1），（a2, b2），（a3, b3） a1同上

a2＝a1-L2/2，b2=b1+ 3L2/2 a3＝a1+L2/2，b3=b1+ 3L2/2

L2＝ 2 1L1

n＝3 3²（a₁, b1），（a₂, b2），（a₃, b3）

（a₄, b4），（a₅, b5），（a₆, b6）

（a₇, b7），（a₈, b8），（a₉, b9）

a1、a₂、a₃同上

a4＝a₁-L3/2，b4=b1+ 3L3/2 a7＝a₁+L3/2，b7=b1+ 3L3/2 a5＝a₂-L3/2，b5=b2+ 3L3/2 a8＝a₂+L3/2，b8=b2+ 3L3/2 a6＝a₃-L3/2，b6=b3+ 3L3/2 a9＝a₃+L3/2，b9=b3+ 3L3/2

L3＝ 2 1L2

表 3-4 Sierpinski gasket 遞迴一到四次的基本概念

(17)

圖 3-8 介紹頂點存放的方式：

k＝1 k＝2

k＝3

圖 3-8 Sierpinski gasket 演算法頂點存放方式

1. 宣告二維陣列 B 存放上頂點的 x 座標及 y 座標 2. K=1 時，由原始的正三角形上頂點畫出第一個三角形 3. 當 K=2 到 n 時，每次邊長減半（

2

L=L），並且藉由上一次遞回的每一個頂點及現在邊長依照下列方式找出左頂點及右頂點。最後可由左頂點：（上頂點—L/2，上頂點＋ 3 L/2），繪出左方三角形；右頂點：（上頂點＋L/2，上頂點＋ 3 L/2），

繪出右方三角形。

(a1,b1) (a1,b1)

(a2,b2) (a3,b3)

(a1,b1)

(a2,b2) (a3,b3) (a4,b4) (a7,b7)

(a5,b5) (a9,b9)

(a₈,b₈) (a₆,b6)

而表中左邊欄位為 Fractal 的規則，右邊欄 位為所繪出的圖形

而表中左邊欄位為 Fractal 的規則，右邊欄位為所繪出的圖形