數學化教學：數型

數學化教學：數型

陳麗萍

東華三院港九電器商聯會小學下午校 馮振業

香港教育學院數社科技學系 引言

對不少小學教師來說，「數型」是一個不容易捉摸的課題。它不像「加」、

「減」、「乘」、「除」或是「四邊形」、「三角形」一樣，有著非學不可的元 素 —— 往後學習數學的預備知識。也就是說，它是學了看不到有何得益，

不學又好像並無不妥的課題。因此，它往往不是教師最關心學生表現的一 課。這種可有可無的地位，令不少人甚至認為大可把它從課程中刪去。對 很多教師而言，學生的學習歷程只是流於背誦公式，掌握不好，亦即背誦 不熟，這樣的學習過程毫無意義可言！記得曾經有教師說過，每年面對這 課題時，總要重新背誦一遍有關公式，才有信心進入課室。教師尚且如此，

何況學生？在新課程之下，數型已由小六的必授部分移至增潤部分（香港 課程發展議會，2000）。可以預期，叫苦的大可不教，不然，總得面對如何 為這課題定位的問題。本文嘗試為這課題重新定位，透過數學化觀點（馮，

2004），揭示數學學習之中，以「形」馭「數」的面相。

重塑學習主軸

依課程文件，數型的學習包括兩項重點：

1. 認識簡單數型如正方形數和三角形數。

2. 認識及欣賞其他簡單數型的規律。

從壞處想，這兩項重點十分概括，並無清楚刻劃實質的學習是甚麼。

要能運用哪些公式？通項公式？求和公式？「其他簡單數型」包括甚麼？

不包括甚麼？要能證明命題嗎？抑或是直觀了事？…… 然而，從好處想，

就是既無太多要求，亦無多少限制。教師大可自由發揮，享受廣闊的自主 空間。

即使沒有任何外加的要求和限制，對學生卻不可能沒有要求。不少學 校愛出類似下列的考題：

（一） 求 1 + 2 + 3 + 4 + … + 50。

（二） 求 11 + 12 + 13 + 14 + … + 50。

（三） 求 1 + 4 + 7 + 10 + … + 64。

擔心題（一）過於淺易的教師，也許會喜歡題（二），而題（三）卻是 用來分出尖子的。在爭分奪秒的筆試環境，最划算還是有公式可代。於是，

本來是中四學習內容的算術級數求和公式，便糊裡糊塗地跑進了小六的課 堂。試想，如果學生運用算術級數求和公式成功計算上述三題，分數儘管 拿足了，這樣的表現又跟學習數型如何扯上關係？退一步說，即使教師不 教，只要測考裡有著類似的問題，又如何阻止家長或補習教師補上一筆？

最終的結果，還不是背誦公式的比賽。為了難到希望只背一式（算術級數 和 =（首項 + 尾項）

 2  項數）走天涯的學生，教師或許會出以下問題：

（四） 求右式的項數：13 + 14 + 15 + … = 1197

這樣的追逐，可算是「生高一尺，師高一丈」，沒完沒了，卻不知所為 何事。最苦的，還是一群被一堆摸不著頭腦的公式，壓得透不過氣的小六 學生。

如果以純符號的方法處理級數問題，是徹頭徹尾的代數手法，完全沒 有幾何味道。這樣的學習經歷，在中學階段多的是，犯不著在小學偷步開 始。筆者等認為，透過圖形理解數列的性質，不但有趣，而且可提供多元 化的思考訓練：

訓練 1 觀察圖形規律，得出數列的通項公式；

訓練 2 以點陣圖表示數列，然後把有關數列的問題轉化成有關點陣的問 題；

訓練 3 由分割或拼砌點陣圖，解決各種有關數列的問題；

訓練 4 學會用圖形證明代數命題。

現舉例說明上述四項訓練的具體內涵：

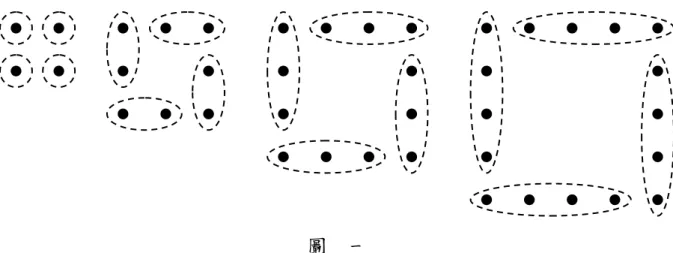
例一 學生透過觀察下列規律（圖一），得出「每邊有 n 點的空心正方形共 有 4(n  1) 點」。

圖 一

例二 學生把「兩連續三角形數的和都是正方形數嗎？」轉化成「圖二兩 三角形點陣是否必定可拼成一個正方形點陣？」

圖 二

例三 學生把「1 , 4 , 7 , 10 , … , 64」轉化成圖三有規律的點陣，然後透過 分割成三個三角形點陣（圖四）的方法（並不唯一），計算 1 + 4 + 7 + 10 + … + 64。

圖 三

當中關鍵的一步，是要找到兩種三角形點陣每邊的點數，這正好回到 第一項訓練。小心觀察點陣圖的規律，不難發現由 (64 + 2)  3 就可找到大

n 層

n 層 n + 1 層

n + 1 層

1 1 + 4 1 + 4 + 7 1 + 4 + 7 + 10

三角形點陣每邊的點數，而小三角形點陣每邊的點數比這數小 1。

圖 四

例四 給學生觀察以下數據，很容易發現三角形數的 8 倍再加 1 都是正方 形數。

n 第 n 個三角形數 第 n 個三角形數 × 8 + 1

1 1 9

2 3 25

3 6 49

4 10 81

5 15 121

6 21 169

7 28 225

8 36 289

9 45 361

對學生而言，挑戰在於如何得知上面列出的並非巧合。用代數方法，

就只有以下一行：

有多少點？

有多少點？

有多少點？

2 ) 1 8  n ( n 

+ 1 = 4n(n + 1) = 4n² + 4n + 1 = (2n + 1)² 用圖入手，就得進行圖五的拼砌：

圖 五

由兩個相同的三角形點陣，必可拼出鄰邊點數為連續數的長方形點陣

（這樣的點數叫「長方形數」）。而四個這樣的長方形點陣，再加 1 點（上 圖中空位置）又可以拼出正方形點陣。慣用代數的人縱然免了這樣的功夫，

卻也錯過了使人觸覺敏銳，思辨靈巧的幾何訓練。

上述四項訓練，可以換個說法如下：

訓練 1 以代數式描述點陣圖的規律；

訓練 2 以點陣圖建立幾何模型，研究數列；

訓練 3 透過拼砌點陣圖，解數學題；

訓練 4 學會不以代數手法，解釋代數命題。

從數學化觀點看，訓練 1 和 2 屬早段學習，旨在建立「形」與「數」

的靈活對應，形成一種新的思考模式。訓練 1 要求由「形」走向「數」，而 訓練 2 則要求由「數」走向「形」。有了這兩項基本功，便可開展後段學習。

訓練 3 和 4 就是要讓學生運用這種新的思考模式，處理多種有關數列的問

題，從而體會以「形」馭「數」的精妙和樂趣。

教學流程

在編排教學流程時，有三點值得關注：

A. 設計要有連貫性，避免予人零碎的感覺；

B. 設計要能抑壓學生背誦公式的傾向，否則將無法走到以「形」馭「數」

的階段；

C. 設計要能令大部分學生掌握形數對應的基本知識。

如果緊跟課程文件，只教授三角形數和正方形數，難免欠連貫性。從 圖形學習的已有知識看，有三角形數和正方形數，是否也該有梯形數、平 行四邊形數、菱形數等等？為了迴避這尷尬一問，筆者等選擇了以點陣入 手。按圖六逐層遞增，要求學生以連加式表示總點數。

圖 六

當通項公式出現後（由 1 + 3 = 2²、1 + 3 + 5 = 3²、1 + 3 + 5 + 7 = 4² …，

推導1 + 3 + … + (2n  1) = n²），除了介紹正方形數的意義，還要令學生注 意這些數都是由 1 開始的連續奇數的和。接著，教師便可順水推舟，要求 學生想想：「由 2 開始的連續偶數的和，是否也可排出有規律的點陣圖？」

如此輕鬆一問，便即開啟了長方形數的研習。於是，學生又要排出下面一 幅一幅的點陣圖（圖七），並回答與前同出一轍的一籃子問題。

圖 七

這樣的佈局，一方面讓形數對應的訓練重複鞏固，另一方面又令發展 顯得順理成章。當完成了由 1 開始的連續奇數及由 2 開始的連續偶數的和 的探討後，學生都會覺得由 1 開始的連續數的和（即三角形數）理應就是 下一個探討的問題。

有了正方形數和長方形數的通項公式（第 n 個正方形數是 n²、第 n 個 長方形數是 n(n + 1)），找三角形數的通項公式，便可循化未知為已知的軌 道完成。教師大可提問：「如果可以把要求通項公式的三角形點陣，以分割 或拼砌的方法造出前面已經找到通項公式的點陣圖，是否便可以利用已知 的通項公式，找到未知的通項公式？」由於加插了長方形數，學生能自己 找到通項公式的機會理應較大。一旦覺察兩個相同的三角形點陣必可拼出 鄰邊點數差 1 的長方形點陣，找通項公式的工作自然水到渠成。

必須一提的，就是工作紙的設計，集中要求形數對應，單單背誦公式，

將無法完成。因此，本文提出的教學流程建議，已充分回應了上述 A、B、

C 三點關注事項。

實踐

如筆者等所料，學生觀察多個對應正方形數的點陣後，很容易便發現 了正方形數的通項公式（訓練 1）。接著，為了抑制學生背誦公式的傾向，

並且令他們有效地進行訓練 2，教師為每位學生準備了一袋黑白鈕扣，要 求學生先用黑白鈕扣逐層排出數列對應的點陣，然後將點陣繪畫出來；例 如：

圖 八

經過一連串排鈕扣、繪畫點陣圖的工作，學生已經掌握了以點陣表示 數列的方法，並熟知下列對應：

連加式

1 + 3 + … + 9 + 11 尾項 連加式的項數

首項 學生由連加式

繪畫出點陣圖

點陣圖 首層

粒數

尾層 粒數

層數

當學生建立了「形」與「數」的靈活對應，形成一種新的思考模式之 後，便開始把有關數列的問題轉化成有關點陣的問題，以體會以「形」馭

「數」的精妙和樂趣。至於有關數列的問題，以正方形數為例，供學生研 習的有以下各類形：

 如果首項是 1

1. 已知尾項，找出項數和總和

例子： 1 + 3 + 5 + … + 105 + 107 =？

這連加式中有多少個奇數及和是多少？

2. 已知總和，找出項數和尾項 例子： 1 + 3 + 5 + … +？= 441

這連加式中有多少個奇數及尾項是多少？

 如果首項不是 1

3. 已知首項和尾項，找出項數和總和

例子： 13 + 15 + 17 + … + 455 + 457 =？

這連加式中有多少個奇數及和是多少？

4. 已知首項和項數，找出尾項和總和

例子： 13 + 15 + 17 + … +？，已知這連加式中共有 24 個奇數，

那麼尾項及總和是多少？

5. 已知項數和尾項，找出首項和總和

例子： ？+ … + 455 + 457，已知這連加式中共有 24 個奇數，那 麼首項及和是多少？

連加式 點陣圖

首 項 首層點數

尾 項 尾層點數

項 數 層 數

總 和 總點數

有多少點？

有多少點？

有多少點？

有多少點？

6. 已知首項和總和，找出尾項和項數

例子： 13 + 15 + 17 + … + ？，已知這連加式的和是 1989，那 麼它由多少個奇數組成及尾項又是多少？

7. 已知尾項和總和，找出首項和項數

例子： ？+ … + 127 + 129，已知這連加式的和是 4000，那麼它 由多少個奇數組成及首項又是多少？

8. 已知項數和總和，找出首項和尾項

例子： ？+ … + ？，已知這連加式是由 40 個奇數組成，且和是 3200，那麼它的首項及尾項各是多少？

在首項不是 1 的問題中，題類 3 至 7 均可通過繪畫多個不同的對應點 陣（如圖九），分別觀察全圖、白色部分與灰色部分三者之間的關係，其中 包括︰層數的相互關係，白色部分的尾項與灰色部分的首項的關係等。

7 + 9 + 11 圖 九

在數值大或項數多的情況下，把點陣圖完整地畫出並不可行。因此，

在工作紙中，加入了讓學生在省略圖中填入適當的資料如下：

圖 十

第一層

第___層(有___粒) 第___層(有___粒)

尾層(有___粒)

共有___層 共有___層

至於題類 8，相信不用點陣圖幫助，是很難找到答案的。學生首先要觀 察以下的排列：

圖十一

在教師的小心引導之下，學生有以下發現︰

發現 1 內的層數不變，且總點數是 和 的點數之和 發現 2 部分的點數分成兩相等部分（左側及上方）

發現 3 部分的層數與 的層數一樣 發現 4 部分的首項 = 部分尾項 + 2

由以上的發現，學生歸納出以下的結果︰

圖十二

a. 由發現 3 得知， 部分有 40 層，即總點數是 1600。

b. 部分內原有總點數 3200，由發現 2 及結果 a 得知， 部分的 首項是 41，尾項是 119。

共有 40 層

有 40 層

有

︿

﹀ 層

有

︿

﹀ 層 有___層

有

︿

﹀ 層

有___層

有___層

依兩年實踐所見，雖然是兩班程度不同的學生，但開始時均表現得有 點不習慣，尤以第一年的學生為甚，他們對於用黑白鈕扣排出對應的點陣 顯得抗拒，每節課都問：「可否不排鈕扣？」起初，教師非常堅持要求他們 先排鈕扣再繪圖，經歷「數學化教學」強調的，由無到有，由粗疏變精密 的演變過程。當他們經歷了約五、六張工作紙後，大概已掌握了操作過程，

學生開始自動作出調節：約有三分之一的學生選擇先繪圖，再排鈕扣驗證；

稍後，約三分之二的學生選擇不排鈕扣，只繪畫簡單的點陣圖來幫助思考，

以完成工作紙中的一些不太困難的部分；然而，能力稍遜的學生仍然堅持 先排鈕扣。這現象是令人高興的：一方面反映鈕扣的設置處理了差異的問 題，學生可以按自己的需要，選擇何時借助學具；另一方面反映學生已找 到一種值得信賴的方法來做學問。接著，學生可以在家完成往後部分的工 作紙，舒緩了超出課時的壓力。至於第二年的學生，因為能力較高，大部 分學生於五、六張工作紙後，已自動作出調節，但當遇到一些較繁複的難 題，鈕扣的作用又再浮現，正如他們所說：「這袋鈕扣是旁身之物。」

當學生完整地經歷了正方形數的數學化過程後，對長方形數及三角形 數的入手再不感到陌生，因此不需要像正方形數一樣地細緻鋪排，可以簡 單一些。礙於課時所限，有關首項不是 2 的長方形數的難題，和首項不是 1 的三角形數的難題，均被省去，但並不代表他們少學了些（一般人均認 為，教師不教，學生就不會懂）。在兩年實踐中，均有學生（雖然只是少部 分）要求教師給予這類難題，尤其是「已知項數和總和，找出首項和尾項」

那一題，對他們來說更是一項自我的挑戰！試問現在有多少學生會要求老 師給他們難題，並追問他們的解題方法是否正確？雖然擠掉了教師的小息 時間，但教學效果卻是令人異常振奮的。

不過，學生的想法有時也難以預計。在完成一張有關三角形數的工作 紙期間，原意希望學生發現下列關係︰

1. 當 n 是偶數時，第 n 個三角形數 = 第

2

n

2 n

2. 當 n 是奇數時，第 n 個三角形數 = 第

2

 1

n

2

 1

n

當 n = 8 時，可以下列拼圖理解：

圖十三 有學生的發現竟然是這樣的：

「如果三角形數的項數是偶數，那麼

三角形數的項數

 正方形數的項數 + 長方形數的項數 = 總點數

三角形數的項數

 正方形數的項數 = 總點數」

對於這個始料不及的發現，教師即場也未能迅速回應。最後，合幾位 同學之力，運用點陣圖向全班解說一番，論據如下︰

如果三角形數的項數是偶數，例如 8

圖十四 如果三角形數的項數是奇數，例如 7 第 4 個

正方形數

第 8 個三角形數

第 4 個 長方形數

正方形數 的項數是 4

三角形數的項數是 8

多出來的 粒數剛是 長方形數 的項數

圖十五

大家對這樣的解說可能覺得不大滿意，或是覺得有點兒造作。當時，

有部分同學亦有同感，且不停加入意見。經過一番激烈的討論後，最終他 們都能歸納出原先預定的結果。但對筆者等來說，這些結論不太重要，最 重要是他們能投入討論的過程，真真正正地經歷一節形神俱備的數學課。

當學生建構了簡單數型的知識，便開始探究有關數型的其他難題，例 如︰

1. 第 n 個長方形數 + 第 n 個正方形數 = 第 2n 個三角形數 2. 兩連續長 方形數之和必定是正方形數的兩倍，反之亦然

3. 三角形數

 8 + 1 必定是正方形數；正方形數卻不一定等於三角形數 

4. 三角形數

 4 + 1 必定是兩連續正方形數之和，反之亦然

當然還有些抽象性沒那麼高的，學生們較喜歡研究的問題，例如︰

5. 波子棋棋盤內有多少個孔﹖ 6. 圖中包含多少個三角形﹖

圖十六 圖十七

正方形數 的項數是 4

三角形數的項數是 7

7. 圖中包含多少個正方形﹖ 8. 圖中包含多少個長方形﹖

圖十八 圖十九

雖然預備了多份有關數型的難題習作，但教師並沒有打算全部發給學 生，由於課時關係，第一年的學生只完成難題 2、3、5、6。由第一年的經 驗所得，學生對於一些抽象性沒那麼高的問題較喜歡研究；另因第二年的 課時比較緊迫，因此，學生只完成難題 5、6、8。

有關「波子棋棋盤內有多少個孔？」這題，兩批學生均能信心十足地 完成，並且毫不猶豫地表示要向全班解說，學生的表達方式各有不同，但 方法大致一樣，如下圖分割棋盤，發現數量有︰12 個 T4（第四個三角形數）

再加 1，所以波子棋棋盤內有 121 個孔。

圖二十

有關「圖中包含多少個三角形？」這題，第二年的學生明顯地較第一 年的完成得更快，他們經過觀察後，不難發現圖中包含三角形數量 = 第（三 角形內加畫線的數量 + 1）個三角形數，如下︰

圖二十一

第二年的學生中，約三分之二的學生很快便完成，且確信自己的方法 是對的，並沒有用其他的方法再驗證，但當他們接觸「圖中包含多少個長 方形？」這題時，雖然透過 2

 2 方格的圖形已有發現（附件一）

以證實自己的發現。在急於求成的大氣候之下，能欣賞學生這股拼勁的教 師和家長可能日見減少。相信有人會說他們很傻，既然已有發現，何不直 接向老師說明，讓老師評定對錯，卻要花時間心力，自己硬數一遍？這裡 必須強調，學生這份執著，顯示他們已完全投入和擁有學習的過程。對他 們來說，努力完成工作已經不再是為了向老師交代，或是討個甲等成績，

而是為了享受親身發掘知識的滿足感。能帶領學生走到這個境界，這兒介 紹的教學設計應記一功。

結語

現在，想讀者最擔心的是課時問題，如前文所述，當學生完整地經歷 了正方形數的數學化過程後，對長方形數及三角形數的入手再不感到陌生 時，部分有關長方形數及三角形數的問題可以省去；另外，有關數型的難 題亦可因應學生興趣及課時而選擇地使用；況且，當學生熟習有關的操作 時，部分的題目可以作為家課（每個學生有一袋鈕扣帶回家使用），第二天 才一起討論，這也省卻不少課時。整體而言，兩年的學生分別約完成了二 十多張工作紙，所需課時約四星期，但依照舊課程課本上的建議，這個課 題原也需約兩星期的課時；因此，只需將六年級下學期的課程進行簡單的

調適，便可以多撥出兩星期的課時。

在這次數型的教學實驗中，原希望學生能真正地認識和欣賞簡單的數 型規律外，還可以繞過盲目背誦公式，掌握如何利用拼砌點陣圖，解決各 種有關數列的問題。經歷了兩年的教學，發現學生不單能達到預期效果，

且能真正體會以「形」馭「數」的精妙和樂趣；而最重的是，透過此課題 的研習，學懂了如何面對數學難題？如何解決數學難題？從何入手？當 然，不是每個學生的進展均是同步的。況且，這兩屆的學生均從未接觸「數 學化教學」，要他們擺脫固有的壞習慣，事事要自己發現，開始時著實有點 困難。然而，只要給予多點時間，筆者等發現部分學生的自學能力原來非 常之高，學生（尤其是第一年的）由最初被動地去面對問題，到後來積極 投入課堂上的討論，鍥而不捨地找尋方法解決問題，這種學習態度的改變，

相對於只是四星期課時，收穫可謂不少。

參考資料

香港課程發展議會（2000）。《數學課程指引（小一至小六）》。香港：教育署。

馮振業（2004，6 月）。〈數學化教學：理論、實踐與前瞻〉，收入 鄧幹明、黃家樂、李 文生、莫雅慈（編）《香港數學教育會議 － 2004 論文集》，78

 88，香港大學教

首作者電郵：pansyclp@yahoo.com.hk

附件二 附件一