Abstract—Fuzzy interpolative reasoning is an important inference technique for sparse fuzzy rule-based systems. In this paper, we present a new fuzzy interpolative reasoning method for sparse fuzzy rule-based systems based on the areas of fuzzy sets. The proposed method can guarantee the normality and the convexity of the conclusion and can deal with fuzzy interpolative reasoning with complicated membership functions, such as hexagons, polygons and Gaussians.
Moreover, the proposed method can deal with the situation when the antecedents and the consequents of fuzzy rules belong to different kinds of membership functions. We use several examples to compare the fuzzy interpolative reasoning results of the proposed method with the ones of the existing methods.
The experimental results show that the proposed method is more suitable to deal with fuzzy interpolative reasoning than the existing methods. The proposed method provides a useful way to deal with fuzzy interpolative reasoning in sparse fuzzy rule-based systems.
I. INTRODUCTION
UZZY interpolative reasoning is an inference technique for sparse fuzzy rule-based systems. It is obvious that the number of fuzzy rules significantly affects the execution time of the fuzzy rule-based system, where the sparser the fuzzy rule bases of the system are, the faster the execution of the system is. In this situation, the input universe of discourse is covered completely by the fuzzy rule bases through the fuzzy interpolative reasoning methods. When an observation occurs, a consequence can be derived by fuzzy interpolative reasoning techniques. In recent years, some fuzzy interpolative reasoning methods have been presented for sparse fuzzy rule-based systems [1]-[11], [14]. Although some existing fuzzy interpolative reasoning methods [4], [5], [7], [8], [11] are presented to deal with the fuzzy interpolative reasoning for sparse rule-based systems, some methods are limited to deal with triangular or trapezoidal membership functions [4], [5], [11], the method presented in [8] gets nonconvex fuzzy interpolative reasoning results in some situations and does not properly deal with fuzzy interpolative reasoning when the fuzzy sets of the
This work was supported in part by the National Science Council, Republic of China, under Grant NSC 95-2221-E-011-116-MY2.
Y.-C. Chang is with the Department of Computer Science and Information Engineering, National Taiwan University of Science and Technology, Taipei, Taiwan, R. O. C. (e-mail: D9315003@
mail.ntust.edu.tw).
S.-M. Chen is with the Department of Computer Science and Information Engineering, National Taiwan University of Science and Technology, Taipei, Taiwan, R. O. C. (e-mail: smchen@mail.ntust.edu.tw).
C.-J. Liau is with the Institute of Information Science, Academia Sinica, Taipei, Taiwan, R. O. C. (e-mail: liaucj@iis.sinica.edu.tw).
antecedents and the consequences in fuzzy rules belong to different kinds of membership functions, and the method presented in [7] can not deal with the fuzzy interpolative reasoning where observations are rectangular membership functions. In [12], Shi et al. pointed out that Koczy-and-Hirota’s fuzzy interpolative reasoning method [8]
does not always lead to convex conclusions. In [13], Tikk and Baranyi compared the modified α-cuts based fuzzy interpolation method [2] and Koczy-and-Hirota’s fuzzy interpolative reasoning method [8] and made a comprehensive analysis.
In this paper, we present a new fuzzy interpolative reasoning method based on the areas of fuzzy sets, which can overcome the drawbacks of the existing methods. Moreover, when the antecedents and the consequents of the fuzzy rules are different kinds of membership functions, the proposed method can generate normal and convex results. In the proposed method, interpolated fuzzy rules are inferred by their adjacent rules and the fuzzy interpolative reasoning results hold the properties of normality and convexity. The proposed method provides a useful way to deal with fuzzy interpolative reasoning in sparse rule-based systems.
The rest of this paper is organized as follows. In Section II, we present a new fuzzy interpolative reasoning method for sparse fuzzy rule-based systems. In Section III, we make some experiments to compare the fuzzy interpolative results of the proposed method with the ones of the existing methods. The conclusions are discussed in Section IV.
II. ANEW FUZZY INTERPOLATIVE REASONING METHOD
In this section, we present a new fuzzy interpolated reasoning method for sparse fuzzy rule-based systems based on the areas of fuzzy sets of given fuzzy rules and observations. In the following, we describe the proposed method by means of different kinds of membership functions.
A. Fuzzy Interpolative Reasoning with Triangular Fuzzy Sets
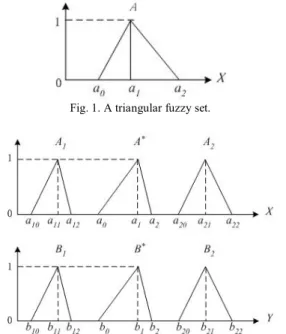
A triangular fuzzy set is denoted by (a0, a1, a2), as shown in Fig. 1, where a0, a1 and a2 are called the left extreme point, the normal point and the right extreme point, respectively.
An interpolative fuzzy reasoning example using triangle membership functions is shown in Fig. 2. Assume that there are two disjoint fuzzy rules A1⇒B1 and A2⇒B2, where A1 and A2 are fuzzy sets of the antecedents of the fuzzy rules in the universe of discourse X, B1 and B2 are fuzzy sets of the
A New Fuzzy Interpolative Reasoning Method Based on the Areas of Fuzzy Sets
Yu-Chuan Chang, Shyi-Ming Chen, Senoir Member, IEEE, and Churn-Jung Liau
F
consequents of the fuzzy rules in the universe of discourse Y, the observation A* occurs between the fuzzy sets A1 and A2, and the fuzzy set B* is the result of the fuzzy interpolative reasoning. Since the fuzzy sets A1, A*, A2, B1 and B2 are triangular membership functions, we can properly assume that the conclusion B* is also a triangular membership function.
Fig. 1. A triangular fuzzy set.
Fig. 2. Fuzzy interpolation with triangular membership functions.
In the proposed fuzzy interpolative reasoning method, the fuzzy interpolated reasoning result B* is obtained as follows:
Step 1: Calculate the normal point b1 of the interpolated fuzzy set B* by the KH method [8]. The linear interpolation is defined as follows:
). , (
) , ( ) , (
) , (
2 1 2
1
B B d
B B d A A d
A A d
∗
∗
∗
∗ = (1)
where d(P, Q) denotes the Euclidean distance between the fuzzy sets P and Q. Therefore, we can get the normal point b1
as follows:
.
21 11
1 11 21 1 21 11 1
21 1 11
1 11 21 1 21 11
1 a a
a a b a a b a a a a
a a b a a
b b = × + ×
+
× +
= × (2)
Step 2: Determine the left and the right extreme points of the interpolated fuzzy set B* shown in Fig. 2. We divide a triangular membership function into the left area SL and the right area SR, as shown in Fig. 3. Then, we use Eq. (1) to get the left area SL(B*) and the right area SR(B*) of the triangular fuzzy set B*, respectively:
= + ∀
+
>
∃
×
=
∑
∑
=
∗
>
=
∗
∗
, 0 ) ( if 1 ,
, 0 ) ( if ), (
) ) ( ( )
(
1 0 ) ( , 1
i K N
i i K K
i K N
A S
i K i
i K K
K
A N S
) (B S ) (A S
A N S
A S
B A S
S B
S
i K
where K∈{L, R} and N denotes the number of given fuzzy
rules (i.e., N = 2). The value of SL(B*) is equal to
2 h dl× , where dl denotes the left bottom length of the triangular fuzzy set B*, the value of SR(B*) is equal to
2 h
dr× , where dr
denotes the right bottom length of the triangular fuzzy set B*, and h denotes the height of B*. Because the value of h is equal to 1 when the membership function is normal, we can obtain the left extreme point b1– 2SL(B*) and the right extreme point b1 + 2SR(B*) of the fuzzy set B*, respectively.
Then, we can obtain the left extreme point b1– 2SL(B*) and the right extreme point b1 + SR(B*) of triangular fuzzy set B* shown in Fig. 2.
Fig. 3. The left area SL(B*) and the right area SR(B*) of the triangular fuzzy set B*.
Step 3: The conclusion B* shown in Fig. 2 denoted by (b1–2SL(B*), b1, b1+2SR(B*)) is derived based on the observation A*, where b0 = b1–2SL(B*) and b2 = b1 + 2SL(B*).
B. Fuzzy Interpolative Reasoning with Trapezoidal Fuzzy Sets
An interpolative fuzzy reasoning example using trapezoidal membership functions is shown in Fig. 4. A trapezoidal fuzzy set A* is denoted by (a0, a1, a2, a3), as shown in Fig. 4, where a1 and a2 are the left normal point and the right normal point, respectively, and a0 and a3 are the left extreme point and the right extreme point, respectively.
Assume that the interpolated fuzzy set B* is a trapezoidal membership function denoted by (b0, b1, b2, b3). Based on Eq. (2), we can get the left normal point b1 and the right normal point b2 of the fuzzy set B*. Then, the left extreme point b0 and the right extreme point b3 of B* are calculated by Eq. (3), respectively. Finally, the conclusion B* denoted by (b1–2SL(B*), b1, b2, b2+2SR(B*)) is derived based on the observation A*.
Fig. 4. Fuzzy interpolation with trapezoidal membership functions.
(3)
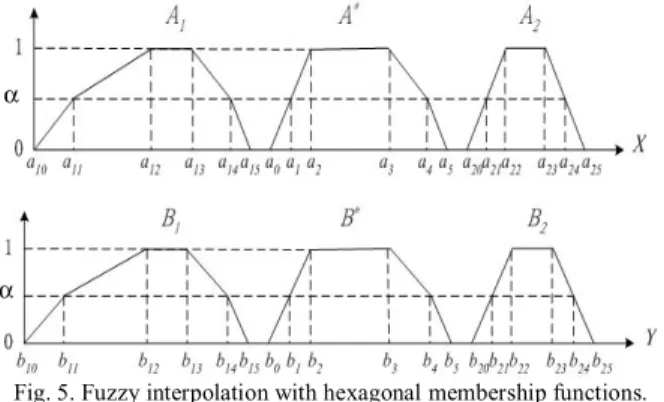
C. Fuzzy Interpolative Reasoning with Hexagonal Fuzzy Sets
An interpolative fuzzy reasoning example using hexagonal membership functions is shown in Fig. 5. A generalized hexagonal fuzzy set A* is denoted by (a0, a1, a2, a3, a4, a5), as shown in Fig. 5, where a2 and a3 are the left normal point and the right normal point, respectively, a0 and a5 are the left extreme point and the right extreme point, respectively, and a1 and a4 are intermediate points (whose membership values are the same and both are between 0 and 1). Assume that the interpolated fuzzy set B* is the hexagonal membership function denoted by (b0, b1, b2, b3, b4, b5). In this case, K ∈{L, L1, R1, R}, SL(B*) denotes the triangular area between b0 and b1 in the trapezoidal membership function B*, SL1(B*) denotes the trapezoidal area between b1 and b2 in the trapezoidal membership function B*, SR1(B*) denotes the trapezoidal area between b3 and b4 in the trapezoidal membership function B*, and SR(B*) denotes the triangular area between b4 and b5 in the trapezoidal membership function B*.
Fig. 5. Fuzzy interpolation with hexagonal membership functions.
The hexagonal fuzzy set interpolation of the proposed method is presented as follows:
Step 1: The left normal point b2 and the right normal point b3
are calculated as follows:
,
22 12
2 12 22 2 22 12 2
22 2 12
2 12 22 2 22 12
2 a a
a a b a a b a a a a
a a b a a
b b = × + ×
+
× +
= × (4)
.
23 13
3 13 23 3 23 13 3
23 3 13
3 13 23 3 23 13
3 a a
a a b a a b a a a a
a a b a a
b b = × + ×
+
× +
= × (5)
Step 2: Calculate the values of the areas SL1(B*) and SR1(B*) by Eq. (3), respectively. Because the value of SL1(B*) is equal to
2 ) 1
(α+ b2−b1 and the value of SR1(B*) is equal to
2 ) 1
(α+ b4−b3 , the value of the intermediate point b1 is equal to
1 ) ( 2 1
2− + ∗
α B
b SL and the value of the intermediate point b4 is equal to
1 ) ( 2 1
3+ + ∗
α B
b SR , where α∈[0,1].
Step 3: The values of the triangular areas SL(A*) and SR(A*) are
2
0
1 a
a −
α and
2
4
5 a
a −
α , respectively. Calculate the
values of the areas SL(B*) and SR(B*) by Eq. (3), respectively.
Because the value of SL(B*) is equal to
2
0
1 b
b −
α and the value of SR(B*) is equal to
2
4
5 b
b −
α , , where α∈[0,1], we can see that the left extreme point b0 and the right extreme point b5
are α
) ( 2
1
∗
− S B
b L and
α ) ( 2
4
+ S B∗
b R , respectively. Finally, The interpolated fuzzy set B* is derived and is denoted by (b0, b1, b2, b3, b4, b5), where 2 ( ),
1 ) ( 2 1
2
0 α α
∗
∗ −
− +
= S B S B
b
b L L
1 , ) ( 2 1
2
1= − + ∗
α B b S
b L ,
1 ) ( 2 1
3
4= + α+ ∗
B b S
b R and
). ( 2 1
) ( 2 1
3
5 α α
∗
∗
+ + +
=b S B S B
b R R
D. Fuzzy Interpolative Reasoning with Polygonal Fuzzy Sets
Let us consider an arbitrary polygonal membership function A = (a0, a1, …, an-1), as shown in Fig. 6. The calculation of the interpolated fuzzy rule A*⇒B* is similar to that of hexagonal fuzzy sets. Assume that the fuzzy sets of the given fuzzy rules A1⇒B1 and A2⇒B2 are polygonal fuzzy sets, where the polygonal fuzzy sets A1 = (a10, a11, …, a1, n-1) and A2 = (a20, a21, …, a2, n-1) are the antecedents and the polygonal fuzzy sets B1 = (b10, b11, …, b1, n-1) and B2 = (b10, b11, …, b1, n-1) are the consequences. The observation A* = (a0*, a1*, …, an-1*) occurs between the fuzzy sets A1 and A2, and B* = (b0*, b1*, …, bn-1*) denotes the fuzzy interpolative reasoning result. There are
− 2 1
n +1 levels including the bottom level and the top level in the fuzzy set, where their membership degrees are
− 2 1 1
0,α ,...,andα n
α , respectively
(i.e., α0 =0 and 1
2
1 =
n−
α ).
Fig. 6. Arbitrary polygonal membership function with n odd points.
The proposed fuzzy interpolative reasoning method with polygonal fuzzy sets is presented as follows:
Step 1: Calculate the left normal point *
2 1
n−
b and the right normal point *
2 1
n−
b of the fuzzy set B* based on Eq. (4) and Eq. (5), respectively, where *
2 1
n−
b and *
2 1
n−
b are the same when n is odd.
α
α
Step 2: Calculate the area SK (B*) of area K of the fuzzy set B* by Eq. (3), where K =
2 1 1−
n−
L ,
2 1 1−
n−
R ,
2 2 1−
n−
L ,
2 2 1−
n−
R , ..., L1, R1, L0, and R0.
Step 3: We also can see that SLi(B*) is equal to 2
)
(αi+αi+1 bi*−bi*+1 and SRi(B*) is equal to
2 )
(αn−i+αn−i−1 bn*−i−b*n−i−1 (i.e., SLi(B*) =
2 ) (αi+αi+1 bi*−bi*+1
and SRi(B*) =
2 )
( * * 1
1 − −−
−
−
−i+ ni ni− ni
n α b b
α ). Finally, the fuzzy
interpolative reasoning result B* denoted by (b0*, b1*, …, bn-1*) is derived, where
−
+
−
+
− + =
− + −
+ −
−
−
− + =
− + −
+ −
−
=
+
∗
−
−
−
−
∗
−
−
−
∗
−
+
∗
−
−
−
−
∗
−
−
−
∗
−
−
−
−
−
−
−
−
−
1 ..., , 2 2 , 1 2 1 if 1 ), ( ... 2 ) ( 2 ) ( 2
, 2 1 , 1 ...
1, 0, if ), ( ... 2 ) ( 2 ) ( 2
1 1 2 2 1 2
1 2
1 1 2
1
* 2
1
1 1 2 2 1 2
1 2
1 1 2
1
* 2
1
*
2 2 1 1
2 1
2 2 1 1
2 1
n n i n
B B S
S B
S b
i n B
B S S B
S b
b
i i
L n
n L
n n
L n
i i
L n
n L
n n
L n
i
i n
n
i n
n
α α α
α α α
α α α
α α
α (6)
E. Fuzzy Interpolative Reasoning with Gaussian and Other Bell-Shaped Membership Functions
Let us consider any Gaussian membership function
2 2
2 ) (
σ c x
e A
−
−
= , as shown in Fig. 7, where c and σ denote the mean and the standard deviation, respectively. The normal point of the Gaussian fuzzy set A is the mean of the Gaussian membership function.
Fig. 7. Gaussian membership function A.
To perform fuzzy interpolation, we assume that the interpolated fuzzy set B* is a Gaussian membership function.
We can calculate the normal point (i.e., the mean) of the Gaussian membership function of the fuzzy set B* by Eq. (2).
The standard deviation of B* can be calculated as follows:
otherwise ,
0 if ,
1 1
∑
>
∑ ×
=
=
=
∗
∗
N N
N
i B
A N
i A
A B
B
i
i i
i
σ σ σ σ σ
σ
where ∗
σB denotes the standard deviation of the interpolated fuzzy set B* and N denotes the number of given fuzzy rules. Once the new mean and the new standard deviation are calculated, the Gaussian membership function of the interpolated fuzzy set 2
*2 2
) (
∗
−
−
∗ = B
cB x
e
B σ is derived.
III.EXPERIMENTAL RESULTS
In this section, we make some experiments to compare the
fuzzy interpolative reasoning results of the proposed method with the ones of the KH method [8], the HCL method [4] and the HS method [7] by using the examples given in [7].
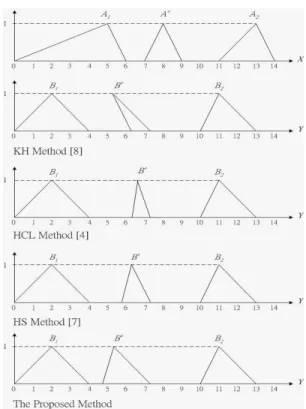
Example 3.1: Assume the triangular fuzzy sets are used in the fuzzy interpolative reasoning scheme. All the conditions and the fuzzy interpolative reasoning results are shown in Table I and Fig. 8. From Fig. 8, we can see that the conclusion of the KH method [8] is nonconvex while the HCL method [4], the HS method [7] and the proposed method have convex results. However, the resultant fuzzy set of the proposed method is more reasonable than the ones of the HCL method [4] and the HS method [7] in terms of the shapes of the original observations.
Example 3.2: Let us consider the situation that fuzzy interpolative reasoning uses trapezoidal fuzzy sets. The conditions and the fuzzy interpolative reasoning results are shown in Table II and Fig. 9. From the Table II, we can see that the HCL method [4] and the HS method [7] can not handle the situation where observations are rectangular membership functions. From Fig. 9, we can see that both the KH method [8] and the proposed method produce the same result.
TABLEI
FUZZY INTERPOLATIVE REASONING RESULTS OF EXAMPLE 3.1 FOR DIFFERENT METHODS
Attribute Values Methods Fuzzy Interpolative Reasoning Results B*
KH Method [8] (6.36, 5.38, 7.38) HCL Method [4] (6.36, 6.58, 7.38) HS Method [7] (5.83, 6.26, 7.38) A1 = (0, 5, 6)
A2 = (11, 13, 14) B1 = (0, 2, 4) B2 = (10, 11, 13)
A* = (7, 8, 9) The Proposed Method ( 4.93, 5.38, 7.38)
(7) c X
A
σ 1
0.5
0
Fig. 8. A comparison of fuzzy interpolative reasoning results of Example 3.1 for different methods.
TABLEII
FUZZYINTERPOLATIVEREASONINGRESULTSOFEXAMPLE3.2 FORDIFFERENTMETHODS
Attribute Values Methods Fuzzy Interpolative Reasoning Results B*
KH Method [8] (4.25, 4.25, 7.5, 7.5)
HCL Method [4] –
HS Method [7] –
A1 = (0, 4, 5, 6) A2 = (11, 12, 13, 14) B1 = (0, 2, 3, 4) B2 = (10, 11, 12, 13)
A* = (6, 6, 9, 9) The Proposed Method (4.25, 4.25, 7.5, 7.5) Note: The symbol “–” denotes the method can not handle the situation.
Fig. 9. A comparison of fuzzy interpolative reasoning results of Example 3.2 for different methods.
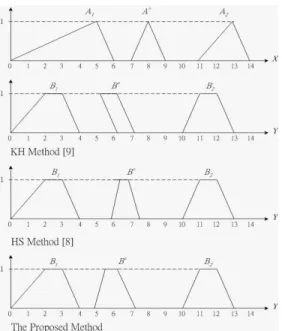
Example 3.3: Let us consider the situation that fuzzy interpolative reasoning uses hexagonal fuzzy sets. The conditions and the fuzzy interpolative reasoning results are shown in Table 3 and Fig. 10. In Table III, the HS1 method
[7], the HS2 method [7], the HS3 method [7] and the HS4 method [7] denote using different strategies (i.e., the average, the compatible, the weighted average and the center of core) to calculate the representative value, respectively.
From Fig. 10, we can see that the KH method [8] produces a nonconvex result. The HS1 method [7] , the HS2 method [7], the HS3 method [7], the HS4 method [7] and the proposed method produce convex results.
TABLEIII
FUZZYINTERPOLATIVEREASONINGRESULTSOFEXAMPLE3.3 FORDIFFERENTMETHODS
Attribute Values Methods Fuzzy Interpolative Reasoning Results B*
KH Method [8] (5.73, 6.00, 5.89, 8.56, 9.59, 10.09)
HCL Method [4] –
HS1 Method (via the average representative value) [7]
(5.64, 5.98, 6.29, 8.63, 9.46, 9.93)
HS2 Method (via the compatible representative value) [7]
(5.69, 6.03, 6.36, 8.69, 9.53, 10.00)
HS3 Method (via the weighted average representative value) [7]
(5.61, 5.95, 6.26, 8.59, 9.42, 9.89)
HS4 Method (via the center of core
representative value) [7]
(5.47, 5.79, 6.08, 8.42, 9.23, 9.70)
A1 = (0, 1, 3, 4, 5, 5.5) A2 = (11, 11.5, 12,
13, 13.5, 14) B1 = (0, 0.5, 1, 3, 4,
4.5) B2 = (10.5, 11, 12,
13, 13.5, 14) A* = (6, 6.5, 7, 9,
10, 10.5)
The Proposed Method (4.96, 5.33, 5.89, 8.56, 9.56, 10.06)
Note: The symbol “–” denotes the method can not handle the situation.
Example 3.4: Let us consider the situation that the antecedents of the fuzzy rules are triangular fuzzy sets and the consequences of the fuzzy rules are trapezoidal fuzzy sets. The conditions and the fuzzy interpolative reasoning results are shown in Table IV and Fig. 11. From Table IV, we can see that the HCL method [4] can not handle this situation. From Fig. 11, we can see that the KH method [8]
produces a nonconvex fuzzy set, whereas the HS method [7]
and the proposed method produce convex trapezoidal fuzzy sets. From this example, we can see that the fuzzy interpolative reasoning results of the HS method [7] and proposed method are better than the one of the KH method [8].
TABLEIV
FUZZYINTERPOLATIVEREASONINGRESULTSOFEXAMPLE3.4 FORDIFFERENTMETHODS
Attribute Values Methods Fuzzy Interpolative Reasoning Results B*
KH Method [8] (6.36, 5.38, 6.36, 7.38)
HCL Method [4] –
HS Method [7] (5.93, 6.36, 6.80, 7.47) A1 = (0, 5, 5, 6)
A2 = (11, 13, 14) B1 = (0, 2, 3, 4) B2 = (10, 11, 12, 13)
A* = (7, 8, 8, 9) The Proposed Method (4.93, 5.38, 6.36, 7.36) Note: The symbol “–” denotes the method can not handle the situation.
Fig. 10. A comparison of fuzzy interpolative reasoning results of Example 3.3 for different methods.
Fig. 11. A comparison of fuzzy interpolative reasoning results of Example 3.4 for different methods.
IV. CONCLUSIONS
In this paper, we have presented a new fuzzy interpolative reasoning method for sparse fuzzy rule-based systems. The proposed method not only can get normal and convex fuzzy interpolative reasoning results, but also can deal with the fuzzy interpolative reasoning with complicated membership functions, such as hexagonal membership functions, polygonal membership functions and Gaussian membership functions. From the experimental results, we can see that the proposed method is better than the KH method [8] , the HCL method [4] and the HS method [7]. Moreover, when the antecedents and the consequents of the fuzzy rules are different kinds of membership functions, the proposed method can generate normal and convex results. The proposed method provides a useful way to deal with fuzzy interpolative reasoning in sparse fuzzy rule-based systems.
REFERENCES
[1] P. Baranyi, T. D. Gedeon, and L. T. Koczy, “A general interpolation technique in fuzzy rule bases with arbitrary membership functions,”
Proc. IEEE Int. Conf. Syst., Man, Cybern, pp. 510–515, 1996.
[2] P. Baranyi, D. Tikk, Y. Yam, and L. T. Kozcy, “A new method for avoiding abnormal conclusion for α-cut based rule interpolation,”
Proc. FUZZ-IEEE’99, pp. 383–388, 1999.
[3] B. Bouchon-Meunier, , C. Marsala, , and M. Rifqi,: “Interpolative reasoning based on graduality,” Proc. FUZZ-IEEE2000, pp. 483–487, 2000.
[4] W. H. Hsiao, S. M. Chen, and C. H. Lee, “A new fuzzy interpolative reasoning method in sparse rule-based system. Fuzzy Set Syst., vol. 93, no. 1, pp. 17–22, 1998.
[5] D. M. Huang, E. C. C. Tsang, D. S. Yeung, “A fuzzy interpolative reasoning method,” Proc. IEEE Int. Conf. Machine Learning and Cybernetics, vol. 3, pp. 1826–1830, 2004.
[6] Z. H. Huang, and Q. Shen, “A new fuzzy interpolative reasoning method based on center of gravity,” Proc. IEEE Int. Conf. Fuzzy Syst., pp. 25–30, 2003.
[7] Z. H. Huang and Q. Shen, “Fuzzy interpolative reasoning via scale and move transformations,” IEEE Trans. Fuzzy Syst., vol. 14, no. 2, pp.
340–359, 2006.
[8] L. T. Koczy and K. Hirota, “Approximate reasoning by linear rule interpolation and approximation,” Int. J. Approx. Reasoning, vol. 9, no.
3, pp. 197–225, 1993.
[9] L. T. Koczy and K. Hirota, “Interpolative reasoning with insufficient evidence in sparse fuzzy rule bases,” Inform. Sci., vol. 71, no. 1, pp.
169–201, 1993.
[10] L. T. Koczy and K. Hirota, “Size reduction by interpolation in fuzzy rule bases,” IEEE. Trans. Syst., Man, Cybern, vol. 27, no. 1, pp. 14–25, 1997.
[11] Y. M. Li, D. M. Huang, C. C. Tsang, L. N. Zhang, ”Weighted fuzzy interpolation reasoning method,” Proc. IEEE Int. Conf. Machine Learning and Cybern vol. 4, pp. 18-21, 2005.
[12] Y. Shi, M. Mizumoto, and W. Z. Qiao, “Reasoning conditions on Kozcy’s interpolative reasoning method in sparse fuzzy rule bases,”
Fuzzy Set Syst., vol. 75, no. 1, pp. 63–71, 1995.
[13] D. Tikk and P. Baranyi, “Comprehensive analysis of a new fuzzy rule interpolation method,” IEEE Trans. Fuzzy Syst., vol. 8, no. 3, pp.
281–296, 2003.
[14] B. Wang, X. Li, W. Liu, and Y. Shi, “A new sparse rule-based fuzzy reasoning method,” Proc. IEEE Int. Conf. Hybrid Int. Syst., pp.
462–467, 2004.