國小中年級自閉症學生學習幾何之個案研究

(1)

國立台中教育大學數學教育系碩士論文

指導教授：陳鉪逸教授

國小中年級自閉症學生學習幾何之個案探究

研究生：蔡仔堂撰

(2)

The mid-level autism student of learning geometry by a case

study in the elementary school

Abstract

1. The purpose of this research:

It mainly discussed about the mid-level autism student of learning geometry by a case study.

The contents contained:

What is the concept of triangle shapes of mid-level autism student in the elementary school?

The comparison of the triangle shape concept in mid-level autism student in the elementary school and the thoughts of geometry by Van Hiele.

2. The methods and tools of research:

The research was by interview, written tests and authentic tests. It was used by seven activities: vision identify, tactile sense identify, plane shape identify, written test, draw triangle, arrange a triangle and do a triangle on the tack board etc.

3. The discovery of research:

It detected that the autism student was learning geometry might:

(1)The concept of triangle shape was by mid-level autism student in elementary school.

It would have abilities to distinguish figures from the shapes. It could not totally realize the features of angles (shrill).

It could not recognize the characteristics of side which was straight. It could not clearly understand the meanings of written questions.

It could not identify the classification of triangles and understand the comprise relationships of triangles.

(2)The mid-level autism student learned geometry arriving at the cognition—the abilities of vision period.

4.Suggestions:

(1)It had to refill the amounts of teachers in special educations without hesitation. The speed of special educations trainings could not catch up the amounts and the species of special students.

(2)It had to be promoted of autism inspect appraisal precisely in hospital in order to predict the errors of appraisal.

(3)

中文摘要

1、本研究的目的：主要是在探討國小中年級自閉症學生學習幾何之個案研究，內容涵蓋： (1)、國小中年級自閉症學生三角形圖形概念為何？ (2)、國小中年級自閉症學生三角形圖形概念與 van Hiele 幾何思考層次的比較。 2、研究方法與工具：本研究是採用晤談、紙筆測驗與實作評量方式進行，共分七個活動研究，包括：視覺辨識、觸覺辨識、平面圖形辨識、紙筆測驗、畫出三角形、排出三角形及在釘板上做出三角形等活動。 4、研究發現：本研究發現自閉症學生學習幾何時具有： (1)、國小中年級自閉症學生三角形圖形概念 c、從圖型外觀有辨視圖形能力；d不能完全了解角特徵（尖尖的）； e、不能瞭解邊的特性是直線性的；f、無法瞭解清楚文字題目的文字意 g、無能力進行三角形的分類及瞭解三角形之間的包含關係。 (2)、中年級自閉症學生學習幾何達到幾何認知層次一視覺期的能力。 5、研究建議：c宜儘速充實特教自閉症師資，特殊生的人數及類型越來越多，特教師資培訓太慢跟不上需求； d醫院自閉症的檢查鑑定應再求精密，避免鑑定錯誤情事的發生。關鍵字：自閉症、幾何、概念。

(4)

附表目次 附圖目次 第一章 緒論`……… 1 第一節研究動機………. 1 第二節研究目的與待答問題……….. 2 第三節名詞闡釋……….. 3 第二章 文獻探討……….. 4 第一節自閉症兒童概觀……….. 4 第二節幾何概念……….. 13 第三節有關幾何概念發展的理論……….. 21 第三章 研究方法與過程………. 28 第一節研究對象………. 28 第二節方法與過程………. 32 第三節研究限制及困難……….. 35 第四章 結果與討論………. 38 第一節自閉症兒童小偉在訪談與操作活動的分析結果……….. 38 第二節小偉的三角形概念分析……… 59 第三節 van Hiele 思考層次分析 ………. 61 第五章 結論與建議……….. 62 第一節結論………. 62 第二節小偉概念學習過程與 van Hiele 的幾何思考層次的比較分析. 64 第三節建議……… 65 參考文獻 一、中文部分……….. 89

(5)

二、英文部分………... 90

附錄………. 92

附錄 1 兒童訪談對象基本資料……… 93

(6)

表目次

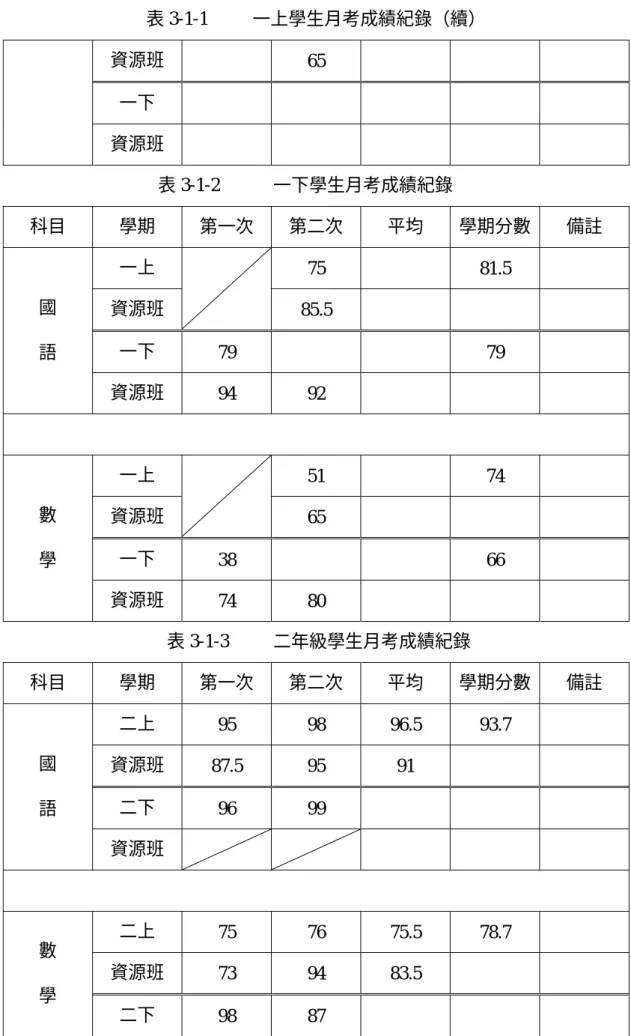
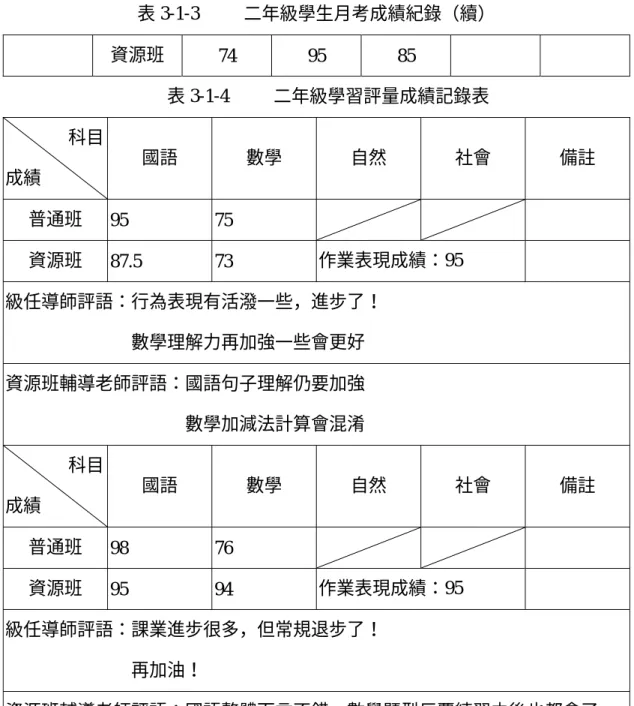
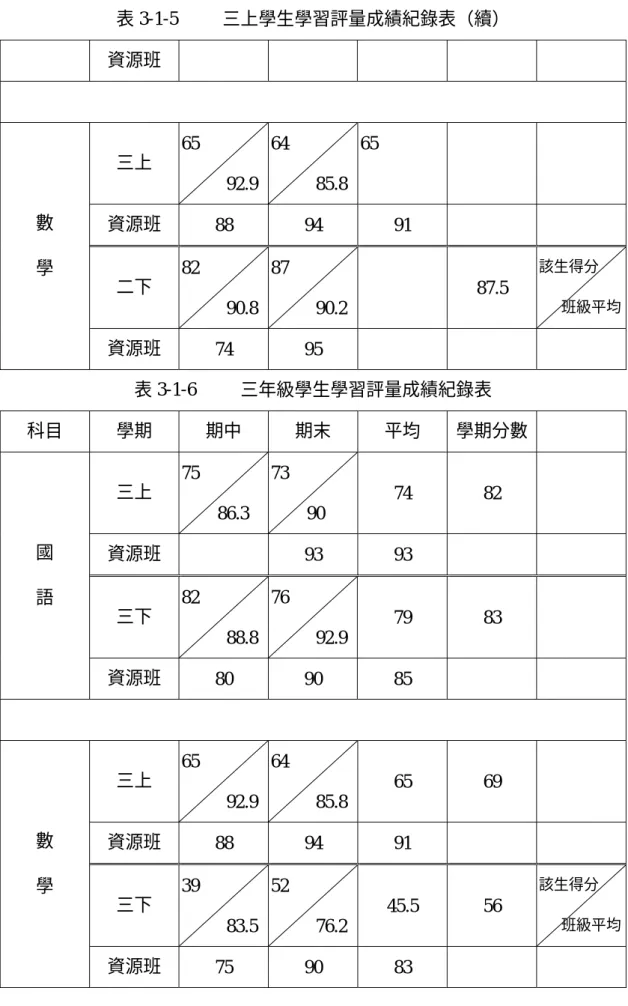
表 2-1-1 九年一貫暫行綱要國小部分平面圖形與空間形體的能力指標……… 22、23 表 2-1-2 九年一貫正式綱要國小部分幾何的能力指標………… 23、24 表 3-1-1 一上學生月考成績記錄……… 39、40 表 3-1-2 一下學生月考成績記錄……… 40 表 3-1-3 二年級學生月考成績記錄……… 40、41 表 3-1-4 二年級學習評量成績記錄表……… 41 表 3-1-5 三上學生學習評量成績記錄表………. 41、42 表 3-1-6 三年級學生學習評量成績記錄表……….. 42 表 3-1-7 四上期中學習成績……….. 43 表 3-1-8 四上期末學習成績……….. 43、44

(7)

圖目次

圖 4-1-1 三角形圖片……… 52 圖 4-1-2 長方形圖片……… 53 圖 4-1-3 圓形圖片……… 55 圖 4-1-4 一堆幾何圖片……… 56 圖 4-1-5 紙箱……… 56 圖 4-1-6 手放入紙箱……… 56 圖 4-1-7 平面組合圖形……… 57、58、59 圖 4-1-8 畫三角形……… 70 圖 4-1-9 畫三角形……….. 70 圖 4-1-10 畫直角三角形（畫成長方形）……… 70 圖 4-1-11 畫等腰三角形……… 70 圖 4-1-12 畫鈍角三角形……… 70 圖 4-1-13 畫三角形……… 71 圖 4-1-14 紅色棒子排成三角形……… 72 圖 4-1-15 第三根棒子太大了的圖形……… 73 圖 4-1-16 調整後的三角形……… 73 圖 4-1-17 綠色棒子排成三角形……… 73

(8)

圖 4-1-18 綠色棒子排成三角形………. 73 圖 4-1-19 拉出兩點………. 74 圖 4-1-20 拉出三角形………. 74 圖 4-1-21 拉出四邊形………. 75 圖 4-1-22 拉出三角形……….. 75 圖 4-1-23 拉出三角形………. 75 圖 4-1-24 請拉出直角三角形，小偉拉出的三角形……… 75 圖 4-1-25 請拉出等腰三角形，小偉拉出的兩點……… 75 圖 4-1-25 請拉出等腰三角形，小偉拉出的三角形………. 75 圖 4-1-26 請拉出等腰三角形，小偉拉出的三角形………. 75 圖 4-1-27 請拉出等腰三角形，小偉拉出的三角形……… 75 圖 4-1-28 拉出三角形……… 75 圖 4-1-29 拉出三角形……… 75 圖 4-1-30 拉出三角形……… 76

(9)

國小中年級自閉症學生幾何學習之個案研究

第一章緒論

本研究在探討國小四年級自閉症學生三角形概念學習過程的表現狀況及其層次結構之形式。本章旨在說明本研究的研究動機、目的、待答問題，並且就本研究的一些相關名詞加以闡釋。

第一節研究動機

人類很幸運的具有各種知覺能力，能看、能聽、能用觸覺來感覺物體，要是人們沒有這些能力，人類便幾乎無法生存。上天又恩賜給我們天賦的直覺能力，賜給人們可以有能力察覺預測事情的發生。甚至可以推測事情可能演變出來的結果。上天這些恩賜使人們有能力去克服生存的障礙。很不幸的是有些人生下來以後某些功能就已經不正常，他們的知覺比正常人遲鈍，他們的學習比正常人遲緩，這些人我們稱為智障，或更嚴重的叫做自閉。看到這些兒童我們心理有另一種難過的感受，同情無助的感受，這也就是引起我想進行自閉症學生學習數學研究的主要動機。甚麼方式的教學對他們最有效？這是人人想知道的，但是教學方式決定於他們學習的習慣和方式，而學習方式與習慣的背後則是由他們的認知的形式所決定，所以本研究決定以觀察和訪談來了解自閉症患者學習數學的方式，了解他們建構幾何概念的方式，於是有了針對校內自閉症學生進行個案研究的想法，從根本來了解自閉症學生認知的形式。本班剛好有一位自閉症的學生，每週在資源班上四節課包含國語及數學，其餘時間均在普通班上課，因此研究者興起對其幾何概念探討的動機。人是視覺的動物，為了生存，研究者認為人類天賦具有的「形」或「幾何」直覺能力，遠比一般人所想像要豐富堅實。人腦的天賦能力實在令人欽佩，它們對典型的視覺影像處理：如

(10)

直線、圖形的邊緣、平行與垂直、對稱、全等操作、放大縮小、圖形識別等，是那麼的輕而易舉，但卻是電腦處理的重大挑戰。幾何不但是各個國家數學教育中的重要課題，實際上幾何本身也是真正很有挑戰性，而且較能挑起學生興趣的教學單元（教育部，2003）。國內數學教育界學者的研究結果指出：兒童在辨識指認圖形的優先順序為三角形、圓形、長方形（吳文如、呂玉琴，2002），再回顧人類幾何知識的發展歷程，由最早期發展出的勾股弦定理、畢氏定理等莫不是以三角形的性質發現來作為一個開端(洪萬生，1999)，所以研究者才決定以三角形作為本研究的主題。

第二節研究目的與待答問題

1. 研究目的 依據上述研究動機，本研究目的有： 1. 了解國小四年級自閉症學生三角形圖形的概念。 2. 國小四年級自閉症學生三角形圖形的概念與 van Hiele 幾何思考層次的比較。 2. 待答問題 根據上述研究目的，本研究在探討下列問題： 1. 國小四年級自閉症學生三角形圖形的概念為何？ 2. 國小四年級自閉症學生三角形圖形的概念與 van Hiele 幾何思考層次的比較情形。

(11)

第三節名詞闡釋

一、身心障礙與自閉症根據特殊教育法，身心障礙指具有下列情形之ㄧ者(教育部，1997)： (1)智能障礙 (2)視覺障礙 (3)聽覺障礙 (4)語言障礙 (5)肢體障礙 (6)身體病弱 (7)嚴重情緒障礙 (8)學習障礙 (9)多重障礙 (10)自閉症 (11)發展性遲緩 (12)其他顯著障礙其中自閉症是因為先天性不明原因（可能因為遺傳、懷孕期間病毒感染、新陳代謝疾病等）的腦傷因素所導致的廣泛性發展障礙，造成他們在認知、語言、知覺等方面發生困難。二、van Hiele 的幾何思考層次

本研究中的 van Hiele 的幾何思考層次指的是 van Hiele 幾何學習的思考五層次，依序如下，層次一：視覺的層次（visual level）、層次二：描述的層次（descriptive level）層次三：非形式化演譯的層次（informal level）層次四：形式化演譯的層次（formal level）層次五：嚴密的層次（rigor level）。國小學生在 van Hiele 的幾

(12)

(13)

第二章文獻探討

本章分成三節，第一節是自閉症兒童概觀；第二節說明幾何概念；第三節說明有關幾何概念發展的理論。

第一節自閉症兒童概觀

一、自閉症的成因 自閉症不是由於父母的養育態度所造成（例如：冷漠），自閉症的成因目前醫學上並無定論，很可能是多方面的因素造成腦部不同地方的傷害。至於造成自閉症的因素則有下列幾項：（一）、遺傳方面 1、20%的自閉症者中，他的家族可找到有智能不足，語言發展遲滯和類似自閉症的症狀。 2、自閉症兒童的兄弟姊妹有較高的機會約五十分之一患有自閉症，而自閉症的一般發病率是一萬分之二~四，同卵雙胞胎當中有一位患有自閉症，另一位也罹患自閉症的機率是 63%~98%，而且有認知障礙的和合率達 80%；異卵雙胞胎同時罹患自閉症的機率是 0~10%，但認知障礙和合率只有 12%。 3、自閉症兒童中約 10%有染色體脆弱症，或是伴隨著某種腦部異常，像是先天性德國痲疹症候群，大多數有這些疾病的人也會同時被診斷患有自閉症。 4、婦女懷孕期間可能因德國麻疹或流行性感冒病毒感染，使胎兒的腦部發育受損傷而導致自閉症。 5、新陳代謝疾病如苯酮尿等先天的新陳代謝障礙，造成腦部細胞的功能失調和障礙，會影響腦神經訊息傳遞的功能，而造成自閉症。 6、母親在懷孕期間窘迫性流產等因素造成大腦發育不全，生產過程中早產、難產、新生兒腦傷，以及嬰兒因感染腦炎、腦膜炎等疾病造成腦部傷害等因素，都可能增加自閉症機會。

(14)

（二）、器質性因素 1、大約四分之一自閉症兒童有羊癲症，發病時間通常在青少年時期，而發病的可能性和弱智的程度有關。 2、腦部影像技術曾用來檢驗自閉症者的腦部結構，發現自閉症的腦部有異常現象，包括：（1）、小腦（Cerebellum）-小腦某些區域有縮小的現象。

（2）、海馬迴與杏仁核（Hippocampus and Amygdala）-體積變小。同樣的這兩個區域的神經細胞變小了，而且堆疊的更加緊密（也可稱為細胞密度變高）。（3）、大腦腦葉（Lobes of Cerebrum）-患者的腦葉比常人的大；（4）、腦室（Ventricles）-變大。（5）、尾狀核（Caudate nucleus）-體積變小。（三）、其他方面 1、男童有自閉症的機會比女童高，大約是五比一，而女童的症狀較為嚴重。 2、自閉症和弱智常常連在一起，大約有三分之二的智商低於七十。 3、不能肯定自閉症是一種固定形式的症狀，還是有進展上的困難。但可知的是症狀有反覆，有時進步到一個階段又會停滯不前，或後退一些，然後又再進步，有時在青少年期又會退步。 4、近幾年又有另一種懷疑是和疫苗保存劑硫柳汞（thimerosal）的使用有關，因此在 2005 年美國的愛荷華、加利福尼亞等州已經廢止疫苗使用硫柳汞了。 二、自閉症兒童的行為特徵 兒童精神醫師之父，美國兒童精神科醫生肯納（Leo kanner）於一九四三年發表「Autistic disturbances of affective contact」一文中詳細描述十一名症狀特殊的兒童，這些病例都未滿二歲即發病，而且具有下列五項行為特徵（Kanner， 1942-43）：

（1）極端的孤獨，缺乏和別人情感的接觸。

(15)

（3）對某些物品有特殊的偏好，且以極好的精細動作玩弄這些物品。（4）沒有語言，或者雖然有語言，但其語言似乎不是用來人際溝通。（5）保留智能，成沉思外貌，並具有良好的認知潛能，在有語言者常以極佳的記憶力來表現，而未具有語言者則由良好的操作測驗表現其潛能。自閉症的研究至今以有五十餘年的歷史，在美國精神醫學協會的診斷標準當中可以給於我們一個明確的定義如下（DSM-IV，1994）：在下列（1）、（2）與（3）中，合計要有六項，其中至少二項屬於（1），一項屬於（2）一項屬於（3）：（1）在社會性互動方面有質的障礙，至少有下列二項以上的情形：（a）在運用下列各種非語言的行為上有著顯著的障礙：例如在用以規範社會互動的眼睛注視、面部表情、身體姿勢、手勢等。（b）不能發展出與其稱度相當的友誼。（c）不能自發地與人互享喜悅、興趣、或成就（例如不會向人展示個人所帶來的東西或指向個人所感興趣的物品）。（d）缺乏社會的或情感上的互動。（2）在溝通上有質的障礙，至少有下列一項的情形：（a）口與發展遲緩或毫無語言（並未嘗試經由其他溝通的管道來加以補救，例如手勢或啞劇手勢）。（b）就已發展出適當語言的兒童來說，他們在與人交談時仍有相當大的困難打開話頭或者使交談持續下去。（c）刻板地或反覆地使用語言，或者以其個人專屬的特別方式使用語言。（d）缺乏與其發展程度相當的各式各樣的自發性的假扮遊戲及模仿性的社會遊戲。（3）在行為、興趣、活動方面有狹窄、重複的、刻板的型式，至少有下列一項以上的行為：（a）偏好一種或多種刻板且狹窄的興趣，然而不論就興趣的強度或興趣的

(16)

集中度來說都是不正常的。（b）很明顯地。他們毫無彈性地執著於特定的、非功能性的日常事務或者儀式。（c）刻板且重複的動作習慣（例如：拍手、扭手、扭手指、全身抖動）。（d）對於物品的各種附件有著持久的偏好。另外，三歲以前，在下列的領域中，至少一項遲緩或者功能上異常：（1）社會互動。（2）社會溝通時的語言使用。（3）象徵性或想像性遊戲。自閉症是因為先天性不明原因（可能為遺傳、懷孕期間病毒或感染、新陳代謝疾病等）的腦傷因素所導致的廣泛性發展障礙，造成他們在認知、語言、知覺等方面發生困難。通常自閉症在幼兒二歲半以前就可以被發現，但目前並無預防方法。自閉症的特徵會隨著年齡、智商及自閉症的嚴重程度不同。發生率為男、女患者比率約為五比一（宋維村，1993）。以下列出自閉症兒童可能出現的特殊行為（中華民國自閉症總會）：

（1）與其他兒童相處困難（Difficulty in mixing with other children）（2）莫名奇妙的笑（Inappropriate laughing and giggling）

（3）目光不與人接觸（Little or no eye contact）

（4）不易與親近（May not want cuddling or act cuddly）（5）喜歡轉動東西（Spins objects）

（6）對疼痛感應遲緩（Apparent insensitivity to pain）（7）不怕危險（No real fear of dangers）

（8）持續怪異的遊戲方法（Sustained odd play）（9）冷漠的態度（Prefers to be alone；aloof manner）

（10）對物體的喜好表現不恰當（Inappropriate attachment to objects）（11）模仿別人說話（Echolalia-repeating words or phrases in place of normal

(17)

language）

（12）形為固定，拒絕變化（Insistence on sameness；resists changes in routine）（13）極端好動或過度被動安靜（Noticeable physical over activity or extreme

under activity）

（14）抗拒正常反應教學方式（Unresponsive to normal teaching methods）（15）聽而不聞，無反應（Not responsive to verbal cues；acts as deaf）（16）以手（姿）勢表達需求（Difficulty in expressing needs；uses gestures or

pointing instead of words）

（17）無特別原因卻表現極度難受（Tantrums-displays extreme distress for no apparent reason）

（18）不願踢球但會堆積木（Unever gross/fine motor skill-May not want to kick ball but can stack blocks ）

由以上可知自閉症兒童通常是行為固定與拒絕變化的而且不容易有新的興趣與活動，各個專家看法不同，難有一致性的意見（張正芬，1997）。台中教育大學黃金源教授就將自閉症兒童的行為依其性質分為：攻擊行為（含自傷行為）、不適當的行為、自我刺激的行為、同一性的行為、怪異行為、過動行為等。現在簡單說明如下： 1、攻擊行為（含自傷行為）自閉症兒童常會撞牆、搥頭、拍耳朵、撞桌子等自傷行為；自閉症兒童也常有傷人（踢、咬、捏、抓、打）的攻擊行為。 2、不適當的行為包括干撓別人、中途闖入他人活動、及不順從、不理人（聽而不聞、像聾子一樣、永遠的孤獨俠）、或情緒亢奮而到處跑、亂吐口水、甚至吐口水到彩色筆盒裡、瘋瘋癲癲的傻笑、公開自慰（玩弄生殖器）。 3、自我刺激的行為這是指自閉症兒童在生活空檔時，表現某種重複的相同動作（可能以奇怪的

(18)

癖好或習慣出現），以滿足感官或心理的需求。這些行為通常不具社會意義甚至干撓人際關係，妨害學習。例如晃頭、搖動或旋轉身體、不停跳躍或繞圈子跑、扭轉手指、喊叫、不停的出怪聲、吐舌頭、作氣喘狀、磨牙、撕紙條、甩紙帶、在沙坑玩沙子、轉動鍋蓋、以頭撞椅背、唱歌、重複而大聲的延宕是鸚鵡語言等。 4、同一性行為所謂同一性行為（又稱為刻板行為或固著行為）是指自閉兒堅持生活中一些不可改變的瑣碎細節，並拒絕改變這些生活細節。如果強硬改變這些生活常規，會引起極度的焦慮或爆發脾氣。常見的同一性的行為如下：出門時一定要帶塑膠袋；走同樣的路回家；使用同一個奶瓶、牙刷；在家中的同一個地方玩或尿尿；蓋同一件棉被；床鋪一定要靠窗戶；到同一個公園玩；早上起床後，固定要先蹲廁所，再做別的事情。自閉兒的挑食（同一性行為之一）常常困擾父母，會堅持光喝牛奶（甚至要求喝同一品牌的牛奶），不吃任何食物；只吃白飯，不吃蔬菜或肉類食品；只吃油炸食物；只吃吐司，其他類的麵包一概不吃；不吃任何水果。自閉兒遊戲的型態也簡單、少有變化，也可視為同一性行為，例如有的自閉兒會花一個上午掏沙，然後觀看沙子從指縫掉下的情形；或用一、兩個小時，甚至更長的時間撕紙條；或一個上午都在旋轉腳踏車的踏板或觀看小輪子轉動。 5、過動行為自閉兒的過動行為包括不停自身旋轉；晃動身體或頭部；在教室或在操場繞著圈跑；爬上、跳下；不斷跳躍或振動身體；在客廳沙發上跳來跳去。三、自閉症教育與治療自閉症因為個別差異極大，加以致病的原因始終不明，因此目前並未發展出任何一套有效的治療方法，只有藉助認知教學、感覺統合訓練、語言溝通訓練等教育來減輕其殘障的程度。其他尚有音樂治療、藝術治療、遊戲治療等方式；但因無法完全獲得治療，故自閉症被視為一種終身殘障（中華民國自閉症總會， 2003）。

(19)

早期療育是目前唯一能補足自閉症患者先天學習能力缺陷的方法。而矯治的目標應為促進其正常發展—彌補加強其學會一般兒童會而他們不會的知識與技巧。一般的矯治原則包括：創造適合學習的情境，也就是誘發學習動機以及實用與生活化，因為自閉症兒童在抽象理解和彈性運用（類化）的能力上有困難；反覆練習，運用養成及增強原理來幫助學習；以及多樣、多變化的安排—相關的人、事、情境作為有計畫的變化配合等方式（中華民國自閉症基金會，2003；中華民國自閉症總會，2003）。另外，對於自閉症兒童常採用的教育與治療有以下幾點（曹純瓊，1998；中華民國自閉症總會，2003）：（1）遊戲治療（2）行為療法（3）感覺統合治療（4）音樂治療（5）藝術治療（6）醫學治療（7） TEACCH 自閉症結構性教學現將這幾種分述如下：（1）遊戲治療遊戲治療（play therapy）是基於心因論的一種心理治療方式。對於兒童無法完全明確的使用語言表達及理解的情況下，治療者用兒童能夠以身體機能表達心理面的遊戲取代語言作為溝通的方式。在遊戲的過程中，兒童可了解人我之分離，並學習人際社交技巧，培養社會適應力。遊戲治療的目的就是藉遊戲的特質發揮兒童本身的自我治癒力，以抒發內在的情結，使人格得以正常發展。（2）行為療法行為療法是自閉症教育治療中最常被採用且有效的方法。其乃是應用個體自發性的行為反應，及所謂的操作制約，來改善與去除自閉症狀與不適應行為或者形成適應行為與日常生活自理及專業技能。

(20)

（3）感覺統合療法感覺統合失常乃是由於腦功能障礙，無法將人類的視覺、聽覺、觸覺、前庭覺及肌肉關節動覺等五種基本感覺的刺激加以統合並適切反應。感覺統合療法的目的即在於提供以上幾種感覺刺激的輸入，並適當的控制，讓孩童以內在驅策力引導自己的活動，自動形成順應性的反應，藉此促成這些感覺的組合和統一。（4）藝術治療藝術治療即一般所謂的繪畫治療。其目的是藉著繪畫及其創造性的自由表現活動將潛意識內壓抑的感情與衝突呈現出來，並且從繪畫過程中獲得紓解與滿足，而達到診斷與治療的效果。（5）音樂治療音樂療法可分為團體治療與個別治療；主要的治療工具為大鼓和銅鈸，讓自閉兒即興、自由的敲打以達到自我宣洩、解放及自我表現的目的。音樂治療可協助自閉者集中注意力、培養想像力、穩定情緒、促進社會化與語言互動、發展新的休閒技能與新的興趣。（6）醫學治療醫學上的治療分成：（a）預防性治療：防止自閉症的出現，包括遺傳學上的輔導；（b）補救性治療：及早診斷，針對生理因素而加以治療。不過（a）、（b）這兩種方法暫時都未有突破性進展。（c）徵狀性治療：藥物治療可以減輕徵狀，例如過分活躍、不集中、情緒不穩定、暴力傾向、睡眠困難等。（7）TEACCH 自閉症結構性教學結構性教學係指物質環境的結構、作息時間的結構、個別工作結構以及視覺結構等四種組織所構成的教學設計。（a）物質環境結構：意旨明確區隔教室空間為四個區域（獨自學習區、轉換區、遊戲區及團體學習區）各區域各司其功能，提供教學、工作、休閒等教學活

(21)

動用途。各區域佈置清楚畫界分明易辨認，有利學生確認不同活動需要在不同區域進行。（b）作習時間結構：標準的作習時間有多種的編排方式，作習內容的呈現方式以符合自閉症者的特徵及需要為前提。作習時間一活動時間長短將一週內的活動時間以圖表呈現並將各時段之時間長短以圖片或字卡呈現的方式按照時間順序由上而下或由左而右排列，使學生極易明瞭其個人作習、活動地點及內容等，卡片大小約六至八公分見方。當作習時間一到，自閉症者即抽取該時段之卡片，了解主要活動內容與時間長短及地點，即可在教師的指導下獨自學習。（c）個別工作結構：本結構依學生功能強弱將每一時段的學習內容進行工作分析，製作卡片以傳達該時段之活動順序與內容，卡片以文字為主，可兼採用圖片或數字，依順序由左而右或由上而下放置於獨立學習桌上學生依卡片排列順序獨自學習或部分時間由教師引導學習。個別工作結構目的在有效的獨自學習之外，最重要的是讓自閉症幼童從個別結構中學到「完成」的概念。此概念是自閉症者所欠缺的，並因有此「完成」的概念，使自閉症者了解有多少工作需完成及如何完成。（d）視覺結構：自閉症者缺乏傳送刺激的能力，因此對外界的口語溝通訊息格式的整體思考，並加上心智理論的缺陷，使其不易認知他人的意圖、願望、信念，更由於缺乏後社表徵能力，使自閉症者無法立即反應他人的對話內容。有鑑於此缺陷，結構性教學本身即充分應用自閉症者不自覺的凝視外界轉動的事物或同時出現手足不斷拍動的自我刺激行為之特徵，重新加以結構性，透過視覺組織學習新的事物（曹純瓊，1998；中華民國自閉症總會，2003）。綜觀以上所述，我們著手研究與發展自閉症兒童的教育甚至於治療，都是預期未來對他們有更多的了解以及提供他們更多的教育機會。四、自閉症者的思考能力自閉症者的行為有一些特徵，其思考能力也有一些特殊的地方現分述如下：

(22)

1、欠缺概念意義自閉症者最根本的問題是個人思考特性欠缺在經驗中歸納意義的能力。他們可以在環境中作出行動、學習不同技巧，甚至有些更可學到應用語言，但卻欠缺能力明白活動的意義，他們不明白事件和事件間的關係。他們的世界中只包含一連串無關的經驗，事件背後的主題、概念、原因、原則，對他們來說是不清晰的，這嚴重的缺損可能與其他認知上的缺損有關。 2、過分集中於瑣碎事、對分辨優先處理瑣碎事情的能力有限自閉症兒童常精於觀察瑣碎事，尤其是視覺上，他們能察覺環境中的物件曾移動過，留意細小的碎垃圾而拾起它；拉起一些線頭；撕剝落的油漆；數算天花板磚塊等。有些亦會專注感官上碎事，例如：風扇、機器的聲音。智商較高的自閉症者是更會專注於認知瑣碎事，例如：電台號碼、國家的首都、區域電話代碼等。要評估這些瑣碎事有無重要性，他們的能力會較弱。他們有可能在橫過馬路時，因專注望著手中懸垂的線而疏忽了將要駛至的巴士，或當他們專注於房中的風扇聲音而忘卻前面的午餐。 3、分心自閉症者因專注於感興趣的感覺上，而忽略老師的授課，更甚的他們很容易把注意力從一個感覺轉移到另一感覺上，能力較低的自閉症兒童其分心源頭多在視覺上，例如一位老師放一支筆在桌上，他們會專注此筆而不再聽教於老師，或有兒童因記掛望著門外的事物而分心，停止他手上的工作。聽覺上的刺激也導致他們分心，一位自閉症兒童會因距離有五間房遠的聲音（老師是聽不到的）而分心於學習。另一些自閉症兒童會因內在產生的刺激而分心，例如：以往渴望的貼紙、線、杯或其他物件等；又或會為曾認識過而記憶起的韻律、數算、背誦事而分心。自閉症者很困難的去解釋或優先處理外來的刺激。他們經常凝視、移動、探索，由如所有感覺刺激都很新鮮和令人興奮的。另一些自閉症兒童對環繞他們的刺激關閉起自己，而將注意力集中於少量事物上。

(23)

4、具體思考

無論認知能力如何，撇除了認知層面上的困難，自閉症者面對抽象、象徵語言的困難更多於一些平鋪直述的事件或描述。在自閉症兒童的文化中，文字只代表一件事而沒有任何額外的含意或聯想。一位十歲擁有一般智商的自閉症兒童，當被問及「早起的鳥兒捉到蟲」（the early bird catches the worm）的意義時他會答道：「如果鳥兒早些起來，牠便能看見一條蟲和捉了牠，並且吃了牠，跟著可再捉另一條。」他們不明白這諺語在說：「早起的人會更成功」；另一個例子，當被問及「不要為倒瀉的奶而哭泣」（do not cry over spilled milk）的意義時，他會答道：「如你倒瀉杯奶，你不要哭，但你應取一塊抹布抹乾它，然後洗淨這塊布後再去另一些奶來飲。」他不明白這諺語在說：「不要為不能彌補的事而悲傷。」 5、串聯、融匯意念的困難自閉症者易於理解個人的事或概念多過將概念有關的資料融匯在一起，尤其當這些概念間看似互相矛盾時。舉例說：有一個自閉症者定時去一營舍，名「山茱萸營」（Camp Dogwood）大多數人都選擇在秋天或初春去宿營，而較少在四月當茱萸開花的時候。這自閉症者每次到「山茱萸營」的時候，他必表達想見到山茱萸開花。最後，他的團友於四月再去「山茱萸營」，管理營地的女士知道他等開花已等了很久，所以將一些營內開著的花放在它的碟上，好讓他在早餐時見到這些花。這自閉症者見到這些花即取起來，直奔至廚房找那營地舍監，似乎要向她道謝，但實際上他教訓了她一頓，應如何保護大自然（因他是環保會社的會員）和不應該採摘花朵。當該舍監解釋她摘下這些花是希望用以表達對他的關懷，該自閉症者仍堅持的說如果她是一位好人的話就不應破壞環境，因此他直斥她也是為她好。這自閉症者不明白為何這兩個矛盾的概念都是好的（保護環境的好人和一位摘花的好人）。 6、組織和排列的困難將多項資料融合的困難正是組織和排列要面對的問題。組織要求將不同元素匯合已達到預定的目的。例如：當一個人計畫去旅行時，他須估計旅程上所需物

(24)

品，並在出發前將所需物件放入行李箱內；另一例子，當要完成一項任務前，我們必須收集達成任務的所需物料。但組織技巧對自閉症者來說相當困難，因他們必須同時專注目前的工作和預期應有的效果。這雙重的要求對著重具體細節的自閉症者來說是難以做得好的。序列對自閉症者來說亦是困難，因它要求同樣的技巧，有時候，他們的一連串行為是缺乏邏輯的及非建設的，舉例說，有某自閉症者早上起來，先會梳頭、再洗澡和洗頭；又某自閉症者吃午餐時，他取二片麵包，然後將一塊肉放在二塊麵包上面，而不是將該塊肉放在二片麵包中間；有時候，他們更會先穿鞋後穿襪。從上述例子，我們可看到他們掌握這些次序是多麼困難。由此可見，他們雖掌握個別步驟，卻不明白個別步驟間的關係。 7、歸納的困難自閉症者很難將某情景中學習到的技巧歸納至不同的情景上。舉例說，他學習用綠色的牙刷去刷牙後，會不願意用藍色的牙刷去刷牙；他學習洗碟的步驟後，卻不懂將此應用於洗杯上；他們學了一些規則的表面意義，卻不明字面背後蘊藏的意義，所以他們很難將規則應用在不同的環境。再舉例：一個智力很高的自閉症青年，他每天很早便到達工作的大廈及如常地更換工作服，有人告訴他雖然大廈未正式開門，但仍會有很多人在那裡做準備的工作，那些人不希望他在他們面前換工作服，表面上他明白了，第二天他開始工作時，他先在外面停車場內換工作服，在那裡有很多人經過，他實際上不明白別人勸告背後的意義。 8、強烈的衝動、過多的憂慮、感官和知覺的理解力不正常除認知上的缺陷外，自閉症者還有一些生理上的特徵。（1）強烈的衝動：自閉症者時常固執得追求他想要的事物。不論這些是最愛的物件、經驗、甚至感覺如觸摸一些物件、完成一些繁複的行為模式，這些強迫性行為特徵很相似，家長和老師們都很難將它們分散或控制。這些行為似乎不受自閉症者本身的控制，如要控制他們這些行為真是一項最大的挑戰。（2）過多憂慮：很多自閉症者容易有過高的憂慮，他們經常在憂心或在憂心的

(25)

邊緣徘徊，有些憂慮可能和生理因素有關，再者，憂慮可能產生於未能預知的事物。由於認知的缺陷，他們常不明白別人對他們的期望，以及週遭發生的事，憂慮和暴躁是可理解的反應，尤其要面對很多不肯定的因素。（3）感知的能力不正常：自閉症者的感覺系統已被知道很多年，他們當中有些對食物有特別的偏好；有些消磨他們的時間去彈手指、用纖維物質去摩擦面頰，；又或將耳朵貼進一些不尋常的聲音，以便能感受到聲音的震動。我們知道自閉症者對聲音的反應與一般人不同，有人以為他們是聾的，而事實上他們的聽覺非常敏銳，有些自閉症者似乎不能分別被打和被搔癢的感覺；有些則似乎沒有痛的感覺；有些會向後或向前搖動個多小時，從各方面來看，自閉症者間的差異，始於他們如何處理每時每刻環境加諸他們身上的感覺。（www.teach.com，周慧玲譯）

自閉症也被稱為「早期幼兒自閉症 early infantile autism」，或「兒童自閉症 childhood autism」，「卡那氏自閉症 Kanner`s autism」和廣泛性發展障礙「pervasive developmental disorder」。

第二節幾何概念

本節先說明一般「概念」的意義，再對幾何與圖形概念及我國國小課程中平面圖形的幾何概念作敘述及探討。

一、何謂概念

什麼是「概念」呢？在 1971 年 Webster 大辭典中有 concept 及 conception 兩種表示方式，concept 只對一連串特殊事例思考過後，所形成的概念；而 Conception 則強調想像的過程或概念形成的過程。

有些專家或研究者對「概念」有不同的說法，例如：心理學家於 Richard R. Skemp 於 1987 年出版的 The Psychology of Learning Mathematics

提到透過分類來說明概念的形成：在較低層次的知覺中，每次將所知覺到的事物做分類，雖然從事物那裡所得到的知覺很少有完全一樣的，但是當這些知覺被

(26)

發現有著相似性，則人類會自然的從這些事物當中抽出這種相似性。接著將抽出的知覺的相似性由抽象而得到的性質，由這些性質再去抽象出更多的共同性質，最後給于這共同的性質就是所謂的概念（陳澤民譯，1995）。因此要形成一個概念就必須先有實際經驗，而這些經驗又有某些相似性、共通性。概念以心理學觀點來看是思惟形式之ㄧ。它反映客觀事物本質的一種理性知識，人類在認知過程中，把所感知的事物共同特點抽象出來，加以概括就成為概念（王明良，1982）。概念以教育的觀點來看是人類思考的一種形式。但是概念並不是一成不變的，隨著社會歷史的發展，有些概念的內涵也不時的都在發展著，並經歷著不斷的變化。概念具有外延和內涵兩個方面。例如：樹的概念的外延是指所有各種不同的樹；樹的內涵包括樹有樹葉和樹是植物等。不同時空、不同身份的人對同一概念都可能有不同的認知。因此，其意義必需是其所使用的脈絡位置才能決定（顏慶祥，湯維玲，1994）。概念是人類思考和了解的工具，也是學習的基本單位，亦即經由有意義的學習而獲得的概念，使得人類能夠具有深入思考的能力（黃台珠，1984）。概念是對具有共同屬性事物的概括性認識。概念分為兩類，一類是具體概念：指示物的共同屬性具體顯現者。如形狀（三角形、長方形）、顏色（藍色、黃色）；第二類是定義概念：它不能用指認的方式來學習的抽象概念，如秩序、悲傷、高興等（張春興，1994）。因此，由於探討研究的角度不同，各學科領域對概念的定義就可能有所偏差，以數學概念來說，學生所要學習的概念是具有共通屬性的科學概念，利用教學中提供足夠的例子，使學生從知覺經驗中將其共通屬性抽離出來，加以概括形成。所以概念是透過有意義的了解與學習，對學生思考能力才有幫助。 二、圖形的幾何概念 數學領域中探討空間關係的學問就是幾何。幾何概念與表徵是數學與真實世界溝通的重要方式，並與數學其他領域緊密連結（左台益，2001）。

(27)

幾何學主要探討的對象為物體之結構和形狀之特性及變化（劉好，1998）。人類生存於世界便需要認識世界的種種性質，人們透過知覺運動與世界互動中，發現有些東西是可以滾、有些是可以堆疊，就加以分析歸納，而分別出平的和曲的兩種屬性，形成平面與曲面的概念（劉秋木，1996）。此外，美國數學教師協會也提出：幾何乃研究空間中的形狀和空間關係，幾何可幫助人們用有條理的方式表現和描述生活的世界（NCTM，1991）。人類依這種探索分析出許多有用的屬性：例如形狀、大小等等。依據這些屬性，幾何學家建立了幾何學問。這些都是對幾何學的一些說明描述，儘管表面敘述形式不同，可是都是強調幾何就是在研究空間中物體的變化和彼此之間的關係，所以內涵都是一樣的。舒茲等人曾指出幾何圖形與物體皆具有其「特質」，如分離性、次序性、包圍性、接近性、空間度數、直或彎、大小尺寸、形狀（面數、點數、線段數、邊數）、位置、方向（上、下、左、右）等（Schultz，Clarusso＆Strawderman，1989）。當圖形或物體以某種方式改變或變化而造成特質隨之改變或變化，這在數學上稱為變形轉換（transformation）。與幾何有關的三種的變形轉換有一、歐幾里德幾何（Euclidean Geometry）：是討論圖形的翻轉、移位及旋轉的特性；二、投影幾何（Projective Geometry）：是討論因不同視覺觀點而產生的特性；三、拓樸幾何（Topological Geometry）：是討論拉扯與壓縮轉換的特徵。在兒童幾何概念的萌發依兒童的學習發展是遵循：拓樸幾何最早建構，再來才是投影幾何與歐幾里德幾何的順序（Paiget，1953；Piaget＆Inhelder，1967；Smock，1976）。但歷史上的幾何發明卻是歐幾里德幾何最先，再來是十七世紀的投影幾何及十九世紀的拓樸幾何。完全是相反的順序。另外劉好（1998）在幾何圖形概念曾有以下說明：圖形並非是實際存在的東西，他是附著於具體存在的物體上，從具體實物中捨棄其顏色、氣味、輕重、大小、硬度等特性的抽象結果。換句話說，他僅是實物外觀的樣子。一般人最常接觸的是立體圖形，而平面圖形是將具體實物的表面拓印出來的結果，常透過立體圖形的面來辨識。一個實物皆可能存在顏色、大小、圖案、擺放的位置、形狀、輕重等等。當中的顏色、大小、圖案等，都可以用肉眼具體明確

(28)

觀察，只有物體的「形狀」對兒童來講是較為抽象，他必須去除這物體各種不相干的屬性，不因物體的大小、顏色或擺放的位置而改變它。由上述的幾何與圖形的概念可了解，幾何與日常生活是息息相關的，在建立空間的概念與圖形間的察覺和辨識時，發現性質與關係是有相互關聯的。 三、國小課程中平面圖形與其相關的幾何概念 檢視我國的數學課程發展，在民國六十四年以前的數學課程，以數、計算、與實測三部份為教材中心的課程結構，而關於幾何部份則分散在計算與實測兩個部分中，並未有規劃獨立的教學單元（教育部，1968）；到民國六十四年修訂的數學課程，將教材內容劃分為數、量、形三個領域，幾何領域的教學才開始受到重視（教育部，1975）。而後在民國八十二年國民小學數學課程標準修改的數學課程，將數學科分為數與計算、量與實測、圖形與空間、統計圖表、數量關係、術語與符號六個領域。其中更將幾何領域的教學以「圖形與空間」規畫獨立為一個主題，並將教材進一步分為平面幾何、立體幾何兩個部份來進行教學（教育部， 1993）；從民國九十年開始實施的九年一貫課程中，數學的學習領域正式以「幾何」名稱成為一個完整的教學主題；由我國歷年數學課程與教材的沿革發展，可以看出幾何獨特的課程與教材，在整體的數學課程中，佔有一席重要的地位（教育部，2003）。自民國八十二年教育部公佈實施國民小學數學課程起，一直到現階段我國實施中的九年一貫課程，有關於數學領域的幾何主題教材，主要依據 van Hiele 夫婦所發展的幾何思考模式與層次理論來編寫（朱建正，1996、吳德邦，1997）；依據這個理論，第一階段（小學一年級到三年級）幾何概念的學習，著重在對於幾何形體的探索、認識與具體操作；第二階段（小學四年級到五年級），重點則在於掌握幾何形體構成的要素，進行形體的分類、認識不同平面圖形的性質，以及全等、對稱的關係等，另外與數、量相關的幾何量（包括角度、邊長、面積），則逐步成為另一個教學重點；而到第三階段（小學六年級到國中一年級）的學習，則以透過形體的分割、拼合、截補等變換操作，更進一步了解形體的性質及非形

(29)

式化的推理（教育部，2003）；在每個階段的學習歷程，因為學童的幾何認知發展狀況不同，而造成學童個別不同的知識架構，一般研究經常以「另有架構」或者是「迷思概念」稱之，關於此一部份的研究，歷來多以陳述不同類型的「迷思概念」為主，並已有相當詳盡的資料（沈佩芳，2002；高耀琮，2002；郭育宓， 2002），然而檢視大部份的研究資料均顯示：部分研究偏重在以成人（教師）的角度思考，而非以兒童本位的立場看待兒童本身的認知發展，對於兒童在學習幾何知識的認知發展的演化歷程更鮮少被論及；究竟兒童形成「迷思概念」的成因為何，以及如何幫助不同發展類型的兒童學習幾何教材，還尚待更進一步的釐清與研究。依據我國九年一貫課程綱要對五大主題幾何部份的說明指出（2005，教育部）：圖形與空間的了解可分為知覺性的了解、操弄性的了解、構圖性的了解、論述性的了解；所以小學階段的幾何教學應可參考幾何歷史發展的軌跡，從應用、操作、實踐中認識各種幾何要素與性質，同時考量兒童認之發展階段，拓展兒童的幾何直覺，讓兒童由具備充足的操弄經驗，以認識各種幾何形體與性質，再加入簡單的推理性質與各種形體間的關係，以銜接國中幾何課程的教學。九年一貫課程綱要所提到的對圖形與空間的四個了解，主要依據 Duval 對幾何圖形了解的認知理論；Duval（1995）提出四個了解的幾何圖形認知理論，是以 123 位 14 歲的學童（約為我國國中二年級學生）為研究對象測試所得結果，而國內以 Duval 理論所進行的研究，目前所見文獻也多以國高中生階段的學生為研究對象（左台益，2003；陳創義，2003），以國小學童為研究對象尚不多見。身心障礙兒童為對象的研究更是少見。但在民國九十三教育部「特殊教育法」（2004）其中第一條即開宗明義「為使身心障礙及資賦優異之國民，均有接受適性教育之權利，充分發展身心潛能，培養健全人格，增進服務社會能力，特制定本法；本法未規定者，依其他有關法律之規定。」以及「身心障礙者保護法」（內政部，1997）之第三章－教育權益內容中也明定「各級政府應規劃設立特殊教育學校、特殊教

(30)

育班或以其他方式教育不能就讀於普通學校或普通班級之身心障礙者，以維護其受教育之權益」。與本研究有關係的課程為九十學年度開始實施的九年一貫課程暫行綱要及九十二年頒布的九年一貫課程正式綱要。其中所包函的平面圖形及相關的幾何概念，分別說明如下：（一）九年一貫課程暫行綱要數學領域在小學部分是第一階段至第三階段，下表 2-1-1 是有關平面圖形與空間形體的能力指標（教育部，2000）。表 2-1-1 九年一貫暫行綱要國小部分平面圖形與空間形體的能力指標能力指標代號內容 S-1-1 能由物體的外觀，辨認、描述與分類簡單幾何形體。 S-1-2 能描繪或仿製簡單幾何形體。 S-1-3 能認識周遭物體的角、直線和平面。 S-1-4 能認識平面圖中的內部、外部及其周角。 S-1-5 能透過操作，將簡單圖形切割重組成另一以之簡單圖形。 S-1-6 能描述物體的相對位置。 S-1-7 能認識生活周遭中水平、鉛直、平行與垂直的現象。 S-2-1 能運用簡單幾何形體的組成要素，作不同形體的分類。 S-2-2 能理解垂直與平行的意義。 S-2-3 能透過操作，認識簡單平面圖形的性質。 S-2-4 能認識平面圖形全等的意義。 S-2-5 能理解旋轉角的意義。 S-2-6 能理解平面圖形的線對稱關係。 S-2-7 能理解長方形面積、周長與長方體體積的公式。（N-2-17）

(31)

表 2-1-1 九年一貫暫行綱要國小部分平面圖形與空間形體的能力指標（續） S-2-8 能運用切割重組，理解三角形、平行四邊形與梯形的面積公式。（N-2-19） S-3-1 能利用幾何形體的性質解決簡單的幾何問題。 S-3-2 能認識平面圖形放大、縮小對長度、角度與面積的影響，並認識比例尺。（N-3-15） S-3-3 能以適當的正方形單位，對曲線圍成的平面區域估算其面積。 S-3-4 能理解圓面積與圓周長的公式，並估算簡單扇形面積。（N-3-16） S-3-5 能認識直圓錐、直圓柱與直角柱。 S-3-6 能理解簡單直立柱體的體積為底面積與高的乘積。（N-3-17）從表 2-1-1 的圖形與空間的能力指標中，小學各階段所要學習的平面概念與性質為：第一階段（一~三年級）的內容是：能辨認及描述正方形、長方形、三角形圓形的外觀、角、鉛垂線、水平線、水平面、直線、平面、圖形的內部、外部、周界及平面舖設；能運用方位語詞描述相對位置。第二階段（四~五年級）的內容是：三角形、四邊形及圓形的構成要素名稱；構成要素間的關係、性質；兩形體的比較；能描述位置及方向；了解平行、垂直、角度；量角器的使用及線對稱圖形的辨識。第三階段（六年級）的內容是：形體性質的描述，圖形間的關係與運用，了解平面上兩直線互相平行、垂直的概念。（二）九年一貫課程正式綱要數學領域在小學部分是第一階段至第三階段。除了將暫綱中「圖形與空間」的主題改為「幾何」主題之外，也有部分內容加以修訂。下表 2-1-2 是正綱有關國小部分「能力」主題能力指標（教育部，2003）。

(32)

表 2-1-2 九年一貫正式綱要國小部分幾何的能力指標能力指標代號內容 S-1-1 能由物體的外觀，辨認、描述與分類簡單幾何形體。 S-1-2 能描繪或仿製簡單幾何形體。 S-1-3 能認識周遭物體的角、直線和平面。 S-1-4 能認識平面圖中的內部、外部及其周角。 S-1-5 能透過操作，將簡單圖形切割重組成另一以之簡單圖形。 S-1-6 能描述物體的相對位置。 S-1-7 能認識生活周遭中水平、鉛直、平行與垂直的現象。 S-2-1 能運用簡單幾何形體的組成要素，作不同形體的分類。 S-2-2 能理解垂直與平行的意義。 S-2-3 能透過操作，認識簡單平面圖形的性質。 S-2-4 能認識平面圖形全等的意義。 S-2-5 能理解旋轉角的意義。 S-2-6 能理解平面圖形的線對稱關係。 S-2-7 能理解長方形面積、周長與長方體體積的公式。（N-2-17） S-2-8 能運用切割重組，理解三角形、平行四邊形與梯形的面積公式。（N-2-19） S-3-1 能利用幾何形體的性質解決簡單的幾何問題。 S-3-2 能認識平面圖形放大、縮小對長度、角度與面積的影響，並認識比例尺。（N-3-15） S-3-3 能以適當的正方形單位，對曲線圍成的平面區域估算其面積。 S-3-4 能理解圓面積與圓周長的公式，並估算簡單扇形面積。（N-3-16） S-3-5 能認識直圓錐、直圓柱與直角柱。

(33)

表 2-1-2 九年一貫正式綱要國小部分幾何的能力指標（續） S-3-6 能理解簡單直立柱體的體積為底面積與高的乘積。（N-3-17）從表 2-1-2 的幾何能力指標中發現角度、邊長、面積等的幾何形體數量性質內容也放入幾何的主題，現在只對國小應學部分的平面圖形與性質做個整理：第一階段（一~三年級）的內容是：能分類、仿製簡單幾何圖形；能認識角、直線、平面及平面圖形的內外部及其周界；能將簡單圖形切割重組成另一簡單圖形；描述相對位置。第二階段（四~五年級）的內容是：能運用組成要素做不同形體的分類；能理解垂直與平行、旋轉角、平面圖形全等、線對稱關係及長方形面積周長與長方體體積公式；能運用切割重組理解其它平面圖形的面積公式。第三階段（六年級）的內容是：能認識比例尺，平面圖形放大與縮小對長度、角度、面積的影響，直圓錐、直圓柱及直角柱；能利用幾何形體的性質解決簡單的幾何問題；能理解圓面積、圓周長及直立柱體體積的公式並計算扇形面積。從上述中我們可以知道正式綱要的「幾何」主題能力指標比暫行綱要的「圖形與空間」能力指標的內容增加了圓心角、扇形、放大與縮小圖、比例尺等。而比較兩個不同時期教材綱要的編排順序，了解其共通點就是都注意到學童幾何思考的發展，並提供多樣化的操作經驗，進而探索形體的性質與關係，依具體到抽象的順序，並重視課程的連貫性。本研究對象的四年級自閉症學生都是接受九年一貫暫行綱要數學領域的課程，從表 2-1-1 九年一貫暫行綱要數學領域課程中可以了解在第一階段（一~三年級）已經能從平面、立體的基本形體外觀做簡單分類並能辨認平面圖形的內部、外部及其周界，其中包括三角形、長方形、圓形。第二階段（四~五年級）能從給定的幾何圖形確認並說出組成要素名稱，也能依基本形體組成要素之間的關係來比較形體的不同。所以研究對象雖然是接受暫行綱要的課程，但是其幾何形體的基本知識並無落差。並沒有因

(34)

為是暫行綱要的課程而有所遺漏或不足。歸納九年一貫暫行綱要或正式綱要的數學領域課程在小學階段其平面圖形概念與性質可以看出，在內容與編排順序大致相同，都是從平面圖形的外觀作辨識，再進一步探討各類圖形組成要素及其關係，了解各類形體的性質，最後理解並對幾何問題加以解決與運用。 四、迷思概念 概念形成的過程，也就是抽象形成的過程，我們稱作是抽象化（abstracting）抽象化是一種心智活動的過程，他使我們了解周圍環境各種經驗間的相似性或共通性。如果在抽象化的過程中，發生了類化錯誤的情況，因而導致抽象結果錯誤，我們便稱這個錯誤的抽象為迷思概念（miss concept/misconception）。概念的迷思通常是思考方向的錯誤造成的（陳鉪逸，1997），他可能是由學生自己的思考方向錯誤所造成，但也可能是教師無心的疏忽，使得學生獲得錯誤的資訊所導致的。例如學生常會用長方形的長、寬的總和來比較長方形的面積，Robert（1993）認為這可能是教師在教室中所舉出的長方形的形狀大致都相同，用這些圖形來比較長和寬的總和，常常就可以比較出長方形的面積大小，使學生誤認為這種方法可行，導致了學生利用長寬相加的方法來求面積，這種概念的迷思往往成為學生學習困難的最大原因（引自陳鉪逸，1997） Driver，Guesne＆Tiberghien 於 1985 年提出了一些迷思概念的特徵（引自劉德明，1993）：（一）、迷思概念是個人化的：對於相同的一些事物在抽象時，一群相同的學童會有各種不同的抽象與解釋，聽完一個故事或看完一本書，不同的人也不一定有相同的概念。所以個體都以自己本位、主觀的方式在接受外界刺激後，用自己獨特的方式來將其變成自己的經驗，他們建構屬於自己所認定的意義，使之變成自己的觀念。這些個人的觀念常是各自為政、各自不同的，迷思概念因人而異，因為個人的經驗與生活環境各不相同。（二）、兒童的個別迷思概念可能是不相連貫的：

(35)

兒童還不了解概念前後一致的需要性，他們的概念和老師或是專家的概念不一定一樣的，例如：對於三角形圖形（以三角形、正三角形、等腰三角形、直角三角形）為例的概念，對三角形圖形達到成熟的人知道這些三角形，並且知道這些三角形之間的關係（像正三角形是等腰三角形、直角形也可以有等腰直角三角形等等）；對於三角形圖形思考未達一定水準的兒童而言，可能未具有三角形的基本圖形完全辨別的能力，可是這並不代表他們不會辨別其他特殊的三角形，如正三角形、等腰三角形、直角三角形等等。（三）兒童的迷思概念是穩定的：兒童的迷思概念，常是穩定的存在他的概念裡，甚至於在重新經歷經驗，有機會澄清迷思概念後，兒童仍不是很容易的修正它。例如：學童認為「等腰三角形恰有兩個角相等」是正確的，對於「等腰三角形至少有兩個角相等」的真正正確的概念卻是遲遲不于認同，這樣的學生大有人在。在經過錯誤概念的澄清機會後，學童們仍舊不能如願的去修正他們的迷思，如同他們常忽略正三角形也是等腰三角形的一種是一樣的頑固。在過去一些研究中指出，國小學童在幾何思考上常產生一些迷思的錯誤概念有：（1）、學生會認為規則的圖形才有面積，學生覺得像不規則的圖形是沒有面積的，在學生的觀念中要長得像或是像規規矩矩的圖形才是有面積的（陳鉪逸，1997）。（2）、學生通常不太會辨別封閉圖形陳鉪逸（1997）指出：學生會認為像的圖形是一個封閉的圖形，所以學生會覺得這樣的一個圖形也可以求面積。而用長寬相加來求面積的錯誤概念也在學生中經常發現，Robert（1993）認為這可能是教師在教室中所舉出的長方形的形狀大致都相同，用這些圖形來比較長和寬的總和，常常就可以比較出長方形的面積大小，使學生誤認為這種方法可行，導致了學生利用長寬相加的方法來求面積，這種概念的迷思往往成為學生學習困難的最大原因（引自陳鉪逸，1997）。

(36)

（3）、對於圖形的底和高，學生也常有迷思概念出現，有些學生認為三角形底一定是水平的線段，因此在圖形經過旋轉後，學生認不出底邊，而使得計算面積的過程上出了問題。甚至於有些學生會覺得圖形中最接近水平的那個邊在水平線上的投影長就是底，而有些學生認為高一定是鉛錘的線段，因此在圖形經過旋轉後，學生找不到高，而使得在計算面積上無法完成任務；在三角形中，學生會認為中線就是高，或是隨便畫一條直線當作高；也有學生也會認為高只有一個，就是通過頂點的那一個（陳鉪逸，1997）。也有學者在訪談實例中發現學生常常找不到圖形中適當的底和高（譚寧君，1998）。（4）、學生仍會以視覺或數數為主，無法了解圖形切割變形後，面積仍然不會改變的事實（譚寧君，1998）。（5）、學童認為正方形不是長方形的一種更是一種常見的現象，林軍治（1992）指出若干國小學生認為正方形不是長方形的一種。上述的迷思概念大多和教師教學時的畫圖方式及位置、或是講解時的方法、用詞有關，少部分和學生的認知結構、理解方式有關，所以教師的教學會影響學生的學習，老師能不謹慎嗎？

第三節有關幾何概念發展的理論

兒童幾何概念之發展，依據 Clement 和 Battista（1992）的分析，指出有：皮亞傑（Piaget）理論、van Hiele 理論。此外九年一貫課程正式綱要也提到的 Duval 幾何圖形認知理論，因此本節將針對這三種理論加以探討。 一、皮亞傑的認知發展理論 瑞士心理學家皮亞傑（Piaget，1896-1980）對兒童的學習發展研究的貢獻最為卓越。他認為兒童的認知是由四個階段來發展，這四個階段是：1、感覺動作期（出生到兩歲）：以反射性動作為基礎發展複雜的行為，兒童的身體與物體的互動提供發展的動力；2、前運思期（兩歲到六或七歲）：透過表徵（心象、語言、

(37)

繪畫）來解決問題，思考和語言均以自我為中心，不能適切的表徵轉換，而只能表徵靜止情境；3、具體運思期（六或七歲到十一或十二歲）：具反推能力，能正確的表徵轉換及靜止情境，對於守恆概念較能理解，但無法將所有合乎邏輯的可能性都考慮清楚，無法了解高度抽象概念；4、形式運思期（十一或十二歲以上）：以邏輯解決各類問題，能合乎科學的思考，在理論的考慮下設計實驗，並在邏輯的架構下加以解釋。依皮亞傑的想法，孩子的認知發展須依順序經過上述四個階段，無法跳過任一階段，只是有些孩子認知發展快，有些可能會在某一階段停留較久，但是認知發展的順序是不會變的。皮亞傑的理論可以歸納如下：人們為了配合環境的需求，會在環境中積極求取新的、有用的訊息來自我修正，並在學習過程中將舊知識組織起來，成為一個整體。而新知識的學習是建立在舊知識基礎上，所以要成為知識體系的一部分，必須新、舊知識融合，因此不正確的舊知識會影響新知識的吸收，也會讓人對新知識產生誤解。因為認知發展有階段性，在不同的時候會有不同訊息需求的種類和了解層次的變化。皮亞傑的認知理論可說明兒童的學習是有階段性、有順序性的，而且和年齡有關，也和幾何概念發展有關聯。（一）、Piaget 的幾何概念皮亞傑等人（Piaget，Inhelder＆Szeminska，1960；Piaget＆Inhelder，1967）研究兒童幾何概念發展，認為兒童認知幾何性質隨著年齡的增長對於空間知覺能力有下列漸進之分化：（1）拓樸性（topological）：幾何形體整體性質，如聯通性、封閉性和連續性等，和大小形狀無關；（2）射影性（projective）：由不同角度觀看物體的臆測；（3）歐幾里德性（Euclidean）：考慮物體的大小距離及方向，涉及角度、平行和長度等。児童空間幾何概念的形成經歷上述三個階段，在 3~4 歲時為拓樸幾何概念，依據圖形是否封閉或開放而定，完全忽視有關邊長、角度、大小等歐氏幾何關係，完全是屬於基本拓樸幾何概念。約 4~6 歲為過度時期是投影性空間概念，一直到 6~8 歲才有歐氏幾何概念。現將這三種幾何體系敘述如下（Piaget，1967；吳貞祥，1990；劉秋木，1996）：

(38)

1、拓樸學概念階段（3~4 歲）：此一階段的兒童與運思前期認知發展階段有關，只能注意圖形的內或外的拓樸學圖形概念，對於直線與曲線，還未具有嚴格區分的能力。對於角度或長度的差異也不能做詳細觀察。例如要求兒童複製長方形或正方形，常常會畫成各邊凹凸不直或劃成接近圓的形狀。另外兒童對左右位置的變換也比較不清楚，他們能感覺左右或曲直的不同，只是在認知上無法了解構成左右或曲直的差異因素罷了。児童只能從接近、分離、包圍、連續、順序等觀點來考慮事物的性質。例如：圓或四邊形都是一個連續簡單封閉圖形，可是這階段的兒童卻不能區分兩者的不同。他們對於物體的角度、形狀、大小等要素都不會留意。 2、投影幾何學概念階段（約 4~6 歲）：此一階段的兒童約相當於運思前期到具體運思期認知發展階段。Piaget 和 Inhelder（1967）認為這個階段的兒童對外界的認知，是以自己本身所在觀點的視覺比其他條件都來的重要，只要是視覺所承認的事物才認為是真實的存在，而在視覺之外的事物都不真實，因為他們深信各種形狀都會照著視覺的感受而變化。例如：教室內排整齊的課桌椅，會覺得近處排的較寬，而遠處排的較窄；或是一張正方形的色紙，將它放在較遠的地方，兒童的心目中會認為變成菱形或長方形，而且也變小。如果又放回原處兒童會認為形狀、大小會回復到原來的樣子。這種因為距離越遠使得平行線變的越窄或是同一物體變的較小甚至形狀改變的情形，對兒童來說是認為真的變窄或形狀真的變小。總而言之，這階段的兒童對界的認知，都以視覺為主，深信形或量都會照著視覺的感覺而變化。 3、歐幾里德幾何學階段（6~8 到 11~12 歲）：歐幾里德幾何學和距離、角度、直線、平行線等的保守量有關，以歐幾里德幾何學的概念建構來說，長度保留不變性質與距離保留不變性質二者是最為基本的。兒童獲得長度與距離保留概念，特別是長度保留概念之後，就自然能發展出測量的概念。児童最早是以本身最熟悉、最靠近自己的工具（自己的手或軀幹）

(39)

來測量，皮亞傑稱這種策略為「手的遷移」及「軀幹遷移」；之後隨著認知的發展，兒童漸漸會用量尺工具來輔助測量，另外，面積保留觀念也大概在本階段發展。小學階段兒童的圖形概念大部分都發展到歐幾里德幾何學概念階段，因此依皮亞傑的說法本階段的兒童應該都具備有線段長短、角度大小或面的大小等的意識。由此可知，皮亞傑理論的重點在於兒童發展幾何概念的思考模式，探討幾何概念形成的運思程序，由最初的拓樸關係到投影再到歐幾里德關係，是年齡取向的階段論，注重發展的過程。 三、van Hiele 幾何思考層次 荷蘭數學家 van Hiele 夫婦，根據完形心理學的結構論，以及皮亞傑的認知理論，在 1957 年提出幾何思考的發展模式包含了五個層次，對於這五個層次國內外有學者有不一樣的說法，一部份學者使用層次零到層次四（譚寧君，1993；劉湘川，1994；劉好，1998），一部份學者則用層次一到層次五（van Hiele，1986；吳德邦，1998）來表示這五種幾何思考層次。甚至 van Hiele 本人在不同年代也有不同的說法，本研究中對層次的說法，一律採用 van Hiele 在 1986 年其最近作品的說法，使用層次一到層次五的說法，並綜合各學者的敘述（譚寧君，1993；劉好，1998；吳德邦，1999），現將這五個層次分述如下：層次一（Level 1）：視覺的層次（visualization）這個層次是視覺層次，此層次的兒童是藉由視覺觀察圖形整體的輪廓，可以分辨圖形的形狀、複製給定的圖形，但無法分析圖形的性質，也不知道圖形的真實意義。例如：像門的形狀是長方形，像盤子的是圓形，正方形是方方的。雖然知道形狀是「長方形」、「圓形」、「正方形」，可是並不能了解真正意義，而且將正方形擺成斜的兒童就認為不是正方形，也不清楚正方形和長方形都有四個直角或對邊是平行。此階段兒童的思考推理受視覺外觀影響很大。層次二（Level 2）：描述的層次（descriptive）這個層次的兒童具有辨別圖形特徵的能力。兒童可依據圖形構成的要素發現

(40)

圖形共有的性質或規則，但無法說明這些圖形之間的關係。例如：能察覺長方形有四個邊、四個直角，而且有兩個長邊，兩個短邊，對邊相等，但無法了解長方形、菱形、正方形之間的關係，此階段的兒童無法推理出邊長不相等時，面積可能相等的關係。

層次三（Level 3）：非形式化演繹的層次（informal deduction level）

這個層次的兒童除了能夠了解、掌握、運用各種圖形的構成要素，並且能夠進一步探究各種幾何圖形的內在屬性以及各圖形間的包含關係，但不能夠了解整體定義或公設，也無法用演繹推理的方式來證明幾何定理的能力。例如：四邊形的兩雙對邊平行就是平行四邊形，不必將所有屬性均描述出來才能確認其圖形。在了解圖形內在關係後，可以建立平行四邊形中有一個角為直角時此四邊形即為長方形；長方形的長邊和短邊相等時，此四邊形即為正方形；可以知道凸 n 多邊形的內角和為（n-2）180 等概念。

層次四（Level 4）：形式化演繹的層次（formal deduction level）

此層次的兒童可以運用演繹邏輯證明定理，用幾何方式推論所理解幾何圖形的意義，不是只記憶圖形的性質和公式；他們知道幾何圖形的充分必要條件及發現正逆命題間的差異性。例如：對三角形兩邊中點連線平行第三邊，且其長為第三邊的一半的幾何證明問題，能確切說出已知的條件是什麼？要證明的是什麼？並且能用多種方法證明，能運用邏輯推理去思考、分析。

層次五（Level 5）：嚴密的層次（rigor level）

這層次的兒童的學習能了解並比較不同的幾何公設系統，也可了解抽象推理幾何，甚至可自創一種幾何公設系統。一般人很難達到這層屬於最高層次的層次，就算是以數學為專業者也不易達成。在教學上並沒有實用的價值，只是理論上的需要而已，因此不是教學研究的重點。根據 van Hiele 研究顯示，上述五個層次有其順序性，學習者必須具備前一層次的先前知識後，老師才能依據該能力，進行更高層次的教學活動。同時，由於教材內容屬性的差異，會影響學習者落入不同層次中。劉好（1998）的研究指

(41)

出國小低年級學童大都在層次一的階段，中年級學童大概可以達到層次二，高年級的學童大約再層次二到層次三之間的過渡時期。本研究中的研究對象為國小四年級學童，其幾何思考層次應屬於層次二的階段。van Hiele（1986）曾指出：幾何思考層次具有某些固定的特性。Usiskin（1982）將這些思考的層次性質分為固定順序性（Fixed Sequence）、毗連性（Adjacency）、特異性（Distinction）、分離性（Separation）及造詣（Attainment）等。另外 Crowley 也曾將這些思考層次特性定義為序列性（Sequence）、進展（Advancement）、內在和外在（Intrinsic and Extrinsic）、語言（Linguistics）及不協調（Mismatch）等性質。現分述如下（Crowley，1987；譚寧君，1993；Wu，1994） 1、序列性（Sequence）兒童幾何思考層次是循序漸進的，任何一個特定層次如果要能成功發展，他必須先具備前一層次的概念和思維。因此學生不可能已達第二層次而第一層次還未達，或已達第四層次而第三層次還未達。 2、毗連性（Adjacency）在幾何思考層次中，前一個層次的隱藏元素為下一個層次的顯現因素，也就是說某一個層次的內在性質為下一個層次的外在因素。 3、特異性（Distinction） van Hiele（1986）指出每一層次均有其特定的語言符號和這些符號有關聯的網絡。像描述層次的語言是「特性」、「性質」，「定義」則是理論層次的語言，但「公理」就屬於理論的層次。 4、分離性（Separation）不同層次的人彼此間是無法互相溝通、了解的。假如學生是屬於第一層次，而教學設計是另外一個層次，那麼所希望的學習效果就不會發生。敎師尤其是在教學時，對教學的內容、教具的選擇、辭彙的使用若是和學生是不同的層次時，學生是無法理解的。 5、進展性（Advancement）