THE IMPACTS OF VIRTUAL MANIPULATIVES AND
PRIOR KNOWLEDGE ON GEOMETRY LEARNING
PERFORMANCE IN JUNIOR HIGH SCHOOL*
CHUN-YI LEENational Taipei University MING-JANG CHEN National Chiao-Tung University
ABSTRACT
Previous studies on the effects of virtual and physical manipulatives have failed to consider the impact of prior knowledge on the efficacy of manipu-latives. This study focuses on the learning of plane geometry in junior high schools, including the sum of interior angles in polygons, the sum of exterior angles in polygons, and the properties of parallel lines. This study adopted a quasi-experimental design of pre-test and post-tests with nonequivalent groups. The participants comprised four classes in the 8th grade. Students were randomly divided into two groups: the virtual manipulatives group and the physical manipulatives group. Two-way factorial analysis of covariance was adopted to compare the impact of manipulatives (virtual vs. physical) and prior knowledge (high vs. low) on learning outcomes and attitudes toward mathematics. Our results demonstrated that students with high prior knowl-edge using virtual manipulatives had better posttest performance than did the physical manipulatives group, and reported taking greater enjoyment in mathematics. These students also perceived the importance of mathematics more strongly than those with low prior knowledge. Students with high prior knowledge also presented stronger motivation to study mathematics and freedom from fear of the subject than those with low prior knowledge.
*The funding of this study was supported by the National Science Council, Taiwan under grant NSC 101-2511-S-305-001-, NSC 102-2511-S-305-001-, NSC 99-2511-S-009-008-, NSC 100-2511-S-009-006-, and NSC 101-2511-S-009-006-MY2.
179 Ó 2014, Baywood Publishing Co., Inc. doi: http://dx.doi.org/10.2190/EC.50.2.b http://baywood.com
1. INTRODUCTION
Physical manipulatives have long been used in the teaching of mathematics, and ongoing research has investigated the efficacy of this practice. Evidence shows that the proper use of physical manipulatives can enhance performance in exploring mathematical concepts (Parham, 1983; Raphael & Wahlstorm, 1989). Balka (1993) proposed the use of physical manipulatives to link conceptual and procedural knowledge, identify the relationship between various mathe-matical topics, view mathematics from a more integrated perspective, explore problems using physical models, and link mathematical procedural knowledge through equivalent representation. Physical manipulatives are usually pur-chased from a store or fabricated by teachers; however, this can be expensive and time consuming. The use of physical manipulatives also tends to disrupt order in the classroom.
To overcome these problems, Moyer, Bolyard, and Spikell (2002) used virtual manipulatives to represent dynamic objects for the development of mathematical concepts. This type of interactive representation can be accessed online. Virtual manipulatives, rather than being just duplicates of physical manipulatives, often provide additional features or options (Clements & McMillen, 1996; Lindroth, 2005), allowing representations that cannot otherwise be accomplished (Steen, Brooks, & Lyon, 2006).
The use of virtual manipulatives remains a relatively new topic in actual class-room applications (Yuan, Lee, & Wang, 2010). The teaching effects of virtual manipulatives have been examined in the form of isolated projects (Lee & Chen, 2009; Moyer, Niezgoda, & Stanley, 2005; Olkun, 2003; Yuan et al., 2010). The previous results show that students using virtual manipulatives perform equally or better than those using physical manipulatives. Prior knowledge has been also identified as an important factor which affects how instructors and students interact with the learning materials (Lin & Huang, 2013). For example, Rittle-Johnson, Durkin, and Star (2009) found that students need sufficient prior knowledge on knowledge of equation solving before they benefit from comparing alternative solution methods. Does prior knowledge also influence the use of manipulatives? Little is known about the interaction between manipulatives and prior knowledge on students’ learning performance in previous studies.
Geometry is an important part of mathematics curriculum. Geometry thinking includes a strong focus on the development of careful reasoning and proof, using definitions and established facts (NCTM, 2000). Geometry helps students gain basic skills such as analysis, comparison, and generalization and is useful in representing and solving problems in other areas of mathematics and in real-world situations. However, many students develop misconceptions and others fail to go beyond simple visualization of geometric figures (Mistretta, 2000). The van Hieles (1984) noticed the difficulties that their junior high school students had in learning geometry. These observations led them to develop a model to
improve students’ geometric thinking understanding. With the emergence of the van Hiele model, most studies related to geometrical thinking were conducted taking this model as the basis (Breyfogle & Lynch, 2010; Erdogan, Akkaya, & Celebi Akkaya, 2009). We also design our teaching materials using manipu-latives based on the van Hiele instruction model because the teaching tech-niques advocated by the van Hieles allow students to learn geometry by means of hands-on activities.
In Taiwan, virtual manipulatives have not been included in the regular mathe-matical curriculum and the impact of prior knowledge on the effectiveness of these manipulatives in learning mathematics has not been addressed. This study integrated manipulatives into the actual teaching of plane geometry in a junior high school based on van Hiele model. A two-way factorial experimental design was adopted to examine the interaction between manipulatives and prior knowl-edge on learning performance and mathematics attitudes.
2. LITERATURE REVIEW 2.1 Prior Knowledge
Prior knowledge has been identified as a key component to consider when evaluating the effects of learning. Previous studies have found that prior knowl-edge influences how instructors and students interact with the learning materials they encounter (Lin & Huang, 2013; Rittle-Johnson et al., 2009). Kim and Rehder (2011) examined how prior knowledge affects selective attention during category learning. Using eyetracking, they found that prior knowledge indeed changes what features are attended, with knowledge-relevant features being fixed more often than irrelevant ones. This effect was not due to an initial attention bias toward relevant dimensions but rather emerged gradually as a result of observing category members, and this effect grew even after a learning criterion was reached. van Loon, de Bruin, van Gog, and van Merrienboer (2013) investigated whether activation of inaccurate prior knowledge before study contributes to primary-school children’s commission errors and overconfidence in these errors when learning new concepts. Their results indicated that inaccurate prior knowledge affects children’s learning and calibration. The level of children’s judgments of learning for recall responses for which they could not receive credit was inappropriately high after activation of inaccurate prior knowledge. Moreover, when judging the quality of their recall responses on the posttest, children were more overconfident when they had activated inaccurate prior knowledge. Also, the children often discarded concepts from further study after activation of inaccurate prior knowledge. Rittle-Johnson et al. (2009) investigated the impor-tance of prior knowledge in learning from comparison. Two hundred thirty-six 7th- and 8th-grade students learned to solve equations by comparing different solution methods to the same problem, comparing different problem types solved
with the same solution method, or studying the examples sequentially. Their results found that students who did not attempt algebraic methods at pretest benefited most from studying examples sequentially or comparing problem types, rather than comparing solution methods. Students who attempted algebraic methods at pretest learned more from comparing solution methods.
The level of prior knowledge has also been shown to interact with repre-sentation format of the instructional materials, amount and type of direct instruction, and type of practice (Kalyuga, 2007; Rittle-Johnson & Kmicikewycz, 2008). An instructional procedure that is relatively effective for novices becomes ineffective for more knowledgeable learners. For example, novices learn more from studying worked examples than from solving problems unaided. But as knowledge increases, independent problem solving becomes the superior learning activity (Renkl & Atkinson, 2003). Cognitive load theory can help explain why constrained tasks and high levels of instructional guidance are often needed to facilitate learning for novices, rather than more experienced learners (Sweller, Ayres, & Kalyuga, 2011). For novices, tasks can easily overload their working memory, as they must deal with many new elements of information at once. In contrast, learners with some experience in a domain can use their existing knowledge structures to interpret and complete the task without overloading their working memory.
However, fewer prior studies have explicitly examined the interaction between prior knowledge and manipulatives on students’ learning performance. It seems plausible that prior knowledge plays an important role in the utilization of manipulatives. For high prior knowledge students, they may organize and integrate more unfamiliar resources into their learning in the virtual environment compared with the physical environment. Therefore, this study examines the interaction between prior knowledge and manipulatives on students’ learning outcomes and mathematics attitudes.
2.2 The van Hiele Instruction Model
The van Hiele model is commonly applied to the instruction of geometry to students in junior high and elementary schools and has been validated as a useful model to design geometry learning activities. (Breyfogle & Lynch, 2010; Erdogan et al., 2009). This model was developed with classroom activities and consisted of five levels of geometric understanding. These levels are visualiza-tion, analysis, informal deducvisualiza-tion, formal deducvisualiza-tion, and rigor. The van Hiele model mentioned the role of the teacher, who organizes and carries out the classroom activities based on the development of students’ geometric thinking. A framework was developed for organizing classroom instruction to help teachers’ structure activities that cultivate their students’ geometric thinking. This framework progresses through a sequence of five phases of learning: infor-mation, guided orientation, explication, free orientation, and integration.
2.2.1 Phase 1: Information
Prior to teaching, instructors must observe and question students to determine what the students already know about the topic. The unique vocabulary, wording, and titles of topics are introduced through conversations and questions can be raised for discussion (Billstein, Libeskind, & Lott, 1993).
2.2.2 Phase 2: Guided Orientation
In this stage, students are gradually introduced to the new concepts and the direction of learning is outlined.
2.2.3 Phase 3: Explication
Through discussion, the main concepts are raised to the level of under-standing. In this stage, the acquisition of knowledge is guided by the correct use of language symbols and the role of the teacher is to help students learn the proper use of vocabulary and language.
2.2.4 Phase 4: Free Orientation
In this stage, students are encouraged to contemplate geometry problems through free orientation. The students are aware of the scope of learning; how-ever, they still need to discover their own direction. Numerous problem-solving methods and topics of greater complexity are introduced. Based on the concepts they have already learned, students attempt to solve problems on their own and thereby gain clarity in their understanding.
2.2.5 Phase 5: Integration
Geometry-related concepts require integration. In this stage, instructors encourage students to utilize these concepts to solve a range of problems. Through this summary of things they have already dealt with, students internalize, absorb, and unify purpose and relationship, and convert them into a new model of thinking.
2.3 Physical Manipulatives and Virtual Manipulatives
Piaget provides a characterization of children’s knowledge at four stages of maturity, termed sensor-motor, preoperational, concrete operational, and formal operational (Corsini, 1994). The sensor-motor stage develops from the age of 0 to 2, when children experience their surrounding environment and explore their body motions and senses. In this stage, they can use deferred imitation and have developed the concept of object permanence. The preoperational stage is from the age of 2 to 7, during which children learn to use symbols to represent their knowledge and experience of the environment; however, they still rely on
specific objects. In this stage, children can begin learning simple text, numbers, and figures. The concrete operations stage is from the age of 7 to age 11, in which children are gradually becoming capable of reasoning, logical thinking, and the comparison of objects according to their characteristics. They are capable of classification and no longer rely on one-sided perception and have formulated concepts of area, volume, and weight. The formal operations stage begins at age 11 and extends into adulthood, in which a series of hypotheses can be proposed for all problem scenarios, and verification sought to obtain the answers they seek. Individual factors can be singled out and formed into combinations to facilitate problem-solving.
Knowledge representation can be divided into three categories: enactive repre-sentation, iconic reprerepre-sentation, and symbolic representation (Bruner, 1966). Enactive representation deals with the experience of learning by doing, in which learners react to external stimuli through action. For example, a child’s understanding of a specific object is based on how this object can be manipulated. When this object disappears or cannot be manipulated, the significance of the object disappears. Physical manipulatives are representations of conceptual actions which can be explicitly manipulated. For instance, flower petals can be counted. Iconic representation refers to experience learned during observation and the mental manipulation of objects. Even if the physical object disappears, a mental image remains in the brain. Symbolic representation deals with the experience of learning by thinking, referring to the use of symbols to grasp concepts and perform thinking. Symbols are not necessarily similar to the physical object they represent. Unlike mental images of physical objects, symbols are abstractions of the characteristics of physical objects or mental images.
Many junior high school students are still unable to use symbols for formal reasoning thinking and justification (Lee & Chen, 2009). In other words, they cannot reach formal operational stage. The representation of knowledge is devel-oped through manipulation. If children are unable to manipulate the environment, it can be very difficult to develop these representations. Action representation and image representation can be formed through the manipulation of specific objects such that the knowledge learned gains a greater number of links to enhance memory. As a result, mathematics instruction in junior high and elementary schools relies heavily on manipulatives (Chang, Yuan, Lee, Chen, & Huang, 2013). The important function of manipulatives is to enable a link between concrete and abstract thinking. Drickey (2000) pointed out that the use of manipulatives can help students to construct mathematical abstract thinking and provide scenarios to connect known and unknown knowledge.
Virtual manipulatives are dynamic objects with interactive features that can be accessed using computers and other devices such as smart phones. The repre-sentation of these objects can provide students with an opportunity to construct mathematical knowledge (Moyer et al., 2002, 2005). The most common represen-tations used in mathematics instruction are concrete/physical, pictorial/visual,
and abstract/symbolic. Virtual manipulatives can provide learners with a visual impression similar to pictorial/visual representation and manipulated like concrete/physical representations. Virtual manipulatives include the following features (Izydorczak, 2003; Yuan et al., 2010):
1. variability, in which the learner can change the properties of the objects, such as colors, or adjust the number of certain objects;
2. unlimited supply, which can solve the issue of insufficient physical manipu-latives during classes; virtual manipumanipu-latives also save teachers from time consuming distribution and organization of teaching aids, and provide convenient arrangement of teaching aids by simply clicking the recycle bin icon to clear all teaching aids on the screen; and
3. simultaneously showing figures and symbols on the screen to help students enhance the link between these two presentations.
Empirical studies related to the comparion of virtual and physical manipulatives for mathematics learning are still relatively new and somewhat limited. Ainsa (1999) observed no significant difference between virtual manipulatives and physical manipulatives in color matching, number matching, shape identification, counting ability, or addition/subtraction. In another study, 3rd-grade students mastered classification and logical thinking equally using virtual manipulatives and physical manipulatives (Clements et al., 1993). Steen et al. (2006) found that virtual manipulatives can be as effective as physical manipulatives in learning geometry-related concepts among 1st-grade students. Yuan et al. (2010) observed no significant difference in the learning performance of students using virtual manipulatives and those using physical manipulatives when dealing with polyominoes; however, new ideas using new symbols to record the results and considering the influence of symmetry and rotation on the figures occurred in the virtual manipulatives. Suh and Moyer (2007) examined the effects of developing students’ representational fluency using virtual manipulatives and physical manipulatives. The results showed that although the different manipulative models had different features, both the physical and virtual environments were effective in supporting students’ learning and encouraging relational thinking and algebraic reasoning.
However, Chang et al. (2013) adopted a non-equivalent quasi-experimental design, and recruited participants from two classes of 3rd-grade students in an elementary school in Taiwan. The results demonstrated the effectiveness of virtual manipulatives over that of physical manipulatives on three subscales of immediate learning performance and all four subscales of retention performance. Reimer and Moyer (2005) also investigated the impact of virtual manipulatives on the instruction of equivalent fractions and the comparison of fraction size. Their results indicated that virtual manipulatives can enhance the learning of fractions compared to physical manipulatives. Moreover, 60% of the students developed a positive attitude toward the use of virtual manipulatives. Most
students appreciated the immediate feedback of this approach, which tends to be more convenient and efficient than using physical manipulatives. Moyer, Niezgoda, and Stanley (2005) discussed virtual manipulatives as a unique technological form of representation for teaching mathematics, and described how two elementary school teachers conducted action research projects in their classroom using this technology. During these projects, a kindergarten teacher and a 2nd-grade teacher taught a series of lessons and documented children’s use of two virtual manipulatives. In these classrooms, teachers used the concrete manipulatives prior to using manipulatives. The findings demonstrated that children using virtual manipulatives were more creative in the formation of geometric patterns.
These studies showed that virtual manipulatives help students to perform equally or better than physical manipulatives. However, most of the participants of these studies were elementary school students and most of these studies were based on independent projects. These were supplementary courses, not included in the regular instruction. Moreover, little is known for the interaction between prior knowledge and manipulatives on learning effects. Therefore, this study uses type of manipulative and level of prior knowledge as independent variables to examine junior high school students’ learning performance of plane geometry, using a curriculum based on van Hiele’s five-stage learning theory. In addition, the course was implemented within the schedule of regular instruction.
3. METHODOLOGY 3.1 Procedure
This study employed a quasi-experimental design using pretest (learning achievement test and intelligence test) and posttest (learning achievement test and mathematics attitudes test) with nonequivalent groups. A delayed posttest (learning achievement test) was conducted 5 weeks after finishing the posttest. We employed the same learning achievement test in the pretest, posttest, and delayed posttest. Two-way factorial analysis of covariance was used with the covariance of mathematics scores in the intelligence test to examine the effects of the types of manipulative and the level of prior knowledge on learning per-formance and attitudes toward mathematics.
3.2 Participants
Four 8th-grade classes in a Taoyuan County junior high school were selected by convenience sampling as research participants. Two classes were randomly designated the virtual group and two classes became the physical group. An independent sample t-test was used to examine differences in the pretest (learn-ing achievement test and intelligence test) between the two groups. The dif-ferences were not significant; therefore, the two groups were deemed to have
equivalent levels of prior mathematical knowledge. To understand the impact of prior knowledge on the type of manipulatives, the median of the pretest score (learning achievement test) was used to divide the research participants into groups with high prior knowledge (scores in the top 50%) and low prior knowledge (scores in the bottom 50%).
3.3 Materials
The virtual manipulatives in this experiment covered basic concepts including the sum of exterior angles of a triangle, the sum of interior angles of a triangle, and the properties of parallel lines. During the development of the manipu-latives, several junior high school teachers and three professors (National Taipei University, National Chiao Tung University, and Chung Yuan Christian University) were consulted to evaluate and suggest modifications. Materials were tested among students with backgrounds similar to those in this study. Modifications were made after collecting opinions and suggestions from students. The virtual and physical manipulatives were based on identical teaching materials. As an example, the virtual manipulatives would allow students to use any triangle (right triangle, acute triangle, and obtuse triangle) to explore the concepts behind the sum of angles, while students in the physical manipulatives group were given only one fixed triangle. In addition, students in the virtual manipulatives group obtained immediate feedback and hints, while those in the physical manipuatives group received such encouragement from the teacher. These differences were inherent in the materials, the characteristics of virtual manipulatives being more flexible and the feedback more immediate than that of physical manipulatives. We developed the teaching materials by the van Hiele instruction model. An example “exploring sum of exterior angles of a triangle” using virtual manipulatives was discussed in detail as the following (see Table 1).
3.4 Instruments
3.4.1 Learning Achievement Test
This test was meant to reveal the learning performance of students after finishing a course in fundamental plane geometry. The test questions were devel-oped by researchers according to specific teaching objectives and learning content. Most of the questions dealt with concepts related to the sum of the exterior angles of a polygon, the sum of the interior angles of a polygon, and parallel lines. The test questions included three sub-levels: basic, understand-ing, and application. To reveal the problem-solving processes employed by the students, they were asked to explain the reason for selecting their answers. A total of 15 questions were to be completed within 30 minutes and most of the students completed the test within 25 minutes. After the official test, consistency among the test questions was analyzed using Cronbach’s a, providing a reliability
Table 1. Instructional Design of Exploring Sum of Exterior Angles of a Triangle
The van Hiele
instruction model Main activities
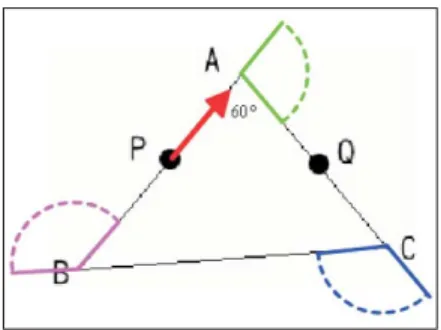
Information A thief ran away from point P on a triangle park but was caught by a policeman on point Q. IfÐA = 60°, what is the angle size the thief turned from P to Q?
Guided orientation Explication
Introduce the concepts of interior angles and exterior angles of a triangle. Posting question: Ask students to guess what is the sum of three exterior angles of a triangle? And encourage students to guess the answer. (Student activity)
Based on students’ discussion results, teacher can propose different strategies to solve the problem. They represent multiple interpretations to help students construct the concept.
Strategy 3: Strategy 2:
Integration Students present their findings and discuss them in class. Teacher can have an integrating discussion with students. Free exploration Posting questions: What is the sum of the exterior angles
of a quadrilateral, or a pentagon, or a hexagon? Students can collaborate with each other to explore the question and verify their answers from the computer.
score of .7602. Thus, the internal consistency of the test questions was verified. The achievement test was reviewed and corrected by two professors in relevant fields and several mathematics teachers in junior high school. Thus, the achieve-ment test was shown to have acceptable validity.
3.4.2 Mathematics Attitude Scale
This scale was adopted from the mathematics attitude scale proposed by Lee and Yuan (2010), used to reveal the learning attitudes of junior high school students after the teaching intervention. The test time was approximately 20 minutes. A total of 24 questions covered four sub-categories: enjoyment in learning mathematics, importance of mathematics, motivation to study mathematics, and fear of mathematics. Each sub-category included six questions: three were positive and three were negative. Scores were calculated using a 5-point Likert scale from “strongly agree” (5 points) to “strongly disagree” (1 point). Higher scores indicated a positive attitude toward mathematics. The Pearson correlation coefficient among the component scales of this test were .50~.86 (p < .001) and test-retest reliability was .78.
3.4.3 Intelligence Test
This test was compiled by Lu, Cheng, and Lu (1991) to measure the common intelligence level of junior high school students for use as a reference in class arrangement, group teaching, and the implementation of counseling activities. The content of this test can be divided into two parts: a language section including two sub-tests of language analog and language induction, each with 38 questions; a mathematics section including two sub-tests of arith-metic calculations and reasoning, each with 36 questions. Thus, the test had a total of 148 questions. The mathematics score of the intelligence test was used as the covariate to conduct two-way ANCOVA analysis. The split-half reliability of this test was 0.80~0.86 and the correlation with the second junior high school intelligence test was 0.39~0.72. Thus, this test was shown to have the acceptable reliability.
4. RESULTS 4.1 Posttest Analysis
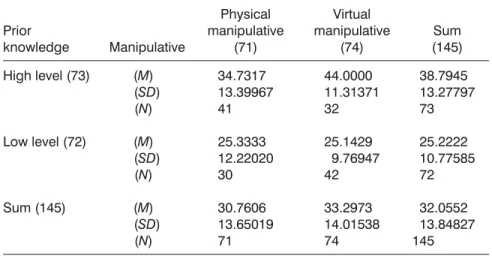
As shown in Table 2, the adjusted mean (mean = 33.3, SD = 14.02) of the posttest in the virtual manipulatives group was higher than that of students in the physical manipulatives group (mean = 30.76, SD = 13.65). The adjusted mean (mean = 38.79, SD = 13.28) of the posttest in the group with high prior knowledge was higher than that of the group with low prior knowledge (mean = 25.22, SD = 10.78).
Two assumptions for the ANCOVA were checked before the analysis pro-ceeded. The test for homogeneity of regression coefficients of the covariate for different types of manipulatives was not significant (F = .56, p = .45). Similarly, the test for homogeneity of regression coefficients of the covariate for different levels of prior knowledge was not significant (F = .62, p = .42). Therefore, it would be appropriate to conduct the two-way analysis of covariance. If the interaction between manipulative and prior knowledge is significant, then the simple main effects should be examined for both manipulative and prior knowledge. If not, then the main effects for each factor (manipulative and prior knowledge) would be conducted respectively. After excluding the impact of the mathematics scores in the intelligence test, there was a significant interaction between the type of manipulative and the level of prior knowledge on learning performance (F = 6.54, p = .012). Therefore, the simple main effects should be conducted with respect to prior knowledge and manipulatives.
As shown in Table 3, among students with high prior knowledge, the posttest performance of the virtual manipulatives group (mean = 44.00, SD = 11.31) was superior to that of the physical manipulatives group (mean = 34.73, SD = 13.40). However, for students with low prior knowledge, no significant difference was observed between the posttest performance of the virtual manipulatives group (mean = 25.14, SD = 9.77) and physical manipulatives group (mean = 25.33,
SD = 12.22). For students in the virtual manipulatives group, those with high
prior knowledge (mean = 44.00, SD = 11.31) outperformed those low prior knowledge (mean = 25.14, SD = 9.77) in the posttest. However, for students in the
Table 2. Summary of Adjusted Means of Posttest Performances of Manipulatives and Prior Knowledge in Plane Geometry Teaching
Prior knowledge Manipulative Physical manipulative (71) Virtual manipulative (74) Sum (145) High level (73) Low level (72) Sum (145) (M) (SD) (N) (M) (SD) (N) (M) (SD) (N) 34.7317 13.39967 41 25.3333 12.22020 30 30.7606 13.65019 71 44.0000 11.31371 32 25.1429 9.76947 42 33.2973 14.01538 74 38.7945 13.27797 73 25.2222 10.77585 72 32.0552 13.84827 145
Table 3. Summary of Two-Way Factorial Analysis of Covariance of Simple Main Effects of Posttest of Achievement Test with Respect to Prior Knowledge and Manipulatives Source of variance SS df MS F Sig Comparison Manipulative High level Low level Prior knowledge Physical manipulative Virtual manipulative 1602.135 6.250 513.427 2288.818 1 1 1 1 1602.135 6.250 513.427 2288.818 10.118* .057 3.058 22.488*** .002 .812 .085 .000 Virtual manipulative > Physical manipulative Virtual manipulative = Physical manipulative High level = Low level High level > Low level
physical manipulatives group, no significant difference was observed between students with high prior knowledge (mean = 34.73, SD = 13.40) and those with low prior knowledge (mean = 25.33, SD = 12.22).
4.2 Delayed Posttest Analysis
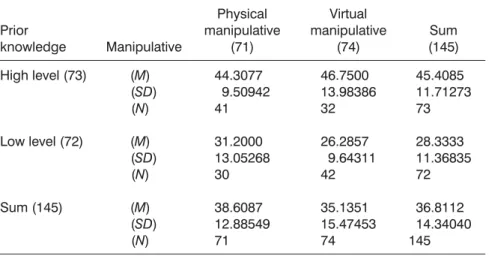
As shown in Table 4, the adjusted mean (mean = 35.14, SD = 15.47) in the delayed posttest performance of students in the virtual manipulatives group was worse than that of students in the physical manipulatives group (mean = 38.61, SD = 12.89). The adjusted mean (mean = 45.41, SD = 11.71) in the delayed posttest performance of students with high prior knowledge was higher than that of students with low prior knowledge (mean = 28.33, SD = 11.37).
Two assumptions for the ANCOVA were checked before the analysis pro-ceeded. The test for homogeneity of regression coefficients of the covariate for different types of manipulatives was not significant (F = .21, p = .65). Similarly, the test for homogeneity of regression coefficients of the covariate for different levels of prior knowledge was not significant (F = .26, p = .63). Therefore, it would be appropriate to conduct the two-way analysis of covariance. After excluding the influence of mathematics scores in the intelligence test, a significant interaction was significant between the type of manipulative and the level of prior knowledge on performance in the delayed learning of geometry (F = 4.55,
p = .035). Therefore, the simple main effects should be conducted with respect to
prior knowledge and manipulatives.
As shown in Table 5, for students with high prior knowledge, no significant difference was observed in the performance on the delayed posttest between
Table 4. Summary of Adjusted Means of Delayed Posttest Performances of Manipulatives and Prior Knowledge in Plane Geometry Reasoning
Prior knowledge Manipulative Physical manipulative (71) Virtual manipulative (74) Sum (145) High level (73) Low level (72) Sum (145) (M) (SD) (N) (M) (SD) (N) (M) (SD) (N) 44.3077 9.50942 41 31.2000 13.05268 30 38.6087 12.88549 71 46.7500 13.98386 32 26.2857 9.64311 42 35.1351 15.47453 74 45.4085 11.71273 73 28.3333 11.36835 72 36.8112 14.34040 145
Table 5. Summary of Two-Way Factorial Analysis of Covariance of Simple Main Effects of Delayed Posttest of Achievement Test with Respect to Prior Knowledge and Manipulatives Source of variance SS df MS F Sig Comparison Manipulative High level Low level Prior knowledge Physical manipulative Virtual manipulative 178.980 256.967 636.184 2796.856 1 1 1 1 179.980 256.967 636.184 2796.856 1.306 2.348 5.362* 21.611*** .257 .130 .024 .000 Virtual manipulative = Physical manipulative Virtual manipulative = Physical manipulative High level > Low level High level > Low level
students in the virtual manipulatives group (mean = 46.75, SD = 13.98) and those in the physical manipulatives group (mean = 44.31, SD = 9.51). Similarly, for students with low prior knowledge, no significant difference was observed in the delayed posttest performance of students in the virtual manipulatives group (mean = 26.29, SD = 9.64) and those in the physical manipulatives group (mean = 31.20, SD = 13.05). For students in the virtual manipulatives group, those with high prior knowledge (mean = 46.75, SD = 13.98) obtained better delayed posttest scores than those with low prior knowledge (mean = 26.29, SD = 9.64). Similarly, among students in the physical manipulatives group, those with high prior knowl-edge (mean = 44.31, SD = 9.51) outperformed those with low prior knowlknowl-edge (mean = 31.20, SD = 13.05) on the delayed posttest.
4.3 Analysis of Attitudes toward Mathematics
The mathematics scores of the intelligence test were used as the covariate to conduct two-way factorial analysis of covariance with the type of manipulative and the level of prior knowledge as independent variables and attitudes toward mathematics as a dependent variable. After excluding the impact of the covariate variable, the interaction between manipulatives and prior knowledge failed to reach the level of significance for three aspects: enjoyment of mathematics (F = 3.12, p = .18), motivation to study mathematics (F = .59, p = .45), and fear of mathematics (F = 4.25, p = .200). By observing the main effects of these three aspects, we determined that there was a significant relationship between type of manipulative and the enjoyment of mathematics (F = 8.62, p = .004), indicating that students in the virtual manipulatives group (mean = 20.82, SD = 4.41) enjoyed mathematics more than did those in the physical manipulatives group (mean = 19.64, SD = 4.64). The level of prior knowledge was only significant in terms of motivation to study mathematics (F = 8.13, p = .005) and fear of mathematics (motivation of mathematics (F = 4.29, p = .040), indicating students with high prior knowledge (motivation to study mathematics, mean = 21.92, SD = 3.46; and fear of mathematics, mean = 19.00, SD = 5.28) were more motivated to study mathematics and experienced less fear of mathematics than those with low prior knowledge (motivation to study mathematics, mean = 19.33, SD = 3.40; and fear of mathematics, mean = 16.14, SD = 3.86).
For the importance of mathematics, the interaction between the type of manipulative and the level of prior knowledge reached significance (F = 5.25,
p = .023). Thus, the simple main effect should be tested with respect to each
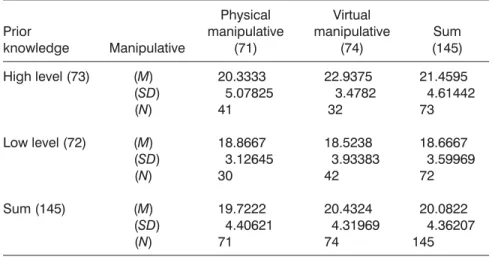
factor. As shown in Tables 6 and 7, among students with high prior knowledge, those in the virtual manipulatives group (mean = 22.94, SD = 3.47) more acutely perceived the importance of mathematics than did students in the physical manipu-latives group (mean = 20.33, SD = 5.08). However, among students with low prior knowledge, no significant difference was observed between students in the virtual manipulatives group (mean = 18.52, SD = 3.93) and those in the physical
manipulatives group (mean = 18.87, SD = 3.13) with regard to perception of the importance of mathematics. In contrast, among students in the physical manipu-latives group, no significant difference was observed between students with high prior knowledge (mean = 20.33, SD = 5.08) and those with low prior knowledge (mean = 18.87, SD = 3.13) with regard to the perception of the importance of mathematics. Among students in the virtual manipulatives group, those with high prior knowledge (mean = 22.93, SD = 3.47) more strongly perceived the importance of mathematics than did those with low prior knowledge (mean = 18.52, SD = 3.93).
5. DISCUSSION AND CONCLUSION
Among students with high prior knowledge, those in the virtual manipulatives group demonstrated better immediate learning performance (via the posttest) than did those in the physical manipulatives group. This effect was not seen in students with low prior knowledge. One reason may be that the ease of operating virtual manipulatives enables students to test themselves repeatedly, thereby gaining more practice with the mathematical concepts. As a result, students with high prior knowledge had more time to integrate the concepts they had learned; however, students with low prior knowledge were still struggling with the basic concepts and were therefore unable to take advantage of the virtual manipulatives. Thus, instructors must take into account the prior knowledge of students and
Table 6. Summary of Adjusted Means of Mathematics Importance of Manipulatives and Prior Knowledge
Prior knowledge Manipulative Physical manipulative (71) Virtual manipulative (74) Sum (145) High level (73) Low level (72) Sum (145) (M) (SD) (N) (M) (SD) (N) (M) (SD) (N) 20.3333 5.07825 41 18.8667 3.12645 30 19.7222 4.40621 71 22.9375 3.4782 32 18.5238 3.93383 42 20.4324 4.31969 74 21.4595 4.61442 73 18.6667 3.59969 72 20.0822 4.36207 145
Table 7. Summary of Two-Way Factorial Analysis of Covariance of Simple Main Effects of Mathematics Importance of Prior Knowledge and Manipulatives Source of variance SS df MS F Sig Comparison Manipulative High level Low level Prior knowledge Physical manipulative Virtual manipulative 184.728 1.802 4.740 214.954 1 1 1 1 184.728 1.802 4.740 214.954 9.928 .135 .264 15.137 .002 .714 .609 .000 Virtual manipulative > Physical manipulative Virtual manipulative = Physical manipulative High level = Low level High level > Low level
provide learning supports (such as scaffolding or problem prompts) for students with low prior knowledge.
No significant difference was observed in the delayed posttest performance of students in the virtual manipulatives group) and those in the physical manipu-latives group, regardless of prior knowledge. This shows that delayed learning performance in the virtual manipulative group was as effective as that in the physical manipulative group. In other words, although the virtual and physical environments had different features, both the virtual and physical manipulatives were effective in supporting students’ delayed learning in different ways. This implies that simply replacing the physical materials with virtual materials does not affect students’ delayed learning performance as long as the method of instruction is preserved. An in-depth examination of this issue should be conducted in the future.
Students with high prior knowledge appeared more motivated to study mathematics and exhibited less fear of mathematics than those with low prior knowledge. Students in the virtual manipulatives group enjoyed mathematics more than did students in the physical manipulatives group. This may explain why students with high prior knowledge in the virtual manipulatives group outperformed those in the physical manipulatives group on the posttest. These results also indicate that using virtual manipulatives could contribute to feelings of enjoyment in the practice of mathematics. These results are consistent with those of Yuan and colleages (2010), in which students were excited and con-fident using virtual manipulatives for problem solving, believing that this approach is easy and effective in revealing problems and finding solutions. Thus, if teachers could arrange learning activities using virtual manipulatives, they could enhance the enjoyment associated with learning mathematics, leading to better learning performance.
Among students with high prior knowledge, those in the virtual manipulatives group more strongly perceived the importance of studying mathematics than did those in the physical manipulatives group. However, among students with low prior knowledge, no significant difference was observed. This may be due to the fact that students with high prior knowledge regard virtual manipulatives as the application of mathematics knowledge, while those with low prior knowledge continue to struggle with the basic concepts. Thus, instructors should emphasize the importance of mathematics and integrating it into the daily lives of students. If students could view mathematics in the context of their own lives, they may better understand its underlying importance. Such applications could include the stories related to importance of learning mathematics. Our results indicate that prior knowledge plays an important role in the use of virtual manipulatives related to plane geometry.
In future studies, the sample size should be increased and this research frame-work can be applied to other topics of mathematics (algebra or probability) or to other fields (physics or chemistry) to verify our findings. In addition, the impact of
individual differences among students (such as learning style) and teaching strategies (such as game-based learning) on the learning performance using virtual manipulatives should also be taken into consideration. Finally, a quali-tative research method can be adopted to understand how virtual manipulatives affect learning to provide a reference for the design of learning activities using virtual manipulatives.
REFERENCES
Ainsa, T. (1999). Success of using technology and manipulatives to introduce numerical problem solving skills in monolingual/bilingual early childhood classrooms. Journal of Computers in Mathematics and Science Teaching, 18, 361-369.
Balka, D. S. (1993). Making the connections in mathematics via manipulatives. Contem-porary Education, 65, 19-23.
Billstein, R., Libeskind, S., & Lott, J. W. (1993). A problem solving approach to mathe-matics for elementary school teachers (5th ed.). New York, NY: Addison-Wesley. Breyfogle, M. L., & Lynch, C. M. (2010). van Hiele revisited. Mathematics Teaching in
the Middle School, 16(4), 232-238.
Bruner, J. S. (1966). Toward a theory of instruction. Cambridge, MA: The Belknap Press of Harvard University Press.
Chang, W. L, Yuan, Y., Lee, C. Y., Chen, M. H., & Huang, W. G. (2013). Exploring the imapct of using Magic Board as a teaching aid in third grader learning of area concepts. Educational Technology and Society, 16(2), 163-173.
Clements, D. H., & McMillen, S. (1996). Rethinking concrete manipulatives. Teaching Children Mathematics, 2, 270-279.
Clements, D. H., Nastasi, B. K., & Swaminathan, S. (1993). Young children and computers: Crossroads and directions from research. Young Children, 48(2), 56-64.
Corsini, R. J. (1994). Encyclopedia of psychology (2nd ed.; pp. 86-89). New York, NY: John Wiley.
Drickey, N. A. (2000). A comparison of virtual and physical manipulatives in teaching virtualization and spatial reasoning to middle school mathematics students. Unpub-lished doctoral dissertation, Utah State University.
Erdogan, T., Akkaya, R., & Celebi Akkaya, S. (2009). The effect of the van Hiele model based instruction on the creative thinking levels of 6th grade primary school students. Educational Sciences: Theory & Practice, 9(1), 181-194.
Izydorczak, A. (2003). A study of virtual manipulatives for elementary mathematics. Unpublished doctoral dissertation, State University of New York-Buffalo.
Kalyuga, S. (2007). Expertise reversal effect and its implications for learner-tailored instruction. Educational Psychology Review, 19, 509-539.
Kim, S. W., & Rehder, B. (2011). How prior knowledge affects selective attention during category learning: An eyetracking study. Memory & Cognition, 39, 649-665. Lee, C. Y., & Chen, M. P. (2009). A computer game as a context for non-routine
mathematical problem solving: The effects of type of question prompt and level of prior knowledge. Computers & Education, 52(3), 530-542.
Lee, C. Y., & Yuan, Y. (2010). Gender differences in the relationship between Taiwanese adolescents’ mathematics attitudes and their perceptions toward virtual manipulatives. International Journal of Science and Mathematics Education, 8, 937-950.
Lin, Y. C., & Huang, Y. M. (2013). A fuzzy-based knowledge diagnostic model with multiple attribute evalulation. Educational Technology & Society, 16(2), 119-136. Lindroth, L. (2005). How to find online math manipulatives. Teaching PreK-8, 35, 24-26. Lu, J. A., Cheng, L. P., & Lu, C. M. (1991). Junior high school instruction manual
of intelligence test. Taipei City, Taiwan: China Behavioral Science Community. Mistretta, R. M. (2000). Enhancing geometric reasoning. Adolescence, 35, 365-379. Moyer, P. S., Bolyard, J. J., & Spikell, M. A. (2002). What are virtual manipulatives?
Teaching Children Mathematics, 8, 372-377.
Moyer, P. S., Niezgoda, D., & Stanley, J. (2005). Young children’s use of virtual manipu-latives and other forms of mathematical representations. In W. J. Masalaski & P. C. Elliott (Eds.), Technology-supported mathematics learning environments (pp. 17-34). Reston, VA: National Council of Teachers of Mathematics.
National Council of Teachers of Mathematics (NCTM). (2000). Principles and standards for school mathematics. Reston, VA: NCTM.
Olkun, S. (2003). Making connections: Improving spatial abilities with engineering drawing activities. International Journal of Mathematics Teaching and Learning, 3(1), 1-10.
Parham J. L. (1983). A meta-analysis of the use of manipulative materials and student achievement in elementary school mathematics. Dissertation Abstracts International, 44A: 96.
Raphael, D., & Wahlstorm, M. (1989). The influence of instructional aids on mathematics achievement. Journal for Research in Mathematics Education, 20, 173-190.
Reimer, K., & Moyer, P. S. (2005). Third-graders learn about fractions using virtual manipulatives: A classroom study. Journal of Computers in Mathematics and Science Teaching, 24(1), 5-25.
Renkl, A., & Atkinson, R. K. (2003). Structuring the transition from example study to problem solving in cognitive skills acquisition: A cognitive load perspective. Educational Psychologist, 38, 15-22.
Rittle-Johnson, B., Durkin, K., & Star, J. R. (2009). The importance of prior knowledge when comparing examples: Influences on conceptual and procedural knowledge of equation solving. Journal of Educational Psychology, 101(4), 836-852.
Rittle-Johnson, B., & Kmicikewcyz, A. O. (2008). When generating answers benefits arithmetic skill: The importance of prior knowledge. Journal of Experimental Child Psychology, 101, 75-81.
Steen, K., Brooks, D., & Lyon, T. (2006). The impact of virtual manipulatives on first grade geometry instruction and learning. International Journal of Computers in Mathematics and Science Teaching, 25, 373-391.
Suh, J., & Moyer, P. S. (2007). Developing students’ representational fluency using virtual and physical algebra balances. Journal of Computers in Mathematics and Science Teaching, 26(2), 155.
Sweller, J., Ayres, P., & Kalyuga, S. (2011). Cognitive load theory. New York, NY: Springer Verlag.
van Hiele, P. M. (1984). A child’s thought and geometry. In D. Fuys, D. Gedders, & R. Tischler (eds. & trans.), English translations of selected writings of Dina van Hiele (pp. 243-252). Columbus, OH: ERIC Information Analysis Center for Science, Mathematics, and Environmental Education. (ERIC Document Reproduction Service No. ED287697.)
van Loon, M. H., de Bruin, A. B. H., van Gog, T., & van Merrienboer, J. J. G. (2013). Activation of inaccurate prior knowledge affects primary-school students’ meta-cognitive judgments and calibration. Learning and Instruction, 24, 15-25.
Yuan, Y., Lee, C. Y., & Wang, C. H. (2010). A comparison study of polyominoes explorations in a physical and a virtual manipulative environment. Journal of Computer Assisted Learning, 26(4), 307-316.
Direct reprint requests to: Dr. Chun-Yi Lee
Center for Teacher Education National Taipei University No. 151, University Rd.
San-Shia Dist., New Taipei City 23741 Taiwan (R.O.C.)