東亞各國股市與美日德三國股市相關係數之非線性研究

全文

(1)國立中山大學經濟學研究所碩士在職專班碩士論文. 東亞各國股市與美日德三國股市相關係數之非線性研究 Nonlinear Analysis of Stock Correlations among East Asian Countries, and The U.S., Japan, and German. 研究生：黃筱雯撰指導教授：翁銘章博士. 中華民國九十七年六月.

(2) 謝詞. 這篇論文得以付梓，衷心感謝指導教授翁銘章博士悉心的指導與諄諄教誨。感謝翁老師於論文撰寫期間給予觀念上的指點與協助，以及寬厚的包容心與耐心，並不因學生的資質駑鈍而嚴厲責罵，另外，每月 AWEE 的 meeting 不僅提供論文撰寫過程中新的想法更讓我接觸到不同領域的課程，使我受益良多，論文也因此得以利完成。此外，感謝口試委員李慶男老師與印永翔老師於口試期間不吝賜教，予以寶貴的建議與指正，使本論文更臻完善，在此感謝兩位老師。感謝所有課堂上的授課老師，由於老師們的悉心教導，讓我學習到相關的專業知識與研究精神。同時，也要感謝所有碩士班的同學們，在求學過程中不斷地相互勉勵。此外，感謝宗穎、信宏、嘉玲、傳強、若蓁學姊等同門，於論文撰寫期間相互鼓勵與扶持，謝謝你們一路上的陪伴。最後，感謝我的家人，謝謝母親、玉如阿姨，我的先生博文以及一對雙胞胎女兒，感謝他們對我的體諒與支持，讓我得以完成學業，謝謝你們！謹以本文獻給所有愛護我的人，再次表達我的感謝之意，謝謝你們！. 黃筱雯謹誌於中山大學經濟學研究所民國九十七年六月.

(3) 摘要. 隨著國際間的政治與總體經濟環境相互依存性逐漸地增強，亞洲部分國家的金融市場採漸進式的改革政策，使金融市場邁向自由化與國際化，然而國際金融市場的整合，也引起學界探討國際股市關聯程度的相關議題。然 Granger and Ter&a&svirta（1993）曾提及多數的經濟變數具有非線性的性質，Chelley-Steeley（2004）以平滑轉換模型探討新興國家股票市場及已開發國家股票市場間的區域性與全球性的整合現象。平滑轉換模型中考量了參數以漸近式變動的可能性，輔以計量方法予以檢定，並於研究之樣本期間內，估計模型參數是否具有漸進式的改變。本文引用 Chelley-Steeley（2004）的平滑轉換模型，進行東亞三國與美日德間股市非線性關係之研究，且探討股市整合的現象，並以線性模型、非線性原始模型與非線性延伸模型進行比較，實證結果發現，非線性延伸模型相較於線性及非線性原始模型之配適度具有較佳的表現。. 關鍵字：股價相關係數、平滑轉換迴歸模型、非線性模型.

(4) Abstract. With gradually increasing interdependence of international political and economic environments, part of Asian countries' financial markets reform adopted progressive policies towards liberalization and internationalization. Therefore, the integration of international financial markets has attracted a bunch of scholars to investigate related topics of international stock market. Granger and Ter&a&svirta (1993) documented that most of the economic variables have nonlinear characters. Chelley-Steeley (2004) uses smooth transition regression model to explore the financial market integration of regional and global markets among emerging and developed countries. Smooth transition regression model considered the possibility of nonlinear changes in regression parameters.. This paper applies the smooth transition regression model to reinvestigate Chelley-Steeley’s (2004) study of nonlinear relationship of stock markets among some East Asian countries and the United States, Japan and Germany. The main difference of our model and Chelley-Steeley’ model is that we relax his constant market index correlation between two countries by allowing the autoregressive process on market index correlation. Empirical evidences of linear model, original non-linear model and our non-linear extension model show that our non-linear extension model outperformedthe other two models in terms of goodness of fit.. Keywords：monthly correlation coefficient, smooth transition regression model, nonlinear model.

(5) 目錄目錄 .................................................................................................................... i 圖目錄 ..............................................................................................................iii 表目錄 ............................................................................................................... v 第壹章緒論 ..................................................................................................... 1 第一節研究動機與目的 ................................................................... 1 第二節研究架構 ............................................................................... 2 第貳章文獻回顧............................................................................................. 3 第一節非線性模相關文獻之探討 ................................................. 3 第二節國際股市關聯性相關文獻之探討..................................... 5 第參章模型介紹與實證研究方法................................................................. 7 第一節模型介紹 ............................................................................... 7 一、平滑轉換迴歸模型 ............................................................... 7 二、原始模型 ............................................................................. 11 三、延伸模型 ............................................................................. 12 第二節實證研究方法 ..................................................................... 15 一、單根檢定............................................................................. 16 二、 STR 模型之建構 ................................................................ 17 三、診斷性分析 ........................................................................ 22. i.

(6) 四、模型選擇之準則 ................................................................ 24 五、非線性模型殘差之 DF-GLS 單根檢定 ............................ 25 第肆章實證分析與結果............................................................................. 26 第一節實證資料來源與處理 ......................................................... 26 一、資料來源與樣本期間 ........................................................ 26 二、資料處理............................................................................. 26 第二節實證結果分析 ..................................................................... 27 一、單根檢定............................................................................. 27 二、非線性模型之估計與檢定 ................................................ 27 三、模型之參數估計 ................................................................ 31 四、線性模型之診斷性分析 .................................................... 56 五、非線性模型之診斷性分析 ................................................ 57 六、配適模型之選擇 ................................................................ 63 七、非線性延伸模型殘差之 DF-GLS 單根檢定 .................... 64 第伍章結論 ................................................................................................... 66 參考文獻 ......................................................................................................... 69. ii.

(7) 圖目錄圖 3.1. LSTR1 轉換函數 .............................................................................. 8. 圖 3.2. LSTR2 轉換函數 .............................................................................. 9. 圖 3.3. ESTR 轉換函數 .............................................................................. 10. 圖 3.4. 股價月相關係數之自我相關程度................................................. 13. 圖 3.5. 研究方法架構圖............................................................................. 15. 圖 3.6. 線性檢定的步驟............................................................................. 21. 圖 4.1. 韓國／德國線性與非線性模型之配適......................................... 34. 圖 4.2. 韓國／德國原始模型 LSTR1 之轉換函數................................... 35. 圖 4.3. 韓國／德國延伸模型 LSTR1 之轉換函數................................... 35. 圖 4.4. 韓國／日本線性與非線性模型之配適......................................... 39. 圖 4.5. 韓國／日本原始模型 LSTR1 之轉換函數................................... 39. 圖 4.6. 韓國／日本延伸模型 LSTR1 之轉換函數................................... 40. 圖 4.7. 韓國／美國線性與非線性模型之配適......................................... 41. 圖 4.8. 韓國／美國原始模型 LSTR1 之轉換函數................................... 41. 圖 4.9. 韓國／美國延伸模型 LSTR1 之轉換函數................................... 42. 圖 4.10 泰國／日本線性與非線性模型之配適......................................... 43 圖 4.11. 泰國／日本延伸模型 LSTR2 之轉換函數 ................................... 43. 圖 4.12 泰國／美國線性與非線性模型之配適......................................... 44 圖 4.13 泰國／美國原始模型 LSTR2 之轉換函數................................... 45 圖 4.14 泰國／美國延伸模型 LSTR2 之轉換函數................................... 45 圖 4.15 泰國／韓國線性與非線性模型之配適......................................... 46 iii.

(8) 圖 4.16 泰國／韓國原始模型 LSTR1 之轉換函數................................... 47 圖 4.17 泰國／韓國延伸模型 LSTR1 之轉換函數................................... 47 圖 4.18 泰國／新加坡線性與非線性模型之配適..................................... 48 圖 4.19 泰國／新加國原始模型 LSTR2 之轉換函數............................... 49 圖 4.20 泰國／新加國延伸模型 LSTR2 之轉換函數............................... 49 圖 4.21 台灣／美國非線性模型之配適..................................................... 50 圖 4.22 台灣／美國原始模型 LSTR1 之轉換函數................................... 51 圖 4.23 新加坡／德國非線性模型之配適................................................. 52 圖 4.24 新加坡／德國原始模型 LSTR1 之轉換函數............................... 52 圖 4.25 新加坡／德國線性與非線性模型之配適..................................... 53 圖 4.26 新加坡／德國 LSTR1 模型之轉換函數....................................... 54. iv.

(9) 表目錄表 4.1. 各股價指數月相關係數水準值 DF-GLS 單根檢定..................... 28. 表 4.2. 股價月相關係數線性模型............................................................. 28. 表 4.3. 原始模型股價月相關係數線性檢定與模型之選擇..................... 30. 表 4.4. 延伸模型股價月相關係數線性檢定與模型之選擇..................... 31. 表 4.5. 韓國／德國股價月相關係數之模型估計..................................... 34. 表 4.6. 韓國／日本股價指數月相關係數之模型估計............................. 38. 表 4.7. 韓國／美國股價指數月相關係數之模型估計............................. 40. 表 4.8. 泰國／日本股價指數月相關係數之模型估計............................. 42. 表 4.9. 泰國／美國股價指數月相關係數之模型估計............................. 44. 表 4.10 泰國／韓國股價指數月相關係數之模型估計............................. 46 表 4.11. 泰國／新加坡股價指數月相關係數之模型估計......................... 48. 表 4.12 台灣／美國股價指數月相關係數之模型估計............................. 50 表 4.13 新加坡／德國股價指數月相關係數之模型估計......................... 51 表 4.14 新加坡／德國股價指數月相關係數之模型估計......................... 53 表 4.15 非線性延伸模型之結構改變可能時間點..................................... 54 表 4.16 1990 年至 2007 年間之國際重大事件一覽表.............................. 55 表 4.17 線性模型診斷性分析-序列相關檢定 P 值................................... 56 表 4.18 線性模型診斷性分析之 ARCH-LM 檢定 P 值............................ 57 表 4.19 非線性原始模型診斷性分析-序列相關檢定 P 值....................... 59 表 4.20 非線性延伸模型之診斷性分析-序列相關檢定 P 值................... 59 表 4.21 非線性原始模型診斷性分析之 ARCH-LM 檢定 P 值................ 60 v.

(10) 表 4.22 非線性延伸模型之診斷性分析-ARCH-LM 檢定 P 值 ............... 60 表 4.23 非線性延伸模型之診斷性分析-無剩餘非線性檢定 P 值........... 61 表 4.24 非線性原始模型之診斷性分析-參數固定檢定 P 值................... 62 表 4.25 非線性延伸模型之診斷性分析-參數固定檢定 P 值................... 62 表 4.26 線性模型與非線性模型配適之 RMSE......................................... 64 表 4.27 非線性延伸模型之殘差 DF-GLS 單根檢定................................. 65. vi.

(11) 第壹章緒論第一節研究動機與目的股市常被喻為一國經濟的櫥窗，反映著國家的經濟概況及未來國家的經濟趨勢，因此，股票市場的動向可說是經濟景氣的領先指標，常言道，「春江水暖鴨先知」，藉由股市的漲跌，來反映一國經濟的狀況。然而金融市場國際化的世界潮流中各國的貿易與資金往來更為頻繁，再加上金融市場上提拱了各式各樣的投資工具，供投資大眾選擇，因此，使得各國的互動往來更加頻繁，由此，國際股市之間是似乎存在某種程度上的關聯性。隨著金融市場趨向國際化的潮流，世界各國的對外貿易與資金往來更為頻繁，進而加速了國際金融市場的結合，也引起學界探討國際股市關聯程度議題。Grubel (1968) 將投資組合的理論應用至國際資本市場上，藉以分散國內資產投資組合的風險，此後，關於投資組合多樣化的議題逐漸地受到重視，希望藉由國際投資組合以達成分散投資風險獲取高額報酬的目的。然而，當國際多角化投資潛在優勢降低後，將焦點移轉到先前未受到重視的新興市場上，卻發現新興市場與已開發市場之間有著相對較低的關聯性，因此提供了可能存在的多角化投資機會，此後開啓相關研究領域之大門， Ripley (1973) 採用因素分析法 (Factor analysis) 衡量已開發國家股價之間的相關性；Parton, Lessig and Joy (1976) 運用群聚分析法 (cluster analysis) 探討國際股價的整合程度；Eun and Shim (1989) 以向量自我迴歸 (VAR) 模型研究國際股市間的關聯性，除了各國股市存在互動關係之外，更發現美國股市對全球市場有顯著的影響； Goetzmann and Jorion (1999) 探討新興市場與全球市場的互動關係，從而得知，新興市場與其他的市場存在著低相關性與較高的報酬，因此，若新興市場與已開發市場之間的整合現象不明顯的話，就投資人而言，或許有潛在多角化分散投資風險的機會。關於國際股市互動關係的文章大多以迴歸分析、Granger 因果關係檢定、光譜分析法、共整合分析或是 GARCH 系列模型等探討股市間的關聯性，然而 Chelley-Steeley (2004) 依 Granger and Ter&a&svirta (1993) 提出的非線性平滑轉換模型 (smooth 1.

(12) transition regression) 探討新興市場及已開發市場間的區域性與全球性的整合現象，在這之前平滑轉換模型則已應用於貿易自由化之相關議題，如 Greenaway, Leybourne, and Sapsford. (1997) ，和 Leybourne and Mizen (1999) 則應用於通貨緊縮的研究，. 因此，九 0 年代之後，國際間的政治與總體經濟環境相互依存性逐漸地增強，亞洲部分國家的金融市場採漸進式的改革政策，使金融市場邁向自由化與國際化，然而政策改革是一個緩慢的過程，對於股市間的影響也極有可能為漸進式的調整過程。即平滑轉換模型中考量了參數以漸近式變動的可能性，進而再以計量方法予以檢定，並於研究之樣本期間內，估計模型參數是否有漸進式改變的現象。此外，近來諸多研究發現，總體經濟變數可能因為環境的變遷或是隨著時間的經過等因素而呈現非線性的現象，是以本文引用 Chelley-Steeley (2004) 的平滑轉換模型，進行東亞三國與美日德間股市非線性關係之研究，且探討股市的關聯性，並以線性模型、Chelley-Steeley (2004) 非線性原始模型與非線性延伸模型進行比較。. 第二節研究架構本文架構可分為五章，第壹章緒論說明研究動機與目的。第貳章為文獻回顧，探討非線性模型與國際股市關聯性的文獻。第參章模型介紹與實證研究方法，首先介紹非線性模型相關估計方法。第肆章為實證分析與結果，詳述實證結果並加以分析。第伍章結論。. 2.

(13) 第貳章文獻回顧第一節非線性模相關文獻之探討 Quandt (1958) 和 Bacon and Watts (1971) 曾提及轉換迴歸模型 (switching regression model) 之概念，爾後，Tong (1978) 及 Tong and Lim (1980) 也提出門檻自我迴歸模型 (threshold autoregressive model, TAR) 。而門檻自我迴歸模型主要是探討當轉換變數 (transition variable) 大於門檻值 (threshold value) 時，係數的改變狀況及調整速度的改變是瞬間的情況。Tiao and Tasy (1994) 研究美國自 1947 年至 1991 年調整後的實質 GNP (real gross national production) 資料，並且分別以線性 AR (autoregressive) 模型及 TAR 模型進行分析比較，實證結果，TAR 模型較 AR 模型更能適當的描述實質 GNP 資料在美國歷經景氣衰退及擴張期間時具有的非對稱性質，再者，以均方誤差 (mean squared error) 作為衡量樣本外預測能力之準則，亦充分顯示 TAR 模型較 AR 模型具有較佳的預測力。與 TAR 模型擁有相似概念之平滑轉換迴歸模型 (smooth transition regression model, STR) 其變數的調整速度是隨著轉換函數而平滑變動，因此，TAR 模型可說是 STAR 模型的特例。STR 模型最早曾於 Goldfeld and Quandt (1972, pp. 263-264) 和 Maddala (1977, p.396) 文章中提及，近期 Granger and Ter&a&svirta (1993)， Ter&a&svirta (1994, 1998)，Franses and van Dijk (2000) 對 STR 模型更是詳加討論，然而 STR 模型若再更進一步延伸即成為平滑轉換自我迴歸模型 (smooth transition autoregressive model, STAR) 模型。Ter&a&svirta and Anderson (1992) 檢驗 13 個 OECD (Organization for Economic Cooperation) 國家景氣循環相關指標能否以非線性 STAR 模型來描述之研究，其結果顯示 13 個 OECD 國家景氣循環指標呈現相似的非線性性質，然而景氣循環的波動於衰退期及擴張期時具有不同的動態調整特性。而在 1994 年， Ter&a&svirta 運用羅吉斯函數 (logistic) 和指數函數 (exponential) 於非線性自我迴歸模型 (nonlinear autoregressive model) 中，並檢驗 STAR 模型之統計檢定及估計，此後，STAR 模型被廣泛地運用於各相關的議題上。 3.

(14) Sarantis (1999) 針對十個主要工業化國家 (G-10) 的實質有效匯率進行測試與建立非線性 STAR 模型，實證結果，除了荷蘭和瑞士，其他八個國家於研究期間內皆拒絶實質有效匯率為線性的假設，即對大部分的國家而言，實質滙率在兩區間 (regime) 內的動態調整過程具有非對稱循環的特性。另外，透過特徵方程式之特徵根估計 STAR 模型之匯率的動態行為，發現實質有效匯率於升值與貶值階段間循環變動，平均而言，循環週期約為 5 至 6 個月，但美國實質有效匯率於 middle regime 的循環週期，則超過了一年。最後，樣本外 (out-of-sample) 之預測，則以誤差均方根 (RMSE) 作為預測能力判斷的指標，其結果顯示 STAR 模型樣本外之預測力優於 Markov regime-switching 模型。 Sarantis (2001) 對七個主要工業國家 (G-7) 應用 STAR 模型研究股票價格是否存在非線性及週期循環的特性，樣本期間自 1966 年至 1999 年股票價格之月資料，並計算股價成長率，結果發現所有國家的股票市場都拒絕線性模型的假設，其中日本、德國、英國、義大利、加拿大的股價成長率可用 LSTAR 模型來描述；美國、法國則以 ESTAR 模型來表示。在配適完各國股價成長率模型之後，計算非線性模型之特徵根，結果顯示除了日本之外，所有國家的特徵根皆為複數根，表示股票市場具有週期變動的特性，並求其各區間 (regime) 的循環週期。另外，由非線性 Granger noncausality tests 得知，只有少數幾個國家的股市短期間會相互影響，但長期間則可忽視。STAR 模型股價成長率之樣本外的預測能力，就短期與中長期而言，STAR 模型亦優於線性 AR 模型 (linear autoregressive model) 和隨機漫步模型 (random walk model)。 Holmes and Maghrebi (2004) 以轉換函數為羅吉斯 (logistic) 函數與指數 (exponential) 函數的STAR模型來估計四個東南亞國家 (韓國、馬來西亞、新加坡、泰國) 分別對日本和美國的實質利率的差額，樣本期間為1977年1月到2000年3月。結果顯示，其實質利率差額均存在非線性，且多為LSTAR模型，然新加坡／日本、泰國／日本實質利率差額之區間 (regime) 轉換為非平滑的過程。另外，若遇到重大外來衝擊時，實質利率平價 (real interest praity, RIP) 能以較快的速度恢復均衡。 4.

(15) Chelley-Steeley (2004) 首先將股價指數月相關係數透過 ADF 單根檢定，選取非定態之序列進行平滑轉換的過程 (smooth transition process) 。主要用意在於股票市場之間可能具有非線性的性質。因此，接著應用平滑轉換羅吉斯 (logistic) 函數檢驗亞太國家股票市場整合 (equity market integration) 的程度。最後，將非線性模型所得之殘差項再次進行 ADF 單根檢定，若為定態序列，則有正當的理由說明此為一平滑的轉換過程，且具非線性的特質，故研究結果顯示韓國、新加坡和泰國不論就區域性或全球性而言，市場分割性較小，即市場整合性較高；台灣地區則沒有明顯的證據顯示在當地或全球有整合的現象。然而，亞洲地區之間的整合速度較全球性的整合速度快。. 第二節國際股市關聯性相關文獻之探討近年來各國逐漸地邁向金融自由化，新的金融商品不斷推陳出新，國際資金移動更加頻繁，造就國際間各國股票市場的關聯性愈來愈密切，而市場的整合程度也隨之提高。關於衡量國際間股票市場整合相關議題研究之計量方法有許多，其一為迴歸分析，探討各國的股價指數相關性，或採Granger因果關係檢定，研究股票市場間的相互關係，亦有利用共整合分析討論股票市場間的長期關係，其它還有運用GARCH系列模型或STAR模型等計量模型進行這方面的研究，相關文獻概略性地探討如下： Eun and Shim (1989) 探討巴黎、法蘭克福、紐約、多倫多、蘇黎世、倫敦、東京、雪梨與香港等九個城市所在地國家的股票市場，運用向量自我迴歸 (VAR) 模型研究國際股市間的關聯性，樣本期間為1979年12月至1985年12月，其結果顯示，美國股市的動向會迅速的傳遞到其他各國的股票市場，顯示出美國股市的領導地位以及各國股市有明確的連動現象。 Kasa (1992) 針對美國、日本、英國、德國、加拿大股價指數進行研究並發現這些國家的股票市場有共同的趨勢，支持長期間具共移的現象，故獲得股票市場報酬整合程度高的結論。 Cheung and Mak (1992) 運用Granger因果關係檢定，研究亞太地區新興市場(澳大. 5.

(16) 利亞、香港、韓國、馬來西亞、菲律賓、新加坡、台灣和泰國) 與已開發市場 (美國、日本) 從1977年1月到1988年6月股市之間的因果關係，其結果因美國股市具有全球性因素 (global factor) 之影響力而引導多數的亞太新興市場的股市，除了韓國、台灣和泰國股市相對較封閉外；而日本僅領先香港、新加坡及泰國股市，故日本股市之影響力僅具區域性因素 (local factor) ，亞太地區市場間即時訊息的傳遞較不具效率，故存在套利空間。 Kanas (1998) 分別針對倫敦、法蘭克福和巴黎三大股票市場從1984年1月1日至 1993年12月7日為樣本期間，運用單變量EGARCH和雙變量EGARCH分析這些股票市場之間是否有資訊傳遞不對稱效果 (asymmetric effect) 與股價報酬率之波動性外溢效果 (volatility spillover effect)。以1987年10月為一分界點，區分為危機發生前後兩段期間，其結果顯示在1987年美股大崩盤之後，各股市之間的連動性更加地強烈。 Ghosh et al. (1999) 以Engle and Granger (1987) 提出共整合 (cointegration) 與誤差修正模型 (error correction model, ECM) 計量方法，進行亞洲金融風暴期間，美國及日本股市對亞洲地區 (香港、印度、韓國、台灣、馬來西亞、新加坡、泰國、印尼、菲律賓) 的股票市場是否具影響力之分析，實證結果顯示香港、印度、韓國和馬來西亞股市皆與美國股市存在長期均衡關係；印尼、菲律賓及新加坡則與日本相連結；然而，台灣和泰國較不受美國與日本股市的影響。另外，處於亞洲金融風暴期間，美國股市仍與香港、印度、韓國和馬來西亞關聯性較強；而印尼、新加坡和菲律賓則受日本股市的影響較為顯著。 Chelley-Steeley (2005) 早期匈牙利、波蘭、俄羅斯和捷克共和國之股票市場是呈現分割的狀態，針對東歐與已開發國家股票市場的報酬率進行向量自我迴歸 (vector autoregressive) 之變異數分解 (variance decomposition) 發現波蘭、匈牙利的股票市場易受其他股票市場的影響，意味著股票市場有整合的現象。並應用平滑轉換模型羅吉斯 (logistic) 轉換函數檢驗東歐國家的股票市場是否有明顯的整合狀況發生，實證結果顯示東歐國家股市有整合的現象，其中以匈牙利的整合速度最快，而俄羅斯則在 1997 年之前是四個東歐國家中整合傾向最不明顯的。 6.

(17) 第參章模型介紹與實證研究方法第一節模型介紹一、平滑轉換迴歸模型平滑轉換迴歸模型 (smooth transition regression model, STR model )最主要的概念在於透過轉換函數使得兩區間的轉換為平滑且連續，在諸多非線性迴歸模型中， Quandt (1958) ，Bacon and Watts (1971) 將轉換迴歸模型進一步延伸發展成為平滑轉換迴歸 (STR) 模型，這與門檻自我迴歸 (TAR, Tong, 1990) 模型或 Markov regime-switching 模型的區間是瞬間轉換的假設而有所不同。本文就 Ter&a&svirta (2004, p.222) 所提出之 STR 的基本模型及其內涵詳加探討。標準 STR 模型： y t = φ ′Z t + θ ′Z t ⋅ G (γ , c, st ) + u t. = (φ + θG (γ , c, s t )) ' Z t + u t , t = 1,2LT. （3.1）. 其中 y t 為應變數， Z t = ( wt′ , xt′ )′ 為解釋變數向量， wt′ = (1, y t −1 ,L, y t − p )′ ，. xt′ = ( x1t ,L , x nt )′ 為外生變數向量。而 φ = (φ 0 , φ1 ,L, φ m )′ ， θ = (θ 0 , θ1 ,L ,θ m )′ 為. ((m + 1) × 1) 之向量， m = p + n ， p 為 AR 模型的落遲項， n 為外生變數個數， γ 為轉換函數的調整速度， c 為門檻值 (threshold value)且 c = (c1, c 2 , L c K )′ ， s t 是轉換變數. (transition variable) ， u t ~ iid (0, σ 2 ) 。 STR 模型依轉換函數型態，可分為羅吉斯函數 (logistic function) 及指數函數 (exponential function) 兩種。這兩種不同型態的轉換函數，分別隱含著時間序列資料具有不同的動態特性，實證上常被應用於經濟與金融相關之分析。. 1.. LSTR 轉換函數 K. G (γ , c, st ) = (1 + exp(−γ ∏ ( s t − c k ))) −1 , γ > 0. （3.2）. k =1. 其中 γ 為斜率參數或轉換函數的調整速度，即 γ 值愈大，反映受到外來衝擊時的制度轉換調整速度或是恢復的速度較快，衝擊的時間相對較短；反之， γ 值愈小，則受衝 7.

(18) 擊時制度轉變的時間則會延長。 c 為位置參數 (location parameter) ，又稱門檻值. (threshold value) 向量， s t 是轉換變數 (transition variable) 。羅吉斯函數 (logistic function) 為一連續之單調轉換函數，其值介於 0 到 1 之間。目前較為廣泛使用的羅吉斯函數 (logistic function) 為 LSTR1 與 LSTR2，分別如下所示：（1） K =1：LSTR1. LSTR1 轉換函數型態：. G L1 (γ , c1 , st ) = (1 + exp(−γ ( st − c1 )) −1 , γ > 0 圖 3.1. （3.3）. LSTR1 轉換函數. LSTR1 模型本身具有不對稱的動態特性，可用來描述時間序列資料依循著景氣循環波動，區間的轉換過程呈現平滑的狀態。在 LSTR1 模型下，僅有一個門檻值，轉換函數 G L1 (γ , c1 , s t ) 值由 0 至 1，因此迴歸參數 φ + θG L1 從 φ 單調轉換成 φ + θ 。從(圖. 3.1) 得知，斜率參數 γ 值影響轉換函數變動的幅度。就 γ 值論之，當 γ → 0 時，. G L1 (γ , c1 , s t ) = 1 2 ， LSTR1 模型即簡化成線性模型 (linear model) ；當 γ → ∞ ， G L1 (γ , c1 , s t ) 在 s t = c1 處瞬間地轉變，LSTR1 模型則退化為 TAR 模型；而 γ 值大小分別可以(圖 3.1)之虛線及實線來約略表示。若以轉換變數 s t 與門檻值 c1 的關係而言，若 s t = c1 時， G L1 (γ , c1 , s t ) = 1 2 ；當 s t 趨近於正無窮大，則轉換函數 G L1 (γ , c1 , st ) = 1 ； 8.

(19) 假如 s t 趨近於負無窮大時， G L1 (γ , c1 , st ) = 0 。另外，在 s t < c1 的情況下，我們稱時間序列資料落在下區間 (lower regime) ；反之，當 s t > c1 時，則為上區間 (upper. regime) 。. （2） K =2：LSTR2. LSTR2 轉換函數型式：. G L 2 (γ , c1 , c 2 , st ) = (1 + exp(−γ ( st − c1 )( st − c 2 )) −1 , γ > 0 圖 3.2. （3.4）. LSTR2 轉換函數. && cal and Osborn (2000) 與 van Dijk and Franses (1999) 在 STR 模型中試著以對 O 稱型態轉換函數之 LSTR2 模型進行實證分析。LSTR2 模型對稱於 (c1 + c 2 ) / 2 ，門檻值 c1 和 c 2 將函數分成三個區間 (regime) 。當 s t < c1 或 s t > c 2 會落在外部區間 (outer. regimes) ，離門檻值愈遠，則轉換函數 G L 2 (γ , c1 , c 2 , st ) 愈趨近於 1；若 c1 < st < c 2 即落在中間區間 (mid-regime) ， G L 2 (γ , c1 , c 2 , st ) 趨近於 0。在(圖 3.2)中，轉換變數 s t 處於兩外部區間 (outer regimes) ，則具對稱的動態經濟行為，但轉換變數 s t 一旦落在中間區間 (mid-regime) ，其動態行為會異於外部區間。又轉換函數調整速度 γ = 0 9.

(20) 時， G L 2 (γ , c1 , c 2 , st ) = 1 2 ，LSTR2 模型即退化成線性模型。因此， γ 值愈大，表示調整所受衝擊的反應速度愈快，(圖 3.2)虛線即愈陗陡；反之，調整的速度愈慢，表現在(圖 3.2)中的實線則就愈平滑。. 2.. ESTR 轉換函數 2. G E (γ , c1 , st ) = (1 + e −γ ( st −c1 ) ) ， γ > 0 圖 3.3. （3.5）. ESTR 轉換函數. 另一種常用的轉換函數為 ESTR (Exponential STR)，其函數圖形與 LSTR2 有些類似，如(圖 3.3)所示。然而，(圖 3.3)說明僅有在 γ 值趨近於無窮大且排除 s t = c1 時，轉換函數 G E (γ , c1 , st ) = 1 。將門檻值 c1 做為區分中間區間 (mid-regime) 及外部區間. (outer regimes) 的分界點，在 s t < c1 或 s t > c1 範疇均屬於外部區間 (outer regimes) ，僅於 s t = c1 ， G E (γ , c1 , st ) = 0 屬於中間區間 (mid-regime) ，故轉換函數對稱於. s t = c1 。ESTR 模型具有 γ = 0 ，G E (γ , c1 , st ) = 0 ，則會退化成線性模型之特性。另外， ESTR 模型和 LSTR2 模型乍看之下好像很相似，但兩模型還是有些許之差異，最主要的差別在於 ESTR 模型在 s t = c1 時， G E (γ , c1 , s t ) 的值為零，然而當 LSTR2 模型之兩門檻值 c1 = c 2 時，G L 2 (γ , c1 , c1 , s t ) ≠ 0，無法簡化成 ESTR 模型，且當 c1 ≠ c 2 時，LSTR2 之中間區間包含 c1 < st < c 2 ，但 ESTR 之中間區間則為一點，即當 s t = c1 時。 10.

(21) LSTR 模型與 ESTR 模型的 γ = 0 時，均退化為線性模型，即不再具有非線性的特質。假如 STR 模型的解釋變數向量 Z t 僅包含其落遲項，那麼 STR 模型則可以延伸為. STAR (smooth transition autoregressive) 模型。簡言之，欲描述具有非線性特性的時間序列資料，LSTR1 模型適合分析具不對稱動態行為的序列資料；ESTR 模型與 LSTR2 模型則可描繪資料型態具對稱特質之區間調整，兩者差異在於 ESTR 模型的中間區間. (mid-regime) 為一個點，而 LSTR2 模型的中間區間 (mid-regime) 可為一點或一個區間，因此，LSTR2 較為一般化，因而本文若是遇有 ESTR 或 LSTR2 之情況時，以採用 LSTR2 之估計為準。. 二、原始模型一九九○年代初期，韓國、台灣、泰國、新加坡等亞洲新興國家，逐漸地開放股票市場且為吸引國外資金的流入進行金融自由化的政策。然而金融市場趨向自由化與國際化後，各國的金融政策已逐漸地放寬對彼此的限制，國際資本的流動更加頻繁，是否因此而加速了全球性金融市場的整合， Chelley-Steeley (2004) 參考 Ganger and Ter&a&svirta (1993) 所建議的平滑轉換羅吉斯趨勢模型 (smooth transition logistic trend. model) ，藉由股價月相關係數來檢視股票市場的整合程度。接著介紹 Chelley-Steeley (2004) 之股票市場相關係數的平滑轉換羅吉斯趨勢模型：. ρ ij ,t = α + βS t (γ ,τ ) + ν t. （3.6）. S t (γ ,τ ) = (1 + exp(−γ (t − τT ))) −1 , = (1 + e. t −γT ( −τ ) −1 T. ). γ >0. ,. （3.7）. ρ ij,t 是亞洲股票市場 i 及已開發市場 j 於 t 時點之月相關係數，α 和 β 為欲估計之迴歸係數， S t 為一連續之轉換函數，即前述之 G 函數，參數 τ 為門檻值，參數 t 為轉換變數，參數 γ 為轉換函數的調整速度且 γ > 0 。 11.

(22) 當(3.7 式)中的轉換變數 t → −∞ 時，轉換函數 S t (γ ,τ ) 為零。轉換變數 t → ∞ ，轉換函數 S t (γ ,τ ) 則為 1。轉換變數 t = τT 時，轉換函數 S t (γ ,τ ) 即為 0.5。若以轉換函數的調整速度 γ 值而言：（1）γ = 0 與 S t (γ ,τ ) = 0 ，其經濟含義說明股票市場間的整合現象沒有任何變動存在。（2）γ 值愈小，轉函變數 S t (γ ,τ ) 在 0 到 1 的區間內的緩慢的移動，表示股票市場間整合的傾向逐漸地有轉變。（3）γ 值愈大，轉換函數 S t (γ ,τ ) 則在. 0 到 1 的區間內快速的移動，顯示整合變動速度較為明顯。（4） γ → ∞ ，轉換函數 S t (γ ,τ ) 幾乎會在 t = τT 時，瞬間地由 0 轉變為 1。從原始模型中的股價月相關係數 ρ ij,t ，即可瞭解股票市場之間的整合現象。若一區間 α 與另一區間 β (若 β 為正) 之整合為 α + β 時，表示其股票市場之間的整合程度是增加；反之，若 β 為負時，股票市場的整合則有趨緩的現象產生。因此，原始模型以亞洲新興國家韓國、台灣、泰國與新加坡和已開發國家加拿大、法國、德國、英國、美國及日本為樣本，探討亞洲國家在區域性及全球性的市場整合的現象。. 三、延伸模型. Chelley-Steeley (2004) 探討亞洲新興國家間的區域整合及與已開發國家間的整合現象時，僅假設股價月相關係數在平滑轉換前後均為一固定數，並無討論股價月相關係數有可能包含自我相關的部分，因此，我們嚐試將股價月相關係數加入自我相關的落後期數條件，即股價月相關係數可能受到前幾期的影響，故重新定義股價月相關係數之平滑轉換自我迴歸模型 (smooth transition autoregression model) 如下：. ρ ij,t = φ ′X t + θ ′X t ⋅ G (γ , c, s t ) + u t , i = 1,2,3,4 , j = 1,2,3 K. G (γ , c, s t ) = (1 + exp(−γ ∏ (s t − c k ))) −1 ,. K=1 or 2 , γ > 0. （3.8）（3.9）. k =1. 其中， ρ ij,t 為 i 與 j 兩國股價於時點 t 之月相關係數，且 i 為本文探討之東亞國家韓國、. 12.

(23) 台灣、泰國及新加坡之一， j 則是美國、日本與德國三國之一。φ = (φ 0 , φ1 , φ 2, ..., φ p ) ' ，. θ = (θ 0 ,θ1 , θ 2 ,...,θ p ) ' ， X t = (1, ρ ij ,t −1 , ρ ij ,t − 2 ,..., ρ ij ,t − p )′ ， u t ~ iid (0, σ 2 ) ， G (γ , c, st ) 為轉換函數， st 轉換變數有可能為 ρ ij,t 落後期數或時間趨勢項， γ 是轉換函數的調整速度且 γ > 0 ， c 為位置參數向量，又稱門檻向量。於前面之原始模型中股價月相關係數 ρ ij,t 僅為一常數項，即假定股價月相關係數在平滑轉換前後皆為固定不變的常數，僅於轉換函數之門檻值附近平滑地改變，表示股價相關係數不會受前期值所影響，故未加入股價月相關係數的落後期數，本文試著將股價月相關係數加入落後期數(如 3.8 式)，主要原因在於影響股價指數波動的總體經濟因素甚多，大多數的國家設有漲跌幅的限制，因此一遇到金融風暴、台灣 921 大地震、美國 911 事件、美國次級房貸、四川大地震等重大的事件時，無法即時反應完畢，延長衝擊股市的期間，股市下跌的時間也隨之而拉長。另外，因為本文之股價月相關係數的計算是以 24 個月兩國股價指數之滾動窗格 (rolling window) 來計算其月相關係數，故隨著衝擊時間的延長加入落後期數，隱含著股價月相關係數可能會產生自我相關 ( 如 3.8 式 ) 的情況，故我們以平滑轉換自我迴歸 (smooth transition. autoregression model，簡稱 STAR) 模型來討論國家間股價月相關係數自我相關的現象以及探討國家之間股市的關聯性。圖 3.4. 股價月相關係數之自我相關程度. 13.

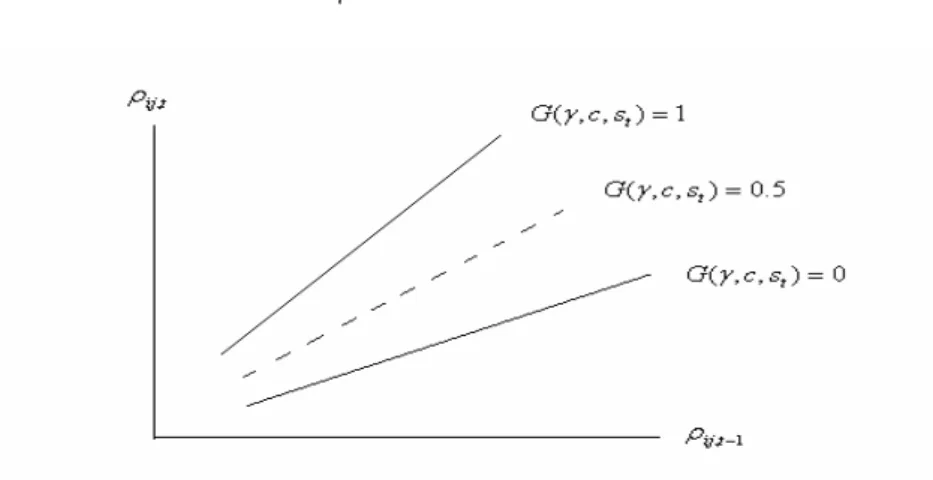
(24) 由於本文中所討論的股價月相關係數 ρ ij,t ，使用兩國間的股價指數且以 24 期為一區間且每一相鄰區間均有 23 期重疊而求得的相關係數，因此，我們合理懷疑股價月相關係數應與前幾期有高度的自我相關，故將(3.8 式)改寫為. ρ ij ,t = (φ 0 + φ1 ρ ij ,t −1 + L + φ p ρ ij ,t − p ) + (θ 0 + θ1 ρ ij ,t −1 + L + θ p ρ ij ,t − p ) ⋅ G (⋅) = (φ 0 + φ1 ρ ij ,t −1 + L + φ p ρ ij ,t − p ) ⋅ (1 − G (⋅)). + ((φ 0 + θ 0 ) + (φ1 + θ1 ) ρ ij ,t −1 + L + (φ p + θ p ) ρ ij ,t − p ) ⋅ G (⋅). （3.10）. 為簡化下列說明，先假設股價月相關係數 ρ ij,t 存在一正自我相關之斜率(表相關程度為正)。轉換函數 G (γ , c, st ) 為一機率函數，值介於 0 到 1 之間，而股價月相關係數 ρ ij,t 視轉換函數 G (γ , c, st ) 所佔權重大小而呈現不同的走勢。就極端狀態而言，當. G (γ , c, st ) = 0 時，(3.10 式)簡化為 ρ ij ,t = (φ 0 + φ1 ρ ij ,t −1 + L + φ p ρ ij ,t − p ) 僅存在線性部分；再者， G (γ , c, st ) = 1 時，股價月相關係數 ρ ij,t 為兩段線性部分之和，即. ρ ij ,t = ((φ0 + θ 0 ) + (φ1 + θ1 ) ρ ij ,t −1 + L + (φ p + θ p ) ρ ij ,t − p ) ；若 G (γ , c, st ) = 0.5 時，則是由線性部分與非線性部分各占轉換函數一部分的權重，因此，股價月自我相關係數會在轉換函數 G (γ , c, st ) = 0 到 G (γ , c, st ) = 1 的區間內依所占的權重大小而改變。欲探討兩國相關係數之自我相關程度的高低(圖 3.4)，則視股價月相關係數 ρ ij,t 自我相關(3.10 式) 斜率的大小而定，若股價月相關係數 ρ ij,t 的自我相關程度愈大 (即 G (γ , c, st ) = 0 移動至 G (γ , c, st ) = 1 ) ，即兩國之間相關係數的自我相關程度愈高；相反的，則股價月相關係數 ρ ij,t 的自我相關程度就愈小 (即 G (γ , c, st ) = 1 變動為 G (γ , c, st ) = 0 )。若股價月相關係數 ρ ij,t 存在負自我相關之斜率 (表兩者相關程度為負) ，其相關程度的大小，分別表示兩國的股價月相關係數 ρ ij,t 的自我相關程度之高低。另外，轉換函數. G (γ , c, st ) = 0.5 所對應的門檻值，恰為轉換函數 G (γ , c, st ) 平滑轉換的中點。 14.

(25) 第二節實證研究方法. 圖 3.5. 研究方法架構圖. 序列資料. 單根檢定. 線性檢定. 線性模型. 非線性模型. 原始模型. 診斷性分析. 延伸模型. 診斷性分析. 配適模型的選擇. 非線性模型殘差之單根檢定. 15.

(26) 一、單根檢定在使用時間序列料資進行實證研究時，首先必需瞭解資料型態是定態(stationary) 或非定態 (nonstationary) 。若序列變數的資料產生過程 (data generating process ,. DGP) 具有不因時間的變動而改變之性質，即表示該變數為定態序列。定態序列之特性，當受到外來的衝擊時，短暫的偏離平均值，但隨著時間的經過長期還是會收斂至均衡水準的調整機能。如果序列變數為非定態序列，則會因時間的變動而變動，一旦遭受到外力的衝擊，因對所受的衝擊具記憶性，故其影響是持續累積而產生永久性的影響。因此，進行實證研究時，確立時間序列資料的定態與否，則顯得相當重要。否則，誤將非定態的變數資料直接進行迴歸分析，則可能會出現 Granger. and Newbold (1974) 所謂的假性迴歸 (spurious regression) 現象發生，造成判定係數 R 2 很高以及 t 值非常顯著，但所估計的實證模型卻不具任何的經濟意義。傳統計量模型理論是建立在資料的性質為定態序列，然而大多數經濟與金融相關之時間序列資料多呈現非定態，因此，可以線性 AR 模型為基礎的 Augmented. Dickey-Fuller (ADF) 檢定檢驗序列資料是否具定態性，但若時間序列變數本身具有非線性之特性時，還是採用 ADF 檢定來驗證時，則可能產生檢定力下降以及型一誤差的問題。通常 Augmented Dickey-Fuller (ADF) 檢定和 Phillips-Perron (PP) 檢定是利用最小平方法 (OLS) 來估計迴歸係數值，然而 Dickey-Fuller GLS (DF-GLS) 檢定、則是採用一般化最小平方法 (GLS) 估計迴歸係數值，而 DF-GLS 單根檢定方法之檢定力較 ADF 檢定和 PP 檢定高。Elliott et al (1996) 運用 GLS 估計確定項係數的想法來修正 ADF 檢定，建立較具效率及檢定力較高的 DF-GLS 檢定。因此，欲檢驗原始序列資料為定態或非定態的序列，令 y t 為時間序列資料並假設：. y = ( y1 , (1 − α L) y 2 ,..., (1 − α L) yT ). （3.11）. z = ( z1 , (1 − α L) z 2 ,..., (1 − α L) zT ). （3.12）. 16.

(27) 且 z t = (1, t ) ' 為確定項， α = 1 +. c ， c 為常數值，當模型包含常數項與時間趨勢項時， T. 則 z t = (1, t ) ' ，常數值 c 為 − 13.5 ；若模型僅有常數項時， zt = (1)′ ，常數值 c 為 − 7 。將 ∧. ∧. y 對 z 進行迴歸，估計出迴歸係數值 ( β 0 , β 1 ) 後，將原始序列資料中的確定趨勢項予以去除。因此，重新定義 y td 為去除確定趨勢項後的序列： ∧. ∧. （3.13）. y td = y t − β 0 − β 1t ∧. ∧. 其中 ( β 0 , β1 ) 為迴歸係數值，最後再依照類似 ADF 單根檢定的方式來進行，其檢定式：. Δy td = a o y td−1 + a1 Δy td−1 + L + a p Δy td− p + vt. （3.14）. DF-GLS 檢定之虛無假設 H 0 : a 0 = 0 ，對立假設 H 1 : a 0 < 0 。檢定結果若無法拒絕虛無假設，意味著序列資料為非定態的序列，即具有單根；反之，如果拒絕虛無假設，則表示該序列資料為一穩定的序列。. 二、STR 模型之建構時間序列料資經過單根檢定，確為定態序列，接著找尋適當的線性模型或非線性模型來配適，若序列無法以適合的線性模型來估計，則應選擇適宜的非線性模型，建構 STR 模型之步驟如下：. 1.. 估計一線性 AR (autoregressive) 模型，並決定最適的落後期數 p 期。. y t = φ ′z t + vt. （3.15）. 其中 φ = (φ 0 , φ1 , φ 2, ..., φ m ) ' ， Z t = ( wt′ , xt′ )′ ， wt′ = (1, y t −1 ,L, yt − p )′ ， xt = ( x1t ,L , x nt )′ ， m = p + n ， vt ~ iid (0, σ 2 ) 。. AIC (Akaike Information Criterion) 或 SC (Schwarz Criterion) 為模型階次(order) 選擇的準則，可用以決定最適落後期數 p。若以 SC 作為落後期數選取的標準，則傾向選擇較精簡的模型，故本研究採取 SC 為落後期數選擇的準則。最適遞延期數 17.

(28) 決定後，最後再針對線性 AR 模型做診斷性檢定 (misspecification test) ，檢查模型是否有序列相關或異質變異的問題存在。分別探討如下：. （1）Ljung-Box Q 檢定若一時間序列資料共 T 個樣本數，在進行迴歸後所得之殘差項數列 εˆt ，並求其自我相關係數 ρ (i ) =. T. ∑ εˆt εˆt −1. t =i +1. T. ∑ εˆ. 2 t. ，故 Ljung-Box Q 統計量之檢定式：. t =1. p. Q( p ) = T (T + 2)∑ ρ (i ) 2 (T − i ). （3.16）. i =1. 統計量為服從自由度 p 之 χ 2 分配。虛無假設為殘差變數從 1 到 p 階均無自我相關。. （2）ARCH-LM 檢定模型診斷檢定之一為 ARCH-LM 檢定，此一檢驗是為了檢查模型之殘差序列是否有異質變異的現象存在。故需將時間序列資料進行迴歸，計算參數估計值及殘差，另將殘差序列平方做一輔助迴歸式： uˆ t2 = β 0 + β 1uˆ t2−1 + L + β q uˆ t2− q + vt. （3.17）. 其虛無假設 H 0 : β1 = L = β q = 0，檢定結果若無法拒絕虛無假設即殘差無條件異質變異。由輔助迴歸式所求出的 R 2 與樣本總數 T 相乘，即可求出 ARCH-LM 之檢定統計量，自由度為 q 的卡方分配， TR 2 ~ χ 2 (q ) 。. 2.. 線性檢定 (linearity test) 若直接對(3.1 式)進行檢定則會產生 φ = (φ 0 , φ1 , φ 2, ..., φ m ) ' ， θ = (θ 0 , θ1 ,L ,θ m )′ 無法. 定義 (unidentified) 的問題，Luukkonen, Saikkonen, Ter&a&svirta (1998a) 提出議建，針對 LSTR1 模型及 LSTR2 模型之轉換函數於 γ = 0 處作 3 階及 2 階之泰勒展開 (Taylor. expansion) 後，再代回(3.1 式)，即得到下列輔助迴歸 (auxiliary regression) ：. 18.

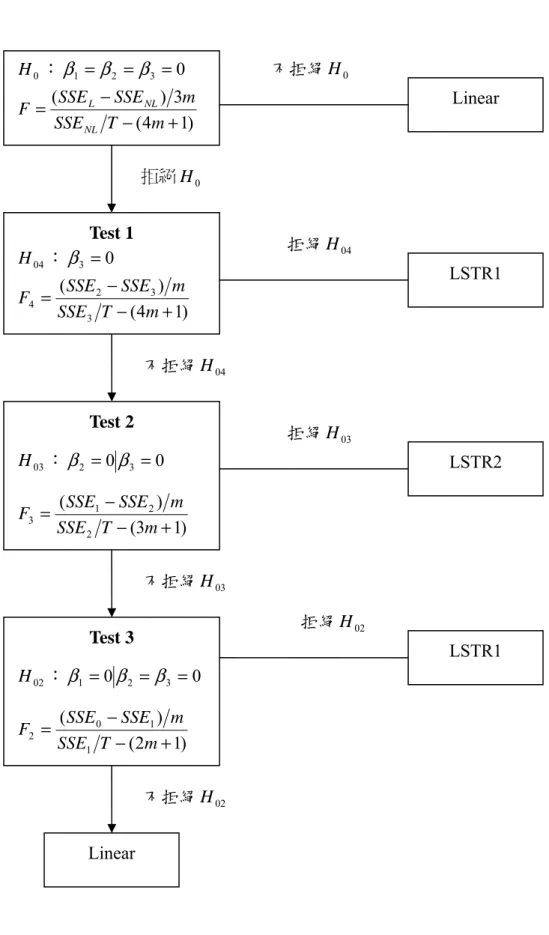
(29) 3. y t = β 0′ z t + ∑ β ′j ~ z t s tj + u t*. （3.18）. j =1. 其中 z t = (1, ~ z t′ )′ ， ~ z t 為 (m × 1) 的向量， β ′j 和 β o′ 為待估參數的係數矩陣，. u t* = u t + R3 (γ , c, st )θ ′z t 為白噪音 (white noise) ， R3 (γ , c, st ) 為多項式近似之剩餘項 (remainder) 。由於轉換函數在 γ = 0 處作 3 階泰勒展開 (Taylor expansion) 之後，不論 c1 值為何， st 的一次方及三次方的值均存在 (即不為零) ；若在 γ = 0 作 2 階泰勒展開 (Taylor expansion) ，無論 c1 和 c 2 值為何， st 之平方項次的值不為零。因此，乃運用此一特性進行檢定。線性檢定之虛無假設為 H 0 : β1 = β 2 = β 3 = 0 ，如果無法拒絶虛無假設，模型即為線性模型，故檢定統計量為 F =. 3.. ( SSE L − SSE NL ) 3m 。 SSE NL T − (4m + 1). 若檢定結果拒絶線性模型，則選擇最適的非線性模型。當虛無假設被拒絶，即線性模型不適用，繼續進行下列檢定程序以決定股價月相. 關係數之非線性關係應以何種轉換模型來配適。檢定步驟為： Test1. H 04 : β 3 = 0. （3.19）. Test 2. H 03 : β 2 = 0 β 3 = 0. （3.20）. Test 3. H 02 : β1 = 0 β 2 = β 3 = 0. （3.21）. 首先針對(3.19 式)做檢驗，若拒絶虛無假設 H 04 ，表示應以 LSTR1 模型來配適，其檢定統計量 F4 =. ( SSE 2 − SSE 3 ) m 。若無法拒絶虛無假設 H 04 ，繼續進行 SSE 3 T − (4m + 1). H 03 : β 2 = 0 β 3 = 0（3.20 式）檢驗，檢定結果為拒絶 H 03，即時間序列資料可以 LSTR2. 模型來描述，檢定統計量為 F3 =. ( SSE1 − SSE 2 ) m 。然而， H 03 之虛無假設如果還是 SSE 2 T − (3m + 1). 無法被拒絶，則接著檢定 H 02 : β1 = 0 β 2 = β 3 = 0 （3.21 式），假使 H 02 的虛無假設被. 19.

(30) 拒絶，則採用 LSTR1 之模型，檢定統計量 F2 =. ( SSE 0 − SSE1 ) m ，若還是無法拒絕 H 02 SSE1 T − (2m + 1). 的虛無假設時，則適用線性模型，其中 SSE1 、 SSE 2 和 SSE3 分別為非線性模型在虛無假設 H 02 ， H 03 ， H 04 為真時的迴歸殘差平方和。不過 Granger & Ter&a&svirta (1993)，Ter&a&svirta (1994) ，Eirheim & Ter&a&svirta (1996) 建議，若按照上述順序來檢定，可能會導致錯誤的判斷，因為在檢定的過程中並未考慮泰勒展開 (Taylor expansion) 的更高次方，故建議分別對(3.19 式)到(3.21 式)計算其. F 檢定的 p 值，選擇三者之中 p 值最小者為最適的 STR 模型。. 20.

(31) 圖 3.6. H 0 ： β1 = β 2 = β 3 = 0 F=. 線性檢定的步驟. 不拒絕 H 0. ( SSE L − SSE NL ) 3m SSE NL T − (4m + 1). Linear. 拒絕 H 0. Test 1 H 04 ： β 3 = 0. 拒絕 H 04. LSTR1. ( SSE 2 − SSE 3 ) m F4 = SSE 3 T − (4m + 1). 不拒絕 H 04. Test 2. 拒絕 H 03. H 03 ： β 2 = 0 β 3 = 0 F3 =. LSTR2. ( SSE1 − SSE 2 ) m SSE 2 T − (3m + 1). 不拒絕 H 03 拒絕 H 02. Test 3. LSTR1. H 02 ： β 1 = 0 β 2 = β 3 = 0 F2 =. ( SSE 0 − SSE1 ) m SSE1 T − (2m + 1). 不拒絕 H 02. Linear. 21.

(32) 三、診斷性分析當時間序列資料進行模型估計時，欲瞭解所配適模型是否得宜，可透過診斷性檢定輔助判斷其模型，分別就下列四種診斷分析檢定方法敘述如下：（1）序列相關檢定 (serial correlation test, SC test) 在古典迴歸模型的基本假設中，殘差需符合無自我相關，然一般實證分析所估計的模型可能出現自我相關的現象，若有此現象存在，將造成模型所估計參數之統計性質不具有效性，即使所估計之參數具不偏性和一致性，終究參數估計值之變異數並非為最小，因此，欲檢定所估模型是否有序列相關之現象存在，可將模型之殘差進行檢驗，即 u t = α ′vt + ε t ，α = (α 1 ,L, α q )′ ， vt = (u t −1 ,L , u t − q )′ ， ε t ~ iid (0, σ 2 ) ，實際操作上是把殘差估計值 uˆ t 對其落遲項 (uˆ t −1 ,L, uˆ t − q ) 進行迴歸，求檢定統計量 F=. ( SSR0 − SSR1 ) q ，其中 SSR0 為 STR 模型殘差平方和 (sum of squared residuals) ， SSR1 (T − n − q ). SSR1 為輔助迴歸式(3.18 式)之殘差平方和， n 為參數個數， q 為落後期數，自由度分. 別為 q 和 (T − n − q ) 之 F 檢定。序列相關檢定之虛無假設 H 0 : α = 0 ，若無法拒絕虛無假設，即表示模型的殘差無序列相關；反之，則存在序列相關的現象。. （2）ARCH-LM 檢定估計參數係數具不具有效性，則要視殘差是否存在自我相關以及是否有條件異質變異的存在，就殘差條件異質變的部分以 ARCH-LM 檢定討論之。利用 OLS 估計一均數方程式，並計算其殘差，將所估計的殘差作一輔助迴歸式： uˆ t2 = β 0 + β 1uˆ t2−1 + L + β q uˆ t2− q + vt. （3.22）. 虛無假設 H 0 : β1 = L = β q = 0 ，檢定結果若無法拒絕虛無假設，即 uˆ t2 = β 0 ，說明所估計之殘差無條件異質變異，也就是說殘差並不會受到前幾期的影響；反之，則具條件異質變異。由(3.22 式)求出輔助迴歸式的 R 2，並將樣本總數 T 與輔助迴歸的 R 2 相乘，即可計算出 ARCH-LM 之檢定統計量，為一自由度為 q 的卡方分配， 22.

(33) TR 2 ~ χ 2 (q ) 。（3）無剩餘非線性檢定 (no remaining nonlinearity test, NRN test) 當我們以非線性模型配適之後，需藉由診斷性檢定判斷所估計的模型是否合適，其一為無剩餘非線性檢定，即檢定模型是否有剩餘的非線性存在。將原 STR 模型加入另一轉換函數，其檢定式：. y t = φ ′z t + θ ′z t G (γ 1 , c1 , s1t ) + ψ ′z t H (γ 2 , c 2 , s 2t ) + u t. （3.23）. H (γ 2 , c 2 , s 2t ) 為另一個轉換函數，ψ = (ψ 0 , L,ψ m )′，u t ~ iidN (0, σ 2 ) 。但若直接對(3.23 式)作檢定可能會比較困難，故可對 H (γ 2 , c 2 , s 2t ) 轉換函數在 γ 2 = 0 處作泰勒展開，得一輔助迴歸： 3. y t = β 0′ z t + θ ′z t G (γ 1 , c1 , s1t ) + ∑ β ′j ( ~z t s 2jt ) + u t*. （3.24）. j =1. 其 u t* = u t + ψ ′z t R3 (γ 2 , c 2 , s st ) ， R3 為剩餘多項式的近似值。當 θ = 0 ，(3.24 式)即退化為(3.18 式)，然轉換變數 s 2t 可為 s1t 或為 Z t 子集中的變數，故虛無假設為(3.24 式)之. H 0 : β1 = β 2 = β 3 = 0 ，若無法拒絕虛無假設，隱含著模型無剩餘非線性存在。. （4）參數不變性檢定 (parameter constancy test, PC test) 檢定以非線性模型來配適之時間序列資料其參數是否會因時間的改變而產生變化，若參數隨時間而變動，則稱參數不具不變性。反之，所估參數若不因時間趨勢的改變而變動，稱參數具有不變性。在估計非線性模型時，若使用樣本期間較長的資料時，需留意參數是否有不變性的狀況存在，以降低模型估計所產生的偏誤，統計檢定式如下：. y t = φ (t )′ z t + θ (t )′ z t G (γ , c, st ) + u t , γ > 0. （3.25）. φ (t ) = φ + λφ H φ (γ φ , cφ , t * ). （3.26）. θ (t ) = θ + λθ H θ (γ θ , cθ , t * ). （3.27）. 23.

(34) 轉換函數 G (γ , c, st ) 假設為固定數，但參數估計值 φ ′ 和 θ ′ 可能會隨時間而改變。. t * = t T (時間趨勢項) ， u t ~ iid N (0, σ 2 ) ， H φ (γ φ , cφ , t * ) 與 H θ (γ θ , cθ , t * ) 同(3.2 式) 的定義，檢定參數不變性的之虛無假設為 γ φ = γ θ = 0 ，且假定 γ 和 c 皆為固定值，並在 γ φ = γ θ = 0 對(3.26 式)及(3.27 式)作泰勒展開，得到一輔助迴歸式： 3. 3. j =1. j =1. y t = β 0′ z t + ∑ β ′j {z t (t * ) j } + ∑ β ′j +3 {z t (t * ) j }G (γ , c, st ) + u t*. （3.28）. 其 β j = 0, j = 1,L,6 ，然參數不變性檢定之虛無假設為 γ φ = γ θ = 0 ，若無法拒絕其虛無假設，則表參數不因時間的改變而有所變動。. 四、模型選擇之準則所謂配適度 (fitness) 係將所搜集的樣本資料透過實證模型進行分析，藉由所估計的模型描述取樣資料，視兩者之間的一致程度，若模型能適當的描述樣本資料，即表該模型的配適度佳。評估模型是否合適，本文以誤差均方根 (root mean square,. RMSE) 做為模型選擇判斷之標準。誤差均方根公式如下： RMSE =. 1 N. T. ∑(y. t. − yˆ t ) 2. （3.29）. t =1. 其中 y t 和 yˆ t 分別表示資料的實際觀察值與模型的估計值，( y y − yˆ t ) 為預測誤差，將配適之線性模型、非線性原始模型與非線性延伸模型分別計算 RMSE 並加以比較其值之大小，若所求得之值愈小，即模型的配適度愈佳。1. 1. RMSR 為模型選擇準則之一，其所求得之值只能比較數值之大小，無法做統計上的假設檢定。 24.

(35) 五、非線性模型殘差之 DF-GLS 單根檢定在配適非線性模型後，將所得之殘差再次以線性單根檢定 DF-GLS 進行驗證. (Leybourne, Newbould, and Vougas, 1998)，若檢定結果為穩定序列，表示先前無法拒絕虛無假設為單根的狀態，是因為序列資料具有非線性的特性，而非資料本身為非定態的序列。. 25.

(36) 第肆章實證分析與結果第一節實證資料來源與處理一、資料來源與樣本期間本文實證研究對象為德國、美國、日本、韓國、台灣、泰國、新加坡之股票市場進而分析其股市之間的關聯性，其中德國股市以 DAX 股價指數，美國股市採用紐約道瓊工業平均股價指數 (JNY) ，日本股市以東京日經平均股價指數 (JTOKYO) ，韓國股市以韓國加權股價指數 (JSEOUL) ，台灣股市以台灣加權股價指數 (JS) ，泰國股市以泰國 Set 股價指數 (JBANGKOK) ，新加坡股市則以新加坡海峽時報股價指數 (JSING) ，以上資料來源取自全球金融資料庫 (The Global Financial Database) 與教育部 AREMOS/PC 經濟統計資料庫。研究期間為 1990 年 1 月 1 日至 2007 年 8 月. 31 日止。並使用 EViews 5 及 JMulTi 4 套裝軟體進行實證分析。. 二、資料處理首先我們將各國股價指數序列之日資料計算日報酬率2後，再求股價指數之月平均報酬率，而相關係數的求算方式係將各國股價指數以兩兩為一組，並以 24 個月 (如. 1990 年 1 月至 1991 年 12 月) 為一區間，計算第 1 個區間的月相關係數 ρ ij ,1，接著 1990 年 2 月至 1992 年 1 月計算出第 2 個區間的月相關係數 ρ ij , 2 ，以此類推至第 189 個區間滾動窗格 (rolling window) 之月相關係數 ρ ij ,189 (2005 年 9 月至 2007 年 8 月) 。我們分別將兩兩為一組的股價月相關係數進行線性 AR 模型與非線性模型的評估，用以分析其整合的程度。. 2. 各國股票市場的股價指數日報酬率計算方式為： ln( Indext +1 26. Indext ).

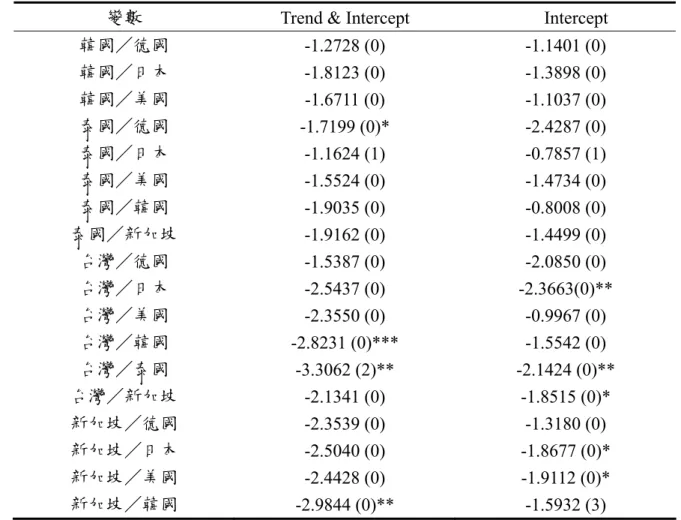
(37) 第二節實證結果分析一、單根檢定由於總體經濟變數多為非定態變數，故在進行實證分析之前，需先針對序列變數的定態與否做進一步的檢驗，本研究採 DF-GLS 單根檢定法檢定時間序列變數是否為定態序列。首先將兩兩為一組之股價月相關係數進行 DF-GLS 單根檢定，在虛無假設為序列具有單根前提下，依據(表 4.1)檢定結果顯示，在具有時間趨勢項及截距項之 10%顯著水準下，除了泰國／德國、台灣／韓國、台灣／泰國、新加坡／韓國之外，其餘的股價月相關係數皆為非穩定的序列；若僅有截距項的狀況下，檢定結果除台灣／日本、台灣／泰國、台灣／新加坡、新加坡／日本、新加坡／美國外，在 10%的顯著水準下皆無法拒絶單根的虛無假設，即時間序列變數為非穩定之序列。排除單根檢定結果為穩定序列外，尚有 10 組 DGP 為非穩定的序列，接著我們繼續針對這 10 組序列進行非線性模型之評估，探究這些序列資料是否是因為資料本身具有非線性的性質，才導致未能通單根檢定，還是序列資料本身即為非定態序列。在進行非線性模型估計後，將所得之殘差再次以線性單根檢定 DF-GLS 進行驗證 (Leybourne, Newbould, and. Vougas, 1998) ，若最終檢定結果為穩定序列，表示先前無法拒絕有單根的虛無假設，即是因為時間序列資料具有非線性的特性，而非資料本身為非定態的序列。. 二、非線性模型之估計與檢定非線性模型建構前先估計線性 AR 模型，並且以 SBC 作為選取之標準，決定最適的落後期數 p 期。依(表 4.2)之結果，針對 10 組股價月相關係數估計線性 AR 模型之最適落後期數的選取，其結果最大落後期數為 1 期，即為 AR(1)模型。. 27.

(38) 表 4.1. 各股價指數月相關係數水準值 DF-GLS 單根檢定. 變數. Trend & Intercept. 韓國／德國韓國／日本韓國／美國泰國／德國泰國／日本泰國／美國泰國／韓國泰國／新加坡台灣／德國. -1.2728 (0) -1.8123 (0) -1.6711 (0) -1.7199 (0)* -1.1624 (1) -1.5524 (0) -1.9035 (0) -1.9162 (0) -1.5387 (0) -2.5437 (0) -2.3550 (0) -2.8231 (0)*** -3.3062 (2)** -2.1341 (0) -2.3539 (0) -2.5040 (0) -2.4428 (0) -2.9844 (0)**. 台灣／日本台灣／美國台灣／韓國台灣／泰國台灣／新加坡新加坡／德國新加坡／日本新加坡／美國新加坡／韓國. Intercept -1.1401 (0) -1.3898 (0) -1.1037 (0) -2.4287 (0) -0.7857 (1) -1.4734 (0) -0.8008 (0) -1.4499 (0) -2.0850 (0) -2.3663(0)** -0.9967 (0) -1.5542 (0) -2.1424 (0)** -1.8515 (0)* -1.3180 (0) -1.8677 (0)* -1.9112 (0)* -1.5932 (3). 說明：1. ( )中的數字是由 SBC (Schwartz Bayesian information criterion) 所選出之最適落後期數。 2. DG-GLS 單根檢定的虛無假設 H 0 :序列具有單根。 3. ***、**、*分別表示 1％、5％、10％的顯著水準。. 表 4.2. 股價月相關係數線性模型. 變數. 線性 AR 模型. 變數. 線性 AR 模型. 韓國／德國韓國／日本韓國／美國泰國／日本泰國／美國. AR（1） AR（1） AR（1） AR（1） AR（1）. 泰國／韓國泰國／新加坡台灣／德國台灣／美國新加坡／德國. AR（1） AR（1） AR（1） AR（1） AR（1）. 說明：以 SC 作為落後期數選取的標準。. 28.

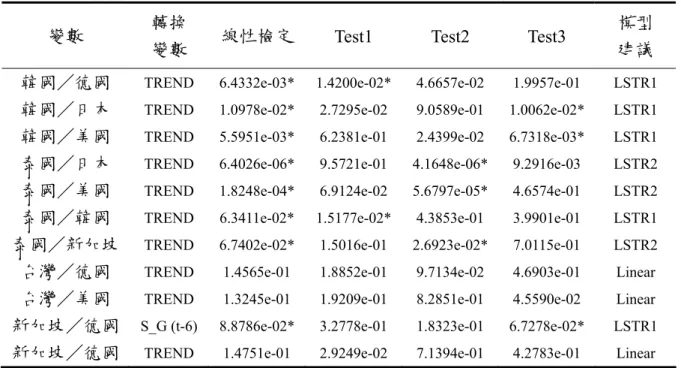
(39) （1）非線性原始模型之估計與檢定原始模型係以時間趨勢項為轉換變數，故線性檢定在於檢驗非線性原始模型應以何種樣態來表示，(表 4.3)結果顯示，泰國／日本與台灣／德國股價月相關係數適合以線性模型估計；而韓國／德國及新加坡／德國股價月相關係數則拒絕了線性模型，且拒絕 Test1 的 H 04 ，判斷為 LSTR1 模型；接著，韓國／日本、韓國／美國、泰國／韓國及台灣／美國股價月相關係數，於 10％顯著水準下，拒絕了線性模型虛無假設，但無法拒絕 Test1 的 H 04 ，Test2 的 H 03 的虛無假設，然而卻拒絕 Test3 的 H 02 之虛無假設，故適合以 LSTR1 模型來描述；最後，泰國／美國、泰國／新加坡之股價月相關係數皆拒絕線性模型虛無假設，且無法拒絕非線性模型 Test1 的 H 04 檢定，但是拒絕. Test2 的 H 03 虛無假設，故判定為 LSTR2 模型。. （2）非線性延伸模型之估計與檢定接著進行延性模型之線性檢定，在確認資料的型態為線性 AR 模型或非線性模型後，即可依照(圖 3.6)線性檢定的步驟選擇適合的模型。另外，在非線性模型中，以股價月相關係數之落後期數或時間趨勢項為非線性模型的轉換變數。(表 4.4)線性檢定結果，台灣／德國、台灣／美國、新加坡／德國之股價指數月相關係數，於 10％的顯著水準下，無法拒絕線性模型之虛無假設 H 0 : β1 = β 2 = β 3 = 0 (如 3.18 式之輔助迴歸式)，故只適合以線性模型來描述。3再者，顯示線性檢定之結果，轉換變數為時間趨勢項 (TREND) 時，韓國／德國、泰國／韓國皆拒絕線性模型，並且拒絕 Test1 的 H 04 ，判斷為 LSTR1 模型；而韓國／日本、韓國／美國亦拒絕線性模型，然無法拒絕 Test1 的 H 04 ，Test2 的 H 03 的虛無假設，但拒絕 Test3 的 H 02 之虛無假設，故適合以 LSTR1 模型來估計。然而新加坡／德國所估計之轉換變數為落後 6 期(S_G (t-6))，拒絕虛無假設 H 0 : β1 = β 2 = β 3 = 0 為線性模型，接著 Test1 的 H 04 ，Test2 的 H 03 之虛. 3. 新加坡／德國之股價月相關係數在 JMulTi 套裝軟體所求出的轉換變數為 S_G (t-6)，欲瞭解其門檻值的時點，故又以時間趨勢項 (TREND) 為轉換變數，再次進行分析，但檢定結果建議以線性模型來估計。 29.

(40) 無假設無法拒絕，但拒絕 Test3 的 H 02 之虛無假設，表示適合的模型為 LSTR1 模型。最後如 ( 表 4.4) 所示，泰國／日本、泰國／美國、泰國／新加坡皆拒絕虛無假設. H 0 : β1 = β 2 = β 3 = 0 之線性模型，繼續進行非線性模型 Test1 的 H 04 檢定，其結果無法拒絕虛無假設，卻拒絕 Test2 的 H 03 虛無假設，即判定適合為 LSTR2 模型。我們利用單根檢定篩選出不穩定的序列，將這些不穩定的序列再透過非線性模型之線性檢定後，發現線性檢定的結果，台灣／德國、台灣／美國、新加坡／德國等股價月相關係數不適合以非線性 STAR 模型來估計，故在此先行略過，不另外加以討論。而其餘的股價月相關係數適合以非線性 STAR 模型來估計，然而針對線性檢定結果，具有非線性性質的時間序列，我們將保留線性模型下之股價月相關係數，以利後續衡量模型的配適度。. 表 4.3. 原始模型股價月相關係數線性檢定與模型之選擇. 轉換變數. 線性檢定. Test1. Test2. Test3. 模型建議. 韓國／德國韓國／日本韓國／美國. TREND. 4.9856e-88*. 6.0175e-51*. 1.8918e-04. 1.7865e-38. LSTR1. TREND. 1.5072e-44*. 1.7186e-08. 3.1080e-03. 3.3879e-38*. LSTR1. TREND. 6.9221e-79*. 2.9310e-14. 4.8851e-01. 2.7101e-59*. LSTR1. 泰國／日本泰國／美國泰國／韓國泰國／新加坡台灣／德國. TREND. NaN. 7.3705e-10. 3.4796e-05. NaN. Linear. TREND. 3.3463e-31*. 1.7486e-05. 2.1094e-15*. 6.9944e-15. LSTR2. TREND. 3.8663e-37*. 6.8951e-03. 3.6415e-14. 2.1205e-14*. LSTR1. TREND. 3.9514e-07*. 2.2463e-02. 3.8488e-07*. 2.0827e-01. LSTR2. TREND. NaN. 2.5313e-14. 2.8527e-02. 6.7998e-02. Linear. 台灣／美國新加坡／德國. TREND. 3.2435e-28*. 8.1627e-01. 2.0360e-04. 1.2879e-14*. LSTR1. TREND. 1.7208e-14*. 3.6415e-14*. 2.7342e-01. 3.3113e-01. LSTR1. 變數. 說明：1.以 10%之顯著水準（*）選擇模型及轉換函數。 2. F 檢定的 P 值為 NaN 表示存在 matrix inversion problem。. 30.

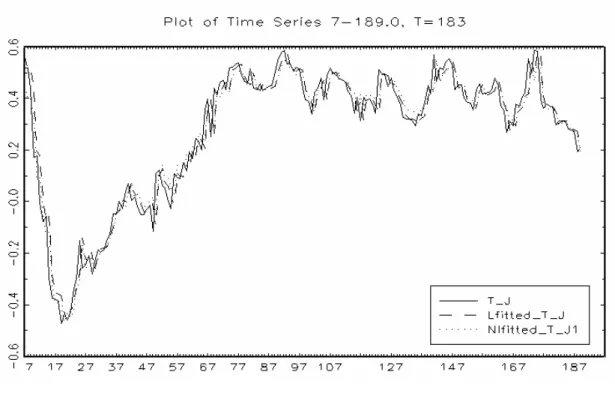
(41) 表 4.4 變數韓國／德國韓國／日本韓國／美國泰國／日本泰國／美國泰國／韓國泰國／新加坡台灣／德國台灣／美國新加坡／德國新加坡／德國. 延伸模型股價月相關係數線性檢定與模型之選擇. 轉換變數. 線性檢定. Test1. Test2. Test3. 模型建議. TREND. 6.4332e-03*. 1.4200e-02*. 4.6657e-02. 1.9957e-01. LSTR1. TREND. 1.0978e-02*. 2.7295e-02. 9.0589e-01. 1.0062e-02*. LSTR1. TREND. 5.5951e-03*. 6.2381e-01. 2.4399e-02. 6.7318e-03*. LSTR1. TREND. 6.4026e-06*. 9.5721e-01. 4.1648e-06*. 9.2916e-03. LSTR2. TREND. 1.8248e-04*. 6.9124e-02. 5.6797e-05*. 4.6574e-01. LSTR2. TREND. 6.3411e-02*. 1.5177e-02*. 4.3853e-01. 3.9901e-01. LSTR1. TREND. 6.7402e-02*. 1.5016e-01. 2.6923e-02*. 7.0115e-01. LSTR2. TREND. 1.4565e-01. 1.8852e-01. 9.7134e-02. 4.6903e-01. Linear. TREND. 1.3245e-01. 1.9209e-01. 8.2851e-01. 4.5590e-02. Linear. S_G (t-6). 8.8786e-02*. 3.2778e-01. 1.8323e-01. 6.7278e-02*. LSTR1. TREND. 1.4751e-01. 2.9249e-02. 7.1394e-01. 4.2783e-01. Linear. 說明：1.以 10%之顯著水準（*）選擇模型及轉換函數。. 三、模型之參數估計若以韓國／德國股價月相關係數為例，首先討論以線性模型配適及探討其相關程度，如 ( 表 4.5) 所列，股價月相關係數之線性 AR 模型估計結果為. ρ ij ,t = 0.2893 + 0.1854 ρ ij ,t −1 + vˆt ，兩國的股價月相關係數呈現低度的自我相關，而相關係數初步呈現先低後高的狀態，即之後才逐漸地回升且呈現緩慢遞增的現象(圖 4.1)。然而在選擇最適的非線性原始模型與延伸模型之後，接著以非線性最小平方法估計模型的參數，先討論韓國／德國股價月相關係數的自我相關現象與相關程度，如(表. 4.5)及(圖 4.1)之非線性原始模型與延伸模型。（1）原始模型之參數估計以韓國／德國股價月相關係數所求得之轉換函數 S t (γ ,τ ) 為 LSTR1 的型態為例，分別就下列狀況討論之：原始模型假設兩國股價月相關係數為固定值，表示兩國的股價月相關係數無自我. 31.

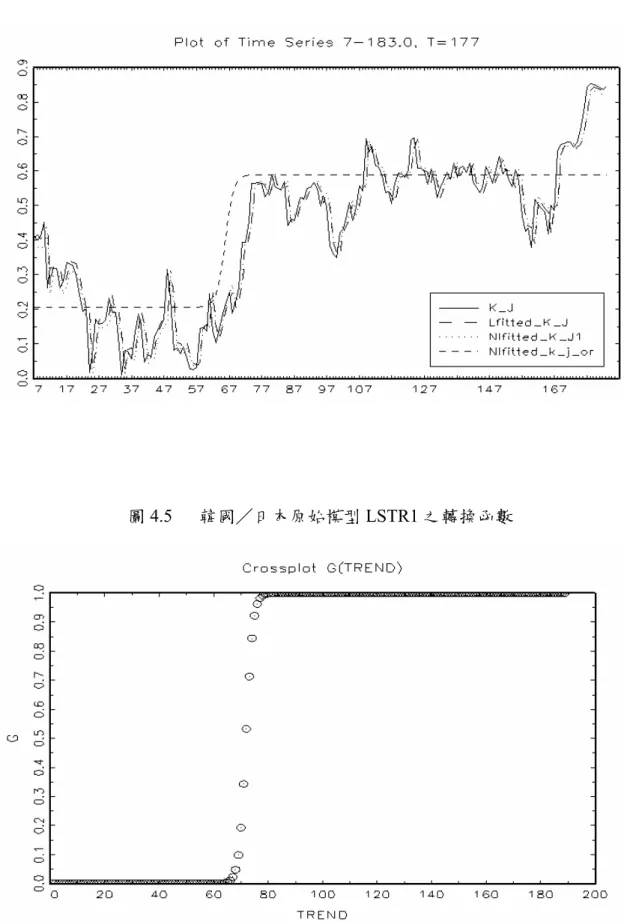
(42) 相關的情況，故韓國／德國之 ρ ij ,t = −0.0292 + 0.7108 ⋅ S t (γ ,τ ) + vˆt 。當轉換函數. S t (γ ,τ ) = 0 時，如(圖 4.1)及(圖 4.2)，約為第 60 期以前， ρ ij ,t = −0.0292 + vˆt 落在下區間且為線性模型；若轉換函數 S t (γ ,τ ) = 1 ，約第 160 期以後， ρ ij,t 則會落在上區間，即 ρ ij ,t = 0.6816 + vˆt 為另一段線性模型；若轉換函數 S t (γ ,τ ) 介於 0~1 的區間內則月相關係數平滑地由下區間轉換至上區間，約為第 61 期至第 161 期之間，表示韓國／德國的股價月相關係數逐漸地上升至 0.7108 左右，顯示經過區間的轉換後相關程度是增加的(圖 4.1)及(圖 4.2)。當轉換函數 S t (γ ,τ ) 於不同的權重之下，將使非線性模型呈現不同的樣態。其中，轉換函數 S t (γ ,τ ) 愈接近 0，表示下區間線性部分所占的權重大於上區間的線性部分；反之，轉換函數 S t (γ ,τ ) 愈接近 1，表示上區間線性部分所占的權重則較大；然而，兩段線性模型需透過轉換函數 S t (γ ,τ ) 於不同的權重下，以平滑的方式來轉換。參照(表. 4.5)，轉換函數以時間趨勢項 (TREND) 做為轉換變數 t ，門檻值 τ = 109.8990 ，調整速度 γ = 4.5748 ，顯示轉換函數 S t (γ ,τ ) 是以平滑的方式來調整，故. S t (γ ,τ ) = (1 + exp(−4.57481(t − 109.8990 ⋅ T ))) −1 。接著，分析非線性原始模型的相關性，韓國／日本、韓國／美國、泰國／韓國、台灣／美國的相關程度是上升的；而泰國／美國的相關程度呈現下降而後上升的狀況；泰國／新加坡的相關程度上升後，再逐漸地下降；新加坡／德國 (TREND) 的相關程度則呈現下降的狀態。在非線性原始模型中，韓國／日本、韓國／美國、泰國／美國、泰國／韓國、泰國／新加坡、台灣／美國與新加坡／德國股價月相關係數之轉換函數 S t (γ ,τ ) ，皆以時間趨勢項 (TREND) 為轉換變數 t ；然而各股價月相關係數的參數調整速度差異頗大，且韓國／日本、泰國／美國、泰國／韓國、泰國／新加坡、新加坡／德國之參數調整速度 γ 值較大，表示參數估計值的轉換速度較快且為明顯。另外，韓國／日本非線性原始模型之轉換函數於第 62 期至第 77 期左右，如(表 4.6)、(圖 4.4)及(圖 4.5)； 32.

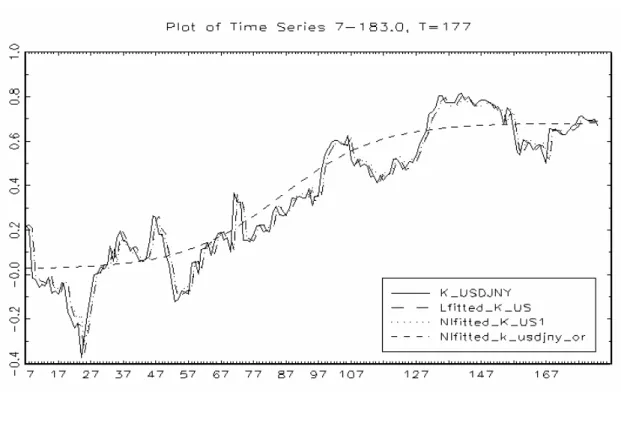
(43) 泰國／美國於第 1 期到第 50 期附近，如(表 4.9)、(圖 4.12）及(圖 4.13）；泰國／韓國於第 67 期到第 72 期附近，如(表 4.10)、(圖 4.15)及(圖 4.16)；泰國／新加坡於第 25 期到第 45 期及第 140 期到第 160 期附近，如(表 4.11)、(圖 4.18)及(圖 4.19)；新加坡／德國於第 1 期到第 20 期左右，如(表 4.13)、(圖 4.23)及(圖 4.24)，呈現區間轉換，但因參數的轉換速度較快，故其圖形較為陡陗。僅有韓國／美國以及台灣／美國之調整速度較緩慢，即區間調整較為平滑。在門檻值的部分，門檻值 τ 為非線性原始模型之參數估計值轉換為另一區間參數之估計值，且恰好為轉換函數 S t (γ ,τ ) = 0.5 之處，因此，韓國／日本的門檻值. τ = 71.8348 ，約略為 1995 年 11 月至 1997 年 10 月左右，如(圖 4.5)；韓國／美國的門檻值為 τ = 91.4860 所對應的時間點大約為 1997 年 7 月至 1999 年 6 月左右，如(圖. 4.8)；泰國／美國的門檻值分別為 τ 1 = 22.8625 及 τ 2 = 22.8625 ，對應時點為 1991 年 10 月至 1993 年 9 月左右，如(圖 4.13)；泰國／韓國的門檻值 τ = 73.3420，約略為 1996 年 1 月至 1997 年 12 月左右，如(圖 4.16)；泰國／新加坡的門檻值 τ 1 = 35.8303 與. τ 2 = 152.1954，大約為 1992 年 11 月至 1994 年 10 月及 2002 年 8 月至 2004 年 7 月左右，如(圖 4.19)；台灣／美國的門檻值 τ = 262.9728 ，如(圖 4.22)，本文發現由軟體自行測出最適之轉換函數的最大值約為 0.24，尚未達到門檻值 (轉換函數為 0.5 時) ，表示於門檻值之前已先行平滑的改變，在此種情況下，已是目前所能找到較佳的非線性原始模型；新加坡／德國的門檻值 τ = 10.5574 ，約略為 1990 年 10 月至 1992 年 9 月左右，如(圖 4.24)。因此，各模型所測出的門檻值並非相同，表示各股價月相關係數受到各種政治因素、經濟發展、政府政策等衝擊的影響，使得兩兩國家間股價的相關程度產生變動。. 33.

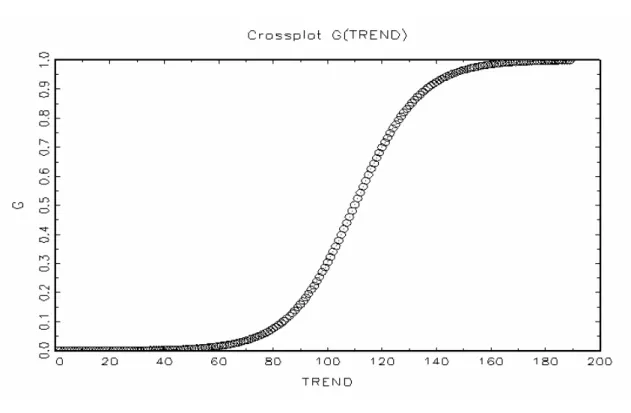
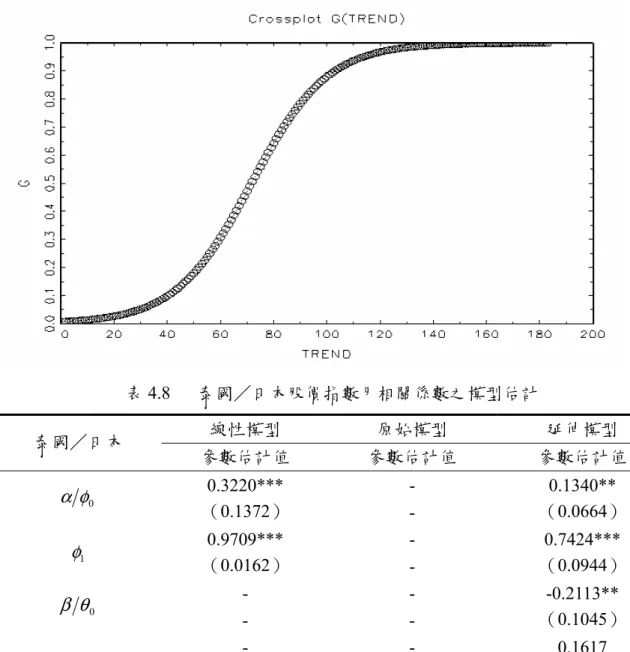
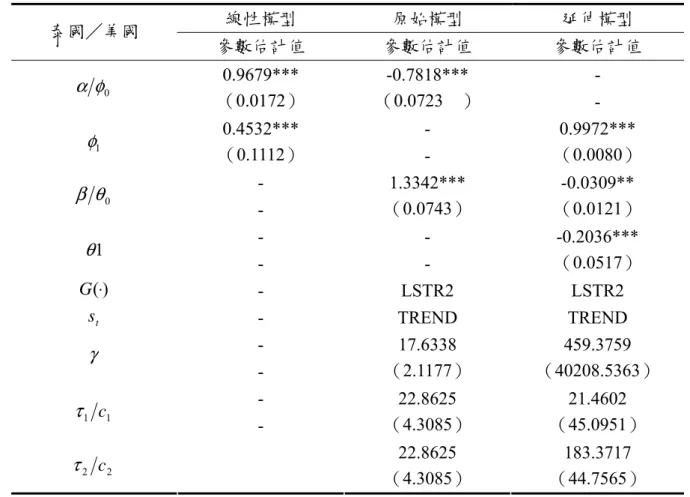
(44) 表 4.5. 韓國／德國股價月相關係數之模型估計線性模型. 原始模型. 延伸模型. 參數估計值. 參數估計值. 參數估計值. α φ0. 0.2893 （0.9820）. -0.0292 （0.0220）. -0.0170 （0.0107）. φ1. 0.1854*** （0.0121）. 0.7108*** （0.0354）. 0.9023*** （0.0422）. LSTR1 TREND 4.5748 （0.7629）. 0.0542 （0.0544）. 109.8990 （2.7229）. 63.9883 （17.4606）. 韓國／德國. -. β θ0 θ1 G (⋅) st. γ τ 1 c1. 說明：1.***、**、*分別表示 P 值小於 1%、5%、10%之顯著水準。 2. 以 10%顯著水準選擇模型及轉換函數。 3.（）內之數值為估計係數的標準差。. 圖 4.1. 韓國／德國線性與非線性模型之配適. 34. 0.0430 （0.0237）. LSTR1 TREND 4.2441 （3.8535）.

(45) 圖 4.2. 韓國／德國原始模型 LSTR1 之轉換函數. 圖 4.3. 韓國／德國延伸模型 LSTR1 之轉換函數. 35.