依據 van Hiele 幾何思考理論探究臺灣中部地區國三學生幾何概念發展之研究

(1)

國立臺中教育大學數學教育系碩士班碩士論文

指導教授：吳德邦博士

依據 van Hiele 幾何思考理論探究臺灣中部地

區國三學生幾何概念發展之研究

研究生：沈紀伶撰

中華民國九十九年六月

(2)

摘要

本研究旨在以自編之「van Hiele 第四幾何思考層次測驗」探討國中三年級學生於 van Hiele 第四幾何思考層次的表現情形，並同時施測前三層次的「吳─薛氏 van Heile 幾何概念測驗」，以進一步分佈台灣中部地區國三學生的 van Hiele 幾何思考層次的分佈情形。研究對象為台灣地區三個縣市的國中三年級學生，共計 357 位。將所蒐集到的資料以描述統計及推論統計的方法分析後，探討不同縣市、不同性別的受試者在第四幾何思考層次測驗表現的差異情形，以及在 van Hiele 幾何層次分佈的差異情形。本研究為國家科學委員會專案研究計畫（計畫名稱：國中學生 van Hiele 幾何思考層次之研究。編號：NSC 87-2511-S-142-003）之部份成果。共有以下幾點發現：一、受試者在第四幾何思考層次測驗的答對率為 53%，乙縣市的答對率為 58 ％，高於甲、丙兩縣市的 56％與 37％，所有樣本女生答對率為 55%，高於男生的 51%。二、從不同縣市學生在「 van Hiele 第四幾何思考層次測驗」中看出，縣市會影響測驗表現，乙縣市學生表現稍優於甲縣市學生，但未達顯著差異，但甲、乙兩縣市的學生表現都明顯優於丙縣市學生。三、從不同性別學生在「 van Hiele 第四幾何思考層次測驗」中看出，在第四幾何思考層次測驗的答對率表現是女生優於男生，但未達顯著差異，即性別因素不會影響此測驗的通過率。四、所有受試者在 van Hiele 幾何思考層次的分佈情形為：層次一：1.4%；層次二：15.1%；層次三：44.5%；層次四：37.0%。而屬於跳躍情形的不到 2.0%。五、在三個不同縣市的受試者表現中，幾何思考層次分佈情形很明顯的存在著城鄉之間的差距，其中不同縣市在層次二與層次四的分佈情形有顯著差異。

(3)

六、在幾何層次的分佈情形中，丙縣市學生多分佈於層次二，甲縣市學生多分佈於層次四。

七、在不同性別的受試者表現中，各層次的分佈情形都沒有顯著差異，即性別不會影響幾何思考層次的分佈情形。

(4)

A study of the van Hiele model of geometric thinking

of Ninth-Grade students from central Taiwan.

Abstract

The purpose of this study was to investigate the van Hiele model of geometric thinking of Ninth-Grade student. The research objects are 357 junior high school students from counties in central Taiwan. The names of the three counties are coded as A, B, C, in this paper. The collected data are analyed by descriptive-Statistics and inferential-Statistics. After data processing, the following conclusions were drawn from this study:

This research has the following findings:

1. The pass rate of the fourth geometric thinking level performance test were 53%. 2. The perfomance of the research objects in 3 counties shows a distinct gap of ability

between cities and counties. The students in City A and B have better performance in the fourth geometric thinking level performance test. Those in County C have the lowest performance.

3. Students of different sex in the fourth geometric thinking level performance test pass rates are girls better than boys, but no significant difference. Gender does not affect the adoption rate of this test.

4. The distributions of the van Hiele levels of geometric thinking of junior high school students, from level 1 to level 4, were: 1.4%、15.1%、44.5%、37.0%

5. The distributions of the van Hiele levels of geometric thinking of the research objects in 3 counties shows a distinct gap of ability between cities and counties, especially in Level 2 and Level 3.

(5)

City A were almost in Level 4. Those in County C were almost in Level 2.

7. The distributions of the van Hiele levels of geometric thinking of the research objects of different sexes have no obvious distinctions in van Hieles’ geometry theory. Gender does not affect the distributions of the van Hiele levels of geometric thinking.

(6)

目

錄

目錄 ...v 圖目錄 ... vii 表目錄 ... ix 第一章緒論 ...1 第一節研究背景與動機 ...1 第二節研究目的 ...4 第三節名詞解釋 ...5 第四節研究限制 ...6 第二章文獻探討 ...7 第一節 van Hiele 理論 ...7 第二節探討九年一貫數學領域課程綱要幾何概念與 van Hiele 理論的關聯 ...15 第三節其他相關研究 ...18 第三章研究方法與實施流程 ...24 第一節研究實施的步驟與設計 ...24 第二節研究對象 ...26 第三節研究工具 ...28 第四節資料處理與分析 ...45

(7)

第四章研究結果與討論 ...48 第一節學生在第四幾何層次測驗的選填分析 ...48 第二節各層次測驗的平均答對題數及通過率 ...62 第三節 van Hiele 幾何思考層次通過情形 ...65 第四節 van Hiele 幾何思考層次分佈情形 ...68 第五節縣市、學校、性別在「van Hiele 第四幾何思考層次測驗」的變異情形...78 第六節不同縣市、學校、性別在 van Hiele 幾何思考層次分佈情形及其卡方檢定 ...85 第五章研究結論與建議 ...91 第一節結論 ...91 第二節反省與建議 ...95 文獻參考 ...98 一、中文部分 ...98 二、英文部分 ...102 附錄一：van Hiele 第四幾何思考層次測驗修改審查表 ...107 附錄二：「van Hiele 第四幾何思考層次測驗」預試題本 ...119 附錄三：「van Hiele 幾何思考層次測驗」正式施測題本 ...137 第一部份. ...137 第二部份. ... 168

(8)

圖

目

錄

圖 3-1-1 研究實施步驟 ...25 圖 3-3-1 測驗工具發展過程圖 ...30 圖 3-3-2 van Hiele 第四幾何層次測驗修改題目 1...35 圖 3-3-3 van Hiele 第四幾何層次測驗修改題目 2...37 圖 3-3-4 van Hiele 第四幾何層次測驗修改題目 3...38 圖 3-3-5 van Hiele 第四幾何層次測驗修改題目 4...39 圖 3-3-6 van Hiele 第四幾何層次測驗修改題目 5...40 圖 3-3-7 van Hiele 第四幾何層次測驗修改題目 6...41 圖 3-3-8 van Hiele 第四幾何層次測驗修改題目 7...42 圖 4-1-1 van Hiele 第四幾何測驗通過率較低題目 1...50 圖 4-1-2 van Hiele 第四幾何測驗通過率較低題目 2...51 圖 4-1-3 van Hiele 第四幾何測驗通過率較低題目 3...53 圖 4-1-4 van Hiele 第四幾何測驗通過率較低題目 4...54 圖 4-1-5 van Hiele 第四幾何測驗通過率較低題目 5...55 圖 4-1-6 van Hiele 第四幾何測驗通過率較高題目 1...56 圖 4-1-7 van Hiele 第四幾何測驗通過率較高題目 2...57 圖 4-1-8 van Hiele 第四幾何測驗通過率較高題目 3...57

(9)

圖 4-1-9 van Hiele 第四幾何測驗通過率較高題目 4...58 圖 4-1-10 van Hiele 第四幾何測驗通過率較高題目 5...59 圖 4-1-11 van Hiele 第四幾何測驗通過率較高題目 6...60 圖 4-1-12 van Hiele 第四幾何測驗通過率較高題目 7...61 圖 4-1-13 van Hiele 第四幾何測驗通過率較高題目 8...61 圖 4-1-14 van Hiele 第四幾何測驗通過率較高題目 9...62 圖 4-4-1 層次分佈情形折線圖 ...70 圖 4-4-2 各校層次分佈相對次數直方圖 ...72 圖 4-4-3 各縣市學生層次分佈百分比直條圖 ...73 圖 4-4-4 不同性別學生層次分佈百分比直條圖 ...74

(10)

表

目

錄

表 2-1-1 van Hiele 層次的評量標準...13 表 2-2-1 第四階段幾何能力指標與 Fuys 等人描述的行為能力對照表 ...16 表 2-3-1 相關研究分析表 1 ...19 表 2-3-2 相關研究中研究對象的層次分佈情形比較 ...20 表 2-3-3 相關研究分析表 2 ...21 表 3-2-1 研究樣本人數分配表 ...28

表 3-3-1 Fuys 針對 van Hiele 幾何思考層次四的描述 ...31

表 3-3-2 「van Hiele 第四幾何思考層次測驗」題型分佈明細表...33 表 3-3-3 預試的難度、鑑別度分析表 ...43 表 4-1-1 「van Hiele 第四幾何思考層次測驗」各題平均答對率...49 表 4-2-1 各層次平均答對題數及答對率（%） ...63 表 4-2-2 各校各層次平均答對題數及答對率 ...64 表 4-2-3 各縣市在各層次測驗的答對率 ...65 表 4-2-4 各縣市在各層次測驗的答對率 ...65 表 4-3-1 各層次通過人數及比例 ...66 表 4-3-2 各縣在各層次通過人數及比例 ...67 表 4-3-3 各校在各層次通過人數及比例 ...68

(11)

表 4-4-1 層次加權得分情形 ...69 表 4-4-2 受試樣本在各層次分佈情形 ...70 表 4-4-3 各校在各層次人數分佈情形及百分比 ...71 表 4-4-4 各縣市學生在 van Hiele 幾何思考層次的分佈情形...73 表 4-4-5 不同性別學生在 van Hiele 幾何思考層次的分佈情形...74 表 4-4-6 層次分佈情形 t 檢定 ...75 表 4-4-7 各縣市層次分佈情形 t 檢定 ...76 表 4-4-8 各校層次分佈情形 t 檢定 ...77 表 4-4-9 不同性別在層次分佈情形 t 檢定 ...77 表 4-5-1 縣市、學校、性別在答對題數的平均數、標準差分析表 ...79 表 4-5-2 不同縣市、學校、性別學生在答對題數之變異數分析 ...80 表 4-5-3 不同縣市單因子變異數 ANOVA...81 表 4-5-4 不同學校單因子變異數 ANOVA...81 表 4-5-5 性別獨立樣本 t 檢定 ...82 表 4-5-6 不同縣市學生在第四幾何思考層次得分的差異情形 ...83 表 4-5-7 不同學校學生在第四幾何思考層次得分的差異情形 ...84 表 4-6-1 縣市在幾何層次分佈情形的列聯表 ...86 表 4-6-2 縣市差異的卡方檢定 ...86 表 4-6-3 各層次間縣市差異的卡方檢定（Chi-Square） ...86

(12)

表 4-6-4 學校在幾何層次分佈情形的卡方考驗 ...88 表 4-6-5 學校差異的卡方檢定 ...89 表 4-6-6 各層次間學校差異的卡方檢定 ...89 表 4-6-7 性別在幾何層次分佈情形的卡方考驗 ...90 表 4-6-8 性別差異的卡方檢定 ...90 表 4-6-9 各層次間性別差異的卡方檢定 ...90

(13)

第一章

緒

論

本研究主要是以 van Hiele 的幾何層次理論為基礎，來探討台灣中部地區國中學生在 van Hiele 幾何思考層次的分佈情形。本章主要說明本論文的研究概述，本章共分成四節，分別來探究本研究的研究動機與目的、待答問題、名詞定義與研究的限制等，第一節介紹本論文的研究動機；第二節介紹本論文的研究目的；第三節為名詞解釋；第四節為研究限制。

第一節

研究背景與動機

人是視覺的動物，為了生存，人類天賦的「形」或「幾何」直覺，遠比一般人所想像要豐富堅實。幾何不但是數學教育中的重要課題，而且也是較易學習、較有趣的教學單元（教育部，2008，p.188）。在 2005 年教育部公佈的數學領域正綱中，明確指出國中幾何教學的目標，首先在於提供學生日後有用的核心幾何知識，其次是提供豐富的背景，可以展示數學推理證明的過程與威力，而推理能力的培養正是國中數學教育的重點之一。幾何教學起初仍以學生的幾何直覺經驗為前導，但從國中階段開始強調幾何觀念的明確定義，及幾何相關量的計算，甚至代數演算，在此同時學生應開始學習閱讀幾何性質的嚴格推理，最後，學習自己動手寫出較短的證明。這對於日後數學邏輯推理能力及以抽象為主的高中數學學習皆很重要（教育部，2005）。我國中小學數學課程從西元 1975 年，將幾何教材的「形」獨立出來至今，歷經三次的課程修訂，自 1993 年教育部公佈實施九年一貫課程，「幾何」正式成為五大主題之一，由許多相關研究（Wu, 1994；朱建正，1996；吳德邦和謝翠玲，1998）可看出有關數學領域的幾何主題教材，主要依據 van Hiele 夫婦所發展的幾何思考模式與層

(14)

次理論來編寫；依據這個理論，將中小學幾何課程分為三階段，第一階段為小學一～三年級，此階段幾何概念的學習，著重在對於幾何形體的探索、認識與具體操作；第二階段為小學四～六年級，學習的重點在於掌握幾何形體構成（如角、邊、面）的要素及其數量性質（如角度、邊長、面積），來描述特殊幾何形體的特徵與性質；第三階段則為國中一～三年級，學習重點由直觀、歸納轉入幾何推理與證明，並開始學習閱讀幾何性質的嚴格推理。由國內外許多關於 van Hiele 幾何思考的研究（紀小玉，2006；吳德邦，1998， 1999，2000a，2000b，2001a，2002，2003，2004，2005；吳德邦、戴五騰和謝翠玲， 2001b；林玉琦，2003；黃盈君，2001；盧銘法，1999；薛建成，2003；Baynes,1998; Clements & Battista, 1992; Fuys, 1985; Golinskaia, 1997; Lee, 1999; Matos,1999; Usiskin, 1982; van Hiele, 1986; Wu, D. B., 1994; Wu & Ma, 2010, 2009, 2005a, 2005b; Wu, Ma, & Lan, 2005），提出有關 van Hiele 理論與該理論的幾何思考層次的相關報告可知， van Hiele 理論中所提到的階層是存在的，學生在學習幾何也有階層性，且學生在幾何的層次存在次序性，這些發現可作為數學幾何教材編寫的參考依據，可見 van Hiele 幾何思考理論相當受到重視。

自 1995 以來，每隔四年舉辦一次的國際數學與科學教育成就趨勢調查（Trends in Mathematics and Science Study 2007，簡稱 TIMSS），在 1999 及 2003 年，國二學生在

數學成就的五個面向，「幾何」在 1999 年排名第四，在 2003 年排名第二，且台灣學生在五個領域中，以「幾何」分數最高（張芳全，2006），最近一次的調查中(2007)，我國國中二年級學生在數學成就整體表現位居世界前五名，數學領域的內容領域主題分為：數（Number）、代數(Algebra)、幾何(Geometry)、資料分析呈現與機率(Data and Chance)，台灣學生在「幾何」主題得分排名第一，且顯著優於新加坡、香港及日本（梁育維和陳芳慶，2009），以教材編擬順序，國二學生正開始學習「幾何」主題，直到國三上學期將「幾何」主題結束。由 TIMSS 的調查結果看到國內學生在「幾何」的表現相當突出，但綜觀國內從

(15)

事 van Hiele 幾何思考層次的研究（吳德邦、沈紀伶、馬秀蘭，2009；左台益、梁勇能，2001；陳進春、吳德邦，2005），卻顯示出國中生、專科生多分佈於 van Hiele 幾何層次中，層次一及層次二的階段，此結果與 TIMSS 的調查似乎有所矛盾，倘若台灣的國中學生能在「幾何」主題勝過其他國家，不應僅停留在 van Hiele 第一及第二幾何思考層次，除此之外，關於 van Hiele 幾何思考層次分佈情形的研究，目前有使用吳德邦（1998）所翻譯的 Usiskin 測驗工具中文版探討國中生及專科學生在 van Hiele 幾何思考層次分佈情形，（吳德邦、沈紀伶、馬秀蘭，2009；左台益、梁勇能，2001；陳進春、吳德邦，2005），也有使用自編題目，探討國小四與六年級學生 van Hiele 幾何思考層次分佈情形（吳德邦、馬秀蘭、陳姿良、許天維，2010；何森豪，2001；李坤達、葉啟村，2005），從文獻中發現測驗工具的不同造成國小學生的幾何思考層次高於國二及專科生。以 van Hiele 理論中各層次的特徵來看，僅用 5 題測驗每一層次的表現，無法精確判斷學生在幾何層次的分佈情形，所以造成多數的學生都停留在較低層次。由文獻中可看出，缺乏統一的測驗工具，使得在測驗不同學習階段學生時，沒有一致的標準，而造成國中生的幾何思考層次竟低於國小學生，目前國內已經有吳德邦、薛建成（2003）共同發展的「吳–薛氏 van Hiele 幾何概念測驗」，可測驗出層次一～層次三的分佈情形，研究者將繼續編擬層次四的題目，使測驗工具更為完整。編制出「 van Hiele 第四幾何層次測驗」後，研究者將以學完全部幾何教材的國三學生為研究對象，並配合「吳–薛氏 van Hiele 幾何概念測驗」，測驗台灣中部地區國三學生在 van Hiele 幾何思考層次的分佈情形。

(16)

第二節

研究目的

本研究計畫之目的是要探討台灣中部地區國三學生是否達到 van Hiele 幾何思考層次的第四層次，研究對象以學完全部幾何教材的國三學生為主，分析其在 van Hiele 第四幾何思考層次的表現，並探討台灣中部地區國三學生在 van Hiele 幾何思考層次的分佈情形。

一、研究目的

（一）根據「van Hiele 幾何理論」發展一套符合 van Hiele 第四幾何思考層次，且具良好信度與效度之工具。（二）探討台灣中部地區國中學生於「van Hiele 第四幾何思考層次測驗」的表現差異。（三）探討臺灣地區之國中學生於 van Hiele 幾何思考層次分佈的差異情形。（四）探討臺灣地區不同性別之國中學生於 van Hiele 幾何思考層次分佈的差異情形。。（五）探討臺灣地區不同縣市之國中學生於 van Hiele 幾何思考層次分佈的差異情形。

二、本研究待答的問題

（一）根據「van Hiele 幾何理論」，編製一套符合 van Hiele 第四幾何思考層次且具良好信度與效度之測驗工具。

(17)

（三）國三學生在 van Hiele 幾何思考發展層次的分佈情形為何？（四）不同性別之國三學生於幾何層次概念上的表現為何？（五）不同縣市之國三學生於幾何層次概念上的表現為何？

第三節

名詞解釋

本節將研究中所提及的相關名詞，做更詳細的定義與說明，茲分述如下：

一、van Hiele 幾何思考層次：

本研究所提及的 van Hiele 幾何思考層次，係指 van Hiele（1986）所提出的五個層次，分別為層次一：視覺的（visual）層次、層次二：描述的（descriptive）層次、層次三：理論的（theoretical）層次、層次四：形式邏輯的（formal logic）層次、以及層次五：邏輯法則本質的（the nature of logical laws）層次。

二、幾何概念：

本研究中的幾何概念包括：三角形、四邊形和圓形及複合平面圖形的概念。

三、甲、乙、丙三縣市

甲縣市：位於台灣省中部，東屏中央山脈、西臨臺灣海峽，地勢大部低平。土地面積約為 2 萬平方公里，行政區域包括有三個市，五個鎮及十三個鄉。乙縣市：位於台灣西北部，三面環山，土地面積 1,400 平方公里，全縣的地形大

(18)

多為丘陵，台地及山地。目前因社會經濟結構改變，使得人口總數迅速成長。丙縣市：本縣位於臺灣的中北部，西濱臺灣海峽。全縣東西寬約 64 公里，南北長約 50 公里，面積約有 1,800 平方公里。境內山多平原少，為標準農鄉，各類農產豐富，居民以米飯、甘藷為傳統主食。

四、國中學生：

係指 2010 年就讀於三縣市之公立國民中學三年級學生，不包括特殊班學生。

第四節

研究

研究限制

研究

限制

本研究因受限於研究經費、時間及人力、物力等因素，故有一些無可避免的限制：一、由於經費及人力的限制，本研究僅限於臺灣地區三縣市之國民中學在學學生，無法擴及全國之樣本研究。二、本研究依據 van Hiele 幾何理論，僅開發第四幾何思考層次的測驗工具，最後一個層次則留待以後有意研究的人再行討論。三、本研究編制的測驗以選擇題為主，無法充分討論學生在證明題表現，多元化題型留待以後有意研究的人繼續編制。四、本研究由於研究對象為台灣三縣市的在學學生，然因台灣中部地區幅員遼闊，誓必存在著嚴重的城鄉差距與語言的隔閡，然本研究不將語言能力的差異列入考量的範圍，留待後續相關的研究再行討論之。

(19)

第二章文獻探討

本章將探討與本研究相關的理論與研究，內容共分三節：第一節介紹有關 van Hiele 的幾何理論，第二節將介紹九年一貫課程綱要中第四階段「幾何」能力指標，與 Fuys 等人（1988）所提出的對於 van Hiele 第四幾何思考層次的描述；第三節探討國內外 van Hiele 幾何思考層次相關研究。

第一節

第一節 van Hiele

van Hiele

van Hiele 理論

理論

本研究所依據的理論基礎為 van Hiele 幾何思考層次理論及 Fuys 等人(1988)提出 van Hiele 層次各層次學生所表現的特質，本節先探討 van Hiele（1986）所提出的幾何思考層次理論及 Crowley(1987)特性，再探討 Fuys 等人(1988)提出 van Hiele 層次各層次學生所表現的特質，分述如下：

一、 van Hiele 幾何思考層次

荷蘭教育家 Piere Marie van Hiele 及 Dina van Hiele-Geldof 夫婦，在西元1957年提出幾何思考層次理論。根據 van Hiele 的理論，幾何思考的發展模式共分為五個層次，每個層次都有各自獨特的發展特徵。對於這五個層次的描述方式，國內外的研究者有兩種不同的表達方式，一部份研究者使用「層次0、層次一、層次二、層次三、層次四」來描述這五個幾何思考層次（黃盈君，2001；盧銘法，1999；Fuys, 1985; Golinskaia,1997），另一部份研究者則使用「層次一、層次二、層次三、層次四、層次五」來描述 van Hiele 的五個幾何思考層次（吳德邦，1998，1999，2000a，2000b， 2001a，2002，2003，2005；吳德邦和薛建成，2004；吳德邦、戴五騰和謝翠玲，2001；

(20)

林玉琦，2003；薛建成，2003；Usiskin, 1982; van Hiele, 1986; Wu, D. B., 1994; Wu & Ma, 2005a, 2005b, 2006, 2007）。 Van Hiele（1986）自己在書中提到，我現在所說的層次二就是以前的層次一，層次三就是以前的層次二，以此類推。本研究採用 van Hiele(1986) 對層次的說法，分別為層次一：視覺的 (visual) 層次、層次二：描述的 (descriptive) 層次、層次三：理論的 (theoretical) 層次、層次四：形式邏輯的 (formal logic) 層次、層次五：邏輯法則本質的 (the nature of logical lows) 層次。茲把這五種層次介紹如下：

（一）層次一：視覺的 (visual) 層次此層次的學童可以分辨、稱呼、比較及操弄幾何圖形。學童可以透過視覺觀察具體實物的整體輪廓，來辨認幾何形體，並依據物體的外觀辨認出物體的形狀，且只要圖形外表特徵差異稍大，就不會誤認長方形為正方形或橢圓為圓形。在視覺下差異不大的圖形，學童也能透過移動或旋轉等方式來協助辨識幾何圖形。（二）層次二：描述的 (descriptive) 層次此層次的學童具有豐富的視覺辨識經驗，除了可以掌握圖形的構成要素，還可以依據觀察形體的結果來分析幾何圖形的構成要素與發現圖形間的共有性質或規則，但是無法解釋性質之間的關係。例如兩個不同的三角形，三邊長都不相等，但面積可能相等，此階段的學生無法經由推理了解其原因為何，只能依其經驗建立同一累圖形所具有之特性，並運用圖形之特性來解題。（三）層次三：理論的 (theoretical) 層次此層次的學生可以透過非正式的論證把先前發現的性質作邏輯的聯結，並依據幾何圖形的性質進行非正式的推演，進而探索圖形內在屬性關係及各種圖形之間的相互包含關係，例如：一個四邊形四個角都為 90°即為長方形，而正方形是長方形的一種，當一個長方形四邊都相等時，它是一個正方形。但此階段

(21)

的的學生還不能進行有系統的證明。（四）層次四：形式邏輯的 (formal logic) 層次能夠經由抽象推理的過程，證明幾何問題及其相互間的關係，且知道證明的方法不只一種，即學生不用拿到實體物，就能夠證明三角形的全等，而是利用邏輯推理的方法，來證明幾何的性質。例如：能證明三角形內角和是 180 度；以及能了解正方形邊長都相等，但邊長都相等的四邊形不一定都是正方形等。（五）層次五：邏輯法則本質的(the nature of logical lows)層次

達到此層次者已可以較嚴謹的程度分析或比較不同的公設體系，建立定理，並比較不同系統的特性，例如歐氏幾何和非歐氏幾何的比較。能夠了解抽象系統的幾何概念並了解公設系統的性質是一致性、獨立性、以及完全性，甚至可以自創一種幾何公設系統。此層次可達到的人並不多，即使是專業的數學工作者也不容易達到。

二、 van Hiele 幾何思考層次之特性

了解學生的認知屬於哪一個 van Hiele 幾何思考層次，可作為教學者在教學時的參考，且 van Hiele（1986）指出：幾何思考層次具有某些基本固有的特性存在，層次的發展不是因為年齡成長或成熟度的增加而進展，主要是依賴教學的引導，是循序漸進的，依據 Crowley(1987) 對 van Hiele 幾何思考層次特性的描述為：次序性 (sequential)、提昇性 (advancement)、內因性與外因性 (intrinsic and extrinsic)、語言性 (linguistics)、以及不配合性(mismatch)。各特性分別敘述如下：

（一）次序性(sequential)：

幾何思考層次的發展是循序漸進的，每一個層次的概念一定是來自於前一個層次的概念基礎。學生必須充分的學習所在層次的各種概念、知識，才能順

(22)

利進到下一個層次的學習。所以學生不可能還沒學會層次一的各項概念、知識，但能力就已經到達層次二，或直接跳過層次二的學習到達層次三。（二）提昇性(advancement)：學生層次的提昇是經由教學，而非個體的年齡成長或個體的成熟而發展，也沒有一種教學方式可以讓學生躍過某一層次而進入下一個較高的層次。 van Hiele (1986) 在書中曾經提到，學生幾何思考層次的進展，主要依賴教學而不是兒童的年齡成長或成熟度的增加。因此由一個層次發展到下一個層次並不是一個自然的過程，它是在教與學課程計畫的影響下而提昇的，也因此在進一步了解幾何層次的發展，可以作為幾何課程編排的參考。

（三）內因性與外因性(intrinsic and extrinsic)：

在幾何思考層次中，某個層次的應有目標，即為下一個層次的研究目標。林軍治(1992)也指出：在每一思考層次上，先前層次的內在性，變為目前層次的外在性。而對某些概念的瞭解，雖然在目前這個層次可能不明顯，但在下個層次卻是明確可知的(Clements & Battista, 1992)。

（四）語言性(linguistics)：每一個層次都有屬於該層次獨特的語言、符號，以及這些符號之間的關聯系統。每一層次有其專屬的獨特語言，在某一個層次中屬於正確的語言，到了另一個層次中，可能就必需經過修正才能符合。（五）不配合性(mismatch)：依據 van Hiele 幾何思考層次的語言獨特性，每個層次有它自己獨特的語言、符號。若學生是屬於層次一，然而教學設計，語言符號的運用，卻是層次二或層次三，那麼學生的學習成效就會不好，老師的教學效果就很差。這也就

(23)

三、Fuys 等人（1988）提出學生在各層次所表現之特質

Fuys, Geddes, & Tischler（1988）所提出針對 van Hiele 層次的描述和學生反應的例子為基礎，更進一步深入探究在每一個層次中，學生所能達到的水準，而提出對應 van Hiele 幾何思考每個層次發展，學生所能表現或達到的具體行為能力：（一）層次一：視覺層次（visualization） 1. 能依據幾何圖形的整體外貌辨識形狀。 2. 能作圖、繪製（draw）或複製（copy）一個圖形。 3. 依據標準或非標準的形式。 4. 能依據圖形整體外貌，進行比較和分類活動，並能用語言描述幾何圖形。（二）層次二︰描述層次（descriptive） 1. 能確認並檢驗圖形組成元素之間的關係。 2. 能說出組成元素的名稱，並使用適當的語彙描述之間的關係。 3. 能依據組成元素之間的關係，比較兩圖之異同。 4. 能經由實驗發現特殊圖形之性質，並能歸納之；能利用圖形的已知性質或洞察隱含的性質去解決幾何問題。（三）層次三︰理論的層次（theoretical） 1. 能辨認某類圖形的各組性質，並檢驗這些性質充分性。 2. 形成並使用某類圖形之定義。 3. 能提出非形式化的論證。 4. 能非形式地辨識敘述及逆敘述之間的不同。 5. 不了解定義及基本假設的需要。 6. 尚未建立定理網路間的內在關係。

(24)

（四）層次四︰形式邏輯的層次（formal logic） 1. 能辨識出正式定義的特性和等價的定義。 2. 在公設系統下，證明在層次二所說明的定理。 3. 學生在一公設系統下，建立定理和定理間的關係，了解公設、公理、定義、定理、未定義名詞及證明的相互關係和角色，了解定理與逆定理的區別和證明的必要與充分條件，可寫出邏輯證明。

（五）層次五︰邏輯法則本質的層次（the nature of logical laws）

1. 學生能嚴格地在不同的公設系統下建立定理，並分析比較這些系統。 2. 找出解決一組問題的一般性方法。

3. 比較公設系統，並自動地探討公設的變動對結果的影響。

四、 van Hiele 層次之評量模式

在評量準則方面，為了解受試者屬於 van Hiele 幾何思考層次的哪一個層次，參考英國 CSMS（Concepts in Secondary Mathmatics and Science Study，簡稱 CSMS）小組，為了分析學生的理解層次而發展了試題層次分析的方法（Hart, 1981），其方法是訂定五個原則，依據此五原則將測驗的試題歸類於各層次，並根據試題層次，將受試學生分屬到各概念層次。其原則敘述如下： 1. 同一層次的試題難度相近。 2. 同一層次試題間的齊性係數(homogeneity coefficient)ψ值，需在可接受的範圍內（約 0.4 左右）。 3. 同一層次的試題與較易及較難層次的試題，利用ψ值或 H 值應該可以互相連貫。 4. 所有試題應具有某些共同的數學概念。 5. 學童答對該層次試題三分之二以上，就算通過該層次。通過某一層次的學

(25)

生，應同時通過所有比該層次為低的層次，否則成為錯誤的學童樣本，錯誤的學童樣本不得超過 7%。依照上述原則將試題歸類於各層次後，才能決定所有學生所屬的層次，其決定的步驟是：先刪除錯誤的學生樣本後，第一個沒有通過之層次的低一層次，就是該學童所屬的層次。按此步驟分完層次就可以知道學童之理解層次的分佈狀況（劉湘川、許天維、林原宏、郭伯臣，1994）。探討 van Hiele 幾何思考層次分佈情形的相關研究中，多數的研究都以受試者在測驗表現上答對的數目為評量的標準。許多研究以通過全部題數的五分之四（Usiskin, 1982; Senk, 1989; Millman, 1973; 吳德邦，1999；左台益和梁勇能，2001），也有研究者（，薛建成 2003；左台益、梁勇能，2001）採取五分之三的標準，或其他如答對 70% 的題目（林軍治，1992）或通過總題數三分之二為標準（盧銘法，1996），不同研究中採取的標準如表 2-1-1。參考相關研究，本研究將以通過某一層次答對題數是全部題數的五分之三作為通過標準。表 2-1-1 van Hiele 層次的評量標準研究者通過標準 Usiskin(1982) 以某一層次答對的題數是全部題數的五分之三或五分之四為達到該思考層次的標準。 Senk（1989）答對子測驗的五分之四為通過的標準。 Millman(1973) 答對子測驗的五分之四為通過的標準。林軍治（1992）在某一層次答對率達 70%為達到該思考層次的標準。盧銘法(1996) 每一概念題中答對的題數超過三分之二為標準。吳德邦（1999）某一層次答對的題數是全部題數以五分之四為達到層次的標準左台益和梁勇能（2001）以某一層次答對的題數是全部題數的五分之三或五分之四為達到該思考層次的標準。

(26)

表 2-1-1 van Hiele 層次的評量標準（續）研究者通過標準薛建成(2003) 某一層次答對的題數是全部題數的五分之三為達到該思考層次的標準。吳德邦、馬秀蘭和沈紀伶（2008）某一層次答對的題數是全部題數以五分之四為達到層次的標準

五、層次的評量與界定

在 van Hiele 模式的研究中，幾何思維層次的評量與界定方式，扮演著非常重要的角色，且大多數研究者是以紙筆測驗上答對的題數作為評量的標準，決定學生之思維層次( Gutierrez & Jaime，1987；Usiskin，1982 )，或者依據訪談期間評定學生在每個活動中所展現的思維特質來加以決定( Burger & Shaughnessy ，1986 )，傳統上，對學生思維層次之評定多屬於單一層次，然而研究發現，學生在回答開放性問題時，多數展現出一個主要的層次，但很多學生也在其答案中清楚的反映出其他層次的存在，且有學生的答案呈現出兩個連續的層次。所以 Gutierrez & Fortuny ( 1991 )提出下面兩個論點︰

1. 為了對於目前學生的幾何推理有更完整的看法，我們必須考慮學生在 van Hiele 每一層次上的能力，而不是只做單一層次的認定。

2. van Hiele 層次的連續性意味著層次的獲得不是立即發生，而是需要一段時間的學習累積。

(27)

第二節

探討九年一貫數學領域課程綱要幾何概念與

van Hiele

van Hiele 理論的關聯

理論的關聯

教育部頒布 95 數學領域正綱，數學學習領域將九年國民教育區分為四個階段：第一階段為國小一至二年級，第二階段為國小三至四年級，第三階段為國小五至六年級，第四階段為國中一至三年級。另將數學內容分為「數與量」、「幾何」、「代數」、「統計與機率」、「連結」等五大主題（教育部，2008）。國中的幾何課程，重點將由直觀、歸納轉入幾何推理與證明，並開始學習閱讀幾何性質的嚴格推理，此與 van Hiele 理論中第四層次：形式邏輯的層次，所提到的此階段的學生需具備抽象思考的推理能力，能理解幾何問題之解決，需具備的充分或必要條件，有相同的概念（教育部，2005）。以下就國中階段「幾何」主題課程綱要介紹中，學生應達到的能力指標，配合 Fuys 等人（1988）對於 van Hiele 第四層次的描述，認為學生所能表現或達到的具體行為能力，相配對之後如表 2-2-1。

(28)

表 2-2-1 第四階段幾何能力指標與 Fuys 等人描述的行為能力對照表第四階段幾何能力指標 Fuys 等人對層次四的行為描述 S-4-01 能理解常用幾何形體之定義與性質 S-4-07 能理解平面上兩平行直線的各種幾何性質。 S-4-11 能理解一般三角形的幾何性質。 S-4-14 能理解圖形縮放前後不變的幾何性質。 S-4-16 能理解三角形內心、外心、重心的意義與性質。 S-4-17 能理解圓的幾何性質。能辨識出正式定義的特性和等價的定義。 S-4-02 能指出滿足給定幾何性質的形體。 S-4-03 能透過形體之刻畫性質，判斷不同形體之包含關係。 S-4-12 能理解特殊三角形 ( 如正三角形、等腰三角形、直角三角形) 的幾何性質。 S-4-13 能理解特殊四邊形(如正方形、矩形、平行四邊形、菱形、梯形) 與正多邊形的幾何性質。 S-4-19 能針對問題，利用幾何或代數性質做簡單證明。在公設系統下，證明在層次二所說明的定理。

(29)

表 2-2-1 第四階段幾何能力指標與 Fuys 等人描述的行為能力對照表（續）第四階段幾何能力指標 Fuys 等人對層次四的行為描述 S-4-04 能利用形體的性質解決幾何問題。 S-4-05 能理解畢氏定理及其逆敘述，並用來解題。 S-4-06 能理解外角和定理與三角形、多邊形內角和定理的關係。 S-4-08 能理解線對稱圖形的幾何性質，並應用於解題和推理。 S-4-09 能理解三角形的全等定理，並應用於解題和推理。 S-4-15 能理解三角形和多邊形的相似性質，並應用於解題和推理。 S-4-18 能用反例說明一敘述錯誤的原因，並能辨識一敘述及其逆敘述間的不同。學生在一公設系統下，建立定理和定理間的關係，了解公設、公理、定義、定理、未定義名詞及證明的相互關係和角色，了解定理與逆定理的區別和證明的必要與充分條件，可寫出邏輯證明。由此節文獻可知，課程能力指標編制符合 van Hiele 幾何思考層次四：形式邏輯 ( formal logic )的層次所描述的具體行為，即學習過國中幾何課程後，學生應可達到 van Hiele 幾何思考層次四，研究者將進一步依照九年一貫分年細目的描述編制本研究工具以測驗研究對象是否達到 van Hiele 幾何思考層次四。

(30)

第

第三

三

三節

三

節

其他相關研究

本節將探討論國內外有關 van Hiele 幾何思考層次相關的研究。

一、國內研究：

國內從事 van Hiele 幾何測驗的相關研究很多，目前測驗層次分佈的工具有研究者使用 Usiskin 測驗工具中文版「van Hiele 測驗」，另一部份研究者則使用自編的工具探討研究對象在 van Hiele 幾何思考層次的分佈情形，以下分兩部份來探討。（一）Usiskin 測驗工具中文版「van Hiele 測驗」

在國內研究 van Hiele 幾何思考層次分佈情形的研究者很多，而測驗的工具目前多以由吳德邦翻譯的 Usiskin 測驗工具中文版，此測驗工具是由 van Hiele 所發展出來的思考模式，採用芝加哥研究計畫中 Usiskin（1982）等人編製之「van Hiele 測驗」，此測驗每一層次共 5 題，總共 25 題，相關研究的結論分述如表 2-3-1。

以下研究（吳德邦、沈紀伶和馬秀蘭，2009；左台益和梁勇能，2001；陳進春和吳德邦，2005）都以某層次答對題數五分之四為通過標準，可看出大部分國中生、專科生都分佈於層次一。相關研究結果的比較如表 2-3-2。

(31)

表 2-3-1 相關研究分析表 1 研究者(年代) 研究對象結果吳德邦、沈紀伶和馬秀蘭(2009) 台灣中部地區國中學生 1723 名大部分樣本（35%）分佈在 van Hiele 幾何思考層次一：視覺的層次。左台益和梁勇能（2001）台北縣的國二學生 222 名以標準 3/5 來看，大部分國二學生達到非型式演繹/抽象的層次（層次二），以標準 4/5 來看，大部分學生卻分佈在未達層次及視覺的層次（層次一）。陳進春和吳德邦 (2005) 台灣南部地區某專科學校一、三年級 464 名大部分的研究對象幾何思考層次分佈情形依序為：視覺的層次(44%)、描述的層次（22%）、未達層次（21%）、跳躍（9%）及理論的層次（5%）吳德邦、沈紀伶、馬秀蘭(2009)以中部五縣市的國中一到三年級學生為研究對象，共得有效樣本 1,723 名。發現大部分樣本（35%）分佈在 van Hiele 幾何思考層次一：視覺的層次，其次依序為層次二(19%)、層次 0 (16%)、層次三 (15%)、層次四 (3%)，屬於跳躍的只有 11%。左台益、梁勇能（2001）以 222 位台北縣的國二學生為對象，研究空間能力與 van Hiele 幾何思考層次相關性。研究發現標準 4/5 來看，大部分國二學生分佈在未達層次（35%）及視覺的層次(33%)，其次依序為層次三(11%)以及層次四(1%)，其研究未列出屬於跳躍情形的學生，以及依據其前測結果所以未施行第五層次的測驗題，所以資料中無數據。陳進春、吳德邦 (2005)，以台灣南部地區某專科學校一年級、三年級共 10 班， 464 位學生為研究對象，研究發現大部分的研究對象幾何思考層次分佈情形依序為：

(32)

視覺的層次(44.2%)、描述的層次（21.6%）、未達層次（20.9%）、跳躍（8.8%）及理論的層次（4.5%）。表 2-3-2 相關研究中研究對象的層次分佈情形比較研究者層次吳德邦、沈紀伶、馬秀蘭 (2009) 左台益、梁勇能（2001） 3/5 標準 4/5 標準陳進春、吳德邦 (2005) 層次 0 16.0 11.2 34.7 20.9% 層次一 34.7 20.8 33.2 44.2% 層次二 19.2 27.0 20.0 21.6% 層次三 15.3 34.3 11.1 4.5% 層次四 3.4 6.7 1.1 0 層次五 0.6 - - 0 跳躍 10.9 - - 8.8% 由以上研究可發現，無論是國中生或專科生，其幾何層次大多屬於層次一，有此結果令研究者認為，以每一層次五題來測驗是否達到該層次水準，會使得大部分的受試者無法通過標準，並不一定是因為該受試者未達到更高的層次，依照 Fuys 等人的描述，每一層次會出現的行為能力是以不同的形式展現，若只以 5 題來推斷是否達到該層次實有所偏頗。（二）不同的自編工具除了使用吳德邦翻譯的 Usiskin 測驗工具中文版外，相關研究者也有自行發展測驗工具，相關研究如表 2-3-3，不同的測驗工具所探討的對象，其分佈情形如表 2-3-4。

(33)

表 2-3-3 相關研究分析表 2 研究者(年代) 研究對象結果何森豪（2001）國小四、六年級各 10 班共 673 位學生四年級多處於層次一：視覺的層次 (51%)，六年級多處於層次二：描述的層次(62%) 李坤達和葉啟村（2005）台南縣、市國小六年級學童各兩班共 123 位大部分的學童幾何思考分佈情形大多為層次二：描述的層次（43.1%）何森豪（2001）利用盧銘法(1996)所編制的「國小學生幾何圖形概念測驗」，內容以「四邊形」概念為主，研究結果發現國小四、六年級學生達視覺的層次、描述的層次、形式演繹的層次分別有 160、254 和 215 人，以年級分類，四年級多處於視覺的層次(51.43%)，六年級多處於描述的層次(62.10%)。而李坤達和葉啟村（2005）以台南縣、市國小六年級學童各兩班共 123 位，實施國小六年級平行線試卷，內容分層次一試卷、層次二試卷、層次三試卷（簡稱 ABC 卷），其中層次一、層次二、層次三為 van Hiele 所稱的視覺、描述以及理論的層次，發現大部分的學童幾何思考分佈情形大多為描述的層次（43.1%），另外，城市型學生主要分佈在視覺的層次、描述的層次及理論的層次，而鄉鎮型學生主要分佈在視覺的層次、描述的層次及未達層次，至於學生在 ABC 三卷的表現上，性別都沒有顯著差異，但城鄉皆有顯著差異。從以上的研究可知，以吳德邦所翻譯的 Usiskin 測驗工具中文版，探討國中生、國二生、專科生的 van Hiele 幾何思考層次分佈情形（吳德邦、沈紀伶、馬秀蘭，2009；左台益、梁勇能，2001；陳進春、吳德邦，2005），發現國中生、專科生大多分佈在視覺的層次，而以自編的工具探討國小學生 van Hiele 幾何思考層次分佈情形（何森

(34)

豪，2001；李坤達和葉啟村，2005），以「四邊形概念」來說，發現小四多處於描述的層次；小六多處於形式演繹的層次。以「平行線概念」來說，發現大部分小六學生的幾何思考層次多位於描述的層次。

綜合以上發現，由於測驗工具的不同，造成國小學生的幾何思考層次高於國二及專科生，不符合 Crowley（1987）對 van Hiele 幾何思考層次特性的描述，所提到的「次序性」、「提昇性」， van Hiele 提到教學的引導是幾何層次提昇的主要原因，但經過學校數學課程的引導，不應該使得國小生在幾何層次的表現優於國中生或專科生。以 van Hiele 理論中各層次的特徵來看，僅用 5 題測驗該層次的表現，讓多數的學生停留在較低層次，目前國內有「吳–薛氏 van Hiele 幾何概念測驗」，可測驗層次一～層次三，研究者將繼續編擬層次四的題目，使測驗工具更為完整。

二、國外研究

Usiskin（1982）提出有 34% 的中學生未達層次一視覺層次的階段，有 26% 的學生在開學初是在層次一的階段，而在學期結束時仍停留在層次一的階段。Fuys 等人（1988）認為兒童屬於某一層次，則必須產生此一層次一致性的行為，但在層次一的兒童卻沒有顯示出相符的行為，如：無法對圖形命名。因此，在層次一視覺層次之前仍有更基本的層次存在。 Clements 等人（1999）研究顯示有比視覺層次更基本的層次存在，那就是第一層次（視覺層次）的前期 (pre-level 1)。在視覺層次前期的兒童能感覺到幾何圖形的形狀，但沒有感覺的活動，及缺乏視覺心像，不能辨別同類圖形的形狀，如不能區別正方形和長方形的不同，但卻可以區別正方形和圓形的不同（林碧珍，1993）。

Denis(1987)發現中學生在不同的幾何概念上，表現不同的 van Hiele 水準層次，且 van Hiele 水準層次是有階層性的。

(35)

Idris(1998)調查研究關於場獨立及場依賴的中學生在 van Hiele 幾何思考層次的影響，實驗組學生透過適當地教學活動能將幾何學習的更好。研究顯示教師可以在設計與選擇適當的教學活動中來提昇學生的幾何層次。

Matos(1999)針對美國 15、16 歲學生，對於角度的概念施予特別的課程學習，再經由紙筆測驗與訪談來探究學生的 van Hiele 幾何思考層次。研究發現 van Hiele 理論對於學生的幾何學習是有階層性的。

Lee(1999)針對學院學生在幾何的理解和證明方面與 van Hiele 幾何思考層次的相關性進行質與量的研究，其中量的研究呈現無顯著差異，但在質的研究中則發現 van Hiele 層次一的學生可提升到層次二，而層次三的學生則停留在原層次。該研究因限於時間因素，只有針對一個學期進行研究，若能進行長期性的研究可能有更多發現。

由國外研究可知， van Hiele 幾何思考層次理論中所提到的階層是存在的，學生在幾何的學習也有階層性、次序性。

從文獻中可知，目前國外的測驗工具有早期 Usiskin 發展的「van Hiele 測驗」，但因測驗題數太少，用以推斷學生在 van Hiele 幾何層次的分佈情形，似乎太過偏頗，容易使得大多數學生停留在層次一或層次二。

(36)

第三章研究方法與實施流程

本研究為探究台灣中部地區國三生在 van Hiele 幾何思考層次的分佈情形，為國家科學委員會專案研究計畫（計畫名稱：國中學生 van Hiele 幾何思考層次之研究。編號：NSC 87-2511-S-142-003）之部份成果。本章主要根據研究的動機、目的及文獻資料來探究研究之設計與實施方式，內容共分為四節。各節的內容茲分述如下：第一節說明本研究架構；第二節說明本研究的研究對象，第三節說明本研究的工具，第四節說明本研究的資料處理與分析。

第一節

研究實施的步

研究實施的步驟與設計

驟與設計

一、研究架構

本研究的實施步驟可分四階段：分別為準備階段、工具發展階段、施測階段與統整階段，分述如下： 1. 準備階段：分析幾何概念相關文獻、文獻探討、擬定研究計劃。 2. 工具發展階段：參考文獻以編擬測驗試題，本測驗工具乃依據「van Hiele 幾何思考理論模式」，開發 van Hiele 第四幾何思考層次的測驗工具、並參考 Fuys 等人（1988）提出針對 van Hiele 層次的描述，試題內容配合九年一貫「幾何」主題分年細目能力指標。測驗工具發展期間為 2009 年 9 月～ 2010 年 1 月，期間請多位數學教育專家（臺中教育大學教授）、臺中教育大學數學教育研究所進修之現職教師，

(37)

以及現職國中數學教師給予意見修正。 3. 施測階段：修訂後的測驗工具於 2010 年 1 ~ 2 月間進行預試，修正測驗試題後，選取正式施測對象，於 2010 年 3 ~ 4 月間進行正式施測。 4. 統整階段：施測結束後進行資料分析、歸納結論，並著手撰寫論文報告。各階段流程如圖 3-1-1 所示：分析幾何概念相關文獻文獻探討擬定研究計畫編擬測驗工具測驗工具編擬過程請參閱圖 3-3-1 選取預試對象抽樣進行預試修正測驗工具選取正式施測對象進行正式測試進行資料分析撰寫論文報告圖3-1-1 研究實施步驟

(38)

第二節

研究對象

本研究主要是以紙筆測驗為主，針對 van Hiele 所提出的幾何思考模式，並參照國內外有關幾何的相關研究來編擬測驗試題，以量的分析（quantitative analysis）來探討國三學生在 van Hiele 幾何思考層次四的表現。預試對象：丙縣某國中三年級學生共 104 位進行試題預試，其中有效樣本有92 位。正試施測對象：以台灣中部地區三個縣市（以下將以「甲、乙、丙」作為縣市的代稱），共 5 間學校（學校代號分別為ㄅ、ㄆ、ㄇ、ㄈ、ㄉ），排除先前已預試過的學校，每所學校隨機選取 1 ~ 4 個國三班級進行施測，其中甲縣的ㄅ校與ㄉ校因數學科採能力分組教學，所以ㄅ校選擇的是數學能力分組後的兩個A組班，而ㄉ校選擇的是分組後 B 組班，其他的ㄆ、ㄇ、ㄈ三校所抽取的班級為常態班。各縣市及各校概況如下：甲縣市：位於台灣省中部，東屏中央山脈、西臨臺灣海峽，地勢大部低平。土地面積約為 2 萬平方公里，行政區域包括有三個市，五個鎮及十三個鄉。選取三校的所在鄉鎮位置及概況如下：ㄅ校：位於甲縣東南隅的市鎮，全市總面積約 120 平方公里，丘陵地面積約佔全市五分之四，目前總人口數為 15 萬人，為人口成長相對快速地區。該校每年級平均 15～19 班，所選取的樣本為該校國三 2 個班，為數學能力分組的 A 組班。ㄆ校：位於甲縣西北方的鄉鎮，全鄉面積為 30 平方公里。鄉內有部份盆地平原與山坡地地形。人口約 8 萬人，人口密度為平均每平方公里約 2 千人，目前為人口高度成長的地區。該校每年級平均 18～19 班，所選取的樣本為該校國三 4 個班，為常態班。ㄉ校：位於甲縣之西北部的鄉鎮，全鎮總面積約 58 平方公里，為台灣西部海岸平

(39)

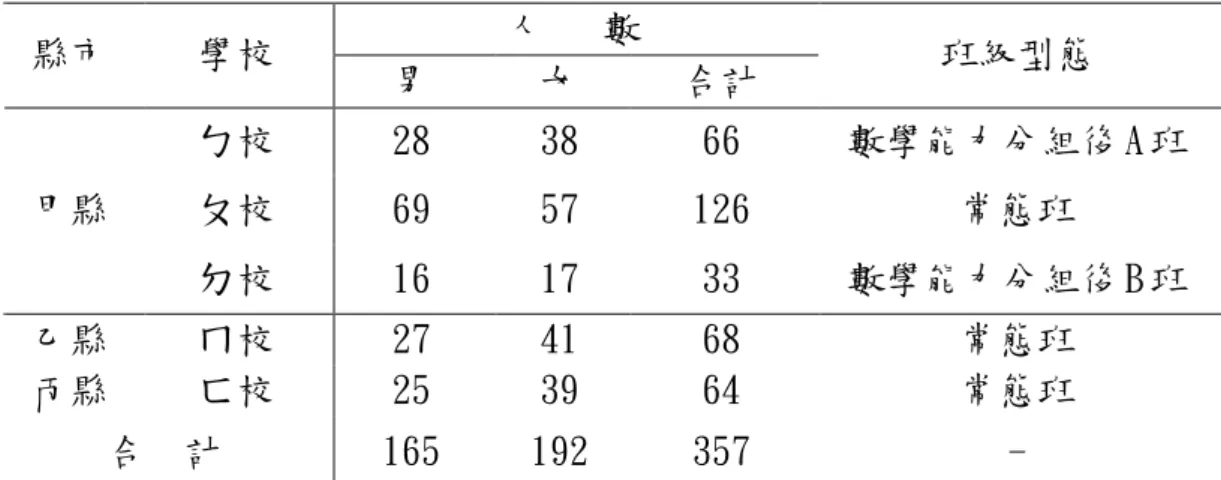
原的最北端。總人口數約為 7 萬人，目前屬於人口成長緩慢地區。該校每年級平均 12～13 班，所選取的樣本為該校國三 1 個班，為數學能力分組的 B 組班。乙縣市：位於台灣西北部，三面環山，土地面積 1,400 平方公里，全縣的地形大多為丘陵，台地及山地。目前因社會經濟結構改變，使得人口總數迅速成長。選取學校的所在位置如下：ㄇ校：位於乙縣市東北山區，西面為帶狀平地，其餘東南北三面連峰，多為丘陵起伏之山坡地。東西長約 21 公里，南北寬約 14 公里。全鎮面積約 125 平方公里，屬乙縣市平地鄉鎮中面積最大者，產業以農業為主。因對外交通便捷，帶動觀光休閒產業的發展。本鎮因幅員遼闊，因特殊環境，經行政院核定為平地原住民地區，境內有原住民、閩、客等族群，為多元族群融合的地區。該校每年級平均 8 班，所選取的樣本為該校國三 2 個班，為常態班。丙縣市：本縣位於臺灣的中北部，西濱臺灣海峽。全縣東西寬約 64 公里，南北長約 50 公里，面積約有 1,800 平方公里。境內山多平原少，為標準農鄉，各類農產豐富，居民以米飯、甘藷為傳統主食。選取學校的所在位置如下：ㄈ校：位於丙縣四個濱海市鎮之一，此市鎮位於丙縣西方，東西最大距離約 10 公里，南北最長寬幅約 20 公里，總面積約為 76 平方公里，為一良好之農牧地區，但因經濟、文化建設落後，尤其文康進修設施甚為缺乏，接受中等以上教育程度之年輕一代，因受農業收入偏低之影響，多不願留鄉工作，目前人口為負成長現象。該校每年級平均 4 班，所選取的樣本為該校國三 2 個班，為常態班。選取的人數分佈情形如表 3-2-1：

(40)

表 3-2-1 研究樣本人數分配表人數縣市學校男女合計班級型態ㄅ校 28 38 66 數學能力分組後 A 班ㄆ校 69 57 126 常態班甲縣ㄉ校 16 17 33 數學能力分組後 B 班乙縣ㄇ校 27 41 68 常態班丙縣ㄈ校 25 39 64 常態班合計 165 192 357 -

第三節

研究工具

本研究採取量的研究立場，將研究工具分為兩部份，第一部份為「吳–薛氏 van Hiele 幾何概念測驗」可探討研究樣本在「van Hiele 幾何思考理論模式」中層次一～層次三的表現情形，第二部份為自編的「 van Hiele 第四幾何思考層次測驗」探討研究樣本在「van Hiele 幾何思考理論模式」中層次四的表現情形，兩部份測驗完成後可綜合討論研究樣本於「 van Hiele 幾何思考理論模式」的分佈情形，兩部份研究工具詳列如下：

一、「吳–薛氏 van Hiele 幾何概念測驗」

此本測驗工具，為四選一之選擇題，在每一層次中皆包含三角形、四邊形及圓形這三種基本幾何圖形概念(詳見附錄（三）第一部份)。此測驗題目共有 70 題，第 1 題至第 25 題屬於層次一的部分，第 26 題至第 45 題屬於層次二的部分，第 46 題至第 69 題（含子題兩題）共25 題。其信度與效度如下（薛建成，2003）。

(41)

（一）信度方面

本測驗之信度考驗採用Cronbach α係數，整份試卷的α值為 .9447，顯示此份測驗的信度相當高。

（二）效度方面

本測驗之效度除了專家效度外，再與吳德邦（1998）所編之「吳氏 van Hiele 幾何思考層次測驗」求效標效度，相關係數為 .5338。本測驗的三個分測驗對總 測驗的一致性係數分別為： .5492、 .7619、 .7222 (p ＜ .01)，顯示三個分測 驗與總測驗的一致性相當高。

二、「 van Hiele 第四幾何思考層次測驗」

此部份的測驗工具為研究者自編的工具，編制歷程參考吳德邦、馬秀蘭、李懿芳（2007）所提出編制一個測驗的歷程，由於研究對象是以國中三年級學生為主，故僅針對 van Hiele 幾何思考層次理論的第四個層次來編製。

本測驗工具乃依據「 van Hiele 幾何思考的理論模式」，及 Fuys 等人（1988）提出針對 van Hiele 層次的描述，配合現行九年一貫課程數學領域分年細目，同時並參考市面上流通之國中數學教科書第四冊、第五冊（康軒版、南一版）、 90 ~ 98 基本學力測驗試題，以及平面幾何相關之研究（吳德邦，1998；薛建成，2003； Fuys, Geddes, & Tischler,1988）等參考文獻編製而成。

編擬試題期間經 5 次修正後，進行預試，根據預試的結果再行修正，成為正式施測題目。

(42)

1. 與教授共同討論編制紙筆測驗預試試卷，接著諮詢數學教育專家、數名實際從事教學活動的國中數學教師以及目前在數學教育學系碩士班進修之現職教師，對試題提供修正與建議，發展過程如圖 3-3-1。 2. 根據各專家的意見再加以編修筆試預試試題（見附錄（一））。 3. 選取國中三年級學生共 3 個班，104 名學生進行筆試預試（2010 年 1 月），再依據筆試預試結果，根據題目的難易度、鑑別度修正試題，編製成正式筆試施測工具（見附錄（三））。國中學生幾何思考層次評量工具相關資料及文獻蒐集試題擬定試題一～二版 (2009年9~11月) 試題三～四版 (2009年12月 ~ 2010年1月) 試題五版 (2010年2月) 專家學者意見修正預試確定試題試題最後修正 _正式施測進行資料分析圖3-3-1 測驗工具發展過程圖

(43)

（二）編製測驗的理論依據與試題重點

本測驗工具主要針對國中三年級學生設計，編制本研究工具的理論依據參考 Fuys 等人（1988）提出針對 van Hiele 幾何思考層次四的描述，各項描述詳如表 3-3-1，並配合教育部九年一貫課程綱要 95 數學正綱五大主題中「幾何」主題，其中第四層次符合第四階段的能力指標，第四階段八、九年級分年細目如表3-3-2。

表 3-3-1 Fuys 針對 van Hiele 幾何思考層次四的描述

層次四：學生在一個公設系統裡建立定理和定理網絡之間的相互關係。層次四：描述層次四:學生反應的例子 L4-1 認識對不定項、定義和基本假設的必要(即：假設) 學生列舉公理、假設，和歐幾里德平面幾何定理，並說明它們如何相互關聯的。 L4-2 辨認形式定義的特徵（例如，充分必要條件）和定義的等價關係。學生用充足的特性辨認確定的形狀（例如，平行四邊形），並推知其他充分的性質。 L4-3 在層次四能證明非正式解釋一個公理設置的關係。學生證明三角形的角度總和等於 180°時用嚴格的方式（例如，使用平行公設、鋸齒圖和梯子圖及有關角度的加法定理）。（鋸齒圖）（階梯圖） L4-4 證明定理及相關敘述之間的關係（例如：可逆、反元素、逆定理）學生證明若一個三角形是等腰，那麼它的底角是相等的，且可逆。應用矛盾證明，學生證明三角形的中線不會互相平分。

(44)

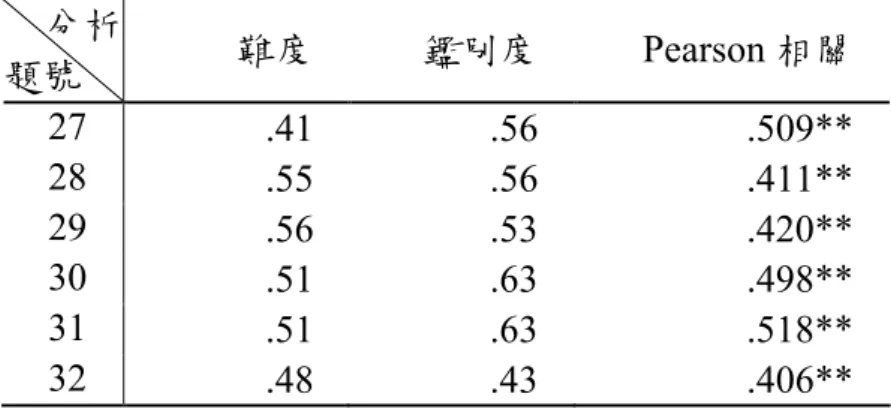
表 3-3-1 Fuys 針對 van Hiele 幾何思考層次四的描述層次四：學生在一個公設系統裡建立定理和定理網絡之間的相互關係。層次四：描述層次四:學生反應的例子 L4-5 建立定理的網絡之間的相互關係。學生能辨認在各種不同的定理(關於四邊形和面積規則的性質)中鋸齒圖和階梯圖的角色。 L4-6 比較和對比不同的證明定理。讓學生由歐幾里德幾何、座標幾何（或向量幾何）證明平行四邊形的對角線互相平分並比較兩種方法的證明。學生比較可供選擇的勾股定理證明 L4-7 審查改變最初的定義或假設的邏輯順序的作用。從〝垂直於同一線的兩條直線是平行的〞開始，學生研究如何證明其他的平行線定理。 L4-8 建立一個統一數種不同定理的一般原則。學生證明下列關係式，頂點位於兩條平行線的圖形面積為：面積 = 中線長 × 高 L4-9 創造從經常使用的簡單的公理模式證明來支持論點。學生在有限的幾何圖形定理提出證明。 L4-10 給予形式演繹的論點，但不探討公理本身或比較公設系統學生不審查一套具獨立性、一致性或完整性的公理。依據表3-3-1，配合九年一貫八、九年級分年細目，編制「 van Hiele 第四幾何思考層次測驗」，問答方式力求精簡、明確，題目敘述盡量口語化，使學生能充分了解題目真正的意涵。本測驗工具之試題分佈明細如表3-3-3，題 16 及題 19

(45)

表 3-3-2 「van Hiele 第四幾何思考層次測驗」題型分佈明細表層次四：描述九年一貫能力指標題號 L4-1 S-4-19 能針對問題，利用幾何或代數性質做簡單證明。 12. 13. 14. S-4-01 能理解常用幾何形體之定義與性質 1. 2. S-4-04 能利用形體的性質解決幾何問題。 3. 5. S-4-12 能理解特殊三角形 ( 如正三角形、等腰三角形、直角三角形) 的幾何性質。 8. L4-2 S-4-13 能理解特殊四邊形(如正方形、矩形、平行四邊形、菱形、梯形) 與正多邊形的幾何性質。 4. 6. L4-3 S-4-06 能理解外角和定理與三角形、多邊形內角和定理的關係。 7. S-4-18 能用反例說明一敘述錯誤的原因，並能辨識一敘述及其逆敘述間的不同。 17. 18. L4-4 S-4-05 能理解畢氏定理及其逆敘述，並用來解題。 23. L4-5 S-4-03 能透過形體之刻畫性質，判斷不同形體之包含關係。 29. 30. 31. 32 L4-6 16. 19. L4-7 S-4-07 能理解平面上兩平行直線的各種幾何性質。 20. 21. L4-8 22. S-4-09 能理解三角形的全等定理，並應用於解題和推理。 9. 10. 11. L4-9 S-4-15 能理解三角形和多邊形的相似性質，並應用於解題和推理。 15. 16. S-4-16 能理解三角形內心、外心、重心的意義與性質。 27. 28. L4-10 S-4-17 能理解圓的幾何性質。 25. 26.

(46)

（三）測驗編制過程

本測驗工具在試題初擬之時，作者們約略以每週討論一次的頻率，常交換意見，並予以修正，修正過程與專家意見詳見附錄（一）。 1. 第一次修正：(2009 年 9 月) 第一次修正內容如下： (1) 使用『方程式編輯器』後的字型、大小都要與本文一致，改為標楷體 14 號字。 (2) 太多題目為『以下哪些敘述不正確？』，改變題目的敘述方式，如圖 3-3-2： (3) 增加「證明三角形全等條件」的相關題型的題目 (4) 增加「圓形」相關題型的題目。 (5) 增加「相似形」相關題型的題目。

(47)

( ) 11.下列四個對四邊形ABCD的判別方式，何者錯誤？ (Ａ) 若OA=OC,OB=OD，可判定此四邊形為平行四邊形。 (Ｂ) 若OA=OC,OB=OD, AC=BD，可判定此四邊形為長方形。 (Ｃ) 若AC=BD, AC⊥BD，可判定此四邊形為正方形。 (Ｄ) 若OA=OC,OB=OD, AC⊥BD，可判定此四邊形為菱形。改為： ( ) 11.下列四個對四邊形ABCD的判別，哪些敘述正確？甲、若OA=OC,OB=OD，可判定此四邊形為平行四邊形。乙、若OA=OC,OB=OD, AC=BD，可判定此四邊形為長方形。丙、若AC=BD, AC⊥BD，可判定此四邊形為正方形。丁、若OA=OC,OB=OD, AC⊥BD，可判定此四邊形為菱形。 (Ａ) 甲乙丙 (Ｂ) 乙丙丁 (Ｃ) 甲丙丁 (Ｄ) 甲乙丁圖3-3-2 van Hiele 第四幾何層次測驗修改題目 1 2. 第二次修正：(2009 年 11 月) 本測驗工具繼續徵詢教授意見，同時也請目前於臺中教育大學數學教育學系碩士班進修之現職教師給予意見修正，修正內容如下： (1) 圖形與題目太緊密，應該將行距擴大。 (2) 選項中圖與圖太接近，會造成混淆，應拉開距離且需個別標示出圖名。 (3) 有些題目敘述太過冗長，建議修改。

(48)

3. 第三次修正：（2009 年 12 月）繼續徵詢教授意見，同時也請服務學校的四位現職國中教師給予意見修正，修正內容如下： (1) 建議修改太過容易的題目，兩雙對邊平行是平行四邊形的性質太容易，應修改為考其他性質，如圖 3-3-3。 (2) 將題目中要選正確或錯誤的敘述改為一致的寫法，例如『正確』、『對的』…都改為一致的「何者正確」，而『錯誤』、『有錯』…都改為一致的「何者錯誤」或改寫題目敘述，盡量要學生選出正確的敘述，且「何者正確」、「何者錯誤」需畫底線強調。 (3) 題目中有『如附圖』、『如右圖』，改為一致的『如附圖（一）』。 (4) 將題目中的「證明過程如下」之後，應稍有間隔或框起作為區分，討論後決定修改為有一行間距。 (5) 題目選項有問題，選不到正確的答案，重新佈題。

(49)

( ) 4. 哪一個是平行四邊形所具備的性質？ (A) 兩雙對邊平行 (B) 四邊相等 (C) 對角線互相垂直 (D) 對角線等長改為 ( ) 4. 以下哪一個敘述可判斷出四邊形ABCD為一平行四邊形？ (Ａ) AB = BC , CD = AD (Ｂ) AB = CD , AD // BC (Ｃ) AB = CD , AB // CD (Ｄ) AC = BD , AC _⊥ BD 圖3-3-3 van Hiele 第四幾何層次測驗修改題目 2 4. 第四次修正：(2010 年 1 月) 本測驗工具接著徵詢兩位臺中教育大學數學教育學系教授之意見，建議修正內容如下。 (1) 選項出現重複的敘述，應稍作修改，如圖 3-3-4。 (2) 題目已寫出部份證明過程是否符合 L4-4？經討論決定重新佈題，如圖 3-3-5，修改方式為將「填空式」的題目敘述改為「配合題型」，將可能的條件全部寫出，讓學生自行選出合適的條件。 (3) 有些題目建議加上附圖，如圖 3-3-6 。 (4) 題型列為「辨識敘述及逆敘述的不同」，但出題方式有誤，敘述為若 p

(50)

則 q，逆敘述則為非 q 則非 p，但選項（A）和（B）都與逆敘述沒有關係，建議重新佈題，討論後重新佈題如圖 3-3-7。 ( ) 1. 下列各四邊形的敘述何者正確？ (A) 平行四邊形的對角線互相平分且等長 (B) 長方形的對角線互相平分且等長 (C) 菱形的對角線互相平分且等長 (D) 等腰梯形的對角線互相平分且等長 改為 ( ) 1. 下列哪一個四邊形的對角線互相平分且等長？ (A) 平行四邊形 (B) 長方形 (C) 菱形 (D) 等腰梯形 圖3-3-4 van Hiele 第四幾何層次測驗修改題目 3

(51)

( ) 11. 如右圖：△ABC 中，若AB＝AC，證明：∠B＝∠C 做BC中點 D，連接AD，已知： AB＝AC； BD＝CD； AD＝AD 所以：△ABD _{≅ ACD(}△ 依據○1 全等性質)，故∠ ＝B ∠ ，試C 問空格○1 應該填寫哪一個全等性質？ (A) SSS (B) RHS (C) SAS (D) ASA ( ) 11.如右圖：△ABC 中，若AB＝AC，證明：∠B＝∠C 證明步驟如下：做BC中點 D，連接AD，要證明 △ABD ≅ △ACD，須用哪些條件？甲、AB＝AC 乙、∠ADB＝∠ADC 丙、BD＝CD 丁、AD＝AD 戊、∠A＝∠A (A) 甲乙丙（SAS） (B) 乙丁戊（ASA） (C) 甲乙戊（AAS） (D) 甲丙丁（SSS）圖3-3-5 van Hiele 第四幾何層次測驗修改題目 4

(52)

( ) 9. 依照以下哪個選項的條件，我們可知△ABC ≅ △DEF (A) ∠A＝∠D；∠B＝∠E；∠C＝∠F (B) ∠A＝∠D；∠B＝∠E；BC = EF (C) AB = DE_{；∠A＝∠D；}BC = EF (D) AB = DE_{；∠C＝∠F；}BC = EF 加上圖示圖3-3-6 van Hiele 第四幾何層次測驗修改題目 5

(53)

( ) 24. 以下有二個敘述。敘述Ⅰ.若一圖形是正方形，則它的對角線互相垂直。敘述Ⅱ.若一圖形的對角線互相垂直，則它是一個正方形。下列哪一個敘述是正確的呢？ (Ａ) 若要證明敘述Ⅰ正確，則只要證明敘述Ⅱ正確即可。 (Ｂ) 若要證明敘述Ⅱ錯誤，則只要證明敘述Ⅰ錯誤即可。 (Ｃ) 若要證明敘述Ⅱ正確，則只要找到一個對角線互相垂直的正方形即可。 (Ｄ) 若要證明敘述Ⅱ錯誤，則只要找到一個對角線互相垂直但不是正方形的四邊形即可。改為： ( ) 24. 關於敘述Ⅰ，以下的討論何者正確敘述Ⅰ.若四邊形ABCD是正方形，則它的對角線互相垂直。 (Ａ) 若一四邊形的對角線互相垂直，則它是一個正方形。 (Ｂ) 若四邊形ABCD不是正方形，則它的對角線不會互相垂直。 (Ｃ) 若一四邊形的對角線沒有互相垂直，則它不是一個正方形。 (Ｄ) 以上說法都不正確，因為敘述Ⅰ不一定正確。圖3-3-7 van Hiele 第四幾何層次測驗修改題目 6 5. 第五次修正：(2010 年 2 月)

依據 van Hiele 幾何思考理論探究臺灣中部地區國三學生幾何概念發展之研究

國立臺中教育大學數學教育系碩士班碩士論文

指導教授：吳德邦 博士