國 立 交 通 大 學
電信工程研究所
碩 士 論 文
應用盲訊號分離法於語音訊號分離之研究
A Study on Applying Source Separation
Algorithms to Audio Signal Separation
研 究 生:黃靖雯 Student: Ching-Wen Huang
指導教授:冀泰石 博士 Advisor: Dr. Tai-Shih Chi
應用盲訊號分離法於語音訊號分離之研究
A Study on Applying Source Separation Algorithms to
Audio Signal Separation
研 究 生:黃靖雯 Student: Ching-Wen Huang
指導教授:冀泰石 博士 Advisor: Dr. Tai-Shih Chi
國立交通大學
電信工程研究所
碩士論文
A Thesis
Submitted to Institute of Communication Engineering
College of Electrical and Computer Engineering
National Chiao-Tung University
In Partial Fulfillment of the Requirements
for the Degree of
Master of Science in
Communication Engineering
March 2012
Hsin-Chu, Taiwan, Republic of China
應用盲訊號分離法於語音訊號分離之研究
學生:黃靖雯 指導教授:冀泰石 博士
國立交通大學電信工程研究所
感知訊號處理實驗室
摘要
本論文探討盲訊號分離法對於語音分離的成效,主要考量經頭部相關傳輸函數 (Head-Related Transfer Function, HRTF)為脈衝響應的摺積混和訊號。此舉是為模擬音 源來自不同方位時,人的左右耳所聽到的聲音,再利用雙耳所收到的混和訊號之間的差 異來做分離。論文中實驗了三種不同的方法,第一種方法為影像分離演算法,將混和訊 號的聲譜圖作為影像訊號來處理,利用影像的邊緣圖具有稀疏的特性,以最大化影像邊 緣圖作為演算法的目標,並以 FastICA 計算疊代法的初始條件。第二種方法加入稀疏成 分分析法的考量,利用非線性投影將影像的邊緣訊號轉成較為稀疏的訊號,作為影像分 離演算法的前置處理。第三種方法將聲譜圖分頻,利用每個頻帶的混和訊號稀疏的特性, 使用非線性函數計算音源對於混和訊號的貢獻值,用非線性遮蔽的方法將音源抽取出來。 實驗結果顯示,當兩個音源分別位於左右兩邊時,三種方法皆可達到良好的分離效果; 當音源來自同一邊的混和情況,所提出的第三種方法也可成功分離音源,與其他現有演 算法的比較結果也顯示此方法的方離效果良好且穩定。A Study on Applying Source Separation Algorithms to
Audio Signal Separation
Student: Ching-Wen Huang Advisor: Dr. Tai-Shih Chi
Institute of Communication Engineering
National Chiao-Tung University
Perception Signal Processing Laboratory
Abstract
In this thesis, we propose audio separation algorithms stemmed from blind source
separation algorithms. The Head-Related Transfer Functions (HRTFs) are used to simulate the convolutive mixing of audio sources to model the sound mixtures perceived by listeners. Three different methods are proposed and investigated. The first method is an image separation method named ISBS, in which we consider audio spectrograms as images. The criterion of this algorithm is to maximize the sparsity of the edges of the signals and the FastICA algorithm is used to initiate its iteration. The second method adopts a nonlinear projection as the pre-processing of the ISBS algorithm. The nonlinear projection transforms the edges onto a sparser domain. The third method considers the frequency bin-wise mixtures and utilizes the sparsity in the time-frequency (T-F) domain. For each T-F unit, we calculate the contributions from each source by a nonlinear function. A masking matrix is formed based on contributions from each source and used to extract original sounds. Simulation results showed that all three methods performed well when sound sources located far apart from each other. When sources are at close locations, only the proposed third method performed well. Comparison with some conventional methods also showed the third method performed better and more robust in most cases.
目 錄
中文摘要 ... i 英文摘要 ... ii 目 錄 ... iii 表 目 錄 ... v 圖 目 錄 ... vi 第一章 緒論 ... 1 1.1 研究背景 ... 1 1.2 盲訊號分離法簡介 ... 1 1.2.1 即時性混和(instantaneous mixing) ... 2 1.2.2 摺積混和(convolutive mixing) ... 3 1.2.3 欠定問題(unter-determined problem) ... 5 1.3 研究方法 ... 5 1.4 章節大綱 ... 6 第二章 獨立成分分析法 ... 7 2.1 發展背景 ... 7 2.2InfomaxICA ... 8 2.3FastICA ... 9 2.3.1 前置處理 ... 10 2.3.2 解分離矩陣 ... 13 第三章 影像分離演算法 ... 143.1Notation and Model ... 14
3.2Sparse Representation ... 15
3.4Initial Condition ... 18 第四章 稀疏成分分析法 ... 21 4.1 發展背景 ... 21 4.1.1 針對即時性混和的 SCA ... 22 4.1.2 DUET ... 23 4.2 稀疏訊號轉換 ... 25
4.3Nonlinear Projection Column Masking ... 27
4.4Proposed Algorithm ... 30 4.5 排列問題(Permutation) ... 32 第五章 模擬結果 ... 35 5.1 實驗設置 ... 36 5.2 模擬結果 ... 37 5.2.1 模擬一 ... 37 5.2.2 模擬二 ... 43 5.2.3 模擬三 ... 47 5.3 結論 ... 48 參考文獻 ... 49
表 目 錄
表 5-1 混和訊號的 SIR ... 38 表 5-2 ISBS 分離結果 ... 39 表 5-3 NP 分離結果 ... 40 表 5-4 NM 分離結果 ... 42 表 5-5 (-5,25)分離結果 ... 43 表 5-6 (40,10)分離結果 ... 44 表 5-7 (-70,-40)分離結果 ... 44 表 5-8 (-30,30)分離結果 ... 45 表 5-9 (15,50)分離結果 ... 45 表 5-10 五種方法的 SIR 平均值 ... 46 表 5-12 DUET 與 NM 的分離結果 ... 47圖 目 錄
圖 1-1 盲訊號分離法示意圖 ... 2 圖 1-2 摺積混和訊號示意圖 ... 3 圖 1-3 CONVOLUTIVE ICA 流程圖 ... 4 圖 1-4 排列問題及膨脹問題 ... 5 圖 2-1 ICA 基本架構 ... 8 圖 2-2 16 個訊號源的統計直方圖 ... 9 圖 2-3 兩個混和訊號的統計直方圖 ... 9 圖 2-4 不同的高斯分布 ... 10 圖 2-5 訊號源的散佈圖及統計直方圖 ... 11 圖 2-6 訊號經過 FASTICA 處理後的變化 ... 12 圖 3-1 影像與邊界圖及其統計直方圖 ... 16 圖 3-2 FASTICA 與 ISBS 流程圖 ... 18 圖 4-1 訊號在時域與頻域的散佈情況 ... 22 圖 4-2 訊號源經過即時性混和後方向的變化 ... 23 圖 4-3 聲譜圖的稀疏特性 ... 23 圖 4-3 聲譜圖的稀疏特性 ... 23 圖 4-4 振幅和相位差之統計直方圖 ... 25 圖 4-5 混和訊號及經過白色化處理後的變化 ... 25 圖 4-6 訊號源位於不同邊的混和情形 ... 26 圖 4-7 訊號源位於同邊的混和情形 ... 26 圖 4-8 長脈衝響應下的混和情況 ... 27圖 4-9 散佈圖上的主要方向 ... 28 圖 4-10 NPCM 所找出的兩個方向 ... 29 圖 4-11 稀疏訊號經過白色化處理後的變化 ... 29 圖 4-12 加入非線性投影的影像分離法 ... 30 圖 4-13 混和訊號聲譜圖分頻 ... 31 圖 4-14 某頻帶的混和訊號分佈圖 ... 31 圖 4-15 訊號源方向對混和訊號散佈圖的影響 ... 33 圖 5-1 HRTF 混和訊號 ... 35 圖 5-2 訊號來源方向示意圖 ... 37 圖 5-3 音源與混和訊號之聲譜圖 ... 38 圖 5-4 ISBS 分離聲譜圖 ... 38 圖 5-5 混和訊號聲譜圖邊緣之散佈圖 ... 39 圖 5-6 NP 分離聲譜圖 ... 40 圖 5-7 音源位於不同邊之非線性投影效果 ... 41 圖 5-8 音源位於同邊之非線性投影效果 ... 41 圖 5-9 NM 分離聲譜圖 ... 42 圖 5-10 (-5,25)分離結果 ... 43 圖 5-10 (40,10)分離結果 ... 44 圖 5-10 (-70,-40)分離結果 ... 44 圖 5-11 (30,-30)分離結果 ... 45 圖 5-12 (15,50)分離結果 ... 45 圖 5-13 五種方法的 SIR 平均值 ... 46 圖 5-14 欠定問題所分離出的聲譜圖 ... 47
第一章 緒論
1.1 研究背景
在日常生活中,常常會遇到多個聲源同時出現的情況,例如在一個吵嘈的環境中, 語音會夾雜著各式的噪音如手機鈴聲、汽機車噪音等,或者是在同一個空間中,有很多 人同時說話,但我們通常都只想要集中在某個人的聲音上面,要如何從吵雜的混和訊號 中抽取出我們想要的訊號源,就是所謂的雞尾酒派對問題(Cocktail-Party Problem)。盲訊號分離法(Blind Source Separation,BSS)為近十幾年來很熱門的一個研究主
題,所謂「盲」指的就是我們只有收到的混和訊號(mixtures),訊號源(sources)和混
和的過程(mixing process)皆為未知,目標就是在只有混和訊號的情況下,分離出原本 的訊號源。因此盲訊號分離法廣泛地應用於未知訊號的處理,如在生醫訊號處理
(Biomedical Signal Processing)的應用,在量測到的腦電波訊號(Electroencephalogram , EEG)中,可能混和著肌肉運動、眼球活動、心臟跳動等訊號源,不同位置所量測到的 EEG 訊號即為混和訊號,BSS 的目的便是從這些混和訊號中分離出原本的訊號源。其 他應用還有特徵擷取(Feature Extraction)、通訊(Telecommunication)、金融序列分析 (Financial Time Series Analysis)等[1][2],在語音訊號處理(Audio Signal Processing) 上的應用大部分為語音分離(Audio Separation),也就是用來解決前段所提的雞尾酒派 對問題,在許多聲源的混和音訊中,個別分離出每個聲音。
1.2 盲訊號分離法簡介
盲訊號分離法的基本架構如(圖 1-1)所示,假設有兩個聲音源 s1、s2,經過了一個 未知的混和過程,兩個麥克風所收到的訊號就是兩個聲源的混和訊號 x1、x2,可以寫成 下式:
其中 a11、a12、a21、a22取決於聲源到麥克風的距離,代表聲源到麥克風的衰減狀況,
這些係數皆為未知,盲訊號分離法的目標就是在混和過程與訊號皆未知的情況下,從混 和訊號中分離出訊號源。
1.2.1 即時性混和(instantaneous mixing)
將盲訊號分離法的數學表示法如下,假設有 N 個訊號源 s1…sN,M 個接收器收到 M 個混和訊號 x1...xM,寫成向量模式即為一個 N x 1 的訊號源向量 s=[s1…sN]T,M x 1 的混 和訊號向量 x=[x1…xM]T,最基本的混和過程假設就是即時性混和(instantaneous mixing), 也就是如(圖 1-1)所示,混和訊號 x 為訊號源 s 和一個混和矩陣(mixing matrix)A 相 乘,其中 A 為一個 M x N 的矩陣,如下式: x=As (1-2) 盲訊號分離法的目的就是找出一個分離矩陣(demixing matrix)W,使此分離矩陣 和混和訊號 x 相乘後,可以分離出訊號源 s(式 1-3)。可看出若是解出的分離矩陣 W 越 接近 A 的反矩陣 A-1,y 就會越接近原本的訊號源 s。 (1-3) (1-1) 圖 1-1 盲訊號分離法示意圖要在只有混和訊號 x 的情況下,分離出矩陣 A 和訊號源 s,也就是對 x 的矩陣分解, 在 A 與 s 都沒有特別限制的情況下,是沒有辦法得到唯一解的,因此通常都會假設訊號 源滿足某種統計特性,利用這種統計特性來做分離,根據不同的假設,就發展出了不同 的演算法。如獨立成分分析法(Independent Component Analysis, ICA)便是假設訊號源 彼此是獨立的(independent)[1-9],從混和訊號中抽取出獨立的成分;稀疏成分分析法 (Sparse Component Analysis, SCA)假設訊號源是非常稀疏的(sparse)[17-20];非負矩 陣分解法(Non-negative Matrix Factorization, NMF)則是用在訊號源皆為非負值的假設 之下[21][22],詳細的方法會在之後的章節裡介紹。
1.2.2 摺積混和(convolutive mixing)
最初 BSS 的基本假設很簡單,混和訊號只是訊號源與混和矩陣 A 的相乘,也就是 訊號源與矩陣係數的相加相乘(式 1-1),但在實際錄音環境下,聲音源到麥克風之間除 了直接路徑(direct path)以外,還會經由不同的反射路徑而產生不同的延遲(delay) 與衰減(圖 1-2),所以麥克風所收到的混和訊號其實是經過摺積混和(convolutive mixing) 的訊號,如(式 1-3)所示,其中 aik代表第 k 個訊號源到第 i 個麥克風的脈衝響應(impulse response),τ為時間延遲。 圖 1-2 摺積混和訊號示意圖(1-3)
(1-4)
(1-5)
因此,原本只須解出一個分離矩陣 W,在此情況下卻變成了一個反摺積
(deconvolution)的問題。針對摺積混和的情況,P. Smaragdis 於 1998 年、S. Ikeda 於 1999 年提出了 Convolutive ICA[13][14],主要概念就是將原本的時域(time domain)訊 號轉到頻域(frequency domain),如此一來在時域上的摺積就會在頻域上變成相乘(式
1-4),因此將混和訊號經過 Short-term Fourier Transform(STFT)後(式 1-5),對於每
個頻帶的成分而言都是即時性混和,此時就可以對每個頻帶的訊號分別使用即時性混和 的分離演算法,最後再用 Inverse STFT 重建回聲音,流程圖如(圖 1-3)[17]。 將摺積混和的訊號轉到頻域,再對每個頻率分別做 ICA,為目前很常見的一個方法 [13-16],但此作法一直存在著一些潛在問題如排列問題(permutation)和縮脹問題 (dilation)。如(圖 1-4)所示,對每個頻帶的訊號都分別視為一個即時性混和的問題來 解,每次解的過程也是互相獨立的,因此每個頻帶所解出來的訊號順序及大小會不一樣, 如此在重建回聲音時,就會產生排列問題和縮脹問題。另外,訊號做了傅立葉轉換 (Fourier Transform)後會有虛數部分,因此若要直接於每個頻帶應用即時性混和的演 算法,也必須將演算法發展成適合虛數計算,如 Complex FastICA[7]。 圖 1-3 Convolutive ICA 流程圖
1.2.3 欠定問題(unter-determined problem)
盲訊號分離法中還有另一個問題,也就是訊號源的數量 n 與混和訊號的數量 m 可能 會不相等。一般最簡單的假設是 M=N,稱為 even-determined problem,此時 A 為方陣, A-1 存在,可以直接將 A-1與混和訊號 x 相乘;當 M>N 時稱為 over-determined problem, 雖然無法直接求得 A-1,但可用 pseudo-inversion。而當訊號源數量大於混和訊號數量, 也就是 M<N 時,稱為 unter-determined problem,此時就無法直接用矩陣計算將訊號源 解回來,因此 ICA 演算法通常都會假設混和訊號的數量要大於或等於訊號源的數量(M ≥ N)。1.3 研究方法
本論文主要針對在實際環境下,人的左右耳所收到的混和訊號來做分離,我們使用 頭部相關傳輸函數(Head-Related Transfer Function, HRTF)作為摺積混和的脈衝響應, 也就是模擬當聲音源來自某個方位角時,雙耳所聽到的聲音,利用雙耳所收到的混和訊 號之間的差異來做分離。我們之所以考慮 HRTF 混和訊號,是希望可以將盲訊號分離法 應用於雙耳助聽器,例如將混和訊號中的語音訊號與噪音個別分離出來,便可以保留語音訊號而捨棄噪音,達到雙耳麥克風降噪的效果。在本研究中,我們首先對於即時性混 和的情況下成功地嘗試了現有的演算法,之後對於此種較為複雜的摺積混和情況,提出 以聲譜圖作為影像訊號所改善的演算法。
1.4 章節大綱
本論文的各章內容如下:第二章為獨立成分分析法的背景簡介,並介紹兩種主要的 ICA 演算法,Infomax 與 FastICA;第三章介紹論文所使用的影像分離演算法-Iterative Sparse Blind Separation,ISBS,以及其在聲譜圖上的實際應用;第四章將介紹稀疏成分 分析法,以及我們利用非線性投影量所提出的遮蔽方法;第五章為實驗結果與相關方法 的比較,以及相關討論與結論。
第二章 獨立成分分析法
2.1 發展背景
獨立成分分析法的想法最早是由 J. Herault 與 C. Jutten 於 1986 年所提出,當初是以 一個簡單的適應性演算法用在類神經網路架構(neural network)上來分離訊號,但並沒 有提出正式的數學理論,之後是在 1994 年由 P. Comon 提出公式定義與證明,並推導出 以最小化混和訊號的共同資訊(mutual information)作為目標函數,這是 ICA 最早期的 歷史[3]。與此同時,1992 年由 Linsker 發展的 Infomax,是一種基於消息理論(Information
Theory)的非監督式學習法(Unsupervised learning rule),主要目的是要最大化類神經網
路的輸入與輸出之交互資訊;而在 1994 年,Nadal 與 Parga 發現當雜訊很小時,在輸入 與輸出的共同資訊為最大時,輸出的訊號會彼此獨立。因此在 1995 年 J. Bell 與 J. Sejnowski 便將這種 Infomax 的技術應用於 ICA 上面,提出了一種有效率的演算法,稱 為 InfomaxICA[8][9]。其他的近似方法也有如 Gaeta 與 Lacoume 於 1990 年提出以最大概 似估計法(Maximum Likelihood Estimation , MLE)作為演算法計算[10],而在 1996 年 Pearlmutter 與 Parra 證明出 MLE 與 Infomax 其實是一樣的[11]。但最原始的 InfomaxICA 只能用來分離超高斯(super-Gaussian)訊號,因此在 1999 年,T.W. Lee 與 Girolami 將 InfomaxICA 繼續做延伸,發展了可用於 sub-Gaussian 與 super-Gaussian 的演算法[12]。
除了以共同資訊作為獨立性的量測外,另一類很熱門的方法為 A. Hyvärinen 與 E. Oja 於 1999 年所提出的 FastICA[4][5],是以訊號的常態性(normality)作為獨立性的判 斷標準,利用語音訊號為超高斯分布的特性,以最大化混和訊號的峰值(kurtosis)作為 演算法目標,並用 fixed-point 演算法求最佳解,收斂速度很快是其優點,缺點是峰值的 計算容易受偏離值(outlier)所影響,作為常態性的量測有時並不穩定。本論文使用 FastICA 作為影像分離演算法的初始條件計算,因此收歛速度快、不影響演算法速度為 主要考量,以下將簡介 InfomaxICA 的基本運算及介紹 FastICA 的詳細運算過程。
2.2 InfomaxICA
ICA 的基本架構如(圖 2-1),訊號源 s1與 s2經過一個未知的混和矩陣 A,得到兩 個混和訊號 x1與 x2,在經過 ICA 的運算後,希望分離出的訊號 y1與 y2就是原本的訊號 源 s1與 s2。 InfomaxICA 主要是用共同資訊做為訊號獨立性的量測,目標是希望能最小化 y1與 y2的共同資訊。共同資訊的計算如(式 2-1),I(y1,y2)代表 y1與 y2的共同資訊,H(y1)為 訊號 y1的熵(entropy),為 y1的不確定性,熵的定義如(式 2-2),其中 pi代表 y 的機率。 (2-1) (2-2) (2-3) 由(式 2-1)可看出要最小化 I(y1,y2),表示要最大化 H(y1,y2),也就是 y1與 y2的聯合熵(joint entropy)(式 2-3),而當 y1與 y2為獨立時,p(y1,y2)= p(y1)p(y2),p(y2|y1)=p(y2),
H(y2|y1)就會等於 H(y2)。而根據消息理論,H(y2|y1) ≤ H(y2),因為在 y1事件發生時,y2
也發生的不確定性會比 y2整體的不確定要來的小,所以當 y1與 y2彼此獨立時,H(y1,y2)
有最大值,I(y1,y2)有最小值。從另一個角度來說,當 y1與 y2為獨立時,表示 y1與 y2沒
有共同的資訊,I(y1,y2)為 0,因此最小化 I(y1,y2)可以作為獨立訊號分離的目標函數。
2.3 FastICA
FastICA 則是以訊號的分佈狀態作為獨立性的量測,通常語音訊號都會有多數的沉 默片段,所以在統計直方圖(histogram)上大部分的值都會在 0 附近,屬於超高斯分布
(Super-Gaussian Distribution)(圖 2-2),經過混和之後,根據中央極限定裡(Central Limit
Theorem),當資料數越來越多時,混和的訊號會越趨近於高斯分布(Gaussian Distribution)。(圖 3-3)顯示 16 個語音訊號的統計直方圖,可以看出混和成 2 個訊號後, 混和訊號會傾向高斯分布(圖 2-3)。因此 FastICA 的目的便是從混和訊號中分離出 Non-Gaussian 的訊號,也就是用常態性(normality)作為獨立性量測的依據。 圖 2-2 16 個訊號源的統計直方圖 圖 2-3 兩個混和訊號的統計直方圖
FastICA 是利用峰值(Kurtosis)來計算 normality,Kurtosis 為四階動差,對不同的 高斯分布(圖 2-4)會有不同的值(式 2-4) (2-4) 因此 Kurtosis 值越大,表示訊號越趨近超高斯分佈,也就越趨近於獨立,FastICA 便以最大化 Kurtosis 為演算法目標。 為了簡化演算法計算,降低需要計算的變數量,我們通常都會假設獨立的訊號源都 是 zero-mean、unit-variance,但實際應用上,收到的混和訊號卻不一定保有這兩種特性, 因此會先對訊號對一些前置處理,如集中變數(centering)以及資料白化(whitening), 使訊號先變成非相關性(un-correlated),之後再解分離矩陣。
2.3.1 前置處理
集中變數(centering)的作法只要將收到的混和訊號 x 減掉它的期望值 E[x](式 2-5), 就可以使訊號的平均值為 0。 圖 2-4 不同的高斯分布x=x-E[x] (2-5)
白化(whitening)的目的是使訊號變成 unit-variance,也就是 E[xxT
]=1,代表 X 的 成分是非相關的,其作法如下: 首先對 x 的共變異數矩陣(covariance matrix)作特徵值分解(eigenvalue decomposition)(式 2-6),分解成由特徵值(eigenvalue)所組成的對角矩陣 D,以及特 徵向量(eigenvector)所組成的矩陣 V,同時定義白化矩陣 U 如(式 2-7)。 (2-6) (2-7) 如此一來白化訊號(whitening signal) z 就是白化矩陣 U 與原訊號 x 相乘(式 2-8), 而 z 的共變異數矩陣就會變成單位矩陣(式 2-9)。 (2-8) (2-9) (a) 訊號源 s1與 s2的散佈圖 (c) s2的統計直方圖 (b) s1的統計直方圖 圖 2-5 訊號源的散佈圖及統計直方圖
訊號源經過混和與 FastICA 處理後的變化如(圖 2-5)~(圖 2-6)所示,(圖 2-5(a)) 為訊號源的散佈圖(scatter plot),橫軸為音源訊號 s1的值,縱軸為音源訊號 s2的值,當 中的點座標為每個時間點 s1與 s2的值,也就是(s1(t), s2(t)),因為訊號源為超高斯分佈, 聚集在 0 附近的點很多,所以兩個訊號的分佈圖會呈現一個十字的狀態;(圖 2-5(b))為 (a)圖對橫軸投影後的統計分佈圖,也就是音源 1 的統計直方圖,(圖 2-5(c))為(a)圖對 縱軸投影後的統計分佈圖,也就是音源 2 的統計直方圖。 訊號源經過混和後的訊號散佈圖如(圖 2-6(a)),(b)圖為經過集中變數後的結果, 在此因為原本的混和訊號就是 zero-mean,所以與(a)圖無異。(c)圖為經過白化的訊號, 可看出 z1與 z2為非相關的,而分離矩陣則是進一步將非相關的訊號轉成獨立的訊號(d), 由(c)到(d)圖可看出分離矩陣其實就是一個旋轉矩陣。 (b) 集中變數 (a) 混和訊號 (d) 分離矩陣 (c) 白色化 圖 2-6 訊號經過 FastICA 處理後的變化
2.3.2 解分離矩陣
前面提到 FastICA 是以最大化 Kurtosis 作為演算法目標,對 zero-mean、unit-variance 的訊號而言,Kurtosis 的公式可簡化為(式 2-10)。 假設分離矩陣為W,當中的每個行向量 wi可以解出一個訊號源,我們希望可以最 大化 的 kurtosis(式 2-11)。因為 W 實為一個旋轉矩陣,我們假設 wi 的 norm 皆 為 1。 (2-10) (2-11) (2-12) 對(式 2-11)取 gradient 會得到(式 2-12),因為||w||=||z||=1, , 根據 fixed-point 演算法,我們可以得到解 的疊代公式如(式 2-13)。 (2-13) FastICA 的整體計算流程如下: (1) 集中變數,使訊號變成 zero-mean。 (2) 白化處理,使訊號變成 un-correlated。 (3) 隨機選擇分離矩陣 W 的初始條件,設定 i=1,k=1。 (4) 計算 (5) 使 wi變成 unit-norm, (6) 若 ,表示 wi尚未收斂,繼續設定 k=k+1,回到(4) 再次疊代。
第三章 影像分離演算法
盲訊號分離法除了用在語音訊號上之外,也有在影像訊號上的應用,如天文影像圖 分離、文字文件重建、fMRI 腦血流量圖分析等,大部分的作法是將二維的影像訊號重 新排列成一維訊號,再使用現有的一維訊號演算法,不過此種作法會破壞影像訊號相鄰 圖素(pixel)間的相關性,因此也有一些演算法直接針對二維訊號做處理[23]。另外也 有利用影像訊號皆為非負值的特性,使用非負矩陣分解法(Non-negative Matrix Factorization, NMF)將影像分離的問題轉換成矩陣分解問題,在演算法內加上訊號源統 計特性的限制,也可以達到影像分離的效果[21][22]。 在 ICA 對語音分離的實驗中,我們確實驗證了演算法在即時性混和的情況下有很好 的分離結果,但對於摺積混和訊號就無法分離。考慮將訊號轉到頻域的作法較為複雜, 並且會產生排列問題及縮脹問題等,我們嘗試將語音訊號的聲譜圖(spectrogram)當作 一個影像訊號,使用影像分離演算法將混和訊號的聲譜圖分離出來,再重建回聲音。我們所使用的演算法為 Iterative Sparse Blind Separation(ISBS)[24],主要是利用影 像的邊緣(edge)會比較稀疏的特性,使用 -2 norm 作為稀疏性(sparsity)的量測,以 最大化混和訊號之邊緣的 -2 norm 作為演算法的目標。實驗中發現疊代法(iteration)的 初始條件會對分離效果有很大的影響,因此我們加入了 FastICA 作為初始條件的計算, 以下將詳細介紹。
3.1 Notation and Model
假設有 N 張大小為 的影像圖 S1….SN,經過混和矩陣 A 得到 M 張混和影像
(3-1) 則 S(m,n)=[S1(m,n)…SN(m,n)]為一個 Nx1 的向量,X(m,n) =[X1(m,n)…XM(m,n)]為 Mx1 的向量,A 為 M x N 的混和矩陣。目標就是找出一個分離矩陣 B,使其乘上混和的 影像 X(m,n)後可以分離出原本的影像 S(m,n)(式 3-2)。 (3-2)
3.2 Sparse Representation
如同 FastICA 將語音訊號視為超高斯分佈,以最大化峰值(kurtosis)作為最佳化演 算法的目標,ISBS 也是先將影像訊號轉到一個稀疏的領域,再以最大化稀疏性作為最 佳化目標。 我們使用拉普拉斯轉換(Laplacian Trasform)作為稀疏域的轉換: (3-3) 寫成離散的形式: (3-4) 可以看出對影像訊號做拉普拉斯轉換,相當於取出一張影像的邊緣部分。選擇拉普 拉斯轉換一來是邊緣訊號會比原本的影像訊號更為稀疏,如(圖 3-1)所示,且聲譜圖 的邊緣訊號也包含了最重要的諧音(harmonic)資訊;二來是因為拉普拉斯轉換為線性 轉換,如此一來在邊緣圖上解出的分離矩陣就可以用回原本的影像訊號。混和訊號經過 拉普拉斯轉換後,表示如下: (3-5)3.3 Algorithm
我們使用 -2 norm 作為稀疏性的量測,定義如下: (3-6) (3-7) 將混和的影像訊號 X(m,n)利用拉普拉斯轉換成邊緣圖 E(m,n),再將 E(m,n)經過白 化處理使其變成非相關性訊號 Z(m,n)。定義 為分離影像 的拉普拉斯轉換,演算法的目標為找到一個分離矩陣 B,使 回復為原影像的邊 緣圖。B 滿足下式: (3-8) (b)邊界圖 (a)原影像 (c)原影像之統計直方圖 (d)邊界圖之統計直方圖 (c)原影像之 histogram 圖 3-1 影像與邊界圖及其統計直方圖我們使用(式 3-9)來疊代計算分離矩陣 B,同時更新 的值如式(3-10)。 (3-9) (3-10) 將(式 3-7)代入(式 3-10)可得到(式 3-11)。假設每次的更新值 都是很小的, 也就是 ,如此一來(式 3-11)可展開成(式 3-12) (3-11) (3-12) 為簡化表示,定義矩陣 R 與矩陣 D 如(式 3-13、3-14),結合(式 3-6)與(式 3-12) 可得(式 3-15),根據 Gradient Method, 可求出如(式 3-16)。 (3-13) (3-14) (3-15) (3-16) 使用 來更新分離矩陣 B,直至 , 為一個很小的閾值,表示 B 已收斂,將 B 乘上白化矩陣即可做為影像的分離矩陣,將此矩陣與原混和影像 X(m,n) 相乘,就可得到原影像 S(m,n)。
3.4 Initial Condition
針對這種用疊代法求最佳解的問題,初始條件通常是很重要的,在此我們用 FastICA 的解當作初始條件,如此一來可以降低疊代的次數,且 FastICA 的收斂速度本身就很快, 因此並不會增加演算法的複雜度,整個流程圖如下:3.5 影像分離演算法用於聲譜圖分離
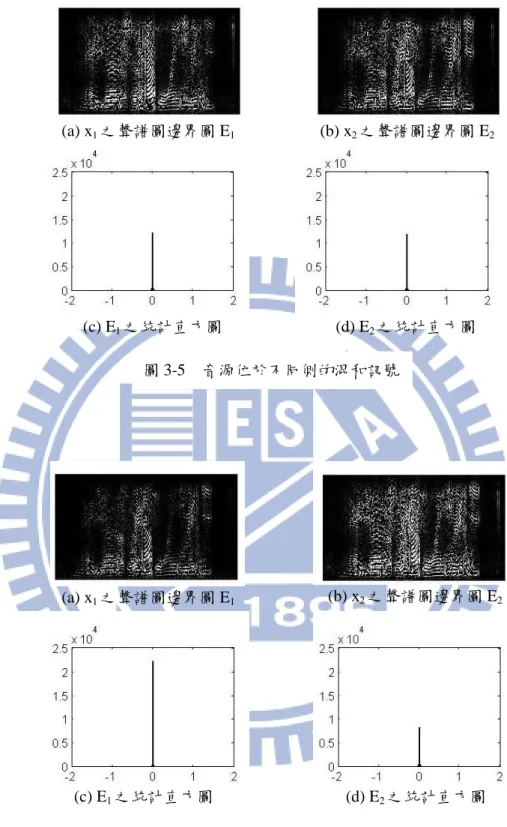
從我們初步的實驗中發現,影像分離演算法在訊號源來自於頭的不同邊時,經過 HRTF 模擬混和的訊號尚可分離,但對於訊號源來自同邊的混和訊號,解出來的效果有 限,第五章中會再顯示詳細的模擬結果。 討論其原因,此方法的概念是將聲譜圖作為影像訊號來處理,希望利用邊界圖會比 原影像訊號來得稀疏的特性來做分離,但結果顯示聲譜圖與影像訊號仍然有不同的特性, 聲譜圖的邊界圖不會如影像訊號的邊界圖那麼的稀疏。(圖 3-3)為一聲譜圖與其邊界圖 的統計直方圖,比較圖(d)與圖(c),可看出邊界圖確實會比原影像圖來得稀疏,但其差異 就不及(圖 3-1)來得明顯,這也可能是影像分離演算法對聲譜圖無法正確分離的原因 所在。 圖 3-2 FastICA 與 ISBS 流程圖在音源方位不同的混和示意圖如(圖 3-4)所示,圖(a)為兩個音源位於頭的不同兩 側,圖(b)為兩個音源於頭的同一側,在這兩種情況下,邊界圖的稀疏情況也會有所不同。 (圖 3-5)為音源位於不同側時,兩耳所收到的混和訊號 x1與 x2,其聲譜圖的邊界 圖 E1與 E2,以及邊界圖的統計直方圖;(圖 3-6)為音源位於同側時的情況。比較(圖 3-5)與(圖 3-6)的圖(c)與圖(d),可看出當音源位於不同側時,E1與 E2的稀疏性會被 降低,因此以提高稀疏性作為分離目標的演算法是可行的;而當音源位於同側時,其中 一個邊界圖 E1本身就較為稀疏,因此在這種情況下演算法較容易失敗。 (b)聲譜圖之邊界圖 (a)原聲譜圖 (c)原聲譜圖之統計直方圖 (d)邊界圖之統計直方圖 圖 3-3 聲譜圖與邊界圖及其統計直方圖 圖 3-4 混和示意圖 (b) 音源位於同側 (a) 音源位於不同側
圖 3-5 音源位於不同側的混和訊號 圖 3-6 音源位於同側的混和訊號 (b) x2之聲譜圖邊界圖 E2 (a) x1之聲譜圖邊界圖 E1 (c) E1之統計直方圖 (d) E2之統計直方圖 (b) x2之聲譜圖邊界圖 E2 (a) x1之聲譜圖邊界圖 E1 (c) E1之統計直方圖 (d) E2之統計直方圖
第四章 稀疏成分分析法
從我們初步的實驗中發現,影像分離演算法在訊號源來自於頭的不同邊時,經過 HRTF 模擬混和的訊號尚可分離,但對於訊號源來自同邊的混和訊號,解出來的效果有 限。因此除了將整張聲譜圖當成影像訊號來做處理外,也該考慮聲譜圖本身所具備的特 性,若能將此特性加入分離的考量,應該會有比較好的效果。 聲譜圖可視為語音頻率成分隨時間的變化,而不同的人講話會有不同的基頻與倍頻, 說話速度與斷句也不一,所以不同音源的聲譜圖的交集是很少的(disjoint),因此混和 訊號聲譜圖的每個 T-F unit 都只來自於其中一個訊號源,也就是有很稀疏(sparse)的特性[20],近年來所發展的稀疏成分分析法(Sparse Component Analysis, SCA),就是適用
於此種訊號分離。
4.1 發展背景
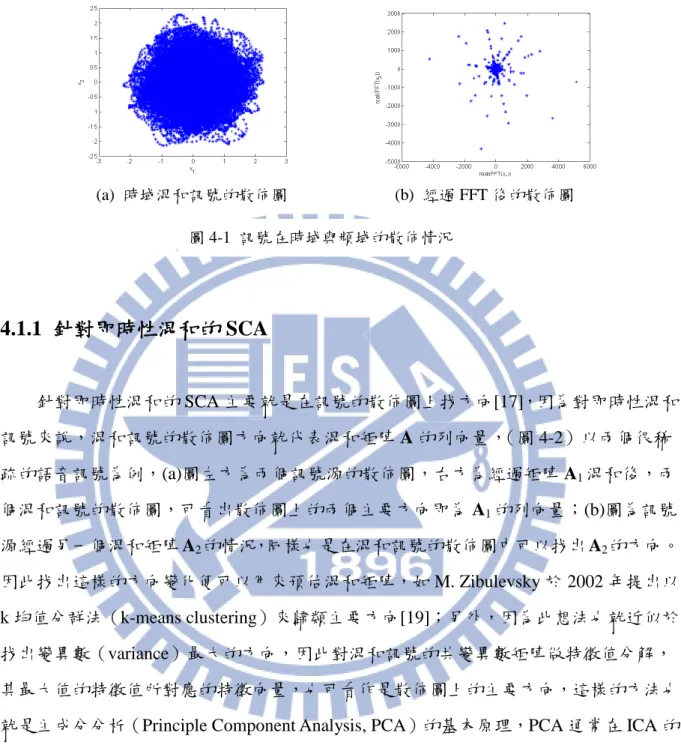
如同緒論中所提到的,在盲訊號分離法中,對於訊號源不同的假設會產生不同的演 算法,有別於 ICA 利用訊號獨立的統計特性作為基本假設,近年來開始有人提出一個新 的假設,也就是假設訊號源在某些 domain 上是非常稀疏的,形成了所謂的稀疏成分分 析法[17-20]。如果一個訊號多數的值都為 0 或是趨近於 0,就稱為稀疏訊號(sparse signal), 其訊號分佈函數在 0 附近會有一個高峰(peak),其餘地方值都很小。將語音訊號轉到sparse domain 的方法多為 Fourier Transform 或是 Wavelet Transform(圖 4-1),圖(a)為 3
個訊號源經過即時性混和成 2 個混和訊號,x1與 x2在時間軸的散佈圖,圖(b)為經過
512-point windowed FFT 後的係數絕對值之散佈圖。當訊號轉到 sparse domain 後,兩個 以上的訊號源同時出現的機率會很低,也就是在同一時間點上大部分只有一個訊號源是 有值的,也就形成了很好的分離條件。
4.1.1 針對即時性混和的 SCA
針對即時性混和的 SCA 主要就是在訊號的散佈圖上找方向[17],因為對即時性混和 訊號來說,混和訊號的散佈圖方向就代表混和矩陣 A 的列向量,(圖 4-2)以兩個很稀 疏的語音訊號為例,(a)圖左方為兩個訊號源的散佈圖,右方為經過矩陣 A1混和後,兩 個混和訊號的散佈圖,可看出散佈圖上的兩個主要方向即為 A1的列向量;(b)圖為訊號 源經過另一個混和矩陣 A2的情況,同樣也是在混和訊號的散佈圖中可以找出 A2的方向。 因此找出這樣的方向變化便可以用來預估混和矩陣,如 M. Zibulevsky 於 2002 年提出以 k 均值分群法(k-means clustering)來歸類主要方向[19];另外,因為此想法也就近似於 找出變異數(variance)最大的方向,因此對混和訊號的共變異數矩陣做特徵值分解, 其最大值的特徵值所對應的特徵向量,也可看作是散佈圖上的主要方向,這樣的方法也 就是主成分分析(Principle Component Analysis, PCA)的基本原理,PCA 通常在 ICA 的 演算法內會作為 pre-whitening 的前置處理,在第二章內有詳細的介紹。(a) 時域混和訊號的散佈圖 (b) 經過 FFT 後的散佈圖
(a)
4.1.2 DUET
針對頻域訊號的 SCA,最著名的就是 S. Rickard 與 O. Yilmaz 於 2000 年提出的 DUET (Degenerate Unmixing and Estimation Technique)[20],其做法也是將訊號利用 STFT 轉 到頻域,利用頻域訊號較時域訊號更為稀疏的特性來做分離。由(圖 4-3)可看出訊號 源的聲譜圖是非常稀疏的,(a)圖為訊號源 s1的聲譜圖 |S1|,(b)圖為 s2的聲譜圖 |S2|,(c) 圖為|S1|與|S2|點對點相乘,可以看出相乘後大部分的值都變得很小,表示|S1|和|S2|同時出 現的時間點是很少的,(d)圖為(c)圖的統計直方圖,圖中也顯示大部分的值都集中在 0 附近。 DUET 是假設訊號經過不同的延遲(delay)和衰減所混和而成的(式 4-1),可以看 作是摺積混和訊號中,只考慮由直接路徑(direct path)傳到麥克風的音源,不考慮音源 (a) 圖 2-6 linear 混和訊號中的主要方 向 圖 4-2 訊號源經過即時性混和後方向的變化 (b) (a) (b) (c) (d) 圖 4-3 聲譜圖的稀疏特性
經過其他反射後的混和情況。若只考慮 x2 相對 x1 的延遲和衰減情況,(式 4-1)可簡化 為(式 4-2),經過 STFT 轉換後可寫成(式 4-3)。 (4-3) 假設每個 T-F unit 都只有來自其中一個音源 si的訊號,表示 X1(ω,τ)和 X2(ω,τ)都只 包含音源 Si(ω,τ)(式 4-4),因此只需利用混和訊號的兩張聲譜圖在當點(ω,τ)的振幅及相 位差,就可以計算音源 si的混和係數(ai,δi),如(式 4-5)所式。 (4-4) (4-5) 針對每個(ω,τ)都可以算出一組混和係數(a,δ),而來自同一個音源的混和係數假設上 都是一樣的,因此若將這些係數作分群,就可以得到音源訊號的混和係數,具體的作法 是將這些係數畫出其統計直方圖,其中每個高峰就會對應出一個音源(圖 4-4)。最後只 要將屬於此音源的 T-F unit 保留,遮蔽掉不屬於該音源的 T-F unit,會得到一個遮蔽矩陣 (masking matrix)Mi(式 4-6),將此遮蔽矩陣與混和訊號的聲譜圖相乘就可以得到訊 號源 si的聲譜圖(式 4-7),再用 inverse STFT 求得原本的聲音源。 (4-6) (4-7) (4-1) (4-2)
4.2 稀疏訊號轉換
我們原先是將聲譜圖從影像訊號的觀點切入,但從模擬結果中發現,影像分離演算 法對於訊號源來自同邊的混和訊號,解出來的效果有限,探討其可能的原因,首先從摺 積混和訊號和即時性混和訊號的語音訊號開始說明。在即時性混和訊號中,每個點加乘 的權重(weight)都是一樣的,因此在散佈圖上會呈現出兩個主要的方向(圖 4-5(a)), 如此在做白化處理後才能確實達到 de-correlation 的效果(圖 4-5(b));而摺積混和訊號 的散佈圖中無法看出有兩個主要的方向(圖 4-5(c)),就算做了白化處理也沒辦法 de-correlation(圖 4-5(d))。 圖 4-4 振幅和相位差之統計直方圖 (b) 白色化處理後之混和訊號 (a) 即時性混和訊號 (d) 白色化處理後之混和訊號 (c) 摺積混和訊號 圖 4-5 混和訊號及經過白色化處理後的變化訊號在做摺積混和時,若是訊號源到麥克風的反射路徑並不多,HRTF 的脈衝響應 長度就不會很長,如果其長度是在 STFT 的音框長度(frame size)及音框位移(frame shift) 足以覆蓋的長度以內的話,摺積混和訊號在經過 STFT 之後,便可以近似於即時性混和 訊號[25];(圖 4-6(a))為脈衝響應長度較短時,對聲譜圖的邊緣所做的散佈圖,可看出 其分佈近似於即時性混和訊號。但是散佈圖的方向其實主要來自於混和訊號 1 與混和訊 號 2 各點數值大小的差異,當兩個聲源訊號分別位於頭的兩側時(圖 4-6(b)),音源 1 在混和訊號 1 比較大聲,在混和訊號 2 比較小聲,而音源 2 則是在混和訊號 2 比較大 聲,在混和訊號 1 比較小聲,如此一來混和訊號 1 和混和訊號 2 在在每個時間點上都 會有不同的主要音源,所以散佈圖上的方向也會較為明顯。 反觀兩個音源訊號在同一邊的情況(圖 4-7(b)),音源 1 和音源 2 都是在混和訊號 1 比較大聲,在混和訊號 2 比較小聲,也就是兩個音源主要都集中在其中一個混和訊號, 因此散佈圖上就不容易找出另一個方向(圖 4-7(a))。 (b) 混和示意圖 (a) 聲譜圖邊緣之散佈圖 圖 4-6 訊號源位於不同邊的混和情形 (b) 混和示意圖 (a) 聲譜圖邊緣之散佈圖 圖 4-7 訊號源位於同邊的混和情形
當摺積混和訊號的脈衝響應越來越長時,在 STFT domain 產生類似即時性混和的特 性也會漸漸消失,因此聲譜圖邊緣的散佈圖也會變得難以辨認方向(圖 4-8(a)),在此情 況下就如同前段所述,白化處理無法達到 de-correlation 的目的。因此我們希望可以找到 一種投影的方法,將分散的點集中到兩個主要的方向上(圖 4-8(b)),如此在經過白化處 理後可以得到兩個非相關的訊號,希望可以達到較好的分離效果。這樣的想法就相當於 將訊號轉到一個稀疏的領域,用此稀疏訊號來做分離。
4.3 Nonlinear Projection Column Masking
為了將訊號投影到稀疏領域,首先要找出其主要的兩個方向。如(圖 4-9)所示, 假設我們想要找到的方向向量為 w,則散佈圖上各點對於 w 的投影量 yt定義如下: (4-8) 其中 xt為各點的座標向量, 表示兩個向量 w 與 xt的夾角。PCA 是對於各個方 向的 w,找出使 E[yt2]最大化的方向向量 w,E[.]代表期望值。如(圖 4-9)所示,此方 法在預估 w 時,會受到另一個方向的訊號點所干擾,雖然當 xt與 w 的夾角很大時, 的值會比較小,但全部的點所加總起來的影響,還是會使求出的 w 稍微偏 離真正所要找的方向(圖 4-9(a))。 (b) 投影成稀疏訊號 (a) 聲譜圖邊緣之散佈圖 圖 4-8 長脈衝響應下的混和情況
為避免此問題,我們可在找方向時,先遮蔽掉遠離 w 的所有訊號點,如此一來就較 不會受到屬於另一個方向的訊號點所干擾,可以較正確地找出 w 的方向(圖(b))。[26] 提出了一個非線性投影的方法將遠離主要方向的點遮蔽掉(Nonlinear Projection Column
Masking, NPCM),其想法是定義出一個閾值 c0(threshold),對於每個點 xt計算 ,當 時表示 xt與 w 較為接近,再對這些點做 PCA。但是在 這樣的定義下,閾值 c0的選擇對效果好壞會有很大的影響,所以文中提出了一個非線性 函數 f(.),將投影量 yt重新定義為: (4-9) 此 f(.)為一遞減函數,並滿足以下三個條件: (1) (2) (3) and if 條件(3)就表示當 xt與 w 在同一個方向上時,f(.)會有最大值,而遠離 w 的點對於 yt 的貢獻值就很小,如此可以達到遮蔽的效果。f(.)可以是任意滿足條件的函數,在此使用 。其中 為常數,根據其值大小可以決定指數函數 f(x)的衰減速度, 若 越大,f(x)衰減越快,表示夾角 一定要很小,xt才不會被遮蔽,也就是 值可 以控制訊號點被遮蔽的門檻。 根據以上的假設,可以定義出目標函數: (4-10) 圖 4-9 散佈圖上的主要方向 (a) PCA (b) NPCM
對各個不同方向的 w 計算 J(w)值,當 J( )有最大值時, 就應該是我們要求的主 要方向。假設有兩個聲源訊號,J(w)就會有兩個高峰(圖 4-10(a)),這兩個高峰也就對 應了主要的兩個方向 w1、w2的角度(圖 4-10(b))。而根據當點 xt所計算出的函數值 的大小,可以決定 x t距離哪個方向比較近,再將此點投影到該方向上(式 4-11)。 (4-11) 對每個點 xt皆投影到 w1或 w2的方向上後,就可以得到一個方向很明確的散佈圖(圖 4-11(a)),此經過投影的訊號 經過白化處理後,就可以達到 de-correlation 的效果(圖 4-11(b)),然後再繼續解分離矩陣。 將投影過的訊號當作新的混和訊號 ,用 所解出的白化矩陣和分離矩陣再回來解 x,流程圖如(圖 4-12)所示,我們將原本聲譜圖的邊緣訊號 E1和 E2作 NPCM,會得 圖 4-10 NPCM 所找出的兩個方向 (a) (b) 圖 4-11 稀疏訊號經過白色化處理後的變化 (a) (b)
到一個新的訊號 和 ,用 、 所解出的白化矩陣與分離矩陣乘上原影像 X1、X2, 就可以得到分離出的聲譜圖 、 。 此方法是將一個新訊號 的解直接用在原訊號 x 上,但因為 x 到 之間的轉換為非 線性的,將 x 轉換成 的過程就破壞了訊號原本的特性,所以也是只有在訊號源位於不 同邊的情況下效果比較好,若是訊號源來自同一邊,還是會因為混和訊號太過相似,導 致分離效果依然有限,詳細的結果會在第五章再作討論。
4.4 Proposed Algorithm
前面所述的方法都是希望可以直接找出一個分離矩陣,乘上混和訊號後就可以解出 原本的訊號。但對摺積混和訊號而言,本身它的混和過程就不是矩陣的相乘,原本希望 轉到影像維度上會比較近似於兩張影像的線性混和,但對於音源來自同邊的混和而言, 因為兩個混和訊號過於類似,所以不太可能用加乘的方法直接解出來。 圖 4-12 加入非線性投影的影像分離法為解決摺積混和訊號之分離,我們參考 Convolutive ICA 的做法,將訊號聲譜圖分 頻,再將每個頻率的訊號當作一組混和訊號,並加入聲譜圖為稀疏訊號的假設來做分離, 個別頻率的訊號都分離完之後,再用 overlap and add 的方法將聲譜圖還原成聲音。
首先,我們將聲音訊號做 STFT(式 4-12),把語音訊號轉成聲譜圖(圖 4-13),將 每一個頻率ωk的訊號X k 1 k 2 k 當作一組混和訊號,在只有兩個音源 的情況下,其散佈圖會有兩個主要的方向(圖 4-14),集中在 w1附近的點表示在混和訊 號 1 較大聲,在混和訊號 2 裡較小聲,反之,集中在 w2附近的點表示在混和訊號 2 較 大聲,在混和訊號 1 裡較小聲。根據稀疏訊號的假設,X 的每個 T-F unit 都只有來 自於其中一個音源,因此我們可以假設 w1附近的點就代表音源 1,在 w2附近的點就代 表音源 2。 (4-12) 圖 4-13 混和訊號聲譜圖分頻 圖 4-14 某頻帶的混和訊號分佈圖
在此假設之下,如果想要分離出音源 1,我們就必須將 w1附近的點放大,並同時 遮蔽 w2附近的點,這些遮蔽值的大小也可以利用先前的非線性函數來計算(式 4-13): (4-13) 由(式 4-13)可以計算出各點對於 w1的貢獻值,其中 為一介於 104~107的常數, 根據其值大小可以決定指數函數的衰減速度,若 越大,u(t)衰減越快,表示訊號點 xt 只有在距離方向向量w 很近時,才會有比較大的遮蔽值,因此 值可以控制訊號點被遮 蔽的門檻。若兩個音源的來源方向相差較大,遮蔽門檻不需要太嚴格就可以分離訊號, 值也就不用太大;若兩個音源的來源方向較近,就需要比較嚴格的遮蔽門檻,就要設 定較大的 值。 最後只要將此遮蔽函數 與混和訊號 1 和混和訊號 2 相乘,就可以解出原本的音 源(式 4-14),其中‧表示點對點相乘。 (4-14)
4.5 排列問題(Permutation)
正如 Convolutive ICA 一樣,我們將每個頻帶的訊號當作一組混和訊號獨立來解, 每個ωk所解回來的 和 的順序是不太一定的(圖 1-4),因此解決此排列 問題是一個很重大的議題。目前一種比較常見的方法是用訊號來源方向(Direction of Arrival, DOA Approach)來分類訊號,利用聲源從不同的方向抵達會有不同的延遲,解 出來的分離矩陣 W( )也會有不同的相位差,利用這些相位差將每個頻帶所解出的訊號 分群,最後歸在同一群的就應該是同一個訊號源。另外,因為聲譜圖具連續性,也有方 法是利用相鄰頻帶的訊號會有比較高的關聯性,用該頻帶訊號與相鄰頻帶訊號的相關性 (correlation)大小作為排列依據(Correlation Approach)。用相關性排序的方法較為直 覺,準確性也較高,因為 DOA 的判斷還要取決於分離矩陣的正確性;然而 DOA Approach會比 Correlation Approach 還要穩健(robust),因為在 Correlation Approach 裡若有其中 一個頻帶判斷錯誤,就很容易造成其他頻帶也出錯。[16] 在我們所提出的演算法中,排列問題變得相對容易解決,因為在運算過程中所找出 的兩個方向,其實就分別是這兩個音源對混和訊號的貢獻,雖然每個頻帶所找出的方向 並不會完全一樣,但當兩個音源的來源角度相差較遠,或是分別來自左右兩方時,因為 音源對於混和訊號的貢獻程度相差較大,所以 w1和 w2的角度也會有比較大的差別(圖 4-15(a))。而集中在 w1和 w2附近的點又分別代表音源 1 和音源 2,所以這時只要將每 個頻帶所解出來的 w1和 w2依角度大小排列,就可以確定 w1所解出的是音源 1,w2所 解出的是音源 2,如此一來就可以解決排列問題。 然而當兩個音源的來源方向太近,兩個音源對混和訊號的貢獻程度相差不大(圖 4-15(b));或是有多個音源的時候,來自不同音源的貢獻值較容易混淆,此時如果只用 w 的角度來排序,還是有可能會有排列錯誤的問題。在此我們利用聲譜圖的連續性作為 判斷的準則,也就是計算該頻帶所解出的訊號和附近頻帶所解出訊號的差異大小來判斷 (式)。如果 Ci的值最小,表示此訊號是與音源 i 的頻譜圖最相像,那此訊號就應該是 屬於音源 i 的。大部分的比較方法是與前一個頻帶的訊號做比較(式 4-15),但因為語 音訊號在 harmonic 之間的空檔有時會造成誤判,所以在(式 4-16)中多設了一個α值, 也就是可以跟前α個頻帶的訊號比較,α值若是可以配合訊號的 harmonic,判斷的準確 圖 4-15 訊號源方向對混和訊號散佈圖的影響 (a) 訊號源相距較遠 (b) 訊號源相距較近
度也會提高。
(4-15)
0 10 20 30 40 50 -0.04 -0.02 0 0.02 0.04 0.06
left ear impulse response for S1
0 10 20 30 40 50 -0.2 -0.1 0 0.1 0.2
right ear impulse response for S1
第五章 模擬結果
我們使用頭部相關傳輸函數(Head-Related Transfer Function, HRTF)作為摺積混和 的脈衝響應,也就是模擬當聲音源來自某個方位角時,雙耳所聽到的聲音。HRTF 包含 聲源到左耳的反射路徑的脈衝響應 hL(t),及到右耳的脈衝響應 hR(t)(圖 5-1),當音源 訊號與 hL(t)和 hR(t)做摺積之後,便會在左右耳產生不同的時間延遲與強度,也就分別模 擬左耳和右耳所收到的聲音。 當聲源位於不同的位置時,對於左右耳會有不同的脈衝響應,因此我們的混和訊號 可寫成(式 5-1): 針對 HRTF 摺積混和訊號,我們嘗試了前面章節所提出的三種分離方法,第一種是 將聲譜圖當作影像訊號,利用 ISBS 作影像分離;第二種是用非線性投影(nonlinear projection, NP),將混和訊號投影到一個較為稀疏的領域,用 ISBS 解出白化矩陣和分離 矩陣後再乘上原混和訊號;第三種則是利用非線性函數計算聲譜圖的每個 T-F unit 來自 圖 5-1 HRTF 混和訊號 (a) 示意圖 (b) 音源到左右耳的脈衝響應 (5-1)
於訊號源的貢獻程度,根據這些值對聲譜圖作非線性遮蔽(nonlinear masking, NM), 把訊號源抽取出來。
在盲訊號分離法中,大多會用 SDR(Signal to Distortion Ratio)、SAR(Signals to
Artifact Ratio)、SIR(Signal to Interference Ratio)作為效能的評比,經過演算法所分離
出的訊號 可分解成(式 5-2):
(5-2)
其中 starget(t)為希望分離出的目標音源,einterf(t)為目標音源以外的音源,也就是沒有
分離乾淨所產生的干擾,enoise(t)為音源以外的雜訊干擾,eartif(t)為經由演算法所產生的人
為干擾,如 musical noise。我們使用 C.F´evotte 所提供的 BSS_EVAL Toolbox[27]將 分 解後,SDR、SAR、SIR 的定義如下: (5-3) (5-4) (5-5) 因為我們的目標為語音分離,所以主要都會以 SIR 作為最重要的指標,SIR 值越高, 表示來自其他音源的干擾很小,也就是分離的效果越好。
5.1 實驗設置
在各個模擬中,我們會分別針對音源來自不同角度的混和情況來做分離,音源來自 右邊的時角度為 0°~ 90°,來自左邊時角度為 0°~ -90°(圖 5-2),以下我們用(θ1,θ2)來表 示音源 1 來自 θ1,音源 2 來自 θ2。第一個模擬實驗首先探討各個方法對於音源來自於頭的左右兩邊、以及來自於同一 邊的結果,使用的語句為一男一女的中文語音,一組的角度為(45,-20),另一組角度為 (30,70),下一節中會詳細的列出分離後的聲譜圖以及其 SAR、SDR、SIR 值,可以看出 聲源方向對分離結果的影響。 第二個模擬實驗為多個分離結果的平均值,我們使用 TIMIT 語料庫中的 12 句話, 分別為 6 個男生與 6 個女生的語音,用其中兩個男生與兩個女生的語音當作音源 1,其 他 4 個男生與 4 個女生的語音當作音源 2,如此總共會有 32 組混和訊號,最後用這 32 組混和訊號所解出的 SDR、SAR、SIR 平均值當作效能的評比。 第三個模擬實驗為欠定問題(unter-determined problem),也就是音源數量大於混和 訊號數量,我們模擬 3 個音源來自不同的方位角,並比較 DUET 與 NM 的分離效果。
5.2 模擬結果
5.2.1 模擬一:一男一女分別位於(45,-20)、(30,70)
圖 5-3(a)為一男一女的音源聲譜圖,圖 5-3(b)為(45,-20)混和情況下的混和訊號,圖 5-3(c)為(30,70) 混和情況下的混和訊號;表 5-1 為兩種不同角度的混和情況下,混和訊 號的 SIR。以下為三種方法之結果。 圖 5-2 訊號來源方向示意圖法一:ISBS 影像分離演算法
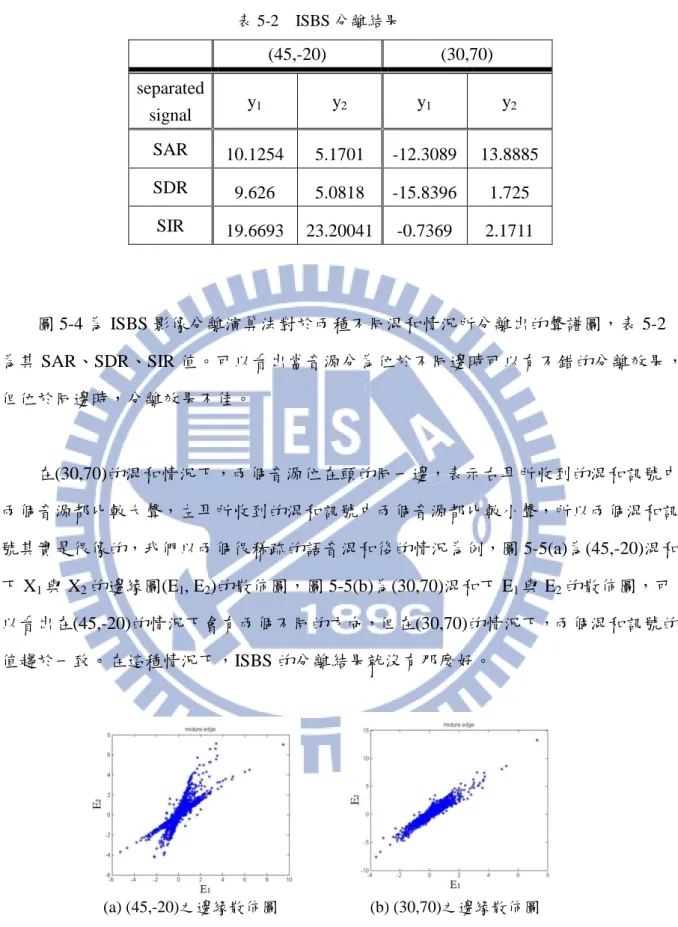
(45,-20) (30,70) mixture x1 x2 x1 x2 SIR -5.4592 -2.9114 -1.6474 3.3033 圖 5-3 音源與混和訊號之聲譜圖 (a) (b) (c) 表 5-1 混和訊號的 SIR 圖 5-4 ISBS 分離聲譜圖 (a) (45,-20)分離出的聲譜圖 (b) (30,70)分離出的聲譜圖圖 5-4 為 ISBS 影像分離演算法對於兩種不同混和情況所分離出的聲譜圖,表 5-2 為其 SAR、SDR、SIR 值。可以看出當音源分為位於不同邊時可以有不錯的分離效果, 但位於同邊時,分離效果不佳。 在(30,70)的混和情況下,兩個音源位在頭的同一邊,表示右耳所收到的混和訊號中 兩個音源都比較大聲,左耳所收到的混和訊號中兩個音源都比較小聲,所以兩個混和訊 號其實是很像的,我們以兩個很稀疏的語音混和後的情況為例,圖 5-5(a)為(45,-20)混和 下 X1與 X2的邊緣圖(E1, E2)的散佈圖,圖 5-5(b)為(30,70)混和下 E1與 E2的散佈圖,可 以看出在(45,-20)的情況下會有兩個不同的方向,但在(30,70)的情況下,兩個混和訊號的 值趨於一致。在這種情況下,ISBS 的分離結果就沒有那麼好。 (45,-20) (30,70) separated signal y1 y2 y1 y2 SAR 10.1254 5.1701 -12.3089 13.8885 SDR 9.626 5.0818 -15.8396 1.725 SIR 19.6693 23.20041 -0.7369 2.1711 表 5-2 ISBS 分離結果 圖 5-5 混和訊號聲譜圖邊緣之散佈圖 (a) (45,-20)之邊緣散佈圖 (b) (30,70)之邊緣散佈圖
法二:Nonlinear Projection
圖 5-6 為加入非線性投影後的影像分離演算法,在兩種不同混和情況下所分離出的 聲譜圖,表 5-3 為其 SAR、SDR、SIR 值。可以看出此方法與只做影像分離的結果相差 不大,都是在音源位於不同邊的情況下可分離,音源位於同邊時效果不佳。且雖然在 (45,-20)狀況下的 SIR 值頗高,但因為訊號經過非線性處理,會使聲音變得比較不自然, 因此 SAR 與 SDR 比原本的 ISBS 方法還要低。 (45,-20) (30,70) separated signal y1 y2 y1 y2 SAR -15.1541 -8.5498 -13.0611 13.9385 SDR -15.4488 -8.5601 -16.3242 1.7358 SIR 11.6672 26.8111 -0.2822 2.1775 圖 5-6 NP 分離聲譜圖 (a) (45,-20)分離出的聲譜圖 (b) (30,70)分離出的聲譜圖 表 5-3 NP 分離結果圖 5-7(a)為混和訊號聲譜圖的邊緣,E1與 E2的散佈圖,用 NPCM 找出兩個主要方 向,圖 5-7(b)為使用非線性投影將所有訊號點投影到該方向上,圖 5-7(c)為圖 5-7(b)做白 化處理後的結果,可以看出因為音源 1 和音源 2 位於頭的兩側,左右耳所收到的聲音有 大小聲之分,所以方向會很明確,投影到兩個方向上的訊號點數量也很平均,因此在做 白化處理後可以達到 de-correlation 的效果。 音源位於同邊的分離結果與 ISBS 類似,因為左右耳所收到的混和訊號很像,所以 找出的兩個方向角度也很接近(圖 5-8(a)),做了非線性投影後,方向也很不明確(圖 5-8(b)),所以經過白化處理後,也很難達到 de-correlation 的效果(圖 5-8(c))。 圖 5-7 音源位於不同邊之非線性投影效果 圖 5-8 音源位於同邊之非線性投影效果 (a) (b) (c) (a) (b) (c)
法三:Nonlinear Masking
由圖 5-9 及表 5-4 的結果中可看出,此方法對於音源位於同邊的混和訊號也可以有 很好的分離效果,在音源位於不同邊的混和情況,SIR 值也比前兩種方法要高。且此方 法並沒有非線性的轉換,只是將混和訊號中來自音源的 T-F unit 抽取出來,因此對聲音 的失真情形並不嚴重,SAR 和 SDR 皆為正值且每個分離出的訊號的情況皆一致。 (45,-20) (30,70) separated signal y1 y2 y1 y2 SAR 6.8963 6.6124 6.2153 9.0356 SDR 6.8886 6.6009 5.6118 8.815 SIR 35.2297 33.2403 15.4121 22.3759 圖 5-9 NM 分離聲譜圖 (a) (45,-20)分離出的聲譜圖 (b) (30,70)分離出的聲譜圖 表 5-4 NM 分離結果-20 -10 0 10 20 30 40
SAR SDR SIR SAR SDR SIR
dB source 1 source 2
(-5,25)
DUET cICA ISBS NP NM5.2.2 模擬二:音源 1-2 男 2 女,音源 2-4 男 4 女,共 32 組混和訊號
以下圖表為三種方法在音源分別位於(-5,25)、(40,10)、(-70,-40)、(30,-30)、(15,50) 混和下的分離結果,與 DUET 及 Convolutive ICA 所做的比較,數據為 32 組混和訊號的 分離數據平均值。(-5,25) s1 s2
SAR SDR SIR SAR SDR SIR
DUET 10.58 10.40 25.33 -11.84 -13.49 9.09 cICA 6.82 4.96 10.71 3.75 3.67 30.46 ISBS 2.81 1.76 16.46 5.53 2.69 13.10 NP 7.48 3.47 13.96 0.08 -8.06 4.93 NM 8.41 8.26 24.84 8.56 8.39 24.16 表 5-5 (-5,25)分離結果 圖 5-10 (-5,25)分離結果
-20 -10 0 10 20 30
SAR SDR SIR SAR SDR SIR
dB source 1 source 2
(40,10)
DUET cICA ISBS NP NM -20 -10 0 10 20 30SAR SDR SIR SAR SDR SIR
dB source 1 source 2
(-70,-40)
DUET cICA ISBS NP NM (40,10) s1 s2SAR SDR SIR SAR SDR SIR
DUET -10.88 -11.33 13.07 8.79 8.55 24.27 cICA 0.97 -1.28 10.50 5.93 4.92 13.16 ISBS 2.81 -5.68 10.99 4.62 0.49 7.90 NP -0.48 -5.10 12.30 5.51 -0.93 9.95 NM 9.39 9.22 24.44 8.10 7.91 23.67 (-70,-40) s1 s2
SAR SDR SIR SAR SDR SIR
DUET 6.45 5.79 21.87 -11.46 -13.24 10.80 cICA -2.63 -4.68 9.43 -1.91 -4.13 6.25 ISBS -2.65 -5.96 2.80 -0.89 -7.25 1.97 NP -5.09 -8.58 2.90 4.79 -9.20 -2.34 NM -3.59 -4.97 10.04 -7.06 -12.71 -0.41 表 5-6 (40,10)分離結果 表 5-7 (-70,-40)分離結果 圖 5-10 (40,10)分離結果 圖 5-10 (-70,-40)分離結果
-40 -20 0 20 40
SAR SDR SIR SAR SDR SIR
dB source 1 source 2
(30,-30)
DUET cICA ISBS NP NM -10 0 10 20 30SAR SDR SIR SAR SDR SIR
dB source 1 source 2
(
15,50
)
DUET cICA ISBS NP NM (-30,30) s1 s2SAR SDR SIR SAR SDR SIR
DUET -20.13 -20.39 17.07 9.46 8.48 23.96 cICA 8.04 7.31 17.37 7.68 7.09 18.79 ISBS -1.51 -2.42 21.80 -4.09 -9.98 8.29 NP -2.59 -7.57 10.49 -0.16 -5.69 13.57 NM 9.17 8.82 25.79 8.95 9.05 26.54 (15,50) s1 s2
SAR SDR SIR SAR SDR SIR
DUET 7.00 3.09 18.11 -6.59 -7.48 21.41 cICA 4.64 3.74 13.47 -2.05 -2.44 16.17 ISBS 1.83 -2.46 4.49 5.18 -4.92 15.70 NP 1.11 -3.87 3.99 -2.46 -5.20 17.57 NM 6.09 5.11 22.50 5.27 5.90 21.76 表 5-8 (-30,30)分離結果 表 5-9 (15,50)分離結果 圖 5-11 (30,-30)分離結果 圖 5-12 (15,50)分離結果
0 5 10 15 20 25 30 (-5,25) (40,10) (-70,-40) (30,-30) (15,50) dB
Average SIR
DUET ICA ISBS NP NM(表 5-10)為只看 SIR 的結果,其值為 s1的 SIR 與 s2的 SIR 平均。
與模擬一的結果類似,ISBS 及 NP 演算法在音源位於不同兩邊時分離結果較好,在 ISBS 本身可分離的情況下,加入 NP 處理後效果稍差;但當音源位於同邊時,ISBS 的 分離結果較差,加入非線性投影後結果會稍好。Convolutive ICA 同樣也是在音源位於同 邊時結果較差,而 DUET 則是在各種角度混和下皆有穩定的分離效果。NM 在大部分的 情況下皆有最高的 SIR 值,且 SAR 與 SDR 值皆很穩定,惟有在(-70,-40)的混和情況下, NM 只能分離出其中一個音源,另一音源 SIR 值很低,可能原因為 NM 考量的是兩個混 和訊號中音源大小聲的差異,當某一音源來自-70°,表示在右耳的混和訊號 xR(t)中,此 音源的音量是很小的,如此一來在散佈圖中會比較難辨認方向,且使用遮蔽的方法也比 較難將此音源抽取出來。而 DUET 演算法中不只考量音量大小,同時考慮每個 T-F unit 之相位差,因此在(-70,-40)的混和情況下,依然有穩定的分離效果。 SIR (-5,25) (40,10) (-70,-40) (30,-30) (15,50) DUET 17.21 18.68 16.33 20.52 19.76 cICA 20.58 11.83 7.84 18.08 14.82 ISBS 14.78 9.45 2.38 15.05 10.09 NP 9.45 11.13 0.28 12.03 10.78 NM 24.50 24.06 4.82 26.16 22.13 表 5-10 五種方法的 SIR 平均值 圖 5-13 五種方法的 SIR 平均值
time fr e q u e n cy time fr e q u e n cy time fr e q u e n cy time fr e q u e n cy time fr e q u e n cy time fr e q u e n cy
5.2.3 模擬三:3 個音源分別位於 (40,-25,10)
在盲訊號分離法中,當音源數量大於混和訊號數量時,因無法使用反矩陣的解法, 大多也是使用頻譜圖遮蔽的方式,因此五種方法中只有 DUET 與 NM 演算法可以解決欠 定問題,以下為兩種方法的分離結果。由(圖 5-14)中可看出兩種方法皆可分離出音源, (表 5-12)中可以看出 NM 對於其中兩個聲源 s1與 s2有較好的分離效果,但在 3 個音 源的情況下,遮蔽矩陣的計算比較容易受到其他訊號點的影響,因此 s3的分離結果相對 DUET 稍差。 DUET NM s1 s2 s3 s1 s2 s3 SAR -13.88 2.74 8.45 -11.75 -1.39 4.64 SDR -14.95 19.68 20.94 -12.01 -1.46 4.27 SIR 5.73 19.68 20.94 12.58 20.05 16.45 表 5-12 DUET 與 NM 的分離結果 圖 5-14 欠定問題所分離出的聲譜圖 (a) DUET 分離結果 (b) NM 分離結果5.3 結論
本論文探討盲訊號分離法對於語音分離的成效,主要針對以 HRTF 為脈衝響應的摺 積混和訊號來做分離,以模擬音源來自不同方位時,人的左右耳所收到的混和訊號。考 慮摺積混和訊號無法直接以時域訊號來做分離,論文中實驗了三種不同的方法,將訊號 轉到頻域後,再以不同特性的演算法加以考量。第一種方法為 ISBS 影像分離演算法, 也就是將混和訊號的聲譜圖作為影像訊號來處理,利用影像的邊緣圖具有稀疏的特性, 以最大化影像邊緣圖作為演算法的目標,並以 FastICA 作為疊代法的初始條件計算,將 解出的分離矩陣乘上原聲譜圖,就可以得到分離出的音源聲譜圖,最後再重建回聲音。 第二種方法在 ISBS 中加入非線性投影的前置處理,利用非線性投影將影像的邊緣訊號 轉成較為稀疏的訊號,希望其所解出的白化矩陣與分離矩陣能有比較好的分離效果。第 三種方法將聲譜圖分頻,利用每個頻帶的混和訊號皆很稀疏的特性,使用非線性函數計 算音源對於混和訊號的貢獻值,遮蔽掉貢獻值較小的訊號點,用非線性遮蔽的方法將音 源抽取出來。 比較三種方法的結果,在音源位於不同邊的混和情況下,三種方法皆可以有不錯的 分離效果,其中又以非線性遮蔽的方法 SIR 值最高,且 SAR 與 SDR 值也很穩定。在音 源位於同邊的混和情況下,因為左右耳所收到的混和訊號趨於一致,ISBS 演算法無法 分離,即使加入非線性投影,也因為無法成功達到 de-correlation 的效果,分離效果依然 不佳;而非線性遮蔽則是只要左右耳的訊號有大小聲的差異,便可以利用此差異將訊號 分離出來,因此對於同邊的混和訊號依然可以做分離。與現有的 Convolutive ICA 及 DUET 演算法來做比較,非線性遮蔽在不同的混和角度下,分離效果穩定且良好,惟有 在某一音源太偏向正左方或正右方時,經過 HRTF 模擬後另一耳的音量太小,造成演算 法沒辦法分出此音源,也就是只能分離出其中一個音源。參考文獻
[1] A. Hyvärinen, J. Karhunen, E. Oja, Independent Component Analysis, John Wiley, 2001.
[2] James V. Stone, Independent Component Analysis: a Tutorial Introduction, MIT Press, 2004.
[3] P. Comon, “Independent Component Analysis, a new concept?” Signal Processing, Elsevier, 36(3):287–314, April 1994.
[4] A. Hyvärinen and E.Oja, “A fast fixed-point algorithm for independent component analysis. Neural Computation, 9(7):1483-1492, 1997.
[5] A. Hyvärinen, “Fast and robust fixed-point algorithms for independent component analysis,” IEEE Trans. on Neural Networks, 10(3):626-634,1999.
[6] A. Hyvärinen, “Survey on independent component analysis,” Neural Computing Surveys, 2:94-128, 1999.
[7] E. Bingham and A. Hyvärinen, “A fast fixed-point algorithm for independent component analysis of complex-valued signals.” Int. Journal of Neural Systems, 10(1):1–8, 2000.
[8] A. J. Bell and T. J. Sejnowski, “A non-linear information maximization algorithm that performs blind separation,” In Advances in Neural Information Processing Systems 7, pages 467–474. The MIT Press, Cambridge, MA, 1995.
[9] A. J. Bell and T. J. Sejnowski, “An information-maximization approach to blind separation and blind deconvolution,” Neural Computation, 7:1129-1159, 1995.
[10] M. Gaeta and J. L. Lacoume, “Source separation without prior knowledge: the maximum likelihood solution,” In Proc. EUSIPCO’90, p. 621–624, 1990.
[11] B. A. Pearlmutter and L. C. Parra, “Maximum likelihood blind source separation: A context-sensitive generalization of ICA,” In Advances in Neural Information Processing Systems, volume 9, p. 613–619, 1997.
[12] T. W. Lee, M. Girolami, and T. J. Sejnowski, “Independent component analysis using an extended infomax algorithm for mixed sub-gaussian and super-gaussian sources,” Neural Computation, 11(2):417–441, 1999.
[13] P. Smaragdis, “Blind separation of convolved mixtures in the frequency domain.” Neuro computing, 22:21–34, November 1998.
[14] S. Ikeda and N. Murata, “A method of ICA in time-frequency domain,” in Proceedings of International Workshop on Independent Component Analysis and Blind Signal
Separation (ICA '99), p. 365–371, Aussions, France, January 1999.
[15] N. Murata, S. Ikeda, and A. Ziehe, “An approach to blind source separation based on temporal structure of speech signals,” Neurocomputing, vol. 41, p.1-24, 2001.
[16] H. Sawada, R. Mukai, S. Araki, and S. Makino, “A robust and precise method for solving the permutation problem of frequency-domain blind source separation,” Proc. Int. Symp. Independent Component Analysis Blind Signal Separation (ICA2003) , p.505-510, 2003.
[17] P.D.O’Grady, B.A.Pearlmutter, and S.T.Rickard, “Survey of sparse and non-sparse methods in source separation,” International Journal of Imaging Systems and Technology (IJIST), vol.15, p.18–33, 2005.
[18] P. Bofill and M. Zibulevsky, “Underdetermined blind source separation using sparse representations ,” Signal Processing, vol. 81, no. 11, p.2353-2362, 2001.
[19] M. Zibulevsky, P. Kisilev, Y. Y. Zeevi, and B. A. Pearlmutter, “Blind source separation via multinode sparse representation,” In Advances in Neural Information Processing Systems 14, p.1049-1056, MIT Press, 2002
[20] A. Jourjine, S. Rickard, and O. Yilmaz, “Blind separation of disjoint orthogonal signals: Demixing N sources from 2 mixtures,” In IEEE Conference on Acoustics, Speech, and Signal Processing (ICASSP2000), vol.5, p.2985-2988, 2000.
[21] D. D. Lee and H. S. Seung, “Learning the parts of objects by non-negative matrix factorization.” Nature, 401(675), 788-791, 1999.