中「多或少」的察覺

(1)

許建銘

高雄市立龍華國民中學

一、前言：

現代人工作忙碌，為了替自己安排出更井然有序的生活步調，「時間管理」、「理財規劃」 … … 似乎成為許多人生活中必修的功課。尤其近幾年來，這種強調「平實活用」、「快又有效」的需求與覺察，也帶給在台灣從事基礎數學教育的有關人員，一股「求新求變」的訊息和行動，於是許多中學數學教師正為耕耘更「生活化」、「實用性」、「多采多姿」的數學教學作改革與努力，而像「精打細算」、「或多或少」這種與日常生活息息相關，不會從腦海中消失的思考問題，就成為設計與解決數學問題時「永不凋零」的題材。記得自己讀國中的時候，曾被問過這道問題：「若吃剩的糖果紙，收集 3 張可再換一顆糖果。那麼買 50 顆糖果，最多可吃到多少顆糖果？」當時為了解出這個問題，我用耐心和細心累加得出了「 74 顆」的答案。不過出題的人卻說我的答案不對。後來即使經我反覆重算還是：「74 顆」，當然出題者還是說：「不對！」最後他說了理由：「吃完 74 顆糖果後，還剩下兩張糖果紙。如果先向朋友借一張而湊足三張，就可以多換一顆糖果來吃，而這顆糖果的糖果紙再拿去還朋友，不就可以吃到 75 顆了嗎！」或許，我們可以把剛才的解題，用比較「開放性」與「趣味性」的角度去看待它。不過事實上，早在數十年前或更早之前，就有人想出相關問題很完整的代數解法了（不含借糖果紙的情形）。例題：某連鎖零食店為了促銷與配合環保，回收糖果紙。每 3 張特定牌子的糖果紙，可以換一顆相同的糖果。如果小傑某年吃了該品牌的糖果 83 顆，那麼他最少買了多少顆糖果？讓我們假設買

x

顆時，最多可以吃到 ) (x f 顆。此時剩下的糖果紙不是 1 張就是 2 張，而且 f(x+2)= f(x)+3，現在讓我先證明這個式子的正確性：如果剩下的糖果紙是 1 張，那再買 2 顆糖果，除了有原先兩顆糖果吃外，還可用 3 張糖果紙再換 1 顆糖來吃，而最後剩 1 張糖果紙。如果剩下的糖果紙是 2 張，那再買 2 顆糖果，除了有原先兩顆糖果吃外，還可用 3 張糖果紙再換 1 顆糖來吃，而最後剩 2 張糖果紙。而 f(1)=1，所以買奇數顆糖果 1，3，5， 7，……可以吃到的糖果數為 1，4，7，10，…… 成等差數列；而 f(2)=2，所以買偶數顆糖果 2，4，6，8，……可以吃到的糖果數為 2， 5，8，11，……也成等差數列。所以歸納得

(2)

到：若買2n−1顆糖果，可吃到 2 3 3 ) 1 ( 1 ) 1 2 ( n− = + n− × = n− f 顆糖果；若買2n顆糖果，可吃到 1 3 3 ) 1 ( 2 ) 2 ( n = + n− × = n− f 顆糖果。由此證得 f(x+2) = f(x)+3的式子成立，而例題也就可以這樣來解： (1)若3n−2=83，則 3 1 28 3 85 = = n (不合) (2)若3n−1=83，則n=28 ⇒2n=56 ，所以買了 56 顆糖果。當然，我們也可以試著用一般的算術求解，不過讓我們先假設糖果是一顆一顆零買，而且只要有 3 張糖果紙就拿去換一顆糖果來吃。同時，也讓我們畫個圖(如下圖 )來輔助說明：83 顆糖果由上而下，由左而右，每 3 個排成 1 行，而 83 除以 3 得商 27 餘數 2，所以共 28 行。而第 2 行至第 28 行最上面的一顆糖果( 加一條斜線段作記號的，共有 27 顆)就是表示用三張糖果紙換來的，所以最少買了 83﹣27=56 顆糖果。

二、本文：

(一)問題 1：

如何在銳角∆ABC的三邊上取四點 M、 N、P、Q，使 MNPQ 為面積最大的矩形？而 P、Q 兩點在BC上，M、N 兩點分別在 AB、 AC上。解法： (1)如圖 1-1，令BC=a，BC上的高AH = h。 (2)假設MN=x h NP h a x： =( − ：) Q hx NP a ah− × = ∴ ) (a x a h NP= − ⇒ (3)MNPQ 面積 ) ( ) ( x2 ax a h x a a h x⋅ − = − + = 4 4 ) 2 (x a 2 ah ah a h ₋ ₊ _≤ − = 2 a x= ⇒ 時，MNPQ 有最大面積 4 ah 也就說當 M、N 為

AB

，

AC

中點時， 矩形 MNPQ 的面積為最大。 另解： (1)剪出與△ABC 為全等形的三張紙。 (2) 摺出每張紙BC上的高，也就是摺痕線 AH。 (3)○1_{取第一張紙，並利用直角△斜邊中點至} 三頂點等距離的性質進行摺紙活動(如圖 1-2)。 ○2_{將紙對摺，並使 A、H 重合。若將紙打} 開，就會出現摺痕線MN，且 M、N 分 別為AB，AC中點。 ○3_{以等腰△MBH、△NHC 之對稱軸 MQ 、} NP為界，分別將紙對摺，則 B、C 皆與 H 重合。也就是說，矩形 MNPQ 的面積 恰為原三角形面積的一半。

○ ○ ○……○……○ ○

○ ○ ○……○……○

B

C

A

H

M

N

P

Q

圖 1-1

(A',B',C')

B

C

A

N

M

H

_P

Q

B

C

A

N

M

H

P

Q

_{圖 1-2}

(3)

(4)○1_{取第二張紙。將紙對摺，使 A 落於} _AH_之延長線上，則摺痕線MN∥

BC

(如圖 1-3)。 ○2_由_∠_ANM₌_∠_MN_A′₌_∠_N_C′_C_， C ANM =∠ ∠ 可推得∠NC′C=∠C C C N ′ ∆ ∴ 為等腰△。同理∆MBB′也是等腰△。 ○3_{分別以等腰}∆_MB_B′_，∆_N_C′_C_之對稱軸 MQ、NP為界，將紙對摺，則 MNPQ 為矩形。但因為斜線部分落在 MNPQ 之 外部，可知 MNPQ 面積小於原三角形面 積的一半。 (5)○1_{取第三張紙。將紙對摺，使 A 落於} _AH_之 上(不含 A、H 兩點)，則摺痕線MN∥ BC(如圖 1-4)。 ○2_{分別以等腰}∆_MB_B′_、∆_N_C′_C(理由同(4) 之○2)之對稱軸_MQ、 NP 為界，將紙對 摺，則 MNPQ 為矩形。而斜線處表示 向內摺的紙，或有部分重疊，或有部分 在 MNPQ 之外部，可知 MNPQ 面積也 是小於原三角形面積的一半。 (6)由以上摺紙活動，可推得當 M 、N 分別為 AB、AC中點時，MNPQ 為最大面積 的矩形。以下問題 2 和問題 3，是我設計給國三生作統整教學的「開放性問題」：

(二)問題 2：

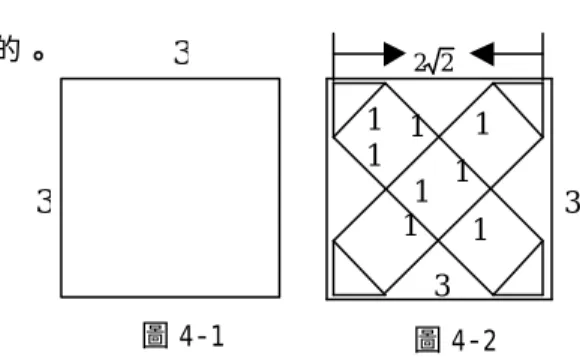
如何在一張 20cm×20cm 的正方形紙上，作出三個兩股長為 1:2 的直角三角形，且讓最大的直角三角形面積是另兩個面積的和，請寫出愈多愈好的作法或想法，同時也希望你能找到三個面積和為最大的直角三角形。解說：讓我們來看看學生和老師對此問題的各種解法及說明： (1)如圖 2-1，這是利用「商高定理」的幾何性質，圖中兩個有虛線邊的正方形面積相加會等於另一個有虛線邊的正方形面積。而三個塗上花色的直角三角形面積皆為該正方形面積的四分之一，且兩股長為 1:2，而其中最大直角三角形面積等於另兩個面積的和。 (2)如圖 2-2，這是利用直角三角形「母子相似」性質，圖中先作兩股長為 8 和 16 的直角三角形，並作其斜邊上的高，此高將原三角形分成兩個小直角三角形，再運用「鏡射原理」，由兩個小直角三角形向外 B C A M N A' C' B' P Q 圖 1-3 B C A M N A' C

'

Q B' P 圖 1-4 圖 2-1

5

10

10 ₁₀

₂

2

5

(4)

各作出全等三角形，自然三個塗上花色的直角三角形的兩股長皆為 1:2，且其中最大直角三角形面積等於另兩個面積的和。 (3)如圖 2-3，這是利用長寬比為 1:2 的長方形，作其對角線得兩個全等直角三角形，並作其中一個直角三角形斜邊上的高，自然三個塗上花色的直角三角形的兩股長皆為 1:2，且其中最大直角三角形面積等於另兩個面積的和。 (4)如圖 2-4，這是利用等腰三角形底邊上的高分原三角形成兩個全等直角三角形，並作其中一個直角三角形斜邊上的高，將得到三個塗上花色的直角三角形的兩股長皆為 1:2，且其中最大直角三角形面積等於另兩個面積的和。 (5)如圖 2-5，這是利用取線段 BC 的中點 E， 連線段 AE 交線段 BD 於 P ，則 2 : 1 :DP= BP (證明容易，不另作證明)。 過 P 點作線段 QR 垂直 BD，且分別交 AB、BC於 Q、R。因為三角形 BPR 為等 腰直角三角形，所以BP =PR ⇒∆QPD， PRD ∆ 皆為 1:2 的直角三角形。若作其中一個直角三角形斜邊上的高，將得到且其中最大直角三角形面積等於另兩個面積的和。 (6)如圖 2-6，將最大直角三角形的斜邊設法 作在正方形對角線上。假設三角形 PRD 為兩股長 1:2 的直角三角形，作PE ⊥BC 交BC於 E。則三角形 PER 相似於三角形 RCD，因為線段 PR 為線段 RD 的二分之 一長，所以線段 ER 等於二分之一線段 CD 圖 2-3 圖 2-4

A

B

C

D

E

P

Q

R

圖 2-5

16

8

4

圖 2-2

(5)

長，所以ER =20÷2=10公分。設BE =x公分，則PE= x公分(因為三角 形 BEP 為等腰直角三角形)，且RC =2x公分。因為 3 10 10 2 = ⇒ = + x x x ， 3 20 2x= 所以只要取 3 20 = CR 公分， 2 3 10 = BP 公分，便可作出兩股長為 1:2 的直角三角形。再運用「鏡射原理」，在對角線另一側作出一個全等直角三角形，並作其斜邊上的高，則圖中三個塗上花色的直角三角形的兩股長皆為 1:2，且其中最大直角三角形面積等於另兩個面積的和。 (7)如圖 2-7，取BC的中點 F，作BE=5公分，連EF、FD、DE。則三角形 EBF 與三角 形 F C D 皆為兩股長為 1:2 的兩相似直角三 角形。又∠BFE+∠CFD=90°=∠EFD，又 FC BF= ，∠FBE+∠FCD=180°，由摺紙性質或簡單的計算可推得： ∆EFD面積 = EBF∆ 面積+∆FCD面積，且圖中三個塗上花色的直角三角形的兩股長皆為 1:2。若試著在正方形內放入一根比DF長的木 條(令長為 l )，我們很容易經由實驗發現， 無法再放入另一根長為 2 l _{的木條( 當然此} 時狀況，兩根木條的一端必須相接且交角 成直角)。由此可以確認三角形 EFD 為正 方形紙上可以作出的最大直角三角形，而這三個直角三角形的面積和也是最大。

(三)問題 3：

(1)圖 3-1 是一塊由矩形與正方形合成的木板，你是否可用三條切割直線將它分成四部分，再拼成一個正方形？請在圖上畫出分割的方式，並在空白處畫其合併後的完成圖。 (2)你也可以利用「三角形全等」性質去作分割，看看切割的長度是否可以少一點，但還是可以切拼成正方形！也請你想一想，並畫出來。圖解(1)：此圖解(或問題設計)的靈感來自：「四個全等的一般直角三角形，加上一個以此直角三角形之兩股差為邊的正方形，則可拼成一個正方形。」

A

B

C

D

E

P

Q

R

圖 2-6

A

B

C

D

E

F

圖 2-7 16 4 4 12 10 6 圖 3-1

(6)

圖 4-3 圖解(2)：說明：圖解(1)和(2)中，雖然都切割成四片，但 (1)的切割線段長度為2 62₊102₊10₌2 136₊10 ，而(2)的切割長度為2 62₊102₌2 136_。讀者可以試著找其它的切割方式，看看有沒有再儘可能小的切割長度。

(四)問題 4：

試從尺寸為

3 ×

3

的正方形中劃出一個圖形(如圖 4-1)，使得它是邊長為 1 的正方體的表面展開圖。解說：這是早期莫斯科數學奧林匹克競試題。國內有許多國中生會知道正方體有十一種展開圖，甚至還可以將它們一一畫出。但對這一題，學生卻束手無策。其實它不是一般的展開方式，我們只要考慮可以摺拼成正方體的外殼即可。我在幾本書上看到的解答都一樣，也很有趣(如圖 4-2)。因為圖中所畫的展開圖，它的長與寬皆為 3 2 2 2 2 2 2 2 < = + + ，所以畫法是可以成立的。然而很明顯的，圖 4-2 絕對不是唯一答案，像圖 4-3 也一定可以摺拼出正方體的外殼，而且有了這種「東牆西補」的觀念，就可以找出「更不一樣」的答案。經筆者實際試驗而找出來的展開圖(如圖 4-4 中，塗黑的部分)，外型像機器人、黑猩猩、變形蟲…… 答案不只可以無限構建，而且都可以摺拼出邊長為 1 的正方體 ( 讀者可以影印此圖，再從中剪幾個摺摺看)。 10 4 4 10 6 6 6 6 ② ① ③ ③ ② ① 圖 4-4 圖 4-1 圖 4-2 1 1 1 1 1 1 1 1 ₃ 3

3

2 2 10 4 4 6 10 6 6 6 6 6 ① ③ ① ② ② ③

(7)

三、結論：

臺灣中學數學教育因為環境與風氣的關係，大多數的家長和老師強調「做多」的練習，相對忽略了「多做」的學習。「做多」的練習指的就是「以量取勝」的練習，「做多」佔據中學生大部分的學習時間，而其中往往包含重覆、死板與雜亂的歷程，例如說：做好幾本參考書，寫各式大量的測驗卷，希望藉由反覆、不斷的練習達到「少錯多對」的「好」成績。但是何謂「多做」的學習呢？它和「做多」的練習有什麼不同呢？就如同上段講的，「做多」的練習的唯一目標就是「成績至上」，而「多做」的學習卻著眼於「有疑必思」、「窮理致知」、「質量並重」的學習態度和規劃，除了重視學生的成績表現，也同時考慮學生理解完整數學知識內涵的教與學，以及終身學習興趣與獨立思考能力的啟發培養。簡單說：「做多」只顧做許多問題；「多做」強調多花時間思考與解決問題(不一定做很多問題，如「一題多解」與「思考啟發」) ，兩者的觀念大不相同。一道外表毫不起眼的美食為何與一只頂級名錶一樣，讓許多人爭相追逐發狂，不只因為「限量」的原因，更重要是這些名廚和工匠用生命在認真生活，他們將智慧與情感投注在工作中的每個細節，而且獲得有品味的人青睞和認證。教育是百年大計，如果教學者能體認並實踐：「『做多』可能是反覆而死板；『多做』才能用心有變化」的道理，「數學之美」才能深入人心，數學教育才能啟迪人類的「善知識」並展現萬物之靈思想的卓然不凡。