臺灣中部地區國小高年級學生vanHiele幾何推理能力之研究

國立臺中教育大學數學教育學系碩士班

碩士論文

指導教授：吳德邦 博士

臺灣中部地區國小高年級學生

臺灣中部地區國小高年級學生

臺灣中部地區國小高年級學生

臺灣中部地區國小高年級學生

van Hiele幾何推理能力之研究

幾何推理能力之研究

幾何推理能力之研究

幾何推理能力之研究

研究生：陳姿良 撰

中華民國九十九年六月

摘

摘

摘

摘 要

要

要

要

本研究旨在探討臺灣中部地區五、六年級學生在 van Hiele 幾何推理層次的表現情 形。 本研究乃行政院國家科學委員會補助專案計畫（吳德邦，2010；馬秀蘭，2009， 2007a，2006，2005）之部份成果，以自編的「van Hiele 非形式幾何推理測驗」為研究 工具，選取臺灣中部地區的國小五、六年級 741 位學生為研究對象，並以百分率統計 法、獨立樣本 t 檢定、三因子變異數分析、交互作用及主要效果檢定、卡方檢定的方 法依整份測驗及批判性、創造性層次的通過率、不同年級、不同性別與不同縣市在 van Hiele 幾何推理層次的表現來加以探討。 本研究的結論如下： 一、van Hiele 非形式幾何推理測驗的總答對率為 70.40%。批判性層次答對率除了四邊 形內角和的概念推理外，其餘試題答對率均在 60%以上。創造性層次的答對率在 60%以下的有 5 題，其中四題是包含關係的推理，一題是圓柱斜切的切面判斷。 二、在批判性層次中，通過率最高的為「梯形的角度推理」，而通過率最低的為「四邊 形內角和的概念推理」。在創造性層次中，通過率最高的為「由已知性質推理出正 確圖形」，而通過率最低的為「圓柱斜切的切面判斷」。 三、在批判性層次中，大多數題目六年級的通過率比五年級增加，但有 3 題（16.67%） 五年級通過率比六年級高，其中屬於平面幾何範圍的有 1 題（5.56%），立體幾何 範圍的則有 2 題（11.11%）。在創造性層次中，大多數題目六年級的通過率仍比五 年級增加，但有 3 題（21.43%）五年級通過率比六年級高，均屬於立體幾何的範 圍。

四、不同縣市、年級與性別之國小學生幾何推理測驗的差異情形 （一）B 市的學生在整份測驗和創造性層次的成績比 A 縣的學生高，有明顯的城鄉差 異，但兩縣市的學生在批判性層次的成績沒有明顯的城鄉差異。 （二）六年級學生在整份測驗、批判性層次和創造性層次的成績比五年級學生高。 （三）男生、女生在整份測驗、批判性層次和創造性層次的成績沒有明顯的差異。 五、縣市、年級與性別之國小學生幾何推理測驗的交互作用情形 （一）在整份測驗中，縣市、年級與性別之間無交互作用、縣市與性別之間無交互作 用以及年級與性別之間無交互作用，但縣市與年級之間有交互作用。 （二）在批判性層次中，縣市、年級與性別之間無交互作用、縣市與年級之間無交互 作用、縣市與性別之間無交互作用、年級與性別之間無交互作用。 （三）在創造性層次中，縣市、年級與性別之間無交互作用、縣市與性別之間無交互 作用以及年級與性別之間無交互作用，但縣市與年級之間仍有交互作用。 六、不同縣市、年級、性別之國小學生在幾何推理層次的分布情形

（一）A 縣和 B 市的學生中，都是分布在創造性層次的學生最多。在 van Hiele 幾何推 理層次中，B 市的表現優於 A 縣，有著明顯的城鄉差異。 （二）五年級和六年級的學生中，都是分布在創造性層次的學生最多，但年級愈高， 分布在較高層次的人數並沒有明顯增多。 （三）男學生和女學生都是分布在創造性層次的學生最多，但在van Hiele幾何推理層 次中，不同性別的學生沒有明顯的差異。 關鍵詞：小學、幾何、推理、van Hiele、思考層次

A Study of van Hiele Geometrical Reasoning of High-Grade Elementary School

Students from Central Taiwan

Abstract

The purpose of this study is to discuss the performance of the high-grade elementary school students from Central Taiwan in van Hiele geometrical reasoning level.

This study is a part of the results of the projects of Executive Yuan National Science Council (Der-Bang Wu: 2010; Hsiu-Lan Ma: 2009, 2007a, 2006, 2005). This study uses self-developing “van Hiele non-formulaic geometrical reasoning test” as the research tool, choosing 741 fifth- and sixth-grade students in Central Taiwan as the subjects. We use percentage change, independent-sample t-test, three-way ANOVA, interaction effects, simple main effects and Chi-Square Test. The discussion is based on the entire test, the pass rate of critical and creative level, to shed light on the performance of the students in different grades, of different genders and from different counties in van Hiele geometrical reasoning level.

The conclusions are as follows:

1. The total correct response rate of van Hiele non-formulaic geometrical reasoning test was 70.40%. Above 60% of the answers are correct in the critical level questions except the angle sum of quadrilateral reasoning. Under 60% of the answers are correct in five creative level questions, four of them is the inclusion relation of reasoning, one of them is the tangent plane of cylinder askew.

2. In the critical level, the trapezoid angle reasoning has the highest pass rate and the angle sum of quadrilateral reasoning has the lowest pass rate. In the creative level, reasoning the correct graph from given properties has the highest pass rate, and the tangent plane of cylinder askew has the lowest pass rate.

3. In the critical level, the sixth-grade students have a higher pass rate in most of the questions. But the fifth-grade students have a higher pass rate in three questions (16.67%). These questions include one of two-dimensional geometry (5.56%) and two of three-dimensional geometry (11.11%). In the creative level, the sixth-grade students have a higher pass rate in most of the questions. But the fifth-grade students have a higher pass rate in three questions (21.43%). These questions are three-dimensional geometry.

4. The variety in the performance of the students from different backgrounds in geometrical reasoning test.

4.1 In the whole test, students from B City get better grades in the creative level than those from A County. An obvious distinction due to urban and rural origins is observed, but not in the grades of the critical level.

4.2 In the whole test, the critical and creative level, scores of sixth-grade students are higher than those of fifth-grade students.

4.3 In the whole test, the critical and creative level, scores of male and female students are not obviously different.

5. The interactions between performance of the students in geometrical reasoning test.

5.1 In the whole test, county, grade and gender did not interact, county and gender did not interact, grade and gender did not interact. But there is interaction between county and grade.

5.2 In the critical level, county, grade and gender did not interact, county and grade did not interact, county and gender did not interact, grade and gender did not interact. 5.3 In the creative level, county, grade and gender did not interact, county and gender did not interact, grade and gender did not interact. But there is interaction between county and grade.

6. In geometrical reasoning level, the distribution of performance from those students. 6.1 Most of A county’s and B city’s students are in the creative level. In the van Hiele geometrical reasoning level, scores of students from B City are better than those from A County.

6.2 Most of fifth- and sixth-grade students are in the creative level, but the number of students is not obviously higher in the higher grade.

6.3. Most of male and female students are in the creative level, but in the van Hiele geometrical reasoning level, the scores of those students in the different genders are not obviously different.

目

目

目

目 次

次

次

次

第

第

第

第一

一

一

一章

章

章

章 緒論

緒論

緒論

緒論 ... 1

第一節 研究動機 ... 1 第二節 研究目的與待答問題 ... 5 第三節 名詞定義 ... 6 第四節 研究的限制 ... 7

第二章

第二章

第二章

第二章 文獻探討

文獻探討

文獻探討

文獻探討 ... 9

第一節 幾何推理的意義 ... 9 第二節 幾何推理發展的理論基礎 ... 11 第三節 幾何推理發展的相關研究 ... 26

第三章

第三章

第三章

第三章 研究方法與步驟

研究方法與步驟

研究方法與步驟

研究方法與步驟 ... 31

第一節 研究對象 ... 31 第二節 研究工具 ... 32 第三節 研究實施步驟 ... 51 第四節 資料分析與處理 ... 54

第四章

第四章

第四章

第四章 研究結果與討論

研究結果與討論

研究結果與討論

研究結果與討論 ... 57

第一節 學生在幾何推理測驗的答題選填分析 ... 57 第二節 學生在幾何推理測驗中整體通過率 ... 81 第三節 學生在各層次答題答對率分析 ... 84 第四節 不同縣市、年級與性別之國小學生幾何推理測驗的差異分析 ... 92 第五節 縣市、年級與性別之國小學生幾何推理測驗的交互作用 ... 98 第六節 不同縣市、年級、性別之國小學生在幾何推理層次的分布情形及其卡方 檢定 ... 111

第五章

第五章

第五章

第五章 結論與建議

結論與建議

結論與建議

結論與建議 ... 119

第一節 結論 ... 119 第二節 建議 ... 125

參考書目

參考書目

參考書目

參考書目 ... 127

一、中文部分 ... 127 二、英文部分 ... 132

附錄

附錄

附錄

附錄 ... 136

附錄一 康軒版、南一版及翰林版教材分析 ... 136 附錄二 預試施測工具 ... 141 附錄三 正式施測工具 ... 159

表

表

表

表 目

目

目 次

目

次

次

次

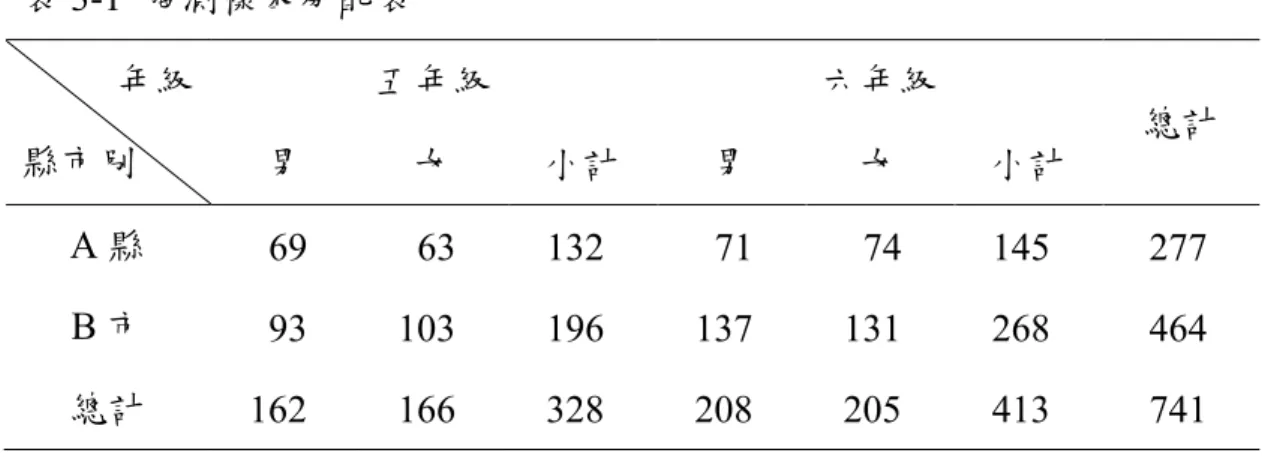
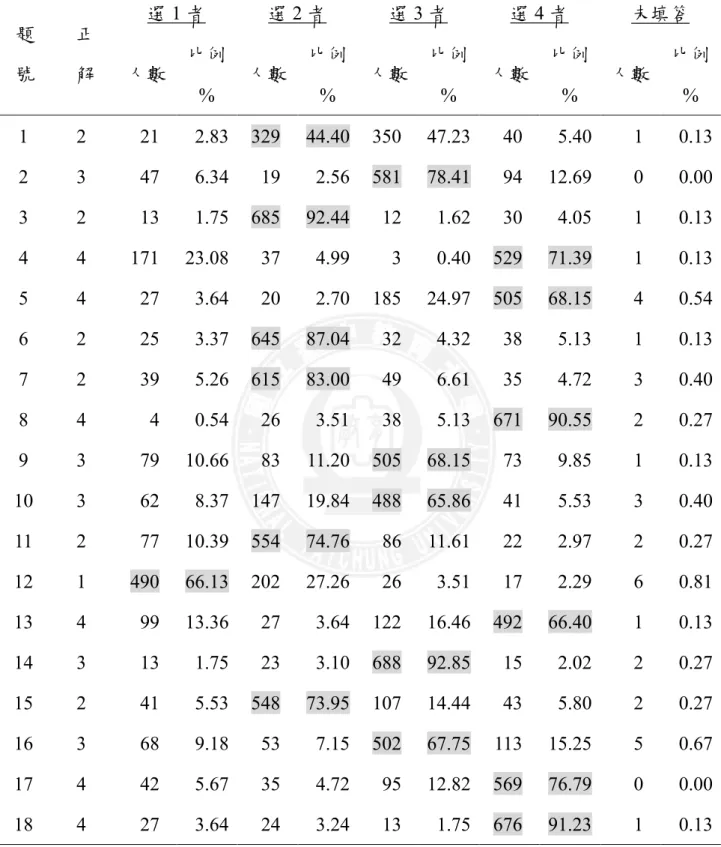
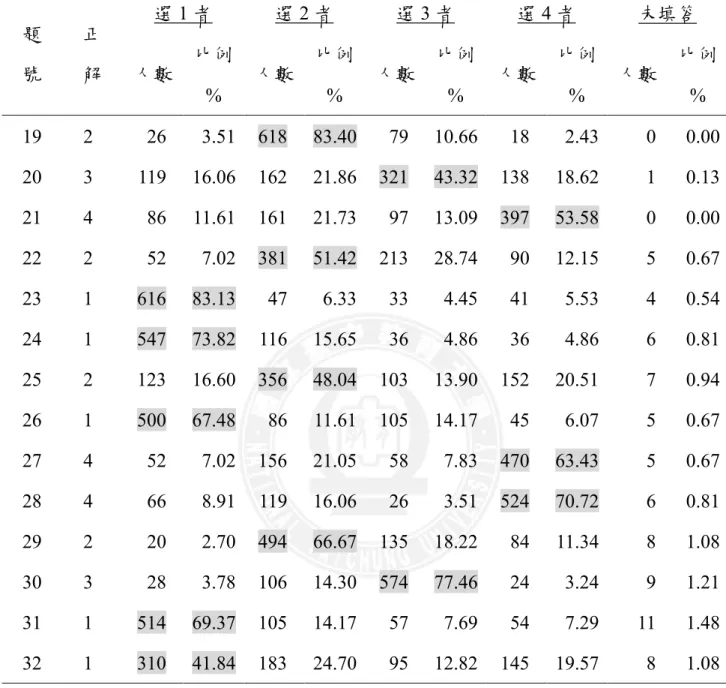
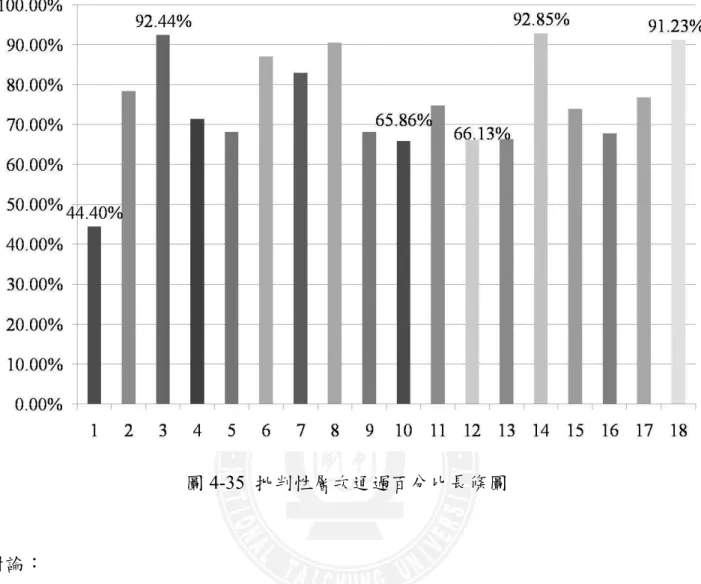
表 2-1 van Hiele 幾何思考層次三的描述 ... 21 表 2-2 國內外數學推理之相關研究... 27 表 3-1 施測樣本分配表 ... 32 表 3-2 van Hiele 幾何推理預試測驗之雙向細目表 ... 44 表 3-3 van Hiele 幾何推理預試測驗之項目分析 ... 46 表 3-4 van Hiele 幾何推理正式測驗之雙向細目表 ... 49 表 4-1 批判性層次各題答案選填情形 ... 59 表 4-2 創造性層次各題答案選填情形 ... 70 表 4-3 批判性層次各題答對人數及通過率 ... 81 表 4-4 創造性層次各題答對人數及通過率 ... 83 表 4-5 批判性層次各題的答對率... 85 表 4-6 創造性層次各題的答對率... 89 表 4-7 不同縣市學生在所有題目得分差異情形 ... 93 表 4-8 不同縣市學生在批判性層次得分差異情形 ... 93 表 4-9 不同縣市學生在創造性層次得分差異情形 ... 94 表 4-10 不同年級學生在所有題目得分差異情形 ... 94 表 4-11 不同年級學生在批判性層次得分差異情形 ... 95 表 4-12 不同年級學生在創造性層次得分差異情形 ... 96 表 4-13 不同性別學生在所有題目得分差異情形 ... 96 表 4-14 不同性別學生在批判性層次得分差異情形 ... 97 表 4-15 不同性別學生在創造性層次得分差異情形 ... 97 表 4-16 縣市、年級與性別在測驗總分上的平均數、標準差分析表 ... 99 表 4-17 不同縣市、年級與性別學生在測驗總分之變異數分析 ... 100

表 4-18 A 縣不同年級學生在所有題目得分差異情形... 101 表 4-19 B 市不同年級學生在所有題目得分差異情形 ... 101 表 4-20 不同縣市的五年級學生在所有題目得分差異情形 ... 102 表 4-21 不同縣市的六年級學生在所有題目得分差異情形 ... 103 表 4-22 縣市、年級與性別在批判性層次上的平均數、標準差分析表 ... 104 表 4-23 不同縣市、年級與性別學生在批判性層次之變異數分析 ... 105 表 4-24 縣市、年級與性別在創造性層次上的平均數、標準差分析表 ... 106 表 4-25 不同縣市、年級與性別學生在創造性層次之變異數分析 ... 107 表 4-26 A 縣不同年級學生在創造性層次得分差異情形... 108 表 4-27 B 市不同年級學生在創造性層次得分差異情形 ... 109 表 4-28 不同縣市的五年級學生在創造性層次得分差異情形 ... 109 表 4-29 不同縣市的六年級學生在創造性層次得分差異情形 ... 110 表 4-30 不同縣市的學生在幾何推理層次的分布情形 ... 111 表 4-31 不同縣市的學生在各個隸屬層次之卡方考驗 ... 113 表 4-32 不同年級的學生在幾何推理層次的分布情形 ... 114 表 4-33 不同年級的學生在各個隸屬層次之卡方考驗 ... 116 表 4-34 不同性別的學生在幾何推理層次的分布情形 ... 117 表 4-35 不同性別的學生在各個隸屬層次之卡方考驗 ... 118

圖

圖

圖

圖 目

目

目 次

目

次

次

次

圖 2-1 推理與批判性和創造性思考之關係 ... 23 圖 2-2 思考層次的階級圖 ... 23 圖 2-3 思考層次的階級圖 ... 25 圖 3-1 修改圖形中角的代號 ... 33 圖 3-2 修改立體圖形的角度 ... 34 圖 3-3 增加圖形的導引線 ... 35 圖 3-4 調整圖形顏色及框線 ... 35 圖 3-5 調整題目敘述及排版 ... 37 圖 3-6 調整題目敘述方式 ... 38 圖 3-7 修改文字敘述及圖形增加輔助線 ... 39 圖 3-8 調整題目中有關方向的敘述... 40 圖 3-9 第 6 題題目 ... 41 圖 3-10 第 8 題題目 ... 41 圖 3-11 第 16 題題目 ... 42 圖 3-12 第 19 題題目 ... 42 圖 3-13 第 25 題題目 ... 43 圖 3-14 第 31 題題目 ... 43 圖 3-15 研究流程圖 ... 53 圖 4-1 批判性層次答題選填分析長條圖 ... 58 圖 4-2 學生在幾何推理測驗第 1 題答題選填情形 ... 60 圖 4-3 學生在幾何推理測驗第 2 題答題選填情形 ... 60 圖 4-4 學生在幾何推理測驗第 3 題答題選填情形 ... 61 圖 4-5 學生在幾何推理測驗第 4 題答題選填情形 ... 61

圖 4-6 學生在幾何推理測驗第 5 題答題選填情形 ... 62 圖 4-7 學生在幾何推理測驗第 6 題答題選填情形 ... 62 圖 4-8 學生在幾何推理測驗第 7 題答題選填情形 ... 63 圖 4-9 學生在幾何推理測驗第 8 題答題選填情形 ... 63 圖 4-10 學生在幾何推理測驗第 9 題答題選填情形 ... 64 圖 4-11 學生在幾何推理測驗第 10 題答題選填情形 ... 64 圖 4-12 學生在幾何推理測驗第 11 題答題選填情形 ... 65 圖 4-13 學生在幾何推理測驗第 12 題答題選填情形 ... 65 圖 4-14 學生在幾何推理測驗第 13 題答題選填情形 ... 66 圖 4-15 學生在幾何推理測驗第 14 題答題選填情形 ... 66 圖 4-16 學生在幾何推理測驗第 15 題答題選填情形 ... 67 圖 4-17 學生在幾何推理測驗第 16 題答題選填情形 ... 67 圖 4-18 學生在幾何推理測驗第 17 題答題選填情形 ... 68 圖 4-19 學生在幾何推理測驗第 18 題答題選填情形 ... 68 圖 4-20 創造性層次答題選填分析長條圖 ... 69 圖 4-21 學生在幾何推理測驗第 19 題答題選填情形 ... 71 圖 4-22 學生在幾何推理測驗第 20 題答題選填情形 ... 71 圖 4-23 學生在幾何推理測驗第 21 題答題選填情形 ... 72 圖 4-24 學生在幾何推理測驗第 22 題答題選填情形 ... 73 圖 4-25 學生在幾何推理測驗第 23 題答題選填情形 ... 74 圖 4-26 學生在幾何推理測驗第 24 題答題選填情形 ... 74 圖 4-27 學生在幾何推理測驗第 25 題答題選填情形 ... 75 圖 4-28 學生在幾何推理測驗第 26 題答題選填情形 ... 76 圖 4-29 學生在幾何推理測驗第 27 題答題選填情形 ... 77

圖 4-30 學生在幾何推理測驗第 28 題答題選填情形 ... 77 圖 4-31 學生在幾何推理測驗第 29 題答題選填情形 ... 78 圖 4-32 學生在幾何推理測驗第 30 題答題選填情形 ... 79 圖 4-33 學生在幾何推理測驗第 31 題答題選填情形 ... 79 圖 4-34 學生在幾何推理測驗第 32 題答題選填情形 ... 80 圖 4-35 批判性層次通過百分比長條圖 ... 82 圖 4-36 創造性層次通過百分比長條圖 ... 83 圖 4-37 批判性層次五、六年級學生答對率長條圖 ... 86 圖 4-38 第 9 題題目 ... 87 圖 4-39 第 15 題題目 ... 87 圖 4-40 第 18 題題目 ... 88 圖 4-41 創造性層次五、六年級學生答對率長條圖 ... 90 圖 4-42 第 27 題題目 ... 91 圖 4-43 第 28 題題目 ... 91 圖 4-44 第 29 題題目 ... 92

第一章

第一章

第一章

第一章 緒論

緒論

緒論

緒論

本研究主要是以 Coles & Robinson（1989）和 Krulik & Rudnick（1993, 1999）所 提出有關推理思考層次，並配合 van Hiele 幾何思考層次為理論基礎，來探討臺灣中部 地區國小五、六年級學生在 van Hiele 幾何推理層次發展之情形。本章共分為四節，分 別來探究本研究的研究動機與目的、待答問題、名詞定義與研究限制。

第一節

第一節

第一節

第一節 研究動機

研究動機

研究動機

研究動機

當你問：「學數學到底要學什麼呢？」以實用性來看，得到的答案是學會數學算術 計算，再加上一點點的幾何與代數。但對大多數的學生來說，在考試至上的氣氛薰陶 之下，認為數學這個科目充滿著許多困難的計算和難懂的公式，懼怕與排斥數學，因 此他們大多認為學數學是背誦及套用公式，做各種（複雜）的計算。 然而做了這麼多複雜的計算之後，學生的數學能力究竟是如何呢？周筱婷（1995） 認為我國的學生在數學方面，優於計算、記憶，卻劣於推理、解題。此外，李源順、 王美娟、蘇意雯與陳怡仲（2009）提到雖然我國歷年來在 TIMSS 的成就或素養表現都 非常優異，但是從 TIMSS 的個別試題表現，仍有許多試題的表現不如理想。像是臺灣 在參與國際教育成就之 TIMSS 2003 試測中，小學四年級學生在「推理」試題表現最 差，平均通過率僅有 43.3%（林碧珍、蔡文煥，2003），或者在 TIMSS 2007 的試題中， 有許多的推理及解題性知識的問題，而學生的答對率不高（李源順等，2009）。可見臺 灣學生對於數學能力的養成偏重於數學公式的記憶與計算過程的訓練，忽略了解題、 推理思考能力的訓練。 早在 1993 年教育部所公佈的國小數學課程標準中便強調：必須將數學視為推理 （教育部，1993）。數學推理是數學的核心，也是數學的基礎。許多國家的數學教育家 認為，在數學教育中，教學生進行邏輯推理的方法，讓他們自己推理出某種結構的教

學比單純告訴他們結論還重要，中國有句古話說：「授之魚不如授之以漁」，意思就是 給一個人一些魚不如教他捕魚的方法。這個道理在當代數學家和教育家引起了共鳴， 而 1993 年國小數學改革就是以這個口號來支持它改革的宗旨。

美國數學教師協會 National Council of Teachers of Mathematics（NCTM, 2000）也 提出推理是學生離開教室及進入真實世界必須跟隨之主技能。把看似無意義的「資料 （data）」加以分析整理，讓它成為有意義的「資訊（information）」，這是推理的能力， 推理思考是指對某些已知的跡象，根據邏輯的原則循序推尋可能導致的結果。因此推 理思考活動是一種尋求因果關係的心理歷程。Coles 和 Robinson（1989）認為推理思 考是一種同時具備批判性思考和創造性思考的思考模式。而 Krulik 和 Rudnick（1993, 1999）則表示推理是思考的一部分，並指出推理是思考的歷程中，高於回憶（recall） 的層次，分為三個層次，從較低層次的基本的（basic）思考，到較高層次的批判性 （critical）思考、創造性（creative）思考。而數學是最能訓練學生推理思考和尋找規 律能力的素材（吳德邦與馬秀蘭譯，2009a，2009b；馬秀蘭與吳德邦譯，2009a，2009b）。 法國數學家何密得曾提到：「在一團亂糟糟的事物中，一條小小規律的察覺，宛如 黑暗中摸索時的一線光明，常引導我們到達新的數學天地。這份經過『柳暗花明又一 村』帶來的喜悅，就是許多學者窮盡畢生之力，研究純粹科學的內在動機。」（黃敏晃， 2000）。這就是數學具有吸引力的原因，它能夠引導學生進行奇妙的推理，推理的培養 讓學生由死記解題過程轉為以理解來解題的方式，在小學數學教育中具有極重要的作 用。 近年來，家長對學習數學的想法已漸有改變，從早期由於考試領導學習，因此解 題只看答案的對錯，不計較答案的來源，到現在漸漸開始認同學數學必須用推理尋求 數與形的規律及過程，且將它看成是學習數學的重要方式（曹亮吉，2003）。而教育部 （2000）所公佈的九年一貫課程在數學科的分段能力指標中，加入了「連結」這個新 主題，就是為了培養學生能夠運用推理的方法達到解題的能力。李源順等人（2009）

為避免連結的主題時常被忽視，更進一步建議在各個年級都增加「連結」這項能力指 標，以增加學生解題的經驗。TIMSS 2007 的數學評量架構在認知領域部份四年級和八 年級都分為知道、應用與推理等三個面向，隨著年級愈高，評量推理的百分比從 20% 提高到 25%(李源順等，2009)。美國麻省理工學院（MIT）將其教育的終極目標區分 為三個層次：推理（reason）、知識（knowledge）與智慧（wisdom），並將其充份的表 現在課程的安排上（林之平、李仙美與林榮泰，2005）。以上種種均顯示出推理能力愈 來愈受到大家的重視。 檢視我國的數學課程發展，幾何和代數是數學的兩大領域，在我們生活的真實世 界中，則處處充滿了幾何形體，這些幾何形體以平面或空間形式放置著或移動著。例 如：長方形的門和窗、三角形的拉環依固定的間隔排列，掛在車廂的半空中、臉上的 圓形眼鏡等等。自然界中，也到處充滿著幾何形體，如行星的橢圓軌道、蜂巢的六角 形，都和平面、空間的幾何有密不可分的關係。也就是說，我們時時刻刻都與幾何同 在。Freudenthal（1973）亦表示：「幾何乃研究空間中的形狀和空間關係，它提供兒童 聯結數學與真實世界一個最佳機會。」因此，幾何不但是數學教育中的重要課題，而 且也是較易學習、較有趣的教學單元（教育部，2003）。 教育部（2000）在《國民中小學九年一貫課程暫行綱要－數學學習領域》的基本 理念中也開宗明義提到：「我們週遭的自然與社會環境中，到處可見數與形，而各種數 與形都有一些規律；而數學探討的就是這一些規律。」數學課程目標第一條即為「掌 握數、量、形的概念與關係」。教育部（2003）頒布的國民中小學九年一貫課程綱要中 明訂數學學習領域的內容為「數與量」、「幾何」、「統計與機率」、「代數」和「連結」 五大主題，足見幾何課程在數學教學中的重要性。 NCTM 除了明定了幾何在數學課程中的重要性：改善空間能力、發展其他數學概 念的橋樑與基礎、學習解題思考的最佳問題來源（周淑惠，1995）。並在學校數學課程 與評量標準（Curriculum and Evaluation Standards for School Mathematics）中指出，培

養幾何能力有助於有條理的表示與敘述世界上的事物（NCTM, 1989）。同時，NCTM （1989）課程標準中，明確指出在幾何主題中，所有的學生必須能：(1)辨識、描述、 比較、仿作、繪製並分類二維及三維之幾何形體；(2)發展空間感；(3)操作研究並預測 圖形經過組合、分解及各種變化之後的結果；(4)理解、應用並推論幾何形體的性質及 其關係，包含全等與相似；(5)發展幾何的應用，作為一種描述並模式化自然世界的方 法；(6)將幾何概念與數字及測量等概念相連結；(7)能在實際生活中辨識並欣賞幾何形 體。數學教育的主要目標是要發展兒童的數學推理及思考能力，使其能夠應用所學的 數學知識和技能來解決在實際的生活中所遭遇的問題情境（NCTM, 2000）。因此小學 的幾何教學，除了盡量讓學童發揮、拓展其幾何直覺，在操作中，認識各種簡單幾何 形體與其性質之外，更要加入簡單的推理性質與彼此之間的關係，為以後銜接國中幾 何的教學，打下良好的基礎（教育部，2003）。 荷蘭數學教育家 van Hiele 夫婦在 1956 年則綜合完形心理學和皮亞傑認知心理學 的論點，研究個體幾何思考層次的發展，共同提出兒童幾何思考的發展層次 van Hieles 模式（van Hiele, 1986），提供小學及中學教師教學前瞭解學生起點行為之參考。Van Hiele 的理論享譽國際，早在 1960 年代蘇俄的教育學家就有興趣於 van Hiele 模式，並 且基於此模式執行了一個廣大的研究，其終極目的在於改進他們學校的幾何課程（Fuys, Geddes & Tischler, 1988）。根據吳德邦（1998）指出其層次分為(1)視覺的（visual）；(2) 描述的（descriptive）；(3)理論的（theoretical）；(4)形式邏輯的（formal logic）；(5)邏輯 法則本質的（the nature of logical lows）（吳德邦，1999，2000b，2004；吳德邦、陳姿 良、馬秀蘭、紀小玉，2009）。

van Hiele 認為幾何思考的發展是與教學因素有關，當學生的能力提升時，思考層 次便會依序地從一個層次移動下一個層次。van Hiele 有關兒童幾何概念發展的理論對 課程都有很大的影響，1993 年起實施的國小數學新課程與 2000 年的九年一貫課程， 在幾何教材的發展順序，即是以 van Hiele 理論為主軸，亦與皮亞傑對七至十二歲具體

運思期兒童的認知發展論點相合（吳德邦，1999；譚寧君，1993）。因此，van Hiele 在幾何課程中佔有一席之地。

基於以上論述，研究者深覺幾何推理在國小數學領域中的重要性，但由於國內相 關 van Hiele 之研究皆顯示國小學童之幾何思考大多介於層次一至三之間（吳德邦， 1999，2000b，2004；林軍治，1992；劉好，1993；Ma & Wu, 2008; Wu & Ma, 2006, 2009, 2010）。大部分中、高年級生對基本幾何圖形概念能達層次二，但只有高年級生能達層 次三（Wu & Ma, 2006, 2009, 2010）。因此本研究以國小五、六年級學生為研究對象， 採用問卷調查，研究臺灣中部地區國小五、六年級學生在幾何推理之發展情形。測驗 工具則依據 Coles & Robinson（1989）和 Krulik & Rudnick（1993, 1999）有關推理的 內涵，以其思考層次的關係與層次，並配合 van Hiele 幾何思考層次理論、Fuys, Geddes & Tischler（1988）提出針對 van Hiele 幾何思考層次的描述（吳德邦、謝翠玲，1998； 吳德邦、李奇荃、馬秀蘭與李懿芳，2009；吳德邦、馬秀蘭與李懿芳，2007；吳德邦、 馬秀蘭與藍同利，2006a，2006b；吳德邦、陳姿良、馬秀蘭與紀小玉，2009），來編擬 本研究中發展的「van Hiele 非形式幾何推理測驗」，用以瞭解國內國小五、六年級學 生幾何推理發展情形，提供國小五、六年級教師課程計畫實施之參考。

第二節

第二節

第二節

第二節 研究目的與

研究目的與

研究目的與

研究目的與待答問題

待答問題

待答問題

待答問題

一 一 一 一、、、、研究目的研究目的研究目的研究目的 依據上述研究動機，本研究的研究目的如下： （一） 分析學生在幾何推理測驗的總答對率及答題選填情形。 （二） 分析學生在幾何推理測驗中各題通過率。 （三） 分析學生在各層次答題答對率。 （四） 分析不同縣市、年級與性別之國小學生幾何推理測驗的差異。 （五） 分析縣市、年級與性別之國小學生幾何推理測驗的交互作用。

（六） 分析不同縣市、年級、性別之國小學生在幾何推理層次的分布情形及其卡方檢 定。 二 二 二 二、、、、待答問題待答問題待答問題待答問題 依據上述的研究動機與目的，本研究主要探討下列相關之問題： （一） 學生在幾何推理測驗的總答對率及答題選填情形為何？ （二） 學生在幾何推理測驗中各題通過率為何？ （三） 學生在各層次答題答對率為何？ （四） 不同縣市、年級與性別之國小學生幾何推理測驗有何差異？ （五） 縣市、年級與性別之國小學生幾何推理測驗的交互作用為何？ （六） 不同縣市、年級、性別之國小學生在幾何推理層次的分布情形及其卡方檢定為 何？

第三節

第三節

第三節

第三節 名詞定義

名詞定義

名詞定義

名詞定義

本節將研究中所涉及到的相關名詞，做更進一步的定義與說明。茲分述如下： 一 一 一 一、、、、中部中部中部中部地區地區地區地區 係指臺灣中部地區，而為顧及研究倫理，因此以 A 縣、B 市之代號定義之。此二 縣市之相關人文背景的描述如下： A 縣：土地面積約為 1074 平方公里，以平地面積最大，農業最為發達，目前總人 口數約為 131.2 萬人。 B 市：土地面積約為 163.4 平方公里，為盆地地形，以工商產業結構為主，是中 臺灣經濟、交通、文化的重鎮，目前總人口數約為 107.4 萬人。

二 二 二 二、、、、國小學國小學國小學國小學生生生生 係指臺灣中部地區 2009 年第二學期在學的國小學生為主，其中並不包含私立國 小、特殊學校以及特殊班級的學生。 三 三 三 三、、、、幾何形體幾何形體幾何形體幾何形體 本研究中所謂的幾何形體，係指國民小學數學中所提到的幾何形體，包含三角形、 正方形、長方形、平行四邊形、菱形、梯形、圓形、正方體、長方體、直角柱、直角 錐、直圓柱、直圓錐。 四 四 四 四、、、、van Hiele 幾何推理層次幾何推理層次幾何推理層次 幾何推理層次

本研究所提及的 van Hiele 幾何推理層次，係綜合 Coles & Robinson（1989）和 Krulik & Rudnick（1993, 1999）有關推理的內涵，以其思考層次的關係與層次，並配合 van Hiele 幾何思考層次理論、Fuys 等人（1988）提出針對 van Hiele 幾何思考層次的描述發展而 來，分為批判性層次和創造性層次。

第四節

第四節

第四節

第四節 研究的限制

研究的限制

研究的限制

研究的限制

本研究的主要限制如下： （一） 由於經費及人力的限制，本研究僅限於臺灣中部地區之國民小學五至六年級在 學學生，無法擴及全國各縣市之樣本。 （二） 由於研究對象為臺灣中部地區的在學學生，然因臺灣中部地區幅員遼闊，勢必 存在著嚴重的城鄉差距與語言習慣，然本研究不將語言能力的差異列入考量的 範圍，留待後續相關的研究再行討論之。 （三） 本研究僅探討九年一貫課程中所論及之三角形、四邊形、多邊形、直柱體、直 錐體、直圓柱、直圓錐等幾何概念。

第二章

第二章

第二章

第二章 文獻探討

文獻探討

文獻探討

文獻探討

本研究的目的在探討國小五、六年級學生在 van Hiele 幾何推理層次發展之情形， 為了對國小五、六年級學生這方面能力的了解，本章就國內外相關理論與文獻進行探 討，主要內容如下：第一節澄清幾何推理的意義；第二節了解幾何推理發展的理論基 礎；第三節探討幾何推理發展的相關研究。

第一節

第一節

第一節

第一節 幾何推理的意義

幾何推理的意義

幾何推理的意義

幾何推理的意義

教育部（2003）在九年一貫課程綱要中，清楚的指出，幾何推理是以「已知條件」 及「已知為正確的幾何性質」，推導出結論。為了更了解幾何推理的意義，本節整理國 內外不同學者的看法，分為幾何及推理兩大部分加以敘述。 一 一 一 一、、、、幾何幾何幾何幾何（（（（geometry））） ） 幾何在數學的各分支中，算是一門歷史久遠且蓬勃發展的學科。早在西元 1607 年（明朝末年）由傳教士利瑪竇和徐光啟合譯歐幾里得的著作「幾何原本」中，就已 經出現「幾何」一詞，「幾何原本」的內容包括平面幾何、立體幾何（余文卿與謝輝光 譯，1989）。 Freudenthal（1973）認為幾何是研究空間中的形狀和空間關係；美國數學教育學 者 Farrell（1987）則認為幾何不但是一個動態發展的學科，它還包含一對不可分離的 基本結構：其一是探索空間數、量、形之間關係的具體事物；另一是分析邏輯推理的 抽象思維。而 ERIC 網站（2009）同樣表示幾何就是研究幾何形體的形狀、大小和相 互位置關係的科學。 一般來說，幾何形體較廣義的定義認為，只要是由點、線、面、體或它們的組合 所成的圖形都可稱為幾何形體。例如：直線、線段、角、長方形、正方形和長方體、 正方體、圓柱體、圓錐等都是幾何形體。

而本研究及九年一貫課程中所探討的幾何形體是指狹義的幾何形體，包括平面幾 何與立體幾何，以下分別簡單介紹平面幾何和立體幾何： （ （ （ （一一一一））））平面幾何平面幾何平面幾何平面幾何 平面幾何所研究之幾何形體上所有的點，也就是一個圖形上所有的點，都會在同 一平面內，例如：正方形、長方形、圓形、三角形等。 （ （ （ （二二二二））））立體幾何立體幾何立體幾何立體幾何 立體幾何所研究之幾何形體上所有的點，也就是一個形體上所有的點，並不全在 同一平面內，例如：球體、立方體、三角錐等（Daintith, J. , & Nelson, R. D. 原著，余 文卿等譯，1989；ERIC 網站，2009）。 高耀琮（2002）提出，2001 年起開始實施的九年一貫課程中，數學領域五個大主 題之ㄧ「圖形與空間」就是「幾何」的總稱。2003 年，教育部（2003）更進一步在所 頒布的國民中小學九年一貫課程綱要中，將「圖形與空間」更改為「幾何」，明訂「幾 何」為數學學習領域的五大主題之ㄧ，由此可知，幾何課程在數學教學中的重要性。 二 二 二 二、、、、推理推理推理推理（（（（reasoning）））） 日常生活中，我們處理問題時並不會特別去注意我們正在使用推理能力，它是一 種自然的、不由自主的反應。然而這種推理能力在我們的日常生活中是非常重要的， 因為 Klenk 指出，推理為我們大部分知識的來源（引自劉福增譯，1997）。 Rosser（1994）表示推理是由舊資料引出新訊息的思考歷程，個體需根據系統性 的原則，在前提間建立起特殊關係。推理可以依是否涉及才智問題被分成兩類，涉及 到才智問題的常被稱為「理論（theoretical）推理」，理論的問題主要是連接到真實的 定理，關連到日常生活問題的則被稱為「實務（practical）推理」（Audi, 1991）。李丹 （1989）和張春興（1991，1995）則認為推理是由一個或數個前提去推演出結論的思 考過程，可分為直接推理和間接推理，間接推理又分為演繹推理和歸納推理兩種形式。

此外，張春興另外提出「捷思推理」，它是一種粗略而實際的經驗法則（張春興，1995）。 綜合以上學者論述，推理可說是根據一個或數個已知的證據，從中推演出另一個 新的適當結論的思考歷程。以下介紹演繹推理、歸納推理以及捷思推理三種不同的推 理類型： （ （ （ （一一一一））））演繹推理演繹推理演繹推理演繹推理（（（（deductive reasoning）））） 依照一般大眾普遍公認的原則或定理為前提，進而推論到特定事例的思考方式。 例如：所有動物都會呼吸，人是動物，人必會呼吸。這就是非常典型三段論方式的演 繹推理。 （ （ （ （二二二二））））歸納推理歸納推理歸納推理歸納推理（（（（inductive reasoning）））） 依照許多項個別事例為前提，進而推論到一個普遍原則的思考方式。例如：秋天 到了，看到第一片樹葉落在地面；接著又看見第二片也落在地面；根據這些現象可以 推論，第三片樹葉脫離樹枝時，也會落在地面。 （ （ （ （三三三三））））捷思推理捷思推理捷思推理捷思推理（（（（heuristic reasoning））） ） 在問題情境中，個人根據以往解決類似問題所累積的經驗去推理思考的方式。它 最大的特徵就是不按邏輯程序去思考，不按常理去看問題。

第二節

第二節

第二節

第二節 幾何推理發展的理論基礎

幾何推理發展的理論基礎

幾何推理發展的理論基礎

幾何推理發展的理論基礎

本節整理幾何推理相關理論，作為本研究之理論基礎，以下分為四大部分加以討 論，分別是認知發展理論、van Hiele 幾何思考層次理論、推理思考層次。

一 一 一 一、、、、認知發展理論認知發展理論認知發展理論認知發展理論 認知發展理論代表人物首推瑞士心理學家皮亞傑（Piaget），他提出兒童認知發展 的階段性理論，從直覺推理發展至邏輯、抽象推理的過程了解兒童，把兒童從出生到 青年初期的認知發展歷程分為四個階段，分別為感覺動作階段、前運思階段、具體運 思階段、形式運思階段，以下將此四階段簡略說明： （ （ （ （一一一一））））感覺動作階段感覺動作階段感覺動作階段感覺動作階段（（（（sensorimotor stage））） ） 從出生到 2 歲左右的幼兒屬於這個階段，主要是指語言出現以前的時期，這個階 段幼兒的特點是只有動作活動而缺乏思考活動，他們依賴身體的動作以及動作所獲得 的感覺，對四周環境的刺激產生反應。沒有保留概念，對於看不見的東西會認為不存 在。一直要到這個階段的後期，幼兒才開始有簡單的語言，動作開始帶有一定的思考 特點。 （ （ （ （二二二二））））前運思階段前運思階段前運思階段前運思階段（（（pre-operational stage）（ ）） ） 屬於此階段的兒童在大約 2 歲到 7 歲之間，這個階段的兒童由於出現了簡單的語 言，開始使用文字、數字、圖形等較為抽象的符號來從事他們的思考。這個時期兒童 的自我中心很強，雖已有物質保留概念，但仍沒有質量、容積等保留概念，且不知道 邏輯的可逆性，雖已能開始思考，但無法進行邏輯思考和推理。 （ （ （

（三三三三））））具體運思階段具體運思階段具體運思階段具體運思階段（（（（concrete operational stage））） ）

7 歲到 12 歲的兒童屬於這個階段，在此階段兒童的特點是能在與具體事物相聯繫 的情況下，進行簡單的邏輯運算及邏輯推理，能排列次序，能用不同的特性進行物的 分類、比較以了解其間的關係。同時已有出現質量、容積等保留概念，也有可逆性的 概念。但這個階段兒童的思考活動只能透過具體物才能理解，還不能靠抽象的符號來 處理事物。

（ （ （

（四四四四））））形式運思階段形式運思階段形式運思階段形式運思階段（（（（formal operational stage））））

12 歲到 15 歲的青少年屬於這個階段，和具體運算階段比較起來，這個階段的青 少年思考能力漸趨成熟，能夠對抽象的問題運用概念的、系統的、邏輯的方式進行推 理，及具有根據假設進行演繹推理的能力，對問題的解答能做出論證，並同時記住許 多變量，進行控制變因的實驗。 在個體的發展中，這四個階段各有其行為上的特徵，各階段成一定的順序，且階 段不能省略，順序不能顛倒（張春興，1977）。各階段的年齡界限只是一個粗略估計的 平均年齡，不同的個人經歷、家庭教育及社會環境會加速、延遲，甚至阻礙一個階段 的出現，但儘管文化的因素可能加速、延緩或停止其發展，從而使個體之間表現出一 定的差異性，但它們並不能改變其順序（歐陽鍾仁，1988）。此外，每一階段有其獨特 的認知結構，代表一定階段的年齡能說明該階段的主要行為模式。整個認知階段是一 個連續的過程，前一階段是後一階段的準備，後一階段是前一階段的發展（孫名符， 1996）。從皮亞傑的認知發展階段性理論來看，本研究的受測學生為國小五、六年級學 生，皆已進入具體運思階段，且大部分學生已進入形式運思階段。因此所有受測學生 應該都能夠根據題目的假設進行非形式的推理，足以回答本研究的測驗題目。

至於兒童幾何認知概念的形成，皮亞傑等（Piaget, Inhelder, & Szeminska, 1960） 認為隨著年齡的成長對於空間知覺的發展可分為拓樸性（topological）、投影性

（projective）、歐幾里得性（Euclidean）三個階段。幼兒在大約 3-4 歲時，先掌握基本 的拓樸學概念，分辨圖形的封閉或開放，忽視邊長、角度等歐幾里得幾何的要素概念； 4-6 歲的幼兒屬於過渡期；6-8 歲之後，兒童才有歐幾里得幾何、投影幾何空間概念（張 英傑，2001）。

（ （ （ （一一一一））））拓樸性幾何概念階段拓樸性幾何概念階段拓樸性幾何概念階段拓樸性幾何概念階段 此一階段的兒童相當於認知發展階段的前運思階段，僅能掌握拓樸性的圖形概 念。所謂拓樸學（topology），是指在不計大小或形狀的情形下，研究空間的關係與形 式，也就是，幾何形體的整體性質，與大小、形狀無關（張英傑，1993）。因此，兒童 只能分辨圖形的封閉或開放，注意到圖形的大概形狀而已，而不會分辨出精確的形狀， 忽視直線、曲線、長度、角度等歐幾里得幾何的要素概念。例如：要求兒童仿畫正方 形或長方形，往往會畫成渾圓的形狀或線條凹凸不直，甚至畫成近乎圓的形狀。也正 是因為拓樸的封閉圖形並無嚴格的形狀，而此階段的兒童所畫出的圓可以被拉長或是 擠壓，形成彼此的形狀，所以拓樸學又俗稱為「橡皮幾何」（周淑惠，1995）。 （ （ （ （二二二二））））投影性幾何概念階段投影性幾何概念階段投影性幾何概念階段投影性幾何概念階段 此一階段的兒童相當於認知發展階段的前運思階段到具體運思階段，此階段兒童 對於外界的認知，以及在視覺的觀點比前一階段優越，他們認為自己所在觀點的視覺 比其他條件占更優越的地位，也就是凡是經由視覺所承認的事物，他們才認為是真實 的存在，而各種事物的形體會因視覺的感受不同而有所變化。例如：正方形紙張一旦 拿開，放在相隔一段距離的遠處，在兒童的心目中則認為變成了菱形或梯形，而且也 變小了，但如果再把它拿回原來的位置，兒童卻又認為形狀及大小都會回復到原來的 大小。其實投影幾何也就是探討各三度空間的物體，最後表現在二度空間的結果。例 如，牆壁上的影子是一個球的投影（張清亮，1986）。所以在實際操作上，教師可以讓 學生由不同角度去觀看一個物體，以進行物體的猜測（張英傑，1993）。 （ （ （ （三三三三））））歐幾里得性幾何概念階段歐幾里得性幾何概念階段歐幾里得性幾何概念階段歐幾里得性幾何概念階段 . 皮亞傑認為當兒童開始形成投影幾何概念的同時，也正學著建構歐幾里得幾何 概念，這兩者是交互作用的（王文科，1989）。所謂的歐式幾何是研究由點、線、面所

構成的點、線段、射線、直線及各種平面或空間的幾何形體。此一階段的兒童對於這 些幾何形體具有長度及距離保留能力，他們知道不論物體怎麼移位，其形狀、大小都 是不會改變的，特別是長度保留能力之後，自然能發展出測量的概念，以最靠近自己 的、最熟悉的工具（自己的手或軀幹）來測量，皮亞傑將此種策略稱為「手的遷移」 及「軀幹遷移」。以後隨著認知發展，兒童漸會使用量尺工具來輔助測量，面積保留概 念大約也在此階段發展完成。 根據皮亞傑的說法，在小學低年級時，兒童的圖形概念大部分都已發展到歐幾里 得幾何概念階段。因此對本研究的受測樣本國小五、六年級學生而言，應都已具備線 段長短、角度大小及面積大小的概念（洪明賢，2003）。 二 二 二 二、、、、van Hiele 幾何思考層次理論幾何思考層次理論幾何思考層次理論 幾何思考層次理論 實際從事教育工作的荷蘭數學教育家 van Hiele 夫婦根據完形心理學的結構論以 及皮亞傑的認知發展理論（Moline, 1990; van Hiele, 1986），歷經多年的努力，終於在 1957 年發展出了幾何思考層次理論。早在 1960 年代起，蘇聯的數學教育家便根據 van Hiele 的理論來改革蘇聯國中小學的幾何課程（Burger & Shaughnessy, 1986; Fuys, Geddes, &Tischler, 1988; Hoffer, 1983; Usiskin, 1982）。但除了蘇聯之外，van Hiele 的理 論在國際間並未受到太多的注意，一直到 1974 年美國數學教育家 Wirszup（1976）將 其理論引進美國，這個理論才普遍受到大家的重視。 van Hiele（1957）曾經說：「教師可以引導學生運用觀察的方式，了解幾何結構， 進而瞭解其中的關係，產生更高層次的思考。」從這句話當中，可以知道相對於皮亞 傑認為兒童之空間概念發展主要是與年齡有關的這個論點，van Hiele 夫婦提出的兒童 幾何思考層次主要認為，幾何的思考有著一定的發展層次，對於學生幾何概念的產生， 教師的教導扮演著重要的角色，透過教師或引導者適當的引導，兒童可以從較低的層

次逐步提升到較高的思考層次，並且要等到前一個層次充分發展之後，才可能晉升到 下一層次（Senk, 1989）。van Hiele 主張，學生幾何概念的發展，是經由「學習歷程」， 而非純粹來自生理的成熟，雖然幼兒的發展通常在第一層次，但也曾發現過國小高年 級學生的幾何思考層次仍處於第一層次。因此，層次的提升與自身經驗、學校教學因 素有關，而教學要配合學生發展的層次。他的觀點與教育心理學家 Bruner（1965）及 Dienes（1969）的教育原理頗為相似，認為兒童受到語言的限制，因此他們所認知的 幾何概念無法以言語明確的表達出來，但透過教師的教學，學生可以將原有的知識結 構再一次重組，進而提升到更高的層次。換句話說，依據 van Hiele 的理論，只要教師 合適的教學引導，學生幾何知識的建構，將循序經歷以下五個層次，而每個層次都有 各自獨特的發展特徵。 對於這五個層次的描述方式，國內外的研究者有兩種不同的表達方式，一部分研 究者使用「層次 0、層次一、層次二、層次三、層次四」來描述這五個幾何思考層次 （黃盈君，2001；盧銘法，1999），另一部份使用者則使用「層次一、層次二、層次三、 層次四、層次五」來描述 van Hiele 的五個幾何思考層次（吳德邦，1998，2000a，2000b， 2001，2004；薛建成，2003；Usiskin, 1982; van Hiele, 1986; Wu, D. B., 1994; Wu & Ma, 2005a, 2005b, 2006）。本研究採用 van Hiele（1986）對層次的說法，分別為層次一：視 覺的（visual）層次、層次二：描述的（descriptive）層次、層次三：理論的（theoretical） 層次、層次四：形式邏輯的（formal logic）層次、層次五：邏輯本質法則的（the nature of logical laws）層次。以下分別就各層次的內容簡單描述： （ （ （ （一一一一））））層次一層次一層次一層次一：：視覺的：：視覺的視覺的視覺的（（（visual）（ ））層次）層次層次層次 屬於這個層次的兒童，主要是藉著視覺觀察各種具體物，從物體的外形輪廓來辨 認形狀，例如：從生活經驗中可得知像太陽的形狀是圓形，像門的形狀為長方形。又 如：◇看起來，不像正方形，在此層次的兒童會認為這不是正方形。兒童的思考推理，

受到視覺外觀的影響很大，所以只要將圖形的外表特徵差異變大，兒童就不會將長方 形看成正方形。但此階段的兒童，雖然可以透過移動或旋轉等方法來辨識圖形的異同， 以及使用非數學的術語，但是他們無法瞭解這些圖形的真正定義，不能根據圖形的性 質或組成要素來進行分析。教師在教學時應提供各種機會，讓兒童透過實際的操作， 藉由視覺感官的協助進行圖形的分類、堆積等活動，以獲得幾何圖形的正確概念。 （ （ （ （二二二二））））層次層次層次層次二二二二：：描述的：：描述的描述的描述的（（（descriptive）（ ）））層次層次層次 層次 兒童在此層次具有豐富的視覺辨識經驗，而且已經具有辨別圖形特徵的能力，更 能依據視覺所觀察到的結果，進而分析圖形的基本要素及這些圖形之間的關係。因此， 他們能夠知道圓形沒有邊，三角形有三個邊，正方形有四個一樣長的邊，也能發現長 方形的角都是直角，三角形的內角和是 180∘等圖形特徵。兒童雖然能夠藉由構成要 素之間的關係對圖形進行分類，依據其經驗建立同一類圖形所具有之特性，並用這些 特性來進行解題，但他們還不能夠過推理來了解圖形特徵之間有何關係存在（例如： 正方形和長方形邊長不相等時，面積卻有可能相等；正方形也是長方形的一種）。沈珮 芳（2002）更進一步的提到，學生要先注意到形體的幾何定義，才可能了解非形式化 的推理。 （ （ （ （三三三三））））層次層次層次層次三三三三：：理論的：：理論的理論的理論的（（（theoretical）（ ）））層次層次層次層次 這個層次的學生，已經很清楚各種圖形的構成要素，並且知道各種幾何圖形的內 在屬性以及各種圖形之間的包含關係。例如：平行四邊形有兩雙平形且相等的對邊， 而長方形是平行四邊形的一種，當平行四邊形其中一個角為 90 度時，這個四邊形就是 長方形。又如：n 邊形的內角和為 180∘×（n－2）。學生能夠將先前發現的性質，整理 成公式或使用定義，並依據圖形的性質進行非正式的推理，但是還不能進行有系統的 證明。

（ （ （ （四四四四））））層次四層次四層次四層次四：：形式邏輯的：：形式邏輯的形式邏輯的形式邏輯的（（（formal logic）（ ）））層次層次層次 層次 這個層次的學生能夠經由抽象推理的過程，來證明幾何問題及相互間的關係，也 能了解這些定理證明的方法可能不只一種。（如：能證明三角形的內角和是 180∘）。 學生能夠理解幾何問題要解決，必須具備的充分或必要條件，並使用邏輯推理的方法， 來證明幾何的性質。 （ （ （

（五五五五））））層次五層次五層次五層次五：：邏輯本質法則的：：邏輯本質法則的邏輯本質法則的邏輯本質法則的（（（the nature of logical laws）（ ）））層次層次層次層次

這個層次是屬於最高層次，達到這個層次的學生，能學習不同的幾何公設系統， 在不同的公設體系中，了解抽象推理幾何，建立定理並且進行分析或比較各種不同的 公設系統，例如：歐氏幾何與非歐氏幾何的比較。

van Hiele（1986）指出：幾何思考層次具有某些基本固有的特性存在，而許多學 者對於 van Hiele 幾何思考層次的特性也有相當程度的描述。根據 Crowley（1987）對 van Hiele 幾何思考層次提出了五個特性，分別為次序性（sequential）、提升性

（advancement）、內因性與外因性（intrinsic and extrinsic）、語言性（linguistics）、以及 不配合性（mismatch）。各項特性分述如下： （ （ （ （一一一一））））次序性次序性次序性次序性（（（（sequential）））） 幾何思考層次的發展是循序漸進的，由於每一個層次的概念都是來自於前一個層 次的概念，因此學生必須充分的學習所在層次的各種概念，才能順利進到下一個層次 的學習。

（ （ （ （二二二二））））提升性提升性提升性提升性（（（（advancement）））） van Hiele（1986）曾經提到，學生幾何思考層次的進展，主要是依賴教學而不是 其年齡成長或成熟度的增加，教師適當的教學和引導能提升學生的幾何思考概念，但 是沒有一種教學方法能使學生跳過某一層次，直接進入到下一個層次。因此由一個層 次到另一個層次的轉變並不是一個自然的過程，它是在教與學課程計畫的影響下而提 升的。 （ （ （

（三三三三））））內因性與外因性內因性與外因性內因性與外因性內因性與外因性（（（intrinsic and extrinsic）（ ）） ）

在某一層次的性質是屬於內在的性質，到了下一個層次，此一性質就有可能成為 外顯的性質。Clements 和 Battista（1992）也指出，對某些概念的瞭解，雖然在目前這 個層次可能不明顯，但在下個層次卻是明確可知的。同理，在每一思考層次上，先前 層次的內在性，變為目前層次的外在性（林軍治，1992）。 （ （ （ （四四四四））））語言性語言性語言性語言性（（（（linguistics）））） 在每一個層次中，都有屬於該層次自己獨特的語言、符號，以及這些符號之間的 關聯系統。在某一個層次中屬於正確的語言，到了另一個層次中，可能就必須經過修 正才能符合。而每一層次中獨特的語言性，不僅代表同一層次有著不同的術語名詞， 甚至有些相同的術語所指的是不同的幾何概念（Eberle, 1989）。例如，正方形也可以 說是長方形，又可說是平行四邊形，這個概念在第二層次的學生可能無法理解，但等 到了第三層次，學生可能就能理解其關連性。 （ （ （ （五五五五））））不配合性不配合性不配合性不配合性（（（（mismatch））） ） 依據 van Hiele 幾何思考層次的語言獨特性，每個層次有它自己獨特的語言、符 號，因而屬於不同層次的人，彼此間不能相互的溝通、了解。假如學生是屬於第一層

次，而教師的教學設計、語言符號的運用，卻是第二層次或第三層次，那麼學生無法 完全理解其過程與結果，其學習成效就會不好，老師的教學效果就很差。這也就是為 什麼老師和學生之間會常常發生誤解或無法溝通的原因之一。因此，老師在教學過程、 教材內容、教具的選擇和語言的運用均要特別注意。

而 Fuys 等人（1988）則依據 van Hiele 幾何思考層次理論為基礎，更進一步深入 探究在每一個層次中，學生所能達到的水準，而提出對應 van Hiele 幾何思考每個層次 發展，學生所能表現或達到的具體行為能力。在本研究中自編的「van Hiele 非形式幾 何推理測驗」屬於 van Hiele 理論的第三層次，Fuys 等人（1988）指出在該層次學生有 系統的說明並使用定義，對於先前發現的性質給予非形式化的論點如同給予推論的觀 點一般。以下表 2-1 則針對第三層次的部份加以陳述。

表 2-1 van Hiele 幾何思考層次三的描述 L3-1-a、定義不同性質的形式用以描繪圖形種類的特性並且檢測這些是充足的 L3-1-b、極少性質形式的定義可以來描繪圖形的特性 L3-1-c、使用定義和用公式來表示來把圖形分類 L3-2、給予非正式的推論（使用圖示，對摺剪下的形狀，或者其他的材料） L3-2-a、使用邏輯關係運算的結論，從給予的訊息描繪出一個結果。 L3-2-b、整理形狀的分類 L3-2-c、整理二個性質 L3-2-d、藉著推論來發現新的性質 L3-2-e、系統（family tree）內一些相關連的性質 L3-3、給予非形式推論的論證 L3-3-a、遵照推論的論證並且能夠支持部分的論證 L3-3-b、給予一個推論論證概括或改變 L3-3-c、自己來給予推論的論證 L3-4、給予超過一個以上的解釋來證明一些正好可以被系統所使用的解釋 L3-5、非正式的認定在說明與交談之間的不同 L3-6、確認和使用策略或具洞察力的理由來解決問題 L3-7、認識到推論的角色和以推論的模式來處理問題，但是 L3-7a、在公理中沒有掌握推論的涵義，因為（例如：沒能暸解定義的需要和基本 的假設） L3-7b、沒有正式的區別陳述和交談間的關係（例如：不能分別＂Siamese twins＂ --陳述和交談） L3-7c、還沒有在定理的網路之間建立關係。

吳德邦、李懿芳與馬秀蘭（2006）更進一步改編Fuys等人（1988）提出針對van Hiele 層次的描述，提出van Hiele立體幾何思考層次的描述。 三 三 三 三、、、、推理思考層次推理思考層次推理思考層次推理思考層次 推理與思考有什麼關係？其實早在 1964 年，Angell（1964）就表示推理是一種動 態的人類活動，它是我們的一種心理活動（思考），這種活動包含解決問題、想出某些 事；它有四項特徵：1.推理一個是有目的的過程；2.要採取何種推理方式會依據推理目 標而決定；3.推理屬於個人的活動；4.推理是一種心智的及內心的活動。張春興（1991） 也曾提出，推理其間經過的心理活動，就是思考，思考和推理歷程是有關的（張春興， 1992）。英國牛津技巧之教學計畫（Coles & Robinson, 1989）則把思考定義為個體從事 解決問題時的心智活動，並以促進兒童的思考能力為其計畫的目的。 在 Gardner（1983）對人類能力的研究中，提出了多元智慧論，每一種都是人類用 來學習、解決問題以及創造的工具，其中他認為人類的能力應可包括邏輯─數學智慧 （logical-mathematical intelligence），也就是能有效地運用邏輯和推理的能力，例如： 數學計算、邏輯思考、問題解決、歸納及演繹推理、及辨別型組和關係（引自馬秀蘭， 2007b）。Gardner 並認為「邏輯─數學智慧」的發展與 Piaget 所提出的認知發展階段與 方面一致。Klenk 則指出邏輯就是要研究推理（引自劉福增譯，1997）。Campell 和 Martin （1995）更進一步提出，用於邏輯─數學智慧的各種步驟包括分類、分等、推論、概 括、計算和假設檢定。

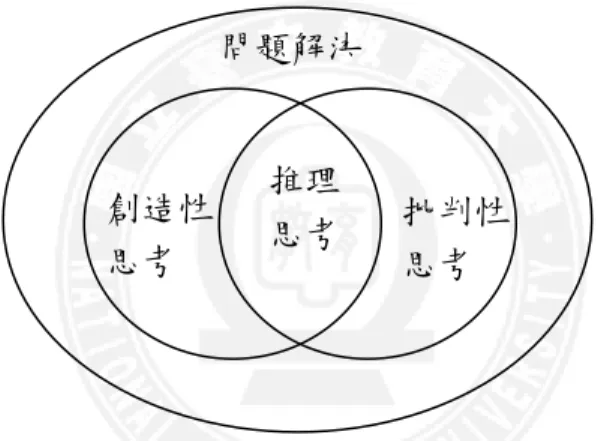
英國牛津技巧之教學計畫（Coles & Robinson, 1989）表示思考的內涵包括批判思 考、創造思考、推理思考和問題解決。Coles 和 Robinson（1989）認為推理思考是一 種同時具備批判性思考和創造性思考的思考模式，兩者都屬於推理思考，其關係如圖 2-1 所示。而 Krulik & Rudnick（1993, 1999）和 Wu & Ma（2010）均表示推理是思考 的一部分，並指出推理是思考的歷程中，高於回憶（recall）的層次，分為三個層次，

從較低層次的基本的（basic）思考，到較高層次的批判性（critical）思考、創造性（creative） 思考，以下以圖 2-2 說明推理的思考層次，因思考可能經常在各層次之間來回移動， 因而各層次並不是完全分離的，每一個層次的思考技能都會外延的，運用到下面層次 的技能。張玉成（1998）同樣認為推理思考是介於認知記憶和高層次思考技巧之間， 而其主要內涵有理解、應用及分析等三項能力。Sternberg（1997）認為，數學推理不 僅要分析思考，還要創造性思考。創造性問題解決的研究者也認為完整的問題解決思 考過程不只是運用推理性思考，也必須並用批判性思考與創造性思考（洪文東，2000； Treffinger & Isaksen, 1992）。

圖 2-2 思考層次的階級圖（引自馬秀蘭與吳德邦譯，2009b，頁 3） 創造性 (creative) 批判性 (critical) 基本的(basic) 回憶性(recall) 推理 reasoning 高層次 higher-order 創造性 思考 推理 思考 問題解決 批判性 思考 圖 2-1 推理與批判性和創造性思考之關係（引自馬秀蘭，2007b，頁 389）

Krulik 和 Rudnick（1993, 1999）認為基本的思考包括對於數學概念的理解以及應 用，例如：除了能運用加法、減法、乘法和除法這些運算來解決問題，還要能夠進一 步運用在解決學校或日常生活問題中。一般認為，學生的數學經驗以真實情境所給予 的真實資料最有價值（Burrill & Romberg, 1998; Garfield & Gal, 1999），因為它提供一 個機會使學生有機會讓自己扮演數學問題解決的主角，讓他們可以在真實世界裡從事 用數學來解決問題（Greer, 2000; Moore, 1998）。 其中批判性思考屬於分析性質，指在遭遇到問題或情境時能夠審查、欣賞或評估。 換句話說，就是能聚焦在一個問題，進而搜集、組織和分析資訊，檢核、連結和評鑑 某一情境或問題的各個面向，然後結合先前已學過的經驗，決定出最合理的答案以及 有效結論的思考（吳德邦與馬秀蘭譯，2009b；馬秀蘭與吳德邦譯，2009b；Coles & Robinson, 1989; Krulik & Rudnick, 1993, 1999）。此外，在有關批判性思考中，Gartenhaus （1984）認為它應包含分析、連結、評鑑；毛連塭、吳清山、陳麗華（1992）則提到 「康乃爾批判思考測驗」（X 級）定義此能力應包括歸納、考察可信度、演繹與確定假 設。張玉成（1998）歸納國外學者對批判思考的定義，將其分為檢視、比較、判斷、 歸納和選擇五個思考過程，並認為批判性思考相近於收斂性和評鑑性運作。 而創造性思考則偏重發散歧異性，它是指一個想法，具有原創性和有效性、擅於 發明、能產生精緻複雜的思考方式。具有創造性思考的人，能綜合其想法、產生創意， 以及能應用概念以解決問題（吳德邦與馬秀蘭譯，2009b；馬秀蘭與吳德邦譯，2009b； Coles & Robinson, 1989; Krulik & Rudnick, 1993, 1999）。張玉成（1998）也認為創造性 思考接近發散性運作。除此之外，有關創造性思考學者有眾多的看法，但內容皆大同 小異，大部分主張流暢性、變通性、獨創性、精進性、敏覺性五種能力為主（陳龍安， 1998；賈馥茗，1976；Guilford, 1977; Torrance & Orlow, 1986）。美國創造力學家 Osbom 甚至把創造力比喻為潛在人類腦中的金礦，最為珍貴。

馬秀蘭（2007b）研究中驗證了 Krulik 和 Rudnick（1993, 1999）的觀點，每個層 次之思考並非分離，而且每個層次是外延的使用到其層次下之技能，因而相鄰層次間 有來動的交集存在。為了表示基本的、批判性和創造性思考的領域大小、各自獨立、 互相含涉以及層次的階級，她修正了 Krulik 和 Rudnick（1993）思考層次的階級圖， 將彼此間之關係表示如圖 2-3，圖中「基本的思考」的範圍較大，表示學生思考過程 大多進行「基本的思考」。 總而言之，國內外學者對推理思考的內容及其涉及的主張雖然略有不同，但大部 分學者皆認為高層次的推理思考包含批判性思考以及創造性思考。因此研究者綜合 Coles & Robinson（1989）和 Krulik & Rudnick（1993, 1999）有關推理的內涵，以其思 考層次的關係與層次，並配合 van Hiele 幾何思考層次理論、Fuys 等人（1988）提出 針對 van Hiele 幾何思考層次的描述，做為本研究中發展「van Hiele 非形式幾何推理測 驗」的理論基礎。 圖 2-3 思考層次的階級圖（馬秀蘭，2007b，頁 408） 創造性思考 批判性思考 基本的思考 推理

第三節

第三節

第三節

第三節 幾何推理發展的相關研究

幾何推理發展的相關研究

幾何推理發展的相關研究

幾何推理發展的相關研究

本研究中探討不同縣市、年級、性別之國小學生在幾何推理能力表現上是否有所 差異。然而儘管國內外有關數學推理的研究幅員廣闊，且理論推理為數不少，但國內 與本研究較為相關的幾何推理之研究僅有杞昭安（1996）和何敏華（2006）兩篇，本 節當中除了整理這兩篇文獻之外，也將國內外近十年有關數學推理之相關研究進行統 整討論，為了方便資料蒐集，將其整理如表 2-2。 杞昭安（1996）在學前兒童圖形推理的研究中，抽取公私立幼稚園及托兒所三歲 至五歲半兒童，共 805 人為研究對象，利用兒童認知發展測驗為研究工具，所得資料 以 SPSS PC+ V5.0 的相關分析、二因子變異數分析、單因子變異數分析、積差相關進 行資料處理。研究結果顯示，不同年齡和不同區域兒童的圖形推理能力有顯著差異， 年齡方面，圖形推理能力隨著年齡的增加而呈直線遞增趨勢呈直線趨勢；區域方面， 則是鄉鎮兒童的圖形推理能力優於城市兒童。但在性別的研究顯示，不同性別兒童的 圖形推理能力沒有顯著差異。然而此結果是否適用於現階段國小高年級學生，有待研 究者進一步探討。 而何敏華（2006）在四邊形包含關係的推理研究中，採立意取樣，選擇國中一年 級下學期的學生 4 人，藉由遊戲競賽「四邊形的獵捕」的方式，透過觀察記錄、資料 的整理，並分析原案的對話，發展學生在四邊形包含關係上的辯證。研究結果發現學 生可非形式的推論與理解長方形也是平行四邊形、長方形是平行四邊形的一個特例、 正方形的集合包含於平行四邊形中，學習者在活動中，充分展現了數學論證、推理和 溝通的技巧。但學生會受長方形字面意義的影響，認為長方形長寬應該是一邊長、一 邊短，因此有「正方形不是長方形」的迷思。此結果雖然僅止於四邊形的包含關係， 但仍可作為研究者在出題時參考的依據，並與本研究的研究結果互相對照。

表 2-2 國內外數學推理之相關研究 研究者（年代） 研究名稱 研究範圍 杞昭安（1996） 學前兒童圖形認知與圖形推理之研究 圖形推理 黃幸美（2001） 兒童解決數學及自然科學問題的問答討論與類 比推理之研究 類比推理 何敏華（2006） 創意教學活動「四邊形的獵捕」─包含關係的推 理 四邊形包含 關係的推理 Halat(2006) Sex-Related Differences In The Acquisition Of

The Van Hiele Levels And Motivation In Learning Geometry van Hiele 幾 何推理層次 馬秀蘭（2007b） 學生思考過程之探究─以實務推理為例 實務推理 黃萬居、邱文鈞、 江帷銓（2007） 國小四年級學生黑白棋力與推理能力、創造力與 問題解決能力之相關研究 類比推理 江淑卿（2007） 從心智模式論點探討兒童邏輯推理能力之發展 邏輯推理 Halat(2008a) Pre-Service Elementary School and Secondary

Mathematics Teachers’ Van Hiele Levels and Gender Differences

van Hiele 幾 何推理層次

Halat(2008b) In-Service Middle and High School Mathematics Teachers: Geometric Reasoning Stages and Gender

van Hiele 幾 何推理層次 馬秀蘭（2008a） 國小高年級學童解樣式題之代數思考：以線性圖 形樣式題為例 樣式推理 馬秀蘭（2008b） 以 van Hiele 理論探討圖形樣式思考層次之研究 樣式思考

除了以上這兩篇文獻，還有眾多數學家對於數學推理能力做了許多貢獻，足以作 為本研究之參考，研究者將諸位學者發現整理如下。 學生的推理能力是否會因為地區的差異而有所不同？杞昭安（1996）認為，不同 地區學前兒童的圖形推理能力有顯著差異，且鄉鎮兒童的圖形推理能力則優於城市兒 童。 學生的年級越高，代表接受數學課程的經驗也越多，然而學生的推理能力是否會 因為接受了教師的教學而有所差異？國外學者 Halat（2006）選取 150 位國小六年級學 生（其中有 66 位男生和 84 位女生）實施以 van Hiele 為理論基礎的數學課程，並利用 自編的多選題幾何測驗進行前、後測，研究結果顯示男生、女生後測的平均數均比前 測的平均數高。 而馬秀蘭（2007b）在實務推理的研究中，利用「自然觀察」法，透過網路觀察臺 中縣某國小五年級二班的 24 位學生，在討論版進行「週休二日任我行」主題的解題活 動，並以學生在網路討論版之解題推理，做為研究的主要資料。研究結果發現到大部 分學生習慣做「基本的思考」，而較好的推理者傾向「批判性思考」和「創造性思考」， 且學生在非數學思考過程中之推理，大多傾向個人對問題之價值觀，因此教師須透過 提問相關之問題情境，適時給予學生實物推理之引導，幫助學生進行五段式推理捷思 之思考，創造實物推理之經驗。由以上兩位學者的研究中均認為，教師的教學能夠提 升學生的推理能力。 除此之外，杞昭安（1996）和江淑卿（2007）認為年齡也會造成學生在推理能力 上的差異。杞昭安（1996）認為不同年齡的學前兒童在圖形推理能力有顯著差異，隨 著年齡的增加而呈直線遞增趨勢。而江淑卿（2007）為了探討受測者邏輯推理的能力 表現及推理反應的差異，採立意取樣，選取屏東縣大班、三年級及五年級的學生，共 227 人為受測對象，利用自編的「三段論分測驗」及「關聯邏輯分測驗」，以 SPSS 的 二因子變異數分析進行考驗，配合臨床晤談記錄。研究結果顯示，兩份分測驗皆隨年