有限長度水槽中孤立波造波與傳遞過程之修正線性解析

全文

(1)國立交通大學土木工程研究所 Institute of Civil Engineering National Chiao Tung University. 碩士論文. 有限長度水槽中孤立波造波與傳遞過程之修正線性解析 A Modified Linear Solution for Solitary Wave Generation and Propagation in a Finite Flume. 指導教授：張憲國博士研究生：賴彥廷中華民國九十六年七月.

(2) 摘要本文根據 Dean 與 Dalrymple（1991）描述造波水槽內部之線性邊界條件，將水槽內部之流速勢分為振盪波與前進波以簡化問題，再以 Fourier 級數展開，可將問題化為二非齊次常微分方程式，在給定造波初始條件的情況下即可解析有限長度造波水槽自靜止開始造波一段時間後停止之線性暫態解。在給定造波板運動方程式的條件下，水槽內部之波浪由開始造波至造波結束後波浪隨時間自由傳遞的過程均可描述，並以步進速度造波（step-velocity）做為此模式之驗證，同時討論了級數的收斂性、收斂項數與水槽長度之關係、以及方程式中各項之物理意義。本文並以弱非線性的孤立波造波問題做為解析之對象，由於孤立波造波板速度為一超越函數，造成解析上的困難；本文以 hypergeometric 函數推求常微分方程式之全解，並與理論波形解比較後，發現由於未考慮非線性及分散性過強等問題，使得線性暫態解較理論波形拉長與歪斜，可能無法有效描述孤立波造波問題，故針對線性之分散關係做出修正。以長波條件做為基準，將 Fourier 級數展開之成份波分為弱分散波（ weakly-dispersive wave ）與非分散波（non-dispersive wave），加上 Hedges（1976）之非線性淺水分散關係式，推得修正後之線性解。並以修正線性解分別對孤立波造波過程後波浪傳遞、尾波及波高衰減現象、以及質量守恆、級數收斂問題進行探討，可發現隨著非線性效應之提高，孤立波造波後尾波效應及波高衰減的量會隨之增加。. i.

(3) ABSTRACT The paper presents a linear transient solution for the solitary wave generated by a piston-type paddle in a finite flume based on the boundary condition derived by Dean and Dalrymple (1991). The wavemaker problem is simplified by decomposing the wave potential into two parts. One is the evanescent wave and the other is progressive wave. The possible solution for the evanescent wave is expressed in form of the Fourier series. The governing equations for velocity potential can be written as two nonhomogeneous ordinary differential equations. The corresponding analytic solution for this problem subjects to initial rest condition. The validity of the proposed solution for step-movement of the paddle is first examined well through the convergence of the series and by a comparison with the previous solution for an infinite flume. The solitary wave can be generated considering Goring and Raichlen’s movement of a paddle. The proposed original linear solution for the solitary wave generation is expressed in the hypergeometric function. Two disadvantages of the original solution with large trailing wave and skewed wave profile are found by comparing with the theory of solitary wave derived from Boussinesq’s equation. The difference between the original linear solution and the solitary wave theory results from the nonlinearity and dispersion of generated waves in the flume. A modification on linear wave speed for weakly dispersive wave is considered following Hedges’ (1976) expression. The other dispersive waves are assumed to move with a constant speed as a linear shallow wave. The modified solution keeps the basic conservation of mass and has good agreement with experimental results. Trailing wave increases with the large movement of a paddle, but the wave comparatively crest decay due to nonlinearity.. ii.

(4) 誌謝研究所兩年的時間轉眼就過去了，即將邁向人生中的另一個階段的我，在這段最後的求學歷程中，首先要感謝恩師張憲國老師的悉心指導與栽培，讓我能夠瞭解做研究應有的態度與方法為何；對於在論文初審時不吝給予批評指導的李兆芳教授與吳永照教授，在此同樣致上誠摯的謝意。特別要感謝遠在成大的同學昶賢不辭辛勞替我尋找參考文獻，感謝你們的幫忙，使得這篇論文能順利完成。感謝研究室中的幾位大家長：喝酒像喝水的勁成學長、認真負責的好朋友立青學長、以及創造 steven 傳說的蔚瑋學長，感謝你們在百忙中仍會關心並指引我們正確的方向，使我獲益良多。在這兩年中的家－歡樂 401 中，感謝已畢業的幼幼班班長阿光、精明幹練的弘偉、專情唯一的江大哥與風采翩翩的明揚等學長的提攜照顧。其次感謝相互幫忙的同學們，雖然總是帶著機車笑容但其實心地很善良的明璋，感謝你碩一替我分擔的工作，真的很不好意思，祝你早日脫離單身生活。家中有無數 nike 珍藏的景鉅，你的反應與笑料讓沉悶的研究生活有了不一樣的顏色，祝你當兵與感情順利。以及隔壁的岡毅與玟豪，你們也讓研究室增加了不少笑語與八卦；更要謝謝可愛的學弟妹們，喜歡在研究室刮鬍子和震地跺的振傑，堅持檔車與和物是男人浪漫的佳裕，每天都在練習卡丁車、合購和網拍的永欣，冷面笑匠彥德，酷似朱....孝天的伯賢，你們在歡樂 401 中帶給我的點點滴滴，是我兩年研究生涯中最好的回憶。最後要感謝我的父母，感謝你們提供的環境與鼓勵，讓我能夠完成我的夢想，尤其要感謝女友在這兩年間的體諒與支持，謝謝妳的體貼，讓我能夠沒有後顧之憂地順利完成學業，由衷感謝曾經幫助過我的每一個人，謝謝你們！. iii.

(5) 目錄中文摘要..................................................................................................... i 英文摘要.................................................................................................... ii 誌謝........................................................................................................... iii 目錄........................................................................................................... iv 圖目錄....................................................................................................... vi 符號說明................................................................................................. viii 第一章緒論...............................................................................................1 1-1 研究動機 ......................................................................................1 1-2 文獻回顧 ......................................................................................1 1-3 研究方法 ......................................................................................3 1-4 文章結構 ......................................................................................3 第二章. 線性水槽控制方程式與解析解 ................................................5. 2-1 控制方程式與邊界條件 ..............................................................5 2-2 暫態解理論解析 ...........................................................................7 2-3 結果與驗證 ..................................................................................9 2-3-1 步進速度造波 ....................................................................9 2-3-2 級數收斂性的探討 ..........................................................10 2-3-3 結果與比較 ......................................................................10 第三章孤立波造波解析 ........................................................................15 3-1 孤立波造波理論 ........................................................................15 3-2 理論解析 ....................................................................................16 iv.

(6) 第四章線性解的分析與修正 ................................................................20 4-1 線性理論的結果與分析 ............................................................20 4-2 線性理論的修正 ........................................................................25 4-3 非線性分散關係 ........................................................................26 4-4 計算結果與討論 ........................................................................30 4-4-1 修正線性解計算結果 ......................................................30 4-4-2 修正線性解之收斂性與質量守恆..................................30 4-4-3 波高衰減與尾波效應 ......................................................30 第五章結論與建議 ................................................................................37 5.1 結論.............................................................................................37 5.2 建議.............................................................................................38 參考文獻...................................................................................................39 附錄. Hypergeometric Function .............................................................43. v.

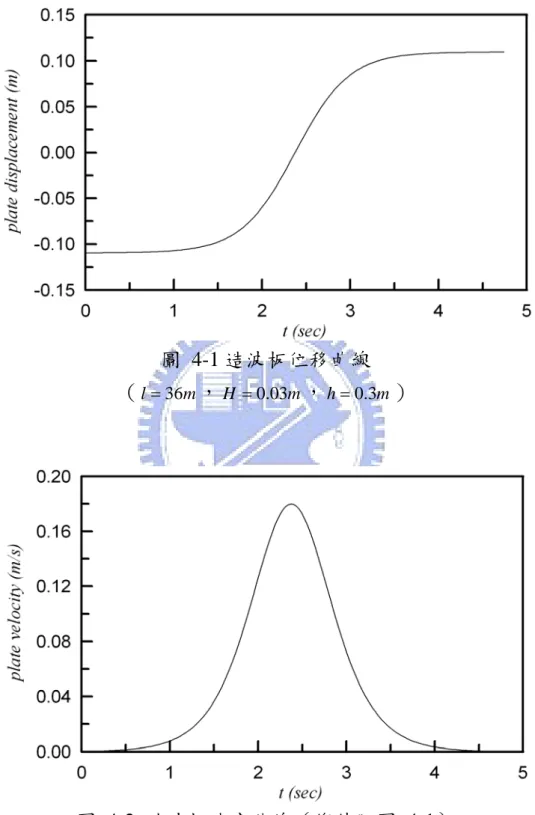
(7) 圖目錄圖 2-1 二維有限長度造波水槽示意圖 ...................................................5 圖 2-2 步進運動時造波板運動速度與時間示意圖.............................12 圖 2-3 級數解係數收斂情形，計算條件為 l = 50m ， s 0 = 0.053m ， h = 0.5m ， τ = 0.27 sec ........................................................................12. 圖 2-4 級數解係數收斂情形，計算條件如圖 2-3（ l = 100m ） ........13 圖 2-5 級數解係數收斂情形，計算條件如圖 2-3（ l = 150m ） ........13 圖 2-6 Moraes et al.（1972，虛線）與本文計算結果（實線）的比較（ l = 50m ， s 0 = 0.053m ， h = 0.5m ， τ = 0.27 sec ） ..........................14 圖 4-1 造波板位移曲線（ l = 36m ， H = 0.03m ， h = 0.3m ） .................22 圖 4-2 造波板速度曲線（條件同圖 4-1）..........................................22 圖 4-3 計算結果與理論波形的比較（ l = 36m ， H = 0.03m ， h = 0.3m ， t = 0.25τ ） .........................................................................................23. 圖 4-4 計算結果與理論波形的比較（條件同圖 4-3， t = 0.5τ ） ......23 圖 4-5 計算結果與理論波形的比較（條件同圖 4-3， t = 0.75τ ） ....24 圖 4-6 計算結果與理論波形的比較（條件同圖 4-3， t = τ ） ..........24 圖 4-7 計算結果與理論波形的比較（條件同圖 4-3， t = 2τ ） .........25 圖 4-8 非線性分散關係比較 ..................................................................29 圖 4-9 長波條件下之非線性分散關係比較 ..........................................29 圖 4-10 修正後計算結果與理論波形的比較（ l = 36m ， H = 0.03m ， h = 0.3m ， t = 0.75τ ） ........................................................................32. 圖 4-11 修正後計算結果與理論波形的比較（造波條件同圖 4-11， t = τ ） ...............................................................................................32. vi.

(8) 圖 4-12 修正後計算結果與理論波形的比較（造波條件同圖 4-11， t = 1.5τ ） ...........................................................................................33. 圖 4-13 修正後計算結果與理論波形的比較（造波條件同圖 4-11， t = 2τ ） .............................................................................................33. 圖 4-14 修正後計算結果與理論波形的比較（造波條件同圖 4-11， t = 3τ ）..............................................................................................34. 圖 4-15 修正線性級數解係數收斂情形（造波條件同圖 4-11）.......34 圖 4-16 造波過程中造波板推移之水體積與自由水面抬升之水體積比較（條件同圖 4-11， t ≤ τ ）.......................................................35 圖 4-17 在不同位置（x=30h、45h、60h、75h、90h）計算通過波峰振幅與第一個尾波波高之相對百分比（ l = 36m ， h = 0.3m ， h / H = 0.1 ~ 0.3 ） ...............................................................................35. 圖 4-18 波峰衰減之相對百分比，造波條件同圖 4-18......................36 圖 4-19 理論孤立波波高、行進波波高與尾波高度之示意圖...........36. vii.

(9) 符號說明 v U. 水分子運動速度. ∇. 梯度運算子. Φ. 流速勢函數. η. 自由水位函數. g. 重力加速度常數. u (t ). 造波板運動速度. S. 造波板位移量. h. 水深. l. 水槽長度. ϕ. 振盪波流速勢函數. φ. 前進波流速勢函數. t. 時間變數. (x, z ). 卡氏直角座標. Ki. 定義可參考（2-11）式. ki. 定義可參考（2-19）式. A0 (t ). 定義可參考（2-20）式. An (t ). 定義可參考（2-20）式. a0. 定義可參考（2-24）式. b0. 定義可參考（2-24）式. A0 p. （2-22）式之特解. an. 定義可參考（2-25）式 viii.

(10) bn. 定義可參考（2-25）式. Anp. （2-23）式之特解. τ. 造波時間. U. 步進造波時之造波板速度. s0. 步進造波時之造波板位移. A1. 定義可參考（2-31a）式. A2. 定義可參考（2-31b）式. C1n. 定義可參考（2-31c）式. C2 n. 定義可參考（2-31d）式. A. 定義可參考（2-31e）式. k. 周波數. n. 成份波數. H. 波高. c. 波速. X 0 (t ). 造波板位移函數. u. 水分子水深平均速度. κ. 定義可參考（3-4）式. α 、 β 、γ. 定義可參考（3-12）式. ( p )n 、 (q )n 、 (r )n. Pochammer symbol. HG1 、 HG2 、 HG3 、 HG4. 定義可參考（3-21a）式. δ. 相對波高. μ. 相對水深. ix.

(11) ωn. 成份波的角頻率. λn. 成份波波長. cn. 成份波波速. (ωm )n. 修正後之成份波角頻率. (ωN )n. 非線性之成份波角頻率. cs. 極限淺水條件之波速. ε. 定義可參考（4-7b）式. D. 定義可參考（4-7c）式. f1. 定義可參考（4-9c）式. f2. 定義可參考（4-9d）式. P. 定義可參考（4-12b）式. Q. 定義可參考（4-12c）式. x.

(12) 第一章緒論 1-1 研究動機在海洋工程的範疇中，經常使用造波水槽來進行波浪運動的物理實驗。在造波水槽中的環境中，造波板運動產生波浪，藉由觀察波浪與特定環境（如動床實驗、水中結構物等）在波浪經過時所造成的改變，得以清楚地描述其物理機制，對於實際海岸工程的問題也有適當的解決方式，因此造波過程的解析和海岸工程研究是息息相關的。造波機所產生的波浪需要理論的支持，來確保其所造出的波浪擁有實驗所需要的特性，以往的文獻已經提供了相當的資訊可供參考。但是在某些非線性波浪的造波過程中，由於造波板邊界以及自由水面邊界均為變動邊界，且自由水面在求解前是未知的非線性邊界條件（nonlinear boundary condition），造成解析上的困難，往往沒有辦法提供一個顯性的解析解，而需仰賴電腦及數值技巧等工具來提供預測解。對造波運動之波浪若可以理論解析之，而不必侷限於數值解析，則更可清楚理解造波之機制。孤立波（solitary wave）是最常被提出來探討的非線性波浪，由於其特性屬於弱非線性淺水長波，往昔研究常以孤立波來表示海嘯、颱風暴潮、以及其它自由水面上非線性與頻散效應幾近平衡之長波現象。然而在實驗水槽中，如何造出完美的孤立波一直是一個尚未解決的問題，其尾端必然會有尾波之產生，目前也尚未有完整之理論解析說明在水槽中根據孤立波條件造波後之自由水面變化，僅有依數值技巧解出之模擬結果。因此若是能提出有效的理論解，對此類問題的理解將有相當大的幫助。. 1-2 文獻回顧現實生活中的波浪多屬於難以計算的非線性問題，為了解析造波水槽問題，其相關的方程式與邊界條件等均需簡化，並假設造波過程中波浪已經發展至穩定狀態以方便解析。Havelock（1929）利用 1.

(13) Fourier 積分首先提出於半無限長度下的二維造波水槽線性理論。 Biesel 與 Suquet（ 1951 ）則提出直推式（ piston-type）與直擺式（flap-type）造波機所造出波浪之線性解。Hyun（1976）、Hudspeth 與 Chen（1981）則驗證並推廣其結果。 Fontanet（1961）在 Lagrangian 座標系統下，提出第一個完整的二階造波理論。Madsen（1970）忽略一階振盪波（evanescent wave）的影響，推導出產生二階 Stokes 波的直推式造波板運動函數。 Hudspeth 與 Sulisz（1991、1993）以特徵函數展開的方式推求完整的二階造波理論的解析解。一些海岸工程的研究著重於某種特定形式（波高、週期等）的單一波浪所造成的影響，為了實驗上的需要，暫態波（transient wave）的造波問題也有許多相關的文獻研究。Kennard（1949）首先提出一階的暫態波造波解析解。Das 與 Wiegel（1972）以考量直推式造波機在指定的造波板速度時驗證 Kennard 的解析解。Moaes 等人（1972）則以控制直推式造波板進行步進運動（step motion）得到暫態波。Lee 等人（1989）以 Laplace 轉換與 Fourier 餘弦轉換求得在有限長度二維水槽中非穩態波（unsteady wave）的一階線性解。Joo 等人（1990）則以 Fourier 積分的技巧提出於半無限長度的二維水槽中自由水面的暫態解。Hughes（1993）對於這些造波理論提出了分析與評論。以上文獻僅為造波理論代表性著作，對於其它相關文獻與相關數值技巧的發展，請再參考相關文獻。關於孤立波造波的部份，Russel（1845）首次觀查到了孤立波現象，並利用重物自水面上自然落至底床的方式造出孤立波。Raichlen （1970）藉由一垂直運動的直推式造波機描述海嘯的波浪如何由底床運動產生。Hammack 與 Segur（1974）以理論與實驗的方式提出孤立波可以由任何因為高於平均水面的水體造成的自由水面邊界運動所產生。以上的理論都可以在實驗室造出孤立波，但是在其造出之孤立波的尾端均跟隨著大小不一，波速較慢的尾波群。在實驗中，尾波必然會對其實驗結果造成影響，為了減少尾波的發生，Goring 與 Raichlen 2.

(14) （1980）基於 Boussinesq 方程式，提出以直推式造波機製造孤立波的理論與實驗驗證。Katell 與 Eric（2002）則由 Rayleigh 的孤立波解導出直推式造波板的運動方程式，並將其實驗結果與 Goring 與 Raichlen（1980）的結果做出分析。相關的孤立波造波數值驗證部份則可參考 Huang et al.（1998）、Woo 與 Liu（2004）、Dong et al.（2004）、張（1997）與李（2004）等人的研究。. 1-3 研究方法實驗水槽的長度通常有限，所以如 Kennard（1949）與 Joo 等人（1990）的結果只適用於水槽很長的情況。為了符合現實情況，發展一有限長度水槽的解析解是有必要的。Lee 等人 (1989) 曾針對有限長度水槽之瞬變造波問題提出一理論解析解，但其解析過程需使用 Laplace 以及 Fourier 轉換法，使得求解較為複雜，且較難對轉換後的變數提出物理解釋。本文基於 Joo 等人（1990）在卡氏座標下解析造波機自靜止開始造波後自由水面暫態解的方法，根據 Dean 與 Dalrymple（1991）描述造波水槽內部之線性邊界條件，將水槽內部之流速勢以 Fourier 級數展開，求解直推式造波機於有限長度水槽中，由靜止開始造波後的暫態解析解，並根據 Goring 與 Raichlen （1980）的孤立波造波板推動方式，解析孤立波之瞬時水面變化。. 1-4 文章結構本文分為下列五個章節，以說明本文研究的解析結果與修正方向，及關於本文的討論與建議。第一章為緒論、研究目的及文獻回顧。第二章為各邊界條件與控制方程式的描述，以及線性理論解的推導過程，並以步進速度造波做為驗證，討論收斂性及方程式中各項之物理意義。第三章應用前章結果，推導以 Goring 孤立波造波理論所提出之造波板運動方程式做為初始條件的線性解析。. 3.

(15) 第四章討論第三章的結果的正確性與修正方式，並將修正後的結果與孤立波理論解比較，以及對修正線性解之波高衰減、尾波現象、質量守恆等方面做出進一步的探討。第五章總結本文所得，並歸納討論與結論以供後續發展之建議。. 4.

(16) 第二章線性水槽控制方程式與解析解 2-1 控制方程式與邊界條件本文考慮之二維水槽如圖（2-1）所示。造波水槽一端為直推式造波機，另一端則為全反射直立壁；所採用之座標系統為固定卡氏座標，x 軸原點定義於造波板移動的平均位置，取向右為正，z 軸原點則定義於靜水面，以垂直向上為正。水槽長度為 l，平均靜水深為 h。 z. − Φ z = ηt gη − Φ t = 0. η. 自由水面邊界條件. 0 造波板. x 水槽底端. 邊界條件. 邊界條件. S. − Φ x = u (t ). h. Φ xx + Φ zz = 0. − Φx = 0. l. 底床邊界條件. − Φz = 0. 圖 2-1 二維有限長度造波水槽示意圖假設流體為不可壓縮（incompressible）、非黏性（non-viscous）、波浪流場運動屬於無旋性運動（irrotational）時，水槽中水體之運動可視為勢能流動，亦即： v U ( x, z, t ) = −∇Φ( x, z , t ). (2-1). v. 其中 U 為水分子運動速度， ∇ 代表梯度運算子， Φ 則為流速勢函數。水槽中之水體由於造波板位移造成流體運動，根據 Dean 與 Dalrymple （1991）推導出的線性邊界條件與控制方程式，描述如下：. 5.

(17) 1.水體控制方程式由於不可壓縮流體的假設，故將流速勢代入連續方程式可推得 Laplace 方程式： Φ xx + Φ zz = 0 , 0 ≤ x ≤ l ,. −h ≤z ≤ 0. (2-2). 2.邊界條件 − Φ x = u (t ),. x=0. (2-3). − Φ x = 0,. x=l. (2-4). − Φ z = 0,. z = −h. (2-5). z=0. (2-6). − Φ z = ηt ,. gη − Φ t = 0,. z=0. (2-7). 式中 η 為自由水面之水位函數。（2-3）式為一非齊次 Neumann 邊界條件，代表造波板上之水分子的法線速度與造波板運動速度相等。（2-4）式為水槽尾端全反射之邊界條件，（2-5）式為底床邊界條件，表示在底床上之水分子沒有垂直底床之速度分量。最後二式（2-6）式及（2-7）式為自由水面運動邊界條件（kinematic boundary condition at free surface）及自由水面動力邊界條件（dynamic boundary condition at free surface）。 3.初始條件假設開始造波前波場完全靜止，則初始條件水位及水流均為零，即為： η = 0,. t=0. (2-8). Φ = 0,. t=0. (2-9) 6.

(18) 2-2 暫態解理論解析為了求解（2-2）式－（2-9）式，我們將 Φ 分解成兩個部份為： Φ ( x, z , t ) = ϕ ( x , z , t ) + φ ( x , z , t ). (2-10). 式中 ϕ (x, z, t ) 為在 z 軸方向為週期性，且隨著與造波板距離增加而呈指數方式衰減的振盪波，φ (x, z, t ) 為隨著 x 軸方向傳遞的前進波。ϕ 可用級數表示為： ϕ=−. 2u ∞ cosh K i (l − x) sin K i z , ∑ h i =0 K i 2 sinh K i l. (2-11). 式中 K i = (i + 1 / 2)π / h 。（2-11）式已經滿足控制方程式（2-2）式與底床邊界條件（2-5）式，將 ϕ 對 x 偏微分，可得到流體的水平速度分量為： −ϕx = −. 2u ∞ sinh K i (l − x) sin K i z . ∑ h i =0 K i sinh K i l. (2-12). 在 x = l 時，（2-12）式可使水槽尾端邊界條件（2-4）式成立，表示（2-11）式滿足水槽尾端邊界條件。而在造波板（ x = 0 ）上之水分子水平速度，若利用如下恆等關係（參考 Spiegel，1999），可使造波板邊界條件（2-3）式成立，亦可證明（2-11）式滿足造波板邊界條件。 sin(2n + 1) y π =− , 2n + 1 4 n =0 ∞. ∑. −π < y < 0 ,. (2-13). 式中 y 為一任意變數。（2-11）式尚未滿足自由水面邊界條件（2-6）式與（2-7）式，若將（2-10）式與（2-11）式代入（2-2）式－（2-7）式，可得： φ xx + φ zz = 0 , 0 ≤ x ≤ l , − φ x = 0,. −h ≤z ≤ 0. x = 0, l. (2-14) (2-15). 7.

(19) − φ z = 0,. z = −h. − φ z − ηt = −. (2-16). 2u ∞ cosh K i (l − x) , ∑ h i =0 K i sinh K i l. gη − φt = 0,. z=0. (2-17). z=0. (2-18). 對（2-17）式等號右側取 Fourier 半幅餘弦展開級數可得： ∞. cosh K i (l − x) h 2 ∞ h tanh k n h ∑ K sinh K l = 2l + ∑ nπ cos k n x i i i =0 n =1. (2-19). 式中 k n = nπ / l。觀察（2-19）式的形式，可以假設 φ ( x, z , t ) 的解以 Fourier 餘弦級數表示為： ∞. φ = A0 (t ) + ∑ An (t ) cosh k n ( z + h) cos k n x. (2-20). n =1. 式中 An (n = 0,1,2,L) 為未知的時間函數。（2-20）式滿足（2-14）式－（2-16）式。若將（2-17）式和（2-18）式結合消去η ，可得聯合自由水面邊界條件為： ⎡h ⎣l. 2 tanh k n h ⎤ cos k n x ⎥, nπ n =1 ⎦ ∞. φtt + gφ z = gu ⎢ + ∑. z=0. (2-21). 將（2-20）式代入（2-21）式，比較等號兩側係數後可得： guh ″ A0 (t ) = l. (2-22). 2 gu tanh k n h ″ An (t ) cosh k n h + gk n An (t )sinh k n h = , nπ. n ≥1. (2-23). （2-22）式與（2-23）式均為二階非齊次常微分方程式，其全解的形式為： A0 (t ) = a 0 t + b0 + A0 p (t ) ,. (2-24). 8.

(20) An (t ) = a n cos ω n t + bn sin ω n t + Anp (t ) ,. (2-25). 式中 ω n 2 = gk n tanh k n h ， a n , bn (n = 0,1,2,L) 為未知的齊次解係數， Anp (n = 0,1,2,L) 則為非齊次微分方程式的特解。當給定造波板速度形式. 的初始條件時，即可解析特解與齊次解。求出 φ (x, z, t ) 後，水面函數η (x, t ) 可由邊界條件（2-7）式求得，即： η ( x, t ) =. ∞ 1 1⎛ ⎞ φt = ⎜ A0 ' (t ) + ∑ An ' (t ) cosh k n ( z + h) cos k n x ⎟ g g⎝ n =1 ⎠. (2-26). 2-3 結果與驗證 2-3-1 步進速度造波此節以步進運動（step-movement）的直推式造波板運動形式來驗證理論解的結果。造波板若以步進速度移動，意謂造波板自靜止開始，依一定速 U 運動，經過 τ 時間之後，造波板位移 s0 的距離後造波板停止運動，如圖 2-2。造波板運動速度可以 U = s0 / τ 表示，將造波板速度表示式代入（2-22）式與（2-23）式，可解得在 t ≤ τ 時流速勢與水位函數的表示式為： φ=. ght 2 s 0 ∞ 2 gs 0 tanh k n h cosh k n ( z + h) +∑ (1 − cos ω n t ) cosk n x, t ≤ τ 2l τ n =1 τ cosh k n h nπωn2. η=. t s 0 h ∞ 2 s 0 tanh k n h +∑ sin ω n t cosk n x, τ l nπω n n =1 τ. t ≤τ. (2-27). (2-28). 在 t ≥ τ 時，造波板停止運動，但波浪依然向水槽底端自由傳遞，此時速度勢與水位函數可以寫為： ∞. φ = A1 + A2 t + ∑ (C1n sin ω n t + C 2 n cos ω n t ) cosh k n ( z + h) cosk n x , t ≥ τ. (2-29). ∞ 1 { A2 + ∑ (C1n cos ω n t − C 2 n sin ω n t )ω n cosh k n h cosk n x} , t ≥ τ g n =1. (2-30). n =1. η=. 式中 A1 ， A2 ， C1n 與 C2 n 為待定係數，當 t = τ 時（2-27）式與（2-28） 9.

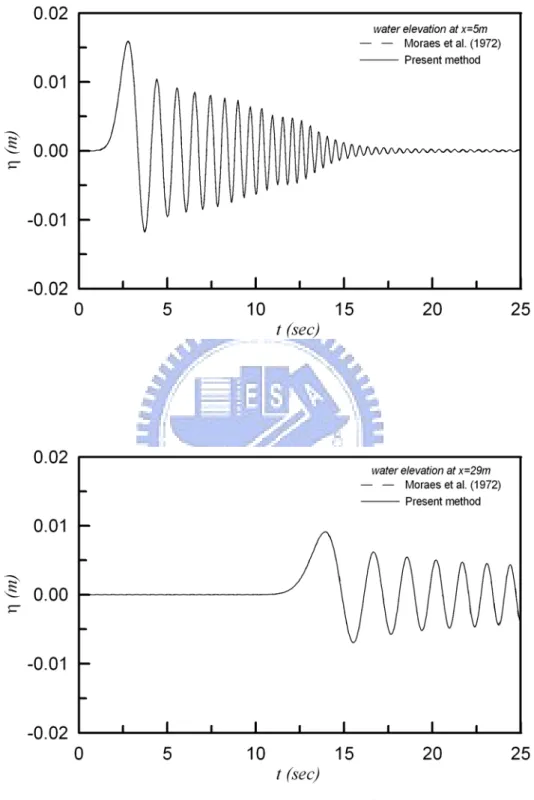
(21) 式會與（2-29）式、（2-30）式相等，比較係數可得： A1 = − A2 =. gs 0 hτ , 2l. (2-31a). gs0 h , l. (2-31b). C1n = A sin ω nτ ,. (2-31c). C 2 n = A(cos ω nτ − 1) ,. (2-31d). 其中 A=. 2 gs0. τ. tanh k n h nπω n2 cosh k n h. (2-31e). .. 2-3-2 級數收斂性的探討理論上，有限 Fourier 級數的項數 n 由 0 至 ∞ ，n 值越大越能描述波浪的變化性，但在實際計算級數時只能取到有限 n 項。圖 2-3～圖 2-5 為在相同造波條件（ s 0 = 0.053m ， h = 0.5m ，τ = 0.27 sec ）下不同長度的造波水槽中，（2-30）式之係數 C1n 與 C2 n 隨項數增加的變化的示意圖，由圖 2-3 可以發現，當 l = 50m 時 C1n 與 C2 n 大約會在 n = 100 項時收斂至 0，但隨著水槽長度增加，在圖 2-4 l = 100m 時 C1n 與 C2 n 大約會在 n = 150 項時收斂至 0，圖 2-5 l = 150m 則表示 C1n 與 C2 n 大約會在 n = 200 項時趨於穩定而收斂至 0，由此可看出隨著水槽長度增加，級. 數收斂項數將會更多，此一結果亦與 Lee 等人（1989）的暫態解析解有著相同的特性。 2-3-3 結果與比較 Moraes 等人（1972）基於 Kennard（1949）提出之造波水槽暫態解析解，推導步進速度造波之水位函數為： η ( x, t ) =. 4U. π. ∫. ∞. 0. ⎛ ⎛ τ ⎞⎞ 1 ⎛ ωτ ⎞ Tanh(kh )Cos(kx )Sin⎜ ⎟Cos⎜⎜ ω ⎜ t − ⎟ ⎟⎟dk kω ⎝ 2 ⎠ ⎝ ⎝ 2 ⎠⎠ 10. (2-32).

(22) 式中 ω = gk tanh kh 。將 2-3-1 節所得結果，與 Moraes 等人（1972）的提出的積分型式解析解在同樣條件下比較（造波條件參考 Moraes et al.，1972），水槽長度 l = 50m ，造波板衝程 s 0 = 0.053m ，靜水深 h = 0.5m ，造波時間 τ = 0.27 sec ，（2-30）式之級數解取 500 項，（2-32）式之數值積分上. 限取 30，計算波浪通過 x = 5m 與 x = 29m 之振幅，如圖 2-4 所示。由圖 2-4 可知，波浪於約 2 秒時到達 x = 5m 處，而波峰於 2.7845 秒時通過 x = 5m，後續之波浪振幅隨時間而衰減；而波浪於約 10 秒時到達 x = 29m 處，且通過 x = 29m 之波浪振幅均小於通過 x = 5m 之波浪。由圖可發現本文計算之結果與 Moraes 等人（1972）相當吻合，證明此解的合理性。根據 Fourier 半幅展開的定義，（2-28）式與（2-30）式之第一項為水槽中之平均水面高度，此值會隨造波板在造波過程中往正向推動水體而增加，至造波結束後（ t ≥ τ ）其增加之量與水槽長度之乘積會與造波板總位移量與平均靜水深相等，由（2-30）式與（2-31b）式可證得： ⎛1 ⎞ l ⎜⎜ A2 ⎟⎟ = Sh ⎝g ⎠. (2-33). （2-28）式與（2-30）式中之第二項為級數和，意指水面之變化可視為 n 個隨時間與空間改變之成份波組合，各成份波波速可能不同，故在傳遞過程中會因波速差異而造成波形之改變。. 11.

(23) 圖 2-2 步進運動時造波板運動速度與時間示意圖. 圖 2-3 級數解係數收斂情形，計算條件為 l = 50m ， s 0 = 0.053m ， h = 0.5m ， τ = 0.27 sec. 12.

(24) 圖 2-4 級數解係數收斂情形，計算條件如圖 2-3 （ l = 100m ）. 圖 2-5 級數解係數收斂情形，計算條件如圖 2-3 （ l = 150m ）. 13.

(25) 圖 2-6 Moraes et al.（1972，虛線）與本文計算結果（實線）的比較（ l = 50m ， s 0 = 0.053m ， h = 0.5m ， τ = 0.27 sec ）. 14.

(26) 第三章孤立波造波解析 3-1 孤立波造波理論孤立波為一弱非線性的淺水長波，其特性為只有單一波峰，波形不會隨著時間改變，且波長為無限大。根據 Boussinesq 方程式，在無限遠處波高為 0 與波形左右對稱的假設下，可以得到孤立波的理論解（參考 Svendsen，2006）為： ⎛ 3H ⎞ (x − ct ) ⎟⎟ 3 ⎝ 4h ⎠. η (x, t ) = HSech 2 ⎜⎜. (3-1). 式中 c 為孤立波理論波速，其理論值為 c = g (h + H )（請參考 Hughes， 1993）。Goring 與 Raichlen（1980）根據淺水造波理論「當造波板移動至某位置時，使造波板速度與造波板上之水分子速度符合該位置上之速度」的假設，由於長波下之水分子垂直速度趨近於 0，而延垂直方向的水平速度近似於常數，故令造波板於某位置 X 0 時的造波板速度與水分子水深平均速度 u 相等，以數學形式表示為： dX 0 (t ) = u (X 0 , t ) dt. (3-2). 基於波浪需滿足連續條件，倘若波形在傳遞的過程中不變，則淺水中水分子水深平均速度可表為： u (X 0 , t ) =. cη (x, t ) h + η ( x, t ). (3-3). 將（3-1）式與（3-3）式代入（3-2）式，可得到孤立波造波板之位移方程式： X 0 (t ) =. H Tanh(κ (ct − X 0 )) κh. (3-4). 式中 κ = 3H 4h 3 。孤立波造波時，造波板的最大位移為： 15.

(27) X 0 (± ∞ ) = ±. H 4 Hh =± κh 3. (3-5). 造波板的總位移可由（3-5）式求得： S = X 0 (+ ∞ ) − X 0 (− ∞ ) =. 16 Hh 3. (3-6). 由於孤立波波長為無限長，但實際實驗造波時間不可能為無限大，故 Goring 與 Raichlen（1980）建議造波時間為： τ=. 2⎛ H⎞ 2 ⎛ H⎞ −1 ⎜ Tanh (0.999) + ⎟ ≈ ⎜ 3.80 + ⎟ κc ⎝ h ⎠ κc ⎝ h⎠. (3-7). 3-2 理論解析孤立波造波板位移方程式（3-4）式為一非線性之隱函式，在解析上有困難，故在此取其線性化後之表示式： X 0 (t ) =. H Tanh(κct ) κh. (3-8). 造波板的速度方程式則為： U (t ) =. dX 0 (t ) cH = Sech 2 (κct ) dt h. (3-9) τ. 為了解析上的需要，造波板的速度方程式需平移時間，故： 2. U (t ) =. dX 0 (t ) cH ⎛ ⎛ τ ⎞⎞ Sech 2 ⎜⎜ κc⎜ t − ⎟ ⎟⎟ = dt h ⎝ ⎝ 2 ⎠⎠. (3-10). 初始條件（3-10）式雖已線性化，可仿照之前的求解過程求解。但其為內含 sec h 函數的雙曲方程式（hyperbolic equation），導致求取特解時的困難。對於 t ≤ τ 的情況，將（3-10）式代入（2-22）式，可解得： A0 (t ) = a0 t + b0 +. ghαLn(Cosh(tβ − β r )) lβ 2. 式中 α 、 β 及 γ 分別代表. 16. (3-11).

(28) H ⎧ = c α ⎪ h ⎪ = c κ ⎨β ⎪ τ ⎪γ = 2 ⎩. (3-12). 齊次解的係數 a0 、 b0 可由代入初始條件： η = 0,. t=0. (3-13). Φ = 0,. t=0. (3-14). ghαTanh(βγ ) lβ 2. (3-15a). 解得 a0 =. b0 = −. ghαLn(Cosh(βγ )) lβ 2. (3-15b). 將（3-15）式代回（3-11）式化簡可得： A0 (t ) =. ghαLn(Cosh(β (t − r ))) − Ln(Cosh(βγ )) + tβ Tanh(βγ ) lβ 2. (3-16). 將（3-10）式代回（2-23）式，其特解可用複數平面的. 2. F1. hypergeometric 無窮收斂級數表示之， 2 F1 hypergeometric 函數的定義為（請參考附錄）：. ( p )n (q )n (r )n n =0 ∞. 2 F1 ( p, q; r ; s ) = ∑. 式中 ( p )n 、 (q )n 、 (r )n 為. ( p )n. sn n!. (3-17) Pochammer symbol ，其定義為. = p( p + 1)( p + 2)L ( p + n − 1) 。. 所以 An (t ) 之解可以表示為： An (t ) = a n cos ω n t + bn sin ω n t +. ⎛ (− HG1 + HG2 ) ⋅ ⎞ ⎜⎜ ⎟ (3-18) nπβω n ⎝ 2igαSech(k n h )Tanh(k n h )⎟⎠ 1. 17.

(29) 式中之 HG1 、 HG2 代表. 2. F1 hypergeometric 函數，分別為：. iω ⎛ iω ⎞ HG1 = 2 F1 ⎜⎜1,− n ;1 − n ;−e 2 β (t −γ ) ⎟⎟ 2β 2β ⎝ ⎠. (3-19a). iω ⎞ ⎛ iω HG2 = 2 F1 ⎜⎜1, n ;1 + n ;−e 2 β (t −γ ) ⎟⎟ 2β ⎠ ⎝ 2β. (3-19b). 齊次解的係數 an 、 bn 同樣可由代入初始條件（3-13）式與（3-14）式求得： an =. 1. nπβω n. bn = −. (2igαSech(k n h )Tanh(k n h )(HG3 − HG4 )). ⎛ 2 gαSech(k n h )Tanh(k n h ) ⋅ ⎞ ⎜⎜ ⎟ nπβω n ⎝ (− 1 + HG3 + HG4 − Tanh(βγ ))⎟⎠ 1. (3-20a). (3-20b). 式中之 HG3 、 HG4 分別代表 iω ⎛ iω HG3 = 2 F1 ⎜⎜1,− n ;1 − n ;−e −2 βγ 2β 2β ⎝ iω ⎛ iω HG4 = 2 F1 ⎜⎜1, n ;1 + n ;−e −2 βγ 2β ⎝ 2β. ⎞ ⎟⎟ ⎠. ⎞ ⎟⎟ ⎠. (3-21a) (3-21b). 將結果代回（3-18）式，化簡可得： ⎛ 2 gαSech(k n h )Tanh(k n h ) ⋅ ⎞ ⎜ ⎟ ⎜ ⎛ − iHG1 + ie itω HG3 + iHG2 − ⎞⎟ An (t ) = ⎟ nπβω n ⎜ ⎜⎜ −itω ⎜ e HG + Sin(ω t )(1 + Tanh(βγ ))⎟ ⎟⎟ 4 n ⎠⎠ ⎝⎝ 1. (3-22). 至此 t ≤ τ 時流速勢的完整解析解可由（3-18）式與（3-22）式代入（2-20）式解得，自由水面函數η (x, t ) 可由（2-26）式求出。 t ≥ τ 時，造波板完全靜止， U (t ) = 0 ，其表示式可參考（2-29）式. 與（2-30）式，在 t = τ 時，令兩方程組相等，可得到（2-29）式與（2-30）式中的係數 A1 ， A2 ， C1n 與 C 2 n 為： A1 = −. ghαLn(Cosh(βγ )) − Ln(Cosh(τ − γ )) + τβTanh(β (τ − γ )) lβ 2. 18. (3-23a).

(30) A2 =. ghα (Tanh(βγ ) + Tanh(β (τ − γ ))) lβ. (3-23b). ⎛ e −iτω gαSech(k n h )Tanh(k n h ) ⋅ ⎞ ⎜ ⎟ 1 ⎜⎛ iτω ⎞ − 1 + 2 HG1 t =τ − 2e (− 1 + HG3 + HG4 − Tanh(βγ )) + ⎟ C1n = ⎟⎟ nπβω n ⎜ ⎜ ⎜ ⎜ Tanh(β (τ − γ )) + e 2iτω − 1 + 2 HG2 + Tanh(β (τ − γ )) ⎟⎠ ⎟⎠ t =τ ⎝⎝. (. C 2n. ). ⎛ ie −iτω gαSech(k n h )Tanh(k n h ) ⋅ ⎞ ⎜ ⎟ 1 ⎜⎛ iτω ⎞ ( ) ( ( ) ) 1 − 2 HG1 t =τ + 2e HG3 − HG4 − Tanh β τ − γ + ⎟ = ⎟⎟ nπβω n ⎜ ⎜ 2iτω ⎟⎟ ⎜⎜e − 1 + 2 HG2 t =τ + Tanh(β (τ − γ )) ⎠⎠ ⎝⎝. (. ). (3-23c). (3-23d). 將上二式代回（2-29）式與（2-30）式，即可得到當 t ≥ τ 時 φ ( x, z, t ) 與η ( x, t ) 的暫態解析解。. 19.

(31) 第四章線性解的分析與修正 4-1 線性理論的結果與分析為了驗證根據前章以輸入孤立波造波板運動方程式作為初始條件推求而得的暫態解，本節取水槽長度為 36m，水深為 0.3m，波高為 0.03m 為孤立波造波之測試條件。根據（3-8）式與（3-9）式，其對應之線性化造波板位移及速度對時間之關係圖如圖 4-1 與圖 4-2 所示。圖 4-3 至圖 4-7 為在不同時間時瞬時水面波形與理論解之比較圖，由此一系列圖可以明顯看出孤立波造波時的水面變化。在造波初期（圖 4-3），造波板位移僅有微量變化（參考圖 4-1、圖 4-2），至圖 4-4 時，造波板速度急遽增加，水面也因此跟著逐漸抬升，此時造波板位移曲線位於反曲點，造波板速度達到最大值，至圖 4-5，造波板速度逐漸遞減至 0，水面抬升量亦跟著下降，圖 4-6 在 t = τ 時造波板靜止，波浪自由向水槽尾端傳遞（如圖 4-7）。由圖中亦可發現，由於分散效應的影響，計算而得的波形相較理論解隨時間增加有分散而拉長的現象，波形亦略有偏斜的現象，同時，在造波過程中波形尾端即有尾波的產生，且隨時間而增大，其整體波速也較理論波速慢。 Boussinesq 方程式與其延伸之 KdV 方程相當適合用來探討淺水長波的運動特性，此點已經被許多文獻證實（可參考 Svendsen， 2006），而根據 Boussinesq 方程式的基本假設： δ ≈ O(1) μ2. (4-1). 式中 δ = H h 代表相對波高， μ = h L 為相對水深。一般在文獻中多以 δ 代表波浪非線性效應強弱與否，而以 μ 代表分散性的多寡。此假設意指 δ 與 μ 2 必須非常接近，且由於 Boussinesq 方程式為一以 δ 及 μ 為微小參數展開之三階方程式， δ 與 μ 必均為小值，Boussinesq 方程式之解才會與現實狀況相符，而孤立波即為此假設下的一個水面波形解，故在波形不變的前提下，孤立波可視為是由於非線性項引起之變形效 20.

(32) 應與分散關係造成之擴展效應相抵消而成的定常波形波浪。前節所提出之線性理論解並未考慮非線性項，且因為對整個水槽的自由水面以 Fourier 級數展開之緣故，其成份波之波長可視為： kn =. 2l nπ ⇒ λn = l n. (4-2). 由（4-2）式中可知成份波波長由 2l 至無限小遞減，週波數 k 則隨成份波數 n 增加而遞增。由第二章理論推導過程中得到之分散關係式： ω n 2 = gk nTanh(k n h ). (4-3). 可知由於成份波波長變化極大之緣故，造成強烈之分散效應而導致前文所述之尾波與波形歪斜，此結果亦與孤立波的原始假設不符合。線性波理論波速為： cn. 2. =. ωn 2 kn. 2. =. g Tanh(k n h ) kn. (4-4). 在長波時， kh → 0 ，故 c = gh 。與孤立波理論波速 c = g (h + H ) 比較之下，可知由於未考慮非線性項的緣故，線性波速將會較非線性波速慢。. 21.

(33) 圖 4-1 造波板位移曲線（ l = 36m ， H = 0.03m ， h = 0.3m ）. 圖 4-2 造波板速度曲線（條件同圖 4-1）. 22.

(34) 圖 4-3 計算結果與理論波形的比較（ l = 36m ， H = 0.03m ， h = 0.3m ， t = 0.25τ ）. 圖 4-4 計算結果與理論波形的比較（條件同圖 4-3， t = 0.5τ ）. 23.

(35) 圖 4-5 計算結果與理論波形的比較（條件同圖 4-3， t = 0.75τ ）. 圖 4-6 計算結果與理論波形的比較（條件同圖 4-3， t = τ ）. 24.

(36) 圖 4-7 計算結果與理論波形的比較（條件同圖 4-3， t = 2τ ）. 4-2 線性理論的修正由前節之討論，可以歸納出本文線性解析解存在兩個問題： 1. 整體波速較非線性波慢。 2. 由於分散效應過強，導致波形產生與現實不符的變化，同時與實際淺水長波為弱分散性的認知相違悖。此二問題都與非線性有關，為了求取更正確的解，可能需要較高階的解析，但由於第三章推導之孤立波線性解析解的型式中含有 hypergeometric 函數，難以用攝動法（perturbation method）的形式推展至高階以探究非線性的影響。 Zhang 與 Schäffer（2004）在其數值造波研究中，曾以修正其分散關係來減少其方程式中高頻波的效應，以符合所套用之 Boussinesq 數值模式之水深限制。為了修正線性解析解與理論孤立波在分散性假設的差異，本文參考 Zhang 與 Schäffer（2004）的方法，將原解析解 25.

(37) 中之線性分散關係式改寫為： ⎧(ω m )n = (ω N )n ⎨ ⎩(ω m )n = c s k n. for. k n h ≤ π 10. for. k n h > π 10. (4-5). 式中 (ω m )n 為各成份波修正後之分散關係， cs 為定值，代表符合淺水波條件的成份波中，波長最短者的波速，相對水深 kh = π / 10 即為一般認知之淺水與中間水深之分界（可參考郭，2001），成份波於 kh ≤ π / 10 時可視為淺水中具有弱分散性之長波群， kh > π / 10 時成份波可視為非線性與分散性平衡之非分散波。而淺水條件可由下述關係求得： knh =. nπh π ≤ 10 l. (4-6). 由（4-6）式可以發現影響淺水條件之變因為波數 n，水槽長度 l，與水深 h。在水槽長度 l=36m，水深 h=0.3m 時，符合淺水條件之波數 n=12，亦即代表 cs 等於 n=12 之成份波波速 c12 。關於波速較理論波形慢的問題，則參考線性化之 Boussinesq 方程式之分散關係需經過修正以減少其在相對水深( H h )增加後造成之波速誤差（請參考 Swendsen，2006）；應用此觀念，（4-5）式中之 (ω N )n 即為受非線性效應所影響之分散關係，將於下節討論。. 4-3 非線性分散關係由於線性的分散關係無法準確的描述水中波浪在不同水深中由於波高造成的波速差異，考慮弱非線性與特定邊界條件的分散關係方程式對於研究被弱非線性效應影響的波場而言是非常重要的，往昔研究亦顯示出此方法在實際應用上有著相當高的準確度（可參考 Hedges，1987）。二階的 Stokes 分散關係式為： ω 2 = gk (1 + ε 2 D )Tanh(kh ). (4-7a). 26.

(38) 式中： ε = kH D=. (4-7b). Cosh(4kh ) + 8 − 2Tanh 2 (kh ) 8Sinh 4 (kh ). (4-7c). 由於（4-7）式只適用於大水深的情況，Hedges（1976）藉由修正線性分散關係，提出了適用於淺水之非線性分散關係的經驗公式為： ω 2 = gkTanh(kh + ε ). (4-8). （4-8）式雖然在淺水條件下有著相當高的精確度，但其只適用於淺水的狀況，在深水中會有明顯的誤差發生（參考 Kirby 與 Dalrymple，1986）。為了克服水深限制，Kirby 與 Dalrymple（1986）平滑地連結二階 Stokes 分散關係式與 Hedges（1976）的淺水分散關係式，提出了一個同時適用於深水和淺水的分散關係式為： ω 2 = gk (1 + f1khε 2 D )Tanh(kh + f 2 khε ). (4-9a). Cosh(4kh ) + 8 − 2Tanh 2 (kh ) 8Sinh 4 (kh ). (4-9b). 式中： D=. f1 = Tanh 5 (kh ) ⎛ kh ⎞ ⎟⎟ f 2 = ⎜⎜ ⎝ Sinh(kh ) ⎠. (4-9c) 4. (4-9d). Hedges（1987）改良（4-9）式在 kh 為小值時結果會不準確的問題，提出了新的聯合分散關係式： ⎛ kh + ε ⎞ 2 ⎟ ⎝ 1+ ε ⎠. ω 2 = gk (1 + ε 2 )Tanh⎜. (4-10). Kirby 與 Dalrymple（1987）同樣提出了新的聯合分散關係式： 27.

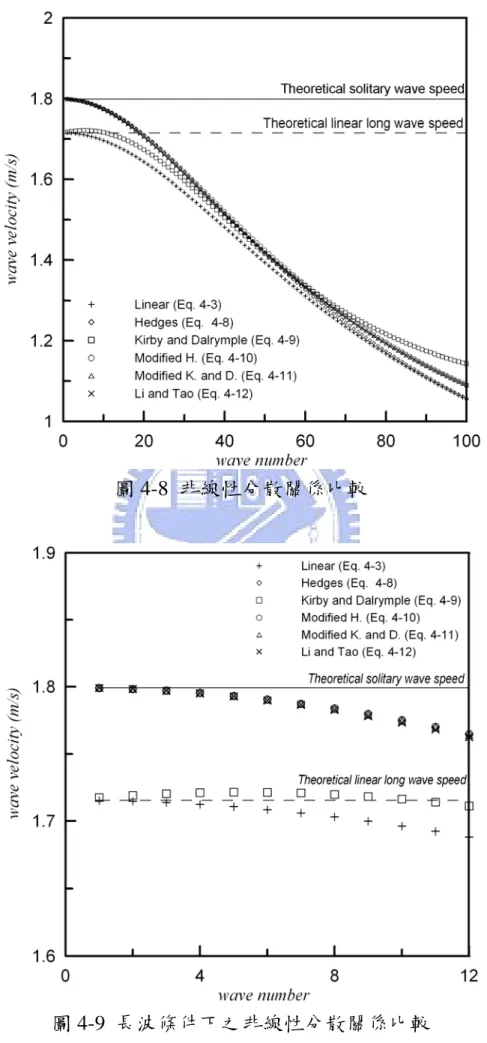
(39) (. ω 2 = gk 1 +. ⎛ kh + ε ⎞ ⎟ f 1ε 2 D Tanh⎜ ⎜1+ ε 2 f D ⎟ 1 ⎝ ⎠. ). (4-11). Li 與 Tao（2004）修正前人提出之聯合分散關係式，以減少其對二階 Stokes 分散關係式在中間水深時的相對誤差： ω 2 = gk (1 + Pε 2 )Tanh(kh + Qε ). (4-12a). 式中： P = Tanh(kh ). ⎛ kh ⎞ ⎟⎟ Q = ⎜⎜ ⎝ Sinh(kh ) ⎠. (4-12b) 2. (4-12c). 圖 4-8 為上述各非線性分散關係與線性分散關係在水槽長度為 36m，水深為 0.3m，波高為 0.03m 時，將成份波波數 n=1～100 之個別波速改用上述之非線性分散關係計算的比較，成份波波速可以下式計算之： cn =. ωn. (4-13). kn. 而圖 4-9 則為長波條件（n=1～12）時的比較。圖 4-8 可以驗證 4-1 節中提到的問題，由於強分散效應造成的成份波分離以及線性波波速較慢的現象。而由圖 4-9 可以發現，除了 Kirby 與 Dalrymple （1986）之結果外，各非線性分散關係式在長波條件下幾無差異，所以為了計算方便，選取 Hedges（1976）之淺水非線性分散關係式做為修正線性理論的修正依據，故（4-5）式可改寫為： ⎧⎪(ω m )n = gk nTanh(k n (h + H )) ⎨ ⎪⎩(ω m )n = c s k n. 28. for. k n h ≤ π 10. for. k n h > π 10. (4-14).

(40) 圖 4-8 非線性分散關係比較. 圖 4-9 長波條件下之非線性分散關係比較 29.

(41) 4-4 計算結果與討論 4-4-1 修正線性解計算結果將（4-14）式套用回原孤立波解析解即可得到修正後之線性解。圖 4-10 至圖 4-14 為在造波中（ t < τ ）至結束後（ t ≥ τ ）水面波浪傳遞的情形，由於減弱其分散效應以及納入非線性分散關係的影響，與未修正之前的結果比較，可發現其尾波大幅減少，波速亦與理論波速相近，但在傳遞過程中由於弱分散性依然存在的緣故，其尾波剛開始並不明顯，但隨著傳遞距離變長仍會逐漸增大，波高亦會因此隨著傳遞距離而逐漸衰減。但在波浪傳遞時間增加後，波形前端會產生水面抬升的現象，波形與理論解亦有一位相差。 4-4-2 修正線性解之收斂性與質量守恆前面於第二章已經討論過線性解的收斂特性，對於修正線性解之收斂性測試可參考圖 4-15。由於水槽長度較短，此修正線性解之係數 -6 -8 C1n 與 C 2 n 在約 40 項時值即小於 10 ，在約 110 項時值即小於 10 。考量級數收斂時係數疊加對收斂值的影響，若以 t = 3τ ， x = 60h 做為測試條件，在相對誤差小於 0.01%的要求下，僅需要 63 項即能達到收斂之要求。根據質量守恆定理，水槽中之水體積需為一定值，線性解之部份已於第二章證明，而修正過之線性解可藉由於造波板運動所抬升之水體積需與水槽內增加之水體積相等判定質量守恆與否，以數學式表達如下： X 0 (t )h = ∫ η ( x, t )dx l. (4-15). 0. 圖 4-16 為造波過程中造波板推移之水體積與水面抬升之水體積比較，可見經過修正後之解依然能符合質量守恆定律。 4-4-3 波高衰減與尾波效應圖 4-17 為波浪於不同相對波高 H h 時，通過水槽不同位置（30h、 30.

(42) 45h、60h、75h、90h）的孤立波波峰高度 H ' 與第一個尾波波高 a' 與之百分比值，圖 4-18 則為波浪在不同相對波高時通過水槽不同位置（條件同上）的波峰高度 H ' 與理論波高 H 的衰減率，對於 H 、 H ' 、 a' 等符號的定義方式，則可參考圖 4-19。由圖 4-17 與 4-18 中可以發現非線性效應對尾波波高以及波峰之影響，會隨非線性效應增加而提高，此結果與 Goring 與 Raichlen （1980）、Katell 與 Eric（2002）等人之實驗結果相近，但 Goring 與 Raichlen（1980）、Katell 與 Eric（2002）分別提出造成尾波的可能原因為水中摩擦力之影響，Katell 與 Eric（2002）之研究中曾利用 Keulegan 公式（1948）推估由黏滯力造成之波高衰減量，而公式預測之平均衰減量較實驗結果為低，故必有其它造成波高衰減之原因； Goring 與 Raichlen（1980）亦曾建議將造波時間（參考 3-7 式）增加 10%，可有效減少尾波產生，推測可能因為造波過程不可能完全滿足其波長與周期均為無限大的特性，其波形在傳遞的過程由於仍有其它成份波存在，故必然會發生變形，但對其尾波變形尚需要進一步的試驗比較。. 31.

(43) 圖 4-10 修正後計算結果與理論波形的比較（ l = 36m ， H = 0.03m ， h = 0.3m ， t = 0.75τ ）. 圖 4-11 修正後計算結果與理論波形的比較（造波條件同圖 4-11， t = τ ）. 32.

(44) 圖 4-12 修正後計算結果與理論波形的比較（造波條件同圖 4-11， t = 1.5τ ）. 圖 4-13 修正後計算結果與理論波形的比較（造波條件同圖 4-11， t = 2τ ）. 33.

(45) 圖 4-14 修正後計算結果與理論波形的比較（造波條件同圖 4-11， t = 3τ ）. 圖 4-15 修正線性級數解係數收斂情形（造波條件同圖 4-11）. 34.

(46) 圖 4-16 造波過程中造波板推移之水體積與自由水面抬升之水體積比較（條件同圖 4-11， t ≤ τ ）. 圖 4-17 在不同位置（x=30h、45h、60h、75h、90h）計算通過波峰振幅與第一個尾波波高之相對百分比（ l = 36m ， h = 0.3m ， h / H = 0.1 ~ 0.3 ）. 35.

(47) 圖 4-18 波峰衰減之相對百分比，造波條件同圖 4-18. 圖 4-19 理論孤立波波高、行進波波高與尾波高度之示意圖. 36.

(48) 第五章結論與建議 5.1 結論本文以勢能流理論與 Fourier 級數展開的方式，推導直推式造波機於有限長度水槽中之暫態解析解，並參考 Zhang 與 Schäffer（2004）對造波問題的研究，藉由修正線性離散關係的方式考量非線性效應之影響，將此解析方式應用至孤立波造波模式中，推導得一修正後之顯性解。對於目前之研究結果，可歸納出以下結論： 1.. 本文參考 Joo 等人（1990）以 Fourier 積分求解半無限長度水槽中直推式造波板造波之自由水面之技巧，在有限長度水槽中以 Fourier 級數展開水槽內之流速勢，與 Moraes 等人（1972）之解比較可印證其在線性造波問題時的正確性。. 2.. 在計算過程中 Fourier 級數所需之收斂項數會隨水槽長度增加而變多，此結論與 Lee 等人（1989）之結果相似；然而 Lee 等人（1989）之解需對時間與空間進行 Fourier 以及 Laplace 轉換，難以對於轉換後之項提出物理解釋，本文提出之理論可避免此項缺點。. 3.. 單純考慮線性項之造波理論可能無法精確描述受弱非線性影響的孤立波造波過程，而修正後之線性解為一易於解析之顯性解，可以有效近似理論波形，且同樣符合質量守恆定律與前述之收斂特性。但由於弱非分散性依然存在，波速仍與理論解不同，其與孤立波理論解之相位誤差會隨時間增加，波前也會產生一不合理之水面隆起。. 4.. 孤立波造波過程中波高衰減與尾波增加的效應會隨非線性效應而增加，推測可能因為波形仍含有其它成份波存在導致波形不會定常，但仍需要進一步的試驗比較。. 37.

(49) 5.2 建議本研究受限於時間之限制，對於非線性效應所產生之諸多影響，僅能反應出波速之改變，對於其它部份並無深入之探討。建議未來可以考量高階解之推導，對非線性效應之影響將會有更精確的描述，同時將結果與實際實驗相比較，以期能夠更加精確地描述造波過程之水面變化。. 38.

(50) 參考文獻 1. 張志華 (1997) 「孤立波與結構物在黏性流體中互制作用之研究」，國立成功大學水利及海洋工程研究所博士論文。 2. 郭一羽 (2001) 「海岸工程學」，文山書局。 3. 李自強 (2004) 「孤立波造波之研究」，國立成功大學水利及海洋工程研究所碩士論文。 4. Biesel, F. and F. Suquet (1951) “Les appareils générateurs de houle en laboratoire,” La Huille Blanche, Vol. 6, No. 2, pp. 4-5. 5. Das, M. M. and R. L. Wiegel (1972) “Waves generated by horizontal motion of a wall,” Journal of Waterways, Port, Coastal and Ocean, ASCE, Vol. 98, pp. 49-65. 6. Dean, R. G. and R. A. Dalrymple (1991) Water wave mechanics for engineers and scientists, World Scientific. 7. Dong, C. M. and Huang C. J. (2004) “Generation and propagation of water waves in a two-dimensional numerical viscous wave flume,” Journal of Waterway, Port, Coastal and Ocean Engineering, Vol. 130, pp. 143-153. 8. Erdélyi, A. (1953) Higher transcendental functions, Vol. I, Dover Publications. 9. Exton, H. (1978) Handbook of hypergeometric integrals: Theory, applications, tables computer programs, Halsted Press. 10. Fontanet, P. (1961) “Théorie de la génération de la houle cylindrique par un batteur plan,” La Houille Blanche, Vol. 16, pp. 3-31. 11. Goring, D. and F. Raichlen (1980) “The generation of long waves in the laboratory,” Proceedings of the 17th Coastal Engineering Conference, ASCE, Vol. 1, pp. 763-783. 12. Hammack, J. L. and H. Segur (1974) “The Korteweg-de Vries equation and water waves. Part 2. Comparison with experiments,” 39.

(51) Journal of Fluid Mechanics, Vol. 65, pp. 289-314. 13. Havelock, T. H. (1929) “Forced surface wave on water,” Philosophical Magazine, Series 7, Vol. 8, pp. 569-576. 14. Hedges, T. S. (1976) “An empirical modification to linear wave theory,” Proceedings Institute of Civil Engineering, Vol. 61, pp. 575-579. 15. Hedges, T. S. (1987) “An approximate model for nonlinear dispersion in monochromatic wave propagation models,” Coastal Engineering, Vol. 13, pp. 87-88. 16. Huang, C. J., E. C. Zhang and J. F. Lee (1998) “Numerical simulation of nonlinear viscous wavefields generated by a piston-type wavemaker,” Journal of Engineering Mechanics, Vol. 124, pp. 1110-1120. 17. Hudspeth, R. T. and M. C. Chen (1981) “Design curves for hinged wavemakers: A comparison of theory and experiment,” Journal of Hydraulics Division, ASCE, Vol. 107, pp. 553-574. 18. Hudspeth, R. T. and W. Sulisz (1991) “Stokes drift in two-dimensional wave flumes,” Journal of Fluid Mechanics, Vol. 230, pp. 209-229. 19. Hughes, S. A. (1993) Physical models and laboratory techniques in coastal engineering, World Scientific. 20. Hyun, J. M. (1976) “Theory for hinged wavemakers of finite draft in water of constant depth,” Journal of Hydronautics, Vol.10, pp. 2-7. 21. Joo, S. W., W. W. Schultz and A. F. Messiter (1990) “An analysis of the initial-value wavemaker problem,” Journal of Fluid Mechanics, Vol. 214, pp. 161-183. 22. Katell, G. and B. Eric (2002) “Accuracy of solitary wave generation by a piston wavemaker,” Journal of Hydraulic Research, Vol. 40, pp. 321-331. 23. Kennard, E. H. (1949) “Generation of surface waves by a moving 40.

(52) partition,” Quarterly of applied mathematics, Vol. 7, pp. 303-312. 24. Keulegan, G. H. (1948) “Gradual damping of solitary waves,” J. Res. Natl. Bureau of Standards, Vol. 40, p. 487-498. 25. Kirby, J. T. and R. A. Dalrymple (1986) “An approximate model for nonlinear dispersion in monochromatic wave propagation models,” Coastal Engineering, Vol. 9, pp. 545-561. 26. Kirby, J. T. and R. A. Dalrymple (1987) “An approximate model for nonlinear dispersion in monochromatic wave propagation models,” Coastal Engineering, Vol. 11, pp. 89-92. 27. Lee, J. F., J. R. Kuo and C. P. Lee (1989) “Transient wavemaker theory,” Journal of Hydraulic Research, Vol. 27, pp. 651-663. 28. Li, R. J. and J. F. Tao (2004) “Analysis of wave nonlinear Dispersion Relations,” China Ocean Engineering, Vol. 19, No. 1, pp. 167-174. 29. Madsen, O. S. (1970) “Waves generated by a piston-type wavemaker,” Proceedings of the 12th Coastal Engineering Conference, ASCE, pp. 587-607. 30. Moraes, C. C., F. S. Ramos and M. M. Carvalho (1972) “Waves induced by Nonpermanent paddle movements,” Proceedings of the 13th Coastal Engineering Conference, ASCE, pp. 707-722. 31. Raichlen,. F.. (1970). “Tsunamis:. some. laboratory. and. field. observations,” Proceedings of the 12th Coastal Engineering Conference, ASCE, Vol. 3, pp.2103-2122. 32. Russel, J. S. (1845) “Report on waves,” Proc. 14th Meeting, Brit. Ass. Adv. Sci., York, pp. 331-390. 33. Seaborn, J. B. (1991) Hypergeometric functions and their applications, Springer-Verlag. 34. Spiegel, M. R. (1999) Schaum’s mathematical handbook of formulas and tables, McGraw-Hill. 35. Sulisz, W. and R. T. Hudspeth (1993) “Complete second-order 41.

(53) solution for water waves generated in wave flumes,” Journal of Fluids and Structures, Vol. 7, pp. 253-268. 36. Svendsen, I. A. (2006) Introduction to nearshore hydrodynamics, World Scientific. 37. Woo, S. and L. F. Liu (2004) “Finite-element model for modified Boussinesq equations. I: Model development,” Journal of Waterway, Port, Coastal and Ocean Engineering, Vol. 130, pp. 1-16. 38. Zhang, H. and H. A. Schäffer (2004) “Waves in numerical and physical wave flumes－a deterministic combination,＂ Proceedings of ICCE 2004, Lisbon, Portugal.. 42.

(54) 附錄. Hypergeometric Function. 對於型如下式之二階常微分方程式： z (1 − z ). d 2u du + [c − (a + b + 1)z ] − abu = 0 2 dz dz. (A-1). 式中 a, b, c ∈ Ζ 。（A-1）式一般稱之為超幾何方程（hypergeometric differential equation），具有三個正則奇點（regular singular point）於. (0,1, ∞ ) 。若利用級數解析，可假設解的形式為： ∞. u ( z ) = ∑ an z n + s. (A-2). n =0. 將（A-2）式代入（A-1）式，可得：. (z − z )∑ a (n + s )(n + s − 1)z ∞. 2. n =0. n+ s −2. n. ∞. [c − (a + b + 1)z ]∑ an (n + s )z n =0. n + s −1. + ∞. − ab∑ an z. (A-3) n+ s. =0. n =0. 整理後可得： ∞ ⎧(n + s + 1)(n + s + c )an+1 − ⎫ n+ s a0 s (s + c − 1)z s−1 + ∑ ⎨ ⎬z = 0 n =0 ⎩[(n + s + a + b )(n + s ) + ab ]an ⎭. (A-4). 若上式等式成立，則必可得到下列關係： a0 s (s + c − 1) = 0 an+1 =. (A-5). (n + s )(n + s + a + b ) + ab a (n + s + 1)(n + s + c ) n. (A-6). 為了得到非顯性解（nontrivial solution）， a0 之值必不為零。若考慮 s = 0 的情況，則（A-6）式可改寫為： an+1 =. (n + a )(n + b ) a (n + 1)(n + c ) n. (A-7). 故由（A-7）式可得到如下關係式： 43.

(55) a1 =. ab a0 c. (A-8). a2 =. (a + 1)(b + 1) a = a(a + 1)b(b + 1) a 1 0 2(c + 1) 2c(c + 1). (A-9). an =. a(a + 1)(a + 2)L(a + n − 1)b(b + 1)(b + 2)L(b + n − 1) a0 n!c(c + 1)(c + 2 )L(c + n − 1). (A-10). 所以（A-1）式之解可表示為： ∞ ⎡ a(a + 1)(a + 2)L(a + n − 1)b(b + 1)(b + 2)L(b + n − 1) n ⎤ u ( z ) = a0 ⎢1 + ∑ z ⎥ (A-11) n!c(c + 1)(c + 2 )L (c + n − 1) ⎣ n=1 ⎦. （A-11）式一般稱為超幾何級數（hypergeometric series）。若利用 Pochammer symbol，可將（A-11）式表示為：. (a )n (b )n (cn ) n =0 ∞. 2. F1 (a, b; c; z ) = ∑. zn n!. (A-12). 式中 Pochammer symbol 之定義為：. (a )n = a(a + 1)(a + 2)L(a + n − 1). (A-13). 根據微分方程的理論，只有方程式的奇點才可能是解的奇點，因此級數（A-11）式在單位圓 | z |< 1 內所表示的解析函數可以解析開拓到全 z 平面，故開拓後以（A-12）式定義之函數 2 F1 (a, b; c; z ) 即為超幾何函數（hypergeometric function），亦意指 hypergeometric 函數為超幾何方程的一個級數解析解（另一解為 z1−c ⋅2 F1 (a + 1 − c, b + 1 − c;2 − c; z ) ）。 Hypergeometric 函數是重要的一類特殊函數，凡具有三個正則奇點的微分方程之解均可以 hypergeometric 函數表達，許多基本函數亦可以 hypergeometric 函數表示，可參考 Erdélyi （ 1953 ）。關於 hypergeometric 函數之推廣及應用，則可參考 Seaborn（1991）與 Exton（1978）等人的著作。故應用參數變異法（method of variation of parameters）求取將（3-10）式代回（2-23）式之特解，設方程式之齊次解為 Anp1 (t ) 與 Anp2 (t )，其特解可假設為：. 44.

(56) Anp (t ) = u1 (t )Anp1 (t ) + u2 (t )Anp 2 (t ). (A-14). 將（A-14）式代回（2-23）式並整理之，可得到： u1 ' (t )Anp1 (t ) + u2 ' (t )Anp 2 (t ) = 0. (A-15). u1 ' (t )Anp1 ' (t ) + u2 ' (t )Anp 2 ' (t ) = δαSech 2 (β (t − γ )). (A-16). 式中： α =c. H h. β = cκ τ γ =. (A-17). 2 2 gTanh(k n h ) δ= nπCosh(k n h ). （2-23）式之齊次解已知為 cos ωnt 與 sin ωnt，故（A-15）式與（A-16）式可解得： u1 ' (t ) =. − δαSech 2 (β (t − γ ))Sinωnt. (A-18). ωn 2. δαSech 2 (β (t − γ ))Cosωnt u2 ' (t ) = ωn 2. (A-19). 應用 hypergeometric 函數，可解得上式中之 u1 (t ) 與 u2 (t ) ： ⎛ 2tω ⎞ ⎞ ⎛ iω iω ⎜ − e 1 + e 2 βγ ⋅2 F1 ⎜⎜1, n ; n + 1;−e 2 β (t −γ ) ⎟⎟ + ⎟ ⎜ ⎠ ⎟ ⎝ 2β 2β ⎟ ⎜ ⎛ iω n iω n − iδαe −itω ⎜ 2 βγ 2 β (t −γ ) ⎞ ⎟ 1+ e ;1 − ;− e u1 (t ) = ⋅2 F1 ⎜⎜1,− ⎟⎟ + ⎟ 2 β 2 β β 1 + e 2 βγ ωn ⎜ ⎠ ⎝ ⎟ ⎜ 2 βγ 2 itω e βγ − Sech(β (γ − t ))Sinh(β t ) ⎟ ⎜ e −1+ e ⎟ ⎜ ⎠ ⎝. (. (. ). (. ). ). (. )(. ). 45. (A-20).

(57) ⎛ 2tω ⎞ ⎞ ⎛ iω iω ⎜ e 1 + e 2 βγ ⋅2 F1 ⎜⎜1, n ; n + 1;−e 2 β (t −γ ) ⎟⎟ + ⎟ ⎜ ⎠ ⎟ ⎝ 2β 2β ⎟ ⎜ ⎛ iωn iωn δαe −itω ⎜ 2 βγ 2 β (t −γ ) ⎞ 1+ e ;1 − ;−e u2 (t ) = ⋅2 F1 ⎜⎜1,− ⎟⎟ + ⎟ ⎟ 2 β 2 β β 1 + e 2 βγ ωn ⎜ ⎠ ⎝ ⎟ ⎜ 2 βγ 2 itω e βγ − Sech(β (γ − t ))Sinh(βt ) ⎟ ⎜e 1+ e ⎟ ⎜ ⎠ ⎝. (. (. ). (. ). ). (. )(. (A-21). ). 將（A-20）式與（A-21）式代入（A-14）式，化簡整理後即可得到特解的表示式為： ⎛ ⎛ iωn ⎞ ⎞ iω ⎜ 2 F1 ⎜⎜1,− ;1 − n ;−e 2 β (t −γ ) ⎟⎟ − ⎟ 2β 2β iδα ⎜ ⎝ ⎠ ⎟ Anp (t ) = − ⎜ ⎟ βω n ⎜ ⎛ iωn iω n 2 β (t −γ ) ⎞ ⎟⎟ ⎟⎟ ⎜ 2 F1 ⎜⎜1, 2 β ;1 + 2 β ;−e ⎠ ⎠ ⎝ ⎝. 46. (A-22).

(58)