射頻金氧半場效電晶體元件佈局對高頻特性與低頻雜訊之影響以應用於射頻與類比電路

i

國 立 交 通 大 學

電子工程學系 電子研究所碩士班

碩 士 論 文

射頻金氧半場效電晶體之元件佈局對高頻

特性與低頻雜訊之影響以應用於

射頻與類比電路

RF MOSFET Layout Effect on

High Frequency Characteristics and

Low Frequency Noise for RF and Analog

Circuit Applications

研 究 生：古智友

指導教授：郭治群 博士

i

射頻金氧半場效電晶體之元件佈局對高頻特性與

低頻雜訊之影響以應用於射頻與類比電路

RF MOSFET Layout Effect on High Frequency

Characteristics and Low Frequency Noise

for RF and Analog Circuit Applications

研究生： 古智友 Student : Chih-You Ku

指導教授：郭治群 博士 Advisor : Dr. Jyh-Chyurn Guo

國 立 交 通 大 學

電子工程系 電子研究所

碩 士 論 文

A Thesis

Submitted to Department of Electronics Engineering & Institute of Electronics

College of Electrical Engineering and Computer Science

National Chiao Tung University

in partial Fulfillment of the Requirements

for the Degree of Master

In

Electronics Engineering September 2010

Hsinchu, Taiwan, Republic of China

i

射頻金氧半場效電晶體之元件佈局對高頻特性

與低頻雜訊之影響以應用於射頻與類比電路

學生：古智友 指導教授: 郭治群 博士

國立交通大學 電子工程學系 電子研究所碩士班

摘要

本論文主要是探討元件佈局造成的 STI 應力，和經由 STI 製程頂邊所產生的圓角 TCR

(Top Corner Rounding)與隨之而來的W 效應對直流 I-V 特性、電導(Gm)，以及載子遷移

率(eff)的影響。同時我們也分析此兩種機制對元件低頻雜訊與高頻特性所產生的影響。

為了提高的 STI 垂直方向的應力，我們設計了狹窄型 OD 和多重 OD MOSFETs 兩種元 件，其概念是由標準多指元件(Standard multi-finger MOSFETs)延伸而來的。而維繞式 MOSFET 是我們所設計的另一種全新結構，它在從垂直方向完全不受到 STI 應力影響，

關鍵就是在於它完全在 width 方向避開了的 STI/OD 界面，並藉此改善低頻雜訊。 但是 在某些元件的量測結果顯示，我們無法從 STI 的應力解釋在極端狹窄的元件的反而有更 低的低頻雜訊。因次我們從 STI 頂邊 TCR 導致的W 的角度去分析，推導出一

semi-empirical 模型，能夠模擬以預測 width 微縮對eff 與 Gm之影響，藉由這些模型可

以準確的求出有效的通道寬度 Weff。 STI 應力愈強將導致介面缺陷電荷(Nit)的增加，但

是此效應確遠不及W 明顯，對於狹窄型元件來說是一項優點。但不幸的是狹窄型元件

的截止頻率還是會因為 Cgg 增加而下降，而且無法經由去寄生的方式改善。

在低頻雜訊與高頻特性之間有著權衡的 RF 元件佈局設計考量。因此基板接點的元件 設計是一個有趣的課題，我們設計各種基板接點結構的 4-port 測試元件並將基板端獨

ii

立接出來，將我們提出新的 body network 模型萃取元件參數如基板電阻，它影響高頻元 件特性與低頻雜訊特性。量測結果顯示愈大的基板電阻會產生愈大的低頻雜訊，我們可 以藉由多重環狀佈局的方式設計基板接點形狀，藉此大量降低基板電阻，但同樣地此舉 也會使閘極至基板接點間的雜散電容增加而降低截止頻率。

iii

RF MOSFET Layout Effect on High Frequency

Characteristics and Low Frequency Noise for

RF and Analog Circuit Applications

Student：Chih-You Ku Advisor：Dr. Jyh-Chyurn Guo

Department of Electronics Engineering Institute of Electronics

National Chiao Tung University

Abstract

The impact of layout dependent STI stress and W from STI top corner rounding (TCR) on I-V characteristics, transconductance (Gm), effective mobility (eff), low frequency noise

(LFN), and high frequency performance has been investigated in this thesis. Narrow-OD and

multi-OD MOSFETs are two structures derived from standard multi-finger MOSFET for

enhancing transverse stress ⊥. Donut MOSFET is another structure created to keep free from

⊥, due to the elimination of STI/OD boundary along the channel width direction.

The compressive stress from STI cannot explain the lower LFN in extremely narrow

devices. STI top TCR induced W is identified as an important factor responsible for the

increase of Gm and the reduction of LFN with width scaling to nanoscale regime. A

semi-empirical model was derived to simulate eff degradation from STI stress and the

increase of effective width (Weff) from W. The proposed model can accurately predict width

scaling effect on Gm based on a trade-off between eff and Weff. The enhanced STI stress may

lead to an increase of interface traps density (Nit) but the influence is relatively minor and

overcome by Weff effect. Unfortunately, the extremely narrow devices suffer fT degradation

iv

deembedding. The trade-off between LFN and high frequency performance provides an

important layout guideline for analog and RF circuit design.

Body contact layout effect on LFN and high frequency performance is one more

interesting topic of research in this thesis. Four-port test structures were implemented to

accommodate 4-terminal MOSFETs with separate body terminal and a new body network

model has been developed to simulate the body contact layout and body biases effects. The

measurement result reveals that the higher body resistance will lead to the worse LFN

characteristic. We can significantly reduce the body resistance by applying multi-ring body

contacts, but this may contribute larger parasitic capacitance from poly gate to body contacts

v

誌謝

首先，我要感謝我的指導教授--郭治群教授。在研究方法及態度上的指導，不斷地 替學生尋找研究資源，並且嚴格要求學生完成許多基礎工作。在這過程中，除了建立許 多研究領域相關的能力，在國際學術會議及期刊發表論文，也體會到許多待人接物的觀 念，相信將會成為我未來工作上或者研究上的準則。 此外，還要感謝 NDL 的研究員—黃國威博士，在研究設備上的支持，讓我能夠接 觸並學習到高頻量測設備。也感謝 RFTC 的工程師們，邱佳松、林書毓、蕭治華在量測 實驗上的協助以及建議，讓我能夠順利完成量測。 感謝 LAB635 中的所有成員們，國良學長、冠旭學長、依修學長、仁嘉學長在研 究上的幫忙，也感謝敬文、弈岑、唯倫、智翔、德昌的陪伴 ，讓我在實驗室的生活更 豐富有趣。 最後，我要感謝一直在背後支持我的家人，他們在我求學與成長的路上付出許多。

vi

Contents

Chinese Abstract

...i

English Abstract

...iii

Acknowledgement

...v

Contents

...vi

Figure Caption

...ix

Table Caption...xvii

Chapter 1 Introduction

1.1 Research Motivation...1

1.2 Thesis Organization...2

Chapter 2 Low Frequency Noise Theory and Measurement Method

2.1 An Overview of CMOS Technology and Low Frequency Noise...4

2.2 Low Frequency Noise Theory...8

2.2.1 Number Fluctuation Theory...9

2.2.2 Mobility Fluctuation Theory...10

2.3 Low Frequency Noise Measurement System...12

2.4 Low Frequency Noise Data Analysis Method...18

Chapter 3 Analysis of Layout Effect on STI Stress and Device Parameters

3.1 STI Stress Mechanics in RF MOSFET...23

3.2 MOSFET Layouts for STI Stress Modulation (Multi-finger, Multi-OD, and Doughnut Structures) ...25

3.3 Layout Effect on DC Characteristics...27

3.4 STI Top Corner Rounding (TCR) Effect on Weff and Gm...36

3.5 STI Top Corner Rounding (TCR) Technique – Stress and W...38 3.6 C-V Characterization and Fringing Capacitances Simulation for Accurate

vii

Mobility Extraction...40

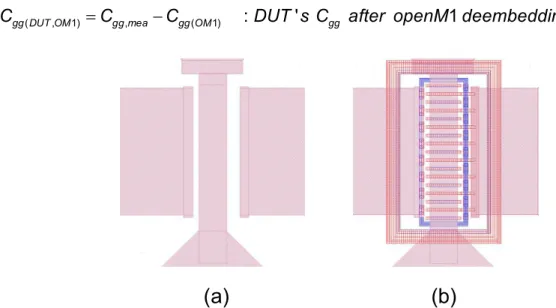
3.6.1 Open Deembedding Methods for Intrinsic Cgg Extraction...40

3.6.2 3-D Fringing Capacitances Simulation and Analysis using Raphael...45

3.6.3 Effective Mobility Extraction for MOSFETs with Various Layouts...51

3.7 CP Current Measurements for Interface States Extraction and Analysis of STI Stress Effect...58

Chapter 4 RF MOSFET Layout effect on Low Frequency Noise

4.1 Low Frequency Noise Analysis in Two-port 3T MOSFET...61

4.2 Narrow-OD MOSFET and Comparison with Standard MOSFET...61

4.3 Multi-OD MOSFET and Comparison with Standard MOSFET1...63

4.4 Doughnut MOSFET and Comparison with Standard MOSFET...66

4.5 Comparison between NMOS and PMOS...68

4.6 Layout Dependence of Interface States and Low Frequency Noise...70

4.7 Low Frequency Noise Model Parameter Extraction for Simulation...74

Chapter 5 RF MOSFET Layout Effect on High Frequency Characteristics

5.1 Two-port S-parameters Measurement and Deembedding...76

5.2 Two-port 3T MOSFET with Multi-finger, Multi-OD, and Doughnut Structures....77

5.2.1 Intrinsic Device and Parasitic RLC Parameters Extraction and Analysis – Layout Effect and Bias dependence...78

5.2.2. High Frequency Performance Analysis (fT, fMAX, NFmin)...83

5.3 Four-port 4T MOSFET with Various Body Contact Layouts...93

viii

5.3.2 Intrinsic Device and Parasitic RLC Parameters Extraction and Analysis – Body Contact Layout Effect and Bias dependence...97

Chapter 6 Conclusion

6.1 Summary...102 6.2 Future Work...103

ix

Figure Captions

Chapter 2

Fig.2.1 Schematical illustration of phase noise spectrum in VCO...7

Fig.2.2 Schematical illustration of electrons in the channel of MOSFET moving in and out of

the traps giving rising to fluctuations in the inversion carrier density and thereby the drain current...10

Fig.2.3 Schematic of SR570 flicker noise measurement system setup with SR570 LNA

(trans-resistance amplifier), Agilent DSA 35670 (dynamic signal analyzer), and HP4142B (DC power supply)...14

Fig.2.4 Schematic of low frequency noise measurement system consisting of model 5184

LNA (voltage amplifier), HP4142B for DC supply, and Agilent 35670 for dynamic signal analyzer...16

Fig.2.5 New solution for using model 5184 LNA (a) Battery (b) ultra low noise DC source

(PA14A1) as a power supply...16

Fig.2.6 Schematic illustration of Celestry 9812B Noisepro system consisting of HP4145 for

DC supply, 9812B for pre-amplifier, and Agilent 35670 for dynamic signal analyzer...17

Fig.2.7 Normalized PSD of drain current noise SID/IDS2 measured from (a) NMOS and (b)

PMOS with increasing frequency, under various VGT (|VGT |=0.1, 0.3, and 0.5V). NMOS and

PMOS fabricated in 90nm low leakage process...21

Fig.2.8 Normalized PSD of drain current noise SID/IDS2 measured from (a) NMOS and (b)

PMOS under increasing |VGT| and fixed |VDS|=0.05V. ...22

Fig.2.9 Normalized PSD of drain current noise SID/IDS2 versus frequency, measured from (a)

NMOS and (b) PMOS under |VGT|=0.3V and |VDS|=0.05V. NMOS and PMOS were fabricated

in 90nm low leakage CMOS process...22

Chapter 3

x

Fig.3.2 Schematics of narrow-OD MOSFETs with three layouts (a) W2N16 (WF×NF=2m×16)

(b) W1N32 (WF× NF=1m × 32) (c) W05N62 (WF× NF=0.5m × 64) corresponding to

Wtot=32m...26

Fig.3.3 Schematics of multi-OD MOSFETs with three layouts (a) OD1 (WOD × NOD=2m×1)

(b) OD8 (WOD × NOD=0.25m×8) (c) OD16 (WOD×NOD=0.125m×16)...26

Fig.3.4 A brief layout of donut MOSFET with two major layers, such as active region (OD)

and poly gate (PO) (a) D1S1 (poly gate to STI edge distance =0.3m (min. rule) (b) D10S10 (poly gate to STI edge distance =3m=10x min. rule), 4-side polygons length is 16 m x4...27

Fig.3.5 Schematics of STI stresses along the longitudinal and transverse directions, defined as

// and ⊥ in MOSFETs with different layouts (a) standard multi-finger MOSFET (b)

narrow-OD MOSFET...30

Fig.3.6 Linear VT versus WOD for narrow-OD NMOS with various layouts like W2N16

(WOD=2m, NF=16), W1N32 (WOD=1m, NF=16), W05N64 (WOD=0.5m, NF=16) under the

biases of VDS=50mV and VBS=0V...31

Fig.3.7 (a) The drain current IDS vs. VGT (b) transconductance Gm vs. VGT measured from

narrow-OD NMOS W1N32 (WF=1m, NF=32) and W05N64 (WF=0.5m, NF=64), and

standard multi-finger NMOS W2N16 (WF=2m, NF=16). All of the devices have the same

total finger width, WF×NF=32m...32

Fig.3.8 Schematics of STI stresses along the longitudinal and transverse directions, defined as



// and ⊥ in MOSFETs with different layouts (a) standard multi-finger MOSFET (b)

multi-OD MOSFET with multiple OD finger and multiple gate finger...32

Fig.3.9 Linear VT versus WOD for multi-OD NMOS with various layout dimensions : OD1

(NOD=1, WOD=2m), OD8 (NOD=8, WOD=0.25m), and OD16 (NOD=16, WOD=0.125m).

Bias condition : VDS=50mV and VBS=0V...33

Fig.3.10 (a) The drain current IDS vs. VGT (b) transconductance Gm versus VGT measured

from multi-OD NMOS OD8 (NOD=8, WOD=0.25m) and OD16 (NOD=16, WOD=0.125m),

and standard NMOS OD1 (NOD=1, WOD=2m). All of the devices have the same finger

xi

Fig.3.11 Schematics of STI stresses along the longitudinal and transverse directions, defined

as // and ⊥ in MOSFETs with different layouts (a) standard multi-finger MOSFET (b)

donut MOSFET with 4-side polygons for gate and OD...34

Fig.3.12 (a) The drain current IDS vs. VGT (VDS=0.05V) (b) transconductance Gm vs. VGT

measured from donut NMOS D1S1 and D10S10 (16mx4) and standard multi-finger NMOS W2N32 (WF=2m, NF=32)...35

Fig.3.13 (a) The drain current IDS vs. |VGT|(VDS=-0.05V) (b) transconductance Gm vs. |VGT|

measured from donut PMOS D1S1 and D10S10 (16mx4) and standard multi-finger PMOS W2N32 (WF=2m, NF=32)...36

Fig.3.14 Schematically drawn cross-sectional view of a MOSFET in the channel width

direction (a) the sharp STI corner without edge recess and top corner rounding (TCR) (b) the rounded STI corner contributes larger Weff due to W from edge recess and

TCR...39

Fig. 3.15 Layout of dummy open test structures for multi-finger MOSFETs (a) dummy

openM3 for open deembedding to M3 (b) dummy openM1 for open deembedding to M1...41

Fig. 3.16 3-D dummy open test structures for Raphael simulation (a) M3 only for openM3

(open deembedding to M3) (b) M3/M2/M1 stack for openM1 (open deembedding to M1)...43

Fig. 3.17 Gate capacitances Cgg(DUT,OM3) and Cgg(DUT,OM1) extracted through openM3 and

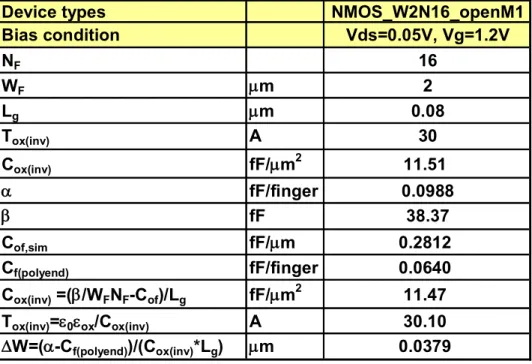
openM1 deembedding on multi-finger NMOS (W2N16, W1N32, W05N64) with fixed WFNF

(a) Cgg(DUT,OM3) vs. NF : linear function '=0.4107 fF/finger, '=38.1 fF (b) Cgg(DUT,OM1) vs. NF :

=0.0988 fF/finger, =38.4 fF...44

Fig. 3.18 Schematical drawing of 3-D MOSFET structure for Raphael simulation. The 3-D

structure incorporates four conducting regions, such as poly gate, channel region, source/drain diffusion region, and contact to source/drain...45

Fig. 3.19 Multi-finger MOSFET structure built in Raphael for 3-D capacitance simulation (a)

xii

Fig. 3.20 Parasitic capacitances Cg,CT, Cg,Diff, Cof, simulated by Raphael for MOSFETs with

square contact versus device geometry parameters (a) gate length, Lg (b) gate to CT space,

Lgct (c) gate electrode thickness, Tg (d) gate dielectric thickness, Tox...47

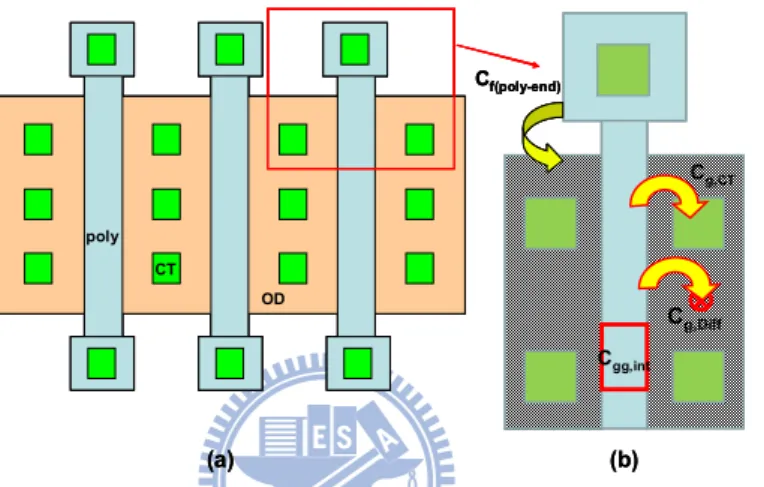
Fig. 3.21 (a) Schematical illustration of multi-finger MOSFET layout (b) three components of

fringing capacitances associated with each gate finger : Cf(poly-end) represents finger-end

fringing capacitance, Cg,Diff, and Cg,CT are gate sidewall fringing capacitances...48

Fig. 3.22 Effective mobility eff versus VGT for narrow-OD NMOS determined with

consideration of W in Weff and Cgg,int for Qint. Narrow-OD NMOS : W1N32, W05N54,

standard : W2N16. Linear operation condition : VDS=0.05V, VGT=VGS - VT...52

Fig. 3.23 Effective mobility eff versus VGT for multi-OD NMOS determined with

consideration of W in Weff and Cgg,int for Qint. Multi-OD NMOS : OD8 (WOD=0.25m),

OD16 (WOD=0.125m), standard : OD1 (WOD=2m)W2N16. Linear operation condition :

VDS=0.05V, VGT=VGS - VT...53

Fig. 3.24 Effective mobility eff versus VGT for donut MOSFET determined with

consideration of W in Weff and Cgg,int for Qint. (a) NMOS (b) PMOS, donut : D1S1, D10S10,

standard : W2N32. Linear operation condition : VDS=0.05V, VGT=VGS - VT...54

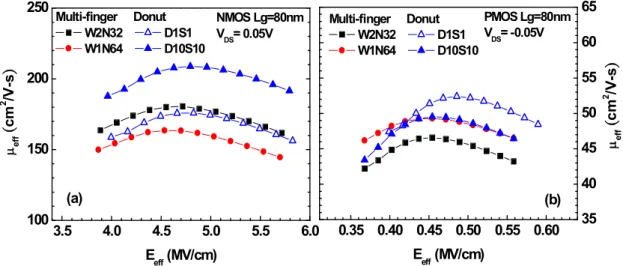
Fig. 3.25 Effective mobility eff versus Eeff for narrow-OD NMOS determined with

consideration of W in Weff and Cgg,int for Qint. Narrow-OD NMOS : W1N32, W05N54,

standard : W2N16. VDS=0.05V, Eeff (VGT 2VT) / 6Tox inv( )...55

Fig. 3.26 Effective mobility eff versus Eeff for multi-OD NMOS determined with

consideration of W in Weff and Cgg,int for Qint. Multi-OD NMOS : OD8 (WOD=0.25m),

OD16(WOD=0.125m), OD1 (WOD=2m). VDS=0.05V, Eeff (VGT 2VT) / 6Tox inv( )...56 Fig. 3.27 Effective mobility eff versus Eeff for donut MOSFET (D1S1, D10S10) determined

with consideration of W in Weff and Cgg,int for Qint (a) NMOS : Eeff (VGT 2VT) / 6Tox inv( ) (b)

PMOSE_eff (V_GT 3V_T) / 9T_{ox inv( )}...56

Fig. 3.28 Effective mobility eff versus Eeff for donut MOSFET (D1S1, D10S10) and a

xiii

( )

( 2 ) / 6

eff GT T ox inv

E  V  V T (b) PMOSE_eff (V_GT 3V_T) / 9T_{ox inv( )}...57

Fig. 3.29 Effective mobility eff versus Eeff for multi-finger NMOS (W2N16, W1N32, W05N64). E_eff (V_GT 2V_T) / 6T_{ox inv( )} . Three regions corresponding to three scattering mechanisms : coulomb scattering in low field, phonon scattering in medium field, and surface roughness scattering in high field...57

Fig.3.30 Schematic of experimental set-up of the charge pumping measurement applied to MOSFET with four terminals...59

Fig.3.31 CP pulse waveform : tr and tf are the rising and falling times, Vbase and Vh are swept from accumulation (Vbase <VFB) to inversion (Vh >VT), under fixed pulse amplitude Va=Vh-Vbase,...60

Chapter 4

Fig. 4.1 The low frequency noise SID/IDS2 measured for the multi-finger NMOS W2N16, W1N32, and W05N64...62

Fig. 4.2 SID/IDS2 vs. IDS under varying |VGT| (0.1~0.7V) for NMOS narrow-OD devices...63

Fig. 4.3 SID/IDS2 vs. IDS under varying VGT (0.1~0.7V) for OD1 and OD16 devices...63

Fig. 4.4 SID/IDS2 vs. IDS under varying |VGT| (0.1~0.7V) for NMOS multi-OD devices...64

Fig. 4.5 The low frequency noise SID/ID2 measured for the multi-OD devices, OD1, OD8, and OD16...65

Fig. 4.6 SID/IDS2 vs. IDS under varying |VGT| (0.1~0.7V) for PMOS multi-OD devices...66

Fig. 4.7 The low frequency noise SID/ID2 measured for the standard and donut devices (a) NMOS (b) PMOS: Standard (multi-finger W2N32), Donut D1S1, and D10S10...67

Fig. 4.8 SID/IDS2 vs. IDS under varying |VGT| (0.1~0.7V) for standard and donut devices (a) NMOS (b) PMOS Standard : multi-finger W2N32, Donut, D1S1 and D10S10...68

xiv

Fig. 4.9 Normalized PSD of drain current noise SID/IDS2 vs. frequency, measured from (a)

W2N32 NMOS and PMOS (b) W1N64 NMOS and PMOS, under |VGT|=0.3V and

|VDS|=0.05V...69

Fig. 4.10 Normalized PSD of drain current noise SID/IDS2 vs. frequency, measured from

multi-OD MOSFET (a) OD8 (WODxNOD=0.25mx8) : NMOS and PMOS (b) OD16

(WODxNOD =0.125mx16) : NMOS and PMOS, under |VGT|=0.3V and |VDS|=0.05V. multi-OD

MOSFET : NF=16, WODxNOD =2 m...69

Fig. 4.11 Comparison of measured charge pumping current with different pulse amplitude

(Va)...71

Fig. 4.12 Charge pumping current measurement of standard and multi OD device...72

Fig. 4.13 Interface trap density Nit of OD1 and OD16 devices extracted by using Weff and W,

measured at VD=VS= VB= 0V and Va = 1.7V...73

Fig. 4.14 Charge pumping current of three narrow OD devices, and maximum charge

pumping current comparison among each measurement die...74

Fig. 4.15 Interface trap density Nit of narrow-OD devices extracted by using Weff and W,

measured at VD=VS= VB= 0V and Va = 1.7V...74

Fig. 4.16 Hooge’s parameter versus gate-over-drive voltage |VGT| for standard and doughnut

devices biased at |VGT|= 0.1~0.7V...75

Chapter 5

Fig. 5.1 General two-port network...76 Fig. 5.2 The extracted Rg of standard and doughnut devices as a function of frequency with

VDS= 1.2V, VGS= 1V...78

Fig. 5.3 Comparison of (a) Z-method and (b) Y-method Rg extraction for NMOS standard and

doughnut devices...79

Fig. 5.4 Comparison of (a) Z method and (b) Y method Rg extraction for PMOS standard

xv

Fig. 5.5 Comparison of (a) Z method and (b) Y method Rg extraction for NMOS narrow-OD

Device...82

Fig. 5.6 Comparison of (a) Z method and (b) Y method Rg extraction for NMOS multi-OD

Device...83

Fig. 5.7 (a) The cut-off frequency fT versus VGT measured for multi-OD devices(b) Cgg versus

VGS extracted from Y-parameters for multi-OD devices...85

Fig. 5.8 (a) Ugain and (b) fMAX extraction for multi-OD NMOS...86

Fig. 5.9 (a) Ugain and (b) fMAX extraction for narrow-OD NMOS...87

Fig. 5.10 The cut-off frequency fT vs. Vgs measured for standard and donut devices (a) NMOS

(b) PMOS. Standard : multi-finger W2N32. Donut : D1S1 and D10S10...87

Fig. 5.11 Cgg vs. Vgs extracted from Y-parameters for standard and donut devices (a) NMOS

(b) PMOS. Standard : multi-finger W2N32. Donut : D1S1 and D10S10...88

Fig. 5.12 Comparison of NFmin measurement result of standard and doughnut devices

of NMOS (left) and PMOS (right)...90

Fig. 5.13 Comparison of Rn measurement result of standard and doughnut devices

of NMOS (left) and PMOS (right)...90

Fig. 5.14 Comparison of Ysopt measurement result of standard and doughnut devices of

NMOS (left) and PMOS (right)...91

Fig. 5.15 Comparison of noise parameters measurement result of standard and narrow-OD

devices, (a) NFmin (b) Rn...92

Fig. 5.16 Comparison of noise parameters Re(Ysopt) and Im(Ysopt) measurement result of

standard and narrow-OD devices...92

Fig. 5.17 Comparison of noise parameters measurement result of standard and multi OD

xvi

Fig. 5.18 Cjs extraction versus frequency (a) without Rbb calibration and (b) after Rbb...97

Fig. 5.19 Cjd extraction versus frequency (a) without Rbb calibration and (b) after Rbb

calibration ...98

Fig. 5.20 Cgs and Cgd extraction versus frequency of ring type body contact layout...99

Fig. 5.21 Cjs extraction versus frequency of ring type body contact layout...99

Fig. 5.22 Cjd (Cbd and Cdb) andCjd (Cbs and Csb) extraction versus body bias (a) standard and

xvii

Table Captions

Chapter2

Table 2.1 (a) RF and Analog Mixed-Signal CMOS Technology Requirements – Near term [4]...6 Table 2.1 (b) RF and Analog Mixed-Signal CMOS Technology Requirements – Long term [4]...7 Table 2.2 Load resistors and filter resistors used in 9812B pre-amplifier...18

Chapter3

Table 3.1 Stress favorable for mobility enhancement in NMOS and PMOS along longitudinal

and transverse directions [29]...24

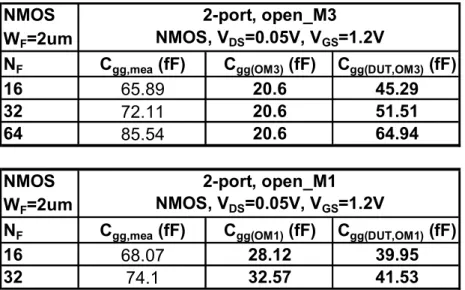
Table 3.2 Gate capacitances measured from multi-finger MOSFET (Cgg,mea), dummy open

structures (Cgg(OM3), Cgg(OM1)), Cgg(DUT,OM3) and Cgg(DUT,OM1) after openM3 or openM1

deembedding...43

Table 3.3 Cgg(DUT,OM3) and Cgg(DUT,OM1), extracted from openM3 and openM1 deembedding on

multi-finger NMOS with NF=16, 32. Cgg(M3) and Cgg(M1~M3) calculated by Raphael simulation

for dummy openM3 and dummy openM1. A comparison of Cgg(M1~M3)=Cgg(DUT,OM3)－

Cgg(DUT,OM1) from measurement and Cgg(M1~M3)=Cgg(M1~M3)－Cgg(M3) from simulation...43

Table 3.4 Multi-finger MOSFET device parameters extracted from DC I-V and RF C-V

characterization flow...51

Chapter5

Table. 5.1 The optimized parameters (Ag and B) for Z method Rg extraction of standard

W2N32 device...80

Table. 5.2 The optimized parameters (Ag and B) for Z method Rg extraction of doughnut

D1S1 device...80

Table. 5.3 The optimized parameters (Ag and B) for Z method Rg extraction of doughnut

D10S10 device...81

Table. 5.4 The layout view and classification of each kind body contacts...95 Table. 5.5 Cjs extraction versus Vgb extraction...98

xviii

Table. 5.6 The increment of Cjs with the body ring number increased...98

Table. 5.7 Body resistance and deep-N-well capacitance with different body

1

Chapter 1

Introduction

1.1 Research Motivation

Recent advances in the CMOS technology, which possesses the advantage of high

integration and low power, is finding more and more important applications in the area of

analog, mixed mode, and RF circuits [1,2]. RF integrated circuit design requires accurate

device models up to the operating frequency, especially when the operating frequency of the

circuit approaches the cutoff frequency (fT) or maximum oscillation frequency (fMAX).

As devices scaled down into the nanometer-scale regime, the stress induced from shallow

trench isolation (STI) process and its impact on the device performance becomes significant

[3]. The longitudinal stress effect has been widely investigated; however, relatively fewer

studies were focused on the transverse stress effects. Besides, STI stresses, either longitudinal

or transverse, exhibits high sensitivity to device layouts, which may significantly impact the

analog circuit performance. Meanwhile, the increase of effective, namely W from STI top

corner rounding (TCR) emerges as an important factor besides STI stress to affect DC

characteristics (drain current and trans-conductance), low frequency noise, and high

frequency performance.

The multi-finger transistors have been widely as the standard layout in RF circuits to

enhance fMAX and reduce RF noise by minimizing the parasitic gate resistance. In this thesis,

three kinds of layouts, namely doughnut (donut), narrow-OD, and multi-OD MOSFETs have

been designed to investigate layout dependence of STI stress, particularly the transverse stress.

A comprehensive characterization was carried out to investigate the transverse stress effect on

mobility, current, low frequency noise (LFN), and high frequency performance. Mullti-finger

2

Four-port test structures adopting five kinds of body contact layouts, denoted as multi-ring,

U-shape, L-shape, parallel, and perpendicular stripe have been designed to explore the

influence on basic device parameters like body resistance and junction capacitances, and the

proliferated impact on low frequency noise and high frequency performance.

1.2 Thesis Organization

This thesis presents our research results of RF MOSFET layout effect on low frequency

noise and high frequency characteristics, with major purpose for RF and analog circuit

applications. The main effect of our focus is the mechanical stress introduced from shallow

trench isolation (STI), which increases with technology scaling and becomes dramatically

significant in nanometer scale devices. In this thesis, three types of new MOSFET layout,

namely narrow-OD, multi-OD, and donut devices are proposed to modulate the transverse

stress from STI.

At first, an overview on low frequency noise theory and measurement methods is presented

in chapter 2. Then, the layout dependence of STI stress and its effect on device parameters

like drain current (IDS), transcondutance (Gm), and effective mobility (eff) are described in

chapter 3. The proposed new MOSFETs with layouts of narrow-OD, multi-OD, and donut

were fabricated in 90 nm low leakage CMOS process. An extensive device characterization

has been carried out through I-V, C-V, S-parameters, and charge pumping (CP) current

measurements. Note that the C-V characterization was performed based on S-parameters

measurement, which can solve the problems of conventional C-V measurement, such as the

parasitic capacitances from pads, interconnection lines, and substrate coupling and gate

leakage induced abnormal C-V fall-off. However, one more parasitic capacitance arising from

3-D gate fringing effect cannot be removed from the open deembedding method implemented

in S-parameters characterization. Thus, 3-D RLC simulator like Raphael was employed in this

3

Based on the mentioned characterization techniques, STI top corner rounding (TCR) is

identified as a key factor affecting I-V, Gm, gate capacitances, LFN, and high frequency

performance, etc.

In chapter 4, MOSFET layouts effect on LFN will be presented, with a

comprehensive characterization on all of the device structures such as standard multi-finger,

narrow-OD, multi-OD, and donut MOSFETs, and covering both NMOS and PMOS. The

layout effect can be examined through an extensive comparison between different device

structures. Also, the interface trap density Nit extracted by CP method is taken as one of key

parameters responsible for flicker noise, i.e. LFN under the condition that number fluctuation

model is the dominant mechanism, tentatively for NMOS. Two more topics to be covered in

chapter 4 are the body contact layouts effect and strain effect on LFN. In this study, totally

five body contact layouts, such as multi-ring, U-shape, L-shape, parallel and perpendicular

stripes are designed for an investigation on their effect on LFN. A review of strain effect will

be classified as stress from strain engineering in 65nm high speed CMOS process and STI

stress from new MOSFET layouts introduced in chapter 3. Chapter 5 will focus on MOSFET

layout effect on high frequency characteristics, such as fT, fMAX, and RF noise parameters. An

extensive characterization will cover different device structures and also the dependence of

frequency and bias. Note that two-port or four-port deembedding is indispensable in high

frequency characterization for parasitic RLC extraction and elimination, which is necessary

for an accurate extraction of intrinsic device performance under high frequency operation. As

for body contact layout effect, four-port test structure is required to accommodate 4-terminal

MOSFETs with separate body terminal and a new body network model has been developed to

simulate the body contact layout and body biases effects. In the end, chapter 6 concludes this

4

Chapter 2

Low Frequency Noise Theory and Measurement Method

2.1 An Overview of CMOS Technology and Low Frequency Noise

It has been well known that noise exists as a fundamental problem in semiconductor

devices and electronic circuits. In electronic devices, noise appears as random fluctuations in

current or voltage around their DC level, due to fluctuations in carriers transport through the

conduction channel. The impact from noise on the desired signal may cause failure of

electronic circuits operation when the noise power becomes too large to keep sufficient signal

to noise ratio (SNR). Furthermore, the mentioned problem becomes increasingly tough in

miniaturized devices accompanied with supply voltage scaling and squeezed dynamic range.

Attributed to the nature of random fluctuations, noise is generally characterized by probability

density function (PDF) based on multiple measurements over time. The time average of the

measured noise currents or noise voltages approaches zero when integrated long enough and

provides no useful information; instead, the square quantities namely power spectral density

(PSD) is used to characterize noise. The PSD is measured with a spectrum analyzer or

dynamic signal analyzer, which will be described in section 2.2.

The experimental indicates that the noise spectral density increases with decreasing

frequency at lower frequencies and becomes white thereafter. The corner frequency between

the frequency dependent noise and white noise is typically from few Hz up to MHz range and

may vary with device types, device dimensions, and bias conditions, etc. The physical

mechanism behind the white noise source is well known. However, the excess noise at low

frequencies, namely low frequency noise (LFN) brings many questions with lot of debates

and open up an interesting research area. Note that the LFN is also known as flicker noise or

5

The aggressive advancement of CMOS technology into nanoscale regime in recent five

years has driven transistor gate delay to below 10 ps and intrinsic cut-off frequency (fT) well

above 100 GHz [4]. According to International Technology Roadmap for Semiconductor

(ITRS) [4], the demand on devices and interconnection lines scaling in the area of analog and

RF is not as stringent as that for high speed logic CMOS. However, much more stringent

criterion on the flicker noise at low frequencies (i.e., LFN) and thermal noise at high

frequencies is required and specified for analog and RF circuit design, as shown in Table 2.1(a)

and (b) for near term and long term, respectively [4]. The yellow blocks marked for

2011~2014 represent that the manufacturing solutions are known but not yet optimized.

Unfortunately, the red blocks marked for 2015 and thereafter highlight the problems for which

the manufacturable solutions do not exist today. Obviously, the 1/f noise, i.e. LFN emerges as

a big roadblock from 2015 and on. As compared with bipolar transistors, CMOS transistors

generally suffer higher flicker noise (LFN), due to the nature of surface channel conduction.

As a result, the solutions to suppressing LFN become more challenging to CMOS technology,

even though CMOS is superior in terms of scalability, high integration, low cost, and low

standby power. To facilitate the extension of CMOS technology into RF and analog domain,

an in-depth study on LFN in MOSFETs and its dependence on layouts and geometry scaling

becomes critically important and is selected as one of research topics in this thesis. It has been

recognized that LFN in transistors introduces particular problem in analog and RF circuits

like voltage controlled oscillators (VCOs) and mixers. For VCOs, the LFN is upconverted to

phase noise at small frequency offsets from the carrier frequency and then sets the ultimate

separation limitation to two channels [5-8]. Fig. 2.1 illustrates schematically phase noise

spectrum and different physical origins. As for mixers, the LFN originated from transistors

may lead to severe degradation of SNR [9,10]. This can be understood if the signal is

6

overwhelm the signal, particularly worse for low voltage operation. The impact from LFN on

mixer may be relieved by using long channel transistors; however the penalty of to be paid is

the degradation of transconductance and circuit speed.

7

Table 2.1(b) RF and Analog Mixed-Signal CMOS Technology Requirements – Long term [4]

8

2.2 Low Frequency Noise Theory

In the past several decades, the origins and physical mechanisms underlying flicker

noise remain an open question, with lot of debates and arguments in the experimental results

and modeling to match the measurement. Number fluctuation model and mobility fluctuation

model appear as two most popular mechanisms to explain and predict the measured flicker

noise [11,12]. In 1957, McWhorter published a flicker noise model based on quantum

mechanical tunneling transitions of electrons between the gate oxide and channel [11]. In

practice, the tunneling time varies exponentially with distance, and it is assumed that trap

density is uniform in both energy and distance from the channel interface to extract the time

constants for generating flicker noise. The McWhorter model, namely number fluctuation

model may be useful due to its simplicity and good agreement with experimental, particularly

for n-channel MOSFETs [12,13]. However, the mobility fluctuation model appears to better

explain the flicker noise measured from p-channel MOSFETs [14,15]. As compared to surface

channel MOSFETs, buried-channel MOSFETs or bipolar junction transistors (BJT)

demonstrate significantly lower flicker noise [16-21]. The published results are in favor of the

number fluctuation model that the flicker noise is originated from the traps in the oxide or at

oxide/channel interface. However, the surface carrier mobility is reduced compared to the

bulk value due to additional surface scattering (acoustic phonon and surface roughness),

which has an impact on the mobility fluctuation. Hooge mobility noise [22], which is

sensitive to the crystalline quality, can be employed to explain the higher flicker noise for

surface channel devices in which the carriers are in close proximity to the gate oxide and may

suffer aggravated mobility fluctuation. In the following, the number fluctuation and mobility

9

2.2.1 Number Fluctuation Theory [11]

The physical mechanism underlying the number fluctuation noise is the interaction

between the channel carriers and slow traps in the gate oxide, which is illustrated in Fig. 2.2.

The dynamic exchange of carriers between the gate oxide and channel causes a fluctuation in

the surface potential (S) and then gives rise to fluctuations in the inversion carrier density

Qinv. This in turn leads to noise in the drain current. Note that Qinv (the fluctuation in the

inversion carrier density) can occur even without a current flowing the channel and the

channel current is only used to sense the fluctuations. The mathematical formulas for

expressing number fluctuation model in different operation regions are provided as follows

In weak inversion region

2 2 2 2 , 1 DS I _{t D it} DS ox B ox S _{N q C C} f m I WLC k T m C        _{ }     (2.1)

In strong inversion region

2 2 1 : m m ox eff DS DS GS T g W linear region g C V L  I V V      _{ } _{ }      (2.2) 2 2 2 2 2 2 2 3 2 1 DS I _{B t m B t ox eff DS} DS ox DS DS S _{q k T N g q k T N WC V} I f WLC I f L I       _{ }    (2.3) 2 2 1 saturation : m m ox sat DS GS T g region g WC I V V       _{ } _{ }      (2.4) 2 ₂ 2 2 2 1 1 DS FB I _{B t} V DS GS T ox GS T S _{q k T N} S I V V f WLC V V       _{ }  _{ }       (2.5) : -t

N the density of traps at quasi Fermi level

The frequency dependence with the exponent  may deviate from 1 under the condition that

the trap density Nt is not uniform in depth. For the case when the trap density near the gate

10

smaller than 1. For the opposite case,  may become larger than 1. As for the bias dependence

predict by the number fluctuation model, the normalized drain current noise SIDS/IDS2 varies

with approximately as 1/IDS2 or 1/(VGS-VT)2 in strong inversion region given by (2.2)~(2.5)

while is nearly independent of bias in weak inversion region, shown in (2.1). In this work, the

LFN in terms of SIDS/IDS2 measured from n-channel MOSFETs just follows number

fluctuation model and varied with IDS according to the relationship of 1/IDS2.

Fig.2.2 Schematical illustration of electrons in the channel of MOSFET moving in and out of the traps giving rising to fluctuations in the inversion carrier density and thereby the drain current.

2.2.2 Mobility Fluctuation Theory

Mobility fluctuation is another mechanism, which can contribute flicker noise. The

mobility fluctuation model was first proposed by F.N. Hooge with an empirical formula given

for the resistance fluctuation [23]. According to the Hooge empirical formula, the drain

current noise generated by fluctuation in the channel carrier mobility can be written as (2.6).

2 DS I _H DS inv S _q I fWLQ   (2.6)

where H is a dimensionless parameter and referred as Hooge parameter. The typical values of

H range between 10-3 and 10-6 for surface channel transistors. H may be down to 10-7 for

buried channel transistors like N+ gate pMOSFETs and even lower to the order of 10-8 for

11

fluctuation noise [22]. The effective mobility eff of the channel carriers is determined by

different scattering mechanisms, which vary in different ways with the effective normal field

E⊥_eff as a function of inversion carriers density Q_INV and body depletion charge Q_B. As a result,

H is not only dependent on technology but also on the bias conditions. In general, each

scattering process generates mobility fluctuation noise with the amount given by each

respective Hooge parameter, denoted as Hj. Assume the scattering processes are independent

of each other and then Matthiessen’s rule can be applied as follows

1 1

j

eff j

 



 (2.7)

The fluctuations in different scattering processes are assumed independent. Then the variation

applied to (2.7) can lead to

2 2 j eff j eff j       

_

(2.8)

The power spectral density can be derived as

2 2 2 j DS I _eff j DS j j S S I        _ _  



(2.9) , 2 j H j j inv S _q fWLQ     (2.10) 2 2 , Hj eff eff H H H j j j inv j inv j q q fWLQ fWLQ              _ _   _ _    





(2.11) It can be understood from (2.11) that H varies with biases due to the bias dependent factor



_eff /_j



2. The total drain current noise is evaluated by adding the noise contribution from each channel segment derived for linear region as follows.

2 2 ₀ 2 DS DS V I _{H eff H eff} DS DS DS DS S _{q W q} dV V I fWL I fL I     

_

 (2.12)

12 2 1 1 ( ) DS I _{H H} DS ox GS T ox GT S q q I f WLC V V f WLC V        (2.13)

The drain current noise contributed from mobility fluctuation as shown in (2.13) predicts that

the larger H and shorter channel length (L) will lead to higher flicker noise whereas the

wider channel width (W) and higher gate overdrive VGT can help reduce the flicker noise. The

thinner gate oxide thickness is another beneficial factor, which can suppress flicker noise. In

our experimental, the mobility fluctuation model can provide much better fit to the flicker

noise measured from p-channel MOSFETs than number fluctuation model.

2.3 Low Frequency Noise Measurement System

Three flicker noise measurement systems with different equipment configurations are

employed in this thesis for characterization of low frequency noise (LFN) in MOSFETs with

different layouts. The conventional one is Celestry 9812B Noisepro system, which is

supported by NDL and has been commonly used in transistor flicker noise characterization

but limited to measurement using DC probes. The other two are new systems built up in our

RF Lab. – one is SR570 system and the other one is model-5184 system. The major difference

from Celestry 9812B is that these two LFN systems can support both RF and DC test

structures, with RF GSG probes and DC probes, respectively. SR570 system shown in Fig.

2.3 is equipped with SR570 LNA (trans-resistances amplifier), Agilent DSA 35670 (dynamic

signal analyzer), and HP4142B (DC power supply). The model-5184 LNA shown in Fig. 2.4

contains 5184 LNA (voltage amplifier), PA14A1 for ultra low noise DC source, low pass filter,

Agilent 35670, and HP4142B. Note that Agilent ICCAP is adopted for measurement

auto-control and data collection.

1) SR570 Low Frequency Noise Measurement System

13

trans-resistances amplifier produced by Stanford Research Systems. Essentially, LNA acts as

a key element in this flicker noise measurement system through which it can provide the

second stage low noise gain to reduce system noise and offer sufficiently large signal

amplitude to dynamic signal analyzer (DSA) without increasing the undesired noises. In

practice, the SR570 LNA can provide an offset current source at the DUT output (i.e., drain

terminal of MOSFETs), which serves as an input to the amplifier. The DUT output current can

be modulated by the low noise offset current source, so as not to drive the amplifier into

saturation. The SR570 is also equipped with a filter with different options, such as low-pass,

high –pass or bandpass filter. In our applications, we typically set bandpass filter to select the

frequency range of our interest, i.e. 1 ~ 100k Hz. The HP4142B DC power supply was

controlled by ICCAP to provide the gate bias for MOSFET through a low pass filter in order

to remove the power supply’s noise within the frequency range of interest that is above 1Hz.

In other words, the supply voltage through the low pass filter is nearly a pure DC voltage

source under the condition that the signal above 1Hz was removed by the low pass filter. The

LNA output is connected to DSA, which can perform dynamic signal (V/ Hz) measurement

and analysis. All the equipments such as 4142B, SR570 LNA, and Agilent DSA 35670 are

integrated together and the measurement can be carried out through the control of ICCAP .

Through a dynamic signal analysis done by DSA, we can obtain the measured noise from

ICCAP. In general, we have to make a simple calculation to recover the original noise

measured from DUT output stage. The measured noise is transformed to current spectrum

14

Fig.2.3 Schematic of SR570 flicker noise measurement system setup with SR570 LNA

(trans-resistance amplifier), Agilent DSA 35670 (dynamic signal analyzer), and HP4142B (DC power supply)

Unfortunately, The measurement system adopting SR570 LNA has a stringent current

limitation of 5 mA. For advanced multi-finger RF MOSFETs, which sometimes have large

total width for sufficient current drivability and transconductance, this current limitation

generally restricts the DUTs to limited operation conditions, such as linear or subthreshold

regions. To solve the mentioned problem, we proposed a new system configuration by using

model-5184 LNA to overcome the current limitation. Unlike SR570, model 5184 LNA is a

kind of voltage amplifier with a separated output bias source. In the following, we will have a

discussion on this new LFN measurement system.

2) New Configuration with Model 5184 LNA and ultra low noise DC source (PA14A1)

An appropriate operation of SR570 LNA requires that the gain setting resistor should be

lower than the output resistance of DUT (rout). As for the new solution using model 5184 LNA

(voltage amplifier), the voltage gain and LNA noise are independent of the output resistance

of DUT. In this way, the LNA noise is independent of the DUT and thus we can obtain a

system noise level from measurement without DUT. The noise floor of the system can be

pushed to 10-20 (V2/Hz), which is well below that of DUT in the frequency range of our

15

DUT output biasing source, thus reducing the system integration level. Therefore, a reliable

and ultra-low noise DC source at DUT output is required to minimize the extra noise

contributed from the system. Battery is one of low noise sources, which can effectively reduce

the noise generated from power supply. Besides the simple setup using batteries, we propose a

new solution using an ultra low noise DC source (PA14A1) instead of batteries. A complete

system configuration incorporating batteries or low noise DC source (PA14A1) is illustrated

in Fig. 2.4. In practice, we implement on a PCB (printed circuit board) the metal lines in three

paths for connecting LNA (model 5184), low noise source (PA14A1), and DUT drain terminal

as shown in Fig. 2.5 (a) and (b).

In Fig.2.5(b), the ultra low noise DC source (PA14A1) was used. The advantage of using

PA14A1 is that it can achieve the desired output voltage but a simple setup with batteries

shown in Fig. 2.5(a) cannot meet the requirement.

In conclusion, we can obtain almost the same measurement results under the same bias

condition by using SR570 LNA and model 5184 LNA either with batteries or PA14A1.

Besides the mentioned achievement, we have extended this work to 4-terminal MOSFET

16

Fig.2.4 Schematic of low frequency noise measurement system consisting of model 5184

LNA (voltage amplifier), HP4142B for DC supply, and Agilent 35670 for dynamic signal analyzer

(a)

PA14A1 Low noise DC soruce

CH1

(b)

Fig.2.5 New solution for using model 5184 LNA (a) Battery (b) ultra low noise DC source

17 3) Celestry 9812B NoisePro System

Fig. 2.6 illustrate the configuration of Celestry 9812B system, later named as ProPLUS

NoisePro system, which consists of 9812B analyzer (hardware), NoisePro software with

automatic control, and built-in 1/f noise SPICE model parameter extraction routine to

provides off-the-shelf 1/f noise system.

Fig.2.6 Schematic illustration of Celestry 9812B Noisepro system consisting of HP4145 for

DC supply, 9812B for pre-amplifier, and Agilent 35670 for dynamic signal analyzer.

Celestry 9812B system can support noise characterization and model parameter extraction

for MOSFETs, BJTs, diodes and resistors, based on either public or proprietary models. This

system offers V-mode and I-mode biasing modes with accuracy specification of user options.

Detachable pre-amplifier unit can be placed closer to DUTs or in the measurement chamber,

which greatly reduces the system noise floor. The battery operated current amplifier provides

as low as 0.5pA/(Hz)1/2 @ 1 KHz floor noise and voltage amplifier provides 1nV/(Hz) 1/2 @ 1

KHz floor noise.

When proceeding a system calibration, NoisePro will automatically perform a leakage

testing, and the system will apply voltage of 1-Volt and measure the leakage current. The

measured values of leakage and load resistors will be saved in a file to be used in the noise

18

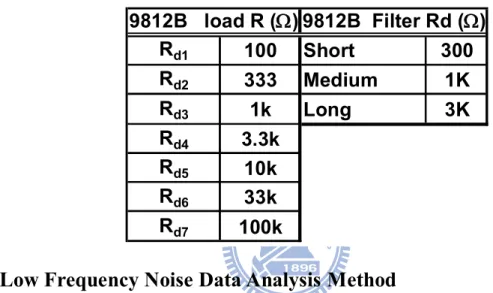
and version of noise amplifier, their values differ. Table 2.2 lists the default values of load

resistors (Rload) used in noise amplifiers and those of filter resistors in load circuit. If 9812B is

selected, user needs to choose the type of amplifier : current or voltage amplifier, internal or

external amplifier. If external amplifier is selected, the user needs to provide method of

converting the A, B, C values.

Table 2.2 Load resistors and filter resistors used in 9812B pre-amplifier

R_d1 100 Short 300 R_d2 333 Medium 1K R_d3 1k Long 3K R_d4 3.3k R_d5 10k R_d6 33k R_d7 100k 9812B load R () 9812B Filter Rd ()

2.4 Low Frequency Noise Data Analysis Method

As mentioned previously, an extensive noise characterization indicates that low frequency

noise (LFN) in nMOSFETs follows the number fluctuation model whereas that in pMOSFET

is in better agreement with mobility fluctuation model. For MOSFETs, the measured LFN is

generally expressed as normalized PSD (power spectral density) of drain current noise,

denoted as SID/IDS2 to identify which model is the dominant one in the devices under test.

According to the normalized PSD derived for number fluctuation model for subthreshold,

linear, and saturation regions in (2.1), (2.3), and (2.5), respectively, the SID/IDS2 is proportional

to 1/IDS2 and increases linearly with oxide trap density Nt. On the other hand for the

normalized PSD governed by mobility fluctuation model, expressed in (2.12) and (2.13) as a

function of IDS and VGT, respectively, the SID/IDS2 is proportional to 1/IDS or 1/ VGT and

19

overdrive VGT can suppress LFN. Sometimes, the experimental present VGS dependence

stronger than what predicted by model. McWhorter’s carrier trapping model may provide one

of mechanisms responsible for the stronger VGS dependence. The oxide trap density Nt is

known to be a function of the potential energy across the band gap of semiconductor substrate.

When VGS is varied, Fermi level of the channel moves accordingly. If the number of particular

traps that cause flicker noise drastically changes along with the VGS, the noise amplitude

could be a stronger function of the bias. Another factor that we should take into account is the

fact that carrier mobility is also a function of VGT. Regarding device scaling effect, both

models reveal dependence of device dimensions in terms of 1/WLCox2, which means the

channel length and width scaling will lead to increase of SID/IDS2 but the oxide thickness TOX

scaling can help reduce LFN in terms of SID/IDS2. Note that W, L, Cox, eff, H, and VGT appear

as key parameters in LFN models and how to accurately extract or determine the mentioned

parameters becomes critical for LFN data analysis and diagnosis. In LFN models, W and L

represent effective channel width and effective channel length, rather than drawn dimensions

on layout or physical dimensions from optical measurement. The accurate extraction of

effective channel dimensions brings additional challenges for miniaturized MOSFETs with

short channel and narrow width to sub-100 nm regimes in 90nm technology and below. STI

top corner rounding (TCR) effect on effective channel width will be described in chapter 3. As

for Cox, it represents the gate capacitance density per unit area, under strong inversion

condition in which Cox is contributed from three major capacitances in series – gate oxide

capacitance, gate depletion capacitance, and inversion channel capacitance. Again, an

accurate extraction of Cox becomes difficult in miniaturized MOSFETs, due to several

complicated factors like deviations in effective channel length and width, gate depletion effect,

inversion channel quantization effect, and more importantly the parasitic capacitances from

20

enough to minimize or even eliminate the deviation of effective channel dimensions is

adopted to solve this problem. Furthermore, a dedicated open deembedding to the bottom

metal, i.e. M1 is necessary to approach an accurate extraction of Cox.

The accuracy or deviation of mentioned basic device parameters will have direct impact

on the determination of eff and H. Furthermore, both eff and H are a function of scattering

mechanisms and biases. The bias dependence ofeff and H comes from electrical field effect

on carriers transport and their scattering through the conduction channel. Note that the gate

bias dependence manifests normal field effect and is expressed in terms of gate overdrive

VGT=VGS -VT in which VT variations from processes, geometries, profiles, and biases can be

taken into account. As shown in Fig. 2.7, the measured LFN in terms of SID/IDS2 decrease with

increasing |VGT| for both NMOS and PMOS. Fig. 2.8 (a) and (b) illustrate SID/IDS2 versus VGT

for NMOS and PMOS, respectively and reveal the difference of VGT dependence between

NMOS and PMOS. The results can be explained by (2.3) and (2.5) for NMOS governed by

number fluctuation, and (2.13) for PMOS dominated by mobility fluctuation.

Frequency dependence is one more key factor for LFN analysis and modeling. Assuming

an ideal condition that trap density Nt is a constant, the frequency dependence of flicker noise

will follow 1/f. However, in most of real cases, the exponent  in frequency dependence may

deviate from 1 due to the fact that the trap density Nt is not uniform in depth. For the case

when the trap density near the gate oxide/channel interface is higher than that in the interior of

the gate oxide,  tends to be smaller than 1. For the opposite case,  may become larger than 1.

Referring to Fig. 2.7, the frequency dependence of PMOS (Fig.2.7(b)) follows 1/f very

consistently but that of NMOS (Fig. 2.7(a)) reveals certain deviation from 1/f , with the

exponent  < 1.

It has been a conventional belief from analog circuit design using N+ poly gate technology

21

buried channel PMOS, attributed to deeper channel and less surface scattering. However, the

advancement of CMOS process has driven phase-out of N+ poly gate technology and

deployment of dual gate technology, i.e. N+ /P+ poly gate for N/P MOSFET, since 0.25m

technology node and beyond. The dual gate technology can realize surface channel for both

NMOS and PMOS and help push VT scaling for low voltage operation. In this way, the

advantage of PMOS over NMOS, in terms of flicker noise can no longer be maintained. Fig.

2.9 makes a comparison of measured LFN (SID/IDS2) between NMOS and PMOS under the

same bias, i.e. |VGT|=0.3V and |VDS|=0.05V. As can be seen clearly that SID/IDS2 of PMOS is

higher than NMOS by around one order at very low frequency (<10 Hz) and the difference

decreases at higher frequency. The results suggest that conventional design using PMOS in

VCO for low phase noise is no longer valid. A detailed analysis of LFN to investigate the

mechanisms responsible for NMOS and PMOS and the optimization design for suppressing

LFN become an important task.

101 102 103 10-12 10-11 10-10 10-9 (a) V_GT=0.2V V_GT=0.3V SID /IDS 2 ( 1 /H z ) Frequency (Hz) UMC90nm-97C W2N32 NMOS Vds=0.05V V_GT=0.1V 101 102 103 10 -12 10-11 10-10 10-9 (b) SID /IDS 2 ( 1 /H z ) Frequency (Hz) V_GT=-0.5V V_GT=-0.3V V_GT=-0.1V UMC90nm_{W2N32 PMOS} Vds= -0.05V

Fig.2.7 Normalized PSD of drain current noise SID/IDS2 measured from (a) NMOS and (b)

PMOS with increasing frequency, under various VGT (|VGT |=0.1, 0.3, and 0.5V).

22 0.1 1 10-11 10-10 (a) V_GT (V) SID /ID S 2 ( 1 /H z ) 90nm NMOS W2N32 W1N64 0.1 1 10-11 10-10 10-9 S ID /I D S 2 ( 1 /H z ) (b) |V_GT| (V) 90nm PMOS W2N32 W1N64

Fig.2.8 Normalized PSD of drain current noise SID/IDS2 measured from (a) NMOS and (b)

PMOS under increasing |VGT| and fixed |VDS|=0.05V.

101 102 103 10-12 10-11 10-10 10-9 S ID /I D S 2 ( 1 /H z ) _PMOS NMOS Frequency (Hz) 90nm W2N32 |V DS|=0.05V, |VGT|=0.3V

Fig.2.9 Normalized PSD of drain current noise SID/IDS2 versus frequency, measured from (a)

NMOS and (b) PMOS under |VGT|=0.3V and |VDS|=0.05V. NMOS and PMOS were fabricated

23

Chapter 3

Analysis of Layout Effect on STI Stress and Device Parameters

3.1 STI stress Mechanics in RF MOSFET

Shallow trench isolation (STI) emerged to replace LOCOS as the standard isolation

technology in CMOS process at 0.25 m node and below [24,25]. The technology transition

proves itself the success that STI enables continuous scaling of active and isolation regions to

far beyond 0.25m node, and realize higher integration level for IC design. Also, STI brings

the advantages like reduced sidewall capacitance for AC performance and improved surface

planarity for high integration [26]. In spite of the mentioned advantages, STI indeed

introduces some other impacts, such as mechanical stress from refilled trench or known as

Length of Oxide Definition (LOD) stress-effect [27,28]. The STI stress may have a significant

influence on MOSFETs’ electrical characteristics, such as threshold voltage (VT), carrier

effective mobility (eff), transconductance (Gm), gate speed, cut-off frequency (fT), and low

frequency noise, etc. The mentioned impacts always increase with devices scaling and

becomes the key factors of consideration in MOSFETs layout for integrated circuit design,

particularly for RF and analog circuits of our focus in this thesis.

The STI module implemented in standard CMOS processes from 0.25m to 65nm

nodes generally introduce compressive stress, either along or transverse to the channel

length, i.e. the current flow direction. The stress along the channel length is defined as

longitudinal stress //, and that transverse to the channel length is denoted as transverse

stress⊥. The reverse type of stress, namely tensile stress will introduce its influence in the

opposite direction with that of compressive stress. The impact from STI stress on device

characteristics is strongly dependent on the device types and orientations. Table 3.1

summarizes the stress favorable for mobility enhancement and reveals fundamental