國 立 交 通 大 學
財 務 金 融 研 究 所
碩 士 論 文
有違約風險的選擇權訂價:對偶問題
Vulnerable Option Pricing:The Dual Problem
研 究 生: 潘政宏
指導教授: 戴天時 博士
有違約風險的選擇權訂價:對偶問題
Vulnerable Option Pricing:The Dual Problem
研 究 生:潘政宏
Student:Zheng-Hung Pan
指導教授:戴天時博士
Advisor:Dr. Tian-Shyr Dai
國立交通大學
財務金融研究所
碩士論文
A Thesis Submitted to Graduate Institute of Finance
National Chiao Tung University
in partial Fulfillment of the Requirements
for the Degree of
Master of Science in
Finance
June 2010
Hsinchu, Taiwan, Republic of China
中華民國九十九年六月
I
有違約風險的選擇權訂價:對偶問題
學生:潘政宏
指導教授:戴天時 博士
國立交通大學財務金融研究所
中華民國九十九年六月
摘要
本文嘗試延伸有違約風險的選擇權評價公式,考慮在首次通過模型的前提 下,推導有違約風險的選擇權之封閉解;以及其對偶問題:考慮在 Merton 結構 式模型的前提下,推導有違約風險的障礙選擇權之封閉解。並且依照本文方法, 利用有違約風險的選擇權之封閉解和 in-out parity 性質,可延伸評價其他型態障 礙選擇權。並將其延伸至結構型債券,如 Reverse exchangeable bond 和 Barrier reverse convertibles 的評價上。
II
Vulnerable Option Pricing:The Dual Problem
Student:Zheng-Hung Pan Advisor:Dr. Tian-Shyr Dai
Graduate Institute of Finance
National Chiao Tung University
June 2010
A
BSTRACTThis paper presents a method of pricing vulnerable vanilla options under the first passage model. Similar approach can be applied to solve the dual problem-pricing barrier options under the Merton’s structural model. By applying the closed-form solution of vulnerable barrier options and the in-out parity, we can derive other types of barrier options. Finally, our formulas can be used to evaluate structural notes, like reverse exchangeable bond and barrier reverse convertibles.
KEYWORDS:Counterparty Risk, Structural Model, First Passage Model, Barrier
III
誌謝
我要感謝指導教授戴天時老師。這一年以來的 meeting,一起研讀 Shreve 的 Stochastic Calculus for Finance 和 John C. Hull 的 Options, Futures, and Other Derivatives 時,每當我們有不太正確的觀念,戴天時老師總是不厭其煩地給予指 正,並因此確定了我研究方向。遇到瓶頸時,老師也常常為我們指點迷津,並鼓 勵我們去多方嘗試。很榮幸能成為老師的學生,老師淵博的學識讓我的碩士生涯 學得紮實,獲益甚多。 感謝王釧茹學姊,遇到問題時,學姊總能想辦法來幫助我,也感謝學姊在論 文及報告上給予的寶貴意見。還要感謝邱俊淵學長,學長強大的數學知識讓我無 後顧之憂的研究論文。感謝呂育道教授和王之彥教授在論文上給予的指正與建 議。感謝一起學習的伙伴們,亮志、敏誠、偲維和雅雯,感謝你們這段日子以來 的鼓勵與相挺。感謝劉彥君以及資管所的同學們,因為有你們的數值模型,才能 讓我的論文更具正確性。也感謝財金所 97 級的全體同學,謝謝你們這兩年來的 陪伴,讓我的人生更加豐富。 最後,由衷地感謝我的父母。謝謝你們不辭辛苦地養育栽培,謝謝你們讓我 享受這麼棒的學習環境,謝謝你們一路以來的鼓勵與支持。最後,再次感謝所有 幫助過我的師長們、學長姊、同學們和我的父母,謝謝你們。 潘政宏 謹誌 國立交通大學財務金融研究所 中華民國九十九年六月
IV
目錄
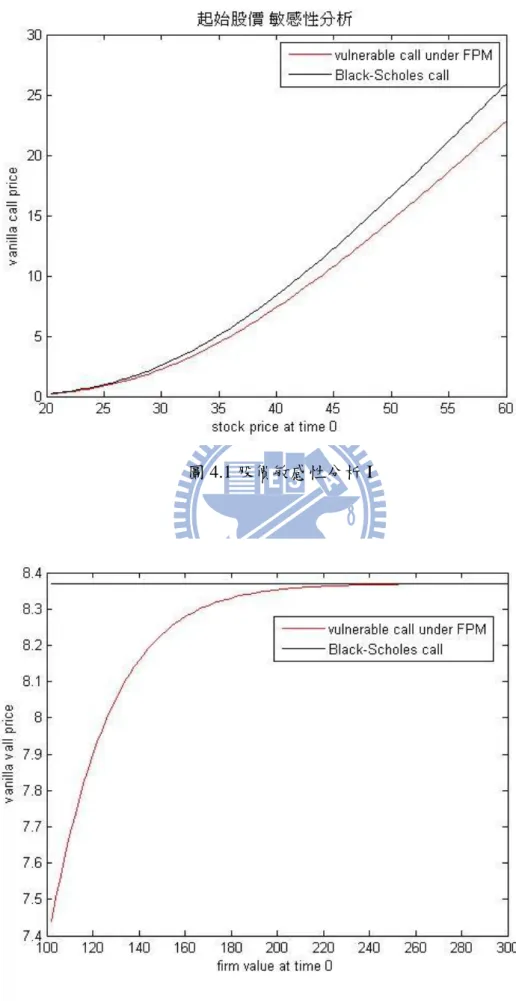
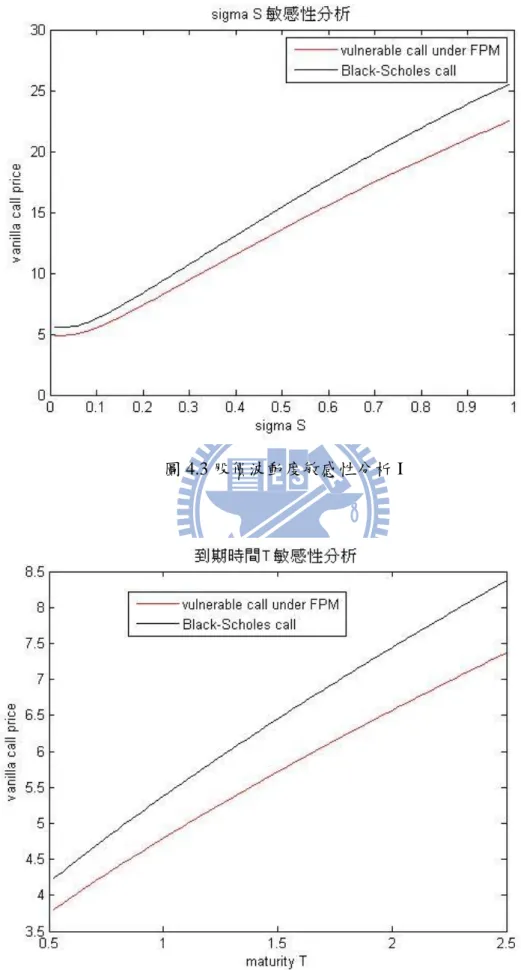
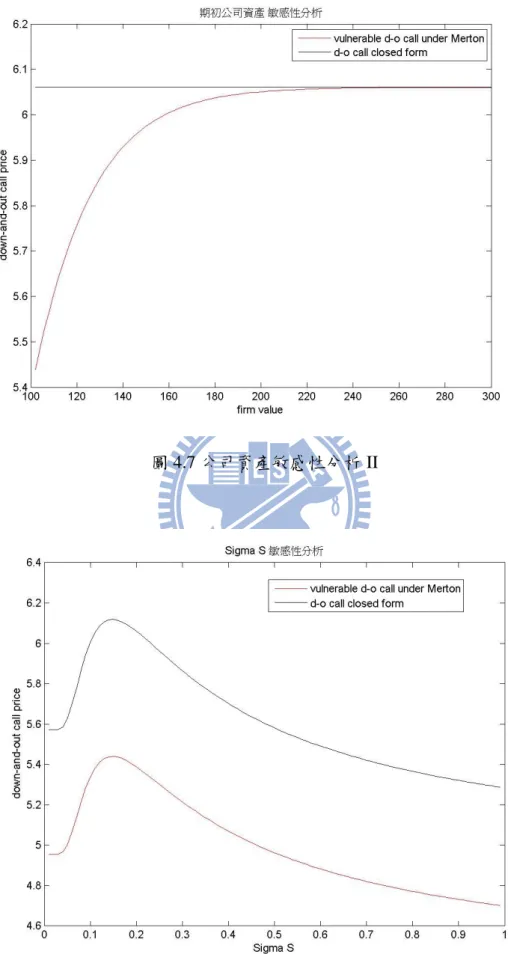
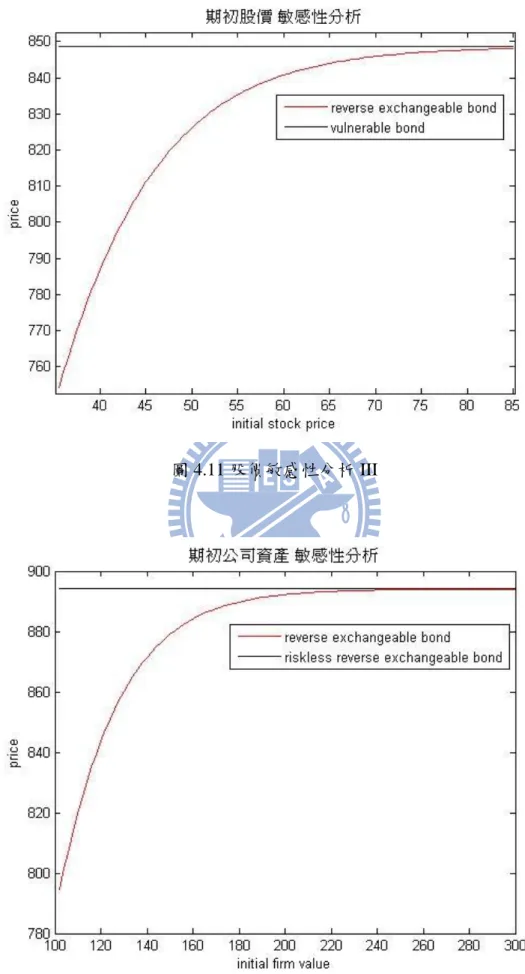
摘要 ... I ABSTRACT ... II 誌謝 ... III 目錄 ... IV 第一章 緒論 ... 1 第一節 研究動機與背景 ... 1 第二節 研究目的 ... 1 第三節 研究架構 ... 3 第二章 文獻回顧 ... 4 第一節 Klein (1996)有違約風險的選擇權評價公式 ... 4 第二節 模型的介紹 ... 6 第三節 論文相關定理 ... 7 第三章 研究方法 ... 10 第一節 定理介紹 ... 10 第二節 在首次通過模型下,有違約風險的選擇權之封閉解... 13 第三節 在 Merton 結構式模型下,有違約風險的下方出局障礙買權之封閉解 ... 22 第四章 模型結果分析 ... 36 第一節 特殊情況參數 ... 36 第二節 有違約風險之下出局買權評價公式與劉彥君 (2010)數值解比較 ... 38 第三節 敏感性分析-在首次通過模型下,有違約風險的買權 ... 39 第四節 敏感性分析-Merton 結構式模型下,有違約風險的下出局買權 ... 42第五節 敏感性分析 Reverse exchangeable bond 和 Barrier reverse convertibles... 46
第五章 結論以及後續研究 ... 53
第一節 結論 ... 53
第二節 後續研究 ... 53
V
表目錄
表 4.1 我們在特殊情況下的封閉解與 Black-Scholes 買權封閉解 ... 36 表 4.2 我們在特殊情況下的封閉解與下出局買權的封閉解 ... 37 表 4.3 我們在特殊情況下的封閉解與 Klein (1996)封閉解 ... 37 表 4.4 我們的封閉解與劉彥君 (2010)數值解... 38圖目錄
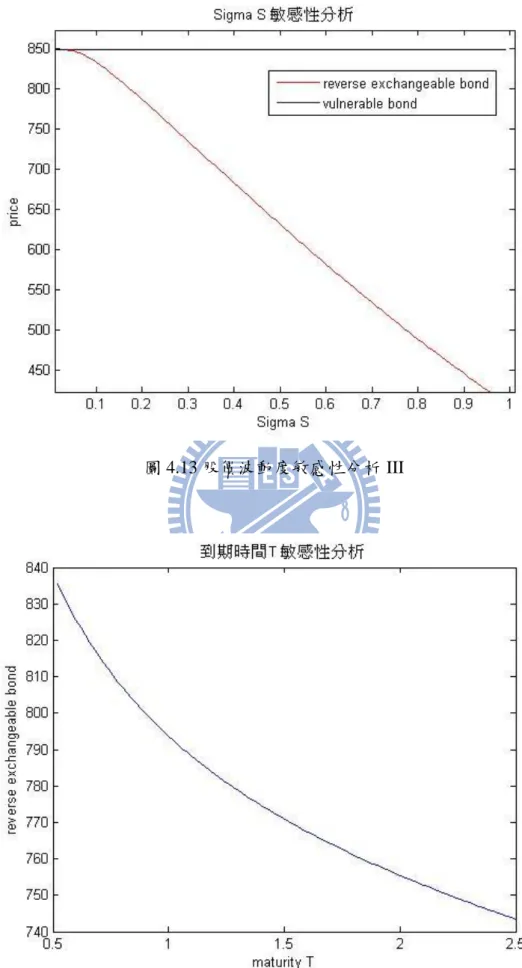
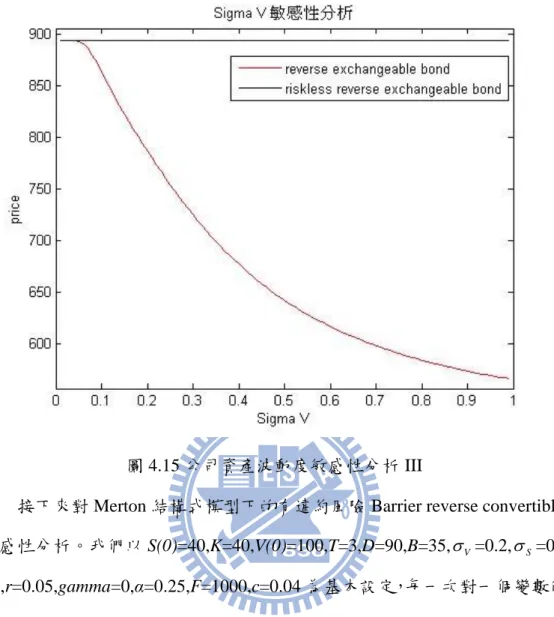
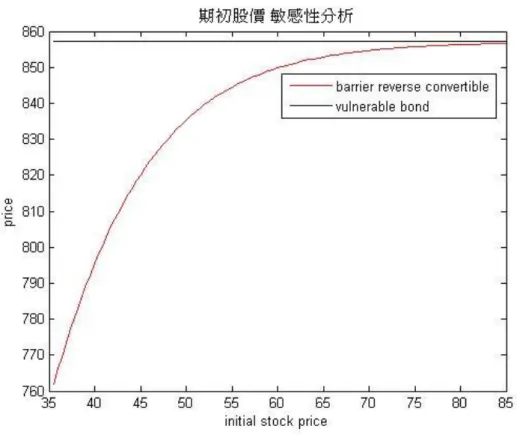
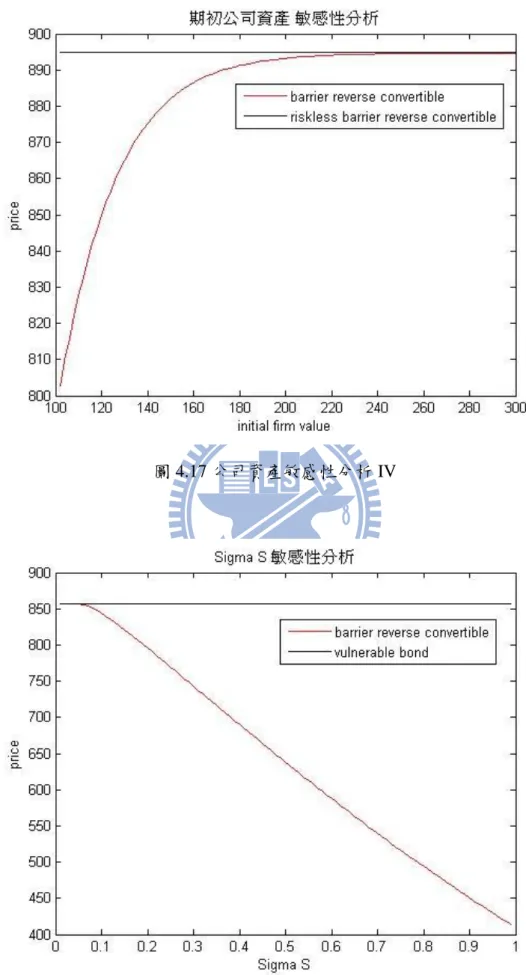
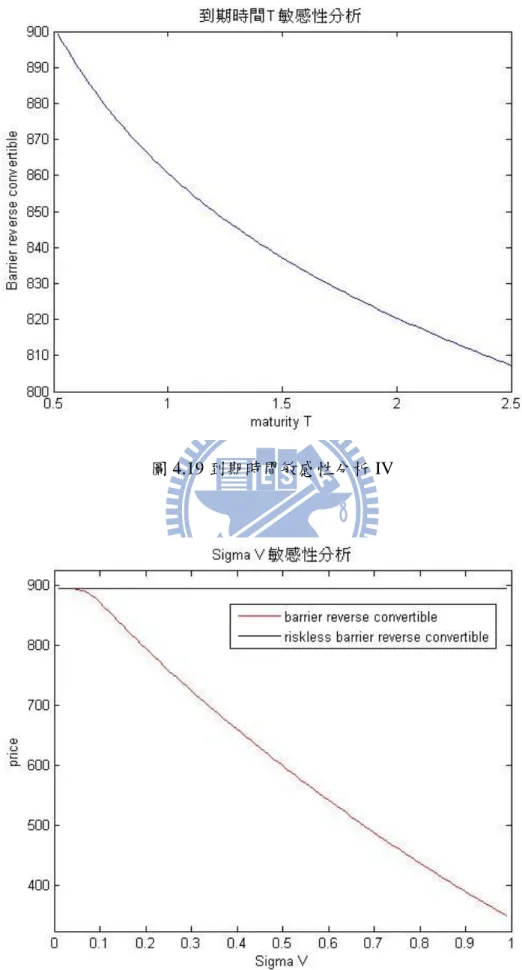
圖 1.1 FPM 下的公司資產與股票價格模擬圖 ... 2 圖 1.2 Merton 結構式模型下的公司資產與股票價格模擬圖... 2 圖 1.3 研究架構 ... 3 圖 2.1 模擬公司價值圖 ... 6 圖 2.2 布朗運動路徑反射圖 ... 7 圖 3.1 積分範圍 I ... 15 圖 3.2 積分範圍 III ... 25 圖 4.1 股價敏感性分析 I ... 40 圖 4.2 公司資產敏感性分析 I ... 40 圖 4.3 股價波動度敏感性分析 I ... 41 圖 4.4 到期時間敏感性分析 I ... 41 圖 4.5 公司資產波動度敏感性分析 I ... 42 圖 4.6 股價敏感性分析 II ... 43 圖 4.7 公司資產敏感性分析 II ... 44 圖 4.8 股價波動度敏感性分析 II ... 44 圖 4.9 到期時間敏感性分析 II ... 45 圖 4.10 公司資產波動度敏感性分析 II ... 45 圖 4.11 股價敏感性分析 III ... 47 圖 4.12 公司資產敏感性分析 III ... 47VI 圖 4.13 股價波動度敏感性分析 III ... 48 圖 4.14 到期時間敏感性分析 III ... 48 圖 4.15 公司資產波動度敏感性分析 III ... 49 圖 4.16 股價敏感性分析 IV ... 50 圖 4.17 公司資產敏感性分析 IV ... 51 圖 4.18 股價波動度敏感性分析 IV ... 51 圖 4.19 到期時間敏感性分析 IV ... 52 圖 4.20 公司資產波動度敏感性分析 IV ... 52
1
第一章 緒論
第一節 研究動機與背景 所謂有違約風險的選擇權(Vulnerable option),是指選擇權的賣方(Option writer)可能發生無法履行其義務的情況。一般在交易所交易的選擇權,在保證金 和結算的制度之下,違約發生的機率很非常小的,也就是其違約風險是可以忽略 的。然而在店頭市場(OTC)而言,若無相關的保證金制度亦無做避險的情況下, 違約風險是存在的。以歐式股票買權為例,若到期日為 T、S T( )為到期日股價、 履約價為 K,當到期日時標的股票價格高於履約價格,買權賣方就必須履行義務 支付S T( )K給予買權買方(Option holder);但若違約發生時,假定回收率為 (0 1) ,則買權買方只能拿到( ( )S T K),而不是S T( )K。 有違約風險的選擇權價值,其風險來自於交易對手的信用風險。選擇權的價 值,不僅取決於標的物價格,亦與交易對手是否會違約有關。在模型上,以交易 對手的公司資產是否低於公司負債來判定違約發生的情形。因此標的物價格與交 易對手公司資產決定了選擇權的價值。過去曾有幾位學者對有違約風險的選擇權 進行了研究。Klein (1996)定義 為破產成本、V T( )為在到期日時的公司資產、 D 為公司負債,並假定回收率 (1 ) ( ) /V T D,提出了在 Merton 結構式模型 下,有違約風險的選擇權之封閉解。而 Rich (1996)也提出在公司負債亦為隨機過 程的假設下,四種不同回收率的有違約風險的選擇權之評價封閉解。 第二節 研究目的我們考量在首次通過模型(First passage model, FPM)下,推導有違約風險的
選擇權封閉解。定義負債折現因子及公司到期日負債 L,若公司資產在到期日 之前的時間 t 時觸碰到負債門檻 (T t) Le ,或在到期日當天的公司價格低於公司 負債 D,則會發生違約。以圖 1.1 為例,由於公司資產在到期日之前皆高於負債 門檻 (T t) Le ,且到期日的公司資產亦高於公司負債 D,而到期日的股價也高於
2 D D ( ) S T ( ) S T 履約價格,因此交易對手不會發生違約,買方可以拿到S T( )K。我們再深入研 究其對偶問題:考量在 Merton 結構式模型下,推導有違約風險的障礙選擇權封 閉解。在 Merton 結構式模型下,只有在到期日的公司資產低於公司負債時,才 會發生違約。以圖 1.2 為例,雖然公司價值曾低於公司負債 D,但在到期日的公 司資產仍高於公司負債,因此不會發生違約,且到期日的股價也高於履約價格, 到期日前的股價高於障礙價格(即 ( ) ( ) T t S t Be ),所以買方可以拿到S T( )K。 該問題相當於將原有的有違約風險選擇權評價問題中,股價S t( )和公司資產V t( ) 的角色對調,並將原來對V t( )的負債門檻Le(T t)轉換成對S t( )的障礙價格 (T t) Be ,以修改有違約風險選擇權評價公式來評價。最後利用 Klein (1996)所提 出有違約風險的選擇權和 in-out parity,可以求得其他形式的障礙選擇權封閉解。 圖 1.1 FPM 下的公司資產與股票價格模擬圖 圖 1.2 Merton 結構式模型下的公司資產與股票價格模擬圖 公司資產 股票價格 T 障礙價格 (T t) Be L T K 公司資產 股票價格 T D T K B 負債門檻 (T t) Le
3 第三節 研究架構 本文主要研究的兩個對偶問題, 1. 在首次通過模型下,有違約風險的選擇權之封閉解。 2. 在 Merton 結構式模型下,有違約風險的障礙選擇權之封閉解。 研究架構如下: 圖 1.3 研究架構 首次通過模型 FPM 有違約風險的陽春買權 在價內且無違約的情況 T S K T V D , 0 t V L t T Merton 結構式模型 有違約風險的下方出局 障礙買權 在價內且無違約的情況 T V D T S K , 0 t S B t T 對偶 有違約風險的 下出局買權 有違約風險的 上出局買權 Klein (1996) 有違約風險 的選擇權評 價公式 In-out parity 有違約風險的 下入局買權 有違約風險的 上入局買權 S:股價 V:公司價格 K:履約價 D:公司負債 L:負債門檻 B:障礙價格 有違約風 險的買權 有違約風 險的賣權 評價 Reverse exchangeable bond 有違約風險的 下入局賣權 評價 Barrier Reverse convertibles 有違約風險的 上入局賣權 有違約風險的 上出局賣權 有違約風險的 下出局賣權
4
第二章 文獻回顧
本文評價有違約風險的選擇權為主。第一節介紹 Klein (1996)所提出的有違 約風險的選擇權評價公式。第二節介紹 Merton 的結構式模型以及首次通過模 型。第三節則介紹評價中所使用到的定理。 第一節 Klein (1996)有違約風險的選擇權評價公式 Klein 在 1996 年,推導有違約風險的選擇權之封閉解,其假設如下: 假設 1:公司價值和標的物價值服從下列的隨機過程, V V V S S S dV dt dZ V dS dt dZ S 其中V和S為公司和標的物期望的報酬,V和S為公司和標的物報酬 的變異數,ZV和ZS為存在著相關性的標準布朗運動。 假設 2:公司只在到期日 T 時,會發生違約的情形。違約與否取決於公司在到期 日的價值是否低於公司負債 D 為準,即V T( )D便違約。其中 D 為公司 不包含選擇權的其他負債,即 D 本身與選擇權的價值無關。 假設 3:假設回收率 (1 ) ( ) /V T D。由於 Klein 假定選擇權的 payoff 相較於 D 而言很小,因此當違約發生時,選擇權持有人依照 payoff 佔總負債比 例來分配扣除破產成本後的公司資產,即 ( ( ) ) ( ( ) ) (1 ) ( ) (1 ) ( ) ( ( ) ) (1 ) ( ) ( ( ) ) ( ( ) ) S T K S T K V T V T D S T K D V T S T K S T K D Klein 利用標的股票價格的 log 值與公司價格的 log 值是一個相關性為的
5 Klein (1996)推導的有違約風險的買權評價公式為: 0 1 2 3 4 ( ) 0 0 5 6 7 8 ( , , ) ( , , ) (1 ) ( S V ( , , ) ( , , )) (2.1.1) rT r T S N a a e KN a a V S e N a a KN a a D Klein (1996) 推導的有違約風險的賣權評價公式為: 0 3 4 7 8 ( ) 0 0 1 2 5 6 (1 ) [ ( , , ) ( , , )] (1 ) [ ( , , ) S V ( , , )] (2.1.2) rT rT r T V e K N a a e N a a D V S N a a e N a a D 其中 2 0 1 2 0 2 2 0 3 2 0 4 2 0 5 2 0 6 2 0 7 2 0 8 1 ln ( ) 2 1 ln ( ) 2 1 ln ( ) 2 1 ln ( ) 2 1 ln ( ) 2 1 ln ( ) 2 1 ln ( ) 2 1 ln ( ) 2 S S V S V V S S V V S S V S V S V V S S V S V S r T K a T V r T D a T S r T K a T V r T D a T S r T K a T V r T D a T S r T K a T V r T D a V T
6 第二節 模型的介紹 1. Merton 結構式模型 Merton(1974)考量違約的情形只有在到期日的時候發生,違約與否取決於公 司資產價值是否低於公司負債。在圖 2.1 中,公司負債為 D,由於藍線與綠 線所代表的公司資產在到期日皆高於負債 D,因此沒有發生違約;反之,紅 線與黑線則會發生違約。 圖 2.1 模擬公司價值圖 2. 首次通過模型
Black and Cox(1976)修正了 Merton 模型,允許公司在到期日之前的任何時間 點違約,違約與否取決於公司價值是否低於某個門檻。在圖 2.1 中,公司負 債為 D,負債門檻為 L,由於藍線與綠線所代表的公司資產不僅在到期日之 前皆高於門檻 L,且在到期日亦高於負債 D,因此沒有發生違約;而紅線雖 然在到期日之前都高於門檻 L,但在到期日卻低於負債 D,因此在到期日發 生違約;黑線則因在時間點 時的公司資產低於門檻 L,故在時間點 便發生 違約。
T
負債 D 門檻 L
公司資產7 第三節 論文相關定理 定理 2.1 反射定理(Harrison (1985)) 圖 2.2 布朗運動路徑反射圖 如圖 2.3,x軸為時間軸,y軸為標準布朗運動的值,固定x軸時間點t以 及y軸一個正值m,m為布朗運動觸碰到 m 的最小時間,我們想要計算在時間 t 之前,標準布朗運動觸碰到m的機率且在時間t,標準布朗運動小於w的機率 如下: { m , ( ) } P t W t w wm情況下,在m之後布朗運動路徑可由對 y m 鏡射至另外一個方向,經反 射之後t時間點布朗運動小於等於w的機率可視為布朗運動大於等於 2 -m w 的 機率: { m , ( ) } { ( ) 2 - } (2.3.1) P t W t w P W t m w 定義時間點t之前的布朗運動最大值如下: 0 ( ) max ( ) s t M t W s 如果m t,則也可表示成M t( )m,因此我們可以將(2.3.1)改寫成:
8 { m , ( ) } { ( ) , ( ) } { ( ) 2 - }, , 0 (2.3.2) P t W t w P M t m W t w P W t m w wm m 由(2.3.2),我們可以推導W t( )以及M t( )的聯合機率分配。 定理 2.2:當t0,(M t W t( ), ( ))的聯合機率分配為: 2 (2 ) 2 ( ), ( ) 2(2 ) ( , ) , , 0. (2.3.3) 2 m w t M t W t m w f m w e w m m t t 證明:因為(2.3.2)的左式寫成積分式如下: ( ), ( ) { ( ) , ( ) } w M t W t ( , ) m P M t m W t w f x y dydx
以及(2.3.2)的右式寫成積分式如下: 2 2 2 1 { ( ) 2 - } 2 z t m w P W t m w e dz t
使得左右兩式相等為: 2 2 ( ), ( ) 2 1 ( , ) 2 z w t M t W t m f x y dydx t m we dz
對左右兩邊對m微分,求得: 2 (2 ) 2 ( ), ( ) 2 ( , ) . 2 m w w t M t W t f m y dy e t
再對兩邊同微w求得: 2 (2 ) 2 ( ), ( ) 2(2 ) ( , ) . 2 m w t M t W t m w f m w e t t 得證之。定理 2.3 (Girsanov, one dimension): 令W t( ),0 t T ,是在機率空間( , , ) F P
上的一個布朗運動,對於W t( )存在一個 filtration F t( )。另外 0 t T 時,存在
9 2 0 0 0 1 ( ) exp{ ( ) ( ) ( ) }, (2.3.4) 2 ( ) ( ) ( ) (2.3.5) t t t Q t u dW u u du W t W t u du
以及假設 2 2 0 ( ) ( ) T E
u Z u du 則在機率測度P下,隨機過程W t( )在 0 t T 屬於一個標準布朗運動。 其中對所有 A F , ( ) ( ) ( ) ( ) ( ) ( ) (2.3.6) ( ) A A A d P w P A d P w dP w Q w dP w dP w
10
第三章 研究方法
本章節討論在首次通過模型下,有違約風險的選擇權之封閉解。並進一步 研究其對偶問題-在 Merton 結構式模型下,有違約風險的障礙選擇權之封閉解。 並延伸到 Reverse exchangeable bond 和 Barrier reverse convertibles 的評價。首先 假設股票價格與公司價格為一隨機過程,負債門檻與障礙價格為和時間有關的指 數函數。利用反射定理與 Girsanov 定理求得聯合機率分配函數,進而積分計算 有違約風險的選擇權價格。 第一節 定理介紹 引理 3.1:對於任意可表達成下式的雙重積分式 2 2 2 2 1 1 exp{ [ 2 2 2 ]} (3.1.1) 2(1 ) 2 1 a b z w pz qw zw dzdw
我們都可以將其改寫成二元常態分配的累積分配函數(cdf)的形式 2 2 2 2 1 1 exp{ [( ) ( ) 2 ( )( )]} 2(1 ) 2 1 a b R z c w d z c w d dzdw
其中 2 2 2 1 exp{ ( 2 )} 2(1 ) R c d cd 。 由於 2 2 2 2 2 2 ( ) ( ) 2 ( )( ) 2( ) 2( ) 2 ( 2 ) (3.1.2) z c w d z c w d z w c d z d c w zw c d cd 根據(3.1.1)與(3.1.2)比較係數,可以得到p q c d, , , 的關係如下: c d p d c q 11 定理 3.2:令k x, , , , , T m n,則 1. 2 2 2 2 2 ( ) 2 2 2 1 1 ( , , ) 2 z w m n T k mz nw T T x w k e dzdw e N d c T T
2. 2 2 2 2 2 ( ) 2 2 2 1 1 ( , , ) 2 z w m n T k x w mz nw T T k e dzdw e N d c T T
其中 2 2 1 (1 ) c x n T m T T d n T 證明: 我們對第 1 式做證明,第 2 式與第 1 式雷同。 首先我們對變數做 Jacobian 變數變換, 令 2 1 2 1 1 [ ( )] 1 , 1 z z x w T w w T 則 2 1 2 1 1 1 1 , T T z z x w w T w 2 2 1 1 2 2 1 1 1 1 | | | | | | | | 1 1 0 z z T T z w T T J w w T z w 因此 2 2 2 2 2 1 2 1 1 2 2 2 1 0 1 1 1 1 1 2 2 2 1 2 ( ) 1 1 1 exp{ 2 2 2 ( ) } 1 1 1 z w k mz nw T T x w k T e dzdw T T T z x w Tw T T T T T T m z x w n T w dz dw
12 2 2 2 2 2 2 1 1 1 2 2 0 2 2 2 1 1 1 1 1 1 1 1 exp{ [ 2( (1 ) ) 2(1 ) 2 1 1 2( (1 ) (1 ) ) 2 ]} x k mx T T e z w x m T z T x m T n T w z w dz dw T
(根據引理 3.1) 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 1 (1 ) 1 (1 ) (1 ) 1 (1 ) 2 (1 ) 2 (1 ) (1 ) (1 ) c d x m T T d c x m T n T T c x n T m T T d n T x c d cd xm m T n T T 2 2 2 2 2 2 2 2 2 2 1 1 2 2 0 1 1 1 1 1 1 exp{ [( ) ( ) 2(1 ) 2 1 2 ( )( )]} x x m T n T k mx mx T T T e z c w d z c w d dz dw
(令 2 1 2 1 z z c w w d ) 2 2 ( ) 2 2 2 2 2 2 2 2 2 2 2 1 1 exp{ [ 2 ]} 2(1 ) 2 1 m n T k d T c e z w z w dz dw
(令z3 z2, dz3 dz2) 2 2 2 2 ( ) 2 2 2 3 2 3 2 3 2 2 2 ( ) 2 1 1 exp{ [ 2 ]} 2(1 ) 2 1 ( , , ) m n T k d c T m n T e z w z w dz dw k e N d c T
得證之。13 第二節 在首次通過模型下,有違約風險的選擇權之封閉解 定義第一個資產-公司價格在風險中立機率測度P下,服從下列隨機過程: 2 1 ( - ) ( ) 2 ( ) (0) r V t VW t , 0 (3.2.1) V t V e t T 第二個資產-股票價格在風險中立機率測度下,服從下列的隨機過程: 2 2 1 ( - ) ( ( ) 1 ( )) 2 ( ) (0) r S t S W t Z t , 0 (3.2.2) S t S e t T 其中為V 與 S 間的相關係數,且W t( )與Z t( )獨立。並定義負債門檻 ( ) ( ) T t , 0 L t Le t T。那麼,在首次通過模型下,有違約風險的買權要在價內 且不發生違約事件,需滿足: ( ) , (3.2.3) ( ) , ( S T K V T D 3.2.4) 和V t( )L t( ), 0 t T (3.2.5)。 我們可以將(3.2.5)改為 2 2 0 1 ( ) ( ) 2 ( ) 0 1 ( ) ( ) 2 0 ( ) min 1 ( ) (0) min 1 min (3.2.6) (0) V V V V t T r t W t T t t T r t W t T t T V t L t V e Le L e e V 令 1 2 ( ) ( ) ( ) 2 V V V r t W t W T , 2 1 1 ( ) 2 V V V r ,使得 W t( )Vt W t( )。並定義 0 M( ) max ( ) t T T W T , 則(3.2.6)可以寫成 ( ) 0 ( ) min (0) (0) 1 ( ) (ln ) (3.2.7) (0) V V W t T t T M T T V L e e V L e e V L M T T l V
14 在到期日 T 的公司價格和股票價格可用 ( )W T 表達如下: 2 2 2 2 1 ( ) ( ) 2 1 1 ( ) ( ) ( ) 2 2 ( ) 1 ( ) [ ( 2 ( ) (0) (0) (0) (3.2.8) ( ) (0) V V V V V V S S r T W T r T r T W T T W T r T W V T V e V e V e S T S e 2 2 2 2 2 ) 1 ( )] 1 ( ) [ ( ( )) 1 ( )] 2 1 ( ) ( ) 1 ( ) 2 (0) (0) (3.2.9) S S V S S V S S T Z T r T T W T Z T r T W T Z T S e S e 因此(3.2.3)和(3.2.4)可以寫成 2 2 ( ) 1 ( ) ( ) 1 ( ) 2 2 ( ) (0) 1 ( ) (ln ) (3.2.10) (0) ( ) (0) 1 ( ) ( ) 1 2 V S S V S S T W T V r T W T Z T S S V S S V T D V e D D W T T d V S T K S e K r T W T 2 2 2 2 2 ( ) ln (0) 1 1 ( ) [ln ( ) ] ( ) (0) 2 1 1 ( ) ( ) (3.2.11) 1 S S V S K Z T S K Z T r T W T S Z T y W T 其中 2 2 1 1 [ln ( ) ] (3.2.12) (0) 2 1 S S V S K y r T S 假定回收率為 ,在首次通過模型下,若買權沒有違約發生,則買方可以拿到 ( ( )S T K)。若違約在到期日 T 發生,則買方拿到( ( )S T K)。若違約在 T 發生,則買方拿到買權在時間 的價值 ( ) [ r T ( ( ) ) | ] E e S T K F 。因此, 根據風險中立定價理論,我們知道在首次通過模型下,有違約風險的買權可以寫 為
15 { } { } ( ) { } { } { } [ ( ( ) ) ] [ ( ( ) ) ] [ [ ( ( ) ) | ] ] [ (1 )] [ ( ( ) ) ] [ ( ( ) ) ] rT rT
not default default at T
r r T
default at
rT rT
not default default at T
C E e S T K I E e S T K I E e E e S T K F I E e S T K I E e S T K I 0 0 { } { min ( ) ( ), ( ) } { min ( ) ( ), ( ) , ( ) } [( ( ) ) ] (1 ) [( ( ) ) ] [( ( ) ) ] (1 ) [( ( ) ) ] [( ( ) ) ] (1 t T t T rT default at rT rT V t L t V T D rT rT V t L t V T D S T K rT e E S T K I e E S T K I e E S T K e E S T K I e E S T K e 2 { ( ) , ( ) , ( ) ( ) 1 ) [( ( ) ) ] [( ( ) ) ] (1 ) [( ( ) ) ] [( ( ) ) ] (3.2.13) rT M T l W T d Z T y W T rT rT C E S T K I e E S T K e E S T K I e E S T K 其中 2 { ( ) , ( ) , ( ) ( ) 1 C M T l W T d Z T y W T I I 為指標函數,若 ( )M T l, ( )W T d且 2 ( ) ( ) 1 Z T y W T ,則IC 1;否則IC 0。 由於(3.2.13)式的E S T[( ( )K) ] 部分可以用 Black-Scholes 的買權訂價公式 帶入,因此只需求解 [( ( )E S T K I) C]的部分。現在考慮IC的積分範圍,由於 l 恆 大於 0,而 d 可正可負,因此積分範圍分為兩種情況,若 0 d l,則積分範圍 如圖 3.1 所示。若d 0 l,則積分範圍如圖 3.2 所示。綜合兩種積分範圍情況, 我們可以將積分範圍寫成 {( , ); m w w m l, - w d} (3.2.14) 圖 3.1 積分範圍 I 圖 3.2 積分範圍 II 接著我們需要 M T W T Z T 的聯合機率分配函數,由於 ( ),( ), ( ) (M T W T( ),( ))與
16 ( ) Z T 獨立,所以 M T W T Z T 的聯合機率分配函數等於 ( ),( ), ( ) M T W T 的聯合( ),( ) 機率分配函數乘上Z T ( )的機率分配函數,即 ( ), ( ), ( )( , , ) ( )( ) ( ), ( )( , ) (3.2.15) M T W T Z T Z T M T W T f m w z f z f m w 定義測度P,使得 ( )W t 在P下是沒有飄移項的布朗運動,根據定理 2.1-反射定 理,可以找到 (M T W T( ),( ))在P下的聯合機率分配函數為 2 (2 ) 2 ( ), ( ) 2(2 ) ( , ) , , 0 (3.2.16) 2 m w T M T W T m w f m w e w m m T T 而 W t( )Vt W t( ),且W t( )與W t( )具有相同的機率分配函數,利用定理 2.3-Girsanov 定理,我們定義測度轉換因子 ( ) 1 2 ( ( )) 1 2 ( ) 1 2 2 2 2 ( ) VW t Vt V Vt W t Vt VW t Vt, 0 Q t e e e t T 根據(2.3.6), 2 1 ( ) 2 ( ) ( ) ( ) VW T VT ( ) A A P A
Q T d P T
e d P T 而 2 1 ( ) 2 ( ) 1 ( ) ( ) ( ) ( ) ( ) ( ) ( ) VW T VT A A A A d P T P A d P T d P T d P T e d P T Q T d P T
找到 (M T W T( ),( ))在P下的聯合機率分配函數為 2 2 1 (2 ) 2 2 ( ), ( ) 2(2 ) ( , ) , , 0 (3.2.17) 2 V V m w w T T M T W T m w f m w e w m m T T 另外在P下,Z T ( )服從期望值為 0,變異數為 T 的常態分配,因此Z T ( )的機率 分配函數為 2 2 ( ) 1 ( ) , - (3.2.18) 2 z T Z T f z e z T 由(3.2.17)和(3.2.18)求得 M T W T Z T 在( ),( ), ( ) P下的聯合機率分配函數為17 2 2 2 1 (2 ) 2 2 2 1 2(2 ) , - , , 0 (3.2.19) 2 2 V V z m w w T T m w T e e z w m m T T T 再由(3.2.14)和(3.2.19),我們對 [( ( )E S T K I) C]求解。 2 2 2 2 2 2 2 2 1 ( ) ( ) 1 ( ) 2 { ( ) , ( ) , ( ) ( )} 1 1 ( ) 1 2 2 1 1 2 [ ( ) ] [ (0) ] 1 (0) 2 2(2 ) 2 S S V S S S S V S S V V C r T W T Z T M T l W T d Z T y W T z r T d l w z T y w w w T E S T I E S e I S e e e T m w e T T
2 2 2 2 2 2 2 2 2 2 2 (2 ) 2 1 1 ( ) 1 2 2 2 1 (2 ) 2 1 1 ( ) 1 2 2 2 1 1 (0) 2 2(2 ) ( ) 2 1 (0) 2 S S V V S S V S S V V S S V m w T z r T T d w z w T y w m w l T w z r T T w z w T y dmdzdw S e e T m w e dm dzdw T T S e e T
2 2 2 2 2 2 2 2 2 2 2 (2 ) 2 1 1 ( - ) 1 2 2 2 2 1 (2 ) 1 2 2 1 ( | ) 1 (0) ( 2 1 2 S S V V S S V S S V m w d m l T m w w z w r T T d w z w T T y w z l w w z w T T y e dzdw S e e dzdw T e dzdw T
2 2 2 2 2 2 2 2 2 2 2 2 1 1 ( - ) 1 2 2 2 2 1 2 2 1 2 2 1 ) 1 (0) ( 2 1 ) 2 S S V V S S V S S V d w z w r T T d w z w T T y w l z lw w d w z w T T T T y w S e e dzdw T e e dzdw T
(前半部的積分令 2 1 , S V S m n ,後半部的積分令 2 1 , S m 2 V S l n T ,再根據定理 3.2) 2 2 2 2 2 2 1 1 1 1 ( - ) 2 2 2 2 1 1 1 1 2 2 2 2 2 2 (0) ( ( , , ) ( , , )) S S V V S V S V S V S V V S r T T T T T T T T l l d S e e N h g T d e N h g T 18 2 2 1 1 2 2 (0) rT ( d , , ) (0) rT Vl l S ( d , , ) (3.2.20) S e N h g S e N h g T T 其中 2 1 1 1 , (3.2.21) V S S V g y T T h T T T 2 2 2 1 2 2 , V S S V l l g y T T h T T T T T 2 2 2 2 2 2 2 2 2 2 2 2 1 (2 ) 2 2 2 1 1 (2 ) 2 2 2 2 2 1 1 [ ] ( ( ) , ( ) , ( ) ( )) 1 1 2(2 ) 2 2 1 1 ( 2 2 V V V V V C z m w d l w T T T y w w z w z l w T d w w T T T T y w y w E K I K P M T l W T d Z T y W T m w K e e dmdzdw T T T Ke e dzdw e T T
2 2 2 1 1 1 2 2 2 2 3 3 4 4 2 3 3 4 4 ) [ ( , , ) ( , , )] ( , , ) ( , , )] (3.2.22) V V V V V d T T T l l dzdw d d Ke e N h g e N h g T T d d KN h g e KN h g T T
其中 2 3 3 1 , (3.2.23) V V g y T h T T 2 4 4 1 2 2 + , V V l l g y T h T T T T 所以,在首次通過模型下,有違約風險的買權在時間 0 的價值為 2 2 1 1 2 2 2 3 3 4 4 1 3 (1 ){ (0) ( , , ) (0) ( , , ) ( , , ) ( , , )]} [ (0) ( ) ( )] V S V l l rT l rT rT d d C S N h g S e N h g T T d d Ke N h g e KN h g T T S N g Ke N g (3.2.24) 且將(3.2.12)式代回的g1,根據(3.2.21),我們可以得到19 2 1 2 2 2 2 2 2 1 { } 1 1 1 { [ln ( ) ] } (0) 2 1 1 (0) 1 [ln ( ) ] 2 1 (0) 1 [ln ( ) ] 2 V S S S V V S S S S V S V S S S S g y T T T K r T T T S T S r T T T K T S r T K T 與 Black-Scholes 訂價公式的d1相同。而將(3.2.12)式代回g3,根據(3.2.23)得 2 3 2 2 2 2 1 { } 1 1 1 { [ln ( ) ] } (0) 2 1 1 (0) 1 [ln ( ) ] 2 V S S V V S S S g y T T K r T T S T S r T K T 與 Black-Scholes 訂價公式的d2相同。而 2 2 2 1 2 1 1 2 [ln ( ) ] (0) 2 V S S S l K l g y T T r T T T T S T 2 2 4 1 2 1 1 2 + [ln ( ) ] (0) 2 V S S l K l g y T r T T T T S T 當 D→0 且 L→0 時, 0 0 1 lim lim[ (ln )] (0) D D V D d T V 0 0 1 lim lim[ (ln )] (0) L L V L l T V 2 2 0 2 0 2 1 1 2 lim lim{ [ln ( ) ] } (0) 2 1 1 2 [ln ( ) ] lim (0) 2 1 1 2 [ln ( ) ] (0) 2 S L l S S L S S S K l g r T S T T K r T l S T T K r T S T T
20 2 4 0 0 2 0 2 1 1 2 lim lim{ [ln ( ) ] } (0) 2 1 1 2 [ln ( ) ] lim (0) 2 1 1 2 [ln ( ) ] (0) 2 S L L S S L S S S K l g r T S T T K r T l S T T K r T S T T 1 1 1 1 0 lim ( , , ) ( , , ) ( ) D d N h g N g N g T 2 2 2 0 lim ( , , ) ( , , ) 0 L d d N h g N h T T 3 3 3 3 0 lim ( , , ) ( , , ) ( ) D d N h g N g N g T 4 4 4 0 lim ( , , )] ( , , )] 0 L d d N h g N h T T 因此,在 D→0 且 L→0 下,首次通過模型的有違約風險買權在時間 0 的價值 2 2 2 1 3 0, 0 1 3 1 3 lim (1 ){ (0) ( ) (0) 0 ( ) 0} [ (0) ( ) ( )] (0) ( ) ( ) Vl l S rT rT Vl D L rT rT C S N g S e Ke N g e K S N g Ke N g S N g Ke N g (3.2.25) 即 Black-Scholes 的買權訂價公式。 同樣的,我們也可求出在首次通過模型下,有違約風險的賣權在時間 0 的價值 2 3 3 4 4 2 2 1 1 2 2 3 1 (1 ){ ( , , ) ( , , )] (0) ( , , ) (0) ( , , ) } [ ( ) (0) ( )] V V S rT l rT l l rT d d P e KN h g e KN h g T T d d S N h g S e N h g T T Ke N g S N g (3.2.26) 接下來,我們延伸這一小節的方法,利用首次通過模型下,對有違約風險 的賣權來對有違約風險的 Reverse exchangeable bond 做評價。Reverse
exchangeable bond 是由債券和賣權兩部分資產所組成(即買債券並賣賣權),其中 賣權的履約價格,即為標的股票的起始價格。如果到期日之標的股票價格是在起 始價格以上,則投資人可在拿回本金與利息;但若標的股票價格在到期日是低於
21
起始價格,投資人在到期日則是拿回股票與利息。現在,我們想求在首次通過模 型下,有違約風險的 Reverse exchangeable bond 價值,即有違約風險的債券減去 有違約風險的陽春賣權。而有違約風險的陽春賣權可以由本小節前面所證的結果 代入,所以我們只需求解有違約風險的債券。假定債券票面價值為 F,票面息率 c,且債息在到期日支付,則有違約風險的債券價值為 { } { } { } { } { } [ ( ) ] [ ( ) ] [ ( ) ] [ (1 )] [ ( ) ] [ ( ) ] [( rT rT
not default default at T
rT
default at
rT rT
not default default at T
rT VB E e F FcT I E e F FcT I E e F FcT I E e F FcT I E e F FcT I e E F F 0 0 { } { min ( ) ( ), ( ) } { min ( ) ( ), ( ) } { ( ) , ( ) ) ) ] (1 ) [(( ) ] ( ) (1 ) [( ) ] ( ) (1 ) [( ) ] ( t T t T default at rT rT V t L t V T D rT rT V t L t V T D rT rT M T l W T d cT I e E F FcT I e F FcT e E F FcT I e F FcT e E F FcT I e F FcT ) (3.2.27) 根據(3.2.14)與(3.2.17)可以得知 2 2 2 2 2 2 1 (2 ) 2 2 { ( ) , ( ) ) 1 (2 ) 2 2 1 (2 ) 2 2 2(2 ) [ ] 2 1 2(2 ) ( ) 2 1 ( | 2 V V V V V V m w d l w T T M T l W T d w m w d w T l T w m w w T m T m w m w E I e dmdw T T m w e e dm dw T T e e T
2 2 2 2 2 2 1 1 (2 ) 2 2 2 2 ( ) [ ( 2 )] 2 2 2 ) 1 1 2 2 1 1 2 2 V V V V V V V d l w l w d w T d w T T T w T w T l d d l T T dw e dw e dw T T e dw e e dw T T
(前者積分令 1 V w T w T ,後者積分令 2 w ( VT 2 )l w T ) 2 2 1 ( 2 ) 2 2 2 2 1 2 2 1 1 2 2 ( 2 ) ( ) ( ) V V V V d T w d T l w l T T l V V e dw e e dw d T d T l N e N T T
帶回(3.2.27)可得在首次通過模型下,有違約風險的債券價值為 2 ( 2 ) (1 )( )[ ( ) Vl ( )] ( ), (3.2.28) rT d VT d VT l rT e F FcT N e N e F FcT T T 22
因此,在首次通過模型下,有違約風險的 Reverse exchangeable bond 價值為
有違約風險的債券減去有違約風險的陽春賣權=(3.2.28)- F(3.2.26) K 。 第三節 在 Merton 結構式模型下,有違約風險的下方出局障礙買權之封閉解 定義第一個資產-股票價格在風險中立機率測度P下,服從下列隨機過程: 2 1 ( ) ( ) 2 ( ) (0) r S t SW t , 0 (3.3.1) S t S e t T 第二個資產-公司價格在風險中立機率測度下,服從下列的隨機過程: 2 2 1 ( ) ( ( ) 1 ( )) 2 ( ) (0) r V t V W t Z t , 0 (3.3.2) V t V e t T 其中為V 與 S 間的相關係數,且W t( )與Z t( )獨立。 並定義障礙價格 ( ) ( ) T t , 0 B t Be t T。那麼,在 Merton 結構式模型下,有違 約風險的下方出局障礙買權在價內且不發生違約事件,需滿足: ( ) , (3.3.3) ( ) , (3.3.4) ( S T K V T D S ) ( ), 0 (3.3.5) t B t t T 我們可以將(3.3.5)改為 2 2 0 1 ( ) ( ) 2 ( ) 0 1 ( ) ( ) 2 0 ( ) min 1 ( ) (0) min 1 min (3.3.6) (0) S S S S t T r t W t T t t T r t W t T t T S t B t S e Be B e e S 令 1 2 ( ) ( ) ( ) 2 S S S r t W t W T , 2 1 1 ( ) 2 S S S r ,使得 W t( )St W t( )。並定義 0 M( ) max ( ) t T T W T , 則(3.3.6)可以寫成
23 ( ) 0 ( ) min (0) (0) 1 ( ) (ln ) (3.3.7) (0) S S W t T t T M T T S B e e S B e e S B M T T b S 到期日 T 的股票價格和公司價格可用 ( )W T 表達如下: 2 2 2 2 1 ( ) ( ) 2 1 1 ( ) ( ) ( ) 2 2 ( ) 1 ( ) [ ( 2 ( ) (0) (0) (0) (3.3.8) ( ) (0) S S S S S S V V r T W T r T r T W T T W T r T W S T S e S e S e V T V e 2 2 2 2 2 ) 1 ( )] 1 ( ) [ ( ( )) 1 ( )] 2 1 ( ) ( ) 1 ( ) 2 (0) (0) (3.3.9) V V S V V S V V T Z T r T T W T Z T r T W T Z T V e V e 因此(3.3.3)和(3.3.4)可以寫成 2 2 ( ) 1 ( ) ( ) 1 ( ) 2 2 ( ) (0) 1 ( ) (ln ) (3.3.10) (0) ( ) (0) 1 ( ) ( )) 1 2 S V V S V V T W T S r T W T Z T V V S V V S T K S e K K W T T k S V T D V e D r T W T 2 2 2 2 2 ( ) ln (0) 1 1 ( ) [ln ( ) ] ( ) (0) 2 1 1 ( ) ( ) (3.3.11) 1 V V S V D Z T V D Z T r T W T V Z T x W T 其中 2 2 1 1 [ln ( ) ] (0) 2 1 V V S V D x r T V 。 根據風險中立定價理論,我們知道在 Merton 結構式模型下,有違約風險的下方 出局障礙買權可以寫為
24 0 0 { ( ) , min ( ) ( ), ( ) } { ( ) , min ( ) ( ), ( ) } [ (( ( ) ) ( ( ) ) (1 ) ( ) )] t T t T rT V T D S t B t S T K V T D S t B t S T K E e S T K I S T K V T I D 2 2 2 2 ( ) { ( ) ( ), ( ) , ( ) } 1 1 ( ) ( )) 1 ( ) 2 ( ) { ( ) ( ), ( ) , ( ) 1 [ (( (0) ) (1 ) (0) ( (0) ) S V V S V V S T W T rT Z T x W T M T b W T k r T W T Z T T W T Z T x W T M T b W T E e S e K I V e S e K I D } 1 2 3 4 )] [ ] k rT T T e E e I I e I I 其中 2 2 ( ) 1 { ( ) ( ), ( ) , ( ) } 1 2 { ( ) ( ), ( ) , ( ) } 1 [ (0) ] [ SW T Z T x W T M T b W T k Z T x W T M T b W T k I E S e I I E K I 2 2 2 2 2 1 ( ) ( ) 1 ( ) ( ) 2 3 { ( ) ( ), ( ) , ( ) } 1 1 ( ) ( ) 1 ( ) 2 4 (1 ) [ (0) (0) )] (1 ) [ (0) V V S V V S V V S V V r T W T Z T W T Z T x W T M T b W T k r T W T Z T I E V e S e D I I E V e K D 2 { ( ) ( ), ( ) , ( ) } 1 )] Z T x W T M T b W T k I 我們考慮積分範圍,由於b0,而k0或k0,因此積分範圍分為兩種情 況,若 0 k b ,則積分範圍如圖 3.2 所示。若k 0 b,則積分範圍如圖 3.3 所示。綜合兩種積分範圍情況,我們可以將積分範圍寫成 {( , ); m w w m b, - w k} (3.3.12)
25 圖 3.2 積分範圍 III 圖 3.3 積分範圍 V 接著我們根據(3.2.16)與定理 2.3-Girsanov 定理,由於 W t( )St W t( ),定 義測度轉換因子 ( ) 1 2 ( ( )) 1 2 ( ) 1 2 2 2 2 ( ) SW t St S St W t St SW t St, 0 Q t e e e t T 我們得到 2 1 ( ) 2 ( ) 1 ( ) ( ) ( ) ( ) ( ) ( ) ( ) SW T ST A A A A d P T P A d P T d P T d P T e d P T Q T d P T
找到 (M T W T( ),( ))在P下的聯合機率分配函數為 2 2 1 (2 ) 2 2 ( ), ( ) 2(2 ) ( , ) , , 0 (3.3.13) 2 S S m w w T T M T W T m w f m w e w m m T T 則 M T W T Z T 在( ),( ), ( ) P下的聯合機率分配函數為 2 2 2 ( ), ( ), ( ) ( ) ( ), ( ) 1 (2 ) 2 2 2 ( , , ) ( ) ( , ) 1 2(2 ) , - , , 0 (3.3.14) 2 2 S S M T W T Z T Z T M T W T z m w w T T T f m w z f z f m w m w e e z w m m T T T 再由(3.3.12)和(3.3.14),我們可以對I I I I1, 2, 3, 4逐一積分求解。26 2 2 2 2 2 2 2 2 2 ( ) 1 { ( ) ( ), ( ) , ( ) } 1 1 (2 ) 2 2 2 1 1 (2 ) 2 2 2 1 [ (0) ] 1 2(2 ) (0) 2 2 1 2(2 ) (0) ( 2 S S S S S S S W T Z T x W T M T b W T k z m w k b w w T T T x w w z m w T k w w b T x w w I E S e I m w S e e e dmdzdw T T T m w S e e e T T
2 2 2 2 2 2 2 2 2 2 2 1 (2 ) 2 2 2 1 1 2 2 2 1 1 (2 ) 2 2 2 ) 1 (0) ( | ) 2 1 (0) 2 1 (0) 2 S S S S S S S S S T z m w T k w w m b T T m w x w z w T k w w T T x w z b w T w w T T x dm dzdw S e e e dzdw T S e e dzdw T S e e T
2 1 k w dzdw
(根據定理 3.2) 2 2 2 2 2 2 1 1 1 2 2 2 1 1 1 1 1 2 2 2 2 2 2 2 (0) ( , , ) (0) ( , , ) S S S S S S S S S S S S T T T T T T T T b b k S e e N d c T k S e e N d c T 2 2 1 2 1 1 1 2 2 2 2 2 (0) ( , , ) (0) ( , , ) (3.3.15) S S S S S S S S T T T T b b k S e N d c T k S e N d c T 其中 2 1 1 1 , S S S S c x T T d T T T 2 2 2 1 2 2 , S S S S b b c x T T d T T T T T 2 2 2 2 2 2 2 2 2 2 { ( ) ( ), ( ) , ( ) } 1 1 (2 ) 2 2 2 1 1 (2 ) 2 2 2 1 [ ] 1 2(2 ) 2 2 1 2(2 ) ( ) 2 S S S S Z T x W T M T b W T k z m w k b w T T T x w w z m w T k w b T T x w w I E K I m w K e e dmdzdw T T T m w Ke e e dm dzdw T T
27 2 2 2 2 2 2 2 2 2 2 2 2 1 (2 ) 2 2 2 1 1 2 2 2 1 1 (2 ) 2 2 2 1 1 ( | ) 2 1 2 1 ) 2 S S S S S S z m w T k w m b T T m w x w z w T k w T T x w z b w T k w T T x w Ke e e dzdw T Ke e dzdw T Ke e dzdw T