正方體的截面 馮振業 香港教育學院數學與資訊科技學系 引言

正方體的截面

馮振業

香港教育學院數學與資訊科技學系

引言

目前香港小學六年級的課程，包括「認識柱體、錐體和球體的不同截 面」（香港課程發展議會，2000，頁 44）。這課題對提高學生的空間想像力 很有幫助，不過要教得出色卻十分困難。難處之一在於教師自己也不清楚 截面可能出現哪些平面圖形，以及在怎樣的切割方向下出現；難處之二在 於不知如何協助學生理解三維空間的幾何體，以至它們之間的關係。三類 立體圖形以球體最簡單，全部截面都是圓形，只是半徑大小不同而已。其 餘柱體和錐體，都夾雜不少變化，非三言兩語可以說得明白。本文收窄討 論範圍，集中考慮角柱體的一個非常特殊的情況 —— 正方體。

試誤找出正方體的截面

如果我們沒有豆腐、涼粉或芝士磚等可供刀子輕易切開的東西，就很 難藉真實的切割找到正方體的截面。沒有了真實的切割，各人憑空想像，

確認答案的步驟，便欠缺了客觀的標準。有些人採用以液體注入透明正方 體的方法來講解，那不失為權宜之計，然而，要以此探討所有情況，就得 不時調整液體的體積，相當費時。再者，肉眼從液體表面看出來的截面，

其幾何特性不易檢測，最後可能流於權威說了作實。

這裡介紹立體動態幾何軟件 Cabri 3D^®（2.0 版），或許可以克服上述困 難。在這個動態平台上，除了可以直接揭示角柱體的截面，還可幫助探討 切割位置的改變對截面形狀的影響。例如以圖 1 的平面切割正方體，就可 以 Cabri 3D^® 展示切割得出的截面（圖 1A）。如果切割平面由圖 2 的三個黑 點定義，只要移動這些點，就會看到切割平面隨之改變（圖 3、4），所得 的截面亦相應地改變（圖 2A、3A、4A）。最有趣的，就是可以看清這個變 化的過程，而非只是看到硬照。軟件還容許改變觀察角度（圖 2B、3B、4B）， 讓大家可以自由地看個清楚明白。有時或許需要測量長度或角度，以檢定 圖形的屬性。軟件備有測量選單，可得出長度和角度（圖 8B、10B、11B、

12A）。為了方便解說，本文的其他截面硬照，都以三個黑點定義切割平面，

而且以圖 mA 表示圖 m 的相應截面，圖 mB 表示改變視點後的圖 mA。

圖 1 圖 1A

圖 2 圖 3 圖 4

圖 2A 圖 3A 圖 4A

圖 2B 圖 3B 圖 4B

小學生碰過的三角形，包括等腰三角形、等邊三角形、直角三角形、

等腰直角三角形、銳角三角形（所有角都是銳角）和鈍角三角形（有一角 是鈍角）。只要碰碰運氣，不難找到造出截面是等腰三角形（圖 5）、等邊 三角形（圖 6）、銳角三角形（圖 7）的切割方法。

圖 5 圖 6 圖 7

小學生碰過的四邊形，包括梯形、平行四邊形、菱形、長方形、正方 形和鷂形（四邊可分成兩對等長的鄰邊），其中梯形還有直角梯形、等腰梯 形（非平行邊等長）等特殊類別。跟三角形截面的探討比較，四邊形截面 要複雜得多。首先，隨便在正方體的三條相鄰的稜上找三點，即有唯一的 一個切割平面通過它們，使得截面正好就是一個以此三點定義的三角形。

相反地，隨便找四點，卻不能保證它們同屬一個平面。其次，只有上述的 切割方法可以造出三角形的截面（解釋見於下文），要窮盡各種可能並不困 難。相反地，存在不同的切割方法，可得出某些四邊形的特類（詳見下文）， 要窮盡各種可能比較費時。例如圖 1 與圖 8 的切割方法儘管不同（圖 8 的 兩個不被切割的面是相鄰的，圖 1 卻不是），卻都可得出長方形的截面。

圖 8 圖 8A 圖 8B

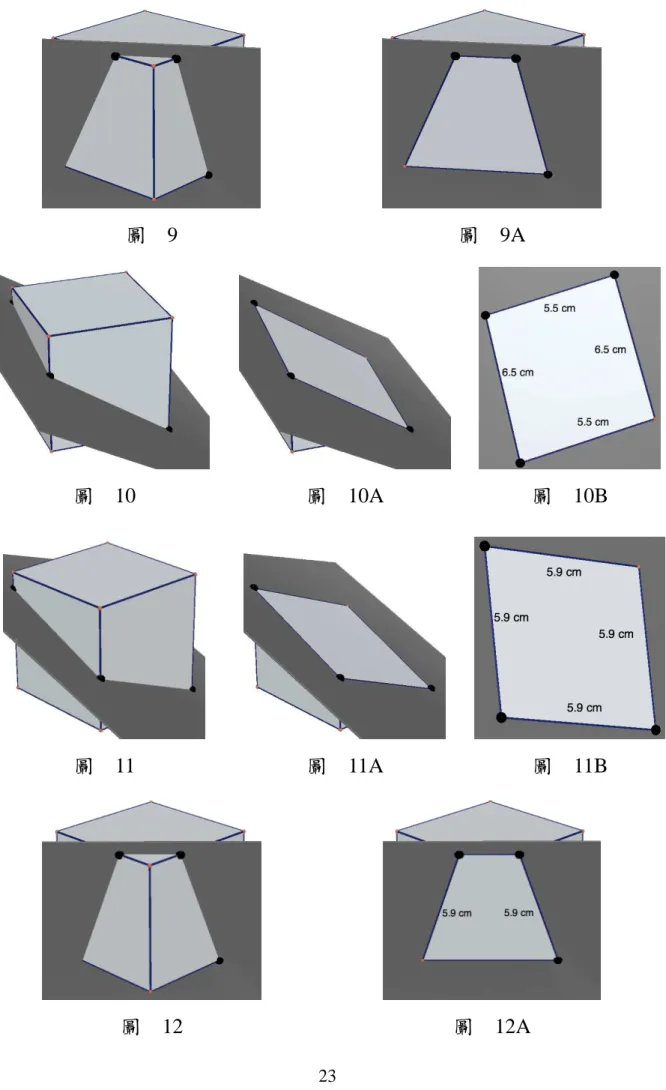
事實上，梯形（圖 9、9A）、等腰梯形（圖 12、12A）、平行四邊形（圖

10、10A、10B）、菱形（圖 11、11A、11B）都是可能得出的截面形狀。

圖 9 圖 9A

圖 10 圖 10A 圖 10B

圖 11 圖 11A 圖 11B

圖 12 圖 12A

除了三角形和四邊形的截面外，正方體還有五邊形（圖 13、13A）和 六邊形（圖 14、14A）的截面，其中包括正六邊形（以稜上中點定義圖 15、

15A 的切割面即得）。

圖 13 圖 13A

圖 14 圖 14A

圖 15 圖 15A

不可能得出的截面形狀

還未找到的截面形狀，包括直角三角形、等腰直角三角形、鈍角三角 形、鷂形、直角梯形和正五邊形。欲探討它們是否存在，需要用上一些高 中數學。

要造出 n 邊形的截面，切割平面必須與正方體的 n 個面相交。因此，

可以肯定截面不可能是邊數大於 6 的多邊形。要造出三角形的截面，切割 平面必須與正方體的三個面相交。三角形的每一對鄰邊，必須來自正方體 上相鄰的面。正方體上三個兩兩相鄰的面，必定連接同一個頂點。因此，

要得出三角形的截面，只可能透過像圖 5、6、7 的切割方法。細心檢視削 去的三角錐 ABCD（圖 16），會發現截面三角形 ABC，與三個直角三角形 ADB、BDC 和 CDA 相鄰，而且直角都在 D 之上。當 C 極度接近 D 時，三 角形 ACB 和 ADB 會接近重疊（如圖 2），表示 ∠ACB 和 ∠ADB 會極度接 近。因此，我們可以想像把 C 點從 D 點開始移向 E 點，∠ACB 會從一個直 角（即 ∠ADB）開始單向變化，直至變成 ∠AEB，過程與圖 2 至圖 4 顯 示的相約。如果把 C 看成是一隻盯著線段 AB 眼睛，當它逐漸遠離 AB，生 活經驗告訴我們：觀察 AB 的視角（即 ∠ACB）就會逐漸縮小。換言之，

當 C 不與 D 重疊，∠ACB 必定小於一個直角！

圖 16

如果不滿意上述那種簡便而粗疏的推論，也可藉畢氏定理得知：

AC ² + BC ² = (AD² + CD²) + (BD² + CD²) = AD² + BD² + 2 CD²

= AB² + 2 CD² ... (1) A

B

C

D

E

再用餘弦公式，可得：

AC ² + BC ² – AB² = 2 AC × BC cos ∠ACB ... (2) 從 (1) 和 (2) 可算得 cos ∠ACB =

BC CD AC

CD × ，是小於 1 的正數（因 CD

< AC及CD < BC），故知 ∠ACB是銳角。

同樣的推論也可確定 _∠CBA 和 _∠BAC 都是銳角，使我們可以肯定地 說：「正方體只有銳角三角形的截面。」

要造出四邊形的截面，切割平面必須與正方體的四個面相交。其餘的 兩個面的相對位置只有兩種情況：（一）兩個面是相鄰的（圖 17 打上陰影 的兩面）；（二）兩個面是相對的（圖 18 打上陰影的兩面）。

圖 17 圖 18

先處理圖 17 的情況，考慮以圖 19 中 H、K、P三點定義的切割平面把 正方體切開，並得出四邊形HKPQ，其中 Q是稜OX上的一點。

圖 19

O

Q X

H Y

P K

Z

設 OH = αOY，OK = βOY+OZ，OP = γOX +OZ，OQ = δOX ， 其中 0 < α , β , γ , δ ≤ 1。則 KP = γ^OX –β^OY，KH = (α–β)^OY –OZ， KQ = δ^OX –β^OY –OZ。Q 與 H、K、P 共面保證存在實數 u、v 使 KQ = uKP+ vKH，即 δOX –βOY –OZ = uγOX + (vα–vβ –uβ) OY – vOZ。 比較係數，即得

α = uβ，uγ = δ，v = 1 (*)

從 (*) 可推論圖 17 的切割方法，可能得出怎樣的截面：

推論 1 圖 17 的截面有一對平行邊。

證 HQ = δOX – αOY = uγOX – uβOY = u(γOX – βOY ) = uKP，其 中 u =

β

α ，因此 HQ 必定與 KP 平行。

推論 2 圖 17 的截面如果有兩對平行邊，它就是矩形。

證 已知 HQ 平行 KP（推論 1），若加上 KH 平行 PQ，即存在非零實數 λ 使 (α –β) OY –OZ = KH = λ^PQ = λ[(δ – γ) OX –OZ]。比較係數，即 得 δ = γ，λ = 1，α = β，使 KP⋅KH = (γOX – βOY ) ⋅ (–^OZ) = 0。因此，

HKPQ 乃含直角的平行四邊形，即矩形。

推論 3 圖 17 的截面如果是鷂形，它就是正方形。

證 推論 1 確定圖 17 的截面有平行邊，而有平行邊的鷂形必是菱形（證明 只涉初中幾何知識，此處從略），由推論 2 可知這圖為有鄰邊等長的矩形，

即正方形。

推論 4 圖 17 的截面如果含有直角，它就是矩形。

證 由 於 HQ 平 行 KP （ 推 論 1 ）， 不 妨 假 設 ∠PKH 為 直 角 。 從 (γOX – βOY ) ⋅ [(δ – γ) OX –^OZ] = KP⋅KH = 0 可得 α = β，加上 (*)

即知 KP = γOX–βOY = δOX – αOY = HQ，表示 HKPQ 為平行四 邊形，最後推論 2 確定它是矩形。

用同樣的手法，考慮圖 18 的情況。先以向量 OX 、 OY 、 OZ 表圖

20 的 向 量 ， 即 OH = α OX +OY ，OK = βOX +OY +OZ ，OP = γOX +OZ，OQ = δOX ，其中 0 < α , β , γ , δ ≤ 1。

圖 20

接著算得 KP = (γ – β) OX – OY ，^KH = (α – β)^OX –OZ，KQ =

(δ – β)^OX –OY –OZ 。由 H、K、P、Q 共面可知存在實數 u、v 使 u(γ – β) OX – u OY + v(α – β) OX – v OZ = uKP+ v KH = KQ = (δ – β) OX – OY – OZ 。比較係數，可得

γ + α = δ + β，u = 1，v = 1 (#)

從 (#) 可推論圖 18 的切割方法，可能得出怎樣的截面：

推論 5 圖 18 的截面是平行四邊形。

證 從 (#) 中 u = v = 1，或 KP = (γ – β) OX – OY = (δ – α) OX –OY

= HQ 可知。

推論 6 圖 18 的截面如果是菱形，則它的其中兩個相對的頂點與打上陰影 的面的距離相等，此距離亦是另外兩個相對的頂點與打上陰影的面的平均 距離。

證 已知 HKPQ 是平行四邊形（推論 5），若 |KP| = | KH |，則 (γ – β)² + 1

= (α – β)² + 1。化簡後得 (γ – α)(γ + α – 2β) = 0，即 γ = α 或 β = 2

α +

γ 。由 (#) 可知 _γ = α 對應 _α = 2

β +

δ ，_β = 2

α +

γ 對應 _δ = β。 兩種情況都顯示推論6 正確。

O Q X

Y

H Z

P K

L

推論 7 圖 18 的截面如果是矩形，則它的其中兩個相鄰的頂點與打上陰影 的面的距離相等，另外兩個頂點與打上陰影的面的距離亦相等。

證 已 知 HKPQ 是 平 行 四 邊 形 （ 推 論 5 ）， 若 ∠PKH 為 直 角 ， 則 [(γ – β)^OX – OY ] ⋅ [(α – β) OX – OZ ] = ^KP ⋅ ^KH = 0。由此得 (γ – β)(α – β) = 0，即 γ = β 或 α = β。由 (#) 可知 γ = β 對應 α = δ，

α = β 對應 γ = δ。兩種情況都顯示推論 7 正確。

要解釋正方體沒有正五邊形截面，只需考慮以圖 21 中 P、Q、G 三點 定義的切割平面把正方體切開，並得出五邊形PQHGF的情況。

圖 21

設 OP = α^OX + OY + OZ（0 < α < 1），OQ = OX + β^OY + OZ

（0 < β < 1），OG = γ^OZ（0 ≤ γ < 1），OF = OY+ δ^OZ（0 ≤ δ < 1），OH

= OX + λ^OZ（0 ≤ λ < 1）。則 QP = (α – 1)^OX+(1 – β)^OY，QG

= –OX– β^OY+ (γ – 1)^OZ，QF = –OX + (1 –β)^OY＋ (δ – 1)^OZ， GF = OY+ (δ – γ)OZ，GH = OX+ (λ –γ)OZ。

F與P、Q、G 共面保證存在實數u、v 使 QF = u QP+ v QG，即 –OX+ (1–β)^OY+ (δ–1)OZ = (uα–u–v)OX+ (u–uβ–vβ)^OY+ (vγ–v)OZ。比 較係數，即得

u(α – 1) = v – 1 (3)

u(1 – β) = (v – 1)β + 1 (4)

v(γ – 1) + 1 = δ (5)

O Y X

Z

P Q

H

G F

先以反證法證明 δ > γ。假設 δ ≤ γ，從 (5) 可得 v(γ – 1) + 1 ≤ γ，即 (v –1)( γ – 1) ≤ 0。由於 γ <1，故知 v – 1 ≥ 0。以此代入 (3) 及 (4)，並注 意到 α < 1 及 0 < β < 1，便可得到 u ≤ 0 和 u > 0 同時成立的矛盾。同理，

亦知 λ > γ。

要證 PQHGF 不可能是正五邊形，只需證明 ∠FGH < 108°（正五邊形 的內角）即可。從 δ > γ 及 λ > γ 可知 cos ∠FGH =

|

|

|

|GF GH GH GF⋅

=

|

|

|

|

) )(

(

GH GF

γ

− λ γ

−

δ > 0，表示 ∠FGH 不大於一個直角，自然小於 108°。

正六邊形截面

前述結果顯示正方體雖有五邊形截面，但不會是正五邊形。那麼正六 邊形截面的存在，便是令人驚訝的巧合。究竟是真有其事，還是美麗的測 量誤差所致？

圖 22

假設圖 22 中，P、Q、H 均為所在稜上的中點，便有 OP = 2

1 OX +

OY + OZ，OQ = OX + 2

1 OY + OZ，OH = 2

1 OY。設 OF = OY

+ α^OZ，OG = OX + β^OZ，OK = γ^OX ，其中0 < α , β , γ < 1。則 QP

= – 2

1 OX + OY，QH = – OX – OZ，QF = – OX + 2

1 OY + (α– 1) OZ。

F 與 P 、 Q 、 H 共 面 保 證 存 在 實 數 u 、 v 使 QF = uQP + vQH ， 即 – OX +

2

1 OY + (α − 1) OZ = − 2

1 uOX + 2

1 uOY− vOX− vOZ。比較

H O K

Y X F

P Q

G Z

係數，即得 −1 = − 2

1 u−v，u = 1，α − 1 = −v。解聯立方程可求得 α = 2

1 。

以相同手法可算得 β = γ = 2

1 ，顯示 P、Q、G、K、H、F 均是所在稜上 的中點。考慮 PQ、QG、GK、KH、HF、FP 各線段與最近頂點生成的直角 三角形都是全等，便知 PQGKHF 是等邊六邊形。從正方體的對稱性可確定 PG = QK = GH = KF = HP = FQ，進而推論 ∆PQG、∆QGK、∆GKH、∆KHF、

∆HFP、∆FPQ 全部全等，表示 PQGKHF 是等角六邊形。所以 PQGKHF 是 正六邊形。

總結

正方體的三角形截面，只能從切割三個有公共頂點的面得出（圖5、6、 7），而且都只有銳角，可以是等腰（於圖 16 設定 AD、BD、CD 其中之二 相等）或等邊（於圖16設定 AD = BD = CD）三角形。正方體的四邊形截 面可以是正方形（於圖19設定 KP = OZ 及 HK ⊥OY 或圖20設定平面 HKP 平行平面 OYZ）、長方形（於圖19設定 KP ≠OZ 及 HK⊥ OY 或圖20設定 LK = YH 及 ZP ≠ YH）、平行四邊形（於圖 20設定 ZP ≠YH，而 LK 不等於 ZP、YH、

2 YH ZP+

任何一個）、菱形（於圖 20設定ZP = YH，而_{LK ≠ ZP}） 和梯形（於圖19 設定ZK ≠ OH）。正方形和長方形均可分別以圖17和圖18 的切割法得出；圖 17 的切割法還可得出梯形，要等腰的話就得在圖 19 中 設定KZ = PZ；圖18的切割法得出的都是平行四邊形，要得菱形就要在圖

20中設定 ZP = YH，如果平面 HKP不與平面OYZ 平行，HKPQ 就是沒有

直角的菱形，否則就是正方形。

多邊形截面的邊數最大是 6；於圖 21 中隨意取 P、Q 和 G，只要不是 稜的端點，都可得到五邊形的截面；於圖22 中隨意取P、Q和H，只要不 是稜的端點，都可得到六邊形的截面；如果於圖22中取P、Q和H 均是所 在稜的中點，所得的截面就是正六邊形；直角三角形、直角梯形及正五邊 形的截面是不存在的；鷂形截面只有菱形和正方形這兩種特殊情況。

參考資料

香港課程發展議會（2000）。《數學課程指引（小一至小六）》。香港：教育署。

作者電郵：cifung@ied.edu.hk