方格告訴我的秘密 － 探討三角形的格線

中華民國第 61 屆中小學科學展覽會 作品說明書

排版\080402-封面

國小組 數學科

佳作

080402-封面

方格告訴我的秘密 － 探討三角形的格線

學校名稱：臺中市豐原區瑞穗國民小學

作者： 指導老師：

小五 林晏宇 徐瑛黛

關鍵詞：格子點、鉛直和、水平和

摘要

本研究由探討三頂點在格子點上的任意三角形鉛直格線長總和與水平格線長總和關係出 發，藉由各種計算法計算、觀察、推論、檢驗、修正、再檢驗、論證、推廣和應用的探究過 程，發現格子點上任意三角形鉛直格線長總和、水平格線長總和與面積的關係為：面積=鉛 直和¹+邊在鉛直格線長×0.5=水平和²+邊在水平格線長×0.5，並將此關係式推廣到簡單多 邊形³，然後應用於地圖上求面積。

壹、研究動機

在和同學玩釘板時，想起在科學研習月刊[1]中發現一個有趣的數學題目，題目是：將整 個平面用直線分成單位正方形，且橫線都是藍色，縱線都是紅色。選定三個正方形的頂點，

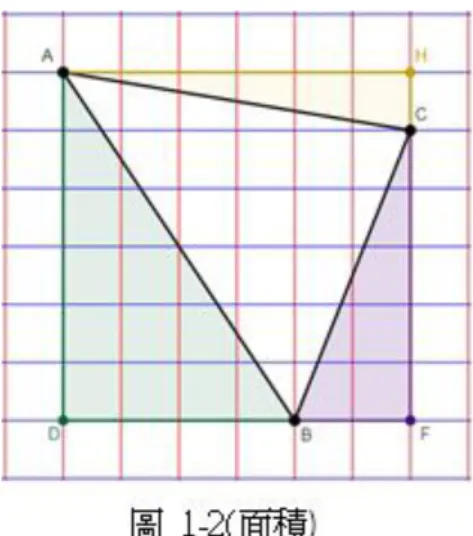
圍成一個三角形，如圖1-1與圖1-2所示，請計算此兩圖中的三角形內部的紅線長總和與藍線 長總和，各是多少呢？請問可以發現什麼？能解釋為什麼嗎？

我用國民小學數學第 6 冊「數格子算面積」單元[2]中估算的方法，驚奇的發現圖1-1與 圖1-2兩個三角形內部的紅線長總和與藍線長總和居然都相等！這使我好奇的想知道是湊巧 嗎？有沒有其他計算方法？除了以上兩個三角形外，其他任意三角形也都有此特性嗎？經過 嘗試後，發現能從中找到許多有趣的結果。於是，我開始進行「三角形中的格線」的研究，

希望深入探討，了解其中奧秘。

1 請參閱名詞定義

2 請參閱名詞定義

圖 1-2 原始題目示意圖 圖 1-1 原始題目示意圖

貳、研究目的

基於以上的研究動機，本研究的研究目的為：

一、找出研究動機中問題的答案。

二、探討任意三角形是否也有同樣的結論。

三、修正研究動機中問題的結論使任意三角形皆滿足。

四、證明任意三角形皆滿足結論，並將此結論推廣到簡單多邊形與應用於地圖上求面積。

參、研究設備及器材

紙、筆、方格紙、方格膠板、直尺、剪刀、口紅膠、電腦、GeoGebra 繪圖軟體。

肆、研究過程及方法

一、名詞定義：

（一）鉛直和：三角形內部的方格線鉛直長總和。

（二）水平和：三角形內部的方格線水平長總和。

（三）邊在鉛直格線長：三角形邊落在鉛直格線的長度，

如圖 1-3 紅線AC 的長度。

（四）邊在水平格線長：三角形邊落在水平格線的長度，

如圖 1-4 藍線AC 的長度。

（五）簡單多邊形：包含凸凹邊形，不能有洞。

（六）標準矩形：長、寬與x 、 y 軸平行的矩形，且頂點在格子點上。

（七）標準直角三角形：兩股與x 、 y 軸平行的直角三角形，且頂點在格子點上。

二、符號對照表：

P 簡單 n邊形，n

n ≥ 3

的正整數 Q 任意三角形

Vl

^{共用邊在鉛直格線長}

Hl

共用邊在水平格線長

V

^鉛直和 VPn P 的鉛直和 _n VQ Q 的鉛直和 H 水平和 HPn P 的水平和 _n HQ Q 的水平和

VL

^{邊在鉛直格線長} VLPn P 的邊在鉛直格線ⁿ 長

VLQ Q 的邊在鉛直格線長

HL 邊在水平格線長 HL_Pn P 的邊在水平格線ⁿ 長

HLQ Q 的邊在水平格線長

A 面積 APn P 的面積 _n AQ Q 的面積

三、文獻探討：

本研究由科學研習月刊中一道有趣的數學題目發展出「計算格子點上多邊形面積的方 法」，並應用在地圖上求面積。首先，我利用科展作品資源網站「科展群傑廳」搜尋歷 屆科展中並無類似的研究。另外，利用 google 搜索引擎搜尋發現了 1975 年高斯證明的 測量員公式(surveyor's formula) [3]與 1899 年皮克提出的皮克定律(Pick's theorem) [4]，此兩 種方法皆是與我的研究同一主題，但方法不同，分別說明比較如下：

（一）測量員公式(Surveyor's formula) ：先將格子點坐標化，再利用行列式計算多邊形 面積，此方法並不局限於格子點上多邊形，是個很棒的方法，但「坐標化」與

「行列式」均非小學學習領域，而我的研究結論只需「算格線長」較適合小學生 計算操作。

（二）皮克定律：是透過數格子點數計算格子點上多邊形面積的方法，這個方法只需

「數格子點數」，也很適合小學生計算操作，但與我的方法「算格線長」並不同。

此外，本研究為了計算和驗證需使用的數學知識，我參閱「史上最強圖解數學」[5]，將 書中提到比與比例(p.44)、數列(p.62) 、多邊形(p.94)、三角形的相似(p.102)的說明加以運 用在本研究中，並利用求_n邊形內角和時，可將_n邊形切割成數個三角形的既有概念與

4

在維基百科中查得的數學歸納法[6]推廣證明。

四、研究架構與流程圖 (綠色 ^→ 藍色 → 粉紅)

分類討論

不滿足研究結果一

修正方法 研究目的一：

找出研究動機中問題的答案

估算方法

研究結果一

研究目的二：

探討任意三角形是否也有 同樣的結論

分類討論

研究結果三 相似形方法

研究結果一

縮放研究動機中問題的圖形邊長大小

研究結果二

發現三角形邊在格線上不滿足結論

研究目的三：

修正結論使任意三角形皆滿足 研究目的二：

探討任意三角形是否也有同樣的結論

證 明 推

廣 結

論

計算

觀察 推論 檢驗

修正

論證、推 廣與應用 再檢驗

研究目的四：

證明、推廣與 應用

檢驗估算方法不滿足的圖形

應 用

剪紙法確認研究結果一

五、以估算方法找出研究動機中問題的答案：

將整個平面用直線分成單位正方形，且橫線都是藍色，縱線都是紅色。選定三個正 方形的頂點，圍成一個三角形，如圖 1-1 與圖 1-2 所示，請計算此兩圖中的三角形內部 的紅線長總和與藍線長總和，各是多少呢？請問可以發現什麼？

由國民小學數學第 6 冊「數格子算面積」單元中估算方法的啟發[7]：我以一格為 1 單位，三角形內格線長完整的一格算 1 單位，不完整的格線長以 0.5 單位估算。

圖 1-1 計算如下：

鉛直和(紅線長總和)

= × + × 10 1 4 0.5 12 =

水平和(藍線長總和)

= × + × 9 1 6 0.5 12 =

鉛直和＝水平和

圖 1-2 計算如下：

鉛直和(紅線長總和)

= × + × 12 1 8 0.5 16 =

水平和(藍線長總和)

= × + × 12 1 8 0.5 16 =

鉛直和＝水平和

此兩個三角形的紅線長總和等於藍線長總和。

以估算方法解答了這個問題，讓我又產生了新的疑問，除了以上兩個三角形外，其他任 意三角形也都有此特性嗎？

六、以估算方法測試任意三角形是否也有同樣的結論

以角度觀點分別測試銳角三角形^、直角三角形、鈍角三角形。因為邊上若有格子 點，則不完整的格線長較少，估算的誤差亦會較小，所以用除了頂點以外，邊上有格子 點通過的邊數進行舉例討論如下表：

角度 格子點通過的邊數 圖形 鉛直和 水平和 結論

銳 角 三 角 形

3 個邊有格子點

（圖 2-1）

1 14 0.5 4 16

× + ×

=

1 14 0.5 4 16

× + ×

= ^相等

2 個邊有格子點

（圖 2-2）

1 12 0.5 6 15

× + ×

=

1 14 0.5 2 15

× + ×

= ^相等

1 個邊有格子點

（圖 2-3）

1 10 0.5 6 13

× + ×

=

1 9 0.5 8 13

× + ×

= ^相等

三邊上無格子點

（圖 2-4）

1 9 0.5 9 13.5

× + ×

=

1 10 0.5 7 13.5

× + ×

= ^相等

角度 格子點通過的邊數 圖形 鉛直和 水平和 結論

直 角 三 角 形

3 個邊有格子點

（圖 3-1）

1 6 0.5 4 8

× + ×

=

1 8 0.5 0 8

× + ×

= ^相等

2 個邊有格子點 (格子點在一股、

一斜邊)

（圖 3-2-1）

1 2 0.5 2 3

× + ×

=

1 3 0.5 0 3

× + ×

= ^相等

2 個邊有格子點 (格子點在兩股)

（圖 3-2-2）

1 11 0.5 8 15

× + ×

=

1 12 0.5 6 15

× + ×

= ^相等

1 個邊有格子點 (格子點在斜邊)

（圖 3-3-1）

1 9 0.5 8 13

× + ×

=

1 10 0.5 6 13

× + ×

= ^相等

1 個邊有格子點 (格子點在股)

（圖 3-3-2）

1 13 0.5 8 17

× + ×

=

1 12 0.5 11 17.5

× + ×

= ^不相等

三邊上無格子點

（圖 3-4）

1 7 0.5 11 12.5

× + ×

=

1 10 0.5 5 12.5

× + ×

= ^相等

角度 格子點通過的邊數 圖形 鉛直和 水平和 結論

鈍 角 三 角 形

3 個邊有格子點

（圖 4-1）

1 8 0.5 8 12

× + ×

=

1 12 0.5 0 12

× + ×

= ^相等

2 個邊有格子點 (格子點在鈍角的 一邊及其對邊)

（圖 4-2-1）

1 7 0.5 10 12

× + ×

=

1 12 0.5 0 12

× + ×

= ^相等

2 個邊有格子點 (格子點在 鈍角的兩邊)

（圖 4-2-2）

1 12 0.5 12 18

× + ×

=

1 18 0.5 0 18

× + ×

= ^相等

1 個邊有格子點 (格子點在

鈍角的對邊)

（圖 4-3-1）

1 10 0.5 13 16.5

× + ×

=

1 14 0.5 5 16.5

× + ×

= ^相等

1 個邊有格子點 (格子點在 鈍角的一邊)

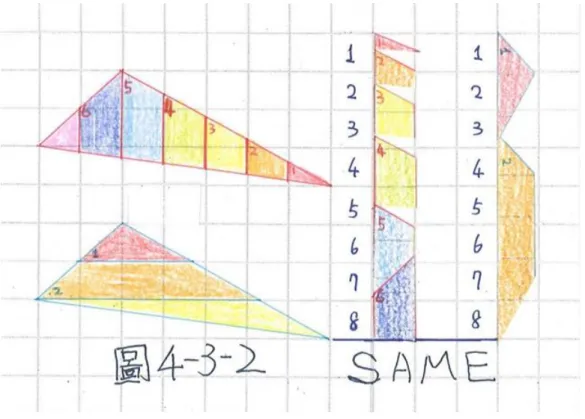
（圖 4-3-2）

1 4 0.5 9 8.5

× + ×

=

1 7 0.5 2 8

× + ×

= ^不相等

三邊上無格子點

（圖 4-4-1）

1 9 0.5 15 16.5

× + ×

=

1 13 0.5 7 16.5

× + ×

= ^相等

三邊上無格子點

（圖 4-4-2）

1 2 0.5 10 7

× + ×

=

1 5 0.5 3 6.5

× + ×

= ^不相等

發現鉛直和^≠水平和的圖 3-3-2、圖 4-3-2、圖 4-4-2，為了確認是「鉛直和等於水平

和」的結論不正確，還是估算方法不適用，我決定進行實際的剪紙法，以確認結論是否 正確。剪紙法的步驟為：

1. 將圖形描繪在方格紙上。

2. 依鉛直與水平方向分別著色與標記數字記號，避免黏貼時搞混淆。

3. 將剪好的鉛直與水平長條依編號黏貼在方格紙上。

我透過實際的剪紙法再確認如下：

圖 3-3-2 剪紙法結果，鉛直和=水平和=17。

圖 4-3-2 剪紙法結果，鉛直和=水平和=8。

圖 4-4-2 剪紙法結果，鉛直和=水平和=6.5。

由上可知「鉛直和等於水平和」的結論依舊成立。推論估算方法會因不完整的格線長產 生誤差，故此估算方法雖然較簡便，但無法確認問題結論，將尋求其他計算方法。

七、以相似形方法檢驗估算方法不滿足的圖形：

計算概念為以三角形頂點為界，將圖形補滿為矩形，先計算矩形內部總格線長，再運用 相似形與比例式計算矩形內部三角形外總格線長，最後將矩形內部總格線長減矩形內部 三角形外總格線長即求得三角形內部的總格線長。

（一）圖 3-3-2 檢驗

鉛直和(紅線長總和)計算如下：

由∆AD ~ ADB_{1 1}E ∆ ，得_{1:2= :81 1= =4}⁸ a ⇒a 2

由∆BFG ~ BF G ~ BF G ~ BF G_{1 1} ∆ _{2 2} ∆ _{3 3} ∆ _{4 4} ~ BF G ~ BFC∆ _{5 5} ∆ ，

得1:2:3:4:5:6= : : : : : 7b b b b b_{1 2 3 4 5 1}= , = , = , =7 ₂ 14 ₃ 21 ₄ 28, =₅ 35

6 6 6 6 6

b b b b b

⇒

由∆AH I ~ AH I ~ AH I ~ AHC_{1 1} ∆ _{2 2} ∆ _{3 3} ∆ ，得1:2:3:4= : : :1_{1 2 3 1}= , = , =¹ ₂ ² ₃ ³

4 4 4

c c c ⇒c c c 鉛直和(紅線長總和) _{=8 5 - (}× _{a b b1}+ +_{1 2}+_{b b3}+ ₄+_b5+ +_{c c1 2}+_c3)

7 14 21 28 35 1 2 3

=40 (4 )

6 6 6 6 6 4 4 4

− + + + + + + + +

=40 23=17 −

水平和(藍線長 總和)計算如下：

由∆BD E ~ BD E ~ BD E ~ BD E ~ BD E ~ BD E ~ BD E ~ BDA_{1 1} ∆ _{2 2} ∆ _{3 3} ∆ _{4 4} ∆ _{5 5} ∆ _{6 6} ∆ _{7 7} ∆ ， 得1:2:3:4:5:6:7:8= : : : : : : : 2a a a a a a a_{1 2 3 4 5 6 7}

1= = , = , = , = , = , = , =2 1 2 2 3 3 4 4 5 5 6 6 7 7

8 4 4 4 4 4 4 4

a a a a a a a

⇒

由∆CFG ~ CF G ~ CF G ~ CF G ~ CF G ~ CF G ~ CFB_{1 1} ∆ _{2 2} ∆ _{3 3} ∆ _{4 4} ∆ _{5 5} ∆ _{6 6} ∆ ，

得1:2:3:4:5:6:7= : : : : : :6_{1 2 3 4 5 6 1}= , = , = , =⁶ ₂ ¹² ₃ ¹⁸ ₄ ²⁴, = , =₅ ³⁰ ₆ ³⁶

7 7 7 7 7 7

b b b b b b ⇒b b b b b b

水平和(藍線長總和) _{=6 7 - (}× _{a a1}+ ₂+_a3+_a4+_a5+_a6+_a7+ +b b b b b b_{1 2}+ ₃+ ₄+ ₅+ ₆₎ 1 2 3 4 5 6 7 6 12 18 24 30 36

=42 ( )

4 4 4 4 4 4 4 7 7 7 7 7 7

− + + + + + + + + + + + + =42 25 17− =

得圖 3-3-2 三角形的鉛直和等於水平和，亦與剪紙法結果相同。

（二）圖 4-3-2 檢驗

同前（一）圖 3-3-2 檢驗，以相似形方法用相似形概念列出比例式，求出不完整格線 長度，即可得：

鉛直和(紅線長總和) _{=3 6 - (}× a b b b b b b₁+ +_{1 2}+ ₃+ ₄+ ₅+ ₆+ +c c_{1 2}+c₃+c₄₎ =18 10 8− = 水平和(藍線長總和) =7 2 (× − a c c₁+ +_{1 2})=14 6 8− =

得圖 4-3-2 三角形的鉛直和等於水平和，亦與剪紙法結果相同。

（三）圖 4-4-2 檢驗

同前（一）圖 3-3-2 檢驗，以相似形方法用相似形概念列出比例式，求出不完整格線 長度，即可得：

鉛直和(紅線長總和)

1 1 2 3 4 5 1 2 3

=8 5 - (× a b b+ + +b b+ +b + +c c +c )=40 23 17− =

水平和(藍線長總和)

1 2 3 4 5 6 7 1 2 3 4 5 6

=6 7 - (× a a+ +a +a +a +a +a + +b b b b b b+ + + + ) =42 25 17− =

得圖 4-4-2 三角形的鉛直和等於水平和，亦與剪紙法結果相同。

由相似形方法準確的算出鉛直和與水平和，檢驗了估算方法不滿足的圖 3-3-2、圖 4- 3-2、圖 4-4-2，並得到「鉛直和等於水平和」這個結論。接著，我想用相似形方法試 試看改變研究動機中問題條件，看看有什麼好玩的特性？

八、縮放研究動機中問題的圖形邊長大小

圖 4-4-2 (水平和) 圖 4-4-2(鉛直和)

首先，以圖 3-3-2 檢驗時的相似形法再次精準計算研究動機中問題的鉛直和與水平和，

以確認估算法中的鉛直和與水平和。

研究動機中問題一：

鉛直和(紅線長總和) _{=6 4 - (}× _{a b b1}+ +_{1 2}+_{b b3}+ ₄+ +_{c c1 2)} =24 12 12− =

水平和(藍線長總和) _{=5 5 - (}× _{a a1}+ ₂+_a3+ + +_{b c c1 1 2}+_c3+_c4+_c5) =25 13 12− = 得圖 1-1 三角形的紅線長總和等於藍線長總和，即鉛直和=水平和=12。

研究動機中問題二：

鉛直和(紅線長總和) _{=6 5 - (}× _{a a1}+ ₂+_a3+ + +_{b c c1 1 2}+_c3+_c4+_c5) =30 14 16− = 水平和(藍線長總和) =6 5 - (× a a₁+ ₂+a₃+a₄+a₅+ +b b b b_{1 2}+ ₃+ ₄) =30 - 14=16 得圖 1-2 三角形的紅線長總和等於藍線長總和，即鉛直和=水平和=16。

（一）將圖形邊長變為 2 倍

依然以一格為 1 單位，將圖形邊長變為 2 倍。

1. 研究動機中問題一之圖 1-1(鉛直和)、圖 1-1(水平和)分別轉為圖 5-1(鉛直和)、

圖 5-1(水平和) ，使用圖 3-3-2 檢驗時相同的相似形法計算，得：

鉛直和(紅線長總和)

1 2 3 1 2 3 4 5 6 7 8 9 1 2 3 4 5

=12 9 - (× a a+ +a + +b b b b b b b b b c c+ + + + + + + + + +c +c +c ) 2 4 6 8 10 12 14 16 18

=108 - (2 4 6 2 4 6 8 10)

5 5 5 5 5 5 5 5 5

=108 - 60 = 48 = 12 4

+ + + + + + + + + + + + + + + +

×

=原鉛直和

× 4

水平和(藍線長總和)

1 2 3 4 5 6 7 1 2 3 1 2 3 4 5 6 7 8 9 10 11

=10 11 - (× a a+ +a +a +a +a +a + +b b +b c c+ + +c +c +c c+ +c +c +c +c +c ) 1 2 3 4 5 6 7 5 10 15 1 2 3 4 5 6 7 8 9 10 11

=110 - ( + + + )

2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2

=110 - 62 = 48 =12 4

+ + + + + + + + + + + + + + + + +

×

=鉛直和(紅線長總和)

=原水平和

× 4

得研究動機中問題一之圖形邊長變為 2 倍，三角形的鉛直和依然等於水平和，但總和 變為 4 倍。

2. 研究動機中問題二之圖 1-2(鉛直和)、圖 1-2(水平和)分別轉為圖 5-2(鉛直和) 、 圖 5-2(水平和)，使用圖 3-3-2 檢驗時相同的相似形法計算，得：

鉛直和(紅線長總和)

1 2 3 4 5 6 7 1 2 3 1 2 3 4 5 6 7 8 9 10 11

=12 11 - (× a a+ +a +a +a +a +a + +b b +b c c+ + +c +c +c +c +c +c +c +c +c ) 3 6 9 12 15 18 21 5 10 15 1 2 3 4 5 6 7 8 9 10 11

=1132 - ( )

2 2 2 2 2 2 2 2 2 2 6 6 6 6 6 6 6 6 6 6 6

= 132-68 = 64 = 16 4

+ + + + + + + + + + + + + + + + + + + +

×

=原鉛直和

× 4

水平和(藍線長總和)

1 2 3 4 5 6 7 8 9 10 11

=12 11 - (a a× + +a +a +a +a +a +a +a +a +a

1 2 3 4 5 6 7 8 9+ )1

b b b b b b b b b c + + + + + + + + + 2 4 6 8 10 12 14 16 18 20 22 2 4 6 8 10 12 14 16 18

=132 - ( + + + 6)

3 3 3 3 3 3 3 3 3 3 3 5 5 5 5 5 5 5 5 5

=132 68 = 64 = 16 4

+ + + + + + + + + + + + + + + + +

− ×

=鉛直和(紅線長總和)

=原水平和

× 4

得研究動機中問題二之圖形邊長變為 2 倍，三角形的鉛直和依然等於水平和，但總和 變為 4 倍。

（二）將圖形邊長變為¹ 2倍

依然以一格為 1 單位，將圖形邊長變為¹ 2倍。

研究動機中問題之圖 1-1、圖 1-2 當圖形邊長變為¹

2倍時，三角形的三頂點無法剛好落 在格子點上，故另外繪圖 6-1，再將圖 6-1 邊長變為¹

2倍得圖 6-2 如下：

使用圖 3-3-2 檢驗時相同的相似形法計算，得：

1. 圖 6-1 如下：

鉛直和(紅線長總和) =6 5 - (× a a₁+ ₂+a b c c₃+ ₁+ ₁+ ₂+ +c₃ c₄+c₅)

=30 - 16 =14

水平和(藍線長總和) _{=6 5 - (}× _{a a1}+ ₂+_a3+_a4+_a5+ +_{b b1 2}+_{b c3+ )1}

= 30 - 16 = 14

=鉛直和

得圖 6-1 滿足鉛直和等於水平和結論。

2. 圖 6-2 (圖形邊長變為¹

2倍) 如下：

圖 6-1(鉛直和) 圖 6-1(水平和)

鉛直和=3 2 ( +× − a c c_{1 1}+ ₂) = 6 2.5 = 3.5− ₌₁₄ ¹

×4 =圖 6-1 鉛直和 ¹

×4 水平和=3 2 (× − a a₁+ ₂+b₁) = 6 2.5 = 3.5− ₌₁₄ ¹

×4=鉛直和=圖 6-1 鉛直和(水平和) ¹

×4

得圖 6-1 之邊長變為¹

2倍，三角形的鉛直和依然等於水平和，但總和變為¹ 4倍。

結論：觀察（一）圖形邊長變為 2 倍，鉛直和與水平和變為_{4 2}= ²倍與（二）圖形邊 長變為¹

2倍，鉛直和與水平和變為¹ _{( )}^{1 2}

4= 2 倍，發現這個變化量和長度改變時面積變 化量相同，所以推論鉛直和與水平和可能跟面積有某種關係。接下來想探究跟面積是 否真的有關？有什麼關係？

九、計算研究動機中問題的面積

計算方法為以三角形頂點為界，將圖形補滿為矩形，先計算矩形面積，再扣除周圍直角 三角形面積，即求得三角形的面積。

（一）研究動機中問題一：

圖 1-1 三角形面積計算如下：

ABC

∆

面積

= 矩形

DFCH − ∆ ABD

面積

−∆ BCF

面積

−∆ ACH

面積

1 1 1

6 5 2 4 5 2 3 6

2 2 2

= × − × × − × × − × ×

= − − − 30 4 5 9

12

= =鉛直和=水平和

（二）研究動機中問題二：

圖 1-2 三角形面積計算如下：

ABC

∆

面積

= 矩形

ADFH ABD − ∆

面積

−∆ BCF

面積

−∆ ACH

面積

1 1 1

6 6 4 6 2 5 6 1

2 2 2

= × − × × − × × − × ×

= − − − 36 12 5 3 16

=

_{=鉛直和=水平和}

結論：發現研究動機中問題的三角形面積=鉛直和=水平和

十、三角形邊在格線上

（一）驚奇的發現

發現「面積 = 鉛直和 = 水平和」後，我開心地請 同學任意畫一個頂點在格子點上的三角形，正想分 享這個發現時，竟意外發現同學畫的這個三角形(圖 7-1 邊在鉛直格線上) 鉛直和^≠水平和。

計算如下：

由∆AD E ~ AD E ~ AD E ~ AD E_{1 1} ∆ _{2 2} ∆ _{3 3} ∆ _{4 4}

~ AD E ~ ADB∆ 5 5 ∆ ，

得1:2:3:4:5:6= : : : : : 4a a a a a_{1 2 3 4 5}

1= = , = , = , = , =4 2 2 4 3 6 4 8 5 10

6 3 3 3 3 3

a a a a a

⇒

由∆CFG ~ CF G ~ CF G ~ CF G_{1 1} ∆ _{2 2} ∆ _{3 3} ∆ _{4 4}

5 5

~ CF G ~ CFB∆ ∆ ，

得1:2:3:4:5:6= : : : : : 2b b b b b_{1 2 3 4 5}

1= = , = , = , = , =2 1 2 2 3 3 4 4 5 5

6 3 3 3 3 3

b b b b b

⇒

鉛直和

1 2 3 4 5 1 2 3 4 5

=6 5 (× − a a+ +a +a +a + +b b b b b+ + + ) 2 4 6 8 10 1 2 3 4 5

=30 ( )

3 3 3 3 3 3 3 3 3 3

=30 15 = 15

− + + + + + + + + +

−

由∆BD E ~ BD E ~ BD E ~ BDA_{1 1} ∆ _{2 2} ∆ _{3 3} ∆

得1:2:3:4= : : : 6a a a_{1 2 3 1}= = , = , =6 3 ₂ 6 ₃ 9

4 2 2 2

a a a

⇒

由∆BFG ~ BFC_{1 1} ∆ ，得1:2= : 6_{1 1}= =3⁶ b ⇒b 2 水平和

1 2 3 1

=6 5 (× − a a+ +a b+ ) =30 (3 6 9+3) 2 2 2

− + +

=30 12=18 15− ≠

鉛直和^≠水平和

我趕緊算面積，計算如下：

∆ ABC

面積₌¹ _{6 6 = 18} 2× ×

得面積 = 水平和 ^≠ 鉛直和，並觀察圖 7-1(鉛直和) ，推論可能是因為_AC邊在鉛直格線 上，故須修正結論。我觀察：

面積−鉛直和=水平和⁻鉛直和_{=18 15 3}− = (鉛直和少

3

)

AC邊在鉛直格線上長為

6

單位

⇒

鉛直和減少的

3

分配給邊在鉛直格線上每一單位，計算為 ^{3 1}_{= = 0.5} 6 2

推論若邊在格線上也要列入計算，每一單位計算為 _0.5。假設結論修正為：

面積=鉛直和+邊在鉛直格線長×0.5=水平和+邊在水平格線長×0.5

令面積為

A

^{，鉛直和為}

V

^{，水平和為}

H

^{，邊在鉛直格線長為}

VL

^{，邊在水平格線長為}

HL

^，則

^{1 1}

2 2

A V= + VL H= + HL ……… (1)式

（二）舉例測試

接著，我測試了一些例子，分別為圖 7-2 邊在水平格線上、 圖 7-3 邊同時在鉛直格線 與水平格線上。

1. 圖 7-2 邊在水平格線上計算如下：

由∆BD E ~ BD E ~ BDA_{1 1} ∆ _{2 2} ∆ ， 得1:2:3= : : 4_{1 2 1}= , =⁴ ₂ ⁸

3 3

a a ⇒a a

由∆BFG ~ BFC_{1 1} ∆ ， 得_{1:2= : 41 1=}⁴ ₂

b ⇒a 2 =

鉛直和 +邊在鉛直格線長×_0.5

1 2 1

=4 4 (× − a a+ +b) + 0

=16 (4 8 2) =16 6 =10

− 3 3+ + −

由∆AD E ~ AD E ~ AD E ~ ADB_{1 1} ∆ _{2 2} ∆ _{3 3} ∆ ， 得1:2:3:4= : : :3a a a_{1 2 3 1}= , = , =3 ₂ 6 ₃ 9

4 4 4

a a a

⇒

由∆CFG ~ CF G ~ CF G ~ CFB_{1 1} ∆ _{2 2} ∆ _{3 3} ∆ ，

得1:2:3:4= : : : 2b b b_{1 2 3 1}= = , = , =2 1 ₂ 2 ₃ 3

4 2 2 2

b b b

⇒

水平和+邊在水平格線長×_0.5

1 2 3 1 2 3

=5 3 - (× a a+ +a + +b b +b )+5 0.5×

3 6 9 1 2 3

=15 - ( + ) +2.5 =10 4 4 4 2 2 2+ + + +

ABC

∆

面積₌¹ _{5 4 = 10} 2× ×

得面積=鉛直和+邊在鉛直格線長×_0.5=水平和+邊在水平格線長×_0.5

2. 圖 7-3 邊同時在鉛直格線與水平格線上計算如下：

由∆BC A ~ BC A ~ BCA_{1 1} ∆ _{2 2} ∆ ，

得1:2:3= _{1 1}: _{2 2}: 4 _{1 1}= ,⁴ _{2 2}=⁸

3 3

AC A C ⇒AC A C 鉛直和+邊在鉛直格線長×_0.5

1 1 2 2 0.5

A C A C AC

= + + × =4 8 4 0.5 = 6 3 3+ + ×

由∆AB C ~ AB C ~ AB C ~ ABC_{1 1} ∆ _{2 2} ∆ _{3 3} ∆ ， 得1: 2 :3: 4=B C B C B C_{1 1}: _{2 2}: _{3 3}:3

1 1= ,3 2 2= ,6 3 3=9

4 4 4

B C B C B C

⇒

水平和+邊在水平格線長×_0.5

1 1+ 2 2 + 3 3 0.5

B C B C B C BC

= + × =3 6 9+3 0.5 = 6

4 4 4+ + ×

ABC

∆

面積= ¹ 3 4 = 6 2× ×

得面積=鉛直和+邊在鉛直格線長×_0.5=水平和+邊在水平格線長×_0.5

進行了一些舉例都滿足此結論，整理如下表：

圖形 ^{1 1}

2 2

A V= + VL H= + HL

VL

^與

HL

邊不在格線上

(圖 1-1) 滿足

VL HL = = 0

邊在鉛直格線上

(圖 7-1) 滿足

VL = 0

邊在水平格線上

(圖 7-2) 滿足

HL = 0

邊同時在鉛直格 線與水平格線上

(圖 7-3)

滿足

VL ≠ 0 0 HL ≠

伍、研究結果

一、找出研究動機中問題的答案為格子點上的三角形鉛直和=水平和。

二、對任意「邊不在格線上」的格子點上三角形有面積=鉛直和=水平和的結論。

三、對任意格子點上的三角形結論修正為：

面積=鉛直和+邊在鉛直格線長×0.5=水平和+邊在水平格線長×0.5

一、證明任意三角形皆滿足

由前面觀察得知，任意三角形可以看成一個外接標準矩形，扣掉多個標準直角三角 形。如圖 8-1：

所以我將證明分成三個部份：

1. 標準矩形滿足(1)式

2. 標準直角三角形滿足(1)式

3. 如果標準矩形與標準直角三角形都滿足(1)式，則標準矩形扣除標準直角三角形的三 角形也滿足(1)式，故任意三角形滿足(1)式。

此處(1)式為面積=鉛直和+邊在鉛直格線長×0.5=水平和+邊在水平格線長×0.5。

（一）證明：標準矩形滿足(1)式

令標準矩形頂點

C

^{為原點，長為}a，寬為

b

，因為四頂點皆在格子點上，故a 、

b

皆為正整數。

標準矩形

ABCD

^面積

=ab

鉛直和+邊在鉛直格線長×0.5 (如圖 8-2)

1 2 1

=b×0.5+y +y ++y_a− + ×b 0.5

=b b a+ × − = +( 1) b ab b ab− =

水平和+邊在水平格線長×0.5 (如圖 8-3)

1 2 1

=a×0.5+x +x ++x_b− + ×a 0.5

=a a b+ × − = +( 1) a ab a ab− =

得面積=鉛直和+邊在鉛直格線長×0.5

=水平和+邊在水平格線長×0.5

=ab

陸、討論

陸、討論

（二）證明：標準直角三角形滿足(1)式

在不失一般性下，令標準直角三角形

∆ ABC

的∠B 為原點，兩股為a 、

b

，因為三頂點皆在格子點 上，故a 、

b

皆為正整數，如圖 8-4。

標準直角三角形

∆ ABC

面積_{= 2=}¹ a b× ÷ 2ab

由∆A BC ~ A BC ~ ~ A BC ~ ABC_{1 1} ∆ _{2 2}  ∆ _{a-1 a-1} ∆ ， 得1 : 2 : : -1: = : : : a a y y_{1 2}  y_a−₁ : b

1= , =b 2 2 b, , _a1=(a 1) b

y y y

a a ⁻ a

× − ×

⇒ 

鉛直和+邊在鉛直格線長×0.5 (如圖 8-5)

1 2 1

= +y +y ++y_a− b×0.5

2 ( 1)

= 0.5b b a b b

a a a

× − ×

+ ++ + ×

[

1 2 ( 1)

]

¹

2

a b b

= + ++ − × + ×a =

[

1 ( 1) (

]

1) 1

2 2

a a b b

a + − × −

× + ×

( 1) 1

= 2 2

a a b b

a

× − × + × = ( 1)

2 2

a− ×b b+ =

2 2 ab b b− + = 1

2ab

由∆AB C ~ AB C ~ ~ AB C ~ ABC_{1 1} ∆ _{2 2}  ∆ _{b-1 b-1} ∆ ， 得1 : 2 : : -1: = : : : b b x x_{1 2}  x_b−₁ : a

1= , =a 2 2 a, , _b 1=(b 1) a

x x x

b b ⁻ b

× − ×

⇒ 

水平和+邊在水平格線長×0.5 (如圖 8-6)

1 2 1

= 0.5x +x ++x_b− + ×a

2 ( 1)

= 0.5a a b a a

b b b

× − ×

+ ++ + ×

[

1 2 ( 1)

]

¹

2

b a a

= + ++ − × + ×b =

[

1 ( 1) (

]

1) 1

2 2

b b a a

b + − × −

× + ×

( 1) 1

= 2 2

b b a a b

× − × + × = ( 1)

2 2

b− ×a a + =

2 2 ab a a−

+ = 1 2ab

得面積=鉛直和+邊在鉛直格線長×0.5=水平和+邊在水平格線長×0.5 = 1 2ab

（三）證明：如果標準矩形與標準直角三角形都滿足(1)式，則標準矩形扣除標準直角三角

形的三角形也滿足(1)式，故任意三角形滿足(1)式。

在不失一般性下，任意三角形與標準矩形依兩者頂點的重合情形可分為：三頂點重 合、兩頂點重合、一頂點重合。我們分別以下面四種可能的情形進行說明：

1. 圖 8-7.1 為標準直角三角形，由（二）已得證明。

2. 如圖 8-8，標準矩形

BCDE

^{扣除兩標準直角三角形}

∆ ABC

與∆ADE為∆ABE。 由

BCDE

^{為標準矩形與}

∆ ABC

、∆ADE為標準直角三角形，得

矩形

BCDE

面積=鉛直和+邊在鉛直格線長×_0.5=水平和+邊在水平格線長×_0.5

= (a b e ab ae+ =) +

ABC

∆

面積=鉛直和+邊在鉛直格線長×_0.5=水平和+邊在水平格線長×_0.5 = 1 2ab ADE

∆ 面積=鉛直和+邊在鉛直格線長×_0.5=水平和+邊在水平格線長×_0.5 = 1 2ae (1)∆ABE面積=矩形

BCDE

^面積−

∆ ABC

面積− ∆ADE面積₌ ^{1 1 1 1}

2 2 2 2

ab ae+ − ab− ae= ab+ ae (2)∆ABE鉛直和+邊在鉛直格線長×0.5

=矩形

BCDE

^鉛直和+邊在鉛直格線長×0.5

−(

∆ ABC

鉛直和+邊在鉛直格線長×0.5)

−( ADE∆ 鉛直和+邊在鉛直格線長×0.5)

1 1 1 1

=ab ae+ −2ab−2ae=2ab+2ae (3)∆ABE水平和+邊在水平格線長×0.5

=矩形

BCDE

^水平和+邊在水平格線長×0.5

−(

∆ ABC

水平和+邊在水平格線長×0.5)

−( ADE∆ 水平和+邊在水平格線長×0.5)

1 1 1 1

=ab ae+ −2ab−2ae=2ab+2ae

得∆ABE面積=鉛直和+邊在鉛直格線長×0.5=水平和+邊在水平格線長×0.5 故圖 8-7.2 滿足(1)式

3. 如圖 8-9，標準矩形

ACBE

扣除兩標準直角三角形

∆ ABC

與∆BDE為∆ABD，

同前圖 8-8計算方法，得：

ABD

∆ 面積=鉛直和+邊在鉛直格線長×0.5

=水平和+邊在水平格線長×0.5 =1 1 2ab−2ae 故∆ABD滿足(1)式，即圖 8-7.3 滿足(1)式

4. 如圖 8-10，標準矩形

BCDE

扣除三個標準直角三角形

∆ ABC

、 ADF

∆ 與∆BEF為∆ABF，同前圖 8-8計算方法，得：

ABF

∆

面積=鉛直和+邊在鉛直格線長×0.5

=水平和+邊在水平格線長×0.5 =1 1 1 2af −2ab+2bd 故

∆ ABF

滿足(1)式，即圖 8-7.4 滿足(1)式

由圖 8-7.1、圖 8-7.2、圖 8-7.3、圖 8-7.4 滿足(1)式得證（三）。 由（一）、（二）、（三）得證任意三角形滿足

面積=鉛直和+邊在鉛直格線長×_0.5=水平和+邊在水平格線長×_0.5。

發現任意三角形皆滿足此結論(1)式後，我想試試簡單多邊形或是旅遊會用到的地圖─不 規則形狀，看看(1)式是否依然成立？以便進行後續的推廣與應用。

二、是否能推廣至簡單多邊形？

因為簡單多邊形可切割為數個共邊的三角形[5]，如圖 9-1，所以只要證明「如果共邊 的簡單n邊形_Pn與任意三角形_Q都滿足(1)式，則兩者合併的簡單

n +1

^邊形P_n+₁也滿足(1) 式」，即可將(1)式推廣至簡單多邊形。例如圖 9-2 為

n =4

^。

令_APn、_VPn、_HPn、_VLPn、_HLPn分別為簡單n邊形P_n的面積、鉛直和、水平和、邊在鉛直格 圖 8-9

圖 8-10

線長、邊在水平格線長；_AQ、_VQ、_HQ、_VLQ、_HLQ分別為任意三角形Q的面積、鉛直 和、水平和、邊在鉛直格線長、邊在水平格線長；_Vl、_Hl分別為共邊落在鉛直格線長與 共邊落在水平格線長。

我先以

n =3

去推論「如果共邊的簡單

3

^邊形P3與任意三角形Q都滿足(1)式，則兩者合併的 簡單

3+1

^邊形P₄也滿足(1)式」，如下：

若

n =3

^，P3與Q為任意三角形，由前面證明知_P3與Q皆滿足(1)式，得

3 3 3 3 3

1 1

2 2

P P P P P

A =V + VL =H + HL ， ^{1 1}

2 2

Q Q Q Q Q

A =V + VL =H + HL

⇒(1)

A

_P4

= A A

_P3

+

_Q

3 3

1 1

2 2

P P Q Q

V VL V VL

= + + + ₃ 1 ₃ 1

2 2

P P Q Q

H HL H HL

= + + +

(2) ₄ ¹ ₄

P 2 P

V + VL ₃ 1( ₃ ) 1( )

2 2

P P Q Q

V VL Vl V VL Vl Vl

= + − + + − + ₃ 1 ₃ 1

2 2

P P Q Q

V VL V VL

= + + +

(3) ₄ ¹ ₄

P 2 P

H + HL = ₃ 1( ₃ ) 1( )

2 2

P P Q Q

H + HL −Hl +H + HL −Hl +Hl ₃ 1 ₃ 1

2 2

P P Q Q

H HL H HL

= + + +

4 4 4 4 4

1 1

2 2

P P P P P

A V VL H HL

⇒ = + = +

=4 n

⇒

滿足(1)式

接著，以數學歸納法[6]證明「簡單n邊形_Pn滿足(1)式」，如下：

1. 若

n =3

^，因為P₃為任意三角形，所以由前面證明知_P3滿足(1)式，命題成立。

2. 設

n k ≥ = 3

^{，命題成立，則}P_k滿足(1)式，得 ^{1 1}

2 2

k k k k k

P P P P P

A =V + VL =H + HL 3. 若n k= +1> 3，因為任意三角形_Q也滿足(1)式，得 ^{1 1}

2 2

Q Q Q Q Q

A =V + VL =H + HL ，則

⇒ (1)

A

_Pk+1

= A A

_Pk

+

_Q ^{1 1}

2 2

k k

P P Q Q

V VL V VL

= + + + 1 1

2 2

k k

P P Q Q

H HL H HL

= + + +

(2) ₊₁ ¹ ₊₁ 2

k k

P P

V + VL 1( ) 1( )

2 2

k k

P P Q Q

V VL Vl V VL Vl Vl

= + − + + − + 1 1

2 2

k k

P P Q Q

V VL V VL

= + + +

(3) ₊₁ ¹ ₊₁ 2

k k

P P

H + HL = 1( ) 1( )

2 2

k k

P P Q Q

H + HL −Hl +H + HL −Hl +Hl 1 1

2 2

k k

P P Q Q

H HL H HL

= + + +

1 1 1 1 1

1 1

2 2

k k k k k

P P P P P

A ₊ V ₊ VL ₊ H ₊ HL ₊

⇒ = + = +

= +1 n k

⇒ 滿足(1)式，命題成立。

由數學歸納法得本命題成立，故本研究的方法可以推廣至簡單多邊形。

三、是否可以應用於求地圖上的面積？

將(1)式推廣到簡單多邊形後，我想起曾經和阿公到台中 公園散步時，阿公說：「台中公園這麼大，如果要量公園面積 不知怎麼量？」我想公園四周的道路都是直線，因此公園是個 被道路圍成的簡單多邊形，於是，我決定將研究結論應用於求 台中公園面積。

（一）首先，我先下載 google map 上台中公園的地圖，依公園四 周道路畫出直線，得成簡單多邊形的台中公園圖形，如圖 10-1。

（二）接著，透過方格膠板(1 單位長為實際 20 公尺)將台中公園圖形畫在方格紙上，如圖 10-2。

（三）將格子縮小¹

2 倍 (1 單位長為實際 10 公尺)，使台中公園 所形成的簡單多邊形頂點都在格子點上，如圖 10-3。

（四）用簡潔的估算法計算出鉛直和後，因為台中公園所形成的 簡單多邊形並無邊在鉛直格線上，所以得面積=鉛直和

1042 1 40 0.5 1062

= × + × =

(1 單位長為 10公尺)，故台中公園 面積約為 106200 平方公尺。

（五）在網路上查得台中公園實際面積約為108724 平方公尺，

與我計算結論相差 6524平方公尺，誤差約 2.3%。以統計學來說，屬於可接受的範 圍，故本推廣應用在地圖上面積的估算，是可接受，並符合小學生可操作的簡便方 法。後續的研究或許可以多比對幾個不同的地圖面積資料，確認誤差值的範圍，再 以此誤差來推論實際面積的範圍，進而得到更準確的面積估算值。

圖 10-1

圖 10-3

柒、結論

這次的研究，從科學月刊的一道題目開始，由於格子點上的三角形鉛直和等於水平和引 發了我的研究興趣，我透過各種計算法計算、觀察、推論、檢驗、修正、再檢驗、論證、推 廣和應用的探究過程，獲得主要研究結果如下：

一、科學月刊中的原命題，格子點上的三角形鉛直和=水平和。

二、使用估算法計算三角形鉛直和與水平和雖然簡便，但易產生誤差。相對而言，相似形方 法雖然計算較繁複，但卻能精準地算出三角形鉛直和與水平和。

三、對任意「邊不在格線上」的格子點上三角形有面積=鉛直和=水平和的結論。

四、對任意格子點上的三角形結論修正為：

面積=鉛直和+邊在鉛直格線長×0.5=水平和+邊在水平格線長×0.5 五、此結論可推廣到簡單多邊形，並應用於估算地圖上面積。

六、未來研究方向：目前此結論除了格子點上的任意三角形外，也可推廣 到格子點上的簡單多邊形。但若圖形為格子點上有洞的多邊形，如圖 11-1，是否依然滿足此結論？或者會有什麼新的規律呢？另外，若將 圖形推廣到非格子點上多邊形或三維空間多面體，會有什麼發現呢？

這些都是未來可以研究的方向。

研究過程中我畫了好幾百個三角形，訓練了耐心與毅力，但其中我覺得最 重要的是觀察與思考，這樣才能在數百個三角形中逐漸找到討論的脈絡與發現

修正方法，並找出正確結論，這一路的研究真是讓我經歷了一趟數學有趣的探索之旅。

捌、參考資料及附錄

一、游森棚（2015）。三角形中的格線。科學研習月刊。第 54 卷第 1 期，49。

二、康軒文教事業（2019）。國小數學第 6 冊第 8 單元數格子算面積。新北市：康軒。

三、吳作樂， 吳秉翰（2017）。圖解向量與解析幾何。台北市：五南。

四、蔡聰明（1994）。談求面積的 Pick 公式。科學月刊。第 25 第 10，749。

五、數學能力開發研究會（2017）。史上最強圖解數學。新北市：漢湘。

六、數學歸納法。維基百科。取自zh.wikipedia.org/wiki/%E6%95%B0%E5%AD%A6%E5%BD%92%E7%BA%B3%E6%B3%95

七、林天相（2015）。國小數學 1-5-3 數格子算面積。學習吧。取自www.learnmode.net/flip/video/5978

圖 11-1

【評語】 080402

本作品從科學研習月刊的一道數學題出發，探討三頂點在格子 點上的任意三角形，其內部以及邊上所包含之鉛直格線長總和與水 平格線長總和及此三角形面積之間的關係。以下是評審委員對此作 品的建議與評析：

1. 作者歷經估算法、剪紙法、相似形法，發現格子點上任意三 角形鉛直格線長總和與水平格線長總和相等，整個研究歷程 清晰呈現、段落分明，值得讚許。

2. 作品「以具體實例台中公園來說明如何將本研究應用於估算 地圖上面積」強化了本研究成果的可應用性！

3. 建議作者應從兩邊都在格線上的格點三角形出發，討論鉛直 格線長總和與水平格線長總和以及斜邊上所含格點數的關 係，這樣應可得到更完整的結果。

排版\評語\080402-評語

作品簡報

方格告訴我的秘密~

探討三角形的格線

國小組 數學科

本篇研究由科學研習月刊中一道「計算三角形內格線長總和」的題目出發，

最後竟然發現一種新的計算格子點上簡單多邊形

¹

面積的方法，即：

面積=鉛直和

²

+邊在鉛直格線長× 𝟎.5=水平和

³

+邊在水平格線長× 𝟎.5 ， 並將此關係式應用於地圖上求面積。

摘要

1 請參閱名詞定義(五) 2 請參閱名詞定義(一) 3 請參閱名詞定義(二)

研究動機

在和同學玩釘板時，想起在科學研習月刊

^[1]

中發現一個有趣的數學題目，題目是：如圖1-1與 圖1-2所示，請計算此兩圖中的三角形內部的紅線長總和與藍線長總和，各是多少呢？請問 可以發現什麼？

圖 1-1 圖 1-2

研究架構與流程圖

發現：

三角形邊在格線上 發現： 不滿足的例子

檢驗不滿足例子：

鉛直和＝水平和 找研究動機中問

題的答案

估算法 發現： 鉛直和＝水平和

探討任意三角形 是否有同樣結論

相似形法

縮放圖形邊長大小

發現：

面積=鉛直和=水平和

測試任意三角形是否 有同樣結論

修正結論：

面積

=鉛直和

+邊在鉛直格線長×0.5

=水平和

+邊在水平格線長×0.5

推廣至簡單多邊形

結論 證明 確認不滿足例子：

鉛直和＝水平和

應用於求地圖上的面積

剪紙法

圖 1-1 圖 1-2

圖 1-1計算如下：

鉛直和(紅線長總和)= 1 × 10 + 0.5 × 4 = 12 水平和(藍線長總和)= 1 × 9 + 0.5 × 6 = 12 鉛直和＝水平和

圖 1-2計算如下：

鉛直和(紅線長總和)= 1 × 12 + 0.5 × 8 = 16 水平和(藍線長總和)= 1 × 12 + 0.5 × 8 = 16 鉛直和＝水平和

此兩個三角形的紅線長總和等於藍線長總和。

以估算法找出研究動機中問題的答案

以估算法測試任意三角形是否也有同樣的結論

為了想確認估算法結論是否正確，我以角度觀點分別測試銳角、直角、鈍角三角形。又因為 邊上若有格子點，則不完整的格線長較少，估算的誤差亦會較小，所以輔以「邊上有格子點 通過的邊數」進行舉例討論如下：

估算法

以估算法測試任意三角形是否也有同樣的結論

角度 銳角三角形

格子點通過的邊數 3個邊有格子點 2個邊有格子點 1個邊有格子點 三邊上無格子點 圖形

結論 相等 相等 相等 相等

角度 格子點通過的邊數 圖形 結論

鈍 角 三 角 形

3個邊有格子點 相等

2個邊有格子點 (格子點在鈍角的

一邊及其對邊)

相等 2個邊有格子點

(格子點在鈍角的兩邊) 相等 1個邊有格子點

(格子點在鈍角的對邊) 相等 1個邊有格子點

(格子點在鈍角的一邊) 不相等

三邊上無格子點 相等

角度 格子點通過的邊數 圖形 結論

直 角 三 角 形

3個邊有格子點 相等

2個邊有格子點

(格子點在股與斜邊) 相等 2個邊有格子點

(格子點在兩股) 相等 1個邊有格子點

(格子點在斜邊) 相等 1個邊有格子點

(格子點在股) 不相等

以剪紙法確認估算法不滿足的例子

以相似形法檢驗估算法不滿足的圖形

相似形法的計算概念為：

透過剪紙法確認估算法不滿足的例子皆

吻合「鉛直和等於水平和」的結論。

檢驗圖 3-3-2

鉛直和(紅線長總和)計算如下：

由Δ𝐴𝐷 ₁ 𝐸 ₁ ~Δ𝐴𝐷𝐵，得1: 2 = 𝑎 ₁ : 8 ⟹ 𝑎 ₁ = 4

由Δ𝐵𝐹 ₁ 𝐺 ₁ ~Δ𝐵𝐹 ₂ 𝐺 ₂ ~ Δ𝐵𝐹 ₃ 𝐺 ₃ ~ Δ𝐵𝐹 ₄ 𝐺 ₄ ~ Δ𝐵𝐹 ₅ 𝐺 ₅ ~ Δ𝐵𝐹𝐶，

得1: 2: 3: 4: 5: 6 = 𝑏 ₁ : 𝑏 ₂ : 𝑏 ₃ : 𝑏 ₄ : 𝑏 ₅ : 7

⟹ 𝑏 ₁ = ⁷

6 , 𝑏 ₂ = ¹⁴

6 , 𝑏 ₃ = ²¹

6 , 𝑏 ₄ = ²⁸

6 , 𝑏 ₅ = ³⁵

6

由Δ𝐴𝐻 ₁ 𝐼 ₁ ~Δ𝐴𝐻 ₂ 𝐼 ₂ ~Δ𝐴𝐻 ₃ 𝐼 ₃ ~ Δ𝐴𝐻𝐶，

得1: 2: 3: 4 = 𝑐 ₁ : 𝑐 ₂ : 𝑐 ₃ : 1 ⟹ 𝑐 ₁ = ¹

4 , 𝑐 ₂ = ²

4 , 𝑐 ₃ = ³

4

鉛直和(紅線長總和)

= 8 × 5 − (𝑎 ₁ + 𝑏 ₁ + 𝑏 ₂ + 𝑏 ₃ + 𝑏 ₄ + 𝑏 ₅ + 𝑐 ₁ + 𝑐 ₂ + 𝑐 ₃ )=17 水平和(藍線長總和)計算方法如上鉛直和，

得水平和(藍線長總和) = 17

故圖 3-3-2三角形鉛直和=水平和=17，亦與剪紙法結果相同。

以相似形法檢驗估算法不滿足的圖形

圖 3-3-2(鉛直和)

相似形法

研 究 動 機 中 問 題 一

鉛直和

=12

=48× ^𝟏

𝟒 相

等 水平和

=12

=48× ^𝟏

𝟒

研 究 動 機 中 問 題 二

鉛直和

=16

=64× ^𝟏

𝟒

相 水平和 等

=16

=64× ^𝟏

𝟒

研 究 動 機 中 問 題 一

鉛直和

=48

=12×4

相 等 水平和

=48

=12×4

研 究 動 機 中 問 題 二

鉛直和

=64

=16 ×4 相 等 水平和

=64

=16 ×4

以一格為1單位

邊長放大2倍

鉛直、水平和變大4倍

邊長縮小 ^𝟏

𝟐 倍

鉛直、水平和變小 ^𝟏

𝟒 倍

縮放研究動機中問題的圖形邊長大小