自動化冠狀動脈分割與註冊方法

國

立

交

通

大

學

資訊科學與工程研究所

碩

士

論

文

自 動 化 冠 狀 動 脈 分 割 及 註 冊 方 法

Automatic 3D Coronary Artery Segmentation

and Registration from MDCT Images

研 究 生：陳建順

指導教授：王才沛 教授

自 動 化 冠 狀 動 脈 分 割 及 註 冊 方 法 Automatic 3D Coronary Artery Segmentation

and Registration from MDCT Images

研 究 生：陳建順 Student：Jian-Shuen Chen 指導教授：王才沛 Advisor：Tsai-Pei Wang 國 立 交 通 大 學 資 訊 科 學 與 工 程 研 究 所 碩 士 論 文 A Thesis

Submitted to Institute of Computer Science and Engineering College of Computer Science

National Chiao Tung University in partial Fulfillment of the Requirements

for the Degree of Master

in

Computer Science February 2009

Hsinchu, Taiwan, Republic of China

自動化冠狀動脈分割及註冊方法

學生：陳建順 指導教授：王才沛

國立交通大學資訊科學與工程研究所 碩士班

摘要

心血管疾病在現代人中罹瘓的機率很高，如果能夠提早發現，及早預防， 才能避免因冠狀動脈阻塞所造成的悲劇 。近年來，多切面電腦斷層 掃 瞄 (multi-detector computed tomography，簡稱 MDCT)的進步，提供我們一項非侵 入式的診斷方法，但是由醫生來判斷一層層的電腦斷層影像，是很耗時費力的 工作。全自動化電腦預診系統是我們研究的主要方向，主要分成冠狀動脈擷取 以及冠狀動脈分析兩大部份。由於前人的相關演算法多省略了自動化找出冠狀 動脈的過程，而以人工標記的方法取代，因此我們的論文改善了這一點，利用 影像處理形態學的方法擷取出可能為冠狀動脈的部份，再以明確均值分類法 (hard c-means)搭配樹狀結構分析，以達到完全自動化擷取冠狀動脈的目標。另 外，同一病患，在攝影心臟電腦斷層掃瞄圖時通常至少會拍攝有顯影劑和無顯 影劑兩組資料，不同的資料會因為心臟跳動的關係，冠狀動脈的形狀會有些微 的變化，因此我們發展了相同位置的定位的演算法，利用 iterative closest point(ICP)將兩組冠狀動脈資料先做基本的比對，再以冠狀動脈縱向剖面影像的 比較，修正兩組資料的位移量，完成不同資料相同位置的註冊，希望可以藉由 不同資料相同位置的資訊，提高預診的準確度。

Automatic 3D Coronary Artery Segmentation and Registration

from MDCT Images

Student：Jian-Shuen Chen Advisor：Tsai-Pei Wang

Institutes of Computer Science and Engineering National Chiao Tung University

ABSTRACT

Cardiovascular disease is common for people. The earlier we discover the disease, the more chance for us to prevent the tragedy caused by myocardial infarction. Recently, the progress of multi-detector computed tomography (MDCT) provides us a kind of diagnostic non-invasive method for coronary. But it is tiring and time-consuming for a doctor to analyze MDCT images layer by layer. Our research is about developing a computer assisted diagnostic system. The inputs are datasets from MDCT. Once we have the inputs, we can segment the coronary artery by computers without human interaction. After that, we can analyze the coronary artery to extract the positions that are in high probability of myocardial infarction caused by calcifications or blood clots. In previous work, in order to simplify the process, the segmentation of coronary artery is made by human. We proposed an algorithm to extract the coronary artery automatically. Firstly we use mathematical morphology to segment coronary candidates. Secondly, we use hard c-means algorithm and tree extraction to reach the goal of fully automatic segmentation. In addition, two different datasets from the same patient will not be the same because of acquiring time. The coronary artery is not rigid, and the shape is slight different

by heart beating. So we also proposed a registration algorithm using iterative closest point (ICP).This algorithm can increase the accuracy of diagnosis by comparing the same position in two different sources.

誌謝

這篇碩士論文能夠順利完成，首先我要感謝我的指導教授王才沛老師，在 我重回學校的這三年碩士生涯，對於我耐心的指導及教誨，當所做的研究遇到 瓶頸和困難時，老師總會給予適當的建議或是可能的解決方向，讓我接觸到這 個領域中前人所發展出對我有用的演算法，使用在我的研究題目上，使得本研 究能夠順利完成，在此要感謝老師的栽培。感謝張北葉醫師及荊宇泰老師擔任 我的口試委員，提供許多寶貴的建議，使得本論文更加完備，特此致謝。在研 究所的修課過程中，張醫師所開的醫學工程課程，讓我對所研究的心臟電腦斷 層掃瞄影像的來源更加清楚，荊老師英文授課的演算法課程，讓我嘗試從另一 種語言中習得各式各樣的演算法。另外要特別感謝國立台灣大學醫學院李文正 醫師提供的心臟電腦斷層掃瞄圖以及相關的醫學資訊。 接下來要感謝的是實驗室一起研究與努力的夥伴們。和我一起口試的詩祐 和聖文，有了你們的陪伴，讓我寫論文的過程不會感到孤獨。昇毅、耿維和劉 強，有了你們，讓我的碩士生活更加充實和精彩。最後我要感謝我的家人以及 交往多年的女友薇生，謝謝你們能夠支持我完成碩士學業，在這途中經歷了休 學、當兵及延畢，總共五年多的時間，沒有你們的支持與鼓勵，就不會有今日 的我。

目錄

摘要 ...i  ABSTRACT ...ii  誌謝 ...iv  目錄 ...v  圖目錄 ...vii  表目錄 ...ix  第一章  簡介 ...1  1.1  研究動機 ...1  1.2  章節概要 ...3  第二章  文獻探討 ...4  2.1  自動化診斷系統 ...4  2.2  血管擷取 ...5  2.3  醫學影像註冊 ...6  第三章  冠狀動脈分割 ...8  3.1  形態學影像處理 ...9  3.2  估計心臟範圍 ... 11  3.3  冠狀動脈候選點 ...14 

3.4  C-MEANS... 18 

3.5  擷取樹狀結構 ...21 

第四章  冠狀動脈註冊 ...27 

4.1  觀察 ...27 

4.2  ITERATIVE CLOSEST POINT... 28 

4.3  調整位移量 ...30 

第五章  實驗結果 ...34 

第六章  結論與未來展望 ...38 

圖目錄

圖 1：冠狀動脈影像 ...2  圖 2：冠狀動脈分割流程圖 ...9  圖 3：估計上層心臟範圍 ...12  圖 4：估計心臟中層範圍 ...13  圖 5：估計心臟下層範圍 ...13  圖 6：取得冠狀動脈候選點 ...16  圖 7：冠狀動脈候選點 ...17  圖 8：資料點轉換為代表點 ...20  圖 9：網狀交織 ...22  圖 10：連通表示圖 ...23  圖 11：冠狀動脈擷取結果 ...25  圖 12：假分支 ...26  圖 13：以ICP找出形狀相似之冠狀動脈...29  圖 14：YZ平面比對圖...32  圖 15：位移調整圖 ...33  圖 16：標點工具 ...35  圖 17：標點驗證結果 ...37 

表目錄

表 1：資料規格 ...34  表 2：資料擷取率 ...36 

第一章 簡介

1.1 研究動機

心肌梗塞是一個在現今的成人中是很常見的疾病，根據衛生署統計，心臟 疾病一直高居國人十大死因前幾位，其中因為冠狀動脈阻塞所引起的缺血性心 臟病，死亡人數更是佔了心臟疾病死亡總數的 50%以上[1]。如果能夠早期發現 冠狀動脈阻塞情況，並以抗血栓藥物做治療，預防心肌梗塞，即能夠大大減低 死亡率。所以如何以便利的方式來診斷冠狀動脈，變成一件很重要的事。近年 來，因為multi-detector computed tomography(MDCT)的概念興起，原本computed tomography(CT)的速度不足以掃瞄跳動快速的心臟，而multi-detector的概念，使 得CT能夠快速地掃瞄全身，而且速度很快，精確度又高，和magnetic resonance imaging(MRI)、positron emissions tomography imaging (PET)相比，它是最適合 用在觀察心臟冠狀動脈中是否存在可能造成阻塞的鈣化產生。但是，也由於它 精確度高的關係，一張張的slice之間的間隔很小，所以光是心臟部份就有上百 張的影像。醫生要從這上百張的影像當中找出是否有鈣化或粥狀斑塊的部份， 是需要消耗相當大的時間以及精力的。因此我們想要透過電腦的幫助，在病人 做完MDCT後，將整組CT影像送到電腦去做處理，經過電腦的計算之後，能夠 自動解讀出病人冠狀動脈鈣化的部份有哪些？是否有心肌梗塞的危險？有可能 阻塞的部位是在哪？這個自動化的過程，即是我們想要做的。能夠在醫生做判 斷之前先預先診斷出有問題的部份，減少醫生花費大量時間及精力，讓醫生能 夠以電腦預先診斷的結果為依據，去做更細部的觀察。 在研究過前人的相關研究之後，我們發現如果想要發展一套全自動電腦預 診系統，最大的問題在於冠狀動脈的擷取，一旦能解決冠狀動脈的擷取，後續

的冠狀動脈診斷與分析，才能夠實行。因此我們的目標就是發展出一套全自動 化冠狀動脈擷取的演算法，只要有心臟斷層掃瞄圖，不需要任何人工的介入， 即可擷取出冠狀動脈。 除此之外，醫生常常使用注射顯影劑前後的影像來做比對，透過不同影像 的比較，有助於判斷的準確性。例如鈣化在無顯影劑的影像中是很明顯的，因 為沒有顯影劑的介入，鈣化的對比度高，而容易被察覺，相對地，在有顯影劑 的影像中，非鈣化阻塞的部份則因為無法被顯影劑增強的關係，和有被顯影劑 增強的區域產生很大的對比。如圖 1(a)為無顯影劑影像，從影像中可以很明顯 地看到冠狀動脈鈣化的部份，而圖 1(b)為有顯影劑的影像，比較圖 1(a)和圖 1(b)，我們發現圖 1(b)在圖 1(a)中出現鈣化部份的周圍呈現出非鈣化的阻塞，這 是從圖 1(a)中看不出來的部份。 (a) (b) 圖 1：冠狀動脈影像 (a)為無顯影劑影像，箭頭所指之處為鈣化的部份。(b)為有顯影劑影像，箭頭所指之 處為鈣化部份，包含非鈣化阻塞，這是從(a)的圖看不出的部份。(b)比(a)對比明顯， 容易看出冠狀動脈的範圍，即圖中長條狀的區域。 為了要結合有顯影劑及無顯影劑中影像資訊的優點，我們的另一個目標是 發展出一套註冊的演算法，只要知道注射前後的影像其中一組的某一個位置， 就能推測出另一組資料中，相對應的位置。在知道注射顯影劑前後影像中的相 對位置及相關資訊後，未來在自動化診斷的應用上，我們就可以透過比較這兩 組相似的影像，取得更精確的資訊，以得到更好的診斷結果。

在本篇論文中，我們將提出兩種演算法，一個是全自動冠狀動脈的擷取， 一個是冠狀動脈的註冊。前者主要的貢獻在於從 MDCT 影像中分割出冠狀動脈 的部份，並且是全自動的，而不是需要人為介入的半自動演算法。後者主要的 貢獻是為了讓以後的自動化診斷更精確，同時可以加速前者在分割無顯影劑冠 狀動脈影像的處理過程。

1.2 章節概要

在第二章我們先介紹前人所做的有關冠狀動脈診斷以及擷取的演算法。第 三章介紹我們所提出的全自動冠狀動脈擷取演算法。第四章介紹相同病人不同 影像的冠狀動脈註冊演算法。第五章為實驗的結果及討論。最後在第六章做總 結以及討論未來可以研究的方向。

第二章 文獻探討

2.1 自動化診斷系統

冠狀動脈自動化預診系統主要分為兩大部份，第一部份是冠狀動脈的擷 取，第二部份是冠狀動脈的分析。由於冠狀動脈在 MDCT 中以三維的方式分 布，如果只是以二維的方式分析一層層的軸狀切面(axial view)，並不容易擷取 出冠狀動脈，這是因為冠狀動脈在每一層軸狀切面沒有固定形狀的關係。冠狀 動脈在有些切面為水平方向分布，有些切面則是以垂直方向分布，如果遇到冠 狀動脈分支的地方，在切面中呈現出來的形狀更是無法預測，因此無法以特定 形狀的擷取方法取出冠狀動脈，要擷取冠狀動脈，主要還是要從三維的方式著 手，如此，就增加了第一部份的困難度。第二部份的目的是分析冠狀動脈的橫 切面，將冠狀動脈切成一個個圓形的形狀，再對此圓形的灰階值做分析，根據 不同的灰階值，來決定冠狀動脈中，這一個位置的成分組成，如果有造成血管 阻塞的鈣化或粥狀斑塊，則根據阻塞情況計算出此位置血液能流通的直徑，如 果直徑過小，則有較高的風險併發心肌梗塞，依此原理做出預診的判斷方式。 Yuji[2]等人利用了診斷肺癌的電腦斷層掃瞄圖，做出冠狀動脈鈣化的診斷 系統。首先，他們將電腦斷層掃瞄圖依心臟的高度分成了三個部份。然後，分 離出屬於心臟範圍的部份。接下來，根據統計結果，設定三個部份中冠狀動脈 可能鈣化的範圍，偵測出鈣化的部份。最後再排除一些雜訊的部分，增加診斷 的準確度。他們的方法只能找到鈣化的部份，無法找到其他造成阻塞的原因。 他們也沒有實際去擷取出冠狀動脈，而是以統計的方式判斷出可能鈣化的範 圍，好處是計算量會比實際找出冠狀動脈少很多，原因是僅使用二維的影像處 理。

董俊良[3]所提出的診斷系統，使用了他們所發展出來的雙邊變形模組 (dual-snake model)，可以自動化並準確地同時擷取出血管內腔及血管外壁的邊 界，並採用區域線性映對分類模組(local linear mapping model)，做為血管組織 分類的依據。他的診斷系統並沒有完全地自動化，仍然需要人為方式，標定出 冠狀動脈的特定位置，才能讓整套系統運作下去，在冠狀動脈擷取的部份，屬 於半自動的系統。

2.2 血管擷取

血管的擷取，在醫學影像處理中是很常見的，最基本的想法，是利用血管 為管狀形狀的特性，除了血管分支處以外，橫切面皆為圓形，將相鄰圓形的圓 心連接起來，即可擷取出血管。

Syoji[4]等人使用了模糊邏輯技術(fuzzy logic technique)從 MR 影像中將血 管擷取出來。他們的方法主要包含兩個部份：(1)量化與特徵擷取，(2)反覆模糊 合 成 。 在 第 一 個 部 份 量 化 的 處 理 ， 是 使 用 了 分 水 嶺 分 割 技 術 (watershed segmentation technique)，並將量化後的血管質、管徑、灰階統計圖做為特徵。 第二部份則利用這些特徵，反覆地合成相鄰的特徵，以增加模糊的等級，最後 利用模糊等級來評定是否為血管或是脂肪。Yan[5]等人也使用模糊邏輯技術， 從 CT 影像中將血管擷取出來。他們利用相鄰層的影像組合和影像差異，將影 像做前處理，之後尋找影像中的環狀物視為可能的血管位置，再對這些位置使 用模糊邏輯技術擷取出血管。使用環狀物當做血管依據的缺點，在於血管分支 或是血管橫向分布時，無法正確找出血管的位置。 Stefan[6]等人提出一種新的三維分割和量化血管的方法。他將血管橫切面 圖的灰階分布，以圓柱狀參數的方法來表示，由於可以透過參數來調整，因此 和以前的高斯分布([7][8])相比，可以更精確地近似血管的灰階值，使得找出來

的血管的管徑、位置、方向等資訊誤差更少、更準確。

2.3 醫學影像註冊

醫學影像中，最常被應用在取得三維的資訊上的，莫過於電腦斷層掃瞄(CT) 以及核磁共震影像(MRI)，常見的應用部位有腦部、心臟、肺…等。有些情況， 因為醫生診斷的需求，會同時需要兩種不同來源的影像資訊，例如利用電腦斷 層掃瞄和核磁共震影像的比對，可以做出更精確的診斷，因此需要影像註冊的 功能來標出不同影像中相同的位置。同一種影像來源也會需要做註冊，例如心 臟的電腦斷層掃瞄圖，由於心臟會隨著心跳做出收縮和舒張的動作，在不同的 時間所得到的電腦斷層掃瞄圖是有些微不同的，因此也會需要影像註冊，來比 對不同時間同一位置的資訊，提升診斷的正確性。 Hsu[9]等人使用了三維的邊界偵測來註冊 CT 和 MR 影像。大部份的註冊 技術是使用表面特徵(如皮膚表面或腦部表面)來做對應，Hsu 等人的方法不止 可以對表面特徵做註冊，還可以應用到組織結構上。以前的方法要做註冊之前 都必須先手動或自動分割出要註冊的表面，而 Hsu 等人的方法則不需要，只要 利用偵測到的邊界，將兩組需要註冊的資料以 iterative closest point 方式找出誤 差夠小的結果，即做完註冊的流程。不過以他們的方法，比較適合在固定不動 的物體，像註冊腦部之類的，對於變化較大的器官則不適用。Petra[10]等人也 使用差不多的方法來做註冊，主要的差別在於所比對的數值是以幾何相關性取 代了邊界資訊。 Jan[11]等人的方法，則適用於變化較大的地方，例如因心臟跳動或肺部呼 吸造成影像有較大的變化時，可以利用血管為樹狀結構的特性，將不同的影像 做註冊。血管系統中的分支位置是註冊的重要目標，利用這項特徵，再以關聯 圖方法(association graph method)，並做了些許的限制，再使用非固態註冊演算

第三章 冠狀動脈分割

本 章 說 明 了 我 們 的 冠 狀 動 脈 分 割 演 算 法 ， 3.1 節 簡 單 介 紹 形 態 學 (mathematical morphology)影像處理。3.2 節估算心臟區域的範圍，藉此排除掉 確定不為冠狀動脈分布的部份。在 3.3 節中我們利用 3.1 節中介紹的形態學影像 處理，分割出 MDCT 每一層軸狀切面中可能為冠狀動脈的部份。在 3.4 節中， 為了減少計算量，我們導入了 hard c-means algorithm，將可能為冠狀動脈的部 份分為很多小群組，以代表點取代數量極多的資料點。最後，在 3.5 節，我們 將代表點之間的關係做分析，判斷其中資料點的分布狀況是否可以連接鄰近的 兩個代表點，再將已建立的連線圖做樹狀分析，得到冠狀動脈的位置。 我們的冠狀動脈分割演算法流程如圖 2 所示，心臟電腦斷層掃瞄圖經過 morphological opening 處理得到可能為冠狀動脈的部份，之後透過事先求得的 心臟範圍圖，排除掉絕對不可能為冠狀動脈的部份。接著將可能為冠狀動脈的 資料點透過 hard c-means algorithm 分成各群組，以代表點稱之，以少量的代表 點取代數量極多的資料點，用來減少大量的計算。之後根據鄰近代表點之間資 料點的分布建立連接圖。最後分析連接圖，找出樹狀結構，即為冠狀動脈，得 到結果。

Identify coronary candidates

MDCT Images

Remove coronary candidates outside the heart region

Obtain a set of representative points

Connect associate representative points

Tree extraction

Results

Identify the heart region

圖 2：冠狀動脈分割流程圖

3.1 形態學影像處理

在本篇論文中，是針對從電腦斷層掃瞄儀器取得的影像來做影像分割，而 我們的影像分割，需要先將一層層的 MDCT 影像，篩選出每一層可能為冠狀動 脈的位置，再將這些可能為冠狀動脈的位置組合成 3D 影像，分析出真正的冠 狀動脈。而要找出每一層可能為冠狀動脈的位置，我們就是利用形態學中 opening 的特性。以下簡單介紹 dilation 和 erosion 兩個形態學的基本運算，以及 此篇論文中對於影像分割所需要的 opening 運算。

Dilation 令 A、B 屬於 2 Z ，表示 A、B 分別為二維的點集合，以 B 做為 structuring element，對 A 做 dilation，定義如下公式： } ) ˆ ( | { ∩ ≠φ = ⊕B z B A A _z (1) 方程式(1)中，⊕為 dilation 的運算符號，Bˆ為 B 集合的鏡像，φ表示空集 合，z 表示二維向量。(B)ˆ z是Bˆ中的點的座標皆位移 z 所得之點集合。當 與 A 交集不為空集合，則將 z 加入 dilation 結果的集合。 z B)ˆ ( 經過 dilation 後的結果，A 會根據 B 的形狀，略為膨脹。 Erosion 令 A、B 屬於 2 Z ，表示 A、B 分別為二維的點集合，以 B 做為 structuring element，對 A 做 erosion，定義如下公式： } ) ( | {z B A B AΟ = _z ⊆ (2) 方程式(2)中，O為 erosion 的運算符號。如果 B 中的點的座標皆位移 z 後 為 A 的子集合，則將 z 加入 erosion 結果的集合。 經過 erosion 後的結果，A 會根據 B 的形狀，而有了被侵蝕的效果。 Opening 令 A、B 屬於 2 Z ，表示 A、B 分別為二維的點集合，以 B 做為 structuring element，對 A 做 opening，定義如下公式： B B A B A_o =( Ο )⊕ (3)

方程式(3)中，_o為 opening 的運算符號。opening 結果為 A 和 B 先做 erosion 運算再做 dilation 運算的集合。

從上面的式子，我們可以很清楚地看到，opening 運算是由 dilation 運算及 erosion 運算所組合而成的。經過 opening 後的結果，影像 A 會根據影像 B 的形 狀，先侵蝕後膨脹，而這樣的效果，等同於將 B 當作是一個固體，將多個 B 塞 在 A 的形狀裡，而不超過 A 的範圍，最後在 B 的形狀所不能涵蓋到的部份， 都會被移除，這樣子的特性，被我們利用做為 smoothing 的工具。我們將 A 從 二維的點集合延伸成為二維的灰階圖 f，將 B 從二維的點集合延伸成為二維的 二元影像 b，形狀為圓形。方程式如下：(詳細內容請參考[12]) } ) , ( ; ) ( ), ( | ) , ( ) , ( max{ ) , )( (f ⊕b s t = f s−x t−y +b x y s−x t−y ∈D_f x y ∈D_b (4) } ) , ( ; ) ( ), ( | ) , ( ) , ( min{ ) , )( (fΟb s t = f s+x t+ y −b x y s+x t+ y ∈D_f x y ∈D_b (5) b b f b f _o =( Ο )⊕ (6) 當 b 移動到 f 的某座標時，會以 b 所在的圓形範圍內中最低的灰階值代表 這個範圍，這意味著高於最低灰階值的部份都會被移除，因此有了 smoothing 的效果。

3.2 估計心臟範圍

在我們的冠狀動脈分割演算法中，最先要做的事即是估計心臟的範圍，因 為冠狀動脈的分布只存在於心臟的表面，而在 MDCT 的軸狀切狀圖中，即從頭 上方往心臟方向看的剖面圖，由於心臟肌肉組織與胸腔的氣體，在 MDCT 中有 很明顯的區隔，但是心臟內部，冠狀動脈和心臟心房心室比較沒有明顯的區分 方法，因此我們先針對容易區分的部份做初步地影像分割。

我們的作法，是利用直徑約 45mm 的圓當作 structuring element，如圖 3(a) 左上角的圓形大小，對 MDCT 的每一層，做 opening 的運算，心臟上半部的 MDCT 中，心臟的範圍大多會與胸骨及脊椎骨連接，但是連接處的寬度並不

大，因此我們利用 opening 的特性，斷開心臟與胸骨和脊椎骨的連接。在做完 opening 之後，還需要取臨界值，以訊號強度區分出心臟及胸腔的氣體空間，在 我們的實驗中，臨界值定為 500，完成後的結果如圖 3(b)所示。圖 3(b)的結果 為我們所得到的心臟範圍。但是，並不是所有的情況都是這麼好的。 (a) (b) 圖 3：估計上層心臟範圍 (a)為心臟上層MDCT影像，左上角的圓為structuring element的形狀及大小。(b)為(a) 影像取出心臟範圍的結果。 在心臟中層的部份，心臟與胸骨和脊椎骨的連接寬度可能大於我們所設定 的 structuring element，所以單純使用 opening 的方法無法找出理想的心臟範圍 (如圖 4(b)所示)。因此，我們利用骨頭在 MDCT 上訊號強度很高的特性，切除 胸骨以上、脊椎骨以下的範圍(實際作法於本節稍後說明)，以求得較好的心臟 範圍圖，在圖 4(a)中，藍線為胸骨中心與脊椎骨的連線，我們要切除的部份就 是落在這條線上最靠近心臟的胸骨及脊椎骨的位置，以紅線表示。圖 4(c)為排 除不可能為心臟區域後，較圖 4(b)好的結果。

(a) (b) (c) 圖 4：估計心臟中層範圍 (a)為心臟中層MDCT影像，藍線為胸骨中心和脊椎骨的連線，紅線為藍線中胸骨和脊椎骨 最靠近心臟的位置，兩條紅線之間為我們所要保留的心臟範圍。(b)為單純用opening取得 (a)中的心臟範圍。(c)為排除不可能為心臟區域後，較好的結果。 對於心臟靠近橫隔膜的部份(如圖 5(a))，由於心肌、心房、心室與橫隔膜 的訊號強度沒有明顯的區分，因此在心臟下半部的範圍取得結果會比較差(如圖 5(b))，雖然會因此增加我們分析冠狀動脈的時間，但是不影響分析後找出冠狀 動脈的結果。 (a) (b) 圖 5：估計心臟下層範圍 (a)為心臟下層MDCT影像。(b)為單純用opening取得(a)中的心臟範圍。

為了增加心臟範圍的準確度，減少處理雜訊的計算量，我們需要自動化找 出每一層 MDCT 中胸骨和脊椎骨中最靠近心臟的部份。第一步為找出胸骨中心 和脊椎骨的連線，利用骨頭在 MDCT 中高亮度的性質，以 1500 為臨界值，取 出二元影像，去掉 1500 以下的部份，再將此二元影像依水平方向分成五等分， 找出所佔 1500 以上點數最多者，再將此等份中所有資料點的水平方向位置取平 均，即為胸骨中心和脊椎骨的連線，圖 4(a)中，以藍線表示這條線。第二步則 是沿著胸骨中心和脊椎骨的連線，找出上半部中，connected component 最大者 中，垂直方向位置最低的地方，做為胸骨與心臟的分界，為圖 4(a)中第 1 條紅 線，另外還要找出下半部中，connected component 最大者中，垂直方向位置最 高的地方，做為脊椎骨與心臟的分界，為圖 4(a)中第 2 條紅線。

3.3 冠狀動脈候選點

在上一節中，我們使用了形態學的方法，利用 opening 有 smoothing 作用的 特性，成功地找出心臟的範圍，避免掉冠狀動脈不可能出現的地方。在這一節， 我們利用 opening 後的影像，以擷取出冠狀動脈候選點。 根據我們的對於冠狀動脈的觀察，冠狀動脈在 MDCT 軸狀切面圖下，會依 心臟由上到下，而有兩種不同的表現方式。第一種方式，是冠狀動脈剛從主動 脈分支出來，在軸狀切面下，由於是橫向分布的關係，會呈現長條狀。同樣的 情況，也存在於心臟下半部靠近橫隔膜的冠狀動脈，一樣是呈現長條狀分布。 第二種方式，是冠狀動脈從心臟上半部表面連接到心臟下半部，在 MDCT 軸狀 切面下，由於是垂直分布的關係，會呈現圓形或橢圓形的樣子，也就是冠狀動 脈的橫切面圖，大部份的電腦診斷方法，就是依據冠狀動脈的橫切面圖來做判 斷。為了成功擷取每層 MDCT 中可能為冠狀動脈的位置，考慮到冠狀動脈在某 幾層是垂直分布，在某幾層又是水平分布，並且可能會有分支的情形產生，如

此不規則形狀下，無法用特定形狀的方式找出冠狀動脈。在嘗試了很多種方法 之後，我們發現 morphological opening 能給我們不錯的效果，通常符合以人眼 觀察後的結果。 我們使用的 structuring element 為一個直徑約 6mm 的圓形二元影像。根據 我們的觀察，冠狀動脈的管壁直徑約在 5mm 左右，為了保留緩衝空間，稍微 加大了它的直徑。我們使用的 structuring element 與 MDCT 軸狀切面圖的比例 大小可見圖 6(a)，左上角的小圓點即為 structuring element。決定好 structuring element 後，我們將一層層 MDCT 的灰階影像做 morphological opening，得到一 張張 smoothing 後的圖(參考圖 6(b))，再以原圖減掉 smoothing 後的圖，所得到 的灰階圖已能清楚看到冠狀動脈的部份已經被擷取出來(參考圖 6(c)的黃色圓 圈)。不過，被擷取出來的不一定都是我們要的冠狀動脈，有些是胸骨或脊椎骨 的骨頭外層，有些是肺血管，有的則是 MDCT 過程中產生的雜訊…等，這些東 西因為直徑大小小於 structuring element，所以也會被擷取出來。此時我們將灰 階圖取臨界值，可初步先排除掉比較明顯，確定不為冠狀動脈的部份，結果如 圖 6(d)所示。臨界值的取法，根據有、無顯影劑而有所不同，有顯影劑為 300， 無顯影劑為 150，會有這樣的區別，是因為無顯影劑的影像對比較差，如果臨 界值設定太高，會將可能為冠狀動脈的部份也一併去除。最後一個步驟，根據 上一節中所得到的心臟範圍圖(如圖 6(e))，移除掉心臟範圍以外，冠狀動脈不 可能存在的位置，得到我們所需要的冠狀動脈候選點，圖 6(f)為最後的結果。

\ (a) (b) (c) (d) (e) (f) 圖 6：取得冠狀動脈候選點 (a)為有顯影劑影像，左上角的小圓圈為structuring element的比例大小。(b)為 opening後的結果。(c)為原圖後opening結果的差異圖，黃色圓圈內為冠狀動脈。(d) 是對(c)取臨界值 300 後的結果。(e)為心臟範圍圖。(f)為(d)中取出心臟範圍內的結 果，為冠狀動脈候選點。

有了每一層的冠狀動脈候選點後，我們可以將這些資料點在 3D 空間下標 示出來，如圖 7 所示，雖然還有很多非冠狀動脈的雜訊部份，但是冠狀動脈在 空間分布的狀況已經很清楚了。不過這些資料點數量極多，少則上萬，多則數 十萬，這樣的數量會讓計算量爆增，因此我們需要方法來簡化這些資料點，並 能利用簡化後的代表點，描述出冠狀動脈的分布。 圖 7：冠狀動脈候選點

3.4 C-Means

為了要將大量的資料點轉換為個數較少的代表點， Yan 的方法[13]可以找 出管狀類型的曲線，利用 fuzzy c-means 的方法，僅用少量的代表點表示所有的 資料點，並且建立代表點之間的連線，找出曲線。而我們為了避免複雜的運算， 決定使用較簡單的 hard c-means 方法，一樣可以找出適當的代表點，取代數量 極多的資料點。

The Hard C-Means Algorithm

令空間中 n 個點分別標示為X ={x₁,x₂,...,x_n}，假設我們要將這 n 個點分成 c 個叢集，則陣列 代表 X 被分群後的結果(hard c-partition of X)，陣列大 小為 。其中 ，當 ] [u_ik U = c n× u_ik∈{0,1} u_ik =1時表示點 屬於叢集 k，當 時表示點 不屬於叢集 k。 i x u_ik =0 i x

hard c-means algorithm 的步驟如下：

1) 初始化 c 個點代表叢集的中心點，以vk表示{vk |k =1,2,...,c}。 2) 根據最短的歐基里德距離(euclidean distance)，計算出陣列 U 中的叢集成員 分布，利用以下的方法判斷： ⎪⎩ ⎪ ⎨ ⎧ = − = ,for alli otherwise || || min arg k , 0 if , 1 i j 2 j ik v x u (7)

3) 更新v_k

∑

∑

= = = _n i ik n i i ik k u x u v 1 1 ) )( ( ₍₈₎ 4) 當更新 後沒有變化時則停止，表示已得到最後分群的結果，否則回到第 2 步驟。 k v

Hard c-means algorithm 很容易實作，但是它的缺點在於對雜訊很敏感，在 雜訊下無法有好的分群結果。 實作演算法 1) 初始化 c 個點代表叢集的中心點vk。 一般在初始化代表點時，是以亂數來產生。因為我們使用的方法是 hard c-means，我們利用它只對最近距離的資料點作用的特性，我們初始化的點 是以正規化(uniform)的分布，如同用正方體分割 MDCT 所涵蓋的三度空 間，正方體的中心做為叢集的中心點。換句話說，相鄰的代表點與代表點 之間，它們的三維座標只會有一個座標是不同的，並且這個不同的座標差 異是固定的。舉例來說，某組資料 MDCT 影像空間為 512x512x309，我們 設定的正方體邊長為 20，因此共有 10816 個叢集分割 3D 影像空間。透過 這樣的方式，我們可以加速我們第一回合的 Hard C-Means 過程，要計算叢 集的中心點的新座標時，只要計算與相鄰代表點之間的空間中所包含的資 料點即可，減少很多不必要的運算。不過這個加速方法只有在第一回合有 效，更新後的代表點即沒有這樣的特性可以應用。 2) 如果代表點沒有包含任何資料點，則刪除此代表點。承上所舉的例子，可

以從 10816 個叢集大幅減少至 585 個叢集，因為大部份的叢集是不包含任 何資料點的。

3) 持續 hard c-means algorithm 的步驟 2 到步驟 4 的過程，並刪除不包含任何 資料點的代表點，直到所有代表點與上一次位置的最大位移不到 3mm，表 示代表點的變化已經不大，趨於收斂，在我們的實驗中可以在 10 次內達到 此條件。 經過以上的演算法之後，我們將數十萬個資料點，改以數百個代表點表示， 如圖 8 所見紅色的點，這些代表點中，有些位於我們欲分割出來的冠狀動脈之 中，有些位於胸骨或脊椎骨的骨頭外層，另外有些位於肺血管，還有的則位於 MDCT 過程中產生的雜訊。如果我們能分析出代表點與代表點之間的關係，則 我們可以分割出我們想要的部份。就我們的觀察，冠狀動脈可以視為兩個樹狀 結構，我們利用這一點，可以分割出冠狀動脈。 圖 8：資料點轉換為代表點

3.5 擷取樹狀結構

代表點間的關係 目前我們所求得的代表點位置，分別表示各種不同的冠狀動脈候選點，而 我們最後所要保留的，是真正的冠狀動脈。首先，我們將代表點分成不同的群 組，為了要區分出不同的群組，我們透過代表點之間的連通性來做判斷。如果 某代表點與相鄰代表點之間的資料成員分布夠均勻，則這兩個代表點之間是連 通的，我們可以視這兩個代表點為同一個群組。我們判斷代表點間資料成員分 布是否的均勻的方法很簡單，將屬於兩代表點的資料成員， 依照兩代表點間的 直線距離分成三等份，超出範圍的資料點不列入，計算各等份所佔有存在三等 份內資料點的比率，只要比率最小的等份大於 10%，則視為均勻分布。為了避 免資料點稀疏時仍滿足我們所設定的條件，我們另外加設一條限制，當最小等 分的資料點數小於 10，兩代表點間為不連通。在實作過程中，為了讓計算量減 少，對每個代表點我們只針對與其最靠近的另 5 個代表點做單方向的連接性測 試，如果兩代表點互相滿足連接的條件，則我們判定此兩代表點為連通，這樣 子的限制是為了避免比較偏遠的代表點，因為連通條件太寬鬆所造成不好的結 果。透過這樣的步驟，我們可以將代表點分成多個 connected components。由於 有時候代表點分布太過密集的關係，會呈現網狀交織(如圖 9)的情況，為了讓之 後的樹狀結構分析更有效，我們從每個 connected components 中任選一點當 root，使用 breadth-first search(BFS)演算法解決網狀交織的問題。圖 10(a)可看出 資料點與連通表示圖，圖 10(b)將連通圖分離出來，綠色的線即為連通。

(a)

(b)

找出樹狀結構 針對每一組 connected components，我們擁有幾項資訊： 1.代表點的數量。 2.每個代表點連通鄰近代表點的數量。 3.每個代表點所有資料點成員的數量。 根據我們的觀察，冠狀動脈是樹狀結構，而冠狀動脈候選點中的其他部位， 則鮮少有樹狀結構，即使存在，所佔的空間也不大。基於以上的資訊，我們可 以推斷出，我們想要找出的 connected components 有兩大特性： 1.代表點存在一定的數量。 由於冠狀動脈在空間中分布範圍大，以我們的方法實作 hard c-means， 冠狀動脈需要一定的數量的代表點才能包含，因此 connected components 所擁有的代表點數量不可能太少。 2. 每個代表點連通鄰近代表點的數量大多為 2。 由於冠狀動脈分布較為細長，代表點之間，會呈現一個接一個的樣子， 只有在樹狀分支點的地方，才會有二個以上的連通數量。因此在這個 connected components 中，連通鄰近代表點的數量大多為 2。我們將連通數 為 2 的代表點稱為 2-node。

我們依照以上的資訊，先計算各 connected components 中 2-node 所佔該 components 代表點總數的比率，將比率小於 40%的去除，接著從剩下的 connected components 中選出代表點總數最多的兩個，成功地找出冠狀動脈所在 屬的兩個 connected components。再根據這兩個 connected components 在空間中 所在的位置，決定左冠狀動脈以及右冠狀動脈。我們成功地以自動化、不需要 人為介入的方式，分割出冠狀動脈，如圖 11 所示。

圖 11：冠狀動脈擷取結果 上圖中的兩組 connected components 並不能完整對應冠狀動脈的樹狀結 構，因為有假分支的存在。由於有時候代表點在冠狀動脈中分布太過密集的關 係，會出現假分支的情況，不過假分支在存在，並不會影響我們的實驗結果。 圖 12 將圖 11 中藍色區塊放大並顯示資料點，可以明顯看出有多個假分支的存 在。

第四章 冠狀動脈註冊

4.1 觀察

在第三章所提出的演算法，一開始，我們的目標是分割出經過顯影劑增強 後的心臟電腦斷層掃瞄圖中，冠狀動脈的部份，而我們也的確成功地分割出冠 狀動脈。但是由於我們從醫院中所取得的心臟電腦斷層掃瞄圖另外還有未經過 顯影劑增強的資料組，而未經顯影劑增強的資料組，因為冠狀動脈與其他部位 的對比不明顯，因此在套用我們的演算法時，會在取得冠狀動脈候選點時，由 於所設定的臨界值太低，而包含了太多雜訊進來。如果將這樣雜訊過多的資料 做 hard c-means，不僅大幅增加計算時間，所得到的結果也不好。針對這樣的 影像資料，我們有另外的處理方法，會在本章中做介紹。 醫生在心臟電腦斷層掃瞄圖的判讀上，之所以會同時需要有顯影劑及無顯 影劑兩種資料，目的就是要做比對之用。比如鈣化在有顯影劑的資料中不容易 看到，因為增強顯影的過程中，有些鈣化的訊號可能會和顯影劑的強度差不多 而被醫生忽略，但在無顯影劑中是很容易被看到的。粥狀斑塊在沒有顯影劑中 不易看到，因為對比不明顯的關係，而在有顯影劑中很容易看到無法被顯影劑 影響的粥狀斑塊，還是保持原本的訊號強度。因此我們想將同一個人有顯影劑 及無顯影劑冠狀動脈做比對，比較同一位置中鈣化及粥狀斑塊的情況。而醫生 在 MDCT 的判讀上，除非有適當的工具，否則需要靠足夠的經驗才能確認有顯 影劑的某一點，是對應到無顯影劑的哪個地方。

4.2 Iterative Closest Point

針對有顯影劑及無顯影劑的比對，我們採用的是同一個人在不同時間所拍 攝出來的結果，因此，即使冠狀動脈會隨著呼吸及心跳所影響，它還是保有它 基本的形狀，可是如果是不同人之間的冠狀動脈要做比對，就會有比較大的差 異，所以我們專注在同一個人不同時間的拍攝資料的處理。我們使用的方法， 是在比對(registration)應用上非常常見的作法─iterative closest point(ICP)[14]。 ICP 的好處，在於它保證可以一步一步地往它當時所測得的最小平方距離 (mean-square distance metric)移動，來達到收斂的結果，而且它收斂的速度非常 地快，通常在幾個步驟內就能完成。由於 ICP 執行速度很快，所以我們利用它 來協助取出在無顯影劑幫助下所拍攝的心臟電腦斷層掃瞄圖。我們可以從容易 取得冠狀動脈的有顯影劑的資料中先取得冠狀動脈的形狀，再以這個形狀為模 形，從無顯影劑的資料中，找到跟這個形狀最相似的位置，如此，即使無顯影 劑中的非冠狀動脈的資料量再大，我們還是可以用 ICP 快速找到冠狀動脈大概 位置，在知道冠狀動脈的分布範圍後，可以進一步刪除非冠狀動脈的候選點， 達到去雜訊的效果。

iterative closest point 演算法如下：

z 令所要比對的資料點的集合為 P，共有Np個點，以{pi} r _{表示每個點。令提} 供做為比對的模型為 X，共有N_x個點。 z 對參數做初始化，令P₀ =P，qr₀ =[1,0,0,0,0,0,0]t且k =0。之後，持續步驟 A~D 直到誤差小於τ，τ為可忍受之最小誤差值。 A. 計算最近點：Y_k =C(P_k,X)。Y_k表示每個P_k從X 中選中最靠近的點。

B. 計算位移矩陣：(qr_k,d_k)=Q(P₀,Y_k)。 C. 乘上位移矩陣：P_k+₁ =qr_k(P₀)。 D. 當

∑

則停止，否則回到步驟 A，且累加 k。 = + < − p N i k i k i p p 1 , 1 , || || r r τ 如圖 13 所示，紅色的點為有顯影劑之冠狀動脈代表點，對應到演算法中的 P，藍色為無顯影劑之冠狀動脈候選點，對應到演算法中的 X。經過 ICP 的演 算法後，紅色的冠狀動脈模型因為從藍色的資料點中找到相似的形狀，逐漸地 位移和旋轉模型後，最後收斂到達黑色點的位置，我們藉此得到兩組資料中冠 狀動脈代表點點大約的對應。 圖 13：以 ICP 找出形狀相似之冠狀動脈

4.3 調整位移量

經過 ICP 的協助，我們能從雜訊極多的情況下，從無顯影劑的資料中，成 功 取 出 冠 狀 動 脈 。ICP 不僅幫助我們去除雜訊，另外還計算出變形矩陣 (transformation matrix)，透過它，我們可以將兩組冠狀動脈展示在空間上，經由 觀察，這兩條冠狀動脈各個部份都很接近，但是因為呼吸以及心臟跳動的影響， 這兩條冠狀動脈的形狀還是有些微的不同，沒有辦法這麼容易就做出對應。接 下來我們想要做的，就是提供對照，給定有顯影劑中的一點，推算出無顯影劑 中相對應的點，反過來亦同。 就我們的觀察，即使同一個人的冠狀動脈在不同的時間下會有不同的變 化，但是冠狀動脈的長度變化是不大的，變化的只是冠狀動脈的高低起伏，總 長度的變化是可以被忽視的。因此我們利用這樣的特性，分別從有顯影劑及無 顯影劑的冠狀動脈中選定同一條路徑，將這條路徑轉換成有用的資訊，藉此來 比對兩組冠狀動脈。 對於這條路徑的選擇，我們採用從主動脈與冠狀動脈的分支做為起點，從 冠狀動脈中找一條最長的分支的結尾做為終點。有了這條路徑後，我們根據從 起點開始行走的路徑長度，將它從 3D 空間中轉換成一維的參數，可以將之視 為一條直線，並透過內插的方式，從 MDCT 原始影像中，取得這條直線的縱向 剖面圖。從縱向剖面圖中，我們可以觀察到起點到終點間的變化，在這之中可 能有冠狀動脈的分支，有鈣化的部份，有粥狀斑塊的部份，還有冠狀動脈之外 的心房、心室也會出現在剖面圖裡，這些圖形的形狀和灰階值，是我們做比對 的重要依據。為了能讓兩組冠狀動脈的剖面圖的資訊具有一致性，我們將兩組 已分割出來的冠狀動脈樹狀結構中所有的節點(代表點)取平均為 ，並以 作為 心臟大約的中心點。對於在冠狀動脈上的某一點 ，以 O O i P OPi 為 X 軸(大略垂直於

心臟表面)，PiPi+1為 Z 軸，Z 軸和 X 軸作外積可求出 Y 軸。XZ 及 YZ 平面為兩 個互相垂直的縱向(沿冠狀動脈)剖面，由於 YZ 比 XZ 平面多了冠狀動脈分支的 資訊，適合做為我們用來比對的平面。 一旦有了有顯影劑和無顯影劑的縱向剖面圖後，由於我們已將兩組冠狀動 脈從曲線轉換成直線，因此我們只要適當調整這兩條直線的位移，即可將兩組 冠狀動脈中的分支、鈣化、粥狀斑塊一一做對應，調整位移的目的是為了對冠 狀動脈起點在兩組不同影像中的位置有誤差而做的修正。計算最佳位移量的方 法如下： 1. 對有顯影劑及無顯影劑的縱向剖面圖以 1024 的數值取臨界值，留下灰 階值大於或等於 1024 的部份，分別以 E(如圖 14(a))和 N(如圖 14(b)) 表示。臨界值決定所要比對的形狀資訊，根據我們的觀察，設定為 1024 可以有比較好的結果。 2. 固定 E，讓 N 沿著垂直方向上下移動，以求得最佳位移量x。令 ，其中 表示固定的 E 影像區域， 表示位移後的 N 影像區域，當 ) ( ) (x E N x z R R R = ∩ R_E R_{N( x)} x為負值表示 影像的起始位置在 E 影像的上方， 當當 ) (x N x為正值表示 影像的起始位置在 E 影像的下方， 表示兩 影像交集的區域。 為我們用來量測兩影像是否相似的方法，分別 從 E 和 N 影像中分離出被 所涵蓋的部份，再做互斥的邏輯運算(以 符號表示)，最後取反轉，得到結果，如圖 14(c)所示，中間部份為 冠狀動脈，冠狀動脈以外的部份，當同時為亮點或同時為暗點時，最 後可以得到最多的亮點，表示此時 E、N 影像最為相似。 ) (x N R_{z( x)} ) (x K ) ( x z R ⊗ (9) ) ( ) (( ) (x R E R N K = ∩ ⊗ ∩

(a) (b) (c) 圖 14：YZ 平面比對圖 (a)為取自有顯影劑的 E。(b)為取自無顯影劑的 N。(c)為 E 與 N 作用的結果K(x)。 3. 令兩組縱向剖面圖寬度為 w， 長度為 。 為 objective function，找出某位移量 ) ( x z R h(x) F(x) x所求得的F(x)為最大值，即為最佳位移量。 ) ( ) ( ) ( x h w x K x F × =

∑

(10) 在經過影像比對，並做位移調整之後，最後的結果，類似圖 15 所示，(a)、 (b)兩圖中，左側為有顯影劑、右側為無顯劑的冠狀動脈的縱向剖面圖，(a)圖為 YZ 平面、(b)圖為 XZ 平面組合而成的剖面圖，在三度空間上是互相垂直的，(a) 圖表示心臟表面，因此冠狀動脈分支處可以比較明顯地觀察到，增加比對的準 確度。最後計算出來無顯影劑的剖面圖的位移量為 13mm，右上角的黑色區塊 為位移後所產生的，經過位移後，從冠狀動脈的的分支，或是非冠狀動脈的區

塊，可以看到有顯影劑和無顯劑的冠狀動脈剖面圖的特徵即互相對應。圖 15(c) 為(a)位移前的狀況，明顯看出所擷取出來的冠狀動脈起點是不同的。 (a) (b) (c) 圖 15：位移調整圖 以上三張圖中，左側為取自有顯影劑影像，右側取自無顯影劑影像。(a)為 YZ 平面中， N 經過位移 13mm 後的結果。(b)為 XZ 平面中，N 經過位移 13mm 後的結果。(c)為 YZ 平 面中，未做位移的情況，用來與(a)做比較。

第五章 實驗結果

在這一章，我們將演算法應用在實際的例子，並對結果做一些討論。透過 國立台灣大學醫學院放射科的協助，我們總共取得了 8 組 MDCT 資料做為測試 之用，這 8 組資料來自 4 個不同的病人，每個人皆有兩組不同的資料，一組為 有顯影劑的，另一組則是沒有顯影劑的，不同的影像有不同的規格，如下表所 示： 表 1：資料規格 編號 病人編號 顯影劑 拍攝區域 (cm*cm) 張數 1 A 有 20x20 193 2 A 無 25x25 256 3 B 有 20x20 212 4 B 無 25x25 288 5 C 有 20x20 207 6 C 無 25x25 256 7 D 有 20x20 181 8 D 無 25x25 224 資料組的編號為 1~8，分別代表不同的心臟電腦斷層掃瞄圖。病人編號為 A~D，分別代表不同的病人。拍攝區域為心臟電腦斷層掃瞄圖所涵蓋的面積， 由於影像解析度皆為 512pixel X 512pixel，因此當拍攝區域為 20x20 時，每 個 pixel 的間距為 0.39mm，而當拍攝區域為 25x25 時，每個 pixel 的間距為 0.49mm。每組資料的拍攝張數不一，但是每一層的間距受到 MDCT 探頭的影 2 cm 2 cm

像，間距固定為 0.625mm。 為了驗證冠狀動脈的擷取效果，我們使用人工標點的方式，在編號 1~8 資 料中，各標上 50 個為冠狀動脈的點。標點工具如圖 16 所示，藍色的圈圈為冠 狀動脈所在位置。有了人工所標示冠狀動脈的位置後，再和電腦自動抓取出來 的冠狀動脈做比較，測量人工標示的點與電腦抓取的冠狀動脈的最短距離。由 於冠狀動脈的直徑大約為 5mm，而人工標點的方式是從一層層的 MDCT 資料 中點出冠狀動脈的位置，標記的時候不一定會標記在冠狀動脈的中間線的位 置，而電腦自動擷取出來的冠狀動脈模型是由點與線所構成，所有的點與線也 不保證通過中間線，因此我們所使用的標準，只要人工標示的點與電腦擷取的 冠狀動脈模型的最短距離小於 5mm，則視為成功的擷取。 圖 16：標點工具

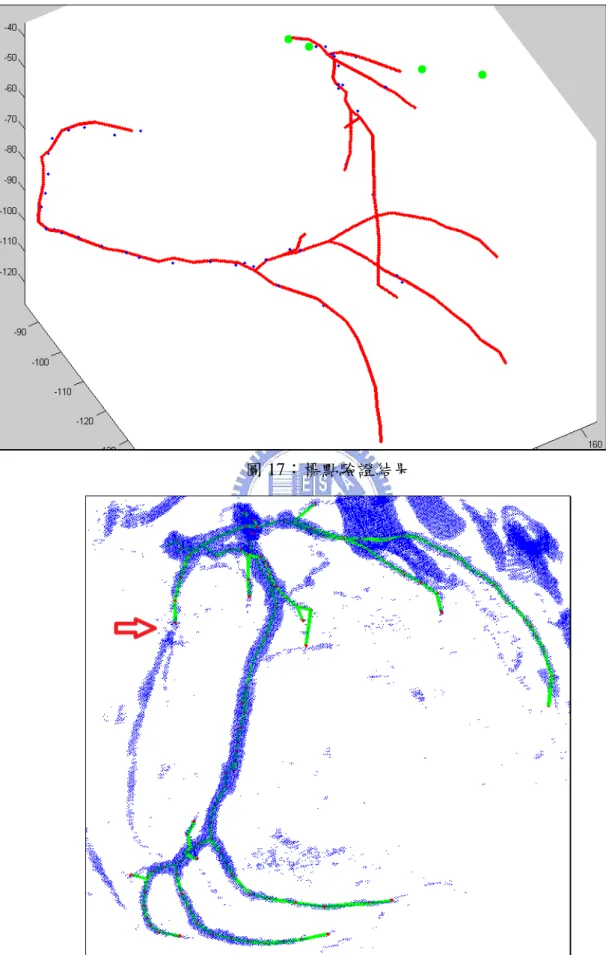
各資料的擷取率如表 2 所示，大多數的資料的擷取成功率在 92%以上，而 少部份失敗次數則明顯偏多。經過觀察之後，發現失敗偏多的原因，在於電腦 自動化所擷取的冠狀動脈，受到雜訊造成資料點不連續的結果，因此自動化冠 狀動脈擷取演算法認為此區域之後的部份，不為冠狀動脈的一部份，如圖 17 所示紅色樹狀圖為編號 1 資料組中所擷取出來的冠狀動脈結構，藍點為距離我 們擷取出的冠狀動脈範圍 5mm 以內的點，而綠點為距離我們擷取出的冠狀動 脈最近點超過 5mm 以上的點，即為失敗的例子。從圖 17 可看右上角有兩個距 離冠狀動脈很遠的標記點，透過圖 18 從另一個角度並加上資料點觀察此冠狀動 脈，發現因為一小段的資料點不連續(紅色箭頭處)，因而沒有連通到下一段冠 狀動脈，才會造成這麼大的誤差。由此我們可以知道，我們的自動化冠狀動脈 擷取演算法，容易受到雜訊的影響，而無法完整擷取出所有屬於冠狀動脈的部 份。 表 2：資料擷取率 編號 成功 失敗 成功率(%) 1 46 4 92 2 44 6 88 3 48 2 96 4 46 4 92 5 50 0 100 6 39 11 78 7 49 1 98 8 49 1 98

圖 17：標點驗證結果

第六章 結論與未來展望

在本篇論文中，我們發展了兩個演算法。第一個演算法，自動化取出冠狀 動脈，完全不需要人為的介入，我們利用了形態學的方法取出電腦斷層掃瞄圖 中可能為冠狀動脈的部份，然後使用 hard c-means 將龐大的資料轉為代表點， 再以樹狀結構分析的方式取得冠狀動脈。第二個演算法，自動化找出兩組冠狀 動脈的對應點，利用 ICP 先將兩組冠狀動脈依照形狀做初步的對應，再以縱向 剖面圖的影像資訊做比對，找出位移量，做為比對的參考。有了這兩套自動化 的方法，自動化預診系統將更容易實現。 由於研究時間有限，我們未能做出一套完整的自動化預診系統，但是最艱 難的部份已經被解決，之後，我們只要針對冠狀動脈的橫切面做分析，可以從 中得知冠狀動脈的直徑、血管的順暢程度、是否有被鈣化或粥狀斑塊阻塞…等， 計算出冠狀動脈任一位置的阻塞率，並將預診的結果提供給醫生做參考，加速 醫生的診斷速度。在兩組冠狀動脈做比對的演算法當中，以位移量做比對的方 式我們還想做改進，因為經過 ICP 後，兩條冠狀動脈不僅位置相近，形狀也差 不多，我們想發展出另一套演算法，直接將其中一條冠狀動脈做一些形變，來 趨近另一條，而不用影像比對縱向剖面圖的方式，可以加速對應的過程。針對 現有的自動化冠狀動脈擷取演算法，主要還有兩個改進的方向，一個是取中間 線，另一個是將樹狀結構做延伸。取中間線的目的是為了讓我們所擷取出的冠 狀動脈樹狀結構連線圖能穿過冠狀動脈的正中心，如此在以距離判斷某點是否 在冠狀動脈的範圍內時，可以從 5mm 降至 2.5mm，增加準確度。而將樹狀結 構做延伸，則是根據影像強度的相關性，追蹤出我們因為雜訊所遺漏的冠狀動 脈部份，增進自動化分割演算法的效果。在驗證我們的冠狀動脈擷取效率上， 未來會使用更多的資料來做測試，並由專業的醫師協助我們判斷冠狀動脈的擷

取準確度是否合乎醫學上的要求。期望未來我們發展出的自動化冠狀動脈預診 系統能夠克服雜訊或訊號不足的問題，在無顯影劑的 MDCT 影像中依然能夠找 出完整的冠狀動脈，並且能從冠狀動脈的橫切圖取出完整的資訊，做出完整的 分析，以得到精確的診斷結果，讓冠狀動脈的診斷不再需要顯影劑的幫助，依 舊能夠找出可能造成冠狀動脈阻塞的鈣化或粥狀斑塊的部份，避免因為顯影劑 對人體造成的影響。

參考文獻

[1] 劉鵬程, “心導管檢查或治療在不同醫院屬性下之醫療資源耗用、死亡率及重返心導管室率之分

析”, 國立臺灣大學醫療機構管理研究所碩士論文, 2005 年 12 月

[2] Yuji Ukai and Noboru Niki, “A Coronary Calcification Diagnosis System Based on Helical CT Images”, in IEEE Transactions on Nuclear Science VOL. 45, NO. 6, December 1998

[3] 董俊良, “三維多重探頭電腦斷層掃瞄之冠狀動脈影像分析與評量系統”, 成功大學資訊工程系

碩士論文, 2004 年 7 月

[4] Syoji Kobashi and Yutaka Hata, “Automatic Segmentation of Blood Vessels from MR Angiography Volume Data by Using Fuzzy Logic Technique”, in Part of the SPIE Conference on Image Processing, February 1999

[5] Changjiang Yan, Shoji Hirano and Yutaka Hata, “Extraction of Blood Vessel in CT Angiography Image Aided by Fuzzy Logic”, in Proceedings of ICSP2000, pp. 926-929

[6] Stefan Wörz and Karl Rohr, “Segmentation and Quantification of Human Vessels Using a 3-D Cylindrical Intensity Model”, in IEEE Transactions on Image Processing , VOL. 16, NO. 8, August 2007

[7] K. Krissian, G. Malandain, N. Ayache, R. Yaillant, and Y. Trousset, “Model Based Detection of Tubular Structures in 3D Images,” Comput. Vis. Image Understand., VOL. 80, NO. 2, pp. 130-171, 2000

[8] H. Noordmans and A. Smeulders, “High Accuracy Tracking of 2D/3D Curved Line Structures by Consecutive Cross-Section Matching,” Pattern Recognit. Lett., VOL. 19, NO. 1, pp.97-111, 1998

[9] Li-yueh Hsu and Murray H. Loew, “Automated Registration of CT and MR Brain Images Using 3-D Edge Detection”, in Proceedings of the 20th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, VOL. 20, NO 2, 1998

[10] Petra A. Van den Elsen, J. B. Antoine Maintz, Evert-Jan D. Pol, and Max A. Viergever, “Automatic Registration of CT and MR Brain Images Using Correlation of Geometrical Features”, in IEEE Transactions on Medical Imaging, VOL.14, NO. 2, June 1995

[11] Jan Hendrik Metzen, “Matching of Anatomical Tree Structures for Registration of Medical Images”, in Image and Vision Computing, 2008

[12] Rafael C. Gonzalez, Richanrd E. Woods, “Digital Image Processing”, second edition, Prentice Hall, 2002

[13] Hong Yan, “Fuzzy Curve-Tracing Algorithm”, in IEEE Transactions on Systems, Man, and Cybernetics—Part B: Cybernetics, VOL. 31, NO. 5, October 2001

[14] Paul J. Besl and Neil D. McKay, “A Method for Registration of 3-D Shapes”, in IEEE Transactions on Pattern Analysis and Machine Intelligence, VOL. 14, NO. 2, February 1992