國小五年級高中低能力兒童機率概念與思考層次之研究

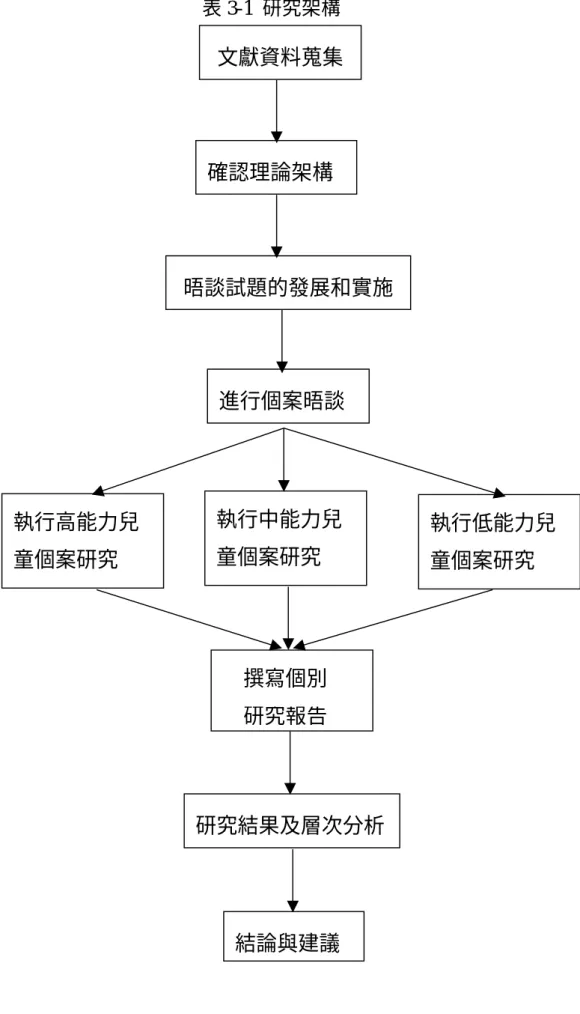
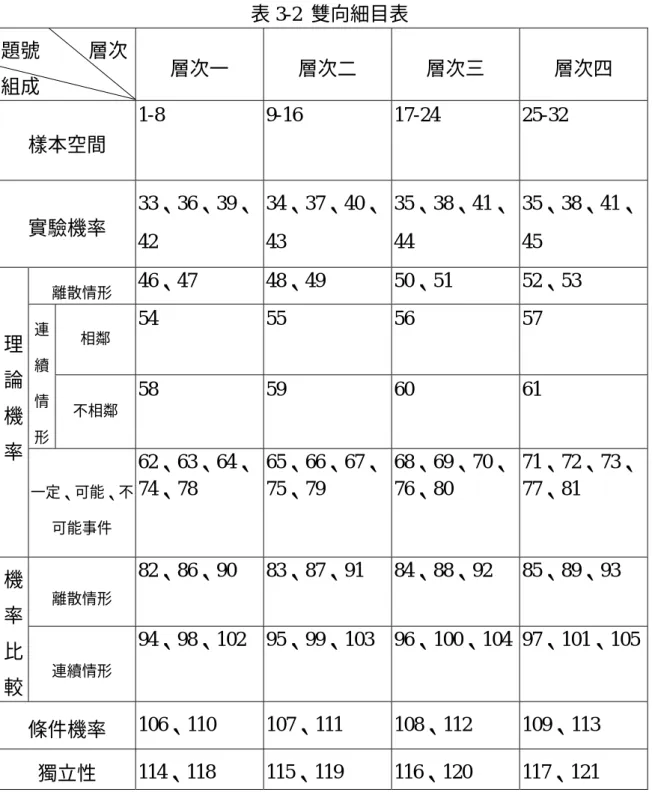
國立台中師範學院數學教育學系理學碩士論文

指導教授：許天維 博士

胡豐榮 博士

國小五年級高中低能力兒童

機率概念與思考層次之研究

研究生：楊怡芳 撰

中 華 民 國 九 十 四 年 六 月

摘要

本研究旨在探討國小五年級兒童，在機率概念中樣本空間、理論機率、實 驗機率、機率比較、條件機率及獨立性的直觀概念及思考層次。本研究以台中 縣某鄉鎮的國小五年級高、中、低能力三位兒童為晤談對象，採用「訪談導引 法」訪談三個個案，利用自編的晤談題目，來了解高、中、低能力兒童在機率 六組成中的直觀概念及思考層次，並綜合兒童答題情形，與國內外相關研究做 比較。 研究結果顯示，在樣本空間方面，中能力兒童和低能力兒童不習慣將所有 情況列出，傾向注意什麼較可能發生，國外研究亦有類似的發現；在實驗機率 方面，高、中、低能力兒童無法從已做出的隨機實驗次數統計表中發現，投擲 次數越多，正反面出現的次數和投擲總次數的比值越接近 1/2，皆沒有大數法 則的概念；在理論機率方面，高、中、低能力兒童大都能清楚判斷事件發生的 可能性，但只有高能力兒童皆能使用分數正確回答最有可能發生事件的機會； 在機率比較方面，中、低能力兒童在離散情境（分母不同），並無考慮母群體 的多寡，採用 Falk 的「更多的目標事件策略」；在條件機率方面，高、中能力 兒童能說出「置回」與「不置回」事件發生的可能性有無改變；在獨立性方面， 高能力兒童能肯定每一次抽糖果的獨立性，中、低能力兒童並不認為每次試驗 的結果是獨立的，對先前的試驗結果做分析以預測下次的結果。 關鍵字：國小兒童、機率概念、機率思考層次

Abstract

The aim of this study is to investigate the intuitive concepts of probability and

levels of thought for 5thgrade elementary school’s students in probability, including

sample space, experimental probability, theoretical probability, probability

comparison, conditional probability, and independence. The researcher interviewed three high-level, mid-level, and low-level students of an elementary school in

Taichung County. The researcher used self-edited problems and adopted the method of interview guide to interview three cases and to understand their intuitive concepts and levels of thought, also, integrated the students’ responses to compare with

related references.

The results of this study show that, in sample space, the mid-level and low-level students are not accustomed to provide a complete listing, but tend to focus subjectively on what is more likely to happen. The results of our study have similar findings with related references. In experimental probability, students are unable to find from random experiments statistics table that the more we throw coins, the more the ratio of positive times and total times is near to 1/2. In

theoretical probability, students are able to distinguish “certain”, ”impossible ”, and “possible” events. Only the high-level student is able to assign a numerical

probability to predict most/least likely events. In probability comparison, the

mid-level and low-level students adopt a strategy called 「more of the target event」 of Falk’s research in discrete situations. In conditional probability, the high-level and mid-level students recognize that the probability of events change or not change in with replacement and without replacement situations. In independence, the

high-level student can understand the independence of drawing candy each time. The mid-level and low-level students do not think that every experimental result is independent, and they analyze previous experimental results to predict next results. Key words: elementary school students, probability concepts, levels of thinking in

目錄

第一章 緒論………1 第一節 問題背景與研究動機………1 第二節 研究目的及待答問題………3 第三節 名詞解釋………4 第四節 研究限制………7 第二章 文獻探討……….8 第一節 理論架構………8 第二節 機率概念之理論性研究………18 第三節 機率概念之實證性研究………24 第四節 我國現行機率課程與 NTCM 機率課程………..43 第五節 綜合討論………51 第三章 研究方法……….52 第一節 研究架構與流程………52 第二節 研究對象………54 第三節 研究工具的發展與實施………56 第四節 資料的蒐集與分析………62 第四章 結果與討論……….66 第一節 晤談結果………66 第二節 個案在機率思考層次上之分析……… .123 第三節 跨個案分析………..128 第五章 結論與建議………...138 第一節 結論………..138 第二節 建議………..144 參考書目……….149 附件一……….155 附件二……….159

第一章 緒論

第一節 問題背景與研究動機

「接下來這個問題我們抽一個小朋友上台做做看」，只見班上小朋友竊竊 私語的說「一定又是他中獎」，而班上有著「籤王」封號的小朋友則是緊張的 面紅耳赤，擔心又是自己被抽中，殊不知每個人被抽中的機率其實是相同的。 機率是生活經驗中的一部分，其實用性及重要性普遍受各國教育家的重視（朱 雅瑋，民 85），兒童卻常存在如上述機率概念的迷思，要解決此問題，當務之 急，應即時給予兒童正確之機率觀念，在這之前，當然必得先了解兒童在機率 的起點行為。 國內機率文獻大都只探討兒童在機率的學習情形或迷思概念（朱雅瑋，民 85；陳欣民，民 91；韓燕言，民 92），歸納出兒童的機率思考情形、迷思概念 及直觀概念類型，很少探討究竟他們的機率概念的起點行為到達何種程度。在 國外，Jones, Langrall, Thornton & Mogill（1997）提出了能具體描述起點行為 程度的機率思考架構，他認為，「雖然已有許多實證性的研究（substantial

research），探討了兒童的機率思考。但卻沒有任何研究能對兒童學習機率的歷

程，提出一個系統性的架構（a systematic framework in probability），進而對兒 童的學習能作適當的預測。再者，缺乏理論架構所進行的教學往往很難達到教 學效果，甚至很多教學活動是不適當的。」（Fennema, Carpenter & Peterson，

1989）。Piaget & Inhelder（1975）提出了兒童機率概念的認知發展階段論；

Fischebin（1975）則從兒童的直觀想法出發，研究兒童機率概念的發展；Tversky & Kahneman（1982）提出了兒童判斷及預測機率時常用到的捷思策略，以上 學者僅探討了兒童在不同年齡層的機率發展及迷思概念（misconception）類 型，並無詳細論述在兒童機率各向度的發展情形。Jones et al.（1997）及 Jones, Langrall, Thornton & Tarr（1999）不但研究了兒童的機率思考，更發展出了機 率思考架構，訂出兒童機率思考四個漸進的發展層次，可以具體描述兒童機率

概念的起點行為。 Jones et al.（1997）根據文獻探討及觀察兒童二年多來，提出了「機率思 考四組成四層次」架構。他們對八位三年級的兒童進行個案研究，分別在機率 教學前後進行訪談，訂出了在「樣本空間」、「理論機率」、「機率比較」和「條 件機率」四個組成（constructs），及「主觀」、「過渡」、「非正式量化」及「量 化」四個兒童的機率思考層次，企圖發展一個最初的架構去描述及預測兒童如 何在機率的情況之下去做思考，並根據這個初始的架構產生評價的調查，再利 用評價的調查精練及確認這一個架構，希望能提供在小學機率的課程設計者一 個理論的根據。而 Jones et al.（1999）將先前的機率架構做更深入的擴充和研 究，又增添了「實驗機率」和由條件機率引伸出來的「獨立性」，提出了「學 生機率推論六組成四層次」架構，目的在闡述小學生與中學生展現出來機率思 考的範圍。這些闡述打算提供一個背景，能夠幫助老師瞭解跟培養兒童的機率 推理。Jones et al.（1997）指出，此研究的思考層次的主張和 Piaget & Inhelder （1975）的認知發展階段是一致的。基於此，研究者欲根據 Jones et al.（1999） 之理論架構，來探討兒童在六個組成之機率思考層次。 在國內的機率課程方面，八十二年版課程在六年級開始有機率課程（單元 目標：認識機率的初步概念），在九年一貫課程暫行綱要，於國中一年級開始 有機率課程（D-3-3 能運用生活經驗來瞭解機會）；依據 92 年 5 月 20 日最新修 訂 94 學年度起生效實施的九年一貫課程綱要草案，到九年級才開始有機率課 程（D-4-05 能以具體情境介紹機率的概念。）。美國教師協會（NCTM）（2000） 的 Grades 3-5（國小 3 到 5 年級兒童）課程標準中，已有機率課程，九年一貫 課程比國外延遲了六年才引入機率課程。八十二年版之前的數學課程在國小就 引入機率的初步概念，國中生尚存有許多機率的迷思概念（林燈茂，民 78，陳 順宇、鄭碧娥，民 82），九年一貫課程將機率初步概念延至國中引入，會不會 讓兒童日後在機率的起步學習產生更大的困難？什麼樣的機率課程適合在國 小先引入及早給予兒童基本的概念？到底國內國小兒童的機率思考層次為

何？林燈茂（民 78）表示，「比值接近」是簡單機率的教學入門之鑰，根據 Piaget & Inhelder（1975）的研究，第三階段形式運思期（11 歲以上）的兒童已能真 正了解比例概念。因此本研究針對國小五年級兒童（形式運思期）高能力、中 能力、低能力各一位兒童在樣本空間、理論機率、實驗機率、機率比較、條件 機率及獨立性六個組成的思考層次，期能提供教師及課程編排者教學上和課程 編排之參考。

第二節 研究目的及待答問題

研究者根據 Jones et al.（1997）的「機率思考四組成四層次」架構及 Jones et al.（1999）的「學生機率理解六組成四層次」架構，選取國小五年級低、中、 高能力兒童各一位兒童進行研究，為了能確實了解兒童的機率思考層次以對照 機率思考架構，本研究以晤談的方式進行。主要研究目的如下： 1. 了解兒童在六個機率組成的直觀概念。 2. 分析高、中、低能力兒童在六個機率組成的思考層次。 3. 綜合兒童答題情形，並與國內外相關研究做比較。 針對上述研究目的，本研究之待答問題如下： 1.高、中、低能力兒童在六個機率組成的直觀概念為何？ 2.高、中、低能力兒童在六個機率組成的思考層次達到 Jones et al.（1999）機 率思考四層次的哪一層次？ 3.綜合高、中、低能力兒童在六個機率組成之答題情形，與國內外相關研究的 相似或差異為何？

第三節 名詞解釋

壹、機率六組成 在本研究中機率六組成分別為樣本空間、實驗機率、理論機率、機率比較、 條件機率及獨立性。 貳、樣本空間 在某一種特定的實驗中，可能出現的所有情形所成之集合，稱之為樣本空 間（sample space），簡寫成Ω。例如擲一顆骰子，所有可能出現的點數是一點、 二點、三點、四點、五點及六點。因此，Ω＝{一點、二點、三點、四點、五 點、六點}為其樣本空間。 參、衍生性策略 衍生性策略（generative strategy）是指兒童在列出隨機實驗之樣本空間結 果時，並非隨意列出，而是採用有系統的方式列出完整的樣本空間，例如使用 里程表策略（odometer strategy）和最大遷移策略（maximal shift strategy） （English，1993）。里程表策略即先固定前項，再變動後項，等後項所有的可 能均出現後，再以相同的方式排出其他不同的結果；最大遷移策略即先固定中 間項，等前後項的可能均出現後，再以相同的方式排出其他不同的結果。 肆、樣本空間一階段二階段及三階段之隨機實驗 一階段（one-stage）隨機實驗，是指例如投擲一枚硬幣一次，可能出現樣 本空間之結果為｛正、反｝；二階段（two-stage）隨機實驗，是指例如投擲一 枚硬幣兩次，可能出現樣本空間之結果為｛（正正）、（正反）、（反正）、（反反）｝； 三階段（three-stage）隨機實驗，是指例如投擲一枚硬幣三次，可能出現樣本 空間之結果為｛（正正反）、（正正正）、（正反反）、（正反正）、（反正反）、（反

正正）、（反反反）、（反反正）｝。 伍、對稱性機率實驗 機率實驗之每一樣本點可能發生的機會，在直觀上沒有理由說它們不相等 時，謂之「對稱性機率實驗」（施能宏，民 86）。例如一個不透明箱子中，有大 小相同的紅球、黃球、籃球各一個，從箱子中抽出一球即屬「對稱性機率實驗」。 陸、時近效應 時近效應（recency effect）是指從一個裝有紅球及黃球各一的箱子中，抽 出一球，在一連串的實驗結果均為「紅球」之後，若兒童預測下一個結果還是 「紅球」，這種現象稱為「正時近效應」（positive recency effect）；反之，若預 測下一個結果是「黃球」，則稱為「負時近效應」（negative efficiency recency

effect）。 柒、事件 樣本空間的部分集合稱之為事件（event）。例如投擲一顆骰子，若A＝ {一點、三點、五點}，則A表示投擲一顆骰子出現奇數點數的事件。 捌、機率 機率（probability）P為一個由事件所成的集合映到[0，1]之函數，且滿 足 _      =

U

_in Ai p 1 ＝

∑

= n i i A P 1 ) ( ，這裡n為任意正整數，Ai為彼此互斥之事件。例如Ω＝ {一點、二點、三點、四點、五點、六點}，A為Ω中之事件，令 P

( )

A = ) ( ) ( Ω n A n ， 則P為一機率。本研究將機率視為「理論機率」。

玖、機率直觀概念

「直觀」（intuition）有時和「發覺」（revelation）、「靈感」（inspiration）、「常

識」（common sense）是等義的（朱雅瑋，民 85）。本研究的定義是採 Fischbein

（1987）的觀點，他將直觀定義為一種每個人自然而發的、幾乎是本能的信念。 它是一種認知的型態，對於擁有直觀想法的人來說，它是由腦中立即出現的意 念，這個想法是不證自明的（self-evident）。 拾、機率思考層次 本研究所指機率思考層次為 Jones et al.（1999）的研究中之四層次，即層 次一：主觀的（subjective）。層次二：過渡的（transitional）。層次三：非正式 量化的（informal quantitative）。層次四：以數字表示的（numerical）。 拾壹、高中低能力兒童 郭換枝以瑞文氏智力測驗成績，來評估兒童在建構式數學教學前後，兒童 的智力進展。因此，本研究選取全班瑞文氏智力測驗成績屬於前 27﹪之兒童一 位，當作高能力兒童。屬於後 27%之兒童一位，當作低能力兒童。屬於中間 46﹪之兒童一位，當作中能力兒童。

第四節 研究限制

壹、研究年級 本研究對象為國民小學五年級尚未接觸過機率單元教學之兒童，對於其他 年級及學習過機率課程的兒童，並未予以廣泛探究。 貳、研究地區 本研究只針對位於台中市近郊之台中縣的某所國民小學兒童來進行，至於 地區的差異，如山地、偏遠、離島地區，是否也有相同現象，則因研究的人力、 物力、時間限制，無法加以探討。 參、晤談對象 因研究人力不足，本研究選取高、中、低能力僅各一位兒童，進行晤談。 本研究不宜過度推論。

第二章 文獻探討

為探討兒童在機率六組成的直觀概念、思考層次及與國內外相關研究比 較，因此，本章共分為五節：第一節介紹本文的理論架構為 Jones et al.（1997） 及 Jones et al.（1999）的理論，第二節論述國外相關機率思考層次之理論，為 理論性研究，為了將兒童的概念與國內外研究做比較，因此在第三節整理了國 內外兒童在機率六組成的想法，並且在第四節比較國內及 NCTM（2000）的機 率課程，最後在第五節提出國內外相關研究不足之處。

第一節 理論架構

Jones et al.（1997）及 Jones et al.（1999）針對八位三年級的兒童所做為期 兩年的研究，及針對小學及中學兒童進行為期三年的教學實驗，並根據國小現 行課程、文獻探討及觀察，洞察兒童的機率思考背景，企圖要（a）發展一個 最初的架構去描述及預測兒童如何在機率的情況之下去做思考（b）根據這個 初始的架構去產生評價的調查（c）使用評價的調查去精練及確認這一個架構， 發展出了「機率思考四組成四層次」架構以及「學生機率推論六組成四層次」 架構。 正如 Jones et al.（1997）所說，「雖然已有許多實證性的研究，探討了兒童 的機率思考。但卻沒有任何研究能對兒童學習機率的歷程，提出一個系統性的 架構，進而對兒童的學習能作適當的預測。再者，缺乏理論架構所進行的教學 往往很難達到教學效果，甚至很多教學活動是不適當的。」（Fennema, Carpenter & Peterson，1989）

Jones et al.（1997）及 Jones et al.（1999）的研究驗證且闡述了機率發展的 架構。在這架構主要的組成是樣本空間、實驗機率、理論機率、機率比較、條 件機率及獨立性。每一項組成有四種發展層次，為直觀到量化的推論。層次一 的兒童在碰到與機率有關的問題時不能辨識隨機的現象而且以主觀的想法來 判斷；兒童在層次二的思考是過渡的，介於主觀和質樸的量化思考（naive

quantitative thinking）之間，嘗試使用量的推理，但有時又返回主觀的判斷； 兒童在層次三嘗試使用定量判斷來決定機率，雖然並不總是使用慣例的（普通 的、協定的）的方式表示機率或是可能性，例如機率是「五個中有三個」；兒 童在層次四開始使用數字來表示機率。 此機率思考的架構，所代表的意義為兒童在每一機率思考層次，有不同的 思考方式，各層次隨著概念的發展漸漸向上提升，且各層次之間是連續的；當 達到最高層次（即第四層次），就具備了正確解決機率問題的基本能力（吳靜 瑜，民 88）。

Jones et al.（1997）及 Jones et al.（1999）之研究發現，機率概念六大組成 中，兒童在四種發展層次上之行為特徵與具體行為表現如下。 壹、樣本空間 一、四種發展層次之行為特徵 此組成中，兒童之行為特徵為： 層次一：在一階段實驗列出不完全的結果。 層次二：在一階段實驗列出完整的結果；在二階段實驗用狹窄的及無 組織的方法列出結果。 層次三：能使用部分衍生性策略完整列出二階段的實驗結果。 層次四：能使用標準的衍生性策略且能列出二階段和三階段的實驗結 果。 二、具體行為表現 在本研究中，對樣本空間的理解是在一階段（例如丟擲一枚錢幣）或二階段（例 如丟擲二枚錢幣）等的實驗中展示所有結果的能力。層次一的兒童很少提供一 個完整的樣本空間結果清單，傾向注意主觀的認為什麼較可能發生，甚至是高 層次的兒童也很少主動的列出所有的結果；層次二的兒童在一階段實驗可以列

出完整的結論，在二階段實驗可能可以列出完整的結論縱使沒有用衍生性策 略；層次三和層次四的兒童能使用衍生性策略列出樣本空間中所有可能的結 果，例如里程表策略（odometer strategy）和最大遷移策略（maximal shift strategy） （English，1993）。里程表策略即先固定前項數字，再變動後項數字，等後項 的所有可能數字均出現後，再以相同的方式排出其他不同的結果；使用最大遷 移策略，如排列 rgy 三個字母，先固定中間項 g，再把前後兩項交換，如 rgy 和 ygr。樣本空間被認為是一個重要的成分，可以引導兒童在機率方面的思考。 然而，研究證據注意到兒童在樣本空間的思考常有矛盾的現象，並且強調研究 孩子在機率背景下對這個組成上的思考是非常需要的（Jones et al.，1997）。表 2-1 是兒童關於樣本空間問題之回答情形，問題如附件一（附件一為 Jones et al. （1997）理論架構中之例題）。 表 2-1 兒童在樣本空間概念上的反應 層次 題號 反應情形 一 壹、一 兒童選擇自己最喜歡的顏色，或是選擇疊在上方的顏 色的熊，甚至把箱子搖一搖，兒童仍不改變他的選擇。 壹、二、（一）兒童能列出所有的結果（紅,藍）、（藍,紅），因為生產 性的策略並不需要。 二 壹、二、（一）兒童總結出結果是(2,3) (1,4)和(1,3)。甚至研究者更進 一步的試探，仍無法說出另一個結果(2,4)。 三 壹、三 兒童使用里程表策略列出的結果(1,3)(1,4)(2,3)和(2,4) 且很有自信的說這是全部了（但是如以下著三種顏色 的題目，就無法列出所有的結果）。 四 壹、四 兒童使用了「最大遷移」策略，列出了三種顏色的交 換排列如下：紅綠藍，藍綠紅；綠藍紅，紅藍綠；藍 紅綠，綠紅藍。兒童說「總共有六種方法，同樣顏色 在中間兩次，指出 2 個綠，2 個藍、2 個紅在中間，先 做一次，然後前後再相反」。 貳、實驗機率 一、四種發展層次之行為特徵

此組成中，兒童之行為特徵為： 層次一：不理會隨機實驗所得來的資料，並且使用主觀的判斷去決定 最可能/最不可能的事件；無法察覺在實驗機率和理論機率間 有任何關係。 層次二：判斷最可能/最不可能的事件，只依據小部分樣本試驗的結 果；當實驗的資料與預想的想法相衝突時，可能會回復到主 觀的判斷。 層次三：能了解欲判斷機率事件必須依據足夠多的廣泛試驗結果；承 認當一個試驗樣本產生一個實驗機率會和理論機率有顯著 的不同。 層次四：蒐集適當的資料去決定實驗機率的數值；從一個大的試驗樣 本決定的實驗機率約等於理論機率；一個事件的機率只有在 實驗上才可以被決定。 二、具體行為表現 實驗機率的重要性是不能被低估的，雖然實驗機率值與理論機率 值是息息相關，但這層關係沒辦法立刻在小學生跟中學生裡面顯現 （Jones et al.，1999）。一個事件的實驗機率值是建立在實驗跟模擬的 基礎上,並且使用相對頻率來決定一個事件的可能，例如，一個箱子裡 有紅、黃、藍、綠、白色 5 種卡片，抽 20 次，抽完放回，紅色卡片 被抽到 8 次，在 20 次的抽籤裡面相對頻率或實驗機率值是 20 次裡有 8 次。具備實驗機率概念要有「收集適當資料以求出機率值」、「了解 實驗機率是根據實驗觀察的結果來判斷一個事件的機率」、「判斷一個 事件的機率要依據足夠多的試驗結果」。表 2-2 是兒童關於實驗機率 問題之回答情形，問題如附件一。

表 2-2 兒童在實驗機率概念上的反應 層次 題號 反應情形 一 貳 女生回答會抽中莫緹娜，因為莫緹娜是女生。她根 據自己的喜好來回答，完全沒有考慮到機率值。 二 貳 兒童覺得斯吉爾最有可能當班長，因為 20 次的實驗 中，他被抽到了 8 次，是最多的。 三 貳 兒童回答，雖然斯吉爾被抽中的次數最多，但那是因 為抽的次數不夠多，珍妮佛、莫緹娜 莫妮卡、菲利普、 斯吉爾卡片都只有一張，所以被抽中當主席的機會應 該都相等。 四 貳 兒童回答，每個人的機會都相等，都是 1/5，如果抽 100 次，每個人有 20 次被抽中的機會。 參、理論機率 一、四種發展層次之行為特徵 此組成中，兒童之行為特徵為： 層次一：藉由主觀的判斷去預測最可能/最不可能的事件；可判斷必然 和不可能事件。 層次二：藉由量化的判斷去預測最可能/最不可能的事件，但有可能會 回復到主觀的判斷。 層次三：藉由量化的判斷去預測最可能/最不可能的事件，其中包含連 續中(continuous)非相鄰的(non-contiguous)情形；使用非正式 數字去比較機率；使用量化判斷「必然」、「不可能」及「可 能」的事件。。 層次四：預測一階段或簡單的二階段實驗最可能/最不可能的事件；能 用分數值表示機率。 二、具體行為表現 在本研究中對於「理論機率」的了解，是能藉由理論和操作來證

明二個或三個事件中，哪一個最有可能或最不可能發生，也包含了能 證明發生機率相同。表 2-3 是兒童關於理論機率問題之回答情形，問 題如附件一。 表 2-3 兒童在理論機率概念上的反應 層次 題號 反應情形 參、一、（一） 兒童選擇黃色，因為喜歡黃色。 參、一、（二）兒童回答紅色，因為箱子搖動過後，紅色的球跑到最 底下了。 一 參、一、（三） 兒童回答，一定會。 二 參、二 兒童回答黃色，因為只有兩個，而且他們比較靠近箱 子的下方。雖然兒童試著使用定量思考，但卻是不嚴 密的且表面上是主觀的。 參、三、（一） 兒童一貫的使用數字來量化機率，他說「綠色最容易， 且拿到機會是 5 個有 4 個」，兒童真正建立了自己的機 率量測。 參、三、（二） 兒童回答「紅色，因為一半都是紅色，只有一些是黃 色，但藍色又多一點，紅色是 4 個中有 2 個，或是 3 個中有 2 個」。缺少分數的知識妨礙他正確的表示出機 率。兒童顯然能夠在離散的情況下（例如糖果遊戲） 反應比連續情況（例如飛鏢遊戲）還快。 三 參、三、（三） 兒童回答，可能，機會是 6 個中有 1 個。 參、四、（一） 兒童會回答，紅色最有可能，機會是 4/5。 四 參、四、（二） 兒童回答，可能，機會是 1/6。 肆、機率比較 一、四種發展層次之行為特徵 此組成中，兒童之行為特徵為： 層次一：在不同樣本空間以主觀想法去比較機率；不能區分「公平」 和「不公平」的機率事件； 層次二：以量化思考來做機率比較（但不一定正確且在連續的情形中 會有所限制）；開始能分辨「公平」和「不公平」的機率事

件。 層次三：以正確的量化推理去比較機率值；以量化推理去判斷，但是 可能在連續情形中會有限制；以明顯的量化推論為基礎去區 分「公平」及「不公平」的機率事件。 層次四：能正確做機率比較並以分數表示；連續中相鄰(contiguous) 及非相鄰事件皆能以分數正確表示機率值；用相同的分數表 示相同可能事件的機率值。 二、具體行為表現 兒童能了解「機率比較」，是指能了解（a）在隨機的刺探下，哪 一種機率情況目標事件較可能發生；（b）目標事件在兩個機率情況下 是否有相同的機率。表 2-4 是兒童關於機率比較問題之回答情形，問 題如附件一。 表 2-4 兒童在機率比較概念上的反應 層次 題號 反應情形 肆、一、（一） 兒童選擇 A 轉盤，因為 A 轉盤比 B 轉盤有較大的紅色 區域，此位兒童和一般典型的層次一兒童想法相同， 都不願意合併不相鄰的結果，完全沒有察覺到 A 轉盤 和 B 轉盤有相同的機會。 一 肆、一、（二） 兒童無法分辨哪一個轉盤是公平的。 肆、一、（一） 兒童使用”更多”策略來判定最有利的情況對於目標顏 色。他在定量此情況時反映出缺少精確度，回答說是 轉盤 A，因為紅色比較多，機會是 50-50。 二 肆、一、（二） 兒童回答第二個是公平的，機會都是 2。

肆、二 兒童選擇轉盤 A，同時說「6 個裡面有 4 個是紅色， 而 6 個裡面有 2 個是白色」。並且說「轉盤 B 中，紅 色是 6 個中有 2 個。」。 肆、一、（一） 兒童無法了解兩個轉盤紅色的機會都是一樣的。他說 「我會選轉盤 A，紅色都串成一串」。他在別的問題上 都可以正確的使用數字來表示，但在這一題的情況下 卻困惑了他。很顯然地，若包含轉盤 B 非相鄰的結果， 將會阻止他使用數字的想法，使他回復到一個不準確 的定量方式。這樣的思考是機率比較層次三的特性。 三 肆、一、（二） 兒童回答第二個是公平的。因為都是 4 個中有 2 個。 肆、一、（一）兒童會認為選擇 A 轉盤（紅色機會 1/2）及 B 轉盤（紅 色機會 6/12），射中紅色的機會是一樣的。 四 肆、一、（二） 兒童回答第二個是公平的，機會是 1/2。 伍、條件機率 一、四種發展層次之行為特徵 此組成中，兒童之行為特徵為： 層次一：只注意到第一次實驗的結果，不能完整列出第二次實驗的可 能情形；使用主觀想法說明「置回」與「不置回」事件。 層次二：認為某些事件的機率在「不置回」的情況下會改變，但其認 知是不完整的且侷限於之前曾發現的事件。 層次三：認為在不置回的情況下，所有的率值皆會改變；可以在不置 回的情況下，量化機率值。 層次四：可用分數表示置回與不置回情況下的機率；在置回以及不置 回的每一個試驗情況下，使用數字的推論去比較事件先後的 機率。 二、具體行為表現 「條件機率」在這個研究中，是藉由兒童是否具有「了解一個事 件的機率會不會隨著另一個事件的結果改變」的能力，來鑑定兒童對

於條件機率的理解。表 2-5 是兒童關於條件機率問題之回答情形，問 題如附件一。 表 2-5 兒童在條件機率概念上的反應 層次 題號 反應情形 一 伍 兒童用主觀的方式回答斯吉爾，我喜歡女生當班長， 他是男生所以不會被選中。 二 伍 兒童認為莫妮卡的卡片被抽走後，再抽中名字是「莫」 開頭的人機會就變少了，但是斯吉爾被抽中的機會沒 變，因為原本就有一張斯吉爾的名字卡片。 三 伍 兒童認為，拿走莫妮卡的卡片後，斯吉爾被抽中的機 會就增加了，原本是五個抽一個，現在是四個抽一個。 四 伍 兒童能了解在抽籤之前，每個人當選班長的機會相 同，都是 1/5，莫妮卡的卡片被抽出後，每個人被抽中 的機會都改變了，是 1/4。 陸、獨立性 一、四種發展層次之行為特徵 此組成中，兒童之行為特徵為： 層次一：有一個傾向去思考連續的事件總是有關係的；一個人可以控 制一個實驗的結果。 層次二：開始承認連續的事件可能有關係的或是沒有關係的；對先前 試驗結果做分析以預測下次結果對先前試驗結果做分析以 預測下次結果。 層次三：可以在置回以及不置回的情況下分出獨立及相依事件；可能 以代表性捷思策略做答。 層次四：可以使用機率數值化去區分獨立以及相依事件。 二、具體行為表現 「獨立性」在這個研究中，是藉由兒童是否能察覺兩事件之關係

為獨立，來鑑定兒童對於獨立性的理解。表 2-6 是兒童關於獨立性問 題之回答情形，問題如附件一。 表 2-6 兒童在獨立性概念上的反應 層次 題號 反應情形 一 陸、一 兒童回答，前四次男生出現比較多，而且老師認為女 生比較乖，所以第五次最有可能抽中女生。 二 陸、一 兒童認為在連續抽出三次男孩後，下一次較有可能是 女孩，因為他覺得太久沒出現女孩了。 三 陸、二 兒童認為下一次的結果並不受上一次結果的影響，但 仍認為出現「正反正正反」的機會比「正正正正正」 的機會大。 四 陸、二 兒童認為第五次出現正、反面的機會各是 1/2，和之前 無關。

第二節 機率概念之理論性研究

Jones et al.（1997）認為在他的機率思考架構中，思考層次的主張與 Piaget & Inhelder（1975）的發展階段認知研究一致的。茲列舉 Piaget & Inhelder（1975） 及其他認知發展理論如下： 壹、認知發展理論 一、皮亞傑認知發展論的階段觀（張春興，民 86） （一） 動作期（0-2 歲）： 1.憑感覺與動作以發揮其基模功能 。 2.由本能性的反射動作到目的性的活動。 3.對物體認識具有物體恆存性概念。 （二） 前運思期（2-7 歲） 1.能使用語言表達概念，但有自我中心傾向。 2.能使用符號代表實物。 3.能思維但不合邏輯，不能見及事物的全面。 （三） 具體運思期（7-11 歲） 1.能根據具體經驗思維以解決問題。 2.能理解可逆性的道理。 3.能理解守恆的道理。 （四） 形式運思期（11 歲以上） 1.能作抽象思維。 2.能按假設驗證的科學法則解決問題。 3.能按形式邏輯的法則思維問題。

二、Biggs & Collis（1991）的認知官能層次

（一） 學習循環中的先前結構層次：雖然學習者能持續進行工作（例 如會回答機率問題），但會轉向或迷失在不恰當的方向。

（二） 單一架構層次：學習者能持續進行工作且朝著某一方面持續進 行。 （三） 多重架構和關係層次：學習者能在工作中挑選一個以上有意義 的特徵，且傾向於整合不同的特徵。 （四） 關係層次：學習者整合工作中恰當的方向成為有意義的結構。 三、Klausmeier（1979）的概念學習與發展理論 層次一：具體層次（concrete level），個體可以辨認出他曾經接觸過或 學過的概念。 層次二：識別層次（identity level），即使是從不同的角度或以不同的 形式呈現個體過去曾接觸或學習過的概念，個體仍然可以辨 認出來。 層次三：分類層次（classificatory level），個體對於相同概念有兩個以 上不同的例子，能歸納出相同種類的特徵。 層次四：形式層次（formal level），個體可以清楚地理解概念所代表 的一般屬性輿獨特屬性，且也能夠分辨與此相似概念差異之 處，進而應用在對問題解決的能力上。 貳、機率認知發展理論

一、Piaget & Inhelder（1975）兒童機率概念的認知發展階段論

在 Piaget & Inhelder（1975）的實驗中，是給兒童兩組代幣，其 中有些代幣做上記號，要兒童估測哪一組代幣中拿到有做記號代幣的 機率比較高。題型呈現的方式有 10 種：(1)兩組的可能性都是「不可 能」 (所有代幣都沒有做記號)；(2)兩組的可能性都是「一定」 (所有 代幣都有做記號)；(3)一組是「一定」、另一組是「不可能」；(4)一組 是「可能」 (某些代幣做記號)、另一組是「一定」；(5)一組是「可

能」、另一組是「不可能」；(6)兩組中有做記號的代幣數一樣，總代幣 數也一樣；(7)兩組的總代幣數不同，但有做記號的代幣數與總代幣數 之「比」是一樣的；(8)兩組中有做記號的代幣數不一樣，但總代幣數 一樣；(9)兩組中有做記號的代幣數一樣，但總代幣數不一樣；(10)兩 組中有做記號的代幣數與總代幣數都不一樣，且比例也不相同。根據 實驗研究結果，他們歸納出「機率概念」發展的層次： （一）階段一（七歲以下） 無法區分事件之必然性與可能性，沒有「不確定」的概念。 年齡在四至六歲的孩童連較簡單的比例也無法區分機率 的大小。例如：兩組代幣中，有做記號的代幣與總代幣數的比 是 1:2 和 2:4、或 l:2 和 l:3 時，兒童無法區分何組較容易拿到 有標記代幣；根據 Piaget & Inhelder（1975）的說法，兒童無 法同時注意到有做記號的代幣數與總數間的關係，而從不重要 的訊息來判斷。例如在 1:2 與 2:4 的這組中，他們認為有做記 號代幣與總代幣數的比是 1:2 時，較有可能拿到有做記號的代 幣。理由是因為兒童比較容易注意到那一個唯一有做記號的代 幣；而在 1:2 與 1:3 一組中，他們認為兩組拿到有做記號代幣 的機率一樣大，因為有做記號的代幣數都一樣多。Piaget & Inhelder（1975）的解釋是，此期的兒童因缺乏「可逆性」，故 不能理解「部份」與「全部」的關係。因此，由於缺乏邏輯結 構的關係，四至六歲的兒童無法在估測勝算(odds)時作比較。 年齡在六至七歲的孩童不能理解的題型有兩種：一是兩組 總代幣數不同，但有做記號代幣與總代幣數之比是相同的(第 7 種題型)；二是兩組中有做標記的代幣數與總代幣數不相同， 且比例也不相同(第 10 種題型) 。依據 Piaget & Inhelder（1975） 的說法，兒童只能處理一個變項，孩童偶爾能答對的原因不是

基於運思的推理，而是來自於「直觀」。 （二）階段二（七歲到十四歲） 已能認清事件之必然性與可能性，但無法以有系統的方法 產生一系列的機率。 上述兩題型中，兒童在此階段能夠同時考慮到兩個變項， 但無法解題，其主要原因乃受智力上的限制，因為這樣的題型 必須同時比較兩個比例，而 Piaget & Inhelder（1975）認為比 較兩個比例之能力是在「形式運思期」才會出現的。 其後，兒童開始能解決雙變項的問題，但仍限於使用試驗 性的方法，而非形式上的推理，他們會輪流考慮到期望事件與 非期望事件。而若缺乏所需的形式運思時，他們就以直觀來判 斷。 （三）階段三（十四歲以上） 開始發展組合的才能，並且了解相對次數之極限（大數法 則）的機率。 兒童雖無法正確使用分數來計算，但仍能正確估計其比 例，兒童開始會利用組合(combination)及排列(permutation)的方 法來計算機率，並以「大數法則」來預測。 由其研究結果可知，在層次一中之孩童無法區分「可能」(possible) 和「必然」(certain)之意義；接著在層次二中之孩童能瞭解「可能」、「必 然」、「機率」之意義，也可量化成機率，但是沒有足夠的解題策略來 計算較複雜的勝算(odds)。最後，在層次三中之學重，能統整推演性 的邏輯，以及機率概念的形式結構，藉以推估事件發生之機率。Piaget & Inhelder（1975）特別指出，在最後層次中，兒童除強化層次二之特 徵外，在對稱性機率實驗裡，兒童已能發現「大數法則」概念。

二、Fischbein（1975）的兒童機率概念學習發展觀點 Fischebin（1975）從兒童的直觀想法出發，研究兒童機率概念的 發展。他提出：即使是前運思期的兒童，也有相對次數和機率的先前 概念暸解，這些概念是由初始直觀建立的，初始直觀是由兒童每天生 活經驗自發性形成的晦隱知識(implicit knowledge)，例如從每天的生 活情境知覺偶發事件。當兒童成熟些後，這些初始直觀可以發展成相 對次數、機會、機率等概念，這個轉化的過程並非自發性或是成長中 自我調整的類自動化的結果，而是經由學校教學介入做為媒介轉化， 若無這樣有目標的介入，可操作的機率概念無法被發展，就算是成人 也一樣。

Piaget & Inhelder（1975）只研究了兒童客觀性的機率概念，因此 在兒童機率概念的發展上，認為需至具體運思期才能夠具備機率概念 之能力，根據 Fischebin（1975）的研究指出 Piaget & Inhelder（1975） 的機率概念發展階層模式有兩個嚴重不足之處，第一是機率學習成長 方面的發現，第二是輕忽了學習導致機率概念形成的過程。

根據 Fischebin（1975）的研究，機率教學對兒童的機率概念形成 佔有舉足輕重的地位。

三、Bognar & Nemetz（1977）的機率教學觀點

（一）在七至八歲時可以教導簡單的機率概念，像確定事件(certain events)、不可能事件(impossible events)及互斥事件(mutually exclusive events)。

（二）在九至十歲時，可依據可能發生的事情，教導較可能事件(more likely events)、較不可能事件(1ess 1ikely events)及次序事件 (order events)。

率事件的圖表如樹狀圖(diagrams)。

（四）在十三至十四歲時可以教導獨立(independent)和相關(correlated) 的實驗和事件。

四、Munisamy & Doraisamy（1998）的機率概念層次特徵

•層次一：屬於本層次的兒童具有機會和機率的直觀概念，對大部分 基本機率概念都能了解。

•層次二：屬於本層次的兒童能了解到機率加法原理和實地的應用。 •層次三：屬於本層次的兒童能了解獨立事件的乘法原理和延伸到條

件機率的推理，並且能成功的應用在新的機率問題上。 歸納上述，Piaget & Inhelder（1975）認為七至十四歲的兒童無法以有系統 的方法產生一系列的機率概念，但 Bognar & Nemetz（1977）卻認為在十一至 十二歲時可教導相對次數(relative frequencies)及畫機率事件的圖表如樹狀圖 (diagrams)，在十三至十四歲時可以教導獨立(independent)和相關(correlated)的 實驗和事件。正如 Fischebin（1975）所述 Piaget（1975）輕忽了學習導致機率 概念形成的過程，因此機率教學對兒童的機率概念形成佔有舉足輕重的地位。

第三節 機率概念之實證性研究

壹、樣本空間 一、國外

Piaget & Inhelder（1975）認為在小學初階段的兒童可以在一階段 的實驗中列出所有可能的結果。但是 Jones（1974）卻認為在大多數 一至三年級的兒童無法列出一階段實驗所有結果且許多孩子出現不 願意去列出結果的情形。

Borovcnik & Bentz（1991）在 Green（1982）的研究中注意到超 過 62﹪的 11 歲兒童無法解決兩題（both of the）關於一階段的樣本空 間試題。

Piaget & Inhelder（1975）聲稱，前運思期的兒童（兩歲到七歲） 只用經驗的方式來組合出結果，一直要到具體運思期（七歲到十一歲） 才嘗試使用有系統的方式來解決二元序對，但他們並不總是使用成功 的，一直要到形式運思期，大約十一歲才能成功的使用。但只要在良 好的學習條件下，具體運思期（七歲到十一歲）的兒童能使用有系統 的方式來解決二元序對及三元序對的問題。 Schroeder（1988）指出四至六年級孩子在二階段實驗上，不情願 去詳盡闡述所有可能的結果。 English（1993）指出大多數七到十二歲的孩子能夠使用有效率的 方法去列出二元序對及三元序對（ordered pairs and ordered triples）， 且解決二元序對的經驗能幫助他們解決三元序對。他們使用的策略從 嘗試錯誤到有效率的步驟列出所有可能組合的情況。

（一）二元的情形： •策略 1

•策略 2 和 3 屬於過渡的階段，比起策略 1，他們更有效率了，但仍 不如策略 4 和 5。 •策略 4 和 5 是最有效率的策略，因為使用了「里程計」（odometer） 的方式。會取名「里程計」（odometer）的方式的原因是因 為這個方式和車輛的里程計很類似。 Ｘ１－Ｙ１ Ｘ２－Ｙ２ Ｘ１－Ｙ２ Ｘ３－Ｙ１ Ｘ２－Ｙ３ Ｘ１－Ｙ３ Ｘ３－Ｙ２ Ｘ３－Ｙ１ Ｘ３－Ｙ３ 策略１ Ｘ１－Ｙ１ Ｘ２－Ｙ２ Ｘ３－Ｙ３ Ｘ１－Ｙ３ Ｘ２－Ｙ１ Ｘ３－Ｙ２ Ｘ２－Ｙ３ Ｘ３－Ｙ１ Ｘ１－Ｙ２ 策略２ Ｘ１－Ｙ１ Ｘ２－Ｙ２ Ｘ３－Ｙ３ Ｘ１－Ｙ２ Ｘ２－Ｙ３ Ｘ３－Ｙ１ Ｘ１－Ｙ３ Ｘ２－Ｙ１ Ｘ３－Ｙ２ 策略３ Ｙ１ Ｘ１ Ｙ２ Ｙ３ Ｙ１ Ｘ２ Ｙ２ Ｙ１ Ｘ３ Ｙ２ Ｙ３ Ｘ２－Ｙ３ 策略４ Ｙ１ Ｘ１ Ｙ２ Ｙ３ Ｙ１ Ｘ２ Ｙ２ Ｙ3 Ｙ１ Ｘ３ Ｙ２ Ｙ３ 策略 5

（二）三元的情形 解決三元的問題中，最有效率的方式是以最少的次數 改變主要常數（major constant 如策略 10 的 x1）及次要常數 （minor constant 如策略 10 的 y2），而不像策略 6 的 x1一直 在改變。 •策略 6 這個策略是嘗試錯誤的且易於犯錯。 •策略 7 兒童嘗試使用一個較有效率的方式，可惜並沒有整題都 使用此種方式。 •策略 8 兒童使用了一致的循環模式，但並沒有讓主要常數 （major constant）及次要常數（minor constant）達到最少的次

數。

•策略 9 和 10

此兩個策略最主要的特點是使主要常數（major constant）及次要常數（minor constant）達到最少的次數，是 最有效率的方式。

Ｙ１－Z₁ Ｘ1 Ｙ２－Z₂ Ｙ3－Z1 Ｘ2 Ｙ1－Z2 X1－Y2－Z1 X2－Y2－Z2 Z1 X1－Y3 Z2 X2－Y1－Z1 X2－Y2－Z1 X1－Y1－Z2 X2－Y3－Z2 策略 6 Z1 Ｙ１ Z2 Ｘ1 Z1 Ｙ２ Z2 Z1 Ｙ１ Z2 Ｘ2 Z1 Ｙ２ Z2 Z1 X1－Y3 Z2 Z1 X2－Y3 Z2 策略 8 Z1 Ｙ１ Z2 Ｘ1 Z1 Ｙ２ Z2 Z1 Ｙ1 Z2 Z1 Ｘ2 Ｙ２ Z2 Z1 Ｙ3 Z2 Z1 X1－Y3 Z2 策略 9 Z1 Ｙ1 Z2 Z1 Ｘ1 Ｙ２ Z2 Z1 Ｙ3 Z2 Z1 Ｙ1 Z2 Z1 Ｘ2 Ｙ２ Z2 Z1 Ｙ3 Z2 策略 10 Z1 Ｙ１ Z2 Ｘ1 Z1 Ｙ２ Z2 Ｙ１－Z₁ Ｘ2 Z1 Ｙ２ Z2 X1－Y3－Z1 Z1 X2－Y3 Z2 X1－Y3－Z2 X2－Y1－Z2 策略 7

Fischbein（1987）表示組合的樹狀圖是強而有力的教學設備，它 在把抽象的觀念轉成直覺的觀念上，扮演著非常重要的角色。但他強 調，對樹狀圖的直覺並不是一個人自然本能的特性。 Fischbein（1991）為了對兒童某些機率思考的直覺障礙有進一步 的了解，同時也為了擬定首度將機率引進小學的義大利數學課程，提 供機率教材設計的心理基礎，乃以國小四、五年級及國中一到三年級 兒童為對象，進行問卷調查，問卷內容包括「必然、可能和不可能事 件之辨認」、「具同一數學結構，但不同機率實驗情境時的兩事件之發 生機率比較」及「兩複合事件之發生機率比較」，發現多數受試兒童 似乎均已發展出「基於事件之樣本點個數，來評估比較同一樣本之間 中兩組複合事件之發生機率的大小」，唯仍欠缺「系統化」建構事件 之所有樣本點的能力，尤其不易將一個無順序的組合事件想成若干個 有順序排列的事件，例如不易將同時投擲兩粒骰子出現 5 點和出現 6 點的事件，想成包含（5,6）和（6,5）兩個樣本點，所以常誤以為「出 現不同元素之事件（如出現 5 點和 6 點）」與「出現相同元素之事件 （如兩個均出現 6 點）」的發生機率是相同的。 歸納上述，在樣本空間一階段的實驗研究上，雖然 Piaget & Inhelder（1975）提示孩子在小學階段能夠判斷一階段實驗所有可能 的結果，但是 Jones（1974）推斷國小一至三年級的孩子不能列出一 階段實驗的結果。與 Jones（1974）發現一致，Borovcnik & Bentz（1991） 在 Green（1982）研究中注意到超過 62﹪的 11 歲兒童無法解決兩題 關於一階段的樣本空間試題。

在二階段的實驗研究上 Piaget & Inhelder（1975）、English（1993）、

Fischbein（1991）一致認為七至十二歲的兒童都能夠使用有效率的方 法去列出二元序對及三元序對，但 Fischbein（1991）卻特別指出，兒 童仍欠缺「系統化」建構事件之所有樣本點的能力，尤其不易將一個

無順序的組合事件想成若干個有順序排列的事件。 Fischbein（1987）、English（1993）皆認為樹狀圖能幫助兒童有 效率的列出二元序對及三元序對。 Jones（1974）及 Schroeder（1988）的研究皆顯示出，兒童「不 情願」列出樣本空間中所有可能的結果。 二、國內 陳順宇、鄭碧娥（民 82）指出大部分國中生已具有樣本空間和機 率事件的觀念，並能列出事件的可能結果。 朱雅瑋（民 85）為了對國小兒童機率的直觀概念做進一步研究， 以國小六級兒童（未正式接觸機率教學）332 位進行筆試及 52 位兒童 進行訪談，研究結果發現：有時兒童不知道樣本空間是如何形成的， 往往只根據猜測，自情境中隨意配取任何給定的訊息或數字來推測事 件的機率。例如：「投擲兩個硬幣，出現一個正面，與投擲四個硬幣， 出現兩個正面，哪一個較容易？」兒童若未考慮到，兩種情形下樣本 發生的機率不等，而只以「實驗次數」和「出現次數」來判斷，就容 易以為這兩種情形，出現正面的機率是一樣的(1/2＝2/4)。 施能宏（民 86）為了解五、六年級兒童在機率教學前後概念的轉 換，對 646 位兒童實施筆測、72 位兒童實施晤談。在其高年級兒童機 率文字題解題表現的研究上，發現兒童對於樣本空間概念比大數法則 較容易理解。 在陳欣民（民 91）的三個訪談個案中（四年級、五年級及六年級 各一位），顯示出孩童在求「同時投擲兩粒骰子」的樣本空間中，該 用乘的運算卻用加的運算，經研究者鼓勵他們寫出所有的情形後，他 們三人皆能馬上發現自己的錯誤而改口成 36 種，顯示出他們已有排 列組合的概念，且能運用「衍生性策略」求出樣本空間了。 歸納上述，陳順宇、鄭碧娥（民 82）、陳欣民（民 91）的研究指

出，國小中、高年級至國中的兒童已能以有系統的策略列出樣本空間 所有可能的結果。但朱雅瑋（民 85）指出，有時兒童不知道樣本空間 是如何形成的，造成從情境中隨意配取任何給定的訊息或數字來推測 事件的機率。所以教師在有關指導樣本空間的問題時，除了注意兒童 是否已會使用系統性策略來解題，更應注意兒童是否確實了解樣本空 間的涵義。 綜合國內外研究，國小兒童在經過教學後，皆能使用有系統的策 略列出樣本空間中所有可能的結果。因此，兒童若想更有效率的列出 樣本空間中二元、三元序對所有可能的情形，應輔以樹狀圖的學習。 貳、實驗機率 一、國外

Piaget & Inhelder（1975）提出兒童知道某一事件成功的機率大的

話（如一個飛鏢有 2 個區域，紅色部分佔 2/3），選擇該事件在長期下

來較為有利。投一個般子、丟一個硬幣、轉一個陀螺，會出現哪一事 件純粹是碰巧的，但大數法則使他們知道，若試驗無數次，則事件成 功的機率相當穩定，例如投一顆骰子很多次，則出現六點的機率是 1/6，所以多次實驗的結果依然有規則管理，亦即受制於機率的規則。

Piaget & Inhelder（1975）指出，在第三層次的兒童（十四歲以上），

在對稱性機率實驗裡，兒童已能發現「大數法則」概念。

Kahneman & Tversky（1972）提出兒童在面對機率問題時，會誤 以為所有次數的分配會有回歸至平均數的順向，甚至產生了所謂大數 法則的迷思。

根據Konold（1983，1989）的研究兒童會有「結果取向」。兒童

會以「可能性相等」來表示「所有的結果都可能發生」且並不認為單 一次的試驗結果是多次試驗結果的其中之一，而是為了下一次結果做

出決定，即一個關於「事件發生的機率」之問題，容易被誤解為「這 樣的事件在下一次試驗當中『會不會發生』？」，以「100﹪」代表「一 定會發生」、「50﹪」代表「不一定會發生」、「0﹪」代表「不可能發 生」，例如：兒童會認為率在50﹪以上不只是可能發生，而且是將要 發生，若氣象預報降雨率是80﹪，但沒下雨，就認為是氣象預報錯了； 兒童也無法從具體情境中抽離相同的數學結構，認為同時進行N 個獨 立實驗和分別進行n個相同的獨立實驗，所得某事件發生的機率不 同。例如：用一枚一元硬幣丟3次，和丟三枚一元硬幣，出現三次正 面的機率是不一樣的。

歸納上述，Piaget & Inhelder（1975）指出，在第三層次的兒童（十

四歲以上），在對稱性機率實驗裡，兒童已能發現「大數法則」概念。

但Kahneman & Tversky（1972）指出，兒童會誤以為樣本空間中的情 形會交錯出現（符合「隨機過程」典型）、所有次數的分配會有回歸 至平均數的順向（符合「理想母群分配」典型），甚至產生了所謂大 數法則的迷思。

Fischbein在1987及1991年的研究皆指出，兒童了解擲硬幣或骰子 時，每次各種情形出現的機率相等，但是仍潛存有下一次較會出現之 前沒有出現的情形之迷思概念，這點與Kahneman & Tversky（1982） 研究中的「負時近效應」相似。 二、國內 根據施能宏（民 86）之研究，兒童存有「結果取向」及「大數法 則」之另有概念。在投幣試驗中，存在「正面與反面出現次數恰為其 試行次數之半的機會，隨著試行次數越多，機會越高」或「正面與反 面出現次數與試行次數之半的絕對次數差異，會隨試行次數之增加而 縮減」之二種另有概念。

林燈茂（民 81）為了瞭解兒童和教師對機率概念的認知與學習， 針對國內數學教材的課程標準和教學目標（依據民國 64 數學科課程 標準所編訂的機率教材）中有關機率的單元作過一系列的研究，並且 設計了相關的情境問題，以探討兒童和教師對機率概念的認知。他曾 採文獻分析及調查研究方式，以國一及高一兒童為對象，探討國內十 一至十六歲兒童之「相對差異」（relative difference）與「大數法則」 的概念，發現目前國小之機率單元「簡單的機率」（依據民國 64 數學 科課程標準所編訂的機率教材）實際教學時會面臨不少問題。且經分 析與比較 124 名受試兒童於機率教學前後在六個相同問題（包括比值 接近、大數法則、機率值等三類）的答題反應。結果顯示：現行國小 機率教學（在課本及坊間國小參考書中所呈現有關大數法則的詮釋， 例如以此種錯誤語句描述：「投擲一粒骰子次數愈多，出現 6 點的次 數就愈接近總投擲次數的 1/6」），不僅未能有改善兒童對於機率教學 前所潛存之有關的迷思想法（部分尚未被強化），反而衍生出一些新 的迷思想法，甚至教師本身亦存在著機率概念的迷思。其研究結果發 現兒童對機率概念知識的了解情形，主要有下列幾項（林燈茂，民 87）： （一）在對稱性機率實驗中，各樣本點出現次數在平均數前後範圍的 發生機會，通常將隨實驗次數增加而提高；但事實上是降低。 （二）基於「絕對差異」觀點來進行「比值接近」程度之比較。林 燈茂（民 78）建議兒童將比值轉換為小數，並在座標圖上標 出正反面比值的位置，兒童在座標上可以觀察到比值接近的 程度。 （三）在對稱性機率實驗中，各樣本點出現次數恰好等於其預期出現 平均次數之機會，通常將隨實驗次數增加而提高；但事實上是 降低。

在陳欣民對四、五、六年級兒童的研究中，研究的個案尚未能 體會「理論機率值」與「大數法則」的意涵，如六年級個案能回答 出「投擲一粒骰子一次，每個點出現的機會是 1/6」，但卻存在有「投 越多次機率不一定會接近 1/6（比值接近），也越不能預測」。僅四 年級的個案能以「小樣本的個數分布臆測大樣本的個數分布」，例 如以「10 顆棋子中有軍 3 顆」預測抽棋子抽後放回，100 次抽中軍 的次數。四、五年級的個案皆能了解「明天的降雨率 70%」，可能 下雨但也有不會下雨的可能，其中五年級的個案有「收集適當資料 以求出機率值的想法」，但四年級的個案卻認為「投一粒骰子可能 出現 5 也有可能不出現 5」，所以投一粒骰子出現 5 的機會是 50﹪， 產生了「二分法的錯誤概念」。 由上述歸納，根據林燈茂（民 87）的研究，因為國小機率教學 （在課本及坊間國小參考書中所呈現有關大數法則的錯誤詮釋，例 如：「投擲一粒骰子次數愈多，出現 6 點的次數就愈接近總投擲次 數的」1/6），易產生如下之迷思概念：（1）在對稱性機率實驗中， 各樣本點出現次數在平均數前後範圍的發生機會，通常將隨實驗次 數增加而提高；但事實上是降低。（2）基於「絕對差異」觀點來 進行「比值接近」程度之比較。（3）在對稱性機率實驗中，各樣 本點出現次數恰好等於其預期出現平均次數之機會，通常將隨實驗 次數增加而提高；但事實上是降低。同樣的，根據朱雅瑋（民 85） 的研究，兒童遇到某些特定問題時，常以「大數法則」做不當推理。 然而在機率教學前之研究方面，陳欣民（民 91）的研究個案卻認為 「投越多次機率不一定會接近 1/6（比值接近），也越不能預測」。 綜合國內外之研究，在 Konold（1983，1989）及陳欣民（民

86）的研究中，兒童會有「結果取向」。Piaget & Inhelder（1975）

兒童已能發現「大數法則」概念，但根據 Kahneman & Tversky （1972）、朱雅瑋（民 85）（國小六年級兒童、未接觸機率教學）、 林燈茂（民 87）（十一至十六歲兒童，機率教學前後）及陳欣民（民 91）（四、五、六年級兒童）的研究皆顯示兒童對大數法則存有迷 思概念。 因此，教師應教導兒童正確的大數法則概念，當出現迷思概念 時，應給予詳細觀念上的指正。 參、理論機率 一、國外

依據 Piaget & Inhelder（1975）的理論，層次一（四至五歲）兒 童對於理解部分－全體間的關係有困難，而部分－全體關係在樣本空 間中比較不同的事件是非常必需的。Perner（1979）也注意到這個現 象但無法確認以下這兩項到底是否有關聯：主觀思考的使用及對部分 全體關係理解的缺乏。在層次三（十四歲以上）中之兒童，能統整推 演性的邏輯，以及機率概念的形式結構，藉以推估事件發生之機會。 Siegler（1981）提出利用比率概念了解機率大小的意義，八歲兒 童一半已具備比率概念，而十二歲以上兒童大部分已有比率概念。 Green（1982）從 3000 位十一至十六歲的受試者中，發現比值的 概念對機率的概念認知相當重要。 Fischbein（1991）發現九至十歲兒童，略經系統教學後，就能像 十二至十三歲一樣，足以正確地比較兩個事件「比例」間的關係、從 而估測某事件發生之「機會」。 Acredolo et al.（1989）給予兒童缺乏比例概念一個令人注目的說 明。他注意到孩子在比較事件機率中束縛他們自己於三個策略中的一 個：例如袋子裡有 3 顆紅球 1 顆白球，比較可能抽中哪一種顏色的球

（a）一個分子策略：他們僅檢查與事件中相符合的部分；（認為抽到 紅色的機率大，因為有 3 顆）（b）一個不完全的分母策略：他們檢查 與事件中的補集相符合的部分（抽到紅色的機率大因為白色只有 1 顆）；（c）一個整合的策略（紅球和白球都有考慮）：他們了解到每一 部份會對其他部分有適當的影響（4 個中，紅色就有 3 個那麼多，白 色只有 1 個，所以紅色比白色多，抽到白色的機率大）。 Green（1987，1988）針對十一至十六歲兒童研究，提出兒童使 用機率語言時，如可能（possible）、不可能（impossible）、確定 （certain）、至少，表現出模糊的概念。

Munisamy & Doraisamy（1998）指出四到六年級兒童對相關的機 率概念在口語能力的表達是不夠的，例如對非常可能(very 1ikely)、確 定的（certain），和不太可能（unlikely）不可能（impossible）這兩組 在機率概念上的運用常常犯錯。

Piaget & Inhelder（1975）指出在層次一（七歲以下）中之孩童無 法區分「可能」(possible)和「必然」(certain)之意義；接著在層次二 （七歲到十四歲）中之孩童能瞭解「可能」、「必然」、「機率」之意義， 也可量化成機率。 Fischbein（1991）針對小學四、五年級及國中一到三年級兒童研 究指出，受試兒童對「可能」、「不可能」、「必然」等名詞之意義，還 沒有明確了解。當關聯到複合事件時，理解「必然事件」似乎遠較「可 能事件」困難。在可能、不可能、確定事件中，確定事件（擲一粒骰 子，出現小於 7 的點數）的答對比率是最低的，甚至是受過基本機率 教學的國中生，也只有 63﹪的答對率，但在另一種題目（擲一粒骰子， 出現大於 0 的點數），答對率較高，超過 80﹪，因為「大於 0」提供 給兒童「全部」（totality）的感覺，是直接的，不需經過頭腦分析的。 也有很多兒童容易混淆了「幾乎不可能的」（rare）和「不可能的」

（impossible），例如「投一粒骰子有可能出現點數 5 嗎？」「不可能， 因為 5 點只佔 6 個點數中的 1 個。」

不可能事件（impossible events）和不確定事件（uncertain events） 混淆，例如，一個箱子裡有 91 個號碼球，分別標上號碼 1 到 91，請

問有可能抽中「偶數號碼嗎？」「不可能，因為不確定一定會抽中。」

確定事件（certain events）和可能事件（possible events）混淆， 例如一個箱子裡有 91 個號碼球，分別標上號碼 1 到 91，請問有可能 抽中「31 號嗎？」「一定會，因為箱子裡有 31 號。」 兒童也傾向用主觀的想法來取代數學上的思考，例如一個箱子裡 有 91 個號碼球，分別標上號碼 1 到 91，請問有可能抽中「31 號嗎？」， 「不可能，因 31 有微乎其微的機會被抽到，根據我的經驗，絕不可 能抽到它。就算有機會抽到，為什麼是別人會抽到，而不是我呢？」

歸納上述，Piaget & Inhelder（1975）、Green（1987，1988）皆認

為部分－全體關係的概念（比值的概念）對機率的概念認知相當重 要。Perner（1979）甚至懷疑，主觀思考的使用及對部分全體關係理 解的缺乏是有相關的。Acredolo et al.（1989）舉出當兒童缺乏比例概 念會使用下列三種策略之一：（1）一個分子策略（2）一個不完全的 分母策略（3）一個整合的策略。

Piaget & Inhelder（1975）、Siegler（1981）、Fischbein（1975）認

為十四歲以上之兒童大部份已有比例概念，能推估事件發生的機率。

Siegler（1981）、Fischbein（1975）更是認為九至十歲的兒童略經系統

教學後，也能具備一樣的比例概念。

Fischbein（1991）、Green（1987，1988）、Munisamy & Doraisamy

（1998）皆指出國小四年級以上兒童對「可能」、「不可能」、「必然」 等名詞，有語意上的理解問題，只有 Piaget & Inhelder（1975）認為

之意義，也可量化成機率。Fischbein（1991）並指出，兒童在判斷一 個事件「可能」、「不可能」或「必然」發生時，傾向用主觀的想法來 取代數學上的思考。 二、國內 陳順宇、鄭碧娥（民82）指出大部分國中生未考慮事件可能出現 之頻率不同而認為k種結果中，每一種結果所出現的機率為1/k。部分 兒童對於事件不發生的機率不知道利用「1－事件發生的機率」求解。 同樣觀念但較抽象或數據較為複雜的問題，兒童的答對率會降低很 多。男生在機率單元的成就表現較優於女生，但差距不大；而城市的 兒童在此單元的成就則明顯優於鄉村兒童。 林燈茂（民87）的研究顯示，兒童在「非對稱性機率實驗」中 會出現「預設機率實驗之樣本空間中各樣本點出現機會均等」來答 題。 朱雅瑋（民 85）指出，兒童在判斷一個事件的機率時，會有「結 果取向」；另外，兒童對於「一定」、「有可能」、「不可能」之意義有 語意上的理解問題。 在陳欣民、劉祥通（民 91b）的研究中顯示，有的兒童以「可能」 會發生來描述「比 7 小的點」，需要研究者反問「有可能的情形有哪 些？」，兒童才能查覺「一定」不會發生。在陳欣民（民 91）的研究 中，五、六年級個案能使用「部分－全體」的分數來表示事件發生的 可能性，其中六年級的個案在「投一顆骰子出現比 7 小的機會」上， 需經教學引導才能正確回答出量化的答案。 歸納上述，陳順宇、鄭碧娥（民 82）、林燈茂（民 87）的研究 皆顯示，國中、國小兒童會傾向認為，每個事件出現的機率皆相同， 而未考慮到是否為「對稱性機率實驗」。

綜合國內外研究結果，Fischbein（1991）、Green（1987，1988）、 Munisamy＆Doraisamy（1998）、朱雅瑋（民 85）及陳欣民、劉祥通 （民 91b）皆指出兒童對「可能」、「不可能」、「必然」等名詞，有語 意上的理解問題，但 Fischbein（1991）指出，兒童在判斷一個事件「可 能」、「不可能」或「必然」發生時，傾向用主觀的想法來取代數學上 的思考，例如「投一粒骰子有可能出現點數 5 嗎？」「不可能，因為 5 點只佔 6 個點數中的 1 個。」，所以教師在指導時，應特別強調這 些名詞在數學上有嚴謹的用法。 肆、機率比較 一、國外

Falk（1983）、Fischbein（1991）及 Piaget & Inhelder（1975）這

些研究者下結論：兒童使用直覺的及非正式量化的策略去對目標事件 （target event）做機率比較。 Falk（1983）的研究中，策略有以下三種（a）更多的目標事件（我 想抽中一顆紅球，左邊的箱子有 4 個紅球，1 個白球；右邊的箱子有 3 個紅球，2 個白球，左邊的紅球比較多，所以左邊的箱子有較大的 機會抽中紅球）；（b）更少的非目標事件（我想抽中一顆紅球，左邊 的箱子有 3 個紅球，1 個白球；右邊的箱子有 4 個紅球，2 個白球， 左邊的白球比較少，所以左邊的箱子有較大的機會抽中紅球）；（c） 同時考慮目標事件和非目標事件（我想抽中一顆紅球，左邊的箱子有 4 個紅球，1 個白球；右邊的箱子有 3 個紅球，1 個白球，左右兩箱白 球一樣多，但是左箱紅球比較多，所以左邊的箱子有較大的機會抽中 紅球）。 歸納上述學者對機率比較的研究中，兒童使用直覺的及非正式量 化的策略來比較機率，包含了（1）更多的目標事件（2）更少的非目 標事件（3）同時考慮目標事件和非目標事件。

二、國內 在陳欣民（民 91）的研究中，國小四年級的個案能解決「從單一 袋中拿球，哪個球被拿到的機會高」的問題，但遇到同時從甲、乙兩 袋抽出紅球（機率分別為 1/2 及 2/4）的問題情境時，因為沒有等值 分數的概念，只考慮目標物的多寡，認為因為乙袋紅球有 2 顆，因此 乙袋抽中紅球的機會比較大。但五年級及六年級個案，因已有能力把 分母擴充至兩者之最小公倍數，而能順利解決問題。在解決問題「兩 轉盤上有紅色白色組成的區塊，兩轉盤紅白兩色區塊面積皆相等，但 甲轉盤紅、白兩區塊分散各四份，乙轉盤紅、白區塊是較集中的各兩 份，哪一個被射中紅色的機會較大？」時，四年級個案因欠缺等值分 數概念無法成功解題。五年級個案認為紅色區塊面積比例相等，因此 兩轉盤機會相等。六年級個案雖能判斷紅色區塊面積比例相等，但仍 返回主觀的判斷，認為甲轉盤紅白區塊分散開來比較容易射中紅色。 根據施能宏（民 86）對未經過機率教學的國小六年級兒童研究， 對於機率性的比較問題，只以目標事件的多寡來作為機率大小的依 據，目標事件較多的那組，被抽到目標物的機率就較大。 歸納上述，兒童若無等值分數的概念，在比較機率時，常只考慮 到目標事件的多寡，且有時雖然認為兩者機率相等，卻仍返回主觀的 判斷，而選擇自己經驗中較可能發生的情形。 綜合國內外研究，Falk（1983）、施能宏（民 86）及陳欣民（民 91）皆認為兒童在比較機率時，常以目標事件的多寡做考量，因此， 兒童在學習機率比較時，應先具備等值分數的概念。 伍、條件機率與獨立性 一、國外

第一次的結果，預測下一次的嘗試會有一樣的結果發生，顯然地不願 意去接受其他結果的機率。其他兒童，為了去保持平衡狀態，預測下 一次的結果將會不同。Borovcnik & Bentz（1991）也對兒童在條件機 率思考做了類似的解釋。Shaughnessy（1992）也注意到兒童對於決定 有條件的事件感到困難，而且可能會被一個條件機率問題的前後關係 所困惑。

Kahneman & Tversky（1982）指出兒童會有代表性捷思策略， 列舉如下： （一）符合「理想母群分配」典型：即在隨機實驗中，不同樣本點出 現的次數比，應與樣本點在理想母群中的機率比是一致的。例 如：兒童認為投擲一枚公正的一元硬幣，「正、反、反、正」 比「正、反、反、反」的結果更易顯出正、反面各佔一半的分 配情形。 （二）符合「隨機過程」典型：在隨機實驗中事件分配的情況應能確 實反映出產生該事件的隨機過程。例如：投擲一枚公正的一元 硬幣，其結果應該是正面、反面交錯出現的。 （三）符合「時近效應」典型：是指由事件出現次數的「多」、或「少」 來預測下個可能的結果，有「正時近效應」和「負時近效應」 兩種。例如，在紅熊、藍熊抽取實驗中，「紅熊」出現的次數 比「藍熊」還多，若兒童預測下一個結果還是會抽中「紅熊」， 就是「正時近效應」；反之，若預測下一個會抽中「藍熊」，則 稱為「負時近效應」。 Fischbein（1987）指出兒童邏輯的且直覺的了解到，當投擲一 枚硬幣好幾次後，正面反面出現的機率是相同的，但是如果反面連續 出現三到四次，兒童還是會認為下一次出現的結果，正面會比反面機 會要大。