國立臺中教育大學數學教育學系
在職進修教學碩士論文
指導教授:林原宏 博士
國小學童比例及機率理解之解題規則
探討-潛在類別及混合 Rasch 模式分析
研究生:蔡嘉豪
撰
中 華 民 國 九 十 七 年 五 月 三 十 日
摘
要
本研究應用潛在類別分析(latent class analysis, LCA)與混合 Rasch 模式(mixed Rasch model, MRM)分析國小學童於比例理解與機率理解的測驗資料, 根據分析 所得各潛在類別之反應組型,與文獻中規則解題所得之規則組型進行比較,藉以了 解各類別受試者所採之解題規則。 研究分別以 25 題果汁濃度測驗及 10 題機率理解測驗,樣本為來自臺灣中部地 區國小四至六年級學童,分析的結果顯示,各類別間的異質性高,而類別內的受試 者同質性高。比例理解測驗經分析後可將受試者分為 6 個類別,而機率理解測驗分 析後可將受試者分為 3 個類別,各類別可與文獻中相關規則相互對應,其類別反應 組型與規則組型相符度極高;不同年齡受試者與採用規則呈顯著差異,而性別與採 用規則則無明顯差異。 本研究之結果與發現,可提供國小中、高年級學童比例理解及機率理解解題規 則的訊息,對於規則使用判斷及補救教學具有參考價值,研究者亦對未來相關研究 提出研究限制及相關建議,可提供後續相關研究之參考。 關鍵字:潛在類別分析 混合 Rasch 模式 柳橙汁濃度測驗 機率理解 比例理解
Rule Usage Analysis for Proportional Reasoning and Probability Reasoning
based on Latent Class Analysis and Mixed Rasch Model
Abstract
The purpose of this study is to apply latent class analysis (LCA) and mixed Rasch model (MRM) to analyze the rule usage of proportional reasoning and probability reasoning for pupils. Latent classes are acquired according to response pattern so that the classification of rule usage is clearly displayed. As to the test of proportional reasoning, there are 25 items. In addition, probability reasoning test consists of 10 items. The sample includes fourth, fifth and sixth graders who are from elementary school in central district in Taiwan. The results show that there is various characteristics among groups, and there is similar characteristics for students within same group.
There are six classes for proportional reasoning and there are three classes for probability reasoning test. Each response pattern of class could be explained by rule pattern. There is obvious difference of rule usage among grade, but there is no difference between gender.
The findings of this research should be helpful for problem solving rule and could be used as references for remedial instruction. Finally, some recommendations and suggestions for future research are provided.
Key words: Latent Class Analysis, Mixed Rasch Model, Orange Juice Test, Probability reasoning, Proportional reasoning
目
次
中文摘要………i
英文摘要………ii
第一章
緒論………1
第一節 研究動機……… 1 第二節 研究目的……… 6 第三節 名詞解釋……… 6第二章
文獻探討………8
第一節 機率概念的相關研究……… 8 第二節 機率理解測驗與解題規則………22 第三節 比例概念的相關研究………25 第四節 柳橙汁濃度測驗與解題規則………33 第五節 規則評量方法………36 第六節 分析模式的探討及適配度的選擇………43 第七節 規則解釋力與規則區別力………54第三章
研究方法………57
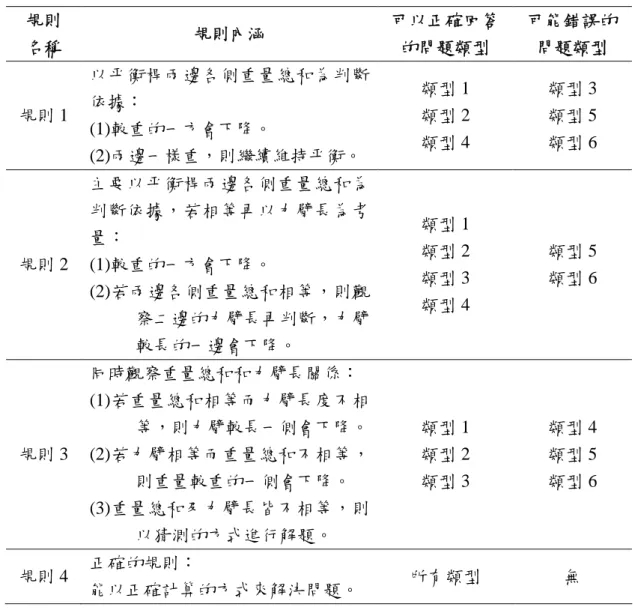
第一節 研究架構………57 第二節 研究對象………60 第三節 應用軟體資料分析步驟………62第一節 OJT 及機率理解測驗試題規則解釋力及規則區別力………63 第二節 OJT 比例理解測驗分析結果………65 第三節 機率理解測驗分析結果………76
第五章
結論與建議………85
第一節 OJT 比例理解概念解題規則分析結論………85 第二節 機率理解概念解題規則分析結論………86 第三節 研究限制………87 第四節 研究結論………88 第五節 研究建議………89參考文獻………91
中文部分………91 英文部分………96附錄
附件一 OJT 施測試卷………107 附件二 機率理解測驗試卷………109表
次
表 1-1 國小數學課程與比例及機率理解概念相關能力指標………..5 表 2-1 Siegler 的題目類型………14 表 2-2 黑球機率問題的四個解題規則……….24 表 2-3 「柳橙汁濃度測驗」的五個解題規則……….………34 表 2-4 四種解題規則及其與各類型問題之對應情形……….………39 表 2-5 潛在類別分析分類概念樣本舉隅……….………43 表 2-6 潛在變項分析方法的分類……….…………44 表 2-7 LCA 應用於各領域研究彙整 ……….………… 47 表 2-8 題目的反應與則的對應關係表……….…………55 表 3-1 本研究「柳橙汁濃度測驗」25 題的組合………58 表 3-2 「機率理解測驗」10 題的組合………59 表 3-3 比例理解測驗施測年級及性別人數列聯表……….…………61 表 3-4 機率理解測驗施測年級及性別人數列聯表……….………62 表 4-1 OJT 比例理解測驗 25 題的組合及其規則解釋力及規則區別力……...63 表 4-2 機率理解測驗 10 題的組合及其規則解釋力及規則區別力…………...64表 4-3 設定類別數下 LCA 分析 OJT 之 AIC、BIC 及 CAIC 值………...65
表 4-4 LCA 分析 OJT 下 6 個類別在各題的答對機率及答題情形…………...66
表 4-5 以 Neolting 研究中 5 個解題規則對應各試題下的答題判定分析…… 67
表 4-6 LCA 分析 OJT 下之各類別與 Neolting 的 5 項規則符合度分析……...68
表 4-9 設定類別數下 MRM 分析 OJT 之 AIC、BIC 及 CAIC 值……….71 表 4-10 MRM 分析 OJT 下 6 個類別在各題的答對機率及答題情形………….72 表 4-11 MRM 分析 OJT 之各類別與 Neolting 的 5 項規則符合度分析……….73 表 4-12 MRM 分析 OJT 之各類別與年級人數分配列聯表……….75 表 4-13 MRM 分析 OJT 之各類別與性別人數分配列聯表……….75 表 4-14 設定類別數下 LCA 分析機率理解受試者反應之 AIC、BIC 及 CAIC 值 ……….77 表 4-15 LCA 分析機率理解反應下 3 個類別在各題的答對機率及判定情形
……….77 表 4-16 以 Bart and Orton(1991)4 個解題規則解決各試題下的答題判定分析
……….78 表 4-17 LCA 分析機率試題反應下之各類別與 4 項規則符合度分析 ………..79 表 4-18 LCA 分析機率理解反應下各類別與年級人數分配列聯表 …………..80 表 4-19 LCA 分析機率理解反應下各類別與性別人數分配列聯表 …………..80 表 4-20 設定類別數下 MRM 分析機率理解受試者反應之 AIC、BIC 及 CAIC 值 ……….81 表 4-21 MRM 分析機率理解反應下 3 個類別在各題的答對機率及判定情形 ……….81 表 4-22 MRM 分析機率試題反應下之各類別與 4 項規則符合度分析………..82 表 4-23 MRM 分析機率理解反應下各類別與年級人數分配列聯表…………..83 表 4-24 MRM 分析機率理解反應下各類別與性別人數分配列聯表…………..83
圖
次
圖 2-1 Siegler 機率理解測驗示例………14 圖 2-2 機率理解測驗範例試題舉隅………23 圖 2-3 比例推理的數學發展結構圖………30 圖 2-4 柳橙汁濃度測驗例題舉例………34 圖 2-5 潛在類別分析分類結果舉隅………44 圖 2-6 反應與規則對應圖………54 圖 3-1 研究架構圖………60第一章 緒論
本研究旨在應用潛在類別分析 (latent class analysis) 及混合 Rasch 模式 (mixed Rasch model) 分析國小四至六年級學童在比例理解及機率理解問題的 規則使用情形,經由觀察各潛在類別的反應組型並和文獻比較,藉以了解受試 者的解題規則。本章說明研究之動機與目的,並對本研究所提及之相關名詞加 以定義及解釋。
第一節
研究動機
九年一貫課程數學學習領域的正式綱要分為「數與量」、「幾何」、「代數」、「統 計與機率」、「連結」等五大主題,強調培養學生帶著走的數學知識,期能成為日 常生活及職場裡應具備的基本能力 (教育部,2003) 。本質而言,此立意良好, 但數學學習領域每週授課時數的減少,對教師而言,則是一大挑戰。因此,如何 進行有效的教學儼然成為一項研究重點。 教學前教師所進行的前測,可藉以了解學生所具備的經驗及知識,是否足以 繼續構築新的概念。而教學後所實施的測驗,目的則在了解學生所學習的概念及 理解情形,進而針對學生個別差異進行補救教學。依據前、後測的測驗結果可獲 得學生的學習成效,並可依其錯誤的題型了解學生個別差異,進行個別化的教 學;但就實務來說,目前現行體制下,國小普通班每個班級平均約有 32 位學生, 教師很難就每個學生學習情形進行個別化教學。而潛在類別分析和混合 Rasch 模 式可根據受試者反應資料,分析學生的潛在知識結構並加以分組,教師即可就各 組的知識結構特性需求進行教學。因此,若能自分析學生的解題情形進行潛在類 別分組,進而獲得各組學生解題規則,及就其解題規則了解其解題所採用的策略 及概念,將有助教師對各潛在類別之學生教學及補救進行準備,此為本研究的動 機之一。日常生活中,我們經常會接觸到有關「比例」 (proportion) 及「機率」 (probability) 的問題。大致而言,凡事以濃、淡、深、淺…等相對性的字詞所形 容的都與比例有所相關,如以藍色為例,深藍色、淺藍色的差異性在於其中所混 合的白色比例多少為區分;果汁的濃淡,是以純果汁和其他液體液量之比例不同 而有所差異;經濟新聞內容所提及的投資比例,所指的亦是部份佔全體間的關係 及大小。上述範例,僅是生活中比例應用的一小部份,而 Lesh, Post and Behr (1988) 提出,在學生數學概念發展過程中,比例推理佔有相當關鍵的地位,是基礎數學 和高階數學的分水嶺。Lamon (1994) 也指出比例概念的建立是學習高等數學的 重要基石。美國「學校數學準則與標準」中提到,在數與計算、測量、機率等領 域,均強調比例概念是六至八年級學童應該學會的課題 (National Council of Teachers of Mathematics, 2000) 。教育部 (2001) 在「國民中小學九年一貫課程綱 要」中指出,期望學生達到數學課程的第一項目為「掌握數、量、形的概念與關 係」,比例即為數量關係的重點之一;教育部於新修定的數學領域正式綱要中指 出,比例是鍛練有理數數感的應用課程之一,更在國小代數課題中,強調協助學 童發展比例推理問題的解題策略,亦有助於國中生理解相似圖形或伸縮圖形的比 例關係 (教育部,2003) 。 「機率」存在於日常生活中的應用之廣也不遑多讓,教師上課時或於各項晚 會進行時的抽獎及摸彩活動,先抽還是後抽的獲獎機率是否有所差異?時下所熱 中的大樂透中獎機率如何與被雷打中的機率進行比較?氣象報告中的降雨情 形,為何不只區分「會下雨」和「不會下雨」兩種情形,而是以數字化的方式來 表示降雨可能性呢?若有興趣於博奕之人,則會自機率關係中理解如何於賽馬活 動中訂定適當的回饋報酬率。以上諸多範例,亦僅是生活應用中之一隅,機率的 重要性,也深受教育界的重視。美國數學教師協會 (National Council of Teachers
納為課程的一部份,因此在其所公佈的課程標準中,可發現每個階段中都有機率 概念的教學 (NCTM, 2000) 。我國教育部 (2003) 於「國民中小學九年一貫課程 綱要-數學學習領域」中將「統計與機率」列為數學領域課程五大主題之一,期 望學童能在具體情境中認識機率的概念,也能察覺數學與人類文化活動相關,並 有助於未來在高中、職階段的數學課程學習。日常生活中的真實問題方能真正引 發學童去關心所處的世界,機率問題所呈現的正是一種生活中的數學,從具體到 抽象的過程,在機率教學時的教學活動及溝通討論也能促進學生對於社會文化的 學習。綜上所述,比例和機率的理解、數學的學習以及生活問題有著密切關係; 因此,對學童的比例與機率理解之探究,有其重要性。 在面對比例和機率問題時,學童若能利用公式法進行解題,其計算及判斷的 結果會是正確的。如判斷「二種果汁混合的比例,A 為 1 杯果汁混合 2 杯白開水, B 為 1 杯果汁混合 3 杯白開水,A 及 B 二種比例混合後的結果何者果汁濃度較濃 或者相等?」此類型的問題,以公式法的方式解題,A 的濃度是 3 1 2 1 1 ,B 的 濃度是 4 1 3 1 1 ,因為 4 1 3 1 ,所以 A 的果汁比例較濃。相同的,判斷「A、B 二個袋子中,A 有 1 顆黑球及 2 顆白球,B 為 1 顆黑球及 3 顆白球,在 A 及 B 中選哪一個袋子的抽出黑球的機率比較大?」A 袋的機率是 3 1 ,B 袋的機率是 4 1 , 所以選擇 A 袋的機率比較大。過程似乎對國小學童有些困難,因為解題的概念 包含「部份-全體」的概念,以及分數計算與比較大小,解決此類比例及機率問 題似乎得先具備分數概念才能解題,但事實不然。就比例問題來看,A 為 1 杯果 汁混合 2 杯白開水,B 為 1 杯果汁混合 3 杯白開水,比較 A 和 B 的果汁杯數是 相同的,進而比較 A 和 B 的白開水杯數,發現 B 的白開水比 A 的還要多,學童 只要知道更多的白開水將會稀釋果汁,就可以理解 A 的濃度較 B 的組合來得高, 這之間的解題過程,進行的僅是整數的比較,而不需經由分數的計算來獲得結 果;同理,學童在解決機率相關問題亦可以其既有經驗及知識進行解題。由於每
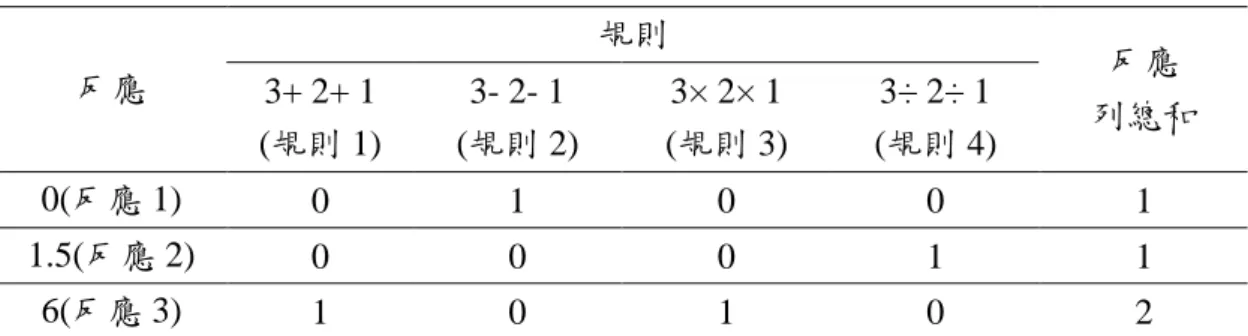
位學童的思考邏輯架構不同,解題時對於各種解題規則的使用情形亦不相同, Siegler (1976) 也指出,解題者受到本身已存在的知識結構的影響,在解題過程 中會依循某種方法進行解題,意即學童在決定解題策略時會產生一定的解題規 則。因此,學童在解題規則的應用亦可象徵其潛在知識狀態。往昔大多耗時地以 晤談方式來獲得學童個別的解題規則,而藉由潛在類別分析及混合 Rasch 模式規 則來獲得學童解題規則使用及潛在知識狀態,有其必要可行之處,此為本研究動 機之二。 知識結構分析屬心理計量所重視的範疇,以往研究中大多以質性晤談的方式 來獲得或以量化的方式進行 (Miller & Fey, 2000) ;而由於近來演算與方法論的 快速進步,藉以取代人工手算的複雜計算過程,因此,根據受試者試題反應情形 獲得受試者潛在知識型態,已有許多不同的方法被提出,其中,潛在類別分析 (latent class analysis, LCA) 及混合 Rasch 模式 (mixed Rasch model, MRM) 即是 廣受重視的分析方法。Siegler (1976) 指出,解題者受到本身已存在的知識結構 的影響,在解題過程中會依循某種方法進行解題,以本身已具備的經驗及知識結 構,擬定解題策略進行解題,並形成一種解題規則來解決同類型的問題;同一概 念的問題中會有不同類型的問題,受試者若採用同一種規則進行解題,正確的解 題規則會產生正確的結果,而不正確的解題規則會產生不正確的結果,亦可能產 生正確的結果。舉例來說,如「3+2+1」,其正確規則為以四則運算中的加法計 算,其正確結果為「6」,而四則運算之另外三種方法為「減法」、「除法」及「乘 法」,此三種方法在算式上為不正確的解題規則,其中的減法和除法所獲得的是 不正確的結果,但應用乘法規則所計算的結果是正確的。而一般傳統測驗之計 分,只能從測驗分數反應出受試者的總分、答對和答錯題數,或以絕對分數來表 示受試者的能力在團體中的相對位置,若欲以結果的正確來判定受試者所應用的 解題規則,則難以達其目的。潛在類別分析 (LCA) 是依據受試者在測驗中的反
應組型進行分析,根據事後機率將受試樣本進行分組,使得各組組內同質性高, 組間異質性高,因此,各組內受試樣本所形成的反應組型可代表各組潛在知識型 態或解題規則。而 Rost (1990) 結合 Rasch 模式與潛在類別分析,假設各組間對 同一試題有不同難度,再進行事後機率分析,進行受試樣本的潛在分組,稱為混 合 Rasch 模式 (mixed Rasch model, MRM) 。本研究即針對比例理解及機率理 解,分析受試樣本所得之反應組型,和文獻中解題規則所獲得的規則組型進行比 較,以獲得各組受試者的解題規則,相對於以晤談方式了解受試者解題規則所耗 費的時間,實有其必要及可行之處,此為本研究動機之三。 解題規則的應用與受試者已存在的知識結構相關,因此,分析現行國小數學 領域課程綱要,與比例和機率概念相關能力指標,如表 1-1 所示 (教育部,2003): 表 1-1 國小數學課程與比例及機率理解概念相關能力指標 指標 代號 分年細目 2-n-03 能用<、=、>表示數量大小關係,並在具體情境中認識遞移律。 3-n-09 能在具體情境中,初步認識分數,並解決同分母分數的比較與加減。 4-n-08 能理解等值分數,進行簡單異分母分數的比較,並用來做簡單分數 與小數的互換。 5-n-04 能用約分、擴分處理等值分數的換算。 5-n-05 能用用通分作簡單異分母分數的比較與加減。 5-n-12 能認識比率及其應用。 6-n-07 能認識比和比值,並解決生活中的問題。 6-n-09 能理解正比的現象,並發展正比的概念,解決生活中的問題。 6-a-04 能在比例的情境或幾何公式中,透過列表的方式認識變數。 表 1-1 顯示,比例推理及機率推理問題並未被直接編入課程綱要中進行教 學,而解題所需工具僅隱涵在能力指標中,而解題規則的應用是否因背景變項而 異,是頗受重視的主題,因此,年齡不同的受試者所採用的解題規則是否會有差
異?性別是否也會影響解題規則使用上的不同呢?林福來、郭汾派、林光賢 (1985) 的研究結果顯示,年級愈高則比例推理能力也隨之成長;Karplus, Pulos and Stage (1983) 的研究結果則顯示,在數值型態為整數之比例問題中,男、女 生之比例推理能力並無差異。因此,解題規則的應用是否因年級的不同而有所差 異,有待進一步的探討,因此,國小學童在比例及機率問題所採用的解題規則是 否會因年齡或性別的差異而有所不同,為本研究的研究動機之四。
第二節
研究目的
基於上述,本研究之目的可臚列為以下三點。 (一)應用潛在類別分析 (LCA) 及混合 Rasch 模式 (MRM) ,分析國小四 至六年級學童,在比例理解問題反應情形,並探討其所採用之解題規 則。 (二)應用潛在類別分析 (LCA) 及混合 Rasch 模式 (MRM) ,分析國小四 至六年級學童,在機率理解問題反應情形,並探討其所採用之解題規 則。 (三)比較不同年級或不同性別的受試者,在上述比例問題及機率問題的解 題規則的差異。第三節
名詞解釋
壹、比例問題
本研究的比例問題,係指 Neolting (1980) 所提出的果汁濃度測驗 (orange juice test, OJT) ,設定二種組合,每種組合皆由不同杯數的純水或不同杯數的果料,係應用林原宏 (2006) 參考 Neolting 所編之果汁濃度測驗,並對中部地區國 小四至六年級學童進行施測所獲得的結果。
貳、機率問題
本研究的機率問題,係指 Siegler (1981) 所提出的機率理解問題,測驗問題 設計有二堆彈珠,每一堆皆由不同數量的黑色及白色彈珠所組合而成,假若在閉 上眼睛的前提下拿出一顆彈珠,讓受試者選擇哪一堆來拿,拿到是黑彈珠的機會 比較大,或是二堆都相等。本研究所分析的資料,係應用 Lin, Yu and Wu (2006b) 參考 Siegler (1981) 及 Bart and Orton (1991) 所編製機率理解測驗,在中部地區 國小四至六年級學童進行施測所獲得的結果,進行爾後的分析。參、解題規則
解題規則係指受試者解決問題時會依循某種方法或策略的心理歷程 (Jansen & Van der Mass, 2002) ,Siegler (1976) 認為解題者受到本身已存在的知識結構的 影響,在解題過程中會依循某種方法或規則進行解題。所以,解題規則可象徵解 題者的潛在知識狀態。
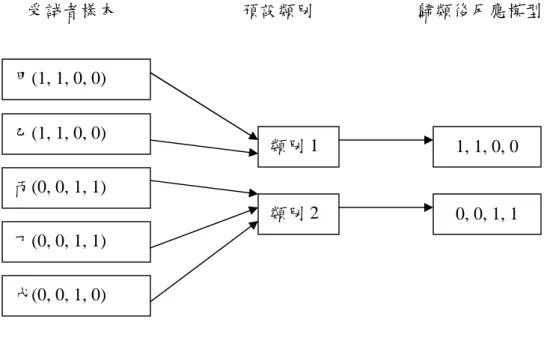
肆、反應組型及規則組型
對於一份測驗,每一位受試者對於各試題的反應結果不一,在二元計分下, 若以「1」表示正確,「0」表示錯誤,則受試者對於此份測驗的各試題將會產生 一種組合,例如對一份有 10 題試題的測驗,受試者可能的答題組型若以向量的 方式表示,可能為 (1, 0, 1, 0, 1, 1, 0, 0, 1, 0) ,表示第 1、3、5、6、9 題答題正 確,第 2、4、7、8、10 題答題錯誤;受試題的答題組型稱為「反應組型」 (reponse pattern) ,而根據某解題規則下進行解題所獲得的答題組型,則稱之為「規則組 型」 (rule pattern) 。第二章
文獻探討
本研究主要應用潛在類別分析及混合 Rasch 模式,分析學童在比例理解及機 率理解問題的反應類型,並和文獻上的規則類型比較,藉以獲得學童可能採用的 解題規則為何,因此,機率概念、比例概念、規則分析方法及所應用之分析模式 相關研究為本章節探討的重點。本章中,第一節先探討機率概念的相關研究;第 二節則說明本研究所應用的機率理解測驗及受試者可能採用的解題規則;第三節 評閱比例概念的相關研究;第四節則說明本研究中所應用的比例理解測驗及其解 題規則;第五節探討規則評量方法;第六節論述本研究所應用的潛在類別分析及 混合 Rasch 模式,並討論如何應用適配度選擇最佳類別數;第七節則說明對於試 題的規則解釋力及規則區別力之分析。第一節
機率概念的相關研究
壹、機率概述
「世界數學簡史」 (凡異,1987) 一書中提及,在十七世紀時,一位賭徒向 數學奇才 Blasise Pascal 提出博奕賭本平分問題,爾後 Pascal 將此問題及解法寄 給 Pierre de Fermat 共同討論,而得知此事的 Christiaan Huygens 亦企圖解決這個 問題,將其研究成果寫成了「論賭博中的計算」(De Rationciniis in Ludo Aleoe) 一 書,成為機率論的最早論著,也開始了研究學者對於機率的探討契機。當人類在觀察或預測某一現象時,會產生兩類情形。第一類情形在某些相同 條件下,其事件發生 (或試驗) 的結果可以預測的,其結果隱含因果關係且具有 決定性者。然而有些現象,雖然在某些相同的條件下,其事件發生 (或試驗) 的 結果並不能事先加以確定,是為非決定性者。「機率」便是一種指標,用來表述
可分為古典機率、經驗機率 (empirical probability) 、主觀或直覺機率 (subjective and intuitive probability) 及形式機率 (formal probability) 等四種類型 (蔡文煥, 1998) ,茲分述如下: 一、古典機率 設一樣本空間由 n 個樣本點所組成,且每一樣本點出現的機會均相等,則 定義事件 A 發生的機率為 A 之樣本點個數與 n 之比,亦即某事件發生之機率為 某事件可能發生的個數與該隨機試驗所有可能發生的總個數比。舉例來說,投擲 一個公正的骰子,其可能出現的結果有 1 點、2 點、3 點、4 點、5 點、6 點等 6 種結果,此為擲骰子可能出現的情形,為機率事件的樣本空間;若想知道投出奇 數的機率,擲骰子出現奇數的事件為 1 點、3 點、5 點共 3 種,則擲骰子出現奇 數的機率即為奇數可能發生的 3 種情形與擲骰子可能發生的 6 種結果的個數比或 比值,即為 6 3 。 二、經驗機率 亦可稱為次數機率,藉著隨機試驗結果的相對次數來預測機率,包含極限和 收斂的理論。例如投擲一枚公平的硬幣,其樣本空間有正反兩種情形,投擲次數 愈多,正反兩面出現的次數比會比較接近 1:1,藉由這樣的實驗結果,可以說 投擲一枚錢幣,其出現正面和反面的機率皆為 2 1 。 三、主觀直覺機率 為二十世紀所產生的名稱,主觀機率指的是個體根據過去客觀的事實來決定 其主觀的機率,因個體所得之經驗 (或是擁有之資料) 不同,因此可能會產生不 同的主觀機率。簡而言之,以觀察者對一件事件的相信程度來定義機率,就是主 觀的觀點。本在測量信仰的程度,依賴可獲得的資訊作為機率修正的理論。例如 一場棒球賽中如何在開賽前估測哪一支球隊獲勝的機率是多少,我們必須用主觀 的觀點,例如參考雙方的投手 ERA (自責失分率) 值、打擊者的打擊率等,給予
一個獲勝的相信程度值;或是依今天的雲量預測明天下雨的機率為 85%、依學生 過去平時測驗的成績預測明天通過檢測的機率是 60%等。 四、形式機率: 利用數學法則 (公理) 來定義機率,以 n A A P( ) 來定義在 n 個樣本點,且 每一樣本點出現的機會均相等時,事件 A 發生的機率。如在擲骰子事件中,出 現點數 1 的機率,為 6 1 ) 1 ( P 。 機率論發展至今,除了應用於博奕外,近來亦應用於科學研究方面,舉凡國 民經濟、醫療、心理學、地震、氣象及近代物理皆是,而企業也以機率來概估經 營的風險及獲利參考,保險金融相關業者亦以機率概述被保人身家風險以獲得最 佳利益比,進而推算各項保費金額。機率論應用之廣,由此可見一斑。
貳、兒童機率概念發展相關研究
一、Piaget and Inhelder 的機率概念發展論
關於兒童機率概念的發展,Piaget and Inhelder (1975) 認為依年齡可將兒童 的機率發展分為運思前期、具體運思期、形式運思期三個階段。 第一個階段在 7 歲前,為運思前期。處於此階段的兒童尚未形成機率的初 步概念,無法區別何謂「可能」 (possible) 或「必然」 (necessary) 的事件。此 階段的兒童也缺乏邏輯推理能力,因此常以自己的偏好,如自己喜好的顏色、數 字等因素來判斷機率的大小。 第二階段在 7 歲至 11 歲間,為具體運思期,此階段的兒童已能夠理解「可 能」、「必然」及「隨機混合」 (random mixture) 的概念,但仍無法以系統性的方 式產生一個有系列性的機率概念,也缺乏組合的技巧或去產生一個機率實驗的抽 象模式。 第三個階段出現於 11 歲後,為形式運思期。此階段的兒童已具有機率概念,
的可能性,並且開始發展組合分析能力,亦能藉大數法則的原理,預測事件的機 率值。
Piaget and Inhelder (1975) 的理論,認知發展是由基本感覺基模,重新建構 為更複雜的認知結構,進入運思前期,爾後再進入具體運思期及形式運思期,階 段的畫分主要為年齡的差異,從一個階段過渡到另一個階段是根據生物學的發 展,而不是受到學習過程的刺激;而 Green (1983a, 1983b) 曾對英國 11 至 16 歲 學生作為期三年有關機率概念的研究,結果顯示,有些學生對於決定機率基礎的 比率概念仍不瞭解,仍有 50%的學生會以單一物體數量決定機率的差異,而未具 備隨機概念,顯見英國學生於 13 歲以後機率概念並無明顯增長。因此,年齡對 兒童機率概念發展的影響,仍有進一步研究的必要性。 二、Fischbein 的機率概念發展論
相對於 Piaget and Inhelder (1975) 認為需至具體運思期才能夠具備機率概念 的能力,Fischbein (1975) 則認為機率概念並非直至具體運思期才出現,而是一 個連續的發展過程。 Fischbein (1987) 將「直觀」 (intuition) 定義為是一種認知的形態,是每個 人自然的、本能的信念。對於擁有直觀想法的人來說,它是腦中立即出現的意念, 不需證明。只是兒童的原始直觀 (primary intuition) 想法深深影響學童機率概念 的發展,若只是直接教導學童客觀性的機率,無助於其直觀想法的轉變,必須藉 由有系統的教學方式將這些原始直觀轉化為第二直觀 (secondary intuition) ,才 能獲得機率概念的意義 (羅友任,2003) 。 此外,Fischbein (1991) 發現,學童在「必然」、「可能」及「不可能」的事 件與「複合事件」時,兒童僅使用直觀想法來判斷機率的大小,因此有必要透過 教學來協助學童區分上述名詞之意義,而非坐視其自然發展 (張捷勝,2002;李 重孝,2004) 。
三、Bognar and Nemetz 的機率教學發展論
Bognar and Nemetz (1977) 的研究是建議針對不同年齡的學童可以提供適當 的機率教學,可分為四個階段:
(一)對 7 至 8 歲的學童可以教授簡單的機率概念,像是確定 (certain) 事 件、不可能 (impossible) 事件、互斥 (mutually exclusive) 事件。 (二)在 9 至 10 歲的學童可以教導「較可能事件」 (more likely events) 、
「較不可能事件」 (less likely events) 或是次序事件 (order events) 。 (三)在 11 至 12 歲的學童可以教相對次數 (relative frequencies) 及製作表 示機率的圖表,如樹狀圖。 (四)對 13 至 14 歲的學童可以教授獨立 (independent) 和相關 (correlated) 事件。例如有一袋中有紅球和白球各 10 個,連續抽取 8 次,若每次 抽取後又放回,則每次抽取的機率不受影響,是為「獨立事件」;若 每次抽取後不放回,則機率受前一次的影響,是為「相關事件」。 四、Jones et al.的機率概念發展論
Jones, Langrall, Thornton and Mogill (1997) 針對八位三年級學童進行個案研 究,為期二年,並對小學及中學學童進行為期三年的教學實驗,其研究架構的組 成依序為樣本空間、實驗機率、理論機率、機率比較、條件機率及獨立性,每一 項組成有四種發展層次,層次為由直觀到量化的推論。四個層次分述如下: 層次一為主觀的 (subjective thinking) 思考層次。學童大多以主觀的判斷決 定機率。例如讓受試者觀察一個有 5 個紅球、3 個黃球的盒子經過搖晃後,要求 受試者選擇抽到哪種球的機率較大,受試者可能因為對某種顏色的喜愛,或試題 圖形中球擺放的上下位置不同來決定機率的大小。 層次二為過渡的 (transitional) 的層次,介於主觀和質樸的量化思考 (naive
如讓受試者觀察一個有 5 個紅球、3 個黃球的盒子經過搖晃後,要求受試者選擇 抽到哪種球的機率較大,受試者可能回應「紅色,因為紅色有 5 個,且紅球在最 上面,因此出現機率較大」,內容雖以數量解釋,但仍以球的位置此類主觀的想 法左右機率的結果,而使得推理不夠精確。
層次三為非正式量化的思考 (informal quantitative thinking) 層次,嘗試使用 定量判斷來決定機率,但並不總是使用慣例的、協定的方式表示機率或是可能 性,例如以分數的方式表達機率的大小。
層次四為數理的推理 (numerical reasoning) ,於此層次的學童開始使用數字 來表示機率。
五、Siegler 的機率概念發展研究
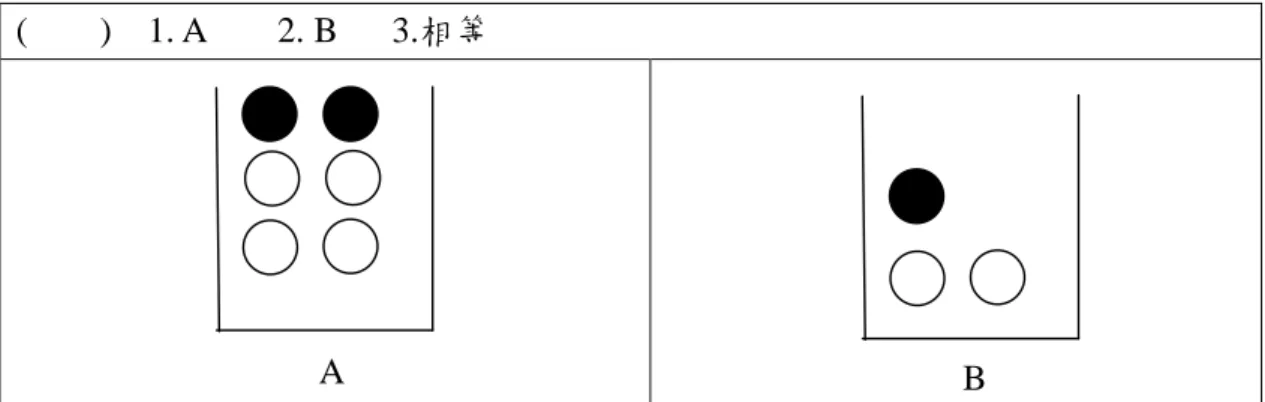
Siegler (1981) 由規則評量的方法 (rule assessment methodology) 出發,自受 試者處理機率問題的訊息中歸納其處理規則。Siegler 認為,若同時有二個向度 (dimension) ,影響一特定事物時,其中一個影響力比較大的向度,稱為「優勢 向度」 (dominant dimension) ,而另一個較不具影響力的向度,就是「次要向度」 (subordinate dimension) 。以 Siegler (1981) 所設計之機率比較類型的測驗說明, 受試者在二堆彈珠中,每一堆彈珠以黑、白二色所組成,請受試者在不同的組合 中,選擇在哪一堆的組合裡抽到黑色彈珠的機會較大,試題範例如圖 2-1 所示。 而所欲取出的目標物為黑色彈珠,則黑色彈珠數即為優勢向度,白色彈珠數為次 要向度。
( ) 1. A 2. B 3.相等 圖 2-1 Siegler 機率理解測驗示例 Siegler (1981) 所設計之測驗試題分為六種類型,若各題的組合以 (a1 , b )1 vs. (a2 , b ) 的組合表示該題測驗中,A 有2 a 個黑色彈珠和1 b 個白色彈珠,B 有1 2 a 個黑色彈珠和b 個白色彈珠,以圖 2-1 之試題為例,則可表示為 (2,4) vs. (1,2 2) 。各類型內容說明及範例如表 2-1 所示。他認為學童使用漸進複雜的四個規 則來處理機率與非機率問題,而 Bart and Orton (1991) 更指出 Siegler 在檢查機率 問題的反應模式是根據四個規則,規則 1 指向最低的認知發展層次,而規則 4 是最高認知發展層次。 表 2-1 Siegler 的題目類型 試題 類型 名稱 說明 範例 A 優勢 二種組合其白色彈珠相同。結 果 為 選 擇 黑 色 彈 珠 較 多 的 組 合,其取得黑色彈珠機率較大。 (4,2) vs (3,2) 結果為 A B 次要 二種組合其黑色彈珠相同。結 果 為 選 擇 白 色 彈 珠 較 少 的 組 合,其取得黑色彈珠的機率較 大。 (3,4) vs (3,3) 結果為 B C 差異-次要 各組間黑色、白色彈珠數皆不 相同,組內黑、白彈珠差異不 相同。結果為選擇白色彈珠較 (3,2) vs (6,3) 結果為 B A B
表 2-1 Siegler 的題目類型(續) 試題 類型 名稱 說明 範例 D 差異-優勢 各組間黑色、白色彈珠數皆不 相同,組內黑、白彈珠差異不 相同。結果為選擇黑色彈珠較 少的組合,其取得黑色彈珠的 機率較大。 (3,1) vs (4,3) 結果為 A E 矛盾-次要 各組間黑色、白色彈珠數皆不 相同,組內黑、白球數差距相 同。結果為選擇黑色彈珠較少 的組合,其取得黑色彈珠的機 率較大。 (3,1) vs (5,3) 結果為 A F 矛盾-優勢 各組間黑色、白色彈珠數皆不 相同,而其中有一組合為黑白 彈珠數相同。結果為選擇黑色 彈珠較少的組合,其取得黑色 彈珠的機率較大。 (4,4) vs (2,1) 結果為 B Siegler (1981) 的研究結果支持著 Fischbein (1975) 的方法,藉著教導學生機 率問題的策略和規則,能使得可操作的機率概念獲得進步和成長。
六、Munisamy and Doraisamy 的機率概念發展研究
Munisamy and Doraisamy (1998) 提出兒童於機率概念各層次所出現的特徵 為何。層次一的兒童具有機會和機率的直觀概念,對大部分基本機率概念都能了 解;層次二的兒童能了解到機率加法原理和實地的應用;層次三的兒童能了解獨 立事件的乘法原理和延伸到條件機率的推理,並且能成功的應用在新的機率問題 上。
綜觀上述,機率概念的形成是漸進且具有發展性的,依年齡的畫分無法完 整敘述兒童於機率概念上的發展,正如 Fischbein (1975) 所述 Piaget and Inhelder
形成佔有舉足輕重的地位。因此本研究藉以規則分析了解學童概念發展,並期望 能於適當的發展時期予以引導,達到最好的教學成效。
參、其它機率概念相關研究
林燈茂 (1992) 的研究澄清 Piaget and Inhelder (1975) 的兒童機率概念發展 理論中,有關「相對差異」 (relative difference) 及「大數法則」項目之研究。「相 對差異」指的是受試者在面對機率試驗時,會依據各樣本點出現次數的差異大 小,或以試驗中各樣本點個數差異來作為判斷的依據;而「大數法則」是機率中 一個重要的基本概念,依現行國小機率教材所呈現,係指「實驗愈多次,各樣本 點出現的比值,將彼此愈來愈接近或愈接近其機率值」的概念。林燈茂的研究發 現,現行國小機率教學,對十二歲左右之學童於「相對差異」概念的理解,尚難 應付於建構「大數法則」概念之所需;而現行教學不僅未能有改善兒童對於機率 教學前所潛存之有關的迷思想法,反而衍生出一些新的迷思想法,甚至教師本身 亦存在著機率概念的迷思。 朱雅瑋 (1996) 以質性研究,探討國小學童機率概念的思考歷程, 並藉以分 析國小學童機率概念的直觀類型。研究結果顯示,國小學生機率概念的直觀類型 可分為八大類型:「符合已出現母群分配典型」、「符合理想母群分配典型」、「符 合隨機過程分配典型」、「正反時近效應」、「樣本空間元素之可獲性不足」、「無法 從不同具體情境抽離出相同數學結構」、「樣本空間之形成不正確」、「結果取向」 等。此外,將職前教師與學童的機率直觀概念作初步比較,發現多數學童存有與 職前教師相同的機率直觀概念。 施能宏 (1997) 探討國小高年級學生在不同概念型式的機率文字題之選答 表現、策略及概念。研究結果發現學生解決機率文字題所使用概念的策略有十 種,分別為「結果取向」、「表徵性誘發」、「有效性誘發」、「以量化絕對差異觀點」、
目標數間差異大小」、「依試行的可控制程度」、「大數法則的另有概念」。其研究 並發現男、女生在機率文字題的得分並無差異。不同年級,及教學前、後的學生 在機率文字題的得分有差異。六年級學生在經過機率單元教學後,整體的學生在 潛在特性的分布上已有顯著的改變,理解程度較佳的學生明顯增多。學生對於機 率文字題中樣本空間概念的題目較易理解,對於大數法則概念的題目則因存另有 之概念而較感困難,對於機率性的比較問題,多以結果取向、量化絕對差異與過 去經驗來作機率大小之判斷,且仍缺乏獨立試行之觀念。 吳靜瑜 (1999) 以 Jones et al. (1997) 機率思考架構研究六年級學童,發現學 童在不同的機率概念測驗中,大部分學童的思考層次尚未達到「數量推理」的層 次;學童的思考仍舊停留在「主觀的」、「過渡的」或是「非正式量化的」想法。 同樣在機率思考架構中,楊珊珊 (2005) 的研究中指出,「樣本空間」、「實驗機 率」、「理論機率」、「機率比較」,學童最高皆能達到層次三的非正式量化思考層 次;而在「條件機率」、「獨立事件」中,最高只能達到層次二的過渡思考層次。 詹淑雯 (2005) 發現四年級的學童可以使用最大位移策略 (maximal shift strategy) 解決樣本空間的問題;國內兒童以樣本空間的表現最為落後,但 Jones, Thornton, Langgrall and Tarr (1999) 的研究結果卻顯示,國外兒童在條件機率組成的表現較 為落後。 韓燕言 (2002) 探討已學習過簡單機率的國小六年級學童,其機率概念學習 之表現,結果發現在不同的教學單元,其機率概念的學習結果有差異;在相同的 教學單元,男、女生以及不同地區的學生其機率概念的學習結果沒有差異。並發 現國小六年級學童在機率概念的答對率普遍不佳,機率的學習結果最佳為樣本空 間,其次依序為機率事件、比值接近、大數法則;雖然男、女生在機率概念沒有 差異,但女生在樣本空間的學習表現優於男生,且不同地區的學生在機率概念的 測驗結果有差異。
張捷勝 (2002) 採用行動研究法 (action research) ,探討兒童的機率學習, 研究結果發現學生在機率學習時,對機率問題的想法有三種類型:想法自然型、 想法接受型及想法整合型。對機率問題類型的解題表現在樣本空間、機率事件、 機率比較、條件機率四個部分,學生在經過學習後,後測成績均較前測為優。且 男、女生在四個部分的答對率都有明顯的進步。答對率不受性別影響。學童對機 率問題的正確解題策略是能對樣本空間有系統的組合分析。正確的求出樣本空間 再利用部分-整體的分數策略;錯誤的解題策略是缺乏對整體結果的完整考慮或 有其自然的想法或對機率存有迷思,且只能用利用部分-部分做比較,較少利用 部分-整體的分數策略,但也因缺乏對整體結果的完整考慮或因對分數值的運用 不熟練而容易出錯。另外研究也發現,學童機率迷思類型有如下十種:「手氣取 向」、「物極必反」、「不太懂題意」、「等機率偏見」、「可獲性啟發」、「結果取向」、 「忽略母群體的改變」、「數量取向」、「等量取向」、「漏列樣本空間」。 張捷勝 (2002) 研究發現,六年級的學童面對「有甲、乙兩個袋子,甲袋中 裝有 12 個黑球、4 個白球,乙袋中裝有 20 個黑球、20 個白球,你認為從哪個 袋子抽到黑球的機會較大?」能正確解題的多用部分—全體的分數值,化成同分 母的形式來進行比較,而答錯的有些認為乙袋的黑球比甲袋多,認為乙袋較易抽 中黑球。 羅友任 (2003) 探討高年級學生機率解題的能力、後設認知的能力與解題溝 通能力的表現與相關。以臺中縣三所國民小學高年級學生共計 331 名。採用自 編的「機率解題測驗」為研究工具,探討學生機率解題能力、後設認知能力與解 題溝通能力之相關,並分析學生在機率問題上所表現的答題類型,藉以瞭解學生 機率解題的理解情形。研究結果發現,高年級學童在「部分─全體」機率試題的 表現上高於「大數法則」試題之表現。五、六年級學生在「可能性大小判斷」機 率試題表現上無顯著差異。在「部分─全體機率大小判斷」、「大數法則」及整體
機率試題的表現上,達顯著差異,六年級高於五年級。 羅友任 (2003) 並以 Siegler (1981) 的規則模式作為探討「二個不透明的箱 子中,甲箱中有相同大小紅彈珠二顆,白彈珠三顆,乙箱中有相同大小紅彈珠三 顆,白彈珠六顆,現在要從當中各抽出一顆彈珠,你認為甲乙兩箱中哪一箱抽中 白彈珠的機會較大?」這類雙重「部分—全體」機率大小試題,在其答題類型分 析上,完全以規則 4 來解題的共 78 位,完全以規則 3 來解題的共 31 位,完全 以規則 2 來解題的共 17 位,完全以規則 1 來解題的的共 44 位。羅友任並發現, 除了這四個策略以外,還有兩種策略,一種是以總和大小為依據,總和大就代表 機會大,完全以此種策略答題者共 12 位,另一種為認為機率就等同於機會都一 樣,而忽略個數不同,完全以此種策略答題者共 9 位。能使用規則 4 的學童, 因分母、分子未加以注意而錯誤者共 9 位,究其原因可能因試題分母均較分子 大,學童未仔細而產生的錯誤;能使用規則 4 的學童,在某些題目卻用規則 1 的 共 13 位,顯示部分學童雖使用規則 4,但其對概念的真正瞭解令人懷疑。 李重孝 (2004) 以臺北市某國小六年級一個班共 25 名學生為教學對象,在 教學前、後對參與教學活動的學生實施機率試題紙筆測驗,發現經過機率教學 後,學生在紙筆測驗卷上的作答表現,明顯較機率教學前為優。另外,選取 6 名 學生進行訪談調查,以了解學生對於機率問題的正確解題思考與錯誤類型,發現 學生對機率問題的正確解題思考是能對樣本空間進行有系統的組合及分析,並運 用到如分數的部分-整體概念來解題;錯誤的類型則有許多種類,較常見的是無 法對樣本空間進行系統性完整考量,結果便是漏列樣本空間,其他如對於機率問 題存有迷思或是強調運氣等都是學生常見的錯誤類型。最後,對全體參與教學活 動共 25 名學生進行問卷調查,結果顯示學生對於機率教學的興趣、教學成效及 上課內容及方式都具有相當正面的看法。因此,李重孝 (2004) 認為在國小實施 機率教學具有相當的可行性。
白惠銣 (2005) 以國小六年級學童為研究對象,研究發現雖然國民小學現階 段正式課程中沒有納入機率概念的課程,但本研究發現學童仍具備該學齡所應發 展的機率概念;研究結果並顯示學童較易犯「以絕對差異的大小來判斷」、「以目 標數大小為依據做機率比較」、「正、負時近效應」之迷思概念。 楊怡芳 (2005) 以國小五年級高、中、低能力三位兒童為晤談對象,探討國 小五年級兒童,在機率概念中樣本空間、理論機率、實驗機率、機率比較、條件 機率及獨立性的直觀概念及思考層次。研究結果顯示,在樣本空間方面,中能力 兒童和低能力兒童不習慣將所有情況列出,傾向注意什麼較可能發生;在實驗機 率方面,高、中、低能力兒童皆沒有大數法則的概念;在理論機率方面,高、中、 低能力兒童大都能清楚判斷事件發生的可能性,但只有高能力兒童皆能使用分數 正確回答最有可能發生事件的機會;在機率比較方面,中、低能力兒童在離散情 境 (分母不同) ,並不會考慮母群體的多寡;在條件機率方面,高、中能力兒童 能說出「置回」與「不置回」事件發生的可能性有無改變;在獨立性方面,高能 力兒童能肯定每一次抽糖果的獨立性,中、低能力兒童並不認為每次試驗的結果 是獨立的。 蔡欣潔 (2005) 從學習機率之基本數學工具觀點探究國小高年級學童機率概 念發展,以瞭解學童的基本數學工具如「點數」、「乘法」、「分數」、「統計」、「比 例」之能力表現,對於機率概念表現是有否其關聯性。研究結果發現學童的基本 數學工具表現會因年級與性別的不同而出現顯著差異,機率概念表現也會因年級 不同而呈現顯著差異,六年級學童的基本數學工具之比例概念明顯比五年級學童 佳,但在大數法則概念的表現上,五年級學童反而略優於六年級學童。 李佳芸 (2007) 採用自編的「彈珠機率測驗」為研究工具,並以次序理論(ord-ering theory) 為理論基礎,再以精緻試題有向圖分析 (refined item digraph
analys-的解題規則次序性之階層結構,結果顯示總分不同的受試者在彈珠機率測驗,其 解題規則結構性有差異,解題規則的次序性亦不同,能呈現個別受試者解題規則 次序性之特色;而與五年級的受試者比較,六年級受試者的解題規則結構圖,與 專家的解題規則結構圖最為相似,但在不同性別的解題規則結構圖,專家的解題 規則結構圖的相似度沒有差異。 Fast (1997) 綜合前人的文獻,歸納出下列五點: 一、對學生來說,機率迷思概念是普遍的。 二、學生在學習時建構他們自己的知識,通常會包含在數學上對的基模跟有 缺陷的基模;學生建構出的知識不管是對或錯,常常很難改變。 三、知識的建構必須考慮到個人先前的知識。個人先前的知識對數學上正確 的基模的去開始建構或再現 (reconstruction) 是有影響的。 四、問題具體的陳述是關係到依學生能力能不能解決問題的關鍵因素,有一 些陳述對問題的解決是適當的活化基模,可有些是活化了建立在迷思概 念的基模。 五、建構主義的學習對學生是有幫助的,特別是克服迷思概念,雖然是以固 定的情境為支持架構。
Rodrigo, Castaneda and Camacho (1999) 對學前兒童 (5 歲) 及五年級 (11 歲) 及高中生 (17 歲) 做預測的測驗,在題目中給予在知覺 (perceptual) 或語義 (se-mantic) 敘述的簡單測驗 (simple task) 或是伴隨給予個別資料的複雜測驗 (com-plex task) ,發現學前兒童 (5 歲) 對簡單測驗可以建立一維的模式。五年級 (11 歲) 及高中生 (17 歲) 也能對簡單工作建立一維的模式,對複雜測驗能建立二維 模式。
Spinillo (2002) 對未接受過機率相關教學的七歲和八歲的兒童,進行判斷機 率大小的研究,證實孩童對三堆混著藍色和粉紅色的彈珠,根據抽取目標的顏色
機會的大小,可以完成排序。這個實驗是可以用部份-部份和部份-全體的比較去 解決問題。在 Spinillo (2002) 設計的三種型式的問題,使用策略 4 可以正確的將 三堆抽到藍彈珠的機率大小做排序。策略 4 跟 Jones et al. (1999) 所提出的機率思 考的層次三相似。
Lopes and de Moura (2002) 基於日益增多的人口將會影響到社會和經濟的發 展,需要有預測跟思考這些不確定的事件的能力。因此,對小學教師在機率和統 計的部份做教育訓練,以教師的教學經驗,分析參與者每一次的訪談、錄影和報 告。這個計畫不只是做統計與機率方面訓練的研究,對教師的成長是有幫助的。
Girotto and Gonzalez (2007) 的研究中,發現學齡前兒童預測一個事件會考慮 事前機率,推翻了認為一定要計算,才能去做機率的推理,這個發現是很重要的, 因為他挑戰了傳統 Piaget and Inhelder (1975) 的觀點:認為學齡前兒童缺乏機率 比值的邏輯推理能力。
綜合上述研究,以量化的方式分析學童機率問題解題規則的研究較為少見。 因此,分析學童解題反應類型,進而獲得學童可能採用的解題規則,了解學童的 解題策略及機率概念,實有必要可行之處。
第二節
機率理解測驗與解題規則
關於機率理解相關的研究中,Siegler (1981) 及 Bart and Orton (1991) 指出學 童在解決機率問題可能採取四個規則,其中有三個規則是不完美的,只有一個規 則是正確的。Bart and Orton (1991) 所設計的機率測驗,試題設計舉例如圖 2-1 所示,請受試者選擇何種組合下抽中黑球的機率較大,若機率相同則選擇「相 等」;其中,各組的組合以 (黑球,白球) 表示,以圖 2-2 為例,A 組可表示為 (2, 4) ,B 組組合可表示為 (1,2) 。
( ) 1. A 2. B 3.相等
圖 2-2 機率理解測驗試題舉例
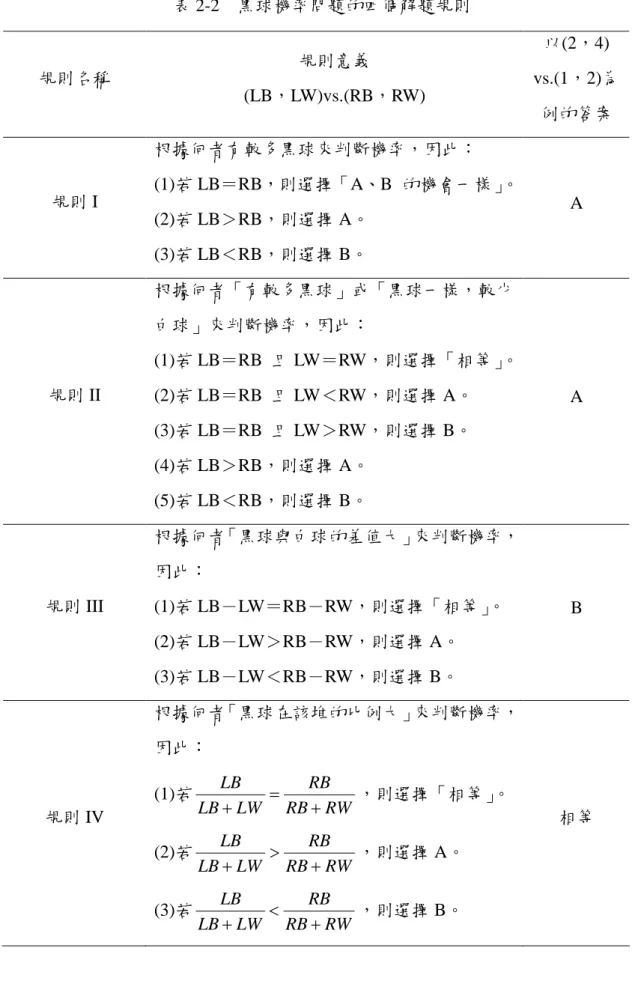
以 RB 代表右側組合 (B 選項中) 黑球數,RW 表右側組合白球數 (B 選項 中) ,LB 表左側組合黑球數 (A 選項中) ,LW 表左側組合白球數 (A 選項中) , Siegler (1981) 及 Bart and Orton (1991) 提到黑球機率問題的四個解題規則,其規 則的意義如表 2-2 所示:
表 2-2 黑球機率問題的四個解題規則 規則名稱 規則意義 (LB,LW)vs.(RB,RW) 以(2,4) vs.(1,2)為 例的答案 規則 I 根據何者有較多黑球來判斷機率,因此: (1)若 LB=RB,則選擇「A、B 的機會一樣」。 (2)若 LB>RB,則選擇 A。 (3)若 LB<RB,則選擇 B。 A 規則 II 根據何者「有較多黑球」或「黑球一樣,較少 白球」來判斷機率,因此: (1)若 LB=RB 且 LW=RW,則選擇「相等」。 (2)若 LB=RB 且 LW<RW,則選擇 A。 (3)若 LB=RB 且 LW>RW,則選擇 B。 (4)若 LB>RB,則選擇 A。 (5)若 LB<RB,則選擇 B。 A 規則 III 根據何者「黑球與白球的差值大」來判斷機率, 因此: (1)若 LB-LW=RB-RW,則選擇「相等」。 (2)若 LB-LW>RB-RW,則選擇 A。 (3)若 LB-LW<RB-RW,則選擇 B。 B 規則 IV 根據何者「黑球在該堆的比例大」來判斷機率, 因此: (1)若 RW RB RB LW LB LB ,則選擇「相等」。 (2)若 RW RB RB LW LB LB ,則選擇 A。 (3)若 RW RB RB LW LB LB ,則選擇 B。 相等
關於機率理解概念的相關量化研究,李佳芸 (2007) 以次序理論 (ordering theory) 為理論基礎,採用自編的「彈珠機率測驗」為研究工具,以精緻試題有 向圖分析 (refined item digraph analysis) 提高試題品質,並以臺中縣市國小高年 級學童共計 362 名為研究對象。探討受試者在彈珠機率機率測驗的表現情形,根 據個人解題規則結構圖的分析,並比較解題規則結構圖與專家的解題規則結構圖 之差異;Lin, Yu and Wu (2006a, 2006b) 以模糊集群分析學童於機率理解概念試 題反應情形,將受試學童進行分群;Lin and Hung (2007b) 利用 SCM (similarity clustering method) 演算法分析學童於機率理解測驗的試題反應,結果指出,將研 究樣本中的學童分為 4 群最為理想,且每一群各與一解題規則相互對應。本研究 則參考 Bart and Orton (1991) 所提及機率理解 4 項解題規則,並應用潛在類別分 析及混合 Rasch 模式二種分析方法,分析 Lin, Yu and Wu (2006b) 對於臺灣中部 地區國小四至六年級學童施測所得資料並進行探討。
第三節
比例概念的相關研究
教育部 (2001) 在「國民中小學九年一貫課程綱要」中指出,期望學生達到 數學課程的第一項目為掌握數、量、形的概念與關係,比例即為數量關係的重點 之一;教育部於新修定的數學領域正式綱要中指出,比例是鍛練有理數數感的應 用課程之一,更在國小代數課題中,強調協助學童發展比例推理問題的解題策 略,亦有助於國中生理解相似圖形或伸縮圖形的比例關係 (教育部,2003) 。比 例概念備受重視,由此可見一斑。壹、比例概念概述
用數學符號a :b來表示兩數量 a 和b之間的對等關係,稱為「比」 (陳竹村、 林淑君、陳俊瑜,2002;劉祥通,2004) , a 稱為比的前項,b為比的後項;而前項 a 除以不為零的後項b的結果,則稱為a :b的「比值」。比例則是兩個比或比 值的等價關係 (劉秋木,1996) 。
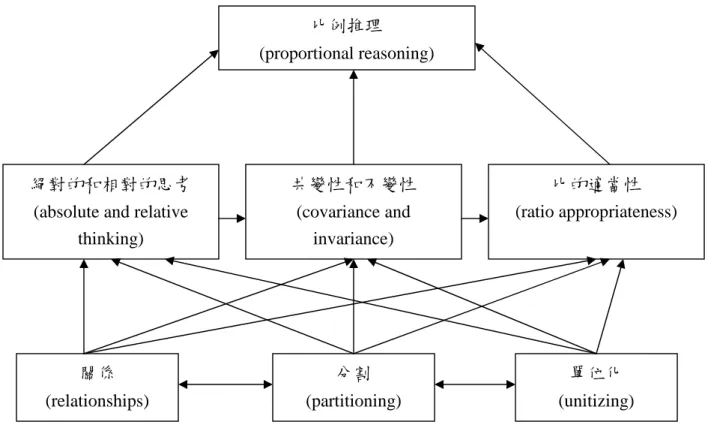
比例關係是兩個量間比的等價關係,Lamon (1995) 認為要了解比例關係的 意涵,要先明白比例概念所包含的三個重要的數學要素,茲分述如下:
一、相對和絕對的改變 (relative and absolute change)
比是表示一個數值對於另一個數值的相對大小 (Nohda, 1984) ,而「相對」 正是比例概念中最重要的成分 (鄭英豪,1990;Lamon, 1995) 。假設有 A、B 二 家公司,A 公司去年賺 50 萬元,B 公司今年賺 200 萬元,經過一年後進行結算, A 公司今年賺 100 萬元,B 公司今年賺 250 萬元。上例中,若以總量來觀察二家 公司的成長率,A、B 二家公司今年各盈利各增加了 50 萬元,成長率看似相同, 這是以「絕對」 (absolute) 的角度來看;但若以「相對」 (relative) 的觀點來看, A 公司盈利自去年 50 萬元上升為今年 100 萬元,今年是去年的 2 倍,而 B 公司 自去年 100 萬元上升為今年 150 萬元,今年僅是去年的 1.5 倍。也就是說,從相 對的觀點來看,這二家公司的成長率是不相同的。 從上述的範例得知,學生在進行比例推理的時候,應該先學會判別要以絕 對或相對的立場來思考問題。然而,這點並非所有的學生均能具備。比例是一個 比較性的指標,它總是說明了一個量和另一個量之間的關係。如果一個人僅以絕 對的角度來思考問題而忽略相對間的關係,則無法掌握比例的意義。 二、比感 (ratio sense) 「比感」是指對比的感知,兒童要能夠分辨哪些情境是由比組成,而哪些 不是。他們需瞭解到,存在於兩量之間的關係是什麼,而且這樣的關係應該是真 實的。同時,兒童應該藉由研究比例關係的實例及非實例來發現構成一個比例情 境的必要條件是什麼。例如,假設知道有兩個量存在著第二個量是第一個量的倍 數關係時,兒童若可以察覺到,只要知道第一個量是多少,就能透過倍數關係找
出第二個量是多少時,那我們可以說兒童已具備比感。 三、共變性和不變性 (covariance and invariance)
Lamon (1995) 認為,組成比例關係的兩個比之比值具有不變性,於是在某 些數量間便會存在「共變性」。例如,市場裡 3 公斤的橘子賣 120 元,12 公斤的 橘子賣 480 元,若以橘子的重量為前項,價格為後項,兩個比分別為 3:120 及 12:480,二個比的比值均為 40 1 ,為比例關係的不變性;但當重量由 3 公斤增為 12 公斤時,為了要維持比值的不變性,價格亦由 120 元變為 480 元,即是屬於 比例關係中的「共變性」。 面對比例問題時,受試者若要能成功解題,其所需具備五項相關基本能力 (林瑋詩,2007) ,分述如下: 一、乘除法概念
Vergnaud (1983) 提出概念體 (concept field) 的觀點,認為比例的理解建立 在乘除概念的結構上;而 Lo and Watanabe (1997) 指出其個案的比例概念深受本 身乘除法概念影響,也支持比和比例概念內嵌於乘法概念體的觀點。Vergnaud (1988) 更進一步提出乘除法問題是比例問題的特例,例如「15 顆糖賣 50 元,10 顆糖賣多少元?」是一個比例問題,而題目改為「1 顆糖賣 3 元,6 顆糖賣多少 元?」則為乘法問題,若改為「4 顆糖賣 8 元,1 顆糖賣多少元?」則是除法問 題。所以,比例概念可說是乘除法概念的上位概念 (劉祥通,2004) ,而對乘除 法的了解,對學生解比例問題有所幫助。 二、因數與倍數概念 「12 顆糖賣 30 元,8 顆糖賣多少元?」屬於比例問題,若受試者的解題過 程,是先將 12 顆糖分為 3 組,每組 4 顆,因此價格 30 元也分為 3 組,每組 10 元;取出其中 2 組,共計 8 顆,價格則為 20 元。這種解法的關鍵是找出價格和 糖數的公因數,進而決定組數為 3,再藉由分解、合成的過程進行解題。解比例
問題通常是先做除法做乘法,就是利用因數與倍數來解決問題 (劉祥通、周立 勳,1999) ,因此,因數與倍數概念的了解有助於比例問題的解題。 三、有理數的相關概念 兒童在進行比例問題的解題過程時通常會以乘除法進行解題,但解題時若 遇到類似「7 除以 3」除不盡的情況時,常會放棄解題 (楊錦連,1999) 。莊玉 如 (2005) 的研究則指出,未受過比例單元教學的學童,解題思維受整數基模影 響,其解題的特徵有避開分數、小數的計算;不熟悉分數概念的學童,在解比例 問題時常會遭遇困難,進而影響解題的成敗,因此,瞭解有理數概念,有助於學 童解比例問題時,用分數表示除法的結果和除不盡的數 (楊錦連,1999) 。 四、相對的 (relative) 思考能力 相 對 的 思 考 能 力 是 學 童 解 比 例 問 題 的 重 要 基 本 能 力 之 一 (Lamon, 1993a) ,具備相對思考能力的學童能了解問題情境中數量間的相對關係 (劉祥 通,2004) ;解比例問題時,亦能避免使用錯誤的加法策略,進而使用單價法、 倍數法等乘法策略來解題 (Lamon, 1993a) 。 五、單位化 (unitizing) 與基準化 (norming) 能力
Behr, Harel, Post, and Lesh (1992) 指出,把單一物體視為一個單位時,這種 單位稱為單項單位 (singleton unit) ;把幾個物體視為一個單位時,這種單位稱 為集聚單位 (composite unit) ;而單位化能力即是建立集聚單位的能力 (Lamon, 1993a, 1993b) 。例如,「4 個蛋糕賣 70 元,12 個蛋糕賣多少元?」的問題,能 把「4 個 70 元」視為一個單位,並以此單位來計數,利用 4 個 70 元、8 個 140 元的方式求得答案,便是具備單位化的能力。由此可知,受試者解比例問題使用 的是累加法策略,也是單位化能力的應用。 而「基準化」則是指以一個固定的單位或標準重新概念化一個系統 (Lamon, 「想像地球就像直徑 1 公厘的
針頭那麼大,則太陽就變成 10 公分的球體,且與地球的距離只有 10 公尺。」像 這樣利用「固定地球縮小為針頭的比例」,重新概念化「太陽的大小」及「與地 球的距離」,便是基準化的過程。Lamon (1994) 指出,解比例問題時所採取的單 價法策略和倍數法策略,都是運用基準化能力解題的好例子。 綜觀上述,具備乘除法觀念是解決比例問題的主要數學要素。林原宏 (2006) 所施測的對象是針對中部地區國小四至六年級學童,依據九年一貫數學課程綱要 (教育部,2003) ,學童在四年級時應能處理二位數乘以二位數及三位數除以一 位數的直式計算,因此在樣本的選擇上相當適當。而研究中所採用的試題為比較 濃度大小,並未要求計算數字,因此,有理數概念理解未必會造成學生解題上的 困難,而本研究以林原宏 (2006) 所施測的資料進行反應類型及解題規則分析有 其適切性。
貳、比例概念的發展
比和比例概念是分不開的概念 (Lo & Watanabe, 1997) ,比的概念可以說是 比例概念的基礎概念,但是要發展出成熟的比例概念,似乎除了對比的概念相當 了解之外,尚需對其他相關概念也要有相當的理解。因此,Lamon (1995) 提出 一個比例推理的數學發展結構圖,如圖 2-3 所示:
圖 2-3 比例推理的數學發展結構圖 (引自陳敏華,1999,p.24)
依據 Piaget and Inhelder (1975) 的說法,比例推理是一種二階 (second-order) 的關係,它包含著介於兩個比之間的等價關係 (Lo & Watanabe, 1997) 。而且比 例推理是以比和比例概念為基礎發展而來的一種數學推理能力,同時也是兒童 在解比和比例問題時,所外顯出來可以讓人觀察得到的解題行為之表現。因此, 當我們在探討比和比例概念時,比例推理也是不可忽略勢的一環 (陳敏華, 1999) 。
參、其它比例概念相關研究
林福來、郭汾派及林光賢 (1985) 以大量筆測方式,了解國中生解題策略的 使用情形;並以不同難易之數字關係問題的通過率代表比例推理能力的層次高 比例推理 (proportional reasoning) 絕對的和相對的思考 (absolute and relativethinking) 共變性和不變性 (covariance and invariance) 比的適當性 (ratio appropriateness) 關係 (relationships) 分割 (partitioning) 單位化 (unitizing)
其次為倍數法和單價法。研究結果之二顯示,年級愈高,則比例推理能力也隨之 成長;而數字關係的難易也影響比例推理能力的發展。 魏金財 (1987) 利用縱貫生長 (longitudinal growth) 研究法,探討國小五、 六年級學童處理比例問題的解題策略類型及解題策略隨生長而變遷的情形。其研 究結果顯示,從解題策略使用頻率較高的觀點,不同層次 (不同數字關係) 之比 例問題與解題策略間有交互作用現象;而對於相同的比例問題,除了六年級發展 出公式法外,其他各解題策略皆未隨年齡改變而有差異。 何意中 (1988) 也以筆測和晤談法了解國小三至五年級的 60 位學童在比例 問題上的解題策略與錯誤類型。其發現之一為學童最常使用單價法和倍數法,最 少使用公式法。這結果與林福來等人 (1985) 之結果不同,可見國中和國小學 童,其解題策略之使用次數多寡不同。研究發現之二為,三年級學童使用累加法 的次數最多,顯示年級愈低欲容易逃避乘法;而在錯誤的解題策略中,則屬任意 運算這一類的使用次數最多,顯示國小學童對加減乘除的運算意義不了解。 楊錦連 (1999) 探究不同城鄉和年級的國小高年級學童在不同數字關係和 語意類型之比例問題的解題表現。其研究採質性和量性並行的的方式,先大量施 測,以學童之答對通過率,作為探討不同數字關係和語意類型之比例問題的困難 度高低之依據,並分析各解題規則的使用率;再訪談 10 位不同解題層次的學童, 了解其解題策略並歸納對解比例問題有幫助的知識和能力。其研究結果顯示,部 分類型之語意問題有困難度高低的差異性,亦即在國小五、六年級學童的解題表 現中,交換問題和組合問題最簡單,密度問題和母子問題次之,而伸縮問題最難; 而交換問題和組合問題的解題表現無顯著差異,其可能原因為交換問題和組合問 題的語意在本質上是非常相似的。再以不同高低層次的學童使用不同之解題策 略,代表其所具備數學知識和能力之難易的觀點,得到學童能力層次由低而高, 依序使用的解題策略為具備約分和擴分的計算能力、單價法、單價法和倍數法混
合使用。另外,大部分解題錯誤者皆使用絕對思考的方式。 翁宜青 (2002) 及翁宜青、劉祥通 (2003) 利用晤談法,針對一位學過乘法 和簡單分數的三年級學童,探討不同數字關係之比例問題,與其所採取的解題策 略之間的關係。研究結果發現此學童能分別依序以累加法、數量分解和單價法及 倍數法解決不同數字關係的比例問題。而對於比例項間彼此皆非整數倍的問題, 則因不了解帶分數與單位量的概念,導致無法解題成功。 莊玉如 (2005) 以訪談法探討未接受過比例教學的 9 位國小四年級學童,其 在比例問題的解題表現。研究結果顯示,不同數字關係和不同題目類型的比例問 題,學童使用的解題策略亦不同;且部分策略被使用的次數多;部分策略則被使 用的次數極少。另外,學童因受整數基模的影響,解題歷程有避開分數和小數計 算的特徵。
Karplus, Pulos and Stage (1983) 探討在不同層次高低之比例問題下,學童使 用解題規則的情形。其研究結果顯示,在數值型態為整數之比例問題上,男、女 生之比例推理能力無差異;在數值型態為分數之問題上,則男生表現較優。 Lamon (1993a) 針對未學過比例概念的六年級學童進行晤談,了解其在不同 語意類型的比例問題之解題思維和策略。其研究發現,對於部分-部分-全體之問 題,學童傾向使用像累加法等較簡單的策略解題;而放大縮小問題是學童感到最 困難的問題類型,因學童不能確認這類問題情境的乘法本質。而在聯想問題 (組 合問題) 上,學童能使用較複雜的解題策略解題,因為這類問題能以具體圖示幫 助解題。 Lo and Watanabe (1997) 針對一位國小五年級學童,探究其解題策略及影響 其解題的因素。研究結果發現,原本只會使用累加法和公倍數法學童,經過教學 實驗後,會因不同的數字關係和語意情境類型,而選擇單價法或倍數法;而遇到 數字關係為非整數倍的問題,便會採取其獨特解題方法,亦即使用累加法和公倍
數法,其相信這兩種方法最後一定會得到正確答案。可見這位學童對於不熟悉的 題目,會有彈性的選擇其有能力解決此問題的解題策略。由此可知,學童解題規 則的使用上具次序性。因此,本研究欲探討個別受試者在比例問題之解題規則的 次序階層結構,有其必要與可行之處。
Misailidou and Williams (2003a, 2003b) 整理相關文獻進行編製試題、並以 Rasch 模式之試題反應理論檢驗,再以晤談提供診斷解釋之依據,發展出診斷比 例推理之解題策略的試題庫。
綜合上述相關文獻,就研究方法而言,分成質性和量性兩大研究取向。一是 以質性的觀察、晤談和記錄,深入了解單一或少數受試者的解題思維 (翁宜青, 2002;翁宜青、劉祥通,2003;莊玉如,2005;Lamon, 1993a; Lo & Watanabe, 1997) ;二是由量性的紙筆測驗和統計分析方法,分析全體受試者資料,歸納出 各種解題規則使用次數的多寡情形 (何意中,1988;林福來等人,1985;楊錦連, 1999;魏金財,1987) 。而本研究從量性研究取向著手,但有別於上述量性研究 之相關文獻,以受試者對比例理解問題的反應,分析其潛在類型,從而了解其解 題規則。 就影響比例問題解題之因素而言,綜合上述文獻 (林福來等人,1985;魏金 財,1987;何意中,1988;楊錦連,1999;翁宜青,2002;翁宜青、劉祥通,2003; 莊玉如,2005; Lamon, 1993a; Lo & Watanabe, 1997) ,大多從不同數字關係或 語意類型之比例問題,探究其與學童解題表現的關係。而本研究分析受試者反應 組型,將所獲得的潛在類型和解題規則比較,進而分析不同年級、性別使用解題 規則上是否有所差異。
第四節
柳橙汁濃度測驗與解題規則
Juice Test, OJT) 探討學童解決此類比例理解問題所採取的五種解題規則,如表 2-3 所示。以 (a1 , b ) vs. (1 a2 , b ) 的組合為例來說明 Neolting 所編製的試題,2 表示該題測驗中,A 有a 杯純果汁和1 b 杯純水,B 有1 a 杯純果汁和2 b 杯純水,2 請受試學童選出此二組合中何者濃度較高或相等。茲以 (2 , 2) vs. (2 , 5) 為例, 其試題範例如圖 2-4 所示: ( ) 1. A 2. B 3.相等 A.