不同標的利率、殖利率曲線、波動結構對標準與亞式利率上限契約價值的影響

行政院國家科學委員會專題研究計畫 成果報告

不同標的利率、殖利率曲線、波動結構對標準與亞式利率上

限契約價值的影響

計畫類別： 個別型計畫 計畫編號： NSC91-2416-H-002-026- 執行期間： 91 年 08 月 01 日至 92 年 07 月 31 日 執行單位： 國立臺灣大學財務金融學系暨研究所 計畫主持人： 李賢源 報告類型： 精簡報告 處理方式： 本計畫可公開查詢

中 華 民 國 92 年 12 月 24 日

不同標的利率、殖利率曲線、波動結構對標準與亞式利率上限契約價值的影響

Impacts of Underlying Interest Rates, Yield Curves and Volatility

Structure on the Values of Standard Cap and Average Cap

計劃編號：NSC 91-2416-H-002-026 執行期間：91 年 8 月 1 日至 92 年 7 月 31 日 主持人：李賢源 國立台灣大學財務金融系(所) 一、 中英文摘要 本文推導不同利率模型下、不同標 的資產的標準利率上限契約的評價封閉 解，並且應用實例驗證各種評價公式的差 異。本文分別在 Hull and White (1990)、 Heath, Jarrow and Morton (1992)、Brace, Gatarek and Musiela (1997) 利率模型下 推導評價公式，標的資產則分別以瞬間短 率(Short Rate)、即期利率(Spot Rate)、 LIBOR 利率當指標。本文的實證則探討 分析在不同利率模型下，標準利率上限契 約價值的比較、利率波動性結構型態對標 準利率上限契約價值的影響、以及標準單 一利率上限契約價值與契約到期期限的 關係。 關鍵字：利率期間結構、利率波動性結 構、利率選擇權、利率上限契約 Abstract：

This paper derives the pricing formula for a standard cap, under different term structure models and using different interest rates as the underlying asset. The term structure models employed include Hull and White (1990), Heath, Jarrow and Morton (1992), Brace, Gatarek and Musiela (1997). In separate cases, the underlying asset is assumed to pay the short rate, the spot rate, and the

LIBOR rate. A unique pricing formula appropriate for each case is derived here and a numerical example is applied to demonstrate their differences. The following empirical studies are conducted ： (1) Computation of premiums of standard caps with various underlying assets and maturities; (2) Impact of interest rate volatility structure on the premium of a standard cap; (3) Relationship between cap premium and maturity.

Keywords：

Term Structure of Interest Rate, Volatility Structure of Interest Rate, Interest Rate Options, Interest Rate Caps 緣由與目的 當公司以舉債的方式籌措資金進行投 資時，利率的波動是影響公司資金成本的 重要因素。尤其是，舉借的若是浮動利率 的債務，則利率上升時，公司的資金成本 變高；利率下降時，公司的資金成本變低。 由於利率的變動並非一成不變，因此公司 的資金成本也具不確定性。公司為了規避 利率變動對營運所產生的風險，可依照自 己對未來利率趨勢的預期、或公司資金成 本規畫的特殊考量等因素，選擇不同的利

率衍生性商品來避險。一般可供避險的利 率衍生性商品如下：利率期貨（Interest Rate Futures）、利率交換（Interest Rate Swap； IRS ） 、 遠 期 利 率 合 約 （ Forward Rate Agreement；FRA）、利率上限（Interest Rate Cap；Cap）、利率下限（Interest Rate Floor； Floor）等。 利率衍生性商品都有避險功能，但由 於報償型態(Payoff Pattern)不同，所以會導 致不同的應用決策。例如上述的浮動利率 債務：若公司希望固定資金成本、且不願 意付避險費用但願意承擔義務，則可以訂 定一個利率交換的契約，支付固定的利 率、收取浮動的利率。由於利率交換契約 的報償型態是一對角線的型態，因此當市 場利率上升時，公司可鎖住資金成本在固 定利率的水準而不會隨市場利率上升；反 之，當市場利率下跌時，公司也必須鎖住 資金成本在固定利率的水準而負擔較高的 資金成本，無法獲得利率下跌所導致資金 成本減少的好處。因此，簽訂利率交換契 約時，雖不用負擔任何避險費用，而且擁 有利率上升時享有好處的權利，但同時也 承擔利率下跌時壞處的義務。另外，若是 公司希望控制資金成本在某一個界限下、 且不願意承擔義務但願意付避險費用，則 公司可購買利率上限契約。由於利率上限 契約的報償型態是一柪折線的型態，因此 當 利 率 上 升 且 超 過 上 限 利 率 (Cap Rate) 時，公司可以執行契約而得到市場利率與 上限利率的差額補償，將資金成本固定在 上限利率的水準；反之，當利率下降且低 於上限利率時，公司可以放棄執行契約， 而享受利率下跌造成資金成本降低的好處 （註1_{）。由上述的兩種利率衍生性商品可} 註1_{: 由於利率上、下限契約的評價與避險原理一} 樣，為節省篇幅，本文主要以利率上限契約為 知，雖然兩種利率衍生性商品都可達到避 險的目的，但是由於使用者願不願意付避 險費用與願不願意承擔義務的態度，會左 右公司選用何種利率衍生性商品來避險的 決策；再者，避險費用的高低以及承擔義 務的輕重也是影響公司決定使用何種利率 衍生性商品來避險的重要因素。因此，選 擇何種利率衍生性商品來避險，其實是因 人、因時、因利率環境而變動，並沒有一 定的準則。 近年來，國內隨著經濟的發展與金融 的自由化，利率的波動較以往益形顯著。 再者，愈來愈多的利率商品內含利率選擇 權 ， 例 如 ： 不 動 產 抵 押 擔 保 債 權 證 券 (Mortgage-Backed Securities; MBS)內含提 早還款(Prepayment)選擇權、或是公司債裏 內含利率賣權或買權(如 Inverse Floater) 等。這些因素促使利率選擇權常被應用來 當做避險工具，且有愈來愈普遍的趨勢； 尤有甚者，由於各種利率期間結構(Term Structure of Interest Rates )的理論模型被蓬 勃的發展，因此可以用來計算利率選擇權 的權利金、以及進行風險管理。本文即因 應這種趨勢，專注推導各種利率期限結構 模型的利率選擇權評價公式，並且以實例 驗證各種利率選擇權評價公式以及比較彼 此之間的差異。本文探討的主題之所以重 要主要是下列原因：(1)國內櫃檯買賣中心 已於民國九十二年八月開放證券商承做利 率 選 擇 權 (Interest Rate Options; 簡 稱 IRO)，目前開放的 IRO 屬於標準型態的利 率選擇權，如 Caps,、Floors、 Collars 等， 這些商品是被應用來交易出指標利率的隱 含波動率(Implied Volatility)，故一般僅需 要用 Black (1976)的評價公式即可；但是， 例來探討。至於利率下限契約的結果，讀者若 有興趣，可來函向主通訊投稿者函索。

預期證券商會衍生出許多的利率選擇權商 品，故需要各種利率期限結構模型的利率 選擇權評價公式。(2) 利率選擇權評價公式 會因依據什麼利率期限結構模型來推導、 以及用什麼指標利率當標的資產而產生不 同的結果，就作者有限之知識範圍內所 知，國內外既存文獻尚未有類似本文主題 之研究，特別是實例之數值比較，故本文 之研究結論可做為理論與實務的參考。 早期對利率選擇權評價公式的推導， 通 常 以 瞬 間 即 期 利 率 (Instantaneous Spot Rate；或稱短率 Short Rate)的利率期限結 構模型來推導。這類利率選擇權的評價公 式一般有三個嚴重的缺陷：(1)應用的利率 期限結構模型與市場現今的利率期限結構 不吻合，這會使得利率選擇權的評價產生 很大的誤差，例如：Jamshidian (1989)應用 Vasicek (1977) 利率期限結構模型解出利 率選擇權的評價封閉解；以及後來應用 Cox，Ingersoll and Ross(1985)利率期限結構 模型所推導出的利率選擇權評價公式等， 都有這個缺陷。(2) 這類利率選擇權的評價 有的是以瞬間即期利率當作利率選擇權的 標的資產，例如：Longstaff (1995)在 Vasicek 模型架構下，推導利率上限契約封閉解； 但是，因為瞬間即期利率是理論值，在市 場上並無法直接觀察得到，以瞬間即期利 率當標的資產會使得利率選擇權的評價公 式不符合實務應用。(3) 利率選擇權的評價 受到利率的波動性結構(Volatility Structure) 影響甚大，特別是利率波動性的型態(例 如：指數遞減型或駝峰型)；但是，瞬間即 期利率的利率期限結構模型，一般並無法 反映利率波動性的型態對利率選擇權的評 價影響。由於這類利率選擇權的評價公式 有上述這些缺陷，因此本文在推導各種利 率期限結構模型的利率選擇權評價公式 時，將針對這些缺陷修正之。 本文用來推導利率選擇權評價公式的 利 率 期 限 結 構 模 型 包 括 ： Hull-White (1990 ； 簡 稱 HW) 、 Heath-Jarrow-Morton (1992; 簡稱 HJM)、Brace-Gatarek-Musiela (1997；簡稱 BGM)等。之所以選用這三個 模型，主要是：(1)它們是學術界與實務界 廣為探討與應用的模型。(2)它們是瞬間即 期 利 率 、 瞬 間 遠 期 利 率 (Instantaneous Forward Rate)、LIBOR 利率的代表性利率 期限結構模型，因此探討比較它們的利率 選擇權評價公式，具有廣泛的價值性與代 表性。(3) 它們都以目前市場上的殖利率曲 線(Yield Curve)做為輸入的資料，因此推導 出來的利率選擇權評價公式都沒有前述的 第一個缺陷。了解這三個模型解決上述第 一個缺陷的優勢之後，本文接著探討以不 同的指標利率當標的資產的影響。 本文推導下列以不同的指標利率當標 的資產的利率選擇權評價公式：(1)在 HW 模型下，以即期利率(Spot Rate) 當標的資 產（註2_{），推導出利率選擇權評價公式。(2)} 在 HJM 模型下，先由瞬間遠期利率推導出 瞬間即期利率的隨機微分方程(Stochastic Differential Equation)，再分別以瞬間即期 利率、以即期利率當標的資產，分別推導 出 對 應 的 利 率 選 擇 權 評 價 公 式 。 (3) 在 BGM 模型下，以 LIBOR 利率當標的資產， 推導出利率選擇權評價公式（註3_）。透過 註2_{: 本文不推導 HW 模型下以瞬間即期利率為標的} 資產的利率選擇權評價公式，是因為這可以參 考 Longstaff (1995)的作品，故不再贅述。 註3_{: 一般而言，最常被用來當利率選擇權之標的資} 產的指標利率是 LIBOR 利率，然而除了 BGM 模型可以直接利用 LIBOR 利率隨機過程來推 導利率選擇權的評價公式之外，HW 模型和 HJM 模型都是應用零息債券價格和 LIBOR 利 率的關係，將 LIBOR 利率轉換成零息債券價格

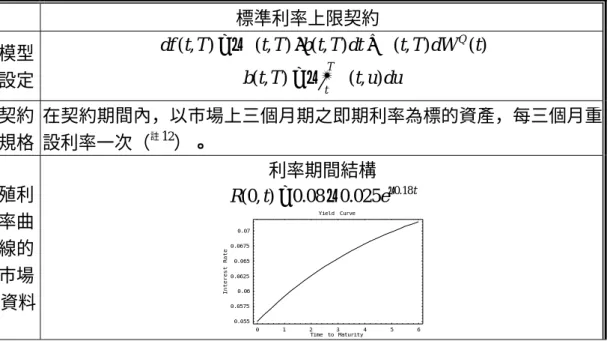
上述這些評價公式的推導，本文即可以用 數值實例來比較不同的模型、不同的指標 利率標的資產對利率選擇權的評價影響。 上述在 HJM 模型及 BGM 模型下推導得 到的不同的指標利率當標的資產的利率 選擇權評價公式，尚可用來探討不同的 利率波動型態對利率選擇權評價的影 響。HJM 模型長久以來即以能彈性的描 述各種型態的遠期利率波動結構而廣為 人知，也因為這項特性而能把 HW 模型 納為特例，使之成為遠期利率波動型態 呈現指數遞減型的 HJM 模型。再者， BGM 模型是間斷型的 HJM 模型，尤有 甚者它是可以直接利用市場上可觀察到 的 LIBOR 利率當標的資產的模型，因此 可以很容易的利用市場的 LIBOR 利率 資料作模型的校準(calibration)，使得模 型不僅符合市場的利率期限結構，而且 也符合遠期利率波動結構，對於利率衍 生性商品的評價與避險有極大的幫助。 二、 結果與討論 本節應用實例驗證不同模型、不同標 的資產的標準利率上限契約的評價差異。 由於利率上限契約是一利率買權(Interest Rate Call)，因此其評價受利率波動結構型 態影響很大，故本節亦探討不同型態的利 率波動結構對利率上限契約的評價影響。 除了 HW 模型因為其利率波動性結構為特 殊型態之外（註11_{），其餘 HJM 模型與 BGM} 表示，再以零息債券價格當標的資產來推導評 價公式，而以零息債券價格當標的資產即是相 當於以即期利率當標的資產來推導評價公式。 註11_{: Hull-White 模型若是從瞬間短率的隨機過程出} 發，其利率波動性結構一般設為常數；但是， 若是從瞬間遠期利率的隨機過程出發，則其 利率波動性結構為指數遞減的特殊型態。因 模型本文將分別考慮利率的波動性結構為 水平型、上升型、下降型、指數遞減型或 駝峰型等型態，探討其對利率上限契約的 評價影響。另外，影響利率上限契約價值 的另一重要因素—殖利率曲線，由於既存 文獻探討已多，故本文只假設目前市場的 利 率 期 間 結 構 為 上 升 型 t e t R(0, )=0.08−0.025 −0.18 ，再根據它討論 不同模型下，標準利率上限契約價值的比 較、利率波動性結構型態對標準利率上限 契約價值的影響、以及標準單一利率上限 契約價值與契約到期期限的關係。 一、Heath-Jarrow-Morton 模型 （一）標準利率上限契約的評價實證分析 在 HJM 模型下評價標準利率上限契 約，其評價公式是(27)式。表 3-1 報告在利 率期間結構為 t e t R(0, )=0.08−0.025 −0.18 、 利率波動結構型態分別為水平型、上升 型、下降型、指數遞減型和駝峰型等不同 狀況下，標準利率上限契約的價值。 由表 3-1 可知，無論利率波動性結構 型態為何，標準利率上限契約的價值有下 列的特徵：(1)隨著上限利率遞增，契約的 價值遞減；(2)隨著契約重設次數愈多 (即 T 愈大)，契約的價值愈大。第一項特徵是因 為利率上限契約是利率買權契約，而執行 價(即上限利率)愈高的買權愈沒價值。第二 項特徵則是因為 T 愈大代表這個利率上限 契約包含愈多個單一利率上限契約，當然 其價值愈大。 另外，由表 3-1 可知，因為所有的利 率波動性結構型態都是從 5%出發，因此可 以比較不同型態的利率波動性結構對利率 此，Hull-White 模型的利率波動性結構對評 價的影響，實證結果可由 HJM 模型裏看出， 不再贅述。

上限契約價值的影響。例如：(1)上升型的 利率波動性結構之利率上限契約價值都比 水平型、下降型和指數遞減型者要高；再 者，水平型的利率波動性結構之利率上限 契約價值都比下降型和指數遞減型者要 高；另外，下降型的利率波動性結構之利 率上限契約價值都比指數遞減型者要高。 這是因為波動性愈大的利率買權，其價值 愈高，而在表 3-1 中，波動性大小排序為 上升型波動性最大、然後依序為水平型、 下降型和指數遞減型，故有這樣的實證結 果。（註14_{）至於駝峰型的利率波動性結構} 之利率上限契約價值，在表 3-1 中是最高 的，比上升型者還高；但是，觀諸附錄的 試算表，駝峰型的利率波動幅度並不是都 比上升型者高，可是利率上限契約的價值 卻比上升型者高。要解釋這種現象必須借 助圖 3-1 的結果，故先分析圖 3-1 的實證結 果以後，再回頭探討為何駝峰型的利率波 動性結構之利率上限契約價值是最高的。 （二）標準單一利率上限契約價值與契約 到期期限的關係 本節探討 HJM 模型下、不同的利率 波動結構型態，標準單一利率上限契約的 到期期限(Time to Expiration)與權利金 (Caplet Premium)的關係。如同上節的起始 資料：利率期間結構仍為上升型 0.18 (0, ) 0.08 0.025 t R t = − e− 、上限利率 K = 註14_{: 欲驗證波動性的大小排序，可以變動 T-t，然} 後計算各種類型的波動結構之波動幅度即可 發現：表 3-1 的波動性大小排序依次為上升 型、水平型、下降型、指數遞減型；但是， 駝峰型之波動幅度最先幾期是比上升型者 高、但是後面幾期則比上升型者低(但仍比其 它類型者高)。(詳見附錄一的各類型波動結 構之波動幅度試算表) 5%、利率波動結構型態仍是那五種型態， 且都是從 5%出發。實證結果繪於圖 3-1。 由圖 3-1 可知，當利率波動結構為上升型 態時，標準單一利率上限契約的權利金隨 著契約的到期期限愈長而遞增；相對的， 當利率波動結構為下降型和指數遞減型 時，標準單一利率上限契約的權利金開始 時隨著到期期限增加而升高，但隨後隨著 到期期限的增加而降低，而且以指數遞減 型者較先反轉、依序為下降型；至於利率 波動結構為水平型時，標準單一利率上限 契約的權利金開始時亦隨著到期期限增加 而升高，但隨後權利金並未隨到期期限的 增加而升高或降低得很明顯。 解釋圖 3-1 的實證結果可由兩個層 面：一為時間價值、另一為利率波動度。 從時間價值的層面來看，因為標準單一利 率上限契約為一利率買權，故契約到期期 限愈長，時間價值愈大，權利金也就愈高。 從利率波動度的層面來看，上升型的波動 結構，因為隨著到期期限愈長，波動度愈 大，權利金也就愈高，故兩個層面的因素 都促使權利金隨著契約的到期期限愈長而 遞增；反觀，下降型和指數遞減型的波動 結構，因為隨著到期期限愈長，波動度不 是線性式的變小、就是指數式的變小，故 標準單一利率上限契約的權利金開始時隨 著到期期限增加而升高，這是因為時間價 值的因素讓權利金隨著到期期限增加而升 高、但是利率波動度線性式變小或指數式 變小的因素尚弱，所以尚不會讓權利金與 契約的到期期限呈反向走勢，這種反向的 走勢會出現在當利率波動度線性式變小或 指數式變小的因素強過時間價值的因素 時，例如：指數遞減型的波動結構其波動 度是指數式的變小，故這種反向的走勢(即 權利金隨著到期期限的增加而降低)最先 出現，依序為下降型。有了上升型、下降

型和指數遞減型的波動結構於圖 3-1 的實 證結果之解釋原因，即不難了解為何水平 型的波動結構，其標準單一利率上限契約 的權利金開始時亦隨著到期期限增加而升 高，但隨後權利金並未隨到期期限的增加 而升高或降低得很明顯。 至於駝峰型的波動結構，其標準單一 利率上限契約的權利金與到期期限的關係 較無一定的型態，主要取決於波動結構的 參數，例如：駝峰出現在哪裡？上升到駝 峰的速度為何？從駝峰下降的速度又如何 等。以圖 3-1 駝峰型的波動結構的實證結 果 ， 因 為 給 定 的 波 動 結 構 為 ) ( 3 . 0 )) ( 04 . 0 5 . 0 . 0 ( ) , (t T = + T−t e− T−t σ ，故其標準 單一利率上限契約的權利金與到期期限的 關係為：權利金開始時隨著到期期限增加 而升高、且升高的幅度比上升型者還大， 但隨後隨著到期期限的增加而降低、且降 低的幅度比下降型和指數遞減型者大。呈 現這種現象，其實都是時間價值與利率波 動度兩個因素交相作用的影響。 根據圖 3-1 的實證結果可以解釋為何 表 3-1 的數值分析中，駝峰型的利率波動 性結構之利率上限契約價值是最高的，甚 至比上升型者還高。觀諸附錄一的試算表 可知，駝峰型的利率波動幅度在 T-t = 2.5 以前都比上升型者高，故到期期限在 2.5 年以內的利率上限契約的價值比上升型者 高並不足為奇；反而比較奇怪的是，到期 期限在 2.5 年以上的利率上限契約的價值 也都比上升型者高，但是駝峰型的利率波 動幅度在 T-t = 2.5 以後都比上升型者低。 要解釋這個『似乎不一致』的現象，必須 看圖 3-1，以便得到一個比較清楚的概念。 圖 3-1 中的駝峰型與上升型的利率波動性 結構設定和表 3-1 者都一樣。由圖 3-1 可看 出，駝峰型的利率波動性結構其到期期限 在 4 年以下的單一利率上限契約的價值都 要比上升型者高，只有到期期限在 4 年以 上的單一利率上限契約的價值上升型者才 比駝峰型者高。因此，要解釋駝峰型的到 期期限在 2.5 年以上的利率上限契約的價 值都比上升型者高，可歸諸於(1)到期期限 在 4 年以下的單一利率上限契約的價值， 駝峰型者都比上升型者高，故駝峰型的到 期期限在 4 年以下的利率上限契約的價值 要比上升型者高；(2)駝峰型的到期期限為 5 年的利率上限契約的價值，是由到期期限 在 5 年以下的單一利率上限契約的價值總 合起來，而到期期限在 4 年以下的單一利 率上限契約的價值總合駝峰型者高於上升 型者，但是到期期限在 4 年以上、5 年以下 的單一利率上限契約的價值總合上升型者 要高於駝峰型者，可是由於到期期限在 4 年以下的單一利率上限契約的價值總合大 於到期期限在 4 年以上、5 年以下的單一利 率上限契約的價值總合，故造成駝峰型的 到期期限為 5 年的利率上限契約的價值高 於上升型者。 二、Brace-Gatarek-Musiela 模型 在 BGM 模型下評價標準利率上限契 約，應用的 LIBOR 利率隨機過程為(33) 式。由(33)式可知，以純粹折價債券價格 ) , (t T_k+1 P 平準，在遠期機率測度 1 + K T F 下， LIBOR 利 率 L(t,Tk) 為 一 平 賭 過 程 (martingale)。現在令ξ(t)為最接近時點t的 利 率 重 設 日 之 指 標 ， 即

{

k T t

}

t)=inf ≥0: k ≥ ( ξ ，當以純粹折價債 券價格P(t,Tξ(t)) 平準時，則 LIBOR 利率L(t,T_k)在遠期機 率測度F_ξ下的隨機過程可改寫為：

[

( , ) (, )

]

( ) ( ) ) ( ) , ( ) , ( ) ( 1 t T dt t dW t T t t T t L T t dL k t k k k k ξ ξ ζ σ σ ζ − + = + (38)

其中W_ξ(t)為遠期機率測度F_ξ下的 Wiener 隨機過程，σ(t,T_k+1)與σ(t,T_ξ(t))分別表示 純粹折價債券價格P(t,T_k+1)與P(t,T_ξ(t))的 波動度。 由(27)式可知純粹折價債券價格波動 度和LIBOR利率波動度的關係為： ) , ( ) , ( 1 ) , ( ) , ( ) , ( 1 k k k k k t T T t L T t L T t T t ζ δ δ σ σ + = − + (39) 將(39)式代入(38)式，可將L(t,T_k)的 隨機過程改寫為

：

) ( ) , ( ) , ( ) , ( 1 ) , ( ) , ( ) , ( ) , ( ) ( t dW T t dt T t T t L T t T t L T t L T t dL k k t j k j j j k k ξ ξ δ ζ ζ ζ δ + + =

∑

= (40) 為了應用BGM模型的(40)式，本文採

用 Hull and White（2000）的做法：假設

) , (t T_k ζ 與該 LIBOR 利率到期前的利率重 設期數有關，若令Λ_k表示第k期時利率重 設 的 LIBOR 利 率 波 動 度 的 值 ， 則 ) ( ) , (t T_{k k ξ t} ζ =Λ − ；再令ωl表示經由 Black 公式所推算、對應於標的利率存續期間為 ] , [T_l T_l+1 的標準單一利率上限契約的即期 波動度(spot volatility)，則Λ_k可由下式推算 得知：

∑

= − − Λ = l k k k l l lT 1 1 2 2 δ ω (41) 將(41)式 代 入(40)式 ， 並 且 假 設 ) , ( lnL t T_k 的漂移項(drift term)在時間區間 ] , [T_k T_k+1 維持固定，則可得到 LIBOR 利率 的近似公式：         _Λ − + Λ Λ = + = − − − − +

∑

_δ δ δ T T L T T L T T L T T L l j k l k j j l j k k j l j l j ) , ( 1 ) , ( exp ) , ( ) , ( 1 2 1 1 1 (42) 其中，n~為標準常態分配的隨機樣本。

(42)式即是Hull and White（2000）實

際應用BGM模型時所推得之LIBOR利率 的解。實務上應用此一近似公式，一般是 先用市場交易的資料來校準(Calibration)出 (42)式的參數，然後再利用Monte Carlo模 擬的方式模擬出LIBOR利率的隨機過程， 然後根據這個模擬出的LIBOR利率隨機過 程進行各類利率商品的評價。 （一）標準利率上限契約的評價實證分析 在BGM模型下評價標準利率上限契約，其 評價公式是(37)式。表3-2報告在利率期間 結構為 t e t R(0, )=0.08−0.025 −0.18 、利率波 動結構型態分別為水平型、上升型、下降 型、指數遞減型和駝峰型等不同狀況下（註 15_{），標準利率上限契約的價值。表} 3-2係 根據(42)式，在給定假設的市場資料下，利 用Monte Carlo模擬方式進行300,000次模 擬，得到不同到期期限和執行價下的標準 利率上限契約的價值，結果如表3-2所示。 由表 3-2 可知，無論利率波動性 結構型態為何，標準利率上限契約的價值 有下列的特徵：(1)隨著上限利率遞增，契 約的價值遞減；(2)隨著契約重設次數愈多 (即T愈大)，契約的價值愈大。這些特徵的 原因與表 3-1 者相同，這表示這些特徵係 利率上限契約的結構性特徵，與應用 HW 註15_{: 此處的利率波動結構型態與表 3-1、圖 3-1 者} 相同，仍為五種型態、但波動函數則不同。 此處的波動結構是指 LIBOR 利率的波動結 構，而表 3-1、圖 3-1 的波動結構是指瞬間遠 期利率的波動結構，兩者是不相同的，故波 動函數不同。

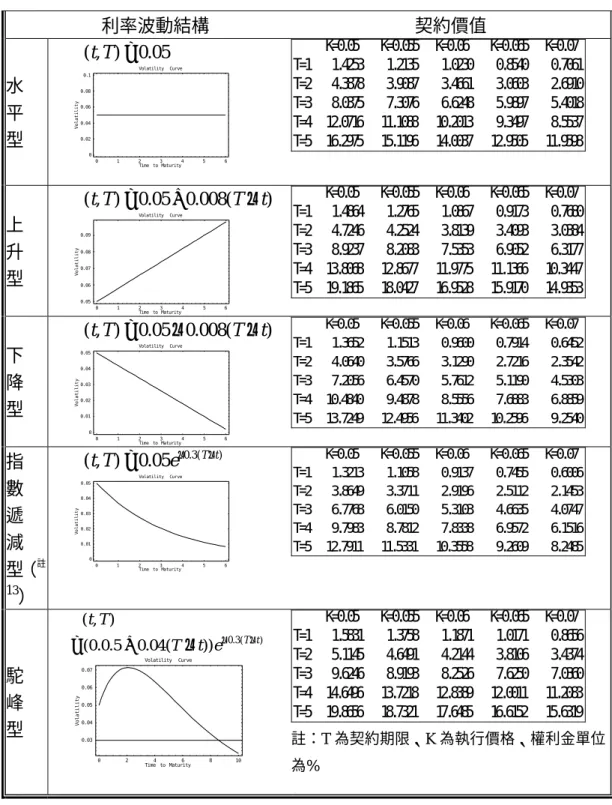
模型、HJM 模型或 BGM 模型無關。再者 值得注意的是：表3-1與表3-2的特徵與成 因雖相同，但是各個標準利率上限契約的 價值並不同，這主要是因為應用不同的利 率模型、以及給定的利率波動性結構的函 數不同所導致。由這些實證的證據顯示， 選擇不同的利率模型與給定不同的利率波 動性結構函數會導致不同的標準利率上限 契約的價值，這衍生出一個重要的問題： 到底應該運用哪一個利率模型？以及應該 給定什麼利率波動性結構函數？才能正確 的評價利率上限契約的價值？針對這個問 題，本文建議應該選擇與市場交易資料愈 貼近的模型愈好，因此BGM模型在理論上 要比HW模型及HJM模型好，這是因為： (1)實務應用時，一般利率模型輸入的殖利 率曲線資料，是由利率交換市場的交換利 率所校準得到，而利率交換市場最大的契 約即是以 LIBOR 為指標利率的契約，又 BGM 模型即是以 LIBOR 利率隨機過程為 基礎的模型，故BGM模型貼近市場交易資 料的優勢是HW模型及HJM模型無可匹敵 的。(2)從利率模型是否可以適用於各種型 態的利率波動性結構來看，BGM 模型及 HJM 模型都要比 HW 模型更有彈性；再 者，由於HJM模型的利率波動性結構是瞬 間遠期利率波動性結構，而瞬間遠期利率 是市場上觀察不到的資料，反觀BGM模型 的利率波動性結構是 LIBOR 利率(或是遠 期利率)的波動性結構，而LIBOR利率是市 場上觀察得到的資料，故在校準利率波動 性結構的函數時，BGM 模型是要較 HJM 模型更貼近市場交易資料，更具實務的應 用性。 另外，由表 3-2 可知，因為所有的利率 波動性結構型態都是從 16.5%出發，因 此可以比較不同型態的利率波動性結構 對利率上限契約價值的影響。例如：(1) 上升型的利率波動性結構之利率上限契 約價值都比水平型、下降型和指數遞減 型者要高；再者，水平型的利率波動性 結構之利率上限契約價值都比下降型和 指數遞減型者要高；另外，指數遞減型 的利率波動性結構之利率上限契約價值 都比下降型者要高。這是因為波動性愈 大的利率買權，其價值愈高，而在表3-2 中，波動性大小排序為上升型波動性最 大、然後依序為水平型、指數遞減型和 下降型(詳見附錄波動幅度試算表)，故有 這樣的實證結果。至於駝峰型的利率波 動性結構之利率上限契約價值，在表3-2 中顯示 T = 2以下的利率上限契約價值 駝峰型者大於上升型者，但是T = 2以上 的利率上限契約價值駝峰型者小於上升 型者，要解釋這種實證現象需先檢視圖 3-2的實證結果。 （二）標準單一利率上限契約價值與 契約到期期限的關係

本節探討 BGM 模型下、不同的

利率波動結構型態，標準單一利率

上限契約的到期期限(Time to

Expiration)與權利金(Caplet

Premium)的關係。如同上一小節的

起始資料：利率期間結構仍為上升

型

0.18 (0, ) 0.08 0.025 t R t = − e−

、上限利率

K = 5%、利率波動結構型態仍是那

五種型態，且都是從 16.5%出發。

實證結果繪於圖 3-2。

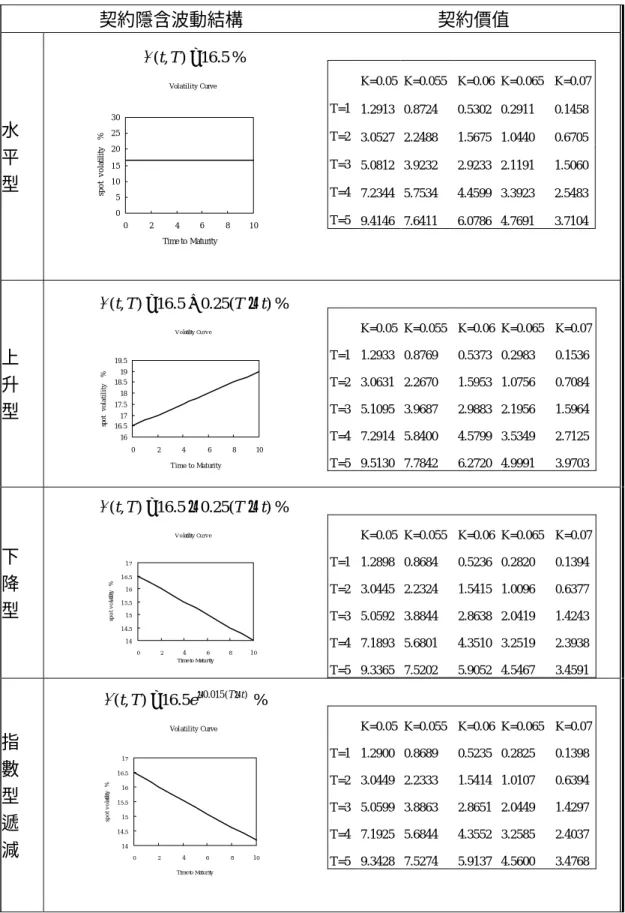
由圖3-2可知，在BGM模型下、不同 的利率波動結構型態，標準單一利率上限 契約價值與契約到期期限的關係大致相 似，即契約到期期限在某段時間內，契約 期限越長，其權利金價值越高；之後，契

約到期期限越長，權利金價值卻隨著到期 期限的增加而遞減。這種實證結果和圖3-1 的駝峰型、下降型、指數遞減型之利率波 動結構的實證結果類似，但迥然不同於圖 3-1 的上升型與水平型之利率波動結構的 實證結果，這又再一次的指出BGM模型與 HJM模型在評價標準單一利率上限契約的 差異。另外，圖 3-2 實證結果的原因其實 與圖 3-1 的原因一樣；亦即，影響標準單 一利率上限契約價值的原因，除了契約到 期期限外，還有利率波動度。圖 3-2 實證 結果的原因其實是：標準單一利率上限契 約的權利金開始時隨著到期期限增加而升 高，這是因為時間價值的因素讓權利金隨 著到期期限增加而升高、但是利率波動度 因素在此階段尚弱，所以尚不會讓權利金 與契約的到期期限呈反向走勢，這種反向 的走勢會出現在當利率波動度線因素強過 時間價值的因素時，此時契約到期期限越 長，權利金價值卻隨著到期期限的增加而 遞減。 有了圖 3-2 的實證結果，接著可以 回頭探討表 3-2 駝峰型波動性結構的利 率上限契約價值。由圖 3-2 的實證結果 以及附錄的試算表可以看出，T = 2以下 的利率上限契約價值駝峰型者大於上升 型者，這主要是因為駝峰型的波動幅度 大於上升型者；但是， T = 2以上的利 率上限契約價值駝峰型者小於上升型 者，主要是因為駝峰型的波動幅度沒有 那麼大於上升型者、而且由圖 3-2 可看 出 T > 2以後上升型的標準單一利率上 限契約權利金都高於駝峰型者，故有此 實證結果。 三、 計劃成果自評 本文推導不同利率模型下、不同標的資產 的標準利率上限契約的評價封閉解。總計 本文推導在HJM模型下、以短率為標的資 產的標準利率上限契約的評價封閉解；再 者，分別推導在HW模型與HJM模型下、 以即期利率為標的資產的評價封閉解；最 後，在BGM模型下、推導以LIBOR利率 為標的資產的評價封閉解。根據推導所得 的評價封閉解，本文應用實例驗證各種評 價公式的差異。發現無論利率波動性結構 型態為何，標準利率上限契約的價值：(1) 隨著上限利率遞增，契約的價值遞減；(2) 隨著契約重設次數愈多，契約的價值愈大。 利率波動性結構的型態對於標準利率 上限契約價值的影響，不論何種利率模 型，只要確定哪一種型態的利率波動性較 大，則利率上限契約的價值較高；例如， 上升型、水平型、下降型和指數遞減型的 波動性結構較容易確定哪一種型態的利率 波動性較大，故這些波動性結構對應的利 率上限契約的價值較容易判斷大小。至於 駝峰型的波動性結構，由於其波動函數的 參數會影響波動性的升降幅度與速度，故 波動性的大小不一致，所以對應的利率上 限契約的價值並無法一致性的判斷大小。 尤有甚者，既存文獻(例如：Ritchken and Chuang (2001))指出，實務上最常見的利率 波動性結構卻是駝峰型結構，這顯示實務 上要評價利率上限契約，非得準確的校準 估計駝峰型的波動函數不可，否則無法判 斷利率上限契約的價值是高估或是低估。 標準單一利率上限契約價值與契約到 期期限之關係，大體上呈現契約到期期限 在某段時間內，契約期限越長，其權利金 價值越高，這主要是時間價值因素造成； 之後若是利率波動度因素蓋過時間價值因 素，則契約到期期限越長，權利金價值卻 隨著到期期限的增加而遞減。 最後值得一提的是：選擇不同 的利率模型與給定不同的利率波動性結

構函數，會導致不同的標準利率上限契 約的價值。這衍生出到底應該運用哪一 個利率模型？以及應該給定什麼利率波 動性結構函數？才能正確的評價利率上 限契約的價值？針對這個問題，本文建 議應該選擇與市場交易資料愈貼近的模 型愈好，因此 BGM 模型在理論上要比 HW 模型及 HJM 模型好，而HJM 模型 又比HW模型更具彈性。 參考文獻

1. Black, F. (1976) “The Pricing of Commodity Contracts,” Journal of Financial Economics, Vol. 3, 167-179.

2. Brace, A., D. Gatarek and M. Musiela

(1997), “The Market Model of Interest Rate Dynamics,” Mathematical Finance, Vol. 7, No. 2, 127-155.

3. Clewlow, L. and C. Strickland (1997),

Exotic Options：The State of the Art,

International Thomson Business Press. 4. Cox, J. C., J. E. Ingersoll and S. A. Ross

(1985), “A Theory of the Term Structure of Interest Rates,” Econometrica, Vol. 3, 385-467.

5. Heath, D., R. Jarrow and A. Morton (1992), “Bond Pricing and the Term

Structure of Interest Rates：A New

Methodology for Contingent Claims Valuation,” Econometrica, Vol. 60, 77-105.

6. Hull, J. (2000), Options, Futures, and Other Derivative Securities, 4th edition, Prentice-Hall, Inc.

7. Hull, J. and A. White (1990), “Pricing

Interest-rate-derivative Securities,”

Review of Financial Studies, Vol. 3, No. 4, 573-592.

8. Hull, J. and A. White (2000), “Forward

Rate Volatilities, Swap Rate Volatilities, and the Implementation of the LIBOR Market Model,” Journal of Fixed Income, Vol. 10, Iss. 2, 46-62.

9. Jamshidian, F., (1989), “An Exact Bond Option Formula,” Journal of Finance, Vol. 44, 205-209.

10. Longstaff, F. A. (1995), “Hedging

Interest Rate Risk with Options on Average Interest Rates,” Journal of Fixed Income, Vol. 4, Iss. 4, 37-45.

11. Pedersen, M. B. (1998), “Calibration

LIBOR Market Models,” Working paper, SimCorp Financial Research.

12. Ritchken, P. H. and I. Chuang (2000),

“Interest Rate Option Pricing with Volatility Humps,” Review of Derivatives Research, Vol. 3, Iss. 3, 231-268.

13. Sidenius, J. (2000), “LIBOR Market

Models in Practice,” Journal of Computational Finance, Vol. 3, No. 3, 5-26.

14. Vasicek, T. (1977), “An Equilibrium

Characterization of the Term Structure,” Journal of Financial Economics, Vol. 5, 179-193.

表 2-1 不同模型、不同標的資產的標準利率上限契約評價封閉解之特徵 利 率 模 型

Hull-White Model

（符合市場利率期間結構，但假 設瞬間短率的波動結構為常數）

BGM Model

（符合市場利率 期 間 結 構 ， 且 LIBOR 利率波動 結構可為任意型 態）

HJM Model

（ 符 合 市 場 利 率 期 間 結 構，且瞬間遠期利率波動 結構可為任意型態） 標 的 利 率 瞬間短率 （理論值；無法 由 市 場 觀 察 得 到，須以市場短 天期即期利率替 代 ； Longstaff (1995)的評價封 閉解即是此類， 故本文並未再推 導） 即期利率 （將 LIBOR 利 率轉換成純粹折 價 債 券 價 格 表 示，以瞬間短率 之隨機過程推導 評價封閉解） LIBOR 利率 （直接由 BGM 模 型 之 LIBOR 利率隨機過程推 導評價封閉解） 瞬間短率 （理論值；無 法 由 市 場 觀 察得到，須以 市 場 短 天 期 即 期 利 率 替 代；Longstaff (1995) 的 結 果 是 本 文 的 特例） 即期利率 （將 LIBOR 利 率 轉 換 成 純 粹 折 價 債 券 價 格 表 示 ， 以 瞬 間 遠 期 利 率 之 隨 機 過 程 推 導 評 價 封 閉 解） 表 2-2 HJM 模型下、以瞬間短率為標的之標準單一利率上限契約評價公式 利率模型 基本隨機過程與標準單一利率上限契約評價公式 HJM Model ) ( ) , ( ) , ( ) , ( ) , (t T t T b t T dt t T dW t df =−σ +σ Q (1)

[

]

_∫

∫

− + + = t t _F t f t u t b u T b u t du u t dW u r 0 0 ( , ) ( , ) ( , ) ( , ) ( ) ) , 0 ( σ σ (5)             − Φ − +      ₋ − = V K M K M V K M V T t P t C ( ) 2 ) ( exp 2 ) , ( ) ( ₂ 2 π δ (11) 其中，M = f( T0, )，V T (u,T)du 0 2

∫

= σ 。

表 2-3 不同模型下、以即期利率為標的之標準單一利率上限契約評價公式 利率模型 基本隨機過程與標準單一利率上限契約評價公式 HW Model ) ( ) ) ( ( t br dt dW t drt = α − +σ Q (14) ) ( ) , ( ) ( ) , ( ) , ( t dW T t B dt t r T t P T t dP = −σ Q (19)       Φ + − Φ = ( , ₊ ) + ( ) (1 ) ( ) ) ( 1 2 2 1 1 2 d K d e T t P t Ck k Mk Vk δ (23) 其中 2 2 1 k k V M e M = + ， k k V V K M d 2 1 2 1 1 ln + + = δ ，d₂ =d₁ −V_k HJM Model ) ( ) , ( ) , ( ) , ( ) , (t T t T b t T dt t T dW t df =−σ +σ Q (1) ) ( ) , ( ) ( ) , ( ) , ( t dW T t b dt t r T t P T t dP = + Q (24)

[

( ) (1 ) ( )

]

) , ( ) (t P t T 1 M d1 K d2 Ck = k+ Φ − +δ Φ (27) 其中其中 2 2 1 1) , 0 ( ) , 0 ( Tk Tk e T P T P M k k −π + χ + = ， k k T T K M d χ χ δ 2 1 2 1 1 ln + + = ， k T d d2 = 1−χ ， =

∫

+ k k T k k T ₀ u T 1 T du 2 ) , , ( 2 1 γ π ，

∫

+ = k k T k k T ₀ u T 1 T du 2 2 ) , , ( γ χ ，γ(u,k,l)=b(u,k)−b(u,l)。

表 2-4 BGM 模型下、以 LIBOR 利率為標的之標準單一利率上限契約評價公 式 利率模型 基本隨機過程與標準單一利率上限契約評價公式 BGM Model       +       ₊ ∂ ∂ = ˆ (, ) ˆ( , ) ( ) 2 1 ) , ( ˆ ) , ( ˆ 2 t dW x t dt x t x t f x x t f d σ σ Q (28)

(

ˆ( , ) ( )

)

) , ( ˆ ) , ( ˆ ) , ( ˆ _{t x L t x t x t x dt dW t} L d = ⋅γ σ +δ + Q (31) dt x t t dW t dWF( )= Q( )+σˆ( , +δ) (32) ) ( ) , ( ) , ( ) , (t T L t T t T dW t dL = ζ F (33) 其中σ(t,T)=σˆ(t,x)，L(t,T)=Lˆ(t,x)，ζ(t,T)=γˆ(t,x)。

[

( , ) ( ( )) ( ( ))

]

) , ( ) (t P t T ₁ L t T d₁ t K d₂ t C_k =δ ⋅ _{k+ k} Φ − Φ (37) 其中， =

∫

Tk t k k(t) (u)du 2 2 ζ θ ， ) ( ) ( 2 1 ) , ( ln ) ( 2 1 t t K T t L t d k k k θ θ + = ， ) ( ) ( ) ( ₁ 2 t d t t d = −θ_k 。

表 3-1 HJM 模型下標準利率上限契約的價值 標準利率上限契約 模型 設定 ) ( ) , ( ) , ( ) , ( ) , (t T t T b t T dt t T dW t df =−σ ⋅ +σ Q

∫

− = T t t u du T t b(, ) σ( , ) 契約 規格 在契約期間內，以市場上三個月期之即期利率為標的資產，每三個月重 設利率一次（註12_）。 殖利 率曲 線的 市場 資料 利率期間結構 0.18 (0, ) 0.08 0.025 t R t = − e− 0 1 2 3 4 5 6 Timeto Maturity 0.055 0.0575 0.06 0.0625 0.065 0.0675 0.07 t s e r e t n Ie t a R YieldCurve 註12_{: 本文僅報告標的資產為即期利率的標準利率上限契約之評價實證結果，不報告標的資產為} 瞬間短率的實證結果，主要是為節省篇幅、以及後者僅是理論結果並不具實用性；然而， 若是讀者有興趣這部分的實證結果，可洽作者函索。

表 3-1 HJM 模型下標準利率上限契約的價值(續) 利率波動結構 契約價值 水 平 型 ( , )t T 0.05 σ = 0 1 2 3 4 5 6 Timeto Maturity 0 0.02 0.04 0.06 0.08 0.1 y t i l i t a l o V Volatility Curve K=0.05 K=0.055 K=0.06 K=0.065 K=0.07 T=1 1.4253 1.2135 1.0230 0.8540 0.7061 T=2 4.3878 3.9087 3.4661 3.0603 2.6910 T=3 8.0375 7.3076 6.6248 5.9897 5.4018 T=4 12.0716 11.1088 10.2013 9.3497 8.5537 T=5 16.2975 15.1196 14.0037 12.9505 11.9598 上 升 型 ( , )t T 0.05 0.008(T t) σ = + − 0 1 2 3 4 5 6 Timeto Maturity 0.05 0.06 0.07 0.08 0.09 y t i l i t a l o V Volatility Curve K=0.05 K=0.055 K=0.06 K=0.065 K=0.07 T=1 1.4864 1.2765 1.0867 0.9173 0.7680 T=2 4.7246 4.2524 3.8139 3.4093 3.0384 T=3 8.9237 8.2083 7.5353 6.9052 6.3177 T=4 13.8068 12.8677 11.9775 11.1366 10.3447 T=5 19.1865 18.0427 16.9528 15.9170 14.9353 下 降 型 ( , )t T 0.05 0.008(T t) σ = − − 0 1 2 3 4 5 6 Timeto Maturity 0 0.01 0.02 0.03 0.04 0.05 y t i l i t a l o V Volatility Curve K=0.05 K=0.055 K=0.06 K=0.065 K=0.07 T=1 1.3652 1.1513 0.9600 0.7914 0.6452 T=2 4.0640 3.5766 3.1290 2.7216 2.3542 T=3 7.2056 6.4570 5.7612 5.1190 4.5303 T=4 10.4840 9.4878 8.5556 7.6883 6.8859 T=5 13.7249 12.4956 11.3402 10.2596 9.2540 指 數 遞 減 型（註 13_） 0.3( ) ( , )t T 0.05e T t σ ₌ − − 0 1 2 3 4 5 6 Timeto Maturity 0 0.01 0.02 0.03 0.04 0.05 y t i l i t a l o V Volatility Curve K=0.05 K=0.055 K=0.06 K=0.065 K=0.07 T=1 1.3213 1.1058 0.9137 0.7455 0.6006 T=2 3.8649 3.3711 2.9196 2.5112 2.1453 T=3 6.7768 6.0150 5.3103 4.6635 4.0747 T=4 9.7983 8.7812 7.8338 6.9572 6.1516 T=5 12.7911 11.5331 10.3558 9.2609 8.2485 駝 峰 型 ) ( 3 . 0 )) ( 04 . 0 5 . 0 . 0 ( ) , ( t T e t T T t − − − + = σ 0 2 4 6 8 10 Timeto Maturity 0.03 0.04 0.05 0.06 0.07 y t i l i t a l o V Volatility Curve K=0.05 K=0.055 K=0.06 K=0.065 K=0.07 T=1 1.5831 1.3758 1.1871 1.0171 0.8656 T=2 5.1145 4.6491 4.2144 3.8106 3.4374 T=3 9.6246 8.9193 8.2526 7.6250 7.0360 T=4 14.6496 13.7218 12.8389 12.0011 11.2083 T=5 19.8656 18.7321 17.6485 16.6152 15.6319 註：T 為契約期限、K 為執行價格、權利金單位 為% 註13_{: 在 HJM 模型架構下，若假設利率波動結構為指數遞減型，則所得到的結果與 Hull-White 模} 型之結果一致。

圖 3-1 標準單一利率上限契約權利金與契約到期期限之關係

表 3-2 BGM 模型架構下標準利率上限契約的價值 標準利率上限契約 模型 設定 dL(t,T) L(t,T) (t,T)dW (t) F ζ = 契約 規格 在契約期間內，以市場上半年期之 LIBOR 利率為標的資產，每半年重設 利率一次。 殖利 率曲 線的 市場 資料 利率期間結構 0.18 (0, ) 0.08 0.025 t R t = − e− 0 1 2 3 4 5 6 Time to Maturity 0.055 0.0575 0.06 0.0625 0.065 0.0675 0.07 t s e r e t n Ie t a R Yield Curve 0 2 4 6 8 10 Time to Maturity 0.4 0.6 0.8 1 1.2 1.4 1.6 m u i m e r P Caplet Premium 水平型 上升型 下降型 指數型遞減 駝峰型

表 3-2 BGM 模型架構下標準利率上限契約的價值(續) 契約隱含波動結構 契約價值 水 平 型 % 5 . 16 ) , (t T = ω Volatility Curve 0 5 10 15 20 25 30 0 2 4 6 8 10 Time to Maturity spot vol at il it y % K=0.05 K=0.055 K=0.06 K=0.065 K=0.07 T=1 1.2913 0.8724 0.5302 0.2911 0.1458 T=2 3.0527 2.2488 1.5675 1.0440 0.6705 T=3 5.0812 3.9232 2.9233 2.1191 1.5060 T=4 7.2344 5.7534 4.4599 3.3923 2.5483 T=5 9.4146 7.6411 6.0786 4.7691 3.7104 上 升 型 % ) ( 25 . 0 5 . 16 ) , (t T = + T −t ω Volatility Cu rv e 16 16.5 17 17.5 18 18.5 19 19.5 0 2 4 6 8 10 Time to Maturity spot vol a ti li ty % K=0.05 K=0.055 K=0.06 K=0.065 K=0.07 T=1 1.2933 0.8769 0.5373 0.2983 0.1536 T=2 3.0631 2.2670 1.5953 1.0756 0.7084 T=3 5.1095 3.9687 2.9883 2.1956 1.5964 T=4 7.2914 5.8400 4.5799 3.5349 2.7125 T=5 9.5130 7.7842 6.2720 4.9991 3.9703 下 降 型 % ) ( 25 . 0 5 . 16 ) , (t T = − T −t ω Vo latility Cu rv e 1 4 1 4 .5 1 5 1 5 .5 1 6 1 6 .5 1 7 0 2 4 6 8 1 0 Time to Maturity sp o t v o la til ity % K=0.05 K=0.055 K=0.06 K=0.065 K=0.07 T=1 1.2898 0.8684 0.5236 0.2820 0.1394 T=2 3.0445 2.2324 1.5415 1.0096 0.6377 T=3 5.0592 3.8844 2.8638 2.0419 1.4243 T=4 7.1893 5.6801 4.3510 3.2519 2.3938 T=5 9.3365 7.5202 5.9052 4.5467 3.4591 指 數 型 遞 減 % 5 . 16 ) , ( 0.015(T t) e T t = − − ω Volatility Curve 14 14 .5 15 15 .5 16 16 .5 17 0 2 4 6 8 10 Time to Maturity sp o t v o la tilit y % K=0.05 K=0.055 K=0.06 K=0.065 K=0.07 T=1 1.2900 0.8689 0.5235 0.2825 0.1398 T=2 3.0449 2.2333 1.5414 1.0107 0.6394 T=3 5.0599 3.8863 2.8651 2.0449 1.4297 T=4 7.1925 5.6844 4.3552 3.2585 2.4037 T=5 9.3428 7.5274 5.9137 4.5600 3.4768

駝 峰 型 % )) ( 75 . 2 5 . 16 ( ) , ( ) ( 105 . 0 T t e t T T t − − − + = ω Volatility Curve 15. 5 16 16. 5 17 17. 5 18 18. 5 0 2 4 6 8 10 Time to Maturity spot vol a ti li ty % K=0.05 K=0.055 K=0.06 K=0.065 K=0.07 T=1 1.2956 0.8800 0.5409 0.3033 0.1609 T=2 3.0688 2.2783 1.6105 1.0911 0.7282 T=3 5.1033 3.9642 2.9810 2.1823 1.5843 T=4 7.2520 5.7894 4.5096 3.4435 2.6137 T=5 9.4201 7.6595 6.1056 4.7912 3.7411 註 1：T 為契約期限、K 為執行價、權利金單位為% 註 2：表列價格之 Standard Error 均小於 0.001 圖 3-2 標準單一利率上限契約權利金與契約到期期限之關係 Ca plet P r em iu m 0.4 0.5 0.6 0.7 0.8 0.9 1.0 1.1 1.2 0 2 4 6 8 10 Tim e t o Ma t u r it y Pr e m iu m 水平型 上升型 下降型 指數型遞減 駝峰型

附錄一 表 3-1、3-2 各類型利率波動性結構之波動幅度試算表 T-t 水平型 上升型 下降型 指數遞減 駝峰型 水平型 上升型 下降型 指數遞減 駝峰型 0.00 0.0500 0.0500 0.0500 0.0500 0.0500 0.1650 0.1650 0.1650 0.1650 0.1650 0.25 0.0500 0.0520 0.0480 0.0464 0.0557 0.1650 0.1656 0.1644 0.1644 0.1674 0.50 0.0500 0.0540 0.0460 0.0430 0.0602 0.1650 0.1663 0.1638 0.1638 0.1696 0.75 0.0500 0.0560 0.0440 0.0399 0.0639 0.1650 0.1669 0.1631 0.1632 0.1716 1.00 0.0500 0.0580 0.0420 0.0370 0.0667 0.1650 0.1675 0.1625 0.1625 0.1733 1.25 0.0500 0.0600 0.0400 0.0344 0.0687 0.1650 0.1681 0.1619 0.1619 0.1749 1.50 0.0500 0.0620 0.0380 0.0319 0.0701 0.1650 0.1688 0.1613 0.1613 0.1762 1.75 0.0500 0.0640 0.0360 0.0296 0.0710 0.1650 0.1694 0.1606 0.1607 0.1774 2.00 0.0500 0.0660 0.0340 0.0274 0.0713 0.1650 0.1700 0.1600 0.1601 0.1783 2.25 0.0500 0.0680 0.0320 0.0255 0.0713 0.1650 0.1706 0.1594 0.1595 0.1791 2.50 0.0500 0.0700 0.0300 0.0236 0.0709 0.1650 0.1713 0.1588 0.1589 0.1798 2.75 0.0500 0.0720 0.0280 0.0219 0.0701 0.1650 0.1719 0.1581 0.1583 0.1803 3.00 0.0500 0.0740 0.0260 0.0203 0.0691 0.1650 0.1725 0.1575 0.1577 0.1806 3.25 0.0500 0.0760 0.0240 0.0189 0.0679 0.1650 0.1731 0.1569 0.1571 0.1808 3.50 0.0500 0.0780 0.0220 0.0175 0.0665 0.1650 0.1738 0.1563 0.1566 0.1809 3.75 0.0500 0.0800 0.0200 0.0162 0.0649 0.1650 0.1744 0.1556 0.1560 0.1809 4.00 0.0500 0.0820 0.0180 0.0151 0.0633 0.1650 0.1750 0.1550 0.1554 0.1807 4.25 0.0500 0.0840 0.0160 0.0140 0.0615 0.1650 0.1756 0.1544 0.1548 0.1804 4.50 0.0500 0.0860 0.0140 0.0130 0.0596 0.1650 0.1763 0.1538 0.1542 0.1800 4.75 0.0500 0.0880 0.0120 0.0120 0.0577 0.1650 0.1769 0.1531 0.1537 0.1795 5.00 0.0500 0.0900 0.0100 0.0112 0.0558 0.1650 0.1775 0.1525 0.1531 0.1789 表3-2波動幅度之試算 表3-1波動幅度之試算