振動台模型邊坡滑移行為之數值模擬

(1)

國立臺灣大學工學院土木工程學系碩士論文

Department of Civil Engineering College of Engineering National Taiwan University

Master Thesis

振動台模型邊坡滑移行為之數值模擬

Numerical Simulation of Landslide Behavior from Shaking Table Test

蕭孙翔 Hsiao, Yu-Hsiang

指導教授：林美聆教授 Advisor: Prof. Lin, Meei-Ling

中華民國 101 年 7 月

July 2012

(2)

(3)

(4)

(5)

I

摘要

邊坡問題通常規模很大，材料組成複雜，並不容易利用全尺寸的現地試驗觀察破壞機制。透過模型相似性與問題的簡化，可以縮小尺度並建立物理模型試驗，

利用振動台試驗與離心機試驗，可以在 1-g 及 N-g 的條件下，觀測大地工程問題的破壞機制。林美聆、王國隆於 2003 年至 2009 年在國家地震工程研究中心進行八組大型振動台試驗，模擬邊坡受震行為。本研究由試驗結果之加速度反應、PIV 影像分析以及標點位移量測，觀察邊坡受震反應，推測破壞時間。以有限差分軟體 FLAC 模擬邊坡模型受震反應，推測可能之破壞面位置，由應力路徑與頻譜分析推測可能之滑動時間及臨界加速度。利用建立之數值模型，針對大型振動台試驗加入垂直振動與否之影響進行討論。

振動加載過程乃由小至大，邊坡開始產生淺層滑動時，滑動範圍僅在邊坡坡面，坡頂及坡趾並無產生明顯位移，試體內部加速度反應並不明顯。邊坡產生大規模滑動時，坡趾開始往下坡方向移動，坡頂後方產生張裂縫，試體內部加速度相位反應不同步。數值模擬由模型內部網格變形呈現夾心狀時定義為大規模滑動之時間，以坡趾延伸至坡頂之剪應變分佈且網格應力碰觸到破壞包絡線做為大規模滑動之範圍。本研究利用數值軟體 FLAC 分別模擬無垂直振動之試驗及加入垂直振動之試驗，發現兩組試驗在水平位移變化及剪應變分佈範圍以加入垂直振動之試驗較為廣泛。最後再比較各組之間不同的加速度歷時及破壞行為，找出大型振動台試驗之淺層破壞及深層破壞之型式，以及各分析方法所對應之破壞時間。

關鍵字：振動台試驗、模型邊坡、破壞面、數值模擬

(6)

(7)

III

Abstract

Geotechnical engineers usually encounter large-scale slope problems with complex material composition. Thus, it is hard to use full-size in-situ test to observe the failure mechanism. By law of similitude and simplification, model tests were established to simulate 1-g gravitational field or n-g gravitational field by shaking table test or centrifuge test. This study utilized to the large-scale model slope shaking table tests of the model slope conducted by Lin and Wang from 2003 to 2009 at NCREE. The failure time was estimated according to the acceleration response record, particle image velocimetry (PIV) analysis, and marker displacement measurements. The failure plane was estimated from results of the finite differentice analysis. The critical acceleration and failure time was estimated based on stress path and frequency spectrum analysis during loading. By using the numerical analysis, the effects of vertical vibration or not were discussed.

Shallow failure sliding occurred on the slope surface, no significant displacement on the crest and toe, and no obvious difference in acceleration responses were observed.

As deep-seated landslide developed, the crest and toe started moving down-slope. The crack occurred behind the crest, and phase of acceleration response became shifted. The failure time was defined when the grid start to deform in deeper. The failure surface was defined by maximum shear strain distribution which is from toe to crest and the stress of grids close to failure envelope. Based on results of numerical simulation of specimen which is without vertical vibration and specimen which is with vertical vibration, it was found that the range of horizontal displacement and shear strain increment of specimen with vertical vibration is more than specimen without vertical vibration.At last, compared with acceleration history and failure behavior were made to determine, find out the mode of shallow failure, deep failure, and failure time, then summarize the data of large shaking table test.

Key word: shaking table test; slope; failure surface; numerical analysis

(8)

(9)

V

表目錄

表 2. 1 1-g 試驗條件下之模型相似律（Iai,1989） ... 19

表 2. 2 1-g 試驗條件下之模型相似律（Meymand,1998） ... 22

表 2. 3 Wartman 所使用之振動模式 ... 23

表 3. 1 試驗砂粒徑分佈 ... 38

表 3. 2 試驗砂基本物理性質 ... 38

表 3. 3 不同相對密度最大剪力模數係數 ... 39

表 3. 4 正規化之動態剪力模數係數 ... 39

表 3. 5 原型邊坡與模型邊之模型相似性 ... 40

表 4. 1 大型振動台試驗之加速度輸入紀錄 ... 64

表 4. 2 邊坡試驗產生大規模滑動之時間比對 ... 64

表 4. 3 坡頂及坡趾移動量之比較 ... 65

表 4. 4 PIV 位移場不同計算與搜尋範圍一覽表 ... 65

表 4. 5 PIV 位移場不同計算與搜尋範圍一覽表 ... 65

表 5. 1 顆粒狀土壤沉積物定性描述（Das, 1995） ... 110

表 5. 2 不同材料之剪脹角（FLAC 5.0 Manual，2005） ... 110

表 5. 3 不同塑性指數對應 K 值（Hardin & Drenvich，1972）... 110

表 5. 4 不同材料之包松比（Das，2001） ... 111

表 5. 5 大型振動台試驗八數值模擬輸入參數 ... 111

表 5. 6 試驗八分析方法之破壞時間與破壞特徵整理 ... 112

表 5. 7 數值模擬坡趾水平位移量與試驗後坡趾延伸量之比較 ... 112

表 5. 8 振動結束之數值模擬水平位移量 ... 113

表 5. 9 原型與模型之比例關係 ... 113

表 6. 1 各組試驗之分析方法破壞時間比較 ... 152

表 6. 2 各組試驗之剪力波速及剪力模數比較 ... 152

(14)

表 6. 3 各組試驗之分析方法的淺層破壞時間比較 ... 153

表 6. 4 各組試驗之淺層滑動時，滑動面深度及位移正規化之比較 ... 153

表 6. 5 各組試驗之分析方法的深層破壞時間比較 ... 153

表 6. 6 各組試驗之深層滑動時，滑動面深度及位移正規化之比較 ... 154

表 C- 1 大型振動台試驗二數值模擬輸入參數 ... 179

表 C- 2 大型振動台試驗三數值模擬輸入參數 ... 180

表 C- 3 大型振動台試驗四數值模擬輸入參數 ... 180

表 C- 4 大型振動台試驗五數值模擬輸入參數 ... 181

表 C- 5 大型振動台試驗六數值模擬輸入參數 ... 181

表 C- 6 大型振動台試驗七數值模擬輸入參數 ... 182

(15)

XI

圖目錄

圖 1.1 研究流程圖 ... 3

圖 2.1 應力－應變相似條件（MONCARZ AND KRAWINKLER,1981） ... 24

圖 2.2 孔隙材料單元土壤有效應力與孔隙水壓方向（IAI,1989） ... 24

圖 2.3 土壤在模型與原型間之應力－應變關係（IAI,1989） ... 25

圖 2.4 振動設備與尺寸示意圖（KOKUSHO,2006） ... 25

圖 2.5 試驗對照示意圖（KOKUSHO,2006） ... 26

圖 2.6 阻尼消散示意圖（KOKUSHO,2006） ... 26

圖 2.7 坡面變位示意圖（KOKUSHO,2006） ... 27

圖 2.8 邊坡試驗基本參數（WARTMAN,2005） ... 27

圖 2.9 邊坡變形示意圖（WARTMAN,2005） ... 28

圖 2.10 加速度與變位隨時間改變示意圖（WARTMAN,2005） ... 29

圖 3.1 粒徑分佈曲線 ... 41

圖 3.2 直接剪力試驗所得剪力摩擦角與相對密度關係圖 ... 41

圖 3.3 實驗室與現地試驗之應變範圍（吳偉特，1985） ... 42

圖 3.4 剪力波元件之構造示意圖 ... 42

圖 3.5 不同應力應變下之剪應力與剪應變遲滯圈 ... 43

圖 3.6 相同初始相對密度下圍壓大小與最大剪力模數關係圖 ... 43

圖 3.7 相同初始相對密度下圍壓大小與最大剪力模數關係圖 ... 44

圖 3.8 正規化之動態剪力模數 ... 44

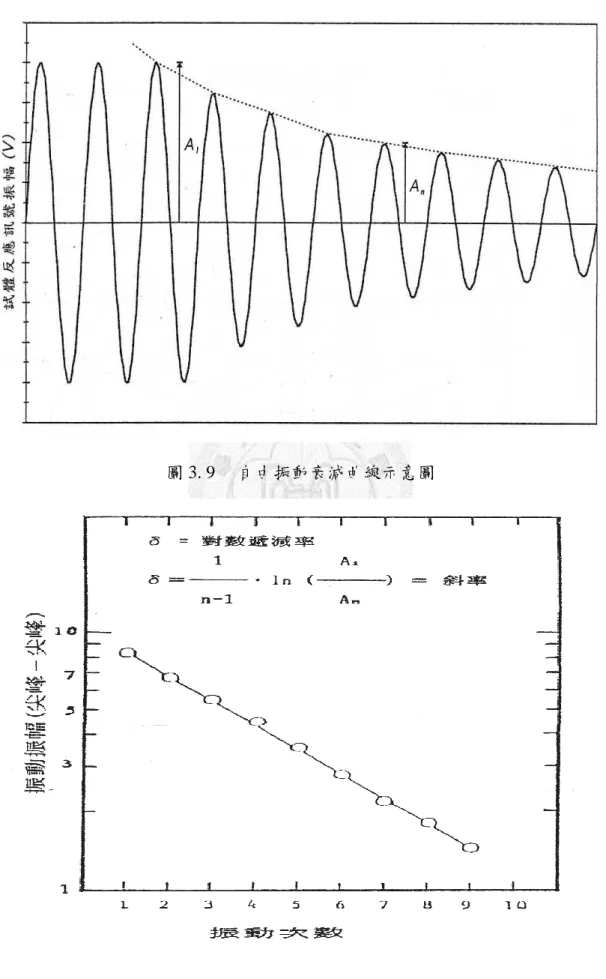
圖 3.9 自由振動衰減曲線示意圖 ... 45

圖 3.10 對數遞減率與振動次數關係圖 ... 45

圖 3.11 正規化之阻尼比 ... 46

圖 3.12 振動台系統透視圖（國家地震工程研究中心） ... 46

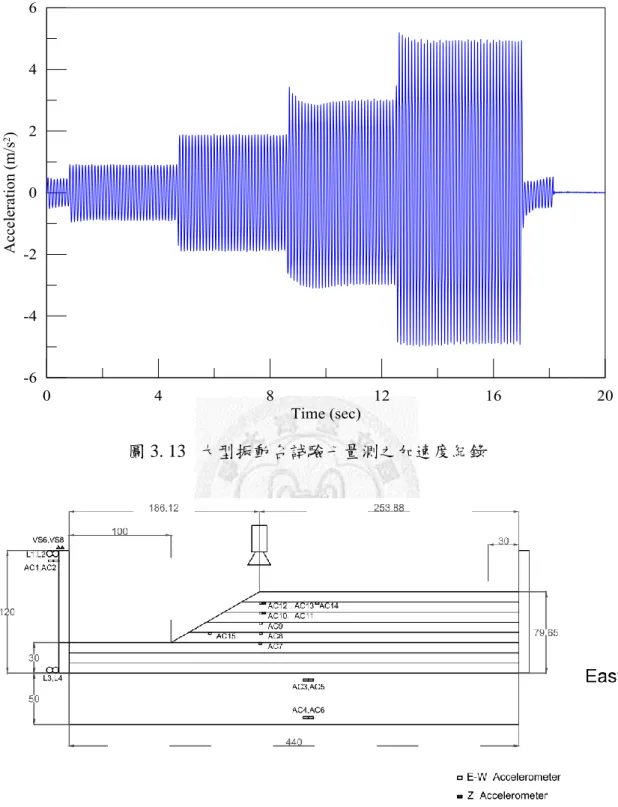
圖 3.13 大型振動台試驗七量測之加速度紀錄 ... 47

圖 3.14 大型振動台試驗七監測系統配置圖 ... 47

圖 3.15 大型振動台試驗側視圖 ... 48

圖 3.16 大型振動台試驗上視圖 ... 48

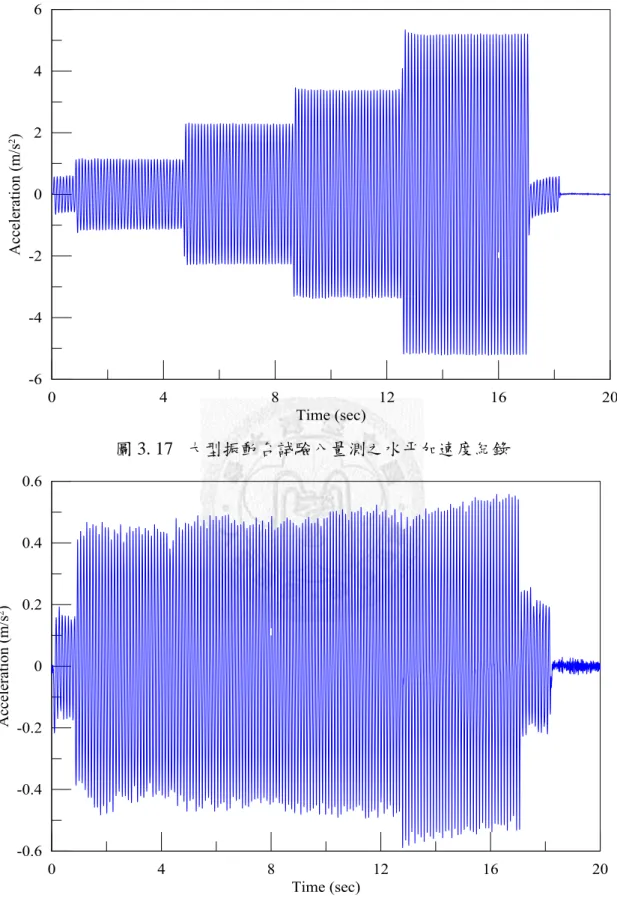
圖 3.17 大型振動台試驗八量測之水平加速度紀錄 ... 49

圖 3.18 大型振動台試驗八量測之垂直加速度紀錄 ... 49

圖 4.1 第八組模型箱外部加速度、速度及位移紀錄 ... 66

(16)

圖 4.2 試驗八之加速度計 AC1 未修正之加速度紀錄與積分的速度及位移 ... 66

圖 4.3 試驗八之加速度計 AC1 之基線偏移量 ... 67

圖 4.4 試驗八之加速度計 AC1 修正後之加速度紀錄與積分的速度及位移 ... 67

圖 4.5 PIV 雙影單一曝光交互關連示意圖 (RAFFEL,1998) ... 68

圖 4.6 試驗八之 PIV 分析截取影像對應運動狀態 ... 68

圖 4.7 試驗八之分析截取影像對應加速度與位移歷時 ... 69

圖 4.8 試驗八之 PIV 影像分析 ... 69

圖 4.9 試驗二之 PIV 分析結果 16.7~17.6 秒，加速度振幅 0.3G ... 72

圖 4.10 試驗二之 PIV 分析結果 21.2~22.1 秒，加速度振幅 0.3G ... 73

圖 4.11 試驗三之 PIV 分析結果 0~15 秒，加速度振幅 0.1G至 0.3G ... 73

圖 4.12 試驗四之 PIV 分析結果 11.3~12.2 秒，加速度振幅 0.2G ... 74

圖 4.13 試驗四之 PIV 分析結果 21.2~22.1 秒，加速度振幅 0.3G ... 74

圖 4.14 試驗五之 PIV 分析結果 0~33 秒，加速度振幅 0.1G至 0.22G ... 75

圖 4.15 試驗七之 PIV 分析結果 13.5~14.4 秒，加速度振幅 0.5G ... 75

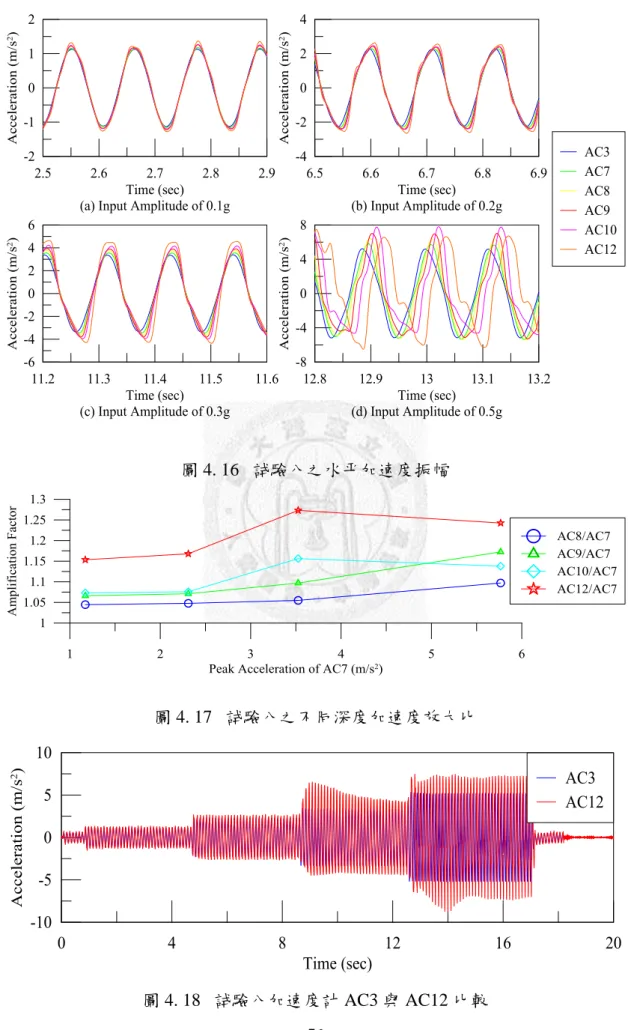
圖 4.16 試驗八之水平加速度振幅 ... 76

圖 4.17 試驗八之不同深度加速度放大比 ... 76

圖 4.18 試驗八加速度計 AC3 與 AC12 比較 ... 76

圖 4.19 試驗二之水平加速度振幅 ... 77

圖 4.20 試驗二之不同深度加速度放大比 ... 77

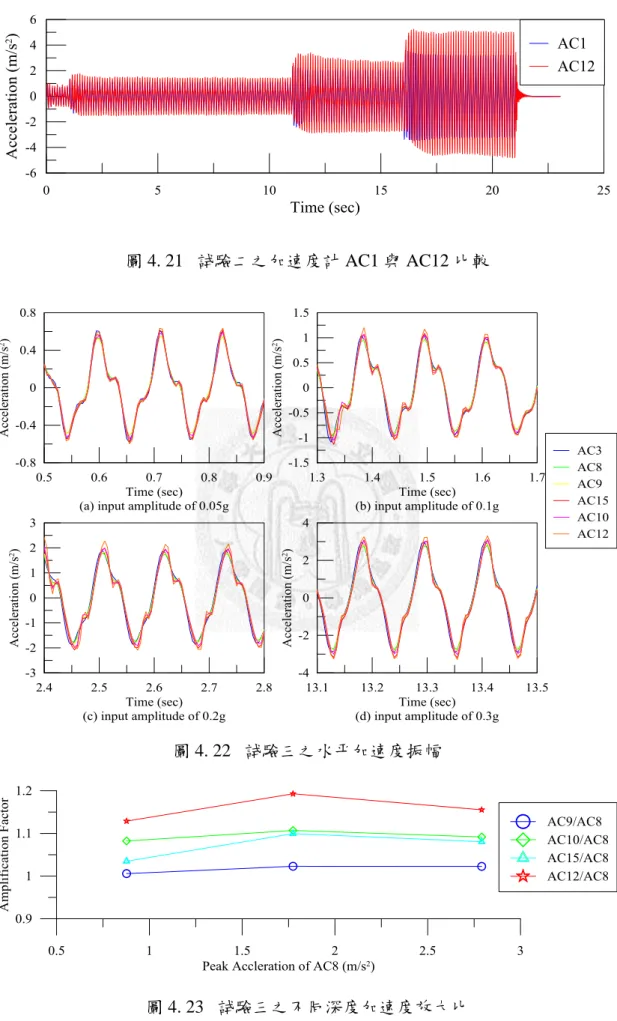
圖 4.21 試驗二之加速度計 AC1 與 AC12 比較 ... 78

圖 4.22 試驗三之水平加速度振幅 ... 78

圖 4.23 試驗三之不同深度加速度放大比 ... 78

圖 4.24 試驗四之水平加速度振幅 ... 79

圖 4.25 試驗四之不同深度加速度放大比 ... 79

圖 4.26 試驗四之加速度計 AC1 與 AC12 比較 ... 79

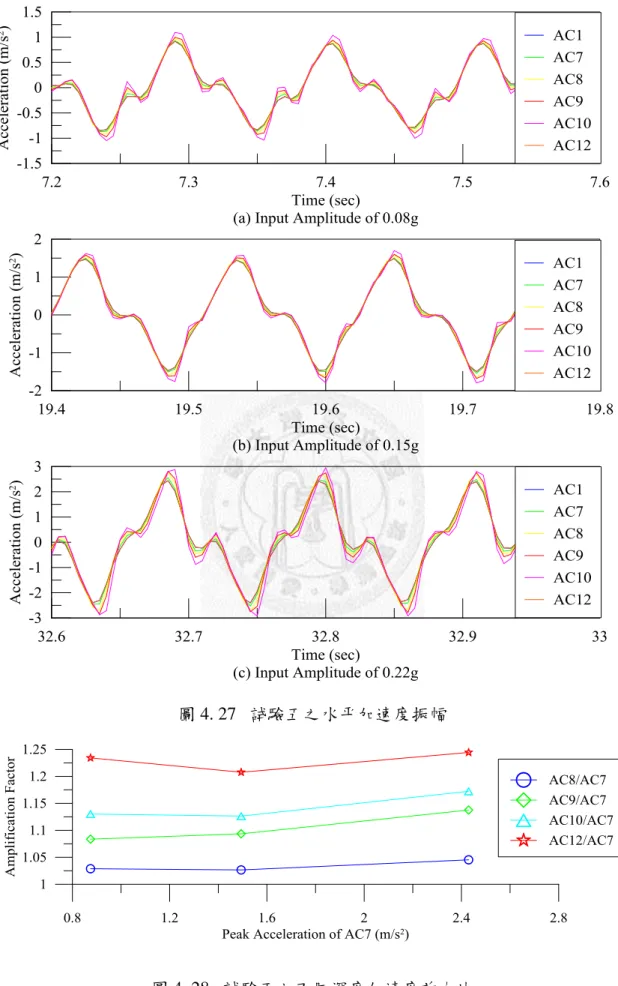
圖 4.27 試驗五之水平加速度振幅 ... 80

圖 4.28 試驗五之不同深度加速度放大比 ... 80

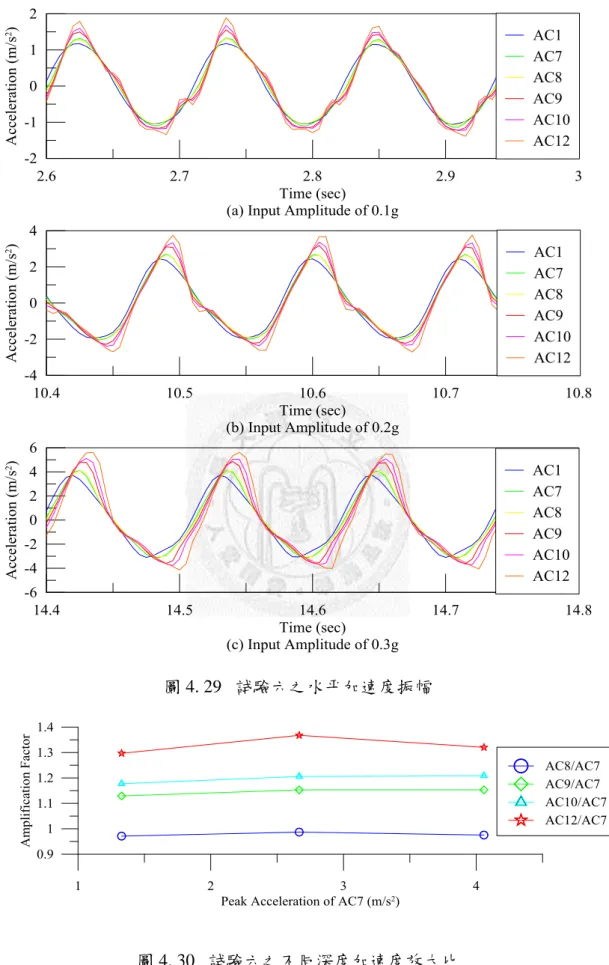
圖 4.29 試驗六之水平加速度振幅 ... 81

圖 4.30 試驗六之不同深度加速度放大比 ... 81

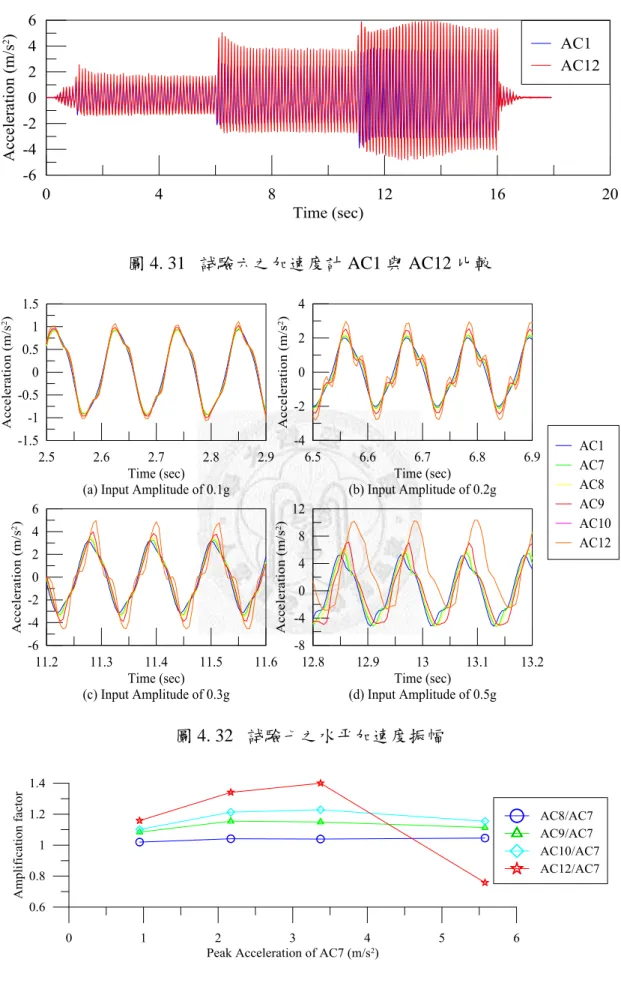
圖 4.31 試驗六之加速度計 AC1 與 AC12 比較 ... 82

圖 4.32 試驗七之水平加速度振幅 ... 82

圖 4.33 試驗七之不同深度加速度放大比 ... 82

圖 4.34 試驗七之加速度計 AC1 與 AC12 比較 ... 83

(17)

XIII

圖 4.35 大型振動台試驗七試驗前之標點編號 ... 83

圖 4.36 大型振動台試驗八試驗前之標點編號 ... 83

圖 4.37 大型振動台試驗七之標點水平位移歷時紀錄 ... 84

圖 4.38 大型振動台試驗八之標點水平位移歷時記錄 ... 84

圖 4.39 大型振動台試驗七之雷射掃描剖面圖 ... 85

圖 4.40 大型振動台試驗八之雷射掃描剖面圖 ... 85

圖 4.41 PIV 影像搜尋範圍 ... 86

圖 4.42 試驗七及試驗八之 PIV 位移場分析之水平位移量 ... 86

圖 4.43 試驗七及試驗八之 PIV 速度場分析之水平速度量 ... 87

圖 4.44 PIV 分析之取點示意圖 ... 87

圖 4.45 試驗七之坡趾、坡面中點、坡頂 PIV 分析水平位移量及標點位移量 .... 88

圖 4.46 試驗八之坡趾、坡面中點、坡頂 PIV 分析水平位移量及標點位移量 .... 88

圖 5.1 基本外顯計算循環（FLAC5.0MANUAL） ... 114

圖 5.2 水平地層示意圖 ... 114

圖 5.3 自重平衡後之水平正應力分佈 ... 114

圖 5.4 垂直振動加載後之正應力分佈 ... 115

圖 5.5 垂直振動加載後之垂直加速度放大效應 ... 115

圖 5.6 水平振動加載後之正應力分佈 ... 115

圖 5.7 水平加載後之水平加速度放大效應 ... 116

圖 5.8 水平振動及垂直振動加載後之正應力分佈 ... 116

圖 5.9 水平振動及垂直振動加載後之加速度放大效應 ... 117

圖 5.10 FLAC 模擬大型振動台之網格設定 ... 117

圖 5.11 邊坡自重平衡後之正應力分佈 ... 117

圖 5.12 邊坡垂直振動加載後之正應力分佈 ... 118

圖 5.13 邊坡輸入垂直振動後之垂直加速度放大效應 ... 118

圖 5.14 FLAC 不同動態輸入(A)絕對座標之位移(B)相對座標之位移(C)剪應變 . 119 圖 5.15 不同動態輸入於加速度振幅 0.3G之最大剪應變分佈 ... 120

圖 5.16 FLAC 決定雷利阻尼輸入最小頻率示意圖（FLAC5.0MANUAL） ... 121

圖 5.17 試驗八之 AC7、AC10 加速度記錄積分一次後之速度反應譜 ... 121

圖 5.18 剪力模數依照平均有效應力調整 ... 121

圖 5.19 大型振動台試驗八輸入修正後之速度歷時 ... 122

圖 5.20 試驗八之加速度振幅(A)0.1G (B)0.2G 結束後之剪應變分佈 ... 122

圖 5.21 試驗八之加速度振幅 0.3G之剪應變分佈 ... 123

(18)

圖 5.22 大型振動台試驗八之標點位移量 ... 123

圖 5.23 試驗八之應力路徑分佈圖 ... 123

圖 5.24 大型振動台試驗八之破壞面整理比較 ... 124

圖 5.25 大型振動台試驗八之坡頂、坡面中點及坡趾網格示意圖 ... 124

圖 5.26 試驗七之加速度振幅(A)0.1G (B)0.2G 結束後之剪應變分佈 ... 125

圖 5.27 大型振動台試驗七之剪應變分佈 0.3G ... 125

圖 5.28 大型振動台試驗七之標點位移 ... 126

圖 5.29 試驗七之應力路徑分佈圖 ... 126

圖 5.30 大型振動台試驗七之破壞面整理比較 ... 127

圖 5.31 試驗二之應力路徑分布圖 ... 127

圖 5.32 大型振動台試驗二之破壞面比較 ... 128

圖 5.33 大型振動台試驗三之剪應變分佈 6 秒 ... 128

圖 5.34 試驗四之應力路徑分佈圖 ... 129

圖 5.35 大型振動台試驗四之破壞面比較 ... 129

圖 5.36 大型振動台試驗五之水平位移分布 35 秒 ... 130

圖 5.37 大型振動台試驗五之剪應變分佈 35 秒 ... 130

圖 5.38 加速度振幅 0.1G之降伏範圍 ... 131

圖 5.39 加速度振幅 0.1G之水平位移分佈 ... 131

圖 5.42 加速度振幅 0.3G之剪應變分佈 ... 132

圖 5.43 加速度振幅 0.5G之剪應變分佈 ... 132

圖 5.44 試驗七之水平位移歷時紀錄 ... 133

圖 5.45 試驗八之水平位移歷時紀錄 ... 133

圖 5.46 原型邊坡示意圖 ... 134

圖 5.47 試驗八原型邊坡之動態輸入速度歷時 ... 134

圖 5.48 試驗八時間與長度正規化後之水平位移歷時 ... 135

圖 5.49 試驗八 MODEL於加速度振幅 0.3G之剪應變分佈 ... 135

圖 5.50 試驗八 PROTOTYPE I 於加速度振幅 0.3G之剪應變分佈 ... 136

圖 5.51 試驗八 PROTOTYPE II 於加速度振幅 0.3G之剪應變分佈 ... 136

圖 5.52 試驗七時間與位移正規化後之水平位移歷時 ... 137

圖 5.53 試驗七 MODEL於加速度振幅 0.3G之剪應變分佈 ... 137

圖 5.54 試驗七 PROTOTYPE I 於加速度振幅 0.3G之剪應變分佈 ... 138

(19)

XV

圖 5.55 試驗七 PROTOTYPE II 於加速度振幅 0.3G之剪應變分佈 ... 138

圖 6.1 大型振動台試驗八 FLAC 之輸出選取位置圖 ... 155

圖 6.2 加速度振幅分段示意圖 ... 155

圖 6.3 大型振動台試驗八 FLAC 網格（27,16）應力路徑 ... 156

圖 6.4 大型振動台試驗八 FLAC 網格（37,15）應力路徑 ... 157

圖 6.5 大型振動台試驗八之各階段加速度振幅頻譜 ... 159

圖 6.6 大型振動台試驗八之各階段加速度振幅的前四個週期頻譜圖 ... 160

圖 6.7 大型振動台試驗七之各階段加速度振幅的前四個週期頻譜圖 ... 160

圖 6.8 試驗七及試驗八在加速度振幅 0.1G階段網格(37,16)之應力路徑 ... 161

圖 6.9 試驗七及試驗八在加速度振幅 0.2G階段網格(37,16)之應力路徑 ... 161

圖 6.10 試驗八之加速度計接收到剪力波 ... 162

圖 6.11 試驗四之 PIV 影像分析及 FLAC 之累計水平位移量比較 ... 162

圖 6.12 試驗五之 PIV 影像分析及 FLAC 之累計水平位移量比較 ... 163

圖 6.13 試驗七之 PIV 影像分析及 FLAC 之累計水平位移量比較 ... 163

圖 6.14 試驗八之 PIV 影像分析及 FLAC 之累計水平位移量比較 ... 164

圖 A-1 試驗二 ... 173

圖 A-2 試驗三 ... 173

圖 A-3 試驗四 ... 174

圖 A-4 試驗五 ... 174

圖 A-5 試驗六 ... 175

圖 A-6 試驗八 ... 175

圖 B-1 試驗七試驗前之雷射掃描 ... 177

圖 B-2 試驗七試驗後之雷射掃描 ... 177

圖 B-3 試驗八試驗前之雷射掃描 ... 178

圖 B-4 試驗八試驗後之雷射掃描 ... 178

圖 D-1 試驗二之加速度振幅頻譜 ... 183

圖 D-2 試驗三之加速度振幅頻譜 ... 183

圖 D-3 試驗四之加速度振幅頻譜 ... 183

圖 D-4 試驗五之加速度振幅頻譜 ... 184

(20)

(21)

1

第一章緒論

前言 1.1

台灣位於環太平洋地震帶上，地震是經常造成台灣的天然災害之一。1999 年 9 月 21 日所發生的集集大地震，造成台灣山區發生大規模的破壞。由於地震產生破壞的規模通常是大尺度，而且很難觀察及量測到內部的破壞行為，僅能藉由地表的特徵改變來判斷，然而問題的尺度太大，很難藉由全尺寸的實驗來了解破壞機制，因此利用模型相似律調整模型的尺寸，透過計算比例關係調整試驗條件，

以期觀察原尺寸的受力狀態、運動行為及破壞機制，使大規模的破壞機制及其行為更容易探討之。

研究動機與目的 1.2

為了解邊坡受震行為及破壞機制，林美聆、王國隆在 2003 年開始在國家地震工程研究中心進行「區域性邊坡受震反應行為分析及振動台模型試驗」，一共試驗了八組大型振動台邊坡模型動態試驗，了解邊坡受震反應及破壞機制。受限於國家地震工程研究中心的作業流程、人力資源不足以及大型試驗的試體在準備上之不易，無法常態性的進行模擬試驗，為了避免受到時間限制及大型試體準備不易之困難，由王國隆（2005）開發了小型振動台設備，王元度（2005）、鄭巽澤（2006）、林京翰（2007）、陳永昇（2009）和許孝源（2010）利用小型振動台模擬邊坡受震反應之研究。鄒銘徽（2011）利用大型振動台試驗及小型振動台試驗的結果進行分析，並探討模型試驗及其原型之動態行為是否照 Meymand（1998）所提出的模型相似性而反應。本研究之主要目的在於透過大型振動台之邊坡模擬試驗，觀察邊坡受震時之動態行為，以及加載垂直振動是否造成破壞行為之差異性。

(22)

研究方法及內容 1.3

本研究針對林美聆、王國隆於國家地震工程研究中心所進行的八組大型振動台試驗，將試驗紀錄、試驗材料參數及試驗配置圖進行整理。透過加速度紀錄、

PIV 影像分析、標點位移量測及快速傅立葉轉換，先對邊坡模型試驗進行動態反應分析，再接著利用 FLAC 軟體做數值模擬分析並結合上述試驗資料分析結果，推測邊坡試驗可能滑動面位置，最後利用垂直振動之加載與否來進行探討。圖 1. 1 為研究流程圖，本論文之研究內容共分為七章：

第一章：緒論。說明本研究之背景、動機、目的及方法。

第二章：文獻回顧。針對王國隆（2006）所使用之模型相似律，其理論背景、假設條件以及推導過程進行整理。

第三章：大型振動台邊坡模型試驗。前人試驗用之材料性質，大型振動台介紹，

試驗簡介、試驗配置及試體尺寸，邊界模型相關設定。

第四章：模型邊坡受震反應及破壞觀測。由加速度紀錄、PIV 影像分析和標點位移量測，分析描述邊坡破壞行為，以及推測可能之破壞時間。

第五章：大型振動台試驗之數值分析。由數值分析軟體 FLAC 模擬大型振動台試驗之受震反應及破壞行為，並推測可能滑動面位置。

第六章：整合加速度歷時記錄配合應力路徑描述振動台之試驗反應，推測其臨界加速度之大小，並整合各分析方法所對應之破壞時間。

第七章：結論與建議。總結本研究之分析結果，並對於未來研究方向提出建議。

(23)

3

圖 1. 1 研究流程圖

(24)

(25)

5

第二章文獻回顧

大地工程中，縮尺模型使得複雜系統能在可控制之條件下進行模擬，提供深入了解系統中力學機制運作的機會。在許多試驗狀況下，縮尺模型提供比全尺寸試驗較經濟的選擇，而縮尺模型與對應原型行為可由模型相似律建立彼此之關聯性。Langhaar（1951 ）提出縮尺模型與原型之關係可被定義為滿足幾何相似

（Geometric Similarity）、運動相似（Kinematic Similarity）與動力相似（Dynamic Similarity），模型與原型間存在對應之物理尺寸稱為幾何相似；對應的顆粒在對應的時間點上位於對應的位置稱為運動相似；對應的部分承受對應的應力大小稱為動力相似。另外，在地震分析時，大部分的地震紀錄儀器是透過加速度計做為紀錄，這些紀錄在透過頻譜轉換所得到的動態資料，一向都是研究地震破壞機制的主要資訊。本章節將對前人研究部分進行整理與介紹，包含模型相似律及傅立葉轉換的介紹。

模型相似律 2.1

許多模型試驗尺寸之設計係實際試驗尺寸之縮減，如何有效地將較小尺寸之模型試驗模擬出真實情況，有賴於模型相似率之牽引，所謂模型相似率係指模型試驗中之模型（Model）與原型（Prototype）間之相似性，通常以幾何相似比



（長度比例因子，原型長度/模型長度）表示。

2.1.1 Moncarz and Krawinkler（1981）

Moncarz and Krawinkler（1981）利用白金漢Π定理推導出在受到加速度歷時之後，應力分量歷時



ij

  r t

^, 以無因次項Π組成之表示式如下：

(26)

( , )

ij

S r t

ij

  

(2.1)

其中，

S

_ij：無因次項目且

i j ,  1, 2,3

，

^r ^

位置向量， t



時間，



₀



應力，

為了達到最佳簡化過程，Moncarz and Krawinkler 假設應力係由下述方程式所表示：



, , , , , , , ⁰, ⁰



F r t E a g l r

   

(2.2)

其中，



密度，E彈性模數，

a 

加速度，g重力加速度，l



長度，以及

r

₀



初始位置向量。

以

l E , , 

為因次參數對其它參數進行無因次化，其推導出之關係式如下：

0 0

, , , , , r

r t E lg a E l l E g E l

  



 

      

(2.3)

反應出真實行為的縮尺模型，必須滿足下列兩項條件：Froude Condition 和 Cauchy Condition，這兩者係指與流體力學、熱傳理論由控制方程式推導出來的無因次項 Froude Number、Cauchy Number 具有相同形式之無因次項必需滿足相似定理。其中 Froude Number 如下：

Fr V

 gl

(2.4)

係應用在自由表面之流動狀態下，為慣性力與重力之比值。

Cauchy Number 如下：

2

v

Ca V E

 

(2.5)

係應用在流體壓縮性對於流動狀態相當重要的情況下，慣性力與壓縮力之比值。

(27)

7

在 1-g 模型試驗條件下，模型重力速度

g 與原型重力加速度

_m

g

_p之比值

g 等於 1

_r （下標 m 代表模型，下標 p 代表原型，下標 r 代表模型/原型之比值），則

r r

1 a  g 

(2.6)

將(2.5)式代入

 ^

^lg/

^E 

_r

^

¹^，則

r r

E l



  

   

(2.7)

(2.7)式亦可表示為一維波傳速度：

r r

r

v E l



     

 

(2.8)

(2.6)式稱之為 Froude Condition，(2.8)式稱之為 Cauchy Condition，(2.7)式為選擇模型材料時十分重要之限制條件。由(2.3)式第二項無因次項可獲得額外的設計條件：

r

r r

r

t l l

E



 

   

 

(2.9)

由於彈性與塑性應變為無因次，因此原型與模型必須是相等的，從位移與尺寸關係可發現：

r

l

r

 

(2.10)

模型與原型之應變自動相等，模擬真實行為之模型必需滿足



_r



1之條件，模型與原型之應力－應變曲線如圖 2. 1 所示，其關係為：

m

E

r p

  

(2.11)

(28)

其中， _r ^m

p

E E

 E

。

2.1.2 Iai（1989）

Iai（1989）利用控制方程式與本構方程式，建立飽和土壤－結構－流體模型在 1-g 試驗條件下振動台試驗之模型相似律。簡單舉例介紹其推導過程，假設孔隙材料單元內部有效應力與孔隙水壓如圖 2. 2 所示，控制飽和土壤行為之方程式如下（Zienkiewicz et al., 1980）：

有效應力定義為：

    ' mp

(2.12) 應變定義

d   Ldu

(2.13)

組成律



⁰



' / 3

_s

d   D d   d   mdp K

(2.14)

整體平衡方程式

T

L    g   u  

f

w

(2.15) 其中，



^T

       

11, 22, 33, 12, 23, 31



：總應力



11 22 33 12 23 31



'^T ' , ' , ' , , ,

       

：有效應力



1,1,1, 0, 0, 0



m

T



(29)

9 p：孔隙水壓



11, 22, 33, 12, 23, 31





T

      

：應變

1 2 3

2 1 3

3 2 1

0 0 0

T

x x x

L x x x

x x x

    

    

 

    

       

    

 

  

 



1, 2, 3



u

T

 u u u

：土壤組構之位移。

D：切線模數，由組成律決定，通常與有效應力以及應變狀態有關。



0：由潛變或溫度對土壤組構產生之應變。

K ：土壤顆粒組成土壤組構之平均統體模數。

s



：飽和土壤密度。



f：孔隙水密度。

1 2 3

( , , )

w

T

 w w w

：孔隙水相對於土壤結構之平均位移。

假設幾何比例與時間比例分別表示為



與



_t，即

  x

p

      x

m

， t

p

 

t

  t

m (2.16)

其中，

x

^T

  x x x

1, 2, 3



：笛卡兒座標系，下標中的 m 及 p 分別代表模型及原型。

假設(2.12)式至(2.15)式之自變數與微分運算子表示成模型與原型之比例關係式：

(30)

           

         

⁰

 

'

0 0

' '

1

s

p m p m p p m

p m p m p u m

D s K s

p m p m p m

p p

L L u u

D D K K

 



      

   



    

  

，，

(2.17)

在上述假設中，應力與應變的假設扮演著相當重要的角色，係由 Rocha（1957）所提出：

在模型與原型間應力與應變分別存在固定之線性比例關係，如圖 2. 3 所示。(2.16) 式、(2.17)式之模型相似條件必須同時滿足於模型與原型間，舉例來說，將(2.12)式以原型表示如下：

    ^

_p

^ ^ ^'

_p

^ ^{m p}  

_p ^(2.18)

將(2.17)式代入(2.18)式，可得

 

'

 

'

 

m m p

m p

m

 

      

(2.19)

為使(2.12)式在模型與原型間皆能滿足，則下述條件也必需滿足：

    ^

_m

^ ^ ^'

_m

^ ^{m p}  

_m ^(2.20)

比較(2.19)式與(2.20)式可得

' p

 

    

(2.21)

依此類推，由(2.13)式可得

u/





  

(2.22)

由(2.14)式可得

(31)

11

' 0

/

D D D p Ks

  

          

(2.23)

由(2.15)式可得

2 2

/

_u

/

_t _f _w

/

_t

   

           

(2.24)

整理結果最後以幾何比例參數



、飽和土壤密度比例參數



_、飽和土壤應變比例參數



_建立起所有模型相似關係，其結果如表 2. 1 所示。

通常



_可由模型與原型之剪力波速準確地決定，當剪應變範圍在 10^-6時，模型與原型之剪力波速可由下述函數所得：

     

2 0

m m s m

p p s p

G V





(2.25)

而剪力模數之比例關係可表示為

       

² ^/ ²

   

^/ ²

D p

V

s p m

V

s m _

V

s p

V

s m

   ^   ^    ^  ^ 

(2.26)

由表 2.1 可知剪力模數之相似律為

D 

/



   

(2.27)

因此可得應變之比例參數

   

²

/

_s

/

_s

p m

V V





  ^  ^ 

(2.28) Rocha（1957）首先有系統地描述縮小尺寸之模型試驗在土壤力學方面所遭遇之問題，Rocha 假設在模型與原型間之應力和應變存在線性關係，由於土壤組成律的決定還是相當具有爭議性的，所以 Rocha 之假設需要小心地評估，而 Iai 由

(32)

Tatsuoka et al.（1986）之試驗結果證明了 Rocha 假設之正確性。Iai 基於以下條件提出模型相似律：

（1）土壤組構視為連續體。

（2）變形量很小以至於變形前後平衡方程式相同。

（3）土壤組構應變量很小，仍然滿足應力應變之線性關係。

因此在應用此模型相似律時亦有兩個使用限制：

（1）無法應用在土壤顆粒間完全失去接觸之現象。

（2）應變量不能太大，以至於不能滿足應力應變之線性關係。

2.1.3 Meymand（1998）

因次分析最簡單的形式係將所有參數表示成質量－長度－時間，三個基本量測單位之比例關係式。舉例而言，彈性模數之單位為力/面積，因次為

ML T

^¹ ^²，由質量、長度、時間三個比例參數



、



、



組合成模型與原型之間應力之比例關係

1 2

 

^ ^ ，其中

  M

_m

M

_p 、

  L

_m

L

_p、

  T T

_m _p；依據相同方法，應變為無因

次項，模型與原型之間應變之比例為 1：1。模型與原型材料密度通常表示成



與



之比例關係，假設



_模型

 

_原型，則

3 3

3

M 1 M

m

m m m p

p p p m

p

L M L M L L

 



^

 

     

 

(2.29)

  

3 (2.30)

在 1-g 試驗條件下，模型與原型之間加速度比例為 1：1，則

(33)

13

2 2

2

1

m

m m P

p p m

p

L

A T T

A L T

T

 

^

 

 

         

   

     

   

 

(2.31)

  

(2.32)

Meymand（1998）為研究土壤－樁－上部結構於軟弱黏土之動態反應，依據試驗條件：（1）1-g 試驗條件下，模型與原型之加速度大小相同；（2）模型與原型試驗用土壤密度相同；（3）試驗材料為飽和黏土，其不排水應力－應變反應與圍壓大小無關，由因次分析與(2.30)式、(2.32)式之關係，以幾何比例參數



建立所有參數之模型相似律，其結果整理於表 2. 2。由表 2. 2 可知剪力波速比例參數等於



，滿足 Moncarz and Krawinkler 所提出之 Cauchy Condition；將



_

 1

、



_



1代入 Iai 之模型相似律，其結果與 Meymand 所推導出之模型相似律亦完全吻合。

林美聆、王國隆於 2003 年至 2009 年於國家地震中心進行八組大型振動台邊坡模型試驗，係依據 Meymand（1988）所提出之模型相似律，以坡高 0.5 公尺，

振動頻率 8.9Hz 之模型邊坡模擬坡高 10 公尺，振動頻率 2Hz 之原型邊坡受震反應。

第三章將對上述試驗之試驗材料、試驗配置以及參數設定進行介紹。

振動台模型試驗 2.2

大部分的模型試驗都有相同之目的，就是了解破壞模式之發展，這樣的概念廣泛地應用在工程科學方面，例如航太工程的風洞實驗、水利工程的水工試驗模型等等，土木工程則以結構工程為最大宗，同樣的試驗概念也應用在邊坡或是壩體之模擬，本小節對於相關之模型振動台試驗做整理回顧。

(34)

2.2.1 Kokusho（2004）之試驗

Kokusho 指出 Newmark 法之邊坡變形係假設滑動體維剛性且土壤之摩擦性質是固定的，但對應於實際之邊坡滑動狀況，並非剛性塊體之行為，在連續性之變動過程中並未產生明顯之滑動面，坡體產生初始破壞後，其土壤強度呈現出非線性行為，從能量觀點來看具有將邊坡破壞程度量化之優點，亦可從能量平衡推估滑動體之變位情形。

Kokusho 所使用的振動台原理與 Uwabe（1986）相同，首先給予一個初始位移量，利用彈簧自由往返之特性來進行振動試驗，其主要裝置與尺寸如圖 2. 4 所示。在試驗過程中 Kokusho 進行一組對照試驗，是為了清楚所用之砂性材料在振動過程中所產生之阻尼效應，利用條型混凝土塊堆疊使其整體重量與重心位置皆與試驗狀況相同如圖 2. 5，分別對混凝土塊與砂性材料所堆疊成的試體進行同樣振動模式，由兩試驗所得到時間與變位的關係，可以從中了解阻尼的消散情形如圖 2. 6 所示。另外，為了取得坡面滑動狀況在試體內部擺置色砂與麵條，在外則使用攝影機配合雷射感應進行量測，結果如圖 2. 7 所示。

2.2.2 Wartman（2005）之試驗

Wartman(2005)所用之振動台尺寸為長 1.219 公尺寬 0.96 公尺，所產生振動特性為單自由度系統之振動行為，其最大荷重為 222kN，最大位移為 15.2 公分。試體主要填築於長 158.2 公分寬 94 公分的樹脂玻璃內，振動台與玻璃箱利用螺栓固定之。

對於此試驗最大的目標在於研究地震機制引致的邊坡變形及利用 Newmark 滑動塊體法估計地震所引致的邊坡變形量，因而填築四種不同型態的邊坡分別討論之，四種邊坡填築方式與基本試驗資料如圖 2. 8 所示，所用之填築材料主要依舊

(35)

15

為高嶺土與膨潤土以 3:1 比例混合而成的複合黏土，並以含水量改變控制試體之不排水剪力強度。在試驗內所使用的量測儀器為加速度感應子及線性位移量測儀，

分別量測試體內部不同位置之加速度變化及坡體受震後之變形量。所輸入之振動模式主要有四種，如表 2. 3 所示，主要包含實際地震記錄及人為產生的振動模式。

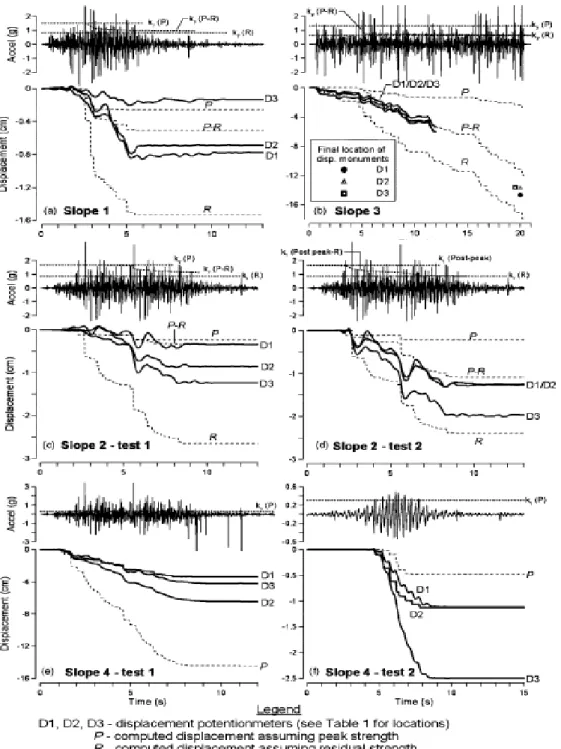
而四種邊坡在受震後之變形狀態如圖 2. 9 所示，圖 2. 10 表示加速度與變形隨時間變化狀況。在各種邊坡模式所產生的破壞型式中以深層的滑動為主要模式。而利用滑動塊體法來估計滑動量，分別利用加速度、尖峰強度及殘餘強度進行計算，

隨著坡體模式的不同各有高、低估的現象，在這一系統試驗中平均估計值為實際量測值之 75%。

傅立葉轉換 2.3

任何週期時間為

T

的有限功率訊號，皆能以正弦波和餘弦波之總何來表示。

一般以下列的三角傅立葉展開式來描述：

 

⁰



0

 

0



1

cos sin

2 n ⁿ ⁿ

x t A A n ^ t B n ^ t





   

^(2.33)

 

/2 /2 0

2 ^T ( ) cos , 0,1, 2

n T

x t n t dt n

A  T 



^  

^(2.34)

 

/2 /2 0

2 ^T ( ) sin , 1, 2,3

n T

x t n t dt n

B  T 



^  

^(2.35)

其中， ( )

x t ：時域訊號函數



₀



2 / T



：頻率

傅立葉展開式可提供訊號一種表現方式，(2.33)式、(2.34)式及(2.35)式說明了彼此之間的關聯。在定義一個週期的時域訊號

^{x t}  

，由(2.34)式及(2.35)式求得傅立

(36)

葉係數後，最後藉由 (2.33) 式可求得時頻訊號，這種表現行為稱之為轉換

（Transformation）。

在不同的研究領域中，傅立葉轉換具有多種不同的形式，如連續傅立葉轉換和離散傅立葉轉換。連續傅立葉轉換，乃是將頻率域的函數

^F   ^

^{表示成時間域的}

函數 ( )

f t 的積分型式，如下所示：

   ^{( )}  ^{( )}

^{i t}

F  F f t

^

f t e

^^

dt

  

 ^(2.36)

連續傅立葉轉換之逆轉換（Inverse Fourier Transformation）乃將時間域之函數 ( )

f t

表示成頻率域之函數

^F   ^

^{的積分，如下所示：}

   

1 1

( ) 2

f t F F  F  e d

i t^





 

      

 ^(2.37)

一般在對信號作分析時，首先須對信號取樣，假設取樣點相當多，則會造成龐大的計算量，為了加快計算時間並減少運算量，大多採用快速傅立葉轉換。傅立葉快速轉換的計算方法是在西元 1965 年由庫利（Cooley）和圖基（Tukey）所提出。快速傅立葉轉換（Fast Fourier Transform，FFT）是以離散傅立葉（Discrete Fourier Transform，DFT）為基礎，將離散傅立葉轉換以下式來表示：

1

0

1 2

( ) ( ) exp( ) 0 1

N

n

j mn

X m x n m N

N N







   ^,   

^(2.38)

其中，

X m ：頻率函數

( )

N ：週期

( )

x n ：時間函數

將上式改寫為：

(37)

17

1

0

( ) 1 ( )

N

mn n

X m x n w

N





 

^(2.39)

(2.39)式中

exp j ²

w N



  

    

， N 需為 2 的次方倍，若

N 

8，則

X

(0) ~

X

(7) 可表示為：

0 0 0 0 0 0 0 0

0 1 2 3 4 5 6 7

0 2 4 6 0 2 4 6

0 3 6 1 4 7 2 5

0 4 0 4 0 4 0 4

0 5 2 7 4 1 6 3

0 6 0 2 0 6 4 2

0 7 6 5 4 3 2 1

(0) (1) (2) (3) 1 (4) (5) (6) (7)

W W W W W W W W X

X W W W W W W W W X N W W W W W W W W X W W W W W W W W X W W W W W W W W X W W W W W W W W

   

  

   

  

 

  

(0) (1) (2) (3) (4) (5) (6) (7)

x x x x x x x x

  

  

   

     

 

(2.40)

快速傅立葉轉換將離散傅立葉轉換中 N 次矩陣，分解成

  (  log )

₂^N 個均為 N 次的矩陣。在分解過程中，將零放置矩陣內部，讓每個矩陣都可以進行複數運算。

例如當

N 

2^點，離散傅立葉轉換需要

N 的複數相乘次數與

²

N N

(



1)的複數相加次數，依照快速傅立葉轉換運算僅需要

N 

/ 2的複數相乘次數與 N



的複數相加次數，透過上述舉例，明顯發現可以大量減少運算次數。

快速傅立葉轉換是由離散傅立葉轉換所衍伸，因此快速傅立葉轉換具有離散傅立葉轉換的特性，在使用上需滿足離散傅立葉轉換的限制條件，這些限制條件如下列：

（1）取樣速率 R （Sampling Rate）需為受測訊號最高頻率的兩倍或兩倍以上，

也就是符合尼奎士取樣定理（Nyquist Sampling Theorem）。

（2）訊號成分頻率需在刻度上，取樣週期須為受測訊號周期的整數倍。

（3）受測訊號具有週期性。

(38)

（4）取樣數須為 2^個資料。

條件（1）、（2）、（3）為離散傅立葉轉換及快速傅立葉轉換之共同條件，當不滿足條件（1）時，因為不符合取樣定理，會使得低頻部分反射至高頻部分，而造成混疊效應（Aliasing Effect）。不滿足條件（2）時，會引起頻譜中信號能量散逸致鄰近周圍之信號刻度上，而出現旁辦（Side Lobe），產生柵欄效應（Picket-fence Effect）及洩漏效應（Leakage Effect）。因 DFT 及 FFT 是以傅立葉轉換為基礎，而信號經過傅立葉轉換需為週期性信號，當不滿足條件（3）時，會導致 DFT 及 FFT 無法計算。條件（4）為 FFT 所增加之限制，如果不滿足該條件則無法計算，必須以 DFT 運算進而造成運算量增加。由於 FFT 之上述限制條件，在分析信號的頻譜時，將不可避免產生些許誤差。

(39)

19

表 2. 1 1-g 試驗條件下之模型相似律（Iai,1989）

Items

Scaling factors (prototype/model)

 

1    

x length

 



density of saturated soil





₁

 strain of soil



_

₁

t

time

 





^0.5



^0.5



0 strain of soil due to creep, temperature, etc.





1

 total stress of soil









' effective stress of soil







D

tangent modulus of soil, which generally depends on histories of effective stress, strain, etc.

 

  

K bulk modulus of the solid grains of soil

s

 

 

 p pressure of pore water and/or external water 





k

permeability of soil

 





^0.5







^0.5

u displacement of soil and/or structure



_



u

velocity of soil and/or structure

 





^0.5



^0.5

u

acceleration of soil and/or structure 1 1

w

average displacement of pore water relative to the soil skeleton







(40)

w rate of pore water flow  





^0.5



^0.5

n porosity of soil 1 1

K

f

bulk modulus of pore water and/or external water

 

  

EI flexural rigidity ( per unit breadth of the beam )   

⁴  

_

⁴

EA

longitudinal rigidity ( per unit breadth of the beam )

2  

   _

²



inclination of the beam



_

1 M

bending moment of the beam ( per unit breadth of the beam )

3 

  _

³

S

shear force of the beam ( per unit breadth of the beam )

2

 



_

²

F

axial force of the beam ( per unit breadth of the beam )

2 

  _

²



f density of pore water and/or external water





₁



b density of the beam ( mass per unit length and breadth of the beam )







T

traction acting on the soil specified on the boundary







u

displacement of the soil and/or the beam specified on the boundary







p

pressure of pore water and/or external water specified on the boundary







(41)

21

w

average displacement of pore water, specified on the boundary, relative to the soil skeleton, often specified as rate of flow on the boundary









inclination of the beam specified at the boundary





₁

M

bending moment of the beam specified at the boundary ( per unit breadth of the beam )

3 

  _

³

S

shear force of the beam specified at the boundary ( per unit breadth of the beam )

2

 



_

²

F

axial force of the beam specified at the boundary ( per unit breadth of the beam )

2 

  _

²

i

hydraulic gradient of external water specified at the boundary





₁

(42)

表 2. 2 1-g 試驗條件下之模型相似律（Meymand,1998）

Entity

Fundamental dimensions

MLT

Scaling factors



3 0.5

    

;





Mass Density

ML

^³



^³ 1 Acceleration

LT

^²



^² 1

Length

L  

Force

MLT

^²



^²

_

³

Shear Wave Velocity

LT

^¹



^¹



Stress

ML T

^¹ ^²

 

^¹ ^²



Stiffness

MT

^²



^²

_

²

Time

T  

Strain

1

1 1

Modulus

ML T

^¹ ^²

 

^¹ ^²



Frequency

T

^¹



^¹ 1



EI

ML T

^¹ ^²

 L

⁴

 

^¹ ^²

 

⁴



⁵

(43)

23

表 2. 3 Wartman 所使用之振動模式

Slope Test motion PGA(g) Mean frequency (Hz)

Significant

duration(s) Notes

1

Modified Kobe port Island;Hyogo-ken Nanbu

EQ

3.03 21.2 5.5 Modified by increasing amplitude and frequency range of recorded motion

2 (Test 1 &

2)

Modified Kobe port

Island;hyogo-ken Nanbu EQ 2.31 21.2 7.8

Modified by increasing amplitude and frequency range of recorded motion and by lengthening

record to increase duration

3 Synthetic 3.46 13.2 19.3 Synthetic motion create in the frequency domain with spectral content from 1 to 20 Hz

4(Test1) Modified Kobe port

Island;hyogo-ken Nanbu EQ 4.02 20 7.9 Modified by increasing amplitude and frequency range of recorded motion

4(Test2) Synthetic 0.49 6 7.6 Synthetic motion create in the frequency domain with spectral content from 1 to 7 Hz

(44)

圖 2. 1 應力－應變相似條件（Moncarz and Krawinkler,1981）

圖 2. 2 孔隙材料單元土壤有效應力與孔隙水壓方向（Iai,1989）

(45)

25

圖 2. 3 土壤在模型與原型間之應力－應變關係（Iai,1989）

圖 2. 4 振動設備與尺寸示意圖（Kokusho,2006）

(46)

圖 2. 5 試驗對照示意圖（Kokusho,2006）

圖 2. 6 阻尼消散示意圖（Kokusho,2006）

(47)

27

圖 2. 7 坡面變位示意圖（Kokusho,2006）

圖 2. 8 邊坡試驗基本參數（Wartman,2005）

(48)

圖 2. 9 邊坡變形示意圖（Wartman,2005）

(49)

29

圖 2. 10 加速度與變位隨時間改變示意圖（Wartman,2005）

振動台模型邊坡滑移行為之數值模擬

國立臺灣大學工學院土木工程學系 碩士論文

Department of Civil Engineering College of Engineering National Taiwan University

Master Thesis