手輪馬達電動輪椅之無力感測器動力輔助控制

(1)

國立臺灣大學工學院機械工程研究所碩士論文

Department of Mechanical Engineering College of Engineering

National Taiwan University Master Thesis

手輪馬達電動輪椅之無力感測器動力輔助控制 Force Sensorless Power Assist Control of Powered

Wheelchair Driven by Rim Motor

劉邦元 Bang-Yuan Liu

指導教授：陽毅平博士 Advisor: Yee-Pien Yang, Ph.D.

中華民國 108 年 6 月 June 2019

(2)

(3)

口試委員會審定書

(4)

(5)

誌謝

在論文的最開始，首先我要對我的指導教授陽毅平博士致上最深的感謝。在我這兩年的碩士生活中，教授在百忙之中仍不忘抽空指導我們，使我從一個懵懂的大學畢業生，逐漸培養出獨立研究並解決問題的能力。在產出論文的過程中，

他也不斷地協助我釐清我研究的方向與目的，並針對研究中的不妥之處提出修正，讓我最終能順利完成論文並畢業。

其次，非常感謝擔任口試委員的黃緒哲教授與郭重顯教授，在百忙中抽空閱讀我的論文並參與口試，並在口試時給了我許多鼓勵與建議，使這本論文最終得以更加完整。

感謝推進控制實驗室的同學們，在這兩年中給予我幫助、與我互相切磋砥礪。首先感謝已畢業的輪椅組學長治緯、詠諭與暉翔等人，在我碩一的一年中教了我許多馬達控制的基礎知識，並在我研究遇到瓶頸時樂意與我討論並協助我解決問題。感謝我的同學泓儒、宇辰與鍾毅，在平時與我討論切磋控制上的知識，

並在我實驗時總是不吝提供協助。感謝學弟彥升、彥廷、冠廷、竣翔在我們忙於論文時協助處理實驗室的事務。其中特別感謝同為輪椅組的泓儒與彥升，與我一起建立新一代的輪椅控制架構，並在輪椅出問題時與我共同探討原因並測試、解決，讓實驗得以順利進行。

此外，特別感謝馬達技術實驗室的冠任學長，在我們遇到馬達控制的問題時不厭其煩的為我們解惑，並提供技術指導，讓各種難題迎刃而解。

最後，再一次感謝以上的所有人，以及雖沒有提到但曾經幫助過我的所有人。做研究雖然是一條孤獨之路，但因為有你們在，讓這條路似乎不再那麼坎坷難行。謝謝你們，謝謝。

(6)

(7)

手輪馬達電動輪椅之無力感測器動力輔助控制

中文摘要

本文主旨在於建立手輪馬達電動輪椅的動力輔助系統，其主要處理的問題分為低速力矩控制的精度提升及動力輔助控制兩部分。在力矩控制上，要達到精確控制需有較準確的轉子位置，過去使用的數位霍爾感測器其解析度較低，難以滿足此需求。另外由於輪椅經常操作在低速區，由數位感測器測得的速度也會有較大落後，使得控制系統的頻寬降低。一般會使用高精度的編碼器來處理上述問題，但考量其成本較高，本文提出使用較便宜的線性霍爾感測器做為解決方案。

在本文應用中，由於馬達內部磁鐵形狀使得感測器訊號有較嚴重的諧波成分，無法直接用於測量，故本文提出一套基於鎖相環的特殊觀測器，其中包含自適應濾波環節，可抑制訊號中主要的諧波成分，達到較穩定的估測。在動力輔助控制部分，本文利用干擾觀測器取代力感測器來估測人力輸入，其後透過阻抗控制的技術來使使用者在推動輪椅時能感受到合適的阻抗特性。輔助控制的目標可分為降低使用者須施加的推力及延長輪椅滑行距離，達成此兩目標需使動力輪對外界干擾力矩分別具有低阻抗及高阻抗兩種特性，故本文設計手推辨識算法來判定使用者是否在推動輪椅，依此來決定兩種阻抗模式的切換。本文方法經模擬驗證可行性，並以實際實驗來證明其效能。

關鍵字：手輪馬達、電動輪椅、力矩控制、霍爾感測器、動力輔助控制

(8)

(9)

Force Sensorless Power Assist Control of Powered Wheelchair Driven by Rim Motor

ABSTRACT

The main objective of this research is to establish the power assist system for the proto-type powered wheelchair driven by rim motor. The main issue can be divided into two parts: improvement on accuracy of torque control in low speed region and design of power assist control sysytem. To achieve precise torque control, it is necessary to know accurate rotor position. However, the digital Hall-effect sensor used in the past research has a low resolution, which is difficult to meet the requirement. In addition, since the wheelchair is often operated in the low speed region, the speed estimated by the digital sensor will also contain large phase lag, which would reduce the bandwidth of the speed control loop. High-resolution encoders are generally used to deal with the above problems, but considering the higher cost, this paper proposes to use cheap linear Hall-effect sensors as a solution. In this application, because of the shape of the magnet using by the rim motor, the sensor signal contained large harmonic components and cannot be directly used for measurement, this paper proposes a specialized observer based on phase-locked loop, which includes adaptive filtering section. It can suppress the main harmonic components in the signal and achieve a more stable estimation. In regard to the power assisted control, this paper uses the disturbance observer instead of force sensors to estimate the human torque input, then through the technique of impedance control, the user could feel the appropriate impedance characteristics during the propulsion of the wheelchair. The objectives of the power assist control can be

(10)

divided into two part: reduce the torque that the user must apply and extend the moving distance of the wheelchair. To achieve these goals, the powered wheel must have different impedance characteristic to the external torque disturbance. An identification algorithm is designed to determine whether the user is pushing the wheelchair, and accordingly determines the switching of the two impedance modes. The method of this paper is verified by simulation and its performance is proved by experiments.

Key words： rim motor, electric wheelchair, torque control, Hall-effect sensor, power assist control

(11)

圖目錄

圖 2-1 手輪馬達電動輪椅整車架構圖 ... 9

圖 2-2 助推模式下控制架構圖 ... 10

圖 2-3 Arduino Due ... 11

圖 2-4 F28069 自製控制卡 ... 13

圖 2-5 自製馬達驅動板實體圖 ... 14

圖 2-6 手輪馬達動力學模型示意圖 ... 17

圖 2-7 手輪馬達轉移函數方塊圖 ... 19

圖 2-8 手輪馬達簡化模型轉移函數方塊圖 ... 21

圖 2-9 車架自由體圖 ... 22

圖 2-10 整車轉移函數方塊圖 ... 25

圖 3-1 無刷馬達基礎控制架構圖 ... 26

圖 3-2 Clarke 變換示意圖 ... 28

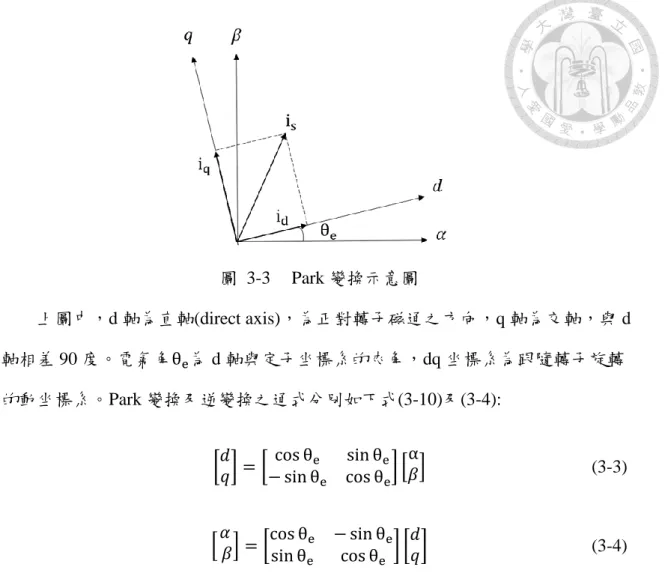
圖 3-3 Park 變換示意圖 ... 30

圖 3-4 PWM 原理示意圖 ... 31

圖 3-5 空間向量六大基底 ... 32

圖 3-6 V4開關狀態下馬達等效電路圖 ... 33

圖 3-7 區域 1 中三相 PWM 波型 ... 34

圖 3-8 SVPWM 等效電壓波型示意圖 ... 36

圖 3-9 磁場導向控制架構圖 ... 37

圖 3-10 電流採樣放大電路 ... 38

圖 3-11 霍爾感測器原理[37] ... 40

圖 3-12 數位霍爾感測器結構圖 ... 41

圖 3-13 理想情況霍爾訊號示意圖 ... 42

(14)

圖 3-14 霍爾訊號與反電動勢相位對齊示意圖 ... 44

圖 3-15 弧形磁鐵示意圖 ... 45

圖 3-16 霍爾訊號之 FFT 分析結果 ... 45

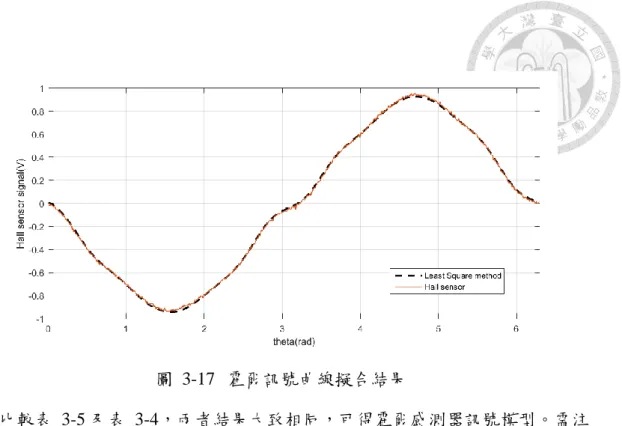
圖 3-17 霍爾訊號曲線擬合結果 ... 47

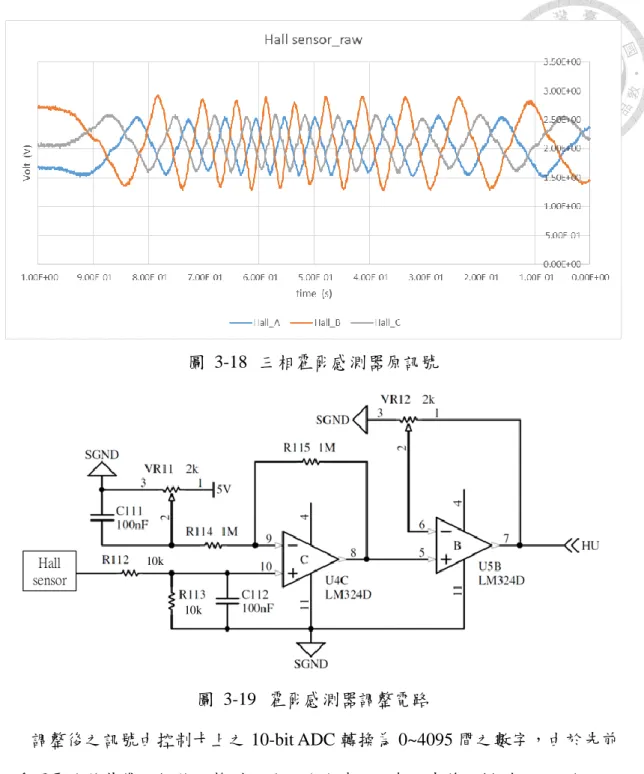
圖 3-18 三相霍爾感測器原訊號 ... 48

圖 3-19 霍爾感測器調整電路 ... 48

圖 3-20 鎖相環架構圖 ... 51

圖 3-21 三階正交鎖相環架構圖 ... 52

圖 3-22 線性化之正交鎖相環 ... 54

圖 3-23 ANF 算法框圖 ... 56

圖 3-24 改進型鎖相環觀測器 ... 57

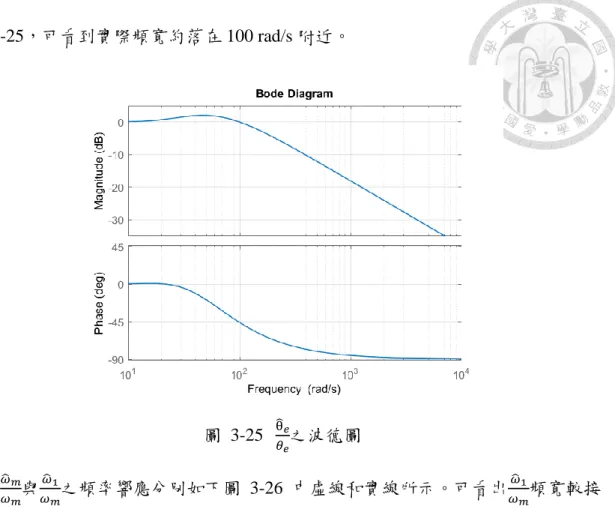
圖 3-25 θ𝑒𝜃𝑒之波德圖 ... 59

圖 3-26 𝜔𝑚𝜔𝑚與𝜔1𝜔𝑚之波德圖 ... 59

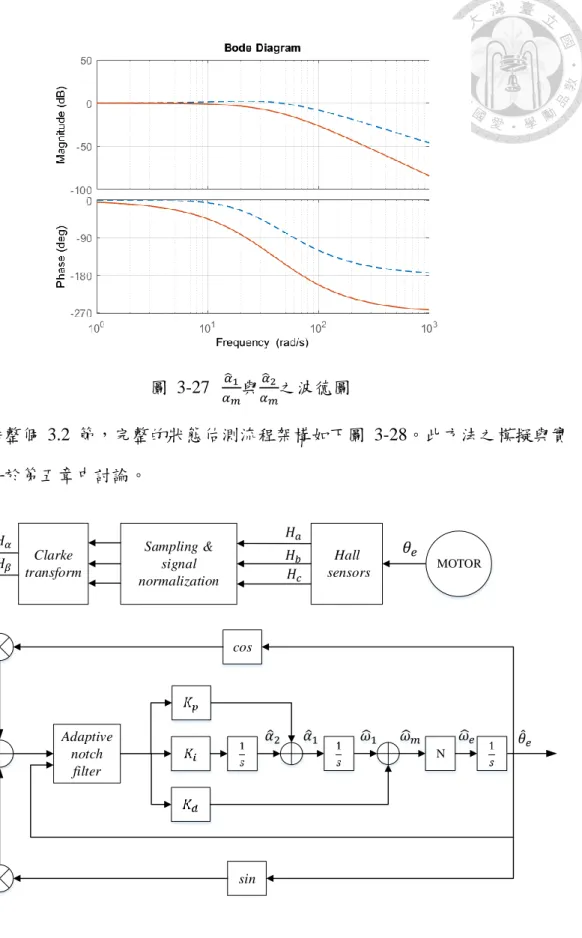
圖 3-27 𝛼1𝛼𝑚與𝛼2𝛼𝑚之波德圖 ... 60

圖 3-28 線性霍爾感測器狀態估測流程 ... 60

圖 4-1 手推過程動力輪狀態示意圖 ... 62

圖 4-2 手推計次算法流程 ... 65

圖 4-3 干擾觀測器系統框圖 ... 69

圖 4-4 摩擦轉矩模型示意圖 ... 70

圖 4-5 阻抗模式切換時機示意圖 ... 74

圖 4-6 無力感測器輔助控制系統架構 ... 74

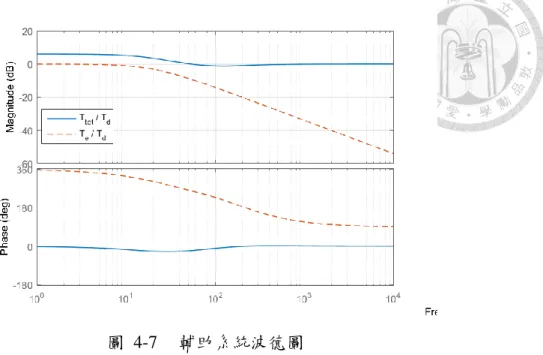
圖 4-7 輔助系統波德圖 ... 78

圖 4-8 慣量參數不準對輔助控制設計之影響 ... 78

圖 4-9 力矩估測頻寬降低對輔助控制設計之影響 ... 79

圖 5-1 Chroma 電源供應器 ... 80

(15)

圖 5-2 Keysight 數位示波器(DSOX4024A) ... 81

圖 5-3 手輪馬達電動輪椅實體圖 ... 81

圖 5-4 鎖相環 Simulink 模擬架構 ... 82

圖 5-5 估測角度與實際角度比較 ... 83

圖 5-6 ANF 輸入及輸出比較 ... 83

圖 5-7 估測速度與實際速度比較 ... 84

圖 5-8 估測加速度與實際加速度比較 ... 84

圖 5-9 感測器有增益誤差時估測速度比較 ... 85

圖 5-10 感測器有增益誤差時估測加速度比較 ... 86

圖 5-11 數位感測器估測速度與本文方法比較 ... 87

圖 5-12 數位感測器估測角度[38]與本文方法比較 ... 87

圖 5-13 動力輪轉速與手推狀態判定(實車實驗) ... 89

圖 5-14 輔助控制 Simulink 模擬架構 ... 90

圖 5-15 有無輔助控制之速度比較 ... 91

圖 5-16 輔助控制之力矩比較 ... 91

圖 5-17 空載時輔助轉矩比較及阻抗模式切換 ... 93

圖 5-18 空載條件下有無輔助控制速度比較 ... 93

圖 5-19 有無輔助控制整車速度對比 ... 94

圖 5-20 左右輪輸出輔助力矩 ... 94

圖 5-21 輔助轉矩與外加轉矩比較 ... 94

圖 5-22 輔助控制下雙輪轉速比較 ... 94

(16)

表目錄

表 2-1 手輪馬達電動輪椅規格表 ... 9

表 2-2 Arduino Due 規格 ... 11

表 2-3 手輪馬達模型參數[37] ... 21

表 3-1 SVPWM 各區域之開關向量作用順序 ... 34

表 3-2 Vref所在區域判斷關係表 ... 35

表 3-3 各區域中基底向量作用時間 ... 35

表 3-4 FFT 所得霍爾訊號諧波成分 ... 45

表 3-5 最小平方法所得諧波成分 ... 46

表 4-1 輔助策略中不同的阻抗模式 ... 73

表 5-1 鎖相環模擬參數 ... 82

表 5-2 手推計次估測次數與實際次數之比較 ... 88

表 5-3 輔助控制主要模擬參數 ... 90

表 5-4 有無輔助控制之車速與推行距離比較 ... 96

(17)

符號表

符號說明單位

B_M 阻抗控制模型黏滯係數 N ∙ m ∙ sec

rad

Bm 馬達黏滯摩擦係數 N ∙ m ∙ sec

rad

ea A 相相反電動勢 V

e_b B 相相反電動勢 V

e_back 反電動勢 V

ec C 相相反電動勢 V

Ha a 相霍爾感測器訊號 V

H_b b 相霍爾感測器訊號 V

H_c c 相霍爾感測器訊號 V

I 相電流峰值 A

ia A 相相電流 A

i_b B 相相電流 A

i_c C 相相電流 A

i_d 定子電流d軸分量 A

iq 定子電流q軸分量 A

i_s 定子電流向量 A

i_sa 定子電流 a 軸分量 A

isb 定子電流 b 軸分量 A

isc 定子電流 c 軸分量 A

i_sα 定子電流α軸分量 A

i_sβ 定子電流β軸分量 A

(18)

J_M 阻抗控制模型慣量 Kg ∙ m²

Jw 動力輪轉動慣量 Kg ∙ m²

Ke 馬達反電動勢常數 V

rad sec⁄

Ki 積分控制參數 NA

K_p 比例控制參數 NA

K_t 馬達力矩常數 Nm A⁄

Kta A 相力矩常數 Nm A⁄

Ktb B 相力矩常數 Nm A⁄

K_tc C 相力矩常數 Nm A⁄

L_a A 相相電感值 H

Lb B 相相電感值 H

Lc C 相相電感值 H

L_s 定子相電感值 H

M_a 振幅調變比 NA

N 單相繞線匝數 NA

Ra A 相繞線相電阻 Ω

R_b B 相繞線相電阻 Ω

R_c C 相繞線相電阻 Ω

Rs 定子相電阻值 Ω

Te 馬達輸出力矩 N ∙ m

T_L 馬達負載力矩 N ∙ m

T_s 取樣時間 sec

van A 相端電壓與中性點電壓差 V

vbn B 相端電壓與中性點電壓差 V

(19)

v_cn C 相端電壓與中性點電壓差 V

Vdc 直流電壓 V

vn 三相 Y 接中性點電壓 V

v_phase 相電壓峰值 V

vs 定子電壓向量 V

vsα 定子電壓α軸分量 V

v_sβ 定子電壓β軸分量 V

θ_e 馬達電氣角 rad

ϕ_m 磁鐵磁通量 Wb

ωe 馬達電氣角速度 rad sec⁄

ω_m 馬達機械角速度 rad sec⁄

∆θ 手推位移量 rad

(20)

.

(21)

第1章緒論

1.1 研究背景與動機

(1)手輪馬達電動輪椅

隨著近年來台灣人口老年化，人們對輔具的需求愈來愈高，考量到在一般環境下使用的機動性，電動輪椅成了許多人的選擇。市面上大部分電動輪椅在制動上採用的是直流有刷馬達搭配齒輪箱的方式，但這也使得整個輪椅的體積及重量難以縮減，對收納及運送造成不便，此外馬達及機械部件的損耗也造成使用年限難以延長。有鑑於此，本實驗室開發的手輪馬達電動輪椅，採用更高效率、低噪音、更耐久的永磁無刷馬達，並將馬達的結構整合在輪子內部，在外觀上與普通輪椅相似，

且達到使電動輪椅輕量化、可收折的目的。

(2)磁場導向控制

磁場導向控制(FOC)採用 SVPWM 合成電壓向量的方式，來達成三相馬達的電流控制，相比原本使用的六步方波控制效率更高，且大幅降低轉矩脈動。然而其需要得知精確的轉子角度這點也使得應用門檻較高。無感測器向量控制因其成本低廉及其在許多應用上的強健性，成為近年馬達控制研究的主流。但無感測器架構因馬達之反電動勢特性限制，使其只能運作於一定速度以上，起轉及低速區的控制則需由其他方式補足，如開路的變頻變壓控制或閉路的轉子高頻注入法等。由於本實驗室開發之手輪馬達屬於表面式永磁無刷馬達(SPM)，其電氣特性使得啟動時由高頻注入法估測角度的做法並不適用，而電動輪椅在操作時負載變化較大，開路控制亦難以保證其運作順利，故而本研究轉而研發有感測器之控制策略。

傳統使用感測器的控制策略仰賴於旋轉編碼器或霍爾感測器產生之脈衝信號

(22)

計算速度，再經由積分估算當前角度，但此作法相當仰賴感測器對角度的解析度，

且只有在速度穩定時才能獲得較好的估計，也就造成了暫態容易有震盪或不穩定的情況。另一種選擇是使用線性霍爾感測器，也是本研究提倡的方法。線性霍爾感測器正如其名，其輸出電壓與施加之磁場呈線性關係，故理論上能直接反映出精確的轉子位置。當然，實際上會有其他因素使得角度估測受影響，此問題的分析與處理會於後文詳述。

(3)動力輔助推行與即時手推計次功能

相較於一般以搖桿作為人機介面之控制方式，動力輔助推行更強調機械與使用者間之協調性，採用更為人性化及符合直覺之操作模式，可縮短一般輪椅使用者適應電動輪椅之週期。且輔助推行模式可以動力輪模組為單位做獨立運行，無需再增加整車之上位控制器，節省成本，同時可以充分發揮本實驗室開發之輕量化手輪馬達模組之優勢，大大提升產品競爭力。

手推計次功能作為輪椅輔助系統功能，可提供使用者及治療師作為運動或復健之參考指標。在本實驗室過去研究中，由於狀態估測精度及演算法設計問題，使得辨別手推之成功率有限，且無法於單晶片中實時運行。本研究將設計一套基於首推角度估測的計次算法，針對這些問題做改善。

(23)

1.2 文獻回顧

 磁場導向控制之角度及速度估測技術

霍爾感測器由於其低成本與結構簡單，在馬達驅動的應用上已行之有年。但一般應用使用的多半是依磁場強度輸出高或低電平的數位霍爾感測器，其解析度較低，僅能用於分辨轉子所在的角度區間，對於要求精確角度資訊的向量控制而言並不適合。解決此問題最簡單作法是將速度積分來獲得死區內的角度，但此作法會受到感測器安裝不準及速度變化的嚴重影響。針對此問題，Zhang 等人[1]在傳統方法上，加入基於最小平方法的擬合機制來降低上述影響。Zaim 等人[2]則結合反電動勢觀測器的估測速度與霍爾訊號來獲得連續角度並保證快速收斂。另外，許多研究結合狀態觀測器以求獲得較好的估計，如 Dalala 等人[3]運用改進型向量追蹤觀測器來彌補霍爾感測器的死區，並利用無感測器控制中常用的磁通觀測器(flux observer)來對估測角度作補償。Zhao 等人[4]建立改進型鎖相環路(enhanced PLL)來估計角度同時降低估測速度的波動。Ni 等人[5]透過設計變取樣頻率的降階觀測器來降低估測速度的抖振。Wang 等人[6]建立非平滑反饋鎖相環(non-smooth feedback PLL)架構，透過前饋消除方波型霍爾訊號的高頻諧波分量，降低估測狀態的震盪。

Liu 等人[7]則將霍爾訊號轉為旋轉向量，並應用同步頻率追蹤濾波器(synchronous frequency tracking filter)來消除高頻成分，由處理過的訊號獲得較佳的位置資訊。

線性霍爾感測器可直接輸出正比於磁場強度的電壓，理論上可精準量測出轉子位置。但也由於其精密性，使其訊號容易受馬達機械結構等不確定性干擾，使角度估測受影響。如[8]中，Jung 等人為解決感測器訊號受三次諧波干擾造成估測角度波動，結合鎖相環路與自適應帶阻濾波器(adaptive notch filter)來濾除諧波。Song 等人[9]則利用同步頻率提取器(synchronus frequency extractor)濾除諧波再直接由反正切函數計算角度。Simpkins 等人[10]應用擴展卡爾曼濾波器(enhanced Kalman filter)優化角度估測，並應用於直流無刷馬達的位置控制。Kim 等人[11]為了處理霍

(24)

爾感測器訊號非理想正弦的特性，採用對訊號建模後作定點迭代的算法估測角度位移量，並以線性馬達平台作實際驗證。同樣在線性馬達的應用，Kim 等人[12]則利用遞迴最小平方法(recursive least square method)，對霍爾訊號的幅值及偏移等作實時的線上補償。 Reigosa 等人 [13] 利用包含動態濾波環節的同步軸鎖相環 (synchronous reference frame -PLL)來估測角度，並分析實際應用中霍爾感測器的偏移、增益差異等特性造成的角度誤差。

 動力輔助控制 (Power Assist Control)

動力輔助控制欲解決問題在於，在一個有人力輸入的系統中，如何依人力輸入的大小匹配馬達的輸出力矩，以達到使人能以更小的力量推動系統的目的。其中最典型的應用是汽車方向盤的輔助轉向(EPS)系統，如[14]中，Lu 等人透過對 EPS 系統建立動態模型並設計 LQR 控制器，提升轉向時的車身穩定性及操作手感。Yin 等人[15]則是由設計可變參數 PID 的方式，增加 EPS 系統對擾動與參數不確定性的強健性與適應性。

在部分產品應用中，力矩感測器由於其價格較高、安裝不易且結構較脆弱等缺點而較不受青睞，故而基於觀測器的無力矩感測器輔助控制(FSPAC)逐漸興起。基於此想法， Hori 及 Oh 等人[16][17] 發展出一套基於擾動觀測器及阻抗控制 (impedance control)的策略，並對控制器設計原則及系統的穩定性與性能作深入的討論，最後以基於線性馬達的輔助系統作實際驗證。Hara 等人[18]為了避免輔助系統放大使用者意料外的擾動，設計一套基於頻率整形的控制架構，過濾可能造成誤動作的信號，提升使用安全性。Salvucci 等人[19]針對低摩擦力的系統，將 FSPAC 架構中的阻抗控制器改為變增益控制，增進穩定性。在醫療機器人的應用上，Ito 等人[20]利用基於位置資訊的擾動觀測及阻抗控制架構，控制馬達出力，以達到幫助護理人員從床上抬起病人並移動的目的。Chen 等人[21]則將基於觀測器的輔助控制用於復健器材，並加入被動速度控制(passive velocity control)來確保安全性。

(25)

在電力輔助自行車的應用上，Hatada 等人[22]針對踩踏板這類週期性的動作，

透過重複控制(repetitive control)方法，優化輔助控制的能量效率。Kai 等人[23]應用干擾估測器調整輔助出力，以達到對負載及坡度變化的適應性。Lee 等人[24]設計比例輔助控制器與基於模糊邏輯的輔助控制器，並透過模擬驗證模糊控制器可輸出較平穩的助力，提供較好的使用體驗。Zhu 等人[25]為了降低路況對騎行影響，

設計基於模型跟隨控制(model-following control)的力矩控制策略，在只用力矩及速度感測器的情況下，仍可對路況及干擾訊號有較好的適應性。Li 等人[26]使用帶通濾波器來估計人為力矩，並依車速決定提供輔助的比例。

在輪椅的應用上，Murakami 等人[27]利用基於模糊控制的演算法，協調兩輪個別的輔助力輸出，以達到優化整車行進軌跡的目的。Nomura 等人[28]設計基於觀測變加速度(jerk)的輔助控制架構，去除重力對擾動觀測的影響，並透過切換不同行駛模式，令使用者在推動輪椅上下坡時能獲得適當的輔助。Seki 等人[29]針對草地、地毯或上坡等阻力較大的路面，設計一套應用模糊控制的輔助策略，調整使用者放開手輪後的助力輸出，以達到讓輪椅能平順行駛的目的。Shibata 等人[30]在無力矩感測器的條件下，利用一組工作區干擾觀測器 (workspace disturbance observer)及人為加速觀測器(human acceleration observer)建立互斥協同控制架構 (repulsive compliance control)，協助輪椅使用者以穩定速度完成在輪椅上推動物體的任務。Ou 等人[31]依據李亞普諾夫理論，設計自適應力矩觀測器應用於輪椅輔助控制系統中，並由實驗驗證此方法之性能優於傳統負載觀測器。Oh 等人[32]針對輪椅在三維地形的運動設計不同的輔助控制策略，並驗證其各自可獨立運行，使操作更為人性化且安全。

 本文貢獻

由前面的回顧可知，在霍爾感測器估測角度上，已有許多不同的算法存在。本研究主要貢獻在於利用目前已安裝於手輪馬達上之線性霍爾感測器，開發一套簡

(26)

單且適用於電動輪椅應用之狀態估測算法，並應用於磁場導向控制。由於在本實驗室過去研究中，採用的控制算法主要為無感測器磁場導向控制及六步方波驅動，透過本研究的改善，可實現在更低速區間的控制，改善過去輪椅在啟動時之不穩定性，

並降低馬達運轉時之震動，提升使用者舒適度。同時狀態估測及控制精度的提升，

也讓更高階的應用功能得以較好的實現，如輪椅之路徑學習控制[39]及本文的手推輔助控制、手推計次功能等，期望能在本實驗室研究中起到繼往開來的作用。

在手推計次功能上，本實驗室過去採用的算法無法於單晶片實時執行，且辨識成功率有限。本研究透過更高精度的狀態估測與全新設計的算法來解決上述問題，

並可成功實現於輪椅控制器中。

輪椅的輔助控制(PAC)對手輪馬達電動輪椅而言則是一套全新的功能，採用更人性化操作且符合當初設計動力輪模組之預想。且本研究採無力矩感測器算法，無須增添額外成本與體積。相較於回顧中提及的研究，其驗證主要用模擬或市售動力輪模組作為測試平台，本研究則專注於將過往提出之算法應用於本實驗室設計之特殊手輪馬達，再由實驗檢驗算法性能，並針對手輪馬達電動輪椅之特性作出合適的修正。

(27)

1.3 章節摘要

本文共分為五章，其內容分述如下。

第一章緒論

說明本論文之研究動機與目的，並回顧磁場導向控制之角度及速度估測技術與動力輔助控制系統之相關文獻，以幫助了解目前的技術發展。

第二章手輪馬達電動輪椅系統架構

簡介手輪馬達電動輪椅整車系統架構，包含輪椅規格表及包括控制器在內的各項硬體，並推導直流無刷手輪馬達之電氣方程式、機械方程式與簡化模型。

第三章手輪馬達之磁場導向控制

本章先對磁場導向控制之基本觀念作一簡單介紹，再說明本研究應用霍爾感測器之狀態估測方法。

第四章手輪馬達電動輪椅之輔助控制與手推計次功能

本章先對手推過程之動態作分析歸納，以此建立手推計次演算法。後半節會對無力矩感測器之輔助控制作詳細介紹，並說明控制架構如何應用於手輪馬達動力輪模組。

第五章實驗數據與討論

本章先對實驗環境作介紹，並將前面章節介紹的算法於動力輪控制器中實作及運行，並對實驗結果與模擬之異同進行分析討論。

第六章結論與未來展望

回顧本研究主要內容，包括:應用於有感測器向量控制之狀態估測、手推計次、輔助控制等，並對運行成效作評估與總結。最後，提出未來可改善的部分及手輪馬達電動輪椅之可能發展方向，以供後人參考。

(28)

第2章手輪馬達電動輪椅之整車系統架構

本章節將簡介手輪馬達電動輪椅整車系統架構，包含輪椅規格表及包括控制器在內的各項硬體組成，並推導直流無刷手輪馬達之電氣方程式、機械方程式與簡化模型。

2.1 整車硬體架構簡介

本實驗室研發之電動輪椅主要特色為使用了本實驗室自主研發之動力輪作為致動器。所謂動力輪事實上為特殊結構之永磁無刷馬達，其核心設計理念在於將輪椅車輪與馬達轉子做結合，因其結構內藏於輪椅車輪中，外轉子部分即為輪框，且外觀上如一般輪椅結構包含手推時握持的輪圈，故又稱手輪馬達。由於其外轉子半徑較大且極數較多的特色，可以較低的電流消耗得到較大的力矩輸出，取代傳統電動輪椅以減速齒輪箱放大力矩的方式。這種直驅式的傳動方式比傳統有刷直流馬達搭配齒輪箱之傳動方式不但可減少能量耗損，更可減輕電動輪椅的整體重量與體積，達到便於搬運與收納的效果。

手輪馬達電動輪椅大致上由幾個部分構成，包含：輪椅車架、動力輪、上控制器、下控制器和電池，如圖 2-1 所示。其中，上控制器負責依搖桿命令協調兩輪輸出，包含人機介面與整車控制器；而下控制器則負責接收上控制器的命令控制動力輪的運轉，由馬達控制器與驅動器組成。動力輪、下控制器、電池結合起來可視為一套可獨立運行之動力輪馬達模組，將兩動力輪模組與上控制器配置於一般輪椅車架上便可成為手輪馬達電動輪椅(各項規格見表 2-1)。

在整車的電池方面採用了鋰鐵電池，並依照手輪馬達的規格 24 伏特(V)、功率 350 瓦特(W)，但要求此電壓規格必須大於手輪馬達之規格，因此選用 25.6V-8Ah- 5C 的電池提供整車使用。

(29)

人機介面與搖桿

鋰鐵電池

機械式煞車

雙動力輪馬達轉子 釋放機構

雙動力輪馬達定子

下控制器與驅動板

圖 2-1 手輪馬達電動輪椅整車架構圖

表 2-1 手輪馬達電動輪椅規格表長/寬/高(cm) 89/65/85 馬達功率(W) 350x2 最大時速(km/hr) 10

爬坡度 7

最大載重(kg) 100

總重/電池重(kg) 45/1

2.2 手輪馬達電動輪椅控制器介紹

手輪馬達電動輪椅之控制器分為上下兩部分，上控制器包含搖桿與觸控螢幕作為人機介面，並以 Arduino Due 作為核心處理器。在搖桿模式下，主要負責控制整車行進方向及速度，並將經差速運算解耦的左右輪速度命令分別傳給兩輪的下控制器以分別控制兩動力輪。在本研究的輔助控制應用中，由於主要人機介面

(30)

為動力輪本身而非搖桿，故上控制器僅負責兩下控制器的通訊中介，並在測試流程中顯示回傳資訊(圖 2-2)。下控制器則使用本實驗室研發之馬達驅動器，配合基於數位訊號處理器(DSP)晶片的自製控制卡作為運算核心。

圖 2-2 助推模式下控制架構圖

2.2.1 上控制器

由於上控制器隨時需要做轉速的運算、通訊以及資料的讀取，需要較高的運算效能以維持系統的順暢運行，因此選用 Arduino 眾多種類裡較高階的 Arduino Due 作為其控制的核心(圖 2-3)。而 Arduino Due 使用 ATMEL 公司所開發的 ARM SAM3X8E Cortex-M3 的晶片，共有 54 個數位輸入/輸出口，12 個數位輸入，4 個通用非同步收發傳輸器，2 個 TWI 口，擁有 84 Hz 的石英震盪器，一個 JTAG 和一個 SPI 接口。Arduino Due 之詳細規格如表 2-2。

(31)

圖 2-3 Arduino Due 表 2-2 Arduino Due 規格

Microcontroller AT91SAM3X8E Operating Voltage 3.3V Input Voltage (recommended) 7-12V

Input Voltage (limits) 6-16V

Digital I/O Pins 54 (of which 12 provide PWM output) Analog Input Pins 12

Analog Output Pins 2 (DAC) Total DC Output Current on all I/O lines 130 mA DC Current for 3.3V Pin 800 mA DC Current for 5V Pin 800 mA

Flash Memory 512 KB available

SRAM 96 KB (two banks: 64KB and 32KB)

Clock Speed 84 MHz

在人機介面部分，使用 AMEL 公司 APEM-9000 系列的類比搖桿作為主要的輸入裝置，另外配有 TFT 顯示器整合記憶卡模組作為輪椅即時資訊的顯示介面。

總體而言，整個上控制器功能包括[39]:

 系統開機與自我檢查安全機制

(32)

 搖桿輸入訊號處理(包含校正與死區運算機制)

 整車緩啟動控制

 上坡起步之電流補償

 差速控制運算

 雙輪轉速耦和控制

 與下控制器間之資料傳輸

 電池殘量、行駛速度與距離顯示

2.2.2 下控制器

輪椅下控制器採用本實驗室研發之馬達驅動器與控制卡。自製控制卡部分(圖 2-4) ，為了滿足向量控制之大量運算需求，選用德州儀器 (TEXAS INSTRUMENTS,TI)生產之 TMS F28069 作為控制晶片，整個控制卡可視為 TI 自行出品的 28069 controlCARD 的精簡縮小版。F28069 屬於 C2000 系列 DSP，專為馬達控制應用設計，具有出色的運算能力及許多特色功能。其主要特色如下:

 高效 32 位元 CPU，主頻率 80 MHz

 浮點數運算，並具有 32 位元浮點數運算加速器，與主 CPU 分離

 嵌入式儲存器，RAM 100 KB ，FLASH 256 KB，OTP ROM 2 KB

 12 位元 ADC，具有雙路採樣保持功能，16 通道，取樣率 3.46 MSPS

 3.3V 單電源，低功耗模式

 支持外設中斷

 3 個 32 位元 CPU 計時器

 8 個增強型 PWM 模塊，每個模塊獨立 16 位計時器，總共 16 個 PWM 通道

 串行接口外設，SCI、SPI、I2C、eCAN、USB2.0

(33)

 54 組可輸入濾波之獨立編程之 GPIO 腳位

 支持 JTAG 邊界掃描

圖 2-4 F28069 自製控制卡

在搖桿控制模式，下控制器中控制卡主要任務為接收上控制器傳送的左右輪轉速命令，並對動力輪進行空間向量弦波控制，其中包括了電流與轉速的閉迴路控制，詳細技術將在第三章中介紹。此外對於當前轉速等訊息亦將回傳給上控制器，以作為整車動態控制的參考。在本文輔助控制中，則包辦所有主要的運算，

僅有整車速度由上控制器處接收。

由於無刷馬達的控制牽涉到大電流的換向，故控制卡無法直接對馬達進行驅動，需有相關的電路作為中介。此外，仍有電流採樣與霍爾感測器等回授訊號在輸入控制卡前須進行預處理，一些周邊系統的管理也需要額外電路。本實驗室開發之馬達驅動板即為此而設計(圖 2-5)，除了基本馬達控制所需的三相逆變器電路，也整合了上述的各種周邊電路，基本上可滿足馬達控制中大部分的硬體需求。此外進行了縮小化與模組化，使整個下控制器模組體積減少，以達到使輪椅可收折的目的。驅動器具體包含之電路模組如下:

 三組半橋及閘極驅動器組成之三相驅動電路

 電流取樣及放大電路

 霍爾感測器訊號調整電路

 機械煞車控制電路

 電源電路(12V/5V)

(34)

 防反電動勢回充電路

 電池電源緩啟動電路

圖 2-5 自製馬達驅動板實體圖

2.3 手輪馬達之數學模型

由於電動輪椅最為核心的部分即為馬達，故此處將推導手輪馬達之數學模型，

以利後續分析及控制器設計使用。而手輪馬達動態方程式可分為電氣動態方程式和機械動態方程式，以下將分別講述。

2.3.1 手輪馬達電氣動態方程式

無刷直流手輪馬達之相電壓、相電流與各相磁通鏈均隨時間與轉子角度改變而變化，以 A 相繞組為例，由能量守恆定律可得:

v_ani_a = i_a²R_a+ i_adλ_a

dt (2-1)

其中v_an、i_a與R_a分別代表輸入 A 相之相電壓、相電流與 A 相繞線的相電阻，

(35)

λ_a則為 A 相磁通鏈。(2-1)式所代表的意義為：輸入功率等於馬達繞線銅損與磁通鍵對時間變化所消耗功率的總和，經整理後可得:

v_an = i_aR_a+dλ_a

dt (2-2)

由於馬達為複激磁結構，其包含轉子磁鐵與定子繞線，故由前述(2-1)式可知，

A 相磁通鏈即為轉子永久磁鐵於 A 相繞組所產生之磁通鍵(λ_m)，與 A 相激磁線圈的相電感(L_a)和相電流(i_a)乘積的總和，如(2-3)式所示。

λ_a = L_ai_a+ λ_m = L_ai_a+ Nϕ_m (2-3) 將(2-3)式代入(2-2)式，並經連鎖律將後兩項轉換為轉子角度的函數，經整理後可得(2-4)式。

v_an = i_aR_a+ L_adi_a

dt + ω_ei_adL_a

dθ_e+ ω_edNϕ_m

dθ_e (2-4)

上式中之前兩項為馬達之電路特性方程式，而第三、四項則為馬達的反電動勢方程式。其中第三項為馬達 A 相電感對馬達轉子位置變化量與相電流和馬達電氣轉速之乘積，但由於一般馬達相電感對轉子位置的變化量並不顯著，此項幾乎接近於零，故在本文中將忽略之，又反電動勢方程式如(2-5)式所示：

e_back = ω_edNϕ_m

dθ_e = K_eω_m (2-5) 整合上述並將(2-5)式代入(2-4)式後，整理可得(2-6)式。

v_an= i_aR_a+ L_adi_a

dt + K_eω_m (2-6) (2-6)式即為馬達 A 相繞組之電氣方程式，在省略下標後，各相繞組之電氣方程式均可以表示為：

v = iR + Ldi

dt+ K_eω_m (2-7) 故(2-7)式即為本文馬達之單相繞組的電氣方程式。

由於馬達為電感性元件，故馬達之單相電流並不會隨著輸入電壓的改變而立刻變化。另一方面，由(2-7)式可知，馬達在有限的輸入端電壓之下，反電動勢振幅

(36)

的增加將會抑制各相的相電流峰值，而由於反電動勢峰值會隨著馬達轉速的增加而上升，因此當馬達處於高速運轉時，電流峰值將會隨之下降，進而降低馬達的輸出力矩；若當馬達的轉速再提高，則反電動勢峰值將會高於電源供應電壓(V_dc)，因馬達反電動勢與供應電壓的極性相反，故會產生電流往電源端逆流的現象，此時馬達之輸出力矩將急遽下降，使轉速無法再提高。故可知馬達的電源供應電壓與反電動勢常數大小將會影響馬達的最高轉速。

因本文中手輪馬達為三相 Y 接之無刷直流馬達，輸入的三相電流(i_a、i_b、i_c)與馬達三相反電動勢波形(e_a、e_b、e_c)皆為正弦波，故可將(2-7)式展開成三維之向量矩陣，整理如(2-8)式所示。

[ v_an v_bn v_cn] = [

R_a 0 0 0 R_b 0 0 0 R_c

] ∙ [ i_a i_b i_c

] + d dt[

L_a 0 0 0 L_b 0 0 0 L_c

] ∙ [ i_a i_b i_c

] + [ e_a e_b e_c

] (2-8)

因手輪馬達之三相的反電動勢波形為各差 120 度電氣角的正弦波，故三相的反電動勢可以定義為(2-9)式、(2-10)式與(2-11)式。

e_a = ω_mK_esin(θ_e) (2-9) e_b= ω_mK_esin(θ_e−2π

3 ) (2-10)

e_c = ω_mK_esin(θ_e−4π

3) (2-11)

將(2-9)式、(2-10)式與(2-11)式代入(2-8)式，並且經拉普拉斯轉換 (Laplace Transform)後，整理可得(2-12)式。故(2-12)式即為無刷直流手輪馬達三相 Y 接形式下的馬達三相電氣方程式。

[ v_an v_bn v_cn] = [

L_as + R_a 0 0 0 L_bs + R_b 0 0 0 L_cs + R_c

] [ i_a i_b i_c

] + ω_mK_e [

sin(θ_e) sin(θ_e−2π

3 ) sin(θ_e−4π

3 )]

(2-12)

2.3.2 手輪馬達機械動態方程式

(37)

手輪馬達的機械動態方程式可藉由對其動力學模型推導而得，而手輪馬達動力學模型則如圖 2-6 所示。藉由動力學模型對馬達 Z 軸作推導可以發現：等號左邊馬達輸出力矩(T_e)與馬達負載力矩(T_L)的總和將會相等於等號右邊，馬達轉動慣量(J_w)與馬達機械角加速度(ω̇_m)乘積和黏滯摩擦係數(B_m)與馬達機械角速度(ω_m) 乘積的總和，整理如(2-13)式所示。

圖 2-6 手輪馬達動力學模型示意圖

T_e− T_L= J_wω̇_m+ B_mω_m (2-13) (2-13)式經拉氏轉換後可得(2-14)式。

T_e− T_L = J_wω_ms + B_mω_m (2-14) (2-14)式即為手輪馬達之機械動態方程式，再者，由於手輪馬達為三相 Y 接之無刷直流馬達，故其輸出力矩為三相相電流分別乘以三相力矩常數(K_ta、K_tb、K_tc) 的總和，經整理後如(2-15)式所示。

T_e = i_aK_ta+ i_bK_tb+ i_cK_tc (2-15) 再根據機電能量轉換守恆原理，馬達的輸入電能與輸出機械能將會相同，如 (2-16)式所示，等式左邊為輸出機械功率，由馬達輸出力矩(T_e)與轉速(ω_m)相乘得到，等式右邊則是輸入電功率，由反電動勢(e_back)與輸入電流(I)相乘得知。

T_eω_m= e_backI (2-16) 又力矩為力矩常數(K_t)乘以電流，如(2-17)式所示：

T_e= K_tI (2-17)

(38)

因此將(2-17)式與(2-5)式代入(2-16)式中並加以整理後即可得(2-18)式。

K_t = K_e (2-18)

由(2-18)式可以發現，馬達之力矩常數與反電動勢常數雖然單位不同，但兩者皆有相同的數值大小，其中力矩常數的單位為力矩除以輸入電流(^N∙m

A )，而反電動勢常數的單位則為電壓除以馬達轉速( ^Volt

rad sec⁄ )。再由手輪馬達之三相反電動勢方程式

(2-9)式、(2-10)式與(2-11)式以及(2-18)式中力矩常數與反電動勢常數之關係，便可知手輪馬達的三相力矩常數分別為：

K_ta= K_esin(θ_e) = K_tsin(θ_e) (2-19) K_tb = K_esin (θ_e−2π

3) = K_tsin(θ_e−2π

3 ) (2-20) K_tc = K_esin (θ_e−4π

3 ) = K_tsin(θ_e−4π

3) (2-21) 再將(2-19)式、(2-20)式與(2-21)式代入(2-15)式，經整理後可得馬達輸出力矩方程式，

如(2-22)式所示。

T_e = i_aK_tsin(θ_e) + i_bK_tsin (θ_e−2π

3 ) + i_cK_tsin(θ_e−4π

3) (2-22)

(39)

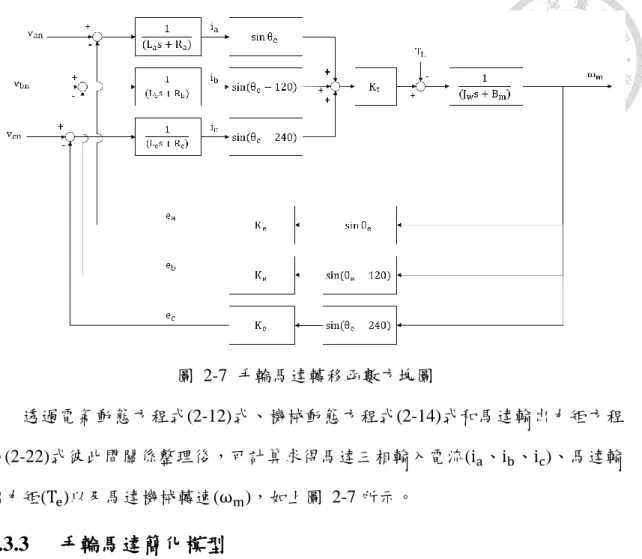
圖 2-7 手輪馬達轉移函數方塊圖

透過電氣動態方程式(2-12)式、機械動態方程式(2-14)式和馬達輸出力矩方程式(2-22)式彼此間關係整理後，可計算求得馬達三相輸入電流(i_a、i_b、i_c)、馬達輸出力矩(T_e)以及馬達機械轉速(ω_m)，如上圖 2-7 所示。

2.3.3 手輪馬達簡化模型

一般來講，經由一些對直流無刷馬達的簡化與條件假設，可以將三相無刷直流馬達模型簡化為直流馬達模式，藉此方便掌握其伺服動態反應與簡化馬達控制器設計。首先，假設輸入手輪馬達之三相相電流波形為與反電動勢波形完全吻合之三相正弦波，如此三相相電流則可以表示為：

i_a = I sin(θ_e) (2-23) i_b = I sin (θ_e−2π

3) (2-24)

i_c = I sin (θ_e−4π

3 ) (2-25)

其中I為輸入馬達之三相相電流振幅，將(2-23)式、(2-24)式與(2-25)式代入(2-22) 式，整理後可得(2-26)式。

T_e = IK_t(sin(θ_e))²+ IK_t(sin (θ_e−2π 3 ))

2

+ IK_t(sin (θ_e−4π 3))

2

(2-26)

(40)

將(2-26)式中iK_t提出，整理為下式：

T_e = IK_t[(sin(θ_e))²+ (sin (θ_e−2π 3))

2

+ (sin (θ_e−4π 3))

2

] (2-27) 觀察(2-27)式，將括號內之三角函數經由差角公式作計算，整理後可得(2-28)式。

T_e =3

2K_tI (2-28)

(2-28)式即為手輪馬達簡化模型之馬達力矩方程式，當輸入馬達之三相相電流波形為與三相反電動勢弦波波形完全相同時，則馬達之輸出力矩可以簡化為輸入三相相電流峰值與馬達力矩常數乘積的 1.5 倍，而無須考慮馬達位置的影響。馬達之三相相電流峰值則可以藉由輸入馬達之相電壓峰值(v_phase)與馬達反電動勢峰值 (K_e∙ ω_m)相減，並透過馬達電氣方程式的運算而得，如(2-29)式所示。

I = v_phase− K_eω_m

Ls + R (2-29)

(2-29)式假設馬達相電阻為R_a = R_b = R_c = R_s，馬達相電感為L_a = L_b = L_c = L_s。當輸入馬達三相端電壓為空間向量弦波輸入時，則馬達三相電壓為輸入電源電壓與振幅調變比的乘積(V_dc∙ M_a)的¹

√3倍，代入(2-29)式整理後可得(2-30)式。

I =

V_dcM_a

√3 − K_eω_m Ls + R

(2-30)

(2-30)式即為手輪馬達簡化模型的電氣動態方程式，將其與簡化模型之馬達力矩方程式(2-28)式以及前一小節所推導之手輪馬達機械動態方程式(2-14)式經整理總和後，即可得到手輪馬達簡化模型之系統方塊圖，如圖 2-8 所示。

(41)

圖 2-8 手輪馬達簡化模型轉移函數方塊圖

上圖中各項馬達參數整理如表 2-3。

表 2-3 手輪馬達模型參數[38]

機械參數單位

轉動慣量(Jw) 0.44 kg ∙ m² 黏滯摩擦係數(Bm) 0.00013 N ∙ m ∙ sec

rad 力矩常數(Kt) 1.388 N ∙ m

A

電氣參數單位

相電阻(R) 0.624 Ω 相電感(L) 0.001016 H 反電動勢常數(Ke) 1.388 volt ∙ sec

rad

2.4 整車動態模型[44]

由於輪椅的左右兩輪受中心車架耦合，因此左右任一手輪馬達之出力皆會同時影響兩輪的運動狀態。故以雙輪轉速比的控制方式來改變輪椅動態，首先必須先分析電動輪椅中兩手輪馬達之出力與輪椅運動狀態間的響應關係，並建立輪椅的數學動態模型以求得系統轉移函數。

(42)

當輪椅左右兩輪皆與地面於純滾動狀態之下，則左輪之輪心線速度V_L可以表示為車輪半徑與左輪之角速度ω_L的乘積；而右輪之輪心線速度V_R亦可以表示為車輪半徑與右輪之角速度ω_R的乘積；如式(2-31)與式(2-32)所示。

𝑣_𝐿 = 𝑅_𝑤 ∙ 𝜔_𝐿 (2-31) 𝑣_𝑅 = 𝑅_𝑤 ∙ 𝜔_𝑅 (2-32) 由於電動輪椅屬於二維平面運動，故共具有兩個方向的自由度，若將座標原點訂於兩輪心之中點 C，如此則可以定義出電動輪椅系統對於幾何中心 C 之車體質量M_C與車體轉動慣量J_C，如圖 2-9 之車架自由體圖所示。而電動輪之車體線速度V_C 與車體轉速度ϕ̇則可以藉由車體寬度W與左右兩輪線速度間的幾何關係求得，整理如式(2-33)、式(2-34)所示。

𝑣_𝑐 = 𝑣_𝐿+ 𝑣_𝑅

2 (2-33)

𝜙̇ = 𝑣_𝐿− 𝑣_𝑅

𝑊 (2-34)

由式(2-33)與式(2-34)可以發現，輪椅之車體線速度與車體轉速度皆可以表示為左右兩輪轉速（ω_L、ω_R）的函數。

W

R_w

R_w V

R



L



 .

Left Wheel

Right Wheel



X Y

C

圖 2-9 車架自由體圖

(43)

為了求得車體之動態方程式，我們必須先計算電動輪車體之拉格朗日量（ℒ），而拉格朗日量的定義為動能（T）與勢能（E）的相減，如式(2-35)所示。

ℒ = 𝑇 − 𝐸 (2-35)

電動輪椅之車體動能可以表示為車體線性移動之動能、左右兩輪之旋轉動能與輪椅車體本身之旋轉動能的總和；由於我們假設電動輪椅處於一水平面上移動，

沒有高度上的變化，故知輪椅車體之勢能可以表示為零，輪椅車體之動能與勢能整理後如式(2-36)與式(2-37)所示。

𝑇 = 1

2𝑀_𝑐𝑣_𝑐²+ 1

2𝐽_𝑐𝜙̇²+ 1

2𝐽_𝑤(𝜔_𝑅² + 𝜔_𝐿²) (2-36)

𝐸 = 0 (2-37)

將式(2-36)與式(2-37)代入式(2-35)，整理後得式(2-38)。

ℒ = 1

2𝑀_𝑐𝑣_𝑐²+ 1

2𝐽_𝑐𝜙̇²+ 1

2𝐽_𝑤(𝜔_𝑅² + 𝜔_𝐿²) (2-38) 式(2-38)即為電動輪椅車體之拉格朗日量，由於本文欲以左右兩輪之轉動角度

（θ_L、θ_R）做為系統的廣義參考座標，故將式(2-33)與式(2-34)中車體線速度與車體轉速度對左右兩輪轉速的關係式代入式(2-38)中，整理後可得式(2-39)。

ℒ = 1

2𝑀_𝑐[𝑅_𝑤

2 (𝜔_𝑅+ 𝜔_𝐿)]

2

+ 1 2𝐽_𝑐[𝑅_𝑤

𝑊 (𝜔_𝑅 − 𝜔_𝐿)]

2

+1

2𝐽_𝑤(𝜔_𝑅² + 𝜔_𝐿²)

(2-39)

由於本文中定義左右兩輪之轉動角度為電動輪椅車體系統之廣義座標，故可以將電動輪椅車體之拉格朗日方程式（Lagrangian Equation）表示為式(2-40)。

{

𝜏_𝑅 = 𝑑 𝑑𝑡( 𝜕ℒ

𝜕𝜔_𝑅) − 𝜕ℒ

𝜕𝜃_𝑅 𝜏_𝐿 = 𝑑

𝑑𝑡(𝜕ℒ

𝜕𝜔_𝐿) − 𝜕ℒ

𝜕𝜃_𝐿

(2-40)

(44)

式(2-40)中，τ_R即為右輪所受之外加力矩，τ_L即為左輪所受之外加力矩。將式 (2-39)代入式(2-40)，經整理後可得式(2-41)。

{

𝜏_𝑅 = 𝑅_𝑤² [(𝑀_𝑐 4 + 𝐽_𝑐

𝑊² + 𝐽_𝑤

𝑅_𝑤²) 𝜔̇_𝑅+ (𝑀_𝑐 4 − 𝐽_𝑐

𝑊²) 𝜔̇_𝐿] 𝜏_𝐿 = 𝑅_𝑤² [(𝑀_𝑐

4 − 𝐽_𝑐

𝑊²) 𝜔̇_𝑅+ (𝑀_𝑐 4 + 𝐽_𝑐

𝑊²+ 𝐽_𝑤 𝑅_𝑤²) 𝜔̇_𝐿]

(2-41)

可以將式(2-41)整理為一二維矩陣，如式(2-42)所示。

[τ_R

τ_L] = R²_w [

M_c 4 + J_c

W²+ J_w R_w²

M_c 4 − J_c

W² M_c

4 − J_c W²

M_c 4 + J_c

W²+ J_w R_w²]

[ω̇_R

ω̇_L] = M_θ[ω̇_R

ω̇_L] (2-42)

式(2-42)中，𝜃̈_𝐿即為左輪角加速度，𝜃̈_𝑅即為右輪角加速度。將式(2-42)中之M_θ 經反置運算後，可以得式(2-43)。

M_θ⁻¹[τ_R

τ_L] = [ω̇_R

ω̇_L] (2-43) 式(2-43)即為本文之電動輪椅車體動態方程式，而輸入車體動態方程式之左右兩輪外加力矩即為左右兩輪之馬達輸出力矩（T_L、T_R）與左右兩輪之負載力矩（T_LD、 T_RD）的總和，又由於輸出力矩與負載力矩的極性相反，故左右兩輪之輸出力矩為正，左右兩輪之負載力矩則為負。整理後如式(2-44)所示。

{𝜏_𝑅 = 𝑇_𝑅− 𝑇_𝑅𝐷

𝜏_𝐿 = 𝑇_𝐿− 𝑇_𝐿𝐷 (2-44) 上述之電動輪椅車體動態方程式(式(2-43))與外加力矩方程式(式(2-44))，經整理總和後，即可得到手輪馬達式電動輪椅之系統方塊圖，如圖 2-10 所示。

(45)

R Ls 

1

2 3K _e

1

M ^s

1 Ke

R Ls 

1

2 3K _e

Ke

s 1 TR

TL

TRD

TLD

VRDC

VLDC

+-

+- +-

+-



R



L

圖 2-10 整車轉移函數方塊圖

(46)

第3章手輪馬達之力矩控制

馬達驅動的基本原理為，透過控制電流在馬達內部線圈中的流動，來產生旋轉磁場，以產生電磁轉矩使馬達轉動。改變電流流向的動作稱為換向(commutation)，

在傳統直流馬達中，此動作由馬達內部的電刷結構實現，當電機旋轉一角度，各線圈與電源導線間的接點便會交替改變，以此實現機械式的換向。此種作法雖然便利，

電刷的磨損也使得馬達壽命降低，其他如電刷造成的能量損耗與噪音也是傳統直流有刷馬達的主要問題。在本研究使用的直流無刷馬達中，由於不存在電刷結構，

也就免除了上述的問題，使馬達更為環保、耐用。但在換向的處理上，就必須使用較為複雜的控制，而不能直接接電使用。以一般三相馬達而言，須由三組半橋電路組成的驅動器，配合微控制器來完成換向的動作，其結構如下圖 3-1。

DRIVER 3-phase MOTOR F28069 MCU

CPU

A ePWM-1

B A ePWM-2

B A ePWM-3

B

SA

SB

SC

Sa

Sb

Sc

圖 3-1 無刷馬達基礎控制架構圖

在驅動器中包含六個開關元件，分別做為馬達三相線圈的上、下橋，由微控制器輸出的開關訊號控制。當上橋開啟時，電流由直流電源 VDC側流入線圈。而當下

(47)

橋開啟時則反之，電流由馬達側流出到地。故分別控制三組線圈的上、下橋開關即可控制電流由哪組線圈流入馬達，又由哪組線圈流出，實現了電流的換向。

如何換向的問題解決後，剩下的問題就是如何決定各個時刻各組線圈的電流方向。我們知道換向的時機對於馬達的運作是相當關鍵的，這是由於只有當定子磁場與轉子磁場間存在夾角，也就是外積不為零時才能產生電磁力矩。在直流無刷馬達中，轉子的磁場由永久磁鐵提供，我們必須控制定子線圈電流產生旋轉磁場來帶動轉子，故換向時機與轉子當前位置直接相關。為了量測轉子位置，霍爾感測器是一種常見的解決方案，其具體細節將於 3.2 介紹。假設已知轉子位置，則需要將電流注入相應位置的線圈，來產生領先轉子磁場一定角度的定子磁場。由外積性質可知，在兩者相差 90 度時，產生的轉矩最大，故如何將定子與轉子磁場夾角保持在此角度將是整個馬達驅動控制的核心。若要改變馬達力矩與轉速，只需在維持上述條件的同時，改變在馬達中流動電流的大小即可，此與有刷直流馬達的控制是相同的。為了達成這個目標，並實現對力矩的精確控制，磁場導向控制是近年來較為流行的作法。本章將先對磁場導向控制之基本觀念作一簡單介紹，再說明本研究如何應用線性霍爾感測器估測諸如轉子角度、轉速等控制相關參數，並將其運用於手輪馬達的控制中，使得控制的效能得到提升。

3.1 磁場導向控制概述

由於三相馬達結構的複雜性，要達到同時對三相電流大小與流向的精確控制，

事實上是極為困難的。在常見的六步方波控制中，並沒有對電流的控制環節，而是根據三相數位霍爾感測器感測到的磁極資訊，粗略的打出方波電壓。此做法與傳統有刷馬達的驅動波型是較為相似的，但在反電動勢波型為弦波的馬達中，此做法將會造成電能的浪費與輸出轉矩的波動。為了解決力矩控制問題，勢必要對定子電流產生的磁通做更精確的控制，此時產生了兩派做法: 磁場導向控制(FOC)與直接轉矩控制(DTC)，這兩者的共同處是都具有電流的採樣與回授控制環節。直接轉矩控

(48)

制利用電壓與電流的回授資訊，估測轉矩與磁通，並以類似開關控制(bang-bang control)的方式來達到對轉矩的直接控制。磁場導向方式又稱向量控制，其以旋轉向量的方式看待定子磁通，並由此實現了對磁通與力矩等問題的解耦處理。向量控制的核心為座標變換，其最大意義在於簡化了原本三相馬達複雜的時變系統特性，

而將其簡化為兩組非時變系統的電流控制問題，以下將針對其中技術分別做詳細的介紹。

3.1.1 座標變換

欲驅動三相馬達，需先產生旋轉磁場，而產生均勻的旋轉磁場需要三相電流波型為弦波。以反電動勢波型為弦波的馬達而言，欲達成上述目的則需產生三組相差 120 度的弦波電壓訊號。並且為了達到對轉矩的穩定控制，三組電壓之幅值與相位須根據三相電流即時做出調整。要同時達成這些目標需要做到大量複雜的運算，且由於系統時變的特性使得控制較為困難。向量控制的核心即為使用座標變換來將三相系統做簡化，使其近似於單相直流馬達的控制。其中使用分別使用了兩種坐標系，以下分別介紹。

圖 3-2 Clarke 變換示意圖

在二維空間中，只要有兩組正交向量便可描述空間中所有向量，此即二軸坐標系的概念。而馬達的三相定子線圈系統則可視為三軸的坐標系，坐標軸間相差