第參章 研究方法

第參章 研究方法

本研究採取質的研究，針對使用 GSP 為解題輔助工具與以紙筆為解題工具之 解題歷程進行比較。資料分析以口語資料為主，輔以部分敘述統計資料，作為說明。

本章有六節，分別介紹研究對象、研究工具、研究設計、研究流程、資料收集與資 料分析。

第一節 研究對象

本研究對象為四位高二學生，兩位熟練操作動態軟體 GSP 的高二學生，兩位 原先不熟悉GSP，但經過 GSP 兩個多月的練習之後能以 GSP 為解題的輔助工具，

選擇這四位高二學生作為本研究的受測者的原因有三：一、幾何能力成熟：高二學 生需選修幾何課程，在該課程中，曾複習平面幾何的性質，並針對各種幾何方法進 行統整。一般學生在高一上時學習解析幾何的基本概念，如：座標化、介紹直線方 程式等；在高一下學習三角學，其中正弦定理與餘弦定理能更進一步描繪三角形中 角度與長度之間的關係；高二上學習向量幾何，向量觀點能提供共線與共點問題更 進一步的描述。因此，相較於其他年級而言，高二學生能擁有較完整的幾何訓練，

較不會受制於幾何知識，且這四位學生數學成績均在全校自然組前10%，應具備成 熟的幾何能力；二、具探究特質：每位受測者具有數學科展經驗，表達能力、探究 能力與解題過程中所展現的毅力，均受到高度肯定；三、研究者和受測者有長期交 流討論的習慣，表現不生怯，能表達出解題過程中的想法。

研究者和四位受測者均有長期互動交流的經驗，以下即為研究者對於四位受測

參與本研究熟練 GSP 的學生有甲生與乙生兩位，其中甲生來自研究者任教的 北縣A 校，甲生在參與科展活動中接觸到 GSP，至今有使用 GSP 一年半的經驗，

他所參與科展主題和幾何解題無關，但研究過程中曾利用 GSP 繪製八十多個不同 種類的幾何圖形(圖 3-1-1 即為其中一例)，因此除了熟練 GSP 基本作圖技能外，還 能利用旋轉、對稱、鏡射與平移等特殊作圖技巧，完成複雜的繪圖任務且迅速確實。

甲生循規蹈矩的個性亦表現在作業活動上，例如以書面呈現解題結果時，均能詳述 解題過程與理由，不會疏漏或跳躍且字跡工整、卷面清晰。

圖3-1- 1：甲生科展作品中利用 GSP 所繪製的圖

乙生來自北縣B 高中數理資優班，專題討論選修數學，並參與科展活動，研究 過程中需要利用GSP 作為探究弧度、弦長與面積關係的工具，有使用 GSP 一年的 經驗。乙生解題時很有毅力且長於化簡計算，一般學生可能會放棄或是尋找另類解 法的化簡與求值問題，他能不畏懼複雜算式而執行冗長的化簡工作，是一個原則上 不放棄解題的人，除非已經嘗試完所有熟悉的技巧且臨時想不到的情況下，才會迫 於無奈而放棄解題 (訪談資料：520070~520074，2007,4,29)。

研究初期以紙筆作答的學生為丙生與丁生兩位，兩生皆來北市C 校，丙生為跳 級生，心思細膩，考試作答有檢查的習慣，邏輯推理能力強，有毅力，曾經多次花 一個小時以上嘗試多種觀點解決一個數學問題而不捨，亦有多次和研究者討論至晚 上十一點半而熱情不減。一般學生對於一年前所學過的數學內容可能感到生疏，丙 生則無這個現象，多次討論過程中，丙生能夠流暢使用高一教過的三角學知識於解

丁生和丙生高一同班，數學成績伯仲之間，丁生聰穎，反應迅速確實，常常提 出令人意外的解題方法，能夠在短時間內，產生數個不同的想法並應用於解題過程 中。他喜歡享受思考問題的樂趣，每次和研究者討論問題時，僅要求指引大方向，

細節部分則自行發揮。丁生特別勇於挑戰難題，對於各種教學資源所提供的挑戰題 則倍感興趣，並常以此和研究者討論。

這四位學生均通過作者所編定的《GSP 操作檢定》(請見附錄一)，其操作熟練 度經作者與另一位任教於同一所學校的GSP 專家(曾多次開授中學數學教師 GSP 研 習課程)檢定之後認可。

第二節 研究工具

本研究共發展並採用兩種評量工具，分別為《幾何評量測驗》及《GSP 操作檢 定工具》。茲說明如下：

一、幾何評量測驗

《幾何評量測驗》是本研究之主要工具，內容為四道幾何問題。探討解題時使 用GSP 與不使用 GSP 之解題歷程有何不同。本研究之四道幾何問題為：

1.銳角 ABC△ 中， AH 是

BC

BC

分線，若 D,E 分別是 AB ,

AC

AC

AHD= AHE

∠ ∠

2.各邊相等的凸五邊形 ABCDE 中，若 ABC=2∠ ∠DBE，求 ABC=∠ ？

3.令 AD 、 BE 、

CF

△ 及△CDE的垂心。試證：△KMN≅ DEF△ 。

4.正三角形 ABC 中內部一點 P，若AP²+PB² =CP²，求∠APB=？ (一).設計理念

幾何問題大致可分成求解題與求證題(Polya, 1957)，因此在問題類型上，各設 計兩個問題。其中GSP 具有計算、測量與動態拖曳之特性能夠預知求解題的答案，

因此特別設計兩個求解題(2,4 題)，藉此觀察在預知答案的情況下如何影響解題歷

個需要精確作圖的問題(1,3 題)。第 1 題有兩個部分可能需要精確作圖，H 與 T 的位 置可能很接近(理論上當 AB 與 AC 相等時，這兩點是重合的)，因此 HD、TD、HE 與TE 四條線段可能產生視覺上的干擾，造成解題困難。同時，題目中的 A,D,H,T,E 五點共圓，在徒手畫圓可能不夠精準，導致連結錯誤訊息。第3 題涉及多組垂心之 間的連線，圖中亦有多組交疊的平行線與平行四邊形，將造成視覺上的干擾。因此 擬藉此觀察是否使用GSP 為解題工具的解題者較容易表徵問題。

解題過程中使用軟體，可能會造成雙刃效應：透過動態幾何軟體雖能作出滿足 題意的例子，有助於理解題目所呈現的幾何關係(Hadas et al., 2000)，但可能因此輕 易看出數學性質，扼殺證明的需求或是發展證明的學習機會(Laborde, 2000)，動態 幾何軟體直接呈現結果，對於推理過程不見得有幫助(Hanna, 1995)。因此設計第 2 題與第 4 題，擬藉此觀察解題者利用 GSP 軟體所提供的測量、計算與拖曳工具得 知答案，在預知答案的情況下，如何重新形成問題表徵、展開解題與證明活動。

GSP 具有探索、實驗等功能，在容易作圖的前提下，解題者才能享受 GSP 所 帶來的便利性。Nunokawa(1994)的研究提出一個值得深思的問題：在難以精確作圖 的情況下，解題者會不會從其他方向尋找表徵問題的方式呢？為了配合本研究受測 者操作GSP 的熟練程度，讓熟練操作 GSP 的受測者施測難度較高的作圖問題。在 研究者與兩位學科專家建立內容效度時，專家們均同意：在動態幾何環境中或是以 尺規作圖的方式下畫一個五邊皆等長的凸五邊形，對於受測者而言均不是件容易的 事，因此將作圖難度高的求解題編定為第2 題，擬藉此觀察受測者如何處理這個燙 手山芋。

此外，為了避免受測者直接應用現有知識解題，將題目視為例行性問題，失去 解題的真正意義，在研究者與兩位學科專家一同建立內容效度時，專家們均同意本 研究之四個問題的難度偏高，解題者需要利用知識與工具探索問題情境，才能找出 隱藏在題意之後的問題結構，如：第1 題的內在結構是五點共圓，第 3 題的內在結

構是平行六邊形(見表 3-2-1)，想藉此觀察是否使用 GSP 為解題工具的解題者較容 易發現問題結構。茲將問題、設計理念與可能涉及的解題關鍵，整理如表3-2-1：

表3-2-1：幾何評量測驗設計表整

題號 類型 目的 問題結構 和問題結構有關的關鍵圖形 1 證明 精確作圖 發現五點共圓，並

從對同弧的觀點證 明角度相等。

D

E

H T

B C

A

2 求解 預知答案 需要重新表徵問 題，才能發現關鍵 的正三角形與平行 四邊形。

3 證明 精確作圖 從複雜圖形中找出 關鍵的平行六邊 形，進而證明全 等。

H

M

N K

F

E

D C

B

A

4 求解 預知答案 透過旋轉或對稱的 觀點求角度

P'

A

P C

B

b

a

a c

c b

b

a c

E F

A P B

C

E D

H T

A

B

C

(二).編碼原則

為了更進一步研究解題歷程，對於各種解題行為的屬性進行歸類，進行資料分 析，將根據第二章第四節的討論以及參考Carlson 及 Bloom(2005)的研究中所彙整 的解題屬性分類表，製作解題歷程的編碼原則以及細部行為歸類表，作為研究之用 (請見表 3-2-2~表 3-2-5)。

表3-2-2：表徵面向的編碼原則與舉例

編碼 定義 舉例

1-1.草圖 以繪圖的方式重新 表達完整或部分的 題目資訊

以圖呈現四點共圓

1-2.符號關係 利用等式、不等式 或方程式等數學算 式表示題目的資訊

透過命名與符號運算後得到

∠AHD= AHE∠ 都為α+β－90∘

1-3.演繹陳述 利用理論、定理(律) 表達、轉換或發現 題目的資訊

AET= ADT

∠ ∠ 都是90∘，對角互補，因 此AEDT 四點共圓且 AT 為直徑

表3-2-3：表徵轉換面向的編碼原則與舉例

編碼 定義 舉例

2-1 表 徵 的 轉 換

2-1-1 透 過 數

學或語意關係 的等價變換

表徵A 轉換成表徵 A’

而A 與 A’是數學等價

1.把文字敘述換成圖 2.表徵 A： 1= 2∠ ∠

1+ 3=90, 2+ 4=90

∠ ∠ ∠ ∠ (題意)

→ 3= 4 ∠ ∠ (表徵A’) 2-1-2

發現新事實後 的重整

原有表徵A 加入新事 實之後成為表徵B

A,D,H,T 四點共圓(表徵 A) A,D,H,E 四點共圓(新事實)

→A,D,E,H,T 五點共圓(表徵 B)

2-1-3 突變

表徵 A 轉換為表徵 B，但表徵 B 的轉換基

礎並不是源自表徵A 表徵A：

表徵B：

表徵A 轉換成表徵 B 是根據過去經 驗而非前兩類方式。

表3-2-4：解題策略執行面向的編碼原則與舉例

編碼 定義 舉例

2-2.

解 題 策 略 的 執 行

啟 思 策 略

2-2-1 嘗試錯誤

沒有明確目標下，摸索題 意

我就隨便試試看啊!

2-2-2 檢驗特例

以滿足題意之部分集合 中元素檢驗命題真確性

先以正三角形來代替一般 三角形來看這題吧 2-2-3

猜測

在某些可能的策略或目 標中擇一實施或檢驗

我猜答案150 度吧 從眾多可能答案中挑選 2-2-4

使用專家知識

直接使用例行性演算程 序而直接獲得答案

轉60 度後，再用全等與畢 氏定理，就是答案了 2-2-5

演繹邏輯

利用A(大前提)與 B(小前 提)，得到 C(結論)

ATD= ATE(

∠ ∠ 大 前 提) 且 ATDE 四點共圓(小前 提)則弧 AD=弧 AE(結論) 2-2-6

從答案逆推

若 B 可推得 A 情況下，

先假設 A 成立，判斷 B 是否成立

如果他們真的全等的話，

則這三角形的三組對邊一 定都要一樣

符 號 策 略

2-2-7a 命名

以文字符號作為幾何物 件的稱號或運算的基礎

令這個角叫做α

2-2-7b 標記

在特定位置上以文字符 號做註記以便辨識

將兩個相同大小的角都標 上○的記號

2-2-7c 運算

以文字符號作為化簡與 計算的工具

∠ ＋2θ=360⇒ A θ=180－1/2 A∠

表3-2-5：解題策略與執行面向的編碼原則與舉例(續)

編碼 定義 舉例

2-2.

解 題 策 略 的 執 行

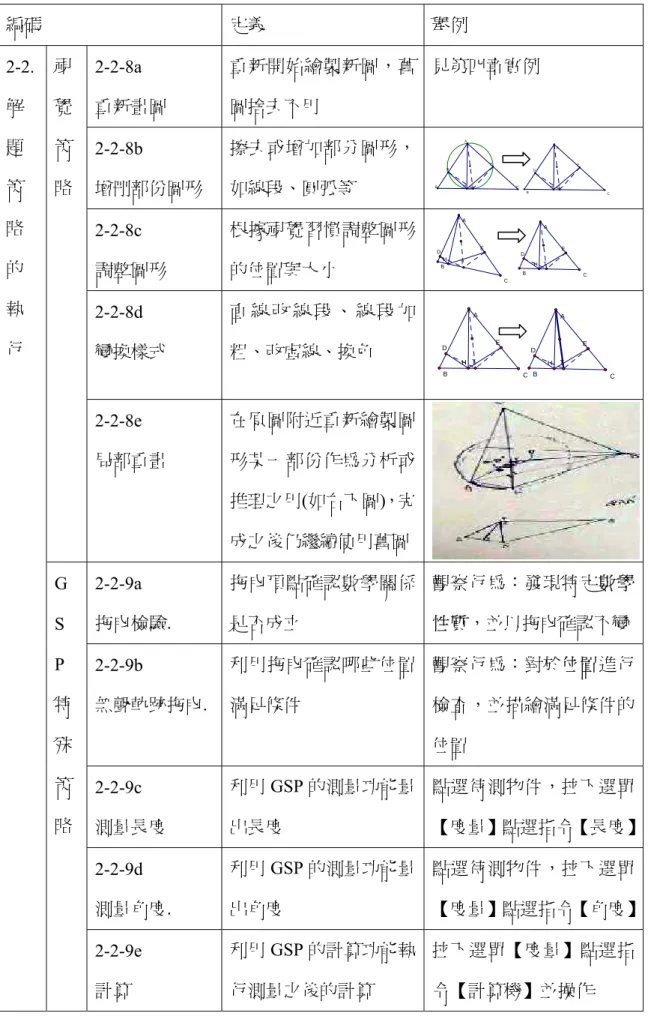
視 覺 策 略

2-2-8a 重新畫圖

重新開始繪製新圖，舊 圖捨去不用

見第四章實例

2-2-8b

增刪部份圖形

擦去或增加部分圖形，

如線段、圓弧等 2-2-8c

調整圖形

根據視覺習慣調整圖形 的位置與大小

2-2-8d 變換樣式

直 線 改 線 段 、 線 段 加 粗、改虛線、換色

2-2-8e 局部重畫

在原圖附近重新繪製圖 形某一部份作為分析或 推理之用(如右下圖)，完 成之後仍繼續使用舊圖 G

S P 特 殊 策 略

2-2-9a 拖曳檢驗.

拖曳頂點確認數學關係 是否成立

觀察行為：發現特定數學 性質，並以拖曳確認不變 2-2-9b

無聲軌跡拖曳.

利用拖曳確認哪些位置 滿足條件

觀察行為：對於位置進行 檢查，並描繪滿足條件的 位置

2-2-9c 測量長度

利用GSP 的測量功能量 出長度

點選待測物件，拉下選單

【度量】點選指令【長度】

2-2-9d 測量角度.

利用GSP 的測量功能量 出角度

點選待測物件，拉下選單

【度量】點選指令【角度】

H

D E

T H

D E

T A

C B

B C

A H D

E

H T D

E

B T C

A

A

B C

H

D E

T H

D E

T

B C

A A

B C

表3-2-6：反思面向的編碼原則與舉例

行為類別 定義 舉例

3-1.

覺 知

3-1-1.

個人覺知

解題者個人對於解題的知 識或經驗

其實，我不大會解幾何題！

3-1-2.

任務覺知

解題者對於解題任務有關 的知識或經驗

通常中線問題都是延長中線 的三分之一

3-1-3.

策略覺知

解題者對於解題策略的知 識或經驗

再多的例子也不足以證明啊 (對證明策略的覺知)

3-2.

評 估

3-2-1.

結果預見

對於解題執行過程或結果 的預先判斷

這些角度好像都不太好算

3-2-2.

策略比較

對於兩種或兩種以上的策 略提出比較

我覺得乘開和代公式都差不 多快

3-2-3.

質疑

對於結果產生懷疑 H 點真的在圓上嗎？

3-2-4.

回顧

針對過往的策略或過程提 出評論

為什麼我剛剛沒有發現角平 分線性質應用在這題上？

3-3.

校 正

3-3-1.發生 偵錯事件

明確指出錯誤，並改正 就是這裡，交點畫錯了！

3-3-2.嘗試 另類解法

解題成功之後，嘗試其他 解法

這題好像也可以從旋轉來做

3-3-3.重新 改變作法

經過評估之後，解題方法 的改變

光 用 角 度 ， 應 該 沒 辦 法(評 估)，應該換新方法

(三).信度與效度

專家效度：本工具請具有三十年教學經驗的K 老師與九年教學經驗的 W 老師 建立專家效度，兩位老師僅以紙筆方式完成這四個問題的解答，針對每一題提出多 種可能的解法以及假想學生可能遭遇的困難與關鍵步驟，分別提出建議，原則同意 表 3-2-1 的內容。兩位專家認為對於一般高二學生而言，題目偏難，但本研究之四 名學生具有特殊性，且在 GSP 的協助下，難度可能有所改變，因此同意研究者的 設計。進行本研究前，已挑選兩名數學程度相近的高二學生(非本研究之四名學生) 進行預試，預試以紙筆為主。由於GSP 操作熟練的學生不容易找到，以 GSP 為解 題輔助工具的預試，則委請兩位實習老師代替。本工具已經針對預試的結果進行修 正，本工具在多位學科專家的協助下，經指導教授核可後進行研究。

評分者信度：研究者與一位任教於國立大學教育研究所的助理教授一起針對本 研究之解題歷程的編碼原則以及細部行為歸類表(請見表 3-2-2~表 3-2-5)進行評分 者信度。第一次選定第一題乙生的原案，兩人分別進行編碼後得到互評信度者為 0.82，經過協商與校正之後，再以丙生第二題的原案進行第二次互評，得到互評信 度為.0.86。

二、GSP 操作檢定工具

在設計《GSP 操作檢定》之前，時常和一位熟悉 GSP 的專家(T 老師)商談，他 曾多次開授中學數學教師GSP 研習課程，對於 GSP 操作功能提供寶貴意見。根據 他的經驗指出：動作技能的檢核不能脫離問題情境，建議將動作技能設計成若干問

根據本研究之《幾何評量測驗》中所出現的四個問題中，整理出學生利用GSP 為解題輔助工具時所可能用到的 GSP 操作技能(請見附錄二)並參酌個人使用 GSP 的經驗，加入標記、換色等技能，編設《GSP 操作檢定》(請見附錄一)，受測者必 須在計時但不限時的情況下，完成《GSP 操作檢定》中的八道作圖題。《GSP 操作 檢定》設計之後，曾經過多次修正，並由該 GSP 專家、研究者與一名實習老師操 作結果的平均值，作為標準，只要受測者的時間沒有超過標準的兩倍且操作過程流 暢，即視為通過。受測者進行檢驗時，研究者、GSP 專家與該實習老師將共同負責 紀錄時間與觀察流暢程度的工作，視受測者的表現與操作時間後，給予通過與否的 認證；如果受試者未通過檢驗，則繼續練習直到通過為止。

1.設計理念

《GSP 操作檢定》之設計係根據本研究之幾何評量測驗中可能用到的 GSP 操 作技能，進行檢測，目的有三：一、確認受測者具備相關幾何知識；二、確認受測 者熟練上述動作技能；三、避免對本研究之幾何問題產生暗示作用，將相關動作技 能重新包裝，作為研究前的演練準備。本工具在正式施測前兩個星期實施，避免對 本研究產生暗示干擾。

2.互評者信度

《GSP 操作檢定》中有八道作圖題，研究者商請 T 老師建立專家效度，並針對

《幾何評量測驗》中的幾何問題及附錄二中所提及的GSP 操作技能進行檢核，T 老 師同意附錄二所列舉的各項技能，亦同意在檢測中加入標記、換色等技能，建議應 多加入分點的作圖，以應付解題時的需求。隨後T 老師與研究者一起針對八道問題 與相關動作技能的雙向細目表建立評分者信度(scorer reliability)，在九十六個答案中 僅有兩個答案不同，一致性為 98%，不一致的部分經過協商後，取得共識，如表 3-2-7 所示。

3.重測信度

四位受測者進行《GSP 操作檢定》之後一星期，挑選甲生與丙生進行重測，以 兩次施測成績之相關係數作為重測信度，得重測信度為 .80。

表3-2- 7：動作技能檢核與動作技能的雙向細目表

技能 項次

標 記

換 色

連 線

中 點

分 角

分 點

垂 直

平 行

旋

轉 圓 測 量

計 算 1.垂直作圖 √ √ √ √ √ √

2.內心作圖 √ √ √ √ √

3.外心作圖 √ √ √ √ √ √

4.重心作圖 √ √ √ √ √

5.垂心作圖 √ √ √ √

6.旋轉作圖 √ √ √

7.平行作圖 √ √ √ √

8.分點作圖 √ √ √ √ √ √ √

第三節 研究設計

本研究的施測順序如下：先施測《GSP 操作檢定工具》，通過者進行放聲思考 的訓練，進行《幾何評量測驗》並針對測驗內容進行訪談。

熟悉GSP 操作的甲生及乙生，先利用 GSP 為解題輔助工具，不會 GSP 的丙生 及丁生以紙筆進行解題；待丙生與丁生學會GSP 操作之後，再輪流以 GSP 為解題 工具，每一個題目均安排兩個人以 GSP 解題，其他兩人以紙筆解題，每位受測者 答題方式，如表3-3-1 所示。

為了使丙生與丁生有充分時間練習 GSP 以及避免延宕研究時間，丙生與丁生 先做完三題紙筆解題之後，再以GSP 解題；甲生與乙生則依表 3-3-1 所列之順序施 測。四位受測者之間並沒有相互聯繫，受測者之間無相互干擾的可能。

表3-3-1：受試者受測試題答題方式安排 題號

受試者 1 2 3 4

甲生 GSP GSP GSP 紙筆 乙生 GSP GSP 紙筆 GSP 丙生 紙筆 紙筆 紙筆 GSP 丁生 紙筆 紙筆 GSP 紙筆

第四節 研究流程

本研究進行的階段可分成五個階段，工作內容及器材列之如下表：

表3-4-1：研究過程

階段 研究步驟 工具與器材

一、

準備 階段

1. 文獻探討 2. 徵詢專家意見 3. 編設評量工具 4. 預測評量工具

5. 受測者參與 GSP 操作能力檢核 6. 訓練放聲思考

GSP 4.04 版；GSP 操作檢定工具

二、

施測 訪談

1. 施測評量工具 2. 解題後進行訪談

自 編 幾 何 評 量 測 驗 、 錄 影 機 (帶)、錄音機(帶)、電腦

三、

資料 騰錄

1. 逐字原案的騰錄

2. GSP 操作動作原案的騰錄 3. 從錄影帶中補充不足的資料

電腦、錄影機、錄音機、錄影帶、

錄音帶等硬體設備

四、

資料 分析

分析解題歷程

五、

撰寫 1. 整理資料 2. 撰寫研究結果

第五節 資料收集

對每一位受測者的施測流程均包括暖身、讀題、解題與測後訪談等部份，分述 如後。

暖身：為了讓受測者熟悉測驗場所中的電腦設備與 GSP 環境，測驗前，會有十到 十五分鐘的時間讓解題者自由操作 GSP 的暖身機會，為了避免提示效果，研究者 並沒有提供任何問題讓受測者練習。紙筆解題則沒有這個活動。

讀題：題目皆以紙本的方式呈現，待受測者閱讀問題之後的兩分鐘，研究者徵詢受 測者的同意開始解題，對於題意沒有爭議的情況下，即開始解題並錄音與錄影。

解題：解題過程中，受測者能自行使用直尺、紅色與黑色筆以及計算紙計算，以 GSP 軟體為解題輔助工具時，受測者可要求使用印表機將螢幕中的圖列印下來。全 程需要放聲思考，研究者並不主動提問，為了避免書寫證明可能對推理過程的排擠 效應(Lange, 2002)，受測者得在放聲思考過程中，以口語解釋的方式說服研究者，

重點在於證明過程的解釋而不是形式(Hanna, 2000)。

(一)放聲思考：每一個受測者在解題過程中均被要求放聲思考，解題過程中研究者

不主動提問，僅在沉默思考時間持續兩到三分鐘後，研究者將以口 頭提醒受測者。

(二)研究者提問：在實行解題過程中，盡量不要去打擾受試者(Hayes,1981)，待解題

者沉默思考時間持續兩到三分鐘後或待有進一步動作時而沒有主 動解釋時，才進行提問；研究者將針對表徵與策略變化有關的動作 進行追問，如：重新畫圖、增刪元素、放棄原有方法而重新開始，

同時，要求解題者對於答案提供解釋。解題者如果沒有及時回應，

則將該問題紀錄下來，等待解題完成之後，立刻追問。為了減少再 次建構或扭曲情況產生，在解題後，立刻針對不足的部分進行訪

表3-5- 1：研究者提問時機與提問語句

提問時機 研究者提問語句

沉默思考時間持續兩到三分鐘 1.你現在有什麼想法嗎？

2.你現在有什麼打算嗎？

有進一步動作時 1.你想到什麼？

2.可不可以解釋一下你在做什麼？

針對特定動作追問理由 1.你要這條線的目的是什麼？

2.你為什麼要重新畫圖？

3.你為什麼要把這圓擦掉？

對於答案要求解釋

1.為什麼它是平行六邊形？

2.為什麼這兩條線段等長？

(三)解釋：解題過程中，要求受測者對於任何發現或答案提供解釋，解題者要解釋 這個發現或結果為什麼是對的(Hanna, 1995)，解釋的目的在於理解與說 服(Hanna, 2000)，研究者透過解釋理解受測者解題歷程的轉變，受測者 透過解釋說服研究者獲得重要發現的理由，研究者以此分辨受測者是根 據推理而獲得結果還是直接從GSP 所提供的視覺資訊解譯而來。

施測時間：

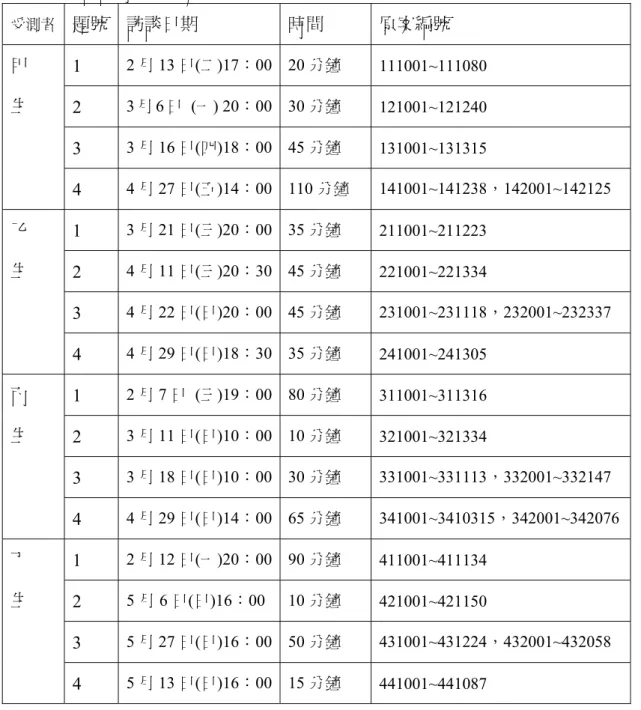
由於四位受測者來自三個不同的學校，無法安排固定時間進行施測與訪談，研 究者視情況與受測者協商施測時間，並於施測之後進行訪談。施測地點多在研究者 任教學校的辦公室或教師專用的電腦教室。施測時間及相關資訊如表3-5-2 所示：

表3-5-2：訪談時間及相關資訊

受測者 題號 訪談日期 時間 原案編號 甲

生

1 2 月 13 日(二)17：00 20 分鐘 111001~111080 2 3 月 6 日 (一) 20：00 30 分鐘 121001~121240 3 3 月 16 日(四)18：00 45 分鐘 131001~131315

4 4 月 27 日(五)14：00 110 分鐘 141001~141238，142001~142125 乙

生

1 3 月 21 日(三)20：00 35 分鐘 211001~211223 2 4 月 11 日(三)20：30 45 分鐘 221001~221334

3 4 月 22 日(日)20：00 45 分鐘 231001~231118，232001~232337 4 4 月 29 日(日)18：30 35 分鐘 241001~241305

丙 生

1 2 月 7 日 (三)19：00 80 分鐘 311001~311316 2 3 月 11 日(日)10：00 10 分鐘 321001~321334

3 3 月 18 日(日)10：00 30 分鐘 331001~331113，332001~332147 4 4 月 29 日(日)14：00 65 分鐘 341001~3410315，342001~342076 丁

生

1 2 月 12 日(一)20：00 90 分鐘 411001~411134 2 5 月 6 日(日)16：00 10 分鐘 421001~421150

3 5 月 27 日(日)16：00 50 分鐘 431001~431224，432001~432058 4 5 月 13 日(日)16：00 15 分鐘 441001~441087

測後訪談：測後訪談的主要問題如下：

1. 要求受測者回顧解題歷程中關鍵想法；

2. 解題超過二十分鐘以上，則要求受測者說明解題困難的原因；

3. 釐清解題過程中不明確之處並針對測驗過程中的特殊問題進行提問。

將訪談過程中每個題目之特殊問題，列之如表3-5-3 所示：

表3-5-3：訪談中的特殊問題

受測者 題號 訪談時間 訪談的特殊問題 甲

生

1 2 月 13 日(二)17：00 解釋發現 AT 為直徑的理由

2 3 月 6 日 (一) 20：00 1.解釋四邊形 ACDE 為正方形的理由 2.GSP 對於解題過程的助益與阻礙 3 3 月 16 日(四)18：00 1.梯形表徵到平行六邊形表徵之轉變歷程

2.說明發現內部平行四邊形的動機 4 4 月 27 日(五)14：00 1.在解題初期即觸及關鍵何以未繼續

2.堅持近九十分鐘的理由 3.局部重畫圖的理由 4.為何想使用餘弦定理 乙

生

1 3 月 21 日(三)20：00 1.釐清 E,A,D,H 共圓的理由 2.解釋作出∆ADH 外接圓的理由 2 4 月 11 日(三)20：30 1.假想不以 GSP 解題時之可能情況

2.對於論證中”反因為果”提出看法

3.GSP 測量的結果能作為論證的理由嗎？

3 4 月 22 日(日)20：00 1.為何堅持以解析法求出垂心？

2.重新思考本題可能的解法

表3-5-3：訪談中的特殊問題(續)

受測者 題號 訪談時間 訪談的特殊問題 丙

生

1 2 月 7 日 (三)19：00 說明解題最關鍵的改變

2 3 月 11 日(日)10：00 假想以 GSP 解題時之可能情況 3 3 月 18 日(日)10：00 假想一般學生解此題可能遇到的困難 4 4 月 29 日(日)14：00 1.預知答案對於推理的影響

2.第一次使用 GSP 為解題工具的心路歷程 3.GSP 對於解題過程的助益與阻礙

丁 生

1 2 月 12 日(一)20：00 1.休息之後重新開始的轉折歷程 2.堅持近七十分鐘的理由 2 5 月 6 日(日)16：00 無

3 5 月 27 日(日)16：00 1.第一次使用 GSP 為解題工具的心路歷程 2.GSP 對於解題過程的助益與阻礙

4 5 月 13 日(日)16：00 畫圖時有考慮到圖形的精確性嗎？

第六節 資料分析

本研究資料主要來自四位受測者的施測結果。包含以紙筆或GSP 為解題工具，

實施《幾何評量測驗》之過程中所產生的口語、動作資料以及施測後的訪談資料。

本節分成兩部份，第一部份說明原案資料處理的流程，第二部份說明資料分析的流 程。

一、原案資料的處理

本研究之口語原案為同時性原案(concurrent protocol, Simon & Kaplan, 1989) 即受測者在解題過程中「同時」說出的想法。原案資料處理的流程如下：

(一) 口語原案由專人騰譯，經研究者確認無誤；

(二) 紙筆解題者的動作原案呈現在錄影帶中，經轉錄成電子檔，GSP 解題者透 過GSP 軟體操弄圖形的過程均由錄影軟體 Camtasia version2 全程紀錄，研 究者根據解題歷程的編碼原則 (請見表 3-2-2~表 3-2-5) 將解題者的動作原 案轉換成文字敘述，寫於原案之「動作原案」欄中(見圖 3-6-1)並給予編碼；

(三) 為了忠實呈現解題者當時所繪製的草圖與解題情境，研究者直接從螢幕翻 拍解題過程中所產生的重要影像資料，稍作影像處理後轉換成圖檔，貼於 原案之「圖示」欄中(見圖 3-6-1)；

(四) 為了讓原案清晰可讀或作為分析的單位，研究者將原案切割成數個解題場 景。解題者所畫的圖反應解題者對於問題情境的理解(Nunokawa, 1994,

歷經數種表徵方式，因此可再以表徵方式作為解題場景；解題過程中，非 成功的表徵亦值得討論，因此非成功的表徵亦能成為解題場景的一部分。

原案中細分成若干個解題場景，搭配草圖、文字符號與算式，搭配口語及 動作，將利於分析解題歷程；

(五) 完成口語原案(如附錄三、四)。

針對口語原案的格式與時間計算方式，詳加說明：

口語原案的格式

將口語原案與自錄影軟體翻拍的草圖資訊彙整成為原案，原案呈解題時間、研 究者與受測者的對話、解題過程中所得到的草圖以及解題歷程編碼，格式如圖3-6-1 所示。原則上以一段形成表徵過程或一個段場景為單位呈現。在每一單位對話之前 均標有編號，以便查閱。

圖3-6- 1：原案格式 時間計算：

掌握學生解題歷程中的時間可分析解題進展的節奏與重要解題特徵出現的次 序(Arzarello, 2000)，因此時間是解題歷程中重要的成分之一。在本研究中，將紀錄 每一道題目之解題歷程中特殊概念或事件產生的時間，做為分析解題歷程的依據。

以第三題為例，紀錄解題過程中「完成草圖」、「發現二條平行線」、「發現三條

「發現外部平行四邊形」、「指出全等」及「證明完成」等時間，擬從發生的時間、

順序與時間差探討兩種解題情境下的差異。

二、 資料分析的流程

由於原案資料的處理已經針對研究問題對於口語資料進行分類與編碼，並切割 成若干解題場景以利於分析，因此，資料分析將針對使用與不使用 GSP 的解題表 現結果進行資料彙整與統計，並針對相異與相近的行為類別進行描述與解釋，資料 分析流程敘述如下：

(一) 部分原案進行評分者信度；

(二) 彙整與比較統計資料，回答研究問題，佐以口語資料支持與解釋。