偶次與三次單項式函數圖形的弦切弧三角不等式

(1)

偶次與三次單項式函數圖形的

弦切弧三角不等式

謝佳叡

1＊

朱啟台

1

李政豐

2

曾政清

3

李政貴

4

陳昭地

1 1_{國立臺灣師範大學}_{數學系} 2_{國立竹南高級中學} 3_{臺北市立建國高級中學} 4_{臺北市立第一女子高級中學}

壹、前言

面積和切線是微積分教學兩大主軸（Larson & Edwards, 2010; Thomas, 2012），而求

平滑曲線的弧長則是積分的重要應用。事實上，早期求圓面積的方法就是利用圓域分別以其內接和外切正n邊形近似，如圖1。對每一個n n



3



值，內接多邊形的面積小於圓的面積，而圓面積又小於外切多邊形的面積，當n增加時，以外切和內接多邊形近似圓的面積會愈來愈好。與其連結在一起的就是圓周長與外切或內接多邊形的周長，內接多邊形周長偏小而外切多邊形周長偏大（參看引理 2-1），但它們都隨著n的增加產生近似圓周長極佳的效果。 6  n n12 圖 1 *為本文通訊作者

(2)

而一般二階可微的函數曲線 y f x( )，a x b  ，不像圓周那麼勻稱，且凹向不一定都是向內的，其弧長的求法則是先取區間

 

a b, 的n1個分割點： 0 1 n 1 n ax x x_ x b_{，取} y_i  f x( )_i ，x_i  x_i x_i_₁_，y_i y_iy_i_₁_，則弧長(PQ)(註一 )近似於曲線上連接P 、 Q 的n條折線的之長度和：  2 2 1 1 1 ( ) n ( _i _i ) ( _i _i ) i PQ x x_ y y_  



    2 2 1 ( ) ( ) n i i i x y  



   2

 

2 2 1 ( ) i i n y i x i i x x  



    

 

2 1 1 i ( ) i n y i x i x  



   





2 1 1 ( ) ( ) n i i i f c x   



  （利用均值定理x_i_₁ c_i x_i）則， 





2 0 1 ( ) lim n 1 ( ) (i i) i PQ f c x  _  



   

（

 max(₁_{ }_{i n} xixi1)

）





2 1 ( ) b a f x dx 

_



.

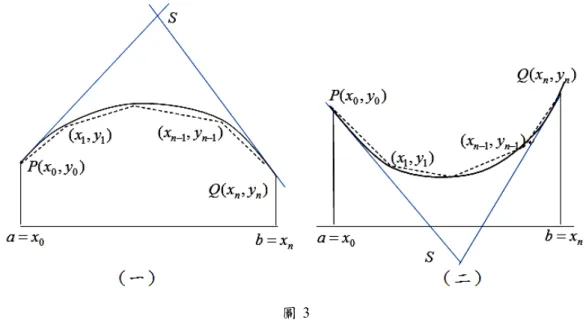
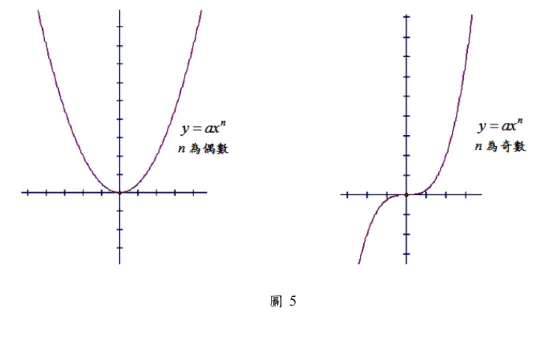
圖 2 由於上述式子中出現了含根號的定積分，因此即便是可積分的式子，能用紙筆演算出來的弧長也相對有限。對於二階可微凹向固定向上或向下的曲線 y f x( ), a x b  ，我們同樣可以用連接 P 、 Q 的內接折線來逼近PQ（如圖 3），但是否和圓一樣可以用外切折線來逼近呢？由圖 3，我們不難理解由於切線交點在求取上不夠直觀便捷，因此藉由外切折線長來逼近弧長並不容易掌握，不過這樣的想法卻提供了一個求弧長上界的方法，亦即：  ( ) SP SQ   PQ （盧思泉，2008）。

(3)

圖 3 而在圓弧的情況，我們發現切線長與所夾圓弧長有著_{SP SQ PQ}_ _ _{ }_{2 (}_PQ₎ 的關係（如圖4），本文稱之為「弦切弧三角不等式」（詳細的敘述與證明參見本文第二節）。而在這個結果的啟發之下，我們自然想知道對於二階可微的函數曲線，若凹向固定，例如 n yax 的單項式函數圖形（如圖 5），是否也有類似的弦切弧三角不等式，這就是本研究關注的焦點！圖 4

(4)

圖 5

貳、基本工具

本節我們先對於圓的情形，依序提出一些觀察的結果，以為本研究的基本工具，再進一步推廣至凹向固定的二階可微分曲線。首先以一個中學常見的不等式作為一系列基本工具介紹的開端，敘述如下：

引理

2-1.

 OPR 為單位圓上的一個扇形， P 在 x軸上，POR , 0 2     ； PS 軸，交x OR於 S ， D 在 OP 上且 RDOP ，則 tan  sin _{，即}PS(PR)RD_。證明：比較圖6 中， OPS ，扇形 OPR 及  OPR 的面積得知：  OPS 的面積  扇形OPR 的面積



 OPR 的面積， tan sin 2 2 2  _{ }  ，故得 tan  sin ，即PS(PR)RD。圖 6

(5)

引理 2-2.

過單位圓外一點S 做圓 O 的切線段 SP 及 SQ（ P 、 Q 為切點），如圖 7 ，則  ( ) SP SQ  PQ PQ。證明： SP、SQ切圓O 於 P 、 Q ， SP SQ   。令POQ2, 0 2     ，連 SO ， 則PQ2sin。令SO 與 PQ 交於R ， 則PRRQ。由引理 2-1 知 tan  sin_，即SQ(QR)1₂PQ，故得SP SQ (PQ)PQ

。

接著引進我們對本研究的一項重要觀察，其本身也深具圓的教學上的意義。

推論

2-3.

平面上三圓兩兩外切於P、Q 、R，如圖 8，則圓弧曲線三角形 PQR 中，任兩弧長 之和大於第三弧。證明：不失一般性，我們僅在此證明    (PQ) (QR) (PR)    的情形。連接PQ、QR、PR ，且過點 P、 R 分 別作兩圓切線，兩切線交於三角形 PQR 內部，令交點為 S 點。 由引理 2-2 可知。 因為點 S 在三角形內部，所以 PQ QR PS SR ，又因為(PQ)PQ, ( QR)QR，所以(PQ)(QR)PQ QR PS SR (PR)，得證。圖 7 圖 8

(6)

接著，我們討論圓的弦切弧三角不等式，請看下列推論2-4。

推論

2-4.

過單位圓外一點 S 做圓 O 的切線， P 、 Q 為切點（如圖 9 ），則 SPQ 中，   (SP SQ )(PQ)(PQ)PQ，即SP SQ PQ   2 (PQ)。證明：(SP SQ )(PQ) 2 tan 2_，且(PQ)PQ22sin 故SP SQ (PQ)(PQ)PQ. tan   sin     tan sin 2    令 f( ) tan  sin2； 0 2     ，則 f(0) 0 ； 2 ( ) sec cos 2 f    (seccos ) 2     ，2 2 0 0 2     ，即 f( ) 0  ，0 2     。故 f 在(0, ) 2  內為嚴格遞增，於是 f( )  f(0) 0 ，0 2     。亦即tansin2，本推論得証。對於單位圓之內接正 n 邊形與外切正 n 邊形，透過直接的計算，其周長分別為： 內接正n邊形周長為2 sinn n  , 外切正n邊形周長為2 tann n  。由內接正n邊形周長 圓周長  外切正n邊周長，且由實數的完備性，取極限得知 sin lim 2 sin 2 lim 2

n n n n n n   _ _       ； tan lim 2 tan 2 lim 2

n n n n n n   _ _       。故單位圓之周長，2   2 ，即2。由上面的結果與推論 2-4，我們可以得到下面的推論 2-5。圖 9

(7)

推論

2-5.

對半徑 r 的圓，若其任一外切正n邊形的周長為T ，而任一內接正_n n邊形的周長為 n K ，則有T_nK_n 4r，且T 的最大下界等於_n K 的最小上界，它們都等於圓周長 2 r_n  。證明：推論2-4 結果的直接應用。我們已經針對圓的情況加以討論，對於凹向固定向下或向上（甚至向左或向右）的二階可微的曲線 y f x( )（ x g y ( )）是否有類似上面推論之性質呢？首先，從引理 2-2 及盧思泉（2008）所提出之結果加以推廣，我們有如下推論 2-6。

推論

2-6.

設 y f x( )為定義於開區間 J 上之二階 可微凹向向下（或向上）的函數，則對 ( ) y f x 圖形上任兩點 P a f a



, ( )



，



, ( )



Q b f b ，S 為過P、Q 之兩條切線的 交點，如圖 10 所示，則  ( ) SP SQ  PQ PQ。證明：過PQ上的任意點C c f c



, ( )



作切線，由於 y f x( )在 P、Q 之間為二階可 微且凹向固定的函數，其切線斜率為嚴格遞增或遞減，因此必交PS 、 SQ 於P及Q ，且 P Q  與 PQ只會交於C 點，如圖 10 所示。 由於SPSQP Q ，故SP SQ PP  P C CQ  Q Q 。再看圖11(1)，    (PQ) (PC) (CQ)    ，僅須證明：P P P C    (PC)，同理，Q C Q Q    (CQ)。對 PC 上異於P、C 的任一點



, ( )



D d f d ，由於 PC 亦為二階可微且凹向固定的 函數圖形，因此過 D作 PC 的切線必 圖 10 圖 11(1)

(8)

交P P 、 P C 於P_{及 C ，且 P C}  與 PC 只會交於D 點，如圖 11(2)。 由P P P D PD    _{； C D C C}   DC，知PP P C PD CD 。     如此步驟逐次進行得知：PPP C 大於任一連接P、C 與 PC 上點的內接折線 段之長度和，其最小上界為弧長 PC ， 故P P P C    (PC)，同理，  ( ) CQQ Q  CQ 。於是SP SQ (PQ)PQ。證明完畢。由上我們有如下的推論2-7。

推論

2-7.

PQS  中，Γ 為連接 PQ 之端點 P、Q 且完全包含於PQS內部的平滑凸曲線（端點除外），如圖 12，則SP SQ  ( )。證明：可仿照推論 2-6 之證明方式加以證明，或參考盧思泉（2008, p. 60）之證明，在此省略證明。

推論

2-8.

PQS  中，PQ、QS及 SP 為三條分別連接 PQ,QS 及SP 之端點且完全包含於 PQS 內部的平滑凸曲線（端點除外），如圖 13，則三弧PQ、QS及 SP，恆有任兩弧長大於 第三弧。證明：推論2-7 的直接結果。

推論

2-9.

設 ,1  及2  為兩兩相切於3 P、Q 、S 的二次曲線，則PQ,QS與 SP 之任兩弧長大於 第三弧。圖 11(2) 圖 12 圖 13

(9)

證明：連接點P、Q 、S ，可直接使用推論 2-8 的結果。（或運用推論 2-6 的性質，仿 照推論2-3 的證明方式加以證明）。

參、主要定理

為了探討二階可微且凹向固定的函數曲線是否也有類似圓的弦切弧三角不等式，首先從我們熟知的二次函數圖形: y ax 2bx c 著手，它有對稱軸，經平移後不妨直接考慮 y ax 2 (a0)的函數圖形。在比對前一節關於圓情況的討論，我們有如下的結果：

定理

3-1

設為拋物線 y ax 2（不妨設a ）的0 圖形(如圖 14)，過對稱軸 y軸的負向上（即頂點O正下方）的任一點

S

作拋物線 的兩條切線，切點為 P 、Q ，則  2 ( ) SP SQ PQ    PQ 。證明：設點S 的坐標為



_{0, at}_ 2



_，其中t ，如圖 15。 0 則可得P t at



, 2



、Q t at



, 2



，設PQ交 y軸於T，因此利用對稱性，我們僅須證明：  2 ( ) SP PT  OP 。由_SP_ _t2_₄_{a t}2 4 __t _{1 4}_ _{a t}2 2 _、 PT 及 t  2 2 0 (OP)

_

t 1 4 a x dx  ，令

 

2 2 2 2 0 1 4 2 t 1 4 f t  t t  a t 

_

 a x dx，則 f

 

0 0，圖 14 圖 15

(10)

而 f t

 

2 2 2 2 2 2 2 2 4 1 1 4 2 1 4 1 4        a t a t a t a t 2 2 2 2 2 2 4 1 1 4 1 4 a t a t a t      2 2 2 2 2 2 2 2 1 4 4 (1 4 ) 1 4 a t a t a t a t       2 2 2 2 1 4 1 ₀ 1 4 a t a t      (t0)，故 f : 0,



  



為嚴格遞增函數，而 f

 

0 0，知 f t

 

0，t ， 0 即SP PT  2 (PQ)。定理 3-1，我們證明對於拋物線_{y ax}_ 2_（_a_{ ），過頂點正下方任一點 S 作拋物線的}₀ 切線，則類似圓的弦切弧三角不等式會成立；事實上，對水平軸x 軸上異於原點的任意 點S 所作的拋物線切線，我們也發現弦切弧三角不等式仍然成立，我們將詳細的證明留 於定理 3-3。而對於更一般的偶次單項式函數 _{y ax}_ 2n_（_a_{ ）的圖形，我們發現}₀ _y_{軸的} 負向上任一點S 作圖形的切線，仍會有同樣的結果。

定理

3-2.

設 為偶次單項式函數 y ax 2n（不妨設a ）的圖形，過對稱軸0 y軸的負向上的任一點S 作拋物線的兩條切線，切點為P、Q ，則SP SQ PQ   2 (PQ) 證明：設 y軸的負向上的任一點S 的坐標為



_{0, (2}_ _n_₁₎_at2n



_{，其中}_t_{ ，}₀ 則_{P t at}



_, 2n



_、_Q



__{t at}_, 2n



_{。設}_PQ_交 _y_{軸於}_T _{，同樣利用對稱性，我們僅須證明：}  2 ( ) SP PT  OP 。因為_SP_ _t2_₄_{n a t}2 2 4n _、_PT _{ ，且由弧長公式可知}_t  2 2 4 2 0 (_OP)_

_

t 1 4_ _{n a x} n _dx  ，同樣令

 

2 2 4 2 2 2 4 2 0 1 4  2 1 4     n 

_

t  n f t t t n a t n a x ，則 f

 

0 0，而

 

2 2 4 2 2 2 4 2 2 2 4 2 2 2 4 2

4 (2

1)

1 1 4

2 1 4

1 4

   





 







n n n n

n

a t

f t

n a t

，由4 (2_n2 _n_1)_{a t}2 4n2 _4_{n a t}2 2 4n2

_，且

2 2 4 2 1 4 n 1 n a t    (t0)

，

故 f t

 

0 (t0)，

(11)

因此 f : 0,



  



為嚴格遞增函數，且 f

 

0 0，故 f t

 

0，t ，於是得0 _{SP SQ PQ}_ _ _{ }_{2 (}_PQ₎_{。證畢。} 進一步針對單項式函數 y ax n (n2)的圖形 ，考量 x 軸上異於原點的任一點 S ， 考慮過S 點的兩條切線（其中一條就是 x 軸本身），則我們有如下的定理：

定理

3-3.

設 為單項式函數 y ax n的圖形（不妨設a ）0 ，n2或

3

，S 為 x 軸上異於原點O 的任一點（如圖 16），則 過 S 點的兩條切線 PS 、 SO ，其中P、O為切點，恆有  2 ( ) SO OP PS    PO 。 (1) (2) 圖 16 證明：先考量a 的情形， 1 令



n 1 _{, 0}



n S  t _為_{x 軸上異於原點的任一點（不妨設}_t_{ ），  過點}₀ _S_{的切線，} 切點為

 

, n P t t ，O

 

0, 0 則SO OP PS   2 (OP) 2 2 2 2 1 2 2 2 0 1 1 n 1 n 2 t 1 n n t t t t n t n x dx n n          

_

 為此，令g: 0,



  



，g

 

0 0且當t 時， 0

 

2 2 2 2 2 2 2 2 0 1 ₁ _n ₁ _n ₂ t ₁ _n n t g t t t t n t n x dx n n          

_



(12)

則

 

2 2 2 2 2 2 2 2 2 2 2 2 2 2 1 ( 1) ( 1) 2 1 1 1 1 1 n n n n n n n n t n n t n g t t n t n _t _{n t} n                     令___t2n2_{，而}___t2n2_{ 時，}₀

 

2 2 1 ( 1) ( 1) 2 1 1 1 (*) 1 1 n n n n n g f n n _n n                         若能證得：

 

0 f   ,    0 則SO OP PS   2 (PO)，即可確認。當n 時，檢核如下： 2

 

0 f   1 2 3 1 1 4 2 1 1 4 2                1  1 4 2(1 ) 1 4 2 1 4 4 1  3(1 4 ) 1               1 4 ( 1  2 4 ) 1 (3 8 )         （兩邊平方再化簡） 2 4 1 (1 2 )(1 4 ) 4 20   28        2 2 1 (1 6 8 ) 1 5 7        （再取兩邊平方化簡） 2 3 4 5 2 3 4 1 13 64 148 160 64 1 10 39 70 49            但由上式知₃__₂₅_2_₇₂_3_₁₁₁_4_₆₄_5_{ 。}₀ （事實上式兩邊比較各項係數，易知左方除了常數項1 以外，恆大於右方。）再對n=3 時，檢核如下：此時

 

2 1 2 6 5 1 9 3 1 1 9 3 f                 (0) 如法炮製， f

 

 0 2 2 6 5 1 1 9 3 1 1 9 3                2 1  1 9 3(1 ) 1 9 6 1 9 18 1  5(1 9 )( 1 )             





1 9 2 1  3(1 ) 6 1 (5 27 )          2 2 (1 9 )(2 1  3 9 ) (1 )(5 27 )         2 12 1 (1 3 )(1 9 ) 12 120   396       

(13)

2 3 4 5 2 3 4 1 25 222 846 1377 729 1 20 166 660 1089            比較上式兩邊係同次項係數易知上面不等式成立。至此，我們完成a 情形的定理證明。 1 至於_:_{y ax}_ n_，_a_{ 的一般情形，同樣令}₀



n1 _{, 0}



n S  t _{（因為考慮}_n_{ 或}₂

₃

_，不妨仍設t0

），

則過點

S

的切線，切點為_{P t at}



, n



_，

_O

 

_{0, 0}

_，

 2 ( ) SO OP PS    PO 2 2 2 2 2 2 2 2 2 2 2 0 1 1 n 1 n 2 t 1 n n t t t a t n a t n a x dx n n          

_



，

令 1 n k t a   代入上式（因為a ，且0 t_{ ，所以知}0 k_{ ）：}0 1 2 2 2 2 2 2 2 2 2 1 1 1 0 1 ₁ ₁ ₂ n ₁ k n n _a n n n n n k k _k k _{n k} _{n a x} _dx n a a n a             



 令

 

2 2 2 2 2 1 2 2 2 2 1 1 1 0 1 ₁ ₁ ₂ n ₁ k n n _a n n n n n k k k F k k n k n a x dx n a a n a              

_

 則

 

2 2 2 2 2 2 2 2 2 1 1 1 2 2 1 1 2 2 2 1 1 ( 1) 1 ( 1) 1 1 1 1 n n n n n n n n n n n n n k n n k F k k n k n a a a k n a a n k                         1 2 2 2 2 1 1 2 1 (n ) n k a n n a a       2 2 2 2 2 2 2 2 2 1 2 2 2 2 2 1 1 ( 1) ( 1) 2 1 1 1 1 1 n n n n n n n n n k n n k n k n k n n a k n k               _       _     故由式子(*) 在n2或 3 的證明，可知當a 時，0 F k

 

0，  。於是定理k 0 3-3 證明完畢！

肆、討論

本研究從圓周長與其外切或內接多邊形周長之間的關係得到啟發，進一步探討切線長與所夾曲線弧長的關係。在第二節中，我們討論了圓弧的情況，發現圓外一點 S 所做 圓的兩切線PS 、 SQ （P、Q 為切點）具有SP SQ  (PQ)以及SP SQ PQ   2 (PQ)之弦切弧三角不等關係，其中，SP SQ  (PQ)的不等關係可以推廣至平滑凸曲線，而弦切弧三角不等關係（亦即SPQ周長大於所夾圓弧長的 2 倍或半周長大於其所夾之弧長）應該可視為觀察圓的切線之基本性質。而對於ABC內之任一點 P而言，其半周長

(14)

（1 2(AB BC CA  )）未必能大於BP PC ，但一定大於以 BC 為底且包含在 ABC 內部之圓弧弧長。有了圓的情況作為基礎，本研究進一步探討平滑凸函數的圖形是否有類似的弦切弧三角不等式性質，並將焦點鎖定在單項式函數圖形，本文提出如下幾個主要結果： 1. 針對拋物線: y ax 2及其外部一點S ，研究發現若 S 位於對稱軸上（在可對做切線情形下）或S 為 x 軸上異於原點的任一點，則過S 點的兩切線 SP 、SQ（P、Q 為切點）具有弦切弧三角不等式：SP SQ PQ   2 (PQ)的關係（定理 3-1 及定理 3-3）。事實上，對於一般情形（即 S 位於拋物線外部任一點）都有弦切弧三角不等 式： SP SQ PQ   2 (PQ)的性質，這是初等數學對於弦切弧三角不等式超乎預期的結果（李政豐、陳昭地，2012）。 2. 針對 y ax n，其中n 或2

3

的單項式函數圖形，若S 位於水平軸上，則函數圖形亦 具有弦切弧三角不等式，此可由定理 3-3 直接證明 f

 

  (0 0)而獲得的結論。但 n4時， f

 

 之正負情況就碰到困難；事實上直接利用 mathematica 計算

 

2 2 2 2 1 2 2 2 0 1 ₁  ₁  ₂ ₁   n   n t  n 

_

t  n g t t t t n t n x dx n n 可得出 g

 

1  (0 n4,5, ) ，換句話說，定理3-3 對n4時並沒有同樣的弦切弧不等式，這也等於宣稱了並非所有的平滑凸曲線都具有弦切弧不等式性質。儘管如此，定理 3-2 至少告訴我們，偶次單項式函數 y ax 2n(n1, 2,3, ) 的圖形，若S 位於特別位置（對稱軸上），則仍具有 弦切弧不等式性質。

備註

一、本文以 PQ 表示圓上或曲線上相異兩點P、Q 之間的一段弧；(PQ)表示 PQ 之弧長 （同理，( ) 則表示曲線 Γ 之曲線長）。

參考文獻

Larson, R. & Edwards, B. H. (2010). Calculus (9th ed.)。台北市：歐亞。

Thomas, G. B. Jr. (2012). Thomas’ Calculus (12 th ed.)。台北市：新月圖書/東華。

盧思泉（2008）：Minkowski 平面三角不等式在凸曲線上的推廣。茂林學院學報，18(4)，

60-61。

李政豐，陳昭地（2012）：拋物線弦切弧三角不等式。教育部高級中學數學學科中心電子報，66 期。 2012 年 9 月 30 日取自： http://mathcenter.ck.tp.edu.tw/Resources/ ePaper/Default.aspx?id=66