國立臺
國立臺
國立臺
國立臺中教育
中教育
中教育
中教育大學
大學
大學
大學數學教育學系
數學教育學系
數學教育學系
數學教育學系
在職進修教學碩士學位班碩士學位
在職進修教學碩士學位班碩士學位
在職進修教學碩士學位班碩士學位
在職進修教學碩士學位班碩士學位論文
論文
論文
論文
指導教授
指導教授
指導教授
指導教授:
:
:胡豐榮
:
胡豐榮
胡豐榮
胡豐榮 博士
博士
博士
博士
國小六年級兒童比概念分析之研究
國小六年級兒童比概念分析之研究
國小六年級兒童比概念分析之研究
國小六年級兒童比概念分析之研究
研
研
研
研 究
究
究
究 生
生
生
生:
:
:郭
:
郭 祈
郭
郭
祈
祈
祈 銘
銘
銘
銘 撰
撰
撰
撰
中
中
中
中 華
華
華 民
華
民
民 國
民
國
國
國 九
九
九
九 十
十 六
十
十
六
六
六 年
年
年
年 六
六
六
六 月
月
月
月
摘 要
本研究之目的在於編製一份具有信度、效度,並且能檢視比概念的優良試題。並藉 由試題關聯結構分析法,對施測結果加以進行分析,並繪製得出國小六年級兒童比概念 結構,應用擴充之邏輯流量測驗計分理論,量化國小六年級兒童比概念結構與教材地位 之比概念結構的差異性。 本研究以彰化縣國小六年級兒童為研究對象,以分層隨機抽樣,選取八所彰化縣國 小,每所國小各一班、共 256 名國小六年級兒童進行施測。並將施測後之資料,以試題 關聯結構分析法,得出國小六年級兒童比概念結構,並根據結構圖,獲以下結論: 壹、六年級兒童在「比的母子意義」上的瞭解,不如「比的組合意義」。 貳、數值範圍在「整數對整數」的比值意義,是數值範圍在「分數對整數」的比值 意義的下位關係。 參、數值範圍在「整數對整數」的前項後項意義,與數值範圍在「分數對整數」的 前項後項意義是等價關係。 肆、六年級兒童在「能將整數除法的商以分數表示」的概念上,是理解並能操作的。 伍、六年級兒童的「相等的比」概念結構主序列為「整數對整數的整數倍轉換之正 向活動問題」→「整數對整數的整數倍轉換之逆溯活動問題」→「整數對整數的單位分 數倍轉換之正向活動問題」。 將獲得之國小六年級兒童比概念結構與教材地位之比概念結構,使用擴充之邏輯流 量計分理論將差異量化,計算出到達度為 25.4 分。 根據以上結論,研究者提出若干建議,以作為教學者及未來研究之參考。 關鍵詞 關鍵詞 關鍵詞 關鍵詞::::國小六年級兒童國小六年級兒童國小六年級兒童國小六年級兒童 比概念比概念比概念 試題關聯結構分析法比概念 試題關聯結構分析法試題關聯結構分析法試題關聯結構分析法 擴充之邏輯流量計分理論 擴充之邏輯流量計分理論 擴充之邏輯流量計分理論 擴充之邏輯流量計分理論Abstract
The purpose of this study is to compile an excellent test sheet, focused on ratio concept, with convinced reliability and validity. The result of tests was further analyzed with Item relational structure analysis, and the ratio concept structure of elementary school six graders was charted. By applying logical flow test-extended theory, elementary school student six graders' difference between ratio concept structure and that of textbooks were put into qualification.
The participants of this research were six graders of elementary school students in Changhua County, and total 256 six graders from seven classes in seven schools (one class for one school) were conducted with a test based on stratified randomly selection. Data obtained from tests were further analyzed with questions-related structure analysis method to gain the ratio concept structure of elementary school students. According to the structure chart, the results were summarized as following:
Firstly, participants of the study had a better understanding in part-part-whole of ratio in comparison of that of associated sets.
Secondly, numerical range from fraction to integer is positioned in the lower status of the ratio meaning of numerical range from integer to integer.
Thirdly, equal level relation was found in between the antecedent and the last term in both numerical range from integer to integer and that of from fraction to integer.
Fourthly, concept of using fraction to descried quotient of division for six graders is understandable and operable.
Fifthly, main sequence for the equal ratio structure of six grader is “positive transfer activity question for integer to integer time”→“reverse transfer activity question for integer to integer time”→“positive transfer activity question for integer to fraction time of integer”
Similarity in the ratio structure concept of six graders of elementary school students' from ratio concept structure and textbooks, compute by Item relational structure analysis, is 25.4.
Suggestions were provided for pedagogical implication and further research based on the conclusion of this research.
Term: Six graders of elementary school, ratio concept,
目
目
目
目
次
次
次
次
摘要……….. i 目次……….. iii 表次……….. v 圖次……….. vii 第一章 緒論……… 1 第一節 研究背景與動機……… 1 第二節 研究目的……… 4 第三節 名詞釋義……… 4 第四節 研究限制……… 5 第二章 文獻探討……… 7 第一節 兒童比概念的發展……… 7 第二節 比概念之數學要素……… 14 第三節 比概念之教材分析……… 16 第四節 比概念之相關實證性研究……… 24 第五節 試題關聯結構分析法……… 30 第六節 邏輯流量計分理論及其擴充理論……… 38 第三章 研究方法……… 46 第一節 研究架構……… 46 第二節 研究對象……… 47 第三節 研究工具……… 48 第四節 資料處理……… 62 第四章 研究結果及分析……… 63 第一節 試題性質的分析..……….. 63 第二節 試題關聯結構圖之繪製……… 67
第三節 試題關聯結構圖之分析與討論……… 70 第四節 擴充之邏輯流量計分理論量化計分……….…… 105 第五章 結論與建議……….… 111 第一節 結論………...……….. 111 第二節 建議……….…… 114 參考文獻…………..……….… 116 中文部分…..………...……….. 116 外文部分……..……….…… 117 附錄 A 試題檢核表…..……….… 119 附錄 B 預試試題……..……….… 120 附錄 C 專家效度問卷..……….… 132 附錄 D 施測試題……..……….… 136
表 次
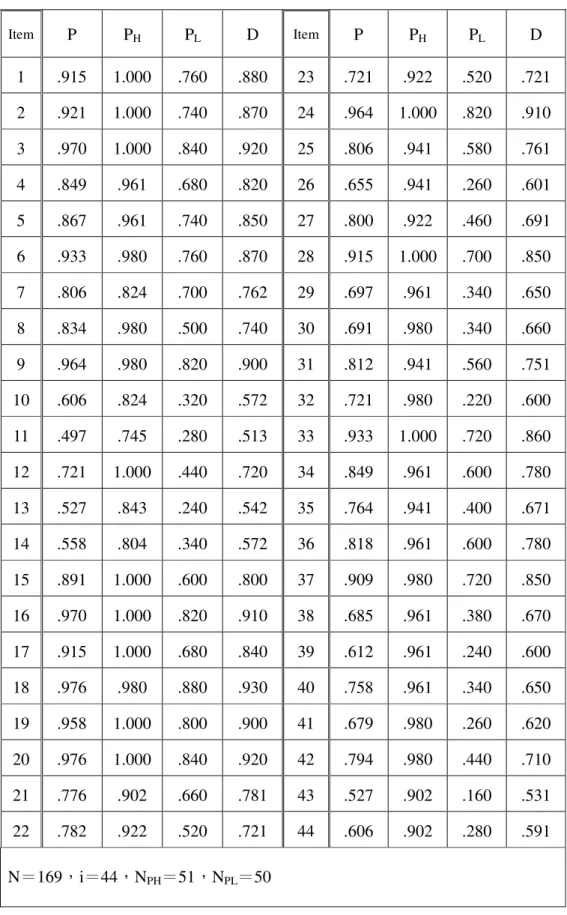
表 2-1-1 INRC 群的邏輯關係……….………... 13 表 2-5-1 A 組學生之答題情形……….….. 31 表 2-5-2 B 組學生之答題情形………... 31 表 2-5-3 A 組、B 組學生之答題情形簡表………... 32 表 2-5-4 A 組、B 組學生之答題情形依得分排序簡表………... 32 表 2-5-5 A 組、B 組學生之答題情形依得分及答對人數多寡排序簡表... 33 表 2-5-6 A 組、B 組學生之試題關聯結構圖...………….………... 34 表 2-5-7 機率的四分割表……….. 35 表 3-3-1 南一版「比與比值」單元教學活動……….. 50 表 3-3-2 康軒版「比與比值」單元教學活動…………...………... 52 表 3-3-3 翰林版「比與比值」單元教學活動………...…... 54 表 3-3-4 仁林版「比與比值」單元教學活動……….. 56 表 3-3-5 各版本之教學活動………..…………..……….. 56 表 3-3-6 施測試題雙向細目表………....……….. 59 表 3-3-7 預試試題難度分析表……….………….….………... 60 表 3-3-8 預試試題鑑別度分析表..………..…...….…...…... 61 表 4-1-1 正式施測 Cronbach'sα
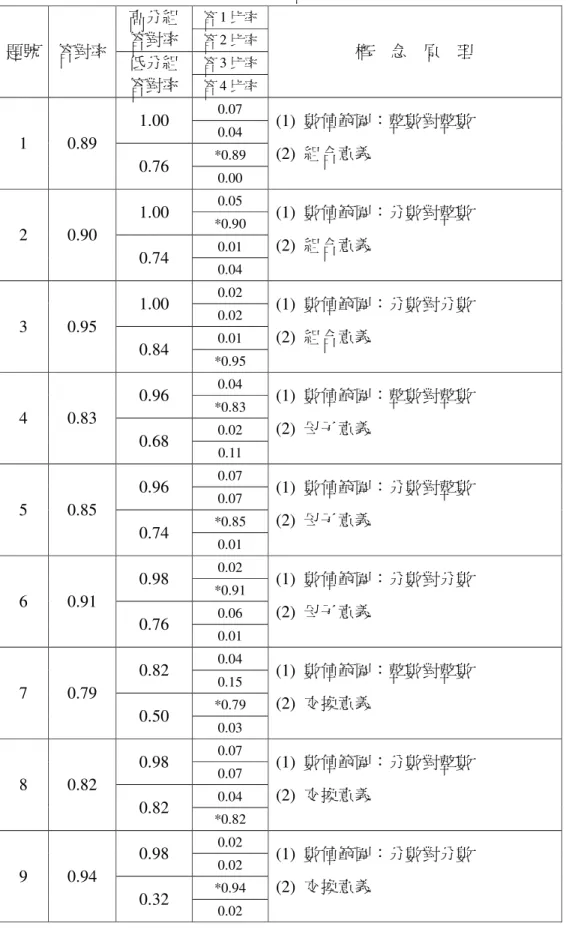
信度分析表………..……….…….. 63 表 4-1-2 正式施測難易度分析表………....….. 65 表 4-1-3 正式施測鑑別度分析表………...…...……….…... 66 表 4-3-1 概念節點答對率………...…... 70 表 4-3-2 「比的意義」概念題目原理及答對率……….……... 74 表 4-3-3 「比值的意義」概念題目原理及答對率……….. 79 表 4-3-4 「前項後項的意義」概念題目原理及答對率…………...……... 82 表 4-3-5 「能將整數除法的商以分數表示」概念題目原理及答對率….. 85表 4-3-6 「因倍數的概念」概念題目原理及答對率…………..………… 88 表 4-3-7 「通分的意義」概念題目原理及答對率……….. 91 表 4-3-8 「相等的比」概念題目原理及答對率…………...………... 94 表 4-3-9 「相等的比」各概念題目原理之平均及高分組低分組答對率.. 96 表 4-3-10 教材地位與施測結果比概念難易編序比較表….……….…….. 98 表 4-3-11 「最簡單整數比」概念題目原理及答對率….………..…….... 102 表 4-4-1 比概念教材地位階層圖之順序性係數 0-1 矩陣表... 106 表 4-4-2 六年級兒童比概念階層圖之順序性係數 0-1 矩陣表….…..….. 108 表 4-4-3 比概念教材地位階層圖的各上下位關係重要度……….... 109. 表 4-4-4 兩概念階層圖之有向邊差異度……….... 110.
圖
圖
圖
圖
次
次
次
次
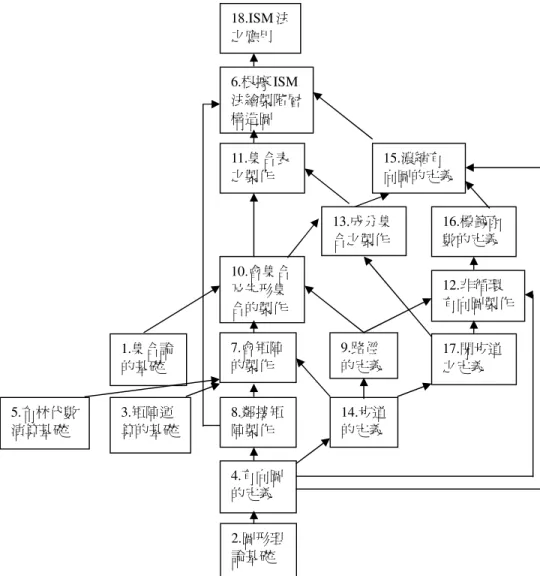
圖 2-6-1 教學者與三位學習者之概念結構圖……….…...………… 38 圖 2-6-2 教學者之 ISM 概念圖……….……….. 42 圖 2-6-3 學習者之 ISM 概念圖………..…. 43 圖 3-1-1 研究架構圖……… 46 圖 3-3-1 南一版「比與比值」單元教材地位……… 49 圖 3-3-2 康軒版「比與比值」單元教材地位………...…. 51 圖 3-3-3 翰林版「比與比值」單元教材地位……….... 53 圖 3-3-4 仁林版「比與比值」單元教材地位………...………. 55 圖 3-3-5 教材地位比概念結構圖……… 57 圖 3-3-6 教材地位比概念結構圖………...…. 58 圖 4-2-1 施測試題概念節點題目分布圖……….... 67 圖 4-2-2 六年級兒童之比概念結構圖………...………. 69 圖 4-3-1 「比的意義」概念試題關聯結構圖……… 76 圖 4-3-2 「比值的意義」概念試題關聯結構圖………...…. 81 圖 4-3-3 「前項後項的意義」概念試題關聯結構圖……….... 84 圖 4-3-4 「能將整數除法的商以分數表示」概念試題關聯結構圖….... 87 圖 4-3-5 「因倍數的概念」概念試題關聯結構圖……… 89 圖 4-3-6 「通分的意義」概念試題關聯結構圖………...…. 93 圖 4-3-7 「比的意義」概念試題關聯結構圖……….….... 100 圖 4-3-8 「最簡單整數比」概念試題關聯結構圖………....……. 104 圖 4-4-1 比概念教材地位階層圖………....……. 105 圖 4-4-2 彰化縣六年級兒童比概念階層圖………..…………..…....……. 107
第一章 緒論
本章先說明本研究的研究背景與動機、研究目的,再針對研究中所提到 的名詞作定義及解釋,最後說明研究範圍及限制,茲分述如下:第一節 研究背景與動機
在二十一世紀來臨前,我國教育部為因應國家發展的需求及對社會期待 的回應,進行自六十四年、八十二年之後的第三次的課程改革,在民國九十 年一月研議出九年一貫課程暫行綱要。基本理念中的終身學習方面,強調主 動探究及解決問題,數學學習領域中就終身學習的演繹是知道如何學而且樂 於學(教育部,2001)。然而就研究者的教學經驗,及國內許多針對兒童所進 行的實證性研究來看,大多數的兒童是不知如何學的,更遑論要樂於學了。 黃寶彰(2003)指出:「根據中小學數學教師的問卷調查結果發現,六、 七年級學童在『因數與倍數』、『分數』、『文字符號』、『比與比例』四個概念 的學習有困難。」比概念是多數數學教師認為兒童學習有困難的概念之一。 黃寶彰的研究亦發現比概念的教學,學童在比與比例主要的學習困難是在應 用比和比值解決有關的問題(如身高問題)、應用比例來解題及判斷比的大小 (如組合問題、濃度問題、身高問題及交換問題等)。 回顧我國數學課程發展,民國六十四年第一次改版的課程標準中,和比 概念相關的教材被歸類集中在高年級第六學年,分別在:(教育部,1975) 「數與量」中的「比例的認識」; 「量與實測」中「用比例關係實測長度」; 「圖形與空間」中「簡易的擴大圖與縮圖」; 「集合與關係」中「比與比值」和「正比與反比的實例」 民國八十二年的課程標準,和比概念相關的教材依然被歸類集中在第六學年,分別在:(教育部,1993) 「圖形與空間」中「透過操作活動,瞭解縮圖與擴大圖的關係」及「瞭 解比例尺的意義及表示方法,並應用於地圖的閱讀」; 「數量關係」中「比、比值、比例的初步認識」及「以實例解釋兩數量 的變化關係」。 民國九十年的九年一貫暫行綱要,與比概念相關的指標仍然在第三階 段,也就是六、七年級,只就六年級的能力指標來看,有:(教育部,2001) 「數與量」中「N-3-15 能在情境中理解比、比例(包括正比例和反比例)、 比值、率(百分率、ppm)的意義」。 民國九十二年的九年一貫正式綱要,六年級的能力指標,與比概念相關 除暫綱原有的指標「N-3-15」在正綱中改為「N-3-05」外,在「數與量」中 還增加了「N-3-07 能熟練比例式的基本運算」,在「圖形與統計」增列了 「S-3-02 能認識平面圖形放大、縮小對長度、角度與面積的影響,並認識比 例尺」(教育部,2003)。 由比概念教材在我國課程發展沿革中,不難看出比概念教材於歷年的課 程綱要中都是置於較高的年級,且在每一次的課程改革中都不曾缺席;在九 年一貫暫綱或是正綱都是跨足六年級到七年級的概念,除了是國小六年級過 渡到國中七年級需要銜接的重要概念,亦是分屬於不同範疇的重要概念:比 概念從整數、小數與分數而來,故是「數與計算」的範圍;從比、比值與比 例的性質來看,又屬「數量關係」的範疇;而從比例尺的觀念來說,就是「圖 形與空間」的題材;從速度、百分比、度量、濃度等觀念來看,「量與實測」 包含著比概念,由此可知比例問題於數學教材中的重要性與複雜性(劉祥通、 周立勲,1999)。 生活中,亦常會用到比概念,例如:要沖泡一杯好喝的即溶咖啡,一定 要知道咖啡粉及水的比例;要判斷那兩班級的學業表現較好,也不能只看考
滿分的有幾個人,而是要看考滿分的人數占了全班人數的多寡;速度也運用 到比概念;地圖要看懂,比例尺的觀念是不可或缺的;就連影印時放大幾倍 或縮小幾倍,都和比概念有關。故比概念是日常生活中常使用的基本概念(林 福來,1987)。 充滿著重要性、複雜性及生活化基本概念的比概念,是六年級數學教育 中重要的一個單元,故有不少研究者針對兒童比概念的進行研究。黃寶彰 (2003)以自編筆試測驗,找出六、七年級兒童在比概念學習困難的部分, 並進行晤談,了解學習困難的癥結。張育萍(2006)以晤談方式探討二位國 小學生在比值問題上的解題表現,並將解題表現加以類化。大多數的研究都 是以晤談方式,找出兒童學習比概念的困難之處,再加以類化,給出教學建 議。但對於瞭解兒童完整的比概念結構,甚或是發現兒童的比概念結構有何 不正確之處,是較少著墨的。研究者認為這一個部分對於站在執行教學第一 線的教師而言,是重要的,也是研究者進行本研究所著重的。 所以,對一個教師來說,知道兒童到底學到的是怎樣的概念結構,甚或 是瞭解兒童學到的概念結構和比概念的教材結構是否一致,是當前重要的課 題。余民寜(1997)提到:「『教學評量』所提供的回饋訊息,可以幫助教師 明瞭兒童的學習類型及學習困難所在,進而採取適當的補救措施。」所以要 知道兒童到底學到的是怎樣的概念結構,甚或是瞭解兒童學到的概念結構和 比概念的教材結構是否一致,必須自編評量工具。但目前針對比概念,自編 評量作概念分析的研究是缺乏的。許天維(1995a)指出,試題關聯結構分析 法(Item relational structure analysis)簡稱 IRS 分析法,有助於教師在進行教 學評量後,瞭解兒童的認知學習構造及概念形成過程、對形成性評量的結果 進行補救教學並提供教科書對課程教材構造之瞭解。而取自兒童的概念圖, 要有效且客觀的進行分析並非易事,Shavelson & Stanton(1975)與佐伯卓 也(1981)提出了能有效量化概念圖的方法,但仍存在許多不合理之處,這
個不合理之處由日本竹谷誠教授提出,並於 1977 年改良發展成新式計分理 論,稱作邏輯流量測驗計分理論(Logical flow test)簡稱 LFT 計分理論(廖
寶貴、曾智鈿、胡豐榮、許天維,2004)。另卓樹樣(2005)在邏輯流量測驗
計分理論的基礎下,考量步道的正確性,修改了 LFT 中部分定義,提出了擴 充之邏輯流量測驗計分理論(Logical flow test-extended)簡稱 LFT-extended 計分理論。綜合以上所述,研究者將針對六年級兒童比概念,進行自編測量 工具,以試題關聯結構分析法繪出兒童學到之比概念結構,並另據學者、專 家意見及現行數學教材,找出教材地位之比概念結構,再以擴充之邏輯流量 測驗計分理論,量化兒童學到之比概念結構與教材地位之比概念結構的差 異,期能對教學者及未來研究有所俾益。
第二節 研究目的
根據研究背景所述,研究之目的如下: 壹、編製一份具有信度、效度,並且能檢視比概念的優良試題。 貳、應用試題關聯結構分析法,得出國小六年級兒童比概念結構。 參、應用擴充之邏輯流量測驗計分理論,量化國小六年級兒童比概念結構與 教材地位之比概念結構的差異性。第三節 名詞釋義
茲將本研究中論及的相關名詞定義如下: 壹、國小學童 本研究中研究對象,係指九十五學年度就讀於彰化縣公立國民小學六年 級的兒童。 貳、比概念 本研究中所稱之比概念,係包含比與比值兩個概念。比(ratio)或比值,指兩數或兩數量的商,用以顯示其相對大小(牛頓數學辭典,1997)。六十四 年版的課程綱要中,「比」定義為「比較量」是「基準量」的多少倍。在 5: 2 中,5 是前項,2 是後項。前項除以後項所得的商,叫做這個比的「比值」。 而八十二年版的課程綱要中,則稱比為對等關係,且定義對等關係是指兩數 量 A、B 之間,由於某種原因,而產生一種配對關係,就稱此兩數量是 A 與 B 有對等關係(此定義於九年一貫課程綱要中仍沿用)。而對等關係的量化即 是比值。對等關係可分為四種類型並舉例如下(陳竹村,1998): 一、組合:一桶積木中有 5 個紅色積木、3 個黃色積木。 二、母子:一箱飲料有 24 杯,其中有 10 杯是綠茶。 三、交換:小明拿了五個蘋果,到市場換了十個橘子。 四、密度:100 立方公分的水重 100 公克。 參、概念分析 本研究之概念分析,係先採日本學者竹谷誠教授所提出之試題關聯結構 分析法,將施測結果,按題目彼此間反應所得的順序性關係,繪製出具有指 向性的兒童比概念階層圖;再以擴充之邏輯流量測驗計分理論,將所得兒童 之比概念階層圖與教材地位之比概念階層圖的差異性量化出來。 肆、教材地位之比概念階層圖 係研究者據教育部八十二年版國民小學課程標準、國民中小學九年一貫 課程暫行綱要及正式綱要,參考現行各家出版社之第十一冊數學教學指引及 徵詢學者專家意見所得出。
第四節 研究限制
茲將本研究的限制,分別依研究内容、研究對象及研究工具上之限制說 明如下: 壹、研究內容本研究僅探討彰化地區國民小學六年級數學科「比和比值」單元的概念 結構分析,因此不宜將本研究之結果,推論到其他單元。 貳、研究對象 本研究旨在透過試題關聯結構分析法及擴充之邏輯流量測驗計分理論, 探討國小六年級兒童在比概念的知識結構,但因本研究受限於人力、經費與 時間等客觀因素,僅以彰化縣之國民小學,以分層隨機抽樣六年級男女兒童 256 名做為研究對象,因選取樣本有地域性限制,故雖可代表多數常態的兒 童,但仍不宜依本研究之結果做過度推論。 參、研究工具 本研究受限於人力、經費與時間等客觀因素,僅能以紙筆測驗施測,如 果時間充足的話,在得到施測結果後,應可在進行晤談觀察等多元評量,使 得到之概念階層圖更臻客觀且能充分正確反應出兒童所學。
第二章 文獻探討
本研究目的在編製一份能充分檢視出國小六年級兒童比概念的優良試 題,並藉由試題關聯結構分析法分析出六年級兒童比概念結構;再由擴充之 邏輯流量測驗計分理論,量化六年級兒童比概念結構與教材地位之比概念結 構的差異性。故瞭解兒童的比概念發展、九年一貫教材內容以及如何運用試 題關聯結構分析法及擴充之邏輯流量測驗計分理論作出有效分析,是本章文 獻探討的重點。因此,本章第一節將先探討兒童的比概念發展,第二節討論 比概念的數學要素,第三節再就現行國小六年級比概念的教科書教材內容作 探討,第四節為比概念之相關實證性研究,最後第五節討論試題關聯結構分 析法,第六節討論邏輯流量測驗計分理論及其擴充理論。第一節 兒童比概念之發展
皮亞傑(Piaget)運用臨床觀察的方法,研究兒童的認知發展,為世界上 兒童心理學的巨擘,更有人將其與心理學大師佛洛依德並列,足可見皮亞傑 認知發展理論在世人心中的地位及不容忽視的重要性。所以提到兒童比概念 的發展,不可不深入瞭解皮亞傑的理論。壹、認知發展理論基礎
生物為了生存,針對環境的變化,必須有適應(adaptation)的產生,隨 著兒童的年齡成長及生活經驗的累積,保持不變的是適應這項生物功能 (functions),但是結構(structure)卻產生變化,且是有系統的變化,這種 變化就是所謂的發展(development)(John L. Phillips, Jr./王文科編譯,1996)。例如:一個嬰兒,看到媽媽來了,就伸出雙手要媽媽抱抱。這一整個事 件中,(看、伸手、抓握)是手段、(從媽媽的懷抱得到安慰的刺激)是目的, 而從手段到目的的關聯,就是「結構」。其中嬰兒動作的功能是適應:就是把 外在感官的輸入,同化(assimilation)於結構中,並調整結構以迎合輸入的 感官刺激。而內容(content)指的是行動的原料,而非行動的模式(John L. Phillips, Jr./王文科編譯,1996)。
在皮亞傑的理論中,有兩個基本的功能:適應(adaptation)與組織(Piaget, 1952)。適應與組織是一個單獨機械作用的兩個層面:適應是和外界的層面相 聯,組織則是關於內在的層面。組織是把簡單的結構形成較複雜的結構。而 適應則包含了同化及調適(accommodation)這兩個功能不變數。 調適和同化是彼此互相影響的關係,人類的大腦在接收訊息或刺激後, 要將此訊息或刺激納入時,須視輸入的訊息或刺激做調適的動作,而當調適 完成時,就是同化的產生。就好比人吃食物,消化系統須依食物的酸甜苦辣、 冷熱軟硬做出如何消化的調適,最後身體獲得食物消化而成的養分就是同化 的完成。換句話說,為了要完成適應功能,結構就必須不斷的調適與同化。 皮亞傑理論中的另一個重要名稱就是基模(scheme or schema)。基模是 同化的一種工具;是一個小型系統(minisystem)(John L. Phillips, Jr./王文科
編譯,1996)。就是說,對某一活動,能被推廣於其他同一種類型的活動,例 如,「看見─撿起」這個基模,就能使人同化各種相類似的活動:看見玩具, 撿起來;看見錢幣,撿起來;看見自己的東西掉了,撿起來。總括來說,基 模是結構的一個單位,任何可重複或可普遍化的行為就是基模(Piaget, 1970)。最初的基模比較簡單,通常指的是反射(reflexes),年歲漸長後,基 模就大部分都是經同化及調適的結果。 結構、功能、與內容三者,是皮亞傑認知理論的中心思想。Wadsworth (1989)曾以交通工具載運貨物來說明這三者之間的關係:交通工具代表運 輸這項不變的功能,而所載的貨物就是內容,但隨著內容的不同,工具的結 構也會隨之不同。 一般而言,影響認知發展的因素有五:成熟(maturation)、物理經驗 (physical experience)、數理經驗(logic-mathematical experience)、社會傳遞 (social transmission)及平衡作用(equilibration),茲分述如下:(John L. Phillips, Jr./王文科編譯,1996)
一、成熟
皮亞傑利用這個詞彙,來描寫一種逐層開展的發展策略。在著作的論述 中,指的是天賦對發展的影響。
兒童利用來抽象各種物體的物理特性,所獲得的經驗稱之。例如:透過 觸摸,發覺物體是柔軟的;透過拿取的動作,發覺物體的重量。 三、數理經驗 當兒童行動,而獲致各種物體間的關係,或者採取行動間的關係,就有 了此種經驗(如:數對應邏輯、加減概念、速度概念…等)。其與物理經驗最 大之不同,物理經驗是當兒童行動後,物體的本質直接反射出來的經驗;而 數理經驗則是物體與所採取之行動之間的關聯。舉例來說,當兒童坐在花園 的地面上,計數石頭,他將石頭排成一列,從一、二、三…開始,一直數到 十,數完後,再從另一頭數過來,又得到十,因此兒童得到十的概念,是數 理經驗;而由拿取石頭排列時,經驗到石頭冰冷、堅硬的物理性質,而得到 石頭的物理經驗。 四、社會傳遞 兒童透過自己學習,從別人所寫的書,或藉由其他媒介所得到知識的過 程,稱為社會傳遞。通常兒童是經由成人所給的社會傳遞得到知識的,學校 就是進行社會傳遞最大的場所。兒童同化了成人所給的知識到自己的結構 中,就是瞭解了成人要給的訊息。 五、平衡作用 平衡作用是一種改變的機械作用,影響兒童的時間超過一個時期以上, 平衡作用是動態的,是穩定狀態的一種維持力量。結構將藉由平衡狀態不斷 地邁向平衡,當基模的平衡狀態愈發穩定時,兒童對該項知識的狀態描述就 愈明顯且清楚。每種基模提供自己有供培育的與採取行動的需求欲,基模開 始就再生、重複自己,並將各類新事物納入自身之中(Piaget, 1972)。所以平 衡作用也可說是發生行動的動機。平衡作用在認知發展五個因素中,扮演的 就是將其他四種因素納入自身之中。 皮亞傑認為,發展是自發性的,而學習是可被激發出來的(Piaget, 1964)。 智力是學習的因,而並非大多數心理學家所認定智力是學習的果。皮亞傑認 為智能的發展,為結構不斷組織與重新組織,而每一次所形成的組織,都將 前一次的組織包含在內。這個過程是連續的,但形成的結果卻是間斷的,隨 著時間的不同,會有或多或少質的變化。所以皮亞傑將整個發展的過程,分
成幾個不同時期: 一、感覺動作期:0 到 2 歲。 二、運思前期:2 到 7 歲。 三、具體運思期:7 到 11 歲。 四、形式運思期:11 到 15 歲。 在這幾期中,年齡組距只是大概的近似值,甚至有許多人並未達到最後 一個時期。能確定的是,每個人發展的順序都是相同的。皮亞傑認為兒童要 完成比概念的發展,須到最後一個時期,形式運思期。故第二部分將就形式 運思期兒童的概念發展作一細部的探究。
貳、形式運思期兒童的比概念
形式運思期的兒童(11~15 歲),係在運思上運思;皮亞傑稱為第二級 運思。也就是形式運思期的兒童知道內省,把自己的思想、感受及知識再拿 來思考。在運思上運思,是達到形式運思期兒童的一大特徵。 比概念問題類型中,第四種對等關係─密度,是用來辨別具體運思期的 兒童是否已達形式運思期的有效工具。 密度概念涵蓋了重量與體積兩個運算,討論的是重量與體積的對等關 係,具體運思期的兒童通常只考慮到其中一項因素,而忽略或對這兩項因素 之間的聯結感到迷感。 在具體運思期未達形式運思期的兒童,考慮密度問題常把重的物體歸為 可以沉下去的那一類(具體運思期的兒童已具備分類的能力)、輕的物體可以 浮起來時,將產生的第一個矛盾,就是有若干大的物體在水中浮起來,若干 小的物體在水中則沉了下去。當提出針為何會沒入水中時,兒童會發現到材 質的影響,但若是兒童不能對重量及體積這兩因素做保留時,是不會想到密 度的。但可以分類,已是發現密度這種比概念的重要進展。 年紀再稍大一些的兒童(依舊未達形式運思期),可以將分類作的更精 密,例如:考慮到像鋁蓋這類型的物體,是可浮可沉的,當鋁蓋上充滿水時, 鋁蓋會沉沒,反之則鋁蓋會浮在水面上;亦會試圖將不同材質,如木頭或鐵 來做比較,但並非等量的比較。而密度的判定就需將重量與體積之一項因素定量,所以做非定量的比較是不會理出頭緒的,只是陷入另一個矛盾。 最後,要達到密度概念的了解,必須了解密度與重量的變化是正比的關 係,但和體積卻是反比的關係,想到此節的兒童,便能將水列入考慮,將同 體積的水及物體拿來比較。但是除非到了形式運思期,否則無法對體積作保 留,也無法理解上述的精密結構,所以一般來說,受試者須至少到十一歲才 有辦法。 再以較簡單的例子來說,具體運思期的兒童可以知道若一籃蘋果有六 顆,三籃蘋果就有十八顆。但要知道 1:6=3:18,在運思上運思,就必須 形式運思期的兒童方能做到。 形式運思期的兒童,思考的另一特徵,就是能以假設(hypotheses)來填 補以前曾為建構完整的結構而產生的矛盾。具體運思期的兒童並不建立假 設,此時期的兒童是在可以想像的條件下想像,是有限度的想像。形式運思 期的兒童可以在心中試驗其假設,無需操弄道具等具體事物,而且可以在所 有變項控制不變的條件下,操縱一個變項,達到其實驗的目的或進行驗證。 形式運思期的兒童,自我中心觀是存在的,但與感覺動作期、具體運思 期及運思前期的自我中心觀是不同的。對感覺動作期的嬰兒,自我中心觀是 以為世界是他伸手可及才是他所謂的世界;而具體運思期及運思前期兒童的 自我中心觀,則是他自己唯一可能獲取表徵的自然物體世界;對於已達形式 運思期的兒童,或許以是青少年,自我中心觀是以自己的邏輯思考方式。延 伸到不可預測,新接觸的領域,當然這常會替他的長輩帶來管教的困擾,因 為青年不認同別人或外在社會加在他身上的邏輯,而只相信自己的思考邏 輯,形成心理學家所謂的青少年叛逆期。
參、比概念的皮亞傑任務(Piagetian tasks)
皮亞傑在著作中,曾運用皮亞傑任務來探索兒童的認知發展程度,本節 將選取兩項與比概念有關的任務來作討論。(John L. Phillips, Jr./王文科編 譯,1996)一、迴紋針任務
(一)內容本項任務在測驗兒童是否具應用比概念的能力。首先給學生一張 8.5 公 分 × 11 公分的厚紙板一張,在紙板的兩邊各畫一個木頭人,但其中一個的 高度是別一個的三分之二。高的木頭人高度有六支大迴紋針高,矮的木頭人 有四支大迴紋針高,先讓兒童以大迴紋針量出木頭人的高度並做記錄後,將 大迴紋針取走,拿小迴紋針拿給兒童,要他以小迴紋針先量出小木頭人的高 度(假設需六支)並做記錄,最後施測者拿走小木頭人,問:「大的木頭人, 如果以小迴紋針來測量,將有多高?」 (二)討論 很顯然的,兒童要成功完成任務,必須知道4:6=6:X 的關係才行。 當然兒童如果是隨意猜測的,表示他未達形式運思期的思考。
二、砝碼任務
(一)內容 給兒童一天平,含間隔數相等的木桿,及數個不同或相同重量的砝碼。 一開始在天平兩端等距離的地方各掛上同為十克重的砝碼,天平是平衡的, 然後將其中一個砝碼移走,問:「利用你面前的砝碼,如何維持天平的平衡?」 等兒童反應後,將其中一邊的砝碼從天平中移走,並把在天平上的砝碼移近 支點,問:「利用砝碼,你如何維持量尺的平衡?你如何證明你的答案是對 的?」 (二)討論 要達成任務,必須會將天平一臂的長度乘上砝碼的重量與另一臂長度乘 上砝碼的重量是相等的概念,也就是槓桿原理,才可完成任務。肆、比例推理五層次
皮亞傑以物理平衡的概念探討兒童的比例推理問題,發現兒童比例推理 的發展共分五個層次。(何意中,1988;陳英傑,1992) 層次一:是完全不瞭解比例推理的人。 層次二:不會同時考量兩個因素間的關係,而常會以加法策略去解決比 例問題。加法策略,但直覺認為若數量增加,則差量也要增加才可能平 衡。
層次四:皮亞傑稱之為邏輯比例期(logical proportions)。能了解 INRC (Identity-Negation-Recirocal-Correlative)群如何運作的概念, 並知道運作的邏輯。INRC 群的關係如表 2-1 所示。 表 2-1-1 INRC群的邏輯關係(引自王文科,1983,p282) I N R C I I N R C N N I C R R R C I N C C R N I 層次五:最高層次是所謂的測量比例期(metrical proportions),到達此 層次的兒童,能自由應用比例概念。 綜上所述,皮亞傑認為比例推理始於定量及加法策略,最後再依序發展 出比例前期、邏輯比例期及最終的測量比例期。
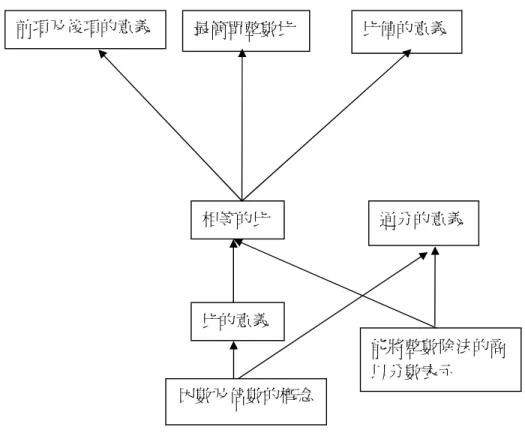
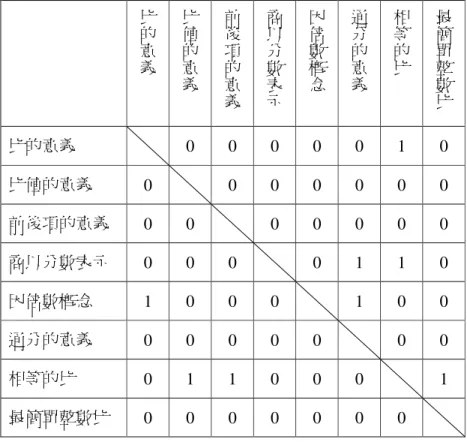
第二節 比概念之數學要素
分別有三個要素,由 Lamon(1995)提出,第一個數學要素為相對的與 絕對的改變(relative and absolute change)、第二個是比感(ratio sense)、第 三個則是共變性及不變性(covariance and invariance)。分別說明如下:
壹、相對的與絕對的改變
比是代表任意兩個數值間的對等關係,故「相對」是比概念中最重要的 部分(鄭英豪,1990)。舉例來說明相對的與絕對的改變:甲校有學生 1000 人,乙校有學生 100 人,甲校的近視人數有 50 人,乙校也有 50 人的近視學 生人數。由絕對的觀念來看,甲校與乙校的近視人數相同,但是可以說甲校 的學生視力不良情形與乙校相同嗎?答案應是否定的,因為如果從相對的角 度來切入問題,也就是說得再考慮到全校總人口數這個因素的影響,如此一 來,甲校的近視人數僅佔全校的 20 1 ,而乙校的近視人口卻佔了全校人口的 2 1 ,可以明顯的看出甲乙兩校的近視率有很大的差距。 因此,兒童在學習比概念的教材時,須學習捨絕對觀念,以相對觀念來 解決比概念的問題(翁宜青,2002)。貳、比感
所謂比感,就是兒童必須知道什麼是比概念的實例(example),或非實 例(non-example)。實例指得是含比例關係的任意兩量,反之則為非實例 (Lamon, 1995)。 例如:「一枝鉛筆賣 10 元,二枝鉛筆賣 20 元」,類似這樣的比例問題, 兒童必須知道這是比概念的實例,因為兒童只要知道一個量,依循比例關係, 兒童可求得另一個量;但是若是以下問題:「80 公分的人重 10 公斤,160 公 分的人重 20 公斤」,就不是非實例問題。所謂的比感,其實是一種直覺,是 一種知道比例情境與數學關係的直覺(Lamon, 1995)。參、共變性及不變性
共變性及不變性是同時存在的。若現有一比的關係式為 A:B=C:D, 這二比的比值是一致的,這是不變性。而 C(或 D)會隨著 A(或 B)改變 而改變,這就是共變性(Lamon, 1995)。 例如:有一材質相同的長圓鐵棒,取 18 公分,就重 3 公斤,那麼取 30 公分,會重幾公斤?其中這兩段鐵棒的長度與重量比都是 6:1,比值是 6, 代表的是比概念的「不變性」。而 30 公分的鐵棒重量會隨 30 公分的鐵棒長度 而變,這是比概念的「共變性」。從另一個角度,就這兩段的鐵棒的長度比來 看,是 3:5,比值是 3/5,這也是一種不變性,而 30 公分的鐵棒重量會隨 18 公分的鐵棒重量而變,這是比概念的「共變性」(劉祥通、周立勲,1999)。第三節 比概念之教材分析
本研究因必須編製比概念之試題,以檢測兒童學習教科書後之比概念階 層圖,與教材地位階層圖有無一致性,故瞭解九年一貫數學教材,對本研究 是重要的。壹、相關名詞的探討
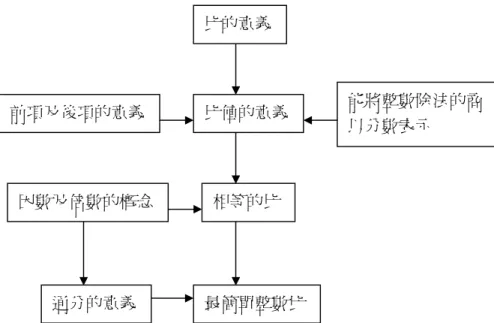
一、比
依據 64 年版部編本國小數學教科書的定義,比是指兩量倍數關係的另一 種說法。例如:「5 塊餅乾是 2 塊餅乾的幾倍,這種關係也可寫做 5:2,讀做 五比二」。 比是指並置的兩對應關係量的紀錄,例如:「小明拿 4 顆蘋果,到菜市場 去換 6 個橘子」可以記為 4:6。這是 82 年版課程綱要的定義。(周筱亭、黃 敏晃,2002)二、對等關係
這是 82 年版課程綱要中,給比的另一個名詞。代表任意兩數量,因某種 原因(不考慮單位是否相同的問題),而產生的關係。數學上的意義等同序對, 序對以(A,B)表示,當然也可用較常見比的符號 A:B 來紀錄。例如:小 明的身高是 140 公分,體重是 40 公斤;一籃水果有 10 顆,一共重 20 公斤; 某班級中男生有 15 人,女生有 12 人…等。諸如此類的描述,都可視為產生 了一個對等關係。140 公分對 40 公斤、10 顆對 20 公斤、15 人對 12 人,…。 記錄成 140:40、10:20、15:12(周筱亭、黃敏晃,2002)。三、對等關係的種類─組合、母子、交換、密度
這四種分類方式是依語意結構的不同來劃分,與 Lamon(1993)依語意 結構而對比概念所做的分類有部分是重疊的。Lamon 將比概念分為熟知的量 數(well-chunked measures)、部分─部分─全體(part-part-whole)、關聯的 集合(associated sets)、擴大縮小(stretchers & shrinkers)四個類型。茲將九年一貫數學領域綱要中對等關係的分類及與 Lamon 所做比較分述於下:(周 筱亭、黃敏晃,2002;翁宜青,2002) (一)組合 若此兩數量是同類量,且同是一全體量的部分時,稱之為組合的對等關 係。例如:一桶積木中有 5 個紅色積木、3 個黃色積木。此部分的定義與 Lamon 分類中「關聯的集合」相似。 (二)母子 若此兩數量是同類量,且其中一數量是全體量,另一數量是全體量的部 分量時,稱之為母子的對稱關係。例如:一箱飲料有 24 杯,其中有 10 杯是 綠茶。此部分的定義與 Lamon 分類中「部分─部分─全體」相似。 (三)交換 兩個具有相同價值的物件,可以進行交換,而形成對等關係,稱之為交 換的對等關係。例如:小明拿了五個蘋果,到市場換了十個橘子。 (四)密度 兩不同類量,重量及體積,用以描述同一物件的密度性質,稱之為密度 的對等關係。例如:100 立方公分的水重 100 公克。此部分的定義與 Lamon 分類中「熟知的量數」相似。
四、比值
64 年版的比值,是直接定義前項除以後項,抽象的定義常使教師在教 學,以及學生在學習上造成困擾。82 年版的課程綱要,則先透過各種對等關 係,產生一個比,並藉由列出與它相同的比,所產生的最簡整數比相同,來 得到最簡整數比的概念。最簡整數比的單位化(unitizing)所產生的數就是比 值。也就是說對於一個比「A:B」,透過找一個後項為 1 且與 A:B 相等的 比,如 A:B=X:1,得到的 X 就是 A:B 的比值。Lamon(1990)認為單 位化是建立複雜單位結構的必經歷程。如果兒童解比概念問題時,能先求出 單位量,再利用此單位量解題,即具備比值的單位化能力(周筱亭、黃敏晃, 2002;翁宜青,2002)。五、比例問題與對等問題
比例問題指的是 64 年版課程所進行類似:已知一比較量對基準量的比, 而且已知一個比較量或基準量,求另一個未知量的問題。而對等問題是指兩 等價的對等關係,「A:B=C:D」其中有一項是未知數的情境文字題問題。 因為對等關係有四類,故對等問題依然可分成四類,分別為組合問題、母子 問題、交換問題及密度問題等。其問題類型舉例如下: (一)組合問題 馬場裡,每二個工人可以照顧五匹馬,有 20 匹馬,需要幾個工人來照顧? (二)母子問題 飲料工廠將飲料裝箱,每 1 箱飲料中有 2 罐可以抽中再來一罐,問如果 要抽中 10 次再來一罐,要買幾箱? (三)交換問題 小明用 10 個菠蘿麵包可以換到 8 個紅豆麵包,如果隔天小明只帶了 5 個菠蘿麵包,可以換幾個紅豆麵包? (四)密度問題 3公升的水重3公斤,幾公升的水重8公斤?(周筱亭、黃敏晃,2002)六、比例式及比例式填充題
「5:8=20:32」即稱為比例式。「5:8=20:32」中若有一數是未知量, 將其列為「5:8=( ):32」則成比例填充題。比例填充題是用在某些數學 具體活動時的記錄,包括教師布題、學生解題及結果的呈現等。(周筱亭、黃 敏晃,2002)七、數量關係與函數
有某一對應關係的兩組數量,例如:多個三角形及其總邊數合、時速 50 公里的車子經過的時間與所走的距離、…等,都可稱為數量關係,可記錄為(X1、X2、X3、…)與(Y1、Y2、Y3、…),特別注意其中的對應順序不可
對調。若存在此兩變項的關係式,使一變項為已知,即可知另一變項,則稱
八、正比例與反比例
生活中存在最簡單的函數,就是正比例及反比例,因為兒童尚未有函數 的概念,故正比例及反比例須透過比與比值的關係來引入。當一數量關係的 所有對應項的比的比值都相同時,稱這兩對應關係為「正比例」;若其中一組 數量先取倒數,與另一組對應數的比的比值相同時,稱這兩個對應關係為「反 比例」。 由上述說明,若甲組數量與乙組數量成正比例,那麼乙組數量與甲組數 量亦成正比例。同樣的若甲組數量與乙組數量成反比例,那麼乙組數量與甲 組數亦成反比例。(周筱亭、黃敏晃,2002)九、百分率、命中率、打擊率
在母子對等關係中,若前項為子、後項為母,例如:「小王投籃球 50 次, 投進了 15 球」,其中的比值,將依不同的情境的社會文化術語,給了不同的 「率」之名稱。如果後項設定為 100,則形成的前項值就可稱為百分率或百 分數。(周筱亭、黃敏晃,2002)貳、比概念問題之兒童解題探討
一、解題的先備知識
翁宜青(2002)認為解比概念的問題,先備知識有五項,分別是:(一) 具有因倍數的能力;(二)熟悉乘除法的問題情境;(三)有理數概念的整體 發展;(四)相對的思考能力;(五)比值的單位化能力。研究者認為,具有 因倍數的能力,乘除法必須熟稔,(一)(二)點其實無須分述,應合為同一 點說明,另(四)相對的思考能力,於第二節中已有說明,故不再贅述,以 下研究者就剩餘三點說明如下: (一)具有因倍數的能力 解比例問題,通常是先做除法再做乘法(劉祥通、周立勲 1999)。例如: 9 顆糖果,賣 15 元,12 顆糖果要賣多少元?類似的問題都必須將 15 元除以 9 顆,得到 1 顆糖的單價是 9 15 = 3 5 元,再以 1 顆糖的單價乘以 12 顆,得到所求的總數 20 元。如果兒童具備因倍數概念時,就可以先將 9 顆糖分 3 堆、15 元分 3 堆,1 堆有 3 顆糖果賣 5 元,亦可解出答案,且更可避免以嘗試錯誤 法去試出公因數。故具備因倍數能力,可以使兒童在解比概念問題時,加快 關鍵解題的要素。 (三)有理數的整體發展 兒童在遇到類似第一點的舉例問題時,如果在第一步以 15 ÷ 9 時得到 一個除不盡的小數,而不知道用分數來代表答案時,表示兒童尚缺乏有理數 的整體發展。兒童對以分數來表示除法的結果並不熟悉,所以無法解決比概 念問題(楊錦蓮,1999)。 (五)比值的單位化能力 「小明買 2 枝鉛筆要 5 元,買 10 鉛筆要花多少元?」。兒童帶遇到類似 比概念問題時,若能將 2 枝 5 元當成一個單位,算出要買 10 枝鉛筆要 5 個單 位(5 從 10÷2 來的),得到 5×5=25 元。則認為兒童已具備比值的單位化能 力。
二、解題關鍵
解題的關鍵在於兒童能具體操作累加及等分割活動(周筱亭、黃敏晃, 2002)。例如:「小王買 4 杯飲料花了 50 元,用同樣的買法,小華買 15 杯飲 料要花多少元?」,兒童必須先把前比例項的兩數量,同時累加 3 次,再把前 比例項的兩數量等分割成 4 分,合成其中的 3 分於之前累加的 3 次上,才可 得到小華所要花的錢數。較不複雜的問題可能只須累加,或等分割即可,又 累加又等分割,最後再合成,應是最複雜的問題了。故無論比概念問題中, 簡單或複雜的問題,解題關鍵都是累加及等分割。累加就是乘法,等分割即 除法,與先前所提先備知識須乘除法及因倍數觀念吻合。而複雜問題的等分 割後再合成,就須先備知識中的單位化能力。此兩部分恰不謀而合。三、難易因素
周筱亭、黃敏晃(2002)等學者們認為,比概念的問題中,有三個難易 因素,分別為:(一)未知數的位置;(二)轉換的方式;(三)前比例項的數 值範圍。茲分述如下:(一)未知數的位置 「5 個蘋果賣 25 元,多少個蘋果賣 40 元?」這類的問題,如果列成比 例式填充題,則可列成「5:25=X:40」;如果是「多少個蘋果賣 25 元時, 8 個蘋果賣 40 元」,列成比列式填充題,可列成「X:25=8:40」。這兩類問 題,不同的只是未知數放的位置,一個放在前比例項,另一個放在後比例項, 以成人的算則來看,這是一樣的題目,但以兒童的角色來看,這是不一樣的 題目。未知數在後比例項時,做為推論基礎的前比例項是已知的,所以這是 一個正向推論,稱為「正向活動」;反之,未知數在前比例項時,做為推論基 礎的前比例項,有部分是未知的,須反向推論來求所求,稱為「逆溯活動」 (周筱亭、黃敏晃,2002)。就兒童的發展而言,正向活動是較早發展的,逆 溯活動是相對較難的,故對兒童解比概念問題時,這是一個重要的難易因素。 (二)轉換的方式 所謂轉換的方式,係指在解比概念問題的正向活動時,前比例項須透過 累加或等分割的轉換方式,得到後比例項,求出未知數。此轉換方式依題目 類不同而不同,分述如下:(周筱亭、黃敏晃,2002) 1、整數倍的轉換:如「5 本書可以換 7 枝筆,15 本書可以換幾枝筆?」 這類型的問題,列成比例式填充題為「5:7=15:X」,通常只須將前比例項 累加 3 次,就可得到答案,稱為整數倍的轉換。 2、單位分數倍的轉換:如「15 本書可以換 21 枝筆,5 本書可以換幾枝 筆?」這類型的問題,列成比例式填充題為「15:21=5:X」,通常只須將 前比例項等分割 3 次,就可得到答案,稱為單位分數倍的轉換。 3、真分數倍或假分數倍的轉換:如「15 本書可以換 21 枝筆,10 本書可 以換幾枝筆?」這類型的問題,列成比例式填充題為「15:21=10:X」,須 透過尋找 10 和 15 的公因數為等分割的次數,得到 10 15 ,約分後成 2 3 的假分數 轉換方式。 依以上 3 種不同的轉換方式,兒童須要的能力不同,亦造成不同的難易 程度。 (三)前比例項的數值範圍 前比例項的數值範圍,亦影響兒童的解題難易,分為:(周筱亭、黃敏晃,
2002) 1、整數對整數。如「2:3=X:6」; 2、分數對整數。如「 2 1 :5=X:10」; 3、分數對分數。如「 2 1 : 3 1 =X:2」。 由於兒童概念發展關係,設計問題時,應由整數對整數範圍漸進到分數 對整數、分數對分數的範圍。
三、難易分類及順序
根據上述難易因素,周筱亭、黃敏晃(2002)等學者認為比概念問題有 四個難易向度:(一)依問題情境來看,交換問題最簡單,因為最接近生活情 境,其次是組合問題和母子問題,最難的是密度問題,因其受物理性質影響; (二)以邏輯推理的正向性來講,正向活動比逆溯活動簡單;(三)前比例項 是後比例項的整數倍時最簡單,再來是單位分數倍及真(假)分數倍;(四) 前比例項的數值,依序以整數對整數、整數對分數、分數對分數由易到難。 依此觀點,學者們將九年一貫比概念教材依編排及難易順序編排如下: (一)整數對整數的整數倍轉換之正向活動問題。 (二)整數對整數的整數倍轉換之逆溯活動問題。 (三)整數對整數的單位分數倍轉換之正向活動問題。 (四)整數對整數的單位分數倍轉換之逆溯活動問題。 (五)整數對整數的真分數倍轉換之正向活動問題。 (六)整數對整數的真分數倍轉換之逆溯活動問題。 (七)分數對整數的整數倍轉換之正向活動問題。(不含帶分數及假分數 對整數) (八)分數對整數的整數倍轉換之逆溯活動問題。(不含帶分數及假分數 對整數) (九)分數對整數的單位分數倍轉換之正向活動問題。 (十)分數對整數的單位分數倍轉換之逆溯活動問題。 (十一)分數對整數的真分數倍轉換之正向活動問題。(不含帶分數及假(十二)分數對整數的真分數倍轉換之逆溯活動問題。(不含帶分數及假 分數對整數) (十三)分數對分數的整數倍轉換之正向活動問題。 (十四)分數對分數的整數倍轉換之逆溯活動問題。 (十五)分數對分數的單位分數倍轉換之正向活動問題。 (十六)分數對分數的單位分數倍轉換之逆溯活動問題。 (十七)分數對分數的真分數倍轉換之正向活動問題。 (十八)分數對分數的真分數倍轉換之逆溯活動問題。
第四節 比概念之相關實證性研究
壹、楊錦蓮的研究
楊錦蓮(1999)的研究在探討不同城鄉和年級的國小高年級兒童在不同 數字型式和語意類型之比例問題的解題表現。 分二個階段進行,第一階段採測驗調查法,以南投縣(市)國小高年級兒 童為研究母群體,採分層叢集抽樣方式抽取有效樣本 441 人,自編「國小高 年級數學比例問題測驗」為工具,了解國小高年級兒童的解題表現。 第二階段以立意抽樣方式訪談 10 位不同解題層次的兒童,探討兒童的解 題策略,進而歸納有助於兒童解決比例問題的知識和能力基礎。 主要的結論如下:一、數字型式比例問題的解題表現
(一)對國小五年級兒童的困難度由簡單到困難依序為第一式、第二 式、第三式及第四式。「A:B=C:X」中,若 C 同時是 A 及 B 的整數倍則 稱第一式、僅 B 是 A 的整數倍則是第二式,第三式則是僅 C 是 A 的整數倍, 最後第四式則定義為 C 不是 A 也不是 B 的整數倍。 (二)對國小六年級兒童的困難度由簡單到困難依序為第一式、第二 式、第三式及第四式。與對國小五年級的施測結果是相同的。 (三)解題通過率:第一層次:五年級 23%,六年級 24%;第二層次: 五年級 14%,六年級 14%;第三層次:五年級 17%,六年級 18%;第四層 次:五年級 5%,六年級 18%。二、語意型式比例問題的解題表現
(一)對國小五年級兒童的困難度由簡單到困難分別是交換問題、組合(二)對國小六年級兒童的困難度由簡單到困難分別是交換問題、組合 問題、密度問題、母子問題及伸縮問題。
三、兒童的解題策略
有單價法、倍數法、疊加法、比例關係式和數量分解等五種策略;解題 錯誤者大都以絕對思考方式解題。四、各層次的兒童數學知識及能力
(一)層次0的兒童具備約分和擴分的計算能力,經由提示會使用單價 法。 (二)層次一的兒童具備約分和擴分的計算能力,會用單價法。 (三)層次二的兒童會用單價法,經由提示會用倍數法。 (四)層次三的兒童會用單價法和倍數法,比較習慣用單價法。 (五)層次四的兒童會用單價法和倍數法,經由提示會用倍數法解相似 圖形題。五、有助於兒童解比例問題之先備知識及能力
(一)不受數字結構因素的影響:如以下所述 1、數字較大時解題錯誤,數字變小則能發現倍數關係而解題成功。 2、非為整數倍時解題錯誤,整數倍時則解題成功。 (二)能正確計算多位數乘、除法問題和不受除數小於被除數的錯誤概 念影響。 (三)了解有理數概念的多義性,明確的以分數表示除法的結果和除不 盡的數。 (四)具有考量答案合理性的後設認知能力。 (五)以相對思考解決比例問題。 (六)了解單位量的意義。貳、Lamon 的研究
Lamon(1995)認為比概念的數學要素,第一個相對的與絕對的改變 (relative and absolute change)、第二個是比感(ratio sense)、第三個則是共 變性及不變性(covariance and invariance)。於本章第二節已有詳述,在此不 再贅述。
參、張育萍的研究
張育萍(2006)的研究旨在探討兩位未接受比值教學的學童,其在處理 比值問題時的解題表現,並將他們的解題活動類型加以分析。研究方法採用 個案研究,並藉工作單來進行訪談以幫助研究資料的搜集,工作單問題共有 9 題,研究者依學生解題後的解題表現加以訪談。 研究一的小亭是一位國小五年級的學生,她在處理比值問題,習慣在兩 階單位的部份整體關係思考下,從等分除的方式,找出「一份所佔的比值」, 因此她在不論遇到比較量大於基準量甚至比較量小於基準量的情況,都使用 此方式解題。 研究二的小奕是一位國小四年級的學生,他在處理比值問題,容易受到 題目中的「語詞」–多少倍、多少、幾分之幾的使用方式而影響解題,尤其是 當題目或是研究者訪談中的語詞出現「多少倍」,會讓他有「大數除以小數」 的迷思產生。當使用「幾分之幾」的方式,他則都可以正確地解題,且不會 有「比值有單位」的問題產生,但是當使用「多少」方式時,他則會受到「等 分除」方式的使用影響,而有「比值有單位」的問題產生,惟這樣的情況不 甚穩定。肆、翁宜青的研究
翁宜青(2002)的研究在探討一位三年級學生解比例問題之表現與接受 教學協助後的解題表現。採個案研究法,以半結構式晤談法進行訪談以深入 了解個案的想法。本研究包含三個時期:一、簡單式比例問題的探討。二、題的探討。 研究對象是一位國小三年級的學生,對數學十分有興趣,數學成績的表 現也很好。受測者只學過乘法問題和簡單的分數問題,但是他尚未學過除法, 也未曾接受過任何有關比例問題的課程及教學。 在第一時期,受測者能以「疊加法」、「數量分解法」、「單價法」、「倍數 法」策略解決四種比值型態之簡單式比例問題中的前三種。但是,因為受測 者不能使用「分數形式」表示兩數相除的結果,以致無法解比值型態第四式 之簡單式比例題目。 在第二時期,受測者能以「倍數法」、「單價法」等策略解決十種比值型 態之多重式比例問題中的前五種。 在第三時期,透過研究者提示協助,受測者能解決「數值型態」第四式 的簡單式比例問題,也能解決十種比值型態之多重式比例問題中的其它三種 問題。 在第三時期,研究者在幫助受測者解決無法解決的問題時,採用的是鷹 架理論,鼓勵受測者做用外在表徴將自己的想法視覺,如果尚無法解決,研 究者會提供線索。如果受測者可以獨立解題,研究者就會拆除鷹架的協助。
伍、侯美玲的研究
侯美玲(2002)的研究,在了解兒童比例概念的發展,以及教材對比例 概念學習的影響。研究者在高雄縣市有效取樣 135 名小學六年級兒童,以面 談和問卷的方式進行三階段研究分析。在比例、比值、比例尺三種的型式下, 分析四個向度,包含中文用語、現實感、等值概念、直觀。 研究結果顯示:一、在中文用語方面
兒童對於「倍」字大多持有「擴大、大於一」的意涵,因此部分兒童會 拒絕「0.8 倍」這類的描述,儘管兒童已經在教材中學過前述用語,也歷經相 關的考試。二、現實生活的量感方面
兒童普遍表現不佳,特別是對重量;雖然兒童對於長度距離的掌握較佳。 但是數學課室裡的教學普遍是遠離現實的。例如以大尺度的比例尺為教學案 例,研究發現,那樣的設計不利於中低成就兒童的現實感發展。
三、等值概念方面
兒童多能掌握具體數量比,低成就兒童在十倍數擴分的表現較好,其次 是約分,最差的是「約分後再擴分」,此與現行教材的安排略有差異;對中、 高成就兒童而言,基於熟練的運算技能,因此約分、擴分正確表現率相當一 致;但是在大數字的表現則不佳,可能來自機械式理解,因此不具解題信心。四、直觀方面
在直觀方面,兒童學得後天直觀,認為「%」代表小於 100 份,因此認 為 150%不合理,顯然脫離真實生活中所使用的意義表徵。 研究中印證 Lamon 所提「相對性思考」為比例運思基礎,樣本中超過 85%的六年級兒童具備該能力。且根據研究發現,兒童在處理比例式、比值, 往往要求給「單位」,特別是低成就兒童,有時甚至是中等成就者。比例式以 非整數比方式出現時,兒童作答的正確率會陡降。因此,研究者認為不適合 以這種表達方式做為引入比值的教學,此與國內教科書的編寫主張不同;又 比例式中的數值型態轉換仍是兒童學習障礙,例如:小數、分數的轉換。低 成就兒童易受學習情境影響;超過 70%的兒童會接受「70%元」,主要來自 日常商業折扣的情境。陸、黃寶彰的研究
黃寶彰(2003)的研究目的在針對六、七年級學生,數學科學習困難的 部分,探討學生在這些學習困難部分的思考方式、錯誤的解題策略或迷思概 念,以及了解學生學習困難的情形及原因為何。 本研究先對中小學數學教師進行問卷調查,整理出教師們認為學童學習 不理想的部分,再針對這些部分設計筆試試題,評量工具為自編的筆試試題, 研究樣本為高屏地區使用南一版數學教材之國小、國中各一所,國小、國中 個三班,共六個班級,其中國小(六年級)109 人,國中(七年級)96 人。根據筆試及晤談結果,發現學童的學習困難所在和錯誤情形及原因,茲將研 究結果說明如下: 根據中小學數學教師的問卷調查結果發現,六、七年級學童在「因數與 倍數」、「分數」、「文字符號」、「比與比例」四個概念的學習有困難。以下僅 針對與本研究相關之「比與比例」的學習困難部分做說明 學童在求兩數量的比、比值、比的相等及求比例式地四項等基本概念較 無明顯的學習困難,學童在比與比例主要的學習困難是在應用比和比值解決 有關的問題(如身高問題)、應用比例來解題及判斷比的大小(如組合問題、 濃度問題、身高問題及交換問題等)。
柒、沈明勲的研究
沈明勲(2003)的研究在透過實踐比例教學模組以幫助學生發展比例問 題概念,以改進學習成效。採用合作行動研究法,探討合作教師對教學模組 的意見、教學模組內各個教學活動的機制、以及學生的學習表現。 研究參與者是南部某國小的一位現職老師與其班上的學生,由研究者提 供比例教學模組的雛形,合作教師提出較可行的教學活動,教學模組分成起 始活動、發展活動、與檢驗活動三個階段。 本研究發現:一、合作教師提出很實際的教學活動以改進教學,二、教 學模組內的教學活動能認識、發展、與檢驗學生的比例概念,三、程度較差 的學生也能在模組教學中建立正確概念,並可利用比例概念解決生活上的應 用問題。第五節 試題關聯結構分析法
壹、試題關聯結構分析法的歷史沿革
試題關聯結構分析法簡稱 IRS 分析法,係日本學者竹谷誠教授於 1980 年所提出。目的在於以試題測驗的結果,按題目反應所得的順序關係,可繪 製成有向性的箭頭圖形,藉以分析試題的特性。 試題關聯結構分析法,是竹谷誠教授為改進美國學者 P. W. Airasian 與W. M. Bart 的「次序理論」(Ordering theory)的缺點而提出的理論。竹谷誠
教授於 1977 年參加美國威斯康辛大學的研討會,因 Baker F. B. 的介紹而得 知次序理論,改進為試題關聯結構分析法後,亦在教育現場進行了七、八年 的實驗,證明是一個有效的分析工具(許天維,1995b)。 試題關聯結構分析法使得教師在實施教學活動之後,能立即窺探出班上 兒童之概念能力在結構上的變化及兒童學習概念結構的訊息,試題關聯結構 分析法也有助於教師進行教學設計、瞭解兒童的認知學習構造及概念形成過 程、對形成性評量的結果進行補救教學並提供教科書編者對課程教材構造之 瞭解(許天維,1995a)。
貳、試題關聯結構分析法的理論
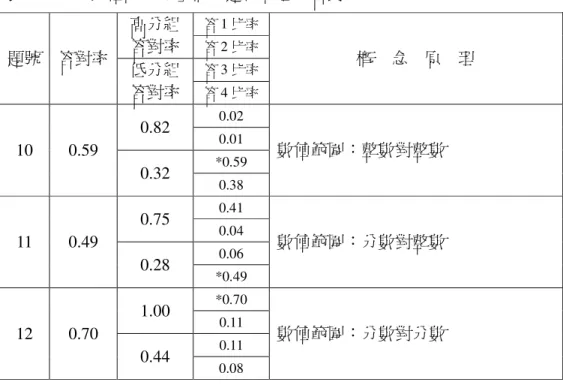
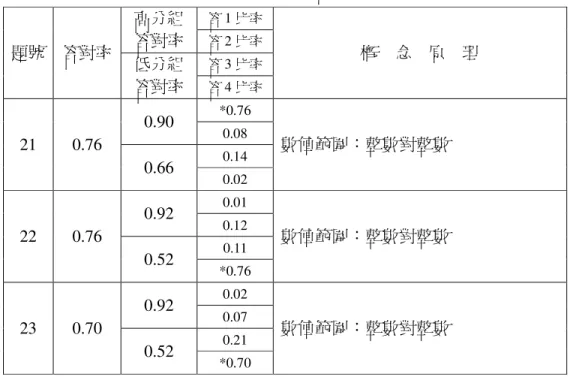
茲將理論直觀上之意義,舉例說明如下:(引自許天維,1995b,p2)表 2-5-1 A 組學生之答題情形 A 組 試題 1 試題 2 試題 3 試題 4 試題 5 試題 6 學生 1 1 1 1 1 1 1 學生 2 1 1 1 1 1 1 學生 3 0 1 1 0 0 0 學生 4 0 1 1 0 0 0 學生 5 0 1 1 0 1 1 學生 6 0 0 1 0 1 1 學生 7 0 0 1 1 1 1 學生 8 0 0 0 1 1 1 學生 9 0 0 0 0 0 0 學生 10 0 0 0 0 0 0 答對人數 2 5 7 4 6 6 表 2-5-2 B 組學生之答題情形 A 組 試題 1 試題 2 試題 3 試題 4 試題 5 試題 6 學生 1 1 1 1 1 1 1 學生 2 1 1 1 1 1 1 學生 3 0 0 1 0 0 0 學生 4 0 0 0 0 0 0 學生 5 0 1 1 1 1 1 學生 6 0 1 1 0 1 1 學生 7 0 1 1 1 1 1 學生 8 0 0 1 0 1 1 學生 9 0 0 0 0 0 0 學生 10 0 0 0 0 0 0 答對人數 2 5 7 4 6 6
為方便說明,改成下表: 表 2-5-3 A 組、B 組學生之答題情形簡表 A 組 試 題 B 組 試 題 1 2 3 4 5 6 1 2 3 4 5 6 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 2 1 1 1 1 1 1 3 0 1 1 0 0 0 3 0 0 1 0 0 0 4 0 1 1 0 0 0 4 0 0 0 0 0 0 5 0 1 1 0 1 1 5 0 1 1 1 1 1 6 0 0 1 0 1 1 6 0 1 1 0 1 1 7 0 0 1 1 1 1 7 0 1 1 1 1 1 8 0 0 0 1 1 1 8 0 0 1 0 1 1 9 0 0 0 0 0 0 9 0 0 0 0 0 0 學 生 10 0 0 0 0 0 0 學 生 10 0 0 0 0 0 0 答對人數 2 5 7 4 6 6 答對人數 2 5 7 4 6 6 再由學生試題所得總分由上而下排序可得下表: 表 2-5-4 A 組、B 組學生之答題情形依得分排序簡表 A 組 試 題 B 組 試 題 1 2 3 4 5 6 1 2 3 4 5 6 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 2 1 1 1 1 1 1 5 0 1 1 0 1 1 5 0 1 1 1 1 1 7 0 0 1 1 1 1 7 0 1 1 1 1 1 6 0 0 1 0 1 1 6 0 1 1 0 1 1 8 0 0 0 1 1 1 8 0 0 1 0 1 1 3 0 1 1 0 0 0 3 0 0 1 0 0 0 4 0 1 1 0 0 0 4 0 0 0 0 0 0 9 0 0 0 0 0 0 高 分 ↓ 低 分 9 0 0 0 0 0 0 學 生 10 0 0 0 0 0 0 學 生 10 0 0 0 0 0 0 答對人數 2 5 7 4 6 6 答對人數 2 5 7 4 6 6
接著,以學生在各試題答對人數多寡,由左至右排列,可得佐藤S-P表 (佐藤隆博,1982)。 表 2-5-5 A 組、B 組學生之答題情形依得分及答對人數多寡排序簡表 A 組 試 題 B 組 試 題 3 5 6 2 4 1 3 5 6 2 4 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 2 1 1 1 1 1 1 5 1 1 1 1 0 0 5 1 1 1 1 1 0 7 1 1 1 0 1 0 7 1 1 1 1 1 0 6 1 1 1 0 0 0 6 1 1 1 1 0 0 8 0 1 1 0 1 0 8 1 1 1 0 0 0 3 1 0 0 1 0 0 3 1 0 0 0 0 0 4 1 0 0 1 0 0 4 0 0 0 0 0 0 9 0 0 0 0 0 0 9 0 0 0 0 0 0 學 生 10 0 0 0 0 0 0 學 生 10 0 0 0 0 0 0 答對人數 7 6 6 5 4 2 答對人數 7 6 6 5 4 2 多 → 寡 多 → 寡 由上表得知兩組學生的總分順序及答對者人數的試題次序都相同;亦即 二組之試題難易分配與試題號碼之對應完全一致,但如果著眼於考慮順序結 構圖,依下列方法加以分析,就會有顯著的不同。 A組中,答對試題 1 的學生是 1 號及 2 號,他們亦同時答對了試題 4, 此時就有試題 4 到試題 1 的箭頭,記作4→1;同理,答對試題4的學生是 1號、2號、7號及8號,他們亦同時答對了試題5、6,所以分別有5→ 4及6→4;另一方面,答對試題1的學生是1號及2號,他們亦同時答對 了試題2,答對試題2的學生是1號、2號、3號、4號及5號,他們亦同 時答對了試題3,所以分別有2→1及3→2;此外,答對試題4的學生有 7號沒答對試題2,故沒有試題2到試題4的箭頭,其餘均依此類推。 同理,在B組中,答對試題1的學生是1號及2號亦答對了試題4,亦 即答對試題1的學生亦答對試題4,此時就有試題4到試題1的箭頭,記作 4→1;答對試題4的學生是1號、2號、5號及7號亦答對了試題2,所
以有2→4;答對試題2的學生是1號、2號、5號、6號及7號分別答對 了試題5、6,所以分別有5→2及6→2;答對試題5、6的學生有1號、 2號、5號、6號、7號及8號亦答對了試題3,故有3→5、3→6;其 餘均依此類推。從以上分析,如果定義答對率為 答對率= 受試全體學生的人數 受試學生答對的人數 則以答對率為縱座標,可將所有相關的指向箭頭標示出來,成為完整的 試題關聯結構圖,如下所示:(許天維,1995b,p4) 表 2-5-6 A 組、B 組學生之試題關聯結構圖 答對率 結 構 圖 答對率 結 構 圖 顯然,A、B兩組試題的關聯結構圖截然不同。值得注意的是,兩個表 的試題答對率雖然相同,但兩組學生的理解結構卻不相同。左圖顯示A組有 兩個系列存在,即試題1、2、3的系列以及試題1、4、5、6系列,而 右圖顯示B組的試題形成一個單純的一元化系列。故試題關聯結構圖可看出 在S-P表裡所觀察不到的各試題間的順序關係,可作有方向性的圖性判讀 (許天維,1995b)。