國立臺中教育大學數學教育學系碩士班碩士論文
指導教授:黃一泓 博士
國小二年級學童的表徵與數概念
知識結構的探討—
以十的合成與分解為例
研究生: 黃志維 撰
中華民國 一○一 年 六 月
謝 辭
終於邁向撰寫論文的最後一個階段──寫謝辭。 兩年的求學時光,一晃眼,竟也邁入尾聲!工作與進修蠟燭兩頭燒的辛勞, 在此劃下一個段落的句點,心情真是五味雜陳……。 首先,要感謝黃一泓教授的指導與協助,在論文的撰寫過程遇到滯礙,老師 總是不厭其煩的給予意見。也感謝口試委員李林滄教授及林冠成教授,提供許多 珍貴的建議與指正,使本論文更臻於完善。 研究過程中,感謝研究所好同學們的加油打氣、感謝學校同事工作業務的支 持。更感謝大學同學筱雲、同事惠卿老師對本研究的大力協助,讓我順順利利完 成各種艱難任務。 最後,謝謝家人以及咅咅的支持與陪伴,讓我在心煩意亂時打起精神,專心 完成研究所的學業。回憶種種,深深覺得自己何其幸運!感謝一路走來幫助我的 每一個人,在此將這份謝意謹獻給這趟生命旅程的貴人。 黃志維 謹誌 2012.06.12中文摘要
本研究旨在藉由ACT-R (Adaptive Control Thought- Rational) 理論探討「十的 合成與分解」活動,分析學童的表徵與數概念之使用知識結構。以國小二年級一 個班級,共27名學生為研究對象,以自編「加減文字題測驗」和「外部表徵測驗」 為測驗工具,探討兩者得分表現相關性;以「認知工作分析」探討學童表徵與數 概念的表現。測驗結果採用質量分析,歸納學童表徵測驗的表現。 研究結果如下: 一、透過認知工作分析,得到學童的表徵與數概念使用的生成規則。 二、學童在加減文字題測驗成績與三種表徵測驗成績,有顯著相關存在。 三、測驗結果,學童在三種表徵測驗當中盒圖的平均得分表現最佳。 四、學童使用圈圈圖與盒圖表徵正確率較高、線段圖表徵正確率較低;但在圈圈 圖與線段圖表徵轉譯數量「零」時易發生困難。 本研究建議:教學者進行數學課程可採用認知工作分析,針對學習內容之概 念進行結構分析,提昇教師教學知能、增進學生學習成效。 關鍵字:認知工作分析、部分整體數概念、表徵
Study on Second Grade Elementary School Students’ Representation
and Number Concept Knowledge Structure:
Using Part-Part-All under Ten as an Example
Abstract
The purpose of the study is to analyze elementary school students’ knowledge structure of representation and numeral concepts by probing into the activity of “part-part-all under ten” based on ACT-R (Adaptive Control Thought- Rational) theory.
The study was performed on a class of the 2nd graders at an elementary school. A total of 27 students participated in this survey.
The researcher designed “Addition-Subtraction Word Problems Test” and “External Representation Test” to evaluate the participants. The evaluation results were used to explore the relationship of their performances between two tests.
“Cognitive Work Analysis" was also adopted to investigate the students’ performances on representation and numeral concept qualitatively.
The finding of this study revealed:
I. Through Cognitive Work Analysis, the production rule of how the students’ representation and numeral concept generated was obtained.
II. There was significant relation between the grades the students gained on Addition-Subtraction Word Problems Test and the three different
Representation Tests.
III. Generally, students gained the best scores on the box diagram test among three Representation Tests.
IV. The higher rate of accuracy was gained when the students used circled and boxed diagram for the representations. In contrast, the rate of accuracy went down when they used the line segment for the representation. However,
students had difficulty in identifying zero when they used circled diagram and line segment representation.
According to the above experimental design and findings, Cognitive Task Analysis could be adopted by teachers as references to analyze conceptual structure of material. Especially when teachers intend to design the mathematics courses to enhance the students’ learning effectiveness.
目 次
中文摘要... I 英文摘要... II 目次... IV 表目次... VI 圖目次... VII 第一章 緒論 ... 1 第一節 研究動機... 1 第二節 研究目的與研究問題 ... 4 第三節 名詞界定 ... 4 第四節 研究限制 ... 5 第五節 章節簡介 ... 5 第二章 文獻探討 ... 6 第一節 表徵與數學學習之探究 ... 6 第二節 表徵與整數加減學習 ... 16 第三節 加減文字題 ... 30 第四節 ACT-R 理論 ... 33 第三章 實驗方法與步驟 ... 40 第一節 研究設計 ... 40 第二節 研究樣本 ... 40 第三節 研究工具 ... 40 第四節 研究步驟 ... 46 第五節 資料處理與分析 ... 47 第四章、實驗結果與討論 ... 48 第一節 量化分析... 48 第二節 質性分析 ... 62 第三節 綜合討論 ... 78 第五章 結論與建議 ... 92 第一節 結論 ... 92 第二節 建議 ... 95 參考文獻... 98 一、中文部分 ... 98二、英文部分 ... 101 附 錄... 107 附錄一、測驗指導語 1 ... 107 附錄二、表徵題試卷一 ... 108 附錄三、應用問題試卷一 ... 109 附錄四、測驗指導語 2 ... 110 附錄五、表徵題試卷二 ... 111 附錄六、應用問題試卷二 ... 112 附錄七、測驗指導語 3 ... 113 附錄八、表徵題試卷三 ... 114 附錄九、應用問題試卷三 ... 116
表目次
表 2-2-1 圖形表徵解題策略之相關研究 ... 26 表 2-3-1 Fuson(1992)的 20 種加減文字題型與示例 ... 31 表 2-4-1 ACT-R 理論三個二分法 ... 33 表 2-4-2 生成規則三階段 ... 36 表 3-3-1 使用盒圖、圈圈圖、線段圖三種外部表徵系統相之關知識架構 ... 45 表 4-1-1 高分組圈圈圖表徵表現人數與得分統計表 ... 49 表 4-1-2 高分組盒圖表徵表現人數與得分統計表 ... 49 表 4-1-3 高分組線段圖表徵表現人數與得分統計表 ... 50 表 4-1-4 低分組圈圈圖表徵表現人數與得分統計表 ... 51 表 4-1-5 低分組盒圖表徵表現人數與得分統計表 ... 51 表 4-1-6 低分組線段圖表徵表現人數與得分統計表 ... 52 表 4-1-7 高低分兩組在各階段表徵測驗平均得分統計表 ... 52 表 4-1-8 學生在文字題及三種表徵測驗得分的描述統計 ... 60 表 4-1-9 文字題得分與三種外部表徵測驗之相關性 ... 61 表 4-3-1 高低分群組在圈圈圖表徵表現之人數與得分統計表 ... 78 表 4-3-2 高低分群組在盒圖表徵表現之人數與得分統計表 ... 79 表 4-3-3 高低分群組在線段圖表徵表現之人數與得分統計表 ... 79 表 4-3-4 高低分兩群組在三種圖形表徵與數概念之錯誤類型 ... 81 表 4-3-5 高低分群組在圈圈圖表徵成功六種分法之人數統計表 ... 87 表 4-3-6 高低分群組在盒圖表徵成功六種分法之人數統計表 ... 88 表 4-3-7 高低分群組在線段圖表徵成功六種分法之人數統計表 ... 89圖目次
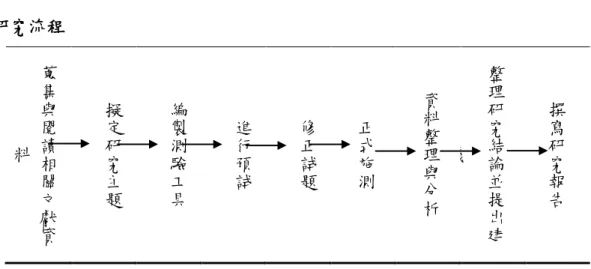
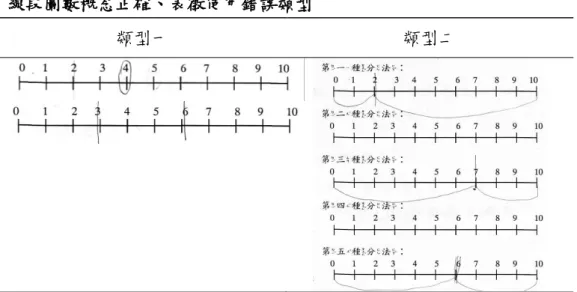
圖 2-1-1 文字與圖像綜合理解之整合模式 ... 10 圖 2-1-2 Lesh 等人(1987)的表徵關係圖 ... 12 圖 2-2-1 新加坡長條圖模式 ... 25 圖 3-4-1 研究流程 ... 47 圖 4-1-1 完整表示圈圈圖表徵以及數概念事例 ... 53 圖 4-1-2 表徵使用錯誤者、數概念正確類型 ... 54 圖 4-1-3 兩群組在圈圈圖表徵與數概念兩者皆錯的錯誤類型 ... 55 圖 4-1-4 盒圖外部表徵及數概念正確表示類型 ... 56 圖 4-1-5 盒圖外部表徵數概念不完整表示類型 ... 57 圖 4-1-6 盒圖錯誤表徵類型 ... 57 圖 4-1-7 線段圖表徵與數概念完整表示類型 ... 58 圖 4-1-8 線段圖數概念正確、表徵使用錯誤類型 ... 59 圖4-1-9 線段圖兩者皆錯類型 ………..59 圖 4-2-1 高分群組學生在圈圈圖表徵編碼 A 的作答類型 ... 62 圖 4-2-2 高分群組學生在圈圈圖表徵編碼 B 的作答類型 ... 63 圖 4-2-3 高分組使用盒圖表徵作答情形 ... 64 圖 4-2-4 高分群組學生在線段圖表徵編碼 A 的作答類型 ... 65 圖 4-2-5 高分群組學生在線段圖表徵編碼 B 的作答類型 ... 66 圖 4-2-6 線段圖編碼B錯誤類型 ... 66 圖 4-2-7 高分群組學生在線段圖表徵編碼 D 的作答類型 ... 67 圖 4-2-8 高分組學生在線段圖之錯誤表徵類型 ... 67 圖 4-2-9 低分群組學生在圈圈圖表徵編碼 A 的作答類型 ... 68 圖 4-2-10 低分群組學生在圈圈圖表徵編碼 B 的作答類型 ... 69 圖 4-2-11 盒圖表徵錯誤類型 ... 70圖 4-2-12 低分群組學生在線段圖表徵編碼 A 的作答類型 ... 71 圖 4-2-13 低分群組學生在線段圖表徵編碼 B 的作答類型 ... 71 圖 4-2-14 低分群組線段圖編碼B錯誤類型 ... 72 圖 4-2-15 低分群組學生在線段圖表徵編碼 D 的表示類型 ... 72 圖 4-2-16 低分群組學生在線段圖表徵編碼 A 的作答錯誤類型 ... 73 圖 4-2-17 圈圈圖數概念編碼錯誤類型 ... 74 圖 4-2-18 高分群組線段圖數概念編碼錯誤類型 ... 75 圖 4-2-19 低分群組圈圈圖數概念知識錯誤類型 ... 75 圖 4-2-20 盒圖數概念編碼錯誤類型 ... 76 圖 4-2-21 低分群組線段圖數概念編碼錯誤類型 ... 77
第一章 緒論
本章旨在闡述本研究相關之動機、目的、名詞釋意、研究範圍與限制,分為 四節:第一節為研究動機;第二節為研究目的;第三節為研究設計與實施;第四 節為名詞解釋;第五節為研究範圍與限制。第一節 研究動機
「數學」這門科目是被公認為科學、技術及思想發展的基石,數學結構之美 除了體現在科學理論的內在結構中,各文明的建築、工藝技術、千古流傳的藝術 作品更是處處留跡。數學,也是一種語言、一種共通的母語,精鍊的數學語句是 人類理性對話最精確的語言。日常生活或是職場生涯裡,數學知識與能力更是不 可或缺。在在顯示,數學舉足輕重的地位。因此,九年一貫課程綱要中指出數學 能力是國民素質的一個重要指標,也是基礎科學的工具;國民教育數學課程的目 標,希冀培養學生正向的數學態度,數學的教學應配合學童不同階段的需求,協 助數學智慧的發展,最後讓數學作為往後更高一層研究的基礎。 國家教育政策強調學生有權利受到良好的數學訓練,並充分認識重要的數學 概念及提升厚實數學能力,讓學生習得「帶著走」的能力。學生能力的發展始於 流利的基礎運算和推演,對數學概念的理解,之後懂得利用推論去解決數學問 題,包括理解和解決日常問題,以及在不熟悉解答方式時,懂得自尋解決問題的 途徑(教育部,2008)。 學生面對數學問題,必須先暸解問題,數學的敘述是一種抽象形式的語言, 開始解題時除了回憶相關問題的知識架構,建構出問題的表徵模式,這種抽象性 的本質更是一般人學習數學的最大障礙。問題解決往往是數學領域最困難的部 分,而許多學者研究發現解題者對問題所形成的表徵是解題的關鍵。美國數學課 程原則與標準(NCTM,2000)提到,表徵是數學學習過程中很重要的一部分,數學表徵提供學習者有效的解題工具,可以幫助孩子達成數學知識的理解、和他人 溝通以及推理的目的(Greeno & Roger, 1997)。學生在數學學習的過程中,對於 抽象的數學概念,若是沒有適當的媒介幫助他們思考以建構自我知識,學生可能 會因此而無法理解算則的意義而發生學習困難,更甚者對數學失去信心而放棄學 習。因此,適當的表徵輔助學習者學習甚至是教學者教學,能促使理解別人使用 表徵所欲表達的數學資訊、自己能夠運用表徵表達想法,也提供教學者傳達概念 以及瞭解學童學習狀況的途徑。 在數學學習中,蔣治邦(1994)提到表徵是用某一種形式(物理或心理),將一 種事、物或想法,重新表現,以達成溝通目的。因此,「表徵」在數學中所扮演 的角色,就是作為內心的想法和外在世界間溝通的媒介。Lesh等人(1987)提出數 學學習與解題五種表徵類型,不僅要瞭解各種表徵系統的意義與運用,還要能在 不同表徵系統間進行轉譯。所以,真正對數學概念暸若指掌,是指能運用多種表 徵來表示同一概念,並在各系統間將概念轉譯。因為在他們能夠掌握這些知識的 意義之後,不管表徵是以其他符號或抽象的形式出現,學生依然可以在之間自由 選擇、運用和轉譯,以達成解題的目的。其他學者相關研究也說明此重要性(遊 自達,1995;謝孟姍,2000;劉曼麗,2003;鄭寰文,2005;Davis, 1984;Putman, Lampert & Peterson, 1990)。所以老師在數學教學時,應該善用各種表徵,為學生 搭起思考的鷹架,使他們在運思階段的過渡能更為順利。學生在學習數個同一系 統的表徵之後,應嘗試依據數個表徵的共通性,將新活動用數學符號系統表徵出 來,倘若學生能夠使用多種不同形式的表徵來代表某一特定的數學概念,或是能 在不同形式的表徵之間進行自由轉換,則代表已經充分的「理解」、「掌握」此 一數概念所代表的意義了。 從小學開始,加減法文字題是學生最早接觸的應用問題,把生活中有關數字 的問題用文字表述,且會在往後課程中不斷反覆出現。加減法概念一向被視為相 關數學概念的基礎,因此,解題教學時應優先以加減法文字題進行訓練。而Riley、 Greeno 和Heller(1983)根據「語意結構」把加減法文字題分為改變、合併和比較
三類,每一類又依未知數性質再細分十四種題型。綜合許多研究發現「合併類」 最簡單;「比較類」最困難(古明峰,1999;蔣治邦、鍾思嘉,1991;Riley, Greeno, & Heller, 1983),雖然國內研究國小學生加減法文字解題之相關研究,多著重「比 較類」(江美娟、周台傑,2003;林淑玲,1999;楊淑芬,2001;鄭人豪,2004), 但考量本研究對象之認知學習能力以及相關數概念,僅採加減法文字題中「合併」 及「改變」兩類題目。 美國人工智慧與心理學專家Anderson提出ACT-R理論中兩類知識的形成,用 於描述個體已有的認知結構,是學習與問題解決的基礎。有關事實性或資料性知 識為陳述性知識(declarative knowledge);一種個體沒有明確提取線索,因而只能 借 助 某 種 活 動 形 式 間 接 推 測 出 來 的 知 識 , 稱 為 程 式 性 知 識 (procedural knowledge)。學習的過程可視為一種「條件─行動規則」,生成規則(production rules) 就是針對問題所給的條件,進行某種特定的認知操作過程。 當個體存在的生成規則不能解決問題時,ACT-R會先搜尋相關舊經驗,以此 作為類比的開始,形成解決新問題的新生成規則;對舊經驗的理解程度影響著舊 經驗的選取和類比的過程,當知識由陳述性形式轉化為程式性形式時,練習在此 過程發揮著重要的作用,經由重複的練習,程式知識漸漸自動化,條件和動作之 間的反應也會隨著精熟而縮短時間並且變得更加準確。 Anderson(2000)透過ACT-R的理論基礎來分析學童表徵使用的知識結構,正 可被用來達成認知工作分析之目的。認知工作分析從認知層面分析個人在完成一 件任務(task)時,腦海中衍生的決策過程、知識,以及目標結構(Schraagen,2002)。 教學者可藉由認知工作分析去擬定個人的教學計畫,分析課程內容,以及學生的 陳述性知識與程式性知識在學習與問題解決過程中交互作用情形,當陳述性知識 發現問題,教學者可以從「學習內容本身的知識」探究;當程式性知識產生混淆 時,可從「問題要怎麼做的知識」把解題步驟具體描述出來,進而加強練習促使 程式性知識的習成。 總體而論,我們嘗試測試概念知識與外部表徵對轉譯能力的影響;其次,我
們想知道:藉由ACT-R理論進行認知工作分析,探討對於10這個數字合理分割的 表達過程,概念是如何被解加減法文字題以及外部表徵類型的知識所引導。最 後,外部表徵的轉譯過程,建構出哪些任務結構,這些知識成分的本質,也是本 研究的目標。
第二節 研究目的與研究問題
基於上述研究動機,本研究之目的在於透過此次研究結果,瞭解外部表徵對 數概念學習之成效。其具體目的分述如下: ㄧ、藉由「認知工作分析」剖析三種外部表徵的知識架構,作為判斷學生使用表 徵歷程的工具。 二、探討加減文字題表現分別在外部表徵測驗的表現上有無相關性? 三、探討學生在三種外部表徵測驗的答題表現,並歸納結果作為往後教學的建議。第三節 名詞界定
為便於本研究之分析與討論,僅就研究中涉及之重要名詞加以界定如下: 一、三種外部表徵 外在表徵:是指解題者利用外在的數學符號、圖形、數表、物體等,做為輔 助或說明解題的工具。 (一)圈圈圖表徵: 本研究圈圈圖是指在計數過程中,保留問題具體物的意義,用「○」模擬實 物變化狀態,形成一個具體的刺激。 (二)盒圖表徵: 本研究盒圖是指在教科書的編排,安排三個方框,讓學生判斷部分─整體關 係,並將一數(整體)拆解兩數(部分)在方框內表示。 (三)線段圖表徵:本研究線段圖是指以直線段來表達數或量及其運算的方式。 二、整數加減法文字題 本研究之整數加減法文字題,主要是依照Fuson(1992)依語意結構及數量運 作方向,將整數加減法文字題歸納分類,分為改變類(起始量未知、改變量未知) 與合併類(部分量未知)。 三、十的合成與分解: 本研究界定「十的合成與分解」概念涵括:1.能完成任意兩數結合為一數的 工作;2.能將十拆解成為兩數的和的理解。 四、認知工作分析: 本研究的認知工作分析是指從認知層面分析個人在完成一個外部表徵時,腦 海中衍生的決策過程、知識,以及目標結構。
第四節 研究限制
本研究採臺中市北區某國小二年級一個班級27人為樣本,研究之樣本人數有 限。研究範圍以國小一年級上學期「分與合」、「加與減」、二年級「二位數的 加減」為範圍,研究結果不宜做過度推論。第五節 章節簡介
以下研究者將分別於第二章文獻探討介紹表徵的相關理論、運用在教學的研 究,說明表徵與整數加減學習與國內外相關研究,加減法文字題相關文獻探討, 最後探討ACT-R理論運用在教學上的相關研究,作為研究討論的參考;第三章實 驗方法與步驟仲介紹研究流程及研究工具;第四章分析實驗結果;第五章則提出 結論與建議。第二章 文獻探討
本章共分為四節:第一節探討表徵的學理基礎,旨在介紹表徵的意涵、功能 與類型,以及表徵轉譯間的重要性,作為本研究之基礎;第二節說明表徵與整數 加減學習與國內外相關研究;第三節加減法文字題相關文獻探討;第四節為探討 ACT-R 理論運用在教學上的相關研究,作為研究討論的參考第一節 表徵與數學學習之探究
學生面對數學問題,必須先瞭解問題的陳述,從工作記憶回憶相關問題的知 識架構,建構出問題的表徵模式。問題解決是數學領域最困難的一部分,而許多 學者研究發現解題的關鍵在於解題者對問題所形成的表徵。一個良好的表徵扮演 著兩種角色:思考與溝通的媒介、除此之外更是解題的工具。教授數學或是教科 書皆使用各種表徵系統來輔助學習,希冀學生能理解各種數學問題;重要的是必 須熟悉各種表徵系統的轉譯,並使用各種表徵系統進行運思與溝通,可見表徵轉 譯能力與數學學習過程有密不可分的關係。本節將說明表徵意義、類型與功能, 以及表徵轉譯的重要性。一、表徵的意義
認知心理學說,表徵是指一種將外在現實環境的事物以較為抽象或符號化的 形式來代表的歷程;從訊息處理觀點來看,表徵指的是訊息處理過程中,將訊息 譯碼而轉換成另一種形式,以便儲存或表達的歷程(張春興,1989)。 Mayer 的解題理論中,表徵的功用亦是從認知觀點出發。數學解題歷程中, 數學表徵除了是內部數學思考歷程亦是外在數學形式的展現。學生須將內部思考 過程轉化為外在解題的表徵,也就是進行表徵的轉譯活動,以作為溝通數學想法 的工具。 Lesh 等人(1987)以溝通及問題解決的角度,指出「表徵」是指心智過程模 式化所使用的符號系統,如圖形、符號、語言文字、具體操作物,也就是學童內心的概念轉為看得見的外在表現。 蔣治邦(1994)以數學的角度,認為表徵是用物理或心理形式,將一種事物或 想法,重新表現出來,以達成溝通的目的。 Ohlsson (1984, 1992)將完形學派的某些想法加入訊息處理的方法中。他的表 徵改變理論的核心在於:連結兩種理論方法,明定引導至頓悟,因而得到問題答 案之過程。其理論處理的是「問題如何解決」──此議題在問題解答者的心中表 達及建構的方式。若表徵被視為對長期知識的一個記憶探測(即是提取儲存在長 期記憶中跟問題相關的知識),則合理的表徵表示被活化的知識對問題的解答是 有幫助的,而不合理的表徵則是沒有幫助的。因此,問題解決者必須努力地將不 合理的表徵轉為合理的表徵。所以,轉變表徵的方式有:對目前的表徵擬定或增 加新的跟問題相關的資訊、放寬限制條件來展開或者重新編碼新的看法,此方式 會重新解釋手上的問題。由於重新解釋的結果,新的長期知識就會被活化,因此 就有一些操作可被支援來達成目標。 綜合上述,許多學者認為表徵是一種將內在思想或是心智過程以物理或心理 的方式重新轉譯(張春興,1989;蔣治邦,1994;Lesh,1987;Mayer,1985; Ohlsson,1992)。解題者對問題做出表徵,是對問題詮釋所建構的一個認知結構, 必須將問題的各種相關訊息統整在一起,當學生能使用適當的數學表徵傳達概 念,找出問題解決的途徑,只要能找出合適的表徵,新的長期知識就會重新內化 成為解題工具。所以,應鼓勵學生採用一些輔助的表徵工具,好比作圖或線段圖 等方式來幫助問題的表徵;學生能使用適當的數學表徵傳達所要表達的概念時, 亦可算是擁有擴充數學思維的技能了。
二、類型與功能
表徵的功能,並非僅止與他人溝通,也是自我溝通的工具,它是記錄個人數 學活動經驗的工具,以便於事後的反省;在解題過程中,亦可以作為前後步驟活動間的溝通聯繫工具。 表徵與解題能力,有其不可分離的關係。如果說每個步驟都涉及一個運思活 動,而每個運思活動都必須存在被運思的材料,前一步驟運思的結果,必須用某 一種形式表達出來,才能成為下一個階段的材料,繼續進行活動,由於表徵是運 思的材料,其形式自然會影響下一個運思活動,進而影響到整個解題方式,或解 題速度(引自蔣治邦,1994)。 (一)從運思歷程的觀點 從個人運思的觀點,Bruner(1966)將表徵區分為動作表徵(enactive representation)、圖像表徵(iconic representation)及符號表徵(symbolic representation)三種。動作表徵,即面對刺激時,我們以所學得的習慣動作做出 反應,當物體不再被操作後,物件意義則不存在,例如:在數學學習過程中,手 指點數或使用外在物件(實物、花片、積木...等實體物教具)這般可以實際外 顯操弄以掌握概念或事物。圖像表徵指的是用心像掌握概念,亦即是可在腦中形 成對圖像進行計數活動。符號表徵指的是受外在實物抽象的影響,代表實物或心 像的某種抽象性質,如在腦中形成數字元號的對應關係(轉引自劉秋木,1996)。 Bruner(1966)認為智慧的成長是運思活動逐漸地不依賴外在的刺激。圖像及 符號表徵都是心智活動的產物,可以留在記憶中,或重新自行建構出來,而不失 外在刺激原本的意義,它可以使人類的運思活動不再受外在刺激呈現的時空限 制,然而這些較為抽象的表徵是在學習經驗中發展出來的,先獲得圖像或符號表 徵的意義,當其意義穩固之後,才可進一步地使用圖像或符號表徵為材料,進行 運思活動(蔣治邦,1994)。 從認知互動的觀點來看,Kaput(1987)將表徵分為:1.認知及感知表徵 (cognitive and perceptual representation):指個體內在對於知識與訊息
的 表 徵 , 亦 即 為 個 體 在 腦 海 中 將 訊 息 及 知 識 轉 換 的 形 式 。 2.解 釋 表 徵 (explanatory representation):指自然語言或心像與其他數學符號間的聯結,用以 描述心理結構的模式,亦即為心理學家所建構的一種假設性實體,用以說明個體
的內在表徵。3.數學內部表徵(representation within mathematics ):指不同數學結 構之間的關聯,亦即以數學的某一結構來呈現另一種結構的特性。4.外在符號表 徵(external symbolic representation):指以外在符號物體來表徵數學概念的系統, 是用來表示抽象的數學概念的物質型式。以上分類,前三種屬於心智活動的產 物,即內在表徵(internal representations);後者屬於外在表徵(external representations)。所謂「內在表徵」是指在解題歷程中,解題者對於語文的解釋 與內在心像所扮演的解題角色;「外在表徵」是指解題者利用外在的數學符號、 圖形、數表、物體等,做為輔助或說明解題的工具(杜佳真,1999)。故,學習者 數學知識的內在表徵會受到外在表徵的影響;相對而言,外在表徵的型式也會反 映出學習者數學知識的內在表徵(蔡志仁,1999;謝孟珊,2000)。 Schnotz et al.(2010)提出表徵的兩種基本形式:描述與描繪。描述藉由符號的 輔助來表示一個對象,比如說透過語言的描述一個物件,或是透過數學符號來描 述牛頓第二定理 F=ma。描述性的表徵由符號組成,與它們要表達的對象並沒有 類似性;相反的,描繪是一種空間上的配置,想要表達的對象有結構上的類似性, 比如,照片、畫圖、地圖等。描繪由圖示來組成,這些圖示藉由類似或結構上的 相似性來表達他的對象,描繪並不會敘述,而是顯示出一個物體的特性。 描述與描繪針對不同的目的有不同的用法,描述表徵較一般化與抽象化,而 描繪較具體化與特定化,描述在表達能力上則比描繪較強大,在表達抽象的知識 時描述的能力比描繪更強。描繪比描述能表達較完整的資訊,比如,畫圖時,我 們不只要畫形狀,還有大小及方向。描述只能確認對象的形狀,無法指明大小或 方向。當使用在推論時描繪則較有用,由於可以直接從表徵讀出訊息,因此描繪 在計算上是較有效率的。 描述的表徵對於以下方面特別有用:以較抽象的方式來描述物件及情節的特 性、事件的解釋及預測、引導個人的注意及認知過程。描繪的表徵對於以下方面 特別有用:物件的外觀、情節與事件的理解、推理討論及問題解決。心智描繪表 徵的建構及處理,稱為心智模式,是條件式演譯及類別推理的核心。
認知心理學家將理解視為建構內部心智表徵的過程,假如理解視為溝通的一 部分,他是依據某人所寫或畫的記號(文字或圖像)。理解就是一個建立在某人所 產生的外部表徵為基礎來建構內部表徵的過程,上述所提有關描繪及描述表徵的 差異也同時應用到內部心智表徵的建構。文字表面結構的心智表徵和文字語意內 容的命題表徵都是描述性表徵,它們都使用符號來描述主題。相對上,視覺的影 像及心智模式都是描繪的表徵,他們的內在結構都可以對應到所要表達主題的結 構。
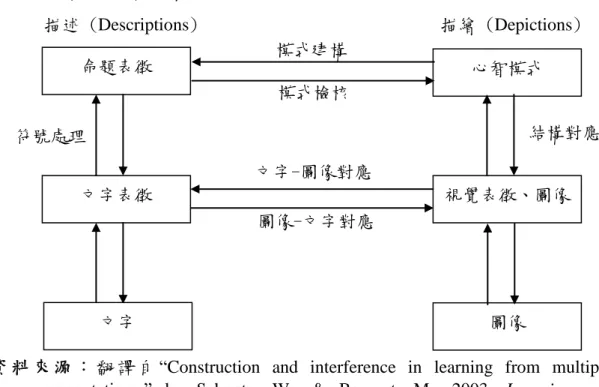
Schnotz and Bannert(2003)為了描述與描繪內外在表徵的差異,提出了文字與 圖畫理解的整合模式。此模式如圖 2-1-1 所示:
圖 2-1-1 文字與圖像綜合理解之整合模式 文字與圖像綜合理解之整合模式
描述 (Descriptions) 描繪 (Depictions)
資 料 來 源 : 翻 譯 自“Construction and interference in learning from multiple representations,” by Schnotz, W., & Bannert, M. ,2003, Learning and Instruction, 13, 141–156. 描述的分支包含了外部的文字、文字表面結構的心智表徵、以及語意內容的 內在命題表徵,這些表徵則依據符號處理來彼此互動。描繪的分支包含了外部的 圖畫及圖示、內部圖形的知覺或圖形顯視的影像,以及所描繪主題的內部心智模 命題表徵 心智模式 模式建構 模式檢核 文字表徵 視覺表徵、圖像 符號處理 文字-圖像對應 圖像-文字對應 結構對應 文字 圖像
式,這些表徵則依據結構對應來彼此互動。 當一個人理解一段文字時,此模式假設他建構三種心智表徵: 1. 他形成文字表面意義的心智表徵,此時他尚未理解文字的意義,但他可 以讀取文字。 2. 根據他讀取的文字,此時他建構命題表徵,此表徵會擷取文字的語意。 3. 最後,他會建構文字內容的心智模式,此模式是一種類物件,用來類比 於所讀取文字的主題。 當一個人理解一幅圖畫時,模式也假設他建構三種心智表徵: 1. 他形成一個視覺的感知,他尚未理解圖形的意義,只是圖形影像的複製。 2. 他建構一個心智模式,此模式擷取影像中的與主題脈絡相關的結構。 3. 最後,他會開始檢核他所建構的心智模型,嘗試從此模型中讀出新的資 訊,而檢測的結果則編碼為命題表徵。 因此,此模式不只用來分析文字與圖形的理解,也可以用來研究從外部表徵 來建構內部表徵的過程。知識的外部化可以用來溝通,例如教學者會藉由畫圖來 輔助講解題意,個人可以將產生的外部表徵視為認知工具來輔助問題解決,將運 思及問題解決過程中所需的認知需求卸載到情境當中。 (二)從溝通的觀點 表徵活動是指將「被表徵」的實體,使用另一種表徵型式,表示一些約定成 俗的共識來描述活動經驗,而不失其重要訊息,溝通並不限於與他人溝通,也是 與自己溝通的工具。Lesh, Post, & Behr(1987)從數學的學習與解題中,進一步具 體化將溝通的表徵區分五種不同類型(如圖 2-1-2)
1. 真實腳本(real scripts):利用實物情境的知識或物品來表示或解釋問題情 境。
2. 具體操作物(manipulative models): 必須配合某些數學概念使用才有意 義的具體物,如古氏積木、分數板、花片、摺紙等以顯示許多數學情境
的內在關係與操作。 3. 靜態圖形(static pictures):一種靜態的圖形模式,如圖形、圖表、圖示 等,指可幫助我們說明或內化為心象的圖形或圖表模式。 4. 口語(spoken language):日常生活用的口語符號,它同時包含此領域的 一些術語與特殊附屬語言(sublanguage),如邏輯推理等。 5. 書寫符號(written symbol):它包含特殊的語句或式子,如常用的數學符 號或算式。例如:5+6=11、6x+y=76、□+5=8…...。 圖 2-1-2 Lesh 等人(1987)的表徵關係圖 Lesh 等人(1987)的表徵關係圖
資料來源:翻譯自“Representations and translations amongrepresentations in mathematics learning and problem solving . In C. Janvier(Ed.),” by Lesh, R., Post, T.& Behr, M. ,1987, Problems of representation in the teaching and learning of mathematics,pp. 30-34. Retrieved from Hillsdale(NJ: Lawrence Erlbaum)
表徵活動即指上述不同表徵系統的轉換。在以上的五個表徵系統中,由於「靜 態圖形」與「具體操作物」與被表徵的實物之間具有較高的相似性,再加上其意 義也比較容易掌握,因此便成為國小階段的學生主要的運思材料。不過,具體操 作物與靜態圖形表徵的缺點是:它們只有在運思的過程中,不喪失所表徵的實物 意義,才能使用它們來進行運思並解決問題(蔣治邦,1994;許良榮,1996)。此 外,Lesh 等人(1987)認為表徵分類強調的並非是區別不同的表徵系統,而是強調
學生能否在不同的表徵方式中自由轉譯,其目的在於:藉由建立從一個表徵到另 一個表徵系統的關聯性,當從手寫的語言轉換為另一種表徵時能保留結構的特性 及意義,來正確地回答問題。藉以顯示出其對概念意義的掌握程度(羅美霞, 1994)。 (三)解題工具 表徵除了扮演運思材料與溝通的媒介外,尚有解題工具的功能。具體物表徵 能夠提供學生作為解題時的思考依據。然而此處的具體物並非為學生安排好現成 的情況,而是要求學生依其所學、所想來說明。透過對具體物的操作,呈現出學 生的數學概念。之後,必須由最初的引導,逐漸提升至抽象概念(Cobb, Yackel & Wood,1992)。數學符號除了溝通的目的,在數學教育的另一個目標,便是用來 解題。亦即在獲得符號初步意義、使符號成為溝通工具之後,要逐步提升學生對 表徵的運用,使數學符號成為解題工具(Mack,1995)。利用數學符號所具有的高 度系統性共通原則,讓學生能更有效率的解題,進而提升數學能力。 儘管表徵的分類觀點眾說紛紜,但表徵在學習上所代表的地位均予以肯定價 值。藉由表徵,學生能正確掌握運思材料的意義,釐清內在思緒,也因為認知思 考的改變或提升而變換表徵的型式,可見數學表徵和解題認知思考是相輔相成 的。
三、表徵轉譯的重要性
現存許多討論「數學中的轉譯」的資料把「轉譯」精準地描述成「全或無」 的活動──不是轉譯成功就是轉譯不正確。舉例來說,在一項針對使用外部表徵 的跨國研究中,Brenner、Herman、Ho 及 Zimmer(1999)調查了中國、日本、臺 灣與美國的 12 歲兒童中轉譯的兩個方面。表現僅以準確與不準確計分。外部表 徵內(同一種形式的外部表徵轉譯,比如同樣是手寫符號的轉譯)分析顯示,通常學生在辨識不同表徵的相似處有困難。外部表徵間(不同形式的外部表徵轉譯)分 析顯示美國學生在視覺外部表徵問題上較亞洲學生表現的要好,除了兩個更困難 的問題以外。當與問題難度有關的差別時,概念式知識在表現上佔了重要的角 色。二擇一的「準確/不準確方法」限制了關於轉譯可做出的推論範圍。因此, 由於方法論的限制,支持轉譯所必備的知識,其本質仍舊不明。 Gagatsis 與 Shiakalli (2004) 檢視了大學生的轉譯來說明解題技巧的不同之 處。在兩個小組活動中,向學生進行兩項有六個直接轉譯任務的測驗,唯有準確 的解答是作為「成功」轉譯的證據而得分。當圖像外部表徵剛開始出現時,轉譯 就更常失敗。而且,外部表徵間的轉譯並不是雙向的。舉例來說,一個學生可以 由文字外部表徵轉譯成圖像外部表徵,並不能預測反向的轉譯(例如,由圖像外 部表徵轉譯為文字外部表徵)。作者強調不同外部表徵系統的特點與結構導致產 生困難。並沒有明確說明學生的數學或外部表徵系統方面知識的特點與結構。然 而,未見學生轉譯表現出雙向性,顯示學生對於應用其知識缺乏彈性。 其他人則使轉譯概念化為一個過程,而不是探討準確性。Pyke(2003)運用了 路徑模組分析的方法(例如,建立一個 X 與 Y 的單向因果關係,當中 X 可能或不 能造成 Y),以檢視八年級學生的轉譯。他提出轉譯的兩個面向:參照策略與變 換策略。前者包含將外部表徵轉換為另一外部表徵,例如由文字轉為圖表,或者 由文字轉為心智模組。後者包含以外部表徵來建構出任務的結構。本路徑分析顯 示參照策略在學生的表現中僅佔了一小部分,但在輔助轉換策略中佔了極大的部 分,並且也相對影響了問題的解決。此發現也告訴我們轉譯過程包含了「較少」 與「較好」的知識成分與學生表現的互動。然而,這項研究並未闡明這些知識成 分的本質,也就是本研究的目標。 許多現行的數學教材將轉譯描述為全同或皆異的活動。幾乎沒有人試著以外 部表徵系統將其敘述為思考的知識或思考用的知識。轉譯的準確度,其狹義描述 有兩項限制:第一,其假定轉譯為單一關聯過程,其中在一外部表徵系統中所見 的訊息自動轉譯至另一外部表徵系統。第二、其排除轉譯是「構成一組產生解答
的知識與技巧的機制」的可能性。目前的研究則將轉譯概念化為兩種知識的結 合:問題敘述中的(例如,問題結構)的數學物件、性質與關係,以及與外部表徵 相關的知識。我們的轉譯模式有一個假說:每一種知識類別是由多種知識成分所 組成。以這種方式來理解,轉譯是一種瞭解數學概念是甚麼與將它呈現在外部世 界之程式間的一個函數。當面對問題時,學生必須能夠表達並結合多種概念與程 式,轉譯必然比全或無或兩部分的過程更為複雜。 Pimm(1990)與 Duval(2006)提出:轉譯不必然能在不同間外部表徵系統得到 完美的結果。轉譯過程不夠理想時,轉譯就被以突變與錯誤來解釋。相同地,當 我們任務中的表現是不甚理想的,我們就以轉譯錯誤來說明。不甚理想的轉譯暗 示:如果全部的知識與技能在處理某一工作上是必需的──僅有該範圍的 1/x─ ─是學生可以表達的。而最佳的轉譯暗示了學生可以完整的表達這項任務所要求 的必需知識與技能(如:x/x)。另一個假說為:轉譯要不是部分的(如:不甚理想) 就是完整的(如:最佳的)。 美國數學教師協會(NCTM)在 2000 年公佈的「學校數學課程之原則和標準 (Principles and Standards for school Mathematics)」一書中,表徵能力區分為:創 造使用表徵去組織、記錄、溝通數學想法;選擇、運用及轉換數學表徵去解決問 題;使用表徵模式及解釋物質的、社會的和數學的現象。NCTM 將發展學生表 徵能力列為教學重點。學生若能適當的運用多樣化的數學表徵,不但能夠增進數 學概念的理解,並且在相關的數學概念之間建立連結,真正理解數學,還能以數 學表徵與他人溝通數學想法,且應用於真實情境當中。 不同的問題需要不同的表徵系統,而不同的表徵系統也將會影響到題目的難 易程度。因此 Lesh 等人認為:無論題目呈現何種表徵形式做為溝通的媒介,學 生都必須能夠在不同表徵形式間自由轉譯──就是用自己的方式重新表徵也不 失其原意。如果學生能掌握這樣的轉譯過程,將有助於解題與數學的學習(蔣治 邦,1994)。Noss and Hoyles(1996)提出僅就單一表徵的學習並不適當,因為在解 題時,不同表徵的角色結構相互牽連,單一表徵在解題時必須要能切換到其他表
徵上。遊自達(1995)認為在數學學習過程中,應該讓學生掌握符號系統做有意義 的操作,更需注意不同表徵系統間的關聯,進而利用多重表徵代表數學概念。教 科書是國中小階段獲得知識的主要來源,因而,在數學教科書中安排合宜的表徵 轉譯活動更顯得重要,除了幫助學生理解不同情境中共同的數學要素,更能提供 學習者一種建立溝通訊息、證明推理的有用工具(Greeno & Hall,1977,轉引自 洪小凡,2008)。 故,教科書中當安排多樣的表徵轉譯活動,讓學習者靈活進行表徵轉譯,選 擇合適的表徵來解題,當學生越能掌握不同表徵的意義,並能自由的運用這些表 徵成為數學思考能力的工具時,對於學習者數學概念的發展是有所幫助的。
第二節 表徵與整數加減學習
表徵系統乃是個人在社會文化影響之下逐步發展而得的思考工具,其一方面 是個人建構的成果,是內在的;另一方面也是社會文化的產物,是外在於個人的 實體,並具有社會約定成俗的意義。因而當學生學習數學之時必須獲得表徵約定 成俗的意義,並使該表徵成為溝通的工具,進而能使用該表徵進行問題的解決。 以此觀點而言,學校進行數學教育的目標之一便在於引導學生去建構或內化社會 共通的數學符號系統,以使能進行數學思考,進行數學溝通(遊自達,1995)。一、表徵與數學學習
表徵是數學學習的重要媒介。學生若能根據問題情境,運用適當的數學表 徵,例如圖像、實物、抽象符號等形式來協助自我與他人溝通,藉由多種表徵表 達同一個數學概念,且在單獨的表徵系統之內以及各個表徵系統之間可以靈活的 轉譯,才能證明學生具有穩固的概念理解(Dreyfus & Eisinberg,1996)。許多研究表示,圖形表徵解題策略對國小學童數學解題有幫助。然而,為 何使用圖形表徵來解題是有好處的? 認知研究已經提出了相當多的論述以及實 驗來驗證這樣的優點。比如 Larkin 與 Simon(1987)提出:以圖形表徵的方式來
解決問題優於使用語詞表徵的三個理由:1.將相關的資訊區域群組化來降低問題 解決的搜尋,也就是說當我們在解決問題時,我們會從頭腦中搜尋相關的資訊, 而圖形表徵會使得我們較容易將相關資訊聚集起來,搜尋與問題相關的知識會較 快。2.圖形表徵相較於符號表徵而言,在比對上較容易,由於圖形表徵較符號表 徵具體,在比對相關知識時較容易。3.圖形表徵可以輔助知覺的推理,而這種推 理的方式要比符號表徵的推理容易。 在數學學習中,若能提供學生不同的表徵與表徵譯活動,引導其將問題情境 轉譯成多種表徵形式,有助於學生思考與問題分析的呈現,幫助學生不僅以一種 有意義的方式來學習數學。透過文字表徵轉譯為圖像表徵的活動,運用合宜的圖 像表徵來呈現問題中隱含的數量關係,能夠增進學生理解文字問題的題意並減少 解題歷程的錯誤(方美珍,2007;林文彥,2006;羅秋霞,2006)。理想的數學學 習需引導學習者在同一個物件上運用數個表徵,並且對該概念有清晰的多重表 徵。Noss and Hoyles(1996)提出僅就單一表徵的學習並不適當,因為在解題時, 不同表徵的角色結構相互牽連,單一表徵在解題時必須要能切換到其他的表徵 上。學生面對一個問題情境若能形成多種表徵,並形成表徵間的連結,將有助於 對問題的理解和解題能力。可見,表徵對於數學學習之重要性。 表徵與數學學習關係密切的另一個因素,便是表徵具有另一種重要的性質─ ─「多義性」。所謂表徵的「多義性」是指相同的數學概念或知識,是可以使用 多種不同的形式來加以表徵的;換言之,原有的數學概念並不會隨著外在表徵型 式的變化而有所改變或差異(蔣治邦,1994;Kaput,1987)。因此,同一個數學概 念可有不同形式的外在表徵,數學概念的存在並不受外在符號表徵的影響。例 如:「3」、「三」、或「○○○」雖是不同的表徵形式,卻是同一種數學概念(遊 自達,1995)。
因表徵代表著多重的意義,所以學生在學習數學的過程中,不但需要瞭解 各種符號所代表的表徵意義,也必須能夠運用不同形式的表徵來進行溝通與運 思,如此方能進行有效的解題(林美惠,1997)。Lesh, Post, Behr(1987)認為:要想
瞭解學生對某數學概念意義的理解程度,最好的方法便是觀察學生是否能夠在不 同的表徵形式之間進行自由轉譯;倘若學生能夠使用多種不同形式的表徵來代表 某一特定的數學概念,或是能在不同形式的表徵之間進行自由轉換,則代表學生 已經充分的「理解」、「掌握」此一數概念所代表的意義了。 數學的概念理解包含兩個面向,除了能夠以一套符號或系統來表徵數學概 念,另一個則是能以多重表徵來呈現一個概念,且能在不同表徵系統間進行轉譯 活動(Davis, 1984)。學生學習數學概念過程中,進行表徵轉譯的過程產生的內心 建構有助於未來學習並且能應用在其他表徵系統,當學生數學概念持續進化,其 表徵系統網絡則會越來越複雜,對於表徵轉譯的能力愈能彈性掌握,其對於概念 學習則是愈成功(Behr, Lesh & Post,1987)。表徵轉譯過程除了產生內心建構且有 助於日後的數學學習之外,Izsak(2000)則提出透過表徵轉譯的過程學生可以反思 自己解題的過程,且表徵能處理問題情境與數學概念間連結的困難。總的來看, 在數學概念學習時,可以透過表徵轉譯活動來幫助學生思考、理解題意、建立不 同表徵系統間的連結、亦能理解題意與記錄題目。因此,表徵轉譯活動對促進學 生的概念學習來有相當大的助益。 根據 Bruner 的研究,認知表徵是隨著年齡發展的,認為智慧的成長是指運 思活動從具體的實務操作逐漸轉換成抽象符號來認知,當不再依賴外在刺激運用 抽象符號之前,學生仍應從具體的學習活動中瞭解抽象符號表徵的意義,才能運 用符號進行運思,這種有意義的歷程對學習運用抽象表徵非常重要(蔣治邦, 2001b;黃幸美,2003)。 Heddens(1984)則以表徵觀點出發,將學生學習分為四個連續階段: 1. 具體表徵階段:運用生活中真實存在的物體,如蘋果、彈珠……等; 2. 半具體表徵階段:利用圖片或照片來代表實際物品; 3. 半抽象階段:利用上同於實體物的符號或圖形來代表實際物品,如畫三個○ 代表三隻貓; 4. 抽象階段:運用符號表徵,如:2+5=7。
Heddens 認為學習者必須在具體階段,將新的知識加以內化,並有系統地沿 著四個學習階段,將新學知識附予抽象化的表徵,學習者才得以在真實世界與抽 象世界建立好連結。 Witzel 則指出美國許多州的數學標準規定數學學習需要讓學生透過操作來經 驗數學,以便建立數學的問題解決與高層次的思考。此外,學生也可以將操作具 體物過程和使用的畫圖表徵兩者來進行連結。未來,當學生面臨到困難的數學問 題時,可藉由具體物操作與圖像表徵間的連結,而將操作具體物的過程畫下來解 決問題,逐漸將其運用表徵能力抽象化。因此,教科書呈現的表徵形式與安排之 表徵轉譯活動須依各學習階段而有所不同,才得以逐漸幫助學生建立運用抽象畫 表徵的運思能力。 低年級學童常透過付諸行動(act out)的表徵轉譯活動呈現文字表徵的情境, 具體呈現出問題中抽象數量間的關係(Carpenter & Moser,1982)。但當問題數字 範圍逐漸增大時,具體操作問題情境的策略,會產生許多運算上的不便。故此, 學生必須形成新的策略,才得以因應與簡化大數量的需求與困難(蔣治邦, 2001c)。 所以,為何教科書中提供不同表徵形式來輔助學習?為何教學者必須讓學生 經由表徵轉譯活動過程中,反思抽象化的活動?皆是希冀藉由教學過程中,教學 者傳達學習者約定俗成的表徵概念,同時也讓學習者瞭解內容或對數學產生論 證,得以透過適當表徵與他人進行溝通,進而促進思考。
二、表徵與整數加減學習
表徵在整數加減學習方面,有以下幾種功能:具體呈現整數加減學習之抽象 概念並促進對整數加減內容意義的瞭解,分述如下: 兒童在未入小學前,即已能利用計算策略來解決簡單的加減問題(蔣治邦, 2001)。具體物加減計算發生於日常生活中,兒童透過生活中的實際物品計數來熟悉計數經驗,得以學得簡易的加減計算技能。然而入小學後,兒童開始接觸正 規運算過程與公式的教學。對兒童而言,這是一些脫離情境的符號學習,較難理 解與運用。因而,低年級教科書中呈現文字表徵轉譯為生活中常見之實際物品(具 體物圖片)的活動,利用生活中實際存在的物品作為表徵,將問題中的訊息視覺 化,讓具體物圖片形成一個具體的刺激,並讓學生從活動中,核對問題中的訊息 與具體物圖片是否一致,進而思考及檢視對問題的理解是否與題意一致,逐漸引 導學生理解加減運算格式的意義,以協助兒童使用正確的解題策略(戴妏純, 2008)。而教科書安排文字表徵轉譯為半抽象符號「○」的活動,讓學生將「○」 視為問題情境中具體物表徵,在計數過程中,保留問題具體物的意義,用「○」 模擬實物變化狀態,用「○」為材料,依循具體物系統的運思法則(例如可被移 動點數),完成計算總數的運思活動,唯有在運思過程中,不喪失具體物所表徵 的實物意義,才能使用具體物的運思,來解決實物的問題(蔣治邦,2000a)。甯 自 強 (1993)提 出 兒 童 能 夠 透 過 把 關 係 放 在 物 中 , 利 用 物 的 建 構 與 解 構 (deconstruction)把內涵的關係藉由具體物操作的過程表徵出來,從而解決涉及關 係問題,他們可以透過物的構成成分來聯絡關係,兒童會利用活動將未知量表現 成已知量,其次進行已知量的確定數值工作。 在低年級階段,學童多半進行動作或圖像的運思活動,在動作運思活動中, 運思材料是實物、具體物、或圖畫,這些材料都可進行外顯的點數行動;在圖像 運思中,運思的材料是實物、具體物、或圖畫的心像,而進行內在的點數活動。 在基本加減運算範圍中,學童可能發展出符號運思,例如在合成情境下,只想到 2 和 3 兩個符號,即聯想到 5,但由於此種聯想是由許多 2 加 3 得到 5 的活動經 驗中提昇出來,學童即使只想到符號,但符號的意義在運思過程中,不會喪失。
如果學童只是背誦加法事實,則令人擔心在提取記憶的過程中,數字元號的意義 是否仍在掌握中? 合成與分解是解決數量問題的兩種最基本的運作,在一年級數學教材中,其 課程內容編排以數數能力為基礎,透過分解與合成的具體問題情境,進行 10 以 內數量的分解與合成之操作活動,增加學生解決數量問題的能力,並從數量的分 解與合成之中,體驗加法與減法的意義。在教科書的編排,學生因為不熟悉 10 的合成與分解,在做 6+7=?此類問題時,如果不透過操作具體物或圖像表徵, 便無法藉助「6 加多少等於 10」的想法來解題。 當學生在開始學習合成與分解的活動時,教學者通常採用分段布題的方式, 引導學生進行活動;透過分段布題與教師的協助,可以將一個較複雜的合成或分 解活動拆成兩個做數活動和一個數數活動,幫助學生對於合成或分解問題的理 解。例如做添加型問題:阿雄有 3 顆蘋果,哥哥再給他 2 顆蘋果,問阿雄有幾枝 鉛筆?教師可以先說:「阿雄有 3 顆蘋果」,要求學生用具體物或圖像表徵做出 3, 教師再說:「哥哥再給他 2 顆蘋果」,要求學生再做 2,最後教師再問;「現在阿 雄有幾顆蘋果?」要求學生說出答案。如果教師意圖使用花片或畫圈圈來表徵蘋 果,詢問學童這裡有多少個蘋果時,則花片或圈圈成為蘋果的具體物表徵,則學 童面臨表徵轉譯的問題,要理解教師的問題,必須將眼中的具體物或圖象表徵, 轉換成心中的蘋果影像,才能在點數花片或圈圈的同時,仍保留其蘋果的意義, 唯有在仍保有其意義時,點數的結果「5 個」,才具有 5 顆蘋果的意義,換言之, 是用具體物或圖象表徵來模擬實物的變化狀態,用圖像為材料,依循具體物系統 的運思法則(例如可被移動點數),完成計算總數的運思活動,唯有在運思過程 中,不喪失具體物所表徵的實物意義,才能使用具體物的運思,來解決實物的問 6 + 7 = ? 4 3 6 + 4=10 10 + 3=13
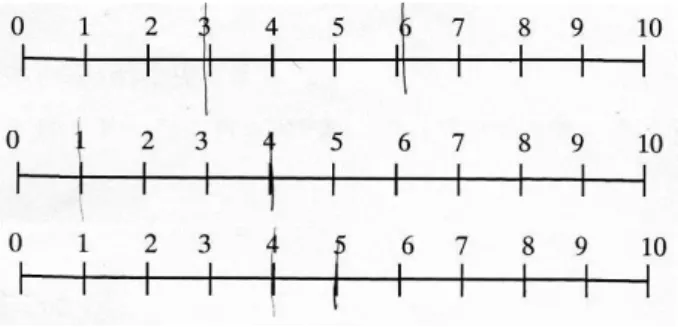
題。洪鬱雯(2006)認為對低年級的學生而言,如果三塊甜甜圈,不管我們用畫圖 的○來表示,或者使用花片來表示,在了解符號表徵所代表的意義之後,他們就 會運用這些表徵來進行運思和運算以解決問題。 除此之外,在教科書整數加減教材的中,為了讓學生『看』見加減運算「部 分-整體」的結構,常使用抽象符號──「線段圖」來表徵問題中數量間的關係。 線段圖可以把情境用圖示表達、呈現數學運算符號及把合成、分解情形表現的更 充分,使得外在表徵-線段圖成為學生理解數學概念或表達想法的溝通工具,但 學生必須發展相關的概念,才得以正確的解讀編輯者透過表徵形式意圖傳達的訊 息。 教育部頒布的國民中小學九年一貫課程綱要數學學習領域分年細目 2-a-04 詮釋說明:能理解加減互逆,並運用於驗算與解題。與 1-a-03 的主要差別是, 這裡可以不再涉入具體情境,在心理上用比較形式的方式,應用加減互逆來解題 或用加法做減法的驗算。在加減互逆的學習裡,可以依情境引入線段圖的說明方 式,讓學生更理解加和減的關係。當應用題中數量關係比較複雜,學生難以釐清, 線段圖可以準確的找出數量間的對應關係,釐清題目的問題,化繁為簡,使得思 考問題的歷程透明化、具體化,發展學生思維能力。線段圖也能進行多種能力的 培養。比如說,一題多解能力的培養、根據線段圖來編應用題,進行溝通能力的 培養,並且直接根據線段圖進行列式計算。不過,國小學童年齡小,理解能力有 限,教導低年級學童,線段圖應只作為教學工具,而且學生還不適合作圖,不宜 要求學生自行繪製線段圖。 數線最重要的概念之一是數與點的對應,如離起點 49 公里的交流道是哪一 個?又如數線上的「1」除了代表在數線上的位置是 1,也代表與原點的距離是 1。
另一個是點與數的對應,如:臺中交流道離起點有多少公里?還有一個是利用座 標算出兩點之間的距離,如從員林交流道到鬥南交流道有多遠?部編教材初步引 入數線時,先暫時以刻度尺的方式去解釋,但要讓學童意識到數線與一般尺稍有 不同。其教材在數線單元中想傳達的概念如下:數線概念最重要的概念是數與點 的對應,例如數線上的「1」除了代表在數線上的位置是 1,也代表與原點的距 離是 1。做加與減的具體操作時,以長度的合成分解為前置經驗,讓學生體認在 數線上做加減運作模式;數線兩點間的距離以「間隔」命名,並融入具體情境包 裝求兩點距離這種較為抽象的問題;透過數線上的運作,觀察到右邊的點所代表 的數會較大,在左邊的點代表的數會較小,進而在數線上做大小比較。 在部編教材,一年級上學期開始,在數的表徵上,出現利用「向上數」或「向 下數」的圖示表徵來做「7+1」或「9-2」的題目。「向上數」的圖示向「右」延 伸,「向下數」的圖示向「左」延伸。有步驟的,引導學生對應到數線圖知識: 從一個數字點跳至下一個數字點,並計算跳了幾次。到了二年級,學生學習概念 的範圍擴增到 1000 以內的數,在認識新數字的序列上,更利用下列表徵來引導 學生數數: 以做為數線正式引入前的 前置經驗。
Gustein & Romberg(1995)提出當看到教科書中呈現之線段圖時,學生是否能 賦予正確意義,這是值得關心的議題。蔣治邦(2000c)指出線段圖並非是學生常 用的溝通表徵,線段圖與文字表徵間的關係,並不如理論中顯而易見,線段圖表 現數量合成、分解或比較的語法,皆可能造成學生看見問題中數量關係或文字表 徵轉譯與線段圖之間表徵轉譯的困難;並且從朱建正與吳昭容(1993)研究發現: 能在圖示中用某種合理方式標示問題的數量關係者,解題率較高,並發現大約至 六年級才有較多學生能運用有效、有意義的空間關係,比如說以線段圖來表徵問 題中的數量關係。 為何要以「十以內數的合成與分解」作為本研究數概念的主題?研究者從文 獻探討的過程中發現,「十以內數的合成與分解」是小學數學課程中「加法」與 995 996 997 +1 +1
「減法」的前置概念。在一年級數學教材中,其課程內容編排以數數能力為基礎, 透過分解與合成的具體問題情境,進行 10 以內數量的分解與合成之操作活動, 增加學生解決數量問題的能力,並從數量的分解與合成之中,體驗加法與減法的 意義。教科書則安排表徵以輔助學習,學生可以將操作具體物的過程和使用畫圖 表徵兩者來進行連結。未來,當學生面臨到困難的數學問題時,可以藉由具體物 操作與圖像表徵間的連結,將操作具體物的過程畫下來解決問題,逐漸將其運用 表徵能力抽象化。 由以上論述可得知,表徵轉譯在整數加減學習過程中扮演著重要角色。學生 在學習數個同一系統的表徵之後,應嘗試依據數個表徵的共通性,將新活動用數 學符號系統表徵出來,不能僅以在具體物操作活度中成功解題為目的,而是以學 生能透過抽象表徵運思活動解決問題為教學的最終目的。換言之,學生必須依據 其運思發展逐步掌握數學符號的多重意義,成為發展更高層運思的經驗基礎。
三、表徵在教學上的相關研究
(一)圖形表徵與解題之關係 在目前國小數學教學而言,學生平日接觸與練習最多的題目表徵型式是「符 號」(包含文字及書寫符號)表徵系統;然而在日常生活中,學生最常接觸的卻是 「圖畫」或「圖像」表徵系統。因此在數學教學上,教師是否可以嘗試使用圖畫 或圖像來表徵數學問題,以達到幫助學生學習數學的目的?而從實徵研究中,卻 獲得了不一致的結果:有些學者認為「圖示」是具像的、同時的與統整的特質, 可以幫助學生在解題時形成恰當的表徵,增進其解題表現(Webb & Sherrill, 1974;Bishop, 1989)。另外有一些學者卻認為「圖示」對於學生形成有效的問題 表徵上,是沒有助益的,甚至會因為圖示具像的特質而造成學生概念抽象化的困 難(Clement, 1981)。representation)和「問題解決」(problem solving)兩大部分。Lewis 和 Mayer(1987) 認為大多數學生不能成功解題,問題在於學生對問題的理解表徵,比問題的求解 還要重要,所以問題的解決教學應注重問題表徵訓練。
學 者 們 (Davis & Mckillip,1980; LeBlance, Proudfit & Putt,1980; Xin & Jitendra,1999)表示圖畫是一種很好的外在表徵,利用圖畫來表示題目是一種有助 於分析題目的教學法,例如在解數學文字題時附上具體的圖示可以減少學生解題 的困難度與閱讀工作記憶的負荷量;圖示表徵策略也可以幫助學生回憶過去相似 的情境,鼓勵學生主動投入理解題意,進而提升其解題能力的表現和幫助解題。 根據國際數學科學研究(Trends in International Mathematics and Science Study) 的結果(TIMSS 2007),新加坡的學生在數學解題的表現持續相當優異,其成功的 原因在於導入了一個稱為新加坡模式的圖形表徵解題策略。此模式利用了一個視 覺的方法讓學生將焦點集中在數學的關係、運思及操作上(Englard,2010)。學生 被教導利用變動長度的長條圖來理解數學的關係及操作。有四個基本模式來輔助 學生運思,用於決定解單步驟問題時要使用哪一種運算,近而簡化學生在面對多 步驟問題的計算。四種基本模式如圖 2-2-1 所示:
圖 2-2-1 新加坡長條圖模式 新加坡長條圖模式 1.部分─全體(加法與減法) 2.比較(加法與減法) 3.部分─全體(乘法與除法) (續下頁) 4.比較(乘法與除法) 全體 部分 部分 較大數量 較小數量 差異量 全體 部分 X 是 Y 的三倍
資料來源:翻譯自“Raise the bar on problem solving,” by Englard, L. ,2010, Teaching Children Mathematics, 17(3), p.156–163.
新加坡的學生在國中小階段都一致地被教導使用此四種基本模式來解決文 字題。從三年級開始導入基本的部分─全體(加法與減法)模式,老師一開始從最 簡單的問題來教導學生如何應用此模式來解題。到了四、五年級,學生便應用他 們所熟悉的技巧來解更複雜的問題。到了六年級時,學生便已具備解更難問題的 能力。有了這樣紮實的基礎,學生很容易地被導入初步的代數概念。此模式不只 教學生如何去解題,他也能引導學生如何用符號來表達代數的概念,這便是代數 理解的主要意義。 目前在美國已有超過 600 所學校採用新加坡的數學教科書。由於新加坡學生 的成功,數學家及老師都相當期待。老師喜愛此模式的簡單極有效率,數學家喜 歡他的邏輯架構、一致的課程編排,以及將焦點放在學習代數概念所需的技能 (Hoven,2007)。 (二)圖形表徵解題策略之相關研究 圖形表徵策略是指解題者在解題過程中,運用畫圖的方法,畫出與題意相關 的圖形或圖案,藉以幫助解題者觀察、推理、思考,是達到解答問題的一種手段 (林香、張英傑,2003),相關的研究如表 2-2-1: 表 2-2-1 圖形表徵解題策略之相關研究 圖形表徵解題策略之相關研究
研究者 研究主題 研究對象 研究結果 方美珍 (2007) 整數加減文 字題 學障生 本研究目的主要在比較「圖片表徵」、「錢 幣表徵」及「線段表徵」三種模式表徵解 題策略教學在教學階段、保留階段對於增 進國小學障學生數學文字解題。三種教學 皆能提升受試者數學文字題之立即學習 成效。 羅秋霞 (2006) 整數加減文 字題 國小三年 級數學低 成就學童 本研究旨在探討圖示表徵策略對提升國 小三年級數學低成就學童加減文字題的 補救教學成效。圖示表徵策略教學能增進 國小三年級數學低成就學童理解題意、正 確列式,減少解題歷程的錯誤。 林文彥 (2006) 整數加減比 較型文字題 六到七年 級學生 本研究依循教學設計模式,發展完成兩套 數位教材,分別引用線圖表徵與圈圖表徵 作為學生理解文字問題的認知鷹架,探討 參與對象在使用線圖和圈圖表徵數位教 材教學後的學習成效之差異,使用不同圖 形表徵數位教材對學生在代數比較類型 文字題解題的學習成效有顯著差異。 林秀燕 (2004) 整數加減文 字題 國小低年 級學生 探討實驗班和控制班採用圖示策略後,在 整體上的學習成效、圖示策略融入教學的 可行性、不同題型文字題的解題表現及不 同數學程度學童的解題表現。在不同面向 合宜的外在表徵有正向效益。 李秀玲 (2007) 加減文字題 二年級學 童 本研究旨在探討「線段圖」引入教學後, 對國小二年級學童在加減文字題的解題 表現,並瞭解其對學童加減互逆概念的建 立是否有幫助。研究發現在學生學習保留 上有顯著影響。 楊馥如 (2012) 加減文字題 國小二年 級學障生 探討線段圖示表徵策略融入教學之後對 學習障礙學生解比較類加減文字題之解 題成效。結果顯示該策略能提升解比較類 加減文字題之整體解題成效、「差異量未 知題型」、「被比較量未知題型」、「參照量 未知題型」之立即成效與維持成效。 林美惠 (1997) 題目表徵型 式與加減法 解題 國小二年 級 學生解題時,題目表徵的形式不同,解題 表現也不同,其中以圖畫題的解題成果最 佳 (續下頁)
研究者 研究主題 研究對象 研究結果 陳美芳 (1995) 「學生因 素」與「題 目因素」對 乘除法應用 問題解題影 響 國小五年 級 高數學能力組在文字題與圖畫題的表現 上均優於中數學能力組學生的表現;中數 學能力組學生在文字題的解題表現優於 圖畫題的解題表現 陳雯貞 (2004) 圖示表徵型 式對學生解 題表現之影 響- 以面 積、周長單 元為例 國小四、 五、六年 級 學生在不同的圖示表徵型式之面積、周長 題目的解題表現有顯著差異。學生的正確 解題策略在不同圖示表徵型式間有部分 差異, 且錯誤類型在不同圖示表徵型式 間也具有些許差異。 林香、張 英傑 (2003) 國小數學資 優生圖畫表 徵解題策略 研究 國小五六 年級亞太 區小學數 學奧林匹 亞競賽台 灣區初賽 錄取學生 前 20% 能夠有效的整合題目條件,轉化成合乎比 例關係的線段圖,並且清楚標示數據數量 關係的學生,有較高的解題成功率 黃芳玉 (2003) 數學表徵能 力與計算能 力 國小六年 級學童 分析國小六年級學生的數學表徵能力與 計算能力,研究結果發現學生具有良好之 計算能力,但不代表他們亦伴隨著計算能 力之精熟,而發展相同之徒刑表徵能力與 符號表徵能力。 陳啟明 (2000) 不同題目表 徵型式及相 關因素學生 解題表現之 影響 國小五年 級學童 探討不同表徵型式(文字題、短語題、圖 畫題)及相關因素(運算步驟、題目訊息和 認知風格)對國小五年級學生數學應用問 題解題表現之影響。研究發現學生在「圖 畫題」上的解題表現顯著優於「短語題」 和「文字題」。 (續下頁)
研究者 研究主題 研究對象 研究結果 李虹韻 (2010) 線圖策略對 兩步驟文字 題之學習成 效 國小四年 級數學低 成就學生 探討線圖策略對國小四年級數學低成就 學生兩步驟文字題之學習成效。研究顯示 線圖策略教學能增進兩步驟文字題整體 解題正確率之「立即效果」、「保留效果」, 以及各題型解題正確率之「保留效果」。 幫助學生理解題意、正確列式、檢核答 案,減少解題歷程的錯誤。 蔣治邦 (2000) 年級因素對 學童解讀線 段圖之影響 國小三四 年級學生 本研究在加減運算範圍內,探討中年級 學童進行文字題與線段圖間轉譯的能力, 以及線段圖在解題過程中的角色。結果顯 示解題能力優於轉譯能力,文字題與線段 圖間轉譯的能力,尚有加強的空間。 研究者歸納表 2-2-1 表徵相關研究後發現:多以個案訪談、團體施測等研究 方法來分析學生在進行數學學習時進行不同表徵間的轉譯活動時的情況,藉以瞭 解學生在理解與解題的學習成效;研究結果歸納出多樣性的表徵可以增進學生數 學學習的成效,透過學生進行表徵轉譯活動可得知其數學學習的情況。從相關研 究發現國內針對表徵轉譯活動之研究多為探究學生數學學習的轉譯情形,或是表 徵對於學習成效有無助益。 許多現行的數學教材將轉譯描述為全同或皆異的活動。幾乎沒有人試著以外 部表徵系統將其敘述為思考的知識或思考用的知識。轉譯的準確度,其狹義描述 有兩項限制:第一,其假定轉譯為單一關聯過程,其中在一外部表徵系統中所見 的訊息自動轉譯至另一外部表徵系統。第二、其排除轉譯是「構成一組產生解答 的知識與技巧的機制」的可能性。目前的研究則將轉譯概念化為兩種知識的結 合:問題敘述中的(例如,問題結構)的數學物件、性質與關係,以及與外部表徵 相關的知識。我們的轉譯模式有一個假說:每一種知識類別是由多種知識成分所 組成。以這種方式來理解,轉譯是一種瞭解數學概念是甚麼與將它呈現在外部世 界之程式間的一個函數。當面對問題時,學生必須能夠表達並結合多種概念與程 式,轉譯必然比全或無或兩部分的過程更為複雜。
轉譯已被描述為在一個外部表徵系統中解決任務的能力,而不是某一個任務 被表達為外部表徵系統的能力(Gagatsis & Shiakalli, 2004;Lesh et al., 1987)。總體 而論,我們想測試知識與外部表徵對轉譯能力的影響;我們想知道:對於 10 這 個數字合理分割的表達,這個概念是如何被解加減法文字題以及外部表徵類型的 知識所引導。因此,本研究旨在分析二年級學童在「十的合成與分解」數概念之 外部表徵答題表現,進而產出使用表徵之認知工作分析;並探討學童在三種外部 表徵使用所遭遇表徵轉譯的問題,希冀提供教學者往後教學時的參考與依據。