認識二次函數 認識二次函數
二次函數圖形的上下移動 二次函數圖形的上下移動
自我評量
y=ax
2的圖形 y=ax2 的圖形
的最大值與最小值
的最大值與最小值 y ax2 k
第二冊我們學過, 在兩個變數 x 與 y 的 關係式中,如果給定一個變數 x 的值,就恰好 可得到一個對應變數 y 的值,則稱 y 是 x 的函數( function ),且 x 為自變數, y 為 應變數 。其中形如 y = ax + b , a≠0 的函數,
自變數 x 最高的次數為一次,稱為一次函數,
例如: y = 3x - 5 , y =- 2x + 1 , y = 5x
等。
而形如 y = ax2 + bx + c , a≠0 的 函數,自變數 x 最高的次數為二次,稱為二 次函數,例如:
(1) 邊長為 x 的正方形,若其面積為 y ,則 可 得關係式 y = x2 ,式中給定一個變數 x 的值 ,就恰好可得到一個對應變數 y 的值,
也就是說 y 是 x 的函數,且為二次函數。
(2) 大小兩數的乘積為 y ,若大數為 x ,且 小數比大數少 3 ,則可得關係式 y = x ( x - 3 )= x2 - 3x ,也就是說 y 是 x 的函數,且為二次函數。
(3) 一個小彈珠從 100 公尺高的地方落下,經 過 t 秒鐘後,它離地面的高度為 h 公尺
,根據物理學的自由落體公式, h 與 t
滿足關係式 h = 100 - 4.9t
2,也就是說
h 是 t 的函數,且為二次函數。
下面哪些是一次函數?哪些是二次函數?
(1) y = 2 - x (2) y = 3
(3) y =- 2x2- 3x + 1 (4) y = x ( x + 1 ) (5) y = x2+ x + 1 (6) y =- 0.2 x + 5
2 3
1 3
一次函數: (1) 、 (6)
二次函數: (3) 、 (4) 、 (5)
當 y 是 x 的函數時,常用符號 y = f
( x ) 來表示它們之間的關係,並用 f ( a ) 代 表 x = a 時所對應的函數值。
例如:二次函數 y = x ( x - 3 ),
可寫成 y = f ( x )= x ( x - 3 )
∴ f ( 0 )= 0 × ( 0 - 3 )= 0 f ( 2 )= 2 × ( 2 - 3 )=- 2
f ( )= × ( - 3) = × ( )
=-
f (- 0.1 )=(- 0.1 ) ×
(- 0.1 - 3 )
=(- 0.
1 ) × (- 3.1 )= 0.31 5 2
2 5
5 2
2 5
1 2
5 4
在一個問題中同時討論幾個函數時,常用 f
( x )、 g ( x )、 h ( x )、……表示不同的 函數。 1 函數值
搭配習作 P5 基礎題 1解 解 ∵ f (- 1 )=(- 1 )
2+ 3 = 4
g (- 2 )=(- 2 + 1 )(- 2 + 2
)= 0
∴ f (- 1 )+ g (- 2 )= 4 + 0 = 4 已知函數 f ( x )= x
2+ 3 , g ( x )=( x
+ 1 )( x + 2 ),試求 f (- 1 )+ g (-
2 )之值。
1. 已知函數 y = 2 ( x - 3 )
2+ 5 ,若此函數 在 x = 2 與 x = 3 的函數值分別為 a 、 b ,試 求 a + b 之值。 x = 2 , y = a = 2 ( 2 - 3 ) 2
+ 5 = 7
x = 3 , y = b = 2 ( 3 - 3 )
2+ 5 = 5
∴a + b = 7 + 5 = 12
2. 已知函數 f ( x )= 3x - 2 ,試求 f ( 1 )+
f ( 2 )+ f ( 3 )+……+ f ( 19 )+ f
( 20 )之值。 f ( 1 )+ f ( 2 )+ f ( 3 )+……+ f
( 19 )+ f ( 20 )
=( 3 × 1 - 2 )+( 3 × 2 - 2 )+( 3 × 3
- 2 )+……+( 3 × 19 - 2 )+( 3 × 20
- 2 )
= 3 ( 1 + 2 + 3 +……+ 19 + 20 )- 2 × 20
= 590
我們知道一次函數在坐標平面上所描繪出 的圖形是一條直線,而二次函數在坐標平面上 會描繪出怎樣的圖形呢?
現在就以如何畫出二次函數 y = x
2的圖形
,當作探討的起點。
首先選擇一些簡易的整數作為 x 值,然 後求出對應的 y 值,以列表方式呈現如下:
x … -
4 -
3 -
2 -
1 0 1 2 3 4 …
y … 16 9 4 1 0 1 4 9 16 …
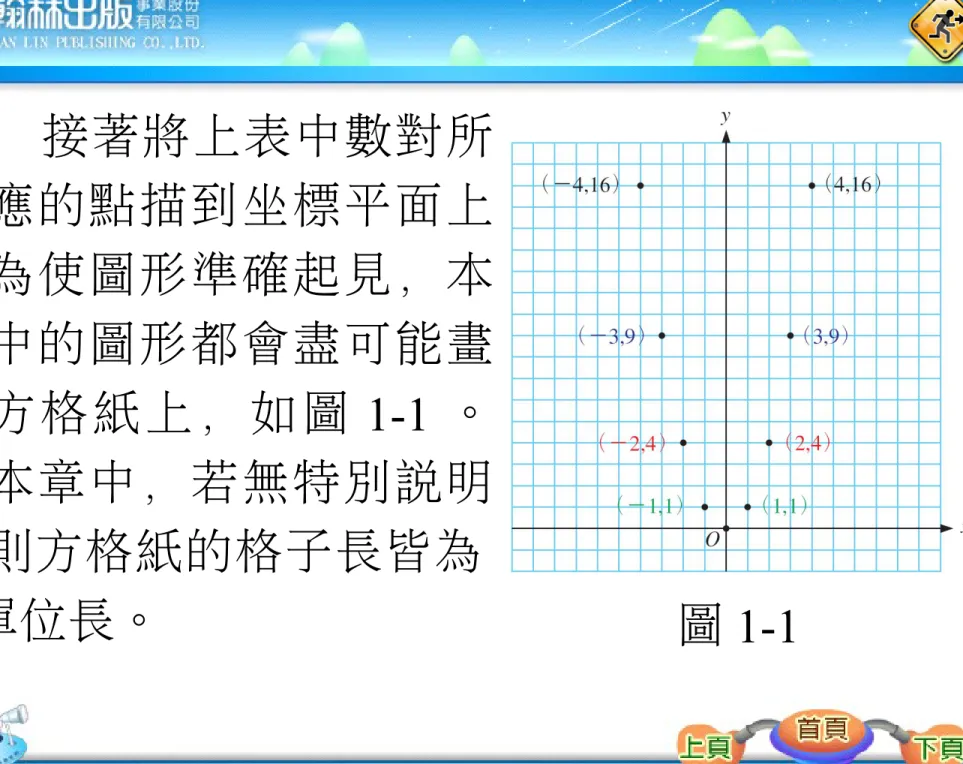
圖 1-1 接著將上表中數對所
對應的點描到坐標平面上
。為使圖形準確起見,本 節中的圖形都會盡可能畫 在方格紙上,如圖 1-1 。 在本章中,若無特別說明
,則方格紙的格子長皆為
1 單位長。
為了更清楚的觀察函數圖形,我們在 0 和 1 之間多取一些 x 值,並求出對應的 y 值,
如下表:
x
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1y
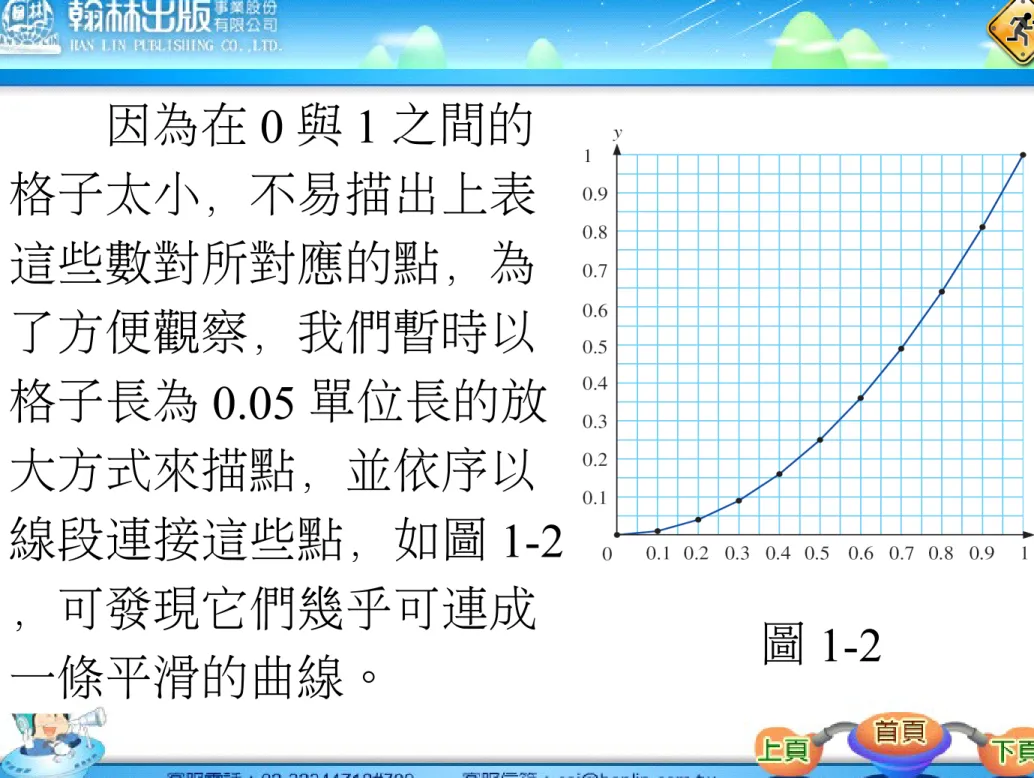
0 0.01 0.04 0.09 0.16 0.25 0.36 0.49 0.64 0.81 1圖 1-2 因為在 0 與 1 之間的
格子太小,不易描出上表 這些數對所對應的點,為 了方便觀察,我們暫時以 格子長為 0.05 單位長的放 大方式來描點,並依序以 線段連接這些點,如圖 1-2
,可發現它們幾乎可連成
一條平滑的曲線。
其實,當我們 取的數對愈多,描 在坐標平面上的點 就愈密,愈容易看 出圖形是一條平滑 的曲線,最後可得 到如圖 1-3 的圖形:
圖 1-3
由圖 1-3 可知: ( - 4 , 16) 的對稱點 (4 , 16) ,
( - 3 , 9) 的對稱點 (3 , 9) ,…… 都在圖形上
,故二次函數 y = x
2的圖形,是以 y 軸為對稱
軸的線對稱圖形,而且這個圖形有一個最低點
(0 , 0) 。因為整個圖形會一直向上延伸,且不會
在上方相交,所以我們說此圖形開口向上。
2 y =- x
2的繪圖
描繪二次函數 y =- x
2的圖形。
首先將 x 和 y 的對應值列表如下:
x
… - 4 -3 - 2 - 1 0 1 2 3 4 …y
… -16 -9 - 4 - 1 0 - 1 - 4 - 9 -16 …解 解
接下來描點,並仿照 y = x
2的圖形畫法,
以平滑的曲線將這些點連接起來,如下圖:
在例題 2 中,二次函數 y =- x
2的圖形,
也是以 y 軸為對稱軸的線對稱圖形,而且這個
圖形有一個最高點 ( 0 , 0 )。因為整個圖形會
一直向下延伸,且不會在下方相交,所以我們說
此圖形開口向下。
當我們投擲物體時,該物體所經過的路線 稱為拋物線 。圖 1-4 中,籃球所經過的路線就 是拋物線的一部分。而在例題 2 中, y =- x
2的圖形也稱為拋物線。
圖 1-4
拿出第 145 頁的附件 1 與附件 2
,試比較右圖中 y = x
2和 y
=- x
2這兩個圖形的形狀、開口方向 與開口大小。
兩圖形的形狀相同,且可完全
疊合,開口方向相反,開口大小相同。
由動動腦可知:
y = x
2與 y =- x
2的圖形可以疊合,開口 大小相同,只是開口方向相反,所以 y = x
2的圖形也稱為拋物線。不論是 y =- x
2圖形 的最高點或是 y = x
2圖形的最低點都稱為拋 物線的頂點,且對稱軸都一定會通過拋物線頂 點。
接著我們將改變 x
2項的係數,探討形如 y = ax2 , a≠0 的二次函數圖形,看看當 a
改變時, y = ax
2圖形的變化情形。
3 y = ax
2的繪圖
描繪下列二次函數的圖形:
(1) y =- x
2(2) y =- 2x
2搭配習作 P4 基礎題 3
1 2
(1) 首先將 x 和 y 的對應值列表如下:
接下來描點,並以平滑的曲線將這些點連接 起來,如圖 ( 一 ) 。
x … -4 -3 -2 -1 0 1 2 3 4 … y … -8 2 9 -2 0 -2 9 2 -8 …
1 2
1 2
解 解
圖 ( 一 )
(2) 首先將 x 和 y 的對應值列表如下:
接下來描點,並以平滑的曲線將這些點連接起 來,如圖 ( 二 ) 。
x … -2 -1 0 1 2 …
y … -8 9 2 -2 0 -2 -8 … 9 2
2
1
1 2
2 3
1 2
1 2
2 3
解 解
圖 ( 二 )
描繪下列二次函數的圖形:
(1) y = x
2x … -
4 -
3 -
2 -
1 0 1 2 3 4 …
y … …
1 2
8 92 2 0 2 8
12
12
92
在例題 3 中,二次函數 y =- x
2與 y
=- 2x
2的圖形也稱為拋物線。 1 2
描繪下列二次函數的圖形:
(1) y = x
22 1
描繪下列二次函數的圖形:
(2) y = 2x
2x … -
2 -
1 0 1 2 …
y … 8 92 2 0 2 8 …
12
12
92 23
12
12
23
描繪下列二次函數的圖形:
(2) y = 2x
21. 拿出第 145 頁的附件 3 與附件 4 ,試比較右圖 中
y = x
2與 y =-
x
2這兩個圖形的形 狀、開口方向與開口大 小。
1 2
2 1
兩圖形的形狀相同,且可完全疊合
,開口方向相反,開口大小相同。
2. 拿出第 146 頁的附件 5 與附件 6 ,試比較右圖 中
y = 2x
2與 y =- 2x
2這兩個圖形的形狀、開 口方向與開口大小。
兩圖形的形狀相同,且可
完全疊合,開口方向相反,開口大小相同。
由動動腦可知:
(1) y = x
2的圖形可和 y =- x
2的圖形 疊合, 開口大小相同,只是開口方向相反。
(2) y = 2x
2的圖形可和 y =- 2x
2的圖形疊合,
開口大小相同,只是開口方向相反。
因此 y = x
2與 y = 2x
2的圖形也都是拋物線。
2 1
2 1
1 2
如圖 1-5 ,把前面所畫的二次函數圖形,都 畫在同一個坐標平面上:
圖 1-5
由圖 1-5 可知,上述的二次函數圖形都是拋 物線,而且都有相同的頂點( 0 , 0 ),與相同 的對稱軸( y 軸)。其中 y = 2x
2、 y = x
2 與 y = x2 的圖形開口向上且愈來愈大,頂點
( 0 , 0 )是最低點;而 y =- 2x
2、 y =- x
2與 y =- x
2的圖形開口向下且愈來愈大,
頂點( 0 , 0 )是最高點。
1 2
1 2
事實上,形如 y = ax
2的二次函數圖形,都是以
( 0 , 0 )為頂點,以 y 軸為對稱軸的拋物線,
且
(1) 當 a > 0 時,圖形的開口向上,頂點是最低點
。
(2) 當 a < 0 時,圖形的開口向下,頂點是最高 點。
(3) | a |愈小,其圖形開口愈大。
4 y = ax2 的圖形比較
試寫出下列二次函數圖形的開口方向、頂點 坐標與對稱軸,並比較其開口大小:
甲: y = 3x
2乙: y =- 3x
2丙: y =- x
2丁: y = x
22 3
4 3
解 解 (1)∵ 甲、丁兩個函數的 x
2係數為正數,
∴ 甲、丁的圖形開口向上。
反之,乙、丙的圖形開口向下。
(2) 各圖形均以( 0 , 0 )為頂點,且均以 y 軸為對稱軸。
(3)∵ | 3 |=|- 3 |>|- |>|
|,
∴開口大小為:甲=乙<丙<丁 2 3
4 3
試寫出下列二次函數圖形的開口方向、頂點 坐標與對稱軸,並比較其開口大小:
甲: y =- x
2乙: y =- x
2丙: y = x
2丁: y =- x
232
13 32
43
(1) 開口向上:丙。
開口向下:甲、乙、丁。
(2) 各圖形均以( 0 ,0 )為頂點, y 軸為對稱軸
。
(3) 開口大小為:丁<甲=丙<乙。
5 y = ax
2的應用
搭配習作 P7 基礎題 5如右圖, A 、 B 兩點分別在 第一、二象限內,且兩點均 在 y = x
2的圖形上,
並與 x 軸相距 4 單位。試求
:
(1) A 、 B 兩點的坐標。
(2) 的長度。
1 2
AB
解一 解一
由圖可知 A 、 B 兩點的 y 坐標均為 4 ,且分 別在第一、二象限內,故可設 A ( a , 4 )、 B
( b , 4 ),其中 a > 0 、 b < 0 。兩點均在 y
= x
2的圖形上,分別將其坐標代入函數得:
4 = a
24 = b
2a
2= 8 b
2= 8
a = ( a > 0 ) b =-
( b < 0 )
因此可得 A ( , 4 )、 B (- ,4 ) =∣ -(- )∣=
2 2
2 2 2
2 4 2
2 2
21
--- --- --- -- AB
21
2 2
2 2
12
解二 解二
由圖可知 A 、 B 兩點的 y 坐標均為 4 ,且均在函數 y = x 2 的圖形上,
∴ 將 y = 4 代入該函數可求得它們的 x 坐標:
4 = x
2, x
2= 8 , x = ± 。
又 A 、 B 兩點分別在第一、二象限內,
因此可得 A ( ,4 )、 B (- ,4 ) =∣ -(- )∣=
12 2 2
12
2
2 2 2
2
2 2 2
AB
4 21. 若二次函數 y = 2x
2的圖形通過坐標 ( - 3 , a) ,而 y = bx
2的圖形通過坐標 ( - 2 ,
- 12 ) ,
試求 a 、 b 之值。
∵ y = 2x
2的圖形通過(- 3 ,a )
∴ 將(- 3 ,a )代入得 a = 2( - 3)
2= 18
又 y = bx
2的圖形通過(- 2 , - 12 )
∴ 將(- 2 , - 12 )代入得- 12 = b( - 2)
2,
b =- 3
2. 如圖, A 、 B 兩點均在 y =- x2 的圖形上,其中 A 點在第三象限內,與 x 軸相距 2 單位, B 點在第 四象限內,與 y 軸相距 2 單位,試求
A 、 B 兩點的坐標。
設 A ( a , - 2 )、 B ( 2 ,b ),其中 a < 0 , b < 0 。 ∵A 、 B 兩點均在 y =- x
2的圖形上,
∴ 分別將( a , - 2 )、( 2 ,b )代入得:
- 2 =- a
2, a =-
b =- 2
2, b =- 4
故 A 點坐標為(- , - 2 ),
B 點坐標為( 2 , - 4 )。
2
2
2.
6 y = ax
2圖形開口大小的應用
在坐標平面上,直線 y = 1 分別與 y = x
2、 y = x
2、 y = x
2的圖形在第一象限內相交
於 A 、 B 、 C 三點,在第二象限內相交於 D
、 E 、 F 三點。試
比較 、 、 長度的大小。
AD BE CF
2 1
1 3
解 解 ∵y = x
2、 y = x
2、 y = x
2的圖 形都是以( 0 , 0 )為頂點的拋物線,
又 x
2項係數均大於 0 , 且| 1 |>| |>| |,
可知圖形的開口向上且愈來愈大
∴ 依題意可圖示如下:
1 2
1 3
1 2
1 3
觀察圖形可發現: CF > BE > 。 AD
坐標平面上 y = x
2的圖形,分別與直線 y = 2 、
y = 3 、 y = 4 在第一象限內相交於 A 、 B 、 C 三點,在第二象限內相交於 D 、 E
、 F 三點。試比較 、 、 三線段長度的大小。
AD BE CF
依題意圖示如右,
觀察圖形可發現:
> > 。 CF BE AD
形如 y = ax
2, a > 0 的二次函數,其圖形 開口向上,有最低點( 0 , 0 ),由圖 1-6 可知,
此類函數在 x = 0 時,有最小值 y = 0 。
相反的,形如 y = ax
2, a < 0 的二次函數
,其圖形開口向下,有最高點( 0 , 0 ),由圖 1-6 可知此類函數在 x = 0 時,有最大值 y = 0
。
圖 1-6
其實不經由畫圖,我們也可由不等式發現 此現象:
1. 若 y = ax
2, a > 0 :
∵ x
2≧ ,∴ ax 0
2≧ , 0 即函數值 y 0 ≧ ,
又 x = 0 時, ax
2= 0 ,
故此函數在 x = 0 時,有最小值 y = 0 。
2. 若 y = ax
2, a < 0 :
∵ x
2≧ ,∴ ax 0
2≦ , 0 即函數值 y 0 ≦ ,
又 x = 0 時, ax
2= 0 ,
故此函數在 x = 0 時,有最大值 y = 0 。
因為拋物線 y = ax2 的開口方向只有向上 或向下,因此當此類函數有最小值時,就不
可能有最大值;若有最大值時,就不可能有 最小值。
為了便於描繪形如 y = ax2+ k , k≠0 的 二
次函數圖形,我們先來練習如何利用不等 式,找出此類二次函數的最大值或最小值。
7 最大值或最小值
試求下列二次函數的最大值或最小值,並寫出 x 的值為多少時,會得到最大值或最小值。
(1) y = 3x
2- 4 (2) y =- x
2+ 2
搭配習作 P5 基礎題 2
(1) 3 ∵ x
2≧ , 0
3x
2- 4 0 ≧ - 4 ,
∴y = 3x
2- 4≧ - 4 ,
又 x = 0 時, 3x
2- 4 =- 4 ,
故函數在 x = 0 時,有最小值 y =- 4 。 (2) ∵ - x
2≦ , 0
- x
2+ 2 0 ≦ + 2 , ∴y =- x
2+ 2 2 ≦ ,
又 x = 0 時,- x
2+ 2 = 2 ,
故函數在 x = 0 時,有最大值 y = 2 。
解 解
試求下列二次函數的最大值或最小值,並寫出 x 的值為多少時,會得到最大值或最小值。
(1) y = 2x ∵2x
2≧ 0
2- 5 (2) y =- 3x
2+ 4 2x
2- 5≧ - 5
∴y = 2x
2- 5≧ - 5
又 x = 0 時, y =- 5 , 故函數在 x = 0 時,
有最小值 y =- 5 。
∵ - 3x
2≦ 0
- 3x
2+ 4 4 ≦
∴y =- 3x
2+ 4 4 ≦
又 x = 0 時, y = 4 , 故函數在 x = 0 時,
有最大值 y = 4 。
(3) y = x 1 3
2+ 1 (4) y =- 4x
2- 2 3
∵ x
2≧ 0
x
2+ 1 1 ≧
∴y = x
2+ 1 1
≧
又 x = 0 時, y = 1 ,
故函數在 x = 0 時
,
有最小值 y = 1 。 1 3
3 1
1 3
∵ - 4x
2≦ 0
- 4x
2- ≦-
∴y =- 4x
2- ≦-
又 x = 0 時, y =- , 故函數在 x = 0 時,
有最大值 y =- 。 2 3
2 3
2 3
2 3
2 3
2 3
一般而言,形如 y = ax
2+ k , k≠0 的 二次函數:
1. 若 a > 0 :
∵ ax
2≧ , 0
ax
2+ k 0 ≧ + k ,
∴ y = ax
2+ k≧k ,
且 x = 0 時, ax
2+ k = k ,
故此函數在 x = 0 時,有最小值 y = k
。
2. 若 a < 0 :
∵ ax
2≦ , 0
ax
2+ k 0 ≦ + k ,
∴ y = ax
2+ k≦k ,
且 x = 0 時, ax
2+ k = k ,
故此函數在 x = 0 時,有最大值 y = k
也就是說,形如 y = ax 。
2+ k , k≠0 的二次函數,
可以得到下面的結論:
(1) 若 a > 0 ,函數在 x = 0 時,有最小值 k 。
(2) 若 a < 0 ,函數在 x = 0 時,有最大值 k 。
接下來,讓我們來看一些形如 y = ax
2+ k , k≠0 的二次函數圖形。
描繪二次函數 y = x
2+ 1 的圖形。
搭配習作 P4 基礎題
8 y = ax2 + k 的繪圖( a > 0 )
3
∵ x
2項係數是 1 ,大於 0 ,
∴ 函數在 x = 0 時,有最小值 y = 1 。
因此從 x = 0 開始,對稱的將 x 和 y 的 對應 列表如下: 值
x … -
3 -
2 -
1 0 1 2 3 …
y … 10 5 2 1 2 5 10 …
解 解
然後描點並畫平滑曲線如右圖:
在下面的坐標平面上,描繪二次函數 y = x
2- 1
的圖形:
x … …
y x … … - …
3 -
2 -
1 0 1 2 3 …
y … 8 3 0 -
1 0 3 8 …
圖形的形狀相同,且可 完全疊合,開口方向、
開口大小也相同。
拿出第 145 頁的附件 1 ,疊在右圖中 y = x
2、
y = x
2- 1 和 y = x
2+ 1 這 三個圖形上,比較它們
的形狀、開口方向與開
口大小。
由動動腦可知:
y = x
2- 1 與 y = x
2+ 1 的圖形均可和 y = x 2 的圖形疊合,所以這三個圖形都是拋物線,
其開口大小相同。且知將 y = x
2的圖形向上移 動 1 個單位,便是 y = x
2+ 1 的圖形;而向下 移動 1 個單位,便是 y = x
2- 1 的圖形,因此 這三個圖形均為開口向上且有相同的對稱軸(
y 軸)。
9 y = ax2 + k 的繪圖( a < 0 ) 描繪二次函數 y =- x
2 - 1 的圖形。
搭配習作 P6 基礎題 3
1 2
解 解 ∵x
2項係數小於 0 ,
∴ 函數在 x = 0 時,有最大值 y =- 1 。 因此從 x = 0 開始,對稱的將 x 和 y 的對 應值列表如下:
x … -
3 -
2 -
1 0 1 2 3 …
y … -
3 -
1 -
3
2
… 11
2 3
2 3
11 2
然後描點並畫平滑曲線如下圖:
在下面的坐標平面上,
描繪二次函數
y =- x
2+ 2 的圖
形: 2 1
… y …
…
… x
2
0 1
0
2 3
… 0
y …
…
- 1
- 2
…
- 3x
2 5
2 3
2 3
2 5
圖形的形狀相同,且 可完全疊合,開口方 向、開口大小也相同
。
拿出第 145 頁的附件 4 ,疊在右圖中 y =-
x
2、 y =- x
2- 1 和 y =- x
2+ 2 這三個圖形上,比較它們的
形狀、開口方向與開口大小。
2 1 1 2
1 2
由動動腦可知:
y =- x
2- 1 與 y =- x
2+ 2 的圖 形均可和
y =- x
2的圖形疊合,所以這三個圖形都 是拋物線,其開口大小相同。且知將 y =-
x
2的圖形向下移動 1 個單位,便是 y =-
x
2- 1 的圖形;而向上移動 2 個單位,便是 y =- x2 + 2 的圖形,因此這三個圖形 均為開口向下且有相同的對稱軸( y 軸)。
2 1 2 1 2 1 2 1 1 2
1 2
由前面的動動腦,我們可整理得表 1-1 ,請 在表 1-1 的空格內,填入適當的文字或符號。
圖形的移動 圖形
形狀 頂點
座標 對稱軸 y = x2 +
1
由 y = x
2的圖 形向上移動 __
_ 個單位可得
。
開口向 上的拋
物線 (0 ,1) 項目
函數
y 軸 (x = 0) 1
表 1-1
y = x
2- 1
由 y = x
2的圖 形向 ___ 移動 1 個單位可得
。
開口向 上的拋 物線
y 軸 (x =
0)
y = - x2- 1
由 y =- x
2的圖形向下移 動 ___ 個單位 可得。
開口向 下的拋
物線 (0 ,-1) (0 ,-1)
y 軸 (x = 0) 下
1
1 2
12y = - x2 + 2
由 y =- x
2的圖形向 ___
移動 2 個單位 可得。
開口向 下的拋
物線 (0 ,2)
(x =y 軸 0)上 2
1
12因此,對於形如 y =
ax2+ k , k≠0 的 二次
函數圖形,由表 1-1 可歸納得:
1. 其圖形都是拋物線,頂點坐標( 0 ,k ),對 稱軸為直線 y 軸(
x = 0 )。(1) 當 k > 0 時,其圖形可由 y = ax
2的圖形向 上移動 k 個單位而得。
(2) 當 k < 0 時,其圖形可由 y = ax
2的圖形向
下移動| k |個單位而得。
2. 其圖形的開口方向與 y = ax
2相同,因此:
(1) 當 a > 0 時,圖形開口向上,頂點是最低 點,函數有最小值為 k 。
(2) 當 a < 0 時,圖形開口向下,頂點是最高
點,函數有最大值為 k 。
我們也可將二次函數 y = ax
2+ k , k≠0 的圖形,整理如下:
條 件
a > 0 a < 0
k > 0 k < 0 k > 0 k < 0
圖
示
1. 若二次函數 y =- 2x
2的圖形向上移動 3 個單位 可得 y = ax
2+ q 的圖形,試求 a + q 之值。
搭配習作 P7 基礎題 4
∵y =- 2x
2的圖形向上移動 3 個單位可得 y =- 2x2 + 3
∴a =- 2 , q = 3 ,
故 a + q = 1 。
2. 試寫出下列二次函數圖形的開口方向、頂點 坐標與對稱軸,並比較其開口大小。
甲: y = 3x
2+ 1 乙: y =- x
2- 4 甲:開口向上,頂點 (0 ,1) ,對稱軸為 y 軸
。
乙:開口向下,頂點 (0 , - 4) ,對稱軸 y 軸
。
開口大小:甲<乙 。
8 3
1. 二次函數:
形如 y = ax
2+ bx + c , a≠0 的函數,
自變數 x
的次數最高為二次,稱為二次函數。
2. y = ax
2+ k 的圖形:
二次函數 y = ax2 + k
a > 0 a < 0
圖形 拋物線
對稱軸 y 軸( x = 0 )
頂點坐標 ( 0 , k )
開口方向 開口向上,
頂點為最低點
開口向下,
頂點為最高點 最大值或最小值 最小值 k 最大值 k
1-1 自我評量
1. 已知函數 f ( x )= x
2- 9x - 190 ,試求 f
(- 10 )+ f ( 19 )之值。
f (- 10 )=(- 10 )
2- 9 (- 10 )- 190 = 100 + 90 - 190
= 0
f ( 19 )= 19
2- 9×19 - 190
= 19 ( 19 - 9 - 10 ) = 0
∴ f (- 10 )+ f ( 19 )= 0
2. 試求下列二次函數的最大值或最小值,並寫出 x 的值為多少時,會得到最大值或最小值。
(1) y = x
2(2) y =- 5x
24 3
∵ x
2項係數 > 0 ,
∴ 函數在 x = 0 時,
有最小值 y = 0 。
4 3 ∵ x
2項係數- 5 < 0 ,
∴ 函數在 x = 0 時,
有最大值 y = 0 。
(3) y = 4x
2- 3 (4)y =- 3x
2- 5 2
∵ x
2項係數 4 > 0 ,
∴ 函數在 x = 0 時,
有最小值 y =- 3 。
∵ x
2項係數- 3 < 0 ,
∴ 函數在 x = 0 時,
有最大值 y =- 5 2
3. 描繪下列二次函數的圖形:
(1)y = x 2 3
21
6 2
… 0
6 y …
… 0
- 1
… - 2
x
2 3
2 3
(2) y = x
2- 2
x … -
2 -
1 0 1 2 … y … 2 -
1 -
2 - 1 2 …
(3) y =- 2x
2+ 1
x … -
2 -
1 0 1 2 … y … -
7 -
1 1 -
1 -
7 …
x … -
4 -
2 0 2 4 …
y … -
7 -
1 1 -
1 -
7 …