應用於正交分頻多工系統之高效能波束形成技術

國 立 交 通 大 學

電子工程學系 電子研究所碩士班

碩 士 論 文

應用於正交分頻多工系統之高效能波束形成技

術

Efficient Design of Beamforming Techniques for OFDM

Systems

研 究 生：張文威

指導教授：陳紹基 博士

應用於正交分頻多工系統之高效能波束形成技

術

Efficient Design of Beamforming Techniques for

OFDM Systems

研 究 生：張文威 Student：Wen-Wei Chang 指導教授：陳紹基 博士 Advisor：Sau-Gee Chen 國 立 交 通 大 學 電子工程學系 電子研究所碩士班 碩 士 論 文 A Thesis

Submitted to Department of Electronics Engineering & Institute of Electronics College of Electrical Engineering and Computer Science

National Chiao Tung University in Partial Fulfillment of the Requirements

for the Degree of Master of Science

in

Electronics Engineering

August 2006

Hsinchu, Taiwan, Republic of China

應用於正交分頻多工系統之高效能波束形

成技術

學生：張文威 指導教授：陳紹基 博士 國立交通大學 電子工程學系 電子研究所碩士班

摘

要

近年來，為了可以增加無線通信系統之資料傳輸速率以及頻譜使用效率， 正交分頻多工系統結合波束形成技術的方式以被廣泛的討論。為了可以獲得最佳 的系統效能，必須解決同頻干擾。使用波束形成技術是一個有效克服同頻干擾的 方式。應用於正交分頻多工之波束形成技術可以分為前置-快速傅立葉轉換型以 及後置-快速傅立葉轉換型兩類。本文中，分別討論前置-快速傅立葉轉換型以及 後置-快速傅立葉轉換型波束形成器之優缺，並提出一個新式結合前置-快速傅立 葉轉換型以及後置-快速傅立葉轉換型之波束形成器。此新式混合型波束形成 器，在有同頻干擾的時變通道之下，相較於前置-快速傅立葉轉換型及後置-快速 傅立葉轉換型之波束形成器可以得到較佳的系統效能。

Efficient Design of Beamforming

Techniques for OFDM Systems

Student: Wen-Wei Chang Advisor: Dr. Sau-Gee Chen Department of Electronics Engineering &

Institute of Electronics National Chiao Tung University

ABSTRACT

For high-speed data transmission and spectral efficiency in wireless communications, the combination of OFDM and beamfroming techniques is being actively studied. In order to maximize the system efficiency, the problem of co-channel interference must be resolved. One technique to overcome the co-channel interference and to increase the system capacity is to use beamfroming algorithm. The techniques are roughly classified into two different types depending on weight installation patterns. The first one is a Pre-FFT type, the second one is a Post-FFT type. In this work, both Post-FFT and Pre-FFT beamformers in OFDM system are studied, and a novel hybrid Pre/Post-FFT beamfromer is proposed. The proposed beamformer yields better performances than Pre-FFT beamformer and Post-FFT beamformer within a multi-path environment with co-channel interference.

誌謝

本論文可以順利完成，首先要感謝我的指導教授陳紹基博士，兩年中 不斷幫我釐清許多觀念，對研究方面提供很多的協助與建議，在此致上由 衷的感謝。 此外要感謝的是實驗室 429 的同學們，很高興有金融、昀震、譽桀、 敏杰這一群很好的夥伴陪我渡過這兩年的碩士班生活，有了你們實驗室裡 就會充滿著快樂，感謝你們陪伴著我這樣一路走來，畢業後，希望你們都 可以利用所學擁有更充實、更精彩的生活；還要感謝建全學長，謝謝建全 學長常常不吝惜的分享他豐富的社會經驗，讓我對未來的方向有更深一層 的了解；感謝學弟、學妹讓實驗室充滿人氣。 最後，要感謝我父母家人及女友，家永遠是世界上最溫暖的地方，感 謝你們的大力支持。

目錄

中文摘要 ... Ⅰ 英文摘要 ... Ⅱ 致謝 ... Ⅲ 目錄 ... Ⅳ 表目錄 ... Ⅵ 圖目錄 ... Ⅶ 第一章 緒論 ... 1 1.1 研究動機 ... 1 1.2 研究目標 ... 2 1.3 論文架構 ... 3 第二章 智慧型天線系統 ... 4 2.1 智慧型天線之基本概念 ... 4 2.1.1 均勻間距線性陣列 ...5 2.1.2 空間濾波器及空間耐奎斯特取樣定理 ...9 2.2 智慧型天線技術 ... 11 2.2.1 切換波束式天線陣列 ...11 2.2.2 適應性天線陣列 ...12 2.2.2.1 權重最佳化之準則 ... 12 2.2.2.2 最小平均平方誤差準則 ... 13 2.2.2.3 最大訊號干擾比 ... 14 2.2.2.4 應用於波束形成之適應性演算法 ... 16 2.2.2.5 倒置取樣矩陣演算法 ... 17 2.2.2.6 最小平均平方演算法 ... 18 2.2.2.7 遞迴最小平方演算法 ... 19 2.3 智慧型天線對系統的改善及主要用途... 21 第三章 正交分頻多工技術 ... 24

3.1 正交分頻多工技術介紹 ... 24 3.2 保護區間與載波正交性 ... 27 3.3 正交分頻多工系統之優缺點 ... 29 第四章 應用於正交分頻多工系統之波束形成技術 ... 31 4.1 通道模型 ... 31 4.2 前置-快速傅立葉轉換型天線系統 ... 32 4.2.1 前置-快速傅立葉轉換型之結構 ...32 4.2.2 理想切換波束天線陣列 ...33 4.2.3 切換波束式天線系統 ...36 4.2.3.1 最大能量法 ... 37 4.2.3.2 最大能量法模擬分析 ... 38 4.3 後置-快速傅立葉轉換型天線陣列 ... 40 4.3.1 後置-快速傅立葉轉換型之結構 ...40 4.3.1.1 倒置取樣矩陣演算法之模擬 ... 43 4.3.1.2 子載波群組化 ... 47 4.3.1.3 子載波波束形成器之內插 ... 51 第五章 新式波束形成器設計 ... 62 5.1 最小平方誤差法 ... 62 5.1.1 頻域最小平方誤差法 ...62 5.1.2 時域最小平方誤差法 ...65 5.1.3 效能分析 ...66 5.1.4 複雜度分析 ...68 5.1.5 前置-快速傅立葉轉換型以及後置-快速傅立葉轉換型之 優缺點比較 ...69 5.2 新式混合型天線陣列結構 ... 71 5.2.1 效能分析 ...72 5.2.2 複雜度分析 ...78 第六章 結論與未來工作展望 ... 79 參考文獻 ... 81

表目錄

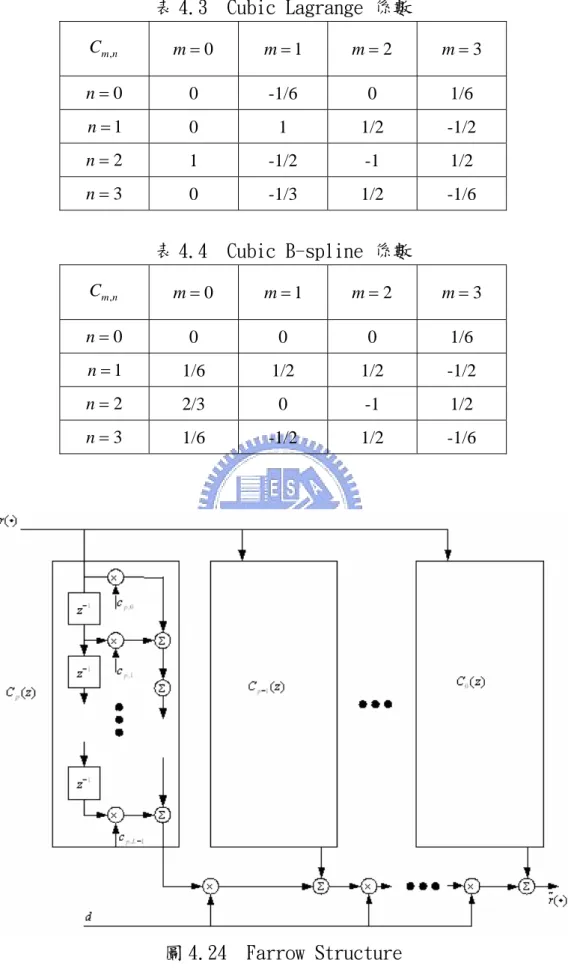
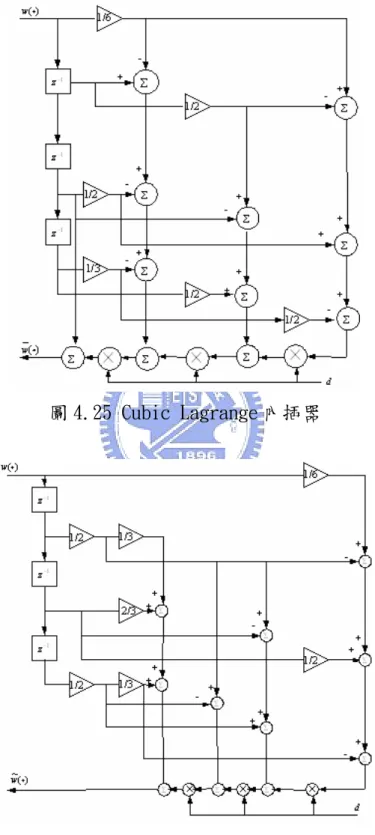
表4.1 系統參數設定 34 表4.2 切換波束式天線陣列之權重向量 37 表4.3 Cubic Lagrange 係數 58 表4.4 Cubic B-spline 係數 58 表4.5 各類型內插法複雜度分析 58 表5.1 最大能量法與最小平方誤差法之複雜度分析 69

表5.2 ETSI Vehicular A channel environment 76 表5.3 比較前置-快速傅立葉轉換型，後置-快速傅立葉轉換型以及混合型

圖目錄

圖2.1 波束形成示意圖 4 圖2.2 (a)線性天線陣列 5 圖2.2 (b)平面天線陣列 5 圖2.2 (c)圓形天線陣列 5 圖2.3 均勻間距線性陣列 6 圖2.4 窄波波束形成器 9 圖3.1 多載波傳輸示意圖 24 圖3.2 傳統分頻多工與正交分頻多工比較圖 25 圖3.3 正交分頻多工系統傳送端調變器示意圖 27 圖3.4 正交分頻多工系統之保護區間示意圖 28 圖3.5 保護區間內不送信號引起載波間干擾之示意圖 28 圖3.6 傳輸延遲延展小於保護區間示意圖 36 圖4.1 (a)正交分頻多工系統之傳送端 32 圖4.1 (b)前置-快速傅立葉轉換型天線陣列 32 圖4.2 理想波束 33 圖4.3 理想切換波束式天線陣列 35 圖4.4 波束對於不同到達角度的增益之示意圖 36 圖4.5 在平坦衰落通道中無同頻干擾最大能量法之模擬 39 圖4.6 在平坦衰落通道中受同頻干擾最大能量法之模擬 40 圖4.7 後置快速傅立葉轉換天線陣列結構 42 圖4.8 正交分頻多工信號之架構 44 圖4.9 在平坦衰落通道中無同頻干擾倒置取樣矩陣演算法之模擬 46 圖4.10 在平坦衰落通道中受同頻干擾倒置取樣矩陣演算法之模擬 46

圖4.11 子載波群組化的結構 47 圖4.12 在平坦衰落通道中無同頻干擾子載波群組化之模擬 48 圖4.13 在平坦衰落通道中受同頻干擾子載波群組化之模擬 49 圖4.14 在頻率選擇性衰落通道中無同頻干擾子載波群組化之模擬 50 圖4.15 在頻率選擇性衰落通道中受同頻干擾子載波群組化之模擬 50 圖4.16 線性內插器 51 圖4.17 在頻率選擇性衰落通道中無同頻干擾子載波群組化與線性內插法 之比較圖 52 圖4.18 在頻率選擇性衰落通道中受同頻干擾子載波群組化與線性內插法 之比較圖 52

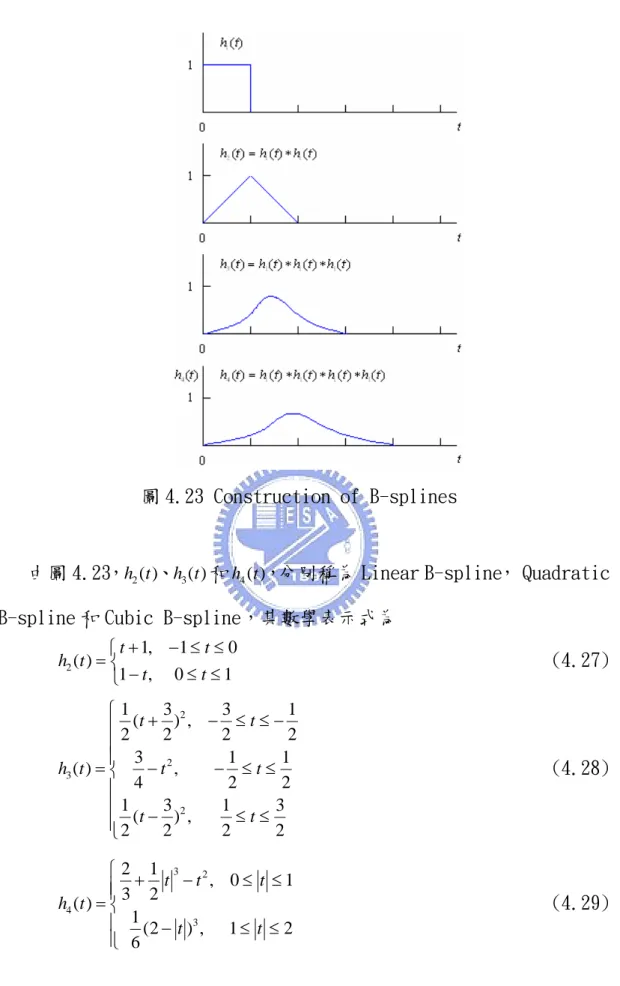
圖4.19 Cubic Spline Interpolator 53

圖4.20 在頻率選擇性衰落通道中無同頻干擾線性內插法與Cubic Spline Interpolation 之比較圖 54 圖4.21 在頻率選擇性衰落通道中受同頻干擾線性內插法與Cubic Spline Interpolation 之比較圖 54 圖4.22 Lagrange Interpolation 示意圖 55 圖4.23 Construction of B-splines 56 圖4.24 Farrow Structure 58 圖4.25 Cubic Lagrange 內插器 59 圖4.26 Cubic B-spline 內插器 59 圖4.27 各類型內插器之比較圖 60 圖5.1 頻域最小平方誤差法之結構 63 圖5.2 在平坦衰落通道中無同頻干擾頻域最小平方誤差法之模擬 64 圖5.3 在平坦衰落通道中受同頻干擾頻域最小平方誤差法之模擬 64 圖5.4 時域最小平方誤差法之結構 65 圖5.5 平坦衰落通道中無同頻干擾最大能量法與最小平方誤差法之比較

圖 66 圖5.6 平坦衰落通道中受同頻干擾最大能量法與最小平方誤差法之比較 圖 67 圖5.7 頻率選擇性衰落通道中無同頻干擾最大能量法與最小平方誤差法 之比較圖 67 圖5.8 頻率選擇性衰落通道中受同頻干擾最大能量法與最小平方誤差法 之比較圖 68 圖5.9 頻率選擇性衰落通道中受同頻干擾前置-快速傅立葉轉換型與後置 -快速傅立葉轉換型之比較圖 70 圖5.10 新式混合型天線陣列結構 71 圖5.11 混合型天線陣列流程圖 72 圖5.12 平坦衰落通道中使用混合式天線陣列無同頻干擾之模擬圖 73 圖5.13 平坦衰落通道中使用混合式天線陣列受同頻干擾之模擬圖 74 圖5.14 頻率選擇性通道中使用混合式天線陣列無同頻干擾之模擬圖 75 圖5.15 頻率選擇性通道中使用混合式天線陣列受同頻干擾之模擬圖 75

圖5.16 ETSI Vehicular A channel environment，使用混合式天線陣列

無同頻干擾之模擬圖 76

圖5.17 ETSI Vehicular A channel environment，使用混合式天線陣列

受同頻干擾之模擬圖 76

圖5.18 ETSI Vehicular A channel environment，無同頻干擾，前置- 快速傅立葉轉換型之切換波束式天線陣列、後置-快速傅立葉轉換

第一章 緒論

1.1 研究動機

近十幾年來，無線通訊發展相當的迅速，也由於現今所需傳輸的資料 包括影像、聲音以及多媒體等，因此需要更大的頻寬，來讓消費者可以享 受更好的服務與品質，如第四代行動通信(4G)在室內傳輸速率要求為 1Gb/s，室外傳輸速率要求100Mb/s，是一個相當高速的無線通訊系統，因 此如何有效利用頻寬是個相當重要的議題，利用智慧型天線即是一個有效 改善頻寬使用效益與通信品質的方法。 智慧型天線工作型態，可大致區分為三個型態，第一類型為將智慧型 天線系統應用於發射端，使其發射端有方向性的發送信號，即在下鏈時， 基地台會根據使用者所在的位置的不同，形成特定的波束，對於使用者所 在之特定方向發送信號；第二種類型為將智慧型天線系統應用於接收端， 使其接收端有方向性的接收信號，即在上鏈時，基地台會根據使用者所在 的位置的不同，形成特定的波束，對於使用者所在之特定方向接收信號； 第三種類型為將智慧型天線系統同時應用於發射端與接收端，智慧型天線 會根據基地台與使用者所處的地理位置與通道環境特性等，傳送端與接收 端同時適應性地調整，以獲得最好之傳輸品質，如802.11n即是屬於此種 類型。不同的工作模式所需的演算法有所不同，本研究主要是針對第二類 之智慧型天線做進一步的研討。 當使用者對基地台的上鏈通訊中，基地台會使用天線陣列接收信號， 利用空間分隔多工的概念，產生特有之訊號空間特徵，基地台可經由訊號 處理的方式，尋找出訊號到達的方向，不同的使用者由於所在的位置不 同，會有不一樣的訊號空間特徵，智慧型天線系統即是利用此差異，在同

樣的頻率與時間的資源裏，區分出不同使用者，達到頻寬重複利用的目 的，即可有效增進頻寬使用效益。 在第二類之智慧型天線中，由於頻寬重複利用的緣故，在相同的頻帶 上會有不同使用者的信號，不同使用者的信號對欲求解的信號而言均視為 同頻干擾，因此如何有效地消除同頻干擾之效應，是第二類型智慧型天線 系統必須研究的重要問題。 目前應用於接收端之智慧天線主要有切換波束式（Switched-beam） 天線陣列和適應性（Adaptive）天線陣列兩種工作模式[1]。適應性天線 陣列雖然有較佳的效能，但複雜的計算加上收斂速度較慢，在通道快速時 變的情況下，可能出現錯誤收斂或無法收斂的缺點，相較之下切換波束式 天線陣列顯然較易實現，演算法既簡單又有不錯的效果，兩種類型的智慧 型天線個具有其優缺點，如何在系統效能與硬體成本之間取得平衡，也是 個重要的議題。

正交分頻多工系統(Orthogonal Frequency Division Multiplexing， OFDM)為多子載波的系統，其將信號分配到不同子載波上，利用分頻多工 的概念，可以滿足高速傳輸的需求，同時具備可以有效對抗多重路徑產生 的失真與干擾等種種優勢，因此正交分頻多工系統為一個被廣泛使用的系 統。本研究主要是探討如何將智慧型天線有效率地應用於正交分頻多工系 統中。

1.2 研究目標

智慧型天線應用於正交分頻多工系統，可區分為兩種類型，一類為在 時域(Time Domain)上做信號處理，稱之為前置-快速傅立葉轉換型天線陣 列；另外一類為在頻域(Frequency Domain)上處理，稱之為後置-快速傅

立葉轉換型天線陣列。我們提出一種新的演算法，是在頻域和時域同時處 理之新式混合型天線陣列，以改善通信品質。

1.3 論文架構

本論文分為六章 第一章 : 介紹研究動機和研究目標 第二章 : 說明智慧型天線的原理及介紹波束形成技術 第三章 : 介紹正交分頻多工系統 第四章 : 將智慧型天線技術應用於正交分頻多工系統並分析其效能 第五章 : 新式波束形成器設計 第六章 : 結論與未來展望

第二章 智慧型天線系統

2.1 智慧型天線之基本概念

對智慧型天線系統的定義如下[1]：「智慧型天線是由一組採特定幾 何排列形式的天線元件所組成，利用切換式、掃描式或適應性的方式控制 主動性元件達成改變無線電波輻射的場型，具有提升載波干擾比、服務區 域範圍、系統容量等系統操作參數的功能。」 最初智慧型天線技術主要應用於雷達、聲納、軍事用途等，用來完成 空間濾波和定位等，90年代以來，陣列信號處理技術逐漸被引入無線通訊 領域。 圖2.1 波束形成(Baeamforming)示意圖 如圖2.1 所示，智慧型天線系統是利用空間分隔多工的概念，在基地 台安置一組天線陣列，用來傳送及接收信號，應用空間分集的特性來區分 與合成不同方位的使用者與路徑訊號，以增加通道容量，提高通訊品質與 消除多重路徑效應。智慧型天線的基本觀念便是以多個具有動態改變能力 的窄波束分別服務多個行動用戶端。用於接收信號時，產生一組特定窄波 束，可由該窄波束接收到最大功率，而落於該窄波束以外的干擾信號則將

被抑制；用於發射信號時，不同於傳統的全向性天線，而是往特定方向傳 輸，除了可讓接收端接收到最大的功率之外，同時也會對其它接收設備產 生較小的干擾。

三種最常見天線陣列幾何排列形式為線性天線陣列(linear antenna array)、 圓 形 天 線 陣 列 (circle antenna array) 、 以 及 平 面 天 線 陣 列 (planar antenna array)[2]。線性天線陣列是由一組擺放成直線的天線 所構成，圓形天線陣列是由一組擺放成圓形的天線陣列所構成，而平面天 線陣列是由擺放成平面的天線陣列所構成，如圖2.2所示。

圖2.2 常見天線陣列(a)線性天線陣列 (b)平面天線陣列 (c)圓形天線陣 列

2.1.1 均勻間距線性陣列(Uniformly Space Linear Array，

ULA)

圖2.3所示,為一組均勻間距線性陣列，其中包含了K根相同的天線， 最右邊的天線為視為參考單位(reference element)。假設單一的信號由 遠端傳送過來，接收信號可以視為一個平面波，相對於天線陣列有一個θ的 夾角，由圖2.3所示平面波最先到達參考單位，而依序經過各根天線，最 後到達第K根天線。第一根天線接收信號用帶通信號(bandpass signal) 表示式來表示 } ) 2 exp( ) ( Re{ ) ( ~ 1 1 t x t j f t x = − π c (2.1)

其 中 x₁(t) 為 接 收 信 號 的 複 數 封 包 表 示 式 (complex envelope

representation)， fc為載波頻率(carrier frequency)。信號由第一根天

線到第二根天線會發生傳遞延遲，其傳遞延遲表示式為 c d θ τ = cos (2.2) 其中c為光速，因此第二根天線所接收到的信號可表示為 )} ( 2 exp( ) ( Re{ ) ( ~ 1 2 t = x t−τ −j πf t−τ x c (2.3) 圖2.3 均勻間距線性陣列

若載波頻率遠大於信號頻寬，則窄波信號模型(narrowband signal model) 將可以被使用，則微小的傳遞延遲將被表示成一個簡單地相角位移。(2.3) 式可表示為 )} ( 2 exp( ) ( Re{ ) ( ~ 1 2 t = x t −j πf t−τ x _c (2.4) 其複數封包表示式為 ) 2 exp( ) ( ) ( ₁ 2 t x t j πfcτ x = − (2.5) 由(2.2)式和(2.5)式可得 ) cos 2 exp( ) ( ) ( ₁ 2 c d f j t x t x = − π _c θ ) cos 2 exp( ) ( 1 λ θ π d j t x − = (2.6)

其中λ為載波波長。由於天線陣列為均勻間距線性陣列，所以第k根天線 所接收的信號可表示成 1 2 ( ) ( ) exp( ( 1) cos ), k x t x t j π k d θ λ = − − k =1,...,K (2.7) 亦可用向量的形式表示: , ] ) ( ... ) ( ) ( [ ) (t = x₁ t x₂ t x_K t T x (2.8) , ] ... 1 [ ) ( ( 1) cos 2 cos 2 T d K j d j e e λ θ π θ λ π θ = − − − a (2.9) 接收信號的複數封包表示式如下 ), ( ) ( ) (t a θ x₁ t x = (2.10) 其 中 a(θ) 稱 為 陣 列 響 應 向 量 (array response vector) 或 引 導 向 量 (steering vector)。需要注意的是，若參考元素在天線陣列的最左邊， 則(2.9)式將表示為 2 2 cos ( 1) cos ( ) [1 j d ... j K d ]T e e π _θ π _θ λ λ θ = − a (2.11) 假設現在有多位使用者同時傳送信號，且信號受可加性白色高斯雜訊 (AWGN)所影響，則接收信號的複數封包表示式為

∑

= + = U i i i s t t t 1 ) ( ) ( ) ( ) ( a n x θ (2.12) 其中U 為使用者總數，θ 為第i i位使用者的到達角度(angle of arrival， AOA)，si(t)為第i位使用者的傳送信號，n(t)為K×1的雜訊向量，且 , ] ... 1 [ ) ( ( 1) cos 2 cos 2 T d K j d j i i i e e λ θ π θ λ π θ = − − − a (2.13) 為第i位使用者的陣列響應向量。使用矩陣表示式，則(2.12)式可表示成 ) ( ) ( ) ( ) (t A s t n t x = θ + (2.14) 其中 ] ) ( ... ) ( ) ( [ ) (θ aθ₁ aθ₂ a θ_U A = (2.15) 為由陣列響應向量所組成的K×U矩陣，且 T U t s t s t s t s( )=[ ₁( ) ₂( ) ... ( )] (2.16) 若多位使用者在多重路徑的環境下，使用相同頻帶，同時傳送信號，其接 收信號可表示成

∑∑

= = + = U i L l i i l i l s t t t i 1 1 , , ( ) ( ) ( ) ) ( a n x α θ

∑

= + = U i i is t t 1 ) ( ) ( n b (2.17) 其中Li為第i位使用者的多重路徑總數，α 為第l ,i i位使用者之第l個多重路 徑之複數振幅(complex amplitude) ，θ 為第l ,i i位使用者之第l個多重路 徑之到達角度，a(θ_l,i)為相對於θ 之陣列響應向量，_{l ,i} b_i為第i位使用者之空 間特徵(spatial signature)，其定義如下

∑

= = Li l i l i l i 1 , , (θ ) α a b (2.18) 我們可以把(2.17)式表示成矩陣表示式 ) ( ) ( ) (t Bs t n t x = + (2.19) 其中 ] ... [b1 b2 bU B= (2.20) B為K×U 的空間特徵矩陣，其行向量和每個傳送信號的空間特徵有關。 假設我們對接收信號x(t)在時間點t₁，t₂，…，t_M 做取樣，可將(2.14)式 表示成 N S A X= (θ) + (2.21) 其中X及N為K×M 之矩陣。 ] ) ( ... ) ( ) ( [x t₁ x t₂ x t_M X= (2.22) ] ) ( ... ) ( ) ( [n t₁ n t₂ n t_M N= (2.23) S為U×M 之信號矩陣 ] ) ( ... ) ( ) ( [s t1 s t2 s tM S= (2.24) 圖2.4為窄波之波束形成器，在第k根天線之第n個時間的窄波信號與 參考單位天線之第n個時間的窄波信號，只在相角上有變化，此相角上的 變化和天線間的距離有關。 波束形成器在時間點n之輸出y n( )為 * 1 ( ) ( ) K k k k y n w x n = =

∑

(2.25) 其中x nk( )為接收信號在第k根天線之第n個時間的複數封包表示式。wk為

複數權重。(2.25)式可用向量的形式來表示: ( ) w xH ( ) y n = n (2.26) 其中 1 2 [ ... ] w T K w w w = (2.27) 1 2 ( ) [ ( ) ( ) ... ( )] x n = x n x n x_K n (2.28) 圖2.4 窄波波束形成器

2.1.2 空間濾波器(spatial filter)及空間耐奎斯特取樣定

理(spatial Nyquist sampling rate)

空間濾波器的概念，相當接近於時間濾波器(temporal filter)的概 念，時間濾波器是在時域上對接收信號做處理，進而區分出使用者的信號 以及干擾信號，而空間濾波器則是利用空間的特性進行信號的濾波[3]。 我們可以使用分接式延遲線濾波器(tapped-delay-line filter)來實現時 間濾波器。我們考慮如何使用分接式延遲線濾波器， 從一個由q個弦波所 組成的波形提取出特定頻率的弦波。輸入分接式延遲線濾波器的信號可表 示為 ) ( )} 2 ( exp{ ) ( 1 t n t f j a t x q k k k k + + =

∑

= φ π (2.29) 其中 fk，ak以及φ 分別代表第k k個弦波之頻率，振幅和相角。假設我們對

輸入信號做取樣，取樣頻率為1/T_s，x(i)定義為在時間點iT_s的信號，則經 過取樣的輸入信號可以表示為

∑

= + + = q k s k s k k j f iT n iT a i x 1 ) ( )} ) ( 2 ( exp{ ) ( π φ (2.30) 信號經過含有P−1個延遲元素之分接式延遲線濾波器後，在第i個取樣的 瞬間可表示為

∑

= + = q i k k s i i f i 1 ) ( ) ( ) ( ) ( a n x (2.31) 其中 T P i x i x i x i) [ ( ) ( 1) ... ( 1)] ( = − − + x T s s s n iT n iT P iT n i) [ ( ) ( 1) ... ( 1)] ( = − − + n T T P f j T f j k s k s k _e e f ) [1 ... ] ( = − 2π − 2π ( −1) a (2.32) ) (i s_k 為第k個複數弦波之第i個瞬時取樣點，表示成 )} ) ( 2 ( exp{ ) ( _{k k s k} k i a j f iT s = π +φ (2.33) 比較(2.31)式、(2.32)式、(2.12)式及(2.13)式可以得到以下關係[4] z 在空間濾波器中之d λ 項相當於時間濾波器中之Ts項 z 在空間濾波器中之cos( )θ 項相當於時間濾波器中之 fk項 根據耐奎斯特取樣定理[5]，時間濾波器為了避免aliasing發生，取樣頻 率至少要大於信號頻寬2倍以上。同理，若應用上述觀念於空間濾波器上， 稱之為空間耐奎斯特取樣定理[6]。由於空間濾波器之 d λ 對應於時間濾波 器之取樣頻率，且最高頻率値為1(因為cos( )θ 的最大值為1) ，則空間耐奎 斯特取樣定理可表為 2 1 d λ _{≥ ×} (2.34) 或者 2 d ≤ λ (2.35) 因此，為了避免aliasing現象的發生，天線間擺放距離必須小於或等於輸

入信號之波長的1 2 。

2.2 智慧型天線技術

智慧天線有依環境來抑制干擾、自動追蹤及數位式波束成型等優點，因此 被認為是第四代行動通信的關鍵技術。一般而言，可分為切換波束式天線 陣列與適應性天線陣列兩種。適應性天線陣列雖然有較佳的效能，但需要 複雜的計算。切換波束天線陣列雖然較易實現，但在提升系統效能方面卻 不及適應性天線陣列。

2.2.1 切換波束式天線陣列[7][8]

切換波束式天線陣列具有有限數目的、固定的、預定先定義的波束， 透過陣列天線技術在同一通道中利用多個波束同時對多個用户傳送不同 的信號，此時系統會檢測信號强度,從幾個預先定義的、固定的波束中選 擇其一進行傳輸，進而提升系統效能。 每個波束都是透過天線陣列預先設計的。根據使用者的方位不同，基 地台選擇其對應的波束，使其接收信號強度為最大。但是，使用者並非每 次都落於波束中心，若使用者位於波束邊緣時，而干擾的信號源卻落於波 束中心，此時接收效果會最差。另外，在多重路徑的考量下，切換式波束 天線陣列其波束是固定的，無法提供針對每個路徑的信號個別處理，容易 降低通信品質。雖然切換式波束天線陣列有上述缺點，不過此系統的構造 相當簡單，不需要複雜的數學運算，即可達到改善系統效能的目的，在硬 體實現上以及經濟成本的考量下有很大的優勢。

2.2.2 適應性天線陣列[7][8]

適應性天線陣列不僅會依據使用者的所在位置來產生特定方向的窄 波束，且可以隨著使用者的移動執行動態調整，其透過權重向量調整波束 場型，將波束場型上具有最高增益的主波束指向使用者的方位，並透過調 整權重向量之振幅及相位，在多重路徑成分與或其他使用者的方位上生成 零強度(null)的場型，以降低多重路徑衰落的程度與抑制同頻干擾的影 響。適應性天線陣列更可以提供空間分集的功能來合成同調的多重路徑訊 號，如此對使用者的訊號能得到更大的增益並增加對系統效能的改善。然 而，相較於切換波束式天線陣列，適應性天線陣列雖擁有上述的多項優點 與好處，但必須付出的代價是較高的運算複雜度與技術需求，這會增加在 硬體實現上的困難度與提高製作成本，而這也是系統業者在選擇使用智慧 型天線系統時需要加以考慮的兩項重要因素。

2.2.2.1 權重最佳化之準則[2]

適應性天線陣列可以根據接收信號的特性而調整權重向量。適應性天 線陣列在干擾出現的方向，會形成零強度場型，進而提高接收信號的訊號 干擾比。若接收信號的特性是不隨時間而改變的，那麼適應演算法將會計 算 出 一 組 固 定 的 權 重 向量 。 一 般 而 言 ， 適 應 性 演 算 法 會 透 過 反 覆 的 (iterative)計算來計算權重向量，一直持續到進行到系統效能到達一定 的 效 能 要 求 為 止 。 幾 個 常 見 準 則 為 最 小 平 均 平 方 誤 差 (minimum mean-squared error ， MMSE) ， 最 大 訊 號 干 擾 比 (maximum signal-to-interference-plus-noise ratio，MSINR)，以及線性限制最 小變異數(linearly constrained minimum variance，LCMV)。以下章節

將會介紹這些準則。

2.2.2.2 最小平均平方誤差準則[2]

最小平均平方誤差準則的目標為使的接收信號 y n( )和欲求的信號 ( ) d n 之間的平均平方誤差値為最小。此準則可表示為 2 [ ( ) ( ) ] J =E d n −y n (2.36) 其中E i[ ]為期望値。將(2.26)式代入(2.36)式可得 2 [ ( ) ( ) ] J =E d n −y n * [{ ( ) ( )}{ ( ) ( )} ] E d n y n d n y n = − − * [{ ( ) w xH ( )}{ ( ) w xH ( )} ] E d n n d n n = − − = 2 _* [ ( ) w xH ( ) ( ) ( )xH( )w w xH ( )xH( ) ]w E d n − n d n −d n n + n n 2 _* [ ( ) ] [w xH ( ) ( ) ] [ ( )xH( ) ]w [w xH ( )xH( ) ]w E d n E n d n E d n n E n n = − − + 2 [ ( ) ] w p p wH H w RwH E d n = − − + (2.37) 其中 [ ( ) ( )] R x xH E n n = (2.38) R為輸入信號x n( )之自相關矩陣(correlation matrix)，其維度為K×K * [ ( ) ( )] p=E x n d n (2.39) p為輸入信號x n( )和欲求的信號d n( )之互相關向量(cross- correlation vector)，其維度為K×1。為了得到J為最小值，必須針對w對J微分使其 結果為零，數學表示式為 2p 2Rw 0 J ∇ = − + = (2.40) 根據(2.40)式，可得最佳化權重向量 1 w_{opt =}R p− _(2.41) 為求得(2.41)式的最佳解，要先求得x n( )之自相關矩陣R以及互相關向量

p。 若我們將自相關矩陣R表示為 R R= _ss+R_uu (2.42) 其中 2 ( ) [ ( )] ( ) R a aH ss = θ E d n θ ，R [ ( )u u ( )] H uu =E n n ，且u n( )為干擾信號，其 維度為K×1。反矩陣原理如下 1 1 2 1 1 [ ] 1 E d n[ ( )] H( )θ _uu ( )θ uu − − − = + R R a R a (2.43) 若我們假設在高的訊雜比之下，則x( )n ≈a( ) ( )θ d n 且 * [ ( ) ( ) ( )] p=E a θ d n d n 2 [ ( )] ( ) E d n θ = a (2.44) 最佳解可表示成 2 1 2 1 [ ( )] [ ] ( ) 1 [ ( )] ( ) ( ) w R a a R a opt H uu uu E d n E d n θ θ θ − − = + (2.45) 1 ( ) MMSE uu β − θ = R a (2.46)

2.2.2.3 最大訊號干擾比[2]

假設天線陣列的輸入信號向量為s n( )，其為維度K×1之向量。經過波 束形成器之輸出信號之信號能量，可表示為 2 2 [w sH ( ) ] s E n σ = * [{w sH ( )}{w sH ( )} ] E n n = [ ( ) ( )] wH s sH w E n n = =w R wH ss (2.47) 其中Rss =E[ ( )s n sH( )]n 為欲求的信號之自相關矩陣，其維度為K×K。同理， 干擾信號之能量可表示為

2 [w uH ( ) ] u E n σ = w R wH uu = (2.48) 其中R_uu =E[ ( )u n uH( )]n 為干擾信號之自相關矩陣，其維度為K×K。輸出之 訊號干擾比可表示為 2 2 ( ) s o u SINR σ σ = w R w w R w H ss H uu = (2.49) 我們將(2.49)式，針對w微分,並使其微分結果為零，可得到 w R w R w R w w R w H ss ss H uu uu = R w_uu λ = (2.50) 最佳的權重向量w，可藉由尋找矩陣_{R R}1 uu ss − _{之最大特徵値而獲得,如下式所} 示 1 max R R wuu ss opt λ wopt − _{= (2.51)} 最大信號干擾比可定義為 ,max ( ) w R w w R w H opt ss opt o H opt uu opt SINR = (2.52) 其中 2 ( ) [ ( )] ( ) R a aH ss = θ E d n θ ，最佳化權重向量可表示成 1 ( ) w_{opt =}β_MSINRR a_uu− θ _(2.53) 其中 2 max [ ( )] ( ) aH w MSINR opt E d n β θ λ = (2.54) 若干擾信號的特性為白色(white)，_R 2_I uu =σ ,其中 2 σ 為白色雜訊的變異數, I為單位矩陣(identity matrix)，則最大訊號干擾比可以等同於最大訊雜 比(maximum signal-to-noise ratio)。輸出的雜訊功率為

2 2_{w w}H n σ =σ (2.55) 且訊雜比為 2 2 ( ) s o n SNR σ σ = 2 w R w w w H ss H σ = (2.56) 將(2.56)式，針對w微分，並使其微分結果為零，可得到最大的訊雜比。 假設 2 1 σ = 並且限制w wH =1_,可得: R w_ss =λw (2.57) (2.57)式為求特徵值得問題。類似於求最大訊號干擾比的情況，最佳的權 重向量可以藉由尋找矩陣Rss之最大特徵値λ 而獲得， max max R wss opt =λ wopt (2.58) 最大訊雜比為 max ,max 2 (SNR)o λ σ = (2.59)

2.2.2.4 應用於波束形成之適應性演算法

先前章節已經討過幾種常見的找出最佳權重向量之準則。為了找出最佳 的權重向量，有時必須知道二階的統計特性，但是統計特性經常是未知的並 且會隨時間而改變其特性。適應性演算法優勢在於可以隨著時間不斷的更新 權重向量，透過權重向量的不斷調整，可以使得系統效能更加接近於最佳化 的準則。以下會介紹幾種經常應用於波束形成的適應性演算法。

2.2.2.5 倒置取樣矩陣演算法(Sample Matrix Inversion

Algorithm，SMI)

倒置取樣矩陣演算法主要概念為持續觀察輸入天線陣列之一段信 號，利用來估測自相關矩陣R和互相關向量p[9][10]，亦稱為最小平方誤 差法(Least Square Error)。表示式為

2 1 2 1 1 ˆ _{( ) ( )} R x x N H n N n n N N = = −

∑

(2.60) 2 1 * 2 1 1 ˆ ( ) ( ) p x N n N n d n N N = = −

∑

(2.61) 其中N₁及N₂分別為觀察區間的起始時刻及終止時刻。權重向量為 1 ˆ _ˆ ˆ w R p= − (2.62) 求得的權重向量將會被使用來接收觀察區間內的信號。為了能適應環境的 改變，每段觀察區間自相關矩陣_Rˆ _{和互相關向量pˆ將為被重新估測。在觀} 察區間以外的信號將不會影響權重向量的計算結果。 為了避免 _ˆ 1 R− 的計算，可以使用反矩陣輔助定理(matrix inversion lemma): 1 1 1 1 1 ˆ _{( 1) ( ) ( )}ˆ _{( 1)} ˆ _{( )} ˆ _{( 1)} ˆ 1 ( ) ( 1) ( ) R x x R R R x R x H H n n n n n n n n n − − − − − − − = − − + − , 1 2 N ≤ ≤n N 1 1 ˆ ₍₀₎ R I ε − _{= ,} 0 ε > (2.63) 必須要有一定的取樣數才能估測較為精準之自相關矩陣_Rˆ _{和互相關向量} ˆ p，一般而言取樣數至少要大於二倍的天線總數[11]。反取樣矩陣演算法

配合反矩陣輔助定理時，每次重新計算權重向量需要 2 3.5M +M 個複數乘 法。其中M 代表權重個數之總數。

2.2.2.6 最小平均平方演算法(Least-Mean-Square

algorithm)

由(2.41)式，要求得最佳權重向量必須計算自相關矩陣R之反矩陣， 需要龐大的運算量。最小平均平方法被用來避免反矩陣的運算[12]，並且 能隨著時間更新權重向量 1 ( 1) ( ) [ ( )] 2 w n+ =w n + µ −∇J n (2.64) 其中µ 為收斂因子(convergence factor)，用來控制收斂速度。最小平均 平方法是建立在最陡峭法(steepest- descent method)[13]上，且利用遞 迴的方式計算並更新權重向量。 要精確的計算出梯度向量(gradient vector)是非常困難的，必須事先知道自相關矩陣R和互相關向量p。我們 利用估測的梯度向量∇ˆ ( )J n 取代梯度向量∇J n( ),其數學表示式為 ˆ_{J n( ) 2 ( ) 2 ( ) ( )pˆ n R}ˆ _{n w n} ∇ = − + (2.65) 其中 ˆ ( ) ( ) ( ) R x xH n = n n (2.66) * ˆ ( ) ( ) ( ) p n =x n d n (2.67) 為(2.38)式以及(2.39)式中R及p之瞬時估測。將(2.65)式、(2.66)式以 及(2.67)式代入(2.64)式中,可得 ˆ ˆ ˆ( 1) ˆ( ) [ ( ) ( ) ( )]ˆ w n+ =w n +µ p n −R n w n * ˆ( ) ( )[ ( ) ( ) ( )]ˆ w x xH w n µ n d n n n = + − * ˆ ( ) ( ) ( ) w n µx n e n = + (2.68) 此即為最小平均平方演算法。最小平均平方演算法每次更新權重向量需要

2M個複數乘法。 收斂因子µ 較小時，收斂速度較為緩慢，當可應用於收斂之資料數目 很多時可以得到較精準的梯度向量之估測值。收斂因子µ 較大時，收斂速 度較快，但是只能得到較為粗略的梯度向量估測值，比較適合應用於可應 用於收斂之資料數目較少時。收斂速度也會和特徵值擴散(eigenvalue spread)χ( )R 有關，其數學表示式為 max min ( )R λ χ λ = (2.69) 其中λ 為_max R之最大特徵值，λ 為_min R之最小特徵值。當訊號特性為白色 時，特徵值擴散χ( )R 會等於1，此時χ( )R 將不會影響收斂速度。在[12]中， 針對收斂速度，有更詳細的討論。

2.2.2.7 遞迴最小平方演算法(Recursive Least-Squares

Algorithm)

使用反取樣矩陣演算法時，必須透過一段觀察區間來估測R和p，而 遞迴最小平方演算法是透過加權總合來估測R和p，其數學表示式為 1 1 ( ) ( ) ( ) R n n x xH i n λ − i i = =

∑

(2.70) 1 * 1 ( ) ( ) ( ) p n n xH i n λ −d i i = =

∑

(2.71) 其中λ為遺忘因子(forgetting factor) ，其範圍為0< ≤λ 1。n為觀察區 間上限,1 i< ≤n。根據(2.70)式以及(2.71)式，可以透過遞迴的方式更新 ( ) R n 及p n( ): ( ) ( 1) ( ) ( ) R R x xH n =λ n− + n n (2.72) * ( ) ( 1) ( ) ( ) p n =λp n− +d n x n (2.73)

應用反矩陣輔助定理: 1 1 1 1 ( ) [ ( 1) ( ) ( ) ( 1)] R R q xH R n λ n n n n − ₋ − − = − − − (2.74) 其中 1 1 1 1 ( 1) ( ) ( ) 1 ( ) ( 1) ( ) R x q xH R x n n n n n n λ λ − − − − − = + − (2.75) 為增益向量(gain vector)。重新整理(2.75)式, 1 1 1 1 ( ) ( 1) ( ) ( ) ( ) ( 1) ( ) q R x q xH R x n =λ− − n− n −λ− n n − n− n 1 1 1 1 [λ− R− (n 1) λ−q( )n xH( )n R− (n 1)] ( )x n = − − − (2.76) 將(2.74)式代入(2.76)式: 1 ( ) ( ) ( ) q n =R− n x n (2.77) 權重向量可以透過下列數學式而被更新: 1 ( ) ( ) ( ) w n =R− n p n = 1 1 1 [R (n 1) q( )n xH( )n R (n 1)] λ− − _{− −} − _{− [} * ( 1) ( ) ( ) p n d n x n λ − + ] 1 1 ( 1) ( 1) ( ) ( ) ( 1) ( 1) R p q xH R p n n n n n n − − = − − − − − 1 * 1 1 * 1 ( )R ( 1) ( )x ( ) ( )q xH( )R ( 1) ( )x d n n n d n n n n n λ− − λ− − + − − − 1 1 ( 1) ( 1) ( ) ( ) ( 1) ( 1) R p q xH R p n n n n n n − − = − − − − − 1 * 1 * 1 [d n( )R (n 1) d n( ) ( )q n xH( )n R (n 1)] ( )x n λ− − − + − − − 1 1 ( 1) ( 1) ( ) ( ) ( 1) ( 1) R p q xH R p n n n n n n − − = − − − − − * 1 ( )R ( ) ( )x d n − n n + 1 * ( 1) ( ) ( ) ( 1) ( ) ( ) ( ) w q xH w R x n n n n d n − n n = − − − + (2.78) 由(2.77)式，q( )n =R−1( ) ( )n x n ，我們透過下面數學式更新權重向量

* ( ) ( 1) ( )[ ( ) ( ) ( 1)] w w q xH w n = n− + n d n − n n− * ( 1) ( ) ( ) w n q n ξ n = − + (2.79)

其中ξ( )n 為事前估測誤差(prior estimation error)，其定義為

* ( )n d n( ) xT( )n w (n 1) ξ = − − =d n( )−w(n−1) ( )x n (2.80) (2.80)式中，ξ( )n 之值主要是由欲求的信號d n( )、輸入信號x n( )與先前在 時間點n−1時，利用遞迴最小平方演算法估測所得的權重向量w n( −1)所建 立產生的。 遞迴最小平方演算法相較於最小平均平方演算法會有較快的收斂速 度，但是相較於最小平均平方演算法需要較複雜的數學運算。遞迴最小平 方演算法每次更新權重向量需要 2 4M +4M +2個複數乘法[4]，其中M 代表 所需的權重個數總數。

2.3 智慧型天線對系統的改善及主要用途

智慧型天線系統利用控制主動元件來改變電波輻射場型，達到空間分 集的功能並實現空間分隔多重進接存取之機制，它可以降低時間延遲擴散 (time delay spread)與多重路徑衰落(multi-path fading)的影響，增加 發射效率與系統蓋範圍及改善通訊品質與系統容量等優點，下面則將對各 項智慧型天線的優點加以描述與分析[14][15][16][17]：

z 改善通道容量及頻譜使用率

在無線通訊系統中如何改善通道容量以及有效利用頻譜是個重要的 議題。在不降低通訊品質為前題之下，增加用戶數量可以提高頻譜使用

率，所以通道容量越大與頻譜使用效率越高，亦即增加通道容量可以使更 多用戶以相同的資料傳輸速率進行通訊進而增加頻譜使用效率。利用智慧 型天線波束合成技術，系統的操作功率比傳統系統低，可增加載波干擾比 (Carrier-to-interference Ratio，CIR)，並提高通道的頻率再使用率， 進而增加系統容量。 z 增加發射功率 由於智慧型天線不同於全向性天線(omni-directional antenna)，具 有在特定方向上形成較大的天線增益之特性，因此在相同細胞(cell)大小 條件之下，可以降低發射機的功率。如此，不僅可減少同頻干擾的現象， 同時可增加電池壽命、縮減電池大小與降低發射機的價格。然而，對接收 機而言，其代價是增加設計複雜度及需要解決較多的零組件形成的空間問 題，所以目前無線通訊系統之應用大多將智慧型天線系統架設在基地站台 之中。當然，倘若行動用戶端能同時使用智慧型天線架構，對系統的整體 效能具有提升的作用。 z 增加系統涵蓋範圍 使用傳統單一全向性天線之系統在傳送信號時，會對360∘方位進行 傳送，因此容易造成功率的浪費。而智慧型天線系統只對使用者所在的特 定方位進行傳送，因此在相同發射功率的條件下，智慧型天線系統可使得 基地台的服務區域擴大而增加系統之涵蓋範圍。上鏈時，因為智慧型天線 擁有較高的天線增益，而對訊號傳播造成的路徑損失所能容忍的值亦較 高，因此在相同的發射功率下，由於對路徑損失容忍度的增加，因此可以 延伸使用者與基地台間的距離；在下鏈時，位於基地台的智慧型天線會依 據使用者所在位置產生一方向較集中、功率較大的窄波束來傳遞訊號，因 此使用者在相同距離的條件下將接收到較大功率的訊號，相對的，相同發 射功率的條件下，使用者能在較遠的距離接收到由基地台所發射的訊號。 z 降低時間延遲擴散及多重路徑衰落的影響 由於電波的多重路徑傳播特性將造成接收天線所收到的信號為各路 徑成份的加成，而每個路徑成份則會因其傳播路徑長度、遮蔽物特性等不

同因素影響，造成其振幅大小、信號相位、到達時間、到達方向等的變化。 智慧型天線系統可使用波束形成技術來抑制多重路徑成分及使用空間分 集機制來降低信號衰落，進而減少多重路徑效應的影響。智慧型天線會依 據使用者所在位置產生一特定方向的窄波束來傳遞訊號，因此使用者將接 收到方向較集中，功率較大的信號，而其它方向則會因為波束場型的限制 而降低其接收功率，利用此多重路徑消除(multi-path cancellation)方 式，可使得在接收信號時，能有效降低延遲擴散、減少多重路徑數目、集 中路徑成分功率及降低同頻干擾的效果；有異於多重路徑消除方式，智慧 型天線可使用天線分集之機制來善加利用每一路徑成分的功率，達到降低 信號衰落的影響，並可利用分集增益(diversity gain)的效應減少發射功 率。 z 提升通訊品質 在通訊系統中，分析通訊品質的方法通常是在一定訊雜比的條件下分 析位元錯誤率(Bit Error Rate，BER)或符元錯誤率(Symbol Error Rate， SER)，或是在一定的位元錯誤率或符元錯誤率條件下比較訊雜比的需求。 一般來說，增加通訊的品質的作法是利用提高訊雜比的方式來達到所要求 的位元錯誤率或符元錯誤率。然而，由於智慧型天線系統可利用其所產生 之特定波束場型來抑制多重路徑或使用空間分集之機制來降低信號衰 落。因此，在不增加發射功率的前題下，使用智慧型天線能增加訊雜比， 進而達到提升通訊品質的目的。

第三章 正交分頻多工技術

3.1 正交分頻多工技術介紹

正交分頻多工系統的基本原理，是將原有的資料傳輸序列分配在多個 不同的子載波上平行傳送，如圖3.1所示。 圖3.1 多載波傳輸示意圖 因此，在時域上，每一子載波上的傳輸時間間隔增為原本時間間隔的 數倍，使得在每個子載波上的符元持續時間(Symbol Duration)增加，因 此 可 以 降 低 由 多 重 路 徑 延 遲 擴 散 所 引 起 的 符 際 干 擾 (Inter Symbol Interference)。在頻域上，若共使用N個子載波，則相對於原本串列傳 輸而言，各個子載波的頻寬相對變小N 倍，於是在遭遇到多重路徑衰落通 道時，通道之同調頻寬(Coherence Bandwidth)便大於子載波的頻寬，因 此對於各別的子載波而言，可視為平坦衰落(Flat fading)的通道。

在 頻 譜 使 用 效 益 上 , 傳 統 分 頻 多 工 (Frequency Division Multiplexing，FDM)子載波頻譜間不相互重疊，如圖3.2(a)所示。而正交 分頻多工系統中，子載波相互維持正交，而子載波間是相互重疊，如圖 3.2(b)所示，藉此來達成頻譜的高利用率。 (a) 傳統分頻多工 (b)正交分頻多工 圖 3.2 傳統分頻多工與正交分頻多工比較圖 分析二種不同的方式之頻譜效益可以得到如下結果。 傳統單載波系統的之頻寬效益： s T W = (1+β) s T M

R=log2 bits/ sec

M W R 2 log 1 1 β + = (3.1)

其中β 為滾邊因子(Roll-off Factor)，M 為字母系統大小(Alphabet

Size)，N為子載波總數。 使用重疊的多載波系統之頻寬效益: s NT N W =( +1)⋅ 1 s T M R= log2 / sec bits M W R 2 log ≅ (3.2) 比較(3.1)式和(3.2)式，使用重疊的多載波系統所得的頻寬效益較傳統單 載波系統約好上(1+β)倍。

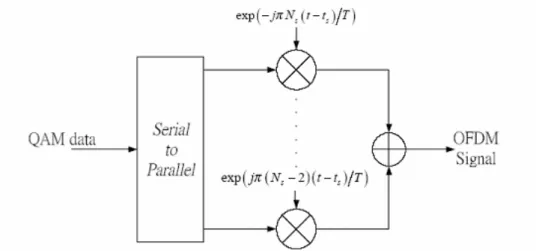
正交分頻多工系統中，子載波上所傳送的符元使用相移鍵(Phase -Shift Keying ， PSK) 或 正 交 振 幅 調 變 (Quadrature-Amplitude Modulation，QAM)，所有子載波的符元一起構成一個正交分頻多工區塊， 其時域信號為所有調變後的子載波總合所組成，其基頻數學表示式為(3.3) 式。 1 2 2 2 exp( 2 ( )), ( ) 0, s s s N N s S S i N i S s i d j t t t T t T d t T t t and t t T π − + =− ⎧ ⎪ _{− ≤ ≤ +} ⎪ = ⎨ ⎪ ⎪ < > + ⎩

∑

_(3.3) 其中di為複數的符元，Ns為子載波的總數，T 為符元區間，ts為符元開始 時間。在時域中，正交分頻多工信號可以視為由多個擁有整數個週期且不 同頻率的正交子載波疊加所組成。圖3.3為正交分頻多工傳送端調變器示 意圖。 上述為基本的類比正交分頻多工系統，需要多組的震盪器傳送正交分 頻多工信號，然而，要同時設計多組的震盪器複雜度太高，不利於硬體實 現。因此，實際上，要實現正交分頻多工系統，是採用數位的快速傅立葉 (IFFT/FFT)的方式，如(3.4)式所示。 1 2 2 2 ( ) exp( 2 ( )) s s s N N s i N s s i i s t d j t t N T π − + =− =

∑

− 1 2 2 2 1 1 ( ) ( ) exp( 2 ) s s s N s N i N s s _i s ik s k s t kT d j N N π N − + =− = = =

∑

, k =0,1,...,Ns−1 2 ( ) { } s N i s k IFFT d + = (3.4)

圖 3.3 正交分頻多工系統傳送端調變器示意圖 由(3.4)式,以時域與頻域的觀點來看分頻正交多工信號，s k( )為時域 的類比波形取樣點，而符元di N+ _s/ 2則為頻域上每個子載波的信號。因此， 正交分頻多工系統可用傅立葉轉換之方式實現。為了使用快速傅立葉轉換 實現正交分頻多工系統，必須對信號取樣，而且取樣信號必須滿足取樣定 理，即取樣頻率必須大於等於兩倍信號頻寬。實際使用正交分頻多工系統 時，經常不會將全部的子載波用來載送信號，而這些不送信號的子載波稱 之為虛擬載波(Virtual Carriers)。

3.2 保護區間(Guard Interval)與載波正交性

多路徑延遲擴散除了造成符元之間的干擾外，也會造成正交分頻多工 系統中不同區塊間的干擾(Inter-Block-Interference，IBI)。為了消除 此干擾，在每一分頻正交多工區塊中加入保護區間，如圖3.4所示。

圖3.4 正交分頻多工系統之保護區間示意圖 保護區間的長度必須大於所預期之最大多路徑延遲擴散，才能確保正 交分頻多工區塊不會受到上一個正交分頻多工區塊干擾。 圖3.5 保護區間內不送信號引起載波間干擾之示意圖 圖3.5[18]為當保護區間內沒有傳送信號時的示意圖,此時會造成引 起載波間干擾(Inter-Carrier-Interference，ICI)。因此為了維持子載 波間的正交性,因此必須在保護區間內加入正交分頻多工信號尾部之一段 信號。 只要傳輸延遲延展小於保護區間，則在一個完整快速傅立葉轉換之區 間中總是有整數倍週期的弦波，如此仍然可維持載波之間的正交性而不會 有載波間干擾現象發生，下面以圖3.6為例子說明。

圖3.6 傳輸延遲延展小於保護區間示意圖 圖3.6[18]為兩個路徑的傳輸，實線部份代表第一路徑，虛線部分代 表第二路徑，也就是實線的正交分頻多工信號延遲。注意在正交分頻多工 符元邊界處會發生相位跳躍的情形，用來表示不同符元之間的不連續。對 於虛線信號而言，其相位跳躍發生在第一個路徑之後的某一特定延遲，當 此延遲小於保護區間，則在完整的快速傅立葉轉換區間中不會有相位跳 躍，因此雖然正交分頻多工信號有相位的變化，因為有週期延伸的保護區 間存在，使得載波之間仍然維持正交性。若是最大傳輸延遲大於保護區 間，則在快速傅立葉轉換區間內會有相位跳躍，使得載波之間失去正交 性，載波間干擾便會出現。 符元同步若是有誤差，造成取到的快速傅立葉區間往前移幾點或者往 後移幾點，只要載波仍然維持正交，僅造成相位偏轉(Phase Rotation)， 可利用通道估測的方式加以補償，因此接收端仍可作正確的解調變。反 之，若是正交性被破壞，則接收端便無法進行正確的解調變。

3.3 正交分頻多工系統之優缺點

綜而言之，正交分頻多工系統主要的優點如下： z 正交分頻多工系統能抵抗多路徑傳輸的干擾，不需要複雜的時域等化 器，可降低複雜度。假設一系統可容忍的延遲擴散固定，正交分頻多工系 統可以簡單的克服延遲擴散所引起的信號干擾，而單載波系統卻需要一個

複雜度相當高的等化器來消除延遲擴散所引起的信號干擾。 z 在緩慢的時變通道中，可以根據各個不同載波的訊雜比，而給予不同 載波不同的調變方式，來增加系統的容量。 z 正交分頻多工系統具有頻率分集(Frequency Diversity)的效果，比單 載波機制更能夠對抗窄頻干擾，因為窄頻干擾只能影響很少比例的載波數 目。 正交分頻多工系統與單載波機制相比，也有一些缺點，可說明如下： z 正交分頻多工系統,會經過快速傅立葉轉換,會將數個載波相加,將會 造成嚴重的之功率峰對平均值(peak-to-average power ratio，PAPR)問 題，造成非線性失真，增加功率放大器設計之複雜度。

z 正交分頻多工系統對於載波頻率偏差、取樣頻率偏差與相位雜訊較為 敏感，容易破壞正交性而造成載波間干擾，因此對同步要求相當嚴格。

第四章 應用於正交分頻多工系統之波束形成技術

本 章 討 論 如 何 將 智 慧 型 天 線 應 用 於 正 交 分 頻 多 工 系 統 。 當 上 鏈 (uplink)時，使用智慧型天線接收正交分頻多工信號，根據結構不同區分 成兩種型態，第一種類型是前置-快速傅立葉轉換型(Pre-FFT type)，第 二種是後置-快速傅立葉轉換型(Post-FFT type)。

4.1 通道模型

介於傳送端天線與擁有K根之接收天線陣列之間之多重路徑通道的 脈衝響應(Impulse response),可以表示為[19][20][21]: 1 ( , ) ( ) exp[ ( )] ( ( )) [ ( )] h a L l l l l l tτ ρ t jβ t θ t δ τ τ t = =

∑

− (4.1) 其中L為路徑的總數量，ρ_l( )t 為第l個路徑之振幅大小，且其分佈為雷利 分佈(Rayleigh distribution)，β_l( )t 為均勻分佈之相角位移，δ( )i 為脈衝 函數(Dirac-delta function)。a( ( ))θ_l t 為陣列響應向量，其數學表示式為 2 2 cos ( ) ( 1) cos ( ) ( ( )) [1 ... ] a j d l t j K d l t T l t e e π _θ π _θ λ λ θ = − − − (4.2) 其中K為天線總數量，θ_l( )t 為到達角度，其機率分布為均勻分布(uniformly distributed)，λ 為載波波長。 l θ 之機率分布為: 1 , ( ) 2 2 0, θ θ l l l l l P otherwise θ ∆ ∆ ⎧ _{Θ − ≤ ≤ Θ +} ⎪ = ∆⎨ ⎪⎩ (4.3) 其中∆為角度擴散(angle spread) ，Θl為第l 個路徑之到達角度之中心

4.2 前置-快速傅立葉轉換型天線系統

4.2.1 前置-快速傅立葉轉換型之結構

前置-快速傅立葉轉換之結構如圖4.1(b)所示。 (a) (b) 圖 4.1 (a)正交分頻多工系統之傳送端 (b)前置-快速傅立葉轉換型天線 陣列 波束形成之基本原理是用一組複數的權重向量w來調整無線電波的 波束場型，其數學表示為 1 2 [ ... ] w= w w wK (4.4) 使用適當的輻射場型收發訊號，以得到空間分集之功能來增強訊號強度與 抑制雜訊及同頻干擾，當權重向量置於快速傅立葉轉換之前，即在時域上

對信號做處理，則稱為前置-快速傅立葉轉換型結構。 關 於 前 置 - 快 速 傅 立 葉 轉 換 型 天 線 陣 列 的 各 種 演 算 法 已 被 提 出 [22][23][24]，各種演算法都有其優缺點。其中若使用切換波束式的做 法，可以滿足低複雜度的需求，並可有效提升系統效能。4.2.2及4.2.3小 節將會介紹前置-快速傅立葉轉換型天線陣列。

4.2.2 理想切換波束天線陣列

在 2.2 節中，已對切換波束天線陣列做了初步的介紹，其主要概念是 在幾組預先設計的權重向量中，選擇出一組最佳的權重向量來接收信號。 圖 4.2 理想波束 切換波束天線陣列重點在於，首先要設計幾組低旁波帶(low sidelobe) 的波束，即是需要事先設計幾組權重向量；其次要能根據使用者信號到達 角度的不同，精準的選擇出使用何組權重向量。 理想切換波束天線陣列即是可以產生理想波束如圖 4.2[25]，波束內 對於任意的到達角度的增益均為 1，旁波帶的增益為波束的 0.1 倍，並且 接收天線可以準確的判斷信號到達角度，進而決定使用者信號所位於的波 束。 前置-快速傅立葉轉換型天線陣列的輸入信號r t( )之數學表示為

, , 1 ( ) ( , ) ( ) ( , ) ( ) ( ) r h U h_{I i I i} n i t ∞ tτ s t τ τd ∞ tτ s t τ τd t −∞ ₌ −∞ =

_∫

− +

∑

_∫

− + 1 2 [ ( )r t r t( ) ... r t_K( )]T = (4.5) 其中h t( , )τ 為使用者信號所經過的通道，s t( )為使用者所傳送的信號， ,( , ) hI i tτ 為第i個干擾源所經過通道，sI i,( )t 為第i個干擾源，總共有U 個干 擾源，n t( )為可加性白色高斯雜訊。 表 4.1 系統參數設定

Antenna array ULA

Antenna spacing 2 λ Number of antenna 4 Center frequency 2.54GHz Signal bandwidth 3.5MHz FFT length 256 Data subcarriers 256 Symbol period 73.14µs Subcarrier spacing 13.67KHz modulation QPSK Channel coding No Angle spread 1∘ Normalized Doppler Frequency 0.001 信號在平坦衰減的通道中傳輸，且使用者信號只受一個同頻干擾(5dB) 所影響，且不受雜訊所干擾，詳細系統參數設定列於表 4.1。模擬下面幾 種情況: (1) 單接收天線的情況。 (2) 使用者信號到達角度為 50∘，同頻干擾信號到達角度 120∘。

(3) 使用者信號到達角度為 50∘，同頻干擾信號到達角度亦為 50∘。 (4) 平均的效能表現。 模擬結果如圖 4.3 所示。 0 2 4 6 8 10 10-3 10-2 10-1 100 SIR (dB) BE R single antenna

S:50 degree ; I:50 degree S:50 degree ; I:120 degree average performance 圖 4.3 理想切換波束式天線陣列 理想的切換波束式天線陣列會根據使用者信號的到達角度選擇其相 對應波束，使用者信號到達角度若和干擾信號的到達角度差異很大時，即 干擾信號的到達角度落於所選擇的波束之外，如(2)的情況，此時干擾信 號會被有效的壓抑，可以大幅改善系統效能(約 10dB)。若使用者信號的到 達角度若和干擾信號的到達角度差異很小時，理想切換波束天線陣列無法 有效區分使用者信號與干擾信號，此時與單天線接收狀況相同，無法有效 改善系統效能。由圖 4.3 模擬圖所示，理想切換波束式天線陣列相較於單 天線系統，可提升約 6dB。

4.2.3 切換波束式天線系統

切換波束式天線陣列，是由幾個固定波束所形成的，每個波束的特性 是由其各自的權重向量所決定，每個波束負責各自的方向以及範圍。如圖 4.2 中低旁波帶之波束要實現是很困難,在實際的設計上，我們只能盡可能 去設計低旁波帶之波束，[26][27][28]均有討論低旁波帶之波束設計。 40 60 80 100 120 140 0 0.2 0.4 0.6 0.8 1 1.2 degree Ga in Direction:45 degree Direction:75 degree Direction:105 degree Direction:135 degree 圖 4.4 波束對於不同到達角度的增益之示意圖 設計一組含有K根天線，四組權重向量之切換波束式天線陣列[29]， ( ) ( ) ( ) ( ) [ (1) (2) ... ( )] wi i i i w w w K = , (i=1...4)，對於均勻線性陣列天線而 言， ( ) 2 ( 1) cos( ) / ( ) j k i d i w k =e π − ϕ λ，(k =1... )K ，其中ϕ 代表第_i ith波束的主要方向。 圖 4.4 為K =4時,波束對於不同到達角度的增益之示意圖。其中ϕ₁=45 ， 2 75 ϕ = ，ϕ3 =105 ，ϕ4 =135 ，權重向量的數值列於表 4.2。 觀察圖 4.4,此設計出的 4 個波束，適合用來接收到達角度介於 30∘ 到 150∘之信號。同一波束對於不同入射角度有不同之增益，且不同波束

間會有部分重疊，這都將導致切換波束式天線陣列的效能下降。3.2.3.1 節及 3.2.3.2 節將會介紹，如何由四組權重向量中決定，適合的權重向量 w。 表 4.2 切換波束式天線陣列之權重向量 (1) w _w (2) _w (3) _w (4) 1st antenna 1.0000 1.0000 1.0000 1.0000 2nd antenna -0.6057 - 0.7957i 0.6872 - 0.7264i 0.6872 + 0.7264i -0.6057 + 0.7957i 3rd antenna -0.2663 + 0.9639i -0.0554 - 0.9985i -0.0554 + 0.9985i -0.2663 - 0.9639i 4th antenna 0.9282 - 0.3720i -0.7634 - 0.6460i -0.7634 + 0.6460i 0.9282 + 0.3720i

4.2.3.1 最大能量法

如圖 4.1(b)所示，在時間點t接收到的信號為r t_i'( )，不同的權重向量 ) (i w 會對應不同的接收信號 ' ( ) i r t 之產生，w(i)表示第

i

組權重向量，r t_i'( )數 學表示式為 ' ( ) ( ) w ri ( ) i r t = t (4.6) 其中 r( ) [ ( )1 2( ) ... ( )] T K t = r t r t r t (4.7) 此時必須從四組預先定義的權重向量中,選擇一組_w(i) ，提升系統效能，此 選擇法則如下: ( ) 1 ( ) 2 0 arg max ( ( )) w w w r i P i t t − = =

∑

(4.8)

( ) 1 ' 2 0 arg max ( ( )) wi P i t r t − = =

∑

, i=1,2,...,4 (4.9) 其中P為觀察區間[29]。由(4.8)式所示,必須在從四組不同的 Beamformed 接收信號能量( ' 2 1 1 ( ( )) P t r t =

∑

， ' 2 2 1 ( ( )) P t r t =

∑

， ' 2 3 1 ( ( )) P t r t =

∑

， ' 2 4 1 ( ( )) P t r t =

∑

)中找出最大的 值，並由此決定相對權重向量w的數值，當w決定之後，即使用此組權重 向量w做信號的接收。經過此天線陣列後之接收信號可表示為: ' ( ) w rH ( ) r t = t (4.10)

4.2.3.2 最大能量法模擬分析

系統主要參數設定如表 4.1 所示，使用者信號在平坦衰落通道中傳 輸，使用者的信號只受可加性白色高斯雜訊所影響，P=100,討論以下幾 種情形: (1) 使用單接收天線系統。 (2) 使用者的信號到達角度為 45∘。 (3) 使用者的信號到達角度為 60∘。 (4) 使用者的信號到達角度介於 30∘於 150∘時之平均效能表現。 模擬結果如圖 4.5 所示。 由圖 4.5，因為設計之波束對於不同到達角度的信號有不同的增益， 所以到達角度為 45∘較 60∘有較佳的性能表現。總體來說使用切換波束 式天線陣列較使用單接收天線系統有較佳的性能表現。切換波束式天線陣 列在訊雜比越高的情況下性能表現會愈來愈好，因為在訊雜比愈高的狀況 下，可以愈準確的選擇波束。 當使用者的信號在平坦衰落通道中傳輸，欲求的信號同時受可加性白 色高斯雜訊所影響以及一個同頻干擾(SIR=5dB)所影響，P=100，討論以 下幾種情形: (1) 使用單接收天線系統。

(2) 使用者的信號到達角度為 50∘，同頻干擾到達角度為 120∘。 (3) 使用者的信號到達角度為 50∘，同頻干擾到達角度為 50∘。 (4) 使用者的信號到達角度為 50∘，同頻干擾到達角度為 40∘。 (5) 使用者與同頻干擾信號到達角度介於 30∘於 150∘時之平均效能表 現。 0 2 4 6 8 10 10-3 10-2 10-1 100 SNR (dB) BE R single antenna S:45 degree S:60 degree average performance 圖 4.5 在平坦衰落通道中無同頻干擾最大能量法之模擬

0 2 4 6 8 10 10-2 10-1 100 SNR (dB) BE R single antenna

S:50 degree ; I:50 degree S:50 degree ; I:40 degree S:50 degree ; I:120 degree average performance 圖 4.6 在平坦衰落通道中受同頻干擾最大能量法之模擬 模擬結果如圖 4.6 所示。由圖 4.6，受到同頻干擾時，使用最大能量 法，因為同頻干擾信號能量太大，以致於無法正確選擇最佳的波束，會發 生誤差持平化(error floor)的現象。

4.3 後置-快速傅立葉轉換型天線陣列[29]

4.3.1 後置-快速傅立葉轉換型之結構

正交分頻多工信號在時域上之第m個取樣點可寫成 1 0 2 exp{ } N m n n mn x X j N π − = =

∑

, 0≤ ≤m N−1 (4.12) 其中N代表子載波的總數，X_n代表第n個子載波上所傳送的信號。假設傳