1
國立交通大學
理學院科技與數位學習學程
碩 士 論 文
應用數位數學教學模式
於國中一年級一元一次方程式的教學成效
Teaching Effectiveness of using Electronic Mathematical Instruction Model
on Seventh Graders in One-Variable Linear Equation
研 究 生:劉建巖
指導教授:李源順 博士
陳明璋 博士
應用數位數學教學模式於國中一年級一元一次方程式的教
學成效
Teaching Effectiveness of using Electronic Mathematical
Instruction Model on Seventh Graders in One-Variable Linear
Equation
研 究 生:劉建巖 Student:Chien-Yen Liu
指導教授:李源順 博士 Advisor:Yuan-Chun Lee
陳明璋 博士 Ming-Jang Chen
國立交通大學
理學院科技與數位學習學程
碩 士 論 文
A Thesis
Submitted to Degree Program of E-Learning
College of Science
National Chiao Tung University
in partial Fulfillment of the Requirements
for the Degree of
Master
in
Degree Program of E-Learning
July 2012
Hsinchu, Taiwan, Republic of China
應用數位數學教學模式於國中一年級一元一次方程式的教學成效
1學生:劉建巖 指導教授:李源順 博士
陳明璋 博士
國立交通大學理學院科技與數位學習學程
摘要
摘要
摘要
摘要
本研究主要目的在探討使用「數位數學教學模式」和「傳統教育模式」兩種 不同教學方式,對國中一年級在單元「一元一次方程式」之學習成效的差異 研究採用準實驗研究法進行教學實驗,研究對象實驗組有 98 位學童,控制 組有 100 位學童,實驗組為研究者原任課班級,控制組則是另一位教學相仿的數 學老師進行教學。實驗組的數位數學教學模式是以 NAEP 評量架構做為數學教 學理論基礎與多媒體教材設計做為數位教材設計理論,過程中特別重視學生溝通 能力的培養。控制組則是一般講述式教學的傳統教育模式。 實驗研究結果獲得以下結論 : 一、整體與不同學業成就學童的學習、保留成效方面,實驗組皆優於控制組。 二、整體與不同學業成就學童在數學能力之概念、程序、解題性知識的立即成效 表現和保留成效方面,實驗組皆優於控制組。 三、學童與不同學業成就學童在數學評量低、中、高複雜度的立即成效表現和保 留成效方面,實驗組皆優於控制組。 四、接受數位數學教學模式的教學後,實驗組學童溝通表現有進步。 五、接受數位數學教學模式的教學後,實驗組學童的數學學習態度是正向的。 關鍵詞:數位數學教學、AMA、一元一次方程式、NAEP 評量架構 1 本論文部分研究成果與國科會專題研究計畫 100-2511-S-009-006- 及 99-2511-S-009-008- 相 關。Teaching Effectiveness of using Electronic Mathematical
Instruction Model on Seventh Graders in One-Variable Linear
Equation
Student:Chien-Yen Liu Advisor:Dr. Yuan-Chun Lee
Dr. Ming-Jang Chen
Degree Program of E-Learning
National Chiao Tung University
Abstract
The purpose of this study was to compare the learning effects in one-variable
linear equation for seventh grade students by using two different teaching methods:
the electronic mathematics instruction and the traditional teaching.
A quais-experimental approach was used in this research. There were 98 students
in the experimental group and 100 students in the control group. The teacher of the
experimental group was the researcher and the teacher of the control group was
another teacher whose teaching method was similar to the researcher’s method. The
teaching method of experimental group was Electronic Mathematical Instruction
which was based on the NAEP assessment framework as a theoretical foundation and
on the Multimedia Principle as electronic teaching materials . Control group used the
traditional teaching method.
The final conclusions are as follows:
1.The experimental group performed better than the control group for the whole
students in the immediate effect and retained effect.
students in the immediate effect and retained effect on the concept, procedures,
problem-solving knowledge.
3.The experimental group performed better than the control group for the whole
students in the immediate effects and retained effects on low, average, high
mathematical assessment complexity.
4.After using Electronic Mathematics Education, the ability of the experimental
group’s communication had been progressed.
5.The Electronic Mathematics Education have positive influence on the experimental
group’s learning attitude.
Keywords:Electronic Mathematics Instruction 、AMA、One-Variable Linear Equation、
誌
誌
誌
誌謝
謝
謝
謝
曾經就讀交大是我的目標,隨後大學聯考的闖關失敗,就讀交大成了我的夢 想,如今從交大畢業是我的驕傲。 兩年的艱辛求學過程,要感謝的人很多。首先感謝兩位指導教授李源順博士、 陳明璋博士,在我教學無法突破產生制式化教學時,引領我進入教材數位化、數 學教學理論合併的教學理論,衝擊了自己的教學方法,這兩年成長很多,謝謝教 授。 感謝 AMA Team---駿碩、世易、依萍、玫琪、淑媛、敏惠,謝謝你們在 FB 上的搞笑聊天,抒解了我不少撰寫論文時的壓力,也謝謝你們分工合作所研究出 來的文件分享,加快了整理數據的效率。感謝有你們的陪伴! 感謝我的母親,在我無暇回台南的時間裡,還專程煮有媽媽味道的飯菜和購 買魚貨寄來給我補身體。媽,謝謝妳,我愛妳! 感謝我的太太---筱娟,這兩年默默辛苦的為家裡付出,因為有妳,強大的後 盾,我才能無後顧之憂的追求學位。 最後,感謝曾經幫助我的人。 僅以此論文獻給數學教育研究者目錄
目錄
目錄
目錄
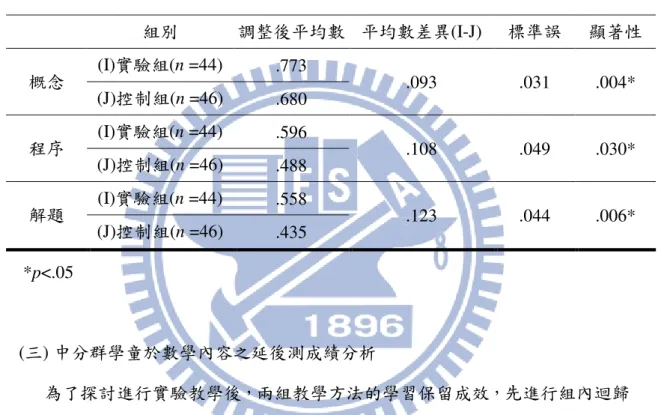
中文摘要 中文摘要 中文摘要 中文摘要 ... IIII Abstract... ... IIIIIIII 誌 誌 誌 誌謝謝謝 ...謝... IIII 目錄 目錄 目錄 目錄 ... IIIIIIII 表次 表次 表次 表次 ... IVIVIVIV 圖次 圖次 圖次 圖次 ... IXIXIXIX 第一章 第一章 第一章 第一章 緒論緒論緒論緒論 ... 1111 第一節 研究動機與背景 ... 1 第二節 研究目的與待答問題 ... 2 第三節 名詞釋義 ... 3 第四節 研究限制與範圍 ... 4 第二章 第二章 第二章 第二章 文獻探討文獻探討文獻探討文獻探討 ... 5555 第一節 數學教學理論 ... 5 第二節 多媒體教材設計理論 ... 11 第三節 一元一次方程式 ... 19 第四節 數學態度 ... 26 第三章 第三章 第三章 第三章 研究方法研究方法研究方法研究方法 ... 33333333 第一節 研究流程 ... 33 第二節 研究對象 ... 34 第三節 研究設計 ... 35 第四節 研究工具設計 ... 37 第五節 資料分析方法 ... 48 第四章 第四章 第四章 第四章 研究結果研究結果研究結果研究結果 ... 51515151 第一節 學習成效分析 ... 51 第二節 數學能力分析 ... 67第三節 數學評量複雜度分析 ... 89 第四節 學童於數學溝通的表現 ... 110 第五節 數位數學教學對數學態度的影響 ... 125 第五章 第五章 第五章 第五章 研究結論與建議研究結論與建議研究結論與建議研究結論與建議 ... 138138138138 第一節 結論與分析討論 ... 138 第二節 研究建議 ... 141 參考文獻 參考文獻 參考文獻 參考文獻 ... 143143143143 中文部分 中文部分 中文部分 中文部分 ... 143143143143 英文部分 英文部分 英文部分 英文部分 ... 147147147147 附錄一 附錄一 附錄一 附錄一 教案教案教案教案 ... 150150150150 附錄二 附錄二 附錄二 附錄二 成就測驗預試成就測驗預試成就測驗預試成就測驗預試、、、前測試卷、前測試卷 ...前測試卷前測試卷 ... 169...169169169 附錄三 附錄三 附錄三 附錄三 成就測驗後測試卷成就測驗後測試卷成就測驗後測試卷成就測驗後測試卷 ... 172...172172172 附錄四 附錄四 附錄四 附錄四 成就測驗延後測試卷成就測驗延後測試卷成就測驗延後測試卷成就測驗延後測試卷 ... 177...177177177 附錄五 附錄五 附錄五 附錄五 數學學習態度量表數學學習態度量表數學學習態度量表數學學習態度量表 ... 180...180180180
表
表
表
表次
次
次
次
表 2-1-1. 2005 年與 1996~2003 年的架構異同處 ... 10 表 2-3-1. 一元一次方程式相關教學研究 ... 24 表 2-4-1. 數學態度的意義 ... 27 表 3-2-1. 各學業成就人數分布 ... 34 表 3-2-2. 數學成績各組能力起始點分析表 ... 34 表 3-3-1. 實驗組與控制組教材差異對照表 ... 37 表 3-4-1. 國中一年級數學一元一次方程式之能力指標 ... 40 表 3-4-2. 國中一年級數學一元一次方程式之分年細目表 ... 40 表 3-4-3. NAEP 複雜度與九年一貫分年細目交互分析表 ... 41 表 3-4-4. 試卷試題信度分析 ... 42 表 3-4-5. 一元一次方程式試卷之數學內容雙向細目表 ... 42 表 3-4-6. 一元一次方程式試卷題號之雙向細目表 ... 43 表 3-4-7. 試卷鑑別度評鑑標準表 ... 45 表 3-4-8. 預試試卷難易度、鑑別度結果 ... 46 表 3-4-9. 學習態度量表內容大綱 ... 47 表 3-4-10. 晤談大綱 ... 48 表 3-4-11. 施測結果統計分析方法 ... 49 表 4-1-1 成就測驗前測獨立樣本 T 檢定表 ... 51 表 4-1-2 學習成效後測組內迴歸係數同質性檢定 ... 52表 4-1-3 學習成效後測共變數分析表 ... 52 表 4-1-4 學習成效後測事後成對比較表 ... 53 表 4-1-5 學習保留成效延後測組內回歸係數同質性檢定 ... 53 表 4-1-6 學習保留成效延後測共變數分析表 ... 54 表 4-1-7 學習保留成效延後測事後成對比較分析表 ... 54 表 4-1-8 高分群成就測驗前測獨立樣本 T 檢定表 ... 55 表 4-1-9 學習成效後測組內迴歸係數同質性檢定 ... 56 表 4-1-10 高分群學習成效後測共變數分析表 ... 56 表 4-1-11 高分群學習成效後測事後成對比較表 ... 56 表 4-1-12 學習保留成效延後測組內回歸係數同質性檢定 ... 57 表 4-1-13 高分群學習保留成效延後測共變數分析表 ... 57 表 4-1-14 高分群學習成效延後測事後成對比較表 ... 58 表 4-1-15 中分群成就測驗前測獨立樣本 T 檢定表 ... 59 表 4-1-16 中分群學習成效後測組內迴歸係數同質性檢定 ... 59 表 4-1-17 中分群學習成效後測共變數分析表 ... 60 表 4-1-18 中分群學習成效後測事後成對比較表 ... 60 表 4-1-19 學習保留成效延後測組內回歸係數同質性檢定 ... 61 表 4-1-20 學習保留成效延後測共變數分析表 ... 61 表 4-1-21 學習保留成效延後測事後成對比較分析表 ... 62 表 4-1-22 低分群成就測驗前測獨立樣本 T 檢定表 ... 63 表 4-1-23 學習成效後測組內迴歸係數同質性檢定 ... 63 表 4-1-24 低分群學習成效後測共變數分析表 ... 64 表 4-1-25 低分群學習成效後測事後成對比較表 ... 64 表 4-1-26 學習保留成效延後測組內回歸係數同質性檢定 ... 65 表 4-1-27 學習保留成效延後測共變數分析表 ... 65
表 4-1-29 學習成效結論統整表 ... 66 表 4-2-1 數學能力三向度前測獨立樣本 T 檢定分析表 ... 67 表 4-2-2 數學能力學習成效後測組內迴歸係數同質性檢定 ... 68 表 4-2-3 學習成效後測共變數分析表 ... 68 表 4-2-4 學習成效後測事後成對比較表 ... 69 表 4-2-5 學習保留成效延後測組內回歸係數同質性檢定 ... 70 表 4-2-6 學習保留成效延後測共變數分析表 ... 70 表 4-2-7 學習保留成效延後測事後成對比較分析表 ... 71 表 4-2-8 數學能力三向度前測獨立樣本 T 檢定分析表 ... 72 表 4-2-9 學習成效後測組內迴歸係數同質性檢定 ... 73 表 4-2-10 高分群學習成效後測共變數分析表 ... 74 表 4-2-11 高分群學習成效後測事後成對比較表 ... 74 表 4-2-12 學習保留成效延後測組內回歸係數同質性檢定 ... 75 表 4-2-13 高分群學習保留成效延後測共變數分析表 ... 76 表 4-2-14 高分群學習保留成效延後測事後成對比較分析表 ... 77 表 4-2-15 數學能力三向度前測獨立樣本 T 檢定分析表 ... 78 表 4-2-16 中分群學習成效後測組內迴歸係數同質性檢定 ... 79 表 4-2-17 中分群學習成效後測共變數分析表 ... 79 表 4-2-18 中分群學習成效後測事後成對比較表 ... 80 表 4-2-19 學習保留成效延後測組內回歸係數同質性檢定 ... 81 表 4-2-20 學習保留成效延後測共變數分析表 ... 81 表 4-2-21 學習保留成效延後測事後成對比較分析表 ... 82 表 4-2-22 數學能力三向度前測獨立樣本 T 檢定分析表 ... 83 表 4-2-23 學習成效後測組內迴歸係數同質性檢定 ... 84 表 4-2-24 低分群學習成效後測共變數分析表 ... 85
表 4-2-25 低分群學習成效後測事後成對比較表 ... 85 表 4-2-26 學習保留成效延後測組內回歸係數同質性檢定 ... 86 表 4-2-27 學習保留成效延後測共變數分析表 ... 87 表 4-2-28 學習保留成效延後測事後成對比較分析表 ... 88 表 4-2-29 數學能力學習成效結論統整表 ... 89 表 4-3-1 數學評量複雜度前測獨立樣本 T 檢定分析表 ... 90 表 4-3-2 學習成效後測組內迴歸係數同質性檢定 ... 90 表 4-3-3 學習成效後測共變數分析表 ... 91 表 4-3-4 學習成效後測事後成對比較表 ... 91 表 4-3-5 學習保留成效延後測組內回歸係數同質性檢定 ... 92 表 4-3-6 學習保留成效延後測共變數分析表 ... 93 表 4-3-7 學習保留成效延後測事後成對比較分析表 ... 94 表 4-3-8 數學評量複雜度前測獨立樣本 T 檢定分析表 ... 95 表 4-3-9 學習成效後測組內迴歸係數同質性檢定 ... 95 表 4-3-10 高分群學習成效後測共變數分析表 ... 96 表 4-3-11 高分群學習成效後測事後成對比較表 ... 97 表 4-3-12 學習保留成效延後測組內回歸係數同質性檢定 ... 97 表 4-3-13 高分群學習保留成效延後測共變數分析表 ... 98 表 4-3-14 高分群學習成效延後測事後成對比較表 ... 99 表 4-3-15 數學評量複雜度前測獨立樣本 T 檢定分析表 ... 100 表 4-3-16 中分群學習成效後測組內迴歸係數同質性檢定 ... 100 表 4-3-17 中分群學習成效後測共變數分析表 ... 101 表 4-3-18 中分群學習成效後測事後成對比較表 ... 102 表 4-3-19 學習保留成效延後測組內回歸係數同質性檢定 ... 102
表 4-3-21 學習保留成效延後測事後成對比較分析表 ... 104 表 4-3-22 數學評量複雜度前測獨立樣本 T 檢定分析表 ... 105 表 4-3-23 學習成效後測組內迴歸係數同質性檢定 ... 105 表 4-3-24 低分群學習成效後測共變數分析表 ... 106 表 4-3-25 低分群學習成效後測事後成對比較表 ... 106 表 4-3-26 學習保留成效延後測組內回歸係數同質性檢定 ... 107 表 4-3-27 學習保留成效延後測共變數分析表 ... 108 表 4-3-28 學習保留成效延後測事後成對比較分析表 ... 109 表 4-3-29 評量複雜度學習成效結論統整表 ... 110 表 4-4-1 學習成就測驗文字解說概念題答對率 ... 118 表 4-4-2 文字解說題作答情形比率 ... 120 表 4-5-1 學習態度問卷統計表 ... 126 表 4-5-2 學習態度問卷統計表(1) ... 127 表 4-5-3 學習態度問卷統計表(2) ... 128 表 4-5-4 學習態度問卷統計表(3) ... 129 表 4-5-5 學習態度問卷統計表(4) ... 130 表 4-5-6 學習態度問卷統計表(5) ... 131 表 4-5-7 學習態度問卷統計表(6) ... 132 表 4-5-8 學習態度問卷統計表(7) ... 133 表 4-5-9 學習態度問卷統計表(8) ... 134
圖
圖
圖
圖次
次
次
次
圖 2-1-1. 美國 NAEP 的數學評量架構圖 ... 6 圖 2-2-1. 多媒體學習理論雙通道模型 ... 14 圖 3-4-1. 控制組計算題教材 ... 38 圖 3-4-2. 控制組應用題教材 ... 38 圖 3-4-3. 實驗組計算題教材 ... 39 圖 3-4-4. 實驗組應用題教材 ... 39 圖 4-1-1. 學習成效進退步曲線圖 ... 54 圖 4-1-2. 高分群學習成效進退步曲線圖 ... 58 圖 4-1-3. 中分群學習成效進退步曲線圖 ... 62 圖 4-1-4. 低分群學習成效進退步曲線圖 ... 66 圖 4-2-1. 數學能力學習成效進退步曲線圖 ... 72 圖 4-2-2. 高分群於數學能力學習成效進退步曲線圖 ... 77 圖 4-2-3. 中分群於數學能力學習成效進退步曲線圖 ... 83 圖 4-2-4. 低分群於數學能力學習成效進退步曲線圖 ... 88 圖 4-3-1. 數學評量複雜度學習成效進退步曲線圖 ... 94 圖 4-3-2. 高分群於評量複雜度學習成效進退步曲線圖 ... 99 圖 4-3-3. 中分群於評量複雜度學習成效進退步曲線圖 ... 104 圖 4-3-4. 低分群於評量複雜度學習成效進退步曲線圖 ... 109 圖 4-4-1. 5(1)文字解說正確 ... 121圖 4-4-3. 5(1)觀念錯 ... 122
圖 4-4-4. 5(2)文字解說正確 ... 123
圖 4-4-5. 5(2)計算解說正確 ... 124
圖 4-4-6. 5(2)觀念錯 ... 124
第一章
第一章
第一章
第一章 緒論
緒論
緒論
緒論
本研究是以一元一次方程式為研究主題,利用數位數學教學模式進行教學, 探究學童學習成效是否有顯著進步。 本章將分為研究動機與背景、研究目的與待答問題、名詞釋義以及研究限制 與範圍等四節。第一節
第一節
第一節
第一節
研究動機
研究動機
研究動機與背景
研究動機
與背景
與背景
與背景
Herscovis&Kieran(1980)認為一元一次方程式是由國小算術思維進入國中代 數思維重要的階段,轉換過程的理解程度將會影響到往後數學學習成效。研究者 教學經驗中,發現多數學生開始放棄數學大多是因為無法有效將算術思維轉換成 代數思維,且在閱讀解題應用問題等題型,因為閱讀能力低落導致題目看不懂進 而無法有解處理應用問題等題型。國內也有多項探討一元一次方程式的研究,無 論是迷思概念或學習過程中學生所面臨的困難,多數學生學習代數的概念及技巧 是記憶性的,尤其是方程式的學習(Kieran , 1992)。九年一貫課程安排階段,早 在小學六年就已接觸未知數問題,以□、x….等依題意來列出算式和利用等量公 理進行基本題型的解方程式,直到國中才進入更進一步的學習複雜的題型。但也 造就一個問題就是國小與國中數學課程銜接的問題,太早接觸文字符號造成無法 有效轉換代數思維的學童,被迫提早放棄數學學習,偏偏對於國內數學教育國一 到國三課程內容來說,又常以解決文字符號作為問題解決能力的重要知識,如果 在國一的文字符號建構代數思維的關鍵時期,學生就遇到學習上的困難,若加上 老師無法適時的提供方法學習、指導,對於學童往後的學習會造成很大挫折。 教育部實施的資訊科技融入數學科教學實驗計畫中指出,數學科是所有學科 中最被學童討厭的科目,而電腦學科卻是深受學童喜愛,且大部分學童都表示因 為喜歡學習電腦,如果能上加利用此資源來學習,會覺得比以前還要快樂。學者 呂玉琴(1991)也指出身為一個數學教師應當省思該如何利用現代資訊科技(如網路、電腦、電算器等)作為輔助工具,以有效幫助學童的學習,因此研究採用 AMA 簡報系統(陳明璋,2008)設計教材,讓教師有更多時間可以和學生進行互動教 學。。 2014 年開始推動 12 年國教,並在九年級進入高中端時舉行一次大會考,會 考成績評比為精熟、基礎、待加強,此評比方式和美國 NAEP(國家教育發展評 量)的評量結果有三個水準:基本(Basic)、精熟(Proficient)、進階(Advanced)類似, 且教育的目的是「培養孩子帶的走的能力」,因此要評量學生的能力,教學上勢 必也要教給他們那些能力。根據李源順、余新富、李勇諭(2006)利用美國 NAEP 評量架構作為教材設計理論,應用於同分母分數加減法的教學研究,發現學童於 數學表現上有顯著的進步,因此利用此評量架構作為一元一次方程式的教學理 論。 培養學生的數學推理、溝通、連結的能力並不是短時間內就能培養出來,因 此本研究只探討利用數位數學教學模式下,學生在溝通上的能力與數學能力之概 念、程序、解題性知識和評量低、中、高複雜度與數學學習態度的改變。
第二節
第二節
第二節
第二節
研究目的
研究目的
研究目的與待答問題
研究目的
與待答問題
與待答問題
與待答問題
一、研究目的
根據上述研究動機,本研究的主要目的數位數學教學模式應用於解一元一次 方程式與應用問題的教學,探討國一學生接受不同教學模式的學習成效及數學學 習態度的改變,以期達到作為提升教師教學之參考。二、待答問題
1. 比較傳統教育與數位數學教學的兩種教學方法,對於國一「整體」與「不同 學業成就」學童於解一元一次方程式單元中的「學習成效」是否顯著差異? 2. 比較傳統教育與數位數學教學的兩種教學方法,對於國一「整體」與「不同 學業成就」學童於解一元一次方程式單元中,NAEP 的「數學能力」的學習成效是否顯著差異? 3. 比較傳統教育與數位數學教學的兩種教學方法,對於國一「整體」與「不同 學業成就」學童於解一元一次方程式單元中,NAEP 的「數學評量複雜度」 的學習成效是否顯著差異? 4. 採用數位數學教學的教學方法後,實驗組學童的溝通能力是否有改變? 5. 採用數位數學教學的教學方法後,實驗組學童的數學學習態度是否有改變?
第三節
第三節
第三節
第三節 名詞釋義
名詞釋義
名詞釋義
名詞釋義
一、NAEP 數學評量架構
美國「國家教育發展評量(National Assessment of Educational Progress)」簡稱 為 NAEP,提出數學內容(Content Strands)、 數學能力(Mathematical Abilities)、數 學威力(Mathematical Power)三個因子的評量架構。數學能力又包含了概念、程序、 解題三個向度。2007 年,評量部分修改為低複雜性、中複雜性、高複雜性三種 題型,本研究測驗題型採用概念、程序、解題、低複雜性、中複雜性、高複雜性 六個向度作為研究內容。
二、多媒體教材設計
本研究多媒體教材設計軟體市立用陳明璋博士於 2002 年以 PowerPoint 簡報 系統作為平台,提供一個按鈕式動態呈現的外掛程式並且不斷改良,如今使用上 不受限於特定科目,因此取名為 Activata Mind Attention 系統(簡稱 AMA),使其 運用更為廣泛(陳明璋 2008)。三、數位數學教學模式
以數學教學理論作為教學的理論依據並配合多媒體教材設計來呈現教材的 模式。本研究是以 NAEP 評量架構做為數學教學理論的依據,並利用陳明璋博 士所研發的 AMA 簡報系統做為多媒體教材設計軟體進行教學。
第四節
第四節
第四節
第四節 研究限制與範圍
研究限制與範圍
研究限制與範圍
研究限制與範圍
一、研究範圍
本研究範圍的課程內容為國中一年級之一元一次方程式二、研究限制
1. 桃園縣某國中一年級學生實驗組 98 位、控制組 100 位,共 198 位學童,此 研究結果僅適宜推論至相同條件的國中生,其餘不宜過度推論。 2. 要培養學生的數學推理、溝通、連結的能力並不是短時間內就能培養出來, 需要長時間進行。本研究教學實驗時間共 3 週 15 節課,僅著重於溝通方面 的培養。 3. 實驗組與控制組施測教師不同,只能盡量控制其他會影響結果的變因。第二章
第二章
第二章
第二章
文獻探討
文獻探討
文獻探討
文獻探討
依據研究目的,本章文獻探討分成四節:第一節為數學教學理論,第二節為 多媒體教材設計理論,第三節為一元一次方程式相關研究,第四節為數學態度第一節
第一節
第一節
第一節
數學教
數學教
數學教
數學教學
學
學
學理論
理論
理論
理論
應用在實際教學設計數學教學相關理論眾多,但各研究要探討其相關理論是 否有效,最後多數研究還是利用評量檢測教學理論是否有效,而數學教學目的是 希望教導學生帶的走的能力,亦即要要培養學生什麼樣的能力就要先看教師是否 能把這些能力交給學生,因此有必要了解教師如何進行解題、推理、溝通、連結 的教學,在「要怎麼收穫,先那麼栽」的理念下,發現 NAEP 這個評量架構中 也特別強調這些能力,因此利用架構用來做為描述教師數學教學的理論。(Lee, Y.S., Lin, F.L., Lee, W.L., Wu, T.F., Hsu, S.F., & Ma, H.Y.,2010)。一、2003 年以前 NAEP 評量架構
美國(National Assessment of Educational Progress [NAEP])從 1996 年起到 2000 年、2003 年的數學教育成就評量提出數學內容(Mathematical Content Strands)、
數學能力(Mathematical Abilities)、數學威力(Mathematical Power)三個因子的評量 架構,如圖 2-1-1。雖然這是一個評量的架構,而要評量這些能力,教師於教學 內容上也必須要教導學生相關能力,因此,我們以此架構為理論基礎,做為探究 解一元一次方程式的教學實驗理念架構。
圖2-1-1. 美國 NAEP 的數學評量架構圖
資料來源:“The 1990–2003 Mathematics Framework”by National Center for Education Statistics, Nationa
http://nces.ed.gov/nationsreportcard/mathematics/previousframework.asp
(一) 數學內容(Mathematical Content Strands)
根據 NAEP 將課程數學內容分成以下五類 1. 數字概念與運算 2. 測量(Measurement) 3. 幾何(Geometry) 4. 資料分析與機率 5. 代數(Algebra) (二) 數學威力(Mathematical Power) 現今數學教育的理念是要培養學童的數學威力 的內涵在我國九年一貫數學領域課程綱要 數學威力是指學童有全面性的能力能結合和使用數學知識去進行探究 邏輯推理、解決非例行性的問題 或其他的學科脈絡進行連結 結(Connections)和溝通(Communication) 1. 推理是指學童能認知數學的基本內容 的數學評量架構圖
2003 Mathematics Framework”by National Center for
Education Statistics, National Assessment of Educational Progress(NAEP
http://nces.ed.gov/nationsreportcard/mathematics/previousframework.asp
(Mathematical Content Strands)
將課程數學內容分成以下五類。 數字概念與運算(Number Properties Operations)
(Measurement)
(Geometry)
資料分析與機率(Data Analysis and Probability)
(Mathematical Power) 現今數學教育的理念是要培養學童的數學威力(Mathematical Power) 在我國九年一貫數學領域課程綱要(教育部, 2003,2008)中也可以看到 學童有全面性的能力能結合和使用數學知識去進行探究 解決非例行性的問題;能進行數學的溝通;以及能在數學脈絡之內 或其他的學科脈絡進行連結。美國 NAEP 認為數學威力是由推理(Reasonin (Communication)三個因子組成。 推理是指學童能認知數學的基本內容,學童能進行探究與數學臆測 2003 Mathematics Framework”by National Center for
NAEP), from http://nces.ed.gov/nationsreportcard/mathematics/previousframework.asp (Mathematical Power)。此向度 中也可以看到。 學童有全面性的能力能結合和使用數學知識去進行探究、臆測、 以及能在數學脈絡之內, (Reasoning)、連 學童能進行探究與數學臆測,學童能
發展對數學論證的評價,學童能選擇使用不同的推理和證明方法。 2. 連結是指學童能理解並進行數學概念間的連結,學童能了解數學概念是環環 相扣的體系,學童能在數學外的領域辨認和使用數學。 3. 溝通是指學童能透過溝通強化數學思維,學童能和同學、老師及他人溝通他 們的數學思維,學童能分析和評估他人的數學思維和策略,學童能使用數學 語言表達他的數學概念。 要培養學童具備這三個能力並不是短暫時間內可以達成的,所以最好在數學 教學過程中持續進行,因此我們將探求一種可以在數學課中培養學童數學威力的 教學脈絡。 (三) 數學能力(Mathematical Abilities) 數學能力可以看成學童在特定的數學知識內展現的數學能力。數學能力包含 有概念性理解(Conceptual Understanding)、程序性知識(Procedural Knowledge)和 解題(Problem Solving)三個因子。 1. 概念性理解 (1). 對於概念符號的正反例能加以辨識。 (2). 能利用模型、圖型及符號來表示概念。 (3). 辨識和應用原理原則。 (4). 知道和應用事實與定義。 (5). 能整合相關概念和原理原則,擴充原本的概念和原理原則。 (6). 能辨識和應用符號表示概念。 (7). 能詮釋概念間相關結論與關係。 2. 程序性知識 (1). 正確地選擇和應用程序。 (2). 能對程序的運用加以說明及判斷其正確性。 (3). 擴充或修正程序,以處理問題中原有的因素。
3. 解題性知識 (1). 在新的情境中能使用數學知識。 (2). 能確認及明確地陳述問題。 (3). 能運用策略數據、模型及相關的數學。 (4). 能創造與使用程序並予以發展和修正。 (5). 能判斷解答的正確性與合理性。
二、2005 年後 NAEP 的評量架構
2005 年後評量架構主要分為框架,其中五個數學內容的標準是數學能力評 量架構中的第一個框架,另一個接續框架是評量中的複雜性程度,區分為低階複 雜性、中階複雜性、高階複雜性的題型。 (一) 低階複雜性(Low complexity) 這個類別非常需要學生去記憶與辨別先前學習過的觀念與原理原則,此種試 題的典型例子是會具體指示出學生需要做到什麼,它常常是要學生去完成有關機 械式操作的程序,不會提供學生原本的數學方法和解決之道。適合低結構性的出 題類型舉例如下: 1. 記憶或辨別一個事實、專有名詞或特性。 2. 能理解一個觀念的例子。 3. 計算出和、差、積或商。4.
能了解相等的代表式子。 5. 完成一個具體說明的過程。 6. 能計算出一個已知變數的算式或方程式。 7. 能解決只有一個步驟的文字問題。 8. 畫出或計算出簡單的幾何圖形。 9. 能從繪圖、表格或圖形中得到訊息。(二) 中階複雜性(Moderate complexity) 中度結構性的試題種類比起低結構性,包含了更多思考上的彈性與選擇性, 它們通常需要一個慣用的、不是具體說明的、不只一個步驟的回答。學生們被期 望去決定該做什麼,使用推理與問題解決等非正式的方法,以得到各領域解題的 技能與知識。以下說明適合中度結構性的出題類型 1. 能以一種以上的方式描述數學的狀況。 2. 依照情況與目的,選擇和使用不同的表現方法 3. 解決需要多個步驟的應用問題。 4. 比較圖形或陳述 5. 在一個解題過程中提供步驟的解釋。 6. 能說明視覺性的表現方法 7. 能延伸數學模式 8. 能從繪圖、表格或圖形中得到訊息,並利用他們來解決需要多重步驟的問 題。 9. 用公式表現一個常見的問題,給予的資料與狀況 10. 能說明簡單的討論主題 (三) 高階複雜性(High complexity) 高度結構性的問題會加諸沉重的要求在學生上,這些學生必須致力於更多抽 象的推理、計畫、分析、判斷與富創造力的思考。對於這類試題而言,令人滿意 的回答是需要透過一個抽象和精熟的方法才能得到。在這個等級的試題或許會問 學生下列的例子: 1. 描述如何針對不同的數學狀況,以不同的表現方法呈現 2. 能展現一個具有多重步驟與結論的過程 3. 分析過程與觀念之間的相似點與不同點 4. 能歸納數學公式
6. 能解決新穎的問題 7. 用一個以上的方法解決問題。 8. 對問題能解釋和證明其解法 9. 能描述、比較和對照解題的方法 10. 對一個複雜的狀況的數學模式能用公式表示 11. 分析在一個數學模式中構成的假設 12. 分析或產生一個推論式的討論主題
三、2005 年與 1996~2003 的數學能力評量架構的異同處比較
2005 年 NAEP 修訂新架構為評量的複雜度程度,不同於 1996~2003 所使用 的架構:數學能力(概念性理解、程序性知識、解題)。為 2005 年與 1996~2003 年的架構異同處。 表2-1-1. 2005年與年與 1996~2003 年的架構異同處年與年與 年的架構異同處年的架構異同處年的架構異同處 評量架構向度 比較說明 評量內容 評量內容相同 認知部分 2005 年架構中,數學能力強調複雜性,指的是數學結 果的正確性取得的難易程度 成就結果呈現方式 仍採用基本層次、精熟層次、進階層次三等級 題目種類 有選擇題、簡答題、問答題、,各種類的回答時間比 例仍維持一樣。 計算過程 2005 年架構中,尤以導出結果的部分為主要評量關鍵 運算過程與工具 需求維持不變 計算機策略 維持不變。2005 年對於 12 年級學生允許測驗時攜帶 課堂上使用的計算機,沒帶者,將提供計算機 資料來源:(引自曾明義,2008)Assessment of Educational Progress(NAEP),2005a, Retrieved October5, 2005, from http://nces.ed.gov/nationsreportcard/mathematics/frameworkcomparison.asp
四、對於本研究的幫助
NAEP 數學評量架構裡提到的數學能力之概念、程序、解題是學生數學知識 中所需具備的三個基本能力。數學教學中,教師在教學過程不也是先強調其數學 概念,進而利用其概念進行程序化的計算問題,最後才結合兩種能力進行解決應 用問題,合乎教師要教給學生很重要的三個能力。此評量架構在數學威力所提到 推理、溝通、連結,更是學生要利用本身既有的數學知識進行探究、臆測、邏輯 推理解決非例行性的問題,過程中利用本身知識與他人進行溝通討論強化其本身 的相關知識,最後利用相關數學脈絡進行其他學科或是生活的連結。NAEP 雖為 一個評量架構,但卻提出學生在追求數學知識中很重要的幾個元素做為數學教學 目標的標的,因此本研究將此評量架構做為數學教學的理論依據。第二節
第二節
第二節
第二節
多媒體教材設計
多媒體教材設計
多媒體教材設計理論
多媒體教材設計
理論
理論
理論
一、認知負荷理論
Sweller(1998)提出「認知負荷理論」 (Cognitive Loas Theorey,CLT),指出
教師課堂授課的安排與教材呈現及教學設計的展演過程,對學習者認知負荷的影 響及教學成效關係,可提供教師教學設計使用何種教學來提升教學成效的依據。 (一) 認知負荷對人類認知架構的基本設定 1. 工作記憶容量是有限的 教材本身設計或演示過程中,如果需要連結很多的訊息或先備知識,會使得 工作記憶負載過大。 2. 長期記憶沒有容量限制 長期記憶體儲存大量基模,學習者若沒有足夠的基模或立即聯想到的解題策
性,將會使學習者有更多的工作記憶空間進行推理與探索。 3. 長期記憶中的內容主要以基模的型態儲存運作 基模式訊息經由簡單到複雜、粗略到精緻的建構而形成,可以將許多複雜的 訊息融合成一個基模,因此基模的運作可以降低工作記憶區的負荷。 4. 自動化是基模建構的重要過程 當基模運作自動化後便可以節省許多記憶體的空間,達到降低運作記憶的負 荷。因此學習者若沒有被活化達到自動化過程,即使已學過相同的主題或概念, 仍然會出現解題上的錯誤(Ayers,2001)。 (二) 認知負荷的類型 1. 內在認知負荷 Sweller(2010)提到內在認知負荷的高低,是指教學過程中所有需要進行運 作的相關元素產生交互作用流量的總量,而非元素交互作用的高低。 2. 外在認知負荷 主要受教材呈現方式、教材設計及教學活動本身影響。教學過程中,如未考 慮訊息的結構及學習者本身的認知架構,教材的呈現方式不恰當,對學習者也就 是訊息接收者來說,很容易產生不同的程度的負荷。 3. 增生認知負荷 主要是促進學習,可以透過訊息提供給學習者的方式、學習活動對學習者的 要求、引導學習者專注於學習內容而達到。 (三) 認知負荷的教學設計原則 Sweller 等人 (1998) 歸納認知負荷理論在各學科領域的研究結果,提出七項 的教學設計原則,而後 Sweller (2004) 再依據眾多實驗證據發展為十一項教學設 計原則;近期 Sweller (2010) 將其延伸為十四項教學設計原則,提供教學設計者 和教學者作為教學設計與教學實施的準則,使其能藉由這些教學設計原則有效地 引領學習者快速學習、深入學習。教學設計原則所產生的效應 (effect)分別如下: 開放目標效應(goal-free effect)、工作示例效應(worked example effect)、完
成問題效應(completion problem effect)、分散注意力效應(split-attention effect)、 重複效應(redundancy effect)、形式效應 (Modality effect) 、專業知識反轉效應 (Expertise reversal effect) 、引導漸減效應 (Guidance fading effect) 、獨立互動元素 效應 (Isolated-interacting elements effect) 、整體-模組效應 (Molar-Modular effect) 、 變化效應 (Variability effect) 、元素交互作用效應 (Element interactivity effect) 、想 像效應 (Imagination effect) 、自我解釋效應 (Self-explanation effect) 。
本研究使用教學原則所產生的效應如下: 1. 開放目標效應(goal-free effect)
應採開放目標方式,學生透過多重表達自己思考過程及解題步驟可以連結相 關的訊息,以降低外在認知負荷。
2. 工作示例效應(worked example effect)
教導程序性知識應呈現適當的解題例子,可以協助學生對於問題狀態和解題 步驟建構出較完整的基模,以降低外在的認知負荷。
3. 完成問題效應(completion problem effect)
若將教學示範過程、教材說明及學生研讀思考的時間同時放入運作記憶,會 造成短期負荷過大。故呈現一半示例,另一半由學習者完成,有降低外在認知負 荷的效果。 4. 分散注意力效應(split-attention effect) 學習者面對多重來源時,必須將來源加以參照整合,才能達到學習或理解。 若這些訊息是分散的,出現時間不一致,會增加認知負荷。 5. 重複效應(redundancy effect) 有些訊息本身訊息量可以自足,可以獨立呈現,不須相互參照整合亦能理解, 若將其安排若在同一空間或時間出現,大量訊息同時進入,會導致運作記憶過度 負荷,降低學習效果。
6. 獨立互動元素效應 (Isolated-interacting elements effect) 當教材包含了很多高交互作用的元素,且同時在工作記憶中處理,會造成大 量的內在認知負荷,導致超出工作記憶容量,造成學習和理解受到極大的阻礙 (Sweller, 2004; Sweller, 2010) 。因此,要將一部份的互動元素分別獨立處理,當 學習者學習該獨立元素之後,原本高交互作用變為低交互作用,才不會造成工作 記憶處理的負荷,也能使基模自動化學習更為深入。
7. 元素交互作用效應 (Element interactivity effect)
當教材的元素交互作用是低的,其內在認知負荷就是低的,即便教材不良的 設計引發了外在認知負荷,其外在認知負荷也不會是影響學習的重要關鍵,因為 總認知負荷不會超過工作記憶容量 (Leahy & Sweller, 2005; Sweller, 2010) 。
二、多媒體學習理論
(一) 多媒體學習認知理論Clark 和 Mayer(2003)將多媒體學習(Multimedia Learning)定義為利用文字與
圖像共同來呈現教材內容的方式進行學習,其中文字部分包括書面、螢幕上的印 刷文字與教師教學話語、旁白的口述文字,圖像則包括靜態與動態,其中圖表、 地圖、坐標圖皆屬於為靜態類,動化、影片則屬於動態類,而這樣共同呈現的多 媒體教材學習理論稱之為雙碼理論(dual-code Theory)。 圖2-2-1. 多媒體學習理論雙通道模型(引自曾椿惠,2000) 多媒體學習理論有三大基本假設,分別為雙通道假設(Dual channels)、容量 文字 圖像 耳朵 眼睛 聲音 圖像 語文模型 圖像模型 先備 知識 整合 組織 文字 組織 影像 選擇 文字 選擇 影像 多媒體呈現 感覺記憶 工作記憶 長期記憶 旁白 字幕 圖像
有限假設(Limited capacity)、主動處理假設(Active processing) (Mayer, 2001)。 1. 雙通道假設
根據 Paivio 所提出的雙碼理論(Dual-coding Theory),Mayer 認為人類視覺 及聽覺訊息的兩個通道是獨立分開的,當訊息被呈現時,可以藉由以文字或是圖 像的形式選擇聽覺或是視覺通道。 2. 容量有限假設 人類的視覺通道與聽覺通道一次所能處理的訊息量是有限的。所以當大量的 訊息湧入時,我們無法完全接收訊息,僅能將少部分的訊息保留於工作記憶中, 這些訊息很可能是片段而非完整的,亦即短期工作記憶區(working memory)的容 量是有限的。 3. 主動處理假設 主動處理假設認為當訊息出現時,學習者會將接收到的訊息根據自己本身已 有的經驗、知識和基模一併整合,而且主動處理的歷程中分成三個階段,如下: (1). 選取(Select): 當學習者接觸到文字或圖像等多媒體訊息時,會先由耳朵與眼睛等感官收錄 後形成視覺與聽覺表徵,接著自動選取對其有意義的文字或圖像,將其儲存在工 作記憶區中。 (2). 組織(Organize): 接著,學習者在工作記憶區中將選取後的文字與圖像加以組織成一個連貫的、 有整體性的模型,分別為語文模型(Verbal Model)和圖像模型(Pictorial Model)。 (3). 整合(Integrate):
學習者在工作記憶區中將語文模型及圖像模型加以配對,建立兩者之聯結, 並與長期記憶中既有的相關知識加以融合,形成外在關聯,即為多媒體學習的認 知過程。
(二) 多媒體教材設計原則(Multimedia Principle)
Mayer(2003)歸納出多媒體教材設計的教學原則,包含有多媒體原則
(Multimedia Principle)、空間接近原則(Spatial Contiguity Principle)、信號原則
(Signaling Principle)、分割原則 (Segmentation Principle)、時間接近原則(Temporal
Contiguity Principle)、形式原則(Modality Principle)、重複原則(Redundancy
Principle)、連慣性原則(Coherence Principle)、個人化原則(Personalization Principle)、
圖像原則(Image Principle)、聲音原則(Voice Principle)、事先訓練原則(Pre-training Principle)共 12 項。本研究僅利用以下原則進行教材設計,如下: 1. 多媒體原則(Multimedia Principle) 教材設計採用文字與圖像並用的學習效果會比僅用文字呈現好。當文字與圖 片一起呈現時,能幫助學習者建構語文及圖像之間的關聯,也就是學習者可以同 時接收較大量的完整訊息,且文字和圖像分別在兩個不同的知識表徵管道,因此 圖像與文字並不會造成通道擁塞。
2. 空間接近原則(Spatial Contiguity Principle)
若相關文字與圖像在畫面中的相對位置較近,學生的學習成效會比相對位置 較遠的好。 3. 信號原則 (Signaling Principle) 當教材含有可以提示重點之信號時,學習者對於教材的理解程度會提高。常 用方式為突顯標題(Heading)與強調關鍵訊息(Key information)(Mayer,2005)。 4. 分割原則(Segmentation Principle) 當教材較為複雜且學習者對於教材不熟悉時,若多媒體已連續未分段呈現, 容易導致學習者認知負荷過載,因此需要教材分割成幾個片段,讓學習者能夠從 每個片段中學習。 5. 事先訓練原則(Pre-training Principle) 當進入正式學習時,學習者若在學習前知道主要概念的名字與特徵,能使學
習者加深對課程之印象,提升其學習效果。
三、代數教材設計原則
謝東育(2009)認為代數領域缺乏視覺情境造成學習者的解題過程容易淪為 制式化的運算,因此提出將教學內容結構化、教材呈現區塊化、建立訊息關聯與 口語簡化的四個原則。 (一) 教學內容結構化 代數教材呈現內容時常是繁瑣的,運算過程往往就是好多個算式,超過工作 記憶所能負荷的,因此設計教材必須針對內容進行結構性分析,將內容主要概念、 訊息進行切割,使得目標明確,其意思雷同 Mayer(2009)提出的分割原則 (Segmenting Principle)。 (二) 教材呈現區塊化 區塊化的概念是將已完成段落切割的訊息,算式未必要由上而下的循序,由 教材設計者依講解需求自行安排訊息的所在位置。在教學內容已結構化切割完畢 後,若仍採取原本展演過程的序列來呈現,上下列算式訊息的對比、引用將較不 容易。區塊化雷同於多媒體教材設計原則的空間接近原則。 (三) 建立訊息關聯 了解各元素間的推演關係,其中包含了上下列算式的關聯、不同區塊的關聯, 因此歸納出兩種操作方式來建立訊息間的連結,兩種方式如下: 1. 對齊 上下列算式的計算演變中,未涉及運算的既有元素(包含文字、數字、運算 符號、等號、性質符號…等)採上下元素對齊。 2. 二維圖像關係 將教材內容分割成數個區塊容易受限於黑板尺寸、電腦版面設定,各區塊並 無法採單一方向連貫式的排列,但不同區塊彼此有對應關係時,若僅採用文字敘 述較不易建立訊息關聯,若能力用曲線、線段適時出現,就能串連訊息區塊,也能達到注意力引導的效果。 (四) 口語簡化解說 代數語言缺乏貼近日常生活的用語,Mayer (2009) 提出個人化原則 (Personalization Principle) 認為口語對話式的說明會比專業術語形式化的講解更 有效用,因此教師講解時應避免缺乏想像的代數語言及專業術語。若直接口述算 式將每一列元素逐一念出,會讓學生更加模糊。
四、對於本研究的幫助
資訊科技融入教學中的有各式各樣的多媒體軟體,搜尋其相關研究中發現不 外乎是電子白板、一般 PTT 或是坊間書商所製作的教材,但其教學過程多數像 是放映影片,比較難以和教師教學互相搭配,特別是對於代數領域又比較缺乏視 覺情境,容易造成學習者的解題過程淪為制式化的運算。有別於這些資訊融入教 學,Sweller(2010)提出教材的呈現方式不恰當,對學習者也就是訊息接收者來說, 很容易產生不同的程度的負荷的看法的認知負荷理論且教學原則會產生的十四 個效應,Mayer(2003)歸納出多媒體教材設計的教學原則,且將理論與效應運用 本研究教學,可了解教師教學前應先複習學生先備知識,以降低學習新單元時的 內在認知負荷,且教師上課前先將教材由易而難分析安排,切割相關元素較高的 教材將其較為複雜運算分割為可獨自處理的運算。教學時,教師應以開放式問題 提問,運用開放目標效應讓學生自由表達思考過程,面對多方訊息需互相參照整 合情形時,應運用分散注意力效應使訊息在同一個空間及同一個時間呈現,減少 學生搜尋訊息所耗費的工作記憶。教師可運用示例效應先呈現適當的例子供學生 參考,逐步建立基模,並依照學生程度運用完成問題效應呈現例子一半的解法, 剩下的部份交由學生完成。第三節
第三節
第三節
第三節 一元一次方程式
一元一次方程式
一元一次方程式
一元一次方程式
一、課程綱要
九年一貫課綱(教育部,2008)已在國小鋪陳代數預備經驗,到國中引入「以 符號代表數」的想法,正式進入代數學習的世界,教師應強調兩個階段解決應用 問題的差異,(例如:國小以線段圖方法解決和國中則以方程式的方法),以及抽 象代數方法的普遍性與優越性(例如:國小許多類問題,從解方程式的觀點,可 能都是一元一次方程式)。另外,代數的能力包含邏輯與符號的推演,可培養學 生的抽象思考能力。即使是幾何推理的素材,也經常需要藉由代數方法來導出新 觀念或新性質。以下為國中一元一次方程式課程題材安排: (一) 以符號代表數 以符號代表數是學習代數的關鍵與難關。這裡有四個層次:首先是國小課程 綱要已要求使用符號來記錄常用的公式,由熟悉的公式入手,可以減輕學生對抽 象符號的恐懼;其次,是用符號來表示運算律(包括指數律),學生在此可體認符 號簡化並釐清數學敘述的威力;第三,是解題時,用符號來表達問題中的數量關 係,作為解方程式的準備,這裡符號所代表的是特別的數,而不是一般的數,因 此認知上更困難;最後,是用一些符號來表示一般的數量關係或函數關係,這不 只是用符號代表數,而是用符號來表示關係,屬於更抽象的層次。 依照此認知難度,綱要建議將第一層次放在國小高年級,第二層次擺在國一 初期,第三層次擺在國一後期解方程式的單元,第四層次則放到國一下中的比例 與函數單元。另外,教師應清楚解釋代數表示式中的常數部分和變數部分的區 別。 (二) 代數演算與分配律 以國小高年級的橫式計算與化簡為基礎,國中要開始學習代數演算,作為所(三) 解方程式 解決應用問題是數學教育的重要目標,而解方程式則是解題活動中,既重要 又較有系統的一環。整個國中的代數教學,應養成學生解題的習慣:觀察題意、 以符號將問題中的數量關係列成方程式,最後在解出方程式,並觀察解是否符合 題意。其中最根本的解方程式原理為等量公理,另外,學生應有機會針對同一問 題(例如:雞兔問題類),觀察以國小方法解題、以一元一次方程式解題,讓學生 思考這些方法的差異。
二、迷思概念
(一) 文字符號 文字符號於國小六年級開始接觸,到國中一年級更是廣加運用,因此數學學 習過程中,學童文字符號的概念是否有建構成功顯得特別重要,Kuchemann(1981) 認為「學生對文字符合是否能有意義的了解,在代數學習時是影響學生非常重要 的因素。」根據研究者教學經驗,國一學童在文字符號的課程內容中和往後學習 課程內容成就是息息相關,如果文字符號無法成為學童於問題解決的工具時,會 間接造成學童不當使用文字符號,也因此影響學習代數課程內容的時機(王如敏, 2004)。 許多學者在研究中提出,當學生在進入代數單元學習時,會遭遇許多問題, 是因為小學過度注重四則運算和算術技巧,到國中階段才突然大量引進代數符號, 讓學童產生適應上的困難,導致產生一些迷思概念。過去三十幾年有許多不同學 者企圖探討學生在文字符號概念加以分類,其中較為完整分類為 Collis(1975)從 學生觀點出發,將問字符號的概念分乘六類不同的使用層次。 1.文字符號代表著一個可以算出的值,如:n+5=8 中的n,n=3。 2.文字符號在數學計算裡是可以忽略而不用,如a+b=43,a+b+2=?在求出 答案的過程裡並不需要考慮到文字符號所代表的意義。3.把文字符號當作物體,例如將h 代表為正方形的一邊,所以只是代表其中的一 邊,而不是邊長是多少,這是不一樣的。 4.把文字符號當做特定的未知數,如一多邊形有n 個邊,而且每個邊長為2,知 道此多邊形周長為2n,這是可以直接用來運算。 5.把文字符號當作一般化的數字,如c+d=10,且c<d,則c 代表小於5 的數, 則此文字符號代表的是一組數字而非單一數值。 6.把文字符號當作變數來使用,亦即該文字符號代表著一個可隨條件變動的未定 數值,如比較n 和2n 的大小,n 可以是任何數,兩者也一定可以做比較。 由上述的 Collins 的分類,前三者的描述,文字符號的使用停留在具體的層 面,而後三者的分類則過渡到抽象的思考模式,在一元一次方程式概念學習,若 學生對文字符號的認知只是停留在具體階段,固然可以解決一些簡單的問題,不 過若遇到結構較為複雜問題時,則往往沒有辦法適當的使用文字符號,因此形成 了解題的困難與概念的迷失。Wagner(1981)在其探究學生是否了解當改變文字 符號的名稱時並不會影響方程式與函數的意義的研究中發現:許多學生仍固著於 所命名之文字符號的刻板性用法,當原有之文字符號一被改變時,則沒有辦法適 應也無法正確地的解題,甚至還會認為整個題意已經改變,由此研究得知學生並 沒有完全瞭解文字符號在問題裡所代表的意義(袁媛,1993)。 郭汾派(1988)曾參考英國 CSMS(中學數學與科學概念)小組所設計的題 目對全國分區抽樣測試國中生在文字符號概念的主要錯誤型態,發現其常見的錯 誤有: 1. 帶分數模式:受到小學7 1 71 2 2 + = 的影響,而有 8+x=8x的迷思 2. 係數、文字分別處理:當學生對符號運算不完全了解時,會認為單項式才是 答案,因此強迫自己對不能進一步合併的多項式進行合併操作,其中最常見 的錯誤類型是係數、文字分別處理,將不同類項的係數先行運算,再將未知
數置於其後。如:學生可能再將2a+5b 化成為7ab、7+ab、7(a+b)或7+a +b 等。 3. 不同類項擺在一起:如h+h+h+h+t=4ht。 4. 不知如何使用括號:如
5 (
×
e
+
2)
=
5
e
+
2
。 5. 忽略數據資料:如假設c+d=10,且c<d,求c 時,答案多為c=10-d,而忽 略c<d 的條件。 6. 文字符號只當不為負數的數字處理:如設c+d=10,且c<d,求c 時,很高比 例的學生會回答為1,2,3,4 或0,1,2,3,4。 (二) 一元一次方程式迷思概念 許多學者研究中提出,當學生在進入代數單元學習時,會遭遇許多問題是因 為小學過度注重四則運算和算術技巧,到國中階段才突然大量引進代數符號,讓 學童產生適應上的困難,導致產生一些迷思概念。蕭宇欽(2006)歸納學生在一元 一次方程式迷思概念分析如下 1. 陳述性概念 (1) 學生對於乘法的基本概念不清楚,只會操作數學符號,不了解數學符號的 實質意義。 (2)「一元一次方程式」與「多項式」的概念混淆。不了解「元」、「次」所 代表的意義或是將多項式當作是方程式來作答。 (3) 學生未能完全理解等號的概念。常有學生採用「式子的化簡」的方式「解 一元一次方程式」,或是作「化簡」的題目,最後變成「解一元一次方程 式」。 (4)對於括號的概念一知半解。當題目需要使用括號時,不知道如何使用括號, 或認為有沒有括號並無差別。 2. 程序性概念 (1) 學生對於「文字符號簡記」的概念產生困擾。不知道如何簡記代數式或根 本不知道簡記代數式所表示的意義。(2) 數的四則運算概念不清楚。發現七年級學生雖然學過數的四則運算,但計 算的技巧並不夠熟練,因此只要在一元一次方程是單元需要「正負數的四 則運算」或「分數的四則運算」時,經常會發生錯誤。 (3) 在「求式子的值」的問題中,部分學生容易將加法或乘法的運算方式混淆, 甚至因為不了解文字符號的意義,代入數字運算之後仍保留文字符號的迷 思概念。 (4) 使用「分配律」時容易產生迷思概念。學生容易錯誤使用分配律,或不知 道括號內的算式要和括號外的哪一項作運算。 (5) 學生對於「移項法則」與「等量公理」的概念易產生迷思。 (6) 學生在「同類項合併」易有迷思概念。學生因不了解同類項的意義或是合 併的技巧,在式子化簡時會將全部相加,或文字符號與係數分開運算。 (7) 「幾何圖形的概念」對部分學生而言較為困難。當幾何圖形出現時,尤其 是求面積與周長,學生容易有迷思概念。 (8) 學生對文字敘述轉成數學符號的概念感到困煣,無法將題目中的條件用數 學的表徵組織成完整的方程式。 3. 構造性概念 (1)學生對於以「文字符號代表數」容易產生迷思概念。當題目出現兩個變量 時,多數學生無法從題目給定的文字符號推得令一個變量所代表的數學表 徵。 (2)學生在「假設」部分的概念不足。不了解「假設」是為了根據題意列式來 解決問題,甚至自己列出的式子與假設毫不相關。 (3)學生的解題策略的概念步構多元。在填充引導式應用問題中,發現部分學 生的解題策略只有一種,若題目設計的解題步驟與學生的解題策略不同時, 學生便感到困擾,甚至放棄作答。除上述的概念之外,經訪談發現學生的 閱讀能力、解題態度、解題耐性與持續的信念等情意的態度,都是影響答
三、相關教學研究
文字符號的使用為代數方程式的基礎。Kuchemann(1981)認為學生對於文字 符號是否瞭解是影響學生代數學習非常重要的因素。在 Resnick(1981)與 Carpenter 等多數學者(1982)的研究中發現,當學生在解決與方程式相關的問 題時,學生習慣利用□來假設未知數,之後寫成關係式來解題,利用此種方式通 常可以很快的解決方程式的問題。但當相類似的方程式問題,學生改以使用文字 符號假設未知數來解題,作答的結果比上述使用□假設未知數解題,答對率明顯 降低,所以使用何種形式的符號或文字來替代未知數,對於學生在解決方程式的 問題上是絕對有關聯的。過去幾年來有許多學者針對這個主題利用各種教學方法 試著解決學生於一元一次方程式所衍生的問題,研究者整理近幾年資料如下。 表2-3-1. 一元一次方程式相關教學研究 一元一次方程式相關教學研究 一元一次方程式相關教學研究 一元一次方程式相關教學研究 作者 題目 研究結論與摘要 邱婉茹 (2001) 以一元一次方程式 情境測驗偵測國中 一年級學生在一元 一次方程式概念發 展之可行性 1. 給予適切的提示語可誘發學生呈現更多與 一元一次方程式有關概念;同時會使不同 程度之數學成就學生所表現之一元一次 方程式有關概念種類次數之差距變小。所 以適當的提示語是有助於學生的概念發 展。 2. 學生所出現的概念並不是片片段段的,對 每一個較高階層的概念,學生無法完整表 達出來,但是卻能表現出一些較低階層的 概念,而且研究中亦發現學生所發展出較 完整的概念為較低階層的概念,精熟度也 較高。 (續下頁)3. 由簡單到複雜的題型,學生大部分的作答 情形也是隨著題形漸複雜,概念愈複雜, 學生愈無法自由運用相關的一元一次方 程式概念,而使用到的解題概念,則是一 直重複使用精熟的較低階層概念。 王如敏 (2004) 國二學生解一元一 次方程式錯誤類型 分析研究 1. 在解應用問題時,多數的學生其解題層次 在了解題意並把相關未知數用文字符號 表達出來這一初始階段已經出現極大困 擾。 2. 不同程度等級的學生在應用問題的解題表 現上有顯著差異。本研究發現程度等級高 的學生,不管傳統組或引導組都有極高的 得分率,但程度等級中或低的學生在解應 用問題時,不管以傳統式或引導式呈現, 其得分率皆不高。 3. 引導式應用問題能適當地引導學生去思 考、幫助學生更了解題意,並從中發現學 生之解題困難點及錯誤的原因。 俞宗賢 (2007) 數學低成就學生一 元一次方程式補救 教學之研究 對於式子的化簡及解一元一次方程式這 兩個偏重計算及運算技巧的單元,本研究的 補救教學另外採取小組合作學習方式,提出 較難的類似題或是思考錯誤答案的作法等問 題讓各小組去進行討論,在小組成員彼此的 討論之中,學生可釐清自己的錯誤,每個單 (續下頁)
元結束後,藉由各小組討論學習任務(練習 題),學生可以強化概念的認知,了解別人的 想法及解題方式。 曾樁惠 (2010) 激發式動態與認知 負荷呈現一元一次 方程式 在激發式動態教學下,教材設計如果讓文字 訊息結構化且加入圖像訊息,對於學童的學 習表現會有明顯的助益,尤其在應用問題列 式的解題過程更為明顯。 李昆霖 (2011) 利用電子白板於一 元一次方程式課堂 教學 使用互動式電子白板教學有助於學童在數學 學習的自我認知態度、學習成效,且利用大 量的動畫與圖形介面可以讓學童經由動畫瞭 解整個運算的原理,更能了解其中的概念。 綜合上述各位學者研究結果可整理出,學生無法妥善解決代數問題原因來自 於不能瞭解題目的意思,解題過程中處理愈高複雜的題目時,使用的依然是低階 的概念,而透過電子數位的教材或是合作學習、引導式的教學皆能有效幫助學生 有效提升在一元一次方程式的學習成效。
第四節
第四節
第四節
第四節 數學態度
數學態度
數學態度
數學態度
態度的改變不只是個人的事而是外界刺激與內在反應的綜合結果,因此幫助 學生培養數學的學習興趣、態度對於學生學習數學來說是有相當的助益,以下分 別就數學態度的意義及相關研究做一些探究。一、數學態度的意義
張春興(1997)認為態度係指個體對人、事、物的內在心理反應的行為取向, 態度包含三個成分:認知性成分、情感性成分,行為性成分。學生如果對數學的 學習有較積極的態度,通常他們的數學成就會比較高(Karen, 1993)。教師如果有積極的數學態度,學生也可能會有積極的數學態度,因此,教師對學生的數學態 度之影響,扮演著重要的角色(Karp, 1991)。關於數學態度的意義,眾多學者皆 有不同的看法,將其個學者定義整理如表 2-4-1。 表2-4-1. 數學態度的意義 數學態度的意義 數學態度的意義 數學態度的意義 學者(年代) 數學態度的意義 Aiken(1976) 指學習數學的興趣、感覺數學的重要性、學數學的動機、免於 數學恐懼等因素的綜合表現。 Fennema 、 Sherman(1976) 數學態度是指對學習數學的信心及成功的態度、父母親及教師 的數學態度、數學是男性的科目、數學的有用性與探究動機及 焦慮等綜合表現。 李默英(1983) 數學態度係指學習數學的信心、對數學成功的態度、數學為男 性的科目、數學有用性、數學探究動機、父母親與教師的數學 態度等綜合表現。 何義清(1987) 數學態度係指個體對於數學所持的一種較具持久性和一致性 的反應傾向。 魏麗敏(1988) 數學態度乃指個人對於數學的喜好程度,包括學習數學的信 心、對數學成功的態度、數學為男性科目、數學的有用性、數 學探究動機各因素之綜合表現。 Sriampai(1992) 數學態度係指對學習數學的信心、教師的數學態度、對數學成 功的態度、數學的有用性等的綜合表現。 譚寧君(1992) 數學態度即對數學的想法與做法。 吳元良(1996) 指學生對數學的看法或喜好程度,是一種既持久又一致的傾 向。
吳明隆(1997) 數學態度指個人對於數學的一般性觀感、看法、喜歡或厭惡的 程度。 高石城(1999) 數學態度是個人基於過去的經驗,對數學所秉持相當一致性與 穩定性的理性認知、情感好惡反應與行動傾向的一種心理特 質。 林承德(2003) 數學態度意旨個人對數學的喜好程度,包含數學學習的信心、 對數學成功態度、數學有用性、數學探究動機等因素的綜合表 現。 曾安如(2004) 數學態度包含認知、情意、行為三個層面,具有一致性及穩定 性的心理特質。 資料來源:洪茂原(2009)。校外數學補習對屏東縣國小高年級學童數學態度與數校外數學補習對屏東縣國小高年級學童數學態度與數校外數學補習對屏東縣國小高年級學童數學態度與數校外數學補習對屏東縣國小高年級學童數學態度與數 學學習策略影響之研究 學學習策略影響之研究學學習策略影響之研究 學學習策略影響之研究。國立屏東教育大學應用數學系碩士班碩士論文。 綜合上述學者觀點,數學態度是個人對於數學的喜好程度,是後天學習環境 逐漸形成的,學習數學是一種認知的過程,然而研究顯示數學態度對學生決定未 來,是否繼續研讀數學或是否從事有關數學行業等,均扮演一個相重要的角色, 往往持較樂觀數學態度者,亦有較高的學習成就發現,且有些學者(魏麗敏,1988; 譚寧君,1992)的看法和張春興(1997)一致,將數學態度分為認知、情意與行 為三個成分,整理如下: (一) 認知性成分 指對數學的信念與有用性的評價,包含下列兩項。 1. 學習數學的信心 指的是學生對自己能力以及數學表現的看法。一般學生總將數學視為一門困 難的科目,對數學感到害怕、排斥甚至有一些消極的反應傾向,是目前數學教育
相當重視且希望改變的。 2. 數學的有用性 指學生對數學實用性的看法,是否可用以解決日常生活的問題,或是幫助未 來的教育與工作。九年一貫課程強調數學課程應該以生活為中心,發展形成數學 問題與解決數學問題的能力,可以幫助學生知道如何學且樂於學習,以幫助其社 會適應。 (二) 情意性成分 指個體對對數學的感覺與情緒的狀態。 1. 數學成就的態度 指學生期待對數學成就的程度,願意去學習數學,建立樂觀的學習態度。 2. 數學焦慮 指學生在學習數學時所引發的緊張、不安、害怕的情緒。而數學焦慮與數學 態度對數學成就具有顯著的預測作用與關係,因此消除學生的數學焦慮,提高數 學態度,是增進學生數學成就的重要途徑(魏麗敏,1989)。 (三) 行為性成分 指對數學的實際行為的探究動機及內在的溝通傾向。 1. 數學探究動機 學習動機指的是引起學生學習活動,維持學習活動,並導致該學習活動趨向 教師所設定的內在心理歷程。數學探究希望能培養學生透過數與形的訊息,主動 分析資料,形成臆測、驗證的判斷能力。 2. 數學溝通傾向 指學生能與他人討論、表達個人的數學想法。九年一貫新課程中,表達、分 享與溝通是基本能力之一,而多元民主的社會,更需要具有理性溝通的素養及培 養學生與他人分享思考歷程與成果,並能尊重他人的意見與想法。
綜合多位學者研究,本研究於數學態度的研究為參考張春興(1997)將數學態 度的意義分為認知、情意、行為,其中內容包含僅對認知性成分的學習數學的信 心、情意性成分的數學成就態度與數學焦慮、行為性成分的數學探究動機與數學 溝通傾向,僅針對這五個向度進行研究。