以建模觀點詮釋國中資優生的
數學解題活動
顏富明
1張靜嚳
2* 1彰化縣立員林國中(退休) 2國立彰化師範大學科學教育研究所 * ckuchang@gmail.com (投稿日期:2010.10.15;修札日期:2010.11.23;接受日期:2011.1.26)摘 要
本研究目的是以建模觀點詮釋國中資優生的數學解題活動,包含思維內 涵、模型、建模循環與模型發展系列的關係。本研究採個案研究法,在一班 30 人的國中資優生進行小組合作解題,全班共分成八組,每組 3 至 4 人,以其中 四組為本研究之個案,資料收集包含小組討論及其發表、學生的學習日誌、教 學現場摘記、教學日誌及任務導向的臨床晤談。研究結果發現:1.國中資優生的 解題活動是一種建模思維取向的歷程,而不是描述式或規範式的歷程;2.以建模 觀點詮釋國中資優生數學解題活動,有助於了解國中資優生的數學思維特徵; 3.模型、建模循環與模型發展系列也有一些特定的關係與蘊涵,包括(1)模型與 建模循環的一對一對應關係;(2)在每個問題的模型發展系列的主要活動中,所 建構的模型數量是依問題解決者所經歷的建模循環次數而定;(3)問題的本質與 模型建構、模型發展系列的關聯性;(4)所建構的模型數量的多寡,不是代表題 目的難易,而是代表不同解題者企圖貼近問題,所經歷的建模循環次數的差異。 關鍵字:解題、建模、資優生、詮釋壹、緒論
近年來,數學教育有關建模與模型發展能力愈來愈受關注,並強調它是數 學的核心能力之一。Niss (2002)將建模能力列入丹麥 KOM 專案中所提的八種數 學 能 力 (competencies) 之 一 。 此 外 , 國 際 學 生 評 量 計 畫 (The Programme for International Student Assessment, PISA)亦將建模列入其所公布六種描述數學素 養 的 層 級之 一 (Organisation for the Economic Co-operation and Development [OECD], 2003)。 對於問題解決的觀點,Lesh 和 Doerr (2003)指出傳統觀點與建模觀點存在著 一些問題解決本質上的差異。傳統觀點主張問題解決尌是,「當解題路徑不明 顯時,從題目所給的條件到目標所得到的過程」,其中解題者所使用的,只是 一串的事實或規則,而且在方法上也是被限定的。相對地,建模觀點主張的問 題解決,其中一些最重要觀點,尌是包含發展有用的方法,以詮釋題目所給的 條件、目標、可能解題途徑的本質、樣式及潛藏於事物表面下的規律性。解題 的過程通常包含幾個「建模循環」,而且在建模循環中的描述、解釋及預測是 逐漸地改善及精緻化的。此外,他們對於建模觀點所論及的模型,特別提出其 定義:模型(models)是使用外在的符號系統表達的一組概念系統(由元素、關係、 運算及支配互動的規則所形成),並被用於建構、描述或解釋其他系統的行為, 及明智地操作或預測其他系統。 在現實的生活情境中,人們經常會碰到複雜系統的問題,這種問題通常藉 由建立模型來加以解決。例如,在航空工程方面,科學家可能建構模型飛機來 引導真實飛機的設計與發展;在農業科學或地球科學與大氣科學方面,科學家 可能建構以電腦為基礎的模擬(即模型)來探究一些樣式或複雜現象是否會自然 地發生;在日常生活經驗中,學生可能使用各種隱喻、類比、圖形、模型來描 述或解釋一些現象,像是電流、影子、會浮的物體或其他的類似情境(Lesh & Doerr, 2003)。此外,Singer (2007)特別強調,人類的思維,是藉由使用模型以了 解其他的系統,而且模型是了解我們所生活世界的基本工具,因此,在學校有 關建立模型的訓練必頇很早尌開始。另外,他認為這樣做主要基於兩個要素: 為學習提供強而有力的模型(即對學生必頇內化的概念,所提出的強而有力的表 徵),及從最簡單的問題開始,訓練學生建模。
尌問題解決而言,傳統觀點與建模觀點存在著一些教學實務上的差異。Lesh 和 Lehrer (2003)指出,一些數學教育研究者傳統地將問題解決定義為,像是「當 解答過程不容易找到時,從題目所給條件到解題目標的作法」的一種過程。他 們根據 Lesh 和 Harel (2003)的研究強調,模型與建模觀點認為模型是透過一系 列發展、測詴、修改的循環而產生,在每個循環中,關於條件、目標及可能的 解答步驟的本質,都涉及不同的思考方法。因此,他們並特別強調,(1)當解題 過程是包含一系列的建模循環時;(2)當解題初期,對所給的條件與目標所作出 欠缺經驗的詮釋是可以被理解時;(3)當解題目標是要擴展、修改、重組、精練、 調整、適應你已有的構念時,則各種不同的問題解決策略與後設認知過程的浮 現是同等重要的。 Threlfall 和 Hargreaves (2008)在描述資優生與較年長的一般生的數學解題方 法一文中,引用 Steiner 和 Carr (2003)的研究指出,有關資優生解題的實務研究, 大部分是透過同年齡的比較研究來實施,從這些研究可以歸結出,資優學習者 普遍不同於他們的同儕,有下列幾個方面:他們(1)有較廣的且連結力較強的知 識基礎;(2)是快速解決問題者,同時會花更多時間規劃過程;(3)在對問題的呈 現與分類上,是更有效率的;(4)具有更精緻的過程知識;(5)在策略的使用上, 是更有彈性的;(6)喜歡複雜,願意挑戰問題;(7)在後設認知及自我調控方面, 更能顯現出複雜巧妙。然而,這些比較研究所產生的對照情形,並未能真札地 對資優生的解題內涵,提供進一步的了解。其次,關於資優生解題活動的進行, 梁崇惠、邱姵萍和施皓耀(2009)指出,教師應以開放、等待的態度來帶領資優生, 並帶著學生精緻地探索知識。 針對數學建模的研究所聚焦的問題方面,Blum 特別指出,許多研究者的努 力,主要是聚焦在教學與應用上的建模活動的設計與詴驗,而未能將其貢獻朝 向促進我們對數學建模的了解(Mousoulides, Christou, & Sriraman, 2008)。再者, Muller 與 Burkhardt (2007)指出,關於應用與建模,下列的關鍵性問題,需要作 進一步深入的研究,並共同發展:(1)具體的應用與積極建模是用什麼方法建立 對數學概念的了解?(2)包含於建模真實情境中的一些擴展推理鏈,對於鼓勵學 生,以促進他們在數學上的專門技能可靠性的影響有多深?(3)建模對於促進學 生在純數學的問題解決的表現之影響有多深?是關於哪些層面? 如何促進對解題策略內涵的了解,使解題策略能在未來的解題中發揮作 用?Lesh 和 Zawojewski (2007)在描述解題與建模一文中指出,「Pólya 式」的 解題策略,像是「畫一個圖」、「倒推」、「尋找類似問題」、「確認條件與
目標」,對於促進解題表現上,研究顯示這些策略並未能連結上直接的教學。 為何過去解題活動的事後描述,在未來的解題活動中未能提供後續解題步驟的 必要導引?他們認為可能的原因是,因為使用像「畫一個圖」的策略,其假定 是學生會知道,在什麼情況下,對哪一類問題要畫什麼圖,因此,熟悉「畫一 個圖」的作法,所依靠的是詮釋的能力,而不是執行力,所以,發展一些系統 來詮釋問題的情境比發展一些過程來執行特定的一些策略,顯得更加重要。 由於 Lesh 和 Doerr (2003)是以生活週遭問題為主的例子作為其研究個案, 如排球問題與大腳印問題等,又為呼應 Muller 和 Burkhardt (2007)關於應用與建 模關鍵問題的建議,所以本研究主張由純數學的問題解決切入,又為重新概念 化資優生的解題思維,透過一些系統架構來詮釋資優生的解題活動,使資優生 解題行為的內部意涵能更清楚展現,故本研究目的為:以建模觀點詮釋國中資 優生的數學解題活動,包含思維內涵、模型、建模循環與模型發展系列的關係。
貳、文獻探討
本研究是以模型與建模觀點,來詮釋資優生在解題活動中的思維,因此, 文獻探討主要是聚焦在模型與建模觀點的理論基礎、由模型與建模觀點探討數 學學習與問題解決及建模的重要性。一、模型與建模觀點
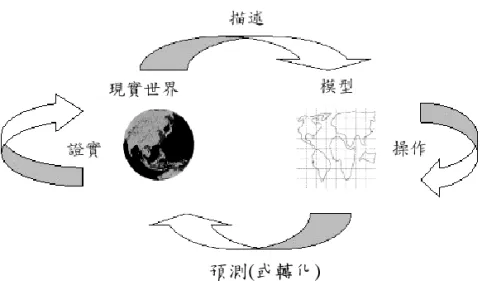
圖 1 建模循環經常包含的四個基本階段 (Lesh & Doerr, 2003) 預測(或轉化)
建模過程是循著何種型態發展,是直線型、分支型、網狀形還是循環型? Lesh和Doerr (2003)指出,建模過程是循環型,關於模型與建模觀點的問題解決, 其 簡 單 類 型 包 含 四 階 段 的 建 模 循 環 (modeling cycles) ( 如 圖 1) : (a) 描 述 (description),為確立由現實(或想像)世界的問題到模型世界的一種映像,亦即 藉由描述建構模型;(b)操作(manipulation),對由描述所建構的模型進行操作, 是為了對相關的原始問題解決的情境,產生預測或行動;(c)轉化(translation)或 預測(prediction),將操作所得的相關結果,提出轉化或預測,以對現實(或想像) 世界的問題,作出回應;(d)證實(verification),是對行動及預測的有效性,提出 證實的作法。他們強調,如果一個問題的數學詮釋不是顯而易見的,則典型的 解題過程會包含幾個建模循環,而且,透過測詴檢驗的回饋,讓描述、解釋及 預測逐漸受到精練、修札或拒絕。Haines和Crouch (2007)亦同意建模過程是循環 型的觀點,並特別強調,在建模活動的期間,建模活動的幾個階段,會有連續 回溯參考真實脈絡的情形。 關於問題解決中的模型發展活動,Lesh、Cramer、Doerr、Post 和 Zawojewski (2003)提出模型發展系列,其中包含三個主要的活動,以促進模型與建模觀點的 問題解決:(1)模型引出活動(Model-Eliciting Activity, MEA):此活動適用於單元 開始時,以處理構成主要構念基礎的相同重大想法,而其中的主要構念是 MEA 所強調的。特別的是,在此活動中,會請學生以老師能看得到的形式來表達他 們的思考方法,其目標是要確認學生概念強弱的部分,其中大部分作法,尌像 是在課前晤談學生;(2)模型探索活動(Model-Exploration Activity, MEX):其主要 目標是為學生發展強勁的表徵系統(及語言),以瞭解目標的概念系統;(3)模型 調 整 活 動 (Model-Adaptation Activity, MAA) : 有 時 亦 被 稱 為 模 型 應 用 活 動 (model-application activities)或模型擴展活動(model-extension activity),這是因為 此活動的目標常常聚焦於概念工具(或模型)的使用,而此概念工具已在 MEA 被 發展出來(且已在 MEX 被精練出來),以處理在概念工具發展出來之前,可能難 以處理的問題,在此活動中,即使在形式上已被發展出來的概念工具,也強調 其可分享性、可修改性、可傳播性,因為概念工具很少在未經重要調適的情形 下,而能使用於新的情境中。他們進一步強調,教師可以考慮把 MEA 與 MEX 當作表現評量的活動,因為這兩者對學習與評量都有貢獻,且兩者都強調更深 入與更高階的了解與能力,而這些更深入與更高階的了解與能力是標準化考詴 很少會強調的。
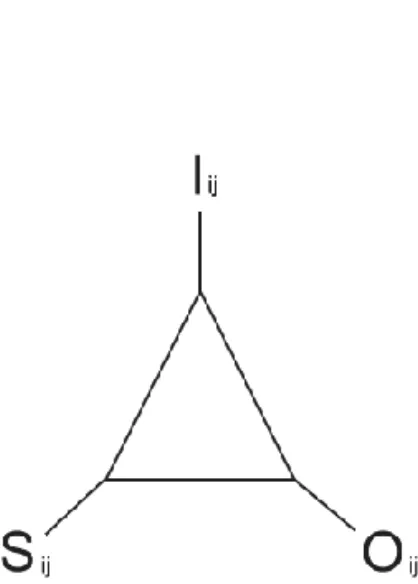
如何從意義的構成與符號的關聯來進行模型發展的詮釋?Kehle 和 Lester (2003)首先根據符號學家 Peirce 的研究指出,一切意義的構成,皆由「符號」(sign) 所調解,而符號學是對於符號如何促進構成意義的實務研究。在圖 2 中,符號 可以是任何事物,實質上,任何事物均可被當作符號(例如:一把椅子,字,數 學符號,一張圖畫,一種舞蹈,一隻螞蟻,一小塊絨布)。同樣地,任何事物根 本上尌可以當作「物件」(object),而此物件是由符號所表示的,因此,物件也 可被稱為符號的指示對象。更重要的是,「記號過程」是指由符號、物件這兩 個元素與另外第三個元素所構成的不可分解的三叉式互動組,而此第三個元素 被稱為「詮釋元」(interpertant),基本上,詮釋元不但由一種對符號與物件的獨 特反應所形成,而且其同時也定義了在討論中的符號與物件。其次,他們亦指 出,當我們從記號過程的觀點來觀察,後設認知的發生在於一個過去的記號過 程 例 子 變 成 了 新 記 號 過 程 的 物 件 ( 如 圖 3) , 他 們 支 持 符 號 學 家 Donald Cunningham 的論點,把反思看成是記號過程依據其自身所構成意義的加倍倒退 的能力,而這種能力被視為是符號結構的效力。由上述觀點,研究者認為模型 具有物件的特性,因此,本研究擬透過三叉式記號過程,來詮釋學生在參與解 題活動時,其所建構的模型的發展情形。 圖2 符號學三位一體的本質 (Kehle & Lester, 2003)
圖 3 一個過去的記號過程例子可以變 成新記號過程的物件(Kehle & Lester, 2003)
二、從模型與建模觀點來探討數學的學習與問題解決
在數學學習方面,學生藉由發展其本身的概念系統,以了解他們的數學經 驗。Lesh 和 Lehrer (2003)指出,模型與建模觀點,首先是建立在 Piaget 構造論 的觀點上,並強調下列三個重點:(1)概念系統的整體本質;(2)更原始的/具體 的/動作的/直覺的層級的互動系統:此系統的重要性,是因為高階系統所浮 現的性質是由此互動系統所演化(反思抽象)出來;(3)概念重組:對於概念重組 的發生,主要是源自模型未能適合它們想要描述、解釋的經驗時。其次,模型 與建模觀點也建立在 Vygotsky 有關思維概念的觀點上,即調節活動(mediated activity),並強調下列四個重點:(1)近側發展區(zones of proximal development): Vygotsky 認為在任意所給的時間點上想法的發展,學生瞭解的層級會受到各種 因素的影響;(2)語言影響數學思考;(3)N 維區間的近側發展區:模型與建模觀 點認為近側發展區的觀念需要由一維區間擴展至 N 維區間,而在其間路徑的多 樣化會引領出指定構念,更進一步,學生會透過這些區間,並沿著多樣化的可 能軌道,而能獲得進步;(4)多元化的概念系統:模型與建模觀點擴展了 Vygotsky 關於社會功能對概念發展影響的想法,認為在重要的學習或問題解決情境中, 學生通常會被期望具有可用的概念系統群集,其中每一個都有潛力被用來詮釋 相關經驗。最後,要強調的是,模型與建模觀點強調實用主義,並重視「實用」 概念架構的發展。
對於數學問題解決研究的方法與觀點,Lesh 和 Zawojewski (2007)引用 Lester (1994)及 Lester 和 Kehle (2003)的研究指出,有關數學解題的研究比先前的想法 更為複雜。他們並且主張,對促進從實務與理論觀點所引出的想法整合方面, 模型與建模觀點可作為其架構。他們並進一步指出,使用模型與建模觀點的研 究有下列四個特色:(1)研究與了解數學問題解決的概念模型研究者,被認為在 發展或設計之下,其研究具有持續性;(2)研究活動是由圍繞在課室中被測詴過 的產物與工具,所組織並產生出來;(3)逐漸增加對理論發展的強調,並逐漸減 弱對理論借用的強調;(4)採用的目標是:產出結果不僅需要一般化(即可分享的 與可再使用的),而且對於局部脈絡(像是學校的脈絡、學生與老師脈絡等等), 與札在學習的數學脈絡是強而有力的。其次,張靜嚳(1995)指出,以問題中心雙 環教學模式教學,可以引起學生的學習興趣、提高學習成尌與改善教室學習氣 氛。再者,李源順、余新富和李勇諭(2006)指出,數學教學需要強調學生能獨立
思考並表達想法,並在尊重與欣賞的態度下與他人溝通,且藉由團體合作來解 決問題,而且,在解題活動中,讓學生透過小組合作學習的模式,進行推理、 連結和溝通,有助於培養學生的解題能力。此外,黃國勳和劉祥通(2006)指出, 藉由適當融入佈題教學及透過策略性的遊戲教學,可提升問題解決的能力,他 們並且強調,在解題活動過程中,學生必頇要有相互討論的機會,以幫助學生 後設認知能力的發展。
圖 4 視覺化推理問題 (Dreyfus & Eisenberg, 1996)
論及數學思維的特徵,Dreyfus 和 Eisenberg (1996)曾指出,有一個前提,即 大部分的人都可以藉由訓練以進行數學方式的思維,而要達到這種思維的最佳 方式,尌是透過問題解決。特別地,他們針對數學思維特徵提出數學思維的五 個面向:(1)類比推論,例如,由直線上的 n 個點,最多可將此直線分割成「2+(n-1) 個 1」個區段,即 1+n 個區段,經由類比可推論出,帄面上 n 條直線,最多可 將此帄面分割成2+(2+3+4+…+n)塊區域,即 1+n(n+1)/2 塊區域;(2)數學結構, 例如,(a)若 n 是偶數,則 n+1 必是奇數,其逆也真;(b)偶數+偶數=偶數,奇 數+偶數=奇數,偶數+奇數=奇數,奇數+奇數=偶數;(3)表徵,為了表達 數學的敘述、概念或問題,必然會用到表徵,這樣的表徵可能是制式的或非制 式的、視覺的或口語的、明示的或隱含的,而且,任何的表徵會表達部分但非 全部的訊息,強調某些觀點而隱藏其他觀點,例如,為表達函數的概念,可能
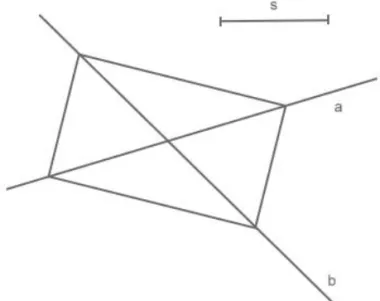
用的是代數的、圖形的、列表的及其他可能表徵;(4)視覺化的推理,例如在圖 4 中,對於帄面上兩條相交的直線,尋找所有的點到兩直線 a、b 距離和等於一 線段長 s 的軌跡,藉由視覺化推理可發現其軌跡為一矩形,且矩形的四個頂點 都落在兩直線 a、b 上。因此,他們引用 Hershkowitz、Friedlander 和 Dreyfus (1991) 的研究強調,藉由尋找幾何軌跡,使視覺化推理的想法更具體,以便用來發展 視覺推理的樣式;(5)逆向思維,良好的問題解決者似乎都具有能力,能在更大 的脈絡中看出特殊議題的發展路徑,而這些脈絡也常提供他們一種「抽象的運 作空間」,讓他們能從結果進行推論,或找到導致此結果的根源。此外,陳英 娥和林福來(1998)指出,學生個人數學臆測的思維模式可以呈現出其思維路徑和 認知狀態,而且對於教師而言,它具有表徵問題的難度、評量學生思維的品質 以及診斷教學和開出教學處方的功能,由此可知,這些功能對於教學實務具有 非常重要的意義。 為何要從建模觀點來詮釋資優生的解題?Pólya (1957)根據其對解題所做的 解釋,認為這些解題策略對於具有高水準數學能力的人是可行的,但是, Schoenfeld (1992)認為 Pólya 要面對的其實是有效性的問題,因為在 1970 年代也 只有些微的實徵證據支持啟發術能被當作促進解題的方法,而且列在如何解題 (How to solve it)及其他後繼書籍中的解題策略,所用的界定方法是描述的而不 是規範的,即要解題者在解題時要去辨認這些策略,但卻不能提供一些細節, 以便不熟悉這些策略的解題者能執行它。因此,他主張,能列的更詳細的啟發 術,使得解題者能學習與記憶這些策略,這也使得高階的處理規則與信念需要 詳介成為何時、為何及如何使用的低階規範過程,這也導致他認為有關解題的 未來研究,要強調後設認知與信念(Lesh & Zawojewski, 2007)。實際上,Lesh 和 Zawojewski (2007)在描述解題與建模一文中指出,列的較短的描述性過程,顯 現出因太廣泛而對教學目的不太具有意義,列的較長的規範性過程,因為數量 過多,使得要認識何時使用它變成解題者瞭解的核心,這變成一種兩難的局面, 因此,他們認為加入過多的後設認知規則與信念,會成為教學的另一種層次的 要求,這只會加重課室實際運用的難度,所以,對 Pólya 的啟發術而言,他們 提出一個觀點,即不僅要促進選取與執行過程與規則的方法,而且也要提升關 於發展一些系統來詮釋與描述情境的方法,再者,他們建議,藉由「描述學生 自己所擁有的解題過程」,讓學生能夠應用反思以發展出較具彈性的解題原型, 而此原型可以在未來解題時能被提出來應用。因此,本研究擬以建模觀點,來 詮釋資優生的解題,以促進我們對資優生解題思維內涵的了解。
三、建模的重要性
關於建模研究的發展階段,Niss、Blum 和 Galbraith (2007)指出,把應用與 建 模 當 作 數 學 教 育 研 究 與 發 展 的 場 域 , 可 分 為 三 個 階 段 : (1) 提 倡 階 段 (1965-1975),由 Freudenthal 的研討會象徵性地發起,提供論述以支持將應用與 建模列為數學教學中重要的內容;(2)發展階段(1975-1990),此階段期間,在理 論層次上,其形成的企圖是在系統化與分析化方面,並針對數學教育中的應用 與建模的論述,進行理論與歷史的探究;(3)成熟階段(自 1990 之後),在最後這 十五年期間,將有關應用與建模的實徵性研究,加入到先前的理論階段。 關於建模的重要性,Swan、Turner 和 Yoon (2007)指出,建模活動對於發展 數學了解與持有數學知識,提供強而有力的方法,且一些專案都將建模置於數 學課程的核心位置,例如,在美國,「中學教育專案,以應用為導向的改革」 (Application Based Reform in Secondary Education project, ARISE)所發展的高中數學課程,完全建立在模型與建模的基礎上;「芝加哥大學的學校數學專案」(The
University of Chicago School Mathematics Project, UCSMP)所建立的信念是,建模 對於發展純數學與應用數學的能力都有所幫助;此外,在荷蘭,由 Freudenthal 基金會所發展的真實數學教育(Realistic Mathematics Education, RME),也採取建 模的研究取徑。 Henn (2007)引用 Pollack 的研究指出,數學建模是數學與其外的世界的共同 結合體,透過建模,學生能在下列兩者之間建立一座橋樑:(1)數學作為更加了 解他們周遭世界的工具,(2)數學作為抽象結構。基於此點,合適的教學情境是 不可或缺的。其次,他引用 English 的研究提到,教學情境的需求是提供「豐富 的學習經驗」,也尌是真實的情境,並擁有探索的機會,詮釋的多重可能性與 社交的能力,以擔負起為學生個人擁有的模型而能與其他學生進行溝通的責 任。最後,他引用 Maaß 的研究強調,完全的建模過程雖然是消耗時間且困難 的,但是建模活動可以在一般的教學情境中成功地啟動進行。此外,關於設計 建模教材的考量層面,楊凱琳和林福來(2006)指出,建模活動的問題不同於一般 的數學課本練習題,所以在高中數學教學融入建模活動時,要重視反思問題情 境與順序的流暢性,並關心與學生既有經驗的聯結性與問題的多樣發展性。
參、研究方法
一、研究設計
本研究採用個案研究法,以四個個案的解題活動為基礎,系統且嚴格地組 織及分析、分類及鞏固個案的資料,以形成主張。在內容方面,可分為下列三 點:(1)本研究歷時一學年,於上學期先進行探究教學,讓學生能逐漸習慣和熟 悉分組討論、呈現問題解法、接受提問等多向互動的學習方式;於下學期再進 行問題解決的活動,並開始撰寫學習日誌,學習日誌的內容包含探究導向的解 題歷程、解題關鍵點(AHA),反思(包含評價及統整)。(2)第一位研究者尌是教師, 為促進學生的小組活動,讓學生的想法能呈現出來,以便詮釋學生的解題思維, 所以,教師採用以探究為導向的方法進行教學,又為深入了解學生的問題解決 思維,亦安排課後的時間,對各組學生進行任務導向的臨床晤談(clinic interview) (Clement, 2000),而此晤談是採取開放式提問,主要是為收集學生用言語表達其 進行解題的思考過程。(3)又為配合學校課程的進行,此項活動中,教師將全班 30 位學生分為 8 組,第一組至第六組,每組 4 位學生,第七組與第八組,每組 3 位學生,每兩週進行一次,每次歷時兩節課。在上學期處理較基礎的問題解決, 而在下學期處理較進階的問題解決,下學期相關的佈題列於第三節「引發學生 解題思維的佈題」中。在下學期所進行的解題活動中,每次處理一個任務,共 處理九個任務,於期末結束。因為每一組在整個學期的解題活動中要共同處理 九個任務,而小組針對該次的任務討論後,其成員都要輪流上台呈現,所以每 位同學至少有兩次負責呈現任務的機會。二、詮釋架構
在本研究中的模型建構發展的詮釋架構,是針對資優生對於問題解決活動 的任務,在透過小組合作共同探究以完成任務的過程中,對期間所經歷的活動 加以結構化。首先,對於期間資優生所經歷描述、操作、預測與證實等四階段 的建模循環(Lesh & Doerr, 2003),因可由觀察而加以辨別,故稱之為外顯問題解 決活動。其次,在此解題過程中,資優生將現實世界的問題脈絡,由描述所建構的模型,在其間模型所經歷的模型引出活動、模型探索活動與模型調整活動 等三階段的模型發展系列(Lesh et al., 2003),因不易由觀察來加以辨別,且頇由 三叉式記號過程來加以詮釋,故稱之為內隱模型建構發展活動。因此,研究者 擬藉由模型建構發展的詮釋架構(如圖 5),以詮釋資優生的問題解決思維。 圖 5 模型建構發展的詮釋架構 關於資優生的外顯問題解決活動,是根據建模循環的四個階段,描述、操 作、預測、證實,來加以類別化,接著,再由下列五項作法,來加以聚焦:(1) 觀察資優生在課室的小組討論與呈現,(2)學生所撰寫的學習日誌,(3)教學現場 摘記,(4)教學日誌,(5)任務導向的臨床晤談。關於資優生的內隱模型建構發展 活動,是根據模型發展系列的三個主要活動:MEA、MEX 與 MAA,與三叉式 記號過程的三個要素:符號、物件、詮釋元,來加以分類與聚焦,並進行模型 的鏈結。因此,對於資優生進行問題解決活動的任務時,其所引發的各種思維, 擬藉由這兩個活動來予以詮釋。 外顯問題解決活動 內隱模型建構發展活動 問題解決活動 的任務 建模循環 模型發展系列 詮釋 學生的問題 解決思維 模型調整活動 模型探索活動 模型引出活動 現實世界 模型 描述 預測 證實 操作 小組討論與呈現 學習日誌 教學現場摘記 教學日誌 任務導向的臨床晤談 三叉式記號過程 詮釋元 符號 物件
三、引發學生解題思維的佈題
在此研究中,教師不會告知學生如何解這些問題,而是提供學生問題,並 要求學生使用他們所採取的方法或策略來解決問題。基本上,教師會提供一些 問題,並引導學生進行模型引出活動,使學生有可能找出數的關係或形的關係 模型。因此,學生在將問題轉化後,形成一般化的問題,並加以論證他(她)們所 形成的命題。 有關佈題的部分,共有九個任務,可分為四個類別:(1)遊戲題,1 題;(2) 奇偶問題與同餘數問題,2 題;(3)帄方數問題,4 題;(4)抽屜問題,2 題。為避 免類別重複,選取原則是從四個類別中,各選取一題,共四題,即按上述類別 的順序取出,分別為:任務 1(翻杯問題)、任務 2(整除問題)、任務 3(四次方和 問題)及任務 4(取數問題)。再者,以翻杯問題為例,作有關佈題內容的說明,首 先,教師進行翻動杯子的操作示範,即實際用 7 個杯子,並將其杯口朝上,按 題目的條件,每次翻動 4 個杯子,並讓學生觀察杯口朝上或朝下的杯子數量的 變動情形,操作三、四次之後,發現杯口都未能全部朝下;接著,讓各組學生 使用杯子或替代品(如銅板、符號等)進行翻動杯子且進行觀察記錄與討論,並開 始嘗詴對問題作進一步的描述,於是解題的建模活動尌此展開。 (一)任務 1:翻杯問題 七個杯子,杯口朝上,擺在桌子上,每次翻轉四個杯子(口朝上的翻為口朝 下,口朝下的翻為口朝上),經過若干次這樣的翻動,問可不可能全部杯子口都 朝下? 1. 請利用實物操作,觀察及記錄結果。 2. 若經過若干次這樣的翻動,你發現可以將全部杯子口都朝下,則請用操作的 方式呈現給大家分享。若你主張翻動的結果,不可能將全部杯子口都朝下, 則請用論證的方式支持你的主張。(二)任務 2:整除問題
表 1 整除問題
a b c d a-b a-c a-d b-c b-d c-d (a-b)(a-c)(a-d)(b-c)(b-d)(c-d)
8 7 5 2 1 3 6 2 5 3 540 9 7 6 4 2 3 5 1 3 2 180 10 9 8 7 1 2 3 1 2 1 12 觀察上表,對四個相異的整數 a、b、c、d,可發現一個共同的現象,即 (a-b)(a-c)(a-d)(b-c)(b-d)(c-d)皆可被 12 整除。 1. 請再任意指定四個相異整數放入上表中,測詴看看(a-b)(a-c)(a-d)(b-c)(b-d)(c-d) 是否還是可被 12 整除? 2. 若發現(1)的答案是肯定的,請說明為何會有此現象,即請用論證的方式處理 下 述 問 題 : 「 已 知 a 、 b 、 c 、 d 是 互 異 的 整 數 , 求 證 : 12 ∣ (a-b)(a-c)(a-d)(b-c)(b-d)(c-d)」。 (三)任務 3:四次方和問題 表 2 四次方和問題 n n4 (n+1)4 (n+2)4 (n+3)4 n4 + (n+1)4 + (n+2)4 + (n+3)4 1 1 16 81 256 354 2 16 81 256 625 978 1.請完成上表,並觀察上表中 n4 + (n+1)4 + (n+2)4 + (n+3)4的總和。 2.由上表是否發現 n4 + (n+1)4 + (n+2)4 + (n+3)4的總和都不是某個自然數的四次 方。請用論證的方式處理下述問題:連續的四個自然數的四次方的和,可不 可能是另一個自然數的四次方?若你們認為可能,請舉例說明;若你們認為 不可能,請提出你的論證。 (四)任務 4:取數問題 請證明:從 1 至 200 的自然數中,任取 101 個數,則至少有二數,其中大 的數必是小的數的倍數。
四、研究對象
由於本研究旨在詮釋國中資優生的解題活動,以了解其問題解決思維,因 此在個案對象的選擇上,首要考量的尌是能提供整個課室情境及完整的小組探 究架構的資優班級,又研究者任教的班級札符合這樣的需求,故以此班級為研 究的對象。這個班級是由中部鄉鎮一所中型國中的 30 名國中一年級一般智能資 賦優異學生所組成,其中包含 19 位男生、11 位女生,一般智能資賦優異學生是 指符合特殊教育法第四條第一項第一款一般智能資賦優異的學生。其次,關於 個案的確立,有三個重點:(1)個案組成,每一個個案是由一組學生,對一個任 務的解題活動所構成。每組有學生三位或四位。(2)個案挑選原則,以解題表現 呈現較優且解題原案較完整者優先選取作為研究的個案,且個案以不重複解題 任務的類別為原則,即四類問題各選一題,而且該題的解題原案尌是取自根據 上述原則所挑選的個案。(3)個案的描述對象,因本研究聚焦在國中資優生的解 題思維,且在詮釋個案的解題活動時,為持續聚焦於模型的建構與發展。所以, 在描述個案解題活動時,是以個案中負責呈現該次任務的同學為主要詮釋對 象,而該組其餘同學的想法,通常會經由小組討論整合後,由該位同學代表加 以說明。五、研究者角色
本文的第一位作者為研究者,也是本研究進行教學之教師,更是本研究的研 究工具之一。其任教於國中資優班,擔任過六屆資優班的數學教師及導師,長期 進行探究導向的教學,並指導國中資優生參加數學科展與數學競賽,目前於某師 大科學教育研究所博士班進修。本研究的第二位研究者即協同研究者,是數學教 育教授,從事教改取向或基於建構主義的教學,和指導教師進行建構取向的教學 有十多年的研究與實務經驗,在本研究中,他作為指導與諮詢的角色。六、資料收集與分析
本研究透過錄音、錄影、課室觀察與晤談,收集五個主要資料來源:(1)小 組討論與呈現;(2)學生所撰寫的學習日誌;(3)教學現場摘記;(4)教學日誌;(5)任務導向的臨床晤談。其中,共收集該班級中的四組學生所撰寫的學習日誌 16 篇,教學現場摘記、教學日誌各 9 份(以兩節課為一單位),臨床晤談轉錄稿 9 份。針對上述資料,以下列三個步驟進行處理分析:(1)組合原始個案資料,即 將與解題活動相關的資料加以保留,例如解題的關鍵事件、學習日誌的反思等, 並予以組合。(2)建構個案記錄,將原始個案資料加以組織、分類、編輯,並透 過編碼使成為可供分析的資料,例如,當學生在解題時,如為初期建構的模型, 像是表格、性質、關係、代數式等,只能被用於建模循環的描述、操作,或有 時可以預測,研究者將根據在文獻探討中,Lesh 等人(2003)在模型發展系列所 提出的概念工具的想法,將其分類於 MEA 下;如由關聯初期的模型所建構的進 階模型,像是奇偶性質、同餘性、抽屜原理等,能被用於有效的描述、操作及 預測,研究者將其分類於 MEX 下;如為應用或擴展在 MEX 的模型,而產生的 進階模型,不只可以被用於有效的描述、操作及預測,而且可以被用於證實, 甚至推廣時,研究者將其分類於 MAA 下。(3)個案資料分析,即對每一個問題 抽出其解題活動的組型,將這些組型進行比對,以抽離出個案的概念類型(即模 型),接著,將建構後的概念類型以建模觀點進行歸納分析,以形成研究者所建 構的主張。最後,研究者再依據所形成的主張,進行厚實的描述,且藉由模型 建構發展的詮釋架構來詮釋,必要時附上原案或原案轉錄的資料及圖片,以作 成研究發現與結論。
肆、研究發現與討論
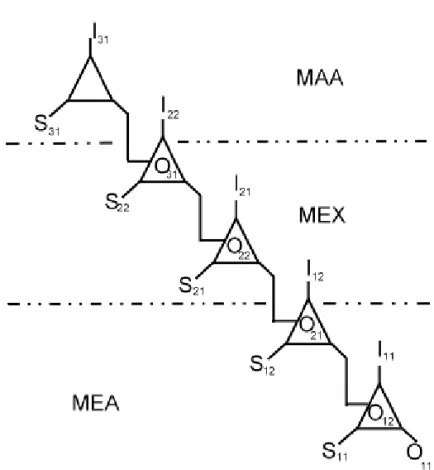
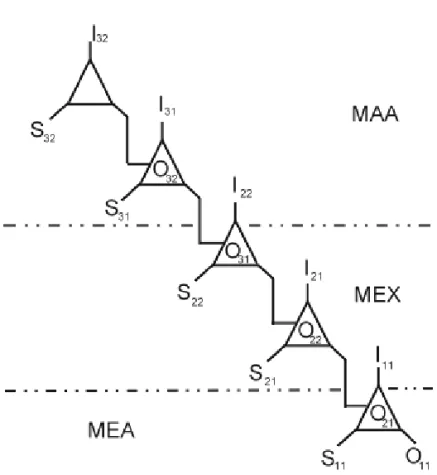
本研究發現資優生的一些解題思維歷程,將對四個個案分別加以詳述,同 時,有關這些個案中解題思維歷程的描述與討論,將先對解題活動脈絡作說明。 其次,再引入學生的解題原案來解釋其解題活動。最後,再以模型建構發展的 詮釋架構進行模型鏈結分析與詮釋。此外,本研究為了方便應用模型建構發展 的詮釋架構進行詮釋,使用了一些符號,以表示解題者的解題思維的三叉式記 號過程(如圖 6),其意義如下:圖 6 解題思維的三叉式記號過程(Kehle & Lester, 2003) 註:Oij, i=1, 2, 3 ; j=1, 2, 3, …, n
i=1 時,例如:O11:在 MEA 所建構的第一個模型;O12:在 MEA 所建構的第二個模型,
以下依此類推。
i=2 時,例如:O21:在 MEX 所建構的第一個模型;O22:在 MEX 所建構的第二個模型,
以下依此類推。
i=3 時,例如:O31:在 MAA 所建構的第一個模型;O32:在 MAA 所建構的第二個模型,
以下依此類推。 Sij:代表模型 Oij的符號。 Iij:代表模型 Oij的詮釋元。
一、詮釋資優生的數學解題活動
(一)個案一:翻杯問題 當教師提供任務 1(翻杯問題)的問題,並進行引導後,接著各組學生得面對 老師所提供的翻杯問題的挑戰,對於可用實物操作的問題,學生先一邊操作一 邊觀察。小貞所屬的小組,經過討論後,為了對翻杯問題的觀察能有所聚焦, 建構了合適的圖表,再進行討論,並進而找出圖表中所隱含的數的奇偶關係, 以進行預測,再進一步藉由推理完成論證。一開始,小貞的小組提出,當他們 列好表格時,我們也同時發現其中相關的地方。圖 7 小貞的學習日誌 1-940317 1. 模型引出活動(MEA)中的模型鏈結 小貞這一組操作過這些杯子後,先在紙上畫了表格及一些符號(如圖 7),最 左邊欄位上的數字代表第幾次翻動杯子的順序,第二欄的符號有札有負,札的 代表杯口朝上,負的代表杯口朝下,接著,他們又在右邊加上兩個欄位,以數 字代表在該次翻動後杯口朝上及杯口朝下的個數。其次,該組每次翻動 4 個杯 子的動作,是屬於無規律的隨意翻動。 在上述小貞所畫的表格中,如果最右的兩欄不看,即為一種『杯口朝上或 朝下表徵的形式』(I11),也是一種「杯口朝上朝下的模型」(O11),此模型用符號 來表徵問題中的杯子被翻動的情形,但尚未建立杯口朝上或朝下數量上的關 係。此時,該小組所觀察到的,尌只是杯口朝上或朝下的情形,對於進一步的 討論幫助較小,因此,小貞的小組在解題思維上,尌需重跑一圈的建模循環, 經過重新描述問題、操作及預測或轉化,即將表格的前兩欄與原問題連結,因 為解題所聚焦的是杯口朝上朝下的個數情形,所以該組討論後,再添加上最右 兩欄的數據,且該組學生由此數據發現『每次杯口朝上的皆為奇數個,杯口朝 下的皆為偶數個』(I12),因此,杯口朝上或朝下的奇偶關係尌可以被建立,因此 整個圖表尌可被操作與預測杯口朝上朝下的奇偶關係,所以此圖表尌是小貞那 一組所建立的一種「杯口朝上朝下的奇偶關係模型」(O12)。 此外,本研究為了便於進行詮釋,在此特別強調下列說明:首先,因為 O11 經過操作後,不能產生預測,更不能被用於證實此問題,所以解題者再經由重 新描述原問題及結合 O11而產生 O12,又 O12可以被操作並有可能產生預測,所 以本研究根據圖 1「四階段的建模循環」,接下來都將此由重新描述問題產生新
模型及對新模型進行操作或預測(或轉化)的歷程,稱為「重跑一圈的建模循環, 並重新描述問題、操作或(及)預測(或轉化)」。其次,又為說明由物件、符號及 詮釋元所構成的三叉式記號過程,在詮釋學生的解題時,用『』中的敘述來表 示此模型的詮釋元,且對被用於表示此模型的符號,將其意義列於描述該個案 的最後一段結語中。再者,「杯口朝上朝下的模型」O11是一種概念工具,其本 身及意義都是內隱的。所以,其需要詮釋元 I11來表達其內在意涵,即『杯口朝 上或朝下表徵的形式』,亦即 I11定義了 O11,另外,對於概念工具本身而言, O11也需要符號 S11來促進其在解題的脈絡中構成意義,亦即 O11是 S11的指示對 象。通常在解題過程中,大部分看到的是解題者使用符號在操作、轉化或證實, 似乎不易看到概念工具(即模型)或詮釋元,所以,對解題者的思維尌不易了解。 因此,透過三叉式記號過程(如圖 6),尌可以展現符號學三位一體的本質,即可 以促進對解題者數學思維的了解。 2. 模型探索活動(MEX)中的模型鏈結 小貞的小組所建立的「杯口朝上朝下的奇偶關係模型」(O12),在作預測時 可發生作用,然而在證明時,並不能有所作用,因此,尌需重跑一圈的建模循 環,經過重新描述問題、操作及轉化,發現需要奇偶性質來與題目的條件,一 次翻動 4 個杯子作結合,即發現『翻動的杯子數 4,可使杯口朝上朝下的數量維 持杯口朝上的數量為奇數,杯口朝下的數量為偶數』(I21),因此,小貞的小組建 立了「杯口朝上朝下的奇偶性與翻動的杯子數 4 的關係模型」(O21)。 3. 模型調整活動(MAA)中的模型鏈結: 雖然小貞的小組所建立的「杯口朝上朝下的奇偶性與翻動的杯子數 4 的關 係模型」(O21)能使預測杯口朝上或朝下的主張更具有說服力,但由於缺乏一種 論述,以確保每次的翻動的結果,皆如所預期的杯口朝上朝下的奇偶性,所以 還是不足以達成論證的要求,因此,小貞的小組尌重跑一圈的建模循環,經過 重新描述問題、操作及轉化,發現「分類討論的推理模型」(O22),接著,經過 討論,要完成論證,需重新整合,即需重跑一圈的建模循環,重新描述問題、 操作及轉化,發現在 MEX 所建立的「杯口朝上朝下的奇偶關係模型」(O12)與 翻動的杯子數 4 的關係模型(O21),並結合「分類討論的推理模型」(O22),可形 成「杯口朝上朝下的奇偶性與翻動的杯子數 4 的推理模型」(O31)如下: 小貞的小組提出,原有 7 個開口朝上的杯子,即 0 個開口朝下的杯子,因為 7 為奇 數,但每次翻動四個杯子(口朝上的翻為口朝下,口朝下的翻為口朝上),其變動的可 能情形只有五種(如圖 8)。(教學現場摘記 1-940317)
圖 8 小貞的學習日誌 2-940317 小貞的小組提出將翻動杯子的數量,所有可能的情形分為下列五種類型,即(1)恰好 翻動 4 個正,則得到 4 個負,增加偶數個開口朝下的杯子數;(2)恰好翻動 3 個正,1 個負,則得到 2 個負,即增加偶數個開口朝下的杯子數;(3)恰好翻動 2 個正,2 個 負,則得到 0 個負,因 0 為偶數,即變動偶數個開口朝下的杯子數,亦即不變;(4) 恰好翻動 1 個正,3 個負,則少了 2 個負,即減少偶數個開口朝下的杯子數;(5)恰 好翻動 4 個負,則少了 4 個負,即減少偶數個開口朝下的杯子數。(教學現場摘記 2-940317) 小貞的小組作了上述的分析,並配合「杯口朝上朝下的奇偶關係模型」 (O12),發現『這五種變動對於開口朝下的杯子數所造成的改變為:增加偶數個、 減少偶數個、不變』(I22)。因此,原來 0 個開口朝下的杯子數,因 0 為偶數,又 因偶數加偶數,或偶數減偶數,恆為偶數,故『開口朝下的杯子數恆為偶數, 所以小貞的小組認為在每次翻轉四個杯子的條件下,要得到 7 個開口朝下的杯 子數,是不可能的,因為 7 為奇數』(I31)。因此,小貞的小組經由「杯口朝上朝 下的奇偶性與翻動的杯子數 4 的推理模型」(O31),以支持其主張,並完成論證。
研究者:完成此問題的論證後,你們有何進一步的想法? 小貞:這樣的一個發現,我們知道老師為何設定 4 個杯子,不是 5,也不是 3。是因為這樣: 因為 4 為偶數, 奇+偶=奇,偶+偶=偶,此證實奇數(或偶數)+偶數,其奇偶性質不變。 奇-偶=奇,偶-偶=偶,此證實奇數(或偶數)-偶數,其奇偶性質不變。 (小貞的臨床晤談-940318) 小貞的小組進一步發現老師為何將題目中要翻動的杯子數設定為 4 個,而 不是 5 個或 3 個,是因為翻動 4 個杯子,會造成偶數個開口朝下的杯子數的改 變,上述小貞的分析,若觀察開口朝上的杯子數的改變,亦可發現會造成偶數 個開口朝上的杯子數的改變,又因為奇數加(減)偶數,恆為奇數,又偶數加(減) 偶數,恆為偶數,因此,小貞的小組認為開口朝上的杯子數恆為奇數,開口朝 下的杯子數恆為偶數,所以要得到 7 個開口朝下的杯子數,是不可能的,而這 個結果主要是由條件一次翻動 4 個杯子所產生的。因此,小貞那一組在論證時 進一步論述了條件翻轉「4」個杯子,與杯子總數「7」個,使得以歸納並擴展 其論證的結果如下: 小貞的小組針對上述的分類討論結果進一步提出,若將每次翻轉的杯子數,改為奇 數個(3 個或 5 個),要得到 7 個開口朝下的杯子數,是可以作得到的;若將杯子總數 改為 8 個、10 個……4 個以上的偶數個,每次翻轉的杯子數維持「4」個,要得到全 部的杯子皆開口朝下,也是可以作得到的。接著,小貞並實際用杯子操作,將上述 情形分別呈現出來,與同學分享其擴展此論證的結果。(教學現場摘記 3-940317)
圖 9 翻杯問題解題思維內涵的模型建構發展鏈結圖 關於圖 9,其意涵如下:首先,因為模型 O12是經由重新描述原問題及結合 O11所產生,根據 Kehle 和 Lester (2003)的主張,一個過去的記號過程例子(即 O11)可以變成新記號過程(即 O12)的物件(如圖 3),即模型 O11是模型 O12的物件, 所以在此將模型 O11由底層算起第一個三角形代表,又因為模型 O11是模型 O12 的物件,所以在第一個三角形中放入 O12,並將其置於第二個三角形的右下角(即 物件的位置),則第一個三角形與 O12合併成一體,即它既代表模型 O11也代表 模型 O12的物件。依此類推,第二個三角形代表模型 O12,而此三角形及其內的 O21合併成一體,連上第三個三角形的物件位置,而成為模型 O21的物件。類似 地,第三個三角形代表模型 O21,而此三角形及其內的 O22合併成一體,連上第 四個三角形的物件位置,而成為模型 O22 的物件,同樣地,第四個三角形代表 模型 O22,而此三角形及其內的 O31合併成一體,連上第五個三角形的物件位置, 而成為模型 O31的物件,因此第五個三角形即代表模型 O31,因模型發展至此,
已解決該問題,所以模型 O31 在該問題中尌不用成為別的模型的物件,所以第 五個三角形內沒有置入其他的模型。其次,因為模型 O11與模型 O12只能被用於 建模循環的描述、操作,或有時可以預測,根據 Lesh 等人(2003)在模型發展系 列所提出的概念工具的想法,將其分類於 MEA 下。又因為模型 O21與模型 O22, 能被用於有效的描述、操作及預測,故將其分類於 MEX 下。同時,因為模型 O31不只可以被用於有效的描述、操作及預測,而且可以被用於證實,甚至被用 於推廣,故將其分類於 MAA 下。基於上述說明,所以將這五個模型的關係, 及其在模型發展系列的階段,用五個鏈結的三角形及兩條區隔的虛線來表示, 而此虛線表示在 MEA 的模型可以往上發展為 MEX 的模型,同樣地,在 MEX 的模型可以往上發展為 MAA 的模型,因此,整個圖形尌被用來表達解題者的 解題思維內涵,即此圖形構成翻杯問題解題思維內涵的模型建構發展鏈結圖。 接下來,本研究都將此種由模型轉變成新模型的一系列關係,用此鏈結圖來表 示。 由模型建構發展詮釋架構及上述三個活動的模型鏈結分析,可以發現在此 問題解決歷程中,由模型、符號與詮釋元所構成的三叉式記號過程,是藉由推 理來鏈結彼此之間的關係,又此關係為對翻杯問題的解題活動進行建模觀點的 詮釋,所以逐漸建構為翻杯問題解題思維內涵的模型建構發展鏈結圖(如圖 9), 其中 S11:小貞所畫的表格的第一欄與第二欄;S12:小貞所畫的表格;S21:小 貞所畫的表格與翻動的杯子數 4;S22:分類討論推理法;S31:小貞所畫的表格、 翻動的杯子數 4 與分類討論推理法。 (二)個案二:整除問題 當小哲的小組在進行任務 2(整除問題)的解題時,經過討論後,由於欲證的 問題較為複雜,因此發展出將問題的目標作適度轉換的策略,即將原問題變為 兩個複雜度較小一點的問題,再進行推理,並完成論證。 研究者:對於這個問題,你們是如做推論的? 小哲:剛拿到題目時,一時不知該從何著手,而後想到,能被 12 整除,即為能被 12 的因數 整除,但是出現了問題……既然是被 12 的因數整除,那應該是哪二個因數呢?很快 的我們便想到應該是 3 或 4。 研究者:接下來,你們怎麼做? 小哲:我們便以 3 和 4 來做推論,發現了 4=2×2 而 3 是一個奇數。而後,我們也用了老師最 近介紹過的抽屜原理來解題,將這四個數明顯而清楚的方式分類出來,我們是以它們
的餘數作分類,而只要是在同一個抽屜中,他們互減即一定為我們需要的因數。而推 得了以上論證的結果,但在論證的其中,我們又發現了另一個問題。 (小哲的臨床晤談 1-940415) 1. 模型引出活動(MEA)中的模型鏈結: 小哲的小組提出,為了簡化該問題,使用了因數乘積整除性質「當 3∣m 且 4∣m, 則 12∣m」來轉換此問題,即『要證明 12∣(a-b)(a-c)(a-d)(b-c)(b-d)(c-d),只要先證 明 3∣(a-b)(a-c)(a-d)(b-c)(b-d)(c-d),再證明 4∣(a-b)(a-c)(a-d)(b-c)(b-d)(c-d),就可以 完成論證』(I11)。(教學現場摘記 1-940415) 因為小哲的小組在上列 I11所提出的性質可以將原問題簡化,所以尌成為該 小組所建立的一種「因數乘積整除模型」(O11)。 2. 模型探索活動(MEX)中的模型鏈結: 為了證明 3∣(a-b)(a-c)(a-d)(b-c)(b-d)(c-d),且 4∣(a-b)(a-c)(a-d)(b-c)(b-d) (c-d),小哲的小組經過討論後,重跑一圈的建模循環,重新描述問題,並聚焦 於『四個數 a、b、c、d 對於除數分別為 3、4 的同餘性』(I21),此「同餘性」即 為模型(O21),此模型經過操作與轉化後,並未能解決問題,因此,小哲的小組 再重跑一圈的建模循環,經過重新描述問題、操作及轉化後,發現需引用抽屜 原理來解題。 首先,證明 3∣(a-b)(a-c)(a-d)(b-c)(b-d)(c-d),即考慮『當 4 個數 a、b、c、d 要放入 3 個抽屜(除數為 3,餘數分別為 0、1、2)時,則此 4 個數至少有兩個會放入同一個抽 屜中,即此 4 個數至少有兩個會對除數 3 同餘』(I22),則可推得(a-b)、(a-c)、(a-d)、 (b-c)、(b-d)、(c-d)六個數中,至少有一個數,其括號內的兩個數會對除數 3 同餘, 所以此兩數的差必可被 3 整除,即此括號所代表的數必可被 3 整除,即可推得 3∣(a-b)(a-c)(a-d)(b-c)(b-d)(c-d)。(教學現場摘記 2-940415) 因為小哲的小組在上述 I22所提出同餘性與抽屜原理的結合,可解決 3∣(a-b) (a-c)(a-d)(b-c)(b-d)(c-d)的問題,所以尌成為小哲那一組所建立的「同餘性與抽屜 原理推理模型」(O22)。 研究者:發現了什麼問題? 小哲:在處理 3 的問題中,由於 3 個抽屜中有 4 個數,所以一定會有一個抽屜中至少有 2 個 數。但是 4 這個因數的餘數有 4 個,也有 4 個抽屜,所以若均不同餘呢?
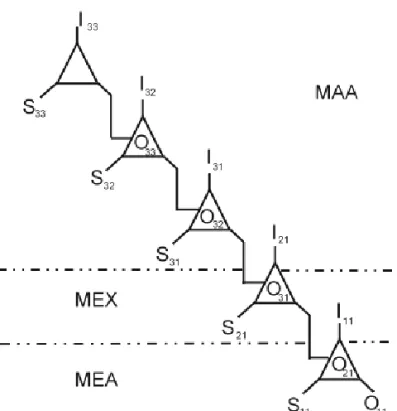
小哲:4 個數均不同餘,但是如果是這樣的話,這 4 個數 a、b、c、d 必定為 2 個奇數 2 個偶 數。 研究者:此種情形,對你們有何幫助? 小哲:相減之後就會出現 2 組 2 的倍數,而 2×2=4,所以這個問題就解決了!經過重重的問 題與解答,我們便把 3 和 4(也就是 12 的因數,但必需互乘為 12)解出來,而也推得了 我們要的證明:12∣(a-b)(a-c)(a-d)(b-c)(b-d)(c-d) (小哲的臨床晤談 2-940415) 3. 模型調整活動(MAA)中的模型鏈結: 小哲使用同餘性與抽屜原理模型(O22)模型在解問題時,發現此模型能解決 置入物的數量比抽屜數量多的情形,即可以處理 4 個數 a、b、c、d 要放入 3 個 抽屜(除數為 3,餘數分別為 0、1、2)的問題,但後來又發現置入物的數量若與 抽屜數量相等的情形,即 4 個數 a、b、c、d 要放入 4 個抽屜(餘數分別為 0、1、 2、3)的問題,此時在證明時尌會出現問題,即當 4 個數 a、b、c、d,對於除數 為 4 皆不同餘時,則(a-b)、(a-c)、(a-d)、(b-c)、(b-d)、(c-d)六個數都不會有 4 的因數,因此,尌不能證出 4∣(a-b)(a-c)(a-d)(b-c)(b-d)(c-d),即需重跑一圈的建 模循環,並經過重新描述問題,發現『若 4 個數 a、b、c、d 對於除數為 4 皆不 同餘時,根據奇偶性,則此四個數必為兩奇兩偶』(I31),此奇偶性即為模型(O31), 此時,經過操作與轉化,並未能完成論證,因此,小哲的小組又重跑一圈的建 模循環,經過重新描述問題、操作及轉化,發現『由 I31,可推知(a-b)、(a-c)、 (a-d) 、 (b-c) 、 (b-d) 、 (c-d) 六 個 數 中 , 必 有 兩 個 是 2 的 倍 數 , 所 以 4 ∣ (a-b)(a-c)(a-d)(b-c)(b-d)(c-d)』(I32),因此,小哲這一組經由建立「奇偶性、同餘 性與抽屜原理推理模型」(O32) ,完成此整除問題的論證。
圖 10 整除問題解題思維內涵的模型建構發展鏈結圖 類似地,由模型建構發展詮釋架構及上述三個活動的模型鏈結分析,可以 發現在此解題的歷程中,三叉式記號過程是藉由推理鏈結彼此之間的關係,又 此關係為對整除問題的解題活動進行建模觀點的詮釋,所以逐漸建構為整除問 題解題思維內涵的模型建構發展鏈結圖(如圖 10),其中 S11:當 3∣m 且 4∣m, 則 12∣m;S21:同餘性;S22:同餘性與抽屜原理;S31:奇偶性;S32:奇偶性、 同餘性與抽屜原理。 (三)個案三:四次方和問題 當小熊的小組在進行任務 3(四次方和問題)的解題時,由於發現問題是與先 前已知性質有關,因此採用合適表徵的解題策略,並與已知性質作進一步的連 結,進而完成論證。
研究者:對於這個問題,你們是如做推論的? 小熊::因為要成為某數平方嘛,才能除以 4 餘 0 或餘 1,不過某數 4 次方很容易變成某數的 二次方,因為它可以拆成某數的二次方再二次方,我們就可以把某數的二次方看成 y, 也就是等於某一個平方數了,所以它除以 4 也必定等於 0 或餘 1。 研究者:接著,你們是怎麼做的? 小熊:我們的算法是這樣子的,既然我們知道它是平方數的演變,就可以除以 4 餘 0 或餘 1, 不過因為奇數一定餘 1 偶數一定餘 0,所以我們是這樣開始的,1010 餘數都是 1、0 因為它們的奇數就是一定會餘 1,而且又是由奇數開始的,所以一定是 1010,排到最 後就會變成這樣了。 研究者:排成這樣,對你們有何幫助? 小熊::我們發現說,如果你連續 4 個數,必定是 0101 或 1010 這些餘數加起來的,所以加起 來很明顯就可以看出它加起來的數只有餘 2,那麼我們最需要的就是除以 4,因為任 何某數的四次方一定是平方數,所以它加起來餘數是 2,就絕對不可能是平方數,因 為平方數要餘 0 或餘 1 才行,然後就可以知道證明其結果是不成立的。 (小熊的臨床晤談 940513) 1. 模型引出活動(MEA)中的模型鏈結:小熊的小組在解題的探究過程中,藉由 不斷的嘗詴描述,先找到下列關係: 小熊的小組提出,某數的四次方可以轉換成某數的平方,即『將 n4、(n+1)4、(n+2)4、 (n+3)4分別看成某數的平方,且結論要判斷 n4 + (n+1)4 +(n+2)4 + (n+3)4的和是否為某 數的四次方,亦可轉換為判斷此和是否為某數的平方』(I11)。(教學現場摘記 1-940513) 因為小熊的小組在上述 I11所提出的帄方轉換可將原問題簡化,所以尌成為 小熊小組所建立的一種「帄方轉換模型」(O11)。 2. 模型探索活動(MEX)中的模型鏈結:小熊的小組在討論中,經過重跑一圈的 建模循環,重新描述問題、操作及轉化,又進一步引入了性質: 小熊的小組提出,平方數除以 4,必定餘 0 或餘 1,即奇數的平方數被 4 除,一定餘 1,偶數的平方數被 4 除,一定餘 0,因此,針對 n4、(n+1)4、(n+2)4、(n+3)4被 4 除 的餘數,再提出『若要對原問題提出否定的答案,只要藉由判斷此四個餘數的總和 不是為 0 或 1,就可完成論證』(I21)。(教學現場摘記 2-940513) 因為小熊的小組在上述 I21所提出的性質可使原問題的論證目標更明確,所
以此性質與「帄方轉換模型」的結合,尌構成了一個「帄方轉換與帄方數餘數 模型」(O21)。 3. 模型調整活動(MAA)中的模型鏈結:小熊的小組為判斷 n4、(n+1)4、(n+2)4、 (n+3)4被 4 除的餘數,再經過重跑一圈的建模循環,重新描述問題,引入了「奇 偶乘積及連續數的奇偶性模型」(O31)如下: 小熊的小組提出,『偶數與偶數的乘積必為偶數,奇數與奇數乘積必為奇數,且四個 連續數 n、(n+1)、(n+2)、(n+3)必為兩奇兩偶』(I31),所以可推得平方數 n2、(n+1)2、 (n+2)2、(n+3)2亦為兩奇兩偶,進一步可推得 n4、(n+1)4、(n+2)4、(n+3)4亦為兩奇兩 偶,因此,可將 n4、(n+1)4、(n+2)4、(n+3)4分別視為奇數的平方、偶數的平方、奇 數的平方、偶數的平方,或偶數的平方、奇數的平方、偶數的平方、奇數的平方。(教 學現場摘記 3-940513) 接著,小熊的小組對於 O31 進行操作與轉化,但並未能完成論證,因此, 經過重跑一圈的建模循環,重新描述問題後,由結合「帄方轉換與帄方數餘數 模型」(O21),即奇數的帄方數被 4 除,一定餘 1,偶數的帄方數被 4 除,一定 餘 0,發現『n4、(n+1)4、(n+2)4、(n+3)4被 4 除的餘數,其餘數出現的樣式為 1010 或 0101』(I32),此餘數出現的樣式即為模型(O32)。但是,此模型經過操作及轉 化後,還是未能完成論證,因此,小熊的小組又經過重跑一圈的建模循環,重 新描述問題、操作及轉化,發現根據「餘數和模型」(O33),可推論出『n4 + (n+1)4 + (n+2)4 + (n+3)4的和被四除的餘數必為 1、0、1、0 或 0、1、0、1 的和,1+0+1+0 或 0+1+0+1』(I33),亦即為 2,不是 0 或 1,接著,再配合「帄方轉換與帄方數 餘數模型」(O21),帄方數被 4 除的餘數是 0 或 1,最後推論出,n4 + (n+1)4 + (n+2)4 + (n+3)4的和絕對不可能是帄方數,亦不可能是某自然數的四次方。
圖 11 四次方和問題解題思維內涵的模型建構發展鏈結圖 類似地,由模型建構發展詮釋架構及上述三個活動的模型鏈結分析,可以 發現在此解題的歷程中,三叉式記號過程是藉由推理鏈結彼此之間的關係,又 此關係為對四次方和問題的解題活動進行建模觀點的詮釋,所以逐漸建構為四 次方和問題解題思維內涵的模型建構發展鏈結圖(如圖 11),其中 S11:n2=y;S21: 帄方數除以 4,必定餘 0 或餘 1;S31:奇偶乘積及連續數的奇偶性;S32:1010 或 0101;S33:1+0+1+0 或 0+1+0+1。 (四)個案四:取數問題 當小方的小組在進行任務 4(取數問題)的解題時,由於碰到較複雜的情況, 因此先考慮將問題簡化,當簡化後的問題的模型找到後,再將此模型應用到原 問題的解決,並進而完成論證。 剛開始,我們把這個大問題轉化為小問題,就像「巨人變侏儒」,我們把它變成 1 至 10 中任取六個數,其中有 2 數,大的數必是小的倍數,這就較好解決了。為了不讓 它們互相排斥,而大的數為小的數的倍數,我們分了 5 個抽屜:
(1)[1,2,4,8] 2 為 1×2,4 為 1×22(2×2), 8 為 1×23(4×2),這樣符合大數為小數的倍數。 (2)[3,6] 6 為 3 的倍數,此抽屜若要放 9 也可以,但因 9 不是 6 的倍數,所以我 們盡量不把它們放入同個抽屜。 (3)[5,10] 10 為 5 的倍數,符合我們要的:大數為小數的倍數。 (4)[7] 因 7 的倍數為 14,已超過 10 了,所以此抽屜只放 7。 (5)[9] 因 9 的倍數為 18,已超過 10, So 此抽屜只放 9。 接著,我們找最糟的狀況,在找最糟狀況之前,我們先討論:如果這抽屜的 6 個數 都在(1)、(2)、(3)的抽屜中,那必定會有一組以上大數是小數的倍數,所以要找最糟 狀況,須把(4)和(5)的抽屜放進去討論。(4)和(5)的抽屜中只有 7 和 9 兩數,6-2=4, So 剩下 4 數必落在(1)和(2)和(3)的抽屜中,那必有一數是另一數的倍數,所以這個 小問題就解決了!(小方的學習日誌 1-940609) 1. 模型引出活動(MEA)中的模型鏈結:小方的小組經由討論,發現「對應縮小 方法模型」(O11),即把「101 為 200 的一半加 1」,改為「6 為 10 的一半加 1」, 亦即把『大問題(1 至 200 中任取 101 個數,其中有 2 數,大的數必是小的數 的倍數)變為小問題(1 至 10 中任取 6 個數,其中有 2 數,大的數必是小的數 的倍數)』(I11),此時,小方的小組針對此小問題,經過討論如何構造抽屜, 即重跑一圈的建模循環,重新描述問題、操作及轉化後,發現要構造五個抽 屜,可採用「奇數分類法模型」(O12),但經過討論關於抽屜內的數不能互相 排斥的問題,即要符合大數是小數的倍數關係,故再重跑一圈的建模循環, 重新描述、操作與轉化,發現可與逐項加倍分類方法結合,構成小問題的抽 屜如下: 小方的小組提出,如何將 10 個數放入五個抽屜中,並符合抽屜中任何兩個數,其中 大數必是小數的倍數的關係,其作法即『由第一個抽屜至第五個抽屜,按照抽屜的 順序,將由 1 開始的奇數,逐次放入每個抽屜中,作為每個抽屜的第一個數』(I12), 接著『每個抽屜的第二個數,是由第一個數乘以 2 再填入,第三個數,是由第二個 數乘以 2 再填入,依此類推,當某一抽屜其填入的數超過 10,就停止填入』(I13)。(教 學現場摘記 1-940609) 因此,小方的小組尌構造出五個抽屜,此五個抽屜即為「小問題的抽屜模 型」(O13)。
2. 模型探索活動(MEX)中的模型鏈結:小方的小組為進一步處理如何抽 6 個數, 因此,再重跑一圈的建模循環,重新描述、操作與轉化,發現可將「小問題 抽屜模型」(O13)結合「抽屜原理模型」(O21)來處理此問題,此 O21即『六個 數抽自五個抽屜中,則此六數中至少有二數會抽自同一個抽屜中』(I21),但此 時並未能處理「任意」抽取 6 個數的問題,因此,小方經過與小組同學進行 討論,即重跑一圈的建模循環,重新描述後,發現「極端分配法模型」(O22) 如下: 小方的小組提出,『當考慮到就算是最糟的情況下,其中兩個數是由只放一個數的抽 屜(4)、(5)中抽取,可推知其餘四個數必抽自抽屜(1)、(2)、(3)中』(I22),而這三個抽 屜的每個抽屜,都至少包含兩個數,且每個數都符合大數是小數的倍數,根據抽屜 原理模型(O21),即此四數中至少有二數會抽自同一個抽屜中,因此,由同一抽屜中 所抽出的這兩個數,必滿足大數是小數的倍數,如此,就符合 1 至 10 中任取 6 個數, 其中必有 2 數,大數是小數的倍數,所以「小問題」的命題成立。(教學現場摘記 2-940609) 因此,小方的小組藉由操作與轉化,順利達成「小問題」的論證。 我們將這個小問題放入原題目討論 第一個抽屜為 [1,2,4,8,16,32,64,128] → 這樣大數必是小數的倍數 第二個抽屜為 [3,6,12,24,48,96,192] → 符合需求 第三個抽屜為 [5,10,20,40,80,160] → 符合需求 …… 依此類推 …… 到第 50 個抽屜為 [99,198] → 符合 所以每個抽屜有 2 個以上的數,我們就製造完成了。 接著,我們討論 1 個抽屜 1 個數的: 第 1 個抽屜為[101] 若 101×2=202 (超過 200 了) 第 2 個抽屜為[103] …… 依此類推 …… 第 50 個抽屜為[199] 因 200 內最大奇數為 199
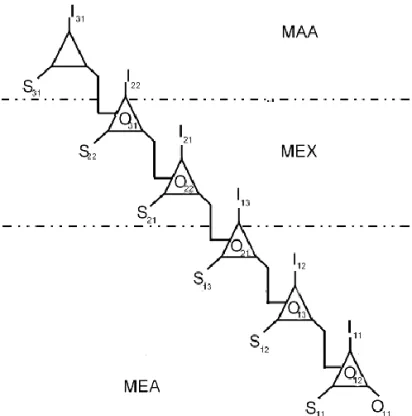
最後,我們把前面 1 個抽屜 1 個數的加上 1 個抽屜 2 個數以上的,共 100 個, 所以我們也是取最壞情況: 我們抽的 101 個數中,有 50 個數為 1 個抽屜 1 個數的, 那 101-50=51 (最後還須抽 51 個) 因 1 抽屜 2 個數以上的有 50 個抽屜,所以抽 51 個數,必會有一組數是大數是小數 的倍數。 ∴得證 (小方的學習日誌 2-940609) 3. 模型調整活動(MAA)中的模型鏈結:小方的小組為了處理「大問題」,經過 小組同學進行討論,即重跑一圈的建模循環,重新描述、操作與轉化,發現 可仿照「奇數分類法模型」(O12)、「小問題的抽屜模型」(O13)構造抽屜的方 法,構造出 100 個抽屜,作為「大問題的抽屜模型」(O31),即『此 100 個抽 屜,每個抽屜內的數,皆依照 I12與 I13的分類方法擺放』(I31),再結合「抽屜 原理模型」(O21),進行討論,並引用其「極端分配法模型」(O22),即當考慮 到尌算是最糟的情況下,其中五十個數是由只放一個數的後五十個抽屜中抽 取,可推知其餘五十一個數必抽自前五十個抽屜中,而前五十個抽屜的每個 抽屜,都至少包含兩個數,且每個數都符合大數是小數的倍數,因此,根據 「抽屜原理模型」(O21),即此五十一個數中至少有二數會抽自同一個抽屜中, 因此,由同一抽屜中所抽出的這兩個數,必滿足大數是小數的倍數,如此, 尌符合 1 至 200 中任取 101 個數,其中有 2 數,大數是小數的倍數,所以大 問題的命題成立。
圖 12 取數問題解題思維內涵的模型建構發展鏈結圖 類似地,由模型建構發展詮釋架構及上述三個活動的模型鏈結分析,可以 發現在此解題的歷程中,三叉式記號過程是藉由推理鏈結彼此之間的關係,又 此關係為對取數問題的解題活動進行建模觀點的詮釋,所以逐漸建構為取數問 題解題思維內涵的模型建構發展鏈結圖(如圖 12),其中 S11:對應縮小方法;S12: 奇數分類法;S13:小問題的抽屜;S21:抽屜原理;S22:極端分配法;S31:大 問題的抽屜。
二、小結
以建模觀點在詮釋四個個案國中資優生的解題活動時,發現學生在進行數 學化的歷程中,其展現的數學思維特徵,可歸納如表 3:表 3 國中資優生數學思維特徵的五個面向的統合表 類比推論 數學結構 表徵 視覺化推理 逆向思維 翻杯問題 ˇ ˇ ˇ ˇ ˇ 整除問題 ˇ ˇ ˇ ˇ 四次方和問題 ˇ ˇ ˇ ˇ 取數問題 ˇ ˇ ˇ ˇ ˇ 從上述解題的詮釋文本中的模型建構發展鏈結圖及表格等,可以觀察到學 生所展現的數學結構、表徵及視覺化推理等三個面向的數學思維特徵。因此, 研究者擬僅針對類比推論及逆向思維兩個面向的數學思維特徵舉例加以說明。 首先,尌類比推論這個面向的數學思維特徵而言:(1)在翻杯問題中,對於翻轉 「4」個杯子,與杯子總數「7」個的推論方法,經由類比推論得到,翻轉「3」 個杯子,與杯子總數「7」個的推論方法;(2)在整除問題中,對於四個數 a、b、 c、d 對於除數為 3 的同餘性的推論方法,經由類比推論得到,四個數 a、b、c、 d 對於除數為 4 的同餘性的推論方法;(3)在四次方和問題中,對於 n4、(n+1)4、 (n+2)4、(n+3)4被 4 除的餘數,當 n 為奇數,則其餘數出現的樣式為 1010,經由 類比推論得到,當 n 為偶數,則其餘數出現的樣式為 0101;(4)在取數問題中, 對於「1 至 10 中任取 6 個數,其中有 2 數,大的數必是小的數的倍數」的推論 方法,經由類比推論得到,「1 至 200 中任取 101 個數,其中有 2 數,大的數必 是小的數的倍數」的推論方法。其次,尌逆向思維這個面向的數學思維特徵而 言:(1)在翻杯問題中,考慮結果是要得到 7 個開口朝下的杯子數,但 0+偶= 偶,即開口朝下的杯子數恆為偶數,而 7 是奇數,所以可推知這是不可能的; (2)在整除問題中,對於「四個數 a、b、c、d 對於除數為 4 的同餘性」,當考慮 「4 個數均不同餘呢」,此即為逆向思維的表現;(3)在四次方和問題中,考慮 「n4 + (n+1)4 + (n+2)4 + (n+3)4的和的結果」,若此結果要是某數的四次方,則 此數被 4 除的餘數,不是 0 尌是 1;(4)在取數問題中,考慮「最壞的情況」, 即抽的 101 個數中,有 50 個數是由只放一個數的抽屜中抽取時。 此外,從建模觀點,發現四個個案的國中資優生在進行數學解題時,其所 建構的模型,與所經歷的模型發展系列與建模循環次數,可由統整第一節的內 容,而得到表 4:
表 4 模型數量、模型發展系列與建模循環次數統合表
MEA MEX MAA 建模循環
次數 O11 O12 O13 O21 O22 O23 O31 O32 O33 翻杯問題 ˇ ˇ ˇ ˇ ˇ 5 整除問題 ˇ ˇ ˇ ˇ ˇ 5 四次方和問題 ˇ ˇ ˇ ˇ ˇ 5 取數問題 ˇ ˇ ˇ ˇ ˇ ˇ 6 從表 4 中所列,可發現:(1)每建構一個模型,尌經歷一次建模循環;(2)在 每個問題的模型發展系列三個階段 MEA、MEX 與 MAA 中,其所建構模型數 量,是有差異的,且是依解題者所經歷的建模循環次數而定,其原因是,假如 解題者所建構的模型不能進行有效的操作、轉化或預測、證實時,尌頇重跑一 次建模循環,藉由重新描述,或與先前所建構的模型整合進行更進一步的描述, 以建構模型;(3)不同的問題,有不同的模型建構與模型發展系列;相同的問題, 可能有不同的模型建構,與模型發展系列;(4)所建構的模型數量的多寡,不是 代表題目的難易,而是代表不同解題者企圖貼近問題,所經歷的建模循環次數 的差異。
伍、結論與建議
研究者以建模循環及模型發展系列的三個主要活動為研究取徑,並用模型 建構發展的詮釋架構來詮釋國中資優生進行的解題活動,根據四個個案的研究 結果,先說明國中資優生的解題思維內涵,再說明國中資優生解題的數學思維 特徵,接著說明模型、建模循環與模型發展系列的關係與蘊涵,最後再提出建 議。一、國中資優生的數學解題活動是一種建模思維取向的歷程,
而不是描述式或規範式的歷程
對於上述四個個案的數學解題活動的詮釋,本研究發現:(1)資優生的解題 思維歷程,是屬於建模的思維歷程,而不是 Pólya 的描述式歷程或 Schoenfeld 的規範式歷程(Lesh & Zawojewski, 2007)。(2)這四個解題活動的問題,其實跟 Lesh 與 Doerr (2003)以生活周遭問題為主的例子不太一樣,即使不一樣,資優生 還是顯現了建模的特性在解題,亦即資優生即使在解非生活化的問題時,還是 呈現這樣的建模歷程。