國
立
交
通
大
學
理學院網路學習學程
碩
士
論
文
以 格 子 謎 題 遊 戲 式 輔 助 小 學 數 學
技 巧 熟 練 之 數 位 學 習 設 計 與 實 作
Design and Implementation of Block Puzzle Digital Game
for Arithmetic Practice
研 究 生:黃憲銘
指導教授:陳德懷 教授
周 倩 教授
以格子謎題遊戲式輔助小學數學技巧熟練之數位學習設計與實作
Design and Implementation of Block Puzzle Digital Game
for Arithmetic Practice
研 究 生:黃憲銘 Student:Hsien-Ming Huang
指導教授:陳德懷 Advisor:Tak-Wai Chan, Ph.D.
周 倩 Chien Chou, Ph.D.
國 立 交 通 大 學
理學院 網路學習 學程
碩 士 論 文
A ThesisSubmitted to Degree Program of E-Learning College of Science
National Chiao Tung University in partial Fulfillment of the Requirements
for the Degree of Master
in
Degree Program of E-Learning June 2006
Hsinchu, Taiwan, Republic of China
以格子謎題遊戲式輔助小學數學技巧熟練
之數位學習設計與實作
學生:黃憲銘 指導教授:陳德懷教授
周 倩教授
國立交通大學理學院網路學習學程碩士班
中文摘要
數位遊戲已經成為最受許多學童歡迎的文化之一,許多教育研究者認為:將 數位遊戲當成教學工具,對學生的學習成效、認知發展能力、學習動機與學習專 注力有正向提升的影響力。 本研究旨在設計及實作一個輔助技巧熟練的格子謎題遊戲(BPDG)。對大多數 的小學學童而言,分數課程是國小數學課程中感到最困難的一部分,如果對分數 不夠理解或熟練,會阻礙學生未來的數學發展。本論文即以「國小數學分數加減 法」為學習內容,設計一個數位遊戲,讓學生在一對一數位學習環境下,觀察學 生是否可以利用這個輔助技巧熟練的遊戲來提高學童們的學習動機與興趣。 為了評估這個遊戲設計及系統設計的可用性,以及觀察 BPDG 對學生學習動 機與興趣的影響,以 30 名的國小六年級學生參加實驗與觀察對象。從實驗結果 可以發現 BPDG 對學生在分數加減法上的專注力、自信心、學習興趣、學習動機 等都有正向的提升。 關鍵字:數位遊戲、遊戲式學習、學習動機、技巧熟練Design and Implementation of Block Puzzle Digital Game
for Arithmetic Practice
Student : Hsien-Ming Huang Advisor:Tak-Wai Chan
Chien Chou
Degree Program of E-Learning
National Chiao Tung University
ABSTRACT
Digital games have become one of the most popular cultures among school children. If digital games are used as instructional tools, as many educational researchers argue, there will be positive effects on the increase of students’ learning achievement, cognitive development, learning motivation, and concentration.
The main objective of this research is to design and implement a block puzzle digital game (BPDG) to enhance students’ fraction skills. For most of the
elementary school children, learning fraction could be one of the most challenging and frustrating parts in their math curriculum. Failure to learn fraction could even lead to the hindrance of students’ latter mathematics development. This thesis will be focused on the design and implementation of a digital game, addition and
subtraction of fraction, in which students can be observed, under 1:1 digital computing environment, to test whether this game-based skill building could raise students’ motivation and interest in learning.
To evaluate the game design as well as the usability of the system design, and to explore the effects of BPDG on students’ motivation and interest, 30 grade 6 students were invited to participate in an evaluation study. The result shows that the level of students’ concentration, confidence, interest, and motivation toward learning addition and subtraction of fraction has been significantly augmented through the use of BPDG.
Keyword : digital game, game-based learning, motivation toward learning, skill
誌 謝
感謝上帝,「只管坦然無懼的來到施恩的寶座前,為要得憐恤,蒙恩惠,作 隨時的幫助」,照著祢的應許,祢給我成全了。 感謝指導我的陳德懷教授,在研究過程中給予我許多關鍵性的指導與建議, 使我獲益良多。 感謝協同指導的周倩教授,在研究期間給予我信心,並在論文的寫作上給我 很多的指導。 感謝柯華葳教授及莊祚敏教授在百忙之中指導與審查論文,並對我的研究提 出了很多寶貴的建議與看法,讓本篇論文可以更加完整。 感謝林秋斌教授給我研究架構及論文簡報的指導,讓我能很快地抓住重點。 感謝衍華學長,在整個的研究裡不厭其煩的指導我,犧牲了自己寶貴的時 間,陪伴我一路走來,給了我最完整的幫助與研究的概念,讓我的獲益也最深。 感謝松濱學長的指導,為我的研究奠定基礎,也在實驗設備上給予我很大的 支援。 感謝學弟柏毅,在實驗過程中協助我架設實驗設備,並在程式開發上與我一 起討論並給我協助,成為我的好幫手。也感謝我的學生韋亨,在程式開發上給我 很好的架構基礎。 感謝教會的楊傳道、弟兄姊妹以及生命小組的成員,在我研究低潮時為我禱 告,讓我能有信心,繼續完成論文,也特別感謝他們分擔了教會及小組的服事。 感謝我服務學校的張碧娟校長、敏芬主任,以及關心我的同仁春吟、鼎國、 瑞鴻、康盟、宏茂…等,能包容我因研究而影響工作,進而給我鼓勵打氣,能有 你們這樣的工作伙伴,實在是人生一大幸福。 感謝桃園縣觀音國小的東宏老師,在實驗期間給予我極大的協助,並且和我 一同探討學生的實驗數據,讓我可以更清楚實驗的結果,還有這一群可愛的學 生,我不會忘記你(妳)們的。 感謝我的父母,給我很大的鼓勵與照顧,並且不時地給我打氣加油。 感謝我的岳父母,關懷我的進度,也給予我很好的建議。 感謝杜娟,引薦我進入觀音國小,得以順利完成實驗。 最後我特別要感謝我的妻子惠娟,這幾年來無怨無悔地照顧家庭及三個孩 子,讓我在毫無後顧之憂地準備我的研究論文;甚至在我一度想放棄時,妳給我 最深的支持與激勵。我要對妳說:「我回來了,從今以後,我不再離開妳及我們 的孩子了。」 我也要對我的三個孩子說:「孩子們,爸爸回來了,從今以後,在你們成長 的道路上,爸爸都不再缺席了!」 黃憲銘 謹於 國立交通大學 中 華 民 國 九 十 五 年 六 月目 錄
中文摘要... I 英文摘要... II 誌 謝...III 目 錄...IV 表 目 錄... VII 圖 目 錄...VIII 第一章 緒論 ...1 1.1 研究背景...1 1.2 研究動機...3 1.3 研究問題...4 1.4 研究目的...4 第二章 文獻探討 ...5 2.1 遊戲教學法...5 2.2 遊戲式的學習...7 2.3 數位遊戲設計...10 2.4 格子謎題遊戲設計理念...13 第三章 系統設計 ...15 3.1 遊戲流程...16 3.2 學習內容設計...16 3.2.1 學習內容等級設計...18 3.2.2 作答區設計...19 3.3 遊戲規則與介面...21 3.3.1 故事與敘述...21 3.3.2 核心機制...21 3.3.3 互動性...23 3.4 遊戲模式...27 3.5 系統架構與規格...30 3.6 系統功能...33 3.6.1 遊戲...33 3.6.2 出題系統與題目驗證...33 3.6.3 答題回饋訊息...34 3.6.4 答題歷程記錄...38 第四章 實驗設計 ...43 4.1 實驗目的...43 4.2 實驗對象與環境...44 4.3 實驗設計...454.4 實驗限制...46 4.5 實驗結果...47 4.5.1 前、後測成績...47 4.5.2 學生答題歷程資料庫...48 4.5.3 學生問卷...49 4.5.4 實驗後學生訪談...61 4.5.5 教師訪談...63 4.5.6 實驗過程記錄...64 第五章 實驗結果討論 ...65 5.1 整體性資料分析...65 5.1.1 前、後測成績比較...65 5.1.2 問卷分析...67 5.1.3 學生訪談...69 5.2 個別受驗者資料分析...70 5.2.1 學生答題概況...71 5.2.2 答對率比較...72 5.2.3 作答時間比較...74 5.2.4 題庫練習率...75 5.3 實驗發現與分析...77 第六章 結論與未來工作 ...78 6.1 結論...78 6.2 未來研究方向...78 參考文獻 ...82 附錄一、學生問卷 ...86 附錄二、教師訪談大綱 ...89 附錄三、學生訪談大綱 ...90 附錄四、學生前測試題 ...91 附錄五、學生後測試題 ...92
表目錄
表 2-1 電腦遊戲的分類(CHRIS CRAWFORD, 1997) ...8 表 3-1 學習內容等級定義...18 表 3-2 作答區設計 ...19 表 3-3 作答獎勵方式(給予亞卓幣數) ...23 表 3-4 BPDG系統規格表...31 表 4-1 實驗組與對照組前後測成績 ...48 表 4-2 BPDG學生答題狀況 ...49 表 5-1 BPDG的系統可用性問卷...67 表 5-2 學生使用BPDG的情境感受問卷 ...68 表 5-3 學生答題狀況表 ...71 表 5-3 學生答題正確率比較表...73 表 5-4 學生作答時間比較表 ...74圖目錄
圖 2-1 遊戲設計的三個領域 ...10 圖 2-2 不同等級的難易度(葉思義,宋昀璐,2003)...12 圖 2-3 挑戰難度增加程度不同的難易度(葉思義,宋昀璐,2003) ...12 圖 3-1 BPDG在教室裡的網路環境...15 圖 3-2 BPDG的遊戲流程 ...16 圖 3-3 國小分數課程綱要圖 ...17 圖 3-4 挑戰關卡 ...20 圖 3-5 第一關的起始畫面...22 圖 3-6 開始練習的畫面 ...24 圖 3-7 第一題答對後,繼續回答第二題 ...24 圖 3-8 學生答錯時,系統會有回饋訊息提示 ...25 圖 3-9 第三題答完,繼續回答第四題 ...26 圖 3-10 四題做完後,遊戲系統的回饋訊息...26 圖 3-11 四題完全答對,可以進入下一關...26 圖 3-12 進階闖關-5×5 階 ...27 圖 3-13 進階闖關-5×5 階加上對角線 ...28 圖 3-14 進階闖關-7×7 階 ...28 圖 3-15 進階闖關-7×7 階加上對角線 ...29 圖 3-16 BPDG的系統架構圖...32 圖 3-17 BPDG的題庫建立系統 ...34 圖 3-18 BPDG的題庫編修(驗證)系統 ...34 圖 3-19 BPDG驗證題目結果及回饋訊息輸入畫面 ...34 圖 3-20 作答區在等號右方,第一次答錯時的回饋訊息 ...35 圖 3-21 作答區在等號右方,第二次答錯時的回饋訊息 ...36 圖 3-22 作答區在等號右方,第三次答錯時的回饋訊息 ...36 圖 3-23 作答區在等號左方,第一次答錯時的回饋訊息 ...37 圖 3-24 作答區在等號左方,第二次答錯時的回饋訊息 ...37 圖 3-25 作答區在等號左方,第三次答錯時的回饋訊息 ...38 圖 3-26 教師監控畫面---學生答題狀況 ...39 圖 3-27 教師監控畫面---檢視學生作答狀況及作答明細 ...40 圖 3-28 教師監控畫面---題庫練習率 ...41 圖 3-29 學生檢視畫面---學生答題記錄 ...42 圖 3-30 學生檢視畫面---學生答題明細 ...42 圖 4-1 BPDG實驗活動-1...44 圖 4-2 BPDG實驗活動-2...44 圖 4-3 實驗順序 ...45 圖 4-4 學生使用電腦頻率統計圖 ...50圖 4-5 學生使用電腦輔助學習的經驗統計圖 ...50 圖 4-6 學生放學後是否有去補習數學統計圖 ...51 圖 4-7 學生每天學習數學時間統計圖 ...51 圖 4-8 畫面說明對於學生操作系統難易性統計圖 ...52 圖 4-9 BPDG的遊戲規則與操作的難易度統計圖 ...52 圖 4-10 提供動畫資訊使學生瞭解自己的答題狀況統計圖 ...53 圖 4-11 整體資訊呈現使學生清楚自己的答題狀況統計圖...53 圖 4-12 BPDG與其他學習分數加減法方式的比較統計圖...54 圖 4-13 激起學生學習興趣比較統計圖 ...54 圖 4-14 練習時的專注用心度比較統計圖 ...55 圖 4-15 將BPDG活動擴展到其他練習課程的意願調查統計圖...56 圖 4-16 使用BPDG有無與他人競爭壓力感受的統計圖 ...56 圖 4-17 BPDG遊戲對學生分數加減法的信心提升統計圖...57 圖 4-18 學生解題速度統計圖 ...57 圖 4-19 學生答錯觀看回饋訊息意願統計圖...58 圖 4-20 解題提示給學生的幫助統計圖 ...59 圖 4-21 學生不再害怕分數加減法考試的統計圖...59 圖 4-22 學生對BPDG遊戲系統的認同度統計圖 ...60 圖 4-23 BPDG對學生答錯後概念修正幫助統計圖 ...60 圖 4-24 BPDG對學生概念的幫助統計圖...61 圖 5-1 BPDG前、中、後段成績進步比較圖...66 圖 5-2 學生在「專注度」、「自信心」、「喜好度」、「學習動機」有正向結果....69 圖 5-3 學生答題狀況與答題明細 ...72 圖 5-4 BPDG前、中、後段學生答題正確率比較圖...73 圖 5-5 (依內容等級分類)學生作答時間比較圖...75 圖 5-6 題庫練習率 ...76
第一章 緒論
1.1 研究背景
由於網路的蓬勃發展,許多學校、甚至家庭都已有電腦,並可以快速的連上網路。 對於大部份國小學習階段的孩童,對電腦的數位遊戲都非常有興趣,他們甚至在數位遊 戲的學習專注力上,更勝於學校所學習的其他科目,數位遊戲已經是受許多孩童非常歡 迎的文化了[1]。這樣的情形引起了家長及教育者的特別關注,深怕學生被數位遊戲影 響過深而有不良影響。然而,也有教育的研究者提出:學生對於數位遊戲有特別的專注 與興趣,這樣的學習動機是否可以把它轉移到教育的目的上[2]? 到底數位遊戲可不可以用在教育的目的上呢[3]?已經有很多的研究指出:將電腦 數位遊戲當成教育的工具來用是有其正向效果的[4][5]。Rosas, Nussbaum, Cumsille, Marianov, Correa 等[6]研究者指出數位遊戲能夠強有力地支持下列四個特性: z 學生在學校的學習成就 z 學生的認知能力發展 z 學生的學習動機 z 學生的專注力 學生在學習了新的課程概念後,接下來就是要熟練概念所衍生出來的技巧。有很多 教育的方法可以讓學生來學習新的課程概念,例如:傳統的教室講授、或者利用一些教 育研究者所研究的一些方法,如 AGQ[7]或 P3T[8]。AGQ(Asking a Good Question)是一 種透過讓學生來問問題,進而達到使學生有更高層次認知的教學模式;而 P3T 則是另一 種的教學模式,是指學生研讀好自己的教學內容後,再教導另一名同學。在新概念的瞭 解後,學生便可以用電腦輔助教學(CAI)軟體來培養更深入的概念思考。而具有反覆練 習(drill-and-practice)功能的數位遊戲,便是一種對學生在技巧熟練習上極為有用的 好工具。將學校教授課程的某些內容予以數位遊戲化,讓學生透過數位遊戲來學習教材內 容,對學生而言,是一項有趣又有意義的學習活動。運用電腦及網路特性,是非常適合 做反覆式的練習方式,特別是適用在練習技能的培養(例:國小數學分數的加減計算)。 近來由於可攜式的電腦設備(如 PDA、筆記型電腦、平板電腦…等)日益普及,加上 無線網路技術的發達。Chan[9]提出了 1:1 的數位教學環境:利用這些資訊科技的技術 與設備,在學校的教室裡設計一個簡單的教學活動,每個學生都有自己的電腦設備來參 加這樣的教學活動,這樣的教學環境可以減去教師做一些繁瑣的時間,例:分派及收集 學生的學習單、簡單的小考,記錄學生在教學活動中的學習歷程,甚至可以觀察整個學 生的學習狀況。 我們觀察到許多孩童都不喜歡學習數學,其中一項理由是孩童覺得數學很難懂。有 研究者指出要幫助孩童學習數學有二個重要因素:1.引發動機來促使孩童願意花時間在 數學的活動上;2.幫助孩童建立起數學的知識[10]。也另有一些研究者建議:透過電腦 的數位遊戲,可以讓孩童在學習數學上有更好的成效及快樂[11]。
在美國科學協會(National Academy of Sciences)出版一本專為幫助孩童學習數學 的報告書:Adding It Up : Helping Children Learn Mathematics [12],裡面針對孩 童學習數學能力的結構,定義出五個要素: 1. 概念的理解 (conceptual understanding) 2. 過程的流暢 (procedural fluency) 3. 策略的能力 (strategy competence) 4. 適性的理由 (adaptive reasoning) 5. 有用的意向 (productive disposition) 本篇論文的主要研究就是針對第二項:過程的流暢──讓學生在解決問題上能培養 出具備彈性、準確性、有效性及適當性的能力。我們運用電腦及網路來建構一個數位化 的學習環境,讓學生能夠快樂並且有成效地建立更熟練的技巧。
1.2 研究動機
1.能否在國小數學「分數的加減法」計算技能上,提供一個有趣的學習活
動,並且也確實能增強技能熟練?
傳統教授國小分數的加減法,無非是要學生多用紙筆運算、反覆練習。對於耐性不 足的學生,可能很快就失去興趣;對於粗心的學生,也可能運算後與答案核對,屢次發 現計算錯誤而失去信心;或對於某些學生練習不夠,但卻自以為練習熟練…等,針對這 些現象,我們設計可以讓學生有充足的題庫、在學生解題錯誤時即時給予適當回饋、加 入某些鼓勵機制(如:獲取金幣),讓學生可以喜歡也有興趣持續練習,達到學習的效果。2.在上述的情境下,能否提供一些教學工具給教師做課前教學預備、課中
教學活動及課後診斷學生的學習狀況?
教師可以利用這套數位遊戲系統來建立自己的題庫、給予題目難易度分類、分派題 目給學生練習、觀察全班學生的學習狀況、檢視低成就學生的學習歷程並給予適當診 斷…等,這些都是在傳統的教法上不易達成的功能。 教師在傳統的方式上授課,對於全班數十位學生的學習活動,僅能詳細觀察到少部 份學生的學習歷程,藉由課後的練習作業或考試,也並不能完全掌握學生的學習狀況。 利用資訊科技的技術,我們可以詳實記錄每位學生在練習分數加減法時的解題過程,除 了可以追踪學生的作答順序外,也可以分析學生是否從中增強了自己的技能?3.在上述的情境下,能否提供一些學習工具給學生,讓學生瞭解自己的作
答歷程?
相對的,學生也可以透過這套系統,檢視自己練習的歷程:瞭解自己答對、答錯題 數及比率,回答每個題目所花費的時間,以及是否正確答對?哪一類的題目犯錯的比例較高?…等,讓學生也能夠瞭解自己的學習狀況。
1.3 研究問題
在本研究中,我們採用了 Block Puzzle Game 為基礎,設計一套個人式學習的教室 內行動學習系統,所以我們的研究問題是:
z 如何建構一套有趣的數位遊戲系統(Block Puzzle Digital Game,BPDG),並 能提升學生在「分數加減法運算」的練習技能? z BPDG 在分數的加減法練習上,是否能提升學生的學習成就、動機與信心? z 如何利用資訊科技來追踪學生的作答行為,藉以提供教師可以更完整掌握學生 的學習狀況? z 學生是否能夠利用 BPDG 系統,追踪自己的學習歷程?
1.4 研究目的
z 嘗試建立一套個人學習式的數位遊戲系統(BPDG),以遊戲方式來提升學生「分 數加減法運算」練習技能。 z 嘗試利用 BPDG 系統,在分數的加減法運算練習上,提升學生的學習成就、動機 與信心。 z 嘗試利用資訊科技來追踪學生的作答行為,讓教師可以更完整地掌握學生的學 習狀況。 z 嘗試利用 BPDG 系統,學生可以自我追踪自己的學習歷程,瞭解自己的學習狀況。第二章 文獻探討
本章將針對在「遊戲教學法」、「遊戲式的學習」及「數位遊戲與設計」三個領域作 一探討,最後再歸納綜合相關文獻,提出研究者自己的看法,並成為本研究的設計理念。2.1 遊戲教學法
教學方法有很多種,而遊戲是一種簡單又好用的教學策略,因為遊戲能給孩童製造 出歡樂[13]。 數學遊戲教學法是把數學科的教學活動轉變成遊戲活動的教學方法。有研究者提出 這樣的遊戲教學法應具備有四個主要的特性[14]: 一、適度的挑戰性:教師設定了某種的任務或目標,學生要設法用自己既有的數學 知能來達成該任務及目標。具有挑戰性的目標通常教師會加上某些限制條件(例:答題 時間、題型難易度...等),學生就必須要在這些限制條件下完成目標,對學生而言 就形成了挑戰性。一個好的遊戲必須要有適度的挑戰性,不能太難而使學生失去挑戰動 機,也不能太簡單使學生不想參與挑戰。 二、競賽性與合作性:多數的遊戲具有某種競賽成份,也造成了挑戰性與趣味。若 在團體的競賽裡,相對地就有團體內合作的成份,形成「組內合作,組間競爭」的合作 學習模式。但在設計有競爭性的遊戲裡,要特別注意到學習後段、低成就學生的內心感 受,以免因為屢次失敗的經驗,反而造成學習負面的效果。 三、機遇性與趣味性:遊戲的過程中具有某種機遇的因素,造成遊戲的趣味性。例 如兩人玩撲克牌,因為每次的洗牌及發牌,每次拿到的牌都不一樣而有不同的機遇性。 但在遊戲的設計裡,也要避免因為不良機遇性的設計而破壞整個遊戲的平衡性,這在稍 後的 2.3 節「數位遊戲與設計」裡會有討論及說明。 四、教育性:前三項是一般遊戲的特性,而「教學遊戲」就須兼具有教育性。好的 數學教學遊戲要能幫助學生養成數學的概念,例如:推理能力、計算能力、創造性思考能力…等。而本研究就是要建立一個數學數位遊戲的系統,這個系統輔助學生在國小分 數加減法的計算能力上能更加熟練。 統整歸納相關遊戲教學法的文獻,(數學)遊戲教學法的優點如下: 一、激發學生學習的興趣與動機[14]:學生在遊戲中應用數學知識,避免枯燥無味 的反覆計算或解題活動。教師建立適當的遊戲情境(故事)及規則,讓學生在其中思考、 計算、遊戲,在輕鬆愉快下學習,減少對數學的排斥。 二、具備趣味化學習及從做中學習的特色[15]:趣味化的學習情境可以激起學生學 習的動機,而做中學的過程讓學生可以親自接觸遊戲的內涵,並且建立具體的經驗。 三、促進自主學習與互動學習[16]:遊戲提供孩童主動學習,允許練習嘗試,也鼓 勵孩童間的互動學習。在個人化學習的數位遊戲裡,犯錯與失敗並不會使孩童在眾人面 前難堪,孩童反而可以在當中多嘗試各種方法,進而找到成功的經驗,並幫助學生建立 自信。 四、幫助學生精熟基本的計算方法與計算能力[14]:傳統的教法中,許多教師往往 以反覆大量的練習方式,讓學生精熟基本的數學概念與數學技巧,但也無形中降低學生 對數學的興趣。透過數位遊戲的環境練習,讓學生完成遊戲裡的任務而間接練習了基本 的計算方法與能力。 五、提供即時的回饋與學習輔導:在個人化學習的數位遊戲裡,孩童在練習的過程 當中,如果完成了階段的目標,系統可以即時地予以獎勵回饋(例:贈予遊戲金幣、加 分…),而學生犯錯時,系統也可以因應不同階段的錯誤而給予不同層次深度的回饋訊 息,讓學生能在「鷹架理論」下逐漸建立自己的數學概念。 遊戲教學法自然也有其缺點與限制,侯禎塘[17]提出如下: 一、與現實情境無法一致; 二、場地秩序不易控制及維持; 三、受場地及材料的限制; 四、價值標準不確定; 五、不易控制學生情緒;
六、耗時間; 七、對某些學生有時難免侵犯; 八、有時不易深入而與教材不能銜接; 九、常因遊戲而忘了學習的目的。 然而這些缺點並不是完全不能克服,我們可以從「教學活動的設計」、「遊戲設計」 及「使用資訊科技」來解決,例如針對第七項「對某些學生有時難免侵犯」,傳統的教 學遊戲方式不管難度設定在何處,都無法讓所有學生滿意:太難,程度好的學生會有很 有興趣去挑戰,但對程度較差的學生,可能就是信心極大的打擊;反之,亦然。然而在 個人化學習的數位遊戲環境下,利用資訊隱藏的技巧,系統可以兼顧學生個人差異,滿 足不同程度的學生難度需求。
2.2 遊戲式的學習
人類天性愛玩,不論大人或小孩。如果能善用人類此種喜好遊戲的天性,引導到各 科的教學與學習,必能增加學習的動機與樂趣[14]。當學生知道將進行的教學活動是以 遊戲方式來進行時,因為競賽富挑戰性並且可能獲勝,他們期待的是有趣、令人愉快的 活動[18]。以遊戲方式透過讓學生與其他同學競爭、或者是讓學生自我挑戰的學習活 動,目的是為了提升學生的學習動機、並且能夠學習的更好,這樣的學習方式,我們可 以稱它為「遊戲式的學習」[19]。 人類設計遊戲與玩遊戲已有幾千年的歷史。早期的遊戲如拼圖遊戲(puzzle game)、 棋盤遊戲(board game)等都有相當長遠的歷史,其中也不乏遊戲很好的遊戲流傳至今, 且仍不斷有人繼續鑽研,例如:圍棋。遊戲基本上是一種創意為主的表現型式,而且是 具有互動性的娛樂型態,例如:打牌、下棋、手機遊戲、蒙古草原上的摔跤比賽等[20]。 遊戲的型態有很多類型,以電腦為媒介的數位遊戲因網際網路的發展如雨後春筍, 各種領域都有。分類電腦遊戲的方式,主要是基於它的玩法與過程,而非遊戲的故事與題材。一般分類電腦遊戲大致如表 2-1[21]:
表 2-1 電腦遊戲的分類(Chris Crawford, 1997)
技巧與動作的遊戲 策略遊戲
戰鬥遊戲(Combat Games) 冒險遊戲(Adventures)
迷宮遊戲(Maze Games) 城堡遊戲(Dungeons and Dragons Games)
運動遊戲(Sport Games) 戰爭遊戲(Wargames)
板拍遊戲(Paddle Games) 機會遊戲(Games of Chance) 競賽遊戲(Race Games) 教育遊戲(Educational and
Children's Games) 其他才藝競賽(Miscellaneous Games) 人際關係遊戲(Interpersonal Games) 由於種類繁多,本研究將聚焦在以數位電腦為媒介的遊戲,運用在教育目的上的研 究為主。 有別於傳統以娛樂為目的的一般數位遊戲,以教育為目的的數位遊戲必須要有明確 的教育目標(例如以布林邏輯數位電路閘所組成的數位遊戲,學生們可以自行組合邏輯 閘以產生不同的電路功能),而且這些俱備教育性的數位遊戲未來極具潛力,教育工作 者也逐漸注意到這些數位遊戲對學生強大的學習動機影響力[21]。 這些富教育性的數位遊戲所包含的反覆練習(drill-and-practice)及模擬 (simulation)特性往往比遊戲規則為多,而「反覆練習」是我們針對本研究技巧熟練的 一個非常重要因素,所以我們也必須瞭解反覆練習的特性及優點,並把這些特性及優點 運用在遊戲上[22]。 z 反覆練習特性: 控制練習的速度:學生應該充份地獲得解題及瞭解回饋訊息的時間。 針對正確答案給予適當回饋:給予學生鼓勵回饋是很重要的。正面回饋要
避免過於複雜、費時以及改變課程原先的用意,否則久了學生仍會厭煩、 失去興致。 強化正確答案:避免因答錯而得到比答對更多令人興奮的反饋,而演變成 反效果。 z 反覆練習優點: 立即回饋:傳統的紙筆方式練習,需要很久的時間才能知道自己的作答是 否正碓。當學生以錯誤的方式完成了作業,他們也許只記得錯誤的技巧。 反覆練習的數位化教學遊戲軟體能馬上在學生答錯時就立即顯示出正確 答案來。 動機:電腦習作能鼓勵學生去做需要的練習,在學生答錯時,電腦也不會 不耐煩或給學生臉色看。 節省教師時間:教師不需要講解或評分,學生即可自行進行,因此教師可 以去應付學生不同的需求。 從以上的各研究者提出對遊戲式學習的相關討論中,可以看到「提升學生的學習動 機」是遊戲式學習一個很重要的焦點。也許獎狀、獎品、免寫週記…等這些外在的獎勵 方式可以暫時激起學生的學習動機,但教育研究者更希望能否讓學生由外在鼓勵的動機 如何能轉化為內在的動機,而讓學生能更主動、更積極的學習。Malone 與 Lepper[23] 就提出在學習活動中,可以提升學生內在動機的四個要素: z 挑戰(Challenge):學生必須要有能力去改變遊戲的難度,而必須要有多元的勝 利目標。在效果上也要有充足的隨機性與一定量的回饋訊息。 z 好奇心(Curiosity):遊戲活動必須提供感官上的刺激與新奇的事物,這樣學生 才會想要繼續停留在這個遊戲裡遊玩。 z 控制權(Control):學生必須能夠做一些選擇,並且也能目睹自己的選擇帶來的 影響或結果。若是選擇不是非常明確時,學生可以蒐集資訊再決定選擇。 z 幻想力(Fantasy):在遊戲的環境裡或角色上,必須讓學生感到引人入勝。 利用這四個要素加入在數位遊戲裡,讓學生原本是因為外在動機因素而能內化成為
了自己的利益而努力學習。
2.3 數位遊戲設計
前一節提到遊戲式學習的相關理論,本節即討論真正在設計一個數位遊戲應當注意 的內容。Rollings 與 Adams[24]提出遊戲設計分成三個不同的領域,如圖 2-1: 圖 2-1 遊戲設計的三個領域 對於這三個領域,分別敘述如下: z 核心機制:描述遊戲運作的方式,而非軟體的運作。有時即稱為遊戲規則。 z 故事與敘述:每個遊戲都有一個故事,故事的複雜度與深度,依據遊戲而定。 而敘述乃遊戲設計者將故事的一部份告訴玩家。 z 互動性:玩家在遊戲世界中看、聽與行動的方式。也就是玩家進行遊戲的方式。 依此三個領域,Rollings 與 Adams[24]便提出了數位遊戲設計時應包括的元素如下: 1. 規則:數位遊戲提供主動性的娛樂,與電影、電視等背動性的娛樂不同。利用 規則來規範整個遊戲的進行。 2. 競爭與挑戰:透過遊戲中的競爭、或是挑戰障礙、關卡,伴隨著玩家遇到它們時所能採取的行動而得到最後的勝利,構成了遊戲性。 3. 任務及目標:整個遊戲必須要有清楚的任務及玩家必須要達成的目標。 4. 模式與結構:模式即為遊戲的方式。不同的模式就會有不同的遊戲進行方式, 自然也會不同的遊戲結果。而結構則為轉換模式的原因及時間點。 5. 背景、互動模式及視角:背景是指遊戲發生的場所;玩家與遊戲世界互動的方 式---採取行動、克服挑戰---稱為遊戲的互動模式;視角則為玩家如何實際地 透過畫面觀察遊戲世界。 6. 真實性:遊戲嚐試以符合真實世界的邏輯描述另一個世界時,即使那是一個想 像的虛擬世界,仍可稱遊戲為寫實的。遊戲設計者需在真實與虛幻中模擬活動 與情境。 7. 故事性:遊戲通常會有故事性的情節,讓遊戲更有意義及趣味。 在瞭解到數位遊戲設計的三個領域及其設計元素後,我們看看在設計數位遊戲時要 注意的事項。Kiili[25]指出在設計一個教育性的遊戲時,要注意到下列三項要點: z 故事敘述:故事是遊戲設計最基本的部份,它把挑戰整合成一個很大的任務或 問題給學生,所以故事的重要性取決於遊戲的複雜度,愈複雜的遊戲相對的故 事就顯的愈重要[24]。有些故事雖然很簡單,但對於使學生專注於遊戲裡卻是 非常重要的。 z 遊戲平衡度:所謂遊戲平衡度指的是遊戲內部的一致性與公平性,也就是不能 讓學生利用了遊戲裡某些設計不良的瑕疵或弱點而得到好處。換句話說,在平 衡的遊戲裡,決定成功破關與否的主要因素是學生的技巧程度。這並非表示遊 戲中不能發生隨機事件,但一名技巧較好的學生應該要比一名技巧較差的學生 更容易成功過關,除非他運氣一直很差[24]。 z 最佳認知負載:多媒體的教材有一個很大的問題就是在呈現畫面或訊息時,常 會放了太多訊息而超過學生所能容納程度的負載[26]。所以可以藉著除去多餘 不相關的多媒體元素、或是利用一些語氣的效果、或者是提供一些可用的使用 者介面和挑戰,來協助學生建立知識或技能熟練。
另外一個在設計數位遊戲時要考慮的重點是:「難易度」。它是指挑戰遊戲由簡單到 困難的程度,必須是一個線性成長的困難度,以便學生可以循序漸進,不致一下遇到很 難克服的關卡,或是突然研到很容易克服的關卡。以下為二種不同類型的難易度[20]: 易 難 遊戲難度 最大難度 中等難度 新手入門 遊戲進行過程 圖 2-2 不同等級的難易度(葉思義,宋昀璐,2003) 易 難 遊戲難度 遊戲進行的過程 新手入門 中等難度 最大難度 圖 2-3 挑戰難度增加程度不同的難易度(葉思義,宋昀璐,2003) 圖 2-2 是一般遊戲裡所看到的難易度分別:比較難的等級,從關卡一開始就比較難, 比較簡單的等級,從關卡一開始也比較簡單。 而圖 2-3 則是另一種不同的難易度:一開始都非常簡單,但是不同等級難度的主要 差異是在挑戰難度增加的速率。難度等級較高者挑戰難度的增加速率增快較多,難度等 級較低者挑戰難度的增加速率增快較少。
2.4 格子謎題遊戲設計理念
根據前述的文獻,我們設計了一個「格子謎題」遊戲(Block Puzzle Digital Game, BPDG)。謎題(puzzle)遊戲是大家熟悉的遊戲,它具有簡單、很容易就能上手操作的特 性;利用格子(block)構成一組彼此前後相關的題目,選擇具有完整定義的數學(分數加 減法)為題目內容,即為「格子謎題」遊戲的內涵。在遊戲過程中,學習者填答事先設 計好的數學問題以完成遊戲,同時增加數學練習的熟練度。這個遊戲的重點並不在於建 立學生的概念理解,而是著重於學生的「計算技能熟練」。我們的目標是讓學生在玩這 個遊戲後,首先可以提高對「分數加減法」的答對率,接下來再提高學生的解題速度。 以下,我們就以文獻中提到的「反覆練習」、「提升內在動機」、「遊戲平衡度考量」、「挑 戰難度設計」等四項在 BPDG 遊戲的設計中加以說明: 1.反覆練習 即然著重在「技能熟練」,Roblyer[22]所提到的「反覆練習」,將是我們設計遊戲 裡一個很重要的練習方式,而透過我們設計 BPDG 遊戲的反覆練習,自然也能得到「立 即回饋」、「動機」、「節省教師時間」等三個優點,這是我們很清楚且可以掌握的。在「立 即回饋」機制裡,傳統上較多的作法僅提供一種「公佈答案」的回饋方式,在 BPDG 遊 戲的設計裡,我們就以鷹架理論提供三次的回饋訊息提示,讓學生在漸進式獲得回饋訊 息的情形下完成學習。 2.提升內在動機 為了讓學生能更主動、更積極的在遊戲中練習,我們也考慮了 Malone 與 Lepper[23] 提到提高學生內在動機四要素的其中二項:「挑戰」與「控制權」。如果遊戲過於簡單或 單調,學生很快就會厭煩而離開,所以在 BPDG 遊戲設計裡,我們由易至難共設計了十 二個關卡讓學生來挑戰,而這些關卡彼此前後也有相關,讓學生不會一下遇到太難的關 卡而失去挑戰的意願與興趣;而另外一項「控制權」,也是每個學生最喜歡的因素之一, 因為學生確實可以選擇不同的遊戲模式,親自操控並且克服關卡、完成任務,達到心理
滿足的目標。而由於 BPDG 遊戲是一個較為簡單的練習遊戲,所以目前在另外二項「好 奇心」及「幻想力」因素並沒有太多的琢磨,也許在將來遊戲發展的更大更複雜時,可 以因遊戲故事深度增加而再將這二項因素設計進來。 3.遊戲平衡度考量 「遊戲平衡度」也是一個很重要的考量,它關乎到學生玩遊戲的過關條件及記分機 制。在 BPDG 遊戲的設計中,採取了較為嚴謹的過關條件---該回合的題目全部答對---這樣有一個優點:學生若通過了某一個等級,則我們可以相信學生已確認俱備了該等級 的相關技能,由於新的等級題目與前一等級彼此有相關,這種較為嚴謹的過關條件可以 確保學生在練習新等級的題目時,不會因為前一等級的技能還未俱備,而又要面臨新的 等級題目。 4.挑戰難度設計 BPDG 遊戲依內容難易度設計成四個等級,共十二關卡(詳如圖 3-4),可以發現和圖 2-2 及圖 2-3 並不相同,但應較為類似於圖 2-3:一開始都較為簡單,之後再隨著不同 挑戰難度增加而有不同的難度增加速率。由於 BPDG 遊戲是一個初始設計的遊戲,目前 尚無針對使用者分別「能力等級」,所以圖 3-4 只有一條類似遞增的難度直線。其中的 四段水平「熟練」是 BPDG 遊戲特意增加的設計:學生在進任下一等級前,會有一個「熟 練」機制,確保學生已俱備該等級的能力且熟練後,才能進入下一個等級。 從以上的文獻探討及運用在 BPDG 遊戲設計裡,可以看到 BPDG 遊戲具有下列三個特 色: z 結構良好的題目(well-structured questions) z 反覆練習(drill-and-practice) z 鷹架式的回饋訊息提示(scaffolding hint) 整個 BPDG 的遊戲設計,將在第三章會有更詳細的說明。
第三章 系統設計
BPDG 是一個可以進行「個人學習」的數位遊戲。每個學生擁有自己的電腦設備(在 本研究實驗中為平板電腦),透過無線存取點(access point) 、無線網路及 BPDG 伺服 器來進行數位遊戲(參見圖 3-1)。在我們的遊戲設計中,學生必須要去練習 BPDG 伺服器 所分派的分數加減法題目計算,以獲取更多的亞卓幣,經過多次反覆的練習後,教師可 以依 BPDG 伺服器所接收到每一筆學生練習的資料來掌握整個學生的練習情形,並且可 以依據數據資料給予有問題的學生課後診斷。 圖 3-1 BPDG 在教室裡的網路環境3.1 遊戲流程
圖 3-2 是 BPDG 的遊戲流程,在遊戲系統開始之前,教師可以依據學生的程度調整 一些系統參數(例:答題時間、題目來源…等)。一開始,系統會給予學生一些簡單的遊 戲介紹及規則說明,接下來學生可以選擇「基本闖關」或「進階闖關」這二項學習活動, 最後也都會有一些統計結果給學生或教師參考。「基本闖關」是在一個 5×5 或 7×7 矩陣 內的四個邊界,一個時間內只出現一題給學生計算,採順時針的順序出題,一個回合有 四題,學生必須在限制的時間內四題全部答對,證明自己已確實具有該階段難度的分數 加減法運算的技能後,才能繼續進入下一關練習;而「進階闖關」與「基本闖關」類似, 但一次即出現全部的題目,並且又再加上對角線的組合,由學生自行判斷答題的順序。 圖 3-2 BPDG 的遊戲流程3.2 學習內容設計
本研究「數位遊戲」採用「國小數學分數加減法」為系統內容,原因如下:1. 分數是國小數學中相當重要的概念,而且在國小數學中也被視為最複雜的部 分。 2. 分數的加減法可依分母的異同、分母之間的關係而達到擴分、約分、通分、最 簡分數的概念理解。 3. 就國小學童而言,分數是複雜且不易學習,如果僅止於概念理解,而無法達到 演算技巧的熟練,對達到學習目標而言似乎是一大缺憾。 圖 3-3 為國小分數課程綱要圖[27],本論文即依其概念元素間之關係,以「通分運 算」、「同分母加減法運算」、「異分母加減法運算」為主要學習內容,設計出適合學生練 習的數位遊戲。 圖 3-3 國小分數課程綱要圖
3.2.1 學習內容等級設計
依據九年一貫課程中國小數學分數能力指標[28](教育部,1998),本研究的內容聚 焦在「真分數」、「假分數」的加減法上 (暫將「帶分數」略去,因「帶分數」可視為「假 分數」的延伸) 。而依據能力指標中的擴分、約分、通分的概念,依據鷹架理論的設計, 本研究將分數加減法設定為四個等級,如表 3-1 之說明。 表 3-1 學習內容等級定義 等級 說明 舉例 Level 1 同分母相加減(兩個分數)13
8
13
5
13
3
+
=
Level 2 異分母相加減,但分母互為倍數 (兩個分數)6
7
6
5
3
1
+
=
Level 3 異分母相加減,其中兩分母相同, 另一分母為另二個之倍數 (三個分數) Level 4 異分母相加減,其中一分母為另二 分母之倍數(三個分數)10
3
10
9
5
4
5
2
=
−
+
4
1
12
3
12
1
3
1
2
1
−
+
=
=
. 在表 3-1 裡,我們可見 Level 1 其實就是「國小整數加減法」的延伸,因為在同分 母的情況下,分數加減法就變成只要分子相加減,分母保持不變即可。 而 Level 2 即為二分數異分母的加減法,但我們限制在這二個分母互為倍數,這樣 可以讓學生先熟悉擴分、通分概念的計算技巧。 Level 3 及 Level 4 皆為三個異分母的分數加減法,但為了避免學生覺得多了一個 分數而增加心理負擔,我們限制了 Level 3 的三個分母中,有二個為相同的分母,而另 一個分母為另二個分母的倍數,這樣學生可以先計算出二個同分母的答案後(即與 Level 1 相同),再與第三個分母計算(即與 Level 2 相同),可見 Level 3 即為 Level 1 與 Level2 的結合。
Level 4 為三個異分母的加減法,其中一分母為另二分母之倍數,由前述的說明可 得知:Level 4 即為二個 Level 2 結合。
當學生熟練 Level 1 後,就可以進入 Level 2 的學習,Level 2 裡一個很重要的概 念即為「通分」,當學生練習會「通分」後,Level 2 的題目就變成 Level 1 一樣容易(同 分母,分子相加減,分母不變)。在學生熟練 Level 2 後,就可以進入 Level 3 的階段, 在前面的說明中,Level 3 的設計即為 Level 1 與 Level 2 的結合;相同的,在熟練 Level 3 後進入 Level 4,Level 4 即為二項 Level 2 的結合。
這樣的學習內容設計理念,有下列二種特色: 1. 概念的連結:呈現出整體的學習概念架構,後面的概念是前面的延伸或結合。 2. 減輕學習壓力:學生只要確認前一 Level 已經熟練,那對現在 Level 就不會有 困難的心理壓力。
3.2.2 作答區設計
傳統的國小數學分數加減法教法中,教師大多由等號的左邊教起,教導學生將等號 左邊的計算式計算完成,即為最後的答案。為了讓這個數位遊戲更有變化,本研究者加 入將等號右邊的作答區移至左邊,詳細的說明如表 3-2: 表 3-2 作答區設計 階段 說明 舉例 Stage 1 作答區在等號右邊的分子 Stage 2 作答區在等號左邊的分子 Stage 3 作答區在等號左邊的分子及分母6
7
6
3
1
=
+
13
13
5
13
3
=
+
10 3 10 7 5 4 = + −Stage 1 即為傳統的教法,學生只要等號左邊的算式算出即可。 Stage 2 將作答區移至等號左邊,學生自己必須要瞭解各分數之間的關係後,最後 可把原計算式調整成 Stage 1 的樣式再計算出來。 Stage 3 除了將作答區移至等號左邊外,另外也將該作答分數的分母列為作答區, 在我們這裡的設計並沒有強制學生一定要將答案化為最簡分數,所以學生回答 10 8 或 5 4 都被視為是相同的。 根據上述「學習內容等級設計」及「作答區設計」二項,每一個「學習內容等級」 可以有三個不同的作答區,所以在四個學習內容等級下,我們就可以得到十二項的學習 階段,在本研究的數位遊戲裡我們就依此建立了十二個挑戰關卡,如圖 3-4 所示: 圖 3-4 挑戰關卡 在圖 3-4 裡,我們增加了四個水平線段的「熟練」階段,這是本研究刻意加上去的: 為了讓學生不是恰巧因為運氣好、做對每個 Level 的最後一個 Stage,而是學生確實已 具備有該 Level 的能力,所以本研究設計特地加上熟練階段。在本研究的數位遊戲系統 裡,這裡的熟練階段是由系統再給學生練習該 Level 裡二回合的題目,學生也必須全部
答對,才能順利進入下一個 Level。
3.3 遊戲規則與介面
依據 2.3 節中 Andrew Rollings and Ernest Adams[24]提到設計一個數位遊戲的三 個領域:「故事與敘述」、「核心機制」、「互動性」,我們來看看遊戲的本數位遊戲的規則 與介面。
3.3.1 故事與敘述
以一個較為龐大完整的數位遊戲來看,應該是要有一個故事,來賦與學生有好奇心 及幻想情境。學生在練習完某一關卡後,會有不同的故事劇情的變化,或是賦予接下來 的關卡有不同的任務或說明,讓學生可以因應故事劇情或任務關卡的轉變,而有更多的 好奇心來挑戰。但 BPDG 遊戲只是一個簡單的練習技能熟練的遊戲設計,所以在這裡我 們暫時將故事省略。也許在將來進階的遊戲設計中,未來的研究者可以把這個故事加入 在更大規模的遊戲內容裡。3.3.2 核心機制
核心機制簡單的說,就是整個遊戲的規則。在 3.2 節中,我們將學習內容設計成四 個等級與三個作答區階段,所以我們的遊戲就設計成十二個關卡---每一個學習內容等 級有三個關卡。學生可以從第一關開始玩起,如圖 3-5:圖 3-5 第一關的起始畫面 從圖 3-5 的遊戲畫面中,可以看到幾個項目: 1. 題目區:即為畫面中央有分成數個畫格的區域,學生必須依據作答區的位置計 算出答案並輸入。 2. 計時區:題目區上方有一隻移動的小狗,會依據題目的方向移動。這個移動的 時間即為該題的計算時間,這個時間的值(t)由教師在出題時依題目的難易度 設定。為了給予學生有更充份的時間練習,系統共給予學生三次的計時方式: 當第一次時間(t)結束而學生未答出來時,系統會給予第二次的計時時間 (1.5t),此時小狗會移回原點繼續計時;若第二次時間結束而學生仍未答出 時,系統會給予第三次的計時時間(2t)。若第三次時間結束而學生仍未答出, 系統會給予該題的解題提示,並在同一等級的題目中再挑一題出來給予學生練 習。 3. 亞卓幣:為了鼓勵學生努力練習,建立一套獎勵機制是有必要的。當學生答對 題目時,系統會針對題目的難易度給予不同的獎勵,目前本遊戲的獎勵方式設 定如表 3-3:
表 3-3 作答獎勵方式(給予亞卓幣數) 等級 第 1 次即答對 第 2 次才答對 第 3 次才答對 Level 1 100 70 50 Level 2 200 140 100 Level 3 300 210 150 Level 4 400 280 200 4. 目前所在關卡:顯示學生目前練習的位置,使學生知道已通過了多少關卡,還 有多少關卡需要努力。
3.3.3 互動性
互動性是指學生在這個數位遊戲中看、聽與行動的方式。也就是學生進行遊戲的方 式。學生透過圖形、使用者界面與遊戲系統互動,其中的內涵包括題目的答對與答錯、 答錯時系統給予的回饋提示、學生依回饋提示再次答題、進入下一關挑戰…等。原則上 是以線性的進行方式挑戰下一關卡,但遊戲系統也會考慮到學生也許因為體力負荷、下 課時間到了…等因素,可以中斷遊戲的進行。但在下回再次進入遊戲系統時,可以考慮 選擇重新開始挑戰、或接續上一次的挑戰關卡繼續下去。 學生在用自己的帳號密碼登入這個數位遊戲系統,在瞭解自己的挑戰任務後,就可 以開始練習。每一關卡各有四題,分別位於畫格四邊的位置,按照「上Æ右Æ下Æ左」 順時針的方向依序出題,每一題學生共有三次的回答機會,如果順利答對,則進入下一 題;如果答錯,則遊戲會有解題的提示供學生練習參考;若回答三次皆無法答對,則遊 戲系統會告知正確的解題步驟及答案,並且繼續完成該 Level 的其他題目。以下的幾個 畫面圖形說明了整個遊戲進行的流程: 學生登入後,就可以開始練習。第一題出現在的題目畫格區的上方,題目的方向為 由左至右,如圖 3-6。圖 3-6 開始練習的畫面 第一題答對後,答案以藍色顯示,並繼續第二題給學生回答。第二題出現在題目區 的右方,題目的方向為由上至下,如圖 3-7。 圖 3-7 第一題答對後,繼續回答第二題 若第二題答對後,遊戲系統會出第三題給學生回答。第三題位於題目區的下方,題 目的方向為由右至左(這裡可能會有人質疑:一般數學的計算式皆是由左至右,這裡的 由右至左出題,會不會使學生混淆?本研究的解釋為:在題目區旁有一隻計時的小狗, 小狗的移動方向就是題目的方向;如果學生仍不清楚,則在遊戲流程裡的「遊戲介紹、
規則說明」時,會特別向學生強調清楚)。如果學生有答錯時,遊戲系統會回饋訊息給 學生,幫助學生解答問題,如圖 3-8。 圖 3-8 學生答錯時,系統會有回饋訊息提示 若第三題學生連續答錯三次,則遊戲系統會提示正確的解題步驟給學生參考。並且 會在作答區內以紅色的字顯示(有別於答對時的藍色)。遊戲系統會繼續出第四題給學生 回答,第四題位於題目區的左方,題目的方向為由下而上。由於等號右邊的作答區已是 第一題的題目,所以第四題的作答區一定位於等號的左方(或下方),如圖 3-9。
圖 3-9 第三題答完,繼續回答第四題 第四題答完後,遊戲系統會依答題狀況給予回饋訊息:若四題沒有完全答對,則本 關必須要重來一次,由遊戲系統再亂數挑取同一 Level 的題目給學生練習,如圖 3-10; 若完全答對,則可以順利進入下一關,如圖 3-11。 圖 3-10 四題做完後,遊戲系統的回饋訊息 圖 3-11 四題完全答對,可以進入下一關
3.4 遊戲模式
本研究所設計出來的遊戲模式有二種:「基本闖關」與「進階闖關」。茲分別說明如 下: 基本闖關:內容與方式如 3.3 節所介紹,同一時間內,一次只出現一個題目,分別 位於題目區的四圍邊界處,依「上方Æ右方Æ下方Æ左方」的順時針順 序出題給學生練習作答。依「學習內容等級設計」與「作答區設計」共 有十二關,其中前六關為 5×5 的方陣(二個分數的加減法),後六關為 7× 7 的方陣(三個分數的加減法)。 進階闖關:方式與「基本闖關」類似,但同一時間內,即把方陣內的所有題目全部 顯示出來,由學生自己來判斷作答的次序,如圖 3-12 至圖 3-15 所示: 圖 3-12 進階闖關-5×5 階圖 3-13 進階闖關-5×5 階加上對角線
圖 3-15 進階闖關-7×7 階加上對角線 由圖 3-12 至圖 3-15 看出,進階闖關是將題目在同一時間內,全部顯示出來給學生 作答。圖 3-12 是 5×5 階的題目,而圖 3-13 是 5×5 階的題目之外,另外再加上一條對角 線的題目,以上二種都是等號左邊只有二個分數的加減法;圖 3-14 是 7×7 階的題目, 而圖 3-15 是 7×7 階的題目之外,另外再加上二條對角線的題目,7×7 階的題目都是等號 左邊會有三個分數的加減法。 進階闖關的答題順序由學生自訂,學生必須要在題目中找出可以計算出所有答案的 順序出來,並且將所算出來的答案輸入所有的作答區內,然後按下「我算完了」按鈕給 遊戲系統。遊戲系統會檢查學生的答案,答對者該作答區的方格會以綠底呈現,表示該 方格答案正確,並且作答區不再讓學生輸入答案;而答錯者該方格會以紅底呈現,表示 訪方格答案錯誤,保留作答區讓學生繼續輸入答案。 由上述設計可知:進階闖關不論在題目的呈現方式上、學生解答的複雜度上、以及 給學生的心理壓力上,都要比基本闖關來的困難的的多,所以我們的設計理念是:在學 生充份練習完基本闖關並且已經熟練後,才來挑戰進階闖關,否則學生會有很大的挫折 感及排斥感。
3.5 系統架構與規格
BPDG 的網路環境中,每個學生使用自己的電腦設備(本研究是使用平板電腦),透過 無線的網路存取點來與 BPDG 伺服器進行資料交流(例:遊戲系統分派問題給學生、學生 輸入答案給遊戲系統、學生端電腦記錄學生的答題狀況及亞卓幣的獲取回傳給 BPDG 伺 服器…等),來完成整個數位遊戲的進行。 圖 3-16 是 BPDG 的系統架構圖,它包含了六個單元:遊戲單元、試題單元、連結單 元、教師介面單元、學生介面單元及資料庫單元。茲分別描述如下: 遊戲單元:由一個遊戲模組所組成,這個遊戲模組就是這整個數位遊戲的核心。它 包含了故事與敘述、遊戲規則、遊戲的畫面配置、遊戲的系統參數設定、 遊戲的任務目標等。 試題單元:試題單元包含了試題模組與訊息回饋模組。當遊戲模組傳來分派試題給 學生練習的命令時,試題模組會挑選試題給學生遊戲,而當學生在遊戲 中答錯時,訊息回饋模組也會負責將答錯次別的訊息傳回遊戲模組,以 供學生參考。 連結單元:連結單元包含一個連結模組,它負責建立學生介面及教師介面與遊戲模 組的連結功能,並處理連結失敗時的狀態記錄。 教師介面單元:教師介面單元包含了教師介面及教師監控模組。教師透過教師介面 與教師監控模組連結,而教師監控模組則將蒐集學生的學習歷程 資料予以處理,並轉化成有用的資訊給教師參考。 學生介面單元:學生介面單元包含了學生介面與遊戲遊玩模組。學生透過學生介面 與遊戲遊玩模組連結,確定遊戲的模式與關卡別後,再透過連結 模組與遊戲模組連結,而開始進行遊戲。 資料庫單元:它是記錄整個 BPDG 活動的資料庫,內含三個主要的資料表:試題資 料表、系統設定資料表及學生答題歷程資料表。試題資料表記錄所有試題的等級與相關回饋訊息;系統設定資料表則記錄 BPDG 的系統參 數;學生答題歷程資料表則記錄整個學生遊戲時的作答歷程記錄,包 含答案對錯、回答時間、回答次數等。 在系統規格方面,分為伺服器端與使用者端,軟硬體需求如下: 表 3-4 BPDG 系統規格表 伺服器端(Server) 使用者端(Client) 硬體需求 軟體需求 硬體需求 軟體需求 z Intel Pentium 2.0 以上之 CPU z 512 MB 以上 RAM z Microsoft Windows Server 2003 + IIS z Mysql 4.1.16 z PHP5 z J2SDK1.4.2_10 z Intel Pentium 以 上的 CPU,有無限 網路功能 z 256 MB 以上 RAM z Windows XP z Jre 5.0 z Microsoft Internet Explorer 5.0
試題單元 題庫模組 訊息回饋模組 學生介面單元 遊戲遊玩模組 遊戲介面 連結單元 連結模組 遊戲單元 遊戲模組 教師介面單元 教師監控模組 教師介面 資料庫單元 試題資料表 系統設定 資料表 學生答題 歷程資料表 圖 3-16 BPDG 的系統架構圖
3.6 系統功能
3.6.1 遊戲
「遊戲」是 BPDG 活動最核心的功能,因為 BPDG 就是建立一個數位遊戲的系統。透 過遊戲,學生可以有興趣地完成學習活動,讓學生在不自覺中達成了學習的目標,而教 師也可以在遊戲中觀察學生的各項反應,並透過遊戲系統提供的其他功能來監控學生的 學習狀況。3.6.2 出題系統與題目驗證
BPDG 提供了出題系統與題目驗證的功能給教師。傳統上出一道分數的加減法並沒有 太大的困難,但由於 BPDG 是在一個 5×5 階或 7×7 的方陣環境下,題目先後是互相關連: 前一題的答案是下一題的題目,所以它的出題難度會比傳統分數加減法為高,稍不小心 就會有出錯題目的情形發生。圖 3-17 是建立題庫的功能畫面,圖 3-18 是編修(驗證)題 庫的畫面,而圖 3-19 則為若驗證題目無誤後,當學生答錯時,遊戲系統要給予的回饋 訊息輸入畫面。圖 3-17 BPDG 的題庫建立系統 圖 3-18 BPDG 的題庫編修(驗證)系統 有了題庫的驗證系統,則可以保證所建立出來的題目是完全正確的,這是非常重要 的一點。因為如果學生練習了有錯誤的題目,除了會造成觀念的混淆外,甚至會造成自 信心的受損,這對達到遊戲教學的效果是相當大的打擊。 圖 3-19 BPDG 驗證題目結果及回饋訊息輸入畫面
3.6.3 答題回饋訊息
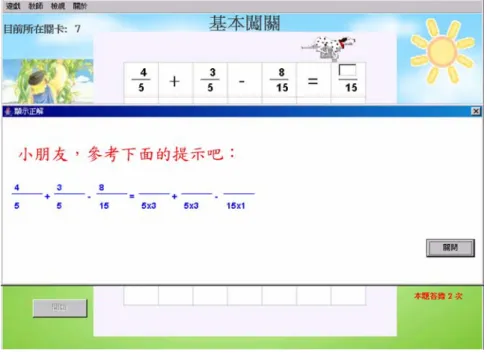
一個良好的數位遊戲系統,必須是學生和遊戲有很好的互動關係。學生透過遊戲系 統提供的回饋機制,可以順利完成挑戰的任務。在 BPDG 裡,學生練習分數加減法題目 時,一定會有答錯的機會,答錯的可能原因有:觀念錯誤、計算錯誤、無法在規定的時 間內計算出答案、輸入了不正確的字元等。BPDG 針對學生不同的答錯情形,會提供不同 的回饋訊息,在這裡,本研究將討論在學生計算錯誤時,BPDG 如何給予學生適當的回饋。 在 3.2.2 節的作答區設計裡,可以看見學生的作答區有三種情形: 1. 作答區在等號的右方分子。 2. 作答區在等號的左方分子。3. 作答區在等號的左方分子及分母。 其中第 2 點與第 3 點因作答區都在等號左方,它們的計算方式是一樣的,所以可以 把第 2 點與第 3 點歸納為同一類,所以我們可以得到二類的情形: 1. 作答區在等號右方 2. 作答區在等號左方 所以在給予回饋訊息提示時,就要依作答區的位置不同而提供不同的回饋訊息。 另外,由於學生每答一題都有三次的答題機會,依據鷹架學習理論,我們便可以依 據學生答錯的次別給予不同程度的回饋訊息提示。以下各圖,將顯示在不同情形下,BPDG 所提供不同的回饋訊息: 圖 3-20 作答區在等號右方,第一次答錯時的回饋訊息
圖 3-21 作答區在等號右方,第二次答錯時的回饋訊息
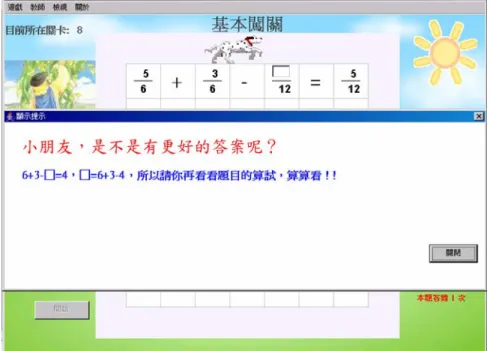
圖 3-23 作答區在等號左方,第一次答錯時的回饋訊息
圖 3-25 作答區在等號左方,第三次答錯時的回饋訊息
3.6.4 答題歷程記錄
學生在遊戲的過程中,所練習的每一個答題記錄,都會從使用者端被送到伺服器儲 存下來。使用者端送來的資料包含:學生登入遊戲系統時間、試題的題號、題目的位置 (上右下左)、學生的答案、標準答案、該題目作答所花費的時間、以及是否正確通過。 藉資訊科技之便,要蒐集學生的答題歷程記錄並不難達成,蒐集上述的記錄是有其 意義的。在傳統的教室裡,針對同一個題目,教師至多只能在同一時間內觀察到一、兩 位學生的整個作答歷程;若以紙筆的考試卷作答情形來看,教師所得到的只是學生交卷 的最終狀態,所能得到學生的學習狀況極其有限。但若是利用資訊科技將上述的資料蒐 集起來,化成有用的資訊,將有以下的二個優點: 課後診斷:將這樣的資訊提供給教師,教師將可以更完整地掌握學生的學習狀況: 某個學生在某一類的題型上屢屢犯錯、哪一類型的題目學生答錯的比例極高、某個學生 在某一題上花費了極多的時間、某個學生確實的練習總時間及練習題目數、某個學生在 練習後解題速度有否變快…?上述的幾個項目若不藉資訊科技來記錄學生的答題歷 程,是很難達到的。檢視學習狀況:學生也可以來檢視自己的學習歷程資料,透過遊戲系統轉化成有用 的資訊,學生可以知道自己在那個環節的觀念是否有問題、在那一類型的題目容易算 錯、學生自己的解題速度有否變快?…等。 以下的幾個附圖說明了記錄了學生答題歷程的應用: 圖 3-26 呈現了學生的答題狀況,教師可根據答錯百比比較高的同學帳號,再進一 步詳細檢視其答題過程。 圖 3-26 教師監控畫面---學生答題狀況 圖 3-27 呈現了某一位學生的答題狀況,除了列出該學生在該日練習的狀況外,也 統計出該學生在四個等級的題目裡練習的題數及答對、答錯情形。若發現該學生在某一 題使用了特別多的時間,教師也可以點選進入檢視更詳細的過程,以獲得更多的資訊來 瞭解學生的問題。
圖 3-27 教師監控畫面---檢視學生作答狀況及作答明細
圖 3-28 顯示了題庫的練習率,其中也列出了各題目的答對與答錯百分比。教師可 以根據答錯百分比特別高的題目來探討,為何學生在這類型的題目上特別容易犯錯,進 而找出學生觀念上的問題。
圖 3-28 教師監控畫面---題庫練習率
圖 3-29 及圖 3-30 是學生的檢視畫面,學生可以看到自己的答題明細,檢視那類型 的題目屢屢犯錯、自己的解題速度有沒有變快?…等。
圖 3-29 學生檢視畫面---學生答題記錄
第四章 實驗設計
本研究所設計出來的數位遊戲系統,必須讓學生實際的使用後才能知道它的價值為 何。經過實驗的檢驗,可以讓我們知道系統那裡有缺失,並根據學生及教師使用的反應, 讓我們可以再做調整。由於這是一個先導性的實驗,所以在實驗設計上是採取較小的規 模及較短的時間進行,也許在未來的研究裡可以進行規模更大或更時間更長久的實驗。 在本章中,先訂出本研究的實驗目的,然後再看看實驗的對象及實驗的環境,接下來再 介紹整個實驗的設計,並且指出整個實驗中的限制有那些,同時做為後續研究及系統發 展的參考,最後將實驗的結果呈現出來。4.1 實驗目的
本研究的實驗目的,包含下列數點: z 測試系統的穩定度及人機介面的操作性 z 學生對 BPDG 的接受度 z 對於班上前、中、後段的學生,在使用 BPDG 後,在下列各個指標上有無提升? 對分數加減法的數學成就 對分數加減法計算的信心 對分數加減法計算的解題速度 z 在數學學習態度,於下列指標上,有無提升? 學習動機 學習堅持性 z 學生作答歷程資料之蒐集,並從中分析: 將結果提供給教師,使教師更完整掌握學生學習狀況 將結果提供給學生,使學生可以追踪自己的歷程4.2 實驗對象與環境
本研究的實驗對象是桃園縣觀音國小六年乙班的學生共 30 名,觀音國小在桃園縣 是較為濱海偏遠的學校,每個年級五個班,全校共 30 班,算是中小型學校。實驗的時 間是 2006 年 3 月中旬連續三週,每週二節課,每節課 40 分鐘。實驗的環境是在教室裡 架設無線網路,每位實驗組學生使用一台平板電腦,在教室裡另架設一台 BPDG 伺服器, 讓學生能登入遊戲系統練習,並蒐集學生的作答歷程資料。以下二張照片是學生在進行 活動時的情形: 圖 4-1 BPDG 實驗活動-1 圖 4-2 BPDG 實驗活動-24.3 實驗設計
在全班 30 名學生中,依前測成績 S 型分成實驗組與對照組二組,每組各 15 名學生。 實驗組學生留在原教室操作(配合 BPDG 伺服器及無線網路架設),而對照組學生則移至 該校另一空教室,進行紙本練習活動,以免實驗進行時,二組學生互相干擾。而該班教 師則於二處教室來回監督學生學習情形。 由於只有 6 節課的時間可供實驗,整個實驗的順序規畫如圖 4-3: 第 1 次實驗活動 前測、分組 第 2 次實驗活動 遊戲介紹、規則說明 基本闖關 第 3 次實驗活動 基本闖關 第 4 次實驗活動 基本闖關 第 5 次實驗活動 基本闖關 (進階闖關) 第 6 次實驗活動 後測、頒獎 問卷、訪談 圖 4-3 實驗順序 扣除第 1 節課與第 6 節課的前後測及問卷訪談,實驗組學生的真正操作時間只有 4 節課。而由於遊戲模式 1 的基本闖關就有 12 關要挑戰,所以所有時間皆讓學生在挑戰 基本闖關(模式 2 的進階闖關在遊戲介紹時,有讓學生練習一段很短的時間)。 前後測皆為紙筆測驗,題目來源皆為遊戲系統內的題庫。每次皆測驗 30 題分數加減法,測驗時間為 30 分鐘。 對照組的學生雖在另一教室,但每次也發下一張 30 題的題目,來源亦為遊戲系統 的題庫。在下課前,會由教師公佈答案,同學互相批改,有錯誤的同學必須自行訂正, 遇有不會的問題可向同學或教師請教。 為鼓勵實驗組學生努力練習答題,遊戲系統設有亞卓幣獎勵機制。在第六節課的頒 獎裡,實驗組學生則依個人獲取亞卓幣的數量取前三名頒獎,而對照組則依每次發下的 測驗卷總分加總取前三名頒獎。 問卷及訪談僅限實驗組學生及教師,詳細內容及結果如第五章。 在整個實驗活動過程中,也使用數位攝影機詳細拍攝學生的活動過程,做為觀察及 蒐集學生在使用 BPDG 的情境感受資料。
4.4 實驗限制
本研究的實驗的限制如下: z 實驗時間限制:由於該班是畢業班,平日已有許多畢業的相關活動,爭取到六 課節課實驗已屬不易,雖曾向該班導師要求再增加二節課實驗,但該班導師言 進度已落後許多,不同意再增加實驗時數。 z 實驗樣本數限制:該班總人數為 30 人,實驗組僅 15 人,若分為前中後三段學 生觀察分析,每段僅 5 人,這樣的樣本數雖然在統計學上較不客觀,但由於本 實驗是「先導性實驗」,為掌握實驗環境,因此實驗樣本數不宜過大。在日後 進行正式的實驗時,較佳的方式為使用二個班級,一個班級為實驗組,另一班 級為對照組,二個班級由同一教師任課。但在現行國小階段,導師多為該班的 主科(國語、數學)教師,非常不易找到教師教授二個班級的數學。 z 實驗工具限制:由於實驗是使用 Tablet PC,學生使用感應筆,對從沒使用過 感應筆的學生會有一點生疏。而且實驗組學生在練習題目時,仍會用到紙筆計算,在感應筆與鉛筆之間的轉換,有時會發生衝突的現象。
4.5 實驗結果
要蒐集什麼樣的實驗結果,端看實驗的目的為何?在 4.1 節中,本研究已經清楚指 明了實驗的目的,便可以在實驗中去蒐集這些實驗的數據資料。這些的實驗數據資料可 以從以下五種資料來源獲得:前後測成績、學生答題歷程資料表、學生問卷、學生與教 師訪談、攝影資料記錄。茲分別陳列於下:4.5.1 前、後測成績
在實驗活動的第一節課與最後一節課有進行前測與後測,依前測成績 S 型分成實驗 組及對照組。二組的前後測成績分別如表 4-1:表 4-1 實驗組與對照組前後測成績 實驗組 對照組 帳號 前測答對題數 後測答對題數 s06 30 30 s13 28 30 s04 27 30 s07 25 30 s05 24 30 s11 23 29 s03 22 29 s08 21 29 s14 20 29 s02 17 28 s12 16 25 s01 10 21 s10 10 13 s09 9 24 s15 8 13 平均 19.33 26.00 學生 前測答對題數 後測答對題數 d28 30 29 d01 28 29 d24 26 28 d05 25 28 d30 24 28 d18 23 30 d10 22 30 d15 21 27 d31 19 28 d04 18 22 d07 15 23 d21 12 26 d26 10 16 d11 9 22 d08 6 19 平均 19.20 25.67
4.5.2 學生答題歷程資料庫
所有學生經遊戲練習作答的資料都會被蒐集在學生答題歷程資料表,內容包含了: 題目編號、題目位置(上、右、下、左)、作答順序、正確答案、學生答案、花費秒數、 是否通過等。這些資料再與其他相關資料表結果,就可以得出一些有用的資訊,相關內 容將在下一章討論說明。表 4-2 為整合學生答題歷程的一例:表 4-2 BPDG 學生答題狀況 帳號 暱稱 答對題數 (百分比) 答對秒 (百分比) 答錯題數 (百分比) 答錯秒 (百分比) 總答題數 總秒數 s01 皓皓 120(75.00) 1950(58.88) 40(25.00) 1362(41.12) 160 3312 s02 小胖 132(90.41) 2683(85.58) 14(9.59) 452(14.42) 146 3135 s03 佑佑 297(90.55) 3957(85.98) 31(9.45) 645(14.02) 328 4602 s04 豪哥 178(84.76) 2049(71.54) 32(15.24) 815(28.46) 210 2864 s05 丫哲 127(87.59) 2099(77.11) 18(12.41) 623(22.89) 145 2722 s06 董事長 327(89.34) 2713(85.29) 39(10.66) 468(14.71) 366 3181 s07 銜銜 151(81.62) 2542(82.56) 34(18.38) 537(17.44) 185 3079 s08 我叫肥肥 272(85.00) 2193(81.25) 48(15.00) 506(18.75) 320 2699 s09 帥帥雲 72(54.55) 959(39.13) 60(45.45) 1492(60.87) 132 2451 s10 君 89(52.66) 821(34.54) 80(47.34) 1556(65.46) 169 2377 s11 小萱 187(96.89) 3307(93.55) 6(3.11) 228(6.45) 193 3535 s12 小麥麥 105(81.40) 2548(78.45) 24(18.60) 700(21.55) 129 3248 s13 小萱萱 148(86.05) 2763(80.04) 24(13.95) 689(19.96) 172 3452 s14 小病毒 188(90.82) 3103(87.51) 19(9.18) 443(12.49) 207 3546 s15 巧克力 64(49.23) 2143(42.79) 66(50.77) 2865(57.21) 130 5008