國小六年級學童因數與倍數概念階層之模糊詮釋結構模式分析

(1)

國立臺中教育大學教育測驗統計研究所

教學碩士學位暑期在職進修專班碩士論文

指導教授：林原宏博士

國小六年級學童因數與倍數概念階層之

模糊詮釋結構模式分析

研究生：吳育楨撰

中華民國九十七年八月

(2)

謝辭

回首三年的研究所生涯，真的是收穫良多，除了領悟到更多的知識與見解外，更重要的是學到了認真與嚴謹的研究態度，這是比完成論文更令人受益的地方，也對我未來的教職生涯有很大的助益，這都應該感謝我的指導教授林原宏老師。從一開始論文題目的擬定到論文的修改完成，林老師總會在百忙之中抽空給予全心全力指導，讓我受益匪淺，點滴記在心頭，並使我在對論文的思考及資料的蒐集上更臻完善，謹此致上最深的謝意。同時，還要感謝教育測驗統計研究所所有教導過我的老師們，因為有他們在各專業領域的授課指導，使得我在學業與未來教學上，獲益良多。而口試委員張宇樑教授以及謝闓如教授的細心指正，使本論文更臻完備以及實用。另外特別感謝研究夥伴，建宏與雅雯同學，大家同甘共苦一起討論、研究及鼓勵才能順利完成論文。最後，要感謝的是我的家人，感謝父親、母親總是在我徬徨不安時給我最大的鼓勵與協助，謝謝姐姐、弟弟、妹妹總是在我心情低落時給予無限的支持，謝謝你們無時無刻的支持與關懷，讓我順利地完成碩士學位。吳育楨謹誌 2008 年 8月

(3)

摘要

因數與倍數概念是學生學習數學備感困難的單元之一，許多研究發現學童對於因數與倍數概念存在學習困難與迷思概念，而本研究旨在應用模糊詮釋結構模式分析法，進行國小六年級學童因數與倍數概念階層結構之探討，以提供數學教材、教學及補救教學之參考。研究者以自編的「因數與倍數概念測驗」為研究工具，針對臺中縣市835名六年級學童進行施測，將所得資料經試題反應理論分析之結果，根據察覺模糊邏輯模式(fuzzy logic model of perception)計算概念之間從屬關係之機率，經由模糊截矩陣(alpha cut)之詮釋結構模式演算，最後獲得個別學童的概念階層結構圖。研究者探討低、中、高三組不同能力值的學童概念結構圖之差異，並檢定不同能力值學童的概念結構圖與專家的概念結構圖間差異性。研究結果如下：一、不同能力值學童的概念結構圖有差異存在。二、不同能力值的學童其試題內概念屬性ISM圖有差異存在。三、答對題數相同但反應組型不同的學童其概念ISM圖不盡相同。四、答對題數相同但反應組型不同的學童其試題內概念ISM圖不盡相同。五、不同能力值學童的概念ISM圖與專家的概念ISM圖有顯著差異。六、不同能力值組間的學童其概念ISM圖相似性係有顯著差異本研究之結果與發現，可幫助教學者瞭解學童的因數與倍數的概念結構，以及概念結構與其能力值高低的不同而產生之差異，依據此差異可提供教師作為分組教學課程規劃之架構，或是進行補救教學課程設計之參考，以提升學生的因數與倍數概念學習成效。最後，研究者提出對未來研究之建議。關鍵字：因數與倍數、試題反應理論、詮釋結構模式、模糊理論

(4)

The Study on Factor and Multiple Concepts for Sixth Graders by

Using the Fuzzy Approach of Interpretive Structural Model

Abstract

The purpose of this study was to analyze the individualized hierarchical structures of factor and multiple concepts for sixth graders in Taiwan by using the the Fuzzy Approach of Interpretive Structural Model (FAISM). The researcher first tested 835 sixth graders of elementary schools by using self-designed factor and multiple concepts test. Secondly, the researcher analyzed the raw data through FAISM based on Fuzzy Logic Model of Perception (FLMP), Item Response Theory (IRT) and the algorithm of Interpretive Structural Model (ISM) of fuzzy alpha-cut. Thirdly, the researcher used FAISM software to get the individualized hierarchical structures of factor and multiple concepts. Finally, the researcher compared the differences of the individualized hierachical structures of factor and multiple concepts among high, middle, low-ability examinees and the experts.

Through the procedures of the analysis, the following conclusions were made. 1. The ISM graphs of examinees varied based on different abilities.

2. The concept structures in each item varied greatly with different-ability examinees.

3. The ISM graphs were different for those who had the same total scores but different response patterns.

4. The concept structures in each item varied greatly for those who had the same total scores but different response patterns.

5. Based on the referenced standard of experts’ concept structures, the ISM graphs of examinees with different-ability were quantitatively different.

6. The similarity indices of ISM graphs between different abilities levels were significantly different.

The findings of this study might be helpful for understanding the learning process of factor and multiple concepts and as references for remedial instruction or group teaching. Finally, some recommendations and suggestions for future research are provided.

Keyword: factor and multiple, item response theory, interpretive structural modeling, fuzzy theory.

(5)

目錄

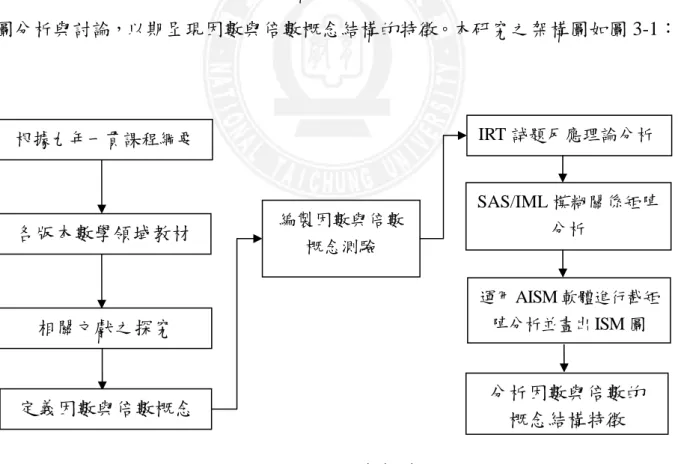
第一章緒論 ... 1 第一節研究動機... 1 第二節研究目的... 4 第三節名詞釋義... 5 第四節研究限制... 7 第二章文獻探討 ... 9 第一節因數與倍數概念研究... 9 第二節知識結構測量理論... 25 第三節模糊理論... 48 第四節模糊取向之詮釋結構模式分析法... 51 第五節試題反應理論... 60 第三章研究方法 ... 67 第一節研究架構... 67 第二節研究對象... 68 第三節研究工具... 68 第四節研究流程... 73 第五節資料分析... 75 第四章研究結果與討論... 79 第一節不同能力值學童的因數與倍數概念 ISM 圖之比較 ... 79 第二節不同能力值學童的因數與倍數試題內概念屬性 ISM 圖之比較... 88 第三節答對題數相同但反應組型不同的學童其因數與倍數概念 ISM 圖之比較 ... 94

(6)

第四節不同能力值組的學童間及其和專家的概念 ISM 圖之量化比較... 107 第五章結論與建議 ... 111 第一節結論... 111 第二節建議... 114 參考文獻 ... 117 一、中文部分... 117 二、日文部分... 124 三、英文部分... 125 附錄 ... 130 附錄一因數與倍數概念測驗... 130 附錄二 A、B、C 三位學生之模糊關係矩陣 ... 133 附錄三計算概念 ISM 圖相似性係數之 SAS/IML 原始碼... 136

(7)

表目錄

表 2-1 因數與倍數相關九年一貫數學課程網要分年細目詮釋 ... 12 表 2-2 九年一貫各版本因數與倍數相關單元教學重點摘要表 ... 14 表 2-3 概念構圖的計分方式... 26 表 2-4 三個網路中各節點的圖形理論距離值 ... 33 表 2-5 根據圖 2-10 之網路一和網路二的 PFC 指數計算... 33 表 2-6 由圖 2-14 認知屬性關聯矩陣Q(2×3)所產生的四種知識狀態... 39 表 2-7 常見的幾種試題反應理論模式摘要表 ... 63 表 3-1 因數與倍數測驗受試樣本人數一覽表 ... 68 表 3-2 因數與倍數概念內容及說明 ... 69 表 3-3 試題與概念屬性之關係矩陣 ... 70 表 3-4 預試工具之項目分析... 71 表 3-5 正式施測工具之項目分析 ... 72 表 4-1 不同能力值的學童代表之答題情形 ... 79 表 4-2 A、B、C 三位學生之概念屬性截矩陣 ... 80 表 4-3 不同能力值在每一概念之平均通過率 ... 83 表 4-4 A、B、C 三生在三個類別的因數與倍數概念階層結構 ... 87 表 4-5 個人化的試題內概念屬性階層結構 ... 88 表 4-6 答對題數相同但反應組型不同的學童之答題情形 ... 94 表 4-7 答對題數相同但反應組型不同的學童之概念屬性截矩陣 ... 95 表 4-8 低能力組之 D1、D2 學生之概念 ISM 圖 ... 97 表 4-9 中能力組之 E1、E2 學生之概念 ISM 圖 ... 98 表 4-10 高能力組之 F1、F2 學生之概念 ISM 圖... 98 表 4-11 答對題數相同但反應組型不同的學童其試題內概念 ISM 圖之比

(8)

較 ... 102

表 4-12 不同能力組學童的相似性係數之單一樣本 t 檢定摘要表 ... 108

表 4-13 不同能力值組概念相似性係數之變異數分析摘要表表 ... 108

(9)

圖目錄

圖 2-1 概念構圖的計分例子... 27 圖 2-2 接近性矩陣與資料網路圖 ... 30 圖 2-3 根據圖 2-8 所產生的距離矩陣和徑路搜尋網路 ... 31 圖 2-4 網路一與另外兩個網路間的 PFC 和 GTD 指數 ... 32 圖 2-5 試題診斷分析圖... 36 圖 2-6 a Tatsuoka 的規則空間 ... 37 圖 2-7 a Tatsuoka 的新規則空間 ... 37 圖 2-8 三題試題和二個認知屬性的關聯矩陣 ... 38 圖 2-9 SAT 測驗 14 個數學認知屬性的知識狀態網路圖 ... 41 圖 2-10 五道數學題目的 Hasse 圖 ... 45 圖 2-11 知識空間K的學習路徑圖... 46 圖 2-12 認知模型之關聯構造階層圖 ... 52 圖 2-13 概念元素的部份關係... 54 圖 2-14 ISM 圖的繪製 ... 55 圖 2-15 四條典型的單參數邏吉斯模式之試題特徵曲線 ... 64 圖 2-16 四條典型的雙參數邏吉斯模式之試題特徵曲線 ... 65 圖 2-17 五條典型的三參數邏吉斯模式之試題特徵曲線 ... 66 圖 3-1 研究架構圖... 67 圖 3-2 研究流程圖... 74 圖 4-1 A 生之因數與倍數概念 ISM 圖 ... 82 圖 4-2 B 生之因數與倍數概念 ISM 圖... 82 圖 4-3 C 生之因數與倍數概念 ISM 圖... 82 圖 4-4 A、B、C 三位學生概念 ISM 圖的概念通過率之比較... 84

(10)

第一章緒論

本研究旨在應用模糊詮釋結構模式分析法，探討國小六年級學童因數與倍數之概念階層結構，以分析不同能力值學童的因數與倍數知識結構，其結果可作為實施補救或分組教學之參考。本章旨在闡述本研究之動機、目的及對本研究所提及之相關名詞作釋義。

第一節研究動機

教育改革是教育發展與進步的動力，歐美先進國家為提升教育品質，促進教育健全發展，紛紛致力於各種教育改革(吳清山，2006)。教育部實施國民中小學九年一貫課程改革是繼九年國民教育之後的教改里程碑(蔡清田，2005)。九年一貫課程強調以學習者為主體，以知識的完整面為教育的主軸，以終身學習為教育的目標，在進入二十一世紀且處於高度文明化的世界中，數學知識及數學能力，已逐漸成為日常生活及職場裡應具備的基本能力(教育部，2003)。依據教育部(2003)所公佈「九年一貫數學領域正式綱要」，在國小階段的數學課程中，數與量概念是非常重要的部分，其中因數與倍數相關概念是五、六年級時數與量概念的教學重點。以因數與倍數教材地位來看，因數與倍數概念對於往後數學的學習有很大的關聯，因數與倍數概念對日後學童學習等值分數、分數加減、比例概念等課程，都是極為重要的，更是國中階段學習因式、倍式、多項式、因式分解、數列與級數的重要基礎(林珮如，2002；邱慧珍，2002)。然而因數與倍數概念是學生學習數學備感困難的單元之一，也是老師教學頗感困難的題材。這是因為它們的概念相當抽象，在學生的生活經驗中也缺乏與因數及倍數概念結合的活動(王詩惠，2003)。根據許多研究發現，國小學童的因數、公因數、倍數、公倍數知識表現並不理想(游麗卿，1998；黃耀興、邱易斌，1999；謝堅，1997；蕭金土，1995)。近年來也有研究發現學童在學習因數、公因數、倍

(11)

數、公倍數時所存在著各種不同迷思及可能的原因(吳彥廷，2005；周文忠，2002；林珮如，2002；邱慧珍，2002；施美多，2006；陳清義，1995；陳標松，2003；黃寶彰，2003；黃國勳、劉祥通，2003；Graeber & Tirosh, 1990; Mayer, 1992; NCTM, 2000; Nevin, 2002; Vergnaud, 1983)。許多中低程度學生往往因為無法有系統學習因數與倍數概念而遭遇瓶頸，導致往後的數學學習產生先備不足的問題，更加深他們對於數學學習的挫敗以及排斥感(陳清義，1995；黃國勳，2004)。因此亦有研究者開始提出補救教學方法，利用學習策略、教學補救等方式，以改善學童學習困難與迷思概念(于國善，2004；王詩惠，2004；蕭正洋，2004；謝哲仁、林榮貴，2006)。而在這幾年的教育改革中，課程的改革、教學方法與課程標準的改變等，學生是否已學得正確的因數與倍數概念？因此進行國小學童因數與倍數概念結構的研究，以提供數學教材、教學及補救教學之參考，實是必要與可能的議題。近年來，認知心理學的興起，使得人們對「人的心理運作」之看法有所改變。尤其在教育領域裡，對知識如何獲得等學習過程的問題，引起心理與教育學者相當大的興趣。在教育的研究上，認知心理學把諸多的焦點放在人類知識結構或概念結構上，配合心理計量學(psychometric)的蓬勃發展，對知識結構的探究方法也有很大的進步。而 Warfield (1976) 所提出的詮釋結構模式(interpretive structural modeling, ISM)是相當重要且有效的方法。ISM 原為社會系統工學(social system engineering)之一種構造模型法(structure modeling)，植基於離散數學和圖形理論，透過二維矩陣(binary matrices)的數學運算，呈現出一個系統內全部元素間的關聯性，及完整的多層級結構化階層(multilevel structural hierarchy) (Warfield, 1974, 1977)。日本學者佐藤隆博於 1980 年提出 ISM 分析法在教育上的課程與學習的應用，將學習者腦中思考的概念要素單位結構，用具體的圖形或數量表示出來。國內亦有運用 ISM 分析法在教育與心理方面的實證研究，鍾靜蓉(2002)以商業職業學校之「經濟學」科目為實例，進行詮釋結構法及構造化學習的研究，建立起更科學化的「學習路徑(learning path)」與「學習地圖(learning map)」。林輝泉(2004)

(12)

運用 ISM 分析法進行教師實施資訊融入教學之素養的需求分析。彭淑珍(2004) 運用 ISM 對智能障礙高職學生職業課程進行「結構化教學設計」。鄭麗娜(2004)運用 ISM 分析法建立地理概念的層級結構圖。因此，ISM 的分析法對於分析教材構造、設計教材內容以及建立學習者的知識概念結構等方面有其卓著效益(林原宏、陳進春、許天維，2005)。但 ISM 分析法礙於其元素關係只限於二元關係，並不完全適用於描述學習者知識結構中概念間的關係。林原宏(2005)提出模糊取向的詮釋結構模式(fuzzy approach of interpretive structural model)，結合了試題反應理論、模糊理論(fuzzy theory)與察覺的模糊邏輯模式(fuzzy logic model of perception)，改進了傳統 ISM 只能分析二元資料的限制，其方法論及實例可提供心理計量或課程單元等有關複雜元素的系統化決定。在實證研究方面，林原宏(2005)應用模糊詮釋結構模式分析高年級學童的網路化分數減法，發現不同能力值的學童之概念結構各有其特徵。陳紹銘(2006)以模糊詮釋結構模式分析國小六年級學童的等量公理概念之階層結構。祝淑梅(2007)以國小高年級小數概念為施測內容，應用模糊詮釋結構模式分析學童的小數概念階層結構圖之特徵。紀順雄(2007)利用模糊詮釋結構模式分析國小六年級學童的分數加法概念結構，發現不同能力值的學童的分數加法概念結構有差異存在。對於知識或概念從屬關係程度的描述，模糊詮釋結構模式的確是一個可行的方法，因此本研究欲應用模糊詮釋結構模式分析方法，進行國小六年級學童的因數與倍數概念階層結構探討，並根據個別學童的概念結構圖，比較低、中、高三組不同能力值的學童概念結構圖之差異。而測驗總分相同的受試者，其認知的結構也會有所差異，因此研究中亦將答對試題題數相同但反應組型不同的學童比較其概念結構圖之異同以瞭解個別學童之差異所在。另外，每一試題內的概念屬性之階層結構圖分析，亦有助於教學者瞭解學生的試題內概念屬性結構、診斷學生的學習困難，因此本研究亦比較不同能力值學童間及答對題數相同但反應組型不

(13)

同的學童，其試題內概念屬性結構之異同。最後，本研究以專家的概念結構圖為參照，將學童的概念結構圖與專家的概念結構圖做比較，以獲得每位學童概念結構圖之相似性係數，並檢定不同能力值組學童的概念結構圖與專家概念結構圖的相似性係數之差異及不同能力值組學童間，其概念結構圖相似性係數之差異。本研究之分析比較，可獲得六年級學童之因數與倍數概念階層結構與概念間的連結關係，及概念結構與其能力值高低的不同而產生之差異，依據此差異，可提供教師作為分組教學課程規劃之架構，或是進行補救教學之課程設計之參考，以提升學生的因數與倍數概念學習成效。

第二節研究目的

基於以上敘述，本研究就因數與倍數相關概念屬性(concept attribute)，以國小六年級學童為研究對象，編製因數與倍數測驗，運用模糊取向的詮釋結構模式將施測所得之資料加以分析，以期呈現因數與倍數的概念結構。本研究之目的有下列六點：一、探討國小六年級學童學習因數與倍數概念之結構特徵。二、探討低、中、高能力的學童其因數與倍數概念結構圖之特徵並分析其概念圖間之異同。三、分析低、中、高能力的學童其因數與倍數試題內概念屬性結構圖之異同。四、分析答對題數相同但反應組型不同之學童，其概念結構圖與試題內概念屬性結構圖之異同。五、比較低、中、高能力組，其因數與倍數概念結構圖與專家概念結構圖的相似性係數之差異。六、比較低、中、高能力組間，其因數與倍數概念結構圖相似性係數之差異。

(14)

第三節名詞釋義

壹、因數與倍數相關名詞

根據教育部(2003)公佈的「九年一貫課程數學課程綱要」之標準用詞與解釋中提到有關因數與倍數的相關名詞如下：一、因數與倍數：一不為零的整數甲若能整除另一整數乙，甲稱為乙的因數，乙稱為甲的倍數。國小階段只學習正因數、正倍數，國中階段則引進負因數、負倍數的學習。二、公因數與最大公因數：一整數甲同為兩個以上整數的因數時，則甲為這些數的公因數。公因數中最大者即稱為最大公因數，最大公因數一定為正整數。三、公倍數與最小公倍數：一整數乙為兩個以上的整數的倍數時，乙稱為這些數的公倍數。在所有正公倍數中最小者稱為最小公倍數。四、質數：一大於 1 的正整數只有 1 及本身兩個正因數時，稱為質數。五、合數：又稱合成數，大於 1 的正整數中不是質數者稱之。六、互質：兩正整數除 1 外無其他公因數者稱為兩數互質。七、質因數：是質數又是某數的因數，稱為某數的質因數。八、短除法：判別一數或一數以上的因數時只寫出除數和商，並不詳細運算除法過程，若除數皆為質數，其過程即稱為質因數分解九、標準分解式：一正整數作質因數分解時將質因數由小至大以連乘式表之，質因數相同者用指數形式簡記，如：12=2×2×3=22_{×3(或 2．2．3)。}

貳、試題反應理論

試題反應理論(item response theory，IRT)是現代測驗理論重要的基礎，係利用數學函數來描述受試者的潛在特質(latent trait)和答題反應機率之間關係的測驗理論(余民寧，1991)。亦即受試者的答題反應機率是受潛在特質所影響，數學函

(15)

數模式中包含了受試者能力 (ability) 與試題的難易度 (difficulty) 、鑑別度 (discrimination)和猜測度(guessing)等參數，而答題反應機率與能力值所繪出的曲線則稱為「試題特徵曲線」(item characteristic curve, ICC)。根據試題參數數目的不同，目前常用的試題反應模式有單參數邏吉斯模式(one-parameter logistic model)、雙參數邏吉斯模式(two-parameter logistic model)以及三參數邏吉斯模式 (three-parameter logistic model)等。

參、能力值

本研究之能力值係根據受試者的作答反應資料，運用試題反應理論數學函數模式進行估計而得，指的是受試者的潛在特質。本研究之能力值的取得由研究者利用 IRT 電腦程式 BLLOG-MG 分析而產生。

肆、知識結構

所謂知識結構是指儲存在長期記憶中的一種結構組織，這種結構組織能清楚的顯示出各概念間的關係。係指學習者透過內在的認知歷程，將數個單一概念組合之後所形成的關聯組織，本研究透過模糊取向詮釋結構模式分析法之運算流程，採用林原宏(2004)開發之 AISM 程式，繪製出學習者之知識結構圖，稱為 ISM 概念圖。

伍、詮釋結構模式

Warfield (1976) 所提出的詮釋結構模式原為社會系統工學之一種構造模型法，植基於離散數學和圖形理論，透過二維矩陣的數學運算，呈現出一個系統內全部元素間的關聯性，及完整的多層級結構化階層(Warfield, 1974, 1977)。

陸、糢糊取向的詮釋結構模式分析

此分析法由林原宏(2005)提出，結合了模糊理論與察覺的模糊邏輯模式(fuzzy logic model of perception)，改進傳統 ISM 只能分析二元資料限制，且可分析個別

(16)

化(individualized)之知識結構圖，其軟體 AISM 程式可以繪製受試者在學習某個領域所習得之概念結構。

第四節研究限制

本研究旨在運用模糊取向的詮釋結構模式將國小六年級學童之因數與倍數測驗予以分析與討論，以期呈現不同能力值學生因數與倍數概念結構的特徵與差異，然而因時間、人力等相關因素，本研究亦有其限制之處，茲分別說明如下。一、因數與倍數知識所涵蓋的概念屬性很多，而本研究只針對九年一貫數學課程綱要能力指標分年細目詮釋中與高年級有關之因數與倍數相關概念，編製因數與倍數知識測驗工具，來瞭解國小六年級學生因數與倍數知識的概念結構。本研究中研究者主觀地將因數與倍數區分為 25 個概念屬性，但這些概念屬性是否就可完整地代表因數與倍數所需的全部能力，則可以再進一步加以探討。二、本研究宥於時間及行政溝通等各方面因素，故採方便抽樣方式選取臺中縣市的六年級學生為研究樣本，所以本研究的受試者概念結構之分析與比較，並無法推論到其他縣市的學生上，為了避免地域性關係所造成的影響，因此後續的研究者可多抽取不同地區的學生作為研究對象，以進行更全面的研究。

(17)

(18)

第二章文獻探討

本研究文獻探討的部分將分五節，針對本研究之相關理論進行文獻探討。各節所探討主題如下：第一節因數與倍數概念研究；第二節模糊理論；第三節模糊取向之詮釋結構模式分析法；第四節試題反應理論；第五節知識結構測量理論。茲將各節內容分述如下：

第一節因數與倍數概念研究

壹、從八十二年版課程標準了解因數與倍數教材的設計原理

八十二年國民小學數學科課程標準教材綱要數與計算部份，所介紹的因數與倍數內容僅僅只有因數、公因數的認識、倍數、公倍數的認識，和六十四年版相較之下，它少了最大公因數、最小公倍數、質數與合數、因數分解與質因數分解、短除法以及2、3、5、11 等質因數的判斷法這些內容。以下針對八十二年國民小學數學科課程標準教材綱要數與計算部份，與因數與倍數有關教材予以介紹，以明瞭因數與倍數相關教材及活動的設計與處理方式。一、因數問題在教導因數時，先由乘法的觀點切入，藉由乘法規則，先讓學童知道「被乘數×乘數＝積」和「因數」關係，接著再讓學童利用除法的技巧來找出並檢驗某數是否為另一數的因數，並讓學童從解決包含除及等分除的問題中，解決剛好分完的情況來建立因數的概念(教育部，1993)。在課程安排上，若直接由數的情境進入因數的意義，學生會出現很大的不適應，因為數的本身相當抽象，而學生的測量運思尚未發展完全，無法將等分除與包含除視為相同的問題(黃國勳、劉祥通，2003；謝堅，1995)，故在課程安排上由情境問題進入，探討因數的意義，待學生累積足夠的經驗後，再正式引入因數

(19)

的意義(于國善，2004；謝堅，1995)。八十二年課程中透過下列三種問題情境(謝堅，1995)，幫助學童逐步形成因數的概念：(一)在方陣排列問題中，探討給定總量的方陣之可能排法，讓學童經驗給定總量的方陣可以有不同的排法；(二)在包含除及等分除的情境問題中，給定總量，要求學童回答可能的等分組方式，幫助學童掌握總量可以由哪些單位量組成的意義；(三)在倍的問題情境中，給定總數，要求學童解決可能組成單位量的數值問題，幫助學童掌握哪些單位量可以組成總量的意義。同時亦透過限制使用除法算式來記錄解決前述問題解題過程的方式，希望學生在各種情境問題中，都能掌握總量可以由哪些單位量組成的意義，並形成以總量為起點，使用除法算式記錄解題過程的共識，課程中不希望學生以部分的觀點，透過合成的方式來看問題，而希望學生由全體的觀點，透過分解的方式來看問題。二、因數和倍數的關係因數與倍數的關係，在數上是以除法原理(若有 a、b 兩個正整數，則必可找到q、r 兩個非負整數，滿足 a＝b×q＋r 的關係，且 b＞r≧0)為基礎，透過判斷 a 是否能整除b(餘數是否為 0)的方式，引入因數與倍數的定義：「設 a、b 是兩個正整數，若a＝b×q＋r，其中 q 是正整數且 r＝0，則稱 b 是 a 的因數，或稱 a 是 b 的倍數」(教育部，1993)。若直接透過因數的意義來引入倍數(若 b 是 a 的因數，就等同於 a 是 b 的倍數)，這時因為成人已發展出測量運思，因此可以彈性地互換單位量與單位數的角色，並已瞭解乘法、除法互為逆運算的關係，因此成人可以掌握因數與倍數的相對關係，明白a 是 b 的因數時，b 就是 a 的倍數的意義。但是對測量運思尚未發展完全的學童而言，並不易掌握因數與倍數的相對關係(黃國勳、劉祥通，2003；黃耀興、邱易斌，1999)，因此在課程安排上不採用此方式來引入倍數，而分別從不同的角度引入因數與倍數的意義。課程中透過下列活動，逐漸培養學童測量運思的發展，幫助學童能察覺因

(20)

數、倍數間的相對關係，並經驗數概念的乘法性結構(謝堅，1995)：(一)透過判斷一個整數是否為其因數的整數倍的方式，讓學童察覺此整數為其所有因數的倍數；(二)透過先求出某數所有的因數，再判斷該數是否為其所有因數的倍數的方式，幫助學童察覺一數是其所有因數的公倍數；(三)透過解決兩數相乘問題，幫助學童察覺兩數相乘的積數為兩數的公倍數，並希望學童能不經過計算的過程，就直接能判斷兩數相乘的積數為兩數的公倍數。三、倍數問題在引入倍數的意義方面，學生於高年級階段已有足夠的經驗，可以直接引入倍數的意義，因此課程中透過乘數未知的乘法算式填充題「2×( )＝10」，先要求學童解題，再經由語言的轉換，2 的 5 倍是 10，所以 10 是 2 的 5 倍，引入倍數的意義。在數學上，如果a 是 b 的倍數(b 是 a 的因數)，則 a，b 要滿足下列三個條件：(一)a，b 都是整數；(二)b≠0；(三)存在一個整數 q，滿足 a＝b×q(教育部， 1993)。四、公因數問題與因數問題一樣，在課程安排上也透過下列三種問題情境，幫助學童逐步形成公因數的概念(謝堅，1995)：(一)在方陣排列問題中，探討兩個方陣的可能連接方式；(二)透過包含除及等分除的情境問題，先要求學童分別找出兩相異量各自的可能等分組的方式，再透過比較各自的等分組方式，解決等分組的可能數值問題；(三)在倍的問題情境下，給定兩總量，透過比較各自可能的單位量數值，找出相同單位量的可能數值。希望學童在各種情境問題中，都能解決兩總量可以有哪些相同單位量的問題，來為形成公因數的概念舖路。而透過先分別找出兩個數的所有因數，再從中找出公因數，從求法中來讓學童知道公因數的意義。五、公倍數問題以探討一個指定正整數有哪些倍數為基礎，可以探討兩個正整數有哪些共同的倍數的問題，這些共同的倍數稱為公倍數。當學童已有求出某數在某一數量範

(21)

圍內的所有倍數，以及求取兩數公因數的經驗後，應該也能夠掌握公倍數的意義。

貳、九年一貫課程綱要數學領域中的因數與倍數教材

九十二年九年一貫課程綱要數學領域的課程中，因數與倍數知識歸屬於五大主題之一「數與量」的「整數」子題中。對於因數與倍數教材內容的編輯及相關基本能力，有明確的說明與規定，其中因數與倍數部分在五年級與六年級的能力指標包括(教育部，2003)： N-2-04 能理解因數、倍數、公因數與公倍數。 N-3-01 能認識質數、合數，並做質因數分解。 N-3-02 能理解最大公因數、最小公倍數與兩數互質的意義，並用來將分數約成最簡分數。進一步分分析在九年一貫數學課程網要能力指標中，分年細目詮釋如表2-1 所示，該表可提供更詳細說明(教育部，2003)：表2-1 因數與倍數相關九年一貫數學課程網要分年細目詮釋分年細目內容說明 5-n-03 能理解因數、倍數、公因數與公倍數。 (1) 以 1-n-07( 幾個一數 ) ， 2-n-08( 九九乘法 ) ， 3-n-04(除法)為前置經驗，理解因數、倍數的概念。 (2)用列表的方式，尋找兩數的公因數與公倍數。學童應知道兩整數的乘積一定是此兩數的公倍數。

(22)

表2-1 因數與倍數相關九年一貫數學課程網要能力指標(續) 分年細目內容說明 6-n-01 能認識質數、合數，並作質因數的分解(質數＜20，質因數＜10，被分解數＜100)。 (1)在 5-n-03，製作整數的因數表時，可以發現有一些整數不能再被分解，這些數稱為質數，他們的因數只有1 與自己而已。大於 1 且不是質數的整數(或有 3 個以上因數的整數)稱為合數。 (2)在對一數做因數分解的練習裡，發現遇到質數就必須停下來。同時在紀錄分解的樣式及整理中 (此時的質因數乘積不寫成指數形式)，發現不管怎麼分解，形式都一樣。 (3)例：60＝6×10＝(2×3)×(2×5)＝2×2×3×5，或 60＝ 15×4＝(3×5)×(2×2)＝2×2×3×5＝2²×3×5 等。 (4)牽涉因數分解的細目(參見 6-n-02)，都應遵循如下原則：質因數＜10，被分解數＜100。 (5)讓學童熟悉 20 以內的質數之倍數(小於 200)。並可從活動中，讓學童掌握2、3、5 的倍數規則。 6-n-02 能認識兩數的最大公因數、最小公倍數與兩數互質的意義，理解最大公因數、最小公倍數的計算方式，並能將分數約成最簡分數。 (1)最大公因數、最小公倍數的初步教學，以列舉觀察為主，待學童熟悉其意義後，再介紹短除法，計算兩數的最大公因數與最小公倍數，數目大小原則參見6-n-01。 (2)兩數的最大公因數是 1 稱為互質。注意區辨互質與質數的不同。例如14 與 15 雖然都是合數，但兩者互質。由上所述可知：最大公因數、最小公倍數、質數與合數、質因數分解、互質，在八十二年版課程標準中並沒有把它列入學習教材中，但在九年一貫數學領域課程綱要中又被列為學習內容。茲將目前使用最普及之南一、康軒、翰林三個版本的教學重點摘要如表2-2，以做作為因數與倍數概念測驗編製之參考。

(23)

表2-2 九年一貫各版本因數與倍數相關單元教學重點摘要表版本冊別翰林版康軒版南一版五上單元三、因數與倍數 1.因數的認識及求法。 2.質數與合數。 3.公因數與最大公因數。 4.倍數的認識及求法。 5.公倍數與最小公倍數。 6.因數和倍數的關係。單元五、質因數分解 1.認識質因數與質因數分解。 2.互質。 3.最大公因數的應用。 4.最小公倍數的應用。單元二、因數與倍數 1.整除的意義與因數的關係。 2.正整數的因數、公因數。 3.整數的倍數、公倍數。 4.因數與倍數的關係。 5. 倍數關係的模式規律 (2、3、5、10 的倍數)。單元六、因數和倍數 1.整除的意義。 2.因數的意義。 3.能找出某數的因數。 4.找出 1 個整數的所有因數。 5.認識相同的因數。 6.能找出 2 個整數的相同因數。 7.能找出 2 個整數的所有公因數。 8.認識倍數的意義。 9.察覺倍數的無限多。 10.能把倍數整理成表。 11. 了解倍數和因數的關係。六上單元三、質因數分解的應用 1.質數及合數。 2.質因數及質因數分解。 3.最大公因數與互質。 4.最大公因數的應用。 5.最小公倍數及應用。單元一、最大公因數與最小公倍數 1.質數、合數的意義。 2.認識質因數，並學會質因數分解。 3.認識最大公因數，並知道兩數互質的意義。 4.用短除法找出兩數的最大公因數。 5.應用最大公因數解決生活中的問題。 6.認識最小公倍數。 7.用短除法找出兩數的最小公倍數。 8.應用最小公倍數解決生活中的問題。單元二、最大公因數和最小公倍數 1.經驗質數和合數的意義。 2.了解質數和合數的意義。 3.了解質因數的意義。 4.將一個數表現成其質因數的連乘積，並加以記錄。 5.了解質因數分解的意義。 6.用短除法將一個數做質因數分解。 7.最大公因數的意義，並能從所有公因數中，找出最大的公因數。 8.從給定兩數，透過列出所有的公因數來探討互質的意義。

參、因數與倍數概念相關研究

國內探討因數倍數問題的研究中，其研究對象幾乎都是國小學童，國外則大都是集中在國中以上的階段。研究者在探討因數與倍數概念的主題時，方向大多

(24)

是有關學生在因數與倍數教材上的學習困難及迷思概念(吳彥廷，2005；周文忠， 2002；林珮如，2002；邱慧珍，2002；施美多，2006；陳清義，1995；陳標松， 2003；黃寶彰，2003；黃國勳、劉祥通，2003；Graeber & Tirosh, 1990; Mayer, 1992; NCTM, 2000; Nevin, 2002; Vergnaud, 1983)，另外亦有研究者分別針對補救教學之策略與原則(于國善，2004；王詩惠，2004；蕭正洋，2004；謝哲仁、林榮貴，2006)、因數與倍數學習表現差異(何欣玫，2004；施美多，2006；陳標松，2003；蕭金土， 1995)、因數倍數教材的編製與創新(黃培甄、葉啟村，2005；黃國勳、劉祥通， 2003；Bassarear, 1997; Kennedy, Tipps, & Johnson, 2004)等方面進行探討，茲將這些研究，分述如下：

一、因數與倍數學習困難與迷思概念之研究

Vergnaud (1983) 在其所提出的乘法概念域(multiplicative conceptual field, MCF)中認為乘法、除法與因數概念的關係是密不可分的，若學生因乘、除法等概念理解不清楚，則會因先備知識的不足、造成因數概念的解題因難。

Graeber and Tirosh (1990) 研究以色列及美國地區四、五六年級學童的乘除法表現，發現學童仍有乘法會變大，而除法會變小的錯誤概念存在。NCTM (2000) 美國數學教師協會在其所發表之「數學課程之原則與標準」(The Principles and Standards for School Mathematics)中亦提到：由於學生受到整數經驗的影響，學生有乘法會變大，而除法會變小的錯誤概念。因此當學生在解題中，需要使用乘法或除法時，此錯誤概念影響了其判斷，導致學習因數概念時會有迷思概念存在，例如學生認為因數就是小的數，所以求因數要用除的方式。 Mayer (1992) 認為語意轉譯能力的不足，對數學名詞意義理解不清，使得學生在問題的閱讀理解及解釋上產生困難，而造成因數解題上的錯誤。 Nevin (2002) 分析38名土耳其小學六年級學生對於因數與倍數的解題策略，結果顯示學生對於問題中的語意、字彙無法完全瞭解，因此不能理解問題；且學生在解決問題的過程，最大的困難是題意理解及符號形式的轉譯，原因為學生在

(25)

問題解決的過程中，使用不正確的錯誤概念。陳清義(1995)運用知識結構分析技術，分析國小五年級數學科因數、倍數兩單元教材的內容概念，據以編製紙筆測驗，並運用無參數試題反應理論所發展出的ICCNP軟體探索試題與受試者的量化特性，然後藉由晤談的方法探討國小五年級學生在因數與倍數這兩個單元的學習瓶頸。研究的結果發現：(一)學生對質數、奇數、合數、偶數等概念的定義、相互之間的關係混淆不清，經常誤用、混用； (二)學生會使用短除法來解決問題，但卻不會使用試除法或是因數分解來解決問題，因此當題目規定不能使用短除法時，學生就發生了學習瓶頸。其原因可能是平時學生練習都只注重短除法，且未能了解此法的真正涵意；(三)在解決文字應用題方面，學生缺乏判斷題意是要求最大公因數或最小公倍數的能力，而當告知學生短除法與除法各數的相互關係後，學生便能判斷要求最大公因數或最小公倍數。

林珮如(2002)依據R. E. Mayer與R. Brainbridge的解題理論(problem solving theory)和直觀法則(intuitive rules)，自編因數迷思概念診斷工具，探討145位五年級學童在因數問題的解題策略、迷思概念及可能成因。其研究發現：(一)國小學童在「因數迷思概念診斷工具」中的答題表現不佳；(二)國小學童在學習因數時的錯誤解題策略和原因，包括用乘除解題時錯誤連結、用一一列出對應方式解題時，粗心或計算錯誤、缺乏閱讀解釋問題能力以致誤解題意、採用關鍵字解題錯誤等；(三)國小學童學習因數時的迷思概念共計有概念混淆不清、概念遺漏與概念錯誤三大類。原因包括先備知識理解不清產生錯誤連結、相類似的知識造成混淆干擾、缺乏閱讀解釋問題能力以致誤解題意、採用關鍵字解題等。邱慧珍(2002)自編倍數迷思概念診斷試題，藉由試題施測結果分析及晤談資料，整理出150位國小五年級學童在倍數的相關知識的錯誤解題策略與迷思概念有三點：(一)國小學童在倍數迷思概念診斷試題的答題表現並不理想；(二)國小學童在解倍數相關知識時的錯誤解題策略有：以乘除符號直接判斷是否為倍數、將

(26)

專有名詞誤解、認為1是倍數、遺漏數字本身是倍數、以及用猜測的方式找解題策略、或用關鍵字解題、計算粗心、空白未作答等不正確的解題策略；(三)因為先備知識不足、概念理解不清楚、解題執行不正確或不了解題意等原因，而造成倍數相關概念混淆、概念遺漏或概念錯誤的迷思概念類型。周文忠(2002)利用診斷工具測驗及採用半結構晤談方式，以深入了解學生對於因數及倍數的解題歷程，及所出現的迷思概念，並探討其成因。結果發現國小高年級學童在學習因數及倍數時所產生之迷思概念，有下列幾項較為明顯之原因：(一)先備知識不足(乘法、除法不精熟)；(二)概念錯誤(因數、倍數概念不完整)； (三)粗心(運算錯誤、遺漏、忽略)；(四)概念混淆不清(如因數、公因數、倍數、公倍數混淆不清)；(五)利用關鍵字解題(以數字的大小來判斷，例如數字大的便代表倍數，數字小的便代表因數)；(六)直觀法則(「因數」就是分的所以要用「除」的，「倍數」就是變大所以要用「乘」的)；(七)語文知識不足，亦即缺乏閱讀問題的能力；(八)問題轉譯能力不足，缺乏解釋問題的能力；(九)策略知識不足，無法以運算式表示問題；(十)不當的遷移，無法將因數、倍數的概念應用於文字題情境上。陳標松(2003)以636名國小六年級學童為研究對象，發現數學學習困難學生主要迷思概念有以下三點：(一)乘除運算概念錯誤，在運算中出現錯誤，而且大都是系統性的乘除運算錯誤，只有少部份學生是粗心的錯誤，顯示學生需要加強乘除運算能力；(二)語言概念存在錯誤，主要錯誤類型可分為題意了解錯誤與專有名詞概念錯誤兩種，而專有名詞錯誤又可細分為因數概念錯誤、倍數概念錯誤、公因數概念錯誤、公倍數概念錯誤和因數倍數關係概念錯誤，顯示這些學生需要加強語言識字和概念學習的能力；(三)策略概念錯誤，主要錯誤類型又可分為解題策略錯誤和隨機反應錯誤，顯示這些學生需要加強解題策略的能力。黃寶彰(2003)以109位六年級和96位七年級學生為研究對象，探討學生在學習困難部分的思考方式、錯誤的解題策略或迷思概念發現六、七年級學童在「因數

(27)

與倍數」這部分的學習困難和錯誤情形為：(一)學童在因數、倍數、兩數的公因數、公倍數、最大公因數、最小公倍數、最小公因數、最大公倍數意義瞭解較無困難，但是在求法上，容易有因為粗心而出現遺漏或多選的情形；(二)因為名詞混淆不清或對陌生名詞的不瞭解，在求法上出現顛倒或錯誤的答案，其中七年級在因數、公因數、最小公倍數較六年級更嚴重；(三)在利用最大公因數及最小公倍數解決文字題方面，兩個年級學童主要困難是轉譯題意有困難，不瞭解是要選擇最大公因數還是用最小公倍數來解決問題。黃國勳和劉祥通(2003)從實務經驗和學童因數教材診斷的探討，發現因數教材對國小學童是很困難的，其困難的原因可歸納為四個方面：(一)從認知運思能力來看：由因數的定義來看，因數屬於R. J. Gagné所提的概念學習，它是由整除概念抽象後再抽象而得概念。從J. Piaget的認知發展論(cognitive-developmental theory)來看，剛升上國小五年級學童尚處於具體運思期，他們的推理思維能力只限於眼見的具體情境或熟悉的經驗，因此對於因數概念的學習是感到困難的；(二) 從先備知識來看：因數是由整數的乘除法等幾個元素所組成，這些組成的元素為「下屬概念」，相對的，因數概念則為其子概念的「上位概念」，因此，因數可說是由複雜概念所組成之更複雜更抽象的概念，學生若未具備整數乘除法的能力則學習因數時會產生困難；(三)從生活經驗來看：因數的概念很抽象，對學生而言，它只是一個獨立於生活之外的數學名詞，比較難透過具體的活動讓學生真正理解因數的意義，學生更因為不了解數學名詞字彙，不理解特定的專有名詞，導致對因數、公因數概念的混淆不清；(四)從語意理解來看：學生在學習數學時，往往因為無法理解特定的專有名詞，以致基本概念混淆不清，或是在問題的閱讀理解和解釋能力不足，而造成學習上的障礙，此外語意知識的不足和錯誤，會影響他對問題的轉譯與解碼，造成解題上的錯誤。吳彥廷(2005) 以33位五年級學童為研究對象，發現學童在因數與倍數這個單元的學習上，存在著許多的錯誤概念，而學童在學習此單元時，也確實存在著許

(28)

多的障礙，其研究歸納因數與倍數迷思概念，分為教學上的不足或錯誤的迷思與學習者自行建構錯誤的迷思二大類。在教與學上的不足或錯誤方面：(一)學生經常使用一種方法解決問題；(二)學生有名詞混淆的情形發生，且學生是因為教師的教學方法有問題或是教學不清楚而產生；(三)學生常常在解決文字應用題時，無法判斷題意是要求最大公因數或最小公倍數的能力。在學習者自行建構錯誤方面：學生有名詞混淆的情形發生，為學生自己類化錯誤而產生。施美多(2006)探討學童學習因數概念的知識結構，並了解學童學習因數概念易犯的錯誤或迷思概念，研究發現學童學習因數概念易犯的錯誤或迷思概念為： (一)只思考一個數的特性(如：質數)比思考二個數的關係(如：互質)，對學童而言是較困難；(二)許多學童在「1是否為質數？」產生迷思；(三)由除法算式引入因數概念會比由乘法算式引入更容易使學童接受；(四)近30％的學童沒有具備周延的過程概念，未具備隱藏性知識的概念，無法彈性思考解題過程中隱藏性知識的意義；(五)近20％的學童在思考因數時，常會把因數的基本成員「1」給遺忘。綜合上述，國小學童在因數與倍數的學習上，確實存在許多學習因難與迷思概念，使其在學習上備感困惑，因此教學者在教學時，若能瞭解這些困難與迷思概念的存在，才能針對這些困難之處，設計一些修正的教學活動，如此不但能避免學生產生迷思概念，更有助於學習的成效。二、補救教學之策略與原則之研究許多研究者對於學童因數、倍數迷思概念之研究後，有研究開始提出補救教學方法，利用學習策略、教學補救等方式，認為都可有效改善學童學習困難與迷思概念所在。于國善(2004)研究設計「國小因數單元」補救教學活動，對三位個案採個別化教學方式進行，教學活動以生活化、情境化、具體化及個別化為設計原則。過程強調以學生為主體，並將學習問題結合其經驗、情境，讓學生能動手操作、實

(29)

際參與，且由學生自己說出「整除」意義，進而逐步建構「因數之概念」。其研究發現：(一)發展因數補救教學活動必須把握三點原則：1. 由學生動手操作實物，以協助其認知發展之不足；2. 運用具體物，建構學生「整除」概念，並強調「順序性」，以避免遺漏或多找的情形產生；3. 結合學生生活經驗與週遭情境(如分裝農業特產等)，使轉譯題目時不致產生困擾；進而瞭解「1」是任何數的因數概念。(二)個案經過補救教學後，在筆試測驗、解題能力與因數概念改變上均有提升的效果；(三)透過補救教學活動後，個案均能說出因數及整除之意義。王詩惠(2004)開發國小數學科因數教學模組運用作為國小五年級補救教學之材料並探討四位學生的學習成效，研究顯示因數教學模組確實能幫助學童突破學習因數概念的困境。其學習成效方面的結果為：(一)在因數窮舉方面，除法心理運作能力快的學童，若能掌握求因數所需的原則，則能將因數完全窮盡；但若對除法心理運作能力慢的學童來說，即使了解因數的概念，但因在判斷兩數是否為整除關係時就需耗費很多時間，無形中增加計算上的複雜性，因而不能將一個數的因數完全窮盡；(二)學童透過具體的因數組成表格自行發覺因數的組成情況，可以改正「數字越大，因數個數就越多」的迷思；(三)學童透過具體的因數組成表格歸納出因數的組成情況，可以理解質數與合成數的概念；但在「1不是質數」的概念上仍有待加強；(四)學童透過察覺每一次公因數的解題結果，不僅改正「比較數字越多時，公因數個數就越多」的迷思；同時也能幫助理解「互質」的概念； (五)學童透過教學模組，可以改正「公因數只指兩個數共同擁有的因數」及「因數一定比本身還要小」的迷思；(六)學童經由具體物的操弄及師生共同討論，皆能增進對文字題的理解，但在解題方面，對部分學童來說仍不能用數學符號清楚表示之。蕭正洋(2004)以筆試測驗調查學童倍數迷思概念及錯誤解法，並設計倍數補救教學活動，探討對三位個案教學實施之歷程及其成效。其研究發現：(一)透過實物對照及操作，著重於單位量、單位數與總量的概念，進而引入總量為單位量

(30)

之倍數概念的教學設計有其成效；(二)在補救教學後，學生原有的迷思概念及錯誤解題情形，例如：認為倍數就是用乘法、認為1是倍數或公倍數、找倍數時遺漏數字本身及利用關鍵字解題等，均已獲得改善。在在筆試測驗、解題能力、數學學習態度方面，亦有明顯的進步及轉變。謝哲仁和林榮貴(2006)針對「國小因數與倍數單元」設計補救教學活動，選取六年級一個低成就生為對象，建構一個可經由操作及探索的視覺化學習環境，藉由電腦的動態情境操作，進行補救教學課程，研究結果顯示以行動為主的電腦設計圖形表徵，讓個案學生在處理因數與倍數問題時，更能理解問題的意義，掌握各種外在表徵之間的關係變化，並產生具體可操作的心靈影像，提升其學習成效。因數與倍數的概念相當抽象，因此生活化、情境化的教材設計配合具體物的操作與電腦輔助的融入，是在補救教學中不可或缺的一環，如此才能順利改善學童認為因數與倍數備感困難之困境。三、因數與倍數學習表現差異之研究蕭金土(1995)針對國小五年級數學學習障礙學生和普通學生，比較其錯誤類型，及探討學習策略教學對數學學習障礙學生之學習成效。研究結果發現部分學生無法理解因數倍數的概念，因其缺乏因數倍數關係形成和類化的能力，而學習策略教學在因數倍數單元教學中，能有效提昇數學學習障礙學生之學習成效。陳標松(2003)研究636名國小六年級學生在因數倍數問題的解題表現，比較數學學習困難和數學表現優異學生在因數倍數問題解題之差異，研究發現：(一)國小六年級學生在因數倍數問題測驗中的總答對率為70％，得分分配情形十分分散，且呈負偏態狀況，在測驗中學生對於運算題目表現較佳，且對倍數和公倍數的觀念較容易著手，但對因數和公因數的學習則較感困難；(二)數學學習困難和數學表現優異學生在因數倍數測驗試題中，無論在得分或是各題的選答狀況上，

(31)

都有明顯的差異存在，而且組別與選項間具有關聯性。數學表現優異學生答對率 89％，得分集中在高分區；數學學習困難學生答對率48％，得分偏低且分散；(三) 數學學習困難學生在因數倍數問題中的主要迷思概念有：乘除法運算概念錯誤(系統性錯誤和粗心錯誤)、語言概念錯誤(題意了解錯誤和專有名詞概念錯誤)、策略概念錯誤(解題策略錯誤和隨機反應錯誤)。何欣玫(2004)根據因數與倍數之數學解題溝通能力的內涵，編製因數與倍數解題溝通能力測驗，以364位六年級學童為施測對象，分析學生的因數與倍數的解題溝通能力。其研究結果摘述如下：(一)研究之溝通層次分為「表達自我想法」、「理解他人想法」與「評價他人想法」，題目類別分為「因數」、「公因數」、「倍數」及「公倍數」。整體而言，「表達自我想法」與「理解他人想法」優於「評價他人想法」；「因數」的溝通能力優於「倍數」的溝通能力；(二)在「表達自我概念」上，「因數」優於「公因數」及「倍數」，「倍數」優於「公倍數」；「符號表徵」的了解優於「理解題意」，「解題」優於「表達溝通」。在「理解他人想法」中，其能力表現依次為「判斷」、「轉化」、「認同說明」、「質疑辯證」。在「評價他人想法」中，「因數」優於「公因數」、「倍數」、「公倍數」，而「公因數」優於「公倍數」；「辨別」優於「澄清與補充」和「評鑑」； (三)其研究溝通類型分為內向表達型、外向理解型、全能優越型及多層障礙型；其中多層障礙型的人數百分比最高，全能優越型最少；(四)因數與倍數概念之錯誤類型分析可分為：1. 語言概念錯誤，包括題意了解錯誤、語意知識不足、專有名詞概念混淆；2. 認知概念錯誤，包括運思能力不足、粗心錯誤、運算系統錯誤、直觀法則影響；3. 策略概念錯誤，包括解題策略錯誤、計劃監控失誤；4. 個人態度錯誤，包括厭惡思考、猜測。施美多(2006)採用自編之因數試題為研究工具，經SPSS/PC統計套裝軟體及試題關聯結構理論之IRS電腦程式進行統計分析後，探討學童學習因數概念的知識結構與專家知識結構的不同，研究發現學童在因數概念之知識結構發展有以下

(32)

的特點：(一)「互質概念」是「質數概念」的下位概念；(二)「合數概念」是「質數概念」的下位概念。；(三)「公因數概念」是「質因數分解概念」的下位概念。因此因數與倍數學習表現優異或是學習表現困難的學生，兩者在解題得分或是知識類型上雖有差異之處，但對於因數與倍數教材仍皆有迷思概念的存在。四、因數倍數教材的編製與創新之研究 Bassarear (1997)認為在學習最大公因數與最小公倍數時，可以使用維恩圖 (Venn diagram)來協助學童對於概念的理解。這種以圖形來展示不同事物群組(集合)之間的數學或邏輯聯繫，可以幫助學童以視覺的方式來理解兩數各自擁有的質因數之間的關聯，即交集和聯集的關係，進而理解最大公因數和最小公倍數的運算。

Kennedy, Tipps and Johnson (2004)認為在因數概念的學習上，樹狀圖的使用可有效的協助學童對於概念的釐清。例如使用因數樹(factor tree)可展示某數的結構，其方法是將一個數以其因數一層一層的分解並往下擴展，直到最底層皆為質數為止。黃國勳和劉祥通(2003)認為因數教材常造成師生教與學的障礙，正因為定義因數和因數教材文字題的語意學童較難理解，且是個抽象、複雜的概念，無法直接透過具體物來說明因數的意義。它的解題與計算過程也較為繁雜，生活中也缺少使用因數概念的經驗，使得學童在因數教材的學習上產生困擾。此外，因數的先備知識是整數乘除法，但除法又是個較難計算的算則和不容易理解的概念，對剛升上五年級的學童來說，部分學童除法問題的知識和測量運思能力仍不完備，因此學習因數教材時，會造成學習的障礙。研究結果提出五點建議，以供教師在因數教材教學的參考：(一)以具體活動來進行整除的教學：教導整除時可藉由實際的生活經驗或具體活動(如人數的分組活動)讓學生清楚的了解整除的意義，進而說明因數的意義，如此可使整除和因數意義的連結更為明確和穩固；(二)因數

(33)

教材教學前注意先備知識是否完整建立：教師不僅在乘除法的計算能力上須留意學童是否完備，同時也需注意學童對於乘除法算式的含意(如等分除和包含除)是否了解，如此才能順遂銜接因數教材的教學；(三)以簡單明確的文字來定義因數：以往定義因數時通常使用「甲數能整除乙數」或「甲數能被乙數整除」的敘述方式，常使許多學童混淆不清，教學時可以「6能被3整除，所以3是6的因數」的敘述來定義因數，學童應該更容易理解；(四)指導學童正確解釋數學問題的題意：教師應就題目的意義逐句的講解，以幫助學童學習。多數學童經由教師的引導，便能從中提升閱讀與語意理解的能力，逐漸領會因數教材問題的意義；(五)重視演算法與意義的連結，以協助學生發展過程概念：因數的計算較為繁複，當然教師有必要教導學童運算的技巧。例如，求因數時無須將整除的算式逐一算完，因為因數通常是配對出現的；或者是教導學童能被2、3、5和11等四個數字整除的判別方法，以減輕學童在計算上的負擔。黃培甄和葉啟村(2005)發現學童在因數與倍數學習上的確遭遇瓶頸與困難，其中因數學習困難更甚於倍數，這樣的學習成效，值得對現行課程架構作一深思。現行國小課程在因數與倍數的編排方式是以先教因數後教倍數的方式來處理，以除法的觀點，由總量為問題的起點，探討可能組成的單位量，來處理因數啟蒙問題等。其研究經由思考學童學習發展及分析課程架構後，研擬異於目前因數與倍數課程之創新架構，其特色共包括三部分：(一)先引入倍數教材再引入因數教材；(二)透過分的記錄引入因數教材；(三)整合強化學童因數與倍數關係。此套創新教材經由實驗教學與筆試測驗後，結果顯示學童學習成效極佳，並可提升低分組學童學習成效，維持中高分組學童學習水平。綜合上述，學童在因數與倍數相關概念的學習上，確實存在許多的學習因難與迷失概念，而透過瞭解不同類型學童的表現差異，設計良好的補救教學方法與學習策略，以及針對現行課程作一深思以提出新的學習架構，皆是改善因數與倍數學習成效的重要環節。

(34)

第二節知識結構測量理論

認知心理學家強調人類大腦中的知識是有組織、具有結構性，而非以雜亂無章的方式來表徵儲存外界訊息。而知識表徵(knowledge representation)的問題向來是認知心理學家所關心的議題。人類在習得知識與技能後，在腦中是如何儲存的？概念之間的關係又是如何？近年來，認知心理學家對於人類知識表徵的研究中，提出了許多知識在大腦中儲存的模式，增進了我們對於知識結構的理解，由此也引發了研究者對於學習如何影響知識結構、知識結構如何影響學習以及如何測量知識結構的興趣(Goldsmith, Johnson & Acton, 1991)，而這些研究和探討則有助於了解個體如何獲得知識的心理歷程，幫助個體找出迷失概念和診斷其學習，以提高學習的成效。

心理研究領域上對知識結構分析方法的探究有很多，本節將針對概念構圖 (concept mapping)、徑路搜尋網路分析法(pathfinder network analysis)、規則空間理論(rule space theory)、線性邏輯測驗模式(linear logistic test model)和知識空間 (knowledge space)等五種知識結構的測量理論，介紹其理論基礎及相關的研究。

壹、概念構圖

隨著認知心理學發展及日益受重視，心理學家嘗試以訊息處理(information processing) 、知識表徵 (knowledge representation) 與知識建構 (knowledge construction)的觀點來解釋學生的學習行為及解題歷程。而概念構圖的研究自 Novaka and Gowin (1984) 的「學習如何學習」(Learning How to Learn)一書中以 Ausubel (1963) 有意義的學習理論(meaningful learning)為基礎發展出一套教學策略與評量工具後，開始受到科學教育界很大的重視。概念構圖以概念與概念間的命題關係結合而成網狀脈絡，以期幫助學習者將新概念的學習和諧的融入原有的認知架構中，當學習者針對所學科目來自行建構概念圖時，會發現許多新的意義，並且可與其原有知識相連結，而進行有意義的學習(余民寧，2002；Novak &

(35)

Gowin, 1984)，其中所謂有意義的學習是指學生主動調整或重新建構新概念，或新概念與先前已學會的認知結構之間所產生的混淆或衝突的過程。概念構圖即是建構概念的歷程，概念圖的內涵包含命題(propositions)、階層 (hierarchies)、交叉連結(cross-links)和舉例(examples)。學生將所要學習內容的概念，先做階層性的分類與分群，含義最廣的概念置於階層的頂端，含義較小的概念依序排列於下，再以連結線將兩兩概念的關係連結起來，此兩個概念的有效連結稱為命題，是概念圖的基本單位，並在連結線上標記連結語，以說明概念間的連結關係。在學習的過程中，概念會不斷分解，形成階層擴增，新舊概念間的關係不斷被修正調整產生新的連結，此種關係稱為交叉連結。交叉連結顯示出對概念的融會貫通與創意，而適當舉例說明，表示對概念正確的瞭解，完成之後的概念構圖有如一幅網狀結構圖。因此，概念構圖是一種有意義的結構化學習法(余民寧，1997；Novak & Gowin, 1984)。

以概念構圖對學生知識進行評量，大致可分為兩個方向：一是將學生的概念圖與專家的概念圖進行比較，找出異同，進行診斷，二是依據準則對構念圖進行計分。關於概念構圖的計分方式Novak and Gowin (1984) 曾提出各種詳盡的教學步驟說明，成為概念構圖教學的重要參考資料，茲將其計分原則摘要如表 2-3。而實務的應用上研究者則可依其研究目的來調整概念構圖的加權計分方式。一個典型的計分方式舉例說明如下圖2-1 所示。表 2-3 概念構圖的計分方式成分描述計分關係連結線和連結語是否表達出兩個概念間的連結關係是有意義且有效的？每個有效且有意義的命題連結關係給一分階層概念圖能顯示出階層嗎？每一個附屬概念是否比其上階層概念更具特殊性？每個有效的階層給五分

(36)

表2-3 概念構圖的計分方式(續)

資料來源：Novak & Gowin, 1984

圖2-1 概念構圖的計分例子

(資料來源：余民寧，2002；Novak & Gowin, 1984)

成分描述計分交叉連結某概念階層的一部分和另一階層的部分概念間的連結關係是否是重要且有效的？每個重要且有效的交叉連結給十分，每個有效但不能指出相關概念之組成的交叉連結給二分階層能否根據自己的理解，舉出特殊且_{具代表性的例子？} 每個特定所舉出的事件_{或物件例子給一分} 連結階層重要概念連結一般化概念一般化概念一般化概念第一階連結連結概念連結連結例子例子事件事件連結連結較具體概念特殊概念連結連結連結連聯概念概念例子例子物件物件較具體概念交叉連結連結第二階概念特殊概念特殊概念交叉連結計分原則：（僅計算有效且重要者）（項目）：（分數） × （個數） =得分關係： 1 × 14 = 14 階層： 5 × 4 = 20 交叉聯結： 10 × 2 = 20 舉例： 1 × 4 = 4 總計： 58 分第三階第四階連結

(37)

概念構圖自J. D. Novak 創立應用在科學學習領域後，開始不斷的被應用於其他學科的教學、學習、評量和研究上。美國的Journal of Research in Science Teaching 期刊曾於1990 年第四季出版一期專門探討「概念構圖的面面觀」(perspectives on concept mapping)，即可證明其卓越的成效。

Seaman (1990) 研究以概念構圖和合作學習為學習策略對於五年級學生自然科學學習成效之影響中發現，運用概念構圖和合作學習為學習策略的學習成效優良。Okebukola (1992) 以概念構圖為學習策略運用於生物學學習之成效研究中顯示，概念構圖的學習策略有顯著的成效。Baugh and Mellott (1998) 研究運用概念構圖於內外科教學後的學習成效，結果顯示 33 位學生均認為概念圖是有效的學習工具。Castellino and Schuster (2002) 評量學生運用概念構圖於臨床照護計畫之效果，學生認為概念圖較傳統的照護計畫更能整合各項資料間之相關性。林明瑞 (1996)在建構國小環境教育概念的研究時認為完整的概念圖，可提供教學者一個完整的課程概念架構。余民寧、陳嘉成(1996)以國小五年級學童為研究對象，發現學習類型不同的學生，其結構圖與概念結構品質有所不同。江淑卿(1997)在探討不同自然科學能力的兒童，閱讀不同規模的經驗式和統計式概念構圖，對知識結構和理解能力之影響時發現不同自然科學能力的兒童，閱讀不同規模的經驗式和統計式概念構圖後，在知識結構和理解能力上有差異。陳嘉成、余民寧(1998) 以國小六年級學生為研究對象，發現合作學習概念構圖的學生比未接受概念圖教學的學生，在較高層次的試題及記憶保留的試題上表現較佳。張俊峰(2001)應用概念構圖於國中學生排球快攻概念的學習上，發現概念構圖的教學比傳統講授式的教學有較佳的成效。時德平(2001)運用概念構圖於自然科教學中，發現利用概念構圖學習的學生在記憶保留上，優於僅接受純文字敘述教學的學生。劉美慧 (2002)研究概念構圖教學對國小學童社會科學習過程與成效，發現概念構圖教學能有效提升學生社會認知成就，尤其對問答題和高層次認知題之成就表現有顯著影響。張秀鳳(2004)在探討藉由概念構圖融入五年級學童數學教學活動中學童解

(38)

題表現的情形及對於概念構圖教學策略之感受中發現，學童大都能接受概念構圖融入數學解題的教學活動，且在理解題意方面很有幫助。但蘇昭博(1998)在探究國內的國中二年級學生使用概念構圖策略學習理化科的成效中，發現使用概念構圖法和傳統學習法，學生的學習成效並無明顯差異。黃萬居(1993)研究國小學生的概念構圖和自然科學學習成就發現學習成效並無明顯差異。陳嘉成(1996)以概念構圖為學習策略之教學對小學生自然科學習之成效研究，發現概念構圖的學習策略並未達顯著的效果。綜合上述，運用概念構圖的成效研究方面，結果並不一致，部份研究顯示概念構圖策略可增進學生的學習效果；然而亦有研究顯示概念構圖策略對學習成效並無顯著的助益。

貳、徑路搜尋法

徑路搜尋是 1985 年由美國新墨西哥州立大學計算研究實驗室領導人 Schvaneveldt 的研究小組根據網路模式和圖形理論(graph-theoretic)所發展而成的徑路搜尋網路量尺化算則(pathfinder scaling algorithm)，並設計知識網路組織工具 (knowledge network organizing tool, KNOT)以執行徑路搜尋。徑路搜尋法是透過一組以節點(node)和連結(linking)相互連接的概念群所構成的知識網路結構，用以建構與分析受試者之知識網路結構型態，並可獲得徑路搜尋網路、圖解理論距離，及藉由量尺化程序來分析專家的知識結構，以專家知識結構做為學習者學習的鷹架，亦可透過客觀數學的公式計算出生手的知識結構與專家的知識結構的相似性係數，進而更精確指出各個知識結構圖之間的差異所在(Jonassen, Beissner & Yacci, 1993)。發展之初大多應用在實驗室研究，爾後才逐漸運用於教育心理學領域。徑路搜尋對於知識結構分析的過程，大致可分成以下三個步驟：

(一)知識結構的引發

知識結構的引出有字義聯想法、卡片分類法、相似性評定法等方法，徑路搜尋法通常採用相似性評定法，依據各概念配對間的相似性、相關性或心理距離，

(39)

透過判斷其相似性程度而給予分數，此分數記載成一種矩陣格式的資料結構，即接近性矩陣資料(proximity matrix data)。透過徑路搜尋量尺化算則，可將此接近性矩陣轉換為資料網路(DATANET)。此資料網路圖形理論上是一完全網路，資料網路每一條聯結鍊的權重等於接近性矩陣元素的值，如果網路中有n 個節點，每 一對節點之間都有連結，則共有_Cn 2條連結鍊，如圖2-2 所示。接近性矩陣 A B C D E A 0 1 3 2 3 B 1 0 1 4 6 C 3 1 0 5 5 D 2 4 5 0 4 E 3 6 5 4 0 圖2-2 接近性矩陣與資料網路圖

(資料來源：Goldsmith, Johnson, & Action, 1991) (二)知識結構的表徵

徑路搜尋法透過量尺化算則，將資料網路轉變成距離矩陣和徑路搜尋網路 (PFNET)。資料網路中的連結鍊包括直接鍊(direct link)和非直接鍊(indirect link)兩種，透過算則，徑路搜尋網路將只會保留接近性數值總和最小的連結鍊，也就是保留「最短長度的徑路」(涂金堂，2003)。徑路搜尋量尺算則的結果主要由r 和 q 兩個參數所決定，參數r 用來決定徑路的長度， r 值的範圍從 1 至∞，對於次序 量數而言r 值通常設為∞，表示路徑的值等於徑路中任何一個錬之最大值 (maximum weight)；參數q 能限制網路連結鍊的數目，其範圍是 2 到n-1之間，n 表示節點數量，當q =n-1時，表示探測所有不同的節點連結路徑，並產生最少徑路的徑路搜尋網路圖(張維珍，2006)。設定不同的r 值和 q 值將影響 PFNET 網路 的連結鍊數目，並產生異種同形(isomorphic)的網路圖(黃湃翔，2002)。例如在圖 DATANET C A B D E 3 ₁ ₂ 3 4 1 5 6 5 4

(40)

2-2 中，節點 A 至 B 至 C 之間的接近值總合為 2，而節點 A 至 C 的接近值為 3，因為非直接鍊接近值總和較小，所以保留節點 A 至 B 至 C 的非直接鍊，如下圖 2-3 所示。距離矩陣 A B C D E A 0 1 1 2 3 B 1 0 1 2 3 C 1 1 0 2 3 D 2 2 2 0 3 E 3 3 3 3 0 圖2-3 根據圖 2-2 所產生的距離矩陣和徑路搜尋網路 (資料來源：Goldsmith, Johnson, & Action, 1991) (三)知識結構表徵的評量

徑路搜尋法的主要重點為知識結構之測量，並比較不同受試者的知識結構之差異。它通常是將受試者的知識結構圖和參照的知識結構圖進行比較，而參照知識結構圖的選取可以依據研究目的以個人或團體平均的知識結構為參照點。 Goldsmith and Davenport (1991) 認為比較兩種不同知識結構圖的相似程度之方法有二：一是以集合理論(set theory)為基礎，計算相鄰節點的交集與聯集關係，可得到相似性指數(closeness index, 簡稱 PFC 或 C 指數)；二是以圖形理論為基礎，計算節點之間距離的相關程度，可得到圖形理論距離指數(graph-theoretic distance, 簡稱GTD)和接近性指數(proximity index, 簡稱 PRX)，藉由這三種指數來判斷受試者知識結構和參照知識結構的相似程度。

茲以Goldsmith, Johnson and Action (1991) 所舉的例子，如圖 2-4 所示。分別說明這三種相似性指數。 PFNET（ r ＝∞，q ＝4） C A B D E 3 1 2 1