國小五年級學童幾何概念階層之概念詮釋結構模式分析

國立臺中教育大學數學教育學系

國小教師在職進修教學碩士班碩士論文

指導教授：林原宏 教授

國小五年級學童幾何概念階層之

概念詮釋結構模式分析

研究生：江孟聰 撰

中 華 民 國 一 ○ ○ 年 六 月

謝誌

漫長的三年，終於要熬過去了，今日的傾盆大雨有如積壓許久的眼淚狂 洩，彷彿在為我的心酸作一註解。 本論文得以順利付梓，特別要感謝恩師 林教授原宏三年來的指導、鞭 策與鼓勵，在身兼系主任處理繁忙校務之際，還常常利用假日撥冗指導論文 寫作，從施測工具的編寫，到論文的修改與完成，恩師的堅持，讓我見識到 身為教授的風範以及對研究態度的執著，這是讓我收穫最多，也是最刻苦銘 心的地方。感謝中臺科技大學資訊管理學系陳教授錦杏與臺中教育大學數學 教育學系黃教授一泓在口試期間，惠賜寶貴意見與指教，讓我的論文更流 暢、完整。 此外，要感謝父母從小對我的栽培與期望，體諒我在事業、課業及家庭 三分壓力齊下的甘苦，在我背後撐起堅實的靠山。感謝老婆及岳父母協助照 顧兩個寶貝。不過每天當馬讓你們騎、一同到學校盪鞦韆、玩沙子，之後洗 個香香的泡泡澡，這要歸功於兩個兒子，因為這是我每天僅有的運動，雖然 這樣的壓力與運動，讓我扎扎實實地針灸了三個月，希望真如施校長所言： 「論文過了，畢業就好了。」 當然在論文製作期間，要感謝學校老師們的相繼配合，讓我的研究能夠 順利進行，感謝施校長孜姿、許主任霞君、林主任淑真、陳主任志宏等主任 們的鼓勵，還有總務處的同仁們在工作上的協助與分憂，及學校的同事：明 周、幸玫、欣男、雅娟、敏彥、旻育等，真的由衷地感謝，還有學校其他同 仁們與我碰面時的寒喧與鼓勵，都是我完成論文的動力。 最後，僅以此論文獻給我摯愛的家人與朋友，感謝您們一直以來的支 持，願與您們一同分享這份喜悅。 江孟聰 謹誌 中華民國一○○年七月

中文摘要

本研究旨在探討國小五年級學童幾何概念的概念結構，根據學童作答 反應資料為基礎，採用多元計分 S-P 表分析理論與多元計分概念詮釋結構 模式來探討同一測驗試題施測後，得分相同的學生間以及得分不相同的學 生間，其概念結構的差異，以協助教師了解學生學習狀況與困難之處，並 可作為教師改進教學的重要參考。 研究者以 625 名已修習完五年級數學幾何課程的學生為研究對象，應 用多元計分概念詮釋結構模式，分析學生幾何的概念階層結構圖，並結合 多元計分 S-P 表分析理論，探討不同學習類型學生的概念階層結構圖之特 徵。研究結果臚列於下列數點： 一、藉由多元計分概念詮釋結構模式分析法，可繪製出受試者個人化的概 念階層結構圖，了解個別受試者的概念階層結構，並可用於不同學習 類型或不同答題反應組型的受試者的概念階層結構圖之比較與分析。 二、不同學習類型或不同反應組型受試者的幾何概念階層結構圖，其概念 階層數、階層內的概念屬性、概念間的連結指向皆有明顯的差異。 三、藉由個人化概念階層結構圖，可以瞭解不同學習類型的受試者在學習 幾何概念時，迷思概念及概念結構的差異，將會有助於教師找出學生 學習困難或迷思概念，進而對學生實施補救教學。 四、從概念階層結構圖中的概念所在之階層位置可以得知，受試者較易精 熟及最難精熟的概念，並由兩兩概念的指向可得知受試者要精熟概念 之上下位關係順序。 五、答對題數相同但反應組型不同的受試者，其整體概念階層結構圖有所 差異。 關鍵字：S-P 表分析理論、多元計分概念詮釋結構模式、幾何

Abstract

This research tries to explore the knowledge structure of geometry concept in the fifth grade curriculum at the elementary school. The polytomous S-P table analysis theory and the concept to annotate the polytomous structure pattern are applied to determine the concept differences between the students with the same scores as well as different scores after attending the identical examination. The purpose of this research is to help teachers understand the learning difficulties of the students, and hopefully to be a major reference in their instructions.

The researcher takes the fifth grade students from 625 primary schools in Taichung who have already studied the geometry curriculum as the target population. The polytomous concept interpretive structural modeling is applied to analyze student’s geometry concept structure, while the polytomous S-P table analysis is also conducted to find out the features of concept structures from different learning style students. Through the procedures of the analysis, the following conclusions were found.

1. It is helpful to apply the polytomous concept interpretive structural modeling to draw individual concept hierarchy structure graph to understand individual’s concept structure. It is also feasible to compare and analyze the concept hierarchy structure graphs between the examinees among different learning styles and response patterns.

2. There are significant differences on the number of the conceptual ranks, conceptual attributes and links between the concept hierarchy structure graphs of the examinees from different study types and response patterns. 3. It is helpful to find out the learning difficulties or conceptual confusions of

students and to apply remedial instructions by using polytomous concept advanced interpretive structural modeling.

4. We can understand the easiest or difficult concepts from responses of examinees and the precondition relationship between concepts.

5. There are differences on conceptual structure among examinees of the same score, thus presented different response patterns.

Key words: student-problem chart analysis theory, polytomous concept advanced interpretive structural modeling, geometry

目 錄

第一章 緒論... 1 第一節 研究動機 ... 1 第二節 研究目的 ... 4 第三節 名詞解釋 ... 4 第二章 文獻探討 ... 7 第一節 幾何概念之相關研究... 7 第二節 模糊理論 ... 15 第三節 詮釋結構模式及其相關研究 ... 17 第四節 概念詮釋結構模式及其相關研究 ... 23 第五節 S-P 表分析理論... 29 第三章 研究方法與設計 ...49 第一節 研究架構 ... 49 第二節 研究對象 ... 51 第三節 研究工具 ... 52 第四節 研究流程 ... 57 第五節 資料分析 ... 58 第四章 研究結果與討論 ...61 第一節 S-P 表分析結果... 61 第二節 學生幾何概念階層結構圖的分析 ... 64 第五章 結論與建議 ...79 第一節 結論... 79 第二節 研究限制 ... 81 第三節 未來研究方向 ... 82 參考文獻...83 壹、中文部分... 83 貳、日文部分... 87

参、英文部分...87

附錄一 幾何概念測驗卷 ...92

附錄二 受試者學習類型一覽表...98

表目錄

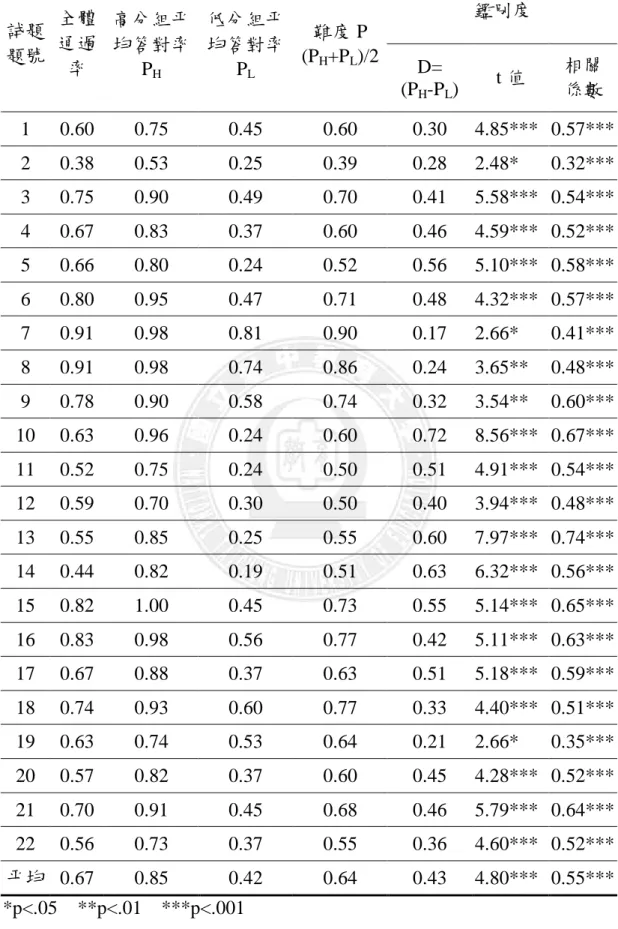
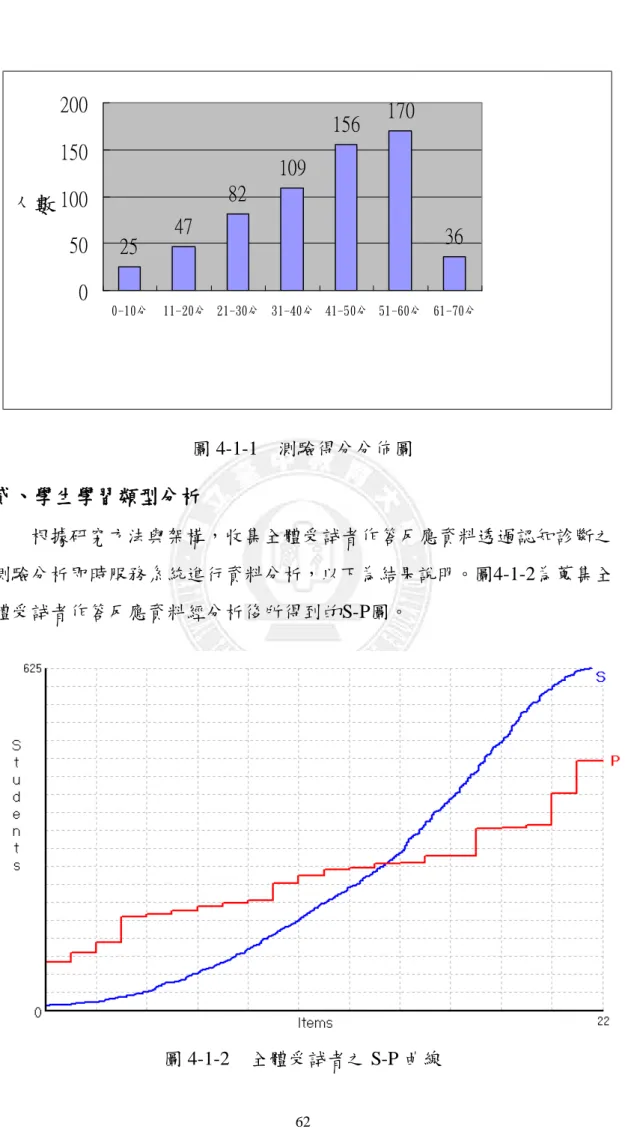
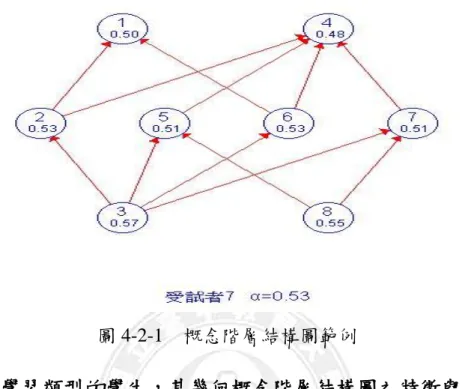
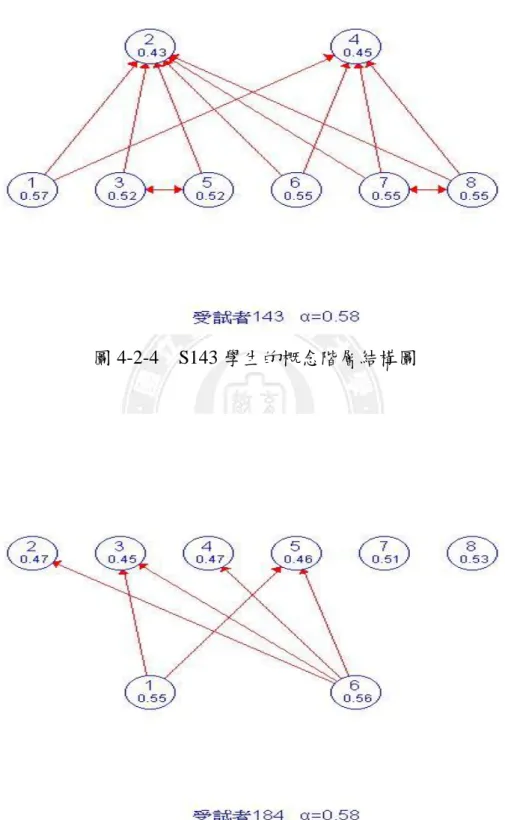
表 2-1-1 國中小九年一貫課程綱要數學領域幾何階段學習表...8 表 2-5-1 學習類型分類表 ... 32 表 2-5-2 試題品質類型分類表 ... ..34 表 2-5-3 原始資料表... 44 表 2-5-4 正規化資料表... 45 表 2-5-5 得分排序後資料表 ... 45 表 2-5-6 學習類型分類表 ... 47 表 2-5-7 試題品質類型分類表 ... 47 表 2-5-8 學生學習類型... 48 表 2-5-9 試題品質類型... 48 表 3-2-1 不同區域學校之受試者人數一覽表 ... 51 表 3-3-1 幾何主題分年細目的概念編號與內容 ... 52 表 3-3-2 施測試卷配分表 ... 53 表 3-3-3 預試施測工具之鑑別度分析... 54 表 3-3-4 幾何主題分年細目試題屬性矩陣資料 ... 55 表 3-3-5 正式施測工具之鑑別度分析... 56 表 4-1-1 施測試卷配分表 ... 61 表 4-1-2 學生學習類型統計 ... 63 表 4-2-1 成績不同之學生答題情況... 65 表 4-2-2 不同得分之學生的各個概念精熟度 ... 72 表 4-2-3 學生得分相同之作答反應組型... 73 表 4-2-4 相同得分之學生的各個概念精熟度 ... 77

圖目錄

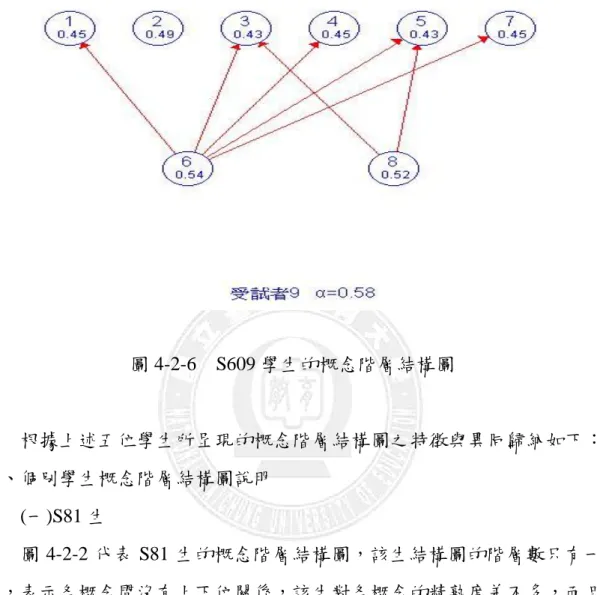
圖 2-3-1 ISM 圖的繪製...20 圖 2-4-1 A 學童之概念階層結構圖...24 圖 2-4-2 B 學童之概念階層結構圖...24 圖 2-4-3 ISM 圖簡化舉例...26 圖 2-5-1 標準化測驗的 S-P 曲線...39 圖 2-5-2 常模參照測驗的 S-P 曲線...40 圖 2-5-3 能力陡降分佈測驗的 S-P 曲線 ...40 圖 2-5-4 編序教學後測驗的 S-P 曲線...41 圖 2-5-5 試題二極化分佈測驗的 S-P 曲線 ...41 圖 2-5-6 教學前測驗的 S-P 曲線...42 圖 2-5-7 多元計分 S-P 曲線圖 ...46 圖 3-1-1 研究架構圖...50 圖 3-4-1 研究流程圖...57 圖 4-1-1 測驗得分分佈圖 ...62 圖 4-1-2 全體受試者之 S-P 曲線...62 圖 4-2-1 概念階層結構圖範例 ...65 圖 4-2-2 S81 學生的概念階層結構圖 ...66 圖 4-2-3 S191 學生的概念階層結構圖 ...66 圖 4-2-4 S143 學生的概念階層結構圖 ...67 圖 4-2-5 S184 學生的概念階層結構圖 ...67 圖 4-2-6 S609 學生的概念階層結構圖 ...68 圖 4-2-7 S5 學生的概念階層結構圖 ...73 圖 4-2-8 S41 學生的概念階層結構圖 ...74 圖 4-2-9 S98 學生的概念階層結構圖 ...74 圖 4-2-10 S164 學生的概念階層結構圖 ...75

第一章 緒論

本研究旨在應用多元計分概念詮釋結構模式，分析國小五年級學童在 「國民中小學九年一貫課程正式綱要」數學領域中有關幾何分年細目的概 念結構，幫助教師瞭解學童的概念結構與學習成就，以便能適性地安排相 關課程，提高教師的教學成效和學生的學習效果。本章旨在說明本研究的 研究動機與目的，以及對於本研究所提及的相關名詞進行釋義。

第一節 研究動機

人類生存於大自然中，透過知覺與世界的互動中，發現有些東西是可 以滾的，有些是可以堆疊的，所以將事物的位置、方向以及相互關係類化 於自我認知結構中，將心中欲表徵的心像加以分解、組合及轉換(劉秋木， 1996)。2000年公布的「國民中小學九年一貫課程暫行綱要」中，數學領域 共分成五大主題，為「數與量」、「圖形與空間」、「統計與機率」、「代 數」、「連結」(教育部，2000)。2003年再公布的「國民中小學九年一貫 課程正式綱要」中，數學領域維持了原先的五大主題架構，只是將「圖形 與空間」改為「幾何」(教育部，2003)。顯示幾何主題逐漸受到重視，其 地位也愈來愈重要。而人是視覺的動物，為了生存，「形」和「幾何」的 天賦直覺就顯得格外重要。「金字塔」的建造如此宏偉以及「萬里長城」 的修築，在在顯示「幾何」在人類生活中占有重要的地位。

van Hiele 幾何思考理論是由荷蘭數學家P.M. van Hiele and Dina van Hiele-Geldof 於1957年所提出的，認為在幾何學習的思考過程中可分為五 個層次，層次一：視覺的層次(visual)、層次二：描述的層次(descriptive)、 層次三：理論的層次(theoretical)、層次四：形式邏輯的層次(formal logic) 以及層次五：邏輯法則本質的層次。這些層次是循序漸進的，也就是說學 生的思考能力到達某一層次之後，才可以依序發展至下一個層次。劉好 (1994)指出國小低年級學童大都屬於最初的視覺辨別層次、高年級的學童

則應漸漸地發展到分析描述的層次。意味著高年級學童應有能力描述周遭 形體。譚寧君(1993)指出「形的教材」表面上雖成功，事實上學生只是強 記了許多抽象的公式，而無法經由實際的操作與推理來建立正確的幾何觀 念，因此相當程度的阻礙了未來在幾何學的學習。 完整的課程規劃是必須建立在有效的「教」與「學」機制上，如此才 能有效的達成教學目標。教師可依據分年細目來訂定教學目標，接著擬定 與發展教學策略。在學生的學習歷程中，測驗是其中的一部份，不管是教 學過程中實施形成性評量或是教學活動結束後實施總結性評量，都是評量 學習成果的方法(曹書豪，2008)。 楊淑菁(2009)指出其在教育現場所觀察有關在數學科教學歷程中的問 題有二：ㄧ、因為「九年一貫課程的實施」，數學領域教學時數下降，教 師常在有限的時間及進度壓力下，只能盲目地趕課，無法了解在群體教學 下，個別學生之學習效果，檢視及適時調整教學內容。二、傳統集體教學 之學後測驗與集體訂正模式仍被大多數的教師採行，教師花很多時間編製 測驗卷與批改考卷，卻無法及時針對學生的錯誤迷思進行補救，更遑論對 個別學生之學習進行診斷。 以往升學主義掛帥，評量著重於紙筆測驗，教師與家長只看分數高 低，對於分數底下所隱含之個人內在知識毫不深究。歷經十年教改後，目 前大部分學校已經不針對國小學童測驗之成績來排定名次，家長僅可獲知 孩童個別的分數，雖然破除了名次的迷思，但是，學童個別分數的意涵之 瞭解仍付之闕如，教師亦然。因此，對於學生所獲得的分數除了重視，更 應探究其內在意涵，因為在相同分數的表象下，隱含著個人化的知識結 構，教師應當針對個人的知識結構進行瞭解，方能有效客製化設計課程， 提升學生學習力。 大部分針對學生知識結構的研究，主要是在評量後，針對特殊少數的 受試者進行晤談，如此偏向質性的研究，需要耗費大量的成本與時間，對 於教學者而言，恐會影響正常的教學進度。因此，根據因材施教的觀念，

個人化的知識結構分析是有其必要性，也更能符合強調及尊重學生個別差 異的精神(陳敏彥，2008)。而近年來在認知診斷評量領域中，已發展出不 少概念結構分析方法，例如：概念構圖(concept mapping)、徑路搜尋法 (pathfinder)、試題關聯結構(item relational structure, IRS)和規則空間(rule space) 、次序理論(ordering theory, OT)、詮釋結構模式(interpretive structural modeling, ISM)、以及察覺的模糊邏輯模式(fuzzy logic model of perception, FLMP)等。這些分析方法主要都是嘗試從試題或元素間的資料中，找出兩 兩有意義的上下從屬關係，以便說明整體受試者的概念特性。 在眾多的方法中，詮釋結構模式分析法是一種有效的概念結構分析 法，惟其法只能得到「整體受試者」的概念結構圖，且其試題或元素間的 關係只能存在二元關係，對於描述知識結構中複雜的概念之間的關係尚無 法完全適用，尤其是數學領域中各單元所隱含之概念，更是無法直接以學 生作答反應進行ISM分析而得到「個人化」的概念結構(陳紹銘，2006；祝 淑梅，2007；鄭佩郡，2008；戴筱玲，2009)。 概念結構的分析有助於評量學習者的學習狀況，並且提供教學者有關 學習者學習缺失的診斷訊息，對於學習者具有正向的補救(Bodolus, 1986; Mikuleck, 1987; Seaman, 1990; Skaggs, 1988; Holley & Dansereas, 1984)。Lin, Hung and Huang(2006) 將 ISM 分析 法 改 良 為概 念 詮釋結構模式 (concept advanced interpretive structural modeling, CAISM)分析法，並與洪文良、黃 國榮共同合作，應用概念詮釋結構模式設計出軟體CAISM程式，以便於將 受試者的測驗資料經過概念向量比對與模糊理論等計算方法，得到受試者 數學概念之兩兩關係矩陣，再利用詮釋結構模式的階層運算法則，用圖形 結 構 和 數 字 呈 現 受 試 者 個 人 化 之 概 念 階 層 結 構 (Lin, Hung & Huang, 2006)。又根據Lin, Hung and Yu(2007)及鄭佩郡(2008)等學者專家對學童數 學概念的研究顯示，概念詮釋結構模式能夠有效圖繪並且分析受試者個人 化的知識結構，使得教師能夠清楚地知道每一位學生的概念結構，有助於 診斷個人認知及進行補救教學。然目前測驗評量試題已呈現多元化，其計

分標準以不同於以往僅有是非題或單一選擇題，而有每題配分不盡相同之 文字題或題組呈現，也就是計分方式呈現多元化。 綜上所述，本研究就幾何的分年細目編製一份多元計分之幾何概念測 驗卷，以已經習得國小五年級幾何課程之學童為對象進行施測，並以多元 計分概念詮釋結構模式分析法來分析測驗結果，再透過多元計分S-P表分析 理論進行學習類型的分類，探討各學習類型學生的概念結構之特徵及差 異，期望能呈現幾何的概念結構，並協助教學者在教學上能得到更大的助 益。

第二節 研究目的

依據上述研究動機，本研究的目的如下： 一、利用多元計分概念詮釋結構模式，探討國小五年級學童的幾何概念詮 釋結構。 二、比較不同學習類型學童之幾何概念詮釋結構之異同。 三、探究相同學習類型學童之幾何概念詮釋結構之異同。 四、探討學童得分相同但作答反應組型不同之幾何概念詮釋結構之異同。

第三節 名詞解釋

壹、模糊理論(fuzzy theory) 「模糊理論」乃於1965年由L. A. Zadeh提出，將人類的事理判斷以及 思考邏輯改用較簡單的數學表現形式來處理，將特徵函數的值域由{0,1} 二值擴展到區間[0,1]，形成一個模糊集合，藉此思維及處理模式來解釋人 類周遭某些實務現象。集合和元素間的關係，以介於[0,1]之間的隸屬度 (membership)來描述，有別於傳統非零即一，非對及錯之二元邏輯觀點。 該理論定義模糊集合U 表示全域， f 為一函數，即f :U→[0,1]，則U 之模 糊子集A的隸屬函數記為μA(x)，表示元素x隸屬於模糊集合A的程度，為一 種用以量化具有不確定性概念的一門學問。

貳、S-P表分析(Student-Problem chart, S-P chart) S-P表分析理論又稱為學生問題表理論，簡稱S-P表分析，由日本佐藤 隆博(Takahiro Sato)於1970年代所創造，此表可以進行調查資料的分析處 理，進行數量化分析、排序比和學習程度判斷等事項(Sato, 1969)。意即此 表可用以分析與診斷學童的學習資料，利用學童針對每份試卷中的每道試 題之作答反應組型，將學童學習類型分成六大類，試題品質分成四大類， 並利用下列四種指標：學生注意係數(student caution index)、試題注意係數 (item caution index)、同質性係數(homogeneity coefficient)以及差異性係數 (disparity coefficient)，來協助教師診斷學童之學習狀況、測驗品質及教師 教學成果，作為改進教學方式與輔導學童之重要參考。

参、詮釋結構模式(interpretive structural modeling, ISM)

為 J. N. Warfield (1976) 所 提 出 用 於 社 會 系 統 工 學 (social system engineering)領域中訊息彙整的建模方法。其分法是就一個集合內各元素之 間的從屬(subordinate) 關係矩陣，植基於圖形理論與離散數學，呈現出元 素間具體化的關聯階層結構圖形(Warfield, 1974, 1977)。

肆 、 概 念詮 釋 結構 模 式 (concept advanced interpretive structural modeling, CAISM)

概念詮釋結構模式(concept advanced interpretive structural modeling, CAISM)分析法是由Lin, Hung and Huang (2006)提出的。此模式乃是將詮釋 結構模式(interpretive structure modeling, ISM)分析法改良，根據受試者的測 驗資料，提供個人化的概念階層結構訊息。且林原宏、洪文良與黃國榮共 同合作應用概念詮釋結構模式設計出CAISM軟體，以便將受試者施測資料 經過概念向量比對(concept vector matching)，並結合模糊理論等計算方 法，得到受試者概念關係矩陣，利用詮釋結構模式的階層結構運算法則， 選定α值輔以計算，得到個人化的概念階層結構圖(individualized concept hierarchy structure) (Lin, Hung & Huang, 2006) 。

伍、多元計分概念詮釋結構模式

多元計分概念詮釋結構模式乃是由Lin, Hung, Huang and Li(2009)為改 進二元計分概念詮釋結構模式所發展的，用以分析多元計分或混合計分模 式的施測資料。且Lin et al.(2009)應用多元計分概念詮釋結構模式設計出 PWCISM軟體，經分析後得到個人化的概念階層結構圖，讓教學者更廣泛 地應用在學生認知診斷，以有效進行補救教學。 陸、幾何概念(geometry concepts) 本研究採自教育部於民國92年11月發布，國民中小學九年一貫課程綱 要數學領域中(簡稱92年版)，國小五年級幾何部分的分年細目當成本研究 之幾何概念，並藉以形成試題進行測驗。

第二章 文獻探討

本研究之相關理論將於本章進行探討，共分五節，各節所探討的主題 如下：第一節幾何概念之相關研究；第二節模糊理論；第三節詮釋結構模 式及其相關研究；第四節概念詮釋結構模式及其相關研究；第五節 S-P 表 分析理論。

第一節 幾何概念之相關研究

人類與外在環境的接觸全靠五官，所謂五官即為採聽官「耳朵」、保 壽官「眉毛」、監察官「眼睛」、審辯官「鼻子」以及出納官「口」。所以 察覺外在事物存在的器官即為眼睛，有無危害人類生命、辨別事物型態(大 小、形狀、輕重、速度)等重要性非眼睛不可。人類與生俱來辨別「形」或 「幾何」等天賦直覺可謂豐富與多元，諸如垂直與平行、對稱、相似與全 等操作及圖形辨識等等。因此在數學教育中，幾何單元之教學非常重要， 亦是較受學童歡迎的單元。美國國家數學教師協會(National Council of Teachers of Mathematics, NCTM)也提出需將幾何形體及其關係、變化、幾 何的模式化與空間推理等概念，包含於學校幾何課程(教育部，2003； Clenents & Battista, 1992; NCTM, 1989, 2000)。

小學的幾何教學，可依據學童認知發展，參酌幾何發展歷史軌跡，拓 展學童幾何直覺，讓學童透過實際手部操弄，在操控過程中逐漸瞭解各種 簡單幾何形體及其性質，之後再導入簡單的推理性質，為銜接國中階段幾 何課程打下良好的基礎(教育部，2003)。 在我國國民中小學九年一貫課程正式綱要中將數學領域的幾何分成 以下四個階段，如表 2-1-1。

表 2-1-1 國民中小學九年一貫課程綱要數學領域幾何階段學習表 階段 年級 學習內容 階段一 一到三年級 強調幾何形體的認識、探索與操作，學童對幾何 形體中的幾何要素，也許能指認，但對於結構意 義尚不完全清楚。 階段二 四到五年級 數 與 量 的 發 展 漸 趨 成 熟 ， 學 童 開 始 結 合 「數」與「形」兩大主題，學習運用幾何形體的 構成要素(如角、邊、面)及其數量性質(如角度、 邊長、面積)。 階段三 六到七年級 透過形體的分割、拼合、截補、變形等操作，了 解形體的特性與幾何量的計算與非制式化推 演。透過方位敘述及立體模型的展開與組合以培 養空間概念及視覺推理。 階段四 八到九年級 開始由具體操作進入推理幾何情境中，學會推理 幾何證明，學習內容採漸進式安排。由基本幾何 概念由淺入深，進入更高層的推理領域。最初的 學習可由填充式推理幾何開始，慢慢養成完整能 力，培養學童自信心，快樂地學習幾何學知識。 教材內含有認識生活中的平面圖形，如三角形、 四邊形、多邊形與圓形；認識點、線、角、符號 及幾何相關名詞；使用基本性質描述某一類形 體；能以最少性質對幾何圖形下定義，並熟練定 義的相關操作；體會邏輯概念：包含關係、敘述 及逆敘述、推理幾何；求角度問題、長度問題、 面積(表面積)問題、體積問題；推理證明、尺規 作圖、全等性質、相似性質、平行性質的應用、 圓的相關性質。 資料來源：修改自教育部(2003)

荷蘭數學教育家 P. M. van Hiele and Dina van Hiele-Geldof 夫婦，在西 元 1957 年，根據完形心理學的結構論以及皮亞傑(Piaget)的認知理論，共 同提出 van Hiele 學習理論。此理論在發表之初並未在國際間受到太多的 注意。直到 1974 年，美國數學教育家 Wirszup(1976)進行一系列相關的研 究，才漸漸受到重視，並依據 van Hiele 的理論模式來改革國民中小學之 幾何課程(Hoffer, 1983)。

茲將相關文獻資料整理成 van Hiele 的理論及幾何思考層次、van Hiele 幾何思考層次的特性、幾何相關研究，分述如下： 壹、幾何概念 一、概念的意義 概念是引導學童進行思考的基礎，適當地運用在教學的過程中，可以 幫助學童發展至更高一層的概念，並習得知識上的原理(薛建成，2003)。 概念是包括主要屬性(attribution)或特徵(features)的同類事物之總稱 (鄭麗玉，1993)。例如：椅子有許多種類與造型，有木頭製的椅子、有石 頭製的椅子、有鐵製的椅子、有的附有靠背的、有的沒有靠背的……等， 但是它們有共同的特徵，都有一個朝上的平面，可以供人席坐，這就是「椅 子」的概念。 概念(conception)是指一個獨特的心智表徵特質(idiosyncratic mental representation)，亦是一個認知學習的動態過程。教育學與心理學的文獻 中，概念(concept)是指一個概括的名稱或具有能被信號或符號以代表所指 共同屬性的一類事物或事件，及一些已明確定義或廣泛為大眾所接受的觀 念(Duit & Treagust, 1995)。

就心理學來看，概念是思維模式的一種。它反應客觀事物本質的一種 理論知識，人類在認知的過程中，把所認知的事物其共同的特點抽象出 來，加以概括而成為概念(沈佩芳，2002)。概念是一個象徵的建構(syambol constrcution)，它用來代表外界事物或事件的共同性，概念之所以形成，是 由於我們能夠對外界的事物進行歸類(categorization)(鄭昭明，1997)。 綜上所述，用一個概括的名稱或符號來描述事物所代表的共同屬性 時，稱這個名稱或符號所代表者為概念。而所有事物的認知過程必須經由 概念來概括、推論、總結。推論者會因時、因地、因時空背景之不同，對 同一概念將有著不同的詮釋，所以概念的意義乃是由所使用的脈絡位置而 決定。

二、概念的發展 俄國心理學維考斯基的概念理論主張每一個人在其生存過程中應該 是一位積極且活力充沛的自然環境參與者，在每一個發展階段中，或多或 少會透過一些方法使自己無論在生理上或心理上都可以得到成長(杜嘉 玲，1999）。 皮亞傑(Piaget)認知發展理論有二個基本要義： (一)個體智能的發展是個體在環境中生活適應的歷程，個人智能高低 乃是遺傳與環境交互作用的結果(張春興、林清山，1992)。主要的四個因 素是成熟(maturation)、經驗(experience)、平衡(equilibration)和個體與社會 互動(social transmisson)(Esler, 1989)。其中「平衡」是建構知識的動力，認 知結構的內在機制(mechanism)主要就是失衡狀態與平衡狀態之間一連串 的同化(assimilation)與調適(accommodation)的歷程。 (二)智力發展有其階段性。皮亞傑將認知發展分為四個階段：感覺動 作期(the sensory-motor stage)、前操作期(the preoperational stage)、具體操作 期(the concrete operations stage)、形式操作期(the stage of formal logic)。兒 童進入四階段的時間或許有各別差異，但此四階段的發展順序是不變的 （歐陽鍾仁，1988）。各階段有其相應的認知內容與思考形式，亦即他認 為不同的認知發展階段或層次，有對應的結構組，各發展階段間的差異， 乃是結構上的差別，這樣的差別不僅是「量」的增加所導致的變化，更有 「質」的改變，這種結構的改變稱為「發展」(development)，亦即認知結 構具有不斷變化的動態性(王文科，1983)。 三、概念分析 概念分析乃是利用系統的方法將概念加以分析，根據分析的結果，診 斷學童錯誤概念之所在，並選取該概念的範例和非範例，同時為每一個範 例和非範例提供理論基礎，以便於教師教學和學童學習(毛連溫、邵尉龍、 楊瑞智，1993)。

貳、van Hiele 的理論及幾何思考層次

van Hiele 幾何思考理論是由荷蘭數學教育家 P. M. van Hiele 和 Dina van Hiele –Geldof 於 1957 年所提出的。茲將其有關理論略述如下：

一、van Hiele 的幾何思考層次 van Hiele 主張學童在學習幾何的歷程上可分成五個思考層次，在教師 適當安排教學情境下，學童的學習將循序經歷此五個層次，而每一個層次 都有其獨特的發展特徵。對於這五個層次的描述方式，研究者有兩種不同 的表達方式：一部分研究者使用「層次 0、層次一、層次二、層次三、層 次四」來表達此五個幾何思考層次(黃盈君，2001；盧銘法，2001)；另一 部分則使用「層次一、層次二、層次三、層次四、層次五」來表達 van Hiele 的五個思考層次(吳德邦，1998；Usiskin, 1982)。本研究採用 van Hiele(1986) 對層次的說法，分別為層次一：視覺的(visual)層次、層次二：描述的 (describptive)層次、層次三：理論的(theoretical)層次、層次四：形式邏輯的 (formal logic)的層次、層次五：邏輯法則本質的(the nature of logic laws)層 次。以下分別描述各層次的內容： (一)層次一：視覺的(visual)層次 屬於這個層次的學童，會藉著視覺觀察物體的外型輪廓來辨認形狀。 例如，從生活經驗當中知道圓圓的東西屬於圓形，像門的東西屬於長方 形，像太陽的形狀屬於圓形的。此層次的學童可辨別具體事物的外形，並 且能學習詞彙或再造出一個與指定圖形相同的圖形，但是學童卻無法利用 構成要素來分析，而且只要圖形的外表稍有變化，學童就無法辨別其之間 的差異所在。教師在教學時應提供各種機會，讓學童透過實際的操作。 (二)層次二：描述的(describptive)層次 屬於這個層次的學童，已經有相當豐富的視覺辨識經驗，能依據視覺 所觀察到的結果辨別圖形，知道圓形沒有邊，正方形有四個一樣長的邊， 三角形有三個邊，三角形的內角和是 180°，也能夠發現長方形的角都是直 角等圖形特徵，但是無法說出這些圖形之間有無關聯存在。位於這個層次

的學童無法經由推理來得知道理(例如：正方形和長方形邊長不相等時，面 積卻有可能相等)。 (三)層次三：理論的(theoretical)層次 這個層次的學童已經清楚圖形的構成要素，利用構成要素探索各種幾 何圖形之間的內在屬性以及不同種類圖形之間的包含關係。例如：菱形有 四個相等的邊，而正方形是菱形的一種，當菱形其中的一個角為 90°時， 這個菱形就是正方形；平行四邊形有兩雙對邊平行且相等的邊，而長方形 是平行四邊形的一種，當平行四邊形其中一個角為 90°時，這個平行四邊 形就是長方形。這個層次的學童能夠依據圖形的性質進行非正式的推演， 但是還不能進行有系統的證明。 (四)層次四：形式邏輯的(formal logic)的層次 這個層次的學童已經能夠經由抽象的推理來證明幾何問題以及相互 間的關係，也可以瞭解幾何定理的證明方法可能不只一種，也知道幾何圖 形的充分條件與必要條件。例如：正方形每一邊長及每一個內角皆相等， 都是 90°，但是邊長相等的四邊形卻不一定是正方形。也就是達到這個層 次的學童可以瞭解正逆敘述之間的異同，能說明題目中已知的條件及要證 明的方向為何，並利用邏輯推理的方法，來證明幾何的性質。

(五)層次五：邏輯法則本質的(the nature of logic laws)層次

此層次是最高的層次，達到這個層次的學童可以在不同的公設體系 中，瞭解抽象推理幾何，並在公設體系中建立定理及比較不同的公設系 統。要達到這個層次是很不容易的，一般人很難達成，所以連 van Hiele, P. M. 本人都認為此層次是理論的價值而已(van Hiele, 1986)。 二、van Hiele 幾何思考的特性 van Hiele(1986)曾經指出：幾何思考層次具有某些固定的特性，不同 的 學 者 對 於 van Hiele 幾 何 思 考 層 次 也 有 著 不 同 的 看 法 及 敘 述 。 Usiskin(1982)定義幾何思考層次的特性為：固定順序(fixed sequence)、毗連 性(adjacency)、特異性(distinction)、分離性(separation)、以及造詣(attainment)

等；Crowley(1987)則稱之為序列(sequential)、進展(advancement)、內在與 外在(intrinsic and extrinsic)、語言(linguistics)、不協調(mismatch)。綜合各 家說法，將幾何思考層次的特性分述如下： (一)序列性(sequential) 幾何思考層次是有一定順序的，每一個層次的觀念的形成都是來自於 前一個層次觀念的建立，所以學童為了能夠順利進到下一個層次，則必須 充分學習之前所有層次的觀念。 (二)毗連性(adjacency) van Hiele(1986)曾經提到，學童幾何思考層次的推演，不是隨著年齡 的增長而增加推進，最主要還是要透過教學，經過教師適當的教學和引 導，則能夠提升學童幾何思考概念。

(三)內在性與外在性(intrinsic and extrinsic)

在某一個層次的性質是內在的，到了下一個層次時，該性質卻有可能 成為外顯的性質。對某些概念的瞭解，雖然在目前這個層次可能不明顯， 但是到了下一個層次卻是明確可知的(Clements & Battista, 1992)。例如：在 層次一中，僅由圖形的外觀來辨別圖形，然而到了層次二時，則是由圖形 的特徵與組成要素來進行分析。 (四)語言性(linguistics) 在每一個層次中都有屬於自己獨特的語言、符號，以及符號彼此之間 的關聯系統。在同一個層次中是正確的語言或符號，到了另外一個層次可 能就必須經過轉換修改才能符合。而每一個層次中獨特的語言性，不僅代 表同一層次有著不同的術語名詞，甚至有些相同的術語，指的卻是不同的 幾何概念(Eberle, 1989)。 (五)分離性(mismatch) 依據 van Hiele 幾何思考層次的語言特性，每個層次都有其獨特的語 言、符號，屬於不同層次的人，彼此間就沒有共通的語言，不能相互的溝 通、傳遞訊息。假如學童的幾何層次屬於第一層次，而教師授課內容、符

號的運用屬於第二層次甚至是第三層次的話，則學童便無法經由相同可溝 通的語言完全瞭解其過程與結果，那麼學童的學習效果將大打折扣。

参、其他相關的研究

Burger and Shaughnessy(1986)對幼稚園兒童一直到大學的學生所做的 晤談觀察，發現學生的幾何思考模式與van Hiele的理論是一致的。 吳德邦(1999)以van Hiele 幾何思考模式為基礎，研究平面幾何圖形 中，正方形、圓形、等腰三角形、直角三角形等概念，探討學生van Hiele 幾 何思考層次分布情形。賴文正(2005)探討國小五年級學童對於角概念的認 知，並分析學童對於角概念的表現與迷失概念情形。 盧銘法(1996)以van Hiele 幾何思考水準為基礎，探討國小高年級的四 邊形幾何概念，以瞭解不同年級、性別的學生在四邊形概念上的差異，和 學生在van Hiele 水準上的分布情形。林碧珍(1993)探討兒童描述兩個相似 圖形常用的語彙，分析兒童辨認，或給兩個相似圖形的認知結構，瞭解兒 童辨認兩個長方形「形狀相同」的發展特徵，從而建立兒童「相似性」概 念的發展特徵。 翁欣瑜(2002)探討影響國小學童幾何解題表現的因素與幾何解題錯誤 的原因。其隨機抽取泰雅族學童138名及六年級平地學童135名，進行幾何 先備知識測驗及幾何解題表現測驗，結果發現：1.國小學童的幾何先備知 識與幾何解題表現呈正相關。2.平地學童的幾何先備知識優於泰雅族學 童，且不同族別的國小學童在幾何先備知識測驗成績達.05顯著差異水準。 3.平地學童的幾何解題表現優於泰雅族學童，且不同族別的國小學童在幾 何解題表現測驗成績達.05顯著差異水準。而且根據研究發現，幾何解題表 現不但受到幾何先備知識的影響，也受族別因素的影響。幾何解題錯誤的 原因，包括不了解題意、缺乏先備知識、計算規則類推錯誤、概念間缺乏 連結或概念混淆不清、根據圖形的解讀由自我想法推測作答、用猜的、沒 看清楚題目等七種。

第二節 模糊理論

壹、模糊理論的意義

模糊理論(fuzzy theory)乃於1965年由L. A. Zadeh提出，將人類的事理 判斷以及思考邏輯改用較簡單的數學表現形式來處理，將特徵函數的值域 由{0,1}二值擴展到區間[0,1]，形成一個模糊集合，藉此思維及處理模式來 解釋人類周遭某些實務現象。而fuzzy一詞存在有「不明確」、「界線不清」 及「模糊」的意義(九章編輯部，1989)。 在古典數學中，同一類元素的聚集形成特定集合(set)，而一個元素是 否屬於某個集合是非常清楚、明確的，沒有模糊地帶。古典集合將元素和 集合關係以特徵函數(characteristic function)來表示，即： C(x)=    ∉ ∈ A x A x ， ， 0 1 可是在現實環境中，利用上述函數關係在描述實務現象時，會發現無 法具體解釋。例如：今天天氣冷或不冷，這家餐廳的菜色好不好等等，回 答會因人而異，沒有絕對的標準答案。 模糊理論在表示集合和元素間的關係，以介於閉區間[0,1]之間的隸屬 度(membership)來描述，有別於傳統非零即一，非對及錯之二元邏輯觀點。 該理論定義模糊集合令U 表示全域，可數集合X為U的一個子集，且X含有 n個元素，表示如下： X⊆U，X={x1,x2,…, xn} 若A定義為X的一個模糊集合(fuzzy set)，對於X中的每一個元素x，隸 屬於A的程度以隸屬度函數稱之，以μA(x)表示，且其值域為閉區間[0,1]， 則在離散(discrete)的情況下，模糊集合A表示法如下：

μA : xi → μA (xi)，μA (xi)

∈

[0,1]，i=1,2,…,n

A=       ∈X x x x i i i A( )_│ µ

=       ⋅⋅ ⋅ n n A A 1 A x x x x x x ( ) , , ) ( , ) ( 2 2 1 µ µ µ 又可表示為： A= n n A A A x x x x x x ) ( ) ( ) ( 2 2 1 1 µ µ µ _{+ +⋅ ⋅⋅+} 其中+是或的意思， i i A x x ) ( µ 表示元素xi 隸屬於模糊集合A的程度。而 當全域是連續(continuous)的情況時，模糊集合A可以表示為：A=

∫

∈A x A x x) ( µ 。 貳、模糊關係矩陣與模糊截矩陣

一、模糊關係矩陣(fuzzy relation matrix)

模糊關係矩陣用來表示兩集合元素之間的關係。假設集合 A 有 I 個元 素，集合 B 有 J 個元素，則兩集合元素 ai和 bj之間的關係程度可以用模糊 關係矩陣 R=

( )

J I j i r × 表示。 論域 X 有 m 個元素，論域 Y 有 n 元素，則由 X 到 Y 的模糊矩陣為： ij r ＝u_R(x_i,y_j)：X ×Y →[0,1] 即 R ＝(rij)m×n＝             mn m m m n n r r r r r r r r r r r r L M M L L 3 2 1 2 23 22 21 1 13 12 11 其中 0≤r_ij ≤1 ， ∀ i=1,2,L,m ∀ j=1,2,L,n 二、模糊截矩陣 在給定α 值之情形下，可進行模糊關係矩陣之截矩陣運算。亦即： α R ＝(r_ijα)_I×J 且 r ＝_ijα     < ≥ α α ij ij r r , 0 , 1 ，其中0≤α ≤1

第三節 詮釋結構模式及其相關研究

壹、詮釋結構模式簡介 當人類處理問題、謀定策略、決定計畫內容與管理組織等不同類型的 事務時，通常需要將重要的關鍵要素通盤考量後，形成階層的模式，再排 列先後解決順序。但人往往都靠「直覺」的意思來處理事務，導致遺失某 些次重要關鍵因素，又或甚至無法決定出詳盡的層級形式(Warfield, 1973)。

詮釋結構模式(interpretive structural modeling, ISM)為J. N. Warfield於 1976年提出用於社會系統工學(social system engineering)領域中訊息彙整 的建模方法。就集合內各個元素之間的從屬(subordinate) 關係矩陣，根據 圖形理論與離散數學，結合行為科學、團體決策(group discussion)及電腦輔 助，透過矩陣的數學運算，呈現出元素間具體化的多層級關聯結構化圖形 (multilevel connection structure ierarchy)(Warfield, 1974, 1977)。日本學者佐 藤隆博在其「ISM構造學習法」一書中，提出為了探究學科內容的知識結 構與其架構的表現，教學者可依學科內容分成數個單元，單元內之教材要 素依照教學目標細分後，產生了學習項目間彼此兩兩關聯性，最後透過ISM 分析法演算後，產生構造化教材的一種設計方法(佐藤隆博，1987)。而想 要進行詮釋結構模式分析前，必須事先建立集合內各個元素間的從屬關 係，此元素可以是腦中知識結構的最基本單位，也可以是教材中最基本的 單元或概念或學習目標及內容(林原宏、陳進春、許天維，2005)。 貳、詮釋結構模式演算介紹 為了瞭解存在於學習者腦中特定概念間的關係，ISM分析法即為將概 念間的關係用具體的圖形或數量表示。傳統的ISM分析法可以系統化表示 整體元素之間的階層結構關係。假設欲分析的集合中含有K個元素，其中 任意兩個元素A 與_i A 的二元關係，以矩陣_j A=(a_ij)_K×K表示。若a_ij =1，表 示A 從屬於_i A ，即_j A 為_i A 的下位元素；反之，若_j a_ij =0，表示A 不為_i A 的_j 下位元素。而ISM分析方法的步驟如下(林原宏，2005)：

一、相鄰矩陣(adjacent matrix)的運算 A=(a_ij)_K×K表示欲分析的集合中，兩兩元素間是否存在關係的矩陣， 稱為相鄰矩陣。 兩個矩陣 A 運算的結果 定義為

( )

K K ij KK K K K K a a a a a a a a a a A × =             = (2) ) 2 ( ) 2 ( 2 ) 2 ( 1 ) 2 ( 2 ) 2 ( 21 ) 2 ( 21 ) 2 ( 1 ) 2 ( 12 ) 2 ( 11 2 L M M M M L L 2 A 矩 陣 內 的 元 素

∑

= = ⊗ ⊕ ⊗ ⊕ ⊕ ⊗ = K k Kj iK j i j i kj ik ij a a a a a a a a a 1 2 2 1 1 ) 2 ( L 上式中⊗和⊕的運算，定義如下：    = = = ⊗ 1 1 , 1 , 0 y and x if else y x    = = = ⊕ else y and x if y x , 1 1 1 , 0 二、傳遞閉包 (transitive closure) 定義 P A A A A Aˆ = ⊕ 2 ⊕ 3⊕L ，且矩陣 Aˆ稱為傳遞閉包。 三、可到達矩陣 (reachability matrix) 定義Aˆ⊕I = A⊕A2 ⊕A3⊕LAP ⊕I =(A⊕I)P，其中 I 表示K×K階的 單位矩陣，則把如下列表示的矩陣 R ，稱為可到達矩陣。 1 ) ( ) ( + ⊕ = ⊕ = P P I A I A R ⊗ 0 1 0 0 0 1 0 1 ⊕ 0 1 0 0 1 1 1 1

四、ISM圖的繪製 以A 至₁ A 元素為例(佐藤隆博，1987)，這五個元素之關係，假設可用₅ 矩陣 A表示；經過步驟一至三運算後，則相對應的可到達矩陣為R，分別 為：                 = 0 0 0 0 1 1 0 1 0 0 0 1 0 0 1 0 1 1 0 0 0 0 0 0 0 A                 = 1 0 0 0 1 1 1 1 0 1 1 1 1 0 1 1 1 1 1 1 0 0 0 0 1 R 為了方便繪製 ISM 圖，將所需要的矩陣整理如下： k A R(Ak) M(Ak) R(Ak)∩M(Ak) 1 A A₁ 0 0 0 0 A₁ A₂ A₃ A₄ A₅ A₁ 0 0 0 0 2 A A₁ A₂ A₃ A₄ A₅ 0 A₂ 0 0 0 0 A₂ 0 0 0 3 A A₁ 0 A₃ A₄ A₅ 0 A₂ A₃ A₄ 0 0 0 A₃ A₄ 0 4 A A₁ 0 A₃ A₄ A₅ 0 A₂ A₃ A₄ 0 0 0 A₃ A₄ 0 5 A A₁ 0 0 0 A₅ 0 A₂ A₃ A₄ A₅ 0 0 0 0 A₅ ) (A_k R ：是 A的可到達矩陣，在可到達矩陣中，若元素為1，則填上表示被 指向的元素代號；在可到達矩陣中，若元素為0，則保持為0。 ) (A_k M ：在R(A_k)矩陣中，M(A_k)的每一列，表示指向該列元素的所有其 它元素。 ) ( ) (A_k M A_k R ∩ ：是R(A_k)和M(A_k)兩矩陣的交集，兩矩陣相對應位置若同 時存在該元素，則填出該元素；否則填上0。

以下介紹繪製圖2-3-1的ISM方法步驟： 一、 比對R(A_k)和R(A_k)∩M(A_k) 比對R(A_k)和R(A_k)∩M(A_k)的每一列，找出列相等的元素。在上表 中，發現第1列A 相等，則在1 R(Ak)、R(Ak)∩M(Ak)中 A 所在的第一行1 (column)與第一列(row)全部刪掉，剩下四列×四行的矩陣，且經過ㄧ次比對 後所剩下的列與行則不再比對與尋找。 二、 重複步驟一動作 重複步驟一的方式，可再找到A 所在的第五列相等，同樣刪除₅ A 所在₅ 的行與列，剩下三行×三列。依此類推，可相繼得到A 、₃ A 一組元素和₄ A₂ 元素。 三、 列出高低層級 依序將步驟一至三各步驟所找到的元素列出高低層級，並依 A 中的元 素間的上下位關係，標示出由上位指向下位的箭頭，如圖 2-3-1 所示，其 中A 、₃ A 是對等元素，至此完成 ISM 圖的繪製。若 ISM 圖形元素多而箭₄ 頭關係複雜，則可視研究者所需而進行圖形簡化。簡化原則為：若元素 Ai 指向 Aj有多條路徑(path)，則去除直接指向並保留間接指向的路徑即可得 簡化之 ISM 圖。 圖 2-3-1 ISM 圖的繪製

参、詮釋結構模式相關研究

ISM分析法主要在於「建立整體概念元素之間的關係，經由部分元素 之間的關係，整合起來形成所有元素整體之關係」(許天維、林原宏，1994)。

蔡秉燁(2004)運用ISM之階層有向圖理論，規劃設置高中階段數學領域 補救教材，將學習項目之順序重新編排，以便建立更科學化的「學習路徑

(learning path)」與「學習地圖(learning map)」。

鍾靜蓉(2002)以商業職業學校經濟學中「需求與供給」單元為實例， 進行詮釋結構模式及構造化學習法的實證研究應用，期能幫助學習者了解 全面知識結構，減少學習時間。結果發現，在確認各概念間的前後因果繼 承關係及關聯程度，以及來回重複實施及修改ISM模型的種種過程中，教 師(教學設計者)可將存於腦中某些模糊籠統或者片段、抽象的知識逐漸清 晰地建構起來。 蕭國強(2008)整合詮釋結構模式與基於影響矩陣乘法方法，針對分析 封裝產業設備工程人員之訓練課程，建構層級化結構及影響相依圖，藉以 發展出規劃課程的適合模式，以提升設備工程人員的訓練成效，精進設備 工程人員各項基礎技能，使有限的資源發揮最大效益。 吳信義(1998)應用ISM分析法，建立職業科目設計教材之模式電腦化， 以協助教師課程規劃與設計。 黃信源(2005)運用詮釋結構模式設計國小數學領域分數概念教材，瞭 解國小學生分數概念學習情形。研究結果發現，透過 ISM 法設計分數概念 教材，可具體化呈現概念構圖之思考脈絡，支援教師教學效能、縮短教師 備課時間，圖像式的呈現 ISM 結構化教材，則可使教師更明確掌握學習 順序以幫助學生學習。 Tatsuoka(1995)運用詮釋結構模式分析出具階層性的知識狀態結構，此 分析方法認為概念和認知具有關聯性，因此屬性之間具有先前需要的關係 (prerequisite relationship)。

Fontela(2003)認為詮釋結構模式分析方法是一種適合整合連結量性和 質性資料的好方法。Nussbaum and Smith(1983)對於職前教師的 TAPE (Teacher and Practicum Elementary Program)訓練課程，採用電腦輔助式的 ISM (computer-aided ISM) 課程設計，用以協助群體中，討論與分析複雜 的教學情境問題，在此過程中電腦對於問題提供解決層級的不同要點。

Saxena, Sushil and Vrat(1992)應用詮釋結構模式分析印度水泥工業之 能源保護計畫中各元素間的分類和階層結構化。

由此可見，詮釋結構模式原是提出用於社會系統工學領域中的建模方 法，如今也可適用於學術領域及教學現場中，有效改善以往人們靠「直覺」 來處理事務時所犯的錯誤，對於團體決策以及各項學習先後順序有極大的 幫助與效益。

第四節 概念詮釋結構模式及其相關研究

壹、概念詮釋結構模式理論簡介 Warfield(1976)提出的詮釋結構模式分析方法中，元素間的關聯指向只 適用二元關係，且概念與概念之間的指向有無並不絕對代表關聯的存在， 也就是說概念之間沒有指向關係並不代表彼此毫無關聯，有指向關係也不 表示有百分之百的關聯性。 林原宏(2005)提出模糊取向的詮釋結構模式分析法，乃是利用模糊理 論的截矩陣和察覺的模糊邏輯模式(fuzzy logic model of perception, FLMP) 以及試題反應理論(item response theory, IRT)，分析概念或解題元素的個人 化階層結構圖，計算其為上下從屬關係(subordination relation)機率計算， 進而進行模糊取向的ISM分析，且元素之間並不受限於二元關係。

Lin, Hung and Huang(2006)提出概念詮釋結構模式(concept advanced interpretive structural modeling, CAISM) ， 針 對 既 有 的 詮 釋 結 構 模 式 (interpretive structural modeling, ISM)，透過模糊理論α截矩陣和察覺的模糊 邏輯模式(fuzzy logic model of perception, FLMP)改進模糊關係矩陣，並且 用概念向量比對(concept vector matching)、精熟度數值等計算方法，針對 受試者對分屬特定概念屬性的每道試題之作答反應進行分析，將個人化概 念階層結構(individualized concept hierarchy structure)以數值和圖形呈現， 提供每位受試者個人化的概念結構訊息。

Lin, Hung, Huang and Li(2009)提出多元計分概念詮釋結構模式，乃是 為 改 進 二 元 計 分 概 念 詮 釋 結 構 模 式 (dichotomopus concept interpretive structural modeling)所發展而成，其分析資料已由二元計分擴展至多元計分 或混合計分模式，且以「概念」(concept)為分析單位，據以呈現個別化 (individualized)的概念結構圖。然而在實際的測驗中，為了統整多個概念於 同一題組，各試題的配分已多元化，於此，將概念詮釋結構模式自二元計 分擴展至多元計分，即為多元計分概念詮釋結構模式(林原宏，2010)。 概念結構圖的呈現會因為每個人的資質以及對概念理解力等因素之

不同而產生不同的概念階層結構圖，如圖2-4-1 A學童的概念階層結構及圖 2-4-2 B學童的概念階層結構(梁錫卿、葉律吟、陳怡汝，2010)。各個概念 方框下方的數字代表受試者對該概念的精熟度。A學童的概念階層結構圖 中，概念1位於第一階層，但在B學童中，第一階層除了有與A學童相同的 概念1以外，還包含了概念2。兩位學童差異較大的地方在於概念2。就A來 說，概念2位於第二階層，對B來說，概念2卻位於第一階層。換言之，三 個概念對於A、B兩學童而言，精熟度不相同，而且針對概念3的精熟，A 學童只要先精熟概念1即可，但是B學童卻要先精熟概念1及概念3。 圖 2-4-1 A 學童之概念階層結構圖 圖 2-4-2 B 學童之概念階層結構圖 概念 2 0.65 概念 3 0.54 概念 1 0.87 → 第一階層概念 → 第二階層概念 概念 2 0.76 概念 3 0.35 概念 1 0.66 → 第二階層概念 →第一階層概念

貳、概念詮釋結構模式演算法則 假設某一個測驗共有S (s=1,2,3,…,S) 位受試者參加，測驗中共有P (p=1,2,3,…,P) 個 多 元 計 分 試 題 ， 而 測 驗 題 中 涵 蓋 的 概 念 共 有 C (c=1,2,3,…,C) 個概念。則概念詮釋結構演算流程說明如下(林原宏，2009)： 一、推導典型反應矩陣 利用受試者測驗後作答的資料建立學生反應矩陣、試題與概念所形成 的試題屬性矩陣及所有概念理解程度可能的組合所形成的典型概念矩陣 等三個矩陣，推導出典型反應矩陣。 二、產生近似值矩陣 將受試者的作答反應矩陣與典型反應矩陣進行相似度比對，產生近似 值矩陣。 三、標準化近似值矩陣 將近似值矩陣進行標準化動作，也就是說讓每一位受試者的答題反應 矩陣與典型反應矩陣的相似程度之值之總和為1。如此經過標準化後之矩 陣稱之為標準化矩陣(standardized closeness matrix, SC)。

四、計算受試者的概念精熟度

每位受試者分別在任一個概念的精熟程度可以構成概念精熟度矩陣。 五、計算概念間從屬關係機率

根據 Luce(1959) 的 選 擇 規 則 (choice rule) 理 論 以及 相 對 適 合 度 準 則 (relative goodness rule, RGR)，配合察覺的模糊邏輯模式(fuzzy logic model

of perception, FLMP)的觀點，以pcc’ 表示對於受試者s而言，概念c為概念c’

的先備概念之機率，從屬關係機率(subordination relation probability)公式如 下(Massaro & Friedman, 1990)：

pcc’ =

( )(

)

( )(

) (

)( )

       − + − − = = = = else d d d d d d d and d d and d sc sc sc sc sc sc sc sc sc sc ， ， ， ' ' ' ' ' 1 1 1 0 0 0 1 1 1

六、計算概念間的關係矩陣

由步驟五求得測驗中所欲測量的c個概念中兩兩概念間的從屬關係機

率後，可得到受試者s的概念間模糊矩陣(fuzzy relation matrix)為Fs

( )

pcc' _C×_C。

七、進行α 截集 (α -cut) 運用α 截集(α-cut)運算方法，依照所選定的α 值

(

0≤α ≤1

)

，將概念間 模糊關係矩陣轉換，公式如下：    < ≥ = α α α ' ' ' 0 1 cc cc cc p p p ， ， ，其中0≤α ≤1 八、建立概念從屬關係矩陣 依照步驟一至七運算方法，可以將複雜的多元資料，經公式轉換成一 個 以 二 元 關 係 (binary relation) 來 表 示 概 念 間 從 屬 關 係 的 關 係 矩 陣

( )

cc C C s p Fα = α_{' ×} 。 九、繪製概念階層結構圖 將步驟八所得到的二元關係矩陣F_sα作為C個概念的相鄰矩陣，經由 ISM分析方法，同時為了提供圖形的可讀性，如圖2-4-3將ISM圖進行簡化， 若元素Ai指向Aj有多條路徑(path)，則去除直接指向並保留間接指向的路徑 (林原宏，2005)，即可獲得每位受試者s的個人化概念階層結構圖。 圖 2-4-3 ISM 圖簡化舉例 C5 C6 C7 C3 C4 C1 C2 簡 化 C5 C6 C7 C3 C4 C1 C2

参、概念詮釋結構模式相關應用研究

戴筱玲(2009)應用概念詮釋結構模式分析法及透過相似性聚類分析演 算法(similarity-based robust clustering method, SCM)分群後，發現不同群組 受試者之速率概念階層結構圖的階層數不盡相同，每一階層內的概念數 量、概念屬性與概念間連結關係也都有所差異。教學者可有效掌握學童的 速率概念知識結構，找出學童學習困難的癥結處，以便有效實施補救教學。 呂秀茹、洪文良、林原宏(2009)應用概念詮釋結構模式及相似性聚類 分析演算法(similarity-based robust clustering method, SCM)將受試者分群， 以分析國小五年級學童時間化聚計算概念。研究指出國小學童時間化聚計 算概念，其知識結構具有階層性，概念之間有連結指向的關係，整體而言， 各群組學童以「日、時、分、秒時間單位的高低階關係」此概念最易精熟； 而以「綜合運用時間的加、減、乘、除計算解決二步驟問題」之概念最難 精熟。 吳玫栞、林原宏、易正明(2008)運用概念詮釋結構模式，針對國小六 年級學童進行四邊形概念結構之圖形化知識結構分析，比較學童的概念詮 釋結構圖發現，對於總分不同之受試者而言，其四邊形概念知識結構圖皆 有所不同，其中以低成就組受試者在概念間的關聯性最為薄弱；而受試者 在總分相同的情形下，其四邊形概念知識結構圖亦會隨著受試者的作答反 應組型不同而產生明顯的差異。整體來說，由國小學童個別化的四邊形概 念階層結構圖可知大多具有階層結構之共同特徵，進而瞭解學童於各概念 的熟悉程度與概念間的關聯指向狀況，因此此診斷訊息可供教學者及教材 設計者作為參考。

Lin, Hung and Yu(2007)應用概念詮釋結構模式，對國小學童等量公理進 行概念結構之分析。研究發現，對於作答反應組型不同或是總分不同的受 試者，其概念階層結構圖也會有所不同。

Yih and Lin(2007) 利用 概 念 詮釋結構 模 式分析大學生在學 習 使 用 MATLAB軟體後，對於該軟體的概念認知結構，結果顯示不同作答反應組

型和不同總分的受試者，在概念結構圖上各有不同的特徵及其差異存在。 其他有關在概念詮釋結構模式分析之實證資料還有診斷選修線性代 數卻學習落後之大學生的知識結構(Yih, Lin & Hung, 2007)、分析三年級學 生數字概念(Lin & Yih, 2008)等。

綜上所述，概念詮釋結構模式為應用察覺的模糊邏輯測量，將概念或 知識間的從屬關係清楚描述，藉由個人化的概念階層結構圖，瞭解不同能 力值或者是得分相同的受試者，在概念階層結構圖上所具有的不同的特徵 及意義。教學者可依此資料進行認知診斷評量的參考，並有助於教學者正 確地找出受試者學習概念或知識時的問題所在，適時實施補救教學，改善 學習效果，提升學習興趣及能力。

第五節 S-P 表分析理論

壹、S-P表的起源 鑑別度與難度是分析試題品質的指標，而信度與效度是施測工具的重 要指標。然而試題品質與使用施測工具測驗後品質分析的結果，無助於協 助教師改進其命題技巧、教學效能或診斷出學童學習的困難所在(余民寧， 2002；蔡小玲，2008)。S-P表(Student-Problem chart)乃是學生問題表的簡 稱，是由日本學者佐藤隆博(Takahiro Sato)於1975年提出。S-P表是在分析 學生的作答反應組型及試題概念屬性的注意係數，含學生注意係數(caution index for students)、試題注意係數(caution index for problems)，整份測驗的 差異係數(disparity index)及同質性係數(homogeneity coefficient)。S-P表屬 於無母數統計方法(nonparametric method)，亦即對母群體特性無任何規定 假設的統計推理法(余民寧，2002；陳騰祥，1988)。適合應用於少人數的、 以班級為單位的之形成性評量資料分析(Takeya, 1980; Tatsuoka, 1984)。

貳、S-P表係數之計算

S-P表內的係數係針對實際測驗所得資料中，用以判斷異常的作答反應 情形之係數，包括學生注意係數(caution index for students, CS)和試題注意 係數(caution index for problems, CP)。當注意係數數值愈大時，代表著學生 或者試題的反應組型之異質成分愈高，意即反應組型不尋常的情形愈加嚴 重，教師可利用這些指標瞭解學生或試題的問題所在，以便適度修正與調 整。以下將就一份測驗如何形成S-P表之過程作一簡介： 對 於 一 個 資 料 矩 陣 而 言 ， 假 設 共 有 N

(

i =1,2,⋅ ⋅⋅,N

)

位 學 生 和

(

j M

)

M =1,2,⋅ ⋅⋅, 的二元計分試題，令矩陣Y =

( )

yij _N×M為N 位學生在M 個試 題上的反應資料矩陣。此外，令

∑

= • = M j ij i y y 1 為第i位學生的總分且學生分數 已經排序為y_1• ≥ y_2• ≥ y_3• ≥⋅ ⋅⋅≥ y_N• 。同樣地，令

∑

= • = N i ij j y y 1 為第j個試題的 答對人數，且試題已經排序為y_•1 ≥ y_•2 ≥ y_•3 ≥⋅ ⋅⋅≥ y_•M。以下為學生注意係

數(CS)和試題注意係數(CP)之計算公式，其中

∑

= • = M j j y M 1 1 ' µ 且

∑

= • = N i i y N 1 1 µ 。 則 第 i 位 學 生 的 注 意 係 數 CSi和 第 j 個 試 題 的 注 意 係 數 CPj分 別 為 ：

( )( )

( )( )

( )( )

' ' 1 1 µ µ • = • • • − − − =

∑

∑

• i y j j M i j ij i y y y y y CS i = ) ' )( ( ) )( ( ) )( 1 ( 1 1 1 u y y y y y y i y j j n y j j ij y j j ij i i i − − −

∑

∑

∑

= + = = =       ×       −                     −           答對人數 試題之平均 之總分 學生 答對人數之和 左方各試題之 曲線 在 學生 之答對人數之和 」的試題 右方答「 曲線 對應於 學生 之答對人數之和 」的試題 左方答「 曲線 對應於 學生 i S i S i S i 1 0 i y ：表示學生i的總分 j y ：表示試題j的答對人數 ij y ：表示學生i在第j試題的答題情況

∑

= = n j j y n 1 1 ' µ ：表示試題之平均答對人數 和

( )

( ) ( )( )

( )

( )

µ µ j y i i N i i i ij j y y y y y CP j i • = • = • • − − − =

∑

∑

1 1 1 =

(

)

( )

( )

( )

( )

j

( )

µ y i i i N y i i ij i ij y y y y y y j j y j − − −

∑

∑

∑

= = = + 1 1 1 1 =       ×       −                     −           平均得分 學生之 之答對人數 試題 總分之和 上方各學生 曲線 在 試題 總分之和 」的學生 下方答「 曲線 對應於 試題 總分之和 」的學生 上方答「 曲線 對應於 試題 j P j P j P j 1 0 i y ：表示學生i的總分 j y ：表示試題j的答對 ij y ：表示學生i在第j試題的答題情況

∑

= = N i i y N 1 1 µ ：表示學生之平均得分 一般而言，學生注意係數(CS)的值應該都是正數，當數值愈大時，表 示學生的反應組型愈不尋常，此時必須提醒教師要更加注意，同時必須探 究其成因(陳騰祥，1986)。佐藤隆博提出下列規則，來判斷學童的作答反 應之組型是否有不尋常的現象。 (一)當0≤CS <0.50時，表示學生的反應組型發生不尋常或異常的情況 並不是很嚴重，還在可容許的誤差範圍之內。 (二)當0.50≤CS <0.75，表示學生的反應組型為不尋常或異常的情況已 經很嚴重，應予注意。 (三)當CS ≥0.75時，表示學生的反應組型發生不尋常或異常的情況已 經非常嚴重，需要特別注意。 利用上述係數的意涵協助教師診斷學生學習成效與檢試測驗之品質 良窳，以期作為改進教學、命題及輔導學生之參考(游森期、余民寧，2006)。 参、學習類型與試題類型分析 根據學生的注意係數與試題注意係數及相關資料，可將學生及試題分 別分為六類學習類型與四類試題類型，如表2-5-1與表2-5-2所示(Sato, 1980; Sato & Kurata, 1997)。

一、學生學習類型 以學生注意係數為橫坐標，學生得分百分比為縱座標，可將所有學生 的學習狀況分成六大類，分別記為A、A'、B、B'、C、C'，如表2-5-1。以 學生注意係數0.50為A與A'、B與B'、C與C'的分界，也就是說A、B、C三類 學生之注意係數介於0至0.50之間，而A'、B'、C'三類學生之注意係數大於 0.50。學生得分百分比75%及50%為A(A')、B(B')、C(C')的分界，也就是說 學生得分百分比大於75%者為A(A')，學生得分百分比介於50%至75%之間 者記為B(B')，而得分百分比小於50%者記為C(C')。

A 學習穩定型 學習良好， 穩定性高。 A’ 粗心大意型 學習稍顯不穩定， 不細心造成錯誤。 B 用功不足型 學習尚稱穩定， 但需要再用功點。 B’ 欠缺充分型 偶有粗心，準備不完全， 需要再努力。 C 學力不足型 學力不足，學習不積極， 需要更加努力用功。 C’ 學習隨興型 學習非常不穩定，具隨性 的讀書習慣，對考前內容 沒有充分準備。 100% 75% 50% 1.00 0.50 學 生 得 分 百 分 比 0 學生注意係數 表 2-5-1 學習類型分類表 茲將各個學習類型之特色分述如下： (一) 學習穩定型(A 類) 此類型學生是屬於學習態度良好且穩定性高的學生，不僅資質較高， 測驗時也常能依其內在能力完全地表現出來，較不會有臨陣擦槍走火，表 現失常的情況發生。 (二) 粗心大意型(A’類) 此類型學生是屬於因為粗心大意，不細心作答而造成錯誤回答的學 生，因此此類學生在應考前，為了提高其應考成績，教師必須事先再三提 醒學生作答時應注意事項，並且需要反覆練習作答，以降低試題答錯率。 (三)努力不足型(B 類) 此類學生是屬於因為學習穩定性較 A 類型略差一點，不過尚稱穩定， 努力程度比較不足。該類型學生只要多花一點點時間於課後複習教師所教 授過之單元，就可以在測驗上獲得更高的成績，在學習狀況也可比較穩定。