國小六年級因數與倍數單元補救教學 之行動研究

國立臺東大學教育學系 文教行政碩士在職專班

碩士論文

指導教授：鄭承昌 博士

國小六年級因數與倍數單元補救教學 之行動研究

研 究 生：葉盛元 撰

中華民國 一○二 年 六 月

國立臺東大學教育學系 文教行政碩士在職專班

碩士論文

國小六年級因數與倍數單元補救教學 之行動研究

研 究 生： 葉盛元 撰 指導教授： 鄭承昌 博士

中華民國 一○二 年 六 月

謝誌

沒想到兩年很快就要過去了，想起前年暑假才剛剛幸運地調回故鄉台東，彷 彿是昨天才發生的事；選擇念臺東的研究所，是剛好搭配著縣外調動的原因，雖 然我不是東大人，但再踏入校園的同時，自己好像回到大學生活般，只是身分不 一樣，是位正式教師也是位在職研究生。回來台東時，其實身旁除了親人外並沒 有其他的同學、朋友，幸好學校的同事們及研究所的同學們一路以來互相關心、

照顧，我很開心有了新同學也有了新朋友。

起初以為念研究所應該是枯燥乏味的過程，但是同學們的開朗活潑、細心體 貼為彼此著想，教授們個個用心地指導我們往畢業論文的方向邁進；尤其要特別 謝謝同組的世斌、家鳳、俊智、鈞元及怡利等同學，每個禮拜大家都準時來老師 家一起互相研究與討論，真是辛苦了！另外也要感謝指導教授鄭老師，每次 meeting 時都給予我很多方面的建議，雖然來回路途遠，不過總是收穫滿滿的回 家，也順便謝謝師母一年來的陪伴，謝謝您泡的茶讓我們精神百倍、思路清晰。

此外也要感謝支持與最愛的家人－爸爸及妹妹，雖然你們遠在台中，但總是 給我加油與打氣；謝謝學校的同事－美娟師、玉卿師、九瓏師，總是幫忙我協助 班上的事務；謝謝能如願和班上一起畢業的 15 位學生；謝謝我的好朋友們－平 等國小的同事們、以及馨尹、銘恩、千珊、宜汝、柔孜、仲修，謝謝你們時時關 心我的進度，並給我精神方面的鼓勵，能夠認識你們真好！

最後想要把這篇論文獻給親愛的奶奶與辛苦的媽媽，謝謝媽媽這四年多來盡 心盡力照顧奶奶，兩年前我毅然決然調回來，也是因為心疼妳捨不得妳太辛苦，

妳說照顧奶奶是甘之如飴的事，叫我要好好如期完成研究所的學業，不用太擔心 奶奶的事，如今要畢業了，也能多花時間照顧奶奶順便盡自己的孝道；親愛的奶 奶，我知道您躺在床上正默默的為我祈禱，我十分感謝您保佑我能一路順利完成 學業，以後我仍會繼續陪伴您走完最後的人生，媽媽、奶奶我愛您們。

葉盛元 謹致 2013 年 6 月

國小六年級因數與倍數單元補救教學 之行動研究

作者：葉盛元

國立臺東大學教育學系

摘 要

本文採行動研究法，以因數與倍數單元進行教學，探討補救教學活動對改善 國小六年級學生於因數與倍數之迷思概念。透過分析迷思概念，設計相關補救教 學課程，檢視其實施的歷程與結果，希望能改變學生觀念與態度，達到澄清因數 與倍數迷思概念之目標。

為達研究之目的，研究者以服務的台東縣曙光國小的六年一班為研究場域，

以研究者擔任級任導師的3位班級學生為研究對象，補救教學時間自102年3月至 102年5月，共計五節課的行動研究。

本研究依據文獻資料的蒐集及探討，經由前測試題了解學生在因數與倍數單 元上有明顯的迷思概念，依據其迷思概念設計相關的教學活動，並輔以適合的教 學軟體進行補救教學，希望幫助學生釐清其在因數與倍數單元上的迷思概念，以 達成九年一貫課綱所要求的能力指標。本研究之教學活動設計以學生生活周遭的 情境為原則，並利用具體物的操作、教學媒體與數學遊戲來引導，期望能解決學 生在因數與倍數概念上的錯誤觀念。教學活動包含五個單元：活動一「判別質數」、 活動二「判別合數」、活動三「質因數與質因數分解」、活動四「最大公因數與 最小公倍數」、活動五「認識互質與最簡分數」等五個活動。

從研究的結果可以發現「最大公因數與最小公倍數」和「互質與最簡分數」

上還是存有迷思概念，而「判別質數、合數」和「質因數與質因數分解」的錯誤 觀念，大部分的學生已獲澄清。整體來說三位學生在補救教學後進步很多，對於 部分的迷思概念尚未釐清，若有足夠的時間與更嚴謹的教學設計，相信能使補救 教學發揮到最大的效果，讓學生的數學能力更上一層。

關鍵詞：六年級學生、因數與倍數單元、迷思概念、補救教學。

Action Research on Remedial Instruction on Factor and Multiple Units for Six Graders

Sheng-Yuan Yeh

Abstract

The action research discussed whether the misconception in factor and multiple units of six graders was improved after remedial instruction was conducted. Through the analysis of the misconception, related remedial courses were designed to examine the process and results of the courses in the hope of changing students’ concepts and attitudes to achieve the objective of clarifying the misconception in factors and multiples.

To achieve the goal of the study, Class One Grade Six at Shuguang Elementary School in Taitung County was where the study was conducted, and three students of this class were the subjects of the study. The remedial instruction started from March to May, 2013 with five courses in total.

On the basis of the collection and discussion of documents and data, the students’

obvious misconception in factors and multiples could be comprehended through a pre-test. Therefore, related instructional activities were designed based on the misconception, and appropriate instructional software was adopted to complement the remedial instruction. It was hoped that by doing so, the misconception of the students in factors and multiples could be clarified to accomplish the competence indicators required by the outline of nine-year curriculum. The instructional activities of the study were designed under a framework of situations surrounding the life of the students, and the operation of concrete objects, instructional media and mathematic games were adopted to assist the students. By doing so, the misconception of the students in factors and multiples was hopefully to be solved. The instructional activities covered five units including Activity One: to differentiate a prime number, Activity Two: to differentiate a composite number, Activity Three: prime factor and prime factorization, Activity Four: highest common factor and lowest common multiple; Activity Five: relatively prime and fraction in lowest term.

It could be discovered that misconceptions still existed in “highest common factor and lowest common multiple” and “relatively prime and fraction in lowest term,” and that the misconceptions in “differentiating a prime number and composite number”

students had improved greatly after the remedial instruction. With respect to certain misconceptions that have not been clarified, if there was sufficient time and more rigorous instructional design, it was believed that the remedial instruction could elaborate its greatest results to improve the mathematic abilities of the students.

Keywords: six graders, factor and multiple units, misconception; remedial instruction.

目 次

摘 要... i

Abstract ... ii

目 次... iv

表 次... vi

圖 次... vii

第一章 緒論... 1

第一節 研究背景... 1

第二節 研究動機... 2

第三節 研究目的... 5

第四節 名詞解釋... 6

第五節 研究範圍與限制 ... 6

第二章 文獻探討... 9

第一節 因數與倍數概念探討 ... 9

第二節 學生常見之因數與倍數迷思概念 ... 12

第三節 因數與倍數教材分析 ... 16

第四節 數學補救教學相關研究 ... 23

第三章 研究方法... 29

第一節 研究設計與架構 ... 29

第二節 研究對象... 32

第三節 研究工具... 33

第四節 教學規畫... 35

第五節 研究流程與實施步驟 ... 36

第四章 研究結果與討論 ... 39

第一節 因數與倍數前測概念結果分析與探討補救學生之迷思概念 ... 39

第二節 因數與倍數補救教學之教學設計 ... 53

第三節 因數與倍數後測概念結果分析與補教教學實施之修正建議 ... 66

第四節 補救教學之行動歷程檢討與教師專業成長之分析 ... 80

第五章 結論與建議 ... 85

第一節 結論 ... 85

第二節 建議 ... 90

參考文獻... 92

中文部分 ... 92

西文部分 ... 94

附錄... 95

附錄一、國民小學數學科補救教學基本學習內容試行版 ... 95

附錄二、六年級因數與倍數概念前測 ... 98

附錄三、教師日誌 ... 99

附錄四、觀察記錄表 ... 100

附錄五、訪談記錄表 ... 101

附錄六、六年級因數與倍數單元補救教學活動－質數判別與應用 ... 102

附錄七、六年級因數與倍數單元補救教學活動－合數判別與應用 ... 105

附錄八、六年級因數與倍數單元補救教學活動－質因數與質因數分解 ... 107

附錄九、六年級因數與倍數單元補救教學活動－最大公因數與最小公倍數 110 附錄十、六年級因數與倍數單元補救教學活動－互質與最簡分數 ... 114

附錄十一、六年級因數與倍數補救教學總結性評量 ... 117

表 次

表 2-1 國民小學九年一貫課程綱要各階段能力指標及分年細目

1 ... 16

表 2-2 九年一貫各版本「因數與倍數」單元教學重點比較

2 ... 17

表 2-3 本研究所欲進行的因數與倍數單元之教材分析

3 ... 19

表 2-4 國小因數與倍數單元補救教學基本學習內容、初階概念及學生常見迷思 概念之分析

4 ... 20

表 3-1 因數與倍數各單元之教學規畫表

5 ... 35

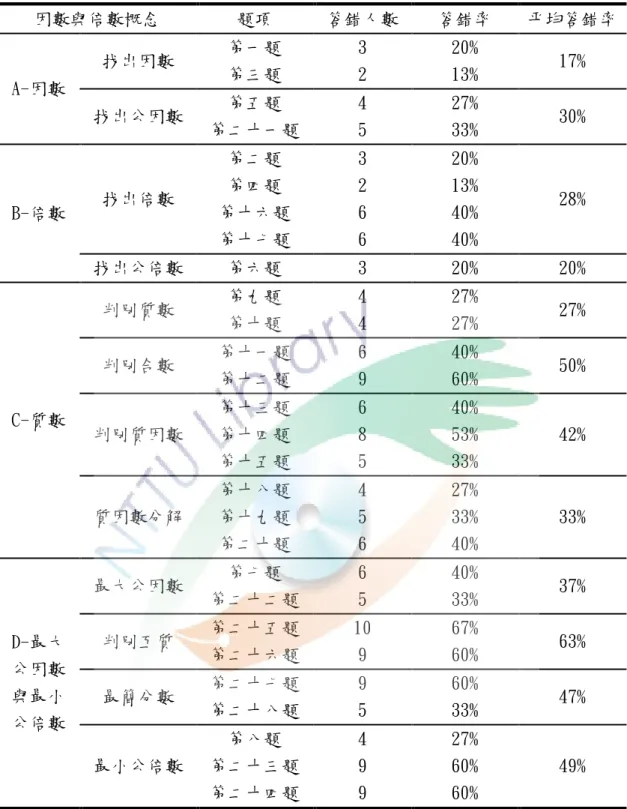
表 4-1 六年級學生因數與倍數迷思概念測驗之結果分析

6 ... 40

表 4-2 受補救教學之前測分析表

7 ... 45

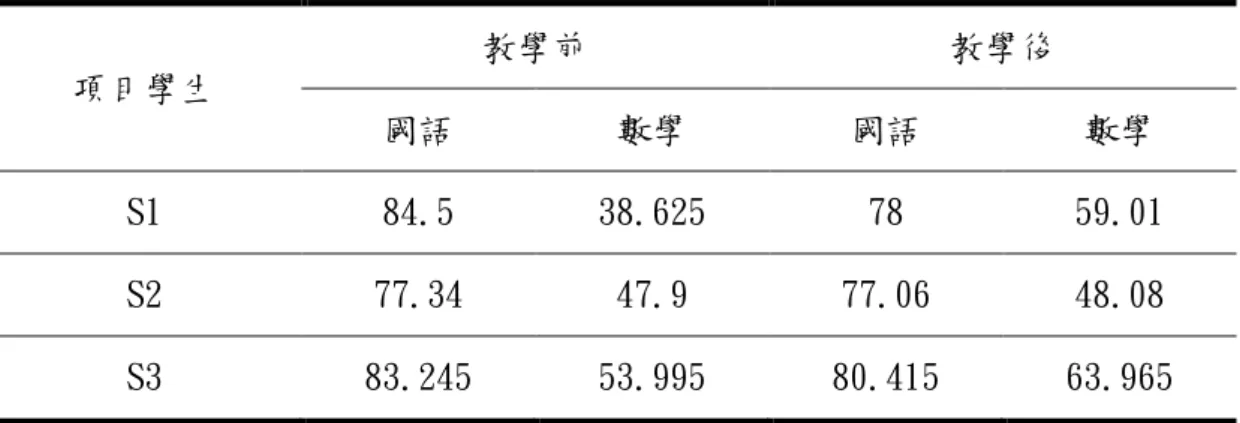
表 4-3 三位學生數理能力與語文成績於補救教學前後統整表現

8 ... 47

表 4-4 A-第二十一題研究對象之答題情形

9 ... 47

表 4-5 B-第四題研究對象之答題情形

10 ... 48

表 4-6 B-第十六題研究對象之答題情形

11 ... 48

表 4-7 C-第九題研究對象之答題情形

12 ... 49

表 4-8 C-第十四題研究對象之答題情形

13 ... 49

表 4-9 D-第七題研究對象之答題情形

14 ... 50

表 4-10 D-第二十四題研究對象之答題情形

15 ... 50

表 4-11 受補救教學學生之前測錯誤率統計表

16 ... 51

表 4-12 受補救教學學生之迷思概念分析簡表

17 ... 52

表 4-13 教學活動設計摘要表

18 ... 53

表 4-14 3 位學生前、後測答對題數對照表

19 ... 66

表 4-15 補救教學前後迷思概念改變之比較

20 ... 67

表 4-16 受補救學生教學前後測迷思概念改變前後對照表

21 ... 69

表 4-17 最大公因數與最小公倍數概念修正前後教學活動設計

22 ... 72

表 4-18 互質與最簡分數概念修正前後教學活動設計

23 ... 75

表 4-19 建議修正後教學歷程之教室觀察記錄表

24 ... 77

表 4-20 建議修正後教學歷程之教師日誌

25 ... 78

表 4-21 學生因數與倍數迷思概念澄清情形之總檢核表

26 ... 80

圖 次

圖 3-1 研究架構圖

1 ... 30

圖 3-2 實施流程圖

2 ... 36

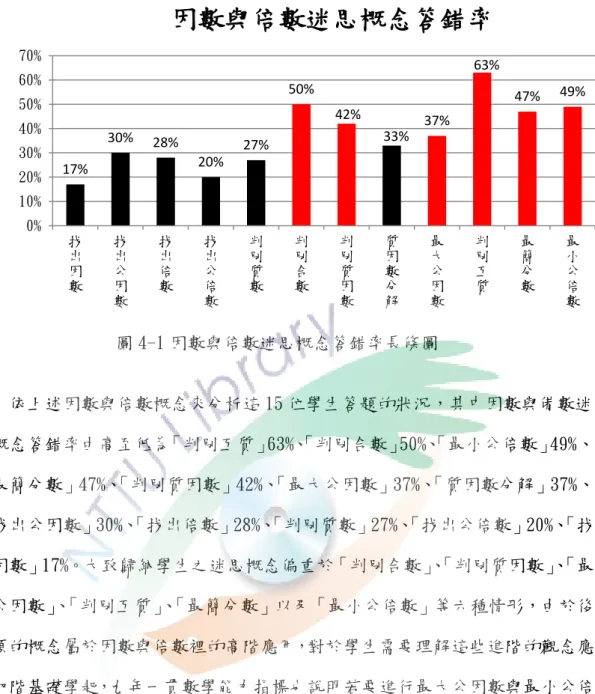
圖 4-1 因數與倍數迷思概念答錯率長條圖

3 ... 44

圖 4-2 學生 S1 判別質數概念課堂學習單之答題情形

4 ... 55

圖 4-3 學生 S3 判別質數概念之數學心智圖

5 ... 55

圖 4-4 學生 S2 判別合數概念課堂學習單之答題情形

6 ... 57

圖 4-5 學生 S2 判別合數概念之數學心智圖

7 ... 57

圖 4-6 學生 S2 質因數與質因數分解概念課堂學習單之答題情形

8 ... 59

圖 4-7 學生 S2 質因數與質因數分解概念之數學心智圖

9 ... 59

圖 4-8、圖 4-9 學生 S1 最大公因數與最小公倍數概念課堂學習單之答題情形

10

圖 4-10、圖 4-11 學生 S2 最大公因數與最小公倍數概念課堂學習單之答題情形

11 ... 62

圖 4-12 學生 S1 最大公因數與最小公倍數概念之數學心智圖

12 ... 62

圖 4-13 學生 S2 最大公因數與最小公倍數概念之數學心智圖

13 ... 62

圖 4-14 學生 S3 最大公因數與最小公倍數概念之數學心智圖

14 ... 63

圖 4-15、圖 4-16 學生 S1 互質與最簡分數概念課堂學習單之答題情形

15 ... 64

圖 4-17 學生 S2 互質與最簡分數概念課堂學習單之答題情形

16 ... 64

圖 4-18 學生 S1 互質與最簡分數概念之數學心智圖

17 ... 65

第一章 緒論

在本章中分為五大節，第一節為研究背景；第二節為研究動機；第三節為研究目 的；第四節為名詞解釋；第五節為研究範圍與限制。

第一節 研究背景

數學是一種螺旋式課程，注重學習的循序漸進，慢慢累積知識經驗，才能穩 定的發展；數學不僅是一切科學、技術及思想的基礎，也是人類最天然的語言，

因此生活在 21 世紀我們，擁有數學能力和數學知識儼然已成為日常生活中重要 的基本能力。目前我們國民教育的數學課程目標，主要反映以下的理念：(1)數 學能力代表國民基本素質；(2)培養學生正向學習數學的態度；(3)數學課程教材 需配合學生在各個階段的不同，幫助學生數學能力的發展；(4)數學具有基礎學 科的工具性特質。

回想起國小的時候，升上五年級的暑假開始上校外的暑期先修班，數學第一 單元令我非常頭痛也非常深刻就是因數與倍數，起初補習班老師在台上講得口沫 橫飛，台下的我卻有聽沒有懂，歷經不斷地反覆練習之後固然學習到了解題的技 巧，但印象中對因數和倍數的概念始終沒有真正的了解。沒想到事隔十多年後，

我成了國小老師，雖然數學的課程內容已不像從前艱澀難懂，但從班上學生的學 習狀況與表現讓我曉得他們對於因數與倍數還是非常陌生。

「為什麼數學這麼難？」、「為什麼不學實用的數學，學這些數學以後長大又 用不到!」這兩句話幾乎是我曾經帶過的學生常常問的，雖然本身於國小任教才 短短五年，知道大部分學生對於學習數學這門課是非常困難也是最沒興趣的，原 因不外乎和他們的生活經驗無法連結，對於做老師的我捫心自問：「如何在數學

領域培養學生帶得走的能力？」而我相信可以培養學生們學習數學的興趣，讓他 們建立自信，解決生活上面臨的問題。生活上有一些和因數與倍數息息相關的例 子，例如：分組、平分東西等等，如果學生能善用這些因數倍數的技巧，很多問 題便能迎刃而解。

倍數的觀念，學生在二年級開始便接觸了九九乘法，對於倍數已有初步的理 解；相對於因數是抽象的概念，大部分學生在學習時易產生混淆不清的迷思，也 很難和他們平日的經驗相連結(林珮如，2002)，對於現在的學生，若學習數學無 法和他們的生活經驗做連結，很難會將數學理解進而熟練，雖然我的學生目前已 經升上六年級，對於因數與倍數的學習已有先備知識，但是仍然不擅長應用。此 外因數、倍數和整數的乘法、除法及分數的計算有關(林榮貴，2006)，學生若能 理解因數、公因數、倍數與公倍數觀念，便能了解分數如何擴分、約分與通分(潘 鳳琴，2008)，如果因數與倍數沒有辦法熟練，那之後學習分數的四則運算可能 會有極大的困難與不方便。

第二節 研究動機

現今九年一貫的課程，主要的目的是希望學生能學習帶得走的能力，所謂「數 學能力」是指擁有統整數學知識與對數學整體感覺的培養；然而在數學領域裡最 重要的基本能力除了培養學生了解數學知識外，以下四種能力是必備的；(1)演 算能力：學生能夠理解並且將計算與概念結合的能力。如果學生有流暢的演算能 力，更能增加學生學習數學的自信心；(2)抽象能力：學生能利用圖形、記號、

模型等其他數學語言，進而解釋量化與增進思考邏輯；(3)推論能力：學生利用 自我的邏輯思考，來分析或推論自己的觀點；(4)溝通能力：學生要理解所學習 的數學概念並且要用數學的語言表達自己的意思。此外學生必須學習如何解決應 用問題，並奠定未來的數學基礎，多方面培養欣賞數學的態度及能力。

目前國小六年級數學課程以九十七年課程綱要為主，將九年國民教育分為四

個階段：第一階段(國小一年級至二年級)，第二階段(國小三年級至四年級)，第 三階段(國小五年級至六年級)，第四階段(國中一年級至三年級)；對於一個國小 六年級的學生而言，須熟悉分數與小數的四則運算；利用所學的數量關係，解決 日常生活中的問題；認識簡單的平面圖形、立體圖形及其性質，如何計算面積與 體積；能夠會繪製簡單的統計圖表等。九年一貫課程所要求的數學基本能力，於 小學畢業前到底還有哪些未完成的目標，此為我想要探討的第一個研究動機。

從皮亞傑的認知發展論來說，國小六年級學生已經開始進入「形式運思期」， 雖然開始慢慢能將所學的知識內化，但仍然有一些學生對於因數倍數的概念混淆 不清，產生學習上的迷思，所以必須讓學生結合舊有的學習經驗，才能理解與融 會貫通。

然而現今九年一貫因數和倍數的學習教材和之前我國小學習的截然不同，對 於因數和倍數學習最快速的方式是從認識質數開始，和九年一貫的能力指標有先 後順序上的差異，如果要配合九年一貫能力指標的分年細目來教導學生，可能需 要很多不同的教學技巧及適合的教材，利用建構的方式一步一步來引導學生，解 決因數和倍數的問題；劉伊祝(2007)於研究中提到學生學習因數與倍數常見錯誤 的情形有以下五種：(1)特定數字的遺漏：學生常常漏寫將 1 或本身的數字；(2) 概念混淆不清：學生會將因數與倍數的概念交錯連結，以致解題上出問題；(3) 計算錯誤：學生會因乘法與除法的計算細節不夠仔細而粗心寫錯；(4)應用題文 字理解上有困難：學生會因為題目看不懂而隨意作答。

黃培甄、葉啟村(2005)則提到學生在因數倍數學習上的困難處有下述四種：

(1)找出關鍵字：研究發現學生認為求因數就要用「除法」的方式，反之求倍數 就用「乘法」；(2)因數倍數概念缺漏：學生會因概念不清而漏寫因數、倍數、公 因數和公倍數；(3)先備經驗不足：學生因為學習因數與倍數的先備經驗不足而 造成解題的障礙；(4)無統整的能力：學生無法將以學習過的因數與倍數的觀念 統整在一起。因此探討學生在學習因數與倍數上還有哪些迷思概念，是我的第二

由上述可知若五年級因數和倍數的先備經驗不足，升上六年級再學習勢必會 更加困難更吃力；國內許多學者提出，對於學生產生因數與倍數的迷思概念可以 藉由一些有效的學習策略和補救教學等方式，改善其錯誤的觀念；補救教學是一 種「評量－教學－再評量」回饋的歷程，實施補救教學必須使用學習診斷工具，

設計適合的教案。希望學生能理解已學得的知識，更能促進學生學習的效果，必 須實施補救教學。一般來說，針對數學進行補救教學，大部分是指導學生如何解 題。

孟瑛如(2009)提出國外研究針對數學學習有困難的學生可分為四類：(1)語 文方面：學生在理解數學專有名詞及觀念上有困難，需幫忙學生釐清或整理常用 名詞或概念；(2)知覺方面：學生在閱讀數字及數學符號，分類上有困難，可利 用一些生活上的口訣幫助學生記憶；(3)注意力不集中：學生會因為上課不專心 而無法理解或混淆所學的觀念，可請學生先說出自己的想法，再進行修正或加強；

(4)數學方面：學生對於計算和推理方面有困難時，學習時容易感到焦慮，必要 時可以利用實物或圖解來進行操作，增強學習印象。如果能分析學生的問題所在，

再進行補救教學則會有事半功倍的效果。例如當學生遇到困難的數學問題時，可 以先請學生再讀一次題目，若學生還是看不懂，則提示學生問題有哪些關鍵字句，

再引導學生利用正確的方式來解題。

關於數學補救教學的原則有以下幾點：(1)教師必須依學生學習有困難的性 質與程度、行為表現與學習型態，設計出適合的教材；(2)實施課程內容初期必 須思考學生本身的個別差異；(3)對於學生學習有困難之問題處理，必須早期發 現、早期修正；(4)對於有效而直接的教學活動必須在適合的課程裡實施；(5) 當學生在學習過程中缺乏學習刺激，可發展適合的教學活動及學習方法；(6)實 施教學活動時須注意前後一致性；(7)培養學生對數學觀念的形成，強化學生對 數學符號的概念；(8)建立學生數學學習的通則；(9)培養學生解決問題的能力；

(10)提醒學生時時建立正確的運算習慣；(11)日常生活經驗可連結相關數學的問 題；(12)教師教導學生應用所學的數學知識；(13)實施數學教學時，教師需注意

發問的語言是否使學生聽得懂；(14)教師要瞭解每個學生學習的程度，並且要適 時評量學生學習的表現。

對於數學學習有困難的學生，不管是利用哪種補救教學方法，均需要因材施 教，做適性化的教學，如此才能夠兼顧每位學生的狀況，學生能快樂學習，學習 更有成就感；要如何才能解決學生在學習因數和倍數的困難，必須先找出學生在 學習因數與倍數上容易犯錯的題型，再進行相關的補救教學，加深學生學習的印 象，這是我的第三個研究動機。

第三節 研究目的

根據以上的研究動機，本研究的目的如下：

一、探討補救教學前後，學生於因數與倍數單元之迷思概念有哪些。

二、探討實施補救教學後，學生於因數與倍數單元中的質數、合數、質因數分解、

最大公因數、最小公倍數、互質與最簡分數等概念是否澄清。

三、探討針對學生產生的迷思概念所發展之因數與倍數補救教學活動實施歷程 與教學省思

因此在分析學生易錯的題型時，需配合教育部國民中小學九年一貫課程綱要 數學學習領域所訂定的能力指標，依據六年級因數與倍數的單元，設計相關的教 學活動，並輔以適切的教具及學習單，協助學生進行補救教學，對於本身數學學 習能力薄弱的學生，期望在進行補救教學後，能澄清錯誤的概念並學到如何解決 基本問題的方法。

第四節 名詞解釋

關於本研究的相關名詞解釋如下：

一、因數倍數單元：依九年一貫課程綱要數學學習領域所訂定的能力指標，將六 年級的因數與倍數課程分為「認識質數、合數與質因數分解」、「最大公因數與最 小公倍數」及「認識互質與最簡分數」三個教學活動。

二、迷思概念：學生在課堂上學到新的知識時，將其轉換成自己認為正確的概念，

但卻與學者專家所判定的觀念不同，這樣的概念大致可稱為「迷思概念」。 三、補救教學：教師進行教學活動中發現學生於認知理解上有困難，經過評量後 發現學生易錯的問題，因此設計並實施相關的教學活動，協助學生解決困難的地 方，以達成預期的教學成效。

第五節 研究範圍與限制

本研究的研究範圍以研究對象、研究設計、課程內容與研究工具四個項目為 主；研究限制則以人力考量、時間因素兩點來敘說。

一、研究範圍：

(一)研究對象：研究對象僅以臺東縣一所國小之六年級學生為對象，本身對於 因數與倍數的學習容易產生錯誤的概念。

(二)研究設計：本研究採行動研究法，先分析受補救教學的學生於因數與倍數 中易錯的題型，再根據這些易錯的題型設計適切的教案進行補救教學，探討補救 教學的實施是否有效。

(三)課程內容：以九年一貫課程綱要數學學習領域所訂定的能力指標為主，其 六年級因數與倍數為實施內容，包含「質數的判別與應用」、「合數的判別與應用」、

「質因數與質因數分解」、「最大公因數與最小公倍數」及「認識互質與最簡分數」

等五個單元。

(四)研究工具：分析六年級學生的易錯的題型，將之擬出因數倍數概念的前測 題目，於班上施測後選擇需要補救教學的學生，了解其迷思概念，進而設計相關 的教學活動，並配合學校硬體設備進行補救教學，其後訪談受補救教學之學生，

了解研究的實施過程與成效如何。

二、研究限制

(一)因本身人力考量，研究對象僅以三位補救教學學生為主。

(二)因本身現為六年級導師，課程也僅限於六年級因數倍數單元之迷思概念。

第二章 文獻探討

本研究目的主要在探討國小六年級學生學習因數與倍數單元產生哪些迷思 概念，進而進行補救教學之行動研究。因此本章之文獻探討分為四個部分，第一 節探討因數與倍數的相關概念；第二節提出學生學習因數與倍數單元中有哪些常 見的迷思概念；第三節針對本研究相關因數與倍數教材進行分析；第四節探討數 學補救教學有哪些相關研究。

第一節 因數與倍數概念探討

本節探討因數與倍數的意涵，以及從八十二年至九十七年數學課程綱要關於 國小因數與倍數的能力指標之修訂過程。

一、因數的意涵

對於因數的概念或定義有很多不同的解釋，從數學辭典中提到因數的意涵是：

整數甲可以被零以外的整數乙整除時，乙便是甲的因數。1 對任何整數而言都是 最小的因數，而整數本身是整數自己最大的因數(小牛頓國小數理辭典，1992)；

而在數學百科中也提到對因數的定義如下：所有能夠整除某整數的商，稱為此整 數的因數(小牛頓數學百科 1，1996)。

另外因數的解釋可以由除法原理(若有 a、b 兩個正整數，則一定可以找到 q、

r 兩個非負整數，滿足 a = b × q + r 且 b > r > 0 或 b > r = 0 )為基礎，透 過判斷 a 是否能夠整除 b(餘數是否為 0)的方式，引入因數與倍數的定義，其定 義如下：設 a、b 是兩個正整數，若 a = b × q + r，其中 q 為正整數，而且 r=0，

則稱 b 為 a 的因數。例如：a = 12、b = 6，滿足 12 = 6 × 2，其中 q = 2，那 麼 6 是 12 的因數。在國小階段因數的討論範圍以正整數為主(國立教育研究院籌 備處，2002)。

然而在九年一貫課程綱要中對於「因數」的標準名詞解釋如下：一正整數 a 若能整除另一正整數 b，a 稱為 b 的因數。如：a = 6、b = 12，12 ÷ 6 = 2(餘

數等於 0)，則 6 是 12 的因數。

因數問題是如設定一個正整數做為單位量，有哪些正整數為單位可以用乘法 方式成為這個正整數。如 8 的因數，一個 8 是 8；二個 4 是 8；四個 2 是 8；八 個 1 是 8，因此 8、4、2、1 皆可以用乘法方式成為 8 的單位量，稱之為 8 的因 數。

二、倍數的意涵

關於倍數的概念與定義，在數學辭典中的解釋如下：某個整數乘以另一個整 數所得的數，就是原來整數的倍數(小牛頓國小數理辭典，1992)；而在數學百科 全書裡提到倍數的定義是整數加倍所得的數稱為此數的倍數(小牛頓數學百科 1，

1996)。

此外對於倍數不同的詮釋，是以除法原理(若有 a、b 兩個正整數，則一定可 以找到 q、r 兩個非負整數，滿足 a = b × q + r 且 b > r > 0 或 b > r = 0)為 基礎，透過判斷 a 是否能夠整除 b(餘數是否為 0)的方式，引入因數與倍數的定 義，其定義如下：設 a、b 是兩個正整數，若 a = b × q + r，其中 q 為正整數，

而且 r = 0，則稱 a 為 b 的倍數。例如：a = 12、b = 6，滿足 12 = 6 × 2，其 中 q = 2，那麼 12 是 6 的倍數。在國小階段倍數的討論範圍一樣以正整數為主(國 立教育研究院籌備處，2002)。

九年一貫課程綱要中對於「倍數」的標準名詞解釋如下：一正整數 a 若能整 除另一正整數 b，b 稱為 a 的倍數。如：a = 6、b = 12，12 ÷ 6 = 2(餘數等於 0)，則 12 是 6 的倍數。

倍數問題是如設定一個正整數做為單位量，此正整數可以用乘法方式成為哪 些正整數。如 8 的倍數，一個 8 是 8；二個 8 是 16；三個 8 是 24；四個 8 是 32…，

因此 8、16、24、32…，稱之為 8 的倍數。

三、因數與倍數能力指標

八十二年國民小學數學科課程標準教材綱要與計算部分，關於因數與倍數概 念部分只著重於認識因數、公因數、倍數及公倍數而已；八十九年九年一貫課程

暫行綱要中有關於因數與倍數的能力指標有二：(1) N-3-18：能察覺整數的因數、

倍數、公因數、公倍數；(2) N-3-20：能察覺整數的最大公因數、最小公倍數、

質數和合數，並能將一個數做質因數分解。其中 N-3-18 屬於六年級課程，N-3-20 屬於七年級課程。從八十二年到八十九年課程綱要中，關於國小因數與倍數的課 程內容並無太大的差異。

九十二年公佈的九年一貫課程綱要裡提到的因數與倍數能力指標關於六年 級分年細目如下：(1) 6-n-01 能認識質數、合數，並作質因數的分解（質數＜

20，質因數＜10，被分解數＜100）；(2) 6-n-02 能認識兩數的最大公因數、最 小公倍數與兩數互質的意義，理解最大公因數、最小公倍數的計算方式，並能將 分數約成最簡分數。從八十九年暫行綱要到九十二年課程綱要中，關於國小因數 與倍數的課程增加了認識質數、合數、質因數分解、最大公因數、最小公倍數、

互質、最簡分數 及短除法等內容。

在九年一貫課程綱要九十七年修訂版中對於六年級因數與倍數部分所應達 成的能力指標如下：(1) 6-n-01 能認識質數、合數，並用短除法做質因數的分解 (質數＜20，質因數＜20，被分解數＜100)；(2) 6-n-02 能用短除法求兩數的最 大公因數、最小公倍數；(3) 6-n-03 能認識兩數互質的意義，並將分數約成最簡 分數。

從九十二年課程綱要到九十七年修訂版綱要中，關於國小因數與倍數的課程 只有質數的內容有些微調整，其他部分均無顯著差異。

第二節 學生常見之因數與倍數迷思概念

關於六年級之因數與倍數迷思概念，綜合國內學者的研究，大致上可歸納出 以下幾點：

一、因數與倍數的意義

1.特定數字的遺漏：學生在求因數、倍數、公因數與公倍數的過程中，常常 出現漏寫將 1 或本身的數字(周文忠，2002；林珮如，2002；邱慧珍，2002)。此 外黃耀興、邱易斌(1999)在探討國小學生在學習因數與倍數單元中，也發現學生 在找因數過程中時而會有缺漏。以因數問題來說，有部分的學生會依九九乘法而 忽略質因數大小撰寫順序，以致漏寫其他的因數。舉例來說：寫出 72 所有的因 數，有部分學生會漏寫因數 1；有些學生會寫 72 = 1 × 72 = 8 × 9 = 3 × 24，

因未按照質因數大小順序而漏寫其他因數。

2.計算錯誤：學生會因乘法與除法的計算細節不夠仔細而粗心寫錯。以倍數 問題來說，學生會因為乘法計算或除法計算錯誤而誤寫答案(周文忠，2002；林 珮如，2002；邱慧珍，2002)。陳標松(2003)從國小六年級學生學習因數與倍數 單元裡指出有些學生因粗心的錯誤，必須加強其乘法與除法的計算能力。舉例來 說：下列哪些是 11 的倍數？6204、5025、594、792；學生會選擇到錯誤的答案 是因為除法計算錯誤沒有仔細檢查，或是少選其他正確的答案。

3.概念混淆不清：學生會將因數與倍數的概念交錯連結，以致解題上出問題 (陳標松，2003；周文忠，2002；林珮如，2002；邱慧珍，2002)。何欣玫（2004）

在國小六年級學生因數與倍數之數學解題研究中，關於學生概念錯誤的類型，其 語言概念錯誤、認知概念錯誤及策略概念錯誤皆會影響學生解題。以公因數與公 倍數問題來說，例如：找出下列各組的公因數及最小的 3 個公倍數(1) 4 和 16 (2) 24 和 36，常見有以下三種錯誤的情形：(1) 因數寫不完整：學生會將題目錯看 成只求 3 個最小的公因數,以致答案多處漏寫；(2)漏寫公倍數：學生答案少寫 3 個公倍數,可能是題目沒看清楚；(3)題目看錯,找公因數寫成最大公因數,找公倍

數寫成最小公倍數：學生將答案寫成兩組數的最大公因數和最小公倍數,並非題 目所要求的公因數及 3 個公倍數,未將題目仔細看清楚再寫。

4.應用題文字理解上有困難：學生會因為題目看不懂而隨意作答(陳標松，

2003；周文忠，2002)。陳筱涵(2004)調查學生在學習因數與倍數的單元之錯誤 類型，發現學生常會因為題目一些無關緊要的訊息而誤解題意，以致無法解決問 題。例如：小平有 30 顆巧克力要分給同學，每個人都要分到一樣多且剛好分完，

他可以分給幾個人？學生的錯誤答案可能有以下三種：(1)學生將答案少漏寫 1；

(2)學生將答案寫成 8 人，不了解題目所要問的意思；(3)學生將答案寫成 4 種，

誤以為題目所求是 4 種情況。

二、質數、合數和質因數分解

1.1 是否為質數？ 1 不是質數也不是合數，1 是任何數的因數。施多美(2006) 在學生學習因數概念的知識結構研究中，發現學生對於「1 是否為質數？」有迷 思概念。質數的定義是一個正整數，除了 1 及本身以外，沒有其他的因數時，

稱為質數；而質因數是指一個數的因數也是質數，稱為該數的質因數。舉例來說：

(○) 81 是合數，81 只有一個質因數。大部份的學生沒選擇對的原因是認為 1 也是 81 的質因數。

2.質因數分解時漏寫質數：Kennedy, L. M. & Tipps, S. (1997) 認為學生 在學習因數概念上，可以利用樹狀圖來幫助其概念的澄清；使用因數樹( factor tree )來做某數的質因數分解，方式是將一個數寫成因數相乘，一層一層往下分 解擴展，直到寫成所有質數相乘。舉例來說：(1) 求 8 × 16 的質因數分解。學 生在寫樹狀圖質因數分解時少寫一個乘以 2；(2) 用質因數分解找出 95 的所有 因數。學生常會漏寫了因數 1 或漏寫了因數 95。

三、最大公因數與最小公倍數

1.只看關鍵字，缺乏閱讀能力(周文忠，2002；林珮如，2002；邱慧珍，2002)：

最大公因數的定義是指一正整數 a 同為兩個以上正整數的因數時，則 a 為這些

有一張廣告紙，長、寬各為 24 公分、16 公分。現在要將此廣告紙分割成大小一 樣的正方形(邊長公分數都是整數) ，正方形的邊長最多是幾公分？可以分割成 幾個？學生將分割的答案寫成最小公倍數,並非題目所求的答案；或將最大公因 數的答案算錯,以致第二個答案也算錯。

又一題如下：要將 126 顆紅球和 108 顆黑球平分裝袋，每袋分到的紅球要一 樣多，黑球也要一樣多，最多可以分幾袋？每袋有幾顆球？學生常見錯誤的寫法 如下：(1)學生將題目 126 顆紅球看成 128 顆紅球，以致答案算錯；(2)學生將最 多分成幾袋答案寫成 7 袋或 6 袋，可能看錯題目所求的意思；(3)學生將每袋有 幾顆球寫成 7 × 6 = 42 顆,看不懂題目要問的意思；(4)學生將每袋有幾顆球寫 成紅球 7 顆，黑球 8 顆，未將紅球與黑球相加。

2.因先備經驗不足，造成解題障礙(陳標松，2003；林珮如，2002；邱慧珍，

2002)：最小公倍數的定義是指一正整數 a 同為兩個以上正整數的倍數時，則 a 稱為這些數的公倍數。在所有公倍數中最小者稱為最小公倍數。黃寶彰(2003) 探討學生在學習因數與倍數的困難和錯誤情形，指出學生在解最大公因數與最小 公倍數問題時，會因為題意理解不清而造成學生不知道要用最大公因數或最小公 倍數的方式來解題。以最小公倍數問題來說：王家的大姊每 15 天回娘家一次，

二姊每 12 天回娘家一次，如果今年元旦，大姊和二姊一起回娘家，今年大姊和 二姊同一天回娘家的日子有幾次？學生常見錯誤的寫法如下：(1)學生將答案寫 成最小公倍數，未將題目的意思看清楚；(2)學生將答案寫成最小公倍數 + 1，

未將題目的意思看清楚；(3)學生將答案寫成 6 次，卻未將元旦那一天算到。

四、互質與最簡分數

1.對於互質的概念混淆不清(施美多，2006)：互質的意義是兩正整數的因數，

除了 1 以外沒有其他公因數，則稱此兩數互質。舉例來說：用質因數分解求 21 和 70 的最大公因數，並判斷是否互質，若不是，求出所有公因數。舉例來說：

學生常會將答案寫成最大公因數 7，而沒把題目求出所有公因數看清楚。

2.未將分數約成最簡分數：最簡分數的定義是指一個分數透過約分，可以將

分數化成分子和分母互質的分數，稱為最簡分數。舉例來說：如將

化成最簡

分數。學生會將答案寫成

，而沒約成最簡分數，可能沒找出兩數共有的因數。

第三節 因數與倍數教材分析

本節主要探討因數與倍數於九年一貫各階段有哪些能力指標及分年細目，進 而比較九年一貫各版本因數與倍數之教學架構；再分析本研究相關因數、倍數之 教材，以及了解教育部國民小學數學科補救教學於因數與倍數單元的基本內容，

最後提出本研究前測之出題方向與綜合心得。

一、九年一貫各階段能力指標與分年細目

國小因數與倍數之概念屬於數學五大主題中的數與量，依據國民中小學九年 一貫課程綱要數學學習領域中提到因數與倍數的能力指標，大多著重於第三階段 (五、六年級)，對於剛升上高年級的學生，對於因數與倍數抽象的觀念如果無法 融會貫通，對於接下來數學課程的學習會有一定的阻礙；相關因數與倍數能力指 標與分年細目如表 2-1：

表 2-1 國民小學九年一貫課程綱要各階段能力指標及分年細目

1

能力指標 分年細目

第 三 階 段

N-3-03 能理解因數、倍數、公因 數與公倍數。

N-3-04 能認識質數、合數，並能 用短除法做質因數分解。

N-3-05 能認識最大公因數、最小 公倍數與兩數互質的意義，並用 來將分數化成最簡分數。

5-n-04 能理解因數和倍數。

5-n-05 能認識兩數的公因數、公倍 數、最大公因數與最小公倍數。

6-n-01 能認識質數、合數，並用短除 法做質因數的分解。

(質數＜20，質因數＜20，被分解數＜

100)。

6-n-02 能用短除法求兩數的最大公因 數、最小公倍數。

6-n-03 能認識兩數互質的意義，並將 分數約成最簡分數。

二、九年一貫各版本教學架構比較

教育部在 97 年公布九年一貫課程綱要修訂版，研究者針對南一、康軒及部 編版的數學教科書，比較三種版本教學重點如表 2-2：

表 2-2 九年一貫各版本「因數與倍數」單元教學重點比較

2

南一版 康軒版 部編版

課程架構 整除→因數和公因 數→倍數和公倍數

→質數和合數→質 因數和質因數分解

→最大公因數→最 小公倍數→覺察 2、

3、5 的倍數

整除→因數→公因 數→倍數→判別 2、

3、5、10 的倍數→公 倍數→質數和合數

→質因數和質因數 分解→最大公因數

→最小公倍數

倍數→公倍數→因 數→公因數→質數 和合數→質因數和 質因數分解→最大 公因數→互質→最 簡分數→最小公倍 數

因數的定 義

用小正方形排成長 方形的情形記錄，了 解整數的因數。

利用整除的概念認 識因數。

利用小方塊排長方 形，以乘法算式列出 兩兩相乘，每一個數 皆為某數的因數。

找出某數 的因數

利用除法找出某數的因數。

公因數 找出兩個數的相同因數，即為公因數。

倍數的定 義

利用某數的幾倍了解倍數的意義，並知道一個數的倍數有無限多 個。

公倍數 從兩個整數的倍數 中，找出相同的倍 數。

從解題中察覺公倍 數。

將各個數的倍數依 序列出來，再挑出共 同的倍數。

因數與倍 從除法的解題紀錄 用乘除互逆了解因 利用整除或乘法算

數的關係 中，了解倍數和因數 的關係

數與倍數的關係 式了解因數與倍數 的關係

質數和合 數的意義

尋找一些數的因數，解釋質數和合數的意義。

質因數 列出某數的因數，從因數中判別哪些是質數，即為質因數、

質因數分 解

將一個數表現成其 質因數的連乘積，並 用短除法做質因數 分解。

由樹狀圖及短除法了解質因數分解。

最大公因 數

從公因數中找出最大的公因數，並利用短除法找出兩數的最大公 因數。

最小公倍 數

從公倍數中找出最小的公倍數，並利用短除法找出兩數的最小公 因數。

互質與最 簡分數

若兩整數互質，最大公因數為 1，最小公倍 數為兩數的乘積。

若一個分數的分子 和分母互質，稱為最 簡分數

從上表 2-2 得知三個版本教材內容中，可以發現於因數的定義、因數與倍數 的關係、質因數分解及互質及最簡分數等四個部分探討的內容不一樣，其餘的內 容大致一樣。在課程的編排上，除了部編版先介紹倍數之外，其他兩種版本皆由 整除的概念帶入因數的定義；此外部編版把最簡分數的概念融入在最大公因數與 最小公倍數單元裡，有別於其他兩種版本的編排(南一版及康軒版將最簡分數概 念放在分數的除法單元裡)。

三、因數與倍數單元之教材分析

根據六年級學生在因數與倍數單元中之迷思概念，來說明本研究進行之補救 教學設計活動如下表 2-3：

表 2-3 本研究所欲進行的因數與倍數單元之教材分析

3

活動 目標

單元 一

認識因數與倍數的意義

1-1 能認識因數與倍數意義。

1-2 能正確找出公因數與公倍數。

1-3 能理解因數與倍數應用題。

單元 二

認識質數、合數和質因數分解

1-1 能認識質數和合數的意義。

1-2 能用短除法做質因數分解。

單元 三

最大公因數與最小公倍數

1-1 能認識最大公因數與最小公倍數 的意義。

1-2 能用短除法找最大公因數與最小 公倍數。

1-3 能理解最大公因數與最小公倍數 應用題。

單元 四 認識互質與最簡分數

1-1 能認識互質的意義。

1-2 能利用約分把分數化成最簡分數。

四、教育部國民小學數學科補救教學基本內容

教育部於 101 年 7 月公布了「國民小學數學科補救教學基本學習內容」試行 版(如附錄一)，其主要目的有三：1.針對學習有困難之學生發展因應之補救教學 教材，以增進國小學生的數學能力；2.當作建構標準化測驗之參考，檢視學生基 本數學能力、篩選需要進行補救教學之學生；3.落實國小數學教育，減低學生學 習數學落差的問題，以加深國人數學能力的基礎。關於國小因數與倍數單元補救 教學的基本學習內容、初階概念與本研究探討之迷思概念統整分析如下表 2-4：

表 2-4 國小因數與倍數單元補救教學基本學習內容、初階概念及學生常見迷思 概念之分析

4

基本學習內容 初階概念 學生常見的迷思概念

透過乘法與整除判斷因 數與倍數。

1. 透過乘法認識因數與 倍數。

2. 透過整除判斷因數與 倍數。

1. 特定數字的遺漏。

2. 計算錯誤。

透過分別列舉因數、倍數 的方式找出兩數的公因 數與公倍數。

透過分別列舉因數、倍數 的方式找出兩數的公因 數與公倍數。

1. 概念混淆不清。

2. 應用題文字理解上有 困難。

透過分別列舉因數、倍數 的方式找出兩數的最大 公因數與最小公倍數。

1. 透過分別列舉因數的 方式找出兩數的最大 公因數。

2. 透過分別列舉倍數的 方式找出兩數的最小 公倍數。

舉例說明質數與合數的 意義。

1. 辨識質數為不能再被 分解的數，其因數只 有1 與自己而已。

2. 辨識合數為大於1 且 有3 個以上因數的整 數，也就是不是質數 的整數。

3. 分辨2、3、5、7、11、

13、17、19 在100 以 內的倍數。

1是否為質數？

進行100 以內的整數的 質因數分解（質因數以 2、3、5、7、11 為主）。

使用樹狀圖進行100 以 內整數的質因數分解（質 因數以2、3、5、7、11 為主）。

質因數分解時漏寫質數。

以短除法進行100以內的 數的質因數分解（質因數 以2、3、5、7、11 為主）。

使用短除法做100 以內 整數的因數分解，並找出 質因數（質因數以2、3、

5、7、11 為主）。

以短除法找出兩數的最 大公因數與最小公倍數。

1. 辨識最大公因數為兩 整數各自擁有的因數 中所共同具有且為最 大的數。

2. 使用短除法求100 以 內兩整數的最大公因 數。

3. 辨識最小公倍數為兩 整數各自的倍數中所 共同具有且為最小的 數。

4. 運用乘法求出兩整數 的最小公倍數。

1. 只看關鍵字，缺乏閱 讀能力。

2. 因先備經驗不足，造 成解題障礙。

舉例說明兩數互質的意 義。

1. 辨識兩數的最大公因 數是1 稱為互質。

2. 區辨兩數可能都是合 數，但兩者互質的情 況。

3. 區辨互質與質數的不 同。

對於互質的概念混淆不 清。

舉例說明最簡分數。 辨識當分子與分母互質 的分數，稱為最簡分數。

未將分數約成最簡分數。

將分數約成最簡分數。 透過約分將分數化成分 子和分母互質的最簡分 數。

五、本研究前測出題方向與綜合心得

根據上述所探討之因數與倍數單元補救教學之教學內容，基於本研究所欲進 行的因數與倍數單元之教學活動與相關擬定前測卷之出題方向說明如下：

1.認識因數與倍數的意義：本單元學生因有特定數字之遺漏與計算錯誤的迷 思，所以出題方向著重於分別列舉因數、倍數、公因數及公倍數之概念澄清；而 學生於應用題文字理解上有困難，將設計相關之應用題以了解其問題的所在。

2.認識質數、合數和質因數分解：學生對於 1 是否為質數與質因數分解時會 漏寫質數之概念上有迷思，因此需要加強其質數、合數與質因數概念，並且要熟 悉 20 以內質數、利用樹狀圖及短除法求出 100 以內整數的質因數分解，為此單 元前測題目所設計之重點。

3.最大公因數與最小公倍數：學生對於利用短除法求出兩數的最大公因數與 最小公倍數上仍有計算錯誤之迷思，因此將加強學生於短除法之運算；由於此單 元之重點偏向於解題，學生常出現先備知識不足，無法解題及只看關鍵字，未能 了解題意等迷思概念，出題方向也會針對文字理解題以探討學生有哪些錯誤的類 型。

4.認識互質與最簡分數：對於互質的概念混淆不清及未將分數約成最簡分數 兩種為學生會出現之迷思概念，所以需要加深其了解互質的意義及最簡分數的觀 念，為此單元出題之參考方向。

綜合以上本研究前測之出題方向，除了透過乘法與整除判斷因數與倍數以及 透過分別列舉因數、倍數的方式找出兩數的最大公因數與最小公倍數等兩項基本 學習內容未納入此補救教學的重點之外，其餘皆因學生存有迷思概念，故依其設 計成相關概念之前測卷，以了解學生有哪些錯誤的觀念，進而實施補救教學。

第四節 數學補救教學相關研究

學生在學習數學有程度上的不同，理解數學概念也不一致，因此老師必須針 對學生在學習產生的困擾分別給予不同指導，幫助學生釐清迷思；在進行數學補 救教學之前，一定要先瞭解學生在數學學習上有哪些困難處，再分析錯誤的類型，

進而設計相關的教學活動；以下從數學補救教學的定義與實施對象、數學補救教 學的歷程及數學補救教學有哪些方式來加以探討。

一、數學補救教學的定義與實施對象 (一)數學補救教學的定義

數學補救教學是指發現學生在學習數學上有困難，並找到其問題所在，針對 問題設計適合的教學活動，幫助學生解決學習上的疑惑，完成應達成的能力指標

（洪素敏，2008）。林榮貴(2006)指出實施補救教學需配合學習診斷工具，設計 合適的課程教材，以讓先備經驗不足與學習能力薄弱的學生有自信的學習；研究 者從事教職工作雖然才短短五年，然而對於指導學生學習數學一直存有疑惑：「為 什麼總是有學生無法把數學學好？」直到帶了高年級，才發現並不是所有學生的 起點行為都相同；對於學習落後的學生，為了讓他們重拾學習的信心、學習更有 成效，數學補救教學的實施勢在必行。

(二)數學補救教學的實施對象

對於補救教學對象之界定，分為以下三類（張新仁，2001）：1.所謂「低成 就學生」是指學生之學業成績明顯低於其應有的標準；2.「低成就」亦指學生之 學業成績明顯低於其班級的平均水準；3.「成績低落( low achievers )」則指 學生學習領域不及格，且學業成績低於其他同學者稱之。學生其成績於全班成績 後百分之五至後百分之二十，方可實施補救教學。

由研究者本身觀察數學學習低落之學生，原因大多是上課學習態度不佳、缺 乏課前預習與課後複習、以及習寫作業不夠認真努力；因此要加強學生學習數學 的動機，多給予學生正面的回饋，教師需要耐心指導是非常重要的。

二、數學補救教學的歷程

補救教學是一種「評量─教學─再評量」的循環歷程（張新仁，2001）。以 理想的情形來說，學生接受一段時間的補救教學，能夠趕上原班級的學習進度。

補救教學的歷程大致分為三個階段(郭玉生，1995、張新仁，2001)：

(一)轉介過程

補救教學的主要工作是篩選、診斷及轉介個案學生，以接受補救教學，以下 為篩選、診斷及轉介的步驟：

1.篩選個案：教師於課堂的觀察與評量，或是經由家長的提出，從班級中 選出需補救教學的學生。

2.蒐集資料：蒐集個案有關的資料，如個案的身心狀況、性向測驗、學習 態度及各領域成績等，來進行診斷與分析。

3.初步診斷：依據學生的日常生活表現，來當作初步判斷學生學習落後及 所需要補救教學措施之參考。

4.家長參與：診斷小組形成決定後與進行評量前，必須通知學生家長，讓 他們了解孩子在學校的學習情形與遇到的困難，進一步再和家長討論孩子接受補 救教學的重要性。惟家長同意後，才可實施正式的評量。

(二)正式評量

評量的目的主要是透過學生學習的過程，找出其遇到的問題與困難處以及補 救方式。

(三)教學

補救教學是一種診療式教學(clinical teaching，也叫做臨床教學)。其主 要是探討學生有哪些學習的困難後，進而設計適當的課程教材與選擇教學類型與 方法，以便達成學生的個別需要。

由上述補救教學的歷程可知，補救教學著重蒐集個案的資料並進行診斷評量，

以了解學生實際的學習情況，並給予適當的幫助。

一般的補救教學課程設計，大致可參考以下幾點(張新仁，2001)：

(一)分析基本能力

任何學習領域目標的達成，一定需要相當的觀察、記憶、想像、知覺、理解、

注意、以及想像力。如果相關的能力不足容易造成學習上發生困難，所以教師在 設計補救教學課程內容時，一定要先瞭解學生學習的能力，再配合教材教法，才 能達到補教教學的成效。

(二)評量學習領域能力

進行補救教學前，需針對學習領域的學習能力進行評量與測試，以當作課程 設計的根據。學習領域能力的評量大多為成就評量，如基本四則運算等。

(三)提高學習動機

學生的學習動機常常會影響其學習成效，因此在進行補救教學之前，教師要 先了解學生學習動機是否強烈，一則可以對學習動機低落的學生提供適度的增強，

二則讓學習低成就的學生列入先補救教學之對象。

(四)擬定教學目標

教學目標往往影響教師選擇其教學方式，自然關係到教學的成果。而教師在 擬定教學目標，要先了解學生的基本能力和學習的客觀條件。此外，教學目標的 訂定，務必指出學習的內容、行為的準則及學習的對象，教學方式與評量的方法。

(五)選擇適合的受試者能力的教材

有效的補救教學課程設計，必須根據學生學習的程度選擇適合的教材內容，

如：將教科書的內容簡化、自行編選坊間的課程教材、訓練有效的學習方式以及 重新設計教材內容等。

有效的補救教學應該遵循以下的原則(Otto，McMenemy、Smith，1973)：

1. 和學生一同合作

2. 教學應依據學生的程度進行 3. 小步驟，循序漸進進行教學 4. 教師提供正面的回饋與增強

6. 幫助學生記憶

7. 鼓勵同學間維持良好的友誼關係 8. 學生能保持強烈的學習動機 9. 提供學生充分的學習機會 10.讓學生累積學習成功的經驗

由上得知，進行補救教學前需考量學生的基本程度，接下來依據學生的基本 能力量身訂做適當的教學目標，進而修改原有的課程內容或自編教材並搭配適當 的學習方式，小步驟，循序漸進進行教學活動，教學活動當中要適時給予學生正 面的回饋與充分的練習，才能達成補救教學的目標。

對於數學補救教學需掌握其知識的性質和教學原則，如以下三點來說明（劉 秋木，民 87；Polloway & Patton, 1997）：

1.生活化的數學：以生活化的問題為教材才能引發學生學習的興趣，由生活 問題的解決中發現數學的概念，熟悉之後便能自然地將數學觀念應用於日常生活 中，學習與生活互有相關的情形下，學生較容易產生濃厚的興趣。

2.數學是由抽象概念所形成的嚴密結構：抽象概念的學習應由觀察與操作具 體事物開始，教學順序應為具體→半具體→抽象學習經驗，同時呈現的教材內容 應與學生的先備知識(prior knowledge)相配合。

3.數學是一種心智歷程的表現：學習數學是期望能在解決問題的過程，學生 能運用各種心理歷程。數學應是在開啟學生的心智，而使其具備解決問題的能力，

而不僅只是灌輸觀念，熟練一種測量或計算方法。學生進行分組討論共同解決問 題，往往有助於學生運用各種方法自行發現解題的方式，同時瞭解數學概念的意 義及各種方法的道理。

除了瞭解學生學習的歷程，學習動機亦是非常重要，對於學習動機薄弱的學 生，和教師本身的數學專業能力並沒有正相關，因此提高學生的學習動機可採取 以下的方式：

1.利用生活中可能遇到的情境或是遊戲使學生能思考運用自己所學的能力

解來決問題。

2. 增加學生成功學習的經驗：教師進行教學過程中可將題目簡化並適當給 與提示，或是採用步驟教學法，使學生能一步一步慢慢學得會，如此學生才能保 持良好的學習動機。

3. 讓學生體會數學帶來的價值，同時能將學習目標具體化：將課堂中的數 學和生活中的數學結合，比較能引起學生學習的興趣，教師的教學方式也能相對 活潑有趣。

4. 教師需給予適時的回饋：教師可設計數學日記讓學生填寫有關今天上課 的內容或心得，使學生慢慢累積自己所學到的經驗，教師也可以從學生的數學日 記中瞭解其學習能力如何。

此外于國善(2004)在設計國小因數單元的補救教學活動裡，提到發展因數 補救教學活動需要注意三點原則：1.學生可藉由具體物的操作，可以加強其因數 的概念；2.學生在具體物的操作之過程中，可以了解「整除」的概念及「順序性」， 以避免因數有漏寫之虞；3.教材內容需和學生的生活經驗相結合，學生在進行解 題時比較容易理解題意，並從中了解「1」是任何數的因數。

三、數學補救教學之方式

張新仁(2001)指出有效協助學習程度落後的學生，可使用直接教學法、精熟 教學、個別化學習及合作學習等教學模式，如下所述：

1.直接教學模式( the direct instrution )：適用於教導學生記憶事實、

學習動作技能。教師主要的工作是統整教材和呈現教材，學生主要的工作是接受 學習。

2.精熟教學模式( the mastery teaching )：這種模式的基本概念是學生在 學習上的程度不同，但只要給予充足的學習時間，學生就可以理解大部分的學習 內容。適用於國中、國小團體教學環境，適用的範圍包含動作技能及認知能力，

然而涉及的層次並不高。

差異，提供適切的教材，做最有效的學習。

4.合作學習教學模式( the cooperative learning )：強調透過小組共同合 作學習的方式精熟學習的內容。在討論的過程中，即使學生產生了錯誤的答案，

在釐清後也能幫助正確觀念的重建。

除了上述所提的四種教學模式，此外針對數學補救教學還有兩種可行的教學 法如下：

1.認知結構激發法：由 Sosniak 及 Ethington 於 1994 年提出，該教學法強 調學生的學習機會(Opportunity To Learn , OTL)。Sosniak 及 Ethington 認為 應不斷給予學生比他們能力程度稍高的教材內容，以激發學生的認知潛能；他們 認為有愈多的機會讓學生解決生活情境式的數學問題，學生愈能有機會奠定真正 的數學概念與技巧。故該教學法的教材內容大都偏向於應用問題及問題解決活動，

不太著重於反覆式的計算題練習。

2.問題解決法：該教學法強調指導學生面對各種數學問題如何解決的方法與 表達技巧。如：(1)教導數學常用詞彙：教師可將數學常用字詞做整理並教導學 生；(2)應用題的解題步驟：再讀題→圈出關鍵字詞→刪除非必要的資訊→標出 關鍵數字→採用圖解方法解題→決定計算方法及步驟→執行計算步驟→檢查答 案→看清楚題目所要求的答案並寫下。

本研究是進行因數與倍數的補救教學，以澄清學生對因數與倍數的迷思概念；

因此本研究主要採取個別化教學模式，希望透過了解學生的個別程度差異而給予 個別的指導，以增進學生在學習數學上的進步。

第三章 研究方法

本研究主要分析六年級學生在因數與倍數單元上的迷思概念，依據其迷思概 念設計相關的教學活動，並輔以適合的教具與教學媒體進行補救教學，希望幫助 學生釐清其在因數與倍數單元上的迷思概念，以達成九年一貫課綱所要求的能力 指標。本研究透過探討相關文獻資料，瞭解六年級學生在因數與倍數上的迷思概 念相關理論後，利用觀察法、訪談學生等方式來蒐集資料，並利用質性的方法來 分析，藉此能更深入的了解學生的學習過程和改善其數學學習的態度。之後透過 記錄、評量、訪談、省思等過程來探討補救教學對學生學習的反應與效果。本章 共分成五節，第一節為研究設計與架構；第二節為研究對象；第三節為研究工具；

第四節為教學規畫；第五節為研究流程與步驟。

第一節 研究設計與架構

本研究採行動研究的方式來進行。研究時間為民國一百零二年三月至五月，

上課時數約 210 分鐘，進行的課程為國民小學六年級數學學習領域因數與倍數單 元部分，教材共分為四個概念，分別為「判別質數與合數」、「質因數與質因數分 解」、「最大公因數與最小公倍數」及「互質與最簡分數」。先利用因數與倍數概 念前測試題對某國小六年級某一班學生進行施測，以了解學生在因數與倍數概念 有哪些迷思情形，並從中找出 3 位在因數與倍數上學習有困難的學生，並設計相 關教學活動，以其進行補救教學。希望透過補救的教學過程能釐清其迷思概念，

並藉由之後的自我省思來提出教學的建議。本研究雖然以個案研究方式來進行，

但考慮研究者本身的人力與時間，無法像行動研究對於未能改善的部分做持續的 修正與澄清，故只探討在教學過程中學生的迷思概念與學習後的觀念轉變。圖 3-1 為本研究之研究架構圖。

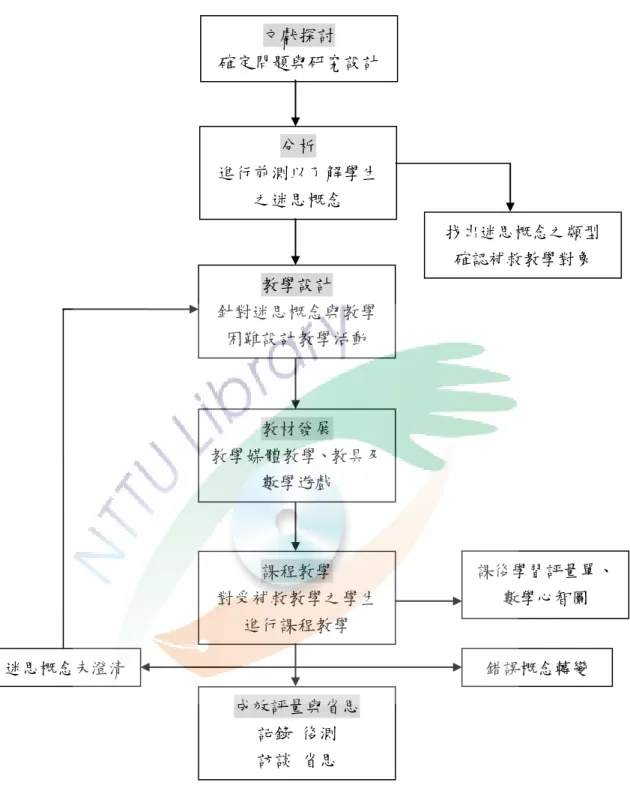
圖 3-1 研究架構圖

1

進行前測以了解學生 之迷思概念

找出迷思概念之類型 確認補救教學對象 教學設計

針對迷思概念與教學 困難設計教學活動

教材發展 教學媒體教學、教具及

數學遊戲

課後學習評量單、

數學心智圖 課程教學

對受補救教學之學生 進行課程教學

錯誤概念轉變 迷思概念未澄清

成效評量與省思 記錄 後測 訪談 省思

文獻探討 確定問題與研究設計

以下分別對研究架構圖中的每一個要素做說明：

一、文獻探討

先探討因數與倍數相關文獻資料，進而分析學生於因數與倍數單元有哪些常 見的迷思概念，形成本研究的研究問題，再確定問題與研究設計的方向。

二、分析

此階段研究者根據課程中會出現的錯誤類型，設計相關概念之前測試題進行 施測，以確實了解學生在因數與倍數單元所產生的迷思概念；此外分析教師在進 行因數與倍數單元教學時會遇到的困難。學生在進行課程學習與教師在教學的過 程中所出現的問題，將其做整體的瞭解與分析，藉此針對問題設計適合的課程教 材與教學活動。

三、教學設計

經由分析學生的迷思概念與教師教學的困難後，形成一個研究的架構圖，依 據分析過後的相關情形來設計教學活動，更能了解學生的需求，進而解決他們在 學習上的常犯錯的問題與混淆不清的概念，教師也能明瞭自己教學上所遇到的瓶 頸；因為知道學生會有哪些問題，所以在進行教學活動時便能單刀直入去處理其 所產生的迷思，不管對學生與教師來說都是有助益的。

四、教材發展

本研究可藉由使用相關教學媒體來提升學生學習的興趣，並利用合適的教具 與數學遊戲來輔助教學，根據每個單元的迷思概念來尋找相關教學媒體教材，幫 助教師在進行補救教學時，可以解決學習落後的學生澄清錯誤的觀念，進而達成 九年一貫現階段的能力指標。

五、課程教學

在此階段將找出學習因數與倍數有困難的學生共 3 位，依據所設計的教學活 動來進行補救教學，透過小組的教學方式，比較能了解所設計的教案是否能達成 補救教學的目標；學生在這樣的課程學習中，本身也比較沒有同儕競爭的壓力，

六、成效評量與省思

實施教學之後最重要的就是評量與省思，評量受補教教學的學生課後學習的 成果如何，了解學生學習前後的差異，並詳實地做記錄，由此可檢視所設計的教 案，根據學生的回饋來做修正。另外透過與學生面對面訪談，來反省整個教學設 計與教學流程，他們是否改變自己的學習態度，並且符合當初所設定的教學目標，

整個研究最重要的部分就是探討學生學習的成效。這個階段所反映出來的數據及 相關資料，都可以當作以後課程與教學活動微調與修正的重要考量。

第二節 研究對象

本節介紹行動研究過程中的教學情境，包含參與學生背景、研究者背景及教 學環境等做介紹。

一、參與學生

本研究以台東縣某國小六年級學生為對象，由因數與倍數概念前測試驗卷的 施測下，挑出 3 位學生其在因數與倍數單元上有一定程度的迷思概念。由於五年 級開始有因數與倍數單元之課程，雖然出現的次數不多，但其中的觀念皆會影響 到其他數學概念的學習，如學生學習分數的四則運算方面。在此階段可說是建立 基礎的黃金時刻，往往因為觀念錯誤、概念產生偏差，常常導致學生在課程學習 上興趣缺缺，一旦出現迷思概念，於理解課程觀念方面就會產生瓶頸。

二、參與教師

研究者本身畢業於某教育大學社會科教育學系後，曾擔任中低年級導師，教 授過數學領域課程，目前擔任六年級導師，會使用相關資訊設備融入教學活動，

教學年資共五年。

三、教學環境

本研究之補救教學之進行利用本班教室，其配有虛擬電子白板與單槍等設備 以方便教學。