第 4 章 《度測》的內容分析（二）

第 4 章 《度測》的內容分析（二）

《度測》書末附有〈開平方說〉及〈開立方說〉，均先詳列開方的原理、方 法及相關納皮爾算籌的運用方法，最後再舉例說明。本章依原書中順序，先列出 開方的原理及方法，再利用現在的數學符號進行解說，並參考徐光啟的《新法曆 書》、方中通的《數度衍》及楊玉星的《清代算學家方中通及其算學研究》還原 相關的納皮爾算籌表，¹以詮釋書中所舉的開方例。

4.1 開平方說

陳藎謨在〈開平方說〉中提及開平方的原理、方法為

開平方者，即自乘還原法實相同之數也。其散積無從置算，故以積求形必 用方法、廉法、隅法商除之。平方籌右行自一至九者，方根也。左行一格 之一者，所謂一^十_个一十，如一百也；二格之四者，二^十_个二，如四百也；以至九 格八一者，九个九，八十一也，此是自乘數；在初商為方根數，在次商以上 為隅數。積數從實尾起算，每間一位作一開，在三位、四位者有兩商，五 位、六位者有三商，七位、八位者有四商，九位、十位者有五商，以上從 此推之。初商曰方根，即自乘方數。其實首單位者，從單數在平方籌之單 位，取初商一格之一，二格之四，三格之九是也；其實首雙位者，從雙數 在平方籌之雙位，取初商四格之十六，以至九格之八一是也；此初商正用 一方法也。次商以往有廉法、隅法，廉同方之長，隅同廉之廣，廉有二，

隅有一。三商居外，其兩廉同次商廉隅之長以為長，其一隅同三商兩廉之

1 參見徐光啟，《籌算》，《新法曆書》第二十二卷，收入《景印文淵閣四庫全書》子部 第 788 冊，

頁 345~354；方中通，《數度衍》，收入靖玉樹主編，《中國歷代算學集成》中卷，頁 2653~2659；

楊玉星，《清代算學家方中通及其算學研究》，頁 47~51。。

廣以為廣。多商之法亦從此推之。商而餘實不盡，以法命之。²

我們可以將上述原理及方法繪製成下圖，並以現在的數學符號說明如下：

設實（被開平方數）為N ，則

（1）初商a：a² ≤ N <(a+1)²；

（2）二商b：(a+b)² ≤N <(a+b+1)²；

（3）三商c：(a+b+c)² ≤N <(a+b+c+1)²；

且(a+b)² =a² +2ab+b²；

2 2

2 2 2

2 ( ) 2( ) 2 2( )

)

(a+b+c = a+b + a+b c+c =a + ab+b + a+b c+c 。

³

對初商a而言，我們稱a 為方法，² ab為廉法，b 為隅法；對二商² b而言，我們 稱(a+b)c為廉法，c 為隅法；涉及多商的算法，以此類推。如為開不盡的平方，² 則稱之為命分。至於開方求值的計算過程，陳藎謨認為珠算不如籌算便捷，他在

《度測》卷下提及：「凡開平方，數少亦罄，數多更繁。初學者若從珠算開方之，

2 引自陳藎謨，〈開平方說〉，《度測》，頁 469~470。

3 《度測》中原無此圖，此圖參考梅榮照、李兆華的《算法統宗校釋》繪製。

圖 4-1 方廉隅法之圖 (a+b)c c²

(a+b)c

b² ab

a² ab

多如前者，竟日不清。省時省力，莫妙籌算。」⁴這裡的籌指的是「納皮爾算籌」，

見下圖。納皮爾算籌是對數發明人納皮爾（J．Napier，英國數學家，1550~1617 年）發明的，它不同於中國古代的算籌，是根據格子算法原理，將格子和數字

⁵

刻在籌上，使用時按需要拼湊使用。籌算經由義大利傳教士羅雅谷（J． Rho，

1590~1638 年）傳入，羅雅谷來華後所著的《籌算》一書中便介紹了納皮爾算籌，

此書收入於《崇禎曆書》中。陳藎謨在開方時，運用納皮爾算籌簡化了繁瑣的開 方工作。

陳藎謨在開平方部份共詳細解釋了七個例子，茲分析如下：

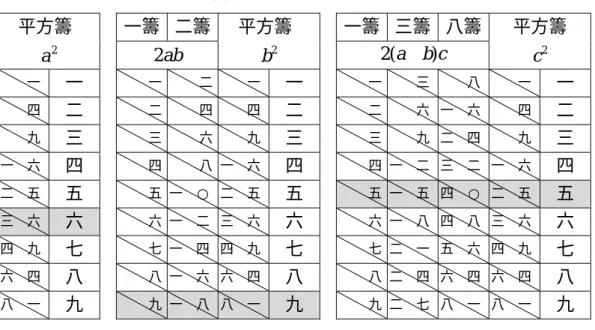
【二商單位例】

積實三百六十一

4 引自陳藎謨，《度測》卷下，頁 437。

5 圖片來源：中國大百科智慧藏（http://210.60.21.117/web34m/Content.asp?ID=15173&Image=數 學&Query=5）。

圖 4-2 象牙製橫排納皮爾籌(清代) （北京故宮博物院藏）

今解：

設實為N ，初商為a，二商為b，則(a+b)² = N，我們可以利用下列算籌表及 數學原理 (a+b)² =a² +2ab+b²解釋開平方步驟：

=361

N ；

（1） 初商a=10，a² =100，餘實 N − a² =261；

（2） 2a=20，取二號籌加平方籌試算得二商b=9，2ab+ b² =261，餘實 0

261 261 ) 2

( )

(N−a² − ab+b² = − = 。 故 361=19。

表 4-1 二商單位例算籌表 平方籌

a 2

二籌 ab 2

平方籌 b 2

一 一 二 一 一

四 二 四 四 二

九 三 六 九 三

一 六 四 八 一 六 四

二 五 五 一 ○ 二 五 五

三 六 六 一 二 三 六 六

四 九 七 一 四 四 九 七

六 四 八 一 六 六 四 八

八 一 九 一 八 八 一 九

【二商雙位例】

積實二千八百○九

今解：

設實為N ，初商為a，二商為b，則(a+b)² = N，我們可以利用下列算籌表及 數學原理 (a+b)² =a² +2ab+b²解釋開平方步驟：

=2809

N ；

（1）初商a=50，a² =2500，餘實 N − a² =309；

（2）2a=100，取一、○兩籌加平方籌試算得二商b=3，2ab+ b² =309，餘實 0

309 309 ) 2

( )

(N −a² − ab+b² = − = 。 故 2809=53。

表 4-2 二商雙位例算籌表

一籌 ○籌 平方籌

a 2 2ab

平方籌 b 2

一 一 一 ○ 一 一

四 二 二 ○ 四 二

九 三 三 ○ 九 三

一 六 四 四 ○ 一 六 四

二 五 五 五 ○ 二 五 五

三 六 六 六 ○ 三 六 六

四 九 七 七 ○ 四 九 七

六 四 八 八 ○ 六 四 八

八 一 九 九 ○ 八 一 九

【三商例】

積實五萬八千○八十一

今解：

設實為N ，初商為a，二商為b，三商為c，則(a+b+c)² = N，我們可以利用 下列算籌表及數學原理

（1）(a+b)² =a² +2ab+b²

（2）(a+b+c)² =(a+b)²+2(a+b)c+c² 來解釋開平方步驟：

58081

=

N ；

（1）初商 a =200，a² =40000，餘實 18081N − a² = ；

（2）2a=400，取四號籌加平方籌試算得二商b=40，2ab+ b² =17600， 餘實 (N−a²)−(2ab+b²)=18081−17600=481 ；

（3）2(a+ b)=480，取四號籌、八號籌加平方籌試算得三商c=1， 481

) (

2 a+b c+c² = ，餘實 [(N−a²)−(2ab+b²)]−[2(a+b)c+c²]=0。 故 58081=241。

表 4-3 三商例算籌表

四籌 八籌 平方籌

a 2

四籌 ab 2

平方籌

b 2 2(a+b)c

平方籌 c 2

一 一 四 一 一 四 八 一 一

四 二 八 四 二 八 一 六 四 二

九 三 一 二 九 三 一 二 二 四 九 三

一 六 四 一 六 一 六 四 一 六 三 二 一 六 四

二 五 五 二 ○ 二 五 五 二 ○ 四 ○ 二 五 五

三 六 六 二 四 三 六 六 二 四 四 八 三 六 六

四 九 七 二 八 四 九 七 二 八 五 六 四 九 七

六 四 八 三 二 六 四 八 三 二 六 四 六 四 八

八 一 九 三 六 八 一 九 三 六 七 二 八 一 九

【升籌例三商】

積實二十二萬八千四百八十四

今解：

設實為N ，初商為a，二商為b，三商為c，則(a+b+c)² = N，我們可以利用 下列算籌表及數學原理

（1）(a+b)² =a² +2ab+b²

（2）(a+b+c)² =(a+b)² +2(a+b)c+c² 來解釋開平方步驟：

228484

=

N ；

（1）初商 a=400，a² =160000，餘實 N− a² =68484；

（2）2a=800，取八號籌加平方籌試算得二商b=70，2ab+ b² =609， 餘實 (N −a²)−(2ab+b²)=68484−60900=7584 ；

（3）2(a+ b)=940，取九號籌、四號籌加平方籌試算得三商c=8， 7584

) (

2 a+b c+c² = ，餘實 [(N −a²)−(2ab+b²)]−[2(a+b)c+c²]=0。 故 228484=478。

表 4-4 升籌例三商算籌表

九籌 四籌 平方籌

a 2

八籌 ab 2

平方籌

b 2 2(a+b)c

平方籌 c 2

一 一 八 一 一 九 四 一 一

四 二 一 六 四 二 一 八 八 四 二

九 三 二 四 九 三 二 七 一 二 九 三

一 六 四 三 二 一 六 四 三 六 一 六 一 六 四

二 五 五 四 ○ 二 五 五 四 五 二 ○ 二 五 五

三 六 六 四 八 三 六 六 五 四 二 四 三 六 六

四 九 七 五 六 四 九 七 六 三 二 八 四 九 七

六 四 八 六 四 六 四 八 七 二 三 二 六 四 八

八 一 九 七 二 八 一 九 八 一 三 六 八 一 九

【隔籌例四商】

積實三千六百○九萬六千○六十四

今解：

設實為N ，初商為a，二商為b，三商為c，四商d，則(a+b+c+d)² =N，我 們可以利用下列算籌表及數學原理

（1）(a+b)² =a² +2ab+b²

（2）(a+b+c)² =(a+b)² +2(a+b)c+c²

（3）(a+b+c+d)² =(a+b+c)² +2(a+b+c)d +d²

=(a+b)²+2(a+b)c+c²+2(a+b+c)d+d² =a² +2ab+b² +2(a+b)c+c² +2(a+b+c)d +d² 來解釋開平方步驟：

36096064

=

N ；

（1）初商 a =6000，a² =36000000 ，

餘實 N− a² =36096064−36000000=96064；

（2）2a=12000，取一號籌、二號籌加平方籌試算得二商b=0，c=0；

（3）2(a+b+c)=12000，取一、二、○、○共四籌加平方籌試算得四商d =8， 96064

) (

2 a+b+c d+d² = ，餘實 96064−96064=0。 故 36096064 =6008。

表 4-5 隔籌例四商算籌表

一籌 二籌 平方籌

a 2 2ab

平方籌 b 2

一 一 一 二 一 一

四 二 二 四 四 二

九 三 三 六 九 三

一 六 四 四 八 一 六 四

二 五 五 五 一 ○ 二 五 五

三 六 六 六 一 二 三 六 六

四 九 七 七 一 四 四 九 七

六 四 八 八 一 六 六 四 八

八 一 九 九 一 八 八 一 九

一籌 二籌 ○籌 一籌 二籌 ○籌 ○籌 c

b a ) ( 2 +

平方籌

c 2 2(a+b+c)d

平方籌 d 2

一 二 ○ 一 一 一 二 ○ ○ 一 一

二 四 ○ 四 二 二 四 ○ ○ 四 二

三 六 ○ 九 三 三 六 ○ ○ 九 三

四 八 ○ 一 六 四 四 八 ○ ○ 一 六 四

五 一 ○ ○ 二 五 五 五 一 ○ ○ ○ 二 五 五

六 一 二 ○ 三 六 六 六 一 二 ○ ○ 三 六 六

七 一 四 ○ 四 九 七 七 一 四 ○ ○ 四 九 七

八 一 六 ○ 六 四 八 八 一 六 ○ ○ 六 四 八

九 一 八 ○ ^{八 一} 九 九 一 八 ○ ○ ^{八 一} 九

【當位例】

積實四十八萬三千○二十五

今解：

設實為N ，初商為a，二商為b，三商為c，則(a+b+c)² = N，我們可以利用 下列算籌表及數學原理

（1）(a+b)² =a² +2ab+b²

（2）(a+b+c)² =(a+b)² +2(a+b)c+c² 來解釋開平方步驟：

483025

=

N ；

（1）初商 a =600，a² =360000，餘實 123025N− a² = ；

（2）2a=1200，取一號籌、二號籌加平方籌試算得二商b = 90 ， 116100

2ab+ b² = ，餘實 (N−a²)−(2ab+b²)=123025−116100=6925；

（3）2(a+ b)=1380，取一號籌、三號籌、八號籌加平方籌試算得三商c=5， 6925

) (

2 a+b c+c² = ，餘實 [(N−a²)−(2ab+b²)]−[2(a+b)c+c²]=0。 故 483025=695。

表 4-6 當位例算籌表

一籌 二籌 一籌 三籌 八籌

平方籌

a 2 2ab

平方籌

b 2 2(a+b)c

平方籌 c 2

一 一 一 二 一 一 一 三 八 一 一

四 二 二 四 四 二 二 六 一 六 四 二

九 三 三 六 九 三 三 九 二 四 九 三

一 六 四 四 八 一 六 四 四 一 二 三 二 一 六 四

二 五 五 五 一 ○ 二 五 五 五 一 五 四 ○ 二 五 五

三 六 六 六 一 二 三 六 六 六 一 八 四 八 三 六 六

四 九 七 七 一 四 四 九 七 七 二 一 五 六 四 九 七

六 四 八 八 一 六 六 四 八 八 二 四 六 四 六 四 八

八 一 九 九 一 八 八 一 九 九 二 七 八 一 八 一 九

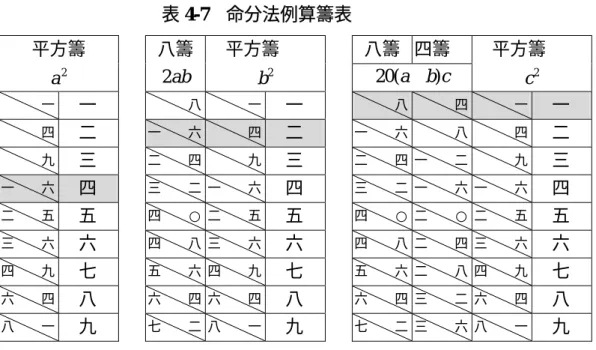
【命分法例】

積實一千八百二十一

今解：

設實為N ，初商為a，二商為b，則(a+b)² +r=N，我們可以利用下列算籌表 及數學式子

（1）(a+b)² =a² +2ab+b²

（2） ₂

1 1 ) ( 20 ) 10

( + + + × +

≈ a b

b r a N

來解釋開平方步驟：

=1821

N ；

（1）初商 a=40，a² =1600，餘實 221N − a² = ；

（2）2a=80，取八號籌加平方籌試算得二商b=2，2ab+ b² =164， 餘實 (N−a²)−(2ab+b²)=221−164=57 ；

（3）20(a+ b)=840，20(a+ b)×1+1² =841。

故 841

42570 1821≈ 。

表 4-7 命分法例算籌表

八籌 四籌 平方籌

a 2

八籌 ab 2

平方籌

b 2 20(a+b)c

平方籌 c 2

一 一 八 一 一 八 四 一 一

四 二 一 六 四 二 一 六 八 四 二

九 三 二 四 九 三 二 四 一 二 九 三

一 六 四 三 二 一 六 四 三 二 一 六 一 六 四

二 五 五 四 ○ 二 五 五 四 ○ 二 ○ 二 五 五

三 六 六 四 八 三 六 六 四 八 二 四 三 六 六

四 九 七 五 六 四 九 七 五 六 二 八 四 九 七

六 四 八 六 四 六 四 八 六 四 三 二 六 四 八

八 一 九 七 二 八 一 九 七 二 三 六 八 一 九

在上述陳藎謨所舉的七個開平方例子中，我們可以看出這些例子呈現的次 序是由簡單至複雜，而且是十分具代表性的。從「二商單位例」、「二商雙位例」、

「三商例」、「升籌例三商」、「隔籌例四商」、「命分法例」中，不難體會出作者解 說詳盡、舉例周延，務期讀者能融會貫通的苦心，但作者所舉的「當位例」一例，

似乎可包含於「升籌例」中，顯然並無另外討論的必要。

此外，在處理「命分法例」——開不盡的平方根時，陳藎謨採用的近似方 法是十分獨特的。如以 N =a² +r 為例，在《周髀算經》及《夏侯陽算經》中，

對於此類開不盡的方根稱之為「有奇」（或「奇」），並未討論平方根的近似值問 題，⁶而在《九章算術》中則有「以面命之」之說。此外，對於此類開方不盡的 問題，傳統中算家採用的近似方法主要有兩種：一是「加借算命分」

1 2 + +

≈ a a r

N ，如《五經算術》、《張丘建算經》卷中、甄鸞注《周髀算經》、 明代周述學的《神道大編曆宗算會》和程大位的《算法統宗》；另一則是「不加

6 參見李繼閔，《《九章算術》及其劉徽注研究》，頁 105。

借算命分」

a a r

N ≈ +2 ，如《孫子算經》卷中。⁷雖然劉徽在註《九章算術》時 便已指出

a a r a N

a r

2 1

2 < < +

+ + 的不等關係式，但以

1 2 + + a

a r 作為 N 的近似值，陳藎謨應該是史上第一人。

事實上，

10 2 1 1

20 10

+ + + =

+

a a r a

a r 且

a a r a

a r a

a r

2 10

2 1 1

2 < +

+ + + <

+ ，

所以當 a

a r N a

a r

2 10

2 1

+

<

<

+

+ 時，

10 2 + 1 +

a

a r 是比

1 2 + + a

a r 更佳的近

似值；但當

10 2 1 1

2 +

+

<

+ <

+

a a r a N

a r 時，

10 2 + 1 +

a

a r 則未必是比

1 2 + + a

a r 更合適的近似值。另一方面，當

10 2 1 1

2 +

+

<

+ <

+

a a r a N

a r 時，

10 2 + 1 +

a

a r 是比

a a r

+ 2 更佳的近似值；但當

10 2 1

2 +

+

<

<

+

a a r a N

a r 時，

10 2 + 1 +

a

a r 則未必是比 a a r

+ 2 更合適的近似值。

然而陳藎謨為何能提出

1 20

10 + +

≈ a a r

N 這個獨特的近似值，由於缺乏相

關資訊，目前無法作進一步討論。

4.2 開立方說

陳藎謨在〈開立方說〉中提及開立方的原理、方法為

7 參見李儼，〈中算家的平方零約術〉，收入《李儼錢寶琮科學史全集》第六卷，頁 96~97。

開立方者，即一數自乘再乘之所積，以六方面總為一實體也。其散積無從 置算，故以積求形必用方法、平廉法、長廉法、立隅法商除之。立方籌右 行為一為四至八一者，自乘數也；左二行為○○一為○○八以至七二九者，

再乘數也。積數從實尾起算，每三位作一開，以自乘再乘每有三位故也。

在四位、五位、六位者有兩開，七位、八位、九位者有三開，十位、十一 位、十二位者有四開，以上從此推之。但實在四位、七位、十位者，再乘 數止于零數一格之○○一、二格之○○八是也，初商即于此兩格內取；實 首在五位、八位、十一位者，再乘數當有十數三格之○二七、四格之○六 四是也，初商即于此兩格內取；實首在六位、九位、十二位者，再乘數當 有百數五格之一二五，以至九格之七二九是也，初商即于此五格內取；所 謂方法用之于初商者也。其次商有平廉法，依方根之旁故曰廉，同方根之 面故曰平。以初商方法數自乘之，自乘為平廉之面，又三倍之，三倍為三 平廉之面。如初商在二格自乘為四，三倍之為一十二；初商在四格自乘為 十六，三倍之為四十八是也。次商又有長廉法，依平廉之旁故曰廉，同方 根之長故曰長，其兩端為自乘方，以初商數三倍之。長廉三倍之高廣，因 長廉之長□以補三平廉之闕。如三則三倍為九，五則五倍為十五是也。以 平廉法數，取其籌列立方籌左；又以長廉法數，取其籌列立方籌右。次視 左籌與方籌橫并之數商其少于餘實者，平行取數為約數，另置之，即以此 格數為為次商；在二格即為次商二，在五格即為次商五是也。又取次商自 乘之數與長廉法數相乘併于約數之內，除其餘實，即為次商取用之法。不 言立隅法者，次商之再乘，即立隅籌上所自有也。三開、四開以上，從此 推之。開而不盡者，以法命之。⁸

我們可以將上述原理及方法繪製成下圖，並以現在的數學符號說明如下：

8 引自陳藎謨，〈開立方說〉，《度測》，頁 485。原文中文字缺漏部分，以□表示。

設實（被開立方數）為N ，則

（1） 初商a：a³ ≤N <(a+1)³；

（2） 二商b：(a+b)³ ≤ N <(a+b+1)³； 且 (a+b)³ =a³ +3a²b+3ab² +b³。

其中a 為方根體，³ b 為立隅體，³ b 為立隅面， ² a為平廉長，a 為平廉面，² a²b為平廉體，

a為長廉長，ab為長廉面，ab 為長廉體， ² 並以3a 為平廉法，² 3a為長廉法。

⁹

陳藎謨在開立方部分共詳細解釋了九個例子，茲分析如下：

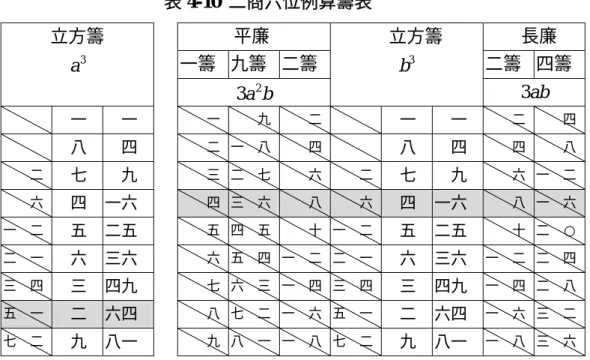
【二商四位例】

積實六千八百五十九

今解：

9 《度測》中原無此圖，此圖參考徐光啟等編的《新法曆書》繪製。

ab2

b3

b a²

a3

ab2

b a²

ab2

圖 4-3 開立方廉隅圖

設實為N ，初商為a，二商為b，則(a+b)³ = N，我們可以利用下列算籌表及 數學原理 (a+b)³ =a³ +3a²b+3ab² +b³解釋開立方步驟：

=6859

N ；

（1） 初商a=10，a³ =1000，餘實 N− a³ =5859；

（2） 平廉法 3a² =300， 長廉法 3a=30，

平廉用三號籌加立方籌試算，得二商b=9， 3429

3a²b+ b³ = ， 2430

3ab² = ，

5859 3

3a²b+ ab² +b³ = ，

餘實 (N−a³)−(3a²b+3ab² +b³)=0。 故 ³ 6859 =19。

表 4-8 二商四位例算籌表

平廉 長廉

三籌 三籌

立方籌 a 3

3a²b

立方籌 b 3

ab 3 一 一 三 一 一 三 八 四 六 八 四 ^六

二 七 九 九 二 七 九 九 六 四 一六 一 二 六 四 一六一 二 一 二 五 二五 一 五 一 二 五 二五一 五 二 一 六 三六 一 八 二 一 六 三六^{一 八}

三 四 三 四九 二 一 三 四 三 四九二 一 五 一 二 六四 二 四 五 一 二 六四二 四 七 二 九 八一 二 七 七 二 九 八一二 七

【二商五位例】

積實九萬一千一百二十五

今解：

設實為N ，初商為a，二商為b，則(a+b)³ = N，我們可以利用下列算籌表及 數學原理 (a+b)³ =a³ +3a²b+3ab² +b³解釋開立方步驟：

91125

=

N ；

（1） 初商a=40，a³ =64000，餘實 N − a³ =27125；

（2） 平廉法 3a² =4800， 長廉法 3a=120，

平廉用四、八號籌加立方籌試算，得二商b=5， 24125

3a²b+ b³ = ， 3000

3ab² = ，

27125 3

3a²b+ ab² +b³ = ，

餘實 (N−a³)−(3a²b+3ab² +b³)=0。 故 ³ 91125 =45。

表 4-9 二商五位例算籌表

平廉 長廉

四籌 八籌 一籌 二籌

立方籌 a 3

3a²b

立方籌 b 3

3ab 一 一 四 八 一 一 一 二 八 四 八 一 六 八 四 二 四 二 七 九 一 二 二 四 二 七 九 三 六 六 四 一六 一 六 三 二 六 四 一六 四 八 一 二 五 二五 二 ○ 四 ○ 一 二 五 二五 五 一 ○ 二 一 六 三六 二 四 四 八 二 一 六 三六 六 一 二 三 四 三 四九 二 八 五 六 三 四 三 四九 七 一 四 五 一 二 六四 三 二 六 四 五 一 二 六四 八 一 六 七 二 九 八一 三 六 七 二 七 二 九 八一 九 一 八

【二商六位例】

積實五十九萬二千七百○四

今解：

設實為N ，初商為a，二商為b，則(a+b)³ = N，我們可以利用下列算籌表及 數學原理 (a+b)³ =a³ +3a²b+3ab² +b³解釋開立方步驟：

592704

=

N ；

（1） 初商a=80，a³ =512000，餘實 N− a³ =80704；

（2） 平廉法 3a² =19200， 長廉法 3a=240，

平廉用一、九、二號籌加立方籌試算，得二商b=4， 76864

3a²b+ b³ = ， 3840

3ab² = ，

80704 3

3a²b+ ab² +b³ = ，

餘實 (N−a³)−(3a²b+3ab² +b³)=0。 故 ³ 592704 =84

表 4-10 二商六位例算籌表

平廉 長廉

一籌 九籌 二籌 二籌 四籌

立方籌 a 3

3a²b

立方籌 b 3

_3ab

一 一 一 九 二 一 一 二 四 八 四 二 一 八 四 八 四 四 八 二 七 九 三 二 七 六 二 七 九 六 一 二 六 四 一六 四 三 六 八 六 四 一六 八 一 六 一 二 五 二五 五 四 五 十 一 二 五 二五 十 二 ○ 二 一 六 三六 六 五 四 一 二 二 一 六 三六 ^{一 二 二 四}

三 四 三 四九 七 六 三 一 四 三 四 三 四九 一 四 二 八 五 一 二 六四 ^八 七 二 一 六 五 一 二 六四 ^{一 六 三 二}

七 二 九 八一 九 八 一 一 八 七 二 九 八一 ^{一 八 三 六}

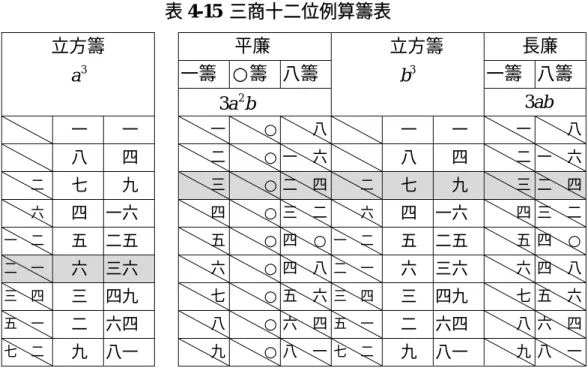
【三商七位例】雖是八位，然在立方籌十數之下，退入于二格單位，仍作七位算。

積實一千九百○三萬四千一百六十三

今解：

設實為N ，初商為a，二商為b，三商為c，則(a+b+c)³ =N ，我們可以利用 下列算籌表及數學原理

（1）(a+b)³ =a³ +3a²b+3ab² +b³

（2）(a+b+c)³ =(a+b)³ +3(a+b)²c+3(a+b)c² +c³ 解釋開立方步驟：

19034163

=

N ；

（1） 初商a=200，a³ =8000000，餘實 N − a³ =11034163；

（2） 平廉法 3a² =120000， 長廉法 3a=600，

平廉用一、二號籌加立方籌試算，得二商b=60， 7416000

3a²b+ b³ = ，

2160000 3ab² = ，

9576000 3

3a²b+ ab² +b³ = ，

餘實 (N−a³)−(3a²b+3ab² +b³)=1458163；

（3） 平廉法 3(a+ b)² =202800， 長廉法 3(a+ b)=780，

平廉用二、○、二、八號籌加立方籌試算，得二商c=7， 1419943

) (

3 a+b ²c+c³ = ， 38220

) (

3 a+ cb ² = ，

1458163 )

( 3 ) (

3 a+b ²c+ a+b c² +c³ = ，

餘實 [(N −a³)−(3a²b+3ab² +b³)]−[3(a+b)²c+3(a+b)c² +c³]=0。 故 ³ 19034163=267。

表 4-11 三商七位例算籌表

平廉 長廉

一籌 二籌 六籌

立方籌 a 3

b a² 3

立方籌 b 3

ab 3 一 一 一 二 一 一 六 八 四 二 四 八 四 一 二 二 七 九 三 六 二 七 九 一 八 六 四 一六 四 八 六 四 一六 ^{二 四}

一 二 五 二五 五 一 ○ 一 二 五 二五 三 ○ 二 一 六 三六 六 一 二 二 一 六 三六 三 六 三 四 三 四九 七 一 四 三 四 三 四九 四 二 五 一 二 六四 八 一 六 五 一 二 六四 ^{四 八}

七 二 九 八一 九 一 八 七 二 九 八一 五 四

平廉 長廉

二籌 ○籌 二籌 八籌 七籌 八籌

c b a )² ( 3 +

立方籌 c 3

3(a+b)c

二 ○ 二 八 一 一 七 八 四 ○ 四 一 六 八 四一 四 一 六 六 ○ 六 二 四 二 七 九二 一 二 四 八 ○ 八 三 二 六 四 一六^{二 八 三 二}

一 ○ ○ 一 ○ 四 ○ 一 二 五 二五三 五 四 ○ 一 二 ○ 一 二 四 八 二 一 六 三六四 二 四 八 一 四 ○ 一 四 五 六 三 四 三 四九四 九 五 六 一 六 ○ 一 六 六 四 五 一 二 六四^{五 六 六 四}

一 八 ○ 一 八 七 二 七 二 九 八一六 三 七 二

【三商八位例】

積實三千○百三十七萬一千三百二十八

今解：

設實為N ，初商為a，二商為b，三商為c，則(a+b+c)³ =N ，我們可以利用 下列算籌表及數學原理

（1）(a+b)³ =a³ +3a²b+3ab² +b³

（2）(a+b+c)³ =(a+b)³ +3(a+b)²c+3(a+b)c² +c³ 解釋開立方步驟：

30371328

=

N ；

（1） 初商a=300，a³ =27000000，餘實 N− a³ =3371328；¹⁰

（2） 平廉法 3a² =270000， 長廉法 3a=900，

平廉用二、七號籌加立方籌試算，得二商b=10， 2701000

3a²b+ b³ = ， 90000

3ab² = ，

10 原文誤作「二百三十七萬一千三百二十八」。

2791000 3

3a²b+ ab² +b³ = ，

餘實 (N−a³)−(3a²b+3ab² +b³)=580328；

（3） 平廉法 3(a+ b)² =288300， 長廉法 3(a+ b)=930，

平廉用二、八、八、三號籌加立方籌試算，得二商c=2， 576608

) (

3 a+b ²c+c³ = ， 3720

) (

3 a+ cb ² = ，

580328 )

( 3 ) (

3 a+b ²c+ a+b c² +c³ = ，

餘實 [(N −a³)−(3a²b+3ab² +b³)]−[3(a+b)²c+3(a+b)c² +c³]=0。 故 ³ 30371328 =312。

表 4-12 三商八位例算籌表

平廉 長廉

二籌 七籌 九籌

立方籌 a 3

b a² 3

立方籌 b 3

ab 3 一 一 二 七 一 一 九 八 四 四 一 四 八 四 ^{一 八}

二 七 九 六 二 一 二 七 九 二 七 六 四 一六 八 二 八 六 四 一六 三 六 一 二 五 二五 一 ○ 三 五 一 二 五 二五 四 五 二 一 六 三六 一 二 四 二 二 一 六 三六 ^{五 四}

三 四 三 四九 一 四 四 九 三 四 三 四九 六 三 五 一 二 六四 一 六 五 六 五 一 二 六四 五 六 七 二 九 八一 一 八 六 三 七 二 九 八一 六 三

平廉 長廉

二籌 八籌 八籌 三籌 九籌 三籌

c b a )² ( 3 +

立方籌 c 3

3(a+b)c

二 八 八 三 一 一 九 三 四 一 六 一 六 六 八 四一 八 六 六 二 四 二 四 九 二 七 九二 七 九 八 三 二 三 二 一 二 六 四 一六三 六 一 二 一 ○ 四 ○ 四 ○ 一 五 一 二 五 二五四 五 一 五 一 二 四 八 四 八 一 八 二 一 六 三六五 四 一 八 一 四 五 六 五 六 二 一 三 四 三 四九六 三 二 一 一 六 六 四 六 四 二 四 五 一 二 六四^{五 六 二 四}

一 八 七 二 七 二 二 七 七 二 九 八一六 三 二 七

【三商九位例】

積實七億七千一百九萬五千二百一十三

今解：

設實為N ，初商為a，二商為b，三商為c，則(a+b+c)³ =N ，我們可以利用 下列算籌表及數學原理

（1）(a+b)³ =a³ +3a²b+3ab² +b³

（2）(a+b+c)³ =(a+b)³ +3(a+b)²c+3(a+b)c² +c³ 解釋開立方步驟：

771095213

=

N ；

（1） 初商a=900，a³ =729000000，餘實 N− a³ =42095123；

（2） 平廉法 3a² =2430000， 長廉法 3a=2700，

平廉用二、四、三號籌加立方籌試算，得二商b=10， 24301000

3a²b+ b³ = ， 270000

3ab² = ，