報告題名:
台灣自來水生產量
之研究分析與預測
作者:李淑如 林芳如 林君亭 張瑋珊 黃郁筑 系級:三年乙班 學號:D9538375 D9561187 D9538358 D9538392 D9561303 開課老師:陳婉淑 教授 課程名稱:統計預測方法 開課系所:統計學系 開課學年:97 學年度第二學期中文摘要
中文摘要
中文摘要
中文摘要
台灣的水資源在時間及空間極其多變且不平均。在近年來,台灣經常發生乾旱,尤其,人為因 素的濫墾、濫伐使得台灣河川逕流在乾季與雨季之間的差異,更形加大,水資源的運用與調配 更加困難。因此我們利用 SAS 軟體並應用本學期所學的統計預測方法,期望能預測出未來一年 自來水的生產量,以供參考。 本報告使用時間序列迴歸法、分解法、指數平滑法、ARIMA 四種方法估計配適模型,並與 保留的 12 筆資料作比較,再利用 MSE、MAE、MPE 及 MAPE 四個準則來判斷四種方法中何者 較佳,並選出最佳模型。 從分析結果來看,明顯看到自來水生產量原本應是逐年增加的傾向,但在近年來有減緩的 趨勢,這應與近年全球氣候變遷有相當的關係。關鍵字
關鍵字
關鍵字
關鍵字:
:
:
:
水資源
水資源
水資源
水資源,
,
,全球氣候變遷
,
全球氣候變遷
全球氣候變遷,
全球氣候變遷
,
,時間序列回歸法
,
時間序列回歸法,
時間序列回歸法
時間序列回歸法
,
,
,分解法
分解法
分解法
分解法,
,
,
,
指數平滑法
指數平滑法
指數平滑法
目
目
目
目
次
次
次
次
第一章 緒論
第一節 研究背景...3
第二節 研究動機...3
第三節 研究目的...3
第四節資料來源...4
第五節 研究流程...4
第二章 研究方法
第一節 時間序列迴歸法...5
第二節 分解法... 11
第三節 指數平滑法...16
第四節 ARIMA...19
第五節 最佳模型...26
第三章 結論與建議
第一節 結論...27
第二節 建議...28
參考文獻...28
第一章
第一章
第一章
第一章 緒論
緒論
緒論
緒論
第一節
第一節
第一節
第一節 研究背景
研究背景
研究背景
研究背景
水資源供給來自於水庫、河川以及地下水,而水資源的需求包括了民生用水、工業用水及 農業用水等三部分。近年來由於全球氣候變遷導致各地的水資源運用益加困難。氣候變遷使得 氣候變異加劇,造成豐水期極端降雨強度增加,而枯水期連續不降雨日也更長,進而影響區域 整體的供水能力。面對此一問題,加強開源節流,推動水資源多元化發展已是各國主要的因應 方式。聖嬰現象在全球各地造成的影響並不相同,某些國家可能會因為降雨量過多,而造成水 災,某些地區可能會因為缺水而有乾旱發生。根據台灣的氣象資料,近 20 年的 聖嬰現象對台 灣的氣候有顯著的影響,其中聖嬰現象對台灣北部地區的春天降雨量(二月及三月的雨量)有正 面的關係,但是反聖嬰則會使得北部地區的降雨量偏低。聖嬰及反聖嬰現象對台灣自來水生產 有怎樣的影響我們期望能透過統計分析來加以探討。第二節
第二節
第二節
第二節 研究動機
研究動機
研究動機
研究動機:
:
:
:
水產量受氣候、緯度及地形等因素的影響甚鉅,因此近年來全球氣候變遷導致各地的水資 源運用益加困難。氣候變遷使得氣候變異加劇,造成豐水期極端降雨強度增加,而枯水期連續 不降雨日也更長,進而影響區域整體的供水能力。 為確保台灣水資源的永續發展,水利署也採取開源與節流雙管齊下的策略。在節流的部分, 推展節約用水政策;而在開源的部分,則推展水資源多元化發展的政策,除持續興建水庫、攔 河堰,開發地下水等傳統水源外,更積極投入推展海水、生活污水、事業廢水,以及貯留雨水 等新興水源的開發利用,以確保水資源穩定供應,減少供水風險。 台灣的主要水源,大多來自夏季的颱風,但為什麼台灣仍然缺水?台灣因為地狹人稠,山 坡地及高山就佔台灣面積的四分之三,其島中間是高山、四周皆為平原,降雨時空分布不均勻, 河川短且陡,雨水一旦降落地面沒過幾天就入海了,便需要蓋水庫來收集雨水。隨著工業技術 的進步,許多的煙囪工業和汽機車所排放的廢氣越來越嚴重,導致空氣污染,讓雨水接觸到酸 性物質變成酸雨,因此人們不能直接使用雨水,需要經過一些水的處理過程,讓水在生活使用 上更為安全,故台灣的水是十分珍貴的。第三節
第三節
第三節
第三節 研究目的
研究目的
研究目的
研究目的:
:
:
:
隨著經濟的發展及國民生活品質的提升,自來水公司於民生、工業用水並重下,辦理各項 自來水新擴建工程,例如:完成南化水庫大壩工程、牡丹水庫主體工程及下游供水工程、南化 水庫越域引水工程、澎湖烏坎海水淡化廠、新竹科學園區供水計畫、平鎮淨水場第二期工程、 鯉魚潭淨水場第二期工程、澎湖望安海水淡化廠、高屏溪攔河堰下游工程、澄清湖高級淨水場 工程……等,滿足民眾的用水需求。 因此我們希望運用統計預測方法來分析,以預測未來一年內自來水的生產量是如何呈現, 並與我們保留一年的實際資料作為比較。期望預測出來的資料能做為未來水資源調配的參考,來使得農業部門和工商業部門及民生部門同時獲利。未來政府可針對此預測配合氣象資訊研擬 不同的因應策略以降低其經濟影響。 若我們預測結果是自來水生產量有越來越向上趨勢,表示民眾需要的用水量也越來越大, 應宣傳「節約用水」的觀念。
第四節
第四節
第四節
第四節 資料來源
資料來源
資料來源
資料來源:
:
:
:
此筆資料主要是記錄台灣自來水生產量 (單位以千立方公尺)。此資料為月資料,分析時間為西元 1982年1月至2008年12月,並保留最後12筆做預測。資料來源為AREMOS經濟統計資料庫。 自來水生產量,代碼:Q3600010.M。第五節
第五節
第五節
第五節 流程圖
流程圖
流程圖
流程圖
第二章
第二章
第二章
第二章 研究方法
研究方法
研究方法
研究方法
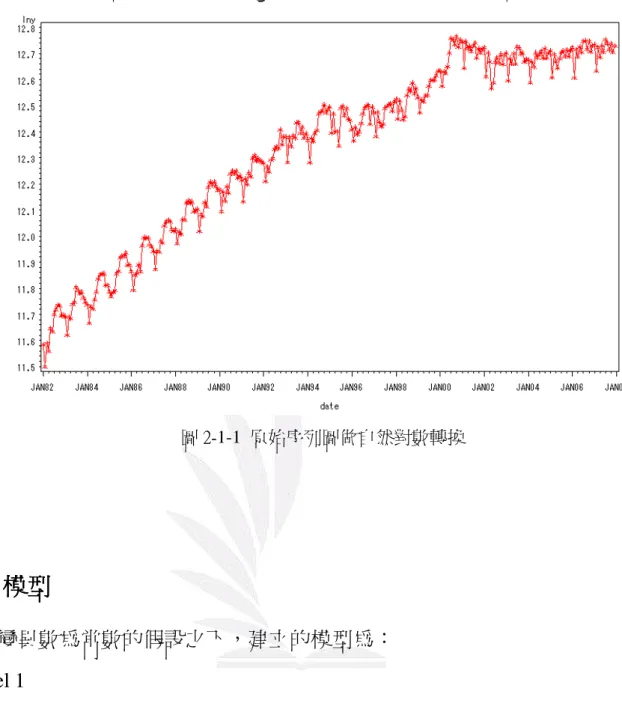
圖 2-1 為自來水生產量原始時間序列圖,座標 X 軸為日期,從 1982 年 1 月開始,至 2008 年 12 月,座標 Y 軸為用自來水生產量,以公噸為單位, 圖 2-1 原始序列圖(1982~2008) 我們使用時間序列迴歸法、分解法、指數平滑法、ARIMA 四種方法估計配適模型,下面四 種方法皆保留最後 12 筆資料,最後使用四種方法估計出來的預測值及 95%上下區間與真實值 做比較,然後使用 MSE、MAE、MPE 及 MAPE 四個準則,來評估這四種方法何者最佳,並選 出最佳模型。第一節
第一節
第一節
第一節 時間序列迴歸法
時間序列迴歸法
時間序列迴歸法(Time Series Regression)
時間序列迴歸法
從圖 2-1 原始序列圖,可看出有明顯上升、增加的趨勢,顯示自來水生產量有逐年增加的 情況,且有明顯的季節變化,這與台灣本身水資源不平衡有關係。台灣雨量多集中在夏季,冬 季則少雨。另外,圖中變異數在 1992 年後呈現不規律的變動,這可能與之後發生的聖嬰及反聖 嬰現象有關,造成豐水期極端降雨強度增加,而枯水期連續不降雨日也更長。因為原始序列圖 變異數不平穩的關係,因此我們必須先對原始資料做轉換,使變異數平穩。圖 2-1-2 即為做對 數轉換後的時間序列圖。由圖中可看出變異數波動較為平穩了。
圖 2-1-1 原始序列圖做自然對數轉換
建立模型
建立模型
建立模型
建立模型
在變異數為常數的假設之下,建立的模型為:
Model 1
y
t* = β
0+β
1t +β
2M
1+β
3M
2+β
4M
3+β
5M
4+β
6M
5+β
7M
6+β
8M
7+β
9M
8+β
10M
9+
β
11M
10+β
12M
11+ε
ty
t* =ln(y
t)
M1= 1 when Jan M2= 1 when Feb M3= 1 when Mar M4= 1 when Apr 0 o.w. 0 o.w. 0 o.w. 0 o.w M5= 1 when May M6= 1 when June M7= 1 when July M8= 1 when Aug 0 o.w. 0 o.w. 0 o.w. 0 o.w.
M9= 1 when Sep M10= 1 when Oct M11= 1 when Nov 0 o.w. 0 o.w. 0 o.w.
ε
t為誤差項
診斷分析
診斷分析
診斷分析
診斷分析
檢測殘差是否有自我相關,DW 為 2 沒有自我相關,DW 值為 0 有正自我相關,DW 值為 4 有 負自我相關。 表 2-1-1 為 Model 1 的殘差項自我相關檢測,其中 DW 值為 0.0586,顯示有正的自我相關。 而 Pr < DW 為檢定是否有正的自我相關, p 值 <0.0001 也顯示確有正的自我相關。所以我們 必須修正模型,對殘差項配適一階自我相關。 表 2-1-1 DW 檢定統計量 Ordinary Least Squares Estimates(lny)SSE 2.36534479 DFE 299 MSE 0.00791 Root MSE 0.08894 SBC -563.13208 AIC -611.79112
Regress R-Square 0.9346 Total R-Square 0.9346 Durbin-Watson 0.0586 Pr < DW <.0001 Pr > DW 1.0000
修正模型
修正模型
修正模型
修正模型
Model 2
y
t* = β
0+β
1t +β
2M
1+β
3M
2+β
4M
3+β
5M
4+β
6M
5+β
7M
6+β
8M
7+β
9M
8+
β
10M
9+β
11M
10+β
12M
11+ε
t 其中y
t* =ln(y
t)
M1,M2,…,M11 為季節虛擬解釋變數
ε
t=
φ1ε
t-1+a
ta
t~
iidN(0,1)
ε
t~
iidN(0,1)
1
φ
為一階自我相關係數,可參表 2-1-2
表 2-1-2 一階自我相關係數 Estimates of Autoregressive Parameters
Lag Coefficient Standard Error tValue
1 -0.956187 0.016959 -56.38
診斷修正後的模型
診斷修正後的模型
診斷修正後的模型
診斷修正後的模型
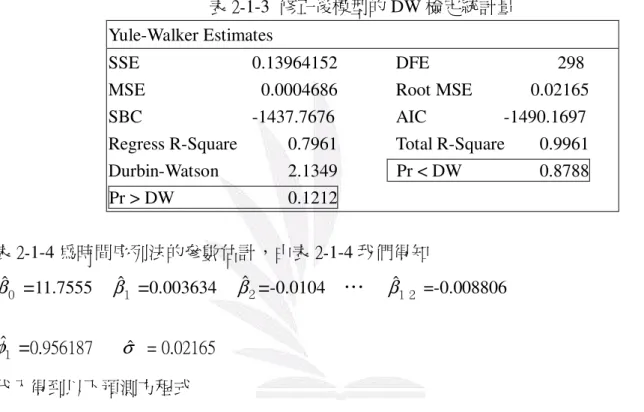
表 2-1-3 為修正後模型的殘差項自我相關檢測,由表 2-1-3,DW 值為 2.1349,P 值也都大於 0.05,顯示殘差項皆無自我相關,所以我們判斷 Model 2 是合適的。 表 2-1-3 修正後模型的 DW 檢定統計量 Yule-Walker Estimates SSE 0.13964152 DFE 298 MSE 0.0004686 Root MSE 0.02165 SBC -1437.7676 AIC -1490.1697 Regress R-Square 0.7961 Total R-Square 0.9961 Durbin-Watson 2.1349 Pr < DW 0.8788 Pr > DW 0.1212 表 2-1-4 為時間序列法的參數估計,由表 2-1-4 我們得知 0 βˆ=
11.7555 βˆ1=
0.003634 βˆ2=
-0.0104…
βˆ12 =-0.008806 1 φˆ=
0.956187 σˆ = 0.02165 代入得到以下預測方程式y
t* =11.7555 + 0.003634t -0.0104M
1-0.0935M
2-0.0240M
3-0.0485M
4-0.0247M
5-0.0301M
6+
0.0250M
7+
0.0312M
8+
0.0142M
9+
0.0280M
10 -0.008806M
11+ε
t whereε
t=
0.956187ε
t-1 +a
tε
t~
iidN(0,1) a
t~
iidN(0,1)
y
t* =ln(y
t)
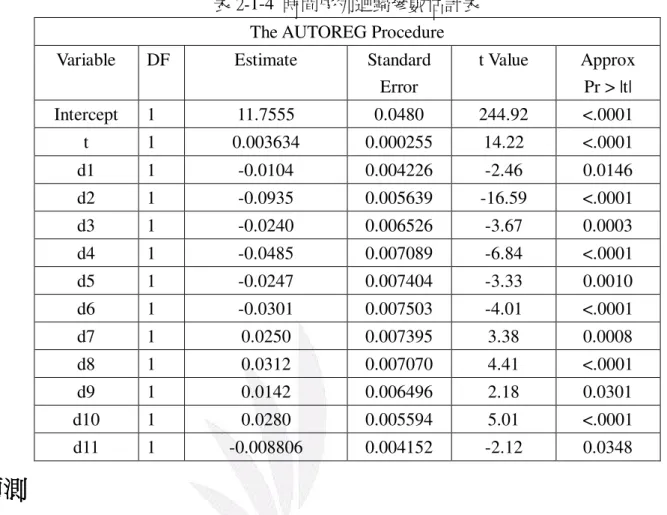
σˆ = 0.02165表 2-1-4 時間序列迴歸參數估計表 The AUTOREG Procedure
Variable DF Estimate Standard
Error t Value Approx Pr > |t| Intercept 1 11.7555 0.0480 244.92 <.0001 t 1 0.003634 0.000255 14.22 <.0001 d1 1 -0.0104 0.004226 -2.46 0.0146 d2 1 -0.0935 0.005639 -16.59 <.0001 d3 1 -0.0240 0.006526 -3.67 0.0003 d4 1 -0.0485 0.007089 -6.84 <.0001 d5 1 -0.0247 0.007404 -3.33 0.0010 d6 1 -0.0301 0.007503 -4.01 <.0001 d7 1 0.0250 0.007395 3.38 0.0008 d8 1 0.0312 0.007070 4.41 <.0001 d9 1 0.0142 0.006496 2.18 0.0301 d10 1 0.0280 0.005594 5.01 <.0001 d11 1 -0.008806 0.004152 -2.12 0.0348
預測
預測
預測
預測
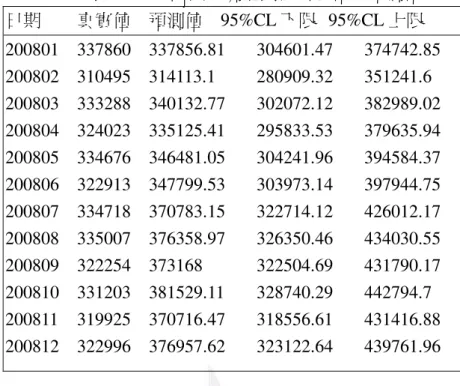
我們保留了 12 筆的真實值,並以我們最後的預測估計式,計算出 12 筆的預測值。我們將 這預測出之 12 筆預測值與 12 筆真實值整理如表 2-1-5,且將預測值與真實值以及估計出之 95% 信賴水準的上下界線,繪製成圖 2-1-3。表 2-1-5 時間序列迴歸法真實值及預測值 日期 真實值 預測值 95%CL 下限 95%CL 上限 200801 337860 337856.81 304601.47 374742.85 200802 310495 314113.1 280909.32 351241.6 200803 333288 340132.77 302072.12 382989.02 200804 324023 335125.41 295833.53 379635.94 200805 334676 346481.05 304241.96 394584.37 200806 322913 347799.53 303973.14 397944.75 200807 334718 370783.15 322714.12 426012.17 200808 335007 376358.97 326350.46 434030.55 200809 322254 373168 322504.69 431790.17 200810 331203 381529.11 328740.29 442794.7 200811 319925 370716.47 318556.61 431416.88 200812 322996 376957.62 323122.64 439761.96 由圖 2-1-3 可看出 在 2008 年的一月至五月基本上預測的不錯,幾乎與實際值非常接近, 但是在 2008 年的九、十、十一、十二月卻相差十分大,都落在 95%信賴區間邊界。另外,大 致上來說,整體預測值皆大於實際值非常多,可見,時間序列法在預測能力上有不足的地方。 圖 2-1-2 時間序列迴歸法的未來一年預測圖
第二節
第二節
第二節
第二節 分解法
分解法
分解法
分解法(Decomposition Method
Decomposition Method
Decomposition Method
Decomposition Method))))
分解法可分為加法模型與乘法模型, 加法模型: yt=TRt+SNt+CLt+IRt 乘法模型: yt= TRt×SNt×CLt×IRt yt:觀察值 TRt:趨勢因子 SNt:季節因子 CLt:循環因子 IRt:不規則因子 當變異數為常數時通常使用加法模型,當變異數不平穩時,通常使用乘法模型,由之前的 原始序列圖 2-2-1 可知序列的變異數有逐漸增大的傾向,所以我們決定使用分解法的乘法模式 作估計。(已使用交易日調整無影響,所以採用原本模式。) 由殘差項的自我相關檢測表 2-2-1 可看出,Pr<DW 為<0.0001 顯著,表示有正自我相關,表示 模型需做修正。接下來表 2-2-2 為配適 AR(1)之後的自我相關檢測表。 表 2-2-1 殘差項自我相關檢測表 Ordinary Least Squares Estimates(dy)
SSE 6.03391E10 DFE 310 MSE 194642148 Root MSE 13951 SBC 6849.93928 AIC 6842.45327 Regress R-Square 0.9638 Total R-Square 0.9638 Durbin-Watson 0.1190 Pr < DW <.0001 Pr > DW 1.0000 由表 2-2-2 可得知配適 AR(1)之後,Pr > DW 的 p 值小於 0.05 為顯著,表示有負自我相關, 所以模式需再作修正,所以我們再配適 AR(2)。 表 2-2-2 配適 AR(1)後的殘差項自我相關檢測表 Yule-Walker Estimates SSE 7030153061 DFE 309 MSE 22751304 Root MSE 4770 SBC 6186.98079 AIC 6175.75178 Regress R-Square 0.5659 Total R-Square 0.9958 Durbin-Watson 2.3480 Pr < DW 0.9988 Pr > DW 0.0012
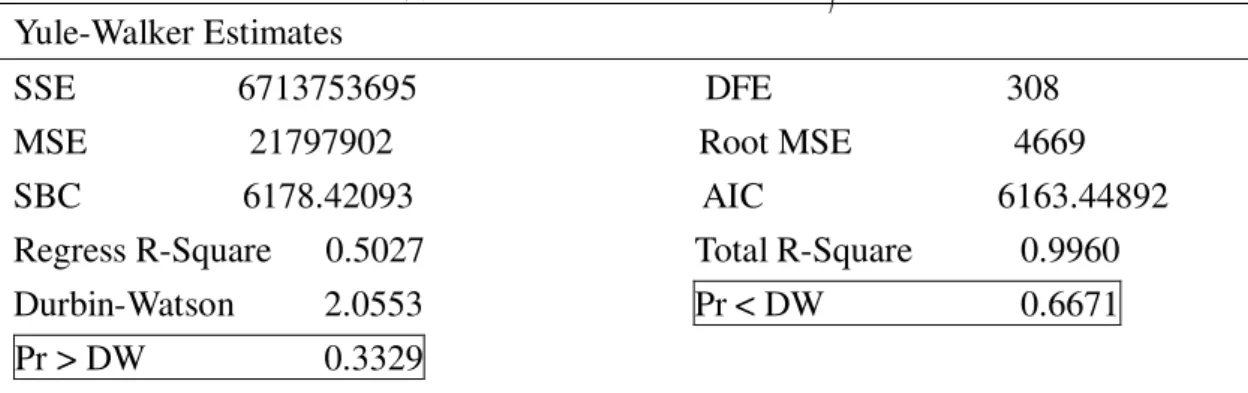
由表 2-2-3 可得知配適 AR(2)之後,Pr < DW 與 Pr > DW 的 p 值皆大於 0.05,沒有正自我相 關及負自我相關,所以我們判斷此模型是合適的。 表 2-2-3 配適 AR(2)後的殘差項自我相關檢測表 Yule-Walker Estimates SSE 6713753695 DFE 308 MSE 21797902 Root MSE 4669 SBC 6178.42093 AIC 6163.44892 Regress R-Square 0.5027 Total R-Square 0.9960 Durbin-Watson 2.0553 Pr < DW 0.6671 Pr > DW 0.3329 由表 2-2-3 可以得知參數估計的 p 值皆顯著,表示此模型為合適。 去季節的估計模式為
TRt=117098+771.9969t+ε
tε
t= 0.765418ε
t-1+ 0.178577ε
t-2+a
tε
t~
iidN(0,1) a
t~
iidN(0,1)
表 2-2-3 參數估計表Variable DF Estimate Standard Error t Value Pr > |t| Intercept 1 117098 8162 14.35 <.0001 t 1 771.9969 43.7475 17.65 <.0001
表 2-2-4 二階自我相關係數 Estimates of Autoregressive Parameters
Lag Coefficient Standard Error t Value 1 -0.765418 0.056064 -13.65 2 -0.178577 0.056064 -3.19
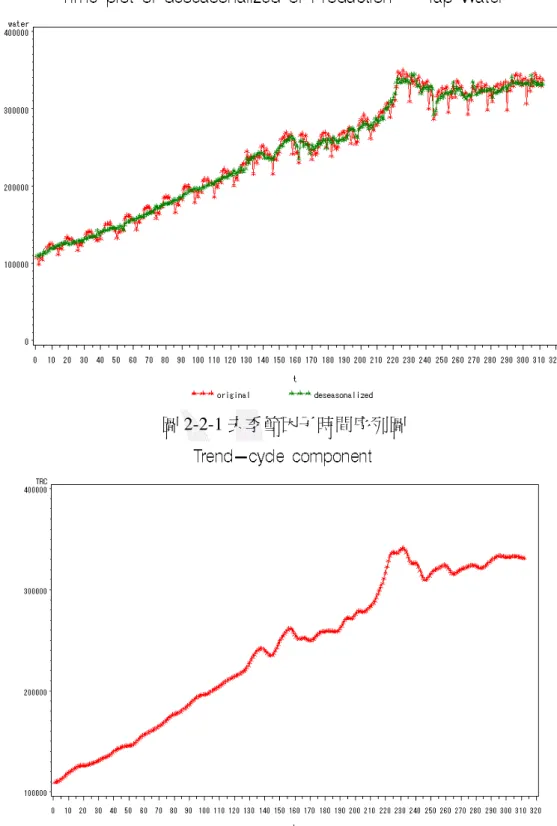
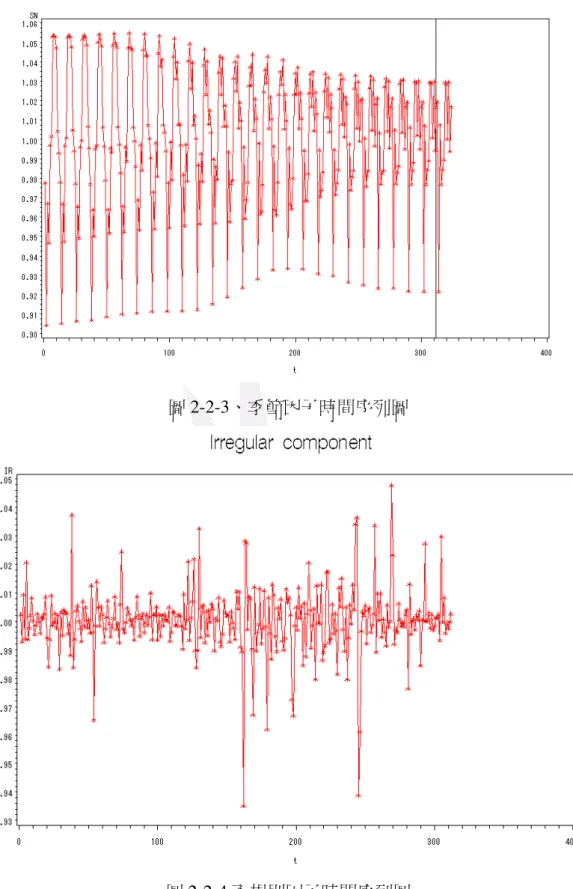
圖 2-2-1 為去季節因子時間序列圖,可由圖看出去季節因素時間序列圖有上升的趨勢,代 表即使沒有季節因素的影響也會隨著時間增加,圖 2-2-2 為趨勢循環時間序列圖可看出有明顯 上升的趨勢,圖 2-2-3 為季節因子時間序列圖可看出有明顯的季節變化。
圖 2-2-1 去季節因子時間序列圖
圖 2-2-3、季節因子時間序列圖
表 2-2-4 是我們使用分解法估計出 12 筆預測值與 95%信賴區間上、下界,並與真實值做比 較。 表 2-2-4 分解法真實值及預測值 時間 真實值 預測值 95%信賴區間下界 95%信賴區間上界 8-Jan 337860 340934.28 322074.67 359793.9 8-Feb 310495 309979.93 291683.98 328275.88 8-Mar 333288 340715.75 319446.57 361984.92 8-Apr 324023 332167.45 310497.03 353837.86 8-May 334676 336478.27 313717.73 359238.81 8-Jun 322913 339929.7 316236.12 363623.28 8-Jul 334718 355338.34 329940.98 380735.69 8-Aug 335007 356615.12 330580.23 382650.01 8-Sep 322254 348510.44 322604.49 374416.4 8-Oct 331203 360272.17 333076.42 387467.92 8-Nov 319925 349324.11 322604.35 376043.87 8-Dec 322996 358802.71 331044.57 386560.86 圖 2-2-5 看出有 3 筆的真實值都超出預測區間之外,分別為 2008 年 10 月,2008 年 11 月 及 2008 年 12 月,若從整體看來,預測值較實際值為偏高,可見,分解法在預測能力上,仍有 不足的地方。 圖 2-2-5 分解法的未來一年預測圖
第三節
第三節
第三節
第三節 指數平滑法
指數平滑法
指數平滑法
指數平滑法((((Exponential Smoothing
Exponential Smoothing
Exponential Smoothing))))
Exponential Smoothing
「指數平滑法」是生產預測中常用的一種方法,也用於中短期經濟發展趨勢預測,所有預測 方法中,「指數平滑法」是用得最多的一種,而「指數平滑法」則相容了全期平均和移動平均 所長,不捨棄過去的資料,但是僅給予逐漸減弱的影響程度,即隨著資料的遠離,賦予逐漸收 斂為零的權數。也就是說「指數平滑法」是在移動平均法基礎上發展起來的一種時間序列分析 預測法,它是通過計算指數平滑值,配合一定的時間序列預測模型對現象的未來進行預測,其 原理是任一期的指數平滑值都是本期實際觀察值與前一期指數平滑值的加權平均為基礎,再加 上預測值與實際值之間差額的百分比。
指數平滑
指數平滑
指數平滑
指數平滑模型
模型
模型:
模型
:
:
:
因為資料有季節變化且變異數有越來越大的趨勢,所以我們使用指數平滑法為 Multiplicative Holt-Winters model。但使用 Multiplicative Holt-Winters model 得其結果沒有 White Noise,此模式不 合適,因此我們再使用 Additive Holt-Winters model 配適且作 log 轉換。模型如下:Lt= α(Yt─St-s)+(1─α)( Lt-1+ bt-1)
bt= γ(Lt ─Lt-1)+(1─γ)bt-1
St= δ(Yt─Lt)+(1─δ)St-s
Ft+m= ( Lt+ btm)St-s+m
Yt *= ln( Yt )
Lt :the level bt:the growth rate st:the seasonal factorof time series
診斷配適模型後之
診斷配適模型後之
診斷配適模型後之
診斷配適模型後之 ACF
ACF
ACF
ACF 圖及
圖及
圖及
圖及 PACF
PACF
PACF
PACF 圖
圖
圖
圖
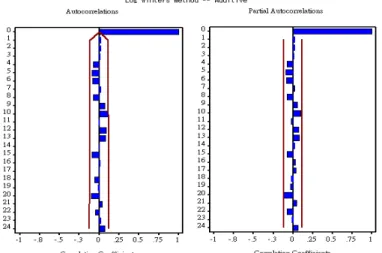
由圖 2-3-1 我們可以看出,每一根 Lag 都在兩倍標準差以內,所以此模式是合適的。
由表 2-3-1 可得知參數估計: = 0.75737 = 0.00100 = 0.00100 2 = 0.0004236 其中 為 水平項的權重、 為趨勢項的權重、 為季節項的權重。 表 2-3-1 指數平滑之參數估計表
Model Parameter Estimate Std.Error T Prob>︱T︱
LEVEL Smoothing Weight 0.75737 0.0391 19.3858 <0.0001
TREND Smoothing Weight 0.00100 0.0026 0.3815 0.7031
SEASONAL Smoothing Weight 0.00100 0.0350 0.0286 0.9772
Residual Variance(sigma squared) 0.0004236 . . .
Smoothing Level 12.71494 . . .
Smoothing Trend 0.00363 . . .
Smoothing Seasonal Factor 1 0.00168 . . .
Smoothing Seasonal Factor 2 -0.08169 . . .
Smoothing Seasonal Factor 3 -0.01226 . . .
Smoothing Seasonal Factor 4 -0.03692 . . .
Smoothing Seasonal Factor 5 -0.01312 . . .
Smoothing Seasonal Factor 6 -0.01854 . . .
Smoothing Seasonal Factor 7 0.03652 . . .
Smoothing Seasonal Factor 8 0.04280 . . .
Smoothing Seasonal Factor 9 0.02590 . . .
Smoothing Seasonal Factor 10 0.03993 . . .
Smoothing Seasonal Factor 11 0.00331 . . .
H0:white noise
H1:not white noise
其檢定規則為若 P-value 大於 0.05,不拒絕 H0,表示是 white noise。
再由圖 2-3-2 可看出有四根 lag 小於 0.05,所以判定此模式不合適。 單根檢定 H0:時間序列不平穩 H1:時間序列平穩 其檢定規則為若 P-value 小於 0.01,拒絕 H0,表示時間序列已達到平穩的狀態。 圖 2-3-2White Noise 和單根檢定
預測
預測
預測
預測:
:
:
:
我們保留了 12 筆的真實值,並以我們最後的預測估計式,計算出 12 筆的預測值。我們將 這預測出之 12 筆預測值與 12 筆真實值整理如表 2-3-2,且將預測值與真實值以及估計出之 95% 信賴水準的上下界線,繪製成圖 2-3-3。 表 2-3-2 指數平滑法真實值及預測值 日期 實際值 預測值 95%信賴區間上限 95%信賴區間下限 2008 年 01 月 337860 334520 348216 321226 2008 年 02 月 310495 308919 324851 293573 2008 年 03 月 333288 332372 352466 313137 2008 年 04 月 324023 325492 347715 304338 2008 年 05 月 334676 334585 359795 310706 2008 年 06 月 322913 334026 361372 308242 2008 年 07 月 334718 354259 385417 325004 2008 年 08 月 335007 357828 391352 326476 2008 年 09 月 322254 353153 388163 320536 2008 年 10 月 331203 359489 396996 324671 2008 年 11 月 319925 347863 385890 3126812008 年 12 月 322996 352347 392555 315269 圖 2-3-3 可看出實際值皆在 95%上下區間內,但是 5 月過後的預測值大於實際值,綜合以 上結果,我們認為此預測的能力不錯。 圖 2-3-3 指數平滑法的未來一年預測圖
第四節
第四節
第四節
第四節 ARIMA
ARIMA
ARIMA
ARIMA
ARIMA 為 AR(AutoRegression ) 模式、差分與 MA(Moving Average) 模式的組合模式。 從圖2-4-1 的原始時間序列圖中,我們得知資料的平均數與變異數皆不平穩,所以變異 數不平穩要做轉換,又平均數不平穩要做差分之後,才可以來判斷為怎樣的 AR 模式與 MA 模式。
圖 2-4-1、原始時間序列圖 首先我們做變數轉換使變異數平穩,圖 2-4-2 為經過對數轉換後的時間序列圖,其 顯示經過對數轉換之後的時間序列,季節變化已保持一致,表示變異數已經達到平穩 了。但由圖2-4-2 可看出資料有上升的趨勢,表示平均數未平穩。 圖 2-4-2、Log 轉換後的時間序列圖 另外,我們也觀察資料的 ACF 與 PACF 圖,判別資料是否平穩。由圖2-4-3 的對數 轉換後的 ACF 與 PACF 圖發現 ACF 圖呈現的是 dies down slowly 的狀態,更確定了此份 資料在經過對數轉換之後,平均數仍是不平穩,所以資料需再作一次差分。
圖 2-4-3、Log 轉換後的 ACF 與 PACF 圖
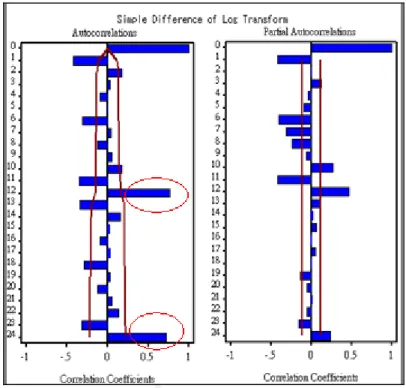
圖2-4-4 為經過 log 轉換及一次差分之後的 ACF 與 PACF 圖,由 ACF 圖可以看出, 殘差在 lag 12 與 lag 24 之處皆有明顯的不顯著,這代表資料有季節波動。如果要解決季 節因素的問題,則需要對資料做季節差分。
圖 2-4-4、Log 轉換與一次差分的 ACF 與 PACF 圖
由圖 2-4-5 可以看出,ACF 圖所呈現的仍是 dies down slowly的狀態表示只經過季節差分之
後,資料仍然是不平穩的,所以我們需要對資料做一次差分與季節差分。
圖 2-4-5、Log 轉換與季節差分的 ACF 與 PACF 圖
由圖 2-4-6 的 ACF 與 PACF 圖可以看出,在經過這些差分與轉換之後,資料已呈現 cut off 的狀態,表示資料已經達到平穩了。
圖 2-4-6、Log 轉換後一次差分與季節差分的 ACF 與 PACF 圖 由圖 2-4-7 的時間序列圖,可看出其資料的變異數與平均數有比較平穩的狀態, 表示資料經過這些轉換是合適的。 圖 2-4-7、Log 轉換後一次差分與季節差分的時間序列圖
我們經過配適 ARIMA(0,1,1)(0,1,1)12後,由圖 2-4-8 的 ACF 與 PACF 圖可看出,資料呈現出良好
圖 2-4-8、配適後的 ACF 與 PACF 圖 建立模型:
(1-B)(1-B12)yt*=(1-θB)(1-ΘB12)at yt*=lnyt
我們做 white noise 檢定、對單根的檢定和 Ljung-Box 檢定,用以判定殘差項 是否有自我相關,並且確定所配適的模式是否恰當。
首先我們做 white noise 檢定,建立假設檢定: H0:white noise
H1:not white noise
其檢定規則為若 P-value 大於 0.05,不拒絕 H0,表示是 white noise。
由圖 2-4-9 可看出所有 Lag 皆大於 0.05,表示殘差項有 White Noise 的現象,其 ARIMA(0,1,1)(0,1,1)12是合適的 。 我們再做單根檢定,建立假設檢定: 單根檢定 H0:時間序列不平穩 H1:時間序列平穩 其檢定規則為若 P-value 小於 0.01,拒絕 H0,表示時間序列已達到平穩的狀態。 由圖 2-4-10 可看出所有 lag 皆小於 0.01,表示時間序列已經達到平穩的狀態,其 ARIMA(0,1,1)(0,1,1)12是合適的 。
圖 2-4-9、White Noise 檢定 圖 2-4-10、單根檢定 接著進行 Ljung-Box 檢定,建立假設檢定: H0:殘差項存在有自我相關 H1:殘差項沒有自我相關 其檢定規則為若 P-value 大於 0.05,則不拒絕 H0,表示殘差項沒有自我相關。 由表 2-4-1 可以看出,所有的 P-value 皆大於 0.05,表示配適後的殘差沒有自我相關,也就 是該模式的配適是合適的。 表 2-4-1、Ljung-Box 檢測表 Autocorrelation Check of Residuals To Chi- Pr >
Lag Square DF ChiSq Autocorrelations
6 3.71 4 0.44660.44660.44660.4466 0.007 -0.02 -0.013 -0.015 -0.105 -0.019 12 10.45 10 0.40170.40170.40170.4017 0.047 -0.018 0.009 0.107 -0.043 -0.076 18 14.73 16 0.54480.54480.54480.5448 0.026 -0.017 -0.098 0.004 0.05 0.02 24 16.04 22 0.81380.81380.81380.8138 0.029 -0.035 -0.004 -0.025 -0.012 -0.035 30 23.62 28 0.70120.70120.70120.7012 0.001 0.136 -0.022 0.016 0.001 -0.06 36 30.84 34 0.62330.62330.62330.6233 -0.078 -0.069 0.001 -0.032 0.047 0.085 42 35.86 40 0.65700.65700.65700.6570 -0.012 0.094 0.022 -0.028 -0.009 -0.064 48 42.79 46 0.60750.60750.60750.6075 -0.096 -0.012 0.055 -0.016 -0.014 0.082
經過以上的 white noise 檢定、對單根的檢定和 Ljung-Box 檢定,又從表 2-4-2 中看出參數的 Pr 值皆小於顯著水準α=0.05,表示參數顯著,應留在模式中。綜合以上的結果可推知,我們所 配適的 ARIMA(0,1,1)(0,1,1)12為一個合適的模型, 我們的預測方程式如下: (1-B)(1- )ln =(1-0.30615B)(1-0.77147 ) =0.0004241 表 2-4-2、參數估計表 Log ARIMA(0,1,1)(0,1,1)s NOINT
ModelParameter Estimate Standard
Error T value Pr ob> |T|
MA factor1 Lag1 0.30615 0.0543 5.6393 <.0001 MA factor2 Lag12 0.77147 0.0418 18.4740 <.0001 Model Variance 0.0004241 . . . 我們保留了 12 筆的真實值,並以我們最後的預測估計式,計算出 12 筆的預測值。我們將這預 測出之 12 筆預測值與 12 筆真實值整理如表 2-4-3,且將預測值與真實值以及估計出之 95%信 賴水準的上下界線,繪製成圖 2-4-11。 表 2-4-3、ARIMA 實際值與預測值表 日期 日期 日期
日期 實際值實際值 實際值實際值 預測值預測值預測值預測值 Upper 95%Upper 95% Lower 95%Upper 95%Upper 95% Lower 95%Lower 95%Lower 95% Jan JanJan Jan----08080808 337860 338270 352128 324820 Feb Feb Feb Feb----080808 08 310495 306817 322165 292016 Mar MarMar Mar----08080808 333288 334914 354251 316369 Apr AprApr Apr----08080808 324023 325758 346797 305678 May May May May----08080808 334676 331945 355452 309609 Jun Jun Jun Jun----080808 08 322913 329821 355075 305920 Jul Jul Jul Jul----080808 08 334718 344733 372985 318096 Aug Aug Aug Aug----08080808 335007 345524 375595 317272 Sep Sep Sep Sep----080808 08 322254 337119 368084 308125 Oct OctOct Oct----080808 08 331203 346018 379391 314867 Nov Nov Nov Nov----08080808 319925 334751 368514 303332 Dec Dec Dec Dec----080808 08 322996 342386 378372 308996
由圖 2-4-11,可看出預測值和實際值大致上都很接近,且都落在 95%上下區間內,認為此 預測能力不錯。 圖 2-4-11、ARIMA 的未來一年預測圖
第五章
第五章
第五章
第五章 最佳模型
最佳模型
最佳模型
最佳模型
表 2-5-1 評估準則
表 2-5-2 分析結果
分析方法 MAD MSE MPE(%) MAPE(%)
時間序列回歸法 28472.53083 1214097224 -8.7144984 8.7146557 分解法 16728.3675 416415916.2 -5.0920669 5.1197147 指數平滑法 14778.41667 369970933.9 -4.2246146 4.5243112 ARIMA 8459.666667 110139254.2 -2.2615063 2.5949351 由表2-5-2可以得知,不論是以何種評估準則來討論,皆是以ARIMA 的預測狀況最佳,再 由四種分析方法的95%信賴水準估計來看,亦為ARIMA 的預測表現最良好。 由於此份資料最適合以ARIMA 來分析,所以我們決定以ARIMA 模式來預測未來的自來水 生產量。
第三章
第三章
第三章
第三章 結論與建議
結論與建議
結論與建議
結論與建議
第一節
第一節
第一節
第一節 結論
結論
結論
結論
在本報告中,使用了時間序列迴歸法、分解法、指數平滑法、ARIMA等四種方法分析台灣 的自來水生產量,並且將實際值與各種方法的預測值作比較,發現ARIMA模式的預測值與實際 值較為接近;且在MSE、MAD、MPE、MAPE 四個評估準則中,結果皆顯示,ARIMA的預測能 力是最佳的。因此我們判定ARIMA配適的模式為最佳模型。 綜觀各種分析結果,在四種方法中對於前半年的預測可以說都是非常良好的,唯其在後半 年,也就是台灣的梅雨季至颱風季節,始出現頗大的偏差。再看圖 2-1 原始序列圖(1982~2008), 由圖中,我們明顯看到自來水生產量原本應是逐年增加的傾向,但在近年來有減緩的趨勢,導 致生產量出現減緩的趨勢有以下幾個原因: 1、近年全球氣候變遷,聖嬰及反聖嬰現象使雨量產生不如以往穩定的現象。 2、人們過度開發水源且未做完善的水源規劃。 3、隨著人口逐漸增加以及工業用水需求量快速增加,而水庫及水源又有限,表示水資源供 應可能已達上限。 再者台灣的用水來源主要仰賴梅雨季與颱風所帶來的雨量,如果梅雨不顯著或侵台颱風太 少( 如 1993 ),則隔年發生缺水的機率相當高。在近年來更是陸陸續續發生乾旱,而根據國際 都市用水量與 GDP 呈正比的趨勢,我們知道未來自來水的需求量仍會持續增加,因此「節約用 水」已經成為不容忽視的重要課題。第二節
第二節
第二節
第二節 建議
建議
建議
建議
隨著人口增加及工業發展,對於水的需求是日益增加,如果不加強開源節流,則可能很快 就會出現供不應求的窘境。尤其近年來因為科技發展的代價-環境變遷又勢必衝擊到台灣的水 資源供給,因此我們建議: 在開源方面,在面對水資源不足的情況下,勢必得再建立新水庫,因為水庫仍是調節水量 的最佳方式,但是建立水庫就得考慮可能會破壞環境。或者應加強尋求替代水源方案,例如目 前自來水公司是以海水淡化、水再生利用、雨水收集貯留、人工湖、越域引水、既有水庫的更 新改善等方式增加供水量。 在節流方面,可推動換成較省水的裝置,比如省水馬桶或是較省水的水龍頭,以避免浪費。 而政府也應在完善的配套措施下推動一些省水方案,宣導節約用水,而民眾也應隨時養成節約 用水的好習慣。 因為自來水取之容易,水龍頭一開便有,因此容易令人忽視它的珍貴性,導致浪費的情形 發生,以至於出現缺水的情況。而出現水資源的不足,也不能全歸咎於自然氣候的變遷,一些 人為的的濫砍濫伐,不當利用水資源擾亂水循環過程導致可利用水源越來越少,這也是現今要 改善的嚴重問題。參考文獻
參考文獻
參考文獻
參考文獻
1. Bowerman ,O’Connell and Koehler,Forecasting, Time series ,and Regression ,Thomson,4th
,2005。
2. AREMOS 經濟統計資料庫系統。
3. 林茂文,時間數列分析與預測,民72年,華泰出版。