正交曲線座標擬似三維水理模式於彎道水流之模擬研究

國

立

交

通

大

學

 

土木工程學系

碩士論文

   

正交曲線座標擬似三維水理模式於彎道水流之模擬研究 

Simulation of Curved Channel Flow Using a Semi-3D Model with

Orthogonal Curvilinear Coordinate System

 

 

研 究 生：洪聖翔

指導教授

：

楊 錦 釧 博士

指導教授

：

謝 德 勇 博士

中 華 民 國 一 ○ ○ 年 七 月

正交曲線座標擬似三維水理模式於彎道水流之模擬研究

Simulation of Curved Channel Flow Using a Semi-3D Model with

Orthogonal Curvilinear Coordinate System

研 究 生：洪聖翔 Student：Sheng-Hsiang Hung 指導教授：楊錦釧 Advisor：Jinn-Chuang Yang

指導教授：謝德勇 Advisor：Te-Yung Hsieh       國  立  交  通  大  學  土  木  工  程  學  系  碩  士  論  文      A Thesis

Submitted to Department of Civil Engineering College of Engineering

National Chiao Tung University in partial Fulfillment of the Requirements

for the Degree of Master in

Civil Engineering July 2011

Hsinchu, Taiwan, Republic of China  

誌謝

承蒙恩師楊教授錦釧及謝博士德勇之悉心指導，使我得以順利完成學業，於 此致上萬分感謝。並感謝口試委員盧教授昭堯、許教授銘熙及賴教授進松給予 寶貴意見與指教，使本研究能更完善。 特別感謝和政學長、夢祺學長、胤隆學長、世偉學長、浩榮學長、建華學長、 弘恩學長、仲達學長、仁凱學長、柏傑學長、鏡如學姊、歆淳學姊、俊宏學長、 昀軒學長、仁猷學長、群玲學姊及綺雯學姊給予的教導與照顧。謝謝同窗彥酉、 家偉、緁玲、唯泰、東洲、紹唐和彥瑜在堅苦的研究所生活互相扶持與關懷， 謝謝學弟妹建翔、昀直、舒勤及芳綺在研究所期間的幫助。感謝好友邦和、元 旎、暐尊和俊廷一直以來的支持與陪伴，讓我的大學生涯充滿難忘的回憶。最 後，感謝家人的照顧與關心，讓我的求學之路得以順利完成。謹將本論文獻給 一路上支持我的朋友，一同分享這份喜悅。  

正交曲線座標擬似三維水理模式於彎道水流之模擬研究

學生：洪聖翔 指導教授：楊錦釧 學生：洪聖翔 指導教授：謝德勇 國立交通大學土木工程學系碩士班

摘要

本研究以垂直水平分離(VHS)演算的方法發展一擬似三維水理模式，探討彎 道流場之水理現象。在水平部份，利用深度平均的控制方程式計算水位與水平 兩方向的水深平均流速值；在垂直部份，先假設任一深度的流速等於水深平均 流速加上一擾動量，帶入三維控制方程式後再扣除深度平均控制方程式即可得 水平兩方向擾動量在垂向(水深方向)的控制方程式；綜合水平與垂直的計算結 果，即可計算不同深度之水平兩方向的流速值。在座標系統上，水平方向與垂 直方向分別採用正交曲線座標與 σ 座標系統，使模式能便利處理不規則的渠道 與底床邊界。在計算步驟上，水平部份採用雙階分割操作趨近法，將水理控制 方程式分割成延散步驟(包含移流項與擴散項)和傳播步驟(包含底床剪應力項與 壓力項)求解，增進模式在實用上的彈性。數值差分上，水平與垂直部分皆採用 隱式法求解，使模式可用較大之演算間距。最後，本研究分別採用緩彎、急彎 及連續彎來模擬彎道流場，並與實驗值與水深平均二維模式模擬結果比較，展 示本模式在不同彎道型態、彎道長度、二次流強度及彎道反曲的情況下，皆能 模擬出合理的結果。 關鍵字：垂直水平分離、擬似三維、彎道水流、正交曲線座標系統、σ座標系統、 隱式雙階分割操作趨近法、二次流    

Simulation of Curved Channel Flow Using a Semi-3D Model with

Orthogonal Curvilinear Coordinated System

Student：Sheng-Hsiang Hung Advisor：Jinn-Chuang Yang

Student：Sheng-Hsiang Hung Advisor：Te-Yung Hsiehaaa

Department of Civil Engineering National Chiao-Tung University

ABSTRACT

This study develops a semi-3D model based on a vertical-horizontal splitting (VHS) method to analyze the flow in open-channel bends. In horizontal, the surface elevation and depth-averaged velocity components are computed by 2D depth-averaged model. In vertical, assume the 3D velocity profile of Navier-Stokes equations is equal to the depth-averaged velocity plus the deviation of velocity profile, and then the vertical governing equations can be derived by subtracting the 2D depth-averaged equations to the 3D Navier-Stokes equations. In order to fit the complex geometry in both side wall and bed slope of channel, the orthogonal curvilinear coordinate system is used in horizontal gird, and sigma coordinate system is used in vertical grid. As for the numerical solution procedure, the two-step split-operator approach, which includes dispersion process (advection and diffusion terms) and propagation process (bed shear stress and pressure terms), is adopted to solve the 2D depth-averaged flow equations to improve the application flexibility. Implicit difference methods are adopted to relax the time step restriction allowing large time steps. Finally, three sets of experimental data including mildly curved, sharply curved and meandering channel are used to demonstrate the capability and accuracy of the semi-3D model, and the results of 2D depth-averaged model are also compared. The simulation results of semi-3D model show well agreement with experimental data considering different curved channels, bend lengths, secondary current and transverse mixing conditions.

Keywords：vertical-horizontal splitting, semi-3D, bend flow, orthogonal curvilinear coordinate system, sigma coordinate system, implicit two-step split-operator approach, secondary current

目錄

誌謝 ... I 摘要 ... II ABSTRACT ... III 目錄 ... IV 表目錄 ... VI 圖目錄 ... VII 符號表 ... IX 第一章 緒論 ... 1 1.1 研究動機與方向 ... 1 1.2 文獻回顧 ... 1 1.3 研究目的與方法 ... 3 1.4 章節介紹 ... 3 第二章 理論基礎 ... 5 2.1 控制方程式 ... 5 2.1.1 三維部分 ... 5 2.1.2 水平二維部分 ... 6 2.1.3 垂直部分 ... 7 2.2 輔助關係式 ... 9 2.2.1 層流與紊流剪應力 ... 9 2.2.2 底床剪應力 ... 9 2.2.3 垂向剪應力與流速梯度之轉換 ... 10 2.3 邊界條件 ... 10 2.3.1 水平二維部分 ... 10 2.3.2 垂直部分 ... 10 第三章 數值架構 ... 13 3.1 水平二維部分 ... 13 3.1.1 隱式雙階分割操作趨近法 ... 13 3.1.2 數值方法 ... 15 3.2 垂直部分 ... 16 第四章 模式測試與彎道模擬分析 ... 21

4.1 模式測試 ... 21 4.1.1 風剪垂直環流場 ... 21 4.1.2 有限深度艾克曼螺旋(Ekman Spiral) ... 22 4.1.3 迴水演算案例 ... 23 4.2 彎道模擬分析 ... 23 4.2.1 緩彎案例 ... 24 4.2.2 急彎案例 ... 25 4.2.3 連續彎案例 ... 27 第五章 結論與建議 ... 63 5.1 結論 ... 63 5.2 建議 ... 64 參考文獻 ... 65

表目錄

表 2.1 曼寧 n 係數與粗糙高度k 對照表 ... 11 _s 表 4.1 彎道案例之幾何資料與水理條件列表 ... 29  表 4.2 de Vriend(1977) u /u 模擬與實驗之均方根誤差(Q = 0.305 cms) ... 29 _m 表 4.3 de Vriend(1977) u /u 模擬與實驗之均方根誤差(Q = 0.61cms) ... 29 _m 表 4.4 de Vriend(1977)u / V_total、v / V_total模擬與實驗之均方根誤差(Q = 0.305 cms) ... 30  表 4.5 de Vriend(1977)u / V_total、v / V_total模擬與實驗之均方根誤差(Q = 0.61 cms) ... 30  表 4.6 Rozovskii(1961) u /u 模擬與實驗之均方根誤差 ... 30 _m 表 4.7 Rozovskii(1961)側壁水深模擬結果與實驗值之均方根誤差 ... 31  表 4.8 Rozovskii(1961)u / V_total、v / V_total模擬與實驗之均方根誤差... 31  表 4.9 Almquist & Holley(1985)u / u_total模擬與實驗之均方根誤差 ... 31  表 4.10 Almquist & Holley(1985)5 號斷面u / u_total、v / u_total模擬與實驗之均方根誤差 .. 32  表 4.11 Almquist & Holley(1985)10 號斷面u / u_total、v / u_total模擬與實驗之均方根誤差 32  表 4.12 Almquist & Holley(1985)13 號斷面u / u_total、v / u_total模擬與實驗之均方根誤差 32   

圖目錄

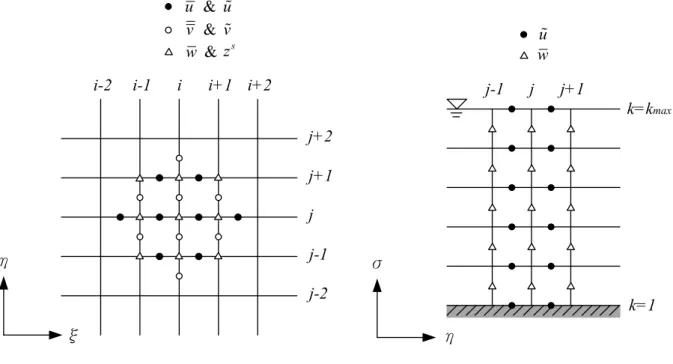
圖 2.1 正交曲線座標轉換示意圖 ... 11  圖 2.2 σ 座標轉換示意圖 ... 11  圖 2.3 水深方向流速剖面示意圖 ... 12  圖 3.1 模式計算流程圖 ... 18  圖 3.2 水平二維模式控制體積法示意圖 ... 19  圖 3.3 交錯格網(staggered grid)示意圖 ... 20  圖 3.4 垂直模式控制體積法示意圖 ... 20  圖 4.1 風剪垂直環流場案例流速比較圖 ... 33  圖 4.2 艾克曼螺旋示意圖 ... 33  圖 4.3 艾克曼螺旋案例流速比較圖 ... 34  圖 4.4 迴水演算案例水深模擬結果圖 ... 34  圖 4.5 迴水演算案例流速模擬結果圖 ... 35  圖 4.6 迴水演算案例垂向流速剖面模擬結果圖 ... 35 

圖 4.7 de Vriend and Koch (1977)實驗案例示意圖 ... 36 

圖 4.8 de Vriend and Koch (1977)計算格網佈置圖 ... 37 

圖 4.9 de Vriend and Koch (1977) u /u 在側方向之比較圖(Q = 0.305 cms) ... 38 _m 圖 4.10 de Vriend and Koch (1977) u /u 在側方向之比較圖(Q = 0.61 cms) ... 39 _m 圖 4.11 de Vriend and Koch (1977)100(zs- s m z )/d 在側方向之比較圖(Q = 0.305 cms) ... 40 

圖 4.12 de Vriend and Koch (1977)100(zs- s m z )/d 在側方向之比較圖(Q = 0.61 cms) ... 41 

圖 4.13 de Vriend and Koch (1977)斷面中間水柱u / V_total之比較圖(Q = 0.305 cms) ... 42 

圖 4.14 de Vriend and Koch (1977)斷面中間水柱v / V_total之比較圖(Q = 0.305 cms) ... 43 

圖 4.15 de Vriend and Koch (1977)斷面中間水柱u / V_total之比較圖(Q = 0.61 cms) ... 44 

圖 4.16 de Vriend and Koch (1977)斷面中間水柱v / V_total之比較圖(Q = 0.61 cms) ... 45 

圖 4.17 Rozovskii (1961)彎道案例幾何示意圖 ... 46 

圖 4.18 Rozovskii (1961)計算格網佈置圖 ... 46 

圖 4.19 Rozovskii (1961)彎道案例實驗量測流速分佈圖 ... 47 

圖 4.21 Rozovskii (1961) u /u 在側方向之比較圖 ... 48 _m 圖 4.22 Rozovskii (1961)側壁水深比較圖 ... 49  圖 4.23 Rozovskii (1961)斷面中間水柱u / V_total之比較圖 ... 50  圖 4.24 Rozovskii (1961)斷面中間水柱v / V_total之比較圖 ... 51  圖 4.25 Rozovskii (1961)案例 65°、100°及 143°斷面側向流速v 分佈之比較圖 ... 52  圖 4.26 以 Rozovskii (1961)案例 65°斷面表示主二次流及小渦流現象 ... 53 

圖 4.27 Almquist and Holley (1985)實驗案例示意圖 ... 53 

圖 4.28 Almquist and Holley (1985)計算格網佈置圖 ... 54 

圖 4.29 Almquist and Holley (1985) u /u_total在側方向之比較圖 ... 56 

圖 4.30 Almquist and Holley (1985)5 號斷面水柱 /u u_total之比較圖 ... 57 

圖 4.31 Almquist and Holley (1985)10 號斷面水柱 /u u_total之比較圖 ... 58 

圖 4.32 Almquist and Holley (1985)13 號斷面水柱 /u u_total之比較圖 ... 59 

圖 4.33 Almquist and Holley (1985)5 號斷面水柱 /v u_total之比較圖 ... 60 

圖 4.34 Almquist and Holley (1985)10 號斷面水柱 /v u_total之比較圖 ... 61 

圖 4.35 Almquist and Holley (1985)13 號斷面水柱 /v u_total之比較圖 ... 62   

符號表

B = 渠道寬度 Cf = 摩擦係數( = g/c2) c = Chezy 係數 d = 水深 fc = 科氏力係數 g = 重力加速度 h = 正交曲線座標轉換係數 ks = 粗糙高度 p = 壓力 Q = 流量 R = 曲率半徑 S = 渠道中心線長度 SI = 二次流強度因子 T = 有效剪應力項 t = 時間 u = ξ 方向流速 u*_{= 剪力速度} total u = 渠道平均流速 total V = 水柱之水深平均流速 v = η 方向流速 w = z方向流速 z = 水位高程 zl = 近底床流速之格網與底床間垂直距離 η = 正交曲線側方向座標軸 κ = von Karman’s 係數 μ 動力黏滯係數 νH = 水平黏滯係數 νl = 層流黏滯係數

νt = 紊流黏滯係數 νV = 垂向黏滯係數 ξ = 正交曲線主流方向座標軸 ρ = 密度 τ 層流剪應力 φ 緯度 ω 地球自轉角速度 上標 b = 底床代號 s = 水面代號 ( ) = 時間平均 ( )  = 時間平均瞬時擾動量 ( ) = 水深平均 ( )  = 物理量之空間微變量 下標 1 = 物理量在 ξ 方向的值 2 = 物理量在 η 方向的值 3 = 物理量在 z 方向的值 m = 物理量之斷面平均值    

第一章 緒論

1.1 研究動機與方向 面對河川水利工程之相關問題，為了尋求解決方案，須對水流在河道中的運 動現象進行分析探討，一般可以利用物理模型試驗或數值模擬來協助瞭解這些 物理現象。物理模型試驗為科學家常用之工具，其為根據原型之縮尺所建造之 模型，試驗結果可信度高，有相當大的助益，然而其設置所需經費龐大、試驗 時間長以及人力與空間的問題，加上模型試驗存在尺度效應(scale effect)、邊界 與量測儀器產生之誤差，且一般僅能針對一、兩種既定方案進行試驗，使物理 模型在應用上有相當的限制和困難。數值模擬乃利用數學模式獲得欲知的物理 現象，在某些假設條件下，仍可求得相當合理的模擬結果，相較於物理模型， 數值模擬具有經濟及高效率之優點，為一非常便利之工具，因此已有許多科學 家致力於數值模擬之發展。 一般淺水的天然河道近似平面水流，即其運動方向近乎水平，深度方向之運 動則相對甚小。對於河川、湖泊及海洋等大範圍之流場分析，一維與二維模式 已廣泛應用在實務上，其相對於三維模式具有計算快速及容易收歛的優點。一 維模式可提供洪水波沿河道方向之運動現象；而二維模式則可提供平面上的流 速分佈。但是當流場在深度方向的分佈為欲探討之問題時，如河川的二次流現 象和水庫泥砂異重流運動等，深度方向的資訊則相對重要而不可忽略，因此在 探討二次流這種局部的現象時，則需要以三維模式進行模擬。相較於全三維模 式，擬似三維模式則具有計算快速和容易收歛的優點，且亦能獲得物理量深度 方向分佈的資訊，適合水利工程實務上的應用。 1.2 文獻回顧 至今已有許多研究利用物理模型及數值模式對河川水流的物理現象進行分 析探討，而其中河川水流在彎道時的流況實為複雜的三維流場，Rozovskii (1957)、Yen (1965)、de Vriend and Koch (1977)、Almquist and Holley (1985)等人

即用物理模型試驗觀測水流在彎道的二次流現象；在數值模式的發展上，水深 平均二維模式已普遍應用在天然河川的模擬上，且有許多研究均已驗證其模擬 結果的合理性。大部分的水深平均二維模式多忽略延散剪應力(dispersion stress) 的效應，然而 Flokstra (1977)指出延散剪應力(dispersion stress)對彎道水流之影 響，Lien et al. (1999)進一步指出如未處理延散剪應力，在模擬彎道水流時，流 場呈現如勢流(potential flow)中之自由渦流(free vortex)，即彎道外岸流速小，而 內岸流速大的情況，如此將無法適當地模擬出彎道二次流現象。處理延散剪應 力則需要有水深方向的流速資訊，因此有許多水深平均二維模式如 Yeh and Kennedy (1993)、Lien et al. (1999)、Hsieh and Yang (2004)等在模式中植入河川彎 道水深方向流速剖面的經驗式，計算延散剪應力項以達到模擬彎道二次流效應 之功能。

近來電子計算機的功能快速成長，許多三維模式開始應用在大型流場如河 川、湖泊及海洋的模擬(Simons, 1974；Falconer and Lin, 1996；Muin and Spaulding, 1997；Ye and McCorquodale, 1998；Gross et al., 1999；Neary et al., 1999；Wu and Falconer, 2000；Fischer-Antze et al., 2001；Li and Gu, 2001；Li and Fleming, 2003； Nicholas and McLelland, 2004；Ge and Sotiropoulos, 2005；Fringer et al., 2006；Song and Hou, 2006； Queutey and Visonneau, 2007；Xia and Jin, 2007；Audusse et al., 2008；Zeng et al., 2008)，Ye and McCorquodale (1998)、Zeng et al. (2008)發展出 三維動壓模式應用在天然河川的模擬，相較於二維模式，其能直接提供水深方 向的資訊。然而三維模式仍需要花費不少的時間來模擬，因此有許多擬似三維 模式的研究提出(Lardner and Cekirge, 1988；Jin and Kranenburg, 1993；Wang, 1994；Blanckaert and de Vriend 2003；Hung et al., 2008；Lin and Huang, 2008； Herzfeld et al., 2010；Zhang et al., 2011)，除了能降低計算成本，在一些假設條件 下，亦能提供合理的三維流速分布資訊。

擬似三維模式中，Lardner and Cekirge (1988)提出的垂直水平分離演算法 Vertical Horizontal Splitting (VHS)受到許多學者引用(如 Wang, 1994；Lin and Huang, 2008 等)，其將水平與垂直流場分開求解，首先利用水深平均二維模式 計算水位分佈與水深平均流速分量，再透過一子模式獲得流速在水深方向之分 佈。VHS 的概念已經應用在海岸、河口及湖泊等大型水體的流場分析(Jin and

Kranenburg, 1993；Wang, 1994；Lin and Huang, 2008；Herzfeld et al., 2010)。應 用VHS 概念探討河川彎道流場的模式中，Blanckaert and de Vriend (2003)提出的 擬似三維模式是在二維模式下，加入一非線性子模式來計算三維效應，其為利 用二次流強度因子與糙度因子計算垂向流速剖面，Blanckaert et al. (2003)利用急 彎案例驗證此非線性擬似三維模式，並與原二維模式及僅適用於緩彎之線性擬 似三維模式比較，證明在急彎這種二次流強度大的案例僅非線性擬似三維模式 能模擬出合理的結果；Zhang et al. (2011)延用並擴展 Muneta and Shimizu (1994) 發展之擬似三維模式，將原模式之卡氏座標系統轉換為非正交曲線座標系統， 並考慮原模式忽略的延散項，然而此模式之水深方向流速剖面則由經驗公式求 得，其實與許多二維模式植入流速剖面經驗式的方法相同。 由以上文獻回顧可看出，在探討河川彎道二次流現象的擬似三維模式中，尚 未有研究是直接以動量方程式求解水深方向的流速，因此，本研究將運用垂直 水平分離演算法的概念，採用正交曲線座標處理不規則幾何邊界的問題，並以 動量方程式求解垂直方向流速剖面應用於彎道流場分析。 1.3 研究目的與方法 本研究之目的為發展一擬似三維水理模式，探討彎道流場中的二次流現象。 基於水深平均二維水理模式(謝德勇, 2003)，應用垂直水平分離演算的概念，加 入垂直水理模式，以動量方程式求解水深方向之流速分佈，另外並在模式中加 入表面風剪力及科氏力之影響。水平方向座標系統採用正交曲線座標，其能適 當表達不規則渠道形狀，且座標軸主軸方向(本研究使用之軸方向)即為主流方 向；而在水深方向則採用σ 座標系統(Blumberg and Mellor, 1983)，其能解決自 由水面在固定格網上變動而影響模式無法準確計算水面之壓力邊界條件的問 題，也能將因為起伏底床產生之不規則格網，轉換為便於計算的矩形格網，如 此可得到精確度較高的模擬結果。為驗證模式的正確性，分別採用具有解析解 或實驗量測數據的案例比較模擬結果。 1.4 章節介紹 前面已闡述本研究之動機與方向、文獻回顧、研究目的與方法，本節將扼要

說明本文章之內容。 第一章為緒論，說明本研究之背景與目的，並回顧相關模式發展的文獻，提 出本研究之方法與研究之重點。 第二章為理論基礎，在正交曲線座標系統下，由三維那威爾-史托克司 (Navier-Stokes)方程式導出模式控制方程式、輔助方程式的使用及邊界條件的設 定，均於本章介紹。 第三章為數值架構，水平二維水理模式及垂直水理模式之數值方法於本章說 明，並簡述模式之計算流程。 第四章為模式驗證，針對模式發展部分，採用具有解析解或實驗量測數據的 案例進行模式的檢定工作，並簡述應用之案例。 第五章為結論與建議，對研究成果作綜合性之歸納說明，並針對研究尚未考 量、不盡完備或日後可繼續研究之處提出建議。

第二章 理論基礎

模式的座標系統方面，為了能適當表達天然河道不規則的幾何形狀，模式在 水平方向採用正交曲線座標系統，如圖 2.1 所示；而在垂直方向則採用 σ 座標 系統(Blumberg and Mellor, 1983)，如圖 2.2 所示，如此能將不規則的計算區域轉 換至矩形計算區域求解，且能便利地處理渠道的側壁、自由液面及底床邊界。 控制方程式方面，透過座標系統轉換，將三維控制方程式轉換為正交曲線座 標系統方程式，再將此控制方程式作時間平均及水深平均後，即可推得水深平 均二維控制方程式(謝德勇, 1994)。將水平二維水理控制方程式從三維控制方程 式中扣除(VHS)，即可求得垂直控制方程式。 2.1 控制方程式 2.1.1 三維部分 基於不可壓縮流之假設下，對那威爾-史托克司(Navier-Stokes)方程式取時間 平均後，得控制方程式如下： 連續方程式 2 1 1 2 (h u) (h v) (h h w) 0 z    _  _  _    (2.1) 動量方程式 ξ 方向： 2 2 2 1 2 2 1 2 1 2 1 2 1 2 1 1 2( ) ( ) ( ) ( u) ( u ) ( uv) ( uw) uv h u h v h t h h z h h h h h h                 _  _  _  _{  }        2 2 2 1 2 2 1 2 1 2 1 2 1 2 1 1 2( ) ( ) ( ) ( u ) ( u v) ( u w) u v h u h v h h h z h h h h h h                    _  _{ }  _{ }             12 1 22 2 2 11 1 12 1 2 13 1 1 2 1 2 1 2 1 1 ( ) ( ) ( ) c h h p f v h h h h h h h z h h h h                       _   _   _   _   (2.2) 1.    

η 方向： 2 2 2 2 1 1 2 1 1 2 1 2 1 2 1 1 2( ) ( ) ( ) ( v) ( v ) ( uv) ( vw) uv h v h u h t h h z h h h h h h                                 2 2 2 2 1 1 2 1 1 2 1 2 1 2 1 1 2( ) ( ) ( ) ( v ) ( u v) ( v w) u v h v h u h h h z h h h h h h                    _  _{ }  _{ }             12 2 11 1 1 22 2 12 1 2 23 2 1 2 1 2 1 2 1 1 ( ) ( ) ( ) c h h p f u h h h h h h h z h h h h                        _   _   _   _   (2.3) z 方向： 在一般淺水的天然水道，垂直方向之動量方程式可用靜水壓分佈來簡化， 0 p g z      (2.4) 而垂直方向之流速可透過連續方程式求得，以減少模式之計算量。 以上諸式中，、、z為三維正交曲線座標方向，其中、為水平方向，z為 水深方向；下標1、2、3 分別代表物理量在、、z方向代號；h₁、h₂分別為、 方向之轉換係數；u、v、w分別為、、z方向流速；g為重力加速度；t 為 時間； 為層流剪應力；( ) 表時間平均；( ) 表時間平均瞬時擾動量；f_c(=2 sin ) 為科氏力係數； 為地球自轉角速度；為緯度； 為密度；p為壓力。 2.1.2 水平二維部分 將 2.1.1 節之三維水理控制方程式(2.1)、(2.2)、(2.3)利用萊布尼茲法則對深 度方向積分，加上運動邊界條件及動力邊界條件，並取深度平均值，可得水平 二維水理控制方程式。 連續方程式 1 2 ( 2 ) ( 1 ) 0 d h h h ud h vd t    _  _  _    (2.5) 動量方程式 ξ 方向：

2 1 2 1 2 1 2 1 2 1 1 1 s s c h h u u u v u uv v p g z f v t h h h h h h h h           _  _  _  _  _{ }  _   _{    }  _{ }   2 1 2 12 11 1 1 11 12 22 1 2 2 1 ( ) 1 1 1 2 s b h h h T T T T T dh h dh dh d                 _   _          (2.6) η 方向： 2 2 1 2 1 1 2 1 2 2 2 1 s s c h h v v v u v uv u p g z f u t h h h h h h h h                           _{    }  _{ }   1 2 1 12 22 2 2 22 12 11 1 2 1 2 ( ) 1 1 1 2 s b h h h T T T T T dh h dh dh d                 _   _          (2.7) 式中， 2 2 11 ( 11 ) s b z z T 



 u u  dz (2.8) 2 2 22 ( 22 ) s b z z T 



 v v  dz (2.9) 12 ( 12 ) s b z z T 



 uvu v dz  (2.10) 以上諸式中，d 為水深；_zs_{為水面高程；z}b_{為底床高程；} s i  為i 方向水面剪應力； b i  為 i 方向底床剪應力；( )表水深平均；( )  表物理量之空間微變量(例： u u u  )；上標 s、b分別為水面及底床代號；T 為有效剪應力項(effective stress term)，其包含層流剪應力、延散剪應力與紊流剪應力。 2.1.3 垂直部分 將 2.1.1 節之三維水理控制方程式(2.2)、(2.3)以靜水壓假設代入，並令 u u u  、v  v v _{(如圖 2.3)，得到之方程式扣掉 2.1.2 節之水平二維水理控制} 方程式(2.6)、(2.7)，即可得到垂直水理控制方程式。 ξ 方向： 1 1 1 2 2 2 u u u u u u u v u v u v u u t h  h  h  h  h  h                                     2 1 1 1 2 2 1 2 1 2 1 2 1 2 1 2 2 h h h h h uv uv uv vv v h h  h h  h h  h h  h h                     

13 ( 1 1) 1 ( ) s b c f v Horizontal Diffusion in d d    _            (2.11) η 方向： 2 2 2 1 1 1 v v v v v v v u v u v u v v t h  h  h  h  h  h                                     2 2 2 2 1 1 1 2 1 2 1 2 1 2 1 2 2 h h h h h uv uv uv uu u h h  h h  h h  h h  h h                       23 ( 2 2) 1 ( ) s b c f u Horizontal Diffusion in d d    _             (2.12) 式中， 1 1 2 2 u u v v w t h h h h z                                (2.13) b z z d    (2.14) d t d t    _{ }    (2.15) 1 _zb _d d d               (2.16) 1 _zb _d d d       _{ }  _     (2.17) 1 z d   _  (2.18) 2 1 2 11 12 22 1 2 1 ( Horizontal Diffusion in ) T h 2T h T h dh h             _   _      2 12 11 2 2 2 2 2 1 1 1 1 2 1 2 2 2 1 T 1 T u _H 1 _H h _H u dh dh h h h h h                         _{  } _    _  _{ }  _  1 2 1 1 1 2 2 1 2 2 2 1 2 _H v h _H h v _H h u h h h h h h h h h                          _{ }  _{   } _{   }  _{ }  _{ } _{ }  _{ } _{ } 2 1 1 2 2 2 2 2 2 2 1 1 2 2 1 1 2 2 1 1 2 H H H h u v u h v h h h h h h h h h  _                       _{ } _{  } _{ }   _{  }  _{ }  _{ }   (2.19)  

1 2 1 22 12 11 1 2 1 ( Horizontal Diffusion in ) T h 2T h T h dh h             _   _      2 22 12 1 2 2 2 2 1 2 2 1 2 2 2 2 2 1 T 1 T v _H 1 _H h _H v dh dh h h h h h                         _{  } _    _  _{ }  _  2 2 1 2 1 2 1 1 2 1 2 1 2 _H u h _H h v _H h u h h h h h h h h h                          _{ }  _{   } _{   }  _{ }  _{ } _{ }  _{ } _{ } 2 2 2 1 2 2 2 2 2 1 2 1 2 2 1 1 2 2 1 1 2 H H H h v v u h u h h h h h h h h h  _                       _{ } _{  } _{ }   _{  }  _{ }  _{ }    (2.20) ； 為水平黏滯係數_H   _{l t}； 為層流黏滯係數；_l  為紊流黏滯係數=κu_t *d/6

(Falconer 1980)；u*為剪力速度；κ 為 von Karman’s 係數(約等於 0.41)；d 為水深。 2.2 輔助關係式 2.2.1 層流與紊流剪應力 採用Boussinesq 之渦流黏性理論，層流與紊流剪應力可合併表示為 2 11 1 1 1 2 1 2 _H u v h u h h h  _           _  _     (2.21) 2 22 2 2 1 2 1 2 _H v u h v h h h  _           _  _     (2.22) 12 2 1 1 2 2 1 2 _H h v h u u v h h h h  _               _{  } _{ }  _{ }  _{ }   (2.23) 2.2.2 底床剪應力 底床剪應力採用French (1986)之經驗式 2 1 _2.5ln 30 2.72 b b b l s z u u k        _{  }      (2.24) 2 2 _2.5ln 30 2.72 b b b l s z v v k        _{  }      (2.25)

式中， b u 、 b v 分別為、方向之近底床流速；z_l為近底床流速之格網與底床間 垂直距離；k_s為粗糙高度，曼寧n 係數與粗糙高度k_s對照如表 2.1。 2.2.3 垂向剪應力與流速梯度之轉換 正交曲線座標上的表示式： 13 1 1 V u w d h          _  _     (2.26) 23 2 1 V v w d h           _  _     (2.27) 式中， 為垂向黏滯係數。 _V 2.3邊界條件 2.3.1 水平二維部分 水平二維水理模式考量三種邊界條件設定，分別為渠道入流、渠道出流與固 體邊界。一般而言，渠道入流邊界條件設定為單位寬度入流量，渠道出流邊界 條件則採用水位高程設定。在固體邊界處，沿固體邊界法線方向採不透水邊界 條件；而沿固體邊界切線方向可分為滑移與非滑移邊界條件。 2.3.2 垂直部分 垂直水理模式考量渠道入流、渠道出流、自由液面及底床邊界條件。在渠道 入 流 及 渠 道 出 流 處 假 設 均 勻 流 邊 界 條 件 。 自 由 液 面 採 風 剪 力 邊 界 條 件 s V u d      _  、 s V v d      _  ； 而 底 床 則 採 用 底 床 剪 力 邊 界 條 件 b V u d      _  、 b V v d      _  。 2.  

表 2.1 曼寧 n 係數與粗糙高度k_s對照表

渠道類型 曼寧n k (mm) _s

Very smooth concrete surface 0.011~0.015 0.15~0.30

Gunite(smooth) 0.016~0.019 0.50~1.5

Rough concrete 0.018~0.022 3.0~4.5 Earth channels(straight, uniform) 0.016~0.02 3.0

Rubble masonry 0.02~0.025 6.0 Untreated gunite 0.018~0.03 3.0~10.0

資料來源”Flow in Open Channels”Second Edition, K. Subramanya

圖 2.1 正交曲線座標轉換示意圖 圖 2.2 σ 座標轉換示意圖 y x η ξ 正交曲線座標轉換 s z b z

圖 2.3 水深方向流速剖面示意圖。(u 為實際流速剖面；u 為水深平均流速；u為 流速微變量)

u

u

u u u

 



u

z

第三章 數值架構

模式之數值計算流程如圖 3.1 所示，首先由水平二維模式求解各水柱之水面 高程以及水深平均流速，然而水平二維深度平均方程式中之擴散項因為須要有 水深方向流速資訊，因此在初次計算時先忽略擴散項。將求得的水面高程以及 水深平均流速代入垂直模式求解水深方向流速剖面，求得的水深方向流速即可 用來計算擴散項，再由水平二維模式求解水面高程以及水深平均流速，如此迭 代直到水平二維模式之水面高程與水深平均流速以及垂直模式水深方向流速剖 面達收歛條件。 3.1 水平二維部分 3.1.1 隱式雙階分割操作趨近法 本研究基於分割操作之觀念，將動量方程式分割成二個步驟(延散步驟及傳 播步驟)，並利用隱式數值方法求解。延散步聚求解移流項和擴散項，傳播步驟 求解壓力項、底床剪應力項和連續方程式。據此，水理控制方程可改寫成 延散步驟 1 1 1 2 2 1 2 ( ) n n n n V V V T t        _{     }  _    (3.1) 傳播步驟 1 1 2 ₁ ( ) n n n b b V V g z d t t d          _  _{    }  _   _      (3.2) 1 ₀ n V     (3.3) 式中，V 表示速度向量；T 表示擴散及延散項；上標 n +1 表示(n +1)Δt 時刻之未 知變數；Δt = tn+1 −tn；上標n 表示 nΔt 時刻之已知變數；上標 n + 1/2 表示在(n +1)Δt 與nΔt 間之未知變數。  

(3.1)~(3.3)的一般式可表示成 延散步驟 2 1 2 1 2 1 2 1 2 h h u u u v u uv v t h  h  h h  h h       _{ }  _  _{ }      _   _ 2 1 2 12 11 11 12 22 1 2 2 1 1 1 1 2 h h h T T T T T dh h dh dh                 _   _         2 11 2 11 1 12 1 12 1 2 1 ( ) ( ) ( ) ( ) s b s b s z b z s z b z h h h h dh h                 _    _       (3.4) 2 2 1 1 2 1 2 1 2 h h v u v v v uv u t h  h  h h  h h            _  _    _   _ 1 2 1 12 22 22 12 11 1 2 1 2 1 1 1 2 h h h T T T T T dh h dh dh                 _   _         2 12 2 12 1 22 1 22 1 2 1 ( ) ( ) ( ) ( ) s b s b s z b z s z b z h h h h dh h                 _    _       (3.5) 傳播步驟 1 1 ( b ) b u g z d t h d     _{ }   _   (3.6) 2 2 ( b ) b v g z d t h d     _{ }   _   (3.7) 和 1 2 ( 2 ) ( 1 ) 0 d h h h ud h vd t    _  _  _    (3.8) 針對n +1 時刻的水深值(d n+1)做線性化處理，且僅保留一階項，(3.8)式可改寫成 1 2 1 1 1 2 2 2 ( ) ( ) 0 d Δd Δd h h Δd Δd t                     _   _ _   _   _  _  _  _ (3.9) 式 中 ， 2 1 1 n h gΔt d C h_    ； 1 1 2 2 2 1 1 ( )b n n n h h gΔt z d u C_ C h_           _  _     ； 1 1 n d   ； 1 2 2 n h gΔt d C h    ； 1 1 1 2 1 2 2 ( )b n n n h h gΔt z d v C_ C h_           _  _     ； 2 2 n d   ； 1 1 2 2 2 2 ( ) ( ) 1 n n f n C u v C Δt d       ； n 1 n Δd d  d ； _/ 2 f C g c 為摩擦係數；c為 Chezy 係數。

3.1.2 數值方法 在數值差分方法選用的考量上，利用顯式數值方法求解時，演算時間間隔將 會受到很大的限制，在模擬天然明渠水流問題時將耗費冗長的演算時間與龐大 的電腦計算量，在應用上有其困難存在。為解決這個問題，本研究採用隱式數 值方法求解。 本模式採用控制體積(control volume)法的觀念來離散控制方程式，控制體積 法的基本概念如圖 3.2 所示，其中(a)圖為實際區域，(b)圖為計算區域，E、W、 N、S 表相鄰格點，e、w、n、s 表控制面。模式計算之變數則放置在交錯網格 (staggered grid)上，如圖 3.3。在控制方程式中，除了移流項採用一階精度混合 型上風法(hybrid scheme) (Spalding 1972)差分外，所有空間差分均採用二階精度 的中央差分法。另外，時間項則採用簡單的前向差分方法。 中央差分法可表示成 e w p Ψ Ψ Ψ Δ     _   _    (3.10) n s p Ψ Ψ Ψ Δ     _  _    (3.11) 式 中 ，Ψ_e 0.5 ( Ψ_E Ψ_P) 0.5 ( Ψ_i1,jΨ_{i j,} ) ；Ψ_w 0.5 ( Ψ_PΨ_W) 0.5 ( Ψ_{i j,} Ψ_i1,j) ； , 1 , 0.5 ( ) 0.5 ( ) n N P i j i j Ψ  Ψ Ψ  Ψ _ Ψ ；Ψ_s 0.5 ( Ψ_PΨ_S) 0.5 ( Ψ_{i j,} Ψ_{i j, 1}) ；Ψ 可 表 為 u、v、h₁、h₂、d、z_s和z_b； i、 j分別代表水平格網上任一點之縱向及橫向 位置。 混合型上風法為上風法(upwind scheme)與中央差分法組合而成，當移流效應 重要時，採用上風法；移流效應不重要時，則採用中央差分法。至於移流效應 重要性的判斷，則採用格網雷諾數(mesh Reynolds number) Rx、Ry作為判斷的因

子，當|Rx|或|Ry|大於 2 時，代表移流效應重要，差分方法採用能反映方向性的上

風法；|Rx|或|Ry|小於等於 2 時，移流效應可視為不重要，差分方法採用中央差分

混合型上風法應用於本研究移流項的處理可表成 , 1 1 1 1 1 , 1, , , 1, 1 1 0.5 (1 ) (1 ) i j n n n n n n n i j i j i j i j i j x x u Φ Φ Φ Φ u Φ h  h  Δ  Δ                _{   }       _  _{   }     _{    } (3.12) , 1 1 1 1 1 , , 1 , , , 1 2 2 0.5 (1 ) (1 ) i j n n n n n n n i j i j i j i j i j y y v Φ Φ Φ Φ v Φ h  h  Δ  Δ                _{   }       _  _{   }          (3.13) 其中 0 2 1 2 1 2 x x x x R R R     _      ； 2 0 1 2 1 2 y y y y R R R     _      (3.14) 上 列 諸 式 中 ， , 1, / i j n i j x u h Δ R     ； , 2, / i j n i j y v h Δ R     ；  為 動 力 黏 滯 係 數(dynamic viscosity)；Φ可表成u或v 。 3.2 垂直部分 在垂直水理模式方面，每一水柱以隱示法分別求解，將(2.11)與(2.12)式改寫 為 ξ 方向： 1 1 1 2 1 1 2 1 2 n n V u h h u u u u uv uv u M t h h h h h d               _  _  _{  }   _    _       _        (3.15) η 方向： 1 2 2 2 2 1 2 1 2 n n V v h h v v v v uv uv v M t h z h h h h d              _  _  _{  }   _    _       _        (3.16) 式中， 1 1 1 1 1 2 2 2 1 2 ( s b) n u c h u u u u v u v u v u uv M f v d h h h h h h h                  _                        2 2 2 1 2 1 2 1 2 ( ) n V h h vv v w Horizontal Diffusion in h h h h dh  _              _     _   (3.17)

2 2 2 2 2 1 1 1 1 2 ( s b) n v c h v v v v u v u v u v uv M f u d h h h h h h h                   _                        2 1 1 1 2 1 2 2 2 ( ) n V h h uu u w Horizontal Diffusion in h h h h dh  _              _     _   (3.18) 式中， 為垂向黏滯係數。 _V 垂直水理模式亦採用控制體積法的觀念離散控制方程式，如圖 3.4 所示，E、 W、N、S、T、B 為相鄰格點，e、w、n、s、t、b 為控制面。模式計算之變數 亦放置在交錯網格(staggered grid)上，如圖 3.3。(3.17)及(3.18)等式左邊採用 Crank-Nicolson method，其時間差分為二階精度；而等式右邊M_u和M_v的空間差 分則採用中央差分法。 3.      

圖 3.1 模式計算流程圖 4.垂直模式-計算剪應力項 (T11、T12、T22) 6.垂直模式-求解水深方向 流速剖面 3.二維收歛 輸入幾何資料與水理條件 1.水平二維-延散步驟 2.水平二維-傳播步驟 否 7.垂直模式收歛 否 9.垂直及二維收歛 是 輸出模擬結果 是 5.垂直模式-計算垂向流速w 8.水平二維(延散、傳播) 否 是

(a) (b) 圖 3.2 水平二維模式控制體積法示意圖。i、j分別代表水平格網上任一點之縱向 及橫向位置；(a)實際區域；(b)計算區域 N S P W E n e w s i , j +1 i , j -1 i -1 , j i +1 , j i , j y x S_{i , j -1} W P N E i , j +1 i +1 , j i -1 , j i , j e n s w η ξ

圖 3.3 交錯格網(staggered grid)示意圖 圖 3.4 垂直模式控制體積法示意圖(計算區域)。i、j分別代表水平格網上任一點 之縱向及橫向位置；k代表在垂向格網上的位置 4.       j j-1 j-2 j+1 j+2 i i+1 i+2 i-1 i-2 ξ η η σ & u u & v v & _s w z _wu k=kmax k=1 j j+1 j-1 s z ξ η P E W S T B e w n s i , j , k i -1 , j , k i +1 , j , k i , j +1 , k i , j -1 , k i , j , k +1 i , j , k -1 N t b k z

第四章 模式測試與彎道模擬分析

本章先採用數個簡單的案例測試模式的基本演算功能，再以實驗案例進行彎 道的模擬分析。 4.1 模式測試 本研究將模式由二維擴展為擬似三維，並加入科氏力及風剪力的影響，雖然 科氏力及風剪力對彎道模擬並不特別重要，但為求模式整體的完整性，在模式 發展時還是考量此二作用力的影響。因此在模式測試部分，首先以風剪垂直環 流場及有限深度艾克曼螺旋兩個有解析解之案例，分別測試風剪力項及科氏力 項的機制；另以迴水演算案例測試垂直模式基本運算功能。 4.1.1 風剪垂直環流場 封閉水池受到風剪力作用時，表面水體朝與風同方向加速，進而帶動更內部 之水體運動，當水流向前運動遇到邊界受阻，表面水體會產生堆升現象，此會 造成底部水平方向壓力不平衡而使底部水體朝與風反方向流動，當水面堆升至 一定程度後，水面坡降造成之壓力差若與風剪應力平衡，則水面坡降不再改變， 而水體內部則形成一穩定之垂直環流場。此一水體由靜止開始運動後各種外力 平衡而產生之內部流場，可用以檢視模式是否具物理機制適度反應其現象。 Heaps (1981)針對定常層流底床不滑移狀況，推導出湖泊環流之水深方向流 速剖面的解析解 (3 2 ) ( ) 4 s V z z d u z d           (4.1) 式中，u z( )表示於高程z 之流速；d 為水深； 為垂向運動黏滯係數；_{V }s 為作用 於湖面之風剪應力。 假設一長度400 m、寬度 160 m 之封閉水槽，水深 2 m，水面受風剪應力 1 0.5 s   N/m2，密度 1013 kg/m3、垂向運動黏滯係數_V 0.015m2/s。流速模擬結果與 解析解比較如圖 4.1 所示，圖中縱軸為高程 z，橫軸為流速u (m/s)，透過風剪

環流場之解析解比較，證明了加入風剪力項後模式能夠反應此現象之機制。模 擬結果與解析解之均方根誤差(root-mean-squar error)為 0.0011，可看出模擬結果 之精度。 4.1.2 有限深度艾克曼螺旋(Ekman Spiral) 水體的流動會因為地球自轉的影響而發生偏轉，瑞典的海洋學家 Ekman 於 1905 年針對此現象推導出一解析解，稱之為艾克曼螺旋。科氏力的影響，會使 得在北半球的水體流動向順時鐘偏轉，如圖 4.2 所示，當風力帶動水體表面流 動，水流因科氏力而向順時鐘方向偏轉，而表層的水流又帶動較下方的水層流 動，此下層的水流亦向順時鐘偏轉，如此往水深方向傳遞，並隨水流的偏轉， 流速漸小。艾克曼螺旋的控制方程式為黏滯力與科氏力之平衡，即 2 2 ( ) ( ) 0 V c d u i v if u i v dz      (4.3) 式中， 為垂向運動黏滯係數；_V i 1；f_c為科氏力係數。其邊界條件在水面 為風剪力邊界條件，而在無限深度底床之流速為零。今考慮有限深度之艾克曼 螺旋，依Ekman 之分析方式，Lin and Huang (2008)推導出一有限深度之解析解。 自由液面邊界條件為 0 du dz  和 2 / s V dv dz     底床邊界條件為非滑移 0 u  和 v 0 有限深度之解析解為

0 _{cos sinh}2 0 _{2 sin sin}2 0

4 4 4 z D V z h z h u e Δ Δ D D D D  _{          }  _{ }  _  _ _  _{ }       

0 _{cos sinh}2 0 _{2 sin sin}2 0

4 4 4 z D V z h z h e Δ Δ D D D D  _{     }          _{ }  _  _ _  _{ }        (4.4)

0 _{cos sin}2 0 _sinh2 0 _{2 sin}

4 4 4 z D V z h h z v e Δ Δ D D D D  _{          }  _{ }  _ _  _{ }  _        

0 _{cos sin}2 0 _sinh2 0 _{2 sin}

z D V z h h z e Δ  _{     }          _{ }  _ _  _{ }  _ (4.5)

式中， 2 V c D f    ； 2 0 / 2 s V D V     ；_{Δ cos}2 h0 _sinh2 h0 D D        _{ } _{ }    ；h0為水深。 假定一水深 30 m 之開放邊界水域，給定科氏力係數 _{1.22 10} 4 c f    、表面風 剪應力 2 1.5 s   N/m2、密度 1013 kg/m3、垂向運動黏滯係數_V 0.0065 m2/s。 流速模擬結果與解析解比較如圖 4.3 所示，圖中縱軸為無因次水深 (z-zb)/d，橫 軸為流速Velocity (m/s)，流速分量u 與v 的模擬結果與解析解之均方根誤差分別 為0.0109 與 0.0126，證明方程式中科氏力項對模擬結果影響之正確性。 4.1.3 迴水演算案例 前兩個案例無法看出流量-水深關係是否合理之問題，然而河川或渠道內之 水流流場不僅傳遞動量，同時也傳輸質量，因此，可藉由此案例觀察模擬結果 之垂向流速剖面是否與二維之平均流速維持質量守恆。 假定一均勻矩形渠道，長8000 m，渠寬 100 m，渠道坡度為 0.0005，曼寧係 數0.035，下游受堰的影響使下游處水深較正常水深抬高 1.5 m。模式上游邊界 條件為單位寬度入流量3.987 m2/s，下游固定水深 4.5 m。在此流況下，河道之 正常水深為3 m，臨界水深為 1.175 m。 水深及流速模擬結果如圖 4.4 及圖 4.5 所示，由圖 4.4 可看出下游為給定的 固定水位邊界條件，沿著往上游方向，距離下游控制斷面愈遠，迴水效應愈小， 水深漸漸趨向正常水深3 公尺。相對地，由圖 4.5 可看出流速從上游的 1.303 m/s 遞減為下游的0.878 m/s。圖 4.6 為垂向流速剖面的模擬結果，圖中由上游至下 游畫出流速分佈及對應水深，分別取距離上游邊界2000 m、4000 m 及 6000 m 處代表上游、中游及下游。由圖可看出愈接近下游整體流速愈慢、水深愈深， 此結果與圖 4.4 及圖 4.5 一致。 4.2 彎道模擬分析 本研究分別採用緩彎、急彎及連續彎案例模擬彎道流場，並以緩彎渠道模擬 不同流量之流況，測試在不同的二次流強度下，模式是否皆能模擬出合理的結 果。模擬結果除了與實驗量測數據驗證，並和二維模式(謝德勇, 2003)比較水深

平均流速與水深之模擬結果，此二維模式採用de Vriend (1977)對二次流速度剖 面之假設，以達到模擬彎道之功能。所有彎道案例之幾何資料與水理條件整理 如表 4.1。

4.2.1 緩彎案例

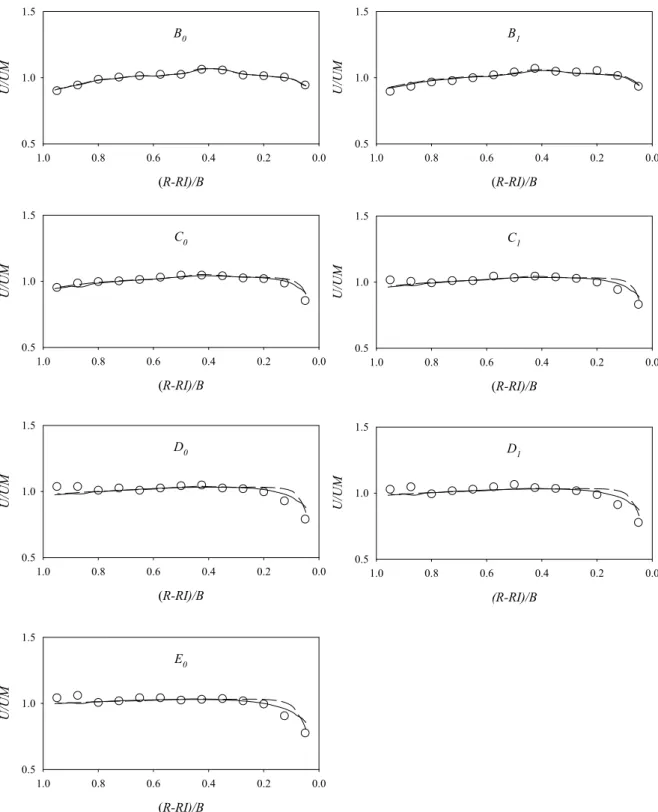
緩彎的驗證採用 de Vriend and Koch (1977)之實驗案例，其實驗水槽佈置如 圖 4.7 所示，從斷面 A0至斷面B0為39 m 之直線道，斷面 B0為彎道之起點，沿 著渠道一直到斷面 E0為一蜿蜒 90 度固定曲率半徑 R 之矩形渠道，渠道寬度 B 為6 m，中心線曲率半徑 R 為 50 m，渠寬與曲率半徑比值 B/R 為 0.12，底床在 直線道為平床，在彎道之縱向坡度為0.0003。模擬之側壁採用非滑移邊界條件， 上游邊界條件為固定入流量，下游邊界條件為實測水位資料。此渠道案例用兩 種流量大小驗證，分別為0.305 cms 與 0.61 cms。流量 Q = 0.305 cms 的案例， Chezy 係數為 50 m0.5/s，平均流速為 0.2 m/s，平均水深為 0.25 m，福祿數為 0.13， 二次流強度因子(relative strength of secondary current) _{SI d/ (R g c/} 2_{)= 0.08；}

流量Q = 0.61 cms 的案例，Chezy 係數為 70 m0.5/s，平均流速為 0.4 m/s，平均水 深為0.25 m，福祿數為 0.26，二次流強度因子 SI 為 0.11。本案例模擬採用 103 ×35 之非均勻計算格網，如圖 4.8 所示。 圖 4.9 及圖 4.10 分別為 Q = 0.305 cms 及 Q = 0.61 cms 之無因次水深平均流 速模擬結果與實驗值比較圖，圖中縱軸無因次參數為比較點之水深平均流速u 除以該斷面的平均流速u_m，橫軸之無因次參數為比較點曲率半徑R 減去渠道內 岸之曲率半徑RI 後再除以渠道寬度 B。圖 4.11 及圖 4.12 分別為 Q = 0.305 cms 及Q = 0.61 cms 之無因次水位模擬結果與實驗值比較圖，圖中縱軸為比較點水 位高程 zs減去該斷面平均水位高程 s m z 除以水深 d 後，再乘上一百倍之放大尺度 無因次參數，橫軸之定義如同流速比較圖。 由圖 4.9 及圖 4.10 可看出，流場受到二次流效應的影響，水流動量由內岸 向外岸傳遞，使彎道中下游段受此效應的影響，外岸縱向流速會明顯大於內岸 的縱向流速。圖中二維模式與本模式的模擬結果趨勢皆與實驗值吻合，其均方 根誤差整理如表 4.2 與表 4.3，從表格可看出誤差值皆很小。如圖 4.11 及圖 4.12

所示，受彎道效應的影響，斷面水面高程會呈現水面超高(super-elevation water surface)的分布，即外岸水面高程會大於內岸的水面高程。此水面超高的現象甚 至從彎道入口處(斷面 B0)即已發生，至斷面 B1時，此斷面水面高程的側向坡度 即已約達穩定的狀態。圖中可看出，水位模擬結果趨勢皆與實驗值吻合，模擬 結果相當接近，其應為緩彎案例水位超高的現象較不明顯。 圖 4.13 及圖 4.14 分別為 Q = 0.305 cms 彎道各斷面中間水柱之無因次水深 方向流速分量u 及v 的模擬結果與實驗值比較圖，圖中縱軸為無因次水深 (z-zb)/d，橫軸之無因次參數分別為比較點流速u及v 除以該水柱水深平均流速之 合向量V total (u2v2 0.5) ；圖 4.15 及圖 4.16 分別為 Q = 0.61 cms 彎道各斷面中 間水柱之無因次水深方向流速分量u 及v 的模擬結果與實驗值比較圖。水深方向 的流速分佈，只有在B0、C0、D0及E0斷面中間提供量測數據，因此只列出這四 個斷面的流速比較圖。由表 4.4、表 4.5 及圖 4.13 至圖 4.16 可看出模擬結果與 實驗值的趨勢吻合、均方根誤差小且能夠適當反應彎道二次流效應側向流速v 在水深方向的分佈。 4.2.2 急彎案例 急彎的驗證採用 Rozovskii (1961)之實驗案例，資料為 Rozovskii (1961)的彎 道實驗1，其實驗水槽佈置，在上游為長 6 m 之直線道，下游為長 3 m 之直線道， 彎道為一蜿蜒 180°固定曲率半徑渠道。渠道斷面為寬度 0.8 m 之矩形斷面，中 心線曲率半徑為0.8 m，渠寬與曲率半徑比值為 1，整個實驗水槽為平床，Chezy 係數為60 m0.5/s，平均流速為 0.265 m/s，平均水深為 0.058 m，福祿數為 0.35， 二次流強度因子SI 為 1.39。上游邊界條件為固定入流量 0.0123 m3/s，下游邊界 條件給定水位資料。側壁為滑移邊界條件，此邊界條件的設定在連和政(1999) “二維水深平均模式應用於彎道水流與泥砂運移模擬之研究＂中指出，如果側 壁邊界條件設為非滑移，其影響會使得內岸的模擬流速結果與實驗值比起來相 對過小，而在外岸則過大，顯然是因為在側壁的邊界處理仍無法適用於急彎的 案例。圖 4.17 為 Rozovskii (1961)彎道實驗水槽示意圖，實驗分別在θ = 0°、65°、 100°、143°及 186°斷面量測數據。本案例模擬採用 61×43 之非均勻計算格網， 如圖 4.18 所示。

圖 4.19 為實驗量測流速分佈圖。圖 4.20 為此急彎案例流速分佈模擬結果， 圖(a)為二維模式模擬結果；圖(b)為擬似三維模式模擬結果。圖 4.21 為無因次水 深平均流速模擬結果與實驗值之比較圖，圖中縱軸與橫軸之無因次參數如圖 4.9 之定義。圖 4.22 為側壁水深比較圖，圖中縱軸為側壁水深，單位為公分，橫軸 之無因次渠長為渠道中心線長度S 除以渠道寬度 B。無因次渠長 0.625 為彎道入 口處，3.767 為彎道出口處。 由圖 4.19 可看出，水流在進入彎道時，內岸的流速會變大，而外岸的流速 則會變小，整個彎道的流速分佈可看出皆為內岸大於外岸，此現象是因為此渠 道之渠寬與曲率半徑比值很大，內岸之路徑又相對較短，自由渦流的效應則較 為明顯。水流在出彎道進入直線道後，內岸的流速變小而外岸的流速則變大， 此現象應為出彎道後，水面不會有超高分佈的情況，且仍有水流動量往外岸傳 遞的影響。由圖 4.20 可看出，二個模式模擬結果愈接近彎道出口，流速分佈差 異愈大，從圖 4.21 可更明顯地看出流速在彎道的分佈，模擬結果皆與實驗值之 趨勢相同，其均方根誤差列於表 4.6，整體來看為擬似三維模式之模擬結果較接 近實驗值。由圖 4.22 可很清楚地看出受彎道效應造成水位超高的現象，由表 4.7 之均方根誤差值可看出擬似三維模式之模擬結果誤差較小，內岸水深變化趨勢 與實驗值較為一致。 圖 4.23 及圖 4.24 分別為彎道各斷面中點之無因次水深方向流速分量u 及v 的模擬結果與實驗值比較圖，圖中縱軸為無因次水深 (z-zb)/d，橫軸為無因次流 速如圖 4.13 之定義。圖 4.25 為彎道內 65°、100°及 143°三個斷面側向流速分佈 之模擬結果與實驗值比較圖，圖中縱軸為無因次水深 (z-zb)/d，橫軸為流速v (m/s)。由圖 4.23 及圖 4.24 可看出，模擬急彎時流速分量u、v 之模擬結果與實 驗值吻合，模擬值與實驗值之均方根誤差列於表 4.8。由圖 4.25 可看出模擬結 果的流速梯度在內岸較大、外岸較小，與實驗值相符，然而實驗顯示出在外岸 接近水面處會出現與二次流反向的小渦流如圖 4.26，因本模式之紊流模式採用 簡單的零方程式模式求解，所以無法模擬出此現象。  

4.2.3 連續彎案例

連續彎的驗證採用Almquist and Holley (1985)之實驗渠道，此水槽為一蜿蜒 之定床矩形渠道，渠寬1.652 m，由一長 2.475 m 之直線渠道連接兩個 125°固定 曲率半徑之彎道，渠道中心線曲率為4.953 m，渠寬與曲率半徑比值為 0.33，渠 道坡度0.001，Chezy 係數為 60 m0.5/s，平均流速為 0.48 m/s，福祿數為 0.45，二 次流強度因子SI 為 0.36。上游邊界條件為固定入流量 0.0991 m3/s，下游邊界條 件給定水位資料，側壁為滑移邊界條件。圖 4.27 為 Almquist and Holley (1985) 實驗案例示意圖，實驗分別在1~15 號斷面量測數據，2 號及 8 號斷面分別為第 一個彎道之入口及出口，10 號斷面為第二個彎道入口。本案例模擬採用 101×35 之非均勻計算格網，如圖 4.28 所示。 圖 4.29 為無因次水深平均流速模擬結果與實驗值之比較圖，圖中縱軸為比 較點之水深平均流速u 除以渠道平均流速utotal，橫軸為比較點之座標Y 減去斷面 中點座標YM 後再除以渠道寬度 B(圖皆為往下游看的方向)。圖 4.30~圖 4.32 分 別為5 號、10 號和 13 號斷面水柱無因次主流流速u / utotal的模擬結果與實驗值比 較圖，圖 4.33~圖 4.35 分別為 5 號、10 號和 13 號斷面水柱無因次側向流速v / utotal 的模擬結果與實驗值比較圖，每個斷面從左岸至右岸取五個水柱比較，分別為 (Y-YM)/B=-0.375、-0.125、0、0.125 及 0.375，圖中縱軸為無因次水深，橫軸為 無因次流速。 由圖 4.29 可看出在進入第一個彎道時(2 號斷面)，斷面最大流速發生在左 岸(內岸)，而在第一個彎道出口處(8號斷面)，斷面最大流速值發生在近右岸(外 岸)處，接著進入第二個彎道，在入口處(10 號斷面)斷面最大流速在右岸(內 岸)，而在 15 號斷面處流速趨近平均分佈。整體模擬結果可看出擬似三維模式 與實驗值趨勢較為符合，特別是在彎道反曲處(5號斷面~13號斷面)，即最大流 速發生處由左岸轉換為右岸的過程，二維模式並無法適當模擬出這幾個斷面的 流速分布，由6號到10號斷面可以很明顯看出模擬結果與實驗值趨勢的不同， 例如在接近第一個彎道出口時，流速最大值已從內岸轉為外岸，而二維模式的 模擬結果顯式，流速最大值仍是在內岸，使得模擬趨勢和實驗值完全相反。模