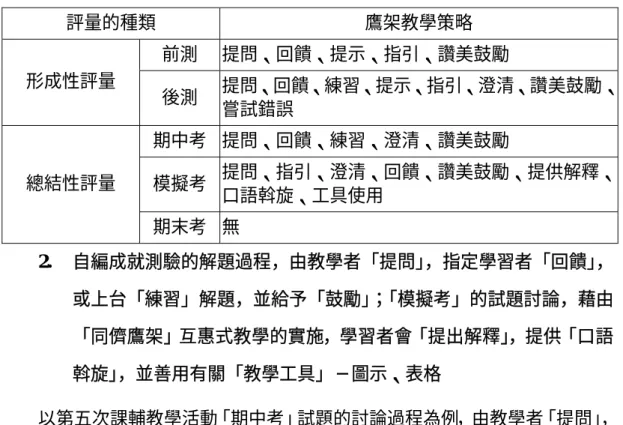
第二節 概念理解歷程的分析與討論
「理解」係對於事物意義的領悟、認識過程或結果的過程(陳碧祥,1998) , 郭為藩(2003)主張,學習的過程不是將知識由外直接灌注到學習的的腦海中,
而是必須經過個體的「思考」 、 「反芻」作用,才得以達到概念理解的程度。本 節為分析《統計學》課後輔導教學活動中,成人學習者在先備條件、語義組織、
思維路徑與概念形成的學習與理解情況,與「鷹架教學」策略應用的情形。
壹•概念理解歷程分析
一、學習者「先備條件」的分析與應用
「先備條件」是指學習者必須具備與所學知識相關的知識。T01 與 T03 都 認為: 「 《統計學》 『先備條件』應該是具備一般國中、高中數學的基本概念就可 以了,如果忘記,學習者應該自行尋找資源,不論是找參考書或是請教其他同 學」 【interview-920528-T01,p.1;17】 【interview-930116-T03,p.3】 。T02 也 主張,成人教育不能像國中、高中講的很詳細,應該是說讓她們自己去找資料,
之後的問題我們用「提示」的。教學者的立場一致,學習者應該要有一般國中、
高中數學的基本觀念,如果忘記,自己應該主動尋求資源,補足《統計學》概 念「先備條件」的不足。
雖說成人學習者應主動尋找學習資源,主動補足自己缺漏的數學基本觀 念,但成人學習者因為多重社會角色的扮演,要實際回到國中、高中的數理學 習資源有限,時間上也不允許,參與課輔教學活動的成人學習者只能藉由「教 科書」或「教學節目」等資源,加強課前預習與課後複習, 「勤能補拙」係少數 成人學習者(S10)突破學習障礙的方法之一【學習者「先備條件」訪談意見參 閱附錄十二,表 12-1】。
此外, 「先備條件」的檢視本身就是一件很困難的工作,教學者在第一階段
四次課輔教學活動中,並未實施「先備條件」的檢視,一方面由於成人學習者
會對質疑其條件的問題感到恐懼,在教與學雙方尚未熟識,學習者尚未培養對
「統計」的興趣前,任何形式的檢視都可能增加學習者負擔;再方面,由於教 學進度應配合空大期中考試成就測驗的評量,以符合學習者參與課輔教學的目 的。本研究既以瞭解學習者「先備條件」的情況,初始即以成人學習者為考量,
減少「先備條件」的檢視,以降低學習過程的焦慮或不安。以下就教學者在《統 計學》概念理解歷程中, 「先備條件」檢視的教學情境、鷹架教學策略的應用與 教學實施成效,列舉分析說明如下:
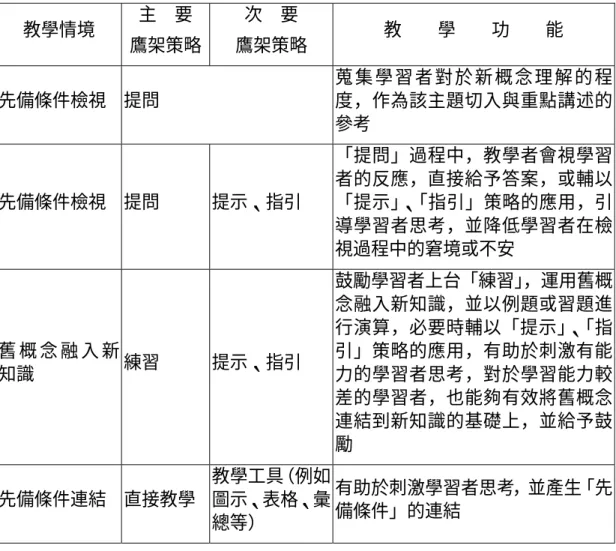
(一) 學習者「先備條件」的檢視與鷹架教學策略的應用
為了解學習者的「先備條件」 ,主要是以「教學者鷹架」為主,逐漸轉移至
「同儕鷹架」 ,其具體策略包括「提問」 、 「提示」 、 「指引」 、 「練習」 ,及輔以「教 學工具」的「直接教學」 ,重點如下:
1. 教學者希望藉由「提問」 ,蒐集學習者對於新概念理解的程度,作為該 主題切入與重點講述的參考
教學者會在每一次的教學活動,實施新主題教學前或教學時,給予學習者 先備知識與條件的測試,測試的方式大多以「提問」及考古題隨堂考試為主。
以 「 樣 本 的 不 偏 與 最 小 變 異 」( 第 七 章 ) 先 備 條 件 的 檢 視 工 作 為 例
【Class-920423,pp.6-7】 ,前測時機是在新概念講解之前實施,教學者希望藉由「提 問」,蒐集學習者對於新概念理解的程度,作為該章主題切入與重點講述的參 考。由於這個主題在「抽樣分配」與往後「估計檢定」有它的重要性,屬於基 礎觀念,同時它與前面「機率」 、 「常態分配」等的學習脈絡息息相關,算是「承 先啟後」的關鍵,教學者檢視的目的在於瞭解學習者對於「抽樣分配」的理解 程度。
鷹架教學 情境
鷹架教學 策略之應用
鷹架教學 實施成效 T02:…有幾個問題還沒教之前,我想
聽你們的瞭解,就你現在的觀念不 管是對或錯,甚麼叫樣本的不偏 性?甚麼叫最小的變異性?…有標 準答案,但是沒有一定的說法…
S06:我覺得樣本的不偏性應該是這 樣,跟眾數的概念一樣,出現最多 的觀察值範圍之內,應該是最不會
提問
指引
學習者回饋
開放性問題,降低學習者 疑慮
S06 以既有的舊觀念(常識
性概念)回應
偏的,
T02:你的不偏就是集中在那邊?
S06:對對對,就跟眾數一樣,
T02:那甚麼叫做最小變異性?最小變 異性就是…彼此之間的差距越小越 好,…就是我們標準差的觀念,標 準差越大是不是整個就不準了?所 以越小越好,那你覺得呢?
S06:標準差的變異?
T02:變異數其實就是標準差,…變異 性就變異性,為甚麼最小?為甚麼 不是最大?不是很清楚是不是?有 沒有人?
S11:就是估計值越接近母體的標準 差,…差異到越小,扣掉裡面的他 最接近的就是標準差,那不偏性就 是說出來的母體跟他原來的母體概 念是一樣的。
T02:對對對,這(位)同學已經講 的很接近標準答案了,非常接近 了。
澄清 提問 提示
學習者回饋 指引
提問 S11 回饋
鼓勵與讚美
T02 協助以圖形解釋
提示、指引標準差「由上 而下」的觀念,引導學習 者思考
S06 顯然無法將舊觀念聯 結,教學者再度指引,刺 激學習者思考,再提問 S11 未看書,直接講出自己 的概念,表現始終就是代 表有預習過,具有一定程 度的先備條件
【Class-920423,pp.6-7】
2. 課前預習可以建立學習者一定程度的「先備條件」,「提問」過程中,
教學者會視學習者的反應,直接給予答案,或輔以「提示」、 「指引」
策略的應用,引導學習者思考,並降低學習者在檢視過程中的窘境或 不安
課前預習在《統計學》科目「先備條件」檢視的過程中具有重要意義,沒 有預習,加上沒有足夠的先備基礎,學習者要憑一般的「常識」概念回答,很 難切中問題的核心;「先備條件」檢視的初始過程中,當學習者無法回應時,
T02 會立刻給予答案,他在課後回憶說: 「一方面是礙於時間的關係,一方面是 他 真 的 不 會 、 又 緊 張 , 如 果 你 一 直 「 指 引 」 的 話 , 他 還 是 … 想 不 出 來 」
【interview-920423-T02】 。過程中「盡可能」不讓學習者產生負面的感覺。
從上述「樣本的不偏與最小變異」的教學情境來看,成人學習者(S06)對 於「提問」會緊張、會手足無措,特別是題目與生活事例或經驗無關,S06 在
母體
x
µ 最小變異數
T(x)前面六章概念並未完全熟悉,第七章又未預習的情形下, 「勉強」以既有常識性 的概念回應,雖經 T02 以「圖示」提示或指引,試圖引導學習者思考,但 S06 仍無法將已教過之「標準差」概念連結起來。課後 S06 在訪談時表示: 「我怕我 答不出來,因為前面那個變異數跟不偏性,我有一點點印象,覺得比較學術,
那整個我是在模糊當中,我怕我講的不好」 【interview-920423-S06,p.1】 。S11 的回應係根據教科書而來,課前預習可以建立學習者一定程度的「先備條件」。
當學習者熟悉教室情境後,教學者會在「提問」後,輔以「提示」 、 「指引」
策略的應用,引導學習者思考,並降低或化解學習者在「提問」過程中的尷尬 或不適應。
3. 鼓勵學習者上台「練習」 ,運用舊概念融入新知識,並以例題或習題進 行演算,必要時輔以「提示」、 「指引」策略的應用,有助於刺激有能 力的學習者思考,對於學習能力較差的學習者,也能夠有效將舊概念 連結到新知識的基礎上,並給予鼓勵
在將舊概念連結到新知識的「先備條件」檢視過程中,教學者採取「直接 教學」與「示範」策略的應用,並無法刺激學習者思考,對於「先備條件」不 足的學習者,只能被動的接受資訊,不斷的抄寫筆記;對於有基礎或認真的學 習者,則會選擇性的接收資訊,抄寫她們認為重要的內容。若教學者能夠鼓勵 學習者上台「練習」【Class-920507,pp.10-11】,運用舊概念融入新知識,並以例 題或習題進行演算,必要時輔以「提示」 、 「指引」策略的應用,雖然教學進度 緩慢,卻有助於刺激有能力的學習者思考,對於學習能力稍差的學習者,也能 夠有效將舊概念連結到新知識的基礎上【Class-920402,p.2】【Class-920507,p.16】
【Class-920514,p.25】。教學過程中,對於成人學習者的「讚美與鼓勵」是不可 少的,它不但有刺激學習的動力,並且能夠加強學習者進步的原動力。
4. 「直接教學」若能輔以教學工具(例如圖示、表格、彙總等)的使用,
有助於刺激學習者思考,並產生「先備條件」的連結
教學者在講解抽樣分配的性質,試圖回顧「離散隨機變數」二項分配、指
數分配、 Poisson 等期望值與標準差的公式,以期解釋「樣本的不偏與最小變異」
基礎上,但部分學習者(S01、S04)「先備條件」不足,專心抄錄筆記;有一些 基礎的學習者(S10、S11、S13),則能夠理解教學者說明的意義,也顯示出學 習者投入程度的不同,影響「先備條件」的差異。
鷹架教學 情境
鷹架教學 策略之應用
鷹架教學 實施成效 T02:我們那時候不是有看到好幾個
分配,…不是有請各未將各個分 配的 E(a)值要去背起來,它的 Variance 好像也是…有請你們
背,有 Poisson 是不是有請你們
背,那這個也是從這裡來的…
直接教學 S01、S04、S12 專心抄筆 記,S10、S11 與 S13 時而 點頭、時而抄錄教學內容
【Class-920430,p.8】
然而,在「直接教學」策略中,若輔以圖示方式,說明點估與區間估計的 差別,複習教科書表 8.1 臨界值正負三個標準差的概念,這種工具的使用有助 於刺激學習者思考統計的「先備條件」 。
鷹架教學 情境
鷹架教學 策略之應用
鷹架教學 實施成效 T02:…其實你去想也知道嘛,…其實
就是 x 加減一個東西嘛,…一定跟標準 差有關係,對不對?…我們以前 是 不是學過,在三個標準差之內的 機 率就佔了 99%,…對不對?就是這個意 思。
直接教學 圖 示 ( 工 具 使 用)
刺激學習者思考
【Class-920514,p.12】
針對「抽樣分配」、 「估計檢定」的相關概念,由於概念間環環相扣,為了 讓學習者能夠前後連貫,由舊概念連結到新知識,課輔教學活動使用較多的方 式仍以「由上而下」進行,教學者會「適時」地以舊概念應用到新概念的觀念 基礎上,例如教學者彙總: 「一個好的估計數是不偏,而且是最小變異,就是一 個好的估計」 【Class-920507,p.21】 。
(二) 鷹架教學策略實施成效
1. 六位學習者參與的動機不同,但是課輔初始具備的「先備條件」卻是 有限的,隨著努力程度的不同,逐漸產生個別差異
第一次上課,教學者即以自我介紹的方式,瞭解學習者參與或修習《統計
2
zα
−
2
zα 2
α
2
1-α α
學》課程的目的,S01 與 S04 都希望修得學分,雖然 S04 對數字很有興趣(喜 歡錢) ,但是對於數理卻很畏懼;S10 對於研讀「統計」缺乏自信,對教學者會 有頗高的期望【Class-920326,pp.15-17】;S11 有自身的規劃,希望多接觸、多吸 收、多改變,因此也就更加要求自己【interview-920402】;S12 是六位學習者中 唯一曾經修過《統計學》課程的學習者(八十七學年度下學期) ,但是挫敗的學 習經驗,使她下定決心再一次接受挑戰【interview-920605,p.6】 ;S13 則是在自行 研習過程中發現困難,必須尋求外力資源解決,而主動參與課輔教學活動
【email-920402】 。六位學習者參與的動機不同,但是在「先備條件」的基礎上,
卻可能不足,她們選擇參與課後輔導教學的目的就在於透過老師的講解,讓「統 計」的概念能夠更清楚、更了解,有不懂的地方也可以有人發問。
彙總成人學習者在《統計學》課程先備條件的多寡【學習者「先備條件」
訪談意見參閱附錄十二,表 12-1】 。少部分的學習者(S01、S08)曾經修過《統 計學》相關課程,但都是很久很久以前的事,或是學習過程中遭遇障礙,到現 在老早就「忘光了」 ,S08 提到:「第一次老師叫我們講的時候,…其實我都忘 了 , … 我 也 忘 記 以 前 是 怎 麼 修 過 的 , 我 真 的 忘 的 很 徹 底 」
【interview-920514,p.2】 。大部分學習者「基礎程度」相當(都沒有學過) , 但是努力程度確有相當大的差別。S10、S11 不但課前預習、課後也複習,收穫 比 較 多 , S10 認 為 :「 我 有 ( 事 先 ) 看 , 這 樣 的 話 比 較 會 有 感 覺 」
【Interview-920521,p.1】。S11 同意 S10 的看法:「…像我上次就沒有看,就很吃 力 , … 幾 乎 都 要事 先看 , 它 根 本 不 等你 ,( 上 課 ) 會 就 會、 不會 就 不 會 」
【Interview-920507,p.2】 。S12、S13 都肯定預習的重要性,「 (看過之後)就 知道老師要上的東西是什麼啊!(在平時預習和複習)我覺得幫助很大」
【Interview-920605-S12,p.1;p.3】 。 「事前備課,在討論的時候或是聽課的時 候,有充分地投入,這樣的收穫當然會加倍的獲得」 【Interview-920528,p.1;p.3】。
S04 是 心 有 餘 力 不 足 , 基 礎 不 夠 穩 固 , 越 到 後 面 的 概 念 越 無 法 消 化
【Interview-920514-S04,p.1】【Interview-920521,pp.2-3】;至於 S01,或許學習動機
不是十分強烈,或是工作忙碌,不但沒有預習,就連課後的複習也往往力不從
心【Interview-920514,p.2】。
2. 教學者會視學習者個人投入的程度, 「適度」的檢視先備條件的多寡,
課前預習與課後複習有助於「統計」觀念基礎的建立,增進進階概念 的理解
第五章離散隨機變數、第六章連續隨機變數開始就有許多公式、定理與演 算步驟的出現,也就是 T01 所稱的「模型」 ;到了第二階段進入真正的統計,學 習者的用功與投入程度就會有明顯的差異,有事前預習或課後複習的同學,他
(她)們會自己捕捉先前教過的觀念、定理或基礎公式,沒有時間投入的學習 者,在教學活動的表現就會比較「木訥」 ,顯示出「先備條件」的不足,無法跟 上進度。也因此,T02 會在第二階段的課輔教學活動,由於學習者「先備條件」
不一,教學者會視學習者個人課前預習與課後複習的程度,適度的「提問」學 習者「先備條件」的多寡,或試圖連結舊觀念到新的知識基礎上。
由於「統計」概念環環相扣,課前預習與課後的複習也可以考量出學習者 下一個觀念先備條件的多寡。習題 7.2 的「提問」時機是在定義、定理(或公 式)講解完畢後進行【Class-920507,pp.2-3】 ,希望學習者能夠「回顧」前一週講 述的公式,學習者依複習與否產生不同的反應,S10、S11、S12 與 S13 有複習 的習慣,也因此能夠「跟隨」教學者的思路,了解 T02 的解題情況;S01、S04 不停的抄寫白板上有關習題 7.2 的解題步驟,根本無暇思考或回顧相關的公式,
更無法顧及理解的過程。
3. 「同儕鷹架」互惠式教學的進行, 「先備條件」已成為課輔教學活動實 施前的必要步驟
第三階段起以「同儕鷹架」互惠式教學進行課輔教學活動,學習者必須課 前預習與課後複習, 「先備條件」已成為課輔教學活動實施前的必要步驟,部分 成人學習者因為無法承受「自學」的壓力,或是自行尋找學習資源,選擇中輟
( 詳 如 第 三 章 第 二 節 說 明 )。《 統 計 學 》 其 實 你 前 面 不 懂 就 真 的 不 懂
【interview-920521-S11,p.2】 ,課前的預習會使整個教學活動的實施會比較「有感 覺」【interview-920521-S10,p.1】,學習者能夠將過去學到的東西做一個充分的連 結【interview-920528-S13,p.3】 ,幫助會很大【interview-920605-S12,p.3】 。S04 認為:
「…要充分準備才能夠上台」 【interview-920521,pp.2-3】。
二、學習者「語義組織」的分析與應用
《統計學》課後輔導教學進行過程中,T01 就一直強調: 「學習統計,我感 覺還是語文問題,你別說我們都是用中文,其實我們都不懂題意…」
【interview-920528,p.3】 。初始,很難體會這句話的意涵,經過幾次的課輔教 學活動,從教科書上的定義、定理,或是例題、習題的文字敘述,觀察教室師 生的互動,教學者與學習者「常常」在題意的解釋與理解上,遭遇到挫折, 「耗 費」了相當長的時間進行理解。
學習者的課後訪談中,幾乎是所有學習者(S04、S10、S11、S13)在《統 計學》課輔教學的學習歷程中,都會有有關「語義」的困擾,在分析題意時,
不了解題目的意思,甚至誤會了題目的真正意涵,不但浪費了寶貴的教學時間,
在 教 學 效 果 上 也 打 了 相 當 大 的 折 扣 【 Email-920409-S04,p.2 ; Interview-920528-S10,p.3;Interview-920528-S11,p.5;Interview-920409-S13,pp.1-2】
【學習者「語義組織」訪談意見請參閱附錄十二,表 12-2】。
教學者在第十次課輔中所強調題意理解的重要性:「…前面你觀念都懂的 話,後面只是小變化,…大部分問題出在你題目看不懂…應用問題是在你要看 得懂題目,不是難在你要如何計算」 【Class-920528,p.22】 。可見「語義組織」
在解題過程中所扮演的角色。
從以上教學者與學習者對「統計」文字的敘述或題目的意義所產生的困 擾,幾乎出現在每一次的課後輔助教學活動中,包括對定義文字敘述的冗長,
無法掌握文句脈絡的精髓,並以自己的語言加以表達;或是對於教科書例題或 習題的文字敘述,無法分辨條件關係,甚或誤解題意,形成錯誤的解題過程。
以下就教學者在《統計學》概念理解歷程中,「語義組織」解析的教學情境、
鷹架策略的應用與教學實施成效,列舉分析說明如下:
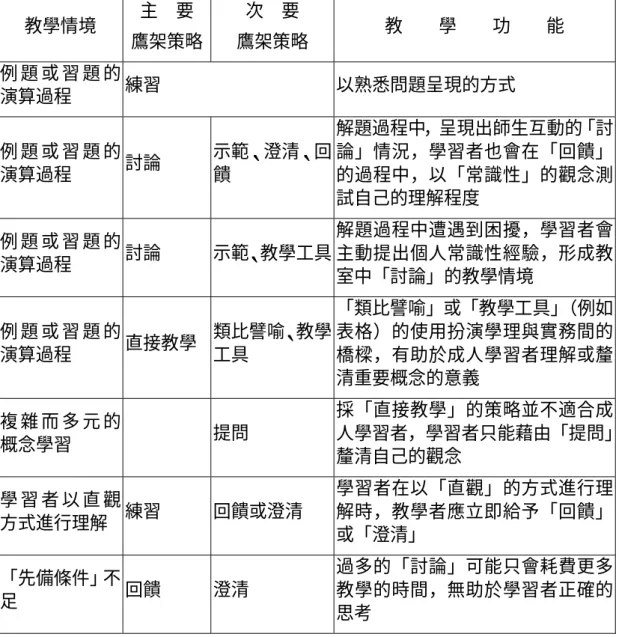
(一)學習者「語義組織」解析與鷹架教學策略的應用
為使學習者了解「統計」的「語義組織」 ,教學過程中,主要以「教學者
鷹架」為主,另以「同儕鷹架」策略為輔,其具體策略包括輔以「示範」 、 「澄
清」 、 「回饋」與「教學工具使用」的「討論」策略,及分享「類比或譬喻」的
「直接教學」 ,教學者建議加強「練習」 ,以熟悉「統計」問題的呈現方式等。
1. 例題或習題的演算過程,首重問題的轉譯,陳述句間的連接詞會造成 問題轉譯過程中的混淆概念,多做題目─「練習」 ,以熟悉問題呈現的 形式
首先以「關係語句」加以說明,中文字有許多連接詞,當兩個以上的字詞 藉由連接詞串接在一起就產生新的意義,常常造成語意理解上的混淆。以第四 章「機率」教學條件機率補充教材範例七為例: 「 『女生且修會計』與『我隨便 找出一個是女生,可是我發現她修會計』的機率,一個是交集,一個是條件機 率,這兩者的意義是不一樣的」 【Class-920402-T02,P.18】。從題目本身來看,都 是「女生」 、 「會計」 ,但是脈絡的前後意義卻不相同,前者係「交集」的概念,
後者則是「條件機率」的觀念,由於學習者對於機率中加法原理、乘法原理的 基本概念還不是十分清楚,題意上所顯示的脈絡意義在區辨上就產生困擾: 「老 師,你是不是再講解一下,為什麼女生修會計的機率是會計又是女生的機 率?…那如果說相反過來的話修會計的女生…」 【Class-920402-S13,P.18】 。 邁阿密商學院院長蒐集了有關該學院大學生的資訊如下:
性別 會計 財政 行銷 管理 合計
男生 170 120 160 150 600 女生 110 100 70 120 400 合計 280 220 230 270 1000
問題
假設隨機選出一學生,該名學生是女生且主修會計學的機率是多少?
已知該學生是女生,她主修會計學的機率是多少?
重述問題已知條件 重述問題解題目標 男女生人數及學生總數
男女生修會計、財政、行銷、管理之人 數
女生且主修會計學的機率是多少?
已知該學生是女生,她主修會計學的 機率是多少?
【Class-920402 補充教材】
《統計學》例題或習題的演算過程,首重問題的轉譯,學習者(或教學者)
應從冗長的文字敘述中,重述問題的已知條件,再列出解題目標,針對字裡行 間關係語詞、前後意義的影響,必須要有清楚的概念,教學者建議多做題目,
熟悉問題呈現的形式,有助於問題轉譯過程中,對題意的理解,T02 以自身經 驗,建議學習者看到題目後,先傻住、再沉澱,以「思考」題意間的脈絡關係
【Class-920430-T02,p.16】。
2. 解題過程中,呈現出師生「討論」互動的情況,教學者首先在「示範」
的過程中, 「釐清」一些觀念,學習者也會在「回饋」的過程中,以「常 識性」的觀念測試自己的理解程度
解題過程中,呈現出師生「討論」互動的情況,教學者首先在「示範」的 過程中, 「釐清」一些觀念,學習者也會在「回饋」的過程中,以「常識性」的 觀念測試自己的理解程度(S04、S13) ,然而關係語句的前後脈絡不同,意義的 產生也會不同,包括教學者也無法給予立即而正確的回應。
鷹架教學 情境
鷹架教學 策略之應用
鷹架教學 實施成效 T02:你隨便抽出一個人她是女生…你
又發覺她是修會計,這跟她是女生 且她修會計是不一樣的道理喔!…
P (會計|女生),…我隨便找出一個 是女生可是我發現她修會計機率,
這意思我不知道你能不能把它釐 清,一個是交集,一個是條件機率 喔!…是在抽出的人當中是女生,
她修很多科目,我現在又要知道她 修會計的機率…
S04:所以這種情況下它的比例會比較 小…
T02:…你是說它的比例還是它的機 率…
S04:就是說這個比 0.1 小…
S13:老師你是不是再講解一下,為什 麼女生修會計的機率是會計又是女 生的機率?…那如果說相反過來的 話修會計的女生…
示範
S04 回饋
澄清
學習者提問
T02「示範」補充教材範 例七,教學者試圖區辨交 集與條件機率的概念,由 於題意乍聽之下條件相 似,學習者對於前後脈絡 的意義無法區辨
學習者「常識性」的「回 饋」,顯然不是十分理解 題意關係語句的脈絡
學 習 者 反 向 思 考 「 提
問」,教學者思考,顯然
無法立即抓住題意的文
辭脈絡與關係語句
T02:修會計,在修會計當中是女生…
(思考中)
S13:是女生。
T02:那就要轉過來,變成這邊是會 計,這邊是女生,等於說我從所 有女生當中…
T02 回饋 討論
思考也會混淆,在語義上 的繞來繞去,愈轉愈亂 學習者主動協助介入討 論
【Class-920402,PP.18-19】
3. 教學者配合「教學工具」的使用(表格),重述問題已知條件,並列明 解題目標;教學者「示範」解題過程中遭遇到困擾,學習者會主動提出 個人常識性經驗,形成教室中「討論」的教學情境
學習者(S11)超越教學進度,提出對於「貝氏定理」習題解題過程的疑問,
在缺乏事前準備的情況下,教學者會以唸題目、分析題意的初始解題步驟著手,
以「示範」的策略瞭解問題的已知條件與解題目標。T02 的解釋是: 「應用問題 題目就是太長了,看到後面,前面又忘記內容是什麼,…其實應用問題它講到 的比較不會難,只是你要去分析就比較麻煩,而且有些敘述性的東西,…它要 解釋老半天…」 【Class-920402,p.21】 。因此,重述問題的已知條件與解題目標 有其必要性。
問題
習題 4.28:已知某大學應屆畢業生有意願考研究所的比率是 0.2,且知應屆畢業 生男女人數的比是 4:6,而應屆畢業之女學生當中,又有意願考研究所的比 率是 0.15。今從該大學應屆畢業生隨機抽出一人,問該學生是男生且有意願 考研究所的機率是多少? 【資料來源:蘇國樑,2003a,p.115】
重述問題已知條件 重述問題解題目標 1. 有意願考研究所 0.2
2. 男女 4:6
3. 女生,有意願 0.15
男生,有意願考研究所的機率?
教學者認為以「自言自語」的方式唸題目、分析題意,有助於個人思考,
並期望以「放聲思考」的方式,希望學習者理解「思維路徑」
【interview-920409,p.5;interview-920423,p.1】 ;教學者再以「樹狀圖」 (圖示工具
使用)解釋「貝氏定理」的基本意涵,以期釐清題意,但是受到問題關係語句
的影響, 「已知…有意願,且知…,又有意願…」 ,使得問題的前後脈絡、意義 始終無法以「樹狀圖」合理呈現。
實施的結果,學習者似乎無法「體會」 ,反而會對於教學者的「自我中心語 言」 ,主動提供協助,根據自己的理解與常識性經驗,提出對於解題過程的意見,
形成教室中由教學者「示範」到師生、同儕「討論」的教學情境。
鷹架教學 情境
鷹架教學 策略之應用
鷹架教學 實施成效 S11:老師,我覺得這一題它的條件已經有給了
一個應屆畢業生女學生當中,這個就是條件 機率…
T02:…其實它已經給了我們一個條件機率,所 以這不一定是貝氏定理,…在男生中且有意 願考研究所的機率,它抽出的男生而且有考 研究所,其實跟貝氏感覺上,有點像條件機 率,比較不像貝氏,…
S04:它說有意願考的是那個部分… (學生討論 中)
T02:是考跟不考。
S04:0.85 跟 0.15。
T02:好,那我們來看這樣的思考對不對,在考 的裡面而且是女生要考的,所以有點是而且 的意思,它現在的題目好像是有點反過 來,…換句話說,這個 0.15 就是整個事 件,…可是題目不是這樣,題目是女生要 考,剛好跟它顛倒過來。
S04:這是男生然後要考。
T02:…我只知道男生跟女生的比例是 4 比 6,
換句話說,在考的不考的當中是 4 比 6,…
男生而且要考的,0.2。是不是剛好就是…
S(?) :0.03。
T02:跟我們的是不是一樣,我考試跟男女是彼 此獨立。
T02:對不對,所以其實題目很簡單,也不必用 貝氏,也不需要用條件機率,就是要畫圖而 已,…來注意看,…應該是這樣處理才對,
這裡沒用到應屆畢業之女生當中有意願考 研究所之比例是 0.15,…那我現在反觀,
提供解釋
回饋
「 自 我 中 心 語言」
討論
回饋
自 我 中 心 語 言
回饋
討論
澄清
工具使用
示範
S11 由題意中引出 另一種思維
T02 在「貝氏定理」
不 得 其 解 的 情 況 下,以「條件機率」
思考,嘗試透過題 意,找出所有關鍵 詞和關係式,並與 學 習 者 一 再 「 推 敲」 ,教室呈現師生
「討論」的情境,
學習者會就自己的 理解提出「回饋」 , 雙方共同思考解題 的過程
學習者亦被帶入教 學 者 解 題 的 思 維 中,教學者「自言 自語」 ,再度遭遇瓶 頸, 「有點是而且的 意思」T02 另起爐 灶,重新思考,但 還是停留在語義上 推敲
有點興奮,演算結
果還是不對
T02 試圖以圖示協
助解題,但仍不得
男生應該我先前畫的是對的,…(停頓,思 考許久)我看這個好了,我們下次來解這個 問題,我們回去想一下,因為現在臨時也浪 費大家太多時間。
停頓
其門而入,決定暫 時放棄,留待下週 分解
【Class-920402,pp.24-26】
4. 當「直接教學」無法使學習者理解時,輔以「類比譬喻」或「教學工 具」的使用,扮演學理與實務間的橋樑,有助於成人學習者理解或釐 清重要概念的意義
定義 4.8 與定義 4.9 的教學過程中,T02 以自己的邏輯思維,藉由投影片「直 接教學」 ,由於並未依照教科書內容順序,學習者十分認真的抄錄投影片內容或 講述內容,由於涉及到兩個關鍵性的概念,教學者會對學習者的「提問」給予 適時、適切的「澄清」 ,並運用「類比」分享方式連結生活事例,由於學習者中 文字義認知理解上的差距,對於生活事例的連結仍舊無法產生具體的思維意 義,學習者的不解,主要在字義的混淆,與前後脈絡文句的意義上,許多數學 符號,即使配合圖示,沒有空間概念也不易進入相關教學情境。
鷹架教學 情境
鷹架教學 策略之應用
鷹架教學 實施成效 T02:…互斥跟獨立不一樣喔,常有人
會搞在一起,…連大學生都搞不 清楚。我跟他不相關應該就是獨 立嘛,可是不一定喔,互斥不代 表獨立,因為互斥代表我做了這 件事,就代表你一定不會來做這 件事,獨立的話是你做你的我做 我的,所以互斥跟獨立不一樣。
S10:老師你剛才講獨立跟互斥,那有 沒有說獨立並不一定互斥,但是 互斥他一定獨立對不對?
T02:不一定喔。…反而互斥是有相 關的,獨立是不相關的,因為互 斥是我做的這件事我就保證你 不會來做,可是獨立是我今天來 到這裡,我不保證你一定不會 來,因為你是自由的個體,行為 跟我是沒有關係的,那互斥是我 來,我就保證你不會來,因為你
直接教學
S10 提問
T02 澄清
直接教學
以生活事例類比互斥與獨 立的意義
S10 會以個人的先備條件 思考,對於互斥與獨立之 間的關係試圖提出個人理 解
教學者澄清,但仍陷入字
義的口頭比較上,亦即教
學者完全從學理的角度解
釋,忽略統計的特殊性
跟我是死對頭,所以是不一樣 的。反而獨立是比較自由的,互 斥比較狹隘。…
【Class-920402,pp.8-11】
從定義 4.8 與定義 4.9 的教學過程,在關鍵概念的解釋比較上,以「直接教 學」的方式並無法使學習者很快進入理解的狀態。S10:「老師,你剛才講獨立 跟 互 斥 , 那 有 沒 有 說 獨 立 並 不 一 定 互 斥 , 但 是 互 斥 他 一 定 獨 立 對 不 對 」
【Class-920402,p.8】?學習者希望就兩者的相關性進行思考,然而,數理的 專業知識與一般常識性的觀念還是有落差,教學者在缺乏圖示與表列的情況 下,可能容易造成學習者觀念的混淆與困擾。若能輔以表格說明,有助於學習 者自行比較「互斥」 、 「獨立」在概念意義上的區別, 「教學工具使用」有其重要 性。
互斥 獨立
教科書
若兩個事件 A 與 B 之間沒有交集
─A∩B 內沒有任何簡單事件─
稱事件 A 與事件 B 互斥,記作 A
∩B=φ
若假設事件 B 發生與否並不會影響 事件 A 發生的機率,則稱事件 A 與 事件 B 相互獨立 P (A│B)= P (A)
教學者
互斥是有相關的,我做的這件事 我就保證你不會來做,我來,我 就保證你不會來,因為你跟我是 死對頭,互斥比較狹隘。
互斥就是不可能,A 發生 B 就不 會發生,B 發生 A 就不會發生,
所以他們的交集是 0,數學叫做 空集合,這是一個例子。
獨立是不相關的,我今天來到這裡,
我不保證你一定不會來,因為你是自 由的個體,行為跟我是沒有關係的,
獨立是比較自由的。
…獨立在統計跟數學的定義就是…
A和B的交集,他的機率會等於A的 機率乘以B的機率,就是獨立。
【Class-920402,pp.8-11】
資料來源:出自蘇國樑(2003a,pp.104-106)
5. 複雜而多元的概念學習,採「直接教學」的策略並不適合成人學習者,
學習者只能藉由「提問」釐清自己的觀念
T02 以「直接教學」的方式說明教科書表 8.2,由於表格的繪製與教科書顛
倒,導致學習者的思維脈絡與教學者無法重疊,因此,以「直接教學」講述相
關概念時,應該以學習者能夠參考(如教科書)或理解的脈絡為主;其次,學
習者會以「直觀」的方式解釋包括虛無、對立,真、不真,拒絕、接受等個別 的涵義,但是四個象限彼此間的關係,卻無法以統計的特殊字義相連結,學習 者只能藉由「提問」釐清自己的觀念,教學者在無法針對型I與型II誤差提出更 合理化的解釋時,T02 試圖再以「直接教學」的策略,就「檢定力」的概念活 化 對 「 型 I 與 型 II 誤 差 」 的 解 釋 , 學 習 者 更 是 將 所 有 概 念 混 淆
【Class-920521,pp.30-31】 ,S11 對於教科書有關「型II誤差計算」的解說反應是:
「我不懂啦!中間看不懂」【Class-920521,p.15】。S04 也認為有看沒有懂
【Class-920521,p.15】。因此,複雜而多元的概念教學,如教科書§8.4「型II誤差 的計算」 ,課本描述冗長,未加標題條列,學習者對於文字與脈絡的理解感到挫 折。
6. 《統計學》觀念有其特殊性,學習者在以「直觀」的方式進行理解時,
教學者應立即給予「回饋」或「澄清」
成人學習者會以「直觀」的方式解題【Class-920402,pp.8-11】,係由於經驗 使然,但是「統計」的概念並不會如此單純,題目背後隱含的意義才是學習者 需要掌握的要點,也才能理解「統計」思維的意義。因此,教學者面對學習者 以「直觀」的方式解釋題目,會是一個正常現象,但應適時給予「回饋」 ,並輔 以正確的解題觀念,理解題目的前後脈絡,才有助於題目或文字敘述「語義組 織」的理解。
型I誤差與型II誤差概念的理解十分重要,屬於估計檢定的基礎,教科書表 8.2 是對假設檢定下可能的四個結果提出說明,虛無假設(H
0)與對立假設(H
a) 在決策(樣本實驗的結果)與實際情況的處理情形,當實際情況虛無假設為真,
樣本實驗結果卻接受對立假設,則會犯下型I誤差;當實際情況對立假設為真,
樣本實驗結果卻接受虛無假設,則會犯下型II誤差;如果實際情況與決策情況 相符,代表判斷正確。然而歷經三次的課輔教學活動,合計超過三十分鐘的討 論過程中,學習者初始即陷入四個象限脈絡思維的比較,對於虛無與對立假設,
決策與實際情況的語義推論上【Class-920521,pp.30-31】。
假設檢定的決策與結果
決策/實際狀況 H
0為真 H
a為真
H
0為真 決策正確 型II誤差 H
a為真 型I誤差 決策正確
資料來源:出自蘇國樑(2003a,p.262)
在教科書表 8.2 的討論過程中,學習者首先對於「虛無假設」與「對立假 設」的字義就無法分辨,從題意上首先決定「對立假設」 ,再反推「虛無假設」,
但 T02 似乎以先建立「虛無架設」,再定義「對立假設」 ,T01 與 T02 教學上有 明顯的不同;其次,就虛無與對立的字義而言,虛無代表空幻、不存在的東西,
對立相對於虛無,似乎是可以理解的觀念,但教學者並未修正一般學習者以「直 觀」的角度所切入的思考方式,以至於學習者深陷其中、不明其意;教學者未 能在後續解釋的過程中,引述適當的類比觀念,或舉實例說明,導致學習者在 字裡行間百思不得其解;最後,教學者在學習者尚未理解型I與型II誤差時,加 入了「檢定力」的觀念,學習者更對於α與β的互為因果性,觀念混淆。在往 後 T02 還花了相當長的時間〈第十次與第十一次課輔教學〉補述型I誤差與型II 誤差的觀念。S13 認為: 「有些題目看樣子還可以去感覺,但是有些題目有時候 就不知道怎麼去下手」 。因此,她強調(題目)整個架構出來,一定要先理解,
T02 也建議學習者看到題目後要做整理的工作【Class-920528,p.17】 。
7. 當「先備條件」不足時,成人學習者會以「常識性」的概念解釋問題,
教學者應立即給予「澄清」 ,過多的「討論」可能只會耗費更多教學的 時間,無助於學習者正確的思考
當學習者「先備條件」不足,成人學習者常以「常識性」的概念,主動提 出自己的想法或觀念,試圖為題意提出解釋,在意見錯綜複雜的情況下,對「統 計」觀念的解題不但沒有幫助,反而會混淆概念,教學者應適時澄清,過多的
「討論」可能只會耗費更多教學的時間,無助於學習者正確的思考。
「貝氏定理」習題 4.25 的解題過程中,教學者事前備課並未觸及,以至於
在理解題意中,耗費了頗多時間【Class-920409,pp.8-11】。
問題
習題 4.25:某項人體血清檢驗,如其結果為陽性,則其罹病率達 90%,如其結果 為陰性,則其未罹病率達 99%。今有一組人員,其中有 5%曾經罹病,自此群 中任取一人,進行檢驗,顯示結果為陽性,求該人未罹病的機率。
【蘇國樑,2003a,p,115】
重述問題已知條件 重述問題解題目標 1. 陽性中,罹病率 0.9
2. 陰性中,未罹病率 0.99
從曾經罹病的 0.05 中,陽性反應的機率
醫學上通常定義「陽性」反應代表有病的機率較高, 「陰性」反應代表可能 沒病,但是運用到其他學科領域,學習者若對上述的醫學概念「先備條件」認 知不足,會以自己的常識性觀念加以解釋,或以自身對語義的理解加以說明,
因為個人的生長環境、教育程度、職業背景、先備知識的差異,造成學習者「先 備條件」上的落差。
對於第四章習題 4.25,教室教學活動中,教學者與學習者對於陽性反應、
陰性反應、有病、無病、罹病與未罹病等語義觀念的「討論」 ,T02 於課後訪談 時提到:
我不是很清楚它的題意,我一看到這個問題,立刻知道(直觀)是用 貝氏定理,絕對不會錯的,可是它的題意,…所以在思考方面就產生 了問題,…到底是陰性就代表有感染,我覺得它應該說清楚才對,應 該 說 「 檢 定 前 」、「 檢 定 後 」 就 很 清 楚 了 , 主 要 是 題 意 啦
【interview-920409-T02,p.2】!
然而,S13 卻強調: 「成年人經歷各方面,理解力較高,剛開始會傻住不曉 得甚麼東西,再慢慢就會想說學到甚麼東西可以拿出來用」
【Interview-920528-S13,p.5】 。換言之,初始的不適應是正常現象,等到練習、
熟練之後,就能夠適應文字的敘述方式,克服解題的困擾。因此,教學者對於 學習者錯誤的「常識性」概念,應給予適時、適切的「澄清」 ,或者是直接給予 明確的定義: 「…在醫學上,陽性就是得病,這樣跟他說就可以了」
【interview-920528-T01,p.6】 。T01 主張,當學習者他的舊經驗所構成的知 識,跟系統化的知識連接不起來的時候,就直接告訴他答案,不需要拐彎抹角,
浪費教學的時間。
(二) 鷹架教學策略實施成效
1. 教學者與學習者事前的備課,可避免語義推敲過程中,忽略關係語句 的相關屬性,概念、定義的理解,有助於解題活動中分析題意的脈絡 關係
學習者「先備條件」不足,在對「統計」概念還是懵懂無知的情況下,對 於教科書「統計」概念文字的敘述冗長,又無條列式標題,會產生語義組織上 的困擾,學習者無法掌握脈落重點;此外,對於教科書的習題,當語義模糊或 與例題無法對應時,在不求甚解的情況下,學習者就無「思考路徑」可循,造 成解題過程的障礙【Class-920521,pp.30-31】。
因此,無論教學者與學習者,事前的備課都是相當重要的,畢竟在眾人面 前思考題意,與課前預習思考題意,感受到的壓力不同,特別是針對教學者而 言,題意釐清,自然就可以避免解題過程中,關係語句相關屬性的遺漏,或細 目轉變的錯誤【Class-920402,pp.24-26】。
此外, 《統計學》解題活動實施前,學習者對於概念、定義應該要有概括的 認識,瞭解定義、公式使用的條件、時機,以便在分析題意時,找出已知條件 與未知條件,再就解題目標套入相關公式,如果概念、定義不瞭解,解題過程 中, 「套公式」 ,不經思考過程的狀況就會出現,對「統計」概念的理解是沒有 幫助的【Class-920402,pp.8-11】。
2. 《統計學》本來就是一種邏輯思維的程序,解題過程中,由唸題目、
分析題意,鼓勵學習者主動參與,課堂「討論」有助於促進學習者思 考,透過思考以釐清題意
《統計學》應用題,題目冗長,教學者建議學習者將題目唸出來,並鼓勵 學習者以自己的意思進行表達,這種「放聲思考」的方式除了有助於教學者或 有能力同儕,針對學習者錯誤的認知給予糾正的機會,並且使學習者透過思考 的過程,釐清題意。
習題 4.25 或 4.28 解題的過程,雖然「耗」去許多教學時間,影響課輔教學
進度,但是教學者(T02)對於這種「討論」卻持正面肯定的意見:「我是覺得 題目本身…讓大家去做一個討論,最後才把結果呈現出來,老師主要站在旁邊 提 示 … 一 個 方 向 , 讓 學 生 自 己 去 想 , … 大 家 表 現 的 還 不 錯 」
【interview-920402-T02,p.1】 。但是,學習者對於 T02 的專業素養卻產生某種 程度的懷疑-解不出來,T02 在研究者委婉轉述後並不以為意,他認為: 「這應 該是很正常的,這種東西並不是說你完全不會的人來接觸還是不會,它是可以 思考的,它是一個方向而已,就算沒有先前的基礎,還是可以來做分析」
【interview-920409-T02,p.3】 。T02 認為, 「統計」本來就是一種思維的程序,
他鼓勵學習者參與思考的過程,提出自己的意見,在數理課程中,解題解不出 來並不是一件丟臉的事,特別是對教學者而言。
鷹架教學 情境
鷹架教學 策略之應用
鷹架教學 實施成效 T02:…好,我們來思考這個樹形圖,
這樣合不合理,如果其結果為陽 性,則患病率達 90%,跟我知道 他已經生病,他是檢查出陽性,
這 樣 子 有 一 樣 嗎 ? 有 點 倒 過 來,題目告訴你說,他的結果是 陽性,檢查出陽性應該是有病,
可是儀器可能是對是錯,…你以 這個想法來想,他本身病患…去 檢查有病 90%,檢查出沒病有 10%,這樣子有沒有一樣 S13 : 這 樣子 好像 是說 有 病的 人 裡
面,檢查出陽性是這樣…
T02:對啊,好像是不太一樣,所以 我說這個樹狀圖好像有點問題
直接教學
討論
自我中心語言 0.05 病
1 . 0
9 . 0 陰性 陽性
0.95 無病
99 . 0
01 . 0 陰性 陽性
「樹狀」圖示有助釐清題 意
學習者以「常識性」概念 回應協助
教學者仍陷入語義解釋的 渾沌之中
【Class-920409,p.10】
三、「思維路徑」的分析與應用
蘇國樑(2003b)強調:「學習統計的重點在學習統計思維(p.49)。」T02 也認為:「統計思維其實就是思考的一種方法,利用數學的方法把思考的方式 解釋出來而已」 【Class-920402,p.20】 。
然而,成人學習者普遍畏懼數理,對於教學者所謂「思維」無法深刻體會,
S04 表示: 「那種思考的模式我害怕它跑出來,這也是我在學習數理的盲點和困 擾」 【interview-920605,pp.3-4】 。 「思維」一般係由問題所引起,在學習過程 中,當教學者或學習者遇到困難,或發生矛盾時,「思維」就開始進行,隨者 問題的不斷展開,「思維」就不斷深入,當問題解決,思維的活動也就告一段 落。因此, 「思維」的具體過程,實際上就是不斷發現問題、解決問題的過程。
S04 畏懼「問題」 、畏懼「思維」 、畏懼「統計」 ,可見一般【學習者「思維路徑」
訪談意見參見附錄十二,表 12-3】。
在第三次課輔教學活動中,師生對於習題 4.28 有關題意、解題的方式(條 件機率或貝氏定理)有相當長時間的「討論」 ,學習者在下課時提到: 「我們不 懂老師的『思考路徑』」【perspective-920409,p.3】。解題首先就是要了解、
分析題意,進而架構出層次,導入公式、算出答案,因此它重視的是概念的邏 輯、分析與理解的過程,這也就是學習者所提的「思考路徑」 。
空大學生大部分都是二十歲以上、步入社會的成年人,在生理、心理的發 展都已經成熟的情況下,解題過程中,到底老師是怎麼想的?思維可不可能學 的會?思維的路徑有沒有可能藉由師生或同儕的互動趨於一致?學習者甚至 能夠透過「思維」的教導而達到「潛移默化」的效果,這是本研究關心的重要 議題,也是學習過程中發現的有趣現象。以下就教學者在《統計學》概念理解 歷程中, 「思維路徑」引導的教學情境、鷹架教學策略的應用與教學實施成效,
列舉分析說明如下:
(一) 學習者「思維路徑」引導與鷹架教學策略的應用
為了解學習者的「思維路徑」,主要是以「教學者鷹架」為主,其具體策 略包括「示範」 、 「提問」 ,輔以「提示」 、 「指引」策略的應用, 「同儕鷹架」策 略中, 「教學工具的使用」有助於解題步驟的內化與驗證解題目標, 「練習」 、 「澄 清」與「回饋」策略的應用,視學習者理解情況彈性運用。
1. 「示範」解題過程中,將題目分解成部分,將過程分解成階段,配合
圖示「教學工具的使用」 ,以解說意義,有助於學習者將解題的步驟「內
化」成為概念知識
問題
一組大小為 n=10 的隨機樣本來自變異數 σ
2 =4的常態母體。求 x 值,使得 a. ) 0 . 01
4 ( 9
2
≤ x =
P s
b.P( s2≦ X )=0.90
重述問題已知條件 重述問題解題目標 n=10; σ
2 =4a. ) 0 . 01 4
( 9
2
≤ x =
P s
b.P( s2≦ X )=0.90
求 x 值
T02 在例題 7.11 的解題過程中,首先將題目分解成部分,包括重述問題的 已知條件,確認解題的目標;並將過程分解成階段,由唸題目、分析題意,將 數值帶入公式,經過標準化的過程、查表,配合圖示解說意義,一系列解題的 過程,試圖使學習者將解題的步驟「內化」成為概念,經過反覆的練習後成為 知識。
鷹架教學 情境
鷹架教學 策略之應用
鷹架教學 實施成效 T02:…例題 7.11,…它說給你一個樣
本大小 n=10,然後隨機樣本變異數
2 =4
σ 的常態母體要求 x…(思考)
我們來看這一個,相對的,它 s
2是在 之前就已經算出來,是在定理 7.3,他 現在想要求什麼?他要求一個 x 值使 得 ) 0 . 01
4 ( 9
2
≤ x =
P s
它 其 實 裡 面 是 由 normal 去組成的東西,對不對,這個 東西我們是可以算出來的,他經過這 個轉換會變成一個 Chi-square ,這蠻 重要的觀念…
T02:…經過這個轉型後我變成一個 Chi-square 會 大 於 , 一 樣 嘛 , 是 (n-1),3,…這邊是不是跟著變了,
我就可以利用查這個表…
T02:…把 x 做一個移向就可以把 x 找 出 來 , 就 會 等 於 這 一 個
526 . 6 ) 6837 . 14 9)(
(4 =
=
x
, 這 就 是 答
案,就是說這一個位置…
示範
提示
指引
示範
演算
工具使用
例題解題過程 1.唸題目
2.釐清題意,引用定理 7.3 公式
數值帶入公式
3.轉化的概念(標準化的 過程)
4.查表
5.解題完成 6.配合圖示說明
0 2 9 , 10 .
4 0
9x=
χ
【Class-920507,pp.8-9】
2. 有能力同儕應用圖表「教學工具的使用」 ,解釋定理、公式的意義,具 系統化思維功能
第三階段「同儕鷹架」互惠式教學策略中,由學習者輪流擔任教學者,S10 提供適切的「工具─表格」 ,應用教科書表 9.6「變異數分析公式表」,以習題 9.29 的實例數值,解釋各個欄位之間的相關,方法帶入算式簡潔易懂,幫助學 習者思考「一因子變異數分析」中複雜的觀念,從變異源經過處理與誤差的程 序後,自由度、平方和與均方和之間的關係,F 值大小的計算;許多學習者縱 然不太了解「單因子變異數分析」的定義,但是對於 S10 以表格形式彙總的 ANOVA table 印象深刻,如果以歷年考古題的題型來看,ANOVA table 可以說是 重點,學習者努力的抄寫,顯然都聽進去了【perspective-920605】。
變異源 自由度 平方和 均方和 F 處理 6(p-1) 16.9 3.886(SST) 3.4083 誤差 4.35(n-p) 28.3 0.80857(SSE) (MSE)
總和 41(n-1) 45
資料來源:蘇國樑(2003a,p.344)
鷹架教學 情境
鷹架教學 策略之應用
鷹架教學 實施成效 S10:因為這個比較簡單,也比較好
記憶,我想這個東西比較好記…
平方和除以自由度為均方和…
自由度的總和係處理差距與誤 差差距…處理均方和乘以誤差 均方和等於 F 值…簡潔易懂「這 個算法比較簡單一點」…
教學工具使用 提供解釋
S10 將公式化繁為簡,並參 考教科書以表格呈現,簡 潔易懂
S10 再以「同儕語言」 ,並 以 實 例 數 值 代 入 公 式 演 算,學習者印象深刻
【Class-920605,p.19】
3. 「圖示」的概念由生活經驗出發,容易望文生義,有助於學習者多重
感官學習,並培養學習者「系統化」思維
系統化是與比較、分類、抽象、概括、具體化等思維方法密切聯繫的。為 了瞭解數字的特性與結構,第一次課輔教學第一個圖示的概念是「枝葉圖」 。枝 葉顧名思義就是枝幹與樹葉,可以就資料中的觀察值或數值的特性列表,將枝 幹的數值由小至大寫成一直行,再將樹葉填入對應的枝幹,以看出資料集的內 在關係,並可以保留數值資料的原始面貌。由於枝幹的概念由生活經驗出發,
容易望文生義,而且圖示的結果清晰可見,有助於學習者多重感官學習與「系 統化」的思維方法,能夠引起學習者興趣,並引發師生互動。
鷹架教學 情境
鷹架教學 策略之應用
鷹架教學 實施成效 T02:…說真的,枝葉真的不難劃,…
它有什麼特性?這才是重點。第 一個你可以知道說它大部分的數 字是集中在那邊。第二個特性 呢?所有資料的原始全部都被我 保留。
S05:老師,如果是一樣的呢?
T02:一樣就排列。比如說 82、82。
S05:那如果..(?)
T02:就是 69 後面再一個 9。只是說如 果不一樣的小的要把它排在左邊。
S05:還是要把它排在…(?)
T02:對,因為它主要可以看出集中 在那邊。它的特性就是說,你看 到這個圖,你還是可以知道它的 原始資料,這就是枝葉圖的很大 的優點。
直接教學 提示
學習者提問 引 發 一 對 一 鷹 架
【枝葉圖】
枝 葉 5 2 6 9
6 0 5 5 5 6 8 9 9 7 1 1 2 2 4 5 5 7 7 8..
8 0 0 1 2 2 2 4 5 8 9 0 2 4 5 5 6 7 9 10 1 5 5 6
11 1 3 7 12
13 2 5 5
學習者能夠一目了然,代 表已經融入了教學內容,
並能提出相關問題,產生 一對一鷹架。
【Class-920326,p.9】
4. 「示範」解題過程中,成人學習者的個別「提問」 ,引發「一對一鷹架」
T02 運用「圖示」 ,說明「枝葉圖」的意義與功能,學習者能以日常生活的
概念聯想到「枝」 、 「葉」的特性,應用在「統計」數字呈現的意義,藉由教科
書的例題,瞭解「枝葉圖」的呈現形式;由於學習者並未直接參與「練習」 ,S05
的個別「提問」 ,引發「一對一的鷹架」 ,教學者能夠針對學習者的問題給予個
別的回應【Class-920326,p.9】。
5. 「示範」解題過程中,輔以「提示」、「指引」教學策略的應用,有課 前預習的學習者會比較「有感覺」
在以「分析」思維解題的過程中,T02 的「示範」,輔以「提示」 、 「指引」
與「工具使用」 (圖示)教學策略的應用,以加深學習者印象,並將解題步驟內 化成為知識。例題的「示範」過程中,學習者有教科書對照,比較容易進入狀 況,對於有預習的學習者而言,也會比較「有感覺」 【interview-920521-S10,p.1】;
但是,對於沒有課前預習,或是習題的演算,部分學習者就只能專心抄錄,過 程中沒有經過「思考」的過程,S04 感概的說: 「對當下還不是很清楚,…我需 要時間…去思考, 『慢慢來』就比較能改變態度」 【interview-920514,pp.1-2】 。
6. 「示範」解題過程中,教學者採「提問」方式引發教室互動,演算時 刺激學習者回饋,最後藉由「教學工具使用(圖示) 」驗證解題目標 為了避免「示範」過程中,教學者的「直接教學」 ,無法反應出學習者的「思 維」是否與教學者同步,T02 採「提問」方式引發教室互動,學習者對於演算 的過程,能夠產生「回饋」 ,最後 T02 再回到「圖示」驗證解題目標,使得解題 過程更加完整。整體而言,教學者以標準化的過程為先備條件,訓練學習者反 向思維,強調問題理解與融會貫通的重要性。
鷹架教學 情境
鷹架教學 策略之應用
鷹架教學 實施成效 T02: (習題)6.9…這個比較難了一
點,…我大概說一下,它說全體 畢業生起薪的最高 5%之內,其最 低起薪應該是多少?
平均數標準差他告訴你了,…他 告訴你說高於起薪內分配最高的 5%,…
假設分配一定是這樣子,高的人 比較少低的人也比較少,然後大 部分都集中在中間,…
那他現在意思就是說你要先找 到…這個 z 啊,…它本來的平均 是多少?
S04:36000。
練習
提示
示範
工具使用 提 問 已 引 起 互 動
習題 6.9
唸題目(佈題)
解釋並釐清題意
配合圖示說明題意
解題過程
0 34%
0.17
0.17
T02:36000 換句話說,假設他原來是 x,x 減掉 36000 再除以他的標準 差是多少?2000 塊,這個才是 z 分數
(公式
2000 36000= −
= x− x
z
σ
µ ) ,
所以如果我去查表,反查,我剛 才是從找 z 然後再查出機率,現 在我要從機率反查出來…這一個 x 才是我真正要的答案,要還原回 去…0.05 我應該查什麼?
S11:0.5 減掉 0.05。
T02:對,沒錯 0.5 減掉 0.05,才是我 要查的,…0.495 大概在哪邊?
Ss:(大家紛紛回答)
S04 回饋 示範
提示
提問 S11 回饋 肯定
教學工具使用 回饋
) (
645 . 1 2000 )
36000 (
2000 645
. 1 . 36000
) 645 . 1 ( 2000 :
36000
x P P x x
x z
− >
×
−
−
利用圖示說明機率的面積 反查表的過程
先有標準化的概念才能談 反標準化的概念
圖示的運用映證解題目標
【Class-920416,pp.8-10】
7. 學習者上台「練習」前,T02 會就題意先行「提示」或「指引」 ,以確 認解題的路徑;學習者上台「練習」時,會以直觀的方式推估「數值」 , 省略公式的步驟,也能得到答案
第四次課輔教學活動中,教學者(T02)針對部分習題,要求學習者上台「練 習」 ,做為即將舉行「期中考」前的總複習。上台「練習」前,T02 會就題意先 行「提示」 ,以確認解題的路徑,若學習者無適當回應時,再給予「指引」 ,以 刺激學習者思考。
鷹架教學 情境
鷹架教學 策略之應用
鷹架教學 實施成效 T02: (習題 5.16)這是甚麼分配,看
一下題目,銷售員在每個禮拜要 跟四個客戶接洽,結果不是成交 就是不買,應該是甚麼?只有兩 種選擇所以是二項式,… P 就是 成功,成交機率 0.2,不買就是 0.8,客戶之間都是獨立的,你 把 它 機 率 分 配 寫 出 來 就 可 以 了…
練習 提問 提示
指引
唸題目 釐清題意
將條件帶入數值 交由學習者 S04 練習
【Class-920416,p.25】
0 34%
0.17
0.17
習題 4.28 當教學者與學習者因「關係語句」在轉譯過程中,忽略重要數值 而未自知,以至於陷入解題的困境,S04 以直觀的思維路徑推估「數值」─學 生人數,反推回去相關的比例,一般我們稱之為「驗算」反推的過程,也能得 到答案,雖然沒有「標準化」的演算程序,但是能以數值的合理性推估,也是 成人學習者遇到問題瓶頸不得已的應變方式。
鷹架教學 情境
鷹架教學 策略之應用
鷹架教學 實施成效 S04:我是把它推斷說男生有 400 個
人,然後女生是 600 個,但是 0.15 是全部女生要考的應屆 90 個人,
那 90 個人,這裡面是 0.15,…應 屆 1000 乘以 0.2 乘以 200,那 200 減掉這個,這就是男生全部的部 分。
T02:對。
S04:但是我代公式就不知道怎麼去 代。但是就等於除以 1000…
T02:對,其實沒錯。
練習
肯定 回饋
S04 坦承使用「數字推斷」
的 方 式 , 過 程 雖 然 有 問 題,但答案是正確的 直接以數值代入「推出」
或「比較」出答案,在數 理課程的選擇題評量中,
或許有些人有這經驗 S04 真正的問題在於不懂 公式,也不願去思考
【Class-920402,p.27】
8. 公式的推導過程以「澄清」、「示範」的方式進行,有助於統計觀念的 理解;將新知識和舊知識以公式推導的方式進行比較,以釐清彼此間 的脈絡關係,以分類方式區辨相關公式,有助於學習者的理解與記憶 成年人「畏懼」數學,對於數學符號的推演更是避之唯恐不及,T02 觀察 到大多數學習者在公式推演的過程中,所顯示的不安與渾沌,T02 強調: 「我覺 得我講出來反而會增加它們的恐懼,…公式導出來的過程…很複雜,而且是要 用積分的,還不是很簡單的積分」 【interview-920416-T02,p.4】 。因此,使用 的教學策略更有其重要性與必要性。
由於公式的產生係許多符號所構成的意義,理解符號所產生的意義將有助
於記憶,在期望值與變異數公式的講解過程中,教學者首先以「澄清」的方式
區辨 x 與
x觀念的差異,再以「示範」的形式演練公式的推導過程,當下或許
了解,但是擔心出了教室就忘記了, 「專心抄錄」成為公式推導過程的重要現象。
T02 建議要以簡單的式子呈現思考的過程: 「我覺得自己用想的一下子就寫出答 案,問題是你要把過程寫出來讓大家去解,我不能直接(解題) ,…沒有把思考 的過程寫下來」 【interview-920402-T02,p.5】 。從 S13 的受訪意見中了解: 「公 式 很 多 , 老 師 將 … 公 式 予 以 分 解 , 以 利 記 憶 , 對 我 們 幫 助 很 大 」
【Email-920416-S13,p.1】 。
在學習者 S13 主動上台演練習題 7.2 後,T02 除了給予肯定外,並就 E ( x ) 、
)( x
E
、 V ( x )與
V(x)等期望值與變異數公式進行彙總,將四個公式彼此間的相 關,以推導的方式進行比較,屬於舊概念與新知識間的比較,以釐清彼此間的 脈絡關係,促進學習者理解。
鷹架教學 情境
鷹架教學 策略之應用
鷹架教學 實施成效 T02:…上次是不是背 E(x)?可是現在
是
x喔,是不一樣的,可是你看 E(x)跟
x竟然都是 n、p 耶,所以 換句話說 E(x)本身也是 n、p 的一 個估計量,…也是不偏的嘛,…
變異數
x的話其實就是等於我們 剛才有講過了是 ( )
2n
σ ,哪這個σ 的話就是 npq,…根號平方之 後,…剩下 n,消掉之後剩下 pq,
所以換句話說,變異數
x就是 p
×q,這個 q 就是 1.7 的意思喔,
q 就是這個成功這個就是不成功 的機率,…你如果覺得 v 這個地 方還不是很熟的話,用這樣子也 可以…它每一個上面都是變成加 了 n 個嘛。
T02:…那我知道σ
2就是剛好 npq,其 實都是一樣的,…我順便把這個 證明都用出來,這個是因為剛才 我們已經說 σ 其實是
xn
1
嘛!
計算式
E(x)=µ
=np2
2
( )
) ( )
(
x nV
= σx = σ pq
npq =n
=