利用Sinc函數為基底分析二維本徵模態

國

立

交

通

大

學

理學院應用科技學程

碩

士

論

文

利用 Sinc 函數為基底分析二維本徵模態

Analysis on Eigenstates in Two Dimensional System by

Expansion method: Using Sinc Function as Basis

研 究 生：詹智淵

指導教授：陳永富教授

利用 Sinc 函數為基底分析二維本徵模態

Analysis on Eigenstates in Two Dimensional System by Expansion method: Using Sinc Function as Basis

研 究 生：詹智淵 Student：Chih-Yuan Chan 指導教授：陳永富教授 Advisor：Yong-Fu Chen 國 立 交 通 大 學 理學院應用科技學程 碩 士 論 文 A Thesis

Submitted to Degree Program of Applied Science and Technology College of Science National Chiao Tung University in partial Fulfillment of the Requirements

for the Degree of Master in

Degree Program of Applied Science and Technology July 2011

Hsinchu, Taiwan, Republic of China

利用 Sinc 函數為基底分析二維本徵模態 學生：詹智淵 指導教授：陳永富教授 國立交通大學理學院應用科技學程碩士班 摘 要 特徵值問題（Eigenvalve problem）普遍存在於自然界中，然而，在求解 的過程中，只有少數情形能得到解析解，如何利用數值方法解出各種情形 的的特徵值問題是一個重要的課題。在這篇論文中，我們利用特徵函數展 開法，以 Sinc 函數為基底，分析物理系統中相當重要的特徵值問題：二維 赫姆霍茲方程式（Helmholtz equation）。 首先為了證實數值方法的可行性，我們以此數值方法解出邊界為二維 方形及圓形的赫姆霍茲方程式，並將模擬結果和解析解比較，發現在同定 態下的圖形是相當接近的；比對特徵能量值（Energy），能量值誤差並不大。 接著我們利用此數值方法解任意邊界的赫姆霍茲方程式，選取的邊界為金 門形狀及小提琴形狀。我們更用此方法推廣研究振盪平板的節線圖騰，並 推算微擾對節線圖騰的影響，比較數值模擬與實際震砂實驗的結果，兩者 之間有良好的對應關係。

Analysis on Eigenstates in Two Dimensional System by Expansion method: Using Sinc Function as Basis

Student：Chih-Yuan Chan

Advisor：Dr. Yung-Fu Chen

Department of Degree Program of Applied Science and Technology Course

National Chiao Tung University

ABSTRACT

Eigenvalue problem has been widely existed in the nature. Unfortunately, due to the complexities of the physical system, analytical solutions to eigenvalue problem can be obtained only in few cases. Some numerical methods must be used to solve the eigenvalue problem. In this paper, we used expansion method based on Sinc function as basis to analyze the famous eigenvalue problem in physical system: 2D Helmholtz equation.

To consider the feasibility of numerical method, we numerically calculated the eigenstates and eigenenergy in rectangular and circular membrane and compared the numerical results with the analytical solutions. We also solved the two dimensional (2D) membranes problems with arbitrary shapes of Kinmen and violin by using the numerical method.

We further used the numerical method to simulate Chladni Nodal line pattern and investigate the influence of perturbation on Chladni Nodal line pattern. It can be seen that there is a good agreement between numerical results and experiment results.

誌

謝

時間很快過去了，感謝這幾年來，有許多人陪著我一起成長，讓我學 的更多、更廣。首先要感謝陳永富老師的指導與鼓勵，承蒙老師在實驗上 悉心的指導與啟發，使得學生得以完成碩士論文，在此獻上最誠摯的感謝。 此外，衷心感謝余彥廷學長在實驗上的教導及敦促，除了在我學習的 路途上給予許多協助與建議之外，讓我對於數值模擬有了更進一步的了 解；謝謝梁興弛學長及李易純學長在論文上的提點，謝謝蘇冠緯老師與其 他學長姐給我許多的協助。 最後，感謝我的父母及家人對我的鼓勵及支持，尤其是我的老婆，在我 心情最低落的時候給我鼓勵，也替我分擔了家裡所有的事，使我得以修完 碩士學業與課程。由衷地謝謝大家陪我走過這一段人生的路程。

目

錄

中文摘要 ……… III 英文摘要 ……… IV 誌謝 ……… V 目錄 ……… VI 圖表目錄 ……… VIII 一、 緒論……… 1 1.1. 研究動機……… 1 1.2. 本文組織……… 3 二、 自然界中的波動及赫姆霍茲方程式……… 4 2.1. 繩波……… 5 2.2. 電磁波……… 8 2.3. 物質波……… 11 2.4 赫姆霍茲方程式（Helmholtz equation）……… 13 三、 數值方法……… 15 3.1. 特徵函數展開法……… 15 3.2. 基底函數……… 18 3.2.1. 基底……… 18 3.2.2 Sinc function……… 19 3.3 一維薛丁格方程式的數值方法推導……… 23 3.4 二維薛丁格方程式的數值方法推導……… 24 3.5 結果與討論……… 26 四、 二維位能勢……… 26 4.1. 二維方形位能勢……… 27 4.1.1. 二維方形位能勢解析解……… 27 4.1.2. 二維方形位能勢數值解……… 33 4.1.3. 二維方形位能勢解析解與數值解比較……… 36 4.2. 二維圓形位能勢……… 40 4.2.1. 二維圓形位能勢解析解……… 40 4.2.2. 二維圓形位能勢數值解……… 45 4.2.3. 二維圓形位能勢解析解與數值解比較……… 48 4.3. 其他二維不規則邊界……… 52 4.3.1. 二維不規則邊界-金門……… 52 4.2.2. 二維不規則邊界-小提琴……… 54 五、 節線研究(Nodal Line)……… 56 5.1. 類比文獻上的 Chladni pattern……… 58 5.1.1. 方形……… 58

5.1.2. 圓形……… 61 5.1.3. 小提琴圖形……… 62 5.1.4 結果與討論……… 63 5.2. 理論計算分析……… 64 5.2.1. 干擾物對圖騰的定性分析……… 64 5.2.2 干擾物對圖騰特徵能量值的定量分析……… 66 5.3. 加干擾物的 Nodal line 波動行為探討……… 70 5.3.1. 類比實驗圖形……… 70 5.3.2 實驗結果討論……… 73 六、 結論與未來展望……… 74 參考文獻 ……… 75

圖目錄

圖 2.1.1 繩波線段示意圖……… 6 圖 3.2.1 單位向量表示圖……… 19 圖 3.2.2 Sinc 函數形式……… 20 圖 3.2.3

( )

2 4 f x = x 圖形……… 21 圖 3.2.4 Sinc function 描述

( )

2 4 f x = x ……… 21 圖 4.1.1 二維方形位能勢圖……… 27 圖 4.1.2 二維方形圖形……… 33 圖 4.1.3 不同 Basis 數量誤差圖……… 39 圖 4.1.4 二維方形解析解與數值解特徵能量關係圖……… 39 圖 4.2.1 二維圓形位能勢圖……… 40 圖 4.2.2 二維圓形圖形……… 45 圖 4.2.3 二維圓形解析解與數值解特徵能量關係圖……… 51 圖 4.3.1 不規則邊界圖形-金門……… 52 圖 4.3.2 不規則邊界圖形-小提琴……… 54 圖 5.1 方形與圓形震動示意圖……… 57 圖 5.1.1 文獻上方形 Chladni pattern……… 58 圖 5.1.2 方形 Chladni pattern 比對圖（一）……… 59 圖 5.1.3 方形 Chladni pattern 比對圖（二）……… 60 圖 5.1.4 圓形 Chladni pattern 比對圖（一）……… 61 圖 5.1.5 圓形 Chladni pattern 比對圖（二）……… 62 圖 5.1.6 小提琴 Chladni pattern 比對圖……… 62 圖 5.2.1 不同距離特徵能量趨勢圖（一）……… 67 圖 5.2.2 不同距離特徵能量趨勢圖（二）……… 67 圖 5.2.3 不同距離的特徵能量趨勢圖……… 68 圖 5.2.4 能量分布形式……… 69 圖 5.3.1 圓形干擾物距圓心 2 cm……… 71 圖 5.3.2 圓形干擾物距圓心 3.8 cm……… 71 圖 5.3.3 圓形干擾物距圓心 5 cm……… 72 圖 5.3.4 圓形干擾物距圓心 7.3 cm……… 73 圖 5.3.5 圓形干擾物距圓心 10 cm……… 73

表目錄

表 4.1.1 二維方形位能勢之解析解(一)……… 31 表 4.1.2 二維方形位能勢之解析解(二)……… 32 表 4.1.3 二維方形位能勢之數值解(一)……… 34 表 4.1.4 二維方形位能勢之數值解(二)……… 35 表 4.1.5 二維方形位能勢解析解與數值解比較表(一)……… 37 表 4.1.6 二維方形位能勢解析解與數值解比較表(二)……… 38 表 4.2.1 二維圓形位能勢之解析解(一)……… 43 表 4.2.2 二維圓形位能勢之解析解(二)……… 44 表 4.2.3 二維圓形位能勢之數值解(一)……… 46 表 4.2.4 二維圓形位能勢之數值解(二)……… 47 表 4.2.5 二維圓形位能勢解析解與數值解比較表(一)……… 49 表 4.2.6 二維圓形位能勢解析解與數值解比較表(二)……… 50 表 4.3.1 二維不規則邊界位能勢數值解-金門……… 53 表 4.3.2 二維不規則邊界位能勢數值解-小提琴……… 55 表 5.2.1 干擾物於不同距離的特徵態（一）……… 65 表 5.2.2 干擾物於不同距離的特徵態（一）……… 65 表 5.2.3 不同距離的特徵能量值……… 66

第一章 緒論

1.1 研究動機

日本 311 芮氏 9.0 大地震發生，撼動了全世界，大地震造成了日本相當 嚴重的損害，所激發的能量也造成了可怕的海嘯，這是人類有史以來第一 次即時的紀錄下海嘯可怕的現場。過去科學家也透過各種研究方法來研究 地震；1985 年墨西哥大地震發生[1- 6]，一群研究量子理論的科學家利用解 薛丁格方程式處理不規則邊界問題的方法，研究震波對於地震產生災害行 為並類比災害現場，發現處於節線位置上房屋倒塌的情形相當輕微，這是 一個很有趣的現象，因而對波的共振行為產生了興趣。

對於波共振行為的研究相當多，其中節線圖騰（Nodal lines patterns） 在科學上是一個相當重要的研究領域，而 Chladni patterns 更是節線圖騰研 究的經典。 Chladni 發現了一種觀察振動波形的方法，他將均勻的細砂撒 在平板上，以小提琴的弓在平板的邊緣拉彈，產生特定頻率的振動，致使 細砂移動至沒有產生振動的節線上，讓人類第一次可以真正的看見聲音。 爾後更有許多科學家以 Chladni patterns 的方法做各種不同方面的運用。郭 政嘉學長也利用了 Chladni patterns 的方法[7]，並在其中加上了干擾物來研 究節線的變化，概念上就有如一座 101 大樓坐落在台北盆地，當震波傳遞 碰上了 101 大樓，看看能量與節線會是如何的變化。諸多的研究也引發對

這些波動行為產生模擬研究的想法。我們知道波動行為在邊界規則的情況 下有解析解可以解釋它，而於複雜的邊界條件下僅能利用數值方法來解釋 這些波動的行為，我們更利用這樣的數值方法去探討不規則邊界的問題及 有干擾物微擾情況下的 Chladni patterns。

1.2 本文組織

本論文共有六個章節，第二章簡介波動行為從繩波到電磁波乃致物質波 的基本概念，以及簡述其代表的運動方程在有邊界條件下的赫姆霍茲方程 式的表示式。第三章介紹 Sinc 函數及其正交性，並以 Sinc 函數為基底利 用數值方法-特徵函數展開法，推導二維定態薛丁格方程式。第四章以此數 值方法得到的解來驗證二維方形、圓形的解析解，並對不規則邊界圖形做 分析。第五章針對 Chladni 經典的節線圖騰作一系列模擬[8]，並類比實際 在 Chladni plate 加干擾物的節線圖驣來做探討。第六章結論與未來方向。 。

第二章 自然界中的波動及赫姆霍茲方程式

在日常生活中，人類無時無刻都可以體驗到許多來自不同介質所產生 的各種波動。波其實是一種擾動，一種平衡狀態中的擾動，這種擾動會隨 著時間的經過，從空間中的某個區域傳到另一個區域。除了拍擊海岸的海 浪是波之外，聲波、光、廣播電台及電視台的無線電波、震撼地面的地震 波、甚至是微小電子的物質波，在在的顯示其實整個自然界到處都是充滿 著波動，換句話說，整個自然界都是被波動所支配。 物理學家將自然界中的波動行為區分為巨觀世界及微觀世界的波動， 描述巨觀世界的波動行為依循的是古典物理中牛頓運動定律準則，主要所 處理的質點系統是建立在力與加速度的觀念，以及描述運動軌跡的運動方 程式的兩項基礎上；而描述微觀世界的波動行為依循的是量子力學的理 論，建立在物質的波粒二象性及能量為不連續態的觀念上。 波既然是一種傳播運動，必然會有符合其行為的運動方程式，稱為波 動方程式，我們將從一般常見的繩波、電磁波及物質波，來導出符合其波 動行為的波動方程式[9]。而在物理系統中任何描述其動態的行為必然有其 對應的微分方程，波動方程亦是其中之ㄧ，而這些重要的微分方程，在有 邊界的條件下皆可以化為特徵值問題的形式。物理界中最常碰到的特徵值 問題的形式其實就是赫姆霍茲方程式，如式（2.1）。

(

2 2

)

0 ∇ +k E = （2.1） 因此我們可以將波動方程式化成赫姆霍茲方程式的形式，來解波動在有邊 界條件下的特徵值問題。

2.1 繩波

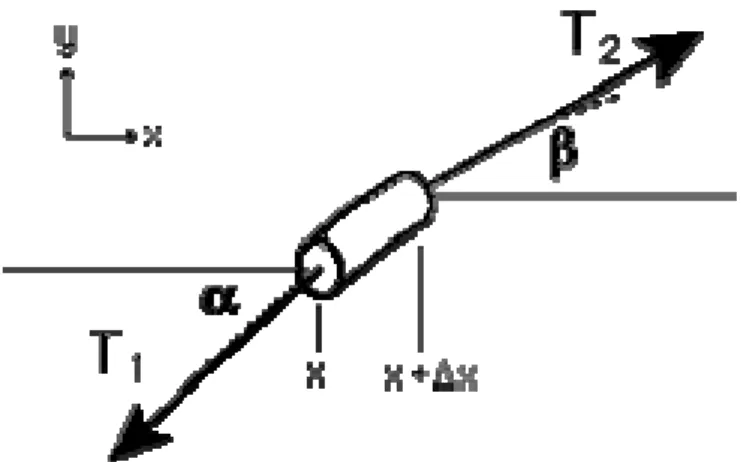
在所有波的種類中，最容易了解的是機械波，這種波是介質從平衡狀態 偏離所引起的效應，使波在這種物質內通過，我們可想像由大量質點所構 成的介質，每一質點都以彈性材料和其附近的質點連接。此介質的一端以 任何形式使其位移，發生位移的地方會使其在旁邊的質點上產生一種彈 力，因此在旁邊的質點也產生了位移，第二個質點又會使旁邊的質點產生 位移，因此這樣的位移會沿著這個介質以固定的速率來傳播[9]。 我們將這個介質換成是一條繩子，在其左端垂直於繩子的方向上施以 外力使其發生位移，此種橫向位移的波我們稱之為橫波，而以一定方向及 速度傳播的波動稱為行進波。 直接從牛頓定律出發，假設均勻且完全彈性之繩索，在兩點張力及斜率 分別為 T₁、tan

α

及 T2、tan

β

之作用下，如圖 2.1.1。

圖 2.1.1 繩波線段示意圖

由橫向力平衡

∑

Fx =0 可知：

T1cosα =T2cosβ = =T constant （2.1.1）

縱向力平衡

∑

F_y =0 可知： 2 2sin

β

1sin

α

( ) 2 ∂ − = ⋅ Δ ⋅ ∂ y T T u x t （2.1.2） 其中， u 為單位質量。將式（2.1.2）除以式（2.1.1）整理可得： 2 2 1 2 2 1 sin sin ( ) cos cos

β

α

β

α

∂ − = ⋅ Δ ⋅ ∂ T T u x T T T y t （2.1.3） 2 2 2 1 +Δ ∂ ⎡∂ ∂ ⎤ ⋅ = _⎢ − _⎥→ ∂ Δ ∂_⎣ x x ∂ x_⎦ ∂ u y y y T t x x x x2 ∂ y （2.1.4） 整理後可得 2 2 2 2 1 ∂ _{= ⋅} ∂ ∂ y 2 ∂ y x v t （2.1.5） 其中 2 =T v u ， 所推導出來的方程式稱為波動方程式，為行進波的波動函數所遵循的 微分方程[10,11]。而 y 為時間 t 與距離 x 的耦合函數，因此利用分離變

數法做時空分離，令 y x t

( )

, = X x T t

( ) ( )

代入式（2.1.5），得 2 2 2 2 2 2 1 1

_λ

⇒ d T = d X = v T dt X dx − （2.1.6） 其中

λ

2 為一常數，整理可得 2 2 2 2 2 2 2 0 0

λ

λ

⎛ ⎞ ⇒_⎜ + _⎟ = ⎝ ⎠ ⎛ ⎞ ⇒_⎜ + _⎟ = ⎝ ⎠ d v T dt d X dx （2.1.7） 只要給定邊界條件就可求得其解。此方程形式就是赫姆霍茲方程式的形式。

2.2 電磁波

最具代表電磁波的理論就是馬克斯威爾方程式（Maxwell equation） [12]，而馬克斯威爾在電磁理論方面的成就可以和牛頓在力學理論的成就相 媲美，他將法拉第等人的實驗結果及理論作為基礎，創造性的提出十九世 紀物理學中最偉大的成就電磁場理論，並預測電磁波的存在。 如何描述波的運動模式在本篇論文中是一項很重要的課題，我們利用 馬克斯威爾方程式（Maxwell equation）來描述電磁波的波動方程式，首先 針對馬克斯威爾方程式來論述。 在 MKS 的單位制度下，馬克斯威爾方程式的微分方程為：

∇ × = −

∂

∂

uv

uv

B

E

t

（2.2.1）

∇ ×

=

∂

+

∂

uv

uuv

D

uv

H

t

J

（2.2.2）

∇ ⋅ =

uv

D

ρ

（2.2.3）

∇ ⋅ =

B

uv

0

（2.2.4） 其中

E

為電場強度（Electric field intensity）， H 為磁場強度（Magnetic field intensity），

D

為電通密度（Electric flux density）亦為電位移為（Electric displacement），

B

為磁通密度（Magnetic flux density）， J 為電流密度 （Electric current density）， ρ 為體電荷密度（Volume charge density）。 電場強度與電位移的關係式為 D=

ε

E ，磁場強度和磁通密度關係式

則為 B=

μ

H，

ε

為介電常數（Permittivity），

μ

為介磁常數（permeability）。 在一無源區域（Source free region），

ρ

、 皆為零，馬克斯威爾方程 式的微分方程可化為

J

∇ × = −

∂

= −

μ

∂

∂

∂

B

H

E

t

t

（2.2.5）

∇ × = −

H

∂

D

=

ε

∂

E

∂

t

∂

t

（2.2.6）

∇ ⋅ =

uv

D

0

（2.2.7）

∇ ⋅ =

uv

B

0

（2.2.8） 對式（2.2.5）取旋度，可得下面的式子：

∇ ×∇ × = −

μ

∂

∇ ×

∂

uv

uuv

E

t

H

（2.2.9） 在

(

)

2 E E ∇ × ∇ × = ∇ ∇ ⋅ − ∇ E 的關係中， ∇ ⋅ =E 0 帶入式（2.2.9），可得 一電場齊次波動方程式如下： 2 2 2

0

με

∂

∇

−

=

∂

E

E

t

（2.2.10） 同理磁場齊次波動方程式: 2 2 2

0

με

∂

∇

−

=

∂

H

H

t

（2.2.11） 式（2,2,10）與式（2.2.11），其形式就是一般的波動方程式的形式，其速率 可表示為: c

1

με

=

c

_（2.2.12） 在 MKS 制 中 ， 介 電 常 數

ε

₀

≈

8.85418 10× -12

s

2

C

2

/

m kg

3 及 介 磁 常 數 -6 2 0 1.25 10

mkg /

C

μ

≈

× 帶入式（2.2.12）可得 8 2.99792 10

/

c

=

×

m

s

此速 率與真空中的光速相等，所以光也是電磁波的一種。 對於這些方程式的解，我們可瞭解到平面行進的 正弦波 就是其一組 解，波的電場和磁場相互垂直，並且分別垂直於平面波行進的方向，以光 速 來傳播。 c 電場和磁場均為時間諧和函數，因此

e

i tω 來表示隨時間的變量，即

E

=

E e

₀ i tω （2.2.13） 因此式（2.2.10）可以二階偏微分方程式來表示為

(

∇ +

2

ω με

2

)

E

=

0

（2.2.14） 同理

(

∇ +

2

ω με

2

)

H

=

0

（2.2.15） 其中 ω με2 表示成 k2 ，則可得

(

∇ +

2

k

2

)

E

=

0

（2.2.16）

(

∇ +

2

k

2

)

H

=

0

（2.2.17） 這就是赫姆霍茲方程式的表示式。

2.3 物質波

描述物質波的微分方程就是薛丁格方程式。當愛因斯坦揭露了光具有波 和粒子的二象性後，一套觀測微觀世界的理論已然悄悄地萌芽。物理學家 德布羅伊（Louis V.deBroglie,1892~1987）提出了突破性的物質波的理論， 每一種粒子都具有粒子與波動的兩象性理論，即帶質量的粒子除了具有粒 子特性外，還具有波的性質，粒子同時也具有波長和頻率，這種質點所具 有的波稱為物質波[13]。 西元1925年，薛丁格（Erwin Schrödinger，1887~1961）研究德布羅伊 的論文，思考著粒子既然具有波粒二象性，其運動應該存在其對應的波動 方程，此方程式可以正確地詮釋粒子的運動行為。西元1926年，薛丁格連 續發表了一系列的論文，提出了滿足粒子系統對應其波函數的波動方程 式，波動力學至此已然產生。薛丁格方程式的提出，成功的描述許多微觀 世界粒子的行為。首先成功解決了重要的氫原子光譜問題。接著利用薛丁 格方程式處理固體的晶格問題，可得到能帶結構，這對於我們了解固體為 何有絕緣體、導體、半導體的區別是非常重要的。還有許多物質的重要物 理及化學性質，都能透過薛丁格方程式得到重要的解釋，也就是說薛丁格 方程式對於近代科學的發展，是具有非常重要的意義[13,14]。 簡單介紹薛丁格方程式，薛丁格在其波動方程式中採用虛數 ’i’ 於時 間項中，其方程式為[14,15]：

∂

ψ

( , )

=

ψ

( , )

∂

h

r t

i

E

t

r t

（2.3.1） ( , )r t

ψ

定義為波函數，代表物質波的粒子在某一時間，出現在特定地點的 機率，

ψ

2代表著出現在特定地點附近機率大小的一個量。 古典物理中，物理系統的總能量 E 是動能與位能的總和，表示式為

E

=

K

+

V

（2.3.2） K 代表著動能勢，V 代表是位能勢。薛丁格依循的這個模式，將空間裡一 個單獨粒子運動於位能勢 V r 中的與時間有關的波動方程式寫為:

( )

( )

2 2

( , )

( , )

2

ψ

∂

_{= −}

⎡

_{∇ +}

⎤

⎢

⎥

∂

_⎣

h

_⎦

h

i

r t

V r

r

t

m

ψ

t

（2.3.3） 接下來令

ψ

( , )r t =

ψ

( )r f t

( )

帶入上式（2.3.3），利用分離變數法處理，可 得方程式，

_{( )}

( )

2 2

1

( )

( )

2

ψ

ψ

⎡

⎤

=

−

∇ +

⎢⎣

⎦

h

h

i

df

V r

r

f t dt

r

m

⎥

（2.3.4） 其中左式及右式分別為時間 t 和位置 r 的函數，互為相等，因此必會等於 一個常數 E，整理可得

_⎢

⎡

∇ +

2

2

₂

⎡

⎣

−

( )

⎦

⎤

⎤

_⎥

ψ

( )

=

0

⎣

h

⎦

m

E V r

r

（2.3.5） 這就是與時間無關的定態薛丁格方程式，其中 E 其實就是定態的特徵能 量，其形式也就是赫姆霍茲方程式的表示式。定態薛丁格方程式將是本論 文對於二維幾何邊界推算特徵能量及特徵態的主要方程式。

2.4 赫姆霍茲方程式（Helmholtz Equation）

從繩波、電磁波到物質波，我們皆可以將其對應方程式化為赫姆霍茲 方程式的形式來求在有邊界條件下的解，因此赫姆霍茲方程式在特徵值問 題中是相當重要的。赫姆霍茲方程式是一個描述電磁波的橢圓偏微分方程 ，其形式如下：

(

∇ +

2

k

2

)

A

=

0

（2.4.1） 在物理的研究中，大部分的物理問題都同時存在著空間和時間的依存 關係，例如波動方程：

( )

2 2 2 2

1

,

ψ

∂

⎛

_{∇ +}

⎞

₌

⎜

_∂

⎟

⎝

c

t

⎠

x t

0

（2.4.2） 對式（2.4.2）進行變數分離

ψ

( , )x t = A x T t( )

( )

，可以得到兩個微分方程：

(

∇ +

2

k

2

)

A

=

0

（2.4.3） 2 2 2 2

0

d

v T

dt

λ

⎛

₊

⎞

⎜

⎟

⎝

⎠

=

（2.4.4） 其中 k 是分離常數波數，A 是振幅。 我們會得到一個具有空間變數x的赫姆霍茲方程式和一個二階時間常 微分方程式。時間解是一個正餘弦函數的線性組合，而空間解則必須依賴邊

界條件，因此只要在給定邊界條件下，我們就可以得到空間解，而我們就 是利用定態薛丁格方程式化為赫姆霍茲方程式的形式，在有邊界的條件下 去求解特徵值問題。

第三章 數值方法

3.1 特徵函數展開法

在一正交系統集合中，定義

{

φ

_m( )x

}

為此正交系統的函數，且具有完備 性及正交性，則此系統中的任意函數 ( )f x 均可以級數展開表示成；

( )

m m

( )

m

f x

=

∑

c

φ

x

_（3.1.1） 因此對於此函數只要找出一組具備正交及完備性質的基底函數，就可 以解出於此系統中任意態的解，其實這就是特徵值函數問題。 解特徵值問題，其實是一種線性轉換的過程，可以表示為；

A

Φ

( )

x

= Φ

E

( )

x

（3.1.2） 其中 A 為此系統集合的特徵空間， E 為特徵值， ( )Φ x 則為特徵函數。 又由上可知，假設 ( )Φ x 為一具備正交及完備性質的函數，我們可以將此 函數作級數展開為；

Φ

( )

x

=

∑

c

m

φ

m

( )

x

（3.1.3） 將式 (3.1.3) 帶入式 (3.1.2) ，得

A

∑

c

m

φ

m

( )

x

=

E

∑

c

m

φ

m

( )

x

（3.1.4） 同乘上 * ( ) n x Φ 並積分 m n*

( ) ( )

m m n*

( ) ( )

m m m

c

φ

x A

φ

x dx

=

E

c

φ

x

φ

x

∑

∫

∫

∑

dx

（3.1.5） 其中 * ( ) n x Φ 與 Φm( )x 彼此正交，所以 m nm n m c

δ

=c

∑

， 又令 *

( ) ( )

n x A m x dx Anm

φ

φ

=

∫

，則式(3.1.5) 改寫為

1 1 2 2 3 3 m n m n m nm m n n n n

c A

Ec

A c

A c

A c

A c

Ec

=

→

+

+

+ +

=

∑

K

（3.1.6） 若將集合展開，n=1, 2,3Km， 11 1 12 2 1 1 21 1 22 2 2 2 1 1 2 2

1

2

m m m m m m mm m

n

A c

A c

A c

E

n

A c

A c

A c

E

n

m

A c

A c

A c

Ec

=

+

+…+

=

=

+

+…+

=

⋅

⋅

⋅

=

+

+…+

=

_m

⎡

⎢

⎢

⎢

⎢

⎢

⎢

⎢

⎢⎣

c

c

我們再將聯立方程式整理，得 11 12 1 1 1 21 22 2 2 2 1 2

m m m m m m mm

A A

A

c

c

A A

A

c

c

E

c

c

A A

A

…

⎡

⎤ ⎡ ⎤

⎡ ⎤

⎢

_…

⎥ ⎢ ⎥

⎢ ⎥

⎢

⎥ ⎢ ⎥

⎢ ⎥

⎢

⋅

⋅

⋅

⋅

⎥ ⎢ ⎥

⋅

⎢ ⎥

⋅

=

⎢

_⋅

_⋅

_⋅

_⋅

⎥ ⎢ ⎥

_⋅

⎢ ⎥

⎢

⎥ ⎢ ⎥

⎢ ⎥

⎢

_⋅

_⋅

_⋅

_⋅

⎥ ⎢ ⎥

_⋅

⎢ ⎥

_⋅

⎢

⎥ ⎢ ⎥

⎢ ⎥

…

⎢ ⎥

⎢ ⎥

⎢

_{⎥ ⎣ ⎦}

_{⎣ ⎦}

⎣

⎦

⋅

（3.1.7） 其中令 11 12 1 21 22 2 1 2

m m m m mm

A A

A

A A

A

A

A A

A

…

⎡

⎤

⎢

_…

⎥

⎢

⎥

⎢

⋅

⋅

⋅

⋅

⎥

⇒

⎢

_⋅

_⋅

_⋅

_⋅

⎥

⎢

⎥

⎢

_⋅

_⋅

_⋅

_⋅

⎥

⎢

⎥

…

⎢

⎥

⎣

⎦

， 1 2 m

c

c

c

c

⎡ ⎤

⎢ ⎥

⎢ ⎥

⎢ ⎥

⋅

=

⎢ ⎥

_⋅

⎢ ⎥

⎢ ⎥

_⋅

⎢ ⎥

⎢ ⎥

⎣ ⎦

，整理得

(

A

−

EI c

)

=

0

（3.1.8） 此即為矩陣的特徵值問題，可藉由解 det

[

A−EI c

]

=0 特徵方程式，

得到相對應的特徵值與特徵向量，亦可得此矩陣中相對應的特徵態，其中 特徵向量為基底向量。由此可知，只要找到某系統的一組具備正交及完備 性質的基底函數，亦可由此方法來找出此系統中的特徵態。而 Sinc 函數即 為具有正交性質的基底函數，但其完備性並不完全，故其數值解有些許的 誤差，雖然如此 Sinc 函數依舊是為基底函數的最佳選擇之ㄧ，所以我們將 以 Sinc 函數作為解定態薛丁格方程式的基底函數。

3.2 基底函數

3.2.1 基底

基底（Basis）在數學上的定義[16] ，簡單來說就是存在一個數學系統 中最小的元素，不能又有其他的元素可以對這個數學系統做線性的組合， 系統內任何狀態皆可以由基底的乘積或疊加而組成來表示。我們最容易理 解的基底就是整數的 1，在整數系定義中它是最小的元素，任何數皆可以 1 的倍數來表示。 以二維向量系統來看，如圖 3.2.1 所示，在二維向量系統中 XY 方向 的基底向量亦可稱為單位向量，其單位向量分別以 及 來表示，而且在這個系統中，任何向量皆可由單位向量 及 來組成，即 可用 來表示，其中a、b 為實數。從 XY 二維的系統中我們 可以理解到既是為 X方向的基底必不可影響到Y方向的向量，亦即為此 XY 二維系統必然具有正交的特質，其 x e = (1,0) e = (1,0)y x e ey (1,0)+ (0,1) a b 空間中兩向量的內積必然為 0；而滿足內 積為 0 的條件，單位向量 ex 及 ey 必然為線性獨立。 而基底不單單是只用向量方式來表示，它當然可以以不同形式的數學 函數來表示，而在二維系統中基底函數的特質如同向量一樣，必須具有正 交及線性獨立的特質。

圖 3.2.1 單位向量表示圖 資料來源[17]

3.2.2 Sinc function

Sinc 函數 [18-23] 在科學上的應用相當廣泛，不論在光學成像系統的 頻率特性、空間濾波、相干光學處理、非相干光學處理、信息光學、光通 信及數位訊號的處理上，都在 Sinc 函數的涵蓋範圍內。我們在處理方波 時，經由傅立葉轉換可得到在時域的訊號，其形狀為一 Sinc 函數的訊號。 首先介紹 Sinc 函數的定義。 Sinc 函數在數學上定義的基本數學形式為： sin

( )

x =sin

( )

x x （3.2.1） sin

( )

α

sin

( )

α

α

= x x x （3.2.2）

其中 Sinc 函數在 x 為 0 點的奇異點定義為 1，如圖 3.2.2， 3 2 1 0 1 2 3 0.4 0.2 0 0.2 0.4 0.6 0.8 1 y x 3 2 1 0 1 2 3 0.4 0.2 0 0.2 0.4 0.6 0.8 1 y x 圖 3.2.2 Sinc 函數形式

Sinc Collection Method 數學符號表示為 Sk，而其數學架構為：

( )

(

)

(

)

( ) sin , 2 π π

π

π

_π

± − − ⎛ ₋ ⎞ ⎜ ⎟ ⎝ ⎠ = = −

∫

h i x kh t k h x kh h h S h x e dt x kh h （3.2.3） 為一 Sinc function 的表示式，其中固定 值，改變 值， 可在 x 軸上的得到不同位置的 Sinc function。很直覺的，任何函數皆可由 這些不同位置的 Sinc function 乘上特定比重所表示，圖 3.2.3 及圖 3.2.4 分 別表示 ( , ) k S h x h k

( )

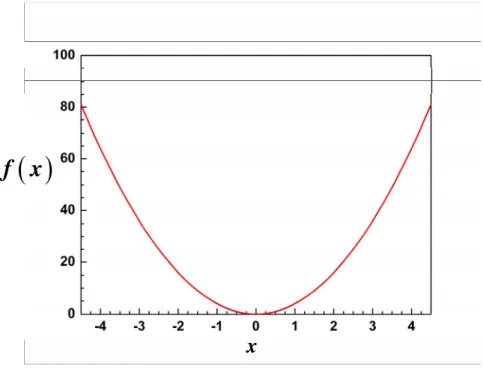
2 4 = f x x 及利用 Sinc function 描述函數

( )

2 4 = f x x 。

x

( )

f x

圖 3.2.3

( )

2 4 = f x x 圖形 圖 3.2.4 Sinc function 描述

( )

2 4 = f x x

Sinc function 也具有正交的特質，接下來我們將接續來了解 Sinc 函數 的正交性質。已知有兩個 Sinc 函數 S h xk( , ) 及 S h xl( , ) ，假設在某一區

間內彼此正交，為驗證其正交性，對 S h xk( , )，S h xl( , ) 做內積運算：

( ) ( )

, , ( ) ( ) 2 2 π π π π

π

π

∞ ∞ ′ − − −∞ −∞ _{− −} ′ =

∫

∫

∫

h i x lh t

∫

h i x kh t l k h h h h S h x S h x dx e dt e dtdx ( ) 2 2 4 π π π π

π

∞ ′ + ′ −∞ − − ′ =

_∫

h ilht

_∫

h ikht

_∫

i t t x h h h e e e dxdtdt （3.2.4）

(

)

( ) 2 2 2 2 π π π π π π

δ

π

π

δ

′ − ′ − − − ′ ′ ′ = + = =

∫

h ilht

∫

h ikht

∫

h i l k ht h h h kl h h e e t t dtdt e dt h 計算結果為 hδ_kl，函數 S h xk( , ) 及 S h xl( , ) 的正交性質因此而得以證明。 從上述討論得知任何函數可以 Sinc function 來表示，而且 Sinc function 彼此間有正交性，也就是說 Sinc function 可以當作任何物理系統的基底函 數。

3.3 一維薛丁格方程式的數值方法推導

以 Sinc 函數為基底代入特徵函數展開法，則一維定態薛丁格方程式 可表示成,

( )

( )

'

( )

( )

(

' 2 ' 2 1 , , , 2 −

∑

k k +

∑∑

_k k k =

∑

k k k k k k d C S h x V k h S h x C S h x E C S h x dx ,

)

（3.3.1） 將式（3.3.1）乘上 S h x 並積分， _l

( )

,

( )

( )

( )

( ) ( ) ( )

( ) ( )

' ' 2 2 ' 1 , , 2 , , , , , − + =

∑ ∫

∑∑

_∫

∑ ∫

k l k k k l _k k k k k l k k d C S h x S h x dx dx V k h C S h x S h x S h x dx E C S h x S h x dx （3.3.2） 將式（3.3.2）整理得 1

(

( )2

( )

' 2

δ

−

_∑

_{k lk} − _lk = k C hC hV k h

)

EhC_l （3.3.3） 其中 ( ) ( ) 2 2 2 2 2 ₃ 1 2 ( ) k l i h lk f l k if l k h k l c π − − = − ≠ − ⎧⎪ ≡ ⎨ ⎪⎩ 式（3.3.3）經由電腦運算，則可計算出特徵函數及特徵能量。

3.4 二維薛丁格方程式的數值方法推導

接著推導二維定態薛丁格方程式，其二維薛丁格方程式的表示為

( )

( ) ( )

(

2 2 2 2 1 , , , 2

ψ

ψ

⎛ ⎞ − _⎜ + _⎟ + = ⎝ ⎠ d d

₎

,

ψ

x y V x y x y E x y dx dy （3.4.1） 而

ψ

( )

x y 及 , V x y 在導入基底函數的表示式為

( )

,

( )

( ) ( )

( )

(

)

( ) (

' ' ' , , , , , ,

ψ

≈ ⎧ ⎪ ⇒ ⎨ ≈ ⎪⎩

∑∑

∑∑

mn m n m n k _k k k x y C S h x S h y V x y V kh k h S h x S h y,

)

（3.4.2） 將式（3.4.2）帶入式（3.4.1）可得

( ) ( )

(

)

( ) ( )

( ) (

( ) ( )

' ' 2 2 2 2 ' 1 , , 2 , , , , , , ⎛ ⎞ − _⎜ + _⎟ ⎝ ⎠ + =

∑∑

∑∑

∑∑

∑∑

mn m n m n k k mn m k k m n mn m n m n d d C S h x S h y dx dy V kh k h S h x S h y C S h x S h y E C S h x S h y

)

, n （3.4.3） 將（3.4.3）同乘上 S_m'

( )

h x 及 , S_n'

( )

h x 並積分， ,

( )

( )

( ) ( )

( ) ( )

( )

( )

( )

' ' ' ' ' 2 2 , 2 2 , , , , 1 2 , , , , ,

+

m n m n mn m n m n m n mn m d S h x S h x dx S h y S h y dy dx C d S h x S h x dx S h y S h y dy dy C S h x ⎡ ⎤ ⎢ ⎥ ⎢ ⎥ − ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦

+

∫

∫

∑

∫

∫

( ) ( ) ( ) ( ) ( )

(

)

( ) ( )

( ) ( )

' ' ' ' ' , , ' , , , , , , , , , , , k m n k n m n k k mn m m _n n m n S h x S h x S h x S h y S h y V kh k h dydx E C S h x S h x dx S h x S h y dx =

∑∑ ∫

∫

∑ ∫

∫

（3.4.4） 整理可得

( ) ( )

₍

₎

}

{

⎡δ δ ⎤ δ δ δ −

∑

_⎣ ' ' + ' ' _⎦+ ' ' =

∑

' ' 2 2 2 2 1 , 2 mn n n m m m m n n m m n n mn m m n n mn mn h C C C V mh nh h E C δ （3.4.5） 其中 ( ) ( ) 2 2 ' 2 2 -' ' 2 ₃ ' ' --1 2 ( - ) m m h m m i i h m m f m m f m m c π ₌ ≠ ⎧⎪ ≡ ⎨ ⎪⎩ ( ) ( ) 2 2 ' 2 ' 2 ' 2 ₃ ' ' 1 2 ( ) n n h n n i i h n n f n n f n n c π − − − − = ≠ ⎧⎪ ≡ ⎨ ⎪⎩ 同樣的，式（3.4.5）經由電腦運算，則可計算出特徵函數及特徵能量。

3.5 結果與討論

對於特徵值問題，我們採用的數值方法就是特徵函數展開法，只要找 出一組具備正交及完備性質的基底函數，我們就可以找到特徵值與特徵向 量，最後就可解出於此系統中特徵態的解。而 Sinc 函數為具有正交性質的 基底函數，但其完備性並不完全，故其數值解有些許的誤差，雖然如此 Sinc 函數依舊是為基底函數的最佳選擇之ㄧ，所以我們將以 Sinc 函數作為解定 態薛丁格方程式的基底函數。

第四章二維位能勢

波在不同幾何形狀邊界的行為探討，一直被科學家所研究著，舉凡 在通訊、雷射及發光二極體等方面，在在都對特定幾何邊界的波動行為有 著相當廣泛的研究。像是光通過光纖進行傳導訊息時，能量在垂直於光傳 遞方向二維平面的行為分布就相當重要，關係著傳導訊息失真與否；發光 二極體在光行進的路徑，在不同的材料的介面上，波在其幾何邊界上所產 生的干涉及反射行為，關係著發光效率高與低。而這些方面的行為研究皆 屬電磁學與量子力學的範疇，因此波在不同幾何形狀二維特定邊界下的基 礎行為探討，在電磁學及量子力學中是相當重要的。

4.1 二維方形位能勢

(Two-Dimensional square potential)

波的運用相當多元，其中最令人熟知的便是運用在光傳輸的光波導，不 同材料的波導會產生不同的模態，在光的傳遞時最不希望高階模態的產 生，高階模態會造成光收斂性不佳，而致使光產生損耗或者訊號轉換失真。 因此波導的形狀及材質也因應產業的發展而廣泛的被研究著，其中矩形對 稱形狀的波導一直是光通訊元件的主流。因此對於二維方形我們將分別以 數值方法及解析解來分析及比較。

4.1.1 二維方形位能勢解析解

經由第三章數值方法的討論，已知二維定態薛丁格波動方程式如下；

(

)

( )

(

)

(

)

2 2 , , 2m

ψ

x y V r

ψ

x y E

ψ

x y, −_{h ∇ +} r ₌ （4.1.1） 現在要解描述粒子行為的波函數

ψ

(

x y,

)

在二維方形位能勢的解析解，位 能勢如圖 4.1.1， V x y

(

,

)

表示如下 2 a − 2 a − 2 a 2 a _x y ( ) 0 2 ; 2 , ; 2 2 a a x y V x y a a x y ⎧ _{< <} ⎪⎪ = ⎨ ⎪∞ > > ⎪⎩ 2 a − 2 a − 2 a 2 a _x y ( ) 0 2 ; 2 , ; 2 2 a a x y V x y a a x y ⎧ _{< <} ⎪⎪ = ⎨ ⎪∞ > > ⎪⎩ 2 a − 2 a − 2 a 2 a _x y 2 a − 2 a − 2 a 2 a _x y ( ) 0 2 ; 2 , ; 2 2 a a x y V x y a a x y ⎧ _{< <} ⎪⎪ = ⎨ ⎪∞ > > ⎪⎩ 圖 4.1.1 二維方形位能勢圖 在方形位能勢中，薛丁格方程式為

)

(

(

)

2 2 , 2m

ψ

x y E

ψ

x y, −_{h ∇ =} （4.1.2） 利用分離變數，令

ψ

(

x y,

)

= X x Y y

( ) ( )

，代入式（4.1.2）

( )

( )

( )

( )

( ) ( )

2 2 2 2 2 2 0 d X x d Y y m Y y X x EX x Y y dx dy ⇒ + + h = （4.1.3） 令 2 2 2mE K = h ，並將式（4.1.3）同除以 X x Y y ，

( ) ( )

( )

( )

( )

( )

2 2 2 2 2 1 1 0 d X x d Y y K X x dx Y y dy ⇒ + + = （4.1.4）

假設

( )

( )

( )

( )

2 2 2 2 2 2 1 -1 -d X x X x dx d Y y Y y dy

α

β

= ⇒ =

⎧

⎪⎪

⎨

⎪

⎪⎩

（4.1.5） 這兩個常係數微分方程式的通解可以表示為

( )

( )

sin cos sin cos X x A x B Y y C y D y x

α

α

β

β

= + ⇒ = +

⎧

⎨

⎩

（4.1.6） 其中 A、B、C、D 為常數。因為我們假設在邊界上，位能勢是無限大，粒 子無法跑出位能勢之外，因此可得知波函數

ψ

(

x y,

)

在方形位能勢的邊界 上的值為零，表示成

( )

( )

, 0 2 2 , 0 2 2 a a x y X Y y a x y X x Y ψ ψ ± ± = = ± ± = = =

⎧ ⎛

⎞

⎛

⎞

⎜

⎟

⎜

⎟

⎪⎪ ⎝

⎠

⎝

⎠

⎨

⎛

⎞

⎛

⎞

⎪ ⎜

⎟

⎜

⎟

⎪ ⎝

⎠

⎝

⎠

⎩

a = （4.1.7） 式（4.1.6）代入邊界條件式（4.1.7），可以解得

( )

( )

sin , 1, 2,3, 2 sin , 1, 2,3, 2 m n m a X x A x m a n a Y y C y n a

π

π

⎧ _{= ′} ⎡ ⎛ ₊ ⎞⎤ ₌ ⎜ ⎟ ⎪ ⎢ _{⎝ ⎠}⎥ ⎪ ⎣ ⎦ ⎨ ⎡ ⎛ ⎞⎤ ⎪ _{= ′ ⎜ + ⎟ =} ⎢ ⎥ ⎪ _{⎣ ⎝ ⎠⎦} ⎩ L L (4.1.8) 其中

A′

和

C′

為常數，可以由歸一化條件

(

)

2 -

ψ

x y dxdy, 1 ∞ ∞ =

∫∫

得到 2 2 2 2 2 2 2 2 sin sin 1 2 2 π π − − ⎡ ⎛ ⎞⎤ ⎡ ⎛ ⎞⎤ ′ ′ ⇒ _{⎢ ⎜} + _{⎟⎥ ⎢ ⎜} + _⎟⎥ ⎝ ⎠ ⎝ ⎠ ⎣ ⎦ ⎣ ⎦

∫

aa

∫

aa m a n a A x dx C y dy a a = 2 4 2 ′ ′ ⇒ A C = = a a

最後可以得知二維方形的特徵態（Eigenstates）的解析解，表示如下

)

(

( ) ( )

,

,

1, 2,3,...

2

sin

sin

1, 2,3,...

2

2

m n

x y

X

m

x Y

n

y

m

m

a

n

a

x

y

n

a

a

a

ψ

π

π

=

=

=

+

+

=

⎧

⎡

⎛

⎞

⎤

⎡

⎛

⎞

⎤

⎨

⎜

⎟

⎜

⎟

⎢

_⎝

_⎠

⎥

⎢

_⎝

_⎠

⎥

⎣

⎦

⎣

⎦ ⎩

（4.1.9） 而二維方形位能勢的特徵態（Eigenstates）對應的能量特徵值（Energy Eigenvalues）

E

_{m n,} 表示為 2 2 2 2 2 , , 1, 2, 3,... 1, 2, 3,... 2 2 m n m n m K m n E n m m a a

π

π

= = = + =

⎡

_⎛

_{⎞ ⎛}

_⎞

⎤

⎧

⎨

⎜

⎟ ⎜

⎟

⎢

_⎝

_{⎠ ⎝}

_⎠

⎥

_⎩

⎣

⎦

h h (4.1.10) 表 4.1.1 及表 4.1.2 為二維方形位能勢的特徵態的解析解及特徵態對應 的特徵能量值。從表 4.1.1 中我們可以看到，當（m,n）為（2,1）及（1,2） 時，所描述的圖形會以簡併態來呈現，所以其 Energy 是相等。

表 4.1.1 二維方形之解析解(一)

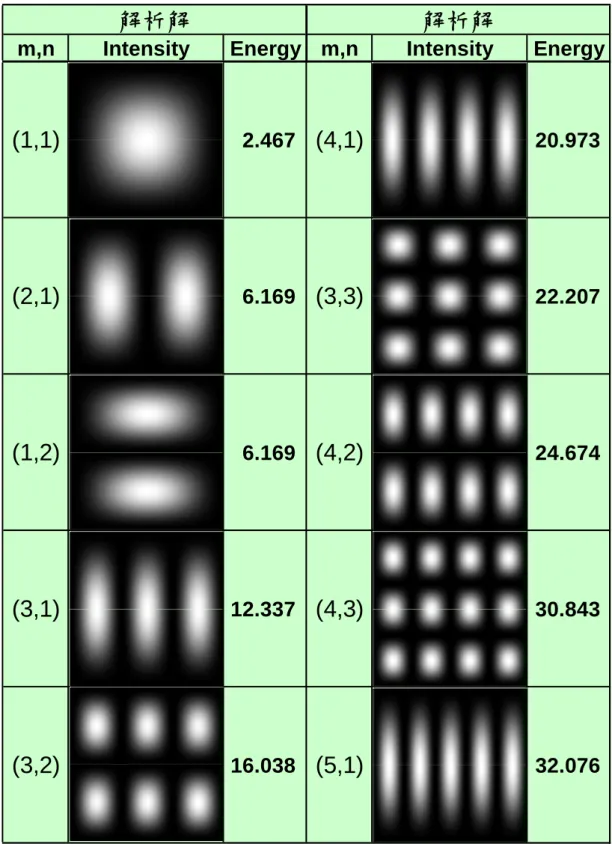
m,n Intensity Energy m,n Intensity Energy

(1,1)

2.467

(4,1)

20.973

(2,1)

6.169

(3,3)

22.207

(1,2)

6.169

(4,2)

24.674

(3,1)

12.337

(4,3)

30.843

(3,2)

16.038

(5,1)

32.076

解析解

解析解

表 4.1.2 二維方形之解析解(二)

m,n Intensity Energy m,n Intensity Energy

(5,2)

35.777

(4,6)

64.152

(4,4)

39.478

(6,5)

75.256

(5,3)

41.946

(1,8)

80.191

(6,2)

49.348

(3,8)

90.060

(3,6)

55.517

(9,4)

119.669

解析解

解析解

4.1.2 二維方形位能勢數值解

將二維方形的圖形，轉化為以點陣圖格式來呈現，點陣圖的灰階呈現由 黑到白可表示為 0 至 255。在二維方形外圍束以白色邊框做為其邊界條件， 如圖 4.1.2，其中以白色為的邊框部份就是我們用以表示為無限位能井，所 有的波動皆束縛在方形位能勢中。 圖 4.1.2 二維方形圖形 將二維方形帶入特徵函數展開法來運算，使用數值方法運算時， Basis 越高其誤差會越低，但由於個人電腦效能的關係，無法處理太大數量的 Basis ，在這裡我們使用的 Basis 數目是 Ｎ＝40×40，得到在不同 State 狀 態下，模擬出的特徵態的圖形及特徵能量值。如表 4.1.3 及表 4.1.4 所示。

表 4.1.3 二維方形位能勢之數值解(一)

State Intensity Energy State Intensity Energy

(1,1)

2.513

(4,1)

21.231

(2,1)

6.256

(3,3)

22.479

(1,2)

6.256

(4,2)

24.975

(3,1)

12.496

(4,3)

31.214

(3,2)

16.239

(5,1)

32.463

數值解

數值解

表 4.1.4 二維方形位能勢之數值解(二)

State Intensity Energy m,n Intensity Energy

(5,2)

36.206

(4,6)

64.908

(4,4)

39.950

(6,5)

76.140

(5,3)

42.446

(1,8)

81.132

(6,2)

49.933

(3,8)

91.116

(3,6)

56.173

(9,4)

121.067

數值解

數值解

4.1.3 二維方形位能勢解析解與數值解比較

由於運算的 Basis 數量越高，其運算結果與解析解的差異會越小，所以 先針對二維方型圖形在不同 Basis 數目的運算下，來比較其運算結果對解 析解的誤差率。定義誤差率為在同一定態下，數值解減去解析解的差值再 除以解析解，並取其絕對值。從圖 4.1.3 的確可以看出，運算的 Basis 數量 越高，其誤差越小。 縱合以上二維方形解析解與數值解的結果，可以從表 4.1.5 及表 4.1.6 中得知，以數值方法模擬所呈現出來在各個不同特徵態的圖形與解析解的 圖形比較，在相同特徵態下的圖形是一致的。比對特徵能量值（Energy）， 從表 4.1.5 及表 4.1.6 中也可以看出二維方形解析解與數值解的特徵能量值 的確相當的接近。 接下來進一步分析解析解與數值解特徵能量值分佈，我們先定義特徵 態（State），由 1 至 100 代表著圖形複雜程度的增加， Energy 為特徵能量 值。從圖 4.1.4 可以看出，隨著特徵態的複雜度遞增，於相同特徵態下解析 解與數值解能量值分別也往上遞增，而其數值解對解析解的平均誤差約為 1.1%。

表 4.1.5 二維方形位能勢解析解與數值解比較表(一)

Intensity Energy Intensity Energy

(1,1)

2.513 2.467

(2,1)

6.256 6.169

(1,2)

6.256 6.169

(3,1)

12.496 12.337

(3,2)

16.239 16.038

解析解

數值解

State (m,n)

表 4.1.6 二維方形位能勢解析解與數值解比較表(二)

Intensity Energy Intensity Energy

(4,1)

21.231 20.973

(3,3)

22.479 22.207

(4,2)

24.975 24.674

(4,3)

31.214 30.843

(5,1)

32.463 32.076

解析解

數值解

State (m,n)

不 同 Basis數 量 誤 差 比 較 0 1 2 3 0 10 20 30 40 50 60 70 80 State Error (%) N : 40 N : 30 N : 22 圖 4.1.3 不同Basis數量誤差圖 解析解與數值解特徵能量關係圖 0 50 100 150 0 20 40 60 80 State Energy 解析解 數值解 圖 4.1.4 二維方形解析解與數值解特徵能量關係圖

4.2 二維圓形位能勢

(Two-Dimensional circle potential)

4.2.1 二維圓形位能勢解析解

現在要解描述粒子行為的波函數

ψ ρ φ

(

,

)

在二維圓形位能勢的解析 解，位能勢如圖 4.2.1，V

(

ρ φ

,

)

表示如下：

a

φ

(

,

)

0 a V a ρ ρ φ ρ < ⎧ = ⎨_{∞ >} ⎩

y

x

a

φ

a

φ

(

,

)

0 a V a ρ ρ φ ρ < ⎧ = ⎨_{∞ >} ⎩

y

x

圖 4.2.1 二維圓形位能勢圖 在

ρ

<a 的位能為零；在

ρ

<a 的區域，其位能則為無窮大。在圓形 位能勢的內部，薛丁格方程式為

(

)

(

)

2 2 2 2 2 2 1 1 + + , , 2m

ρ

ρ ρ ρ φ

ψ ρ φ

E

ψ ρ φ

⎡ ⎤ − ∂ ∂ ∂ ₌ ⎢_{∂ ∂ ∂} ⎥ ⎣ ⎦ h _（4.2.1） 利用分離變數，令

ψ ρ φ

(

,

)

=R

( ) ( )

ρ

Φ

φ

，代入式（4.2.1），

( )

( )

( ) ( )

( )

( )

( ) ( )

2 2 2 2 2 2 0 d R dR R d m d d d ER 2

ρ

φ

ρ

ρ

φ

φ

ρ

ρ

ρ

ρ

φ

ρ

φ

Φ Φ ⎡ ⎤ − ⇒ _⎢Φ + + _⎥ ⎣ ⎦ + Φ = h （4.2.2）

令 2 2 2mE K = h ，並將式（4.2.2）同除以

( ) ( )

2 R ρ φ ρ Φ

( )

( )

( )

( )

( )

( )

2 2 2 2 2 2 2 1 1 0 d R dR d R K R d d d ρ ρ φ ρ ρ ρ ρ ρ ρ ρ φ φ Φ ⇒ + + + Φ ⎡ ⎛ ⎞⎤ ⎢ ⎜ ⎝ ⎠ ⎣ ⎟⎥⎦= （4.2.3） 假設

( )

( )

2 2 2 1 -d m d

φ

φ

φ

Φ = Φ ，代入式（4.2.3）並重新整理，可得徑向跟軸向兩 個方向的微分方程式

( )

( )

( )

2 2 2 2 2 1 0 d R dR m K R d d

ρ

ρ

_ρ

ρ

ρ

ρ

ρ

⎡ ⎛ ⎞ ⎤ ⇒_⎢ + +_⎜ − _{⎟ ⎥} ⎝ ⎠ ⎣ ⎦= （4.2.4）

( )

( )

2 2 2 0 d m d

φ

φ

φ

Φ ⇒ + Φ = （4.2.5） 現在先解式（4.2.5）微分方程式。已知此微分方程式的通解為 ⇒ Φ_m

( )

φ

= Acos

(

m

φ θ

+

)

（4.2.6） 其中 A,

θ

為常數。在此我們令

θ

= 。又因為在 0

φ

方向圓對稱，故有 邊界條件 Φ

(

φ

+2

π

)

= Φ

( )

φ

，代入式（4.2.6），可以得到 ， 因此其通解為 0, 1, 2... m= ± ± ⇒ Φ_m

( )

φ

= Acos

( )

m

φ

, m= ± ±0, 1, 2... （4.2.7） 接下來，要解徑向方向微分方程式。令 x=K

ρ

，則式（4.2.4）可改寫 成

( )

( )

( )

2 2 2 2 1 1 d R x dR x m R x dx x dx x ⎡ ⎛ ⎞ ⎤ ⇒_⎢ + + −_{⎜ ⎟} ⎝ ⎠ ⎣ ⎦⎥ =0 （4.2.8） 式（4.2.8）即 m 階 Bessel 微分方程式，其通解為

⇒R x

( )

=BJ_m

( )

x （4.2.9） 其中 B 為常數且 為 m 階 Bessel 函數。跟方形一樣，波函數在邊 界上值為零，也就是

( )

m J x

(

)

_m

( )

0 R x=Ka =BJ Ka = 。並非所有的K 都可滿足 ，只有某些特定的不連續

( )

0 m J Ka = K 值才滿足，即當 K a_mn =α_mn 時， ，

( )

0 m mn J α = α_mn 可由查表得知。最後我們得到徑向方向的通解為 ⇒R

( )

ρ

=BJ_m

(

K_mn

ρ

)

（4.2.10） 不同

(

m n,

)

_{可對應到特定的特徵狀態}

(

)

(

) ( )

, , c m n ABJm Kmn os m ψ ρ φ = ρ φ ， AB 可以由歸一化條件

(

)

2 - ψ ρ φ ρ ρ φ, d d 1 ∞ ∞ =

∫∫

得到

(

)

1 1 m mn AB aJ K

π

₊

ρ

⇒ = （4.2.11） 最後可以得知二維圓形位能勢的特徵態（Eigenstates）解析解，表示如下

)

(

( ) ( )

(

) ( )

(

)

, 1

,

cos

,

0, 1, 2..

m n m mn m mn

R

J

K

m

aJ

K

m

ψ

ρ φ

ρ

φ

ρ

φ

π

₊

ρ

⇒

=

Φ

=

= ± ±

_（4.2.12） 而二維圓形位能勢的特徵態（Eigenstates）對應的能量特徵值（Energy eigenvalues）

E

_{m n,} 表示為 2 2 ,

,

0, 1, 2..

2

mn m n

E

m

m

a

α

⎛

⎞

=

_⎜

_⎟

=

⎝

⎠

h

_{± ±}

（4.2.13） 表 4.2.1 及 4.2.2 為二維圓形位能勢的特徵態解析解及特徵態對應的能量特 徵值。

表 4.2.1 二維圓形位能勢之解析解(一)

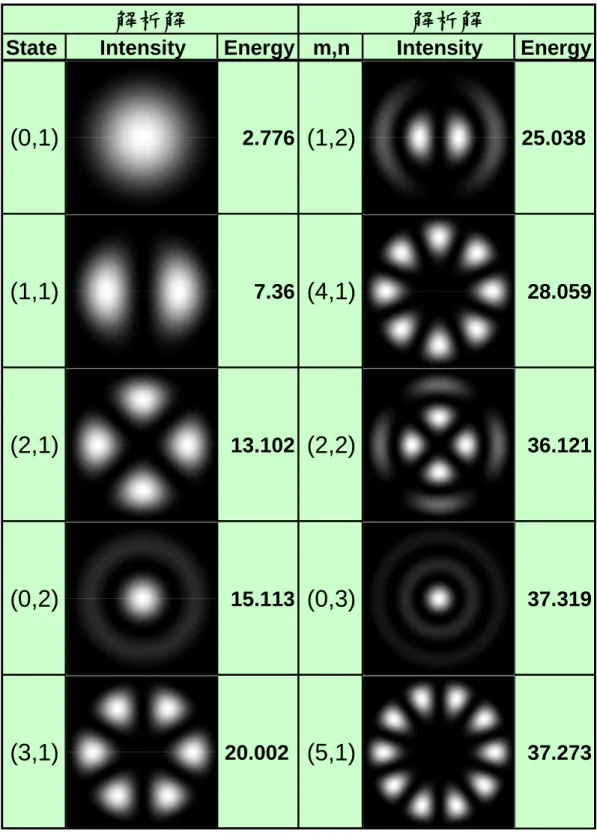
State Intensity Energy m,n Intensity Energy

(0,1)

2.776

(1,2)

25.038

(1,1)

7.36

(4,1)

28.059

(2,1)

13.102

(2,2)

36.121

(0,2)

15.113

(0,3)

37.319

(3,1)

20.002

(5,1)

37.273

解析解

解析解

表 4.2.2 二維圓形位能勢之解析解(二)

State Intensity Energy m,n Intensity Energy

(4,1)

28.059

(3,3)

86.590

(4,1)

37.319

(6,2)

92.027

(6,1)

47.645

(4,3)

105.329

(4,2)

61.759

(5,3)

125.225

(0,4)

69.396

(1,5)

137.289

解析解

解析解

4.2.2 二維圓形位能勢數值解

將二維圓形的圖形，化為矩陣的方式來呈現，處理方式與方型一致，在 圓形外圍束以白色邊框做為其邊界，其中白色部分的位能勢視為無窮大， 黑色部分位能勢設為零，如圖 4.2.2， 圖 4.2.2 二維圓形圖形 將此圖形帶入數值方法來做運算，可以得到在不同 State 狀態下，其模 擬出的不同特徵態圖形及特徵能量 Energy 。如表 4.2.3 及表 4.2.4 所示。

表 4.2.3 二維圓形位能勢之數值解(一)

State Intensity Energy m,n Intensity Energy

(0,1)

2.865

(1,2)

25.111

(1,1)

7.456

(4,1)

29.226

(2,1)

13.344

(2,2)

35.799

(0,2)

15.503

(0,3)

38.067

(3,1)

20.724

(5,1)

39.076

數值解

數值解

表 4.2.4 二維圓形位能勢之數值解(二)

State Intensity Energy m,n Intensity Energy

(3,2)

48.333

(3,3)

85.875

(6,1)

50.128

(6,2)

93.759

(4,2)

62.294

(4,3)

104.63

(0,4)

70.715

(5,3)

125.21

(5,2)

77.246

(1,5)

137.34

數值解

數值解

4.2.3 二維圓形位能勢解析解與數值解比較

縱合以上二維圓形解析解與數值解的結果，可以從表 4.2.5 及表 4.2.6 中 得知，以數值方法模擬所呈現出來在各個不同 State 的圖像與解析解的圖 像作比較，在相同 State 下的圖形，數值解的圖形近似解析解的圖形。比 對特徵能量值（Energy），從表 4.2.5 及表 4.2.6 中也可以看出二維圓形解析 解與數值解的特徵能量值相當的接近。 接下來進一步分析解析解與數值解特徵能量值分佈，與二維方形一 樣，定義 State 由 1 至 100 代表著圖形複雜程度的增加， Energy 為特徵能 量值。從圖 4.1.3 可以了解，隨著 State 的複雜度遞增，於相同 State 下解 析解與數值解能量值分別往上遞增，其數值解對解析解的誤差約為 2.39%。

表 4.2.5 二維圓形位能勢解析解與數值解比較表(一)

Intensity Energy Intensity Energy

(0,1)

2.865 2.776

(1,1)

7.456 7.36

(2,1)

13.344 13.102

(0,2)

15.503 15.113

(3,1)

20.724 20.002

解析解

數值解

State (m,n)

表 4.2.6 二維圓形位能勢解析解與數值解比較表(二)

Intensity Energy Intensity Energy

(1,2)

25.111 25.038

(4,1)

29.226 28.059

(2,2)

35.799 36.121

(0,3)

38.067 37.319

(5,1)

39.076 37.273

解析解

數值解

State (m,n)

解析解 與數值 解特徵 能量關 係圖 0 50 100 150 200 0 20 40 60 80 State Energy 解 析 解 Sinc數 值 解 圖 4.2.3 二維圓形解析解與數值解特徵能量關係圖

4.3 其他二維不規則邊界

從上述二維方形及圓形位能勢的解析解與數值解比較來看，以數值方法 所運算出來的數值解，的確可以近似二維方形及圓形位能勢的解析解。 接下來我們將利用這個數值方法對於不規則形狀邊界的圖形做運算，解出 在各個不同定態下的圖形及特徵能量值。

4.3.1 二維不規則邊界-金門

選擇一個金門地形的地圖，再將地圖轉化為二維不規則的矩陣圖形，如 圖4.3.1，再帶入數值方法運算，可得二維不規則邊界的特徵態及特徵能量 值。 圖4.3.1 不規則邊界圖形-金門

表 4.3.1 二維不規則邊界-金門

Intensity Energy Intensity Energy Intensity Energy

11.704 43.334 150.047 18.680 49.818 200.569 25.015 54.614 236.512 29.724 61.825 280.848 34.955 83.892 329.290 40.745 106.822 362.464 數值解

4.3.2 二維不規則邊界-小提琴

選擇一個小提琴的圖形，再將小提琴圖形轉化為二維不規則的圖形，如

圖4.3.2，帶入數值方法運算，可得小提琴形狀的二維不規則邊界的特徵態 及特徵能量值。