融入動態幾何軟體的合作學習模式對國中學生學習二次函數圖形的影響

(1)

國立交通大學

理學院科技與數位學習學程

碩士論文

融入動態幾何軟體的合作學習模式

對國中學生學習二次函數圖形的影響

The Effects of Integrating Cooperative Learning Model with the

Dynamic Geometry Software on Junior High School Students’

Learning of Quadratic Function Graphics

研究生：陳弘昌

指導教授：袁媛教授

李榮耀教授

(2)

融入動態幾何軟體的合作學習模式對國中學生學習二次函數圖形的影響

The Effects of Integrating Cooperative Learning Model with the Dynamic Geometry Software on Junior High School Students’ Learning of

Quadratic Function Graphics

研究生：陳弘昌 Student：Hung-Chang Chen 指導教授：袁媛 Advisor：Yuan Yuan 李榮耀 Jong-Eao Lee 國立交通大學理學院科技與數位學習學程碩士論文 A Thesis

Submitted to Degree Program of E-Learning College of Science

National Chiao Tung University in partial Fulfillment of the Requirements

for the Degree of Master

in

Degree Program of E-Learning

June 2013

Hsinchu, Taiwan, Republic of China

(3)

摘要

本研究主要探討在融入使用動態幾何軟體的教學環境下，比較合作學習法和個別學習法的兩種模式，對國中學生學習二次函數圖形是否因為不同的數學學業能力及不同性別而有不同的影響。本研究採用不等組前測後測的準實驗研究法，研究對象為新竹市某國中九年級學生，研究者將任教的兩個班隨機分派為實驗組及控制組，兩組皆為學生自行操作 GSP 幾何軟體，實驗組使用合作學習法之教學，控制組使用個別學習法之教學。教學前先對兩組的學生實施「二次函數單元先備概念理解測驗」(即前測)，確認兩組學生的二次函數先備概念理解能力相同，並於教學後實施「二次函數單元成就測驗」(即後測)作為檢驗學習成效之工具。本研究的主要發現如下：一、在學生自行操作 GSP 幾何軟體下學習二次函數圖形，融入異質分組之合作學習法的教學模式顯著優於個別學習的教學模式。二、在學生自行操作 GSP 幾何軟體下學習二次函數圖形，融入合作學習法的教學模式，有助於提升學生的概念理解能力。三、在學生自行操作 GSP 幾何軟體下學習二次函數圖形，融入合作學習法的教學模式，有助於提升學生的問題解決能力。四、在學生自行操作 GSP 幾何軟體下，融入合作學習法的教學模式和個別學習的教學模式，對於男女生在學習二次函數單元的概念理解能力都一樣好。五、在學生自行操作 GSP 幾何軟體下，融入合作學習法的教學模式和個別學習的教學模式，對於男女生在學習二次函數單元的問題解決能力都一樣好。最後，本研究依據研究結果，提出具體建議，以做為數學教學、教材設計及未來研究上的參考。關鍵字：二次函數、GSP 動態幾何軟體、合作學習法

(4)

Abstract

This study focuses on integrating cooperative leaning mode with the dynamic geometry software on junior high school students’ learning of quadratic function graphics. The result is compared with individual leaning mode. This study tries to find out if different math proficiency and different genders will influence the learning result.

In this study, we apply quasi-experimental design of ranging groups to do pretest and posttest, and we also take ninth graders in two classes of Hsinchu

City Junior High School as objects. We then have randomly assigned a class to

be an experimental group and the other class to be a control group to conduct teaching. The students in each group apply GSP geometry software by themselves. The experimental group is taught with cooperative learning method, and the control group is taught with individual learning method. Before teaching, the students do the pre-test of quadratic function concept, and the teacher has to make sure the students in both groups have the same understanding of quadratic function. After teaching, the students have to take quadratic function proficiency test (the post-test) as a tool to check the learning outcomes.

This study finds out:

1. When the students learn quadratic function with GSP geometry software by themselves, cooperative learning mode in heterogeneous groups is better than individual learning mode.

2. When the students learn quadratic function with GSP geometry software by themselves, cooperative learning can help the students improve concept understanding ability.

3. When the students learn quadratic function with GSP geometry software by themselves, cooperative learning can help the students improve the ability of solving problems.

4. When the students learn quadratic function with GSP geometry software by themselves, applying cooperative learning mode and individual learning

(5)

mode in teaching are both good for the boys and girls to learn quadratic function concept.

5. When the students learn quadratic function with GSP geometry software by themselves, applying cooperative learning mode and individual learning mode in teaching are both good for the boys and girls to answer quadratic function questions.

At last, according to the research results, this study offers suggestions for teaching math, designing of teaching materials, and doing further researches.

Key words: Quadratic Function, the Geometer’s Skectchpad Dynamic Geometry Software, Cooperative Learning

(6)

(7)

誌謝

為了充實自己，選擇碩士在職專班就讀，這種忙碌的生活，終於在兩年之後劃下句點，在這之中，受到很多人的幫助，完成了我的論文。首先要感謝的是指導教授袁媛老師，從論文題目的選擇，到最後完成論文，當中遇到的每個問題及每個小細節，都是和藹可親的您用您的耐心帶領著我去面對、去探討、去解決，最大功勞要歸功於您。再來要感謝的是指導教授李榮耀老師，在論文研討課時，給了我許多建議與看法，讓我能有不同面向的思考。接著，感謝口試委員孫之元教授，您仔細地閱讀我的論文，提供了許多意見與想法，讓我的論文更臻於完美。接著要好好感謝我的同事兼好友泓葆、有聖、佩錦，一起念這個碩班，可以互相鼓勵與討論課業，回憶起除了在新竹上課，甚至還曾經每個星期到桃園去和袁媛老師討論論文，結束時，大家都拖著疲憊的身軀，還願意讓我開車送各位回新竹，共同打拚兩年的日子，我不會忘記的，也再次特別感謝泓葆及同辦公室的彤曲，你們和我一起留晚自習並督促我要認真寫論文了，不能再混了。也謝謝怡菁，幫助我完成英文摘要。最後要感謝的是我的家人，有你們默默的支持，是我堅持進修最大的動力，真的很謝謝你們。

(8)

(9)

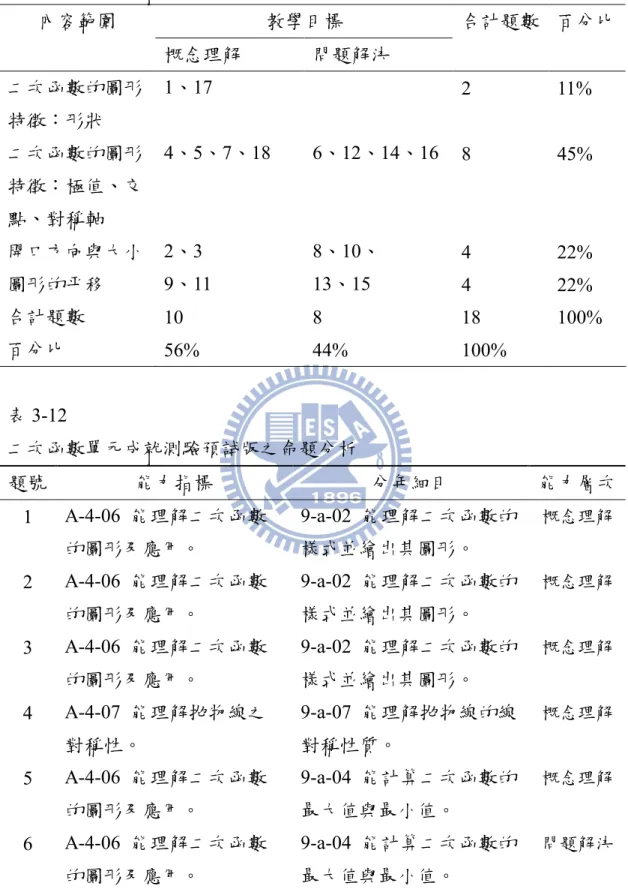
第一章緒論………...1 第一節研究背景與動機……….1 第二節研究目的與待答問題……….4 第三節名詞解釋……….5 第四節研究範圍與限制……….6 第二章文獻探討………...7 第一節二次函數課程的內涵及學習問題探討……….7 第二節動態幾何軟體教學………...12 第三節合作學習………...16 第三章研究方法……….21 第一節研究設計………...21 第二節研究對象………...27 第三節研究工具………...29 第四節資料分析………...40 第四章研究結果與討論………41 第一節資訊融入的不同教學模式與學業能力對學習成效的交互作用影響………...41 第二節資訊融入的不同教學模式與性別對學習成效的交互作用影響………...48 第五章結論與建議………55 第一節結論………...55 第二節建議………...56 參考文獻……….……….59 一、中文部分………59 二、英文部分………62 附錄………...65 附錄一二次函數學習單………...65 附錄二二次函數 GSP 教材………..70 附錄三二次函數單元先備概念理解能力之測驗………...84 附錄四二次函數單元成就測驗………...86

(10)

(11)

表次

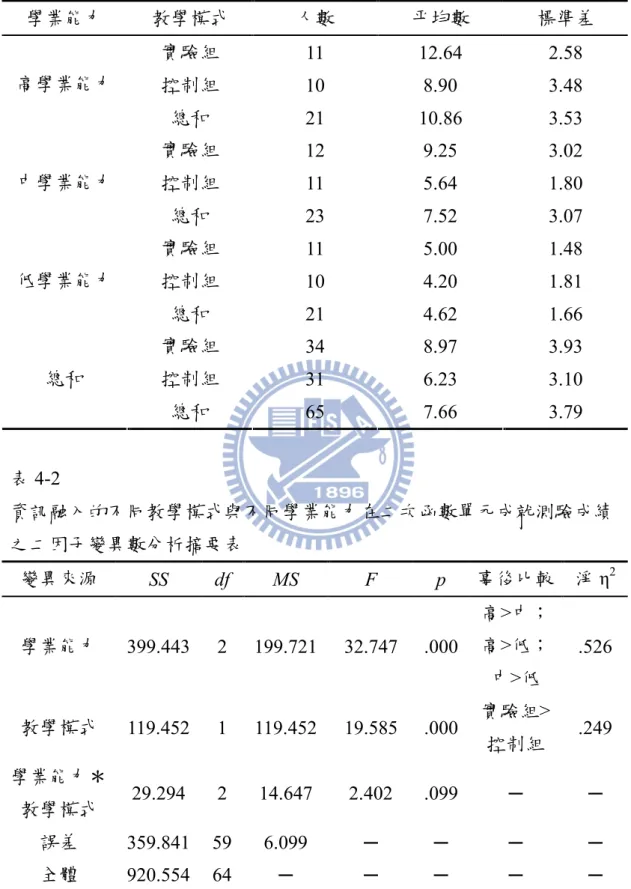
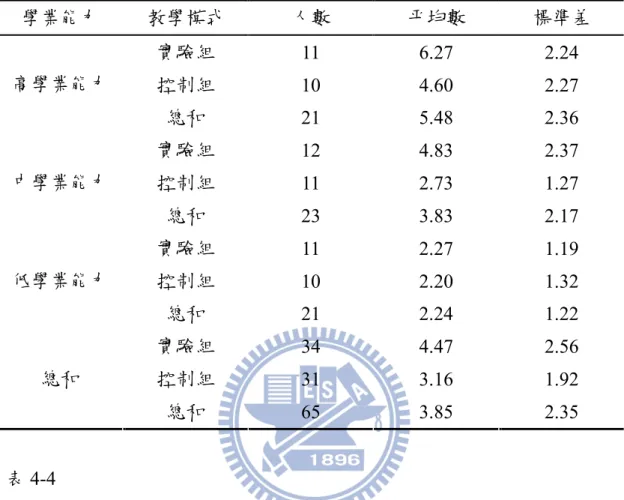
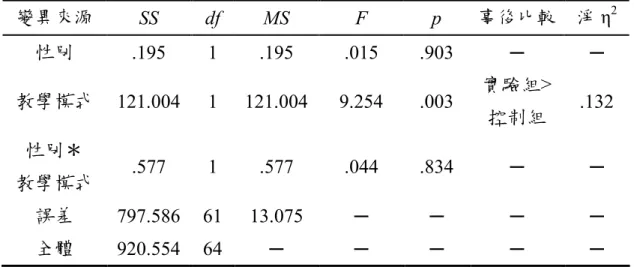
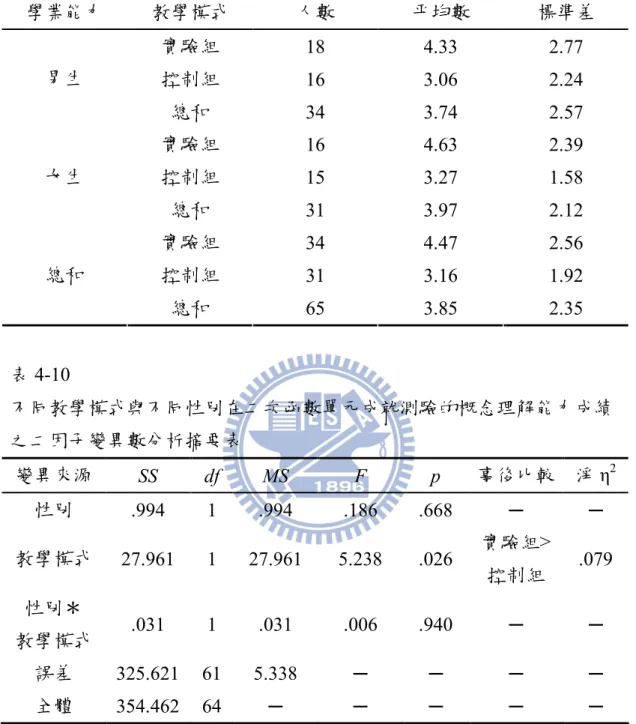
表 3-1 實驗設計表………..22 表 3-2 實驗研究各組之各學業能力人數統計表………..23 表 3-3 研究樣本人數統計表………..27 表 3-4 實驗研究各組前測成績之獨立樣本 t 檢定摘要表………...28 表 3-5 自編二次函數單元的分年細目及能力指標對應表………..30 表 3-6 自編二次函數單元的分年細目及教學目標對應表………..31 表 3-7 專長教師建議教材修改內容………..32 表 3-8 二次函數單元先備概念理解能力測驗預試版之雙向細目表……..33 表 3-9 二次函數單元先備概念理解能力測驗預試版之命題分析………..34 表 3-10 二次函數單元先備概念理解能力測驗預試試卷難度及鑑別度摘要表……….36 表 3-11 二次函數單元成就測驗預試之雙向細目表………..37 表 3-12 二次函數單元成就測驗預試之命題分析………..37 表 3-13 二次函數單元成就測驗之預試試卷難度及鑑別度摘要表………..39 表 3-14 實驗研究的虛無假設及統計方法表………..40 表 4-1 不同學業能力學生在二次函數單元成就測驗的成績表現分配表..42 表 4-2 資訊融入的不同教學模式與不同學業能力在二次函數單元成就測驗成績之二因子變異數分析摘要表……….42 表 4-3 不同學業能力學生在二次函數單元成就測驗的概念理解能力成績表現分配表……….44 表 4-4 不同教學模式與不同學業能力在二次函數單元成就測驗的概念理解能力成績之二因子變異數分析摘要表……….44 表 4-5 不同學業能力學生在二次函數單元成就測驗的問題解決能力成績表現分配表……….45 表 4-6 不同教學模式與不同學業能力在二次函數單元成就測驗的問題解決能力成績之二因子變異數分析摘要表……….45 表 4-7 不同性別學生在二次函數單元成就測驗的成績表現分配表……..48 表 4-8 資訊融入的不同教學模式與不同性別在二次函數單元成就測驗成績之二因子變異數分析摘要表……….49

(12)

表 4-9 不同性別學生在二次函數單元成就測驗的概念理解能力成績表現分配表……….50 表 4-10 不同教學模式與不同性別在二次函數單元成就測驗的概念理解能力成績之二因子變異數分析摘要表……….50 表 4-11 不同性別學生在二次函數單元成就測驗的問題解決能力成績表現分配表……….51 表 4-12 不同教學模式與不同性別在二次函數單元成就測驗的問題解決能力成績之二因子變異數分析摘要表……….51

(13)

圖次

圖 2-1 二次函數教材地位分析圖………....8

圖 3-1 研究架構圖………..22

圖 3-2 研究流程圖………..26

(14)

(15)

第一章緒論

本研究主要探討在融入使用動態幾何軟體的教學環境下，比較合作學習法和個別學習法的兩種模式，對國中學生學習二次函數圖形的影響。本章共分為四節，第一節為研究背景與動機，第二節為研究目的與待答問題，第三節為名詞解釋，第四節為研究範圍與限制。

第一節研究背景與動機

資訊時代的到來，教育部持續補助並提升國民中小學教學現場的資訊設備，以便能夠透過資訊科技的介入，提升教師在教學上的成效。教育部 (2008)在提出的「中小學資訊教育白皮書」中也確實提出三大願景：(一) 學生能運用資訊科技增進學習與生活能力；(二)教師能善用資訊科技提升教學品質；(三)教室能提供師生均等的數位機會。在現行的九年一貫課程當中，也明確揭示以培養學生運用資訊科技進行邏輯思維的習慣，以有效解決日常生活與學習的問題，以及培養學生使用資訊科技，進行資料的搜尋、處理、分析、展示與溝通的能力，增進合作學習、主動學習的能力，來做為資訊教育的課程目標(教育部，2003)。但鐘樹椽與黃任怡(2005)提到，所謂資訊融入教學不是意味著只要在課堂中使用到電腦、網路或是單槍投影機等設備，而是教師能運用科技的優勢來活化教材，加深學童對於教材方面的學習及延伸式學習，才能達到資訊融入教學的真正精神。由此可知，教師將資訊融入教學時,不該只是著重在資訊科技的使用，而是要做高層次的融入應用(袁媛、林意晨，2008)。教育部在九年一貫課程綱要中，將數學課程內容分為數與量、幾何、代數、統計與機率和連結等五大主題(教育部，2003)。美國數學教師協會

(Nation Council of Teachers of Mathematics [NCTM], 1989)出版的《中小學數

學課程與評量標準》(Curriculum and Evaluation Standards for School Mathematics)中指出函數概念是代數課程的基礎，而且強調函數概念當作中學與高等數學課程的中心組織原則。Eisenberg(1992)則明確地指出中學和大學的主要目標應該是發展「函數感」(sense of functions)。Yerushalmy 與 Schwartz(1993)認為函數在現行中學課程中，佔有重要的部分，且有充分理由說明函數是代數學習的基礎。謝豐瑞與陳材河(1997)也認為函數這

(16)

個概念是本國學生從國中到大學都必須學習的。因此，函數在數學的學習上佔有重要地位。雖然函數在數學的學習如此重要，但部分學生在學習函數相關單元時，依舊倍感困難，更甚至是感到沮喪，因為函數的概念是如此的抽象以及複雜。Dreyfus 與 Eisenberg(1982)提出函數的概念不只是單一的概念，而是有其他相關的子概念，例如：變數、定義域、值域和極值、…等，且函數可用多種不同的表徵來表示，像是表格、集合映射圖(arrow diagram set)、圖形、式子和語意敘述等五種表徵。Markovits, Eylon 與 Bruckheimer(1986) 的研究發現，九年級的學生在函數表徵轉換上有嚴重的困難。大多數的學生對函數的想法都停留在抽象代數符號的操弄，而忽略了函數在坐標幾何上的意義(林星秀，2001)。Zaslavsky(1997)指出，如果學生在學習二次函數的過程中，能將代數與幾何圖形表徵間成功地轉換，將會促進函數概念的學習。 NCTM(1989)出版的《中小學數學課程與評量標準》中強調數學教學要使用具體視覺化模型以促進概念的學習。NCTM(2000)出版的《中小學數學原則與標準》(Principles and Standards for School Mathematics)中指出利用電腦及計算器繪製函數圖形，可以有助於學生觀察當參數改變時，圖形的變動關係。國內也有學者提到，應用動態幾何軟體，佈置幾何實驗環境，提供學習者模擬探究幾何概念，是一可行教學模式(左台益，2002)。研究者也是有感於在教學現場上，進行二次函數 2

(

)

y



a x



h



k

的教學時，在黑板上繪製二次函數圖形時，不易呈現參數a、

h

和

k

在改變時，二次函數圖形會如何跟著改變，往往需要大量的時間在黑板上將二次圖形畫出，再比較其中的差異，每次教學都需耗費大量時間，如能使用 Geometer’s Skectchpad(簡稱 GSP)動態幾何軟體來教學，想必能更清楚明瞭二次函數圖形會因參數a、

h

和

k

改變而隨之如何變動，也能縮短在黑板上繪製二次函數圖形的時間，所以想藉由資訊融入教學，利用 GSP 動態幾何軟體進行教學，來彌補傳統講述教學上的缺失。而且許多研究顯示，使用 GSP 動態幾何軟體來進行教學，對學生的數學學習成效是有助益的(尤冠龍，2006；張美珠，2003；郭昭慧，2004；楊子賢，2011；戴錦秀，2002)。但探討目前的相關研究中，多是著重於資訊融入教學的方法和傳統講述法的比較，且教學實驗中的實驗組和控制組在學習表現上，顯著與無顯著差異的實驗結果數量各半，部分研究進而考慮學生的性別及學習成效(分

(17)

成高、低、中三種程度) ，則出現明顯差異現象，例如郭昭慧(2004)在數學學習成就方面發現，對於中分群學生，實驗組明顯優於控制組，而高、低分群學生，實驗組與控制組無顯著差異。但尤冠龍(2006)的實驗結果發現，在數學學習成就上，只有高分群的實驗組與控制組有顯著差異。而吳鳳萍(2002)的實驗在性別方面發現，男生在實驗組與控制組的後測成績上有顯著差異。另外，臺灣國中二年級學生在 TIMSS 2003 中的數學成就來看，女生的分數(589 分)雖然比男生的分數(582 分)稍微高一點，但無顯著差異，但在代數和幾何上的平均得分都較男生高，並且達到顯著水準(曹博盛，2005)。而臺灣的八年級學生在 TIMSS 2007 年的數學得分，女生(599 分)雖然比男生(598 分)略高，但並未達統計上的顯著水準，在代數和幾何的主題上，女生平均得分較男生高，但都未達顯著水準，但以國際平均來看，女生在代數和幾何上的表現都顯著優於男生(Mullis, Martin, & Foy, 2008)。因此，性別和不同程度的變項加入動態幾何軟體教學是可以多做探討的。另外，大部份研究的實驗組多為教師直接操作及展示 GSP 來進行教學，但根據楊子賢(2011)的研究，他將實驗組分成兩組，一為「GSP 動態教師展示組」，另一為「GSP 動態學生操作組」，而研究結果顯示接受 GSP 融入數學教學的學生，在平行四邊形單元成就測驗上的得分，的確顯著高於未接受 GSP 融入數學教學的學生，這結果顯示 GSP 融入數學教學確有助益學生學習平行四邊形。但值得注意的是，其結果有一項為在「GSP 動態教師展示」教學模式比「GSP 動態學生操作」教學模式更適合國中階段學生。分析其原因，「GSP 動態學生操作」教學模式可能是學生個別操作，在沒有同學之間進行討論下，也許是造就學習成效不彰的因素。而國外學者 Skemp(1989)也曾提出數學學習可藉由討論，透過意見交流的方式進行合作學習。另外國內學者朱敬先(1999)也提出合作學習強調學生以主動合作的學習方式，取代教師主導的教學，藉以培養學生主動求知的能力，發展合作過程中的人際溝通能力，從而養成其團隊精神。因此研究者想探討是否能藉由合作學習法，來進行小組內的討論，讓學生更能透過討論來了解 GSP 幾何軟體所呈現的教材內容，進而提升學習成效。因此，研究者以二次函數的圖形做為本次研究的主題，利用 GSP 動態幾何軟體來進行學生動手操作的學習，進而探討學生在合作學習與個別學習模式下，兩組學生在學習成效上的差異，也探討將學生分成高、中、低

(18)

三種學業能力和不同教學模式下，是否有交互作用影響，再者，也進行不同性別和不同教學模式下，是否有交互作用的影響之研究。

第二節研究目的與待答問題

一、研究目的本研究旨在探討學生在自行操作 GSP 幾何軟體的方式下學習「二次函數的圖形」的單元，是否能藉由合作學習法來提升學生的學習成效，因此本研究的目的如下： (一)探討學生在自行操作 GSP 幾何軟體的方式下，接受不同教學模式(合作學習和個別學習)，對於不同學業能力(高、中、低)的學生，學習二次函數圖形的影響。 (二)探討學生在自行操作 GSP 幾何軟體的方式下，接受不同教學模式(合作學習和個別學習)，對於不同性別的學生，學習二次函數圖形的影響。二、待答問題根據本研究的研究目的而相對應形成的待答問題如下： (一)接受不同教學模式(合作學習和個別學習)與不同學業能力(高、中、低) 的學生，對於學習二次函數圖形是否有顯著的交互作用？ 1.接受不同教學模式(合作學習和個別學習)與不同學業能力(高、中、低)的學生，對於學習二次函數圖形在概念理解的題型上是否有顯著的交互作用？ 2.接受不同教學模式(合作學習和個別學習)與不同學業能力(高、中、低)的學生，對於學習二次函數圖形在問題解決的題型上是否有顯著的交互作用？ (二)接受不同教學模式(合作學習和個別學習)與不同性別的學生，對於學習二次函數圖形是否有顯著的交互作用？ 1.接受不同教學模式(合作學習和個別學習)與不同性別的學生，對於學習二次函數圖形在概念理解的題型上是否有顯著的交互作用？ 2.接受不同教學模式(合作學習和個別學習)與不同性別的學生，對於學習二次函數圖形在問題解決的題型上是否有顯著的交互作用？

(19)

第三節名詞解釋

針對本研究所提及之重要名詞，其解釋如下：一、二次函數(quadratic function) 在兩個變數 x 與 y 的關係式中，如果給定一個變數 x 的值，就恰好可 得到一個對應變數 y 的值，則稱 y 是 x 的函數，且 x 為自變數，y 為應變數， 而形如 2 yax bx (一般式)和c ya x( h)2 k(標準式)，a  的函數，0 自變數 x 的最高次為二次，稱為二次函數(quadratic function)。 二、GSP

GSP 為動態幾何畫板(The Geometer’s Sketchpad)的簡稱，是一個適用於幾何教學與研究的軟體，可以針對所繪製的幾何圖形進行操作，並能將操作結果作為教師和學生提供一個觀察和探索幾何圖形的環境，其最大特色是能以動態的方式呈現。本研究使用 GSP4.03 版作為教學媒體來進行實驗教學。三、教學模式教學模式是指教師在教學上使用不同的方式來進行教學。本研究使用兩種教學模式，其一為「合作學習法」，係指採用合作學習法的分組方式，學生在電腦教室根據老師的引導，小組一起討論並自行操控滑鼠進行學習，其二為「個別學習」，係指在未分組的情形下，學生在電腦教室根據老師的引導，一個人操作一台電腦自行操控滑鼠進行學習。四、學習成效學習成效指的是學習者經過學習之後，應用知識來解決問題的能力。本研究採用自編二次函數的圖形單元階段性成就測驗之分數來探討學習成效。五、合作學習所謂合作學習法，是將學生分組來進行學習的方法，其分組方式是考量能力、性別或其他因素，小組內的成員彼此協助，以提升組內每個人的學習成效，並且透過分工來共同合作完成教師指定之目標。本研究採用異質性分組，以 S 形的分組方法，讓各小組內皆有高、中、低三種程度的學生，以及不同性別的學生，以三至四人為一組。

(20)

第四節研究範圍與限制

一、研究範圍 (一)研究母體與樣本由於人力、時間、經費及資源等因素，本研究選定新竹市某國中為研究母體，並以便利抽樣選定九年級兩個班級學生作為研究樣本。 (二)研究主題本研究之主題僅限於國民中學數學領域第六冊第一章「二次函數」第一節「二次函數的圖形」及第二節「配方法與二次函數的圖形」，包含幾個概念，如：

y



ax

2的圖形、

y



ax

2



k

的最大值與最小值、二次函數圖形的上下移動、

y



a x

(



h

)

2



k

的圖形及二次函數圖形的左右移動，但不包含配方法的探討，因配方法較屬於代數算式的操弄，和圖形較不相關，故不在本研究主題之內。二、研究限制本研究內容是以二次函數的圖形為主，其他單元不在本研究範圍內，對於其他單元須進行其他研究，不宜作過度推論。

(21)

第二章文獻探討

本研究主要是在探討學生在自行操作 GSP 幾何軟體的方式下，融入合作學習法對學生學習二次函數的圖形的學習成效，因此本章進行相關的文獻探討，總共分成三節。第一節為二次函數課程的內涵及學習問題探討，第二節為動態幾何軟體教學，第三節為合作學習法。

第一節二次函數課程的內涵及學習問題探討

本研究主題與二次函數的圖形相關，本節就「二次函數課程的教材地位分析」、「學生學習二次函數的困難之處」及「二次函數的相關研究」來進行探討。一、二次函數課程的教材地位分析函數是臺灣學生從國中到大學都必須要學習的數學概念(謝豐瑞、陳材河，1997)。其實函數的概念在國小階段第十二冊「數量關係與解題」就有初步的介紹，例如一些生活中的例子，一杯奶茶 20 元，兩杯多少元？三杯多少元？四杯多少元？更甚至 10 杯共多少元？抑或是月份和天數的概念，除了二月，大月如一、三、五、七…等月分，天數是 31 天，四、六、八…等月分，天數是 30 天，雖然未正式介紹「總價是數量的函數」以及「天數是月分的函數」，但這些例子都具有函數的概念在內，只是學生要進入國中階段，才會對函數的相關名詞和定義做完整的介紹。而國中階段函數相關概念會從七年級的「變數與函數」開始介紹起，接著會介紹「線型函數的圖形」，到了九年級才會介紹「二次函數」。學習二次函數須具備許多先備概念，先要學習「一元一次方程式」的「以符號列式」的概念；學過「直角坐標平面」的概念，並會畫出「二元一次方程式的圖形」；接著可以畫出「線型函數的圖形」，並且已具備「一元二次方程式」以及「線對稱圖形」的概念，有了這些相關的先備概念，對於二次函數的學習，才不會有太大的阻礙。而二次函數主要分成三個小節，第一節簡易二次函數的圖形、第二節配方法與二次函數的圖形及第三節二次函數的應用問題，本研究採用翰林版第六冊第一章二次函數的第一節和第二節來進行教學實驗，而在未來發展，會應用到的相關課程有高中課程的多項函數、圓錐曲線以及大學課程的微積分，所以在國中二次函數單元算是承先啟後的重要章節，既是將之前所學的課程加以應用，也為未來的課程

(22)

奠定良好基礎，其二次函數教材地位分析如圖 2-1。二、學生學習二次函數的困難之處 Zaslavsky(1997)認為在二次函數的學習過程當中，如果先學習線型函數及一元二次方程式的相關概念，之後再學二次函數，以這樣的學習順序，反而容易造成學生學習二次函數的阻礙。Zaslavsky 同時提出在二次函數的學習時，學生最常出錯的五種迷思概念，如下所示： (一)學生在學習二次函數時，經常只看到部分的函數圖形，而忽略了眼睛所見的只是完整的函數圖形的一部份而已，實際上，其函數圖形是無限延伸的。 (二)學生可能在學習的次序上，先學習一元二次方程式之後，再學習二次函數，往往導致將一元二次方程式及二次函數之間的概念理解不清楚。就像某兩個等價關係的一元二次方程式，如 2 3 4 0 x  x  和 2 2x 6x 8 0     ，其所得的解是一樣的；但若以二次函數來看， 2

3

4 y



x



x



和 2

2

6

8 y

 

x



x



卻是兩個不同的二次函數，其圖形的開口方向、開口大小、頂點及與兩軸的交點坐標等相關概念都不相圖 2-1 二次函數教材地位分析圖

先備概念

一元一次方程式

二次函數

未來發展

直角坐標平面二元一次方程式線型函數及其圖形一元二次方程式圓錐曲線 (高中課程) 微積分 (大學課程) 簡易二次函數的圖形配方法與二次函數的圖形二次函數的應用問題線對稱圖形多項函數 (高中課程)

(23)

同。但學生在學習過程中，可能因其先學了一元二次方程式，其解是相同的，而誤解二次函數也是相同的。 (三)學生在二次函數的學習過程當中，容易將線型函數的先備經驗類推至二次函數之中，例如，線型函數上任三點共線，因此常常誤以為二次函數的圖形也是一條直線。 (四)學生可能會認為

y



ax

2



bx



c

，其中

a 

0

，此為一個二次函數，但當 b = 0 及 c = 0 時，反而就認為這種函數就不是二次函數了，因此學生無法將二次函數的概念做有效地運用。 (五)學生可能會認為只要任意找到其中一個坐標值，就可以決定二次函數的頂點的坐標，例如學生可能認為

y



ax

2



bx



2

和

y



ax

2



bx



5

會有相同的頂點。除了Zaslavsky 提出上述的五種迷思概念，徐敏媛(2011)在她所做的研究中也歸納整理出九年級學生在學習二次函數概念時，常犯的錯誤類型分成四類型，共 11 種： (一)對二次函數代數式解釋的錯誤： 1.不了解二次函數中「二次」所代表的意義。 2.將二次函數

y



ax

2



bx



c

和一元二次方程式ax2 bx c 0的概念混淆。 3.在將一般式

y



ax

2



bx



c

轉換成標準式 2

(

)

y



a x



h



k

，將係數a當成 1，或是從標準式中確認對稱軸為何的時侯所發生的錯誤。 (二)對二次函數圖形解式的錯誤： 1.只關心圖形看得到的部分，忽略圖形隱含的解析性質。 2.認為拋物線的部分圖形是線性的。 3.對稱軸概念的錯誤。 (三)二次函數代數式表徵與圖形表徵之間轉換的錯誤： 1.不了解

y



ax

2的係數a與圖形的關係。 2.不了解圖形的左右平移與代數式

y



a x

(



h

)

2



k

中，係數

h

和

k

的意義。 (四)二次函數的特殊點(與兩軸的交點以及頂點)的錯誤： 1.認為二次函數的頂點都在

y

軸上。 2.不了解二次函數

y



ax

2



bx



c

中判別式 2 4 b  ac與x軸交點個數的關係。 3.不了解二次函數

y



a x

(



h

)

2



k

的頂點坐標( , )h k 與 2

y



ax



bx



c

的

(24)

關係。研究者在教學現場上也發現了幾個學生常犯的錯誤類型： (一)線型函數描繪出兩點即可畫出其圖形，學生可能會以線型函數的方式，描繪出兩點即畫出二次函數的圖形，但實際上必須多描繪幾個坐標點才能確定二次函數圖形的模樣，這與 Zaslavsky(1997)所提出的觀點，學生常將線型函數的經驗類推到二次函數上來使用是相符的。 (二)二次函數是一條平滑的曲線，學生常常將找到的坐標點以折線連接起來，將折線的圖視為二次函數圖形，這也是和 Zaslavsky(1997)所提到的將線型函數的經驗類推到二次函數圖形上來使用是相符的。 (三)二次函數延伸至遠方的部分實際上還是平滑的曲線，因看起來很像直線段，學生常誤解遠方為直線。 (四)學生在將 2 ( ) ya xh k的圖形左右平移時，常常將向右平移 m 個單 位當作在 x 項之後 m ，將向左平移 m 個單位當作在 x 項之後 m ，例如：將 2 2( 3) 5 y x  向右平移 2 個單位，新的二次函數應是 2 2 2( 3 2) 5 2( 5) 5 y x    x  ，但學生常誤認為向右為加，向左為減，即 2 2 2( 3 2) 5 2( 1) 5 y x    x  ，這和徐敏媛(2011)所提及的第三類第二種錯誤類型有著相同看法。綜上所述，研究者藉由整理二次函數教材地位分析以及學生常犯的錯誤類型，盼能在研究的教學實驗中減少學生在二次函數單元上學習的錯誤，並且讓學生更能了解二次函數所需要學習的性質。三、二次函數的相關研究分析近年來國內所做關於二次函數的研究，研究者歸納以下幾點特性： (一)新舊教學法的比較大多數研究在比較新的教學方法與傳統講述法的教學成效，例如林佳慧(2003)和林星秀(2001)都研究使用 GSP 輔助教學和傳統講述教學對國二學生學習函數課程的成效；黃昱霖(2012)比較「GeoGegra 電腦輔助教學」與「傳統講述教學」對國三生學習二次函數圖形之成效；葉慧玲(2011) 探討利用 Excel 電腦輔助教材，結合問題中心教學的數位學習教學模式，與「傳統講述教學」進行二次函數圖形教學的比較。除了林星秀(2001)的實驗組和控制組的學習成就沒有顯著差異外，其他的新方法學習成效多數顯

(25)

著優於傳統教學法，代表新的教學法有其優勢存在，能提升學生的學習成效。 (二)教材動態呈現與傳統講述教學法比較，教材多可動態呈現(林佳慧，2003；林星秀， 2001；黃昱霖，2012)；另外，廖家瑩(2010)比較激發式動態呈現與非激發式動態呈現的教學，探討學生的學習成效，其實驗組學習成效顯著優於控制組；而謝謹謙(2011)利用認知診斷測驗探討激發式動態教學的成效，其實驗組與控制組無顯著差異，這兩位也都將教材動態呈現。 (三)研究範圍大小不同二次函數在學校課程內容基本上分成三小節，第一節為簡易二次函數的圖形，第二節為配方法與二次函數的圖形，第三節為二次函數的應用問題。國內有關二次函數的研究，教學範圍有所不同，有的是整個二次函數單元(林佳慧，2003；林星秀，2001；黃昱霖，2012)，有的只取第一節，簡易二次函數的圖形(廖家瑩，2010；謝謹謙，2011)，來進行教學的研究。 (四)研究方向多元除了新舊教學方法的比較，徐敏媛(2011)進行二次函數錯誤類型的分類及探討補救教學成效，其研究結果主要有：1.二次函數概念有 11 種錯誤類型。2.二次函數概念補救教學對於改善學生常犯的錯誤類型有顯著成效而且有保留效果；而胡惠茹(2008)探討的是國三學生在不同表徵型式如：圖形、數對、代數和文字敘述的二次函數問題的解題表現，其研究主要發現：1.不同數學能力學生在解題策略異同，高數學能力學生最喜歡文字敘述題，而中、低數學能力組最喜歡數對表徵題；2.不同性別的學生在不同表徵型式的解題表現沒有顯著交互作用。綜合以上的文獻分析，給了研究者一些啟發：1.除了研究與傳統講述教學的比較，還是有許多題材是二次函數單元可以進行關注的。2.關於二次函數單元，學生在學習過程中，其中的各個概念形成，如果有將教材作動態呈現，對於學生多有助益，因此研究者想藉由 GSP 動態幾何軟體將二次函數單元的教材作動態呈現，讓學生能有更好的學習成效。

(26)

第二節動態幾何軟體教學

在這二十一世紀的開端，資訊科技的發展快速，國人使用資訊科技已趨於普遍，而在教育上，資訊科技的快速成長使得融入教學已成為全球教育共同的趨勢，國內建立各種教學模式以探討學習成效的研究也同時蓬勃發展(袁媛、許錦芳，2007)。教育部(2008)提出的「中小學資訊教育白皮書」中也確實提到「培養學生應用資訊科技解決問題的能力」和「培訓具備資訊科技應用能力的教師」的目標。實際上，近幾年也愈來愈多教師願意嘗試資訊科技融入教學，而在數學的領域裡，最常使用「動態幾何軟體」來進行教學，而在眾多的動態幾何軟體中，又以The Geometer’s Sketchpad(簡稱GSP)發展的時間最早，所以相關研究也累積較多，如：「高雄市高職學生運用GSP軟體學習三角函數成效之研究」、「國小五年級學生使用電腦軟提GSP學習三角形面積成效之研究」、「探討GSP軟體融入數學教學對國小五年級學童學習複合圖形面積之成效」、「幾何動態軟體融入教學的模式對國中學生學習平行四邊形的影響研究」、「高雄市國二學生使用GSP電腦輔助教學學習三角形全等成效之研究」、「國中相似形GSP電腦輔助教學之成效研究」等，皆是使用GSP幾何軟體融入數學教學來探討學習成效(余酈惠，2003；李春生，2006；曾意鈞，2012；楊子賢，2011；戴錦秀，2002；蘇聖文，2007)，徐千和(2013)更是蒐羅近年來多篇有關GSP的研究，並以後設分析來探討GSP融入數學教學的學習成效，從中可以知道，使用GSP 來進行的研究不在少數。對研究者本身而言，GSP動態幾何軟體的操作甚為熟捻，且GSP在資訊呈現設計上較容易為操作者所接納。因此本節就「動態幾何軟體GSP的特色及功能」以「GSP探討教學成效的相關研究」分別做探討。一、動態幾何軟體 GSP 的特色及功能

動態幾何軟體 GSP 是由美國 Key Curriculum Press(簡稱 KCP)公司在美國國家科學基金會(National Science Foundation)資助幾何研究計畫下而問世的產品，從 1987 年推出第 1 版，隨著時間的演進，2001 年推出第 4 版，內容加入遞迴迭代的工具，擴大程式分析和繪圖能力，拓展了代數和微積分的相關應用，目前還是以第 4 版為最多人使用，至今，GSP 已發展至 5.05 版，其特色分述如下：

(27)

(一)操作介面簡易 GSP 採用尺規作圖的方式，利用滑鼠來操作點、線、圓等作圖工具，來創造出各式各樣的幾何圖形，並且創造出更精準的圖形，能降地學生的認知負荷，其操作功能簡易，國小學生也能順利操作，適合各階段的學生使用，更適合教師在教學中使用。 (二)動態視覺化動態視覺化(dynamic visualization)是 GSP 軟體最重要的特色，使用者可以觀察到幾何圖形，在保持幾何性質的不變性，而產生的動態呈現，有助於學生建立完整的幾何圖形概念心像，了解幾何性質的意義。 (三)多重表徵的呈現 GSP 提供文字表徵、數值表徵、圖形表徵、表格表徵等多重表徵的呈現，讓學生能在代數與幾何的多種不同表徵之間，做有效的連結，來進行不同表徵的轉換。 (四)記錄作圖功能使用者在繪製幾何圖形時，GSP 會記錄每一個繪圖步驟，隨時可以取用先前繪製好的物件，來繪製之後想繪製的圖形，除了省時的好處外，也可看到不同時間所繪出圖形的異同，也可查看學生的思考歷程，是否出現錯誤觀念而導致畫出不同的圖形。 (五)按鈕的設計教師可以設計按鈕，來佈置 GSP 的學習環境，讓學生除了 GSP 提供的環境功能外，可直接點選按鈕，顯現或隱藏幾何圖形或文字說明，來進行學習，讓學生的操作更為簡單，教師也可設計按鈕，配合教學的進度，隱藏尚未出現的內容，或是佈置學習環境時，不必要出現的內容。由以上可知，GSP 所提供的直覺操作、多樣性、互動及便利性，可以提供更多空間讓學生進行探究活動(Bennett,1999)。GSP 的功能強大且眾多，其最重要的動態功能是研究者想要在研究中利用的，藉由此功能的呈現來提升二次函數單元的學習成效。二、以 GSP 探討教學成效的相關研究 GSP 在臺灣的發展已超過十年，所累積的實徵性研究也達到相當的數量(徐千和，2013)。此部分即是對以 GSP 探討教學成效的研究進行文獻探討，大部分的研究基本上是以教師展示 GSP 模式和傳統教學法做比較，或者是以學生自行操作 GSP 模式和傳統教學法做比較，來探討教學成效，尚

(28)

未有人對「教師展示 GSP 模式」和「學生自行操作 GSP 模式」兩種模式的教學成效做比較。直到楊子賢(2011)探討 GSP 融入教學的兩種模式，對國中學生學習平行四邊形的影響，才有了比較，其實驗採用準實驗研究法，有兩組實驗組，一為 GSP 動態教師展示組，另一為 GSP 動態學生操作組，並安排控制組接受傳統講述教學，其研究結果發現：（一)在成就測驗上，實驗組顯著優於控制組；（二）「GSP 動態教師展示」教學模式比「GSP 動態學生操作」教學模式更適合國中階段的學生；（三）接受不同教學模式與不同性別的學生，在數學學習成就上沒有顯著的交互作用。楊子賢(2011)認為「GSP 動態教師展示」教學模式比「GSP 動態學生操作」教學模式更適合國中階段的學生，他並分析其原因，可能「GSP 動態學生操作」教學模式是學生個別操作，在沒有同學之間進行討論下，也許是造就學習成效不如預期好的因素，但楊子賢也提到可以使用不同的教學策略或方法，使 GSP 學生操作教學模式達到更好的學習成效，因此研究者希冀能藉由其他方法來提升「GSP 動態學生操作」教學模式的學習成效。在此先將國中階段使用 GSP 學生操作教學模式的研究進行整理分析，主要有以下特點： (一)多為準實驗研究國內對於學生自行操作 GSP 來進行融入數學教學的研究顯示，大多採用量化的準實驗研究法，在不同的數學單元上，探討 GSP 輔助教學和傳統講述教學的學習成效(尤冠龍，2006；李春生，2006；林佳慧，2003；林星秀，2001；姚文仁，2007；楊子賢，2011；葉進安，2010)。 (二)研究主題多元研究主題相當地多，分別為函數圖形與二元一次方程式圖形(尤冠龍， 2006)、三角形(李春生，2006；姚文仁，2007)、二次函數(林佳慧，2003；林星秀，2001)、平行四邊形(楊子賢，2011)、圓(葉進安，2010)…等主題，但都是與幾何相關的課程。 (三)研究結果不一有研究顯示，實驗組學生的學習成就顯著優於控制組(李春生，2006；林佳慧，2003；葉進安，2010)；但也有研究顯示，實驗組學生的學習成就和控制組無顯著差異(尤冠龍，2006；林星秀，2001；姚文仁，2007)，這和楊子賢(2011)的研究中實驗組二「GSP 動態學生操作組」和控制組沒有

(29)

顯著差異的結果是相符的，其中要考慮不同程度(高、中、低分組)，才可能有顯著差異。另外，有些研究有關注於不同性別是否在學習成效上有所差異，其結果發現性別不是主要因素(楊子賢，2011；葉進安，2010)，但吳鳳萍(2002) 的實驗研究在性別方面發現，男生在實驗組與控制組的後測成績上有顯著差異，兩組女生則無顯著差異。另外，臺灣八年級學生在 TIMSS 2003 中的數學成就來看，女生的分數(589 分)雖然比男生的分數(582 分)稍微高一點，但沒有達到顯著差異，但在代數和幾何上的平均得分都較男生高，並且達到顯著差異(曹博盛，2005)。而臺灣的八年級學生在 TIMSS 2007 年的數學得分，女生(599 分)雖然比男生(598 分)略高，但並未達顯著差異，在代數和幾何的主題上，女生平均得分較男生高，但也都未達顯著差異，但以國際平均看來，女生在代數和幾何上的表現都顯著優於男生的表現。盧雪梅和毛國楠(2008)在國中基測性別差異的分析研究結果發現，全體受試者的男生和女生在概念理解以及代數和幾何的分項上是沒有顯著差異的，但在問題解決的能力表現上是顯著優於女生的。盧雪梅和毛國楠在國中基測差別試題功能(DIF)分析中提到，女生在代數的部分比較占有優勢，而男生是在幾何的部分以及問題解決比較占有優勢的，就本研究主題而言，二次函數雖屬於代數的部分，但函數圖形又屬於幾何的部分，算是橫跨兩大主題，所以代數和幾何，都是研究者必須要關注的。另外，盧雪梅和毛國楠的研究是以國中基測為範圍，當中包含了國中三年所有主題的題目，當然也涵蓋所有主題的問題解決能力層次的題目，其牽涉到的概念性相對而言是非常複雜的，所以在問體解決能力上，就出現了顯著差異的情形。因此，研究者想要研究的主題─二次函數的圖形中，二次函數不僅是代數的範疇，其函數圖形也可歸類為幾何的內容，所以研究者想要將動態幾何軟體融入此次的教學研究裡，並在研究中加入性別和不同程度(高、中、低分組)的變項。除此之外，根據上述文獻整理，對於國內學者研究學生自行操作 GSP 來進行融入數學教學，實驗組和控制組的學習成效無顯著差異的，也不在少數。而且楊子賢(2011)也提到可以使用不同的教學策略或方法，使學生自行操作 GSP 的方式達到更好的學習成效。因此，研究者欲探討是否能藉由融入合作學習法，來提升學生自行操作 GSP 融入教學的學習成效。

(30)

第三節合作學習

合作學習從 1970 年代以來，隨著時代潮流蓬勃發展，在學術領域上也有相當的成果，有許多不同面向及角度切入的研究都是探討關於合作學習；近年，資訊融入教學來提升教學成效，也多有研究持正向的肯定；將兩者做結合，資訊融入教學輔以合作學習法的研究也是許多人關注的焦點，其成效也是不錯的。而本研究想要進行的是在動態幾何軟體融入下，比較不同的教學模式，探討國中學生學習二次函數圖形的學習成效，實驗組所使用的教學模式即為合作學習，因此本節就「合作學習的特質」和「結合資訊融入教學與合作學習的實徵性研究」來做深入地探討。一、合作學習的特質在教學過程當中，學生以主動合作的學習方式，取代教師主導的教學方式，來培養學生主動求知的能力，發展合作過程中人際溝通的能力，進而培養團隊精神，其特質有下列六項(黃政傑、林佩璇，1996)： (一)異質分組依學生的學習能力、性別、特質及社經背景……等因素，將學生分配到不同的小組之中，使每一小組內有不同程度、不同性別……等相異特質的學生，其目的是希望學生能有不同的學習對象，分享彼此的經驗和看法，讓學生能吸取更多樣的觀點，進而達到學習目標。 (二)積極互賴積極互賴是指學生能夠了解自己和小組內的同學是一個生命共同體，個人的成功是基於整個小組成功。彼此相互了解與信賴，小組成員之間的互動也會提升(黃政傑、吳俊憲，2006)當然，倘若小組失敗，個人也就失敗，因此，小組間的每個人必須共同努力，積極完成自己的任務，才能產生互相依賴的關係，達成小組目標。 (三)面對面的助長式互動透過面對面的助長式互動，小組內的學生可以藉由共同討論或切磋來互相幫助，並且可以互相鼓勵，來達成共同目標，藉此助長彼此學習的成功。 (四)評鑑個人學習績效小組的成功是取決於組內每一個人的成功，而不是以小組內某一個人成員的成功來代表整個小組的表現，因此評鑑小組內每一個學生的學習情

(31)

形，來幫助整個小組達到共同的目標。 (五)人際技巧合作學習的小組成員要學習的有兩項，一為與學業相關的任務工作，另一為人際技巧和小團體技巧，此種合稱為小組工作，基於團體動力學的觀點，小組工作能力愈高，任務工作完成度也愈高，人際技巧包含彼此認識並互相信任、相互接納並支持、正確無誤地進行溝通，並且能有建設性地解決衝突，將有助於合作學習。 (六)團體歷程小組內學習效能的展現，有賴於每個人檢討和反省學習過程及其表現，並回饋於小組，使其增進團體效能。Johnson 和 Johnson(1994)認為當小組遇到困難或問題時，小組成員回饋得愈多，愈能增進學習成效。本研究根據以上合作學習的特質，採異質性分組，以三至四人為一組，以 S 形的分組方法，讓各小組內皆有高、中、低三種程度的學生，以及不同性別的學生，希冀小組內不同特質的學生，透過此分組方式，有效地進行溝通與討論，並且互相給予鼓勵，從中找到學習數學的樂趣，達成學習目標。二、合作學習的實徵性研究本研究是在探討在動態幾何軟體融入下，比較合作學習和個別學習兩種不同的教學模式，對國中學生學習二次函數圖形的影響。因此，此部分對「使用資訊融入教學輔以合作學習探討數學學習成效」的研究作分析，發現有以下特點： (一)有效提升學習成效王永賢(2004)進行結合資訊融入教學與合作學習於國中數學課之行動研究，發現學生的前後測有顯著的進步。龍榕淑(2006)則採用準實驗法探討同儕合作學習與電腦輔助教學對國一學生學習統計單元之成效，其研究發現：實驗組學生在學習成就進步分數大於控制組。許文松(2009)也以準實驗法比較「資訊融入教學輔以合作學習」與「傳統講述教學法」對國三學生數學學習成效，實驗組顯著優於控制組。而謝怡倫(2009)同樣以鷹架學習對學習成效之影響的研究，其中利用合作學習搭配 GSP 融入教學的組別，其成就測驗顯著優於單純使用 GSP 融入教學的組別，也就是說加入了合作學習，確實提升 GSP 融入教學的成效。

(32)

(二)多為量化研究除了王永賢(2004)的研究為行動研究外，研究此方面主題大多數採用準實驗研究法(許文松，2009；龍榕淑，2006；謝怡倫，2009)，多為量化研究，可以明確控制許多變項，來探討學習成效上的差異。 (三)資訊工具種類眾多在使用資訊融入教學輔以合作學習探討數學學習成效的研究裡，研究者使用的資訊工具不同：王永賢(2004)使用的資訊工具為網路教學以及自行設計的 e 化環境；龍榕淑(2006)使用 Excel 軟體來進行教學；許文松(2009) 使用的則是 PowerPoint 以及 Geogebra 幾何軟體；謝怡倫(2009)則使用 GSP 幾何軟體來進行教學。相關研究使用到的資訊工具種類眾多，但都是可以融入合作學習來探討教學成效。 (四)研究主題多元在數學課程上所要探討的主題非常多元：有直角坐標平面(許文松， 2009)、統計圖表(龍榕淑、2006)、三角形與四邊形(王永賢，2004)、平面圖形(謝怡倫，2009)等主題。由此可知，使用資訊融入教學輔以合作學習探討數學學習成效的研究主題，是可以使用在不同的數學課程內容之下的。 (五)分組方式不一過去的研究分組方式不大相同，王永賢(2004)所研究的為行動研究，只有一組學生施以資訊融入加合作學習法，探討對學生的影響；龍榕淑 (2006)的研究分成兩組，實驗組實施同儕合作學習與電腦輔助教學，控制組實施電腦輔助教學，比較兩組的學習成效差異；許文松(2009)分成兩組，實驗組施行「資訊融入教學輔以合作學習」，控制組施行「傳統講述教學」，並比較兩組的學習成效；謝怡倫(2009)將學生分成三組，第一組為合作學習加資訊融入教學，第二組為資訊融入教學，第三組為合作學習法的教學，並探討三組學生的學習成效。根據以上研究探討「使用資訊融入教學輔以合作學習探討數學學習成效」，雖然使用的研究方法不盡相同，使用的資訊工具也不相同，但都配合合作學習的使用，而學生的學習成效有顯著提升(王永賢，2004)，或是實驗組顯著優於控制組(許文松，2009)，有研究為合作學習加資訊融入教學的組別顯著優於資訊融入教學的組別(謝怡倫，2009)，有的研究雖未在統計上探討顯著性，但其實驗組學生進步分數大於控制組，也算在某種程

(33)

度上達到效果(龍榕淑，2006)。總體來說，這樣的教學方式皆能提升學生的學習成效，因此更增進了研究者想要介由合作學習的教學模式，來進行教學實驗，檢視融入 GSP 動態幾何軟體的教學，是否能提升國中學生自行動手操作 GSP 動態幾何軟體的學習成效。合作學習自從 1970 年代以來開始蓬勃發展，許多方法相繼問世，例如學生小組成就區分法(STAD)、小組遊戲競賽法(TGT)、拼圖法(Jigsaw)、拼圖法第二代(Jigsaw II)、團體探究法(GI)、小組協力教學法(TAI)、共同學習法(LT)及協同合作法(Co-op Co-op)，合作學習雖然有許多方法，而且各種方法都有其特色及適用時機與範圍，教師在教學時，可以根據不同的時機、年級或教材而採取不同的設計(黃政傑、林佩璇，1996)。而本研究設計採用的合作學習教學模式為學生小組成就區分法，是由 Slavin 在 1978 年發展出來的，此法是教學現場當中最容易實施的一種合作學習方法，因為它所使用的教材內容、標準和評鑑方式都和傳統的教學方法沒有太大的差異，是教師最容易上手、學生最容易融入情境的方法之一。其方法的實施步驟為教師先進行全班性的授課，介紹教材內容，接著是分組學習，教師依照學生的學業能力、特質、性別及社會背景等因素，進行異質性的分組，一起學習教師指定的教材內容，透過討論、發現及釐清問題以達到精熟該單元內容，再來是學習評量，實施測驗來評鑑每個人的學習成果，最後給予表現較好的小組獎勵。

(34)

(35)

第三章研究方法

本章進行研究方法的討論，總共分成四節。第一節為研究設計，第二節為研究對象，第三節為研究工具，第四節為資料分析。

第一節研究設計

本研究的研究目的主要是探討在不同教學模式下融入動態幾何軟體對國中學生學習二次函數圖形的影響，本節分為四個部分，分別為使用的研究法、研究架構、研究變項與假設及研究流程。一、準實驗研究法本研究因考量到現有的班級無法變動，各班的班級課表也有所不同，因此無法將接受實驗的學生以隨機分派的方式，分成等組的實驗組和控制組。因此研究者從新竹市某國中九年級 25 個班當中，選取兩個班，此國中入學時即以新生能力測驗，採 S 型常態編班，所以指定一個班為實驗組，另一班為控制組，故研究者採用的研究法是不等組前測後測的準實驗研究法來探討使用動態幾何軟體融入教學的不同模式，對國中學生學習二次函數的影響。實驗設計如表 3-1。實驗組與控制組學生於實驗前均接受二次函數先備概念理解能力之測驗，來確定兩組學生是否具備相同的二次函數先備概念理解能力。實驗組在前測之後，實施學生自行操作 GSP 幾何軟體，並使用合作學習法之教學來學習二次函數單元；控制組在前測之後，實施學生自行操作 GSP 幾何軟體，並使用個別學習法之教學來學習二次函數單元，教學時間皆為兩節課，實驗結束後，兩組皆進行二次函數單元的成就測驗，即後測，分析兩組後測成績是否有顯著差異。在實驗研究裡，常常發生受試者效應(subject effects)，這會對受試者的行為表現有所影響，進而影響實驗結果。受試者效應分別有霍桑效應 (Hawthorne effect)、強亨利效應(the John Henry effect)以及控制組憤慨性的意志消沉(resentful demoralization)。霍桑效應指的是研究者通常在實驗組使用新的教學方法，實驗組學生得知為實驗組，受到特別關注，容易表現得更好；強亨利效應則是指控制組學生得知本身是被拿來與實驗組做比較，

(36)

為了不甘示弱，想要贏過實驗組，反而更積極表現；憤慨性的意志消沉指的是控制組得知實驗組使用新的教學方法，而自己這組卻沒有，感到憤恨不公平，甚至表現不積極，導致在後測上遜於平常(王文科、王智弘，1986)。研究者為避免受試者效應的發生而影響實驗結果，沒有讓兩組學生得知哪一組為實驗組，哪一組為控制組，意即不讓學生知道其中一班有使用合作學習法，另一班則沒有，這樣的處理也就避免了受試者效應的發生。表 3-1 實驗設計表組別前測實驗處置後測實驗組 TE1 XE TE2 控制組 TC1 XC TC2 XE 表示學生自行操作 GSP 幾何軟體，並使用合作學習法之教學。 XC 表示學生自行操作 GSP 幾何軟體，並使用個別學習法之教學。 TE1 表示實驗處置前對實驗組學生實施的二次函數先備概念理解之測驗。 TE2 表示實驗處置後對實驗組學生實施的二次函數單元的成就測驗。 TC1 表示實驗處置前對控制組學生實施的二次函數先備概念理解之測驗。 TC2 表示實驗處置後對控制組學生實施的二次函數單元的成就測驗。二、研究架構本研究架構說明如圖 3-1。 自變項 1.教學模式合作學習法個別學習法 2.學業能力 (高、中、低) 3.性別 依變項 二次函數單元成就測驗成績圖 3-1 研究架構圖 控制變項 1.教學時間 2.教學進度 3.教材內容 4.前測成績

(37)

三、研究變項 (一)自變項 1.教學模式：實驗組使用學生自行操作 GSP 幾何軟體，並使用合作學習法之教學，控制組使用學生自行操作 GSP 幾何軟體，並使用個別學習法之教學，兩組皆學習二次函數單元，來檢驗不同的教學方法是否會造成學生學習成效上的差異。 2.學業能力：分成低學業能力、中學業能及高學業能力三組。分組方式以 101 學年度上學期第一次與第二次段考數學成績平均為依據，由低至高排列，前 33% 為低學業能力組，後 33%為高學業能力組，中間剩餘部分為中學業能力組。實驗組與控制組之各學業能力人數表如表 3-2。表 3-2 實驗研究各組之各學業能力人數統計表組別低能力中能力高能力總和實驗組 11 12 11 34 控制組 10 11 10 31 總和 21 23 21 65 3.性別：探討不同性別的學生在接受對於不同的 GSP 動態軟體融入的教學模式是否產生不同的學習成效。 (二)控制變項 1.授課教師：本研究實驗組與控制組的授課教師為同一人，亦為本研究之研究者，且授課教師有三年數學科教學經驗，能夠確實掌握授課時間，也能注意兩組間的教學進度是否一致。 2.教材內容：兩組的教材內容都是同樣單元，皆為二次函數，並使用相同的 GSP 幾何軟體教材，教材內容包含現行國民中學數學科第六冊第一章第一節簡易

(38)

二次函數的圖形，以及第二節配方法與二次函數的圖形，第二節所取的教材內容範圍主要是

y



a x

(



h

)

2、二次函數圖形左右平移和 2

(

)

y



a x



h



k

，但不含配方法，因配方法較屬於代數式的運算，比較不適合動態幾何軟體的融入教學。 3.前測成績：前測採用的是二次函數單元先備概念理解之測驗，包含「直角坐標平面」、「二元一次方程式的圖形」、「函數與其圖形」、「線對稱圖形」，來檢測兩組學生在學二次函數單元之前，是否具備了相同的先備概念理解能力。 (三)依變項本實驗研究的依變項為二次函數單元成就測驗的成績。四、研究流程本研究自民國一百年六月開始進行資料的收集，並與指導教授討論後，確定研究主題及方向。其實施的步驟分成三大階段，分別為準備階段、實驗階段和分析階段，分別敘述如下： (一)準備階段自民國一百年六月至十月，研究者收集資料及相關文獻，確定研究主題後，即進行研究設計之規劃，主要供作如下所述： 1.收集相關資料及閱讀文獻：研究者探討文獻當中資料，並與指導教授充分討論，以確定研究主題及研究問題，本研究之文獻探討共計三節，分別為「二次函數的內涵及學習問題探討」、「動態幾何軟體教學之相關研究」以及「合作學習法教學之相關研究」。 2.編修研究工具：本研究所使用到的研究工具有：研究者自編二次函數先備概念理解測驗、以二次函數為教學內容之 GSP 動態幾何軟體教材以及研究者自編二次函數單元成就測驗。 3.進行二次函數先備概念理解測驗及成就測驗之預試為讓本研究工具更趨於完備，經過專家(包含一位教授及三位在職國中數學教師)對先備概念理解測驗及成就測驗進行指導和修正，以確認測驗之題目，於試卷編製完成後，在研究對象之外，找三個九年級的班級，共計

(39)

93 位學生進行前測之預試，並找新竹地區某高中其中一個高一的班級，共計 41 位學生進行後測之預試，預試後即進行難度及鑑別度分析，以修改或刪除不適宜之題目。 4.進行 GSP 動態幾何軟體教學之教材編修設計適合本研究之 GSP 動態幾何軟體教學之教材及學習單，經過專家 (包含一位教授及三位在職國中數學教師)對教材及學習單進行多次指導及修正，並先找三位學業能力分別為低、中、高的學生進行操作，再將學生的意見作為教材及學習單的修正，最後再與指導教授討論，使教材更為完善。 (二)實驗階段 1.選定研究對象本研究選定研究者所教的兩個班級之學生作為研究對象，一班為實驗組，並先依據一百零一學年度前兩次段考成績平均將學生分成低、中、高三種學業能力，再分成數個小組，每組皆有不同學業能力的學生，來進行合作學習的教學，另一班為控制組，採個別學習。 2.實施前測本研究於一百零一年十二月進行實驗教學，於實驗教學前一週進行二次函數先備概念理解之測驗(即前測)。 3.教學實驗教學實驗於一百零一年十二月進行，兩組皆在電腦教室進行教學，使用兩次上課，每次上課時間 45 分鐘，第一次包含熟悉 GSP 軟體的操作，其餘時間為正式上課。本實驗以二次函數為單元，探討在不同教學模式下融入動態幾何軟體對國中學生學習二次函數圖形的影響。 4.實施後測為了解在不同教學模式下，實驗組學生和控制組學生對於二次函數單元的學習情況是否有所差異，所以於教學實驗後，進行二次函數單元成就測驗(即後測)。 (三)分析階段後測結束後，於一百零二年一月，研究者將研究其間內所蒐集到的資料、教學過程、前後測之數據，加以彙整及分析，並進行論文的撰寫，包含實驗結果與討論以及結論與建議的部分。本研究之研究流程整理如圖 3-2：

(40)

確定研究主題進行文獻探討前測預試發展研究工具資料分析圖 3-2 研究流程圖完成論文後測預試選定研究對象實施前測(二次函數單元先備概念理解測驗) 整理實驗數據實施後測(二次函數單元成就測驗) 教學實驗準備階段分析階段實驗階段

(41)

第二節研究對象

本研究是以新竹市某國中九年級兩個班學生為研究對象，該校九年級共有 25 個班，其分班方式是依新生入學測驗成績採 S 型常態編班及男女合班。其中隨機選取一班為實驗組，進行 GSP 融入的合作學習，其實驗的實施方式為學生配合著學習單的問題引導，自行操作 GSP 幾何軟體，各小組透過合作學習，進行組內互相討論來研究答案；而選取另一班為控制組，進行 GSP 融入的個別學習，其實驗的實施方式為學生配合著學習單的問題引導，自行操作 GSP 幾何軟體，不進行小組的討論，個人研究出答案來進習學習，其各組人數如表 3-3。表 3-3 研究樣本人數統計表組別男生女生人數實驗組 18 16 34 控制組 16 15 31 合計 34 31 65 實驗組及控制組的教學實驗教師為同一位教師，來進行 GSP 融入的教學活動，教學實驗的教師亦為研究者本身，具有三年的數學科教學經驗，能確實掌握教學時間與進度。在教學實驗前，為了解學生對於二次函數單元的先備概念的學習情況，先實施前測，以「組別」為自變項，以「二次 函數單元的先備概念前測」為依變項，採用獨立樣本 t 檢定方法檢定學生 具備的先備概念程度是否一樣，資料分析結果如表 3-4。

(42)

表 3-4 實驗研究各組前測成績之獨立樣本 t 檢定摘要表 學業能力教學模式人數平均數標準差 t p 實驗組 34 7.06 2.82 全部控制組 31 6.90 2.45 .236 .814 實驗組 11 9.18 .75 高控制組 10 9.10 .88 .231 .820 實驗組 12 8.08 1.24 中控制組 11 7.36 1.12 1.456 .160 實驗組 11 3.82 2.48 低控制組 10 4.20 2.04 -.382 .706 由表 3-4 可知，獨立樣本 t 檢定的資料，實驗組與控制組兩組的「全 部學生」p 值為.814，「高學業能力」的 p 值為.820，「中學業能力」的 p 值 為.160，「低學業能力」的 p 值為.706，所有的 p 值皆大於.05，代表實驗組 與控制組兩組，不管是「全部學生」、「高學業能力」、「中學業能力」和「低學業能力」的平均皆無顯著差異，因此，各組在先備概念上可視為具備了相同的理解能力。

(43)

第三節研究工具

本研究工具包含：自編二次函數 GSP 教材、二次函數單元先備概念理解能力之測驗及二次函數單元成就測驗。一、自編二次函數 GSP 教材 (一)教材地位分析本研究是以二次函數為主題，利用 GSP 動態幾何軟體作為教材設計，來探討在不同教學模式下融入動態幾何軟體對國中學生學習二次函數圖形的影響，所以必須先了解這次的教學實驗會利用到哪些先備概念，以及在這次的教學實驗中能學習到哪些概念，自編二次函數 GSP 的教材地位分析如圖 3-3： (二)確認教學目標及範圍本研究以國民中學數學科第六冊第一章第一節及第二節為教材設計範圍，因為是使用 GSP 動態幾何軟體為教材，主要是希望學生能透過觀察 GSP 軟體的動態呈現來學習二次函數，所以不包含第二節有關配方法的部分。設計的內容則依據九年一貫數學學習領域課程綱要(教育部，2003)的能力指標及分年細目，自編二次函數單元所使用到的分年細目及能力指標的對應表如表 3-5：先備概念：直角坐標平面二元一次方程式的圖形函數與其圖形線對稱圖形 2

y



ax

的圖形 2 y ax k 的圖形二次函數的上下平移 2

(

)

y



a x



h

的圖形二次函數的左右平移 2

(

)

y



a x



h



k

的圖形圖 3-3 自編二次函數 GSP 教材之教材地位分析圖

(44)

表 3-5 自編二次函數單元的分年細目及能力指標對應表分年細目能力指標 9-a-02 能理解二次函數的樣式並繪出其圖形。 A-4-06 能理解二次函數的圖形及應用。 9-a-04 能計算二次函數的最大值與最小值。 A-4-06 能理解二次函數的圖形及應用。 9-a-06 能理解二次函數的圖形與拋物線的概念。 A-4-06 能理解二次函數的圖形及應用。 9-a-07 能理解拋物線的線對稱性質。 A-4-07 能理解拋物線之對稱性。根據九年一貫數學學習領域課程綱要的能力指標及分年細目，將教材內容分成四個主題，繪製二次函數圖形、比較二次函數開口方向及大小、上下平移、左右平移，並整理出教學目標，分年細目及教學目標的對應表如表 3-6：

融入動態幾何軟體的合作學習模式對國中學生學習二次函數圖形的影響

國立交通大學

理學院科技與數位學習學程

碩 士 論 文