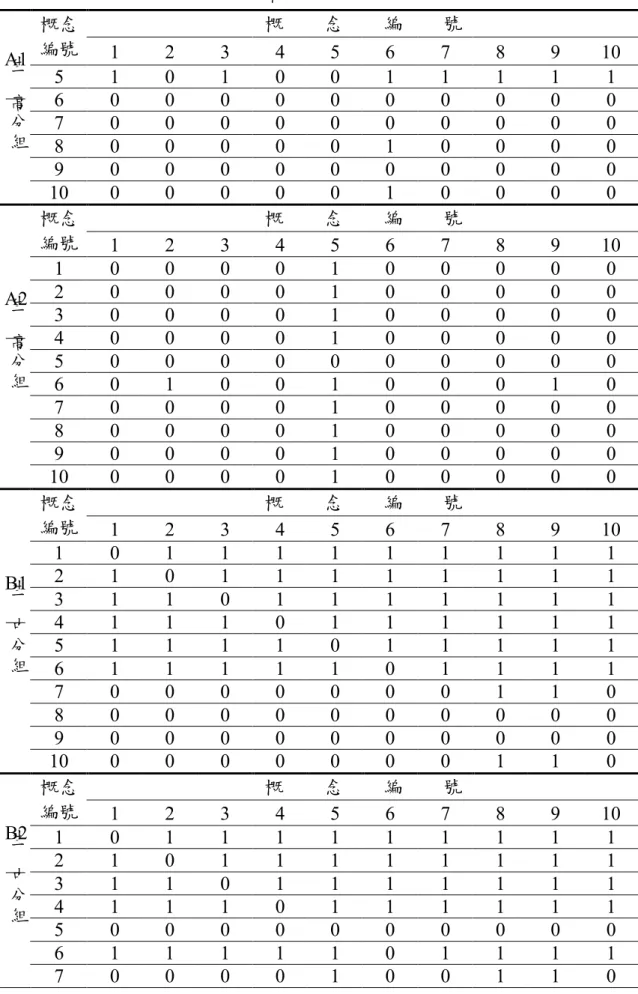
國立臺中教育大學數學教育學系在職進修
教學碩士學位班碩士學位論文
指導教授:林原宏 博士
研究生:詹家明 撰
中
華
民
國
九
十
八
年
六
月
國小五年級數與量分年細目之圖形化
認知診斷探究
中文摘要
本 研 究 旨 在 應 用 概 念 詮 釋 結 構 模 式 (concept advanced interpretive structural modeling, CAISM),分析國小五年級學生在九年一貫數學領域中數 與量分年細目的概念結構圖。此分析法乃結合察覺的模糊邏輯模式和詮釋結 構模式,分析個別化概念階層結構。本研究以自編「數與量概念測驗」為研 究工具,以中部四個縣市共 602 位國小五年級學生為研究對象,探討其個別 化的數與量概念階層結構,研究者並比較總分相同但反應組型不同的受試者 之概念階層結構異同。研究結果發現: 一、概念詮釋結構模式分析方法,對數與量概念分析是可行的分析方法。 二、學生的數與量概念結構圖因能力值的不同而有所不同。 三、總分相同但反應組型不同的學生,其知識結構亦不盡相同。 四、概念連結關係表示受試者對概念的熟悉度,可提供教學者做教材呈現的 參考。 本研究的結果與發現,有助於教師瞭解學生在五年級數與量分年細目的 知識結構,以及實施補救教學或課程設計之參考。最後,研究者根據研究心 得,提出對未來研究的相關建議。 關鍵字:數與量、分年細目、詮釋結構模式、知識結構
Abstract
The purpose of this study is to use concept advanced interpretive structural model (CAISM) in analyzing concept structure of mathematics indicators on number and quantity for fifth graders in the Elementary Schools’ Nine Year One Curriculum. This method integrates algorithm of fuzzy logic model of perception (FLMP) and interpretive structural model (ISM), to analyze the individualized concept structure. In order to explore the individualized structure of numbers and quantities, the researcher first tested 602 fifth graders of elementary schools by using self-designed numbers and quantities test. Secondly, the researcher compared the ISM graphs of the examinees who got the same scores with different response patterns.
Through the procedures of the analysis, the following conclusions were found.
1. The CAISM was a feasible way for analyzing the concepts structures of number and quantity.
2. The ISM graphs of examinees varied based on different abilities.
3. The ISM graphs were different for those who have the same total scores but different response patterns.
4. The linkage among concepts could be as references for group teaching and remedial instruction.
The findings of this study should be helpful for understanding the learning process of numbers and quantities for fifth graders and as references for remedial teaching or courses design. Finally, some recommendations and suggestions for future research are provided.
Keywords: numbers and quantities, mathematics indicators, interpretive structural modeling, knowledge structure.
目錄
第一章 緒論………1
第一節 研究動機………..1 第二節 研究目的………..4 第三節 名詞釋義………..4第二章 文獻探討………7
第一節 九年一貫數學領域課程………..…7 第二節 模糊理論………13 第三節 詮釋結構模式分析法………15 第四節 概念詮釋結構模式………23 第五節 知識結構測量………29第三章 研究方法與步驟………..45
第一節 研究架構……….45 第二節 研究工具……….46 第三節 研究對象……….55 第四節 研究流程……….56 第五節 資料分析……….56第四章 研究結果與討論………..59
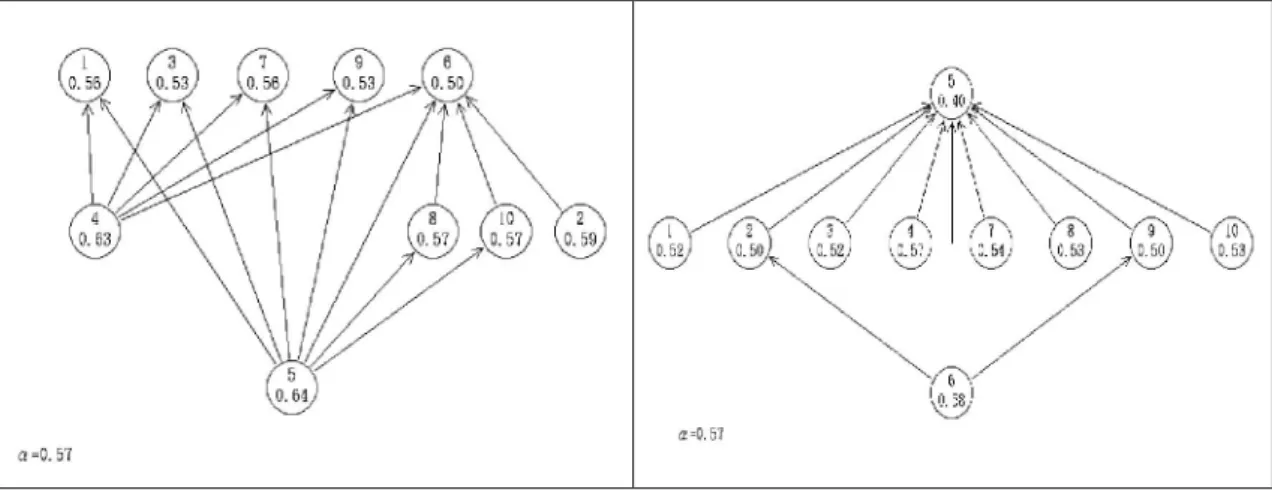
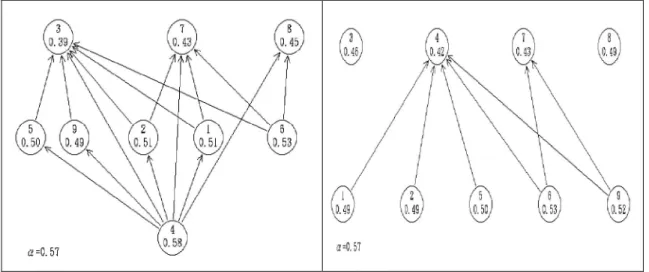
第一節 不同能力的學生在數與量上概念 ISM 圖之比較……….59第二節 答對題數相同但反應組型不同的學生其概念 ISM 圖之比 較……….69
第五章 結論與建議………..89
第一節 結論……….89 第二節 研究限制……….90 第三節 建議……….91參考文獻………..93
附錄………103
附錄一 數與量概念測驗……….………..103 附錄二 不同能力受試者的模糊關係矩陣……….……..107表目錄
表 2-1 五年級數與量的分年細目………...9 表 2-2 試題屬性矩陣Y及受試者反應矩陣X ………...27 表 2-3 網路一和網路二各節點的距離值………...35 表 2-4 網路一和網路二的 PFC 指數之計算………..36 表 3-1 分年細目的內容及群組………...46 表 3-2 A 卷試題概念屬性矩陣………...47 表 3-3 B 卷試題概念屬性矩陣………49 表 3-4 預試學生人數一覽表………...50 表 3-5 A 卷試題難度………50 表 3-6 B 卷試題難度………51 表 3-7 A 卷鑑別度分析………....51 表 3-8 B 卷鑑別度分析………52 表 3-9 數與量測驗之概念屬性矩陣………...53 表 3-10 試題通過率……….54 表 3-11 試題鑑別度……….…54 表 3-12 受測學生人數一覽表……….…55 表 4-1 不同能力的受試者代表之答題情形………...59 表 4-2 不同能力六位受試者第Ⅰ群組之概念模糊關係截矩陣……...59表 4-3 不同能力六位受試者第Ⅱ群組之概念模糊關係截矩陣…..….61 表 4-4 答對題數相同但反應組型不同之答題情形………...……69 表 4-5 高、中、低分組十二位受試者第Ⅰ群組之概念模糊關係截矩 陣………..………69 表 4-6 高、中、低分組十二位受試者第Ⅱ群組之概念模糊關係截矩 陣………..73
圖目錄
圖 2-1 ISM 圖的繪製……….….19 圖 2-2 兩位受試者之概念 ISM 圖………27 圖 2-3 概念圖計分例子……….32 圖 2-4 近似值矩陣與徑路搜尋網路……….34 圖 2-5 知識結構比較之 PFC 和 GTD 指數………..35 圖 2-6 知識空間k的學習路徑圖………..43 圖 3-1 研究架構圖………...45 圖 3-2 研究流程圖………..……….56 圖 4-1 A1、A2 受試者之第Ⅰ群組(數的計算)概念 ISM 圖………….67 圖 4-2 B1、B2 受試者之第Ⅰ群組(數的計算)概念 ISM 圖………….67 圖 4-3 C1、C2 受試者之第Ⅰ群組(數的計算)概念 ISM 圖…………..67 圖 4-4 A1、A2 受試者之第Ⅱ群組(量的換算)概念 ISM 圖………….68 圖 4-5 B1、B2 受試者之第Ⅱ群組(量的換算)概念 ISM 圖………….68 圖 4-6 C1、C2 受試者之第Ⅱ群組(量的換算)概念 ISM 圖………….68 圖 4-7 D1、D2 受試者之第Ⅰ群組(數的計算)概念 ISM 圖(高分組)...83 圖 4-8 E1、E2 受試者之第Ⅰ群組(數的計算)概念 ISM 圖(高分組)..…83 圖 4-9 F1、F2 受試者之第Ⅰ群組(數的計算)概念 ISM 圖(中分組)..….84 圖 4-10 G1、G2 受試者之第Ⅰ群組(數的計算)概念 ISM 圖(中分組)...84圖 4-11 H1、H2 受試者之第Ⅰ群組(數的計算)概念 ISM 圖(低分組)…84 圖 4-12 I1、I2 受試者之第Ⅰ群組(數的計算)概念 ISM 圖(低分組)..…85 圖 4-13 D1、D2 受試者之第Ⅱ群組(量的換算)概念 ISM 圖(高分組)...85 圖 4-14 E1、E2 受試者之第Ⅱ群組(量的換算)概念 ISM 圖(高分組)…85 圖 4-15 F1、F2 受試者之第Ⅱ群組(量的換算)概念 ISM 圖(中分組)…86 圖 4-16 G1、G2 受試者之第Ⅱ群組(量的換算)概念 ISM 圖(中分組)...86 圖 4-17 H1、H2 受試者之第Ⅱ群組(量的換算)概念 ISM 圖(低分組)...86 圖 4-18 I1、I2 受試者之第Ⅱ群組(量的換算)概念 ISM 圖(低分組)….87
第一章 緒論
本 研 究 旨 在 應 用 概 念 詮 釋 結 構 模 式 (concept advanced interpretive structural modeling, 簡稱 CAISM) ,分析國小五年級學生在九年一貫數學領 域中數與量的分年細目之知識結構。研究者藉由 CAISM 圖繪出不同能力的 學生之個別化概念結構圖,探討其數與量分年細目上知識結構之異同。本章 旨在闡述本研究之動機、目的及對本研究所提及的相關名詞作釋義。
第一節 研究動機
概念分析的方法在教育心理學及認知科學上是很重要的議題,概念被認 為是以有關係和階層的特性之網路形式貯存於大腦中。但在傳統紙筆測驗 上,學生的測驗分數結果只能反應出答對與答錯的題數,而這種分數能提供 學生的能力在團體中所佔的相對位置,或判定學生是否通過預定的標準,並 由學生的作答反應無法顯示學生是否精熟某種概念的訊息,亦無法得到學生 學習過程中如何組織所了解的概念,及概念間的關係結構等訊息,且其學生 分數相同,並不代表學生之間的概念結構相同,如此的測驗結果,未能提供 診斷的訊息 (余民寧、林曉芳、蔡佳燕,2001;涂金堂,2003;游森期、余 民寧,2006;黃瓊瑩,2002;Lin, Hung & Yu, 2007) 。余民寧、陳嘉成 (1998) 指出傳統評量無法讓教師得知學生是如何組織知識的訊息,且也難以得知學 生的知識中迷思概念 (misconception) 。余民寧 (1997) 認為傳統的紙筆測驗 方式,太過重視統計技術的分析而忽略測量背後所具有的心理學建構。所以 如何測量並分析學生的概念結構,是一個值得探討的問題。 余民寧、陳嘉成 (1998) 指出在認知診斷中,「質化」與「量化」的方法 皆不可以偏廢,但以質化為主的認知診斷方式十分依賴教師本身在學科知 識、測驗理論及教學 (認知) 心理學方面的專業知識與經驗,而數學科知識 對一般教師而言是較沒有問題,可是後兩者卻非一般教師皆能完全具備的。因此,採用量化的研究,可以幫助教師短時間獲得學生的學習訊息,以利於 安排補救教學。
在心理計量領域,有關測量學生在學習知識後的概念結構分析上有很多 不同的方法,除了古典測驗理論 (classical test theory) 與試題反應理論 (item response theory) 之外,常見的還有概念構圖 (concept mapping) 、次序理論 (ordering theory) 、 詮 釋 結 構 模 式 (interpretive structural modeling, 簡 稱 ISM) 、試題關連結構 (item relational structure) 、徑路搜尋 (pathfinder) 、 知識空間 (knowledge space) 和規則空間 (rule space) 等。大多數的分析方 法的目的是從元素或試題間關係的資料中,找出有意義的上下從屬關係,來 說明整體受試者的概念特性。其中,ISM分析法由日本學者佐籐隆博於1987 年所提出,其主要意義,是要將學習者腦中思考的概念單位結構,用具體化 的圖形階層結構表示出來。許天維、林原宏 (1994) 指出 ISM 分析法可表 示出概念思考單位元素的高低層次和順序關係。林原宏 (2005) 亦認為 ISM 是一個相當重要且有效的方法。不過 ISM 分析法中的元素關係只限於二元 關係,且只能得到整體受試者概念的結構圖,使 ISM 的應用有所限制。林 原宏 (2005) 提出在心理計量所獲得的概念或解題能力單位之關係,不是只 用二元關係就能描述。阮亨中、吳柏林 (2000) 認為在人文與社會科學的測 度裡,模糊相關性日漸受到重視,這是複雜的人文社會科學無法以傳統二元 數值模型充分合理解釋的一種自然發展結果。尤其是用於描述學習者所獲得 的概念或解題能力之關係,Lin, Hung and Huang (2006) 提出概念詮釋結構模 式 (concept advanced interpretive structural modeling, 簡稱CAISM) ,基於模 糊觀點的察覺的模糊邏輯模式 (fuzzy logic model of perception, 簡稱FLMP) 的觀點,及利用 ISM 的階層結構演算法,進行模糊截矩陣 (α-cut) 運算, 可繪製出個別化概念階層結構。
與常模參照測驗 (norm-referenced) 不同,常模參照測驗結果僅能提供個別 學生在群體表現的相對地位,但此個別學生的測驗結果會受到樣本抽樣不同 有所影響。因此,本研究的方法與常模參照測驗最大的不同在於可提供個人 潛在特質 (latent trait) 的測量,不會因為不同樣本群而繪製出不同的概念階 層結構。 在九年一貫數學課程正式綱要中指出數與量在國民教育的數學課程中 具有最重要的位置,其主要概念的形成與演算能力的培養均奠基於國小階段 (教育部,2003) 。在國小階段中數與量又可分為「整數」、「量與實測」、「有 理數」和「估算」等子題。然而,根據國內許多研究報告及結果顯示,國小 五年級學生在各個子題方面的學習表現並不理想,存在許多迷思概念 (支毅 君,1996;江愛華,2002;呂玉琴,1996;阮麗蓉 曹雅玲,2005;林麗雲、 姚如芬,2002;林怡靜、曹雅玲,2005;洪素敏,2003;黃國勳、劉祥通, 2003;劉曼麗,2001,2002,2003,2005;潘亭蓉、曹雅玲,2007;蕭正洋, 2004) 。但上述研究者僅針對單一子題進行研究,未能提供國小五年級學生 在數與量上的整體表現,所以藉本研究可了解學生在五年級數與量上的知識 結構。 教育部 (2003) 提出分年細目供教師教學與教科書編輯的主要參考依 據。張燕滿 (2007) 認為「分年細目」是評量與檢定學生達到該能力階段的 重要參考依據,且目前坊間各版本教材大致上符合課程綱要上所列舉的基本 能力,並將這些能力指標轉化為課程內容呈現,因此研究者以分年細目為依 據編製試題測驗,將能測驗出學生的學習情形。 基於上述,研究者欲以九年一貫數學課程正式綱要五年級數與量的分年 細目為例,運用 Lin et al. (2006) 所提出的概念詮釋結構模式來繪製出受試 者個別化的數與量概念詮釋結構圖,藉此了解國小五年級學生在數與量上各 個分年細目之概念不足之處,以利於補救教學。
第二節 研究目的
分別就下列二項,探討學生在五年級數與量上的個別化概念結構圖上的特 徵。 一、分析高、中、低能力的學生在個別化概念結構圖的差異。 二、就高中低不同能力群組,比較在答對題數相同,但反應組型不同的學生, 其個別化概念結構圖之異同。第三節 名詞釋義
本節內容係將本研究所涉及的重要名詞,分別說明與界定如下: 一、模糊理論 (fuzzy theory) 模糊理論是由 L. A. Zadeh 於 1965 年提出,以介於[0,1]之間的隸屬度 (membership) 來描述元素和集合之間的關係。早期使用在控制工程、資訊 工程、人工智慧等,且此理論的觀點很符合人心察覺測度 (perception measure) 的觀點,而逐漸被應用於社會科學資料分析上 (黃瓊瑩,2002) 。二、詮釋結構模式 (interpretive structural model, 簡稱 ISM)
詮釋結構模式是由 J. N. Warfield 於 1976 年所提出,原是一種社會系統 工學(social system engineering) 之彙整訊息的建模方法。根據圖形理論和 離散數學,以二維矩陣的數學運算來呈現整體元素之間的階層結構關係 圖。
三、概念詮釋結構模式 (concept advanced interpretive structural modeling, 簡 稱 CAISM)
及試題屬性矩陣 (item attribute matrix),根據概念向量比對 (concept vector matching) 和模糊理論等計算方法,計算出兩兩概念之間的從屬關係機率 (subordination relation probaility) ,並構成一個模糊關係矩陣 (fuzzy relation matrix) ,利用α截集運算進行 ISM 分析,可獲得個別化的概念階層結構圖。
第二章 文獻探討
第一節 九年一貫數學領域課程
壹、基本理念
數學的學習注重循序累進的邏輯結構,由於此嚴謹的結構性,教材的變 動常會引起牽一髮而動全身的效應。因此,過去國內外數學教材的演進,概 能遵循此邏輯結構,以保證數學教育的穩定性。再者,數學是較能進行國際 性評比的學習領域,教學的成效亦有較客觀的標準,因此,數學教育成效的 評估應有其客觀基礎。 數學學習領域為國民教育的基礎課程,有三個重要的原因 (教育部, 2003): 一、數學是人類最重要的資產之一 數學被公認為科學、技術及思想發展的碁石,文明演進的指標與推手。 二、數學是一種語言 簡單的數學語言,融合在人類生活世界的諸多面向,宛如另一種母語。 三、數學是人類天賦本能的延伸 人類嘗試錯誤、尋求策略、解決問題的生存本能,形與數的初等直覺。 經過文明累積的陶冶與教育,使這些本能得以具體延伸為數學知識,並形成 更有力量的邏輯思維能力。 九年一貫課程強調以學習者為主體,以知識的完整面為教育的主軸,以 終身學習為教育的目標。數學知識及數學能力,成為日常生活及職場裡應具 備的基本能力。基於以上的認知,國民教育數學課程的目標,必須能反映下 列理念:(一)數學能力是國民素質的一個重要指標;(二)了解數學是人類重 要資產;(三)教學應配合學童不同階段的需求,協助學童數學智能的發展;(四) 數學作為基礎科學的工具性特質。基於上述理念,協助學童數學智能的發展,需要長期及多面向的關照。
貳、課程目標
九年一貫數學領域的課程綱要,是由下列四個原則來界定 (教育部, 2003): 一、參考施行有年且有穩定基礎的傳統教材。 二、採用國際間數學課程必備的核心題材。 三、考慮數學作為科學工具性的特質。 四、現有學生能夠有效學習數學的一般能力。 具體而言,九年一貫數學學習領域的教學總體目標為: 一、培養學生的計算能力、抽象能力及邏輯推演能力。 二、學習應用問題的解題方法。 三、奠定下一階段的數學基礎。 四、培養欣賞數學的態度及能力。 其中,國民小學階段目標為: 一、在第一階段(一至三年級)能掌握數、量、形的概念。 二、在第二階段(四至五年級)能熟練自然數直式運算與混合四則運算,培 養流暢的數字感。 三、在小學畢業前,能熟練正數的混合四則運算、理解估算的概念,並運用 在演算上;能認識簡單幾何形體的幾何性質、並理解其面積與體積公 式;能報讀簡單統計圖形並理解其概念。參、分年細目
九年一貫課程綱要的能力指標係依主題及階段學習能力而訂定,然因多 數指標須採分年進階式教學方能達成其教學目標。因此,由階段能力指標演 繹出更細緻的分年細目及詮釋,以利分年進階式教學進度目標的明確掌握。分年細目以三碼編排,其中第一碼表示年級,分別以 1,…,9 表示一 至九年級;第二碼表示主題,分別以小寫字母 n、s、a、d 表示「數與量」、 「幾何」、「代數」和「統計與機率」四個主題;第三碼則是分年細目的流水 號,表示該細項下分年細目的序號。 與第二階段五年級數與量的分年細目,請參見表 2-1。 表 2-1 五年級數與量的分年細目 編號 分年細目 能力指標 5-n-01 能在具體情境中,解決三步驟問題。 N-2-03 A-2-01 5-n-02 能熟練整數四則混合計算。 N-2-03 A-2-01 5-n-03 能理解因數、倍數、公因數與公倍數。 N-2-04 5-n-04 能用約分、擴分處理等值分數的換算。 N-2-08 5-n-05 能用通分作簡單異分母分數的比較與加減。 N-2-09 5-n-06 能在測量情境中,理解分數之「整數相除」的意涵。 N-2-06 5-n-07 能理解乘數為分數的意義及計算方法,並解決生活中的問題。 N-2-11 5-n-08 能認識多位小數,並作比較與加、減的計算,以及解決生活中 的問題。 N-2-10 5-n-09 能用直式處理乘數是小數的計算,並解決生活中的問題。 N-2-12 5-n-10 能用四捨五入的方法,對小數在指定位數取概數,並做加、減、 乘、除之估算。 N-2-05 5-n-11 能將分數、小數標記在數線上。 N-2-06 N-2-13 5-n-12 能認識比率及其應用(含「百分率」、「折」)。 N-2-14 5-n-13 能解決時間的乘除計算問題。 N-2-15 5-n-14 能認識重量單位「公噸」及「公噸」、「公斤」間的關係,並作 相關計算。 N-2-15 N-2-16 5-n-15 能認識面積單位「公畝」、「公頃」、「平方公里」及其關係,並 作相關計算。 N-2-15 N-2-16 5-n-16 能運用切割重組,理解三角形、平行四邊形與梯形的面積公 式。(同 5-s-05) N-2-19 S-2-08
表 2-1 五年級數與量的分年細目(續) 編號 分年細目 能力指標 5-n-17 能認識體積單位「立方公尺」,及「立方公分」、「立方公尺」 間的關係,並作相關計算。 N-2-15 N-2-16 5-n-18 能理解長方體和正方體的體積公式。(同 5-s-07) N-2-17 S-2-07 5-n-19 能理解容量、容積和體積間的關係。 N-2-18
肆、數與量相關研究
數與量在國民教育的數學課程中具有最重要的位置,其主要的形成以及 演算能力的培養均奠基於國小階段。國小數與量的範圍較大,因此分為整 數、量與實測、有理數、估算等子題 (教育部,2003)。 一、整數 在國小階段,整數指的是非負整數,所處理的是離散量的計數與計算, 並且整數計算是一切數學學習的基礎。而計算的能力是包含加、減、乘、除, 在小學階段是重要的關鍵 (Klausmeier, 1985)。在教學中,學童經由活動、 情境掌握計算的意義,藉著各種例子體驗計算的規則與策略。流暢的計算能 力,有如語文學習中,基本的文字駕馭能力,不僅可以內化學童的數字感, 並且是日後(國、高中)學習抽象運算及形式推導的基礎,這樣的能力固然 是學習科學所必須,也是能夠有效處理日常生活的基本能力之一。 二、量與實測 「量與實測」是國小數學的核心課程之一,量的學習是學生學習連續量 的入口,可以與有理數的學習相互加強。教學中的量包含長度、重量、容量、 時間、角度、面積、體積等生活中常用的七種量。其中,長度、容量、角度、 面積、體積屬於幾何(視覺)量,可依賴學生的幾何經驗。重量除了依靠身 體的感覺,也相當依賴測量工具。在量 的測量上,Piaget, Inhelder andSzeminska (1960) 針對長度、面積、容量、重量等概念歸納出三個階段:直 接的視覺比較、應用位置改變、量的間接比較。因此可以從實物存在性質上 入手的量為感官量,且學生對此六種量概念的發展進度不是一致的,是有前 後的 (鐘靜,2001)。但是時間的學習卻完全依賴計時的約定,因為時間的量 感不是建基在「實物的感覺存有性質」的量,是必需直接由比對刻度觀點入 手,藉比對刻度建立相對於刻度的量感,故稱時間為工具量 (王文良,2005)。 因此時間以外六種量的學習,大致上要經歷初步概念與直接比較、間接比較 與個別單位、常用單位的約定、常用單位的換算等四個階段(教育部,2003)。 三、有理數 「有理數」是小學的核心課程之一。有理數教學的困難主要在於:它牽 涉兩種非常不同的表現形式─分數與小數。從 Dickson, Brown and Gibson (1984) 的觀點,分數具有下列五種意義:(1)是全部範圍中的部分;(2)子 集和整個集合的比較;(3)數線上的點;(4)除法運算的結果;(5)比較兩 個物體或測量結果的大小。Kieren (1976) 則提出分數的五種概念:部分-全 體、比、商、測量及運算元 (引自林怡靜、曹雅玲,2005)。依據洪素敏 (2003) 分析有關之文獻及自我以往教學經驗,將分數的迷思概念分為「等分的觀念 薄弱」、「忽略單位量」及「受整數基模的影響,視分數為兩個獨立的數」三 方面。 小數的概念起源於測量和分數的部分全體關係,其記數系統又是從整數 的十進位制擴充而來。從小數與分數的關係來看,小數可以視為不帶分母的 十進位分數,雖然小數和分數都可以用來代表不滿一個單位量的量,但在其 符號表示上,卻有著極大的不同:分數的分母代表切割的份數,而分子則代 表得到的數目,但小數的數字卻只代表得到的數目,而其切割的份數則被隱 藏在位值裡;分數的分割是隨著分母的不同而得到不同的分數,但小數的分 割則被限制在10 的冪次方裡 (阮麗蓉、曹雅玲,2005;劉曼麗,2005)。小
數與分數的不同處以及小數與整數的不同處,正是干擾學童建構小數概念的 原因 (劉曼麗,2003)。且學生學習小數極易產生的迷思概念大都集中在四、 五年級 (劉曼麗,2002)。 四、估算 「估算」在國民教育中可粗分為離散量的估算(自然數四則運算的估算) 與連續量的估算。估算是得到一個計算題的粗略答案的一種過程,是一種猜 出合理的近似值的技能。估算的特點包括:短時間內得到答案、不用紙筆、 以合理的猜測代替精確的計算結果 (支毅君,1996)。 估算是過去數學教學中,較被忽略的課題。一般來說,數字感較好的學 生,通常都能夠使用估算的技巧,來協助計算、驗算與解題。而經由估算課 題的教學,也更能促使學生對數學概念、程序計算、解題三者間的連結,有 更深入的理解 (教育部,2003)。 五、數與量的相關研究 黃國勳、劉祥通 (2003) 發現國小學生對因數的學習是很困難的,根據 實際的教學經驗及因數教材的分析,進而剖析困難的成因,提出建議供教師 教學時之參考。蕭正洋 (2004) 以紙筆測驗及個別晤談了解學生倍數迷思概 念及解題過程與想法,搭配相對應的補救教學活動,探討教學歷程及其成 效。江愛華 (2002) 針對國小五年級學生運用診斷教學三步驟,進行小數教 學,探討實施情形及其成效。劉曼麗 (2005) 透過資料蒐集及資料分析(包 括量性及質性的分析),探討小數診斷教學的實施情形及學生在迷思概念的 改變情形。張淑怡 (2004) 以紙筆測驗、實作及訪談活動蒐集研究資料,分 析國小五年級學生其容量概念的瞭解情形及所呈現之迷思概念。洪素敏 (2003) 以紙筆測驗與訪談,了解國小五年級學生其分數迷思概念情形,並對 分數迷思概念的學生進行補救教學,探討分數概念改變的情形。林麗雲、姚 如芬 (2002) 自編試題並進行分析,探討國小五年級學生的小數迷思概念。
林怡靜、曹雅玲 (2005) 進行分數數感實驗教學,結果發現實施教學活動後, 確實增進學生分數數感的能力。阮麗蓉、曹雅玲 (2005) 以筆試及訪談,瞭 解四到六年級學生在小數概念發展過程中,所產生的迷思概念及其產生的可 能原因。潘亭蓉、曹雅玲 (2007) 透過筆試探討國小五年級學生在面積概念 上的表現,並進一步對學生訪談,以瞭解其解題情況與可能迷思。 綜合上述研究,僅針對數與量中的某一子題作探討,且研究方法上大多 使用晤談,以瞭解學生在數與量某一子題上的迷思概念,這樣的研究方法必 須耗費大量的時間、人力及物力,才能獲得學生個別的認知結構或迷思概念 的情形。所以本研究應用概念詮釋結構模式與軟體,以數與量進行整體性分 析,將有助於教師快速且完整的了解學生的概念連結情形,進而提供教師進 行認知診斷、補救教學或課程設計之參考。
第二節 模糊理論
壹、理論介紹
現今科學所欲研究的物件之結構複雜性日益增加,包括人類的知識、語 言、思維、決策,都存在模糊性,有時不適用於傳統二元邏輯的分析,若硬 要把模糊的事物進行二元邏輯分類,將會無法得到滿意的結果。換句話說, 憑藉模糊模式的呈現方式比直接指定單一物體的特定值,較合適於評估物體 間的相關特性。因此,L. A. Zadeh 於 1965 年提出模糊理論 (fuzzy theory), 以隸屬度的概念來描述元素和集合之間的隸屬關係。近來來,模糊理論已經 廣泛運用於農業方面、氣象預測、經濟管理、資訊科技、統計方法及人工智 慧等等。以下就模糊理論的基本定義,進行說明:隸屬度函數A
x 和α截集(-cut) 的定義說明如下:【定義 2-1】令U 表示全域 (universal set),為一映至
0,1 的函數,則U之模糊子集 A的隸屬函數記為A
x ,表示元素隸屬 x 於模 糊集合 A的程度。可表示成:
1, 2, , n
X x x x
1 1 2 2 1 2 n n n x x x A x x x 【定義 2-2】模糊子集 A的α截集定義為:
| A
, 0 1 A x x A 的α截集的隸屬度函數A
x 為:
1 , 0 , A A A x x x 貳、模糊關係矩陣與模糊截矩陣 兩個集合元素之間的相似程度,稱之為模糊關係 (fuzzy relation) ,可用 矩陣方式來表示,即為模糊關係矩陣 (fuzzy relation matrix) ,其定義如下:【定義 2-3】假設論域 X 有 m 個元素,論域Y 有 n 個元素,則用來描述 X 與Y 兩極和元素間關係模糊關係矩陣可表示為:
1 1 1 1 n ij m n m m n r r R r r r 在給定α值之情形下,可進行模糊關係矩陣之截矩陣運算,亦即:
ij m n R r 且 1 , 0 , ij ij ij r r r ,其中 0 1 藉由模糊理論之隸屬度的觀點來描述元素和集合之間的關係,改善以二 元邏輯只有 0 和 1 之兩種選擇方式來描述現象,而此研究分析方法運用此模 糊關係矩陣之α-cut 運算來表示兩兩概念之間的從屬關係。第三節 詮釋結構模式分析法
壹、詮釋結構模式
詮釋結構模式 (interpretive structural model, ISM) 是由Warfield (1976) 所提出,原是一種社會系統工學 (social system engineering) 之彙整訊息的建 模方法。根據圖形理論和離散數學,以二維矩陣的數學運算來呈現整體元素 之間的階層結構關係圖。 一、ISM 分析法 ISM 分析法主要功能是建立整體概念元素之間的關係,即經由部分元 素之間的關係,整合起來形成所有元素整體之關係,亦即是在建立整體概念 要素之間的指向關係結構 (林原宏、陳進春、許天維,2005;許天維、林原 宏,1994) 。例如: Wu, Liu, Chang, Chang and Li (2006) 應用 ISM 發展個 人化知識導航服務,提供給學生在自我學習上一個依據,研究結果顯示該服 務能提供不同的學生在自我學習的認知層次地圖,以理解學生的學習目標和 概念的認知層次。林靖宇 (2006) 針對大學生上課睡覺原因進行 ISM 法分 析,其結果顯示學生上課睡覺的各種原因形成一個相互影響的系統,並對最 根本的原因提出相對應建議及解決策略。王從陸、吳超及李樹清 (2004) 應 用 ISM 法,將事故原因分為五個層次,明確了解事故原因不同層次之間關 係,藉由階層關係圖清楚顯示事故發生的直接原因或間接原因大多是因為人
的不安全行為。王振琤 (2007) 運用 ISM 法建立一種需求管理輔助模式, 能有效協助設計者釐清需求要素之間的關係,且以整體性視覺化觀點理解需 求要素。 而 ISM 法在教育上的課程與學習應用,則是由日本學者佐藤隆博 (1979) 所提出,主要是探討學科內容的知識架構與結構的表現,首先將學習 單元內的教材要素依學習目標明確的細分出來,再精確的決定全部學習項目 的兩兩關聯性,最後透過 ISM 分析法,產生構造化的教材 (佐藤隆博, 1987) 。 許天維、林原宏 (1994) 提出 ISM 方法在教育上用途,主要有以下三 個方面: (一)教材內容的結構化:將教材目標「由上往下」的分析,決定出年級間或 各單元間教材內容的結構。 (二)編授教材內容:教學者決定教材內容的目標層次關係,是「由下往上」 累積元素關係的方式,幫助教學者了解目標之間的順序關係和發展。 (三)學習者學習內容的結構化:指的是學習者本身對知識的概念結構,可從 已知學習者概念元素兩兩之間的關係,利用 ISM 分析法,得到整體概 念的結構圖。 而 ISM 法應用在國內外教育上有許多研究,如徐賢德 (2004) 在客家 語教材方面進行教材結構化,應用 ISM 法繪製出客家語教材構造圖,有助 於學生建立客家語學習路徑,以及作為教師教學及編輯教材的參考。蔡秉燁 (2004) 運用 ISM 法,以高中數學補救教學教材進行結構化教材之設計,建 立 起 更 科 學 化 的 「 學 習 路 徑 (learning path) 」 與 「 學 習 地 圖 (learning map) 」。其研究結果顯示,圖像式的階層結構化教材,有助於教師明確掌 握學習順序,以及增進補救教學的成效。鍾靜蓉 (2002) 以商業職業學校經 濟學中「需求與供給」單元為例,進行 ISM 法及構造化學習的實證研究,
使教師能確認本身的知識體系,以及進行教學時能更富邏輯與合理性。廖信 德 (1998) 在原住民國小四至六年級數學基本學歷指標初探研究中,以 ISM 法統整數學教育專家們對國小四至六年級數學概念的意見,繪製成數學概念 結構圖,作為設計問卷之參考。Hawthorme and Sage (1975) 針對五種不同團 體成員的討論過程,以 ISM 方法整合高等教育課程計畫的意見。 因此,運用 ISM 在教學及分析認知結構上,可使腦中片斷、籠統而抽 象化的要素重新排列順序,轉變成具體化、全面化的關聯構造階層圖 (吳育 楨,2008)。林原宏、陳進春及許天維 (2005) 指出 ISM 分析法對於分析教 材構造、設計教材內容以及建立學習者的知識概念結構等方面貢獻卓著。 二、ISM分析步驟 1.矩陣的運算 兩個矩陣A的運算的結果定義為
2 2 2 11 12 1 2 2 2 2 2 21 22 2 2 2 2 1 2 K K ij K K K K KK a a a a a a A a a a a 2 A 矩陣內的元素 2 1 1 2 2 1 K ij ik kj i j i j iK Kj k a a a a a a a a a
上式中 和 的運算,定義如下: 0 else 1 if 1 and 1 x y x y 0 if 0 and 0 1 else x y xy 2.傳遞閉包 (transitive closure) 定義 ˆ 2 3 P A AA A A ,且矩陣 ˆA稱為傳遞閉包。 3.可到達矩陣 (reachability matrix) 定義 ˆ 2 3 P
P A I A A A A I AI ,其中 I 表示 K K 階 的單位矩陣。把如下的矩陣 R ,稱為可到達矩陣。
2 3 1 2 3 1 ˆ p p p p p R A I A I A A A A I A I A A A A A I 4. ISM圖的繪製 以A 至1 A 元素為例 (佐籐隆博,1987) 。這五個元素之關係,假設可用5 矩陣 A表示;經過上述的傳遞閉包運算後,則相對應的可到達矩陣為 R ,分 別為: 0 0 0 0 0 0 0 1 1 0 1 0 0 1 0 0 0 1 0 1 1 0 0 0 0 A 1 0 0 0 0 1 1 1 1 1 1 0 1 1 1 1 0 1 1 1 1 0 0 0 1 R 為便於繪製ISM圖,將矩陣整理如下: k A R A
k M A
k R A
k M A
k 1 A A 0 1 0 0 0 A 1 A 2 A 3 A 4 A 5 A 0 0 1 0 0 2 A A 1 A 2 A 3 A 4 A 0 5 A 0 0 2 0 0 A 0 2 0 0 3 A A 0 1 A 3 A 4 A 0 5 A 2 A 3 A 0 0 4 0 A 3 A 0 4 4 A A 0 1 A 3 A 4 A 0 5 A 2 A 3 A 0 0 4 0 A 3 A 0 4 5 A A 0 1 0 0 A 0 5 A 2 A 3 A 4 A 0 5 0 0 0 A 5
k R A :是 A 的可到達矩陣,在可到達矩陣中,若元素為1,則填上表示 被指向的元素代號;若元素為0,則保持為0。
k M A :就R A 矩陣中,
k M A 的每一列,表示指向該列元素的所有
k 其他元素。
k
k R A M A :是R A 和
k M A 兩矩陣的交集,兩矩陣相對應位置
k 若同時存在該元素,則填出該元素;否則填上0。 而製作圖2-1的 ISM 的方法步驟為: 【步驟一】針對R A 和
k R A
k M A
k 的每一列,找出列相等的元素。在 上 表 中 , 先 找 到 相 對 應 的 第 1 列 A , 則 在1 R A
k 、
k
k R A M A 中 A 所在的行 (column) 與列 (row) 全部1 刪掉,刪除後的列與行則不再比較和尋找。 【步驟二】以相同方法再找到第5列A ,以此類推,我們再次得到5 A 、3 A4 一組元素和A 元素。 2 【步驟三】將找到的元素依序列出高低層級,並依 A中的元素關係,劃 上箭頭,如圖2-1所示,圖2-1中A 、3 A 是對等元素。在此,4 完成 ISM 圖的繪製。若 ISM 圖形元素多而箭頭關係複 雜,則可視研究者所需而進行圖形簡化。 圖2-1 ISM 圖的繪製 綜合上述,ISM可在各領域上應用,ISM呈現出整體元素間的階層結構 關係,亦可幫助使用者分析元素之間的關聯指向,進而提供診斷之用。貳、模糊取向的詮釋結構模式
ISM 分析法中的元素關係只限於二元關係,但從認知心理學的觀點來 看,人的思維具有多元邏輯的特性,難以用非對即錯的二元的明確數值來加 以描述。尤其在心理計量所獲得的概念或解題能力單位之關係,非單用二元 關係即能描述。而傳統詮釋結構模式 (ISM) 僅能針對二元關係的元素進行 1 A 2 A 3 A A4 5 A 1 A 2 A 3 A A4 5 A分析,這對於 ISM 的應用性有所限制。阮亨中、吳柏林 (2000) 認為在人 文與社會科學的測度裡,模糊相關性日漸受到重視,這是複雜的人文社會科 學無法以傳統二元數值模型充分合理解釋的一種自然發展結果。因此,改進 ISM 法之限制,並融入心理計量的分析資料,有其必要及可行之處。
Tazaki and Amagasa (1979) 以模糊理論為基礎,發展出模糊結構模式 (fuzzy structural modeling, FSM)。Yih and Lin (2007b) 結合試題反應理論 (item response theory, IRT) 、察覺的模糊邏輯模式 (fuzzy logic model of perception, FLMP) 和模糊結構模式 (FSM) 分析國小三年級學生的幾何概 念結構,研究證實此種方法可提供在教育應用,且圖繪其結構化階層圖能夠 解釋學童個人知識結構。Yamashita (1997) 根據模糊推理 (fuzzy reasoning) 與模糊結構模式 (fuzzy structural modeling) ,發展一套有關高中畢業生的升 學與就業輔導的生涯決定模式 (career decision-making modeling) 量表。溫坤 禮 (2000) 藉由模糊理論的模糊集,將 ISM 法的二值關係改為0到1之間的 集合,並取0至1之間的任意值為元素的特徵值,即為模糊集合的隸屬度 (membership),以精確掌握不確定的因素。 林原宏 (2005) 所提出的模糊取向詮釋結構模式,結合察覺的模糊邏輯 模式 (FLMP) 和試題反應理論 (IRT) ,基於模糊觀點的察覺的模糊邏輯模 式,衡量配對刺激屬於某一典型的機率,計算出不同能力值的受試者概念或 試題間的模糊關係矩陣,並將其模糊關係矩陣進行α截矩陣,以概念屬性截 矩陣繪製出該能力值之受試者個人化的概念 ISM 圖。 模糊取向詮釋結構模式針對模糊關係元素,計算其為上下從屬關係 (subordination relation) 機率計算,進行模糊取向的 ISM 分析,呈現個人化 (individualized) 的概念屬性矩陣。其分析步驟如下 (引自林原宏,2005): 【步驟一】確定所分析的元素單位為試題或概念,假設共有 M 個試題或所
【步驟二】在選定的試題反應理論模式下,能力值k受試者在第m題的答對 機率為Pm
k ,依察覺的模糊邏輯模式,計算該受試者的模糊關 係矩陣如下: 1. 若 所 分 析 的 元 素 單 位 為 試 題 , 則 能 力 值k受試者 的模 糊關 係矩 陣為
k ij
k M M D p ,pij
k 為符合試題 i 指向試題 j 的機率。依察覺的模 糊邏輯模式意義,令ci P
k 且oj 1 Pj
k ,所以可得:
1 , 1 1 1 1 i k j k i j ij k i j i j i j i k j k i k j k P P c o p p c o c o c o P P P P 2. 若 所 分 析 的 元 素 單 位 為 概 念 , 則 能 力 值k受試者 的模 糊關 係矩 陣為
k ij
k L L D p ,pij
k 為符合概念 i 指向試題 j 的機率。依每一試題 測得該概念與否的關係,設概念個數為L個,可形成一個二元關係的概念 屬性矩陣 (attribute matrix) A
aml
M L ,aml 表示第1 m 題包含概念l , 亦即有測到概念 l ;aml 表示第0 m 題沒有包含概念l ,亦即沒有測到概念 l 。令
1 1 1 M ml l L m L SA a a
表示每一概念被測得出現的總數之矩陣。因 此 , 能 力 值 k 之 受 試 者 在 每 個 概 念 精 熟 的 機 率 為
1 ml
1 k m k M l k L l M L a MA P ma a 。依察覺的模糊邏輯模式意 義,令ci mai
k 且oj 1 maj
k ,所以可得:
1 , 1 1 1 1 i k j k i j ij k i j i j i j i k j k i k j k ma ma c o p p c o c o c o ma ma ma ma 【步驟三】選定值且 0 ,將模糊關係矩陣為1
k ij
k M M D p 或
k ij
k L L D p 進行截矩陣分析。例如分析的單位為試題, 則:
k ij
k M M D p 且
1 , 0 , ij k ij k ij k p p p ,其中 0 1 【步驟四】將步驟三所得的模糊關係截矩陣進行 ISM 分析,為提供圖形可 讀性,可進行 ISM 圖簡化,假設元素 A 指向i A 有多條 路徑 j (path) ,則去除直接指向並保留間接指向的路徑。例如: 【步驟五】在給定值,可獲得能力值k之受試者的 ISM 圖。因此,可獲 得不同能力值之個人化試題或概念的 ISM 圖。 林原宏 (2005) 以網路化分數減法施測系統對852名國小高年級學生進 行施測,結果發現不同能力值的學生其分數減法的概念結構各有其特徵,且 傳統計分相同的情形下,學生的分數減法之概念結構亦有所不同。陳紹銘 (2006) 應用模糊取向的詮釋結構模式,分析國小六年級學生的等量公理概念 之階層結構,結果發現國小六年級學生等量公理的知識結構具有階層性,且 因學生的能力值不同而有明顯的差異存在,而傳統計分之總分相同但反應組 型不同的學生,其知識結構不盡相同。紀順雄 (2007) 利用模糊取向的詮釋 簡化結構模式,分析國小六年級學生的分數加法概念結構,結果發現不同能力值 的學生之分數加法概念結構亦有所差異。祝淑梅 (2007) 應用模糊取向的詮 釋結構模式分析國小高年級學生的小數概念階層結構圖之特徵,結果顯示學 生的能力值不同其小數概念結構亦有明顯差異存在。吳育楨 (2008) 應用模 糊詮釋結構模式分析法,分析國小六年級學童因數與倍數概念階層結構,研 究發現不同能力值學生的概念結構圖有差異存在。 綜合上述研究可知,模糊取向的詮釋結構模式可得到學生的概念階層結 構圖,在分析知識結構上是一個可行的方法。
第四節 概念詮釋結構模式
對於知識或概念從屬關係程度的描述,模糊取向的詮釋結構模式的確是 一個可行的方法。但此模式的數學演算模型會因受試者在群體表現的相對地 位影響此受試者的概念結構圖,亦即個別學生的測驗結果會受到樣本抽樣不 同有所影響。因此,Lin, Hung and Huang (2006) 結合模糊理論 (fuzzy theory) 和察覺的模糊邏輯模式 (FLMP) 提出概念詮釋結構模式 (concept advanced interpretive structural modeling, CAISM) ,此模式可以數值和圖形結構呈現個 人化概念階層結構 (individualized concept hierarchy structure) 。其方法不但 改進傳統ISM分析法受限於二元關係的限制,且提供個人潛在特質 (latent trait) 的測量,不會因不同樣本群而繪製出不同的概念階層結構。壹、理論與演算
本研究應用 Lin et al. (2006) 提出的概念詮釋結構模式理論,進行國小 五年級學生在數與量的個別化概念階層結構之分析。假設某測驗是二元計分 (dichotomous) ,測驗的試題有 M 個 (m1, 2,,M ) ,其所測驗的概念有 A個 (a1, 2,,A) ,而受試者有 N 位 (n1, 2,,N) ,假設其矩陣及意義說 明如下 (Lin, Hung & Huang, 2006) :
1.根據測驗結果可得受試者反應矩陣為 X
xnm
N M ,xnm 表示受試者 n1 答對試題 m;xnm 表示受試者 n 答錯試題 m。 0 2.根據試題概念雙 向細目表 可得試 題屬 性矩陣 (item-attribute matrix) 為
ma
M A Y y ,yma 表示試題 m 測量概念 a;1 yma 表示試題 m 未測量0 到概念 a。 3.此測驗所測得的概念有 A 個概念下,總共有2A個典型概念向量 (ideal concept vector) ,可構成典型概念矩陣Z
zia I A ,其中以zi
zia 1A表示 第 i 個典型概念向量,而i 1, 2,,I且I 2A。亦即表示每個典型概念向量 為某個典型受試者所具備的概念結構。z 表示此種典型概念向量有具ia 1 備概念 a;z 則表示此種典型概念向量未具備概念 a。 ia 0 4.在 I 個典型概念向量下,對應於試題概念屬性矩陣Y
yma
M A ,可構成反 應 矩 陣
im I M R r 。 其 中
1 i im M r r 為典 型 反 應 向 量 (ideal response vector) 。其計算如下: 1 0 im r
zia yma
yma, a 1, 2, ,A else , , (1) 若r =1 表示典型概念向量im z 能答對試題 m;i r =0 表示典型概念向量im i z 答錯試題 m。 5.受試者的反應矩陣 X
xnm
N M 與典型反應矩陣
im I M R r 的標準化近似 值矩陣 (standardized closeness matrix) 以SC
scni
N I 表示。其中sc 表示ni受試者 n 的試題反應向量 (item response vector)
xnm
1M與典型反應向量
rim 1M 的近似值 (closeness) 。 針對上述所定義的矩陣意義,則概念詮釋模式的演算步驟如下: 1. 就 受 試 者 n , 計 算 其 試 題 反 應 向 量 與 典 型 反 應 向 量 的 近 似 值 矩 陣
ni N I C c 和標準化近似值 (standardized closeness) 矩陣SC
scni
N I , 其演算公式如下:
1 M ni nm im m c x r M
(2) 其中
1 0 nm im nm im nm im x r x r x r , , (3) (1)根據c 值,若存在ni c =1,且假設有 k 個ni c 滿足ni c =1,則表示存在明確辨ni 識 (crisp recognition) ,令標準化近似值sc 如下: ni 1 1 0 ni ni k c sc else , , (4) (2) 根 據 c 值 , 若ni cni 1 i 1, 2,,I , 則 表 示 存 在 模 糊 辨 識 (fuzzy recognition) ,令標準化近似值sc 如下: ni 1 I ni ni ni i sc c c
(5) 2. 令 D
dna
N A 表 示 受 試 者 n 在 概 念 a 的 精 熟 程 度 , 所 以 可 定 義
na
N A
D d SC Z ,其計算如下:
1 I na ni ia i d sc z
且 0dna (6) 1 3.依 Luce (1959) 的選擇規則 (choice rule) 理論和相對適合度準則 (relative goodness rule, RGR) 以及察 覺 的模 糊邏 輯模 式 (fuzzy logic model ofperception, 簡稱 FLMP) 的觀點,對受試者 n 而言,其概念為概念 a 的 先備概念(即概念指向概念 a 的機率)之從屬關係機率 (subordination relation probability) 如下 (Massaro & Friedman, 1990):
1 1 1 0 0 0 1- 1-na na aa na na na na na na na na d and d p d and d d d else d d d d , , , (7) 4.對每個受試者 n 而言,其所有兩兩概念之間的從屬關係機率可構成模 糊關係矩陣 (fuzzy relation matrix) Fn
paa
A A 。且利用截集 (-cut) 運算 後,可獲得二元關係矩陣 (binary relation matrix) 的相鄰矩陣 (adjacent matrix) 如下:
a a n aa A A F p 且 1 0 aa a aa aa p p p , , ,其中 0 (8) 1 5.將截集運算所得的二元關係矩陣進行 ISM 分析,可繪製出受試者 個別化概念結構圖。貳、程式與舉例說明
概念詮釋結構模式的軟體程式為 CAISM,進行分析前需先建立兩個資 料檔:一是受試者反應矩陣 X ;另一是試題屬性矩陣Y 。程式讀取此兩個資 料檔即可進行分析,以下舉例說明: 假設某測驗有 6 個試題,所測量的概念有 4 個,受試者人數為 6,其試 題屬性矩陣Y 和受試者反應矩陣 X ,分別如表 2-2 所示。表 2-2 試題屬性矩陣Y 及受試者反應矩陣 X 試題屬性矩陣Y 受試者反應矩陣 X 1 1 0 0 1 0 0 1 0 1 1 0 0 1 0 1 1 0 1 0 1 0 1 1 1 1 0 0 0 1 1 1 1 1 1 0 1 1 0 1 1 0 0 0 0 0 1 0 1 0 0 1 1 0 0 0 1 1 0 0 則第一位受試者和第五位受試者的概念 ISM 圖分別如圖 2-2 所示。由圖 2-2 可知兩位受試者的概念 ISM 圖截然不同,且由表 2-2 得知,第一位和第 五位受試者的總分都一樣是 3 分,但兩位受試者的試題反應組型完全不相 同,第一位受試者的試題反應組型是(1 1 0 0 0 1),第五位受試者的試題反應 組型是(1 0 0 1 1 0)。顯示傳統總分相同但反應組型不同,其認知結構不相同。 第一位受試者 第五位受試者 圖 2-2 兩位受試者之概念 ISM 圖
參、概念詮釋結構模式的相關研究
Yih, Lin and Hung (2007) 應用概念詮釋結構模式,分析大學生的線性代 數概念之知識結構。Yih and Lin (2007a) 以大學生為對象,分析電腦輔助 MATLAB 之學習數學相關概念的知識結構。此外,Lin, Hung and Yu (2007) 分國小學生的等量公理之概念階層結構,結果均發現傳統分數總分相同但反 應組型不同的受試者,其概念詮釋結構圖不盡相同,且能有效診斷學習者的
認知結構,並進行補救教學。黃雅琦、易正明及林原宏 (2008) 應用模糊詮 釋結構模式進行「電腦化數感診斷測驗」以檢測六年級學生在分數及小數的 數感發展,研究發現(1)形成數感能力的概念具有階層性,概念間存有關 聯性及方向性,而高分組受測者的概念間存在縝密的關聯結構,但是低分組 受測者的概念間存在的關聯性較薄弱。(2)概念結構圖具有個別性,總分 不同的受試者其概念的階層數、各階層的概念內容、概念的指向,皆不相同, 且相同總分的受試者也並未意謂著受試者的能力或概念發展順序相同。莊惠 雯、林原宏及易正明 (2008) 應用概念詮釋結構模式,分析國小一年級學生 的加減文字題之概念結構;王佩芬、易正明及林原宏 (2008) 應用概念階層 結構模式,分析國小四年級學生的除法概念結構。研究結果皆發現概念圖具 有階層結構,且總分不同的受試者的概念結構圖有所差異,總分相同但反應 組型不同的受試者其概念結構圖也不盡相同。梁錫卿、黃釋緯、廖敏妃及林 聖學 (2008) 以建置一套高互動性的數位教學平台-整合式即時回饋系統 (Integrated Personal Response System, IPRS) ,利用概念詮釋結構模式進行分 析,幫助教師了解學生對每個概念的學習情況,並針對學習成就較差者給予 個人化的補救教學。 綜上所述可知,應用概念結構模式(CAISM),可得個人化概念結構圖, 是一個可行的方法。因此,本研究應用概念結構模式,分析國小五年級學生 數與量分年細目概念的認知結構,以了解學生的概念關聯情形,作為教師進 行認知診斷、補救教學與課程設計之參考。
第五節 知識結構測量
壹、概念構圖 (concept mapping)
Novak and Gowin (1984) 提出概念構圖 (concept mapping) 方法,建立 在 Ausubel (1963) 所主張的認知同化理論之「有意義的學習」 (meaningful learning) 基礎上。概念構圖要求學生將所要學習內容的概念,先做階層性的 分類和分群,並以聯結線將兩兩概念間的關係作聯結,且在聯結線上標記聯 結語,此聯結語用來輔助說明兩兩概念之間的聯結關係,最後形成有如一幅 網狀結構圖 (Novak & Gowin, 1984) 。
概念構圖是強調學生將所具備知識以結構性、組織性、完整性的方式表 達出來,可直接就知識的組織與結構情形,了解學生的學習狀態 (宋德忠、 林世華、陳淑芬、張國恩,1998) 。因此概念構圖是建構概念的歷程,也是 一種有意義的結構化學習法。從學生建構出的概念圖,可視為他對某特定領 域的知識結構,進而從此知識結構可看出其理解程度及是否存在有迷思概 念。 概念構圖對學生知識進行評量,大致可分為兩個方向:一是將學生概念 圖與專家概念圖作比較;一是利用概念構圖以了解學生學習時,知識結構改 變與建構的情形 (宋德忠、林世華、陳淑芬、張國恩,1998) 。其計分方式 大多根據 Novak and Gowin (1984) 所發展出來的計分方式為藍本,再根據 個別研究目的的採取修正的模式或不同的加權計分方式 (余民寧、陳嘉成、 潘雅芳,1996; Markham, Mintzes & Jones, 1994; Novak & Gowin, 1984, Ruiz-Primo & Shavelson, 1996; Stuart, 1985) 。茲將其計分原則簡述如下:
(一)關係 (relationships):指將兩個概念聯結成一道命題的聯結關係;在 評分時,只針對每個有效且有意義的命題聯結關係給予一分,反之則不予計 分,亦不扣分。
只計算有意義的階層關係,並給予相對於有效聯結關係三到十倍的分數,但 概念圖若呈現出「不對稱」,則以分支較多的那一個架構來計算有效的階層 個數,而每一個有效的階層,給予五分。 (三)交叉聯結 (cross-links):指概念圖中某階層的一部分概念和另一階層 的部分概念呈現有意義的聯結,而所呈現的聯結關係必須是重要且有效的。 在評分時,每一個重要且有效的交叉聯結,給予十分;每一個有效但不能指 出相關概念(或命題)之組成之交叉聯結,則給予二分,但交叉聯結亦可作 為創造力的指標,因此獨特的或具創造力的交叉聯結可以給予特別的認可或 額外的加分。 (四)舉例 (examples):指學習者能根據自己的理解,舉出特殊且具代表 性的例子,而所舉出的例子必須是學習者知識統整後,以特定的事件或物件 (但非教材上的現成例子)作為例子才行。在評分時,學習者的每一個舉例 若能標明出其概念間的關係,給予一分。 根據概念構圖的計分原則,將學生所繪製的概念圖分別逐項計分,在將 各項分數加總起來,得到一個總分,此總分代表學生在概念學習後所習得該 概念間關係結構的一項成績或成就指標。概念構圖的總分越高,即表示學生 的概念學習越好,對概念之間的關係理解越透徹、越清楚;反之,則表示學 生的概念學習愈差,對概念之間的關係理解較缺乏完整性及正確性,或甚至 是具有錯誤、偏差,或是迷失概念的情況存在。一個典型的概念圖計分例子, 可參考圖 2-3 所示。 Novak (1990) 認為概念構圖是一種學習方法、教學策略、評量工具,亦 是設計課程的依據。例如江淑卿 (2001) 探討不同自然學業能力的兒童以閱 讀概念構圖方式,對知識結構、理解能力與學習反應的影響,結果發現中、 低能力的學生對閱讀概念構圖的理解能力有較佳的表現,而高能力的學生會 因教材的難易有所差異。薛雅惠 (2000) 應用概念構圖在地理教學上,發現
在學生的學習上給予較明確的學習方向及指引,增進對學習內容的了解,且 可診斷出學生在探討地理現象時的困難與迷思。Chang, Chiu, Lin and Heh (2003) 提出一套藉由領域專家制定的概念圖及分析題目知識概念的方法,藉 著網路評量系統給予學生線上評量,即時診斷學生的迷思概念。Chiu, Huang and Chang (2000) 針對在職老師及實習老師進行網路合作概念構圖的研 究,發現過程共同協調的行為和結果有關聯。李博宏、王薰巧 (2004) 將概 念構圖融入在自然與生活科技領域上,結果顯示學習概念構圖後,學生構圖 表現有 1/3 以上學生構圖表現優異。余民寧、陳嘉成 (1996) 在探討概念構 圖評量法的可行性,及學習概念構圖後態度改變對學業成就之影響中發現, 概念構圖可當成一種有效的學習方法,且概念構圖評量法也可以當成一種有 效的評量工具,以取代傳統的評量方式。 不過相關研究亦顯示概念構圖的應用是否均有成效則有不相同的結 果。Seaman (1990) 以五年級學生為對象,進行合作概念構圖及個別概念構 圖的研究,結果發現不論是合作或是個別建構概念圖均有助於學生學習,但 低成就的學生無法透過概念構圖學習到教材內容。黃萬居 (1993) 以國小高 年級學生的概念構圖和自然科學習成效之研究中發現,以概念構圖教學與一 般傳統教學在自然科之教學成效中,並無顯著差異。羅廷英 (2001) 以國小 一年級學生為對象,結果發現概念構圖策略對學生學習成效沒有明顯差異。 蔡天民、王美芬 (2002) 以概念構圖為後設認知策略,對「自然科學習成就」 並沒有顯著的提昇效果,但進一步分析,對低推理能力的學生,則有較正向 的結果。 綜上所述可知,概念構圖可做為課程設計、學習方法、評量診斷、補救 教學的工具,學生運用概念構圖可以是一種結構化的學習,但從一些相關研 究中發現其應用成效有不顯著的結果。不過在分析知識結構上,概念構圖不 失為一個可行的方法。
圖2-3 概念圖計分例子 (資料來源:修改自余民寧 (1997:486) ) 重要概念 聯 聯 聯 一般化概念 一般化概念 一般化概念 概念 聯結 概念 聯結 聯結 聯結 聯結 聯結 概念 概念 聯結 例子 事件 聯結 例子 事件 較不 一般 化概 念 較不 一般 化概 念 聯結 聯結 聯結 交叉聯結 例子 例子 交 叉 特 殊 化 概 念 特 殊 化 概 念 特 殊 化 概 念 物件 物件 聯結 階層 第一階 第二階 第三階 第四階 計分:(僅計算有效且重要者) (分數) (個數) 關係: 1 × 14 =14 階層: 5 × 4 =20 交叉聯結: 10 × 2 =20 舉例: 1 × 4 = 4 總計: 58 分
貳、徑路搜尋法 (pathfinder)
徑路搜尋法於1985年由美國新墨西哥州立大學計算研究實驗室領導人 Schvaneveldt 與其研究小組,根據圖形理論和網路模式,研究發展出徑路搜 尋量尺化算則 (pathfinder scaling algorithm) ,用來建構和分析知識結構,且 設 計 知 識 網 路 組 織 工 具 (Knowledge Network Organizing Tool , 簡 稱 KNOT) ,來輔助建構、分析和評量徑路搜尋網路。
徑路搜尋開始多應用於實驗室,近年來逐漸運用於教育心理學領域,林 原宏 (1996) 認為徑路搜尋可運用此三個方面:(一)表達概念的關係,(二) 預測記憶搜尋 (memory retrieval) 及記憶組織 (memory organi-zation) ,(三) 分析專家和生手的表徵不同及轉換。
徑路 搜尋 法 評量 知識 結構 的 過程 大致 可 分為 三個 步 驟 : 引出 知 識 (knowledge elicitation)、表徵知識結構 (knowledge representation) 與評價知 識結構 (evaluation of knowledge representation) ,茲將這個三個程序簡述如 下: 一、知識結構的引出 由受試者針對某個領域知識之概念進行判斷兩兩概念間的相似性、關聯 性或心理距離值,以獲得近似值矩陣 (proximity matrix, PRX) ,近似值矩陣 是一種完全網路 (complete network) 。 二、知識結構的表徵 徑路 搜尋 法 透過 量尺 化算 則 ,將 近似 值 矩陣 轉換 成 徑路 搜尋 網 路 (PFNET),徑路搜尋網路是由一組概念以節點和鍊結所連接而成的網路結 構,如圖2-4所示。
圖2-4 近似值矩陣與徑路搜尋網路 (Goldsmith, Johnson & Acton, 1991) 三、知識結構的評價 徑路搜尋法主要是將受試者的知識結構和參照結構 (referent structure) 進行比較,而比較知識結構的相似程度的方法有兩種,一是以集合理論 (set theory) 為 基 礎 , 計 算 相 鄰節 點 的 交 集和聯 集 關 係 , 可 得到 相 似 性 指 數 (closeness index, 簡稱PFC或C指數) ;另一種是以圖形理論為基礎,計算節 點之間距離的相關程度,可得圖形理論距離指數 (graphic-theoretic distance, 簡稱GTD) 和近近性指數 (proximity index, 簡稱PRX) ,藉這三種指數可 判 斷 受 試 者 知 識 結 構 和 參 照 結 構 的 相 似 程 度 (Goldsmith & Davenport, 1990)。以下將以Goldsmith, Johnson and Acton (1991) 所舉的例子,如圖2-5 所示,分別說明這三種相似指數。 近似值資料矩陣 (proximity Data) A B C D E A 0 1 3 2 3 B 1 0 1 4 6 C 3 1 0 5 5 D 2 4 5 0 4 E 3 6 5 4 0 PFNET A B E D C
圖2-5 知識結構比較之PFC和GTD指數 (改寫自Goldsmith et al., 1991) GTD指數是根據圖解理論的算則,計算兩徑路搜尋網路相同節點間的距 離值的相關係數,如表2-3所示,GTD指數的數值介於由0至1之間,數值越 大表示兩個網路越相近。 表2-3 網路一和網路二各節點的距離值 網路一 節點 A B C D E F G A — 1 1 2 2 2 2 B — 2 1 1 3 3 C — 3 3 1 1 D — 2 4 4 E — 4 4 F — 2 G — 網路二 節點 A B C D E F G A — 1 2 1 1 3 3 B — 1 2 2 2 2 C — 3 3 1 1 D — 2 4 4 E — 4 4 F — 2 G — 網路一 網路二 網路三 A B C G E F D A B C G E F D A B C G E F D PFC=.43 GTD=.79 PFC=.74 GTD=.42