國立台中教育大學教育測驗統計研究所
教學碩士論文
指 導 教 授:胡豐榮 博士
國小六年級學童分數乘除概念與
運算錯誤類型之研究
研 究 生:林榮煌 撰
中 華 民 國 九 十 五 年 八 月
摘 要
本研究主要是探討小六學生在分數乘法與除法運算的學習表現,以及可能產 生的錯誤類型與原因。 本研究樣本分布在台中縣山、海、屯三區共六所國小,每所學校選取兩班六 年級的學生共 381 人,研究工具採用分數乘除法運算評量試題,針對學生在分數 乘除法概念及運算上的表現及錯誤類型情形,進行調查。並整理、歸納出學生之 錯誤類型,並進一步分析學生在分數乘除法運算錯誤之原因。 研究結果發現主要有下列六個部份: 一、學生在分數乘除概念與運算的學習成果答對率表現平均為 0.63。 二、學生在分數乘除的分類學習上,以分數乘整數表現最好,分數乘分數及分數 除整數表現次之,而整數除整數等於分數及分數除分數的表現不佳。 三、學生在分數乘除法能力指標習得的能力來看,在概念建構能力與基本運算能 力上,學生的表現較佳;而分數乘除法概念理解能力與問題解決能力的表 現,仍有進步空間。 四、台中縣三個區域的學生及性別在分數乘除概念與運算的學習成果表現上,並 無顯著差異。 五、學生在分數乘法概念與運算上的錯誤類型與原因 六、學生在分數除法概念與運算上的錯誤類型與原因 此外,研究者亦就研究發現提出,教師在教學、學生在學習以及分數乘除法 未來研究上的建議。 關鍵字:分數 乘除法 國小六年級 錯誤原因Abstract
The main goal of this research is to probe into the six grade students’ learning multiplication and division of mathematical fractions and to explore the potential mistakes and reasons while students operate mathematical fractions.
The subjects in this research were from six primary schools, three districts in Taichung county, and there were total 381 subjects chosen from two six grade classes in each school. The research instrument was employed the measurement which focused on students’ constructs of multiplication and division of mathematical fractions, students’ performances of mathematical operation, and students’ potential mistakes while operating mathematical fractions. After collecting the data, the researcher classified students’ mistakes on mathematical operation, and further, analyzed the reasons for these mistakes.
The results of this research included six parts which were presented as follows.
1.The average rate of accuracy of student's constructs and operating performances of multiplication and division of mathematical fractions was 0.63.
2.In the classification of fractional operation, students performed the best on the operation of fraction-multiply-integrate. Students’ performances on the operation of fraction-multiply-fraction and fraction-divided-by-integer were in the second place in the order. Students did not perform well on the operation of
integer-divided-by-integer and fraction-divided-by-fraction. 3. Based on the standards of students’ learning multiplication and
division of mathematical fractions, students performed well on the ability of construct-built and basic operation. However, students’ performances on the understanding of multiplication and division of mathematical fractions and on the problem-solving had a room for being improved.
4. Students from three districts and the gender did not have a significant difference on the performance of learning multiplication and division of mathematical fractions.
5.The mistakes students made while operating multiplication of mathematical fractions and reasons for these mistakes.
6. The mistakes students made while operating division of mathematical fractions and reasons for these mistakes.
Furthermore, based on the results of the research, the researcher proposed the recommendations for future researchers with regard to students’ learning multiplication and division of mathematical fractions.
Key word: fraction, multiplication and division, Grade six of primary school, Wrong reason
目 錄
第一章 緒論
……… 1 第一節 研究動機……… 1 第二節 研究目的與待答問題……… 2 第三節 研究範圍與限制……… 3第二章 文獻探討
……… 4 第一節 分數的來源與意義……… 4 第二節 數概念與分數的概念……… 7 第三節 乘除法類型之研究………16 第四節 國小分數教材分析………27 第五節 分數乘除法運算的錯誤類型與成因………32 第六節 試題編製之理論………43第三章 研究方法
………50 第一節 研究架構………50 第二節 研究對象………52 第三節 研究工具………52 第四節 資料分析………58第四章 結果與討論
………59 第一節 分數乘除概念與運算的施測試卷分析………59 第二節 分數乘除法學習的表現結果………61 第三節 分數乘除法學習的錯誤類形與原因………85 第四節 分數乘除法學習的錯誤原因………91第五章 結論與建議
………93 第一節 結 論 ………93 第二節 建 議 ………95參考文獻
中文部份 ………97 英文部份 ………99
附錄 A
表 目 次
表 2-1 Vergnaud 的量數同構型關係表………17 表 2-2 Vergnaud 量數同構型的問題類型表………17 表 2-3 Vergnaud 叉積型關係表………18 表 2-4 Vergnaud 叉積型問題類型表………18 表 2-5 Vergnaud 多重比例型關係表………19 表 2-6 Vergnaud 多重比例型問題類型表………19表 2-7 Schwartz (I, E, E’)問題類型表………20
表 2-8 Schwartz 的(E, E’,E’’)結構表………21
表 2-9 Schwartz 的(I, I', I'')結構表………21
表 2-10 Schwartz 的(S, E, E')結構表 ………21
表 2-11 Greer 的 STS 乘除問題類型(屬於不對稱型)表………22
表 2-11 Greer 的 STS 乘除問題類型(屬於不對稱型)續表………23
表 2-12 Greer 不同數值型態的乘除情境類型表………24
表 2-13 Nesher 的映像規則(mapping rule)說明表………24
表 2-14 Nesher 的比較型(compare) 問題說明表………25
表 2-15 Nesher 的乘法叉積(cartesian)問題說明表………25
表 2-16 Usiskin & Bell 的 Schwartz 的比例因子類或相同等集合問題 (I, E, E’) 結構表………26
表 2-17 Usiskin & Bell 的 Schwartz 的交叉運作問題表 ………26
表 2-18 Usiskin & Bell 的大小改變類或常量問題表………26
表 2-19 乘除法類型之比較表………27 表 2-20 82 年版新課程綱要表………28 表2-21 九年一貫課程暫行綱要表 ………29 表2-22 92年頒布之九年一貫課程綱要數學能力指標表 ………30 表 2-23 國小六年級學童學得的分數課程內容表………31 表 2-24 有關分數概念的研究報告內容表………32 表 2-24 有關分數概念的研究報告內容表(續)………33 表 2-24 有關分數概念的研究報告內容表(續)………34 表 3-1 正式施測學校、學生數一覽表 ………52 表 3-2 預試試題難度及鑑別度一覽表 ………54 表 3-3 預試試題雙向細目表 ………55 表 3-4 期中數學評量成積與預試測驗成績的 Pearson 積差相關表 …………56 表 3-5 期末數學評量成績與預試測驗成績的 Pearson 積差相關表…………56 表 3-6 預試答題結果的難度表 ………57
表 3-8 正式試題雙向細目表………58 表 4-1 正式施測試題的難度及鑑別度表………59 表 4-2 台中縣三區學生學習成果 95%信賴區間表………60 表 4-4 男女學生的學習比較 T 檢定表………61 表 4-5 分數乘除概念與運算的學習答對率排序表………63 表 4-6 分數乘除概念與運算的學習成果統計表………63
圖 目 次
圖 3-1 研究流程圖………51 圖 4-1 分數乘除概念與運算的學習表現統計圖………62
第一章 緒 論
第一節 研究動機
教育部自 93 年 5 月起委託國立教育研究院籌備處,針對國民中小學學生學 習成就建立常態性的資料庫,每年追縱、分析學生學習成就表現,並在 94 年 5 月 26 日先針對國小 6 年級學生在國語、數學、英語三科進行第 1 年抽樣測驗, 根據正式對外公布的學生學習成就評量抽測結果發現,小六學生在數學科有 19.1%(約五萬九千人),未達到小六基礎水準,數學科成就水準在基礎以下,沒 有達到小六數學應有的知能,必須補救教學(教育部國教司,2006)。 國立台北教育大學副校長王富祥指出,現今國小學生數學程度明顯下降,國 立師院附小一名高年級老師也說,高年級學生開始接觸「分數」,分母通分、擴 分、等值分數等概念,多數學生常搞不清。王富祥還說,學生數學出現學習落差, 以分數四則運算概念為例,小六或國一的老師如果沒有補救教學,學生成績就很 明顯出現兩極化(聯合報,2006)。 分數,是多數國小學童的夢靨,也讓部分國小老師視為畏途,德國人甚至將 遭遇困難問題描述為「如墜分數中」(劉秋木,民 85),國外學者 Behr, Harel, Post & Lesh(1992)亦說:「學習分數為兒童數學發展上的嚴重障礙」。可見國內外學 者都有「分數在國小數學中,是複雜又重要的概念」,國小學童分數學習有困難, 會阻礙學生在國小後的數學發展。所以國內將分數乘除法運算安排在九年一貫課 程的第三階段數與量的主題中,適合從具體運思期過渡到形式運思期的學生(國 小六年級到國中一年級)學習;美國數學教師協會(NCTM)的學校數學課程原則 與標準(Principles and Standard for School Mathematics),也將分數的學 習放在中年級(6-8)的數與運算中,學習的項目包括:(一) 數的了解和數的呈現方式及數與數之間的關係和數的系統: 運用分數解決問題與了解分數在數線上的位置。
(二) 數運算的含義與關係: 了解分數運算的意義與功能。 (三) 數的運算技能: 學生能選擇適合的方法和工具來計算分數的運算,提升分數運算技能。 因此分數的學習可以分成兩大項,一項是分數的概念,另一項則是分數的運 算(NCTM, 2000)。此外,國外學者 Gagne’(1985)也提到數學的基本能力包括概 念理解和計算能力兩大部分。因此,學生在學習分數運算時,必須兩者並重,若 是一項不注意,錯誤就容易發生,而學生不論是概念上或計算上的錯誤,都透露 出學生的想法,這時,教師可藉由學生的錯誤類型,診斷出學生錯誤類型發生的 原因,進而設計補救教學內容,讓學生的學習錯誤改善( Borais,1987) ,讓學 生在學習達到應有的程度。 綜合以上所述,研究者將探討目前小六學生在分數乘除法上的學習成果,以 及在分數乘除法上的運算概念與技能錯誤的類型,了解學生的學習困難和錯誤成 因,以提供教師教學上的參考,並能針對其錯誤行為進行補救教學,讓學生在分 數乘除法運算上的學習達到應有的程度。
第二節 研究目的與待答問題
本研究的目的是了解台中縣小六學生在分數乘除法運算中的學習成效以及 運算中存在哪些錯誤類型並分析其成因。透過文獻探討使用一份適合小六學生分 數乘法及除法之診斷試卷,調查學生在分數乘除法運算之表現,並分析學生存在 分數乘除法運算之錯誤類型,進而探討造成學生錯誤類型可能成因,提供教師教 學與評量的參考。基於上述的研究動機,本研究之研究目的具體言之為: (一)了解台中縣國小六年級學生在分數乘除法的學習表現。 (二)了解台中縣國小六年級學童在分數乘除概念與運算的錯誤類型。(三)探討台中縣國小六年級學童在分數乘除概念與運算發生錯誤的原因。 因此基於研究目的提出下列的待答問題: (一)台中縣國小六年級學生在分數乘除法的學習表現為何? (二)台中縣國小六年級學童在分數乘除概念與運算的錯誤類型為何? (三)台中縣國小六年級學童在分數乘除概念與運算的錯誤形成的原因為何?
第三節 研究範圍與限制
本研究以九年一貫國小數學科課程綱要為主,研究期間為九十五年二月到九 十五年六月。此時為九年一貫課程六年級數學科課程施行的第二年。研究內容主 要是國小六年級學習分數的乘除法概念及運算,至於不同版本內容未列入本研究 之範圍。研究目的只討論國小六年級學童在分數乘除概念與運算的學習成果及錯 誤情形與錯誤形成的原因,沒有探究其他的變項如年級、使用教科書版本及教師 的教學方式等對錯誤情形或原因的影響。研究對象僅為台中縣六所國小共十二班 381名六年級學童,因此推廣性有其限制。第二章 文獻探討
要探討學童分數乘除法概念與運算及錯誤類型的相關內容,必須先了解以 下內容:分數的意義和概念,分數概念的發展,乘除法概念的相關研究, 國民小 學分數教材的內容,國小學生學習分數時容易發生的迷思與錯誤類型,以及測驗 編制及命題原則,如此方能探討目前小六學生在分數乘除法上的學習成果,以及 在分數乘除法上的運算概念與技能錯誤的類型,了解學生的學習困難和錯誤成 因。第一節 分數的來源和意義
欲探究學生的分數學習成果,必須先對分數有充分的了解,本節將從分數的 來源和意義概念來說明分數的內容。(一)分數的來源
人類生活中,因為整數的不夠用,才產生了分數。分數(fraction)一詞來 自拉丁文的「fangere & fractus」,意思是碎裂、分開,通常用來描述一個被分 開全體之各部份(羅鴻翔,1980),或是一個小於1的數。在計數系統的發展上以 「1」為計數單位,對於大數量的計數,發展出比「1」大的計數單位數,例如5、 10、100、1000、…等,而面臨到不足「1」的量必須計數、測量及比較時,必須 發展比「1」小的計數單位,例如 2 1 、 3 1 、 4 1 …等等(周筱婷及黃敏晃等,民90), 早期人們因為社會趨於多元與複雜化,以至單位元素「1」的不夠用,分數也藉 由計數上的需要孕育而生。Hunting(1986)對分數的最初概念是以一個連續物 品細分(如蘋果、蛋糕、派)。呂玉琴(民84)認為分數概念起源於「分」,是用來解決不滿一個單位量的量數值的問題。甯自強(民84)主張分數是一物件等 分割活動的紀錄與結果。透過將原單位量加以分割,得到單位分量的重複,因而 得到與被測量量等價的量,以分割份數和重複單位分量的次數並置,作為被測量 量指標。因此,分數是為了要解決比「1」小的計數單位問題而產生的。
(二)分數的意義
在數學上是以有理數來定義分數,分數是指能化為 p q 的型態,且p、q 皆為 整數者,其中p≠0(Corwin, Russel, & Tierney, 1990;教育部,民92),文 獻中亦有關於分數多重意義的各家說法。 劉曼麗(民85)「部分與全體」關係是用來詮釋分數意義中的一種,將一個整 體等分後,分數是表示或記錄其中被指定的部分與全體關係。例如:「 5 4 」可表 示一個整體被分成五等分後的四分。Behr, & Post(1988)解釋分數為: 1.「部分/全部」的概念。 2.比率:強調兩個數量的關係。 3.比值:用一個量值來代表兩個數量的關係。 4.商:兩數相除的結果。 林碧珍(民79)定義分數包含下列五種: 1.部分-整體模式:全部區域的部分區域,以連續量(長度、面積、容積)為主。 2.子集合-集合模式:集合中的部分集合。 3.數線模式:數線上的一個數值。 4.商模式:兩個整數相除的結果。 5.比值模式:二個集合或二個度量相除的結果。
綜合 Kieren(1980)、Behr,Lesh,Post,& Silver (1983)、Ohlsson(1988)、 楊瑞智(2000)等學者的研究,可知分數較常用的定義有以下五種:
1.部分--全體的關係。 2.兩個整數相除的除法。 3.比:兩個數的比較值。 4.運算。 5.測量。 教育部國立編譯館依據82年課程標準所編的國小數學科教學指引也有如下 的說明:當使用分數數詞(字)來描述有理數時(以 5 3 為例),至少可以從下列 六種角度,來討論分數數詞(字)的意義: 1.部分與全體的比較:全體為5時,3是5的部分。 2.除法的活動:3除以5活動的另一種記法。 3.運算元:對於物件1,進行一個運作,將1等分割成5份,再取出其中的3份。 4.小數的另一種記法。 5.比的意義:表示兩數量的相對關係(3:5)。 6.測量:用來測量一個不滿一個單位量的量的數值問題,或是對兩量的對等關係 進行數值化(比值)。 教育部編製之92年版九年一貫課程綱要則指出有理數即是分數,小學有理數 教學,必須釐清、練習並且連結下述有理數的四種意涵: 1.平分的意涵 2.測量的意涵 3.比例的意涵 4.部分/整體的意涵。 最後歸結成日後數學學習中,有理數最核心的意涵----「除的意涵」。(教 育部,民92)。
綜合學者們的觀點與數學教材分析可知,分數是一個複雜而重要的數學概 念。分數可以是個「數」、量的分割,又涉及兩個量的比較,其意義是豐富而多 樣的,而且,因為教學的情境或是單元的不同,分數也會有不同的意義,因此, 教師在教學前應該深入了解教學的情境與單元所要呈現的問題,配合不同意義的 解釋,讓學生在分數的理解上更具體的明白其中所含的意義。
第二節 數概念與分數的概念
在了解分數的來源與意義之後,本節將進一步了解兒童對分數的概念,但是 數概念對兒童的分數概念發展有所影響,因此本節先對兒童數概念的模型做一探 討,接著再分析兒童分數概念的結構。一、數概念的發展
數概念的模型是指兒童因為運思方式及層次的不同,使學童對應出對數的意 義亦有所不同。當兒童能熟練的運用某一種運思方式時,才能表示其擁有此階段 的數概念。根據兒童對數的意義之不同,可以區分兒童數概念類型的種類為:數 的前置概念、起始數、內嵌數、合成巢狀數、以及測量單位數。 以不同的數概念模型分析兒童的運思方式,可區分為序列性合成運思、累進 性合成運思、部分-全體運思、測量運思、與比例運思(甯自強,民81,民83)。 茲將兒童的運思方式與對應的數概念模型說明如下: (一)數的前置概念 數的前置概念類型中,數概念的意義為標準數詞序列上的一個「位置」或是 「特定的空間圖形」,並不具備約定成俗的數概念性質。例如:給兒童5個花片,問他花片有多少個時,兒童只能指出第五個花片(位置數)而不知整體「五個」 才是5,兒童僅能依據經驗來對特定的空間圖形作一區分而尋出答案。 此階段兒童以「位置」或「圖形」來認識「數」。也就是,兒童此時所指的 5 並未具有基數的概念,即此階段的兒童尚未具有數保留概念(Piaget,1965), 故稱為「數的前置概念」。數數是兒童在此階段的解題活動,尚無法解決數的合 成、分解、比較等問題。
(二)序列性合成運思(sequential uniting operations)與起始數
合成運思是指兒童將構成事物的元素合成為一事物的能力或運思(甯自強, 民81)。例如兒童能指出整體5個花片是5,此5是由5個1所組成,這就是兒童將 構成事物的元素合成為一事物。依發展的先後,合成運思又可分為序列性合成運 思與累進性合成運思。合成運思被兒童運用於量的情境中以建構數的概念,將抽 象的計數動作(counting acts)合成為一集聚單位。 序列性合成運思是指兒童能依數詞所指示的量依序全盤表現以進行量的合 成或分解,並將結果重新合成予以數值化,所以將此種性質的數稱為「起始數」。 起始數概念的意義為兒童在數詞序列中,一段由1 開始的有限數列,一一對應的 一個以「一」為元素的群體,或是集聚「一」所成的單位,而且此集聚單位的數 值是有限數列的最後一項(甯自強,民83)。此運思將數個「1」合而為一,形 成一個集聚單位(例如:10 或16)。 序列性合成運思階段的兒童對數概念的掌握,必須透過標準數詞序列,將一 的物件對應一個數詞的方式而得。換言之,兒童必須透過使用單位「一」,將物 件累算後才能確定數的大小。此時兒童在聯絡兩數時,至多只是將兩數加以並置 (juxtaposed),也就是將兩數看成是獨立無關的。
(三)累進性合成運思(progressive uniting operations)與內嵌數 累進性合成運思是指兒童能將構成事物的元素合成一集聚單位,並以此集聚 單位為起點,進一步累加另一物件以形成另一新的集聚單位。例如以16 為起點, 繼續合成3個「1」,而形成19。 此階段兒童利用累進性合成運思建構「內嵌數」概念。內嵌數概念的意義為 兒童在數詞序列中,一段非由1 開始的連續有限數列,一一對應的一個以「一」 為元素的集聚單位,而且此集聚單位的數值是有限數列的項數(甯自強,民83)。 累進性合成運思的兒童能以一個數為起點開始往上數,但是當兒童往上數 時,舊的集聚單位是內嵌於(embedded)新的集聚單位之中。然而,累進性合成 運思中,蘊含的內嵌關係只是隱約的「部分-全體關係」,因此此階段的數一再 複製尚未穩固,兒童一再複製數時,會產生單位之間混淆的現象。此時兒童所建 構的兩數之間關係,是集合間的包含關係。 (四)部分-全體運思(part-whole operations)與合成巢狀數 部分-全體運思是累進性合成運思和的重組。以累進性合成運思所製成的集 聚單位為基礎,將內嵌於集聚單位中的部分複製(copy)後脫嵌(disembedded), 再置回原集聚單位中,同時保持原有的全體不變。由部分-全體運思所孤立出的 部分不會影響原來的全體,而由累進性合成運思所建構出的部分,一經孤立則使 原有的全體不復存在(甯自強,民81)。 此運思掌握「1」單位與以「1」為單位量所合成的集聚單位(例如:10 或 100)間的部分-全體關係,明顯地區分兩者的意義,故在混合使用兩種以上的 被計數單位時,不混淆其計數的意義,可以將數個集聚單位和數個「1」單位合 而為一,形成新的集聚單位。例如:能區辨3個「十」與3個「一」這兩個3具有 不同的意義,而將33 視為3個「十」與3個「一」的合成結果,發展由多單位的 觀點,來解讀數字(詞)的意義。
部分-全體運思階段的兒童具有合成巢狀數概念。合成巢狀數概念指示的集 聚單位,可以由1 與其他高階單位聯合而成,合成時重複的高階單位與1不會產 生混淆(甯自強,民83)。 雖然此階段兒童對於單位之間不會產生混淆的現象,但是此時所建立的「部 分-全體關係」只是單方向的。如問3×4+5×4=?的問題,兒童是先分別求出3× 4的結果和5×4的結果,然後再將兩結果相加,而非以自全體看局部的方式,自行 調整結構過程使用8×4得到結果;又如將108塊積木分成三份的問題,兒童則是先 行估計每一份的數量,再重複製作三份,並求其總合,若總合數與108不符,則 調整估計量重新求解,直至重複製作的總合數與108 相同為止。 (五)測量運思(measurement operations)與測量單位數 測量運思是二個部分-全體運思的遞迴運用,在重複的運用部分-全體運思 以重組同基數的次階集聚單位後,把內嵌於最高階集聚單位中的次階集聚單位都 當成部分,加以複製後予以脫嵌外提,再行置回原處,並且同時保留原有的最高 階集聚單位與「一」的部分-全體關係(甯自強,民81)。 此運思以掌握「1」與集聚單位(例如10 或100)間的部分-全體關係為基 礎,進而能掌握集聚單位(例如:「十」)與以此集聚單位為單位量所合成的另 一個新集聚單位(例如:10 個「十」,也就是「百」)間的部分-全體關係, 故而是同時掌握兩個層級的部分-全體關係,換言之,在運思上,可以把任何整 數(例如10或16)當作單位量,而此整數成為測量單位。以8×3=6×?為例,兒童 不但能將6看成是構成24 的單位量,6也是異於1 的單位量「2」所構成的,因此 6不但是構成一整體的部分,同時也是由別種部分所構成的整體,故其具有測量 單位的性質,稱為測量單位(measurement unit),而由測量單位構成的數稱為 測量單位數。
間的轉換。換言之,一單位可同時為另一單位的高階單位,且同時為另一單位的 低階單位。此階段兒童具有測量單位數概念,測量單位數是指兒童具有保留概念 的合成巢狀數(甯自強,民83)。 (六)比例運思(proportion operations) 比例運思掌握兩個集聚單位間的關係,形成一種新的單位來描述此關係,亦 即掌握比值或有理數的概念,以關係即為運思的對象,蘊含著對共變性質的掌 握,被此關係聯絡的兩個集聚單位,如果產生等比例的變化,並不會改變此關係。 由數概念模型分析兒童的運思方式,可知兒童一開始由「位置」或「圖形」 來認識「數」,在有了序列性合成運思能力後,才具備起始數概念;有累進性合 成運思能力後,才能具備內嵌數概念;有單向的部分-全體運思能力後,才能具 備合成巢狀數概念;當兒童有測量運思能力後,此時部分-全體關係是雙向可逆 的,合成巢狀數概念才能過渡至測量單位數概念。 在了解兒童的數的概念後,我們就可以進行分數概念發展的探討。
二、兒童分數概念的發展
Piaget,Inhelder & Szeminska(1960)曾經使用連續量的具體物,研究4到 7歲兒童對面積的分割行為,以探討兒童如何建構部分與全體的關係,來形成分 數的概念,其研究發現兒童的分數概念發展分期為: (一)四歲到四歲半的兒童,對一物分為兩半甚為困難,在分割之前沒有預想的 計畫或基模(Skema)。此階段的最大特徵是缺少部分與全體之間的任何關 係,兒童不會注意到他所接觸的部分是某個比較大的全體之中所含的元素。 對於不同形狀之分割,為長方形比較容易,圓形次之,正方形較難。 (二)四到六歲的兒童對於規則的與小範圍的東西有分半的能力,但將物體分成
相等的三部分的能力尚未表現。如果原來全體的大小增大了,期分成一半的 能力更要延緩,在分割圖形中利用長方形的比較容易解決。 (三)六到七歲的兒童已經能夠成功的實施三等分的分法,而不必利用嘗試錯誤 的方法,但其操作的了解,還是在具體的操作層次,在這個階段的兒童具有 整體性的保留概念,以一個餅為例,他們能夠了解各個分割塊數集聚所得到 的總量與整個餅是一樣的。 (四)十歲左右的兒童能進行六等分的分法,首先是用三等分法分一個餅,然後 再將所分得的三塊餅,每塊用二分法再分一次。 Piaget et al.(1960)並指出,兒童在瞭解分數運算之前必須具有下列七 個子概念: 1.必須有一個可以除盡的全體。 2.一個分數包含各部分的限定數(determinent),分配東西時,各部份必須與 接受者相對應。 3.子分割活動中,全體必須被耗盡,沒有餘數。 4.全體被切割成各部分的數與切割數間,有一固定的關係。 5.分數的概念意指分割後的每一部分都是相等的。 6.當兒童操作了再細分的概念時,瞭解到此細分的一部分是全體的一部分,同時 此一細分的部分本身也是一可再分割的全體。 7.因為分數是從全體而來,其全體始終不變。
此外,Hiebert & Tonnessen(1978)曾經以一對一的方式研究九位五歲四 個月到八歲兒童的分數概念發展情形,發現與Piaget et al.(1960)的七個子 概念相符,但結果並不一致。以面積模式呈現問題,兒童分數概念的發展次序為, 2 1 → 4 1 → 3 1 → 5 1 → 6 1 ,與Piaget等人相同。但使用長度模式時,其順序為 2 1 → 3 1 → 1 →1→1,則與Piaget等人的研究結果1→1→1→1→1不相同。
根據兒童在不同階段的運思方式所呈現的數概念與分割活動為基準,利用分 數詞做為區分而將兒童的分數概念分為:一、分數概念的前身;二、起始單位分 數;三、加法性分數;四、巢狀分數;五、有理數(Ning,1992)。以下分別將 概念說明如下: (一)分數概念的前身 當兒童僅能使用序列性合成運思時,即數概念只是序列性合成運思,雖然兒 童具有分割經驗,但分割活動未能將子分割單位數值化,因為此層次的兒童並未 具有分數概念,故稱之為分數概念的前身。 此階段兒童分數詞的意義為「並置類型」(juxtaposed pattern)。舉例來 說,分數詞 4 1 ,此時的意義為1和4,或是4和1,若拿8個積木給兒童,要求他取 出其中的 4 1 時,則答案不是1個積木,就是4個積木。 在分數概念的前身時,兒童只是靠直覺作判斷,將一物撕裂使成為一個撕得 的部分和一撕剩下的部分,撕得的部分與撕餘的部分不一定相等,也不一定窮 盡。且只有部分而缺乏部分與全體的概念,例如兒童可以知道 3 1 是三份中的一份, 但是如果將這一份再放回去,問兒童全部是多少時,兒童會回答四份。此外,兒 童亦無法使用不同分數詞去表示不同分割情境的意義。 (二)起始單位分數 當兒童能夠引入累進性合成運思於分數的情境時,他們則如同在整數情境中 聯絡兩個整數一般,將由子分割單位所構成的分子部分內嵌於由子分割單位所構 成的分母部分,此時的分數詞意義稱之為「內嵌並置類型」。舉例來說, 4 1 是指 由1 所指涉的集聚單位,而此集聚單位內嵌於由4 所指涉的集聚單位之中,即 4 1 是指「4 中間的1」。但「內嵌並置類型」的並置關係,並不是明顯的部分-全
體關係,而是隱約的部分-全體關係,這種部分-全體關係可稱之為部分在全體 之中(part-in-whole)。 以「內嵌並置類型」為分數詞意義的兒童無法進行單位分數的累積活動。舉 例來說,要求兒童將兩個 4 1 加以合成,對兒童而言,分子僅是內嵌於分母的一部 分,尚無法脫嵌而出,成為可以獨立於分母之外單獨被累積運作的單位,此時 4 1 尚非可以被使用的分數單位(fractional unit),因此稱為起始單位分數。而 兒童在算 4 1 + 4 1 時,由於當1 被複製時,分割數也同被複製,因此會以 8 2 來回答。 (三)加法性分數 當兒童將部分全體運思引入子分割活動中,造成子分割活動的質變。這時子 分割活動的結果不但是可以被集聚的計數單位,同時也是用子分割單位集聚而成 的集聚單位中的獨立部分單位,子分割單位已成為所謂的單位分數單位,此時的 分數詞意義稱為加法性分數。舉例來說,兒童認為兩個 4 1 可以構成 4 2 ,而非 8 2 。 雖然此階段兒童能同時使用部分全體運思及子分割單位的轉換活動於分數 情境之中,但仍無法聯絡兩個以上的子分割活動。例如,要兒童從8個積木中, 取出其中的 4 3 ,兒童回答6個,並不表示「4份中之3份」,而是「每4個中之3個」。 雖然8個積木的 4 3 和8個積木的 8 6 是相同的,但3/4 和6/8是不同的。 在加法性分數時,兒童能夠理解單位分數的內容是一個離散量的問題(離散 量是3個,兒童知道 3 1 是1個),以及單位分數的內容是多個離散量的問題(如離 散量是6個,兒童知 3 1 是2個);能夠理解集聚分數的內容是多個的離散量問題(如 離散量是6個,兒童知6個的 6 2 和 6 3 是 6 2 + 6 3 = 6 5 ,所以是5個);亦能夠理解集聚
兒童知12個的 6 2 和 6 3 是 6 2 + 6 3 = 6 5 ,所以是10個)。 由於兒童這時的部分全體運思是單向的,所以當全部中拿走兩個次部分時, 兒童會失去全部,而且再計算單位分數累加時會失去累加次數,亦無法掌握單位 分數與部份分數(非單位分數)之間的關係。 (四)巢狀分數 當兒童進入測量運思的階段時,他們能察覺等值分數的情形,知道兩個等值 分數同為一分量的測量值,分數單位就會由加法性分數質變成巢狀分數(甯自 強,民82)。舉例來說,兒童已察覺到8個積木的 4 3 和8個積木的 8 6 是相同的,同 時也認為 4 3 和 8 6 是同一分量的測量值。 在巢狀分數時,兒童具有雙向的部分全體運思與子分割單位化概念,因此, 兒童可以利用單位分數的再次分割,察覺等值分數的情形,例如:知道 3 1 可以分 割成 6 2 ,所以 3 1 = 6 2 。但是,因為兒童缺乏彈性思考,對於非以再次等分單位分 數而產生的等值分數,則無法判定,尚未能真正具備等值的分數概念,例如知道 2 1 = 6 3 , 2 1 = 8 4 ,但無法擴展到 6 3 和 8 4 是等值分數的概念。 此時兒童的部分全體運思是雙向的,所以當全部中拿走兩個次部分時,兒童 不會失去全部。此外,兒童具有共變的概念,如1 比25 可以等於10 比250。亦 具有分數乘法的概念。 (五)有理數概念 所謂的有理數是兩個部分全體的重組,兒童不僅具有部分全體的雙向運 思,更能以分數做為測量的單位。舉例來說,比較 6 3 和 8 4 ,兒童知道二者均是 24 12 ,
所以 6 3 等於 8 4 (兩個巢狀分數比較)。由於能同時思考兩個分數,有等比例運思 的共變概念,此概念即為密度的觀念,因此稱為有理數概念。 在有理數概念時,兒童具有彈性思考的能力,能將不同分母的分數經由等分 割活動加以比較,具有等值分數的概念,如1/2=2/4=3/6……。 所以可以了解兒童對分數概念的發展為:在分數概念的前身時,無法進行等 分割活動,亦無法將等分割後的分得量與單位量做並置比較;當兒童能進行等分 割活動,且能將等分割後的分得量與單位量做並置比較時,便具備起始單位分數 概念,但對於單位量的掌握並不明確;當兒童已能明確的掌握單位量與分量之間 的關係時,便具有加法性分數的概念,但此時尚缺乏通分的概念;當兒童能以通 分的概念來進行分數的解題活動時,則具備了巢狀分數概念,但仍缺乏等值分數 的概念;然而,當兒童能以共測單位理解不同分數詞之間的等值或次序關係,知 道分數詞之間的稠密性,便進入有理數概念的階段,與教育部編製之92年版九年 一貫課程綱要指出有理數即是分數的意涵相同了。
第三節 乘除法類型之研究
對於乘除法類型之研究,分析的方式很多,基於學生轉換文字表徵時會依 其對語意結構的瞭解來進行文字題的編寫(李承華,民91),許多學者對乘除法 問題著重在語意結構的分析,因其採用的觀點不同而有不同之模式,以下針對五 種模式的分析來加以說明。一、Vergnaud 模式
Vergnaud(1988)認為學生概念的發展,單一概念無法被單一種情境所解釋,域(conceptual field)的觀點來探討。所謂的概念域就是分析某一概念所需要 的一組情境,乘除結構的概念域就是用簡單比例與多重比例加以分析的各種情境 所組成的。因此,Vergnaud(1988)從度量空間和向度的觀點,將乘法的結構分為 量數同構型(isomorphisms of measures),叉積型(product of measures)和多 重比例型(multiple proportion)三種。 (一)量數同構型 將二個度量空間 M1 與 M2 的直接相比。其中同一度量空間內 x1 與 x2、f(x1) 與 f(x2)存在有放大常數倍或縮小的關係;或在不同的兩個度量空間 M1 與 M2 之 間存在有一函數關係,其關係如表 2-1: 表 2-1 Vergnaud 的量數同構型關係表 M1 M2 x1 f(x1) x2 f(x2) 當x1=1時,已知三個值中的二個值,則依照未知數的位置,分類為乘法、等 分除和包含除三種問題。若是已知四個值中的三個值,則歸類於「3的規則」的 問題。整理如表2-2: 表 2-2 Vergnaud 量數同構型的問題類型表 問題類 型 乘法問題 等分除問題 包含除問題 「3 的規則」 問題 問題舉 例 每人有 4 枝 筆,請問 6 個人 共有幾枝筆? 15 枝筆平分給 3 個人,請問每 人可以得到幾 枝筆? 15 枝筆平分給 小朋友,每人可 以得到 5 枝,請 問可分給幾個 人? 某糖果店 4 枝 筆賣 15 元,志 傑買 9 枝筆需 付多少元? M1 {人} {人} {人} {枝} M2 {枝} {枝} {枝} {價錢 (元)} x1 1 1 1 4 f(x1) 4 求 f(1) 5 15 x2 6 3 求 x2 9 f(x2) 求 f(6) 15 15 求 f(9)
Vergnaud(1988)認為這四種問題的學習層次以「3 的規則」最高,乘法問題 最容易。 (二)叉積型 由二個度量空間M1 與M2 的叉積合成,而產生第三個度量空間M3,屬這類的 問題必須涉及到三個度量空間。叉積(cross products)是兩集合的積集合,由有 序對(order pair)所構成的集合。其關係如表2-3: 表 2-3 Vergnaud 叉積型關係表 (M2) x2 (M1) x1 F(x1, x2) (M3) 而依未知數所在的位置不同,可以分為乘法問題和除法問題,如表2-4: 表 2-4 Vergnaud 叉積型問題類型表 問題類型 乘法問題 除法問題 問題舉例 長方形的長為 5 公分,寬為 7 公分,則長方形面積為多少平 方公分? 長方形的面積為 30 平方公 分,長為 6 公分,則長方形的 寬為多少公分? M1 {長} {長} M2 {寬} {寬} M3 {面積} {面積} x1 5 6 x2 7 求 x2 f(x1,x2) 求 f(5,7) 30 (三)多重比例型 涉及到三個度量空間M1、M2與M3,而M3度量空間與另外兩個獨立的度量空間 M1和M2成比例關係,是探討四個值的關係。如表2-5:
表 2-5 Vergnaud 多重比例型關係表 (M2) x2 x2' f(x1, x2) f(x1', x2') (M1) x1 x1' (M3) 同樣的依未知數所在的位置不同,可以區分為乘法問題、等分除、包含除和 5 的規則等類型,如表2-6: 表 2-6 Vergnaud 多重比例型問題類型表 問題類型 乘法問題 等分除問題 包含除問題 「5 的規則」問 題 問題舉例 小明家裡有 5 個人,每人每 天吃掉 3 塊麵 包,請問這 5 人 7 天一共吃 掉多少塊麵 包? 小明家裡有 5 個人,每人每 天吃的麵包數 一樣,7 天一 共吃掉 105 塊 麵包,請問每 個人每天要吃 掉多少塊麵 包? 小明家裡的 人, 7 天一共 吃掉 105 塊麵 包,而每人每 天吃 3 個麵 包,請問小明 家裡共有多少 人? 小明家裡有 5 個人,每人每天 吃的麵包數一 樣,每天共吃掉 15 塊麵包,如 果小明家裡有 8 個人,請問 7 天共要吃掉多 少塊麵包? M1 {天} {天} {天} {天} M2 {人} {人} {人} {人} M3 {麵包} {麵包} {麵包} {麵包} x1 1 1 1 1 x2 1 1 1 5 f(x1,x2) 3 求 f(1,1) 3 15 x1' 7 7 7 7 x2' 5 5 求 x2' 8 f(x1',x2') 求 f(7,5) 105 105 求 f(7,8)
二、Schwartz 模式
Schwartz(1988)的乘法結構是從問題中的內涵量(intensive measures)和外 延量(extensive measures)考慮。Schwartz(1988)將乘法以語意關係的三元組分 為(I, E, E’)、(E, E’, E’’)、(I, I’, I’’)及(S, E, E’)的結構。
其中的E代表外延量,只包含一個向度,用以計算、測量數值,如:50公里、 3人,可以直接相加且是整體測量的;而外延量又區分為(1)離散量以D表示, 有自然單位,呈離散的狀態,是一個一個獨立的呈現,如:人、輛;(2)連續 量以C表示,沒有自然單位,須使用約定的測量工具,才能描述,如:公里。 I代表內涵量,內涵量包含二個向度,源於外延量,是由二個外延量組成的, 不可以直接相加,而且是局部可測量的,依外延量的組合情形可分四種情形: (1)D/D,如:人/組;(2)C/D,如:公斤/人;(3)D/C,如:輛/小時;(4)C/C, 如:公里/時。 Schwartz(1988)乘除問題分類如下: (一)(I, E, E’) 結構
依三個量是已知或未知的關係,分為I ×E = E’、E’/E=I、E’/I = E 三種 類型(表2-10),相當於Vergnaud(1988)量數同構型,此處內涵量相當於函數關係。
表 2-7 Schwartz (I, E, E’)問題類型表
類型名稱 乘法問題 等分除問題 包含除問題 (I, E, E’) 結構類型 I × E = E' E'/ E = I E'/ I = E 問題舉例 每人有 5 顆糖果, 請問 3 個人共有幾 顆糖果? 15 顆糖果平分給 3 個人,請問每人可 以得到幾顆糖果? 15 顆糖果平分給小 朋友,每人可以得 到 5 顆,請問可分 給幾個人? I 代表意義 5 顆/人 未知量(顆/人) 5 顆/人 E 代表意義 3 人 3 人 未知量(人) E'代表意義 未知量(顆) 15 顆 15 顆
(二) (E, E’, E’’) 結構
E ×E’=E’’,是由一個外延量(E)和另一個外延量(E’)相乘而產生第三 個外延量(E’’)。相當於Vergnaud(1988)的叉積型。例如表2-8
表 2-8 Schwartz 的(E, E’, E’’)結構表
問題舉例 有一塊長方形土地,長 7 公分,寬 5 公分,請問這塊土地的 面積是多少平方公分?
E 代表意義 長 7 公分 E'代表意義 寬 5 公分 E''代表意義 面積是多少平方公分?
(三) (I, I’, I’’) 結構
I ×I’=I’’ 是由一個內涵量(I)乘上另一個內涵量(I’)而產生第三個內 涵量(I’’)。例題參見表 2-9:
表 2-9 Schwartz 的(I, I', I'')結構表
問題舉例 哥哥打工每小時的薪水是 80 元,他每天打工 4 小時,一天 可賺多少錢? I 代表意義 80 元/時 I'代表意義 4 時/天 I''代表意義 一天可賺多少錢(元/天) (四) (S, E, E’) 結構 S 為一常量(scalar)是沒有向度的量,S 值通常是倍數、折扣、加成等。 例題參見表 2-10: 表 2-10 Schwartz 的(S, E, E')結構表 問題舉例 弟弟有 60 元,哥哥的錢是弟弟的 5 倍,則哥哥有多少元? S 代表意義 5 倍 E 代表意義 60 元 E'代表意義 未知量(哥哥有多少元)
三、Greer 模式
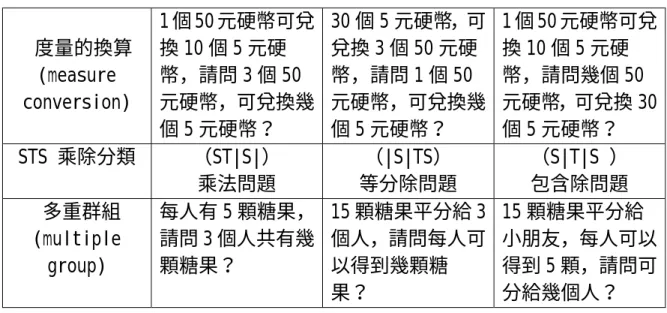
Greer(1987)是以符號STS、SSS、SRS乘法結構將乘除法問題分類。 (一)STS 最初量 S 受到一種變換 T(transfornation)造成另一個量 S。而依未知數所 在的位置不同,又可以分為乘法問題(ST|S|)、等分除(|S|TS)、包含除(S|T|S) 三種類型。例題參見表 2-11: 表 2-11 Greer 的 STS 乘除問題類型(屬於不對稱型)表 STS 乘除分類 (ST|S|) 乘法問題 (|S|TS) 等分除問題 (S|T|S ) 包含除問題 多重群組 (multiple group) 每人有 5 顆糖果, 請問 3 個人共有幾 顆糖果? 15 顆糖果平分給 3 個人,請問每人可 以得到幾顆糖 果? 15 顆糖果平分給 小朋友,每人可以 得到 5 顆,請問可 分給幾個人? 度量的連加 (iteration of measure) 每條繩子長度是 5 公尺,請問 3 條相 同的繩子長度共 是幾公尺? 一條繩子長度是 15 公尺,等分成 3 等份,請問每等份 的長度是幾尺? 一條繩子長度是 15 公尺,等分成每 等份是 5 公尺的繩 子,請問可分成幾 等份? 大小的改變 (change of scale) 照片中的房子寬 5 公分,若將照片放 大 3 倍後,請問房 子的寬度變成幾 公分? 照片中的房子放 大 3 倍後,寬度變 成 15 公分,請問 房子放大前的寬 度是幾公分? 照片中的房子寬 5 公分,照片放大 後,房子寬度變成 15 公分,請問照片 放大了幾倍? 比例 (rate) 小明騎腳踏車的 速度是 20 公里/小 時,請問如果他以 相同速度騎 3 小 時,請問共騎了幾 公里? 小明騎騎腳踏車 3 小時後,共騎了 60 公里,假設他的速 度保持不變,請問 小明每小時騎了 幾公里? 小明騎腳踏車的 速度是 20 公里/小 時,他用相同的速 度騎了 60 公里,, 請問小明騎了幾 小時?表 2-11 Greer的STS 乘除問題類型(屬於不對稱型)續 度量的換算 (measure conversion) 1 個 50 元硬幣可兌 換 10 個 5 元硬 幣,請問 3 個 50 元硬幣,可兌換幾 個 5 元硬幣? 30 個 5 元硬幣,可 兌換 3 個 50 元硬 幣,請問 1 個 50 元硬幣,可兌換幾 個 5 元硬幣? 1 個 50 元硬幣可兌 換 10 個 5 元硬 幣,請問幾個 50 元硬幣,可兌換 30 個 5 元硬幣? STS 乘除分類 (ST|S|) 乘法問題 (|S|TS) 等分除問題 (S|T|S ) 包含除問題 多重群組 (multiple group) 每人有 5 顆糖果, 請問 3 個人共有幾 顆糖果? 15 顆糖果平分給 3 個人,請問每人可 以得到幾顆糖 果? 15 顆糖果平分給 小朋友,每人可以 得到 5 顆,請問可 分給幾個人? (二)SSS 由二個量結合而成為第三個量,分為乘法和除法。相當於Vergnaud(1988)的 叉積型與Schwartz(1988)的(E,E’,E’’)結構。 (三)SRS 有一種關係R(relation)存在於二個量中。相當於Schwartz(1988)的(S,E, E’) 結構。 Greer(1987)主要的興趣在於討論如何使學生整數乘除概念得以擴展到有 理數。他認為造成學生的乘除運算之迷思概念主要來自於不同的數值型態,因此 他從不同的數值型態來分析有理數的乘除法問題情境,Greer 不同數值型態的乘 除情境類型,請參見表 2-12。
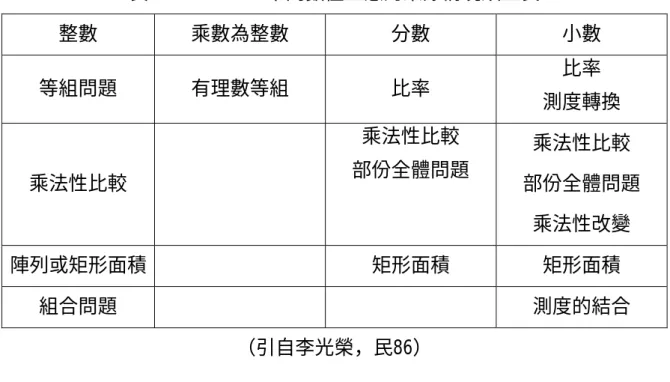
表 2-12 Greer 不同數值型態的乘除情境類型表 整數 乘數為整數 分數 小數 等組問題 有理數等組 比率 比率 測度轉換 乘法性比較 乘法性比較 部份全體問題 乘法性比較 部份全體問題 乘法性改變 陣列或矩形面積 矩形面積 矩形面積 組合問題 測度的結合 (引自李光榮,民86)
四、Nesher 模式
Nesher (1988)認為學生對於文字題的解題困境在於無法將自然語言所表徵 的情境轉化為數學語言表徵,所以他對乘除文字題的研究著重在問題中所涉及的 內文如何轉化成為數學語言之探討。他參考Vergnaud 和Schwartz 乘法結構模 式,將乘法問題分類為三種,並探討其中的邏輯結構: (一)映射規則(mapping rule)問題 例如:小明有5 包巧克力,每包巧克力有15 顆,小明共有幾顆巧克力? 參見表 2-13 的說明:表 2-13 Nesher 的映像規則(mapping rule)說明表
說明 命題結構 第一部份 說明一般的術語,有 n1 個 x,每一 個 x 有 y,即存在有一個敘述是描 述值 p(x,y)。 每包有 15 顆巧克力。 第二部份 呈現一個映像規則,是每一個 x 對 應到 y 的關係,說明 p(x,y)中 x 與 y 的關係 小明有 5 包巧克力。 第三部分 求出題目的答案:共有多少個 y? 小明共有幾顆巧克力?
(二)比較型(compare)問題 例如:弟弟有60 元,哥哥的錢是弟弟的5 倍,則哥哥有多少元? 參見表 2-14 的說明: 表 2-14 Nesher 的比較型(compare) 問題說明表 說明 命題結構 第一部份 有一參考集合 y 有 n1 個元素。 弟弟有 60 元。 第二部份 有一特殊的函數關係,將每一個參 考集合 y 中的元素對 應到比較集合 x 的關係 哥哥的錢是弟弟的 5 倍。 第三部分 求出題目的答案:求出比較集合的 元素個數。? 哥哥有多少元? (三)乘法叉積(cartesian)問題 例如:有一塊長方形土地,長7公分,寬5公分,請問這塊土地的面積是多少 平方公分?參見表2-15的說明: 表 2-15 Nesher 的乘法叉積(cartesian)問題說明表 說明 命題結構 第一、二部份 描述兩個獨立的集合 x,y。 長方形土地,長 7 公分,寬 5 公分。 第三部分 求出題目的答案:有多少 z?z 是一個 x 與一個 y 的叉積。 土 地 的 面 積 是 多 少 平 方 公 分?
五、Usiskin & Bell(1983)的觀點
Usiskin & Bell(1983)以乘法應用的觀點,將乘法意義分為:
(一)比例因子類或相同等集合問題此類型與連加法關係密切,基本算式為: 比例因子×數量=另一個量 ,這類問題相當於 Schwartz 模式的 (I, E, E’) 和 Greer 的 STS 以及 Nesher 的函數規則問題。參見表 2-16 的說明:
表 2-16 Usiskin & Bell 的 Schwartz 的比例因子類或 相同等集合問題(I, E, E’) 結構表 問題舉例 每人有 5 顆糖果,請問 3 個人共有幾顆糖果? 比例因子 5 顆/人 數量 3 人 另一個量 未知量(共有幾顆糖果?) (二)交叉運作或叉積 兩量交互運作之後,會得到一具有複合單位的量,相當於 Schwartz 模式的 (E, E’, E’’)。參見表 2-17 的說明:
表 2-17 Usiskin & Bell 的 Schwartz 的交叉運作問題表
問題舉例 有一塊長方形土地,長 7 公分,寬 5 公分,請問這塊土地的 面積是多少平方公分? 第一個量 長 7 公分 第二個量 寬 5 公分 複合單位的量 面積是多少平方公分? (三)大小改變類或常量問題 原始量×改變大小的比率=改變後的量,其中改變大小的量是一個數值,沒 有單位,運算中的因子可以有二個或二個以上,相當於 Schwartz 模式的 (S, E, E’)和 Greer 的 SRS 以及 Nesher 的比較型問題。參見表 2-18 的說明:
表 2-18 Usiskin & Bell 的大小改變類或常量問題表
問題舉例 弟弟有 60 元,哥哥的錢是弟弟的 5 倍,則哥哥有多少元? S 原始量 5 倍 改變大小的比率 60 元 改變後的量 未知量(哥哥有多少元) 以上各種乘法模式的意義是相同的,但其所分類的觀點又有所不同。 將其分析比較如表2-19:
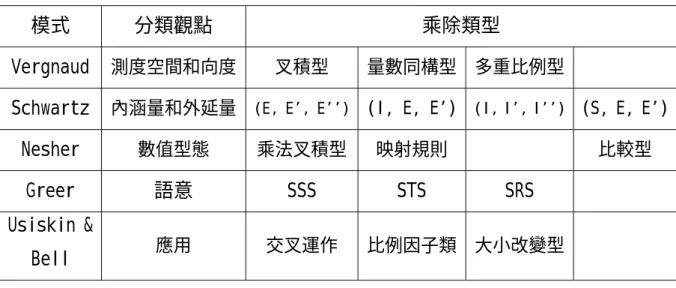
表 2-19 乘除法類型之比較表
模式 分類觀點 乘除類型 Vergnaud 測度空間和向度 叉積型 量數同構型 多重比例型
Schwartz 內涵量和外延量 (E, E’, E’’) (I, E, E’) (I, I’, I’’) (S, E, E’)
Nesher 數值型態 乘法叉積型 映射規則 比較型 Greer 語意 SSS STS SRS Usiskin & Bell 應用 交叉運作 比例因子類 大小改變型
第四節 國小分數教材分析
本研究的研究目的主要是討論國小六年級學童在分數乘除運算的學習成果 及錯誤情形與錯誤形成的原因,因為國小課程的編排是有連貫性的,不能光只從 一個學年來了解全部,必須對其他學年的教材也有所研究,才能對六年級學童分 數概念的學習過程,有一整體性的瞭解。 現在在國小就學的學童,研究者根據教育部所頒布的教學綱要,將其分成三 派:第一派是一至三年級接受82年版新課程綱要,四至五年級接受90學年度實行 的九年一貫課程暫行綱要,到94年學年度接受92年最新頒布之九年一貫最新的數 學能力指標的學童,也就是本研究的研究對象;第二派則是一部分接受90學年度 實行的九年一貫課程暫行綱要,到94年學年度接受92年最新頒布之九年一貫最新 的數學能力指標的學童;第三派則是94年度入學的學童,接受92年最新頒布之九 年一貫最新的數學能力指標的學童。由於本研究的研究對象—國小六年級學童,經歷過的數學課程綱要多達三種,但本研究之範圍在「分數」,故僅列出數與計 算中與「分數」相關的部分,以下為分數教材綱要表。 茲將82年版新課程綱要、89年九年一貫課程暫行綱要、92年最新頒布之九年 一貫最新的數學能力指標中有關分數的能力指標整理為以下三表: 表2-20 82年版新課程綱要表 年級 有關分數的能力指標 一年級 二年級 1.分數概念的初步認識。 2.分數的讀法轉換成記法。 三年級 1.分母為20 以內的真分數的認識。 2.分母為10 的真分數。 四年級 1.分數的種類。 2.真分數的概念。 3.假分數的認識。 4.同分母的加減。 五年級 1.等值分數。 2.分數的數線。 3.把分數視為整數除法的結果。 4.分數乘以整數的乘法。 六年級 1.約分和擴分。 2.通分。 3.分數除以整數的除法。
表2-21 九年一貫課程暫行綱要表 階段(年級) 有關分數的能力指標 第一階段 1-3年級 N-1-7 在等分好、整體1 能明顯出現之具體生活情境中(包含連續量、 離散量),能以真分數(分母在20 以內)描述內容物為單一個物 的幾份,並能延伸真分數的意義,進行同分母真分數的合成、 分解活動(和<1)。 N-1-8 在一個整體1 被明確十等分的具體生活情境中(包含離散量、連 續量),能以一位小數描述其中的幾分,並能進行一位小數的合 成、分解活動(和及被減數<1)。 第二階段 4-5年級 N-2-5 在等分好、整體1 能明顯出現之具體情境中,能以真分數來描 述單位分數內容物為多個個物的幾份,進行同分母真分數的合 成、分解活動,並理解等值分數的意義。 N-2-6 在具體情境中,能以假分數或帶分數描述具體的量,並能解決 分數的合成、分解以及簡單整數倍的問題。 N-2-19 能利用等分好的線段上,做出一條簡單的整數數線,並能進一 步延伸至簡單的分數和小數的數線。 第三階段 6-7年級 N-3-3 在具體情境中,理解通分的意義並運用通分解決異分母分數的 合成、分解問題。 N-3-4 在具體情境中,解決分數乘以分數的問題,進而形成分數倍的 概念。 N-3-6 在具體情境中,能用分數、小數表示除的結果(除的結果為有限 小數)。 N-3-7 能用分數倍的概念,整合以分數為除數的包含除和等分除的運 算格式。
表2-22 92年頒布之九年一貫課程綱要數學能力指標表 階段(年級) 有關分數的能力指標 第一階段 1-3年級 N-1-09 能在具體情境中,初步認識分數,並解決同分母分數的比較與 加減問題。 第二階段 4-5年級 N-2-06 能理解分數之「整數相除」的意涵。 N-2-07 能認識真分數、假分數與帶分數,作同分母分數的比較、加減 與整數倍計算,並解決生活中的問題。 N-2-08 能理解等值分數、約分、擴分的意義。 N-2-09 能理解通分的意義,並用來解決異分母分數的比較與加減問題。 N-2-11 能理解分數乘法的意義及計算方法,並解決生活中的問題。 N-2-13 能做分數與小數的互換,並標記在數線上。 第三階段 6-7年級 N-3-02 能理解最大公因數、最小公倍數與兩數互質的意義,並用來將 分數約成最簡分數。 N-3-03 能理解除數為分數的意義及計算方法,並解決生活中的問題。 N-3-11 能熟練正負數的混合四則運算。 A-3-01 能做基本的代數運算。 第三階段 6年級 分年細目 6-n-02 能認識兩數的最大公因數、最小公倍數與兩數互質的意義,理 解最大公因數、最小公倍數的計算方式,並能將分數約成最簡 分數。對應能力指標N-3-02 6-n-03 能理解除數為分數的意義及計算方法,並解決生活中的問題。 對應能力指標N-3-03 6-n-05 能作分數的兩步驟四則混合計算。對應能力指標N-3-11及對應 能力指標A-3-01 分年細目是指九年一貫課程綱要的能力指標係依主題及階段學習能力而訂
定,然因多數指標須採分年進階式教學方能達成其教學目標。因此,由階段能力 指標演繹出更細緻的分年細目及詮釋,以利分年進階式教學進度目標的明確掌握 綜合整理國小六年級學童經歷過的三種數學課程綱要內容,可知其在國小階 段學得與分數相關的課程內容如附表 2-23 所示: 表 2-23 國小六年級學童學得的分數課程內容表 年級 有關分數的能力指標 一年級 二年級 1.分數概念的初步認識。 2.分數的讀法轉換成記法。 三年級 1.分母為20 以內的真分數的認識。 2.分母為10 的真分數。 第二階段 4-5年級 N-2-5 在等分好、整體1 能明顯出現之具體情境中,能以真分數來描述 單位分數內容物為多個個物的幾份,進行同分母真分數的合成、 分解活動,並理解等值分數的意義。 N-2-6 在具體情境中,能以假分數或帶分數描述具體的量,並能解決分 數的合成、分解以及簡單整數倍的問題。 N-2-19 能利用等分好的線段上,做出一條簡單的整數數線,並能進一 步延伸至簡單的分數和小數的數線。 第三階段 6年級 6-n-02 能認識兩數的最大公因數、最小公倍數與兩數互質的意義,理 解最大公因數、最小公倍數的計算方式,並能將分數約成最簡 分數。對應能力指標N-3-02 6-n-03 能理解除數為分數的意義及計算方法,並解決生活中的問題。對 應能力指標N-3-03 6-n-05 能作分數的兩步驟四則混合計算。對應能力指標N-3-11及A-3-01
第五節 分數乘除法運算的錯誤類型與成因
一、分數概念與運算錯誤情形之研究
由於分數概念的語意相當豐富,且在日常生活的應用中有許多不同的解釋意 義,因此易形成多樣化的理解,也容易產生多種的迷思概念。 (一) 分數概念錯誤情形之研究 研究者參考分數概念的研究報告,將分數概念學習較困難、容易犯錯的情形 及各種錯誤類型綜合整理如下表2-24: 表2-24 有關分數概念的研究報告內容表 作者(年代) 內容 比值模式的概念發展比較慢 Novillis(1976) 在「部分-整體」模式中,斜線區域不是連續時,學生 會發生轉換錯誤 Bruni & Silverman(1977) 學童對形狀不同的圖形較難決定是否等分 逃避處理分數 無法將相同分數概念的應用題與計算題相連結 12 到15 歲的兒童不熟悉「等價分數」 單位量指認有困難,例如:學生無法瞭解在不同的單位 量中,較小分數所佔的量可能比較大分數所佔的量多 認為分數不是一個數。例如: 5 3 是3 和5 的組合 Hart(1981) 圖形能幫學生瞭解某方面的分數概念,但也會對別的方 面的分數概念造成困擾表2-24 有關分數概念的研究報告內容表(續) Booth(1984) 學生認為分數是兩個整數 Hunting(1986) 在處理比較分數的大小及等價分數時,學生經常會受自 然數的影響,只依據分子或分母的大小來比較,或將分 子、分母同加一數來比較,或分別比較二個分數的分子、 分母等。 Kerslake(1986) 12 到14 歲的學生無法確認 4 3 =3÷4 Bergeron et al. (1987) 在處理「部份/全部」的分數問題時不知道各部份均需等 分 Booth(1987) 11 歲的學生對分數是除法運算結果的概念很弱 Kerslak(1987) 學生對分數的意義比較能接受「部分-全部」這一種意 義,但無法將「部分-全部」的意義遷移到分數是二個 相除的結果及子集-集合的意義上 Bright et al. (1988) 不注意單位的標示 Hunting & Sharply(1988) 3歲10個月到4歲10個月的兒童只有少數能了解一半的意 義,大部分兒童只知道一半就是分成兩塊,卻沒有等分 的概念
表2-24 有關分數概念的研究報告內容表(續) Figueras et al. (1987), Figueras(1989) 對單位量的指認有下列錯誤類型: (1)忽略給定的單位量,例如:在一堆磚塊中(有28 塊)將 7 1 的磚塊著色時,學生會圈出7塊磚塊。此 種錯誤答案就是忽略給定的單位量。 (2)受分子控制,例如:在30 顆葡萄中指出其中5顆著 色葡萄是全部的幾分之幾時,學生的答案為「5 份」、「 5 1 」,這就是學生解題時受分子控制。 (3)受分母控制;例如:在8朵花中圈出 4 3 的花朵時, 只考慮問題中的分母,而圈出4朵花。 此外,楊壬孝(民78)在「國民中小學生分數概念的發展」研究中指出學生 在作答困擾及觀念偏差有下列的情形: 1. 在分數比較大小的排序中,分子相同以分母做比較的題目較以分母相同用分 子做比較的題目,使學生感到困難。例如:在「比較 4 1 與 4 3 的大小」與「比較 2 1 與 3 1 的大小」此兩個題目中,學生在「比較 2 1 與 3 1 的大小」這個題目較容易 產生錯誤。 2. 通分時,以分母已知求分子以及分子已知求分母兩者方式比較下,前者學生 較易接受,後者犯錯的學生較多。 3. 同題中,題意轉換造成難度增加的因素。 4. 使用數線在國小學生的分數學習上較國中感到困難。 5. 數與量的觀念混淆不清,例如:甲數的 4 1 誤為甲數是 4 1 ,或 2 1 誤為 2 1 元。
7. 對題意不明白,因此以猜答方式答題。 8. 題組中,前一題的答案影響後一題的答案。 9. 未能把握題意。 吳相儒(2001)也指出兒童常過於依賴連續量部分-整體模式,反而抑制了 他們將分數視為一個數,並抑制了其他分數解釋的發展。 因此,綜合上述學者專家的研究,學生在分數概念較容易產生的錯誤情形有 單位量的指認、部份-全部的區分、數量的觀念、分數數線的觀念、題意的瞭解、 等值分數概念等。 (二) 分數運算錯誤情形之研究 在分數的運算常犯的錯誤(Tatsuoka,1984;Painter,1989)如下: 1、 帶分數方面的錯誤: (1) 帶分數化成假分數的錯誤。 (2) 借位的錯誤: 向整數借1時,卻加10到分子。 向整數借1時,最後計算時卻忘了減1。 (3) 求同分母的錯誤。 (4) 等值分數的錯誤。 (5) 簡化的錯誤。 (6) 加減運算的錯誤: 將帶分數化成假分數後,分子與分母各自分別運算。 通分後,分子不變並直接處理分子及整數部分的運算。 直接作分子及分母的運算時,若求出的值為0,則省略0值的部分。 計算時,完全用大的減小的數。
2、向整數借位問題: (1)從整數所借的1,直接在分子加10。 (2)借位時,將原整數部分加到分子去。 3、分數的加法運算錯誤: (1)直接分子加分子,分母加分母。 (2)求出同分母後放在分母,而分子為原分子相加。 (3)分母相乘,分子相加。 (4)分母相乘,分子相乘。 4、分數的減法運算錯誤: (1) 通分後,分子為大數減去小數。 (2) 分母減分母,分子減分子而且是大數減小數。 (3) 求出公分母後放在分母,而分子為原分子相減。 分數乘法錯誤情形(Lankford,1972;Edwards,1983;Painter,1989)如 下: 1. 先通分後,再計算。 2. 將第二個分數顛倒後,再計算。 3. 交叉相乘而得到分子與分母。 4. 分母相乘,分子卻作加法運算。 5. 分數乘整數時,分數不變,只處理整數部分。 6. 帶分數乘整數時,分數不變,只處理分數部分。 7. 帶分數乘整數時,整數、分數分別自行做乘法運算。 分數除法錯誤情形歸納(Brueckner,1931;Lankford,1972;Painter,1989) 如下:
2. 計算錯誤。 3. 不瞭解計算步驟。 (1)被除數倒置。 (2)除數及被除數均倒置。 (3)加分子,乘分母。 (4)忽略被除數中的分母。 例如:2 4 1 ÷1 3 1 = 4 9 × 3 4 =12,把被除數中的4 給忽略了。 4. 假分數化成帶分數,計算錯誤。 5. 帶分數化成假分數,計算錯誤。 6. 消去時發生錯誤。 (1)分母相消。 (2)分子相消。 (3)相消得0。例如:2 4 1 ÷2 4 1 = 4 9 ÷ 4 9 =0 7. 分母不變,但分子直接做除法運算。 8. 帶分數除以整數時,只做整數之間的運算。 9. 帶分數除以一個分數時,整數不變,只處理分數的部分。 10. 未求出第二個分數的倒數,而直接做乘法運算。 例如: 4 1 ÷ 3 2 = 4 1 × 3 2 = 12 2 12. 帶分數除以帶分數時,整數與分數分別運算。 例如:4 3 1 ÷2 5 2 =2 6 5 13. 除數沒有先求出其倒數,便直接計算。 例如: 5 4 ÷ 5 2 = 25 2 14. 帶分數除以整數時,只以分子除以整數,其餘都不變。
15. 分母不變,但分子相減。 劉天民(82)對國一學生在分數四則運算的錯誤類型研究結果如下: 1. 整數運算的錯誤。 例如:5 3 2 -2 3 1 =4 3 1 2. 帶分數化成假分數的錯誤。 例如:-2 3 2 =-3 4 3. 通分的錯誤。 例如:-1 4 3 + 2 5 1 =-1 20 3 +2 20 1 4. 約分的錯誤。 例如:-1 4 3 ×4 3 2 =-1 2 1 ×4 1 1 5. 直接計算的錯誤。 例如: 5 3 -1 2 1 = 5 3 -2 3 = 3 0 =3 6. 除法改為乘法,除數未倒置的錯誤。 例如:-1 5 3 ÷3=-5 8 ÷3=-5 8 ×3=-5 24 7. 學生誤認A/A=0。 8. 運算不完全。 綜觀學者之研究,學生在分數加減法運算的錯誤情形有帶分數方面的錯誤、 向整數借位的問題、分數的加減法運算錯誤、整數運算錯誤、通分與約分的錯誤 等。而在分數乘除法運算錯誤情形有乘法用除法計算、除法用乘法計算、乘法分 子分母交叉相乘、分母用乘法運算而分子卻用加法運算、只做整數部份或只做分 數部份、整數與分數分別用乘法運算、帶分數除以帶分數時,整數與分數分別運 算、分子直接相除,通分與約分的錯誤等。
二、分數概念與運算錯誤原因之研究
學生在數學學習上所犯的錯誤都是系統性的、有規律性的、標準化的、很少 隨機或善變的,且應該有正確的理論以解釋之(Brown & Burton,1978; Ginsburg ,1977;劉秋木,民85)。 (一)錯誤概念的原因分類 學生在概念犯錯的原因可能有: 1. 缺少完整的先備知識: 2. 使用不當的數學規則 3. 學習知識互相干擾 4. 兒童採用兒童法Sutton & West(1982), Head(1986),Blosser(1987a,1987b)等人 都曾提出產生錯誤概念的主要原因有七種:1、與生俱來;2、從日常生活而來的; 3、從隱喻而來的;4、從類比產生的;5、來自同儕文化;6、正式或非正式的教 學;7、字義的聯想、混淆、衝突或缺乏知識。 呂溪木(1983)認為學生錯誤概念的產生有可能來自學生日常生活所學得 的,也有些是來自學生對於教師機械式教學的一知半解。 Ginsburg(1989)& Harding(1986)認為當學生不了解教師所教授的知識 和書本的說明時,往往因為缺少完整的概念或不當的使用數學規則,因而造成錯 誤。 Baxter & Dole(1990)則指出錯誤是由於不完全的學習和漸漸養成習慣 所造成的。 建構主義主張學生的知識是由學生自行建構而成的,學生的先前知識對其知 識建構正確與否影響甚大。當先前知識與正統概念相去甚遠時,不僅將會干擾課 堂學習,影響最後的解答,也會影響思考過程,形成錯誤概念(張鳳燕,1991)。
Confrey(1994)指出每一個學生在學習數學時,為使所學能對他們有意義, 因此建造許多理論使得它們能自我解釋。學生他們使用新的訊息,修定原先他們 既有的想法。因此每一個學生的數學知識各具有其獨特性,而學生所學到的數學 則只在他們能夠自己建構出的數學。這種知識或概念常因:1、經驗不足;2、教 師或環境的引導與現行廣受接納的知識無法相容或有相當的差距,造成學習的困 難而產生錯誤概念。 綜合國內外學者對於錯誤概念的成因有:1、日常生活的錯誤印象;2、架構 異取的錯誤(frame-retrieval errors)例如;在小數時適用將數線每一單位長 分成10 段,但在分數時就不適用; 3、「二元逆轉」(binary reversions), 此種錯誤主要是退回到先前的學習領域,也就是學生以過去學過的問題來對待新 近學習知識,例如:利用部份-全部的概念在數線上表示分數;4、同化範型 (assimilation paradigms),指視覺刺激的「熟悉度」所造成的影響,例如: 將2×2 算成2+2;5 正式或非正式的教學影響;6、遺忘或解除演算公式的限制 條件,導致錯誤的規則產生;7、對相關知識不足所產生;8、語言的不正確和含 糊所導致;9、用不完全算則而遭遇僵局所產生的解題方式(Resnick,1987; Davis,民79;呂玉琴,民83,Resnick & Ford,1981;鄭昭明,民82)。 Ginsburg(1989)也指出學生會覺得使用自己發明的方法解決問題讓他們感 到滿意、有意義。學生在課堂上學習數學並不是單純地將老師教導的銘印在大腦 中,學生會以過去的生活經驗來解決問題,建構出個人的數學意義,在此建構同 時,正是學生產生迷思概念的主因,例如:Hart(1989)發現學生對分數概念不 清楚,主要因解題傾向採用學童法(child methods)或初學法(naive methods) 所造成。這兩種方法的主要特徵是:1.傾向於使用整數;2.包括數數或疊加的方 式;3.只針對手邊的問題來解決,無法發展成一般性的解法;4.當遇到較難的問 題時這些方法就不適用了。顏啟麟(民81)也發現四年級學生在處理分數的加減、