國
立
交
通
大
學
理學院科技與數位學習學程
碩
碩
碩
碩
士
士
士
士
論
論
論
論
文
文
文
文
七年級學生的等號概念與
其對代數學習之影響研究
The Study of Seventh Graders' Equal Concept
and How Does it Affect Student’s Learning of Algebra
研 究 生:吳佩錦
指導教授:袁 媛 教授
李榮耀 教授
中
中
中
中
華
華
華
華
民
民
民
民
國
國
國
國
一
一
一
一
○
○
○
○
二
二
二
二
年
年
年
年
六
六
六
六
月
月
月
月
七年級學生的等號概念與其對代數學習之影響研究
The Study of Seventh Graders' Equal Concept
and How Does it Affect Student’s Learning of Algebra
研 究 生:吳佩錦 Student:Pei-Chin Wu
指導教授:袁 媛 Advisor:Yuan Yuan
李榮耀 Jong-Eao Lee
國 立 交 通 大 學
理學院科技與數位學習學程
碩 士 論 文
A ThesisSubmitted to Degree Program of E-Learning College of Science
National Chiao Tung University in partial Fulfillment of the Requirements
for the Degree of Master
in
Degree Program of E-Learning
June 2013
Hsinchu, Taiwan, Republic of China
摘
摘
摘
摘
要
要
要
要
本研究主要在探究七年級學生的等號概念,並分析不同等號概念的七年級學生 在一元一次代數式學習上的影響。本研究的主要目的有四項:(一)探討七年級新 生的等號概念以及對於等號意義的理解;(二)瞭解不同等號概念的七年級新生對 典型等式與非典型等式的判讀與解題策略;(三)瞭解「運算型」學生在學習等量 公理後,其等號概念的拓展情形;(四)瞭解不同等號概念的七年級學生在一元一 次代數式中解題策略與其學習成效。 本研究採問卷調查法,以國中七年級學生為調查與研究對象,由研究者自編前 後測以及一元一次代數式學習成就測驗分析得到以下研究結論: 一、七年級學生在尚未正式接觸代數課程前,只有近五成的學生可以理解等號除「運 算」意涵外,還有更深一層的等量「關係型」概念。 二、七年級學生多數能夠正確判讀非典型等式問題,唯獨「等號自反性」的題型僅 有三成學生能夠理解。 三、七年級的關係型學生比運算型學生更能理解等號的特性,但擁有關係型概念不 代表完全擁有解決非典型等式問題的能力。 四、七年級的運算型學生在處理典型或非典型等式時,所採用的解題策略傾向於「求 得一個結果」,無法跳出計算的思考框架。 五、七年級的關係型學生在處理典型或非典型等式時,能運用「等號的替代意義與 等價意義」進行解題,同時展現較多元的解題策略。 六、七年級的運算型學生在化簡一元一次式時往往會忽略要維持等號兩邊等價的關 係,並固著於計算出一個最後的數值。 七、部份運算型學生認為等號是一種計算過程的連結,因此習慣在所有解題步驟中 加入等號,而忽略了等號兩邊必須等價的概念。 八、七年級關係型學生在一元一次代數式的學習成效優於運算型學生。 最後,本研究根據研究結果,提出具體建議,以做為未來相關研究、教材設計 與等號概念教學的參考。 關鍵字:等號概念、非典型等式、代數學習
Abstract
This study aimed to explore the concept of seventh graders’ equal sign , and how does it affect student’s learning of algebra. There are four main purpose of this study:1. To realize the seventh graders' understanding of the equal sign concept;2. To analysis of seventh graders' who have different equal concept problem solving strategies on standard or nonstandard equation;3.To analysis the operational students how to change the concept of the equal sign by learning through equality axioms;4. To analysis of seventh graders' who have different equal concept problem solving strategies on algebra and how does it affect student’s learning of algebra.
The study used questionnaire survey to analysis of seventh graders' equal concept.
Through some test designed by the researcher can get the following conclusions:
1. Before learning algebra, there is only 50% of seventh-graders can really understand the relational meaning of equal sign.
2. Most of seventh-graders can distinguish the nonstandard equation, but only 30% of them can understand the equal sign reflexive Quiz.
3. In understanding the concept of equal sign, the relational seventh-graders are better than operational ones.But has a relation concept is not the same as having the ability to solve problems.
4. When the operational-seventh graders solve the nonstandard equation, they are used to calculate a result or to do something.
5. When the relational seventh-graders solve the nonstandard equation, they have a variety of problem-solving ability.
6. The operational seventh-graders always ignore the equivalence equal significance when they solve algebra problems.
7. A part of operational seventh-gradersconsider the equal sign is a link of calculation process.
8. In the effect of learning algebra, the relational seventh-graders are better than the operational ones.
In conclusion, the findings of this study show that specific proposals are offered to be used in the design of instructional materials and the equal sign concept as reference. Key words:equal concept、nonstandard equation、learning of algebra
誌 謝
沒想到自己也能勇敢的跨出那一步,並順利地走到這一天。提筆的此刻,心中 瀰漫著無以言喻的激動與喜悅,卻無法全然化成片片字句。 一直以來,讀書不甚靈巧的我總是在學習的路途上跌跌撞撞,雖然如此,我始 終熱愛著校園中相互砥礪又蘊含書卷香氣的氛圍,也一直期待著有朝一日能繼續完 成那暫時被現實生活擊敗的夢想。工作一段時日,看著身旁的夥伴一個個又重新走 入校園,那份熱情與執著也再度燃起我心中的小小燭光。就這樣擁著家人與同事們 的祝福,挾著幾分美好憧憬與小小的莫名恐懼,回憶起初踏入交大校園的那一刻, 李榮耀教授的殷殷叮囑,彷彿還在眼前。而如今,我竟已在此細數說不盡的感謝。 回首這兩年來的每一步,時而溫馨時而憂愁,幸好所有的喜怒哀樂與焦躁不安 都有有聖、泓葆、弘昌陪著我一起走過:在每份報告與實驗中、在每個週末從白天 到黑夜的相守;更要感謝的,是悉心帶領著我一路前行的指導老師袁媛教授:總是 竭盡心力、無私無我的指導與傳授所學,不僅在學術中惠予良多,更在兩年研究生 涯裡亦師亦友的引領著我們渡過一次又一次的考驗與難題。 最後,感謝口試委員孫之元教授不吝給予指導,讓我釐清自己所學的盲點,並 給予我未來研究更多的方向。也感謝我可愛又乖巧貼心的班級,能讓我無後顧之憂 的在課餘之中充實自己。吳佩錦謹識
于 交通大學理學院碩專班中華
民國一0二年六月
目次
第
第
第
第一
一
一
一章
章
章
章
緒論
緒論
緒論
緒論
...............................1 第一節 研究背景與動機..........................1 第二節 研究目的與待答問題........................4 第三節 名詞釋義 ............................5 第四節 研究範圍與限制 .........................9第
第
第
第二
二
二
二章
章
章
章
文獻探討
文獻探討
文獻探討
文獻探討
... ........................11 第一節 等號概念的發展背景 .......................11 第二節 等號概念的相關研究 .......................15 第三節 等號概念與代數學習的關連 ....................17第三
第三
第三
第三章
章
章
章
研究設計與實施
研究設計與實施
研究設計與實施
研究設計與實施
........................21 第一節 研究設計與架構 .........................21 第二節 研究步驟與流程 .........................24 第三節 研究工具 ............................31 第四節 資料蒐集與分析 .........................36第四章
第四章
第四章
第四章
研究結果與討論
研究結果與討論
研究結果與討論
研究結果與討論
........................45 第一節 初探七年級學生的等號概念 ....................45 第二節 運算型學生的等號拓展與迷思概念............ .....53 第三節 不同等號概念對代數學習的影響................. .60第五章
第五章
第五章
第五章
結論與建議
結論與建議
結論與建議
結論與建議
..........................61 第一節 結論..............................61 第二節 建議..............................62
參考文獻
參考文獻
參考文獻
參考文獻
中文部分................................65 英文部分................................67
附錄
附錄
附錄
附錄
附錄一 等號意義理解與等號概念發展前測初稿...............72 附錄二 等號意義理解與等號概念發展前測正式問卷.............74 附錄三 一元一次代數式錯誤類型分析與等號迷思概念後測..........75
表次
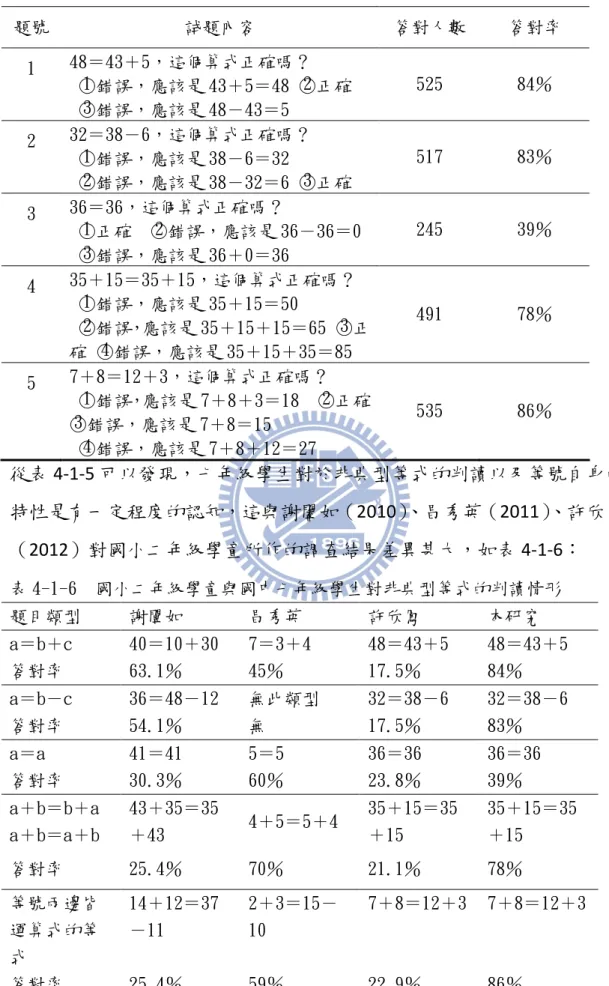
表 3-4-6 等號意義理解類型分析.....................40 表 3-4-7 等號意義理解和等號概念類型的描述...............40 表 4-1-2 學生在等號意義與認知的表現情況................46 表 4-1-3 國內各研究者等號概念研究百分比例表..............47 表 4-1-5 非典型等式測驗內容與學生表現統計表..............50 表 4-1-6 國小二年級學童與國中七年級學生對非典型等式的判讀情形.....50 表 4-1-7 七年級學生在第一二大題的作答情形...............52 表 4-2-2 國中七年級學生等號概念和認知調查結果.............54 表 4-2-3 七年級 A、B、C 三班第一大題作答情形 .............54 表 4-2-5 不同等號思維學生的解題策略統計表...............56 表 4-2-6 第二大題測驗內容以及整體七年級學生作答情形..........57 表 4-2-7 不同等號概念的七年級學生在第二大題作答情形..........58 表 4-2-8 不同等號概念學生的解題思維情形................59 表 4-3-1 不同等號概念與一元一次代數學習成效的獨立樣本 t 檢定摘要表...60圖次
圖 3-2-1 研究流程圖.........................24 圖 3-2-2 前測問卷第二大題等號概念心像測驗內容............27 圖 3-2-3 前測問卷第二大題數學態度測驗內容..............27 圖 3-2-4 後測第二大題等號迷思概念測驗內容..............30 圖 3-3-1 後測第二大題等號迷思概念測驗內容..............33 圖 3-4-1 等號意義理解與認知測驗內容.................37 圖 3-4-2 非典型等式測驗內容.....................38 圖 3-4-3 等號的自反性測驗內容....................38 圖 3-4-4 等號的對稱性與等價概念測驗內容...............38 圖 3-4-5 不同等號概念的解題思維測驗內容...............39 圖 3-4-8 後測第一大題等號的意義認知與理解內容............41 圖 3-4-9 後測第二大題等號的迷思概念和誤用測驗內容..........42 圖 3-4-10 後測第三大題等號誤用與錯誤類型測驗內容 ..........42 圖 4-1-1 等號意義理解與認知第一大題測驗內容.............45 圖 4-1-4 陳嘉皇等號意義解釋的題目內容................48 圖 4-2-1 一元一次代數式錯誤類型分析與等號誤用測驗第一大題內容....53 圖 4-2-4 等號概念理解與等號意義認知測驗第三大題測驗內容.......55
第一章 緒論
在教育部所揭示的九年一貫數學學習領域課程能力指標中,指出六年 級的學生應能夠理解等量公理,並瞭解等式左右同時加、減、乘、除一數 (除時此數不能為零)時,等式仍然會成立(教育部,2003)。而「等式」 代表等號左右兩邊物件「等價」的想法,是學生能夠由算術順利進入到代 數的重要轉戾點,亦是學生學習等量公理的重要基石(王志銘、康淑娟, 2006)。由此可見,學生對於等式的概念心像與學習等量公理之間有著密 不可分的關係存在。故本研究主要在探討七年級新生的等號概念拓展情 形,以及不懂等號概念對於學習代數的影響。本章分為四節,分別為研究 背景與動機、研究目的與問題、名詞釋義、研究範圍與限制。第一節 研究背景與動機
近年來有許多研究發現,國內有不少學生對於「等號」的真正意涵, 仍處於一知半解的狀態,例如:一個將等號視為「運算型」關係的學生, 在面對「等式」的時候,會誤認等式右邊應該是等式左邊運算出來的結果, 而未經運算的數字應該擺放在等式左邊(邱志賢、毛國楠,2001)。Seo 與 Ginsburg(2003)也指出將等號視為運算符號的觀點,容易限制學生學習 數學時的思考層級。簡單地說:一個只將等號視為「運算型」關係的學生, 多半能夠理解 3+2=5 這種典型等式,但是卻不一定能夠接受 5=3+2 或 4+1=3+2 這種非典型等式的寫法。一般而言,國小學生對於等號的 認知,通常還是停留在將等號視為「操作符號」去進行由左而右的計算, 這些視等號定義為運算型的學生,也多半會將等號界定為「待解決的結 果」,或是「應算出的答案」,並未將等號視為一種具有等價關係的符號 (Behr,Erlwanger & Nichols,1976;Warren,2004)。因為「=」早在國小一年級上學期的數學教材裡頭,就被普遍介紹與大量 使用在算術式當中。因此對國小的學童來說,「=」出現的時候,學生的 概念心像出現的是「do something 」的意象,認定必須要做某事,並且尋 求的是一種結果。國內學者謝堅(1997)也認為學生在處理數學課運算教 材的時候,會過於著重得到答案,這樣的課程脈絡可能會導致學生誤以為 「等號」僅僅只是代表著「運算後的結果」或「計算後的答案是…」的情 形,而這樣的教材編排與教學也使得學生在日後學習代數式判讀其等價關 係時產生了困擾。國內學者廖學專(2002)在他的研究中也曾呼應這樣的 說法:學生由算術進入到代數領域的困難之一,其實是根源於學生對於「等 式」缺乏了一種「等價概念」,意即學生缺乏「=」右邊的物件會等於「=」 左邊的物件,同時「=」左邊的物件也會等於「=」右邊的物件的想法。 所以,當學生在國中進入到代數式學習的時候,往往會沿用過往運算型關 係的認知,認為「=」是掌控一個算術運算的執行命令,需要 do something 並得到一個最後的結果,而不認為「=」是比較兩個相等的量的關係符號。 而諸如此類的迷思觀念,也往往是日後造成學生在代數學習上產生困難與 疑惑的重要因素之一(廖瓊菁,2001)。 無獨有偶,早在中國清朝晚年就有數學家華蘅芳體悟出影響代數學習 的成效,其實應該要根源於等號意義的理解上,而非全然植基於未知數的 操弄上(上官瑋茵, 2010)。近年來也有越來越多學者投入與等號相關的 研究,確認算術式當中的「等號」和代數式裡頭的「等號」,其意義是不 盡全然相同的(洪萬生,2007)。縱觀內外,有許多的研究都紛紛不約而 同指出,許多學生從算術式到代數式的學習過程中產生了困難,是因為學 生對等號概念理解的局限性(Carpenter & Franke,2001;Warren,2002;
Warren,2003)。簡單地說,就是學生沒有辦法正確轉換等號的意義,認
為看到等號就一定是要找出結果,而不是要維持「=」左右物件數量上的 平衡。因此,研究者在教學現場當中,也常常會發現學生在處理代數式運 算的時候,會出現以下兩種的迷思狀況,而追根究柢不是學生不能掌握文 字符號操弄,而是學生的等號概念仍然停留在操作型的運算型定義中:
7x-3=2x+7 7x+3x+2-5 = 7x-2x=7+3 = 10x+2-5 = 5x =10 = 10x-3 = x=2 = 7 (迷思一:習慣運算後接等號) (迷思二:等號後要有運算結果) 因此,不管是國內或是國外,有許多學者的研究結論都支持:學生 對於「=」的理解,如果能夠從「運算型」轉化為「關係型」,了解「=」 除了具有運算結果的特性外,仍具有「替代性」、「自反性」、「對稱性」和 「遞移性」,就能促進學生由算術式到代數式的提昇與連接(Falkner, Levi & Carpenter,1999)。而從這些例子我們也不難發現,「代數式的學習」 與「等號概念」是有一定程度的相關性存在。再者,研究者從近幾年相關 調查研究中發現,國內多數中小學的學生並未全然具有「等式」即為一種 「等價關係」的概念,而學生對於「等式」的理解以及「等號概念」也不 一定會隨年級增長而有所擴展。探究其原因,也許根源於教材的鋪陳並未 強化「等號」的真正意涵。而有不少的研究也顯示,能夠將「等號」視為 「關係型」的學生,在解題表現上會明顯優於視「等號」為「運算型」的 學生(楊喻惟,2009;劉佩綺,2010;詹佳縈,2010;楊絮媛,2010;昌 秀英,2011;許欣鳳,2012)。除此之外,在學生的觀念當中,許多學生 認為「=」的出現代表著他們必須做某種程度的運算動作,這也導致了學 生在學習等號右邊有未知數的方程式或是在做非典型等式的時候,會產生 某種程度的混淆與困惑,這樣的迷思概念也導致學生在化簡代數式的時 候,容易產生錯亂和非得尋求ㄧ種結果的固著(莊松潔,2005)。國外的 學者 Alibali、Knuth、McNeil 和 Stephens( 2007 )更表示,唯有學生真 正理解及掌握等號的意義,才是代數學習成功的關鍵。
對於等量公理的學習,不僅是代表著等式兩邊存在一種等價的關 係,裡頭更包含了學生對文字符號概念的理解。因此,研究者認為要 讓學生對於代數式的運算以及等量公理的學習更加順利,就應該要先 瞭解學生對於「等號」的概念理解,到底存在於哪一種階段。Ausubel (1968)曾經說過:影響學習最重要的因素就是確認學習者已經學到 甚麼而據以教之,而林福來(1991)也曾指出教師要幫助學生學好數 學的最佳參考依據就是在教學中適時的進行診斷評量,瞭解學生的想 法、程度、解題策略以及犯錯的原因,也才能對於學生的學習做即時 的補救與調整。因此本研究首部份將先針對七年級新生做一份研究者 自編的等號概念理解問卷調查,以瞭解學生對於等號的概念心像到底 存在於哪種階段,並分析學生現有等號概念中,對於典型等式以及非 典型等式的掌握與處理策略有何異同。並初步暸解對等號固著於「運 算型」以及無法處理「非典型等式」的學生,在進入到代數式學習時, 會產生甚麼樣的盲點與混淆做探討,在學期末學生學習過等量公理之 後,再進行第二次研究者自編的問卷調查,以探討七年級新生的等號 概念拓展情形以及代數式的學習成效是否會因其等號概念不同而有 所差異。最後,對身為教學現場第一線的教師該如何進行等號概念的 擴展以及後續補教教學,便成了本研究的重要目的之一。
第二節 研究目的與待答問題
一、研究目的:
國內學者李宜蓉(2009)與國外學者McNeil等人(2006)都曾分析國 內外教科書中等號的使用方式,發現中學教科書的版本中對於等號(equal signs)的呈現方式鮮少有引出「關係型」詮釋的脈絡,所以學生即便上了 國中以後,仍然會將等號解釋為一種操作符號或是維持一種必須要「do something 」運算型的定義。而針對不同等號概念的學生,在由算術進入 到代數的學習中,究竟又扮演著何種舉足輕重的角色,是否真會因等號
概念的不同而對其學習成效產生影響,著實令研究者感到好奇。因此, 根據以上動機,本研究主要研究目的如下: (1) 初探七年級新生的等號概念以及對於等號意義的理解 (2) 瞭解不同等號概念的七年級新生對典型等式與非典型等式的判讀 與解題策略 (3) 瞭解「運算型」學生在學習等量公理後,其等號概念的拓展情形 (4) 瞭解不同等號概念的七年級學生在一元一次代數式中解題策略與 其學習成效
二、待答問題:
依據本研究所提出的研究目的,列出以下幾個待答問題,期許能透過 研究者自編的兩次問卷調查統計,瞭解目前七年級新生等號的概念階段以 及代數式學習時的各個面向: (1) 探究七年級新生的等號概念與對等號意義的理解有何差異存 在? (2) 探究不同等號概念的七年級新生,對於典型等式與非典型等式的 認知與解題策略為何? (3) 觀察七年級「運算型」學生在學習完等量公理後,其等號概念是 否能由「運算型」提昇到「關係型」? (4) 探討七年級學生在一元一次代數式的解題策略與學習成效是否 會因等號概念的不同而有所差異?
第三節 名詞釋義
在本小節當中,研究者將針對本研究中所提及的一些名詞作簡單的介 紹與定義,本小節將分成三個部份做解釋,第一部分為與「等號」概念相 關的名詞,包含了文中所提及的「運算型」與「關係型」的界定與分類以 及「等號概念心像」的意涵:第二部份是與「等式」有關的名詞,包含了 典型等式與非典型等式的部份;最後第三部份是「等號」本身具有的特性, 包含了等號的「替代性」、「自反性」、「對稱性」與「遞移性」的基本性質 說明。一、與「等號」概念相關的名詞:
本研究依陳嘉皇(2008)及 Knuth、Stephens、McNeil 與 Alibali (2006) 的定義,依據學生不同的等號概念心像,將學生區分為「運算型學生」以 及「關係型學生」,其定義闡述如下: 1.運算(operational)型學生: 將「=」視為一種運算結果的表現,也就是認為「=」是運算過程與 答案之間的ㄧ種連結符號。對於等式的判讀,只侷限於典型等式當中。意 即認定「=」的處理必須是由一種左到右的過程,會將等號定義為「答案 是…..」、「結果是……」、「要算出答案是……」等。 2.關係(relational)型學生: 在本研究當中,「關係」意義代表的是等號兩邊等量,也可以視為 等號兩邊一樣多的概念,也就是以ㄧ種等價平衡的關係來判讀等式。對 「關係型」的學生來說,等號不再ㄧ定是運算結果的連結符號。因此, 此類型的學生對於等號的理解可以是「左右兩邊相等」、「左右兩邊一樣 多、「左右兩邊一樣大」等,這也意味著學生能夠理解接受等號兩邊數值 相等、並有等號兩端數值平衡的概念。3、等號概念心像: 本研究是根據 Vinner(1983)的定義:所謂的概念心像(concept image) 指的是當我們聽到一個詞彙或是概念時,在心中或腦海中對此詞彙或概念 名稱所聯結產生的非言辭實體(enity),我們稱之為概念心像。簡單的來 說,概念心像指的是與這個概念有關的印象或是經驗的集合體。舉例來 說:當我們聽到蘋果這個詞彙,每個人在心中所浮現的意像或是概念聯結 可能是不盡相同的;有人對於蘋果的印象與聯結在於他的視覺表徵,所以 當提及蘋果時所產生的概念心像為紅色或是綠色;也有人對於蘋果的聯結 在於他接觸蘋果時的味覺表徵,所以當提到蘋果時心中所產生的概念心像 就是微酸帶點香甜;更有人對於蘋果的印象聯結在於一種心靈影像或是記 憶,因此當提到蘋果時心中所浮現的概念心像便是一段回憶或某個具有代 表性的人、事、物。
二、典型等式以及非典型等式
在本研究中對於等式所界定的「典型等式」以及「非典型等式」,是 參考陳嘉皇(2009)及 Nicole M. McNeil et al.(2006)的分類,其相關的 定義闡述如下: 1.典型等式(Standard equations) 是為學生最熟悉的ㄧ般等式,意即等號左邊為運算過程,右邊為運算 結果的呈現,例如:5+2=7、10-4=6。此種等式是將等號界定在操作 符號的學生最為習慣及能夠掌握的等式。 2.非典型等式(Nonstandard equations) 除了等號左邊為運算過程,右邊為運算結果的等式之外,其餘不同 呈現方式的等式,在本研究中均界定為非典型等式。其中分典型等式又可 以細分為三大類:包括等號右邊為運算過程,左邊為運算結果,例如:7 =2+5、6=10-4;或等號左右兩邊皆為運算過程,如:2+5=3+4、10 -3=6+1;抑或是具有等號自反性的式子,如:6=6。三、等號本身具有的特性:
1.等號的「替代性」: 對任意數 a ,b 和函數式 F(x),若 a = b,則 F(a)= F(b)(假設等 式兩邊都具有其意義)。在一階邏輯中,不能量化像 F 這樣的表達式(它 可能是個函數謂詞)。一些例子: 對任意實數 a,b,c,若 a = b,則 a + c = b + c (這裡 F(x)為 x + c); 對任意實數 a,b,c,若 a = b,則 a - c = b – c (這裡 F(x)為 x - c); 對任意實數 a,b,c,若 a = b,則 a × c = b × c(這裡 F(x)為 x × c); 對任意實數 a,b,c,若 a = b 且 c 不為零,則 a ÷ c = b ÷ c (這裡 F(x)為 x ÷ c)。 2.等號的「自反性」:對任意量 a,a = a。這個性質通常在數學證明中 作為中間步驟。 3.等號的「對稱性」:對任意量 a 和 b,若 a = b,則 b = a。 4.等號的「遞移性」:對任意量 a,b,c,若 a = b 且 b = c,則 a = c。第四節 研究範圍與限制
本研究採用調查法,並以研究者任教學校的七年級學生為研究對象, 主要在探討七年級學生的等號概念以及不同等號概念對學生學習一元一 次代數式的影響。在研究中所使用與等號概念有關的測驗是改編自國內研 究者許欣鳳(2012)對國小二年級學生所做的等號相關研究;研究中與等 號概念相關的典型與非典型等式則是採用陳嘉皇(2009)及 McNeil 等人 (2006)的試題與分類,在分類過程中都是由研究者自己評定與分類,容 易有研究者主觀因素介入,未來後續研究者或許可改採用評分者間信度; 而等量公理與一元一次代數式學習教材則是採用十二年國教中百綱的能 力指標為限,以研究者任教學校的七年級學生為研究範圍,而本研究結果 是否可以推論到其他對象或其他學校,則應審慎考量。第二章
第二章
第二章
第二章
文獻探討
文獻探討
文獻探討
文獻探討
根據本研究的動機與目的,本章節將針對研究內容,依序彙整與本研 究相關之文獻基礎,並分為三個面向進行相關文獻探討。因此本章將分為 三個小節,第一節為「等號概念的發展背景」,主要探討等號的起源、意 義與分類;第二節為「等號概念的相關研究」,主要探索具有不同等號意 義思考對等號概念形成的影響;第三節為「等號概念與代數學習的關連」, 主要以代數的角度出發,去探究其不同等號概念思維與代數學習的關連。
第一節
第一節
第一節
第一節 等號概念的發展
等號概念的發展
等號概念的發展
等號概念的發展背景
背景
背景
背景
本節主要目的在介紹等號概念的發展背景,並分別針對「等號的起 源」以及「等號的意義與分類」,加以陳述與探討。
一、等號的起源
相等( equal ) 是數學概念裡頭重要的觀念與關係之一,它意味著一種 相等的意涵。而等號(sign of equality)的出現其實與方程式有相當的關 連性存在。數學史上,早在數學萌芽時期就已經有了方程式的記載,因此 也有了表示相等關係的方法。綜觀內外,在中國古代也有所謂的方程式概 念,但它是以「列表」(算籌布列)的方法解決,因此不需要使用到等號, 而在記錄書寫上則是以漢字「等」或「等於」表示。在阿默斯紙草書中以 「 」符號來表示相等的概念;在丟番圖中則是以「 」或「 」為等號; 在巴赫沙里殘簡中則是以相當於「pha」的字母為等號代表;一直到了十 五世紀,阿拉伯人蓋拉薩迪以「 」表示相等;雷格蒙塔努斯則以水平之 破折號「──」為等號,如 表示 x2 +3x=30;帕喬利亦以破折 號為等號,但較長且記於數字之下,如 表示 x2-y2=36(引自百度百科 http://baike.baidu.com/view/428835.htm)。
等號(sign of equality)最早是出現在西元 1557 年英國雷考特教授 (Rebort Record,1510~1558)的勵志石(Whetstone of Witte)ㄧ書當中, 而這本代數課本也是英國第一本使用「+」、「-」符號的英文書。Recorde 為了避免重複使用枯燥乏味的「等於」這個介詞,因此創用了「=」這個 符號來取代「等於」。在當時 Record 也認為沒有其它符號可以比「平行而 且等長的兩條直線」更適合用來代表「等於」的意涵,因此「=」又被稱 之為 Record’s sign。而等於這個符號「=」的創立,無庸置疑是 Recorde 對數學界最大的貢獻。 然而「=」這個符號被雷考特創立之後,在當時並沒有被廣泛的接受 與使用,它的推廣十分地緩慢。ㄧ直到 1631 年,英國的奧特雷德(William Oughtred)出版了一本對數學界極具影響力的書籍-數學之鑰(Clavis Mathematicae),並在書中強調數學符號的重要性,才使得「+」、「-」、 「=」這些符號成為數學最終通行的標準記號(林炎全等譯,1983)。
二、等號的意義:
等號所表示的最基本意義為「保持式子左右等量」,也就是相等 (sameness)的等量關係。在數學上,等號本身具備有替代性(符合等量 公理的特性,即:a=b則a+c=b+c)、自反性(1=1、2=2、3 =3…等符合恆等式型態的式子)、對稱性(若a+b=c則c=a+b) 和遞移性(若a=b且b=c則a=c)等性質。 依據 McNeil等人(2006)針對等號概念所作的相關研究分類,將學 生對等號概念的認知區分為運算型及關係型。所謂的運算型指的是一種運 算定義,代表等號的右邊是一種運算結果;而關係型則是指學生能以平衡 的觀點來看待等號左右兩邊的物件。有許多研究發現,不管在哪一種年級 階層中都有許多的學生尚未對等號有完備的認識與發展(Baroody& Ginsburg,1983;Behr,Erlwanger&Nichols,1980;Kieran,1981)。簡單地說:學生往往將等號誤解為只是一種運算符號,意即一定要「做某件 事情(doing something)」,而非總是將等號視為一種等價或是等量的關 係(Behr et al.,1980)。 McNeil 和 Alibali(2006)也曾在其研究中指出,學生通常會依據自 身的經驗來詮釋並建構其等號概念,當學生在小學階段初次接觸等號時, 因為學習經驗與範疇有限,所以會因課程編排而傾向於將等號解釋定義為 運算符號。也正因為國內九年一貫數學領域教材課程綱要的編排以及課程 內容的鋪陳沒有對於等號真正的意涵做完善的引導與拓展,所以多數的學 童都會直接將等號定義為一種運算符號的代表,而缺乏了等價的關係意 義。NcNeil 的論點也和 Seo 和 Ginsburg(2003)所提出的論點不謀而合: 這兩位學者認為在小學數學教材中,因為等號常常搭配著算術運算出現, 所以學生往往會將等號定義為求得的「總數量」、或運算後的「結果與答 案」,而潛移默化地限制了學童對等號真正意涵的理解。根據這些學者的 論點,倘若我們持續在這樣的教學模式下學習,學生的確會容易根深蒂固 的把等號直接與「運算符號」畫上等號(McNeil&Alibali,2006)。
三、等號的分類:
在上一小節等號的意義中,我們可以理解等號的基本意涵指的是「保 持式子左右相等」,但是在算術當中,等號的使用卻常常是要求學生求出 一個最終答案。所以等號在算術中除了具有「保持相等」的意義外,有時 也蘊含著「運算」的意義。蔣治邦、謝堅、陳竹村、林昭珍與吳淑娟(2002) 都曾在其相關研究中指出等號的意義有二:一為「得到答案」:如「2+6 =8」式子中,表示「2個和6個和起來,得到的答案是8個」;另一個意義 為兩邊一樣大的「等價關係」:如「5+3=2+6」式子中,表示「5+3」 和「2+6」這兩項經過數量大小的比較活動,可以發現這兩者一樣大的結 果。因此,等號可因其在典型等式與非典型等式中而給予不同的分類。依據陳嘉皇(2008)及Knuth、Stephens、McNeil 與 Alibali(2006) 對等號概念的分類法則,將學生對於等號概念的認知區分為「運算型定義」 及「關係型定義」。「運算型定義」是指學生只將等號視為運算後與得到 結果之間的連結符號,具有宣告結果的意義存在,是故等號後方必須跟隨 出現的一個答案或結果。而所謂的「關係型定義」則是指學生能夠將等號 視為一種左右兩側等價的關係符號,因此不尋求必須要有結果,只要是兩 邊符合關係對等的式子。而許多研究(楊喻惟,2009;黃富麟,2010;潘 亨足,2010;劉佩綺,2010;昌秀英,2011)在探討等號概念時,皆根據 陳嘉皇(2008)及Knuth、Stephens、McNeil 與 Alibali(2006)等人的分
類法,將學生對等號的認知區分成「運算型」以及「關係型」。因此,當 本研究探討學生的等號概念時,將參考陳嘉皇(2008)及Knuth、Stephens、 McNeil 與 Alibali(2006)等人的分類法,將學生對等號的認知主區分為
第二節
第二節
第二節
第二節
等號概念的相關研究
等號概念的相關研究
等號概念的相關研究
等號概念的相關研究
研究者在此將探討國內外等號概念的相關研究,並分析不同等號概 念類型對等號概念形成的影響,並在此小節當中,將等號類型依照陳嘉皇 (2008)及 Knuth、Stephens、McNeil 與 Alibali(2006)等人的分類法,
把學生對等號的認知區分為「運算型」及「關係型」兩種意義來解釋。 一、「運算型」:將等號視為運算符號 根據國外許多學者的研究發現,不管在哪一種年級當中,都有不少學 生對於等號意義理解尚未完全發展完備(Baroody&Ginsburg,1983;Behr, Erlwanger&Nichols,1980;Kieran,1981;Rand,2003)。而此種未完備 的緣由不外乎學生總將等號認定為一種必須「do something」的運算符號, 意即等號的出現就代表著必須要「做某件事情」,而正因為這樣的狹隘認 知,學生往往無法將等號進一步認定為等價或是等量的概念(Behr et al., 1980)。McNeil 和 Alibali(2006)曾在他們的研究中指出,學生在詮釋 以及建構一些概念的時候,多半都是根據自己本身的學習經驗來做演繹與 歸納,當學生在小學初次接觸到等號的時候,因為他們的學習經驗相當有 限且狹隘,加上課程編排的脈絡偏向於運算型意義的鋪陳,因此在此階段 的學生多半傾向於將等號解釋為一種運算型的符號,鮮少能有學生會將其 轉化成一種等價的概念,而正因為這樣的課程編排,導致學生無法對等號 產生完備的觀念。 無獨有偶,學者 Seo 和 Ginsburg(2003)也認為在小學數學課程當中, 等號常常搭配著算術運算的出現,使得小學生容易將等號定義成為求得 「答案」以及「總量」的一種結果連結符號,而忽略了等式左右亦存在著 一種等價或等量的關係。也因為初次接觸等號時總是在加減法問題中呈 現,進而促使學生更加將等號建構歸納成一種運算結果,因為解決這樣單 純加減法的運算問題時,是不需具備等式兩邊等價的概念,僅需針對數字 做運算便可得到正確的結果,長期浸濡在這樣的情境中,自然容易使學生
將等號的意義建構成一種單純的運算結果(McNeil & Alibali,2006)。 曾有國外學者在研究中指出,對初次接觸代數的學生而言,他們心中 所預期的方程式是一種左邊為單純運算過程,右邊為唯一結果且中間由等 號做為連結的一種特定形式,意即本文中所指的典型等式,例如:6+5 =11(Baroody & Ginsburg,1983)。在早前不少關於等號的研究中, 當中學生被要求對「等號」下一個定義時,大多數的中學生對「等號」理 解的表現和小學生一樣,均對等號做出運算型的定義,只有極少數的中學 生能夠兼及關係型的意義。而這樣的不成熟的等號概念思維不只存在於中 學生,更是有可能延續到大學生的階段(Kieran,1981)。Herscovics 和 Linchevski(1994)更在其研究中明確指出:儘管在一般運算式中,學生 只將等號視為運算型符號並不會對解題過程及結果造成立即的影響,但在 後續的學習過程當中,一旦需要將等號視為關係型的等價概念時,學生就 會有所迷惑及認知的障礙存在。而為了驗證這樣的假設,Essien 和 Setati 在 2006 年時曾將研究對象由小學轉移至中學,果不其然發現八年級甚或 是九年級的學生多將等號視為一種求解的運算工具符號,較難將等號視為 一種比較數量的關係型符號。 二、「關係型」:將等號視為等價關係符號 綜觀內外,其實並非所有的研究結果都對於等號概念存在著負面不樂 觀的想法。Knuth、Alibali、McNeil、Weinberg 和 Stephens(2006)就曾 在其研究中表示,學生對於等號意義的理解會隨著中學年級的增加而有所 拓展,最後終將發展出關係型的等號概念。McNeil 和 Alibali(2006)在 探討學生等號意義理解對經驗數學和等號情境產生作用時,預期數學經驗 的層次與等號情境會交互影響,因此七年級的學生在單獨或加減法的運算 當中,會自然的將等號視為一種運算型符號;而在需要比較數量的等價題 型當中,學生也會自然的將等號視為一種關係型的等價符號;而對大學生 而言,不管今天面對的是一種什麼樣的題型,因為其本身的等號意義理解
已臻完備,因此都能夠以一種等價的思維來解題。在 McNeil 和 Alibali (2006)的研究中更指出,中學生(研究中指的是七年級學生)的表現可 以被用來預測數學經驗的層次與等號情境的互動性。這也呼應了 Izsak (2003)所提出的研究結果,這些學者認為學生在中學階段具有良好的知 識背景與組織結構能力,而這樣的能力恰好能夠用來學習並建構較高層次 的數學問題,而適時佐以中學階段所發展的邏輯概念,更可用來協助等價 關係的建立。藉由這樣的關係,我們更能幫助學生察覺複雜的相似關係, 所以從發展學的角度來觀看,中學生比小學生更容易形成等號關係型意義 的理解(McNeil,Grandau,Knuth,Alibili,Stephens,Hattikudur & Krill, 2006)。Herscovics(1980)和 Kieran(1981)也曾以年齡的觀點來做研 究,他們認為 12 到 14 歲的學生即便最初對等號抱持著運算的概念,但經 過解說以及訓練過後,學生便會開始對等號建立所謂的等價關係,Kieran 的研究更進一步明確的指出,13 歲是接受等號成為等價概念的最佳過渡 時期。 早期在一些國外學者的研究中都曾指出:學生對於非典型等式的方程 式容易感到困擾以及混淆,而追根究柢發現,其源自於學生接觸非典型的 機會較少(Weaver,1973)。更有研究報告顯示,七年級的學生多半難以 將等號視為一種等量等價的關係型符號,但是在等號兩邊都具有運算方程 式的等價脈絡之下,便可以將等號視為一種數量比較的等價型意義符號 (McNeil & Alibili,2005)。在後續的研究中,等號通常被視為運算後 接答案的一種連結符號,這樣的標準情境即為本研究中的典型等式(例 如:6+3=9),很少被視為兩邊非標準操作情境(例如:3+6=4+5) 或其他具有自反性的非典型等式(例如:9=9),而這些非標準情境中的 非典型等式包含了「等號兩邊運算」、「等號右邊運算」、「等號兩邊均 不運算」和「不全等」四種,而這些非典型等式往往會比典型等式更容易 引發學生理解等號的等價概念(McNeil,2006)。
第三節
第三節
第三節
第三節
等號概念與代數學習的關連
等號概念與代數學習的關連
等號概念與代數學習的關連
等號概念與代數學習的關連
「代數」在中學數學課程裡常被視為一種「廣義算術 generalized arithmetic」(Booth,1988),從引入文字符號開始,到對文字符號施行運 算,最後有系統地解決算術四則運算問題,都算是代數的一種範疇。而代 數與算術之間有許多共同使用的符號,例如:+、-、=;但實際上,這 些符號在代數與算術兩者之間的意義卻不盡全然相同。一、等號意義與學生對於等號的認知
國外學者 Sfard(1991)曾在其研究中指出,當人類在思索一個抽象 的數學概念時會有兩種不同層次的面向出現,ㄧ個是運算層面的,另一個 則是結構層面的。舉例來說:當我們去處理一個情境化的題型時,倘若採 取的策略是用ㄧ序列的還原法倒回來推算答案,而不是將問題情境或解題 方法形式化,只是單純的去推算出結果,那麼在這樣的解題過程裡,數學 的概念便是停留在單純的運算過程,然而這樣的還原推算不見得可以解決 所有的數學題型。而國內學者謝孟珊(2000)更在其研究中擴展說明:當 學生沒有辦法成功地以算術方法解題時,他必須學習將問題形式化,建立 方程式,並在方程式左右實際處理運算,這才算是真正進入到代數的階 段,對於數學的處理也才正式進入到結構層面。二、代數與等號學習的關連
Kieran(1989)與 Vergnaud(1997)都曾在研究中表示:學生對於等 號概念的學習與理解都將影響往後他如何處理一個代數式。不約而同地, 學者 Alibali、Knuth、Hattikudur、McNeil 和 Stephens(2007)也都認為代 數學習在數學教育中佔了不可或缺的重要角色,然而若學生對於等號概念 理解有限,則終將成為其學習代數的絆腳石。當我們細細檢視方程式在數 學中所扮演的本質與角色,事實上,所有代數方程式的操作都必須瞭解等 號是一種關係型的表徵(上官瑋茵,2010)。除此之外,等式在學校各階段的數學課程編排中無所不在,等式的理解在代數的學習中必然扮演著舉 足輕重的角色,更確切地說,等式中等號意義的判讀直接或間接的都影響 著未來代數的學習成效。Byers 和 Herscovics(1977)認為在學習代數的 解題策略時,必須要能夠將等號視為一種等價型的概念,如此才能夠賦與 代數學習的意義而非流於一種形式上的記憶。 Chaiklin 與 Lesgold(1984)研究約莫 11 歲左右的學生如何判斷等式 是否相等(例如:685-492+947、947+492-685、947-685+492、947 -492+685 中,那些式子是相等的?),結果發現學生在判斷過程中習慣 以「計算出結果」來作判讀,而不是以一種數量相等的關係來研判,這代 表著學生尚存留在一種運算型的概念當中,因此面對這樣題型的題目時, 無法快速的以等價概念作答。反觀 Knuth、Alibili、Hattikudur、McNeil 和 Stephens(2008)所提出的研究結果,即使是六七年級未正式接觸過代 數學習的學生,只要他們具有等價型的等號概念時,他們便可以順利的解 決代數方程式類型的數學問題。同時這些學者也提出,若學生想要瞭解並 能使用代數來解決數學問題,那麼他們就必須仰賴正確的數學觀念,而其 中最重要的觀念之一,便是等號等價的概念。Soh(1994)指出,有些學 生認為「2x+14=6x」這種方程式是錯的,因為等式的左邊應該要有比較 多的未知數。而 Sfard 與 Linchevski(1994)在研究學生解方程式的迷思 時也不約而同的發現,學生能處理「3x+17=24」這種典型的等式,但是 卻無法完全處理像「24=3x+17」這種非典型等式,因為學生覺得式子不 像它本來應該有的常見的樣子。這些研究再再地說明,學生對等式有其必 然的刻板印象,因此學生必須要先理解「等號」的真正意涵,並接受等號 的存在是保持一種平衡等價的概念而非總是要計算出一個結果,如此完備 了自身的等號概念後,才能真正處理一個代數式子(許欣鳳,2012)。
第三章
第三章
第三章
第三章 研究設計與實施
研究設計與實施
研究設計與實施
研究設計與實施
本研究首部分主要在探究國中七年級學生對於等號意義的理解及其 等號概念發展,而研究後半部將聚焦於運算型學生在學習等量公理前後的 等號概念擴展情形,並希望透過研究者自編後測研究分析調查,瞭解國中 七年級學生是否會因其等號意義認知差異,而在學習一元一次式化簡及一 元一次方程式求解時產生不同的迷思概念與錯誤類型。最後透過期末的成 就測驗瞭解七年級學生的代數學習成果是否會因其等號概念而有所不 同。在本章節中,依本研究之研究目的與待答問題進行研究設計與實施之 說明。本章共分四小節,第一節為研究方法與研究對象;第二節為研究步 驟與流程;第三節為研究工具;第四節為資料蒐集與分析。第一節
第一節
第一節
第一節
研究方法
研究方法
研究方法
研究方法與研究對象
與研究對象
與研究對象
與研究對象
杜威(Dewey,1933)曾指出,當一個研究者面對待處理的問題時, 其解決程序有五個步驟與階段:遭遇困難與問題、界定和認定困難與問 題、提出解決問題的假設與方法、沙盤推演假設的結果、最後進行假設的 考驗。而這五個程序也被視為科學方法的基本步驟。一個符合科學精神的 研究,應具有系統性、客觀性和實證性三個特徵。調查法是所有量化的科 學研究中最常用的方法之一,它是一種有目的、有計劃、有系統地蒐集有 關研究對象現實狀況或歷史狀況的方法。而調查法也是科學研究當中最常 用的基本研究方法,它綜合運用歷史法、觀察法等方法以及談話、問卷、 個案研究、測驗等科學方式,對教育現象進行有計劃的、周密的和系統的 了解,並對調查蒐集到的資料進行分析、綜合、比較、歸納。 在所有的調查法當中,蒐集初級資料最普遍被採用的是問卷調查法 (Kotler,1998),它是以書面提出問題的方式再蒐集資料的一種研究方 法,即調查者就調查項目編制問題組成問卷,分發或郵寄給相關人員,經由文字引導說明後由受試者填寫答案,然後回收整理、統計和研究,以便 研究者能夠全盤的瞭解受試者的現況,從而能針對其現況提出假設再設計 相關性的實驗進行驗證。國內多位學者在進行國中學生等號概念的教學研 究時,也曾採用問卷調查法以瞭解受試者對於等號意義的認知階段並觀察 其對代數方面的學習成效影響(廖學專,2002;楊喻維,2009;劉佩綺, 2010;潘亨足,2010),這與本研究首部分探討國中七年級新生的「等號 意義與等號概念發展」,並依其對等號概念理解的不同而區分為「運算型 學生」及「關係型學生」有異曲同工之妙,因此研究者在本研究第一部份 將採用問卷調查法進行研究資料的蒐集。而為了降低樣本學生各種特質的 差異,諸如:城鄉差距、學校規模、社經背景等等,在研究者與指導教授 討論後決定選取同一所國民中學為本研究之樣本學校。同時為了考量樣本 學生選取之可行性及便利性,本研究採非隨機抽樣中的方便抽樣,選取研 究者所任職的新竹市立新新國中為研究樣本學校,且為了方便研究者在同 一時間進行施測,因此樣本選取時採用立意抽樣的方式在 25 個班級中, 選取 20 個班級學生為樣本學生,合計約 660 人接受研究者所自編的「等 號意義理解與等號概念認知」測驗調查,透過研究者自編測驗問卷資料的 蒐集分析,將學生依其「等號的意義理解」與處理「典型等式」、「非典型 等式」的結果與認知概念將樣本學校中的七年級樣本新生區分為「運算型 學生」及「關係型學生」。 在過去的研究當中,國內有不少研究者針對國小學童進行等號概念理 解與教學的行動研究,而這些研究者均發現等號概念的拓展有助於國小學 童正確學習爾後的數學代數知識(陳嘉皇,2009;楊絮媛,2010;昌秀英, 2011;許欣鳳,2012)。然而研究者卻時常在教學現場中發現即便上了國 中以後,學生的等號概念也並未如預期將隨著時間的增長而有所拓展,以 致於學生在國中階段接觸代數以後,往往無法以正確的概念進行解題,或 雖能順利解題但卻常常出現令人啼笑皆非的式子,尤其是在一元一次多項 式與一元一次方程式中,常常會有等號誤用的情況產生,即便最後結果為
正確解答,但細看其運算式卻常出現前後不等的情況。例如以下兩個例子: (1)將等號放置在方程式之前 (2)認為等號必定為結果論 3x+4x-3=2x+7 3x+2x+7=5x+7=12 =7x-3=2x+7 即認定等號之後必定要有 =7x-2x=7+3 ㄧ個計算後的結果 =5x =10 =x=2 探究其迷思根源,在於學生對於等號概念的一知半解而造成往後代數的學 習困難與混淆(廖學專,2002;楊喻維,2009;劉佩綺,2010;潘亨足, 2010)。追本溯源,學生應當在七年級正式接觸代數前就具備有完整的等 號概念,因此,在本研究的第二部分,研究者將把研究過程聚焦於「運算 型樣本學生」與「關係型樣本學生」在處理「一元一次多項式」與「一元 一次方程式」時的解題策略與等號迷思誤用情況,並透過一元一次式定期 評量成果觀察兩組學生的代數學習成果,更希望能透過兩次自編測驗分 析:等量公理教學前後「運算型樣本學生」對於等號概念理解的擴展以及 等號意義認知的變化,以期有助於教師將來在針對學生學習算術過渡到代 數的內容教學,能夠掌握學生的迷思概念並完備運算型學生的等號概念。
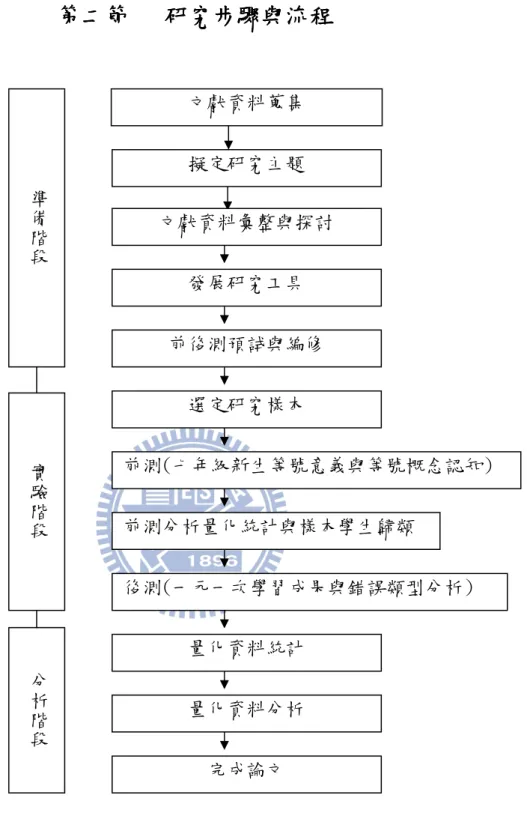
圖 3-2-1 研究流程圖 文獻資料蒐集 擬定研究主題 發展研究工具 文獻資料彙整與探討 量化資料分析 完成論文 前後測預試與編修 選定研究樣本 前測(七年級新生等號意義與等號概念認知) 量化資料統計 後測(一元一次學習成果與錯誤類型分析) 前測分析量化統計與樣本學生歸類 準 備 階 段 分 析 階 段 實 驗 階 段
第二節
第二節
第二節
第二節 研究步驟與流程
研究步驟與流程
研究步驟與流程
研究步驟與流程
本研究主要研究目的在於探討國中七年學生對於等號意義的理解與 等號概念的發展情形,依照杜威(Dewey,1933)科學研究的方法與精神, 研究者將本研究的研究步驟與流程(圖 3-2-1),主要區分為三大階段;階 段一是為準備階段:包含了文獻資料的蒐集與彙整、研究主題的擬訂、研 究工具的發展與編修;階段二為實驗階段:包含樣本學校與樣本學生的選 定、等號意義理解與等號概念發展的前測問卷調查、量化分析統計與樣本 學生歸類、以及學習完等量公理後的ㄧ元一次學習成果與錯誤類型分析問 卷;最後階段三為分析階段:將階段二中的前後測問卷作資料分析探討, 並從中探究學生的等號概念類型與學習代數式的迷思。以下研究者將分別 依照研究三個階段做詳細描述: 階段一 準備階段 : (ㄧ)文獻蒐集與彙整: 研究者依據過去在教學現場所觀察到的現象以及國內外專家學者的 研究,發現學生的等號概念認知在學生學習代數時扮演著舉足輕重的角 色,近年來國外學者 Jones、Pratt 和 Tayler(2012)也在期刊上再次對等 號作了意義類別的區分與定義,由此可見等號(equal sign)在數學學習與 教學鋪陳上的確有值得我們重新深入研究探討之處。故研究者在 2012 年 3 月與指導教授多次討論後,決定將研究主題訂為探討國中七年級新生對 於等號意義的理解以及運算型學生學習等量公理前後等號概念認知的拓 展情形,並期許藉由研究者自編的試題可以觀察並分析不同等號認知概念 的學生在學習代數的迷思概念以及錯誤類型分析,最後透過專家教師所編 製的成就測驗觀察不同等號類型的學生在代數上的學習成果。而在研究問 題形成後,研究者便著手擬定研究方向、研究目的、以及相關的待答問題。 為確認此主題之可行性與重要性,研究者在 2012 年 2 月尚未真正確定研 究主題時,便先行蒐集閱讀其相關文獻,以利研究確立後之彙整,並與指 導教授作定期討論以確定本研究的範圍與理論基礎。
(二)發展研究工具: 在本研究中,研究者所採取的研究方法為調查研究法,而蒐集初級資 料最普遍被採用的便是問卷調查法(Kotler,1998),因此在本研究中所重 的研究工具主要為三項:第一部分為研究者自編的等號意義與等號概念認 知理解測驗;第二部分為研究者自編的一元一次代數式錯誤類型分析與等 號謬用測驗;最後一部分為專家教師所編纂的一元一次代數式學習成就測 驗。期許透過這些量化資料彙整分析,可以幫助研究者瞭解國中七年級學 生的等號意義理解與等號概念拓展情形。而在發展研究工具的過程當中, 研究者也參閱了國內學者潘亨足(2010)、許欣鳳(2012)等人所編製與 等號或一元一次代數式相關的試卷,並與國中現職數學教師進行討論,以 期完備兩份問卷調查試卷的準確度。 (三)預試與試題俢編: 為使本研究的研究工具更趨於完備,研究者在預試前便與多位教學經 歷三~五年的現職國中數學教師共同編修試題,並經過專家教師-指導教 授的分析與建議後,於 2012 年 5 月初步確立前測:等號意義與等號概念 理解的預試試題。為使預試更具有準確性,因此在預試學生的挑選上,研 究者採用與正式施測時所選定的樣本學校為基準,隨機挑選 25 個班級中 的一個七年級班級學生(2012 年 10 月正式施測時,此班級學生已成為八 年級學生)做為預試樣本,以期與正式進行施測時的樣本學生達最小差 異。並在預試後挑選三名運算型學生與三名關係型學生:分別依其七年級 五次段考成績平均為標準劃分為高、中、低成就,再分別進行晤談並瞭解 題目對學生是否有誤導或語意不明之處,以利研究者在正式施測時能將學 生因題意誤解而影響作答的誤差降至最低。在預試時研究者原本希望透過 題目的引導讓學生描述關於等號的概念心像,如圖 3-2-2 前測問卷第二 大題。
圖 3-2-2 前測問卷第二大題等號概念心像測驗 但因學生對於概念心像一詞多半感受生澀難懂,無法以白話文詞流暢回 答,因此研究者在與指導教授討論後將此題目移除,並將題目更替為學生 對於數學的態度測驗,如圖 3-2-3, 圖 3-2-3 前測第二大題數學態度測驗 讓學生透過日常接觸到的食物來比擬心目中對於數學的態度與喜愛程 度,藉此題目可使研究者更加瞭解學生對於數學的接受程度,並在其中挑 選出適當的個案以利後續研究發展。 關於本研究後測問卷:一元一次代數式錯誤類型分析與等號謬用測 驗,研究者編製時謹遵前例,避免冗詞贅字與艱難生詞,以減少受試者的 閱讀認知負荷,並於 2012 年 9 月在樣本學校中 25 個八年級班級中隨機挑 選一個班級進行預試,經由指導教授再次審閱無誤後,後測問卷於是確立。 對於數學這個科目,我覺得它像哪一種食物? _____________________________ 原因: _____________________________ _____________________________ 當我們提到牛頓,有人會聯想到蘋果、地心引力;當我們提到華盛 頓,有人會聯想到櫻桃樹、誠實;那麼當老師提到"等號"的時候, 你又會聯想到甚麼呢?或者,等號對你來說,具有甚麼樣的意義呢? 請你試著把它寫下來。 當我聽到或看到 當我聽到或看到 當我聽到或看到 當我聽到或看到「=」、「「=」、「「=」、「「=」、「等號等號等號等號」」我會想到」」我會想到我會想到我會想到::: :
階段二 實驗階段 : (一)實施對象與實施時間: 本研究首部分欲瞭解剛升上國中的七年級新生,對於等號意義的理解 及其等號概念發展,為避免七年級新生在尚未接觸正式課程前已有先修其 相關課程而影響研究結果,故關於國中七年級新生對於等號意義的理解及 其等號概念發展之前置研究將於 2012 年 10 月份第一次段考後的早自習時 間統一施測。而在本研究中參與研究的樣本學校選擇上,研究者最後選定 研究者所任職的新竹市立新新國民中學作為樣本學校。新竹市立新新國民 中學在新竹市屬於市區型的大型學校,每個年級班級數有 25 個班級,每 班人數約為 29~33 名學生,由於地理位置鄰近交通大學、清華大學、新竹 大學、食品研究院、工研院、以及新竹科學園區,故家長素質與其社經背 景也較為一致。再加上新新國民中學辦學風格多元且特色顯著,所以也有 不少重視教育的家長跨區將孩子送到此處就讀。在本研究中為了降低研究 時樣本的內部因素差異,並衡量研究進行的時間與地域便利性,因此研究 者與指導教授多次討論後共同選定研究者所任職的新竹市立新新國民中 學作為樣本學校。並在新新國民中學的新生 25 個班級中,採非隨機抽樣 中的立意抽樣方式,選取時間可配合的 20 個班級共約 660 名學生作為樣 本學生。 而本研究第二部分希望透過等量公理的教學前後,觀察「運算型樣本 學生」等號概念的拓展情形,隨後將研究聚焦於「運算型樣本學生」與「關 係型樣本學生」在處理「一元一次多項式」與「一元一次方程式」時的解 題策略與等號迷思與誤用情況。因此在第二部分的研究中,研究者將在 2012年 12 月同樣對樣本學校中進行前測的 660 名樣本學生進行一元一次 代數式錯誤類型分析與等號迷思概念,最後於 2013 年 1 月對這 660 名樣 本學生進行一元一次代數式學習成就測驗,希望透過這兩次的自編測驗分 析:等量公理教學前後「運算型樣本學生」對於等號概念理解的擴展以及 等號意義認知的變化,並分析不同等號概念學生在學習一元一次代數式時 的解題策略與學習成效是否會有所差異。
(二)前後測問卷調查: 在本研究當中,研究者將針對樣本學生進行三次與等號概念相關的研 究測驗,分別為前測:等號意義理解與等號概念發展測驗、後測:一元一 次代數式解題策略與等號概念迷思測驗,以及學期末由數位專家教師所編 製的一元一次代數式學習成就測驗。在這三次的測驗當中,研究者將分別 分析七年級新生的等號概念與其數學學習成就之相關性,並探討不同等號 概念的樣本學生在學習等量公理與一元一次代數式時所產生的迷思概 念,最後藉由期末的學習成就測驗去探討不同等號概念對與代數學習之影 響。 在本研究中所使用的前測與後測測驗工具為研究者參考國內外學者 McNeil 與 Alibali(2005)、Knuth、Stephens、Alibali (2006)、陳嘉 皇(2009)、謝闓如(2010)、昌秀英(2011)、許欣鳳(2012)等人的相 關研究後所設計,相關內容與編製過程將於第三節研究工具中詳細說明。 階段三 分析階段: 在本研究當中,前測所進行的等號意義理解與等號概念發展測驗主要 是想瞭解學生對於等號認知的現況,因此在首部分的調查研究中,研究者 將採用描述性統計的方式,分別針對學生對於等號意義理解的狀況與非典 型等式的認知狀況作百分比統計與描述性解釋;第二部分的一元一次代數 式錯誤類型分析與等號迷思概念則是欲瞭解學生在學習完等量公理之 後,其對於等號概念的拓展情形,是否能有效從運算型提升為關係型。從 這份調查當中,研究者也想探討不同等號概念的學生在面對一元一次代數 式時所產生的等號迷思概念為何,因此,第二部分的資料分析亦是採用描 述性統計的方式作說明,更想透過此份調查研究探討運算型學生與關係型 學生在面對一元一次式化簡時所產生的迷思概念為何?檢測內容如圖 3-2-4 所示:
圖 3-2-4 後測 第二大題 等號迷思概念測驗內容 最後,研究者想藉由專家教師所編製的一元一次代數式學習成就測驗探討 不同等號概念的學生在代數學習上的影響,因此這部分研究者將利用獨立 樣本t考驗作資料的統計分析。 二、李小衡在練習化簡x的一元一次式時,採用了以下方法,請你幫 李小衡檢查看看整個化簡的過程是否有錯誤? 7 37 37 7 37 7 25 35 12 28 4 5 4 7 5 3 5 7 = = = + = + + + − = + + + − x x x x x x x …步驟一 同乘分母最小公倍數20 …步驟二 同類項合併 …步驟三 使用移項法則 …步驟四 解得x 口 沒有錯誤 口 有錯誤,我認為在步驟___開始錯誤,應該為________
第三節
第三節
第三節
第三節 研究工具
研究工具
研究工具
研究工具
本研究旨在探究國中七年級學生對於等號意義的理解與等號概念的 發展,與探討不同等號概念的七年級學生在經過等量公理學習後,其對一 元一次代數式的解題策略與等號誤用情形。在這個小節當中,將針對研究 中研究者所自編的兩份研究工具作詳細說明:分別為研究工具的編製過 程、研究工具的內容、研究工具的信度與效度、以及研究工具的使用方式。 一.國中七年級學生等號意義理解與等號概念發展測驗 (一)等號意義理解與等號概念發展編製過程: 本研究首部分所採用的等號意義理解與等號概念發展測驗,是研究者 參考國內外學者 McNeil 與 Alibali(2005)、Knuth、Stephens、Alibali (2006)、陳嘉皇(2009)、謝闓如(2010)、昌秀英(2011)、許欣鳳(2012) 等人的相關研究,自行設計「國中七年級新生等號意義理解與等號概念發 展測驗」,經過多位任職於教學現場的專家教師討論,以及指導教授編修 而成前測初稿(如附錄一),而後研究者再以樣本學校為基準,隨機挑選 25個班級中的一個七年級班級學生共 29 名進行實際測驗,以了解學生對 測驗試題語意描述之接受程度與作答情形,以便研究者做進一步的修正。 在 2012 年 5 月前測初稿施測的過程當中,研究者發現第二大題描述 等號概念心像的部分,對於國中七年級學生在作答上具有相當難度,探究 其原因為學生多半不瞭解何謂概念心像,即便題幹中有給予例子參考說 明,學生多半仍舊對於概念心像一詞一知半解,更無法以文字描述。所以 在與指導教授討論過後,研究者將原本試題修更替為學生對於數學的態度 測驗,讓學生透過日常接觸到的食物來比擬心目中對於數學的態度與喜愛 程度,藉此題目可使研究者更加瞭解學生對於數學的接受程度,並在其中 挑選出適當的個案以利後續研究發展以選擇題方式呈現。在第三大題等式 正確值的判斷當中,研究者參考陳嘉皇(2009)、謝闓如(2010)、許欣鳳 (2012)的研究結果,將學生的等號認知概念依照其「運算型」與「關係
型」思維而編製不同的選項,希望透過兩種不同的解題歷程,可以幫助研 究者瞭解學生對於等號概念的思維存在於何種階段。同樣為了更加釐清學 生對於等號意義的理解,因為研究者在前測的第四大題中採用勾選的方式 讓學生回答心目中等號可能代表的意義為何,透過這個可使研究者與前測 第三第五兩大題相互對應,更能協助研究者判定學生的等號類型停留在何 種階段。而在第五大題中研究者依循學者陳嘉皇(2009)、謝闓如(2010)、 許欣鳳(2012)的測驗試題模式,將「典型等式」與「非典型等式」而其 類別分別編製,並在其中融入學生可能常見的等號錯誤迷思類型為誘導選 項;最後經過預試發現,學生多半反應第三大題與第五大題的過於類似, 最後在與指導教授討論後,採用指導教授的建議,雖然題目類似,但在第 三大題中可以清楚的判斷學生對於等號解題的概念式採用運算或是等量 推理,因此仍舊決定保留此題型。只將第一大題與第二大題合併為同一大 題以方便對照學生先備數學成就與其對於數學喜愛程度的相關性。最後交 由指導教授再次審閱後成只有四個大題的正式前測試卷(如附錄二)。 (二)等號概念檢測工具內容 本研究首部分等號意義理解與等號概念發展的測驗工具內容共分為 四個大題,第一大題的施測目的主要是想瞭解七年級新生過去的數學學習 成就以及其對於數學的學習態度;第二大題的施測目的則是要瞭解學生對 於等號的認知存在何種階段;第三大題則是藉由典型等式與非典型等式的 區別來判斷學生對於等號左右兩側數值的關係理解,並依據樣本學生的作 答內容將其分別歸類為不同類型,最後第四大題則是幫助研究者釐清不同 等號概念的學生在處理等式問題是所採用的解題策略為何,透過此大題研 究者更能夠掌握過渡型的學生在處理非典型等式的部分會較傾向於哪種 解題模式(如附錄二)。