國立臺中教育大學數學教育學系
在職進修教學碩士學位班碩士學位論文
指導教授:林原宏 博士
國小四年級學童之幾何表現的概念
結構探討
研究生:劉建宏 撰
中
華
民
國
九
十
九
年
六
月
摘要
本研究旨在應用模糊取向的詮釋結構模式,分析國小四年級學童之幾
何概念結構。依據察覺的模糊邏輯模式 (fuzzy logic model of perceptions, FLMP) 、試題反應理論 (item response theory) 和模糊截矩陣之 ISM 運 算,繪製學童的個別化幾何概念結構圖。 本研究以 504 名國小四年級學童為研究對象,依能力值區分為高、中、 低三組,繪製學童個別化的幾何概念階層結構圖。研究結果顯示: 一、藉由模糊取向的詮釋結構模式,可繪製並有效分析個別化的幾何概念 結構圖。 二、不同能力值的學童,其幾何概念結構圖在階層數、概念關聯指向上皆 有差異。 三、測驗分數相同但反應組型不同的受試者,其概念結構圖會有所不同。 四、由受試者的概念結構圖中可知,愈上位的概念屬性,其精熟的程度較 低,下位的概念屬性,其精熟的程度較高。 五、比較專家和高、中、低能力值受試者的概念結構圖,可發現其間有明 顯差異。 六、由個人化的概念結構圖,可以了解受試者的概念關聯指向與各概念之 精熟度。 根據本研究的結果與發現,提供教學者在了解學童的學習情況之後 ,能使教學者依學童學習成就的不同,準備教材與課程設計。 關鍵字:幾何概念、試題反應理論、模糊理論、詮釋結構模式
Abstract
The purpose of this study was to adopt fuzzy approach of interpretive structural modeling to analyze the structure of the geometric of elementary fourth grade students. This study was based on Fuzzy Logic Model of Perceptions (FLMP), Item Response Theory (IRT) and the algorithm of Interpretive Structural Model (ISM) of fuzzy alpha-cut to draw the student’s individualized structure of geometry concept.
This study included 504 students of fourth graders. According to the student ability, three groups are divided, which were high, medium, and low ability, so that the researcher drew the student’s individualized structure of geometry concept. Based on the procedures of the analysis, the following conclusions were found.
1. This study effectively drew and analyzed the individualized concepts structures of geometry by Fuzzy Approach of Interpretive Structural Model.
2. There were significant differences on the number of concept hierarchies and concept linkage among different IRT theta values.
3. There were differences on conceptual structure among examinees of the same total score but different response pattern.
4. We can see that it’s lower mastery on the top concepts and higher mastery on the bottom concepts by the subject’s conceptual structure.
5. There were significant differences in comparing the expert’s concept structures with different-ability groups.
6. it was easy to understand the subject’s concept linkage and mastery of concepts by the individualized concept structure.
According to the results and finding of this study, this study can be the reference of preparation for teaching materials and curriculum design in accordance with different learning achievements of students.
Keyword: geometric concept, item response theory, fuzzy theory, interpretive structural model.
目 錄
第一章 緒論
...1 第一節 研究動機 ...1 第二節 研究目的 ...4 第三節 名詞解釋 ...4第二章 文獻探討...
7 第一節 van Hiele 幾何概念 ...7 第二節 試題反應理論 ... 13 第三節 模糊理論 ... 24 第四節 詮釋結構模式 ... 27 第五節 模糊取向的詮釋結構模式 ... 33第三章 研究方法
... 37 第一節 研究架構 ... 37 第二節 研究對象 ... 38 第三節 研究流程 ... 39 第四節 研究工具 ... 40 第五節 資料分析 ... 44第四章 研究結果與討論...
47 第一節 不同能力值學童的幾何概念 ISM 結構圖比較 ... 47 第二節 總分相同但反應組型不同的幾何概念 ISM 結構圖比較 ... 56 第三節 不同能力值學童的幾何概念 ISM 圖之相似性係數比較 ... 65第五章 結論與建議
... 67第一節 結論 ...67 第二節 建議 ...68
參考文獻
...71 壹、 中文部分 ...71 貳、 英文部分 ...76 參、 日文部分 ...81附錄一 幾何概念測驗卷
...83附錄二 SAS/IML 原始碼
...87附錄三 2PL 試題參數值...
91表目錄
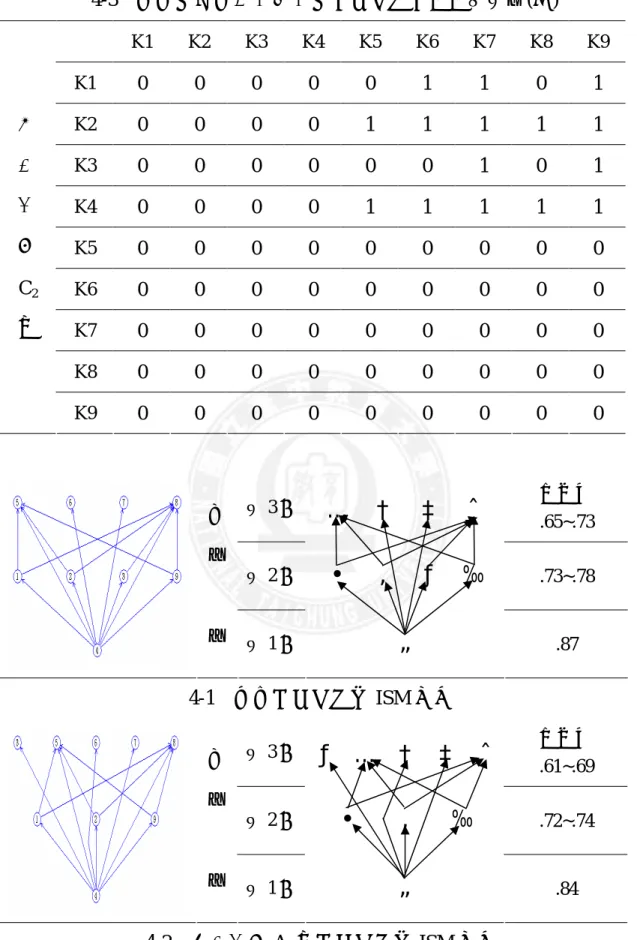
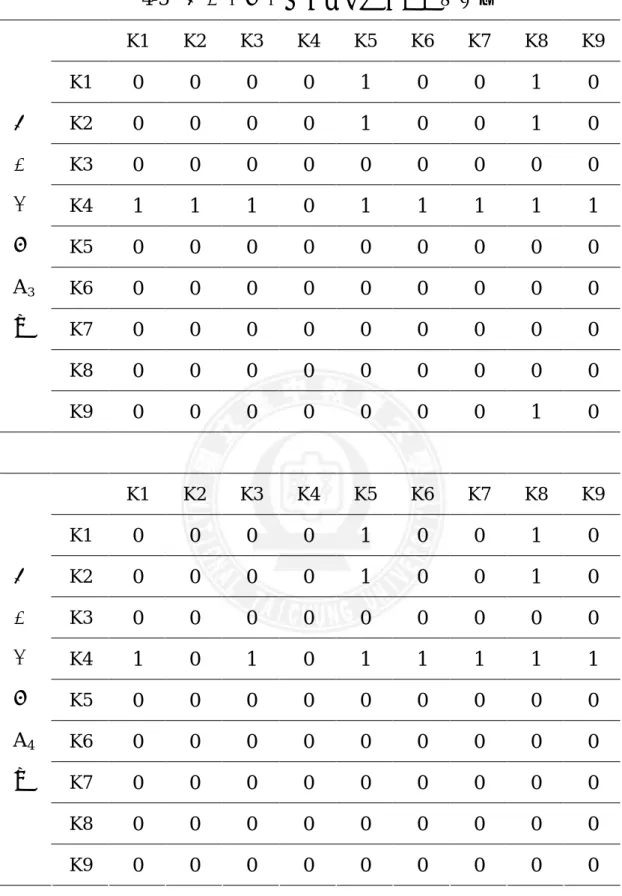
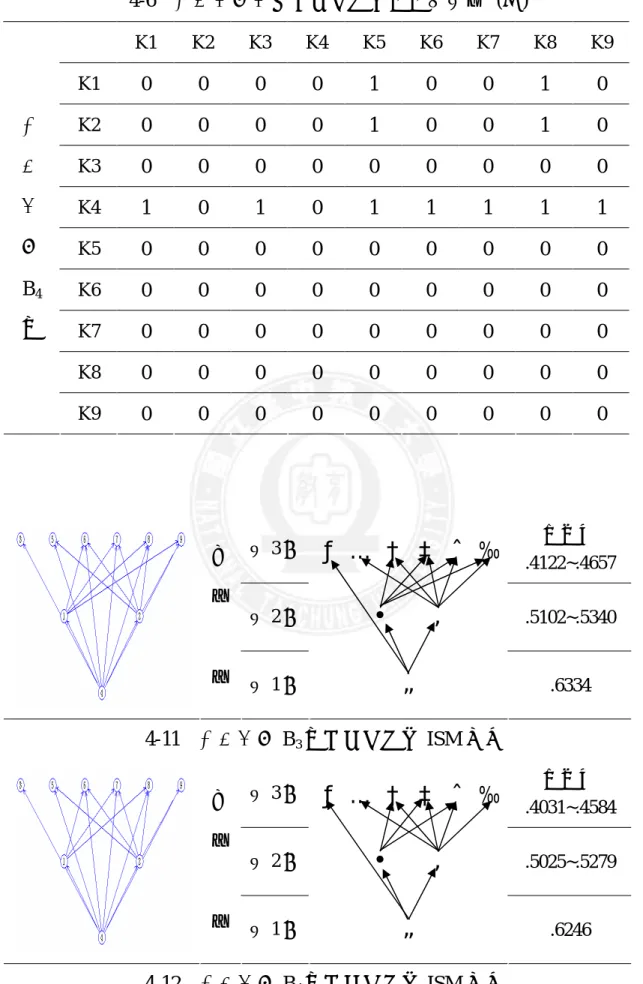
表 2-1 常見的試題反應模式 ...20 表 3-1 各學校班級人數統計表 ...38 表 3-2 九年一貫數學課程正式綱要四年級幾何能力分年細目 ...40 表 3-3 試題與四年級分年細目概念關係表 ...41 表 3-4 預試結果分析 ...42 表 3-5 正式施測結果分析 ...43 表 4-1 學生能力值分組表 ...47 表 4-2 不同能力值學童之能力值及作答情形 ...48 表 4-3 專家及不同能力值學童之幾何概念屬性截矩陣 ...49 表 4-4 總分相同但反應組型不同的六名學童作答情形 ...57 表 4-5 高能力組學童之幾何概念屬性截矩陣 ...58 表 4-6 中能力組學童之幾何概念屬性截矩陣 ...60 表 4-7 低能力組學童之幾何概念屬性截矩陣 ...63 表 4-8 不同能力組學童與專家 ISM 圖相似性係數單一樣本 t 檢定摘要 表 ...65 表 4-9 不同能力組之 ISM 圖相似性係數單因子變異數分析...66 表 4-10 不同能力組之 ISM 圖相似性係數事後比較...66圖目錄
圖 2-1 六種不同的試題特徵曲線 ...16 圖 2-2 三條典型的單參數邏輯斯模式的試題特徵曲線 ...21 圖 2-3 三條典型的雙參數邏輯斯模式的試題特徵曲線 ...22 圖 2-4 三條典型的三參數邏輯斯模式的試題特徵曲線 ...23 圖 2-5 教師知識概念之關聯構造階層圖 ...28 圖 2-6 ISM 圖之繪製...31 圖 2-7 簡化後之 ISM 圖...35 圖 3-1 研究架構圖 ...37 圖 3-2 研究流程圖 ...39 圖 4-1 專家之幾何概念 ISM 結構圖...52 圖 4-2 高能力組 A1生之幾何概念 ISM 結構圖 ...52 圖 4-3 高能力組 A2生之幾何概念 ISM 結構圖 ...53 圖 4-4 中能力組 B1生之幾何概念 ISM 結構圖 ...53 圖 4-5 中能力組 B2生之幾何概念 ISM 結構圖 ...53 圖 4-6 低能力組 C1生之幾何概念 ISM 結構圖 ...53 圖 4-7 低能力組 C2生之幾何概念 ISM 結構圖 ...54 圖 4-8 不同能力受試學童之精熟度折線圖 ...56 圖 4-9 高能力組 A3生之幾何概念 ISM 結構圖 ...59 圖 4-10 高能力組 A4生之幾何概念 ISM 結構圖 ...59 圖 4-11 中能力組 B3生之幾何概念 ISM 結構圖 ...61 圖 4-12 中能力組 B4生之幾何概念 ISM 結構圖 ...61 圖 4-13 低能力組 C3生之幾何概念 ISM 結構圖 ...64 圖 4-14 低能力組 C4生之幾何概念 ISM 結構圖 ...64第一章 緒論
本 研 究 主 要 以 模 糊 取 向 的 詮 釋 結 構 模 式 (fuzzy approach of interpretive structural modeling, FAISM) ,針對國小四年級學童之幾何分年 細目概念結構進行分析,描繪學童個別化的概念 ISM 結構圖,並對不同 能力之學童 ISM 圖進行探討與比較,以期了解學童的概念知識結構,提 供教學者在教學上能依學童學習狀況的不同,採用不同的教學策略或進行 補救教學。本章共分三節,旨在說明研究動機、研究目的及名詞解釋。
第一節 研究動機
人類文化的發展上,許多事物都和幾何有關係。從早期象形文字的應 用、建築物的建立,甚至繪畫藝術的發展,都包含著幾何因素在其中。人 類對於幾何的認識,首先是經由觀察、經驗,再進而整理歸納與應用。幾 何為數學課程的必要內容,藉由幾何的學習,可幫助人們以有條理的方式 來表現、描述生活的世界 (NCTM 1989, 2000) ;幾何也可增進解決問題的 能力,幫助孩童表徵周遭的事物及提升算術的理解能力 (Shaugnessy & Burger, 1985) 。因此在小學的幾何教學中,盡量讓學童發揮、拓展其幾何 直覺,在操作中認識各種簡單幾何形體與構造,再慢慢加入推理性質,為 銜接國中幾何打下良好的基礎 (教育部,2003) 。 在九年一貫課程綱要中,數學學習領域區分為數與量、幾何、代數、 統計與機率、連結五大主題,而其中幾何領域的「圖形與空間」更規劃為 一獨立主題,並參考 van Hiele 幾何思考層次規劃課程架構;在九年一貫 數學學習領域的教學目標中,一年級至二年級為對長度與簡單圖形之認 識;三年級至四年級則要認識幾何圖形之基本要素及性質;五年級至六年 級能認識簡單平面與立體形體的幾何性質,並理解其面積或體積之計算; 七至九年級則要學習三角形及圓的基本幾何性質,認識線對稱與圖形縮放
的概念,並學習簡單的幾何推理 (教育部,2003) 。薛建成 (2003) 指出愈 高年級的學童在 van Hiele 幾何層次的表現愈好,學童的幾何層次表現是 經由「學習的過程」,使得較低層次的學生可以藉由學習而達到較高的層 次。三年級至四年級時期為學生初步了解幾何性質之階段,因此更須在此 階段奠定學童對幾何概念之基礎與興趣,提升學童學習之成就感,以期加 強學童學習幾何之興趣與動力。 九年一貫之教學評量逐步走向多元化評量,雖可從多方面對學生之學 習狀況進行評量,但未能確實了解學生在許多概念的學習情形,各評量之 間無關聯性,而最後仍以總分來評斷一個學生的學習狀況,但卻無法從分 數中了解各學生的學習困境,以致教師在教學上,無法針對學生所不了解 的問題進行補救加強。若只是不斷在評量型式上求變化,卻不知為何而 做、有何意義,那麼可能會失去教學評量的功能與目的。所以評量品質應 是實施教學評量的基本核心,高品質的教學評量對學生的學習表現,能提 供可信、有效和有用的量數,並促進學生的學習 (江文慈,2001) 。 幾何概念對國小學童的數學學習有其相當的重要性,且中年級為銜接 低年級與高年級的時期,奠定良好的幾何概念基礎,才能讓學生在往後的 學習更為確實與穩固。為了瞭解學童在幾何概念的學習狀況,尋求合適且 有效的概念診斷方法,實為一相當重要的課題。且學童在幾何分年細目概 念中,必須先理解前置概念,才能在學習下一層次的概念時了解其意函, 使其概念階層能前後連貫。 鑒於不同能力的學童其概念結構上的差異,因此了解學童的概念結 構,找出學童在不同概念上的學習困難,才能確實的幫助學童突破學習的 瓶頸。劉湘川、林原宏 (1995) 在其研究中指出,不同能力值的學童,在 答題反應上會有所差異,其個人的知識結構上蘊含著某種意義,值得深入 探討;汪慧瑜、余民寧 (2006) 亦指出,答對題數相同但答對題目的組型 不同的學生,其概念結構也會有所不同,均顯示每個學童在學習上的表現
情況不一,每位學童皆有其學習概念上的差異,當了解不同能力的學童的 學習情況與概念結構之後,便可藉由探討不同能力學生的概念結構圖,了 解不同能力學生之間的差異,對於能力較低的學生便可經由適當的教學方 法與引導,協助其解決學習上的問題,使其概念結構能更具組織性、系統 性和階層性,Simon and Gilmortin (1973) 及 Leinhardt (1983) 於研究中亦 指 出 , 經 由 合 適 的 訓 練 , 能 力 較 低 的 學 童 也 能 成 為 能 力 較 高 的 專 家 (expert)。
探討知識結構的心理計量方法很多,其中Warfield (1976) 所提之詮釋 結構模式法 (interpretive structural modeling, 簡稱ISM) ,能將不同類型元 素之間的關係,轉變為關聯構造階層圖。依圖中各階層概念之指向,來描 述不同類型元素之間的關係。如此可使複雜系統中片段、抽象化的不同元 素,轉變為具體化、全面化的關聯構造階層圖。但ISM分析法受限於二元 關係,無法合理解釋複雜的人文社會現象,阮亨中、吳柏林 (2000) 提出 在人文與社會科學的範疇裡,以模糊相關性來描述解題能力或複雜的概念 階層結構關係,是較符合實際狀況的。因此林原宏 (2005) 提出模糊取向 的詮釋結構分析模式,以模糊理論 (fuzzy theory) 及察覺的模糊邏輯模式 (fuzzy logic model of perception, 簡稱FLMP) ,改進傳統ISM圖受限於二元 資料的缺點。 綜合上述,本研究以四年級學童的幾何分年細目概念結構進行探討, 依林原宏 (2005) 所提之模糊取向詮釋結構分析模式,以自編試題施測並 經試題反應理論軟體 BILOG-MG 分析受試學童資料,依學童能力分成 高、中、低三組,再從各組中選取樣本,進行模糊關係矩陣詮釋結構模式 分析,繪製學童分年細目概念結構圖,分析不同能力學童在幾何分年細目 之概念結構,比較高、中、低三組不同能力值學童之ISM圖之異同,並與 專家之概念結構圖進行探討比較,以期了解不同能力之學童在學習上之困 難,以協助教師在教學時能針對學童較不熟悉之單元、概念進行加強與補
救教學。
第二節 研究目的
依據上述研究動機,本研究主要目的如下: 一、分析高、中、低不同能力值的學童,在四年級幾何分年細目ISM結構 圖差異。 二、分析在答對題數相同而答題組型不同的學童,在幾何分年細目ISM結 構圖之差異。 三、探討專家與不同能力值的學童,在幾何分年細目ISM結構圖之差異。
第三節 名詞解釋
本研究所涉及之相關名詞說明如下: 一、幾何分年細目 本研究以九年一貫四年級幾何分年細目指標為依據,能力指標是依主 題與階段的學習能力而訂定,分年細目則進一步細分,明確掌握分年教學 的目標。分年細目的編排採三碼制定,第一碼表年級,第二碼表示主題, 第三碼則是分年細目的流水號,如「1-n-03」表示一年級幾何概念的第三 項分年細目。 二、試題反應理論 心理計量學上常以某些測驗工具來測量受試者的心理特質,而測驗結 果可大致分為心理測驗和教育測驗兩大類 (Linn, 1989) 。理論的發展也漸 由古典測驗理論 (classical test theory) 邁向試題反應理論 (item response theory) ,應用上也較著重測驗的連結等化、適性測驗,甚至電腦化適性測 驗 (王寶墉,1995) 。試題反應理論主要是認為受試者在試題上的表現與
其某種潛在特質 (或能力) 之間有著某種關係存在,這種關係可由一條連 續遞增的數學函數來表示,這數學函數便稱為「試題特徵曲線」 (item characteristic curve, ICC) ,透過這條迴歸線 (regression line) 來解釋受試者 在試題或測驗中所得的分數。
三、模糊理論
模糊理論 (fuzzy theory) 由 Zadeh 於1965年提出,引入隸屬度函數 (membership function) 的概念,將特徵函數的值域由{0,1}二值擴展到區間 [0,1],形成一個模糊集合,其定義說明如下:元素x隸屬於模糊集合A, 則模糊集合A可表示為
( )
( )
≤ ≤ = = x i n x x A A i i i A 0 µ 1 , 1,2,L, µ 四、詮釋結構模式詮釋結構模式 (interpretive structural modeling) 由 Warfield 於1976年 提出,將不同元素之關係,透過0和1之矩陣表示各元素之間的從屬關係, 進而轉變為具體化的有向性構造階層圖,能將複雜且抽象的元素轉而為具 體的關聯構造階層圖。
五、模糊取向的詮釋結構模式
模糊取向的詮釋結構模式 (fuzzy approach of interpretive structural modeling) 由林原宏於2005年提出,結合模糊理論與察覺的模糊邏輯模 式,改進傳統詮釋結構模式受限於二元資料的限制。利用模糊理論截矩陣 獲得學童概念階層關係之資料矩陣,透過AISM軟體進行截矩陣分析,繪 製個別受試者之概念結構圖。
六、專家概念階層結構圖
本研究以答對全部試題之受試者為專家,並以其概念結構圖為專家概 念結構圖。
第二章 文獻探討
本章將對本研究所涉及之相關理論進行探討,共分五節。第一節為幾 何相關研究;第二節為試題反應理論;第三節為模糊理論;第四節為詮釋 結構模式;第五節為模糊取向的詮釋結構模式。各節分述如下:第一節 van Hiele 幾何概念
壹、van Hiele 幾何發展理論
民國八十二年部編本國小教材中的幾何課程以 van Hiele 幾何發展理 論為依據設計,故在此針對其理論做探討,其幾何思維發展分為五個層次 :視覺的 (visual/visualization) 、分析或描述的 (analytic/descriptive) 、非 形式演繹 (informal deduction/abstract) 、形式演繹 (formal deduction) 、嚴 密 (rigor) 。各層次分述如下: 一、層次一:視覺的 此層次的兒童依據感官所察覺到的實物外觀來分辨形體,直觀的認為 正正方方的就是正方形,長長扁扁的就是長方形,而無法了解正方形的條 件為四邊等長且四個角都是直角,長方形為兩兩對邊等長且四個角亦為直 角這些幾何圖形的定義,其他如三角形或圓形亦是如此。因此,這層次的 兒童可以透過生活中接觸到的實物來認識圖形,並藉此加深對圖形的認知 。 二、層次二:分析或描述的 當兒童熟練層次一的概念之後,便對圖形具有分類的能力,能分辨不 同圖形之間的特徵,如圓形沒有邊、三角形有三個角三個邊、正方形有四 個直角四個邊,長方形各有一對等長的邊,四個相同的角,兒童便藉由這 些圖形的基本構造將其分類,但兒童還無法理解圖形中各構成要素之相互 關係,如長方形兩兩對邊相等且四個角都是直角時,其對邊也互相平行。三、層次三:非形式演繹 此層次的學童能辨認圖形內的各組性質,並能利用圖形定義辨認圖形 ,了解不同圖形之間的包含關係。如「矩形的對角線互相平分且相等」,「 兩兩對邊相等是平行四邊形」,此時學童也能了解,在平行四邊形中,如 果有一個角是直角的話,此圖形也一定是矩形,藉由透過理解構造性質的 定義,對各性質能作有系統、邏輯化的聯結。 四、層次四:形式演繹 此層次的學童除了理解幾何性質之間的關係之外,亦能對定理作有系 統的推理演繹證明,能在一個公設系統下,了解定理、定義等的相互關係 ,並可區別定理和逆定理,了解一個定理的充分或必要條件,例如學童可 藉由平行公理證明三角形的內角和為 180 度,對於圖形已有能力去檢驗其 幾何性質。 五、層次五:嚴密性或公理性 此層次的學童能以較嚴密的程度分析比較不同公設系統,如歐式幾何 和非歐幾何,了解抽象的幾何概念,在公設系統中建立定理,了解公設系 統的性質具有一致性、獨立性及完整性。此層次為 van Hiele 幾何思考的最 高層次,一般人較難達成此層性。 van Hiele (1986) 曾對其幾何思考層次提出其具有某些固定特性,許多 研究學者對 van Hiele 幾何思考層次的特性也有不同的解釋,Usiskin (1982) 提出固定順序 (fixed sequence) 、毗連性 (adjacency)、特異性 (distinction) 、分離性 (separation) 、以及造詣 (attainment) 等;Crowley (1987) 提出 了序列性 (sequential) 、進展性 (advancement) 、內在與外在 (intrinsic and extrinsic) 、語言性 (linguistics) 、不協調性 (mismatch) 。研究者依據上 述特性及國內外相關研究 (吳德邦,1999;林軍治,1992;譚寧君,1993 ;Crowley, 1987;Usiskin, 1982;Clements & Battista, 1992;Shaughnessy &
一、次序性 幾何思考層次必須按照一定的順序依序漸進,學童須將原本層次的概 念精熟之後,才能往下一個層次學習,每個層次若要順利學習,則必須掌 握上一個層次的概念。 二、內在與外在 在每個層次中,前一層次的內在元素將轉為下一層次的外在元素。如 學童在視覺層次時,能透過觀察圖形的外觀而分辨圖形,但對圖形的特質 和構成要素並無法掌握,而到了描述層次時,這些圖形的特質和構成要素 學童已能掌握操弄,即原本層次一中的內在元素 (圖形的特質和構成要素) 到了層次二中即轉為可掌握的外在元素,亦即學童能在前一層次中的概念 內化為自我概念,並成為下一層次的使用工具。 三、語言性 每一層次中皆有專屬的符號或語言,而隨著層次的改變,有些語言或 符號就需做適當的修正,如描述層次的學童無法了解長方形亦可稱為平行 四邊形,而到了非形式演繹層次就可理解其之間的關係。 四、分離性 教學過程中是師生互動的,教師的幾何認知層次必然和學生不同,因 此需站在學生的立場,分析學生的幾何思考層次,從學生的角度給予適當 的教材,否則容易造成師生之間的溝通障礙。如教師在教導面積公式時, 若直接給予公式背誦,學生未能先了解面積的意義,而無法建立面積的概 念。 五、進展性 從一個層次提升到另一個層次,需經過教學課程計畫的安排,並不是 自然提升的 (van Hiele, 1986) ,相較於學童的年齡或成熟度,適當的教學 課程安排更顯的重要。因此學童在某個層次尚未精熟之前,若強行加強下 一層次的概念是沒有效果的。
六、不連續性 學童的學習有時會出現不連續的跳躍,當由一個層次要提升到更高層 次時,學童會遭遇所謂的思考危機,若克服了思考危機,那麼學童便能建 立一套新的思考概念。學生的學習可能會有斷層,但在學習的過程中較少 出現。
貳、相關研究
國內外有相當多對於 van Hiele 幾何思考理論的研究,九年一貫課程之 幾何課程也依據其理論設計,故在此將相關研究結果簡介如下: Mason (1989) 在研究中指出,學童在學習不同的幾何概念時,其所呈 現出來的層次也會有所差異,且經由個別晤談結果,可以得知學童在學習 幾何時的錯誤觀念,且高年級的幾何思考層次也較高。Golinskaia (1997) 指出van Hiele理論有其簡單和應用的優點,並將van Hiele理論應用到課程設計中,證明其理論能適切的描述課程架構與內容, 但在較高層次的描述則較不明確。
Baynes (1998) 在如何提升學童的幾何思考層次研究中指出,學童的幾 何層次發展具有低層次往高層次發展的趨勢,且學童的幾何思考層次是有 階層性。
Idris (1998) 在van Hiele幾何思考層次對於場獨立及場依賴的中學生 的影響的研究中指出,實驗組的學生透過課程設計的教學活動能學習的較 好,顯示教師可以經由課程設計、選擇及準備教學,幫助學生提升其思考 層次。 Larew (1999) 於研究中對實驗組27位使用自動繪圖工具學習幾何與 控制組36位使用標準教材學習幾何的學生進行比較,研究結果顯示,組別 之間並無顯著差異,但實驗組在層次0進入層次1有顯著差異,控制組在層
次0進入層次1無顯著差異。
Angela (2008) 以四年級學童為研究對象,應用Realistic Mathematics Education (RME) 和van Hiele理論,探討學童在角的幾何概念上的學習情 況,研究顯示透過這兩種理論,可以幫助學童在角概念上的學習。 盧銘法 (1996) 在國小中高年級幾何概念之分析研究中,以406名中、 高年級學童為樣本,發現學童幾何概念在年級別、圖示題與文字題兩種項 目上達顯著差異;van Hiele水準層次上則受年級不同之影響,未受性別不 同而有明顯差異。 何森豪 (1999) 在van Hiele幾何發展水準之量化模式-以國小中高年 級學生在四邊形概念之表現研究中,結合無母數試題反應理論及模糊理論 ,針對van Hiele幾何思考模式提供另一種方法論,使van Hiele幾何思考模 式量尺化,對學生的思考水準能更準確的測量。研究中發現,層次一的學 童 (40.39%) > 層次二 (34.18%) > 層次三 (25.43%) 。教師透過量尺能更 了解學童的能力與學習狀況。 左台益、梁勇能 (2001) 在國二學生空間能力與van Hiele幾何思考層 次相關性研究中,發現222位國二學生空間能力與van Hiele幾何思考層次, 及學生解決幾何空間問題均呈現正相關,因此在幾何教學適當的融入空間 視覺與操作活動以增進學生幾何學習效果。 林玉琦 (2003) 在國小高年級學童的梯形認知成份與VHL發展層次之 研究中,以721名國小五、六年級學生為樣本,研究顯示不同年級在層次 上的分佈達顯著,6.7%學生在梯形幾何層次上屬逆階層類型,違反van Hiele 幾何思考層次理論,這類學生可能多使用猜測的方式作答。 張永杰 (2003) 在實作評量取向的幾何思考研究中,針對國小四、五 、六年級共459名學生進行四邊形幾何概念的認知情形與層次研究。愈高 年級的學生在幾何思考層次上的表現愈好,幾何思考層次愈好的學生,其 後設認知的表現也愈好。學生的測驗分數相同時,其認知結構可能會有差
異。 薛建成 (2003) 在依據van Hiele幾何思考理論-探究臺灣中部地區國 小學童幾何概念發展之研究中,以中部四縣市共722名學生為樣本,測驗 學生在九大類不同圖型上的表現,其中在直線與曲線上的判別表現最好, 在圖形旋轉上的判別表現較差。高年級的表現優於中年級,中年級的表現 則優於低年級。不同城市的表現上,城市與鄉村的學童在表現上達顯著差 異。 李昆達 (2005) 在從van Hiele發展層次分析國小六年級學童平行概念 之研究中,以城市、鄉村共123名六年級學童為樣本,研究顯示六年級學 童在層次一 (43.1%) > 層次二 (23.6%) > 層次三 (18.7%) ,男女生在層次 上的分佈則無顯示差異。城市、鄉村學童在層次上的分佈達顯著差異,城 市學童多偏向高層次,鄉村偏向低層次。 陳進春、吳德邦 (2005) 在醫護專科學生van Hiele幾何思考層次上之 研究,以464名學生為樣本,層次一至層次五之分布分別為:44.2%、21.6% 、4.5%、0.0%、0.0%。學生在不同性別及科別之幾何思考層次上並無顯著 差異 (p=0.377,p=0.675) ,在年級上則有顯著差異 (p=.038) 。 紀妙貞 (2005) 在基於模糊理論與試題反應理論來探討國小中高年級 學童三角形的概念發展中,發現四年級學童大多位於van Hiele幾何思考層 次的第一、二層次,五六年級則位於第二、三層次;並利用試題通過率顯 示,四、五、六年級在van Hiele幾何層次一、二、三上的分佈是有明顯差 異的,在性別上無差異,年級上則是五、六年級優於四年級,但五、六年 級之間並無顯著差異。 紀小玉 (2005) 在探討接受九年一貫學童幾何思考層次上,以國小一 至六年級學童為樣本,發現學童在層次一中以四邊形凹與凸的判別通過率 最低,層次二中以四邊形角度關係的認知通過率最低,層次三中以正方形 的對角線互相垂直且平分和兩圓心間的距離認知通過率最低。各年級的表
現中,高年級優於中年級,中年級優於低年級,顯示其幾何層次發展是循 序漸進的。跳躍情形以四邊形最多,圓形次之,三角形發生的情況最少。 在基本平面幾何圖和van Hiele幾何層次表現上,地區和年級別的表現上有 顯著差異,性別上則無顯著差異。 李懿芳 (2006) 在探討臺灣中部地區國小四至六年級學童立體幾何概 念-從van Hiele理論的觀點中,以中部五縣市共1351名學生為樣本,四至 六年級的答對率中,六年級高於五年級,五年級高於四年級,且在總分、 各層次、角柱、角椎、圓 (柱、椎、球) 之表現皆達顯著差異 (p<.001) 。 在城市的表現上,可能因城鄉差距而使學童在立體幾何層次上有所差異。 不同性別的學童在van Hiele立體幾何思考層次的表現上無顯著差異。四年 級學童之表現多分佈在未達層次一 (43.88%) 及層次一 (35.75%) ,五年 級 分 佈 在 層 次 二 (40.81%) 及 層 次 一 (24.83%) , 六 年 級 分 在 層 次 二 (54.59%) 及層次三 (31.00%) 。顯示中部地區學童在van Hiele立體幾何思 考層次上是有階層性。 吳德邦、馬秀蘭、李懿芳 (2006) 在van Hiele立體幾何思考層次測驗 之歷程中,以國小四到六年級共183名學童為對象,施測題目範圍從層次 一至層次三,研究結果顯示,以分布在層次二的學生最多,共有39.3%, 而不同年級在立體幾何思考層次上的表現,四年級多分布在層次一,共 45.2%,五年級多分布在層次二,共44.2%,六年級多分布在層次二及層次 三,各佔52.2%及45.0%,顯示學生在van Hiele立體幾何思考層次上是有階 層性的,年級的高低在層次的表現上就有明顯不同,顯示符合van Hiele的 理論。 吳德邦、沈紀伶、馬秀蘭、許天維 (2009) 在臺灣中部地區國中學生 van Hiele幾何思考層次分佈情形之調查研究中,以中部五縣市共1723名一 至三年級國中生為樣本,研究結果顯示,所有學生分佈型態為正偏態,由 層次一至層次五遞減。未達層次一的學生共佔16.02%,有「跳躍現象」的
學生佔10.85%。不同年級的表現上達顯著差異;性別上則在層次二及層次 三達顯著差異,皆男生表現較佳。 綜合上述,可以知道學童在學習幾何概念時,其幾何概念的表現是有 層次性,不同年級的學童在van Hiele幾何發展層次皆有不同,依據學童的 幾何概念發展層次給予適切的教學課程,對於提升學童在幾何學習上的興 趣與成就具有相當大的幫助。
第二節 試題反應理論
心理與教育測驗理論之發展,經過長久時間演變,現今主要可分為古 典測驗理論 (classical test theory, CTT) 與現代測驗理論 (modern test theory)。古典測驗理論又稱真分數理論 (true score theory) 或傳統測驗理論 (conventional test theory) ,主要以真實分數模式為架構,以數學公式表示 :x=t+e,其中x表實得分數,t表真實分數,e為誤差分數。但古典測驗 理論在實施上會有幾項缺點,如同一份測驗試題的難度會依受試樣本的程 度高低而有不同,即當同一份試題給資優班與普通班施測時,資優班反應 出來的結果是試卷簡單,而普通班卻是試卷困難。同樣的,若難度不同的 試卷給同一位學生作答,困難的試卷反應出來的是學生能力較低,而簡單 的試卷結果是學生能力較高,造成學生的能力判斷不一。 針對古典測驗理論的缺點,便發展出現代測驗理論,主要以試題反應 理論 (item response theory, IRT) 為其架構,理論與公式雖較為複雜深奧, 但目前較受測驗學者所青睞,已逐漸取代古典測驗理論,成為目前的主流 測驗理論 (Hambleton, 1989; Drasgow & Hulin, 1990) 。壹、IRT的基本概念
或能力) 之間有著某種關係存在,這種關係可由一條連續遞增的數學函數 來表示,這數學函數便稱為「試題特徵曲線」 (item characteristic curve, ICC) ,透過此條曲線來解釋受試者在試題或測驗中通過的機率。 在試題反應理論中,有許多不同的試題反應模式,通常由一個或多個 參數來描述試題的特性或受試者的潛在特質。最簡單的IRT模式為一參數 邏輯斯模式,如下所示 (Rasch, 1980) :
( )
( ) ) ( 1 i i b b i e e P − − + = θ θ θ 其中Pi( )
θ 為任何一位能力值為θ 的受試者在第i試題做出正確反應的機率,bi為試題i的難度參數 (item difficulty parameter) ,當受試者的能力
值等於試題難度參數時 (即θ −bi =0) ,受試者答對該試題的機率只有50% [即Pi
( )
θ =0.50] ,當能力值小於試題難度參數時 (即θ −bi <0) ,受試者答 對該試題的機率就會低於50% [即Pi( )
θ <0.50] ,當能力值大於試題難度 參數時 (即θ −bi >0) ,受試者答對該試題的機率就會高於50% [ 即( )
θ >0.50 i P ] 。貳、試題特徵曲線
試題特徵曲線所代表的涵義為某種潛在特質的程度與在某一試題上 正確反應的機率,當潛在特質的程度愈高時,答對某一試題的機率就愈高 ,反之則愈小,潛在特質通常指的是精熟度、知識、技巧、態度等。在試 題反應理論中,不同的試題反應模式會有其相對應的試題特徵曲線,當採 用的試題反應模式不同時,所繪製出來的試題特徵曲線便有所不同,常見 的試題特徵曲線如圖2-1所示:
圖2-1 六種不同的試題特徵曲線 資料來源:Hambleton & Cool, 1977
參、試題反應理論的基本假設
試題反應理論具有幾項基本假設,只有在這些基本假設都成立的情形 下,試題反應模式才能具備良好的測驗特性 (余民寧,1992;Embretson & Reise, 2000; Hambleton, 1989; Hambleton & Swaminathan, 1985; Hambleton, Swaminathan, & Rogers, 1991) 。
一、單向度 單向度 (uni-dimensionality) 假設是指在一份測驗中,每個試題都能測 出同一種能力或潛在特質,而不包含測試其他能力或潛在特質。例如在一 份數學試卷中,要測驗的是學生的數學能力,但如果試卷題目的語意較為 完美量尺曲線
( )
θ i P 試題 1 試題 2 潛在距離曲線( )
θ i P 試題 試題 潛在直線曲線( )
θ i P 試題 1 試題 2 單參數邏輯斯曲線( )
θ i P θ 試題 1 試題 2 雙參數邏輯斯曲線( )
θ i P 試題 1 試題 2 三參數邏輯斯曲線( )
θ i P θ 試題 1 試題 2艱澀難懂,對於語文程度較低的學生在作答上便有所困難,使得同一份數 學試卷中,同時測驗了學生的數學和語文能力,這便不算是單向度的測驗 。當一份測驗中的試題所測量的能力或特質不只一種時,便稱為「多向度 假設」 (multidimensionality assumption) 。所以含有單一因素測驗資料的 試題反應模式便稱作「單向度模式」 (unidimensional model) ,也簡稱作 「IRT模式」;而含有多項因素測驗資料的試題反應模式,便稱作「多向度
模式」 (multidimensional model) ,亦簡稱「MIRT模式」。雖然有許多學者 提出多向度試題反應模式 (如:Ackerman, 1989; McDonal, 1981; 王文中, 2004) ,但目前仍以單向度假設的試題反應模式較為普遍。 二、局部獨立性 局部獨立性 (local independence) 是指當受試者在任兩題試題上的作 答情形是不互相影響時,便稱局部獨立性,即在考量受試者的能力因素後 ,受試者在各個試題上的反應情形是各自獨立而不互相影響的,也就是說 試題反應模式裡的能力因素,是影響受試者作答反應的唯一因素,此能力 因素即代表整個潛在空間 (complete latent space) ,此潛在空間可能包含一 種能力因素 (單向度假設) 或一種以上的能力因素 (多向度假設) 。滿足局 部獨立性者,可以公式表示如下:
∏
= = = n i i n n U P U P U P U P U U U P 1 2 1 2 1 ) ( ) ( )... ( ) ( ) ,..., , ( θ θ θ θ θ通常當單向度假設成立時,局部試題獨立性也會成立 (Lord, 1980; Lord & Novick, 1968),但當資料不是單向度時,局部試題獨立性也可能成立,只 是整個潛在空間需被界定清楚。但在影響測驗的能力向度不只一種時,局 部試題獨立性便無法成立,如:題組型試題、學習時間不同、身體疲憊、
答題格式不一、試題提供答案線索等 (Yen, 1993) ,在這種情形下便需要 特殊的試題反應模式才能加以分析。 三、非速度測驗 非速度測驗 (non-speedness test) 是指當受試者在接受一份測驗時,並 不會因時間限制而導致受試者無法完成測驗,也就是說,影響受試者表現 的因素只有受試者的能力高低,而不是因為時間不夠無法完成測驗。亦即 試題反應模式測驗的實施是在受試者不受速度限制下所完成,受試者的表 現完全由其能力高低決定。 四、知道-正確假設 知道-正確假設 (know-correct assumption) 是當受試者知道某一試題 的正確答案時,便會答對該試題,而當受試者答錯該試題時,便表示受試 者不知道該試題的答案,即受試者在作答時,不受其他因素所影響,如粗 心大意、作弊、跳題等, 由以上的IRT基本假設可知,試題反應模式須在單 (或多) 向度假設、 局部試題獨立性、非速度測驗及知道-正確假設的情形下才能適用,若測 驗不符合這些假設時是無法適用的。
肆、試題反應理論的特色
試題反應理論能取代古典測驗理論,顯示其有優於古典測驗理論的特 色,以下介紹兩種試題反應理論所具有的特色,分別為「參數不變性」 (parameter invariance) 和「訊息函數」 (information function) 概念。當試題反應模式適合一份欲分析的資料時,其試題參數的估計值不受 受試者能力所影響,也就是不管受試者的能力高低,其獲得的試題特徵曲 線均相同,即此參數估計值是一種「樣本獨立」 (sample independent) 特 性,在估計時不會因樣本不同而有所差異。
二、訊息函數
訊息函數有分為試題的訊息函數 (item information function) 和測驗 的訊息函數 (test information function) 兩種,前者是試題特徵曲線微分的 平方與該試題變異數的比值,後者為試題訊息函數的總和,訊息函數可作 為試題的挑選和測驗的編製的依據,對於電腦化適性測驗及評鑑測驗的相 對成效等均有很大的幫助 (余民寧,2009) 。
伍、試題反應理論的模式
在常見的測驗資料中,計分的類型可分為三種,分別為二元化計分 (dichotomous scoring) 、多元化計分 (polytomous scoring) 及連續性計分 (continuous scoring) ,依據計分模式的不同,分別介紹幾種常見的試題反 應模式,如下表所示:
表2-1 常見的試題反應模式
資料測量屬性 試題反應模式
潛在線性模式 (latent linear model) 完美量尺模式 (perfect scale model) 潛在距離模式 (latent distance model)
單、雙、三參數常態肩形模式 (1, 2, 3 parameter normal ogive models)
單、雙、三參數邏輯斯模式 (1, 2, 3 parameter logistic models)
二元化計分
四參數邏輯斯模式 (4 parameter logistic model) 等級反應模式 (graded response model)
名義反應模式 (nominal response model) 評定量表模式 (rating scale model) 多元化計分
部分計分模式 (partial credit model)
連續計分模式 連續反應模式 (continuous response model) 資料來源:Hambleton & Swaminathan, 1985
在目前的測驗資料中,二元化計分是較常採用的,其作答反應只有「 對」和「錯」兩種,而在二元化計分中,又以1PL、2PL、3PL的試題反應 模式較常使用,以下分別介紹這三種常用的模式。
一、單參數邏輯斯模式
單參數邏輯斯模式 (one-parameter logistic model, 1PL) 又稱「Rasch模 式」,為George Rasch (1960/1980) 所提出,其公式如下:
( )
i n e e P i i b b i 1,2, , 1 ( ) ) ( ⋅⋅ ⋅ = + = θ−θ− θ 其中P( )
θ 表能力值為θ的受試者答對第i試題的機率,b為試題i的難度參數 (item difficulty parameter) ,e為以2.718為底的指數 (exponential) ,n為 該份測驗的總題數,Pi
( )
θ 為介於0和1之間的值,其圖形為一條S形的曲線 。當受試者能力值θ等於試題難度bi時,其答對該試題的機率只有50% ( 即Pi( )
θ =0.50) ;受試者能力值θ大於試題難度bi時,其答對該試題的機率 便會大於50% (即Pi( )
θ >0.50) ;受試者能力值θ小於試題難度bi時,其答 對該試題的機率就會小於50% (即Pi( )
θ <0.50) 。由Rasch模式我們可以繪 出其試題特徵曲線如下圖所示: 圖2-2 三條典型的單參數邏輯斯模式的試題特徵曲線 資料來源:Hambleton, Swaminathan, & Rogers, 1991由圖2-2中可知,當受試者的能力值愈高時,其答對該試題的機率也愈 高,以圖中三題試題為例,從答對機率0.5畫一橫線與三條試題特徵曲線相 交,其交點對應到的能力值則被定義為該試題的難度參數,亦稱作「位置 參數」 (location parameter) ,圖中試題1至試題3的試題難度參數分別為 1 1=− b 、b2 =1、b3 =2,當bi值愈大時,表示試題愈困難,反之則愈簡單。 1.0 0.9 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1 0 -4 -3 -2 -1 0 1 2 3 4 正 確 反 應 機 率 試題 1 試題 2 試題 3 能力值
二、雙參數邏輯斯模式
雙參數邏輯斯模式 (two-parameter logistic model, 2PL) 為Birnbaum (1968) 修改Lord (1952) 的雙參數常態肩形模式 (normal ogive model) 而 來,已成為目前主流的試題反應模式之一,其公式如下所示:
( )
i n e e P i i i i b a b a i 1,2, , 1 ( ) ) ( ⋅⋅ ⋅ = + = θ−θ− θ 雙參數邏輯斯模式較單參數邏輯斯模式在公式中多了ai參數,即試題鑑別度參數 (item discrimination parameter) ,ai值與Pi
( )
θ 在θ =bi點上的斜率成某種比例關係,其試題特徵曲線如圖2-2所示: 圖2-3 三條典型的雙參數邏輯斯模式的試題特徵曲線 資料來源:Hambleton et al., 1991 在圖2-3中可以發現,試題2和試題3的試題難度參數相等,b2 =b3 =1, 但試題2的試題特徵曲線較為平緩,試題3則較為陡峭,顯示當受試者的能 力愈高時,答對試題3的機率會高於試題2,反之則答對試題3的機率會低 於試題2,即試題特徵曲線愈陡的試題,較平緩的試題具有較大的試題鑑 別度參數。 1.0 0.9 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1 0 -4 -3 -2 -1 0 1 2 3 4 正 確 反 應 機 率 試題 1 試題 2 試題 3 能力值
三、三參數邏輯斯模式
三參數邏輯斯模式 (three-parameter logistic model, 3PL) 是由Lord (1952) 所提出的三參數常態肩形模式而來,其公式可表示如下:
( )
i n e e c c P i i i i b a b a i i i 1,2, , 1 ) 1 ( ( ) ) ( ⋅⋅ ⋅ = + − + = θ−θ− θ 其中ci為「機會參數」 (pseudo-chance parameter) ,ci值使得試題特徵曲 線的下限值可能會大於0,因為當受試者遇到不會的試題時,可能會採取 猜題的解題策略,一般來說 i i A c ≤ 1 ,其中Ai為試題i的選項數目,因為命 題者可能會在試題中佈置誘答選項,由於這個緣故,ci值不應該完全等同 於「猜題參數」。三參數邏輯斯模式的試題特徵曲線如圖2-3所示如下: 圖2-4 三條典型的三參數邏輯斯模式的試題特徵曲線 資料來源:Hambleton et, al., 1991由圖2-4中可發現,當受試者能力很低時,還是有機率答對試題,三參 數邏輯斯模式考慮了鑑別度和猜題因素,較適用於答錯不倒扣且為四選一 的單選題測驗資料的分析。 1.0 0.9 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1 0 -4 -3 -2 -1 0 1 2 3 4 正 確 反 應 機 率 能力值 試題 1 試題 2 試題 3
第三節 模糊理論
壹、模糊理論簡介
在古典集合論中,要求元素對集合的屬性是二者之中必選其一,不可 模稜兩可,表現出「非此即彼」的概念,但在一般的日常生活中,許多事 物的認定並不符合這個概念,如美醜、快慢、滿意度、年輕與年老等,因 人類思想看法的不同,許多事物存在著「既此又彼」的關係 (林原宏,2007) ,其關係的界定並不是傳統邏輯概念的非對即錯,而是存在著一條不明確 的界線,模糊理論 (fuzzy theory) 便是在探討這些概念,模糊理論首先由 Zadeh (1965) 提出,引入隸屬度函數 (membership function) 的概念,將特 徵函數的值域由{0,1}二值擴展到區間[0,1],形成一個模糊集合,其理論已 應用到社會科學、教育、電子器材等許多領域 (林清平,2005;林基興, 2007;汪惠健,2006;馮國臣、任麗偉,2007;Kosko, 1999) 。貳、模糊隸屬度函數和
α截集
有關模糊隸屬度函數和α 截集 (α-cut) 的定義如下: 【定義2-1】令U表示全域 (universal set) ,µ為一函數,即µ:U →[ ]
0,1 , 則U 之模糊子集A的隸屬函數記為µA( )
x ,表示元素x隸屬於 集合A的程度,在離散的情形下,模糊集合A可表示成:( )
( )
≤ ≤ = = x i n x x A A i i i A , , 2 , 1 , 1 0 µ L µ 【定義2-2】模糊集合A的α 截集定義為: Aα ={xµA( )
x ≥α} , 0≤α ≤1 A的α截集的隸屬度函數µAα( )
x 表示為:( )
( )
( )
< ≥ = α µ α µ µ α x x x A A A , 0 , 1參、模糊關係矩陣與截矩陣
模糊關係 (fuzzy relation) 指的是兩個集合元素之間的某種關聯特性 ,可以模糊關係矩陣 (fuzzy relation matrix) 來表示兩個集合元素之間的關 係,可表示如下: 【定義2-3】假設論域X 有m個元素,論域Y有n個元素,則X與Y兩集合 元素的關係可表示為:( )
ij m n mn m n r r r r r R = × = L M M K 1 1 11 其中rij =µR( )
x,y :X×Y →[ ]
0,1 【定義2-4】給定α 的情形下,可以進行模糊關係矩陣之截矩陣運算,可表 示如下:( )
rij I J R × = α 且 , 0 1 , 0 , 1 ≤ ≤ < ≥ = α α α α ij ij ij r r r肆、模糊理論在教育領域相關研究
Biswas (1995) 利用模糊理論,建立以六個級距的方法,來表示學生評 量分數程度的高低。Perdikaris (1996) 認為van hiele幾何發展層次無法明確的細分學童概 念,遂利用模糊集合隸屬度函數理論,將其幾何發展層次數學化,以細分 學童的幾何思考層次。
非完全的明確了解,因此採用ISM模式,延伸至模糊理論,建立一套高中 畢業生的升學與就業輔導的評量生涯決定模式。 Nolan (1998) 將模糊理論應用於作文評分系統中,可事先讓教師輸入 詞彙及評分標準,接著讓學生輸入所欲評估的文章,利用此系統來進行作 文的自動評分,在此方法下,可避免教師的個人主觀因素而影響到作文批 改的成績。 Zhou (2002) 在評量期刊的系統中,以模糊理論為基礎,整合主觀與 客觀相關因素,進而對期刊的等級進行評分。 何偉雲 (1995) 應用模糊統計的方法,對學生學習成就的評量進行分 析,以模糊理論探討評量工作本質的模糊性,並利用三相模糊統計方法, 對評估對象進行模糊評判,顯示基於模糊理論的評量方法下,能有效且客 觀地精確反映學習情況,有別於傳統評量的方式,能在教師主觀的經驗判 斷下,提供了另一種精確評量的方法。 Law (1996) 將模糊隸屬度函數的定義應用於建立數學教育指標系統; Law (1997) 指出模糊理論已成為科技、人工智慧、測驗統計等領域的重要 方法。何偉雲 (1996) 亦提出模糊理論在教育方面的應用,均拓寬和加深 了模糊理論在各方面的應用。 胡悅倫、吳柏林 (2002) 將模糊隸屬度概念應用到測驗量表中,使受 試者能在選項中填寫隸屬度,改進傳統量表無法精確反應出受試者樂觀程 度的缺點。 王元仁 (2003) 應用模糊理論中的模糊綜合評估到CIPP評鑑模式,能 將課程評鑑中所獲得主觀和不明確的信息加以合理的量化,以作為課程調 整的參考之用。
羅 豪 章 (2005) 利 用 模 糊 理 論 發 展 出 改 良 的 CSA (Cognitive Style Analysis) 數值處理的模糊推論系統,顯示以此系統在分析傳統數值與模糊 推論處理下的認知風格衡鑑結果是適切可行的。
葉秋呈 (2007) 將模糊隸屬度函數應用到威克生等級和檢定當中,分 析學生學習微積分的動機和學習策略,分析結果並可作為老師了解學生與 營造學習環境之參考。 劉威德、梁姿茵 (2008) 以模糊理論和管制圖建構一套繪畫科目多元 評量成績管控系統,探討模糊理論在多元評量的適用性,顯示透過模糊理 論能使學習成效評量更具客觀化。 綜合上述,可知模糊理論在各個領域的應用相當廣泛,在教育與心理 統計中,利用模糊理論則可改進傳統二元計分的方式,使評量的結果能更 符合學生的學習情況。
第四節 詮釋結構模式
壹、理論基礎
詮釋結構模式 (interpretive structural modeling) 首先由Warfield (1976) 提出,原本是應用在社會系統工學 (social system engineering) 中的一種結 構化模型法,理論基礎為離散數學和圖形理論,並結合行為科學、數學概 念、團體決策 (group discussion) 及電腦輔助等領域,再考慮學習的歷程 (Warfield, 1974a, 1974b,1979) ,透過二維矩陣 (binary matrices) 的數學運 算來呈現出一個系統內完整的多層級結構化階層圖,稱為「地圖 (map) 」 (蔡秉燁、鍾靜蓉,2003) 。Warfield (1982) 進一步提出了ISM分析法非常 適用於龎大資料的推演與運算,能應用在社會學、人文學、心理及哲學等 方面。 佐藤隆博 (1987) 提出了將ISM分析法應用在探討教育的課程與學習 架構上,利用ISM分析法將教師腦中片斷、抽象化的教材概念加以編排, 轉而為具體的關聯構造階層圖,並可藉由此結果編排教學課程,有效的連 結學童腦中片斷、零散的概念知識,協助學童建立完整的概念聯結構造。
如圖2-5所示。 圖2-5 教師知識概念之關聯構造階層圖 參考自:蔡秉燁、鍾靜蓉 (2003)
貳、ISM分析法
傳統的ISM分析法可將元素間的階層結構關係有系統化的表現出來, 若欲分析的系統內有K個元素,已知其中任意兩元素Ai與Aj的二元關係, 可以A=( )
aij k×k表示。若Aij =1,表示Ai從屬於Aj,即Ai為Aj的下位元素; 若Aij =0,則表示Ai不屬於Aj下位元素。依據許天維與林原宏 (1994) 所 整理提出的ISM分析法,其要點敘述如下: (一) 矩陣的運算 兩個矩陣A運算的結果定義為: ( ) ( ) ( ) ( ) ( )( )
ij k k kk k k a a a a a A = × = 2 2 2 1 2 1 2 11 2 L M M L 2 A 矩陣內的元素: ( ) iK Kj K k j i j i kj ik ij a a a a a a a a a =∑
= ⊗ ⊕ ⊗ ⊕ ⊕ ⊗ = ... 1 2 2 1 1 2 上式中的⊗與⊕的運算定義如下: = = = ⊗ 1 1 1 0 y and x else y x = = = ⊕ else y and x y x 1 0 0 0 教師腦中的知識概念 外部表現之構造化結果 學童腦中零散的知識(二) 傳遞封包 (transitive closure) 假設Aˆ為傳遞封包,則定義Aˆ = A⊕A2⊕A3⊕⋅ ⋅⋅⊕AP (三) 可到達矩陣 (reachability matrix) 定義 P p I A I A A A A I A ⊕ = ⊕ ⊕ ⋅⋅ ⋅ ⊕ ⊕ ⊕ = ⊕ ˆ ˆ 2 3 ,其中 I表示K×K階的 單位矩陣。滿足如下關係的矩陣R則稱為可到達矩陣。
(
)
(
)
I A A A A A I A I A A A A A I A R P P ⊕ ⊕ ⊕ ⋅⋅ ⋅ ⊕ ⊕ ⊕ = ⊕ = ⊕ ⊕ ⋅⋅ ⋅ ⊕ ⊕ ⊕ = ⊕ = ⊕ = + + 1 P 3 2 1 P 3 2 P I ˆ (四) ISM圖的繪製 以A1至A5五個元素為例,假設可用矩陣A表示這五個元素的關係, 經過上述的傳遞封包運算後,相對應的可到達矩陣為R,可表示如下 (資 料修改自佐藤隆博,1987) : = 0 0 0 0 1 1 0 1 0 0 0 1 0 0 1 0 1 1 0 0 0 0 0 0 0 A = 1 0 0 0 1 1 1 1 0 1 1 1 1 0 1 1 1 1 1 1 0 0 0 0 1 R 矩陣R的轉置矩陣T及兩矩陣的交集矩陣表示如下: = 1 1 1 1 0 0 1 1 1 0 0 1 1 1 0 0 0 0 1 0 1 1 1 1 1 T = ∩ 1 0 0 0 0 0 1 1 0 0 0 1 1 0 0 0 0 0 1 0 0 0 0 0 1 T R 為了方便繪製ISM圖,將概念資料A1、A2、A3、A4、A5融入矩陣R中 ,若矩陣中的元素為1,則填上指向的元素代號,可得到概念元素代號的 矩陣R( )
Ak 、T( )
Ak 及R( ) ( )
Ak ∩T Ak ,如下所示:( )
= 5 1 5 4 3 1 5 4 3 1 5 4 3 2 1 1 0 0 0 0 0 0 0 0 0 A A A A A A A A A A A A A A A A A R k( )
= 5 4 3 2 4 3 2 4 3 2 2 5 4 3 2 1 0 0 0 0 0 0 0 0 0 A A A A A A A A A A A A A A A A A T k( ) ( )
= ∩ 5 4 3 4 3 2 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 A A A A A A A A T A R k k 根據矩陣R( )
Ak 、T( )
Ak 及R( ) ( )
Ak ∩T Ak 中的元素代號,加以圖像化,繪 製成如圖2-6的ISM結構圖,繪製步驟如下: 1、比較R( )
Ak 及R( ) ( )
Ak ∩T Ak 的每一列,找出每一列中皆相等的概念元素 ,可首先找到R( )
Ak 及R( ) ( )
Ak ∩T Ak 的第一列元素A1相等,則在R( )
Ak 及( ) ( )
Ak T Ak R ∩ 中A1所在的行、列皆刪除,刪除之後可得到以下矩陣:( )
= 5 1 5 4 3 1 5 4 3 1 5 4 3 2 1 1 0 0 0 0 0 0 0 0 0 A A A A A A A A A A A A A A A A A R k( ) ( )
= ∩ 5 4 3 4 3 2 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 A A A A A A A A T A R k k 刪除後( )
= 5 5 4 3 5 4 3 5 4 3 2 0 0 0 0 0 A A A A A A A A A A A A R k( ) ( )
= ∩ 5 4 3 4 3 2 0 0 0 0 0 0 0 0 0 0 A A A A A A A T A R k k 2、再以同樣的方法,找到第五列的A5,並刪除A5所在的行和列,得到以 下矩陣:( )
= 4 3 4 3 4 3 2 0 0 A A A A A A A A R k( ) ( )
= ∩ 4 3 4 3 2 0 0 0 0 A A A A A A T A R k k 3、重複同樣方法最後可得到以下矩陣: R( )
Ak =[ ]
A2 R( ) ( )
Ak ∩T Ak =[ ]
A2 4、由以上步驟可以得到概念的階層關係,由上而下分別為:A1、A5、A3及 4 A 、A2,繪製成ISM圖如下所示: 圖2-6 ISM圖之繪製參、ISM相關研究
Hawthorme & Sage (1975) 將ISM分析法應用於高等教育課程計畫的 整合,針對五名成員所組成的課程小組討論過程,提出對於高等教育的建 議。
Nussbaum & Smith (1983) 應用電腦輔助式的ISM課程設計,協助群體 中討論與分析較為複雜的教學情境,可對於問題提供解決層級的不同要點 ,根據研究結果顯示,透過此項課程設計,可有效且迅速的協助小組團體 形成課程要點,增加解決問題的創造思考能力,減少時間與討論成本的浪 費。 A1 A5 A3 A4 A2 A1 A5 A3 A4 A2
Tatsuoka (1995) 應用ISM分析法,獲得具階層性的知識概念結構,指 出概念和認知之間具有關聯性,屬性之間也有先前需要 (prerequisite relationship) 的關係存在。
Wang, Girel & Leighton (2006) 在研究中指出,經由評量訊息階層化以 及教材的結構化,可以獲得更多的認知診斷訊息,協助學習者建立知識概 念結構。 吳信義 (1998) 利用ISM分析職業教育中「基本電學」科目中各教學單 位元素的階層關係,並將所獲得的階層關係利用電腦化進行分析,使課程 編排更為簡潔方便。 戴筱玲、洪文良、林原宏 (2009) 應用概念詮釋結構模式,分析學童 的速率概念知識結構,探討學童個人化的速率概念階層結構,顯示應用此 方法能有效的表徵速率概念及進行結構分析。 呂秀茹、洪文良、林原宏 (2009) 應用SCM及CAISM分析五年級學童 在時間化聚計算的概念結構,顯示經CSM演算法分群後,進而進行CAISM 分析,可有效表徵學童時間化聚計算概念結構,並進行分析比較。 應紀來、李炳軍、胡知、賈勇、劉新萍 (2003) 利用投入產出表關係 ,分析各產業部門結構,並以此為基礎建立投入產出詮釋結構模式,利用 此模式對河南省1987、1992、1997年的投入產出表中的各工業產業部門進 行實證研究,找出河南省在此期間的一些基礎產業部門。 蔡秉燁、鍾靜蓉 (2003) 以商業職業學校經濟學中的「供給與需求」 單元為實例,利用ISM中的階層有向圖 (hierarchical digraph) ,提出具有 構造化及階層化的教學方法,建構出學習單元的「學習地圖」 (learning map) 及「學習路徑」 (learning path) 。
王熙松、劉述舜、張睦雄、梁樾 (2005) 利用詮釋結構模式針對公路 邊坡整治工程實際案例進行分析,並建立分析要素之層級架構。
許多相關研究,顯示將其應用在分析學童的概念結構上,可以了解學童的 知識概念結構,進而分析學童在各概念的學習程度,提供教學者在編排課 程與進行補救教學上的資訊。
第五節 模糊取向的詮釋結構模式
壹、理論
傳統的ISM分析法中的元素關係,受限於二元資料的處理,使ISM分 析法的應用受限,無法解釋許多複雜的人文社會科學現象,林原宏 (2005) 結合了模糊理論與察覺的模糊邏輯模式,提出了模糊取向的詮釋結構模式 ,解決傳統ISM分析法只適用於二元關係的限制,應用在心理計量分析, 可針對模糊關係元素,計算出上下從屬關係 (subordinate relation) ,提供 個人化的概念關聯分析。貳、模糊取向的ISM分析法
模糊取向的詮釋結構模式分析方法,其步驟如下 (林原宏,2005) : 一、確定欲分析的元素單位為試題或概念,假設共有M 個試題,L個概念 。 二、在選定的試題反應模式之下,能力值θk的受試者,其在第m題的答對 機率為Pm( )
θk ,依察覺的模糊邏輯模式,計算該受試者的模糊關係矩 陣,方法如下: 1、若所分析的元素單位為試題,則能力值θk的受試者的模糊關係矩陣為( )
k pij( )
k M M Dθ =[ θ ] × ,Pij( )
θk 為符合試題i指向試題 j的機率,依察覺的模 糊邏輯模式意義,令ci =Pi( )
θk 且oj =1−Pj( )
θk ,可得以下公式:
( )
( )
(
)
(
)
( )
[
( )
( )
[
]
[
( )
( )
]
]
( )
k j k j k j k i k j k i j i j i j i j i k ij p p p p p p o c o c o c o c p p θ θ θ θ θ θ θ − + − − = − − + = = 1 1 1 1 1 , 2、若所分析的元素單位為概念,則能力值θk的受試者的模糊關係矩陣為( )
k pij( )
k LL Dθ =[ θ ] × ,Pij( )
θk 為符合概念i指向概念 j的機率,依每一題試 所測得該概念與否的關係,假設概念個數為L個,可形成一個二元關係 的概念屬性矩陣 (attribute matrix) A=( )
aml M×L, aml =1表示第m題含有 概念l,即有測到概念l;若aml =0則表示第m題沒有包含概念l,即沒 有測到概念l。令( )
l L L M m ml a a SA • × × = = =∑
1 1 1 表示每一概念被測得出現的總 數 之 矩 陣 。 因 此 能 力 值θk 的 受 試 者 在 每 個 概 念 精 熟 的 機 率 為( )
[
( )
]
[
l( )
k]
L L M l ml M k m k a ma a P MA × × • × = = θ 1 θ 1 θ 。依察覺的模糊邏輯模式意義 ,令ci =mai( )
θk 且oj =1−maj( )
θk ,所以可得:( )
( )
(
)
(
)
( )
[
( )
( )
[
]
[
( )
( )
]
]
( )
k j k i k j k i k j k i j i j i j i j i k ij ma ma ma ma ma ma o c o c o c o c p p θ θ θ θ θ θ θ − + − − = − − + = = 1 1 1 1 1 , 3 、 選 定 α 值 且 0≤α ≤1 , 將 模 糊 關 係 矩 陣 為 D( )
θk =[pij( )
θk ]M×M 或( )
k pij( )
k L L Dθ =[ θ ] × 進行截矩陣分析。例如分析單位為概念,則: D( )
θk =[pij( )
θk ]L×L α 且( )
( )
( )
, 0 1 , 0 , 1 ≤ ≤ < ≥ = α α θ α θ θ α k ij k ij k ij p p p 4、將步驟3所得的模糊關係截矩陣進行ISM分析,為使圖形便於閱讀,將 各元素之間的指向加以簡化,去除直接指向而保留間接指向的路徑, 如下圖所示:簡 化 →