多元表徵應用於二元一次聯立方程式文字題列式教學之研究

(1)

國立交通大學

理學院科技與數位學習學程

碩士論文

多元表徵應用於二元一次聯立方程式

文字題列式教學之研究

A Study of an Instructional Design by Using Multiple

Representations to Translate Word Problems of Two

Variables into A System of Linear Equations

研究生

：

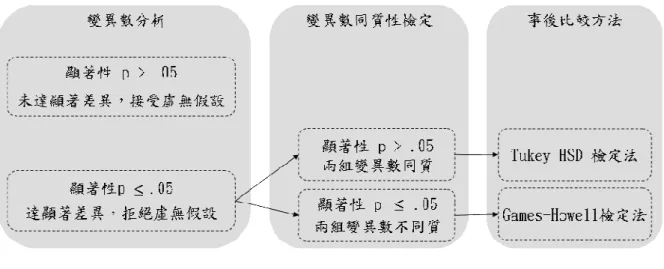
廖真瑜

指導教授

：

陳明璋博士

(2)

多元表徵應用於二元一次聯立方程式文字題列式教學之研究

A Study of an Instructional Design by Using Multiple

Representations to Translate Word Problems of Two

Variables into A System of Linear Equations

研究生：廖真瑜

Student ： Chen-Yu Liao

指導教授：陳明璋

Advisor ： Ming-Jang Chen

國立交通大學

理學院科技與數位學習學程

碩士論文

A Thesis

Submitted to Degree Program of E-Learning

College of Science

National Chiao Tung University

in partial Fulfillment of the Requirements

for the Degree of

Master

In

Degree Program of E-Learning

July 2011

Hsinchu, Taiwan, Republic of China

(3)

多元表徵應用於二元一次聯立方程式文字題列式教學之研究

學生：廖真瑜指導教授：陳明璋博士

國立交通大學理學院科技與數位學習學程

中文摘要

本研究目的在分析不同表徵之教學設計模式對於常態編班學生其學習成效及認知負荷之影響，並以整體學生、學過與未學過學生及不同數學學習成就學生作為樣本區隔，針對國中七年級「二元一次聯立方程式文字題列式」進行研究，進而對教學現場中不同的教學對象提出其適用之教學設計模式建議。本研究採準實驗研究設計，以研究者任教之常態編班國中七年級四個班的學生為研究對象進行實驗，依據不同的教學設計模式分為四組進行實驗，分別為(1)串流式教學組、(2)代數教材設計原則組、(3)動態圖像組、(4)代數教材設計原則輔以動態圖像組。實驗結果分析得到：(1)將結合代數教材設計原則及動態圖像之教學設計教材運用於常態編班中整體學生、未學過之學生及中學習成就、低學習成就學生之教學，能有效提升其學習成效，並降低認知負荷；(2)代數教材設計原則能降低學生在搜尋相關訊息之認知負荷；(3)動態圖像表徵有助於低學習成就學生理解題意，進而正確的將文字表徵轉化為代數表徵；(4)將僅有動態圖像表徵而未具代數教材設計原則之教材設計運用於常態編班中整體學生、未學過學生及中學習成就、高學習成就學生之教學，其學習成效表現不佳且認知負荷較高；(5)在實驗教材中皆未產生專業知識反轉效應。關鍵字：二元一次聯立方程式文字題、多元表徵、認知負荷

(4)

A Study of an Instructional Design by Using Multiple Representations

to Translate Word Problems of Two Variables into A System of

Linear Equations

Student：Chen-Yu Liao Advisor：Ming-Jang Chen

Degree Program of E-Learning

National Chiao Tung University

Abstract

The purpose of this study was to analyze the effects of four different instructional design models on learning effectiveness and cognitive load among students in a normal grouping system. The experimental lesson was about translate word problems of two variables into a system of linear equations. The sample was divided by experience of learning the lesson and math learning achievement into various groups to find the suitable instructional design model for each group of students.

The quasi-experimental research design was adopted. Four seventh-year classes of students from the school where the researcher served as a teacher participated in the experiment. The students were divided into four groups based on four instructional design models, including (1) streaming instruction, (2) algebra lesson design principles, (3) dynamic graphic represrntations teaching, and (4) algebra lesson design principles with dynamic graphic represrntations teaching.

The experimental results showed: (1) the instruction based on algebra lesson design principles with dynamic graphic represrntations teaching could effectively enhance the learning effectiveness and reduce the cognitive load among overall students, students who have never learnt the experimental lesson, students with intermediate math learning achievement, and students with low math learning achievement in a normal grouping system; (2) the instruction based on algebra lesson design principles could reduce the cognitive load on students in seeking related information; (3) dynamic graphical representations were helpful for students with low learning achievement in comprehension of problems and translation of word representations into algebraic representations; (4) the instruction designed with dynamic graphic representations but without algebra lesson design principles caused poor learning effectiveness and higher cognitive load among overall students, students who have never learnt the experimental lesson, students with intermediate math learning achievement, and students with high math learning achievement in a normal grouping system; (5) no expertise reversal effect was found in this study.

Keywords: word problems of two variables into a system of linear equations, multiple representation, cognitive load/

(5)

誌

謝

自從大學畢業後即踏入工作的我，在兩年前走回校園進修，歷經了兩年的光陰，終於在此刻把睽違已久的論文順利完成了，期間遇到許多挑戰與磨鍊，所幸有眾人的支持和鼓勵，讓我能夠將論文順利地完成。在碩士班的兩年中，我學到的不只是能實用於課堂教學的技巧及研究的方法，更重要的還有團隊合作、努力不懈的精神。首先最感謝的是我的指導教授陳明璋老師，老師在忙碌之餘，每周一定會跟我們進行研究討論，並且用他最敏銳的感官與專業的判斷，不厭其煩的指導我們將教材修改到盡善盡美，尤其在口試這個最後關頭，經過老師的指點我才能將複雜的研究結論做出完整的歸納。另外，每當我因為忙於工作、課業及結婚大事而感到挫折時，老師總是給予我溫暖的鼓勵，讓我有勇氣再面對這些人生的課題，真的很感謝老師的提攜與包容，著實讓我成長許多。另外，要特別感謝袁媛教授、譚寧君教授及盧鴻興教授在百忙之中撥空擔任我的口試委員，並提出精闢的見解與寶貴的建議，使得本研究能更加嚴謹，在此致上我最誠摯的謝意。感謝研究室中一同奮鬥的夥伴忠韻、嘉惠、勃毅、志青、怡君、于芳及純慧，讓我在研究的過程中感到不孤單，感謝你們無私的分享，讓我能順利的完成這份研究，也讓我重溫學生時期那種單純美好的快樂。此外，還要深深感謝我的上司吳惠濱校長，因為您的信任、體諒及鼓勵，讓我得以在兩年內完成碩士論文，還有我工作上最重要夥伴怡萱、彥蓉、步剛及元平，在我分身乏術之際給予我最大的幫助，讓我放心的完成學業。最後，要感謝長久以來一直支持我雙親及家人，總是給予我莫大的勇氣面對一切、感謝體貼陪我熬夜寫論文的丈夫宗德及幫我誠心祈求能順利畢業的外公、外婆及公公、婆婆，衷心的感恩眾人的協助讓我能順利完成學業，謝謝你們！

(6)

目

次

中文摘要中文摘要中文摘要中文摘要 ... IIII ABSTRACT ABSTRACT ABSTRACT ABSTRACT ... IIIIIIII 目目目目次次次次 ... IVIVIVIV 表表表

表次次次次 ...VIII...VIIIVIIIVIII 圖

圖圖

圖次次次次 ... ... XIIXIIXIIXII 1 1 1 1、、、、緒論緒論緒論緒論 ... . 1111 1.1 研究動機 ... 1 1.2 研究目的 ... 3 1.3 研究問題 ... 3 1.4 研究範圍 ... 4 1.5 研究限制 ... 4 2 2 2 2、、、、文獻探討文獻探討文獻探討文獻探討 ... ... 5555 2.1 二元一次聯立方程式的文字題 ... 5 2.1.1 迷思概念 ... 5 2.1.2 二元一次聯立方程式文字題列式常見之錯誤形式 ... 5 2.1.3 二元一次方程式解題歷程 ... 7 2.2 多媒體學習理論 ... 8 2.2.1 多媒體學習的定義 ... 8 2.2.2 訊息處理的過程 ... 8 2.2.3 多媒體學習理論的三大基本假設 ... 9 2.2.4 多媒體學習理論教學設計原則 ... 10 2.3 代數教材設計原則 ... 14 2.3.1 教學內容結構化 ... 15 2.3.2 教材呈現區塊化 ... 16 2.3.3 建立訊息關聯 ... 16 2.3.4 口語簡化解說 ... 17

(7)

2.4 多元表徵 ... 17 2.4.1 表徵的意義 ... 18 2.4.2 表徵的分類 ... 18 2.5 認知負荷理論 ... 20 2.5.1 認知負荷的意義 ... 20 2.5.2 認知負荷的基本假定 ... 20 2.5.3 認知負荷的類型 ... 22 2.5.4 認知負荷教學設計原則 ... 23 3 3 3 3、、、研究方法、研究方法研究方法研究方法 ... ... 27272727 3.1 研究流程 ... 27 3.1.1 準備階段 ... 28 3.1.2 實驗階段 ... 28 3.1.3 分析階段 ... 28 3.2 研究設計 ... 28 3.2.1 實驗流程 ... 29 3.2.2 研究變項與假設 ... 29 3.3 研究對象 ... 31 3.3.1 整體學生立足點一致 ... 31 3.3.2 各組未學過學生與各組已學過學生立足點一致 ... 34 3.3.3 各組不同學習成就之學生立足點一致 ... 38 3.4 研究工具 ... 46 3.4.1 實驗教材修改與製作 ... 46 3.4.2 學習成就測驗 ... 54 3.4.3 認知負荷量表 ... 55 3.5 資料分析方法 ... 57 3.5.1 ANOVA ... 57 3.5.2 Effect Size ... 58 3.5.3 學習效率（Instructional Efficiency） ... 59

3.5.4 投入分數（Instructional Involvement Score） ... 60

3.5.5 綜合學習效率與投入分數 ... 61

(8)

4 4 4 4、、、、研究結果與發現研究結果與發現研究結果與發現研究結果與發現 ... ... 63636363 4.1 不同表徵模式教材對學生學習成就表現之影響 ... 63 4.1.1 在整體學生階段學習成效方面 ... 63 4.1.2 在未先學過學生其階段學習成效方面 ... 66 4.1.3 在已先學過學生其階段學習成效方面 ... 69 4.1.4 在低數學學習成就學生其階段學習成效方面 ... 71 4.1.5 在中數學學習成就學生其階段學習成效方面 ... 74 4.1.6 在高數學學習成就學生其階段學習成效方面 ... 77 4.2 不同表徵模式之教材對學生認知負荷之影響 ... 79 4.2.1 在整體學生的認知負荷方面 ... 79 4.2.2 在未先學過學生其認知負荷方面 ... 89 4.2.3 在已先學過學生其認知負荷方面 ... 97 4.2.4 在低數學學習成就學生其認知負荷方面 ... 104 4.2.5 在中數學學習成就學生其認知負荷方面 ... 111 4.2.6 在高數學學習成就學生其認知負荷方面 ... 118 4.3 經不同表徵模式教材教學之學生其後測成績與認知負荷相關性分析 ... 125 4.3.1 串流式教材組 ... 126 4.3.2 代數教材設計原則組 ... 128 4.3.3 動態圖像表徵組 ... 130 4.3.4 代數教材設計原則輔以動態圖像表徵組 ... 132 4.4 學習成就與認知負荷暨專業知識反轉效應分析 ... 134 4.4.1 對整體學生而言 ... 135 4.4.2 對未學過與已學過學生而言 ... 136 4.4.3 對不同學習成就之學生而言 ... 138 4.5 研究結果與分析 ... 140 4.5.1 綜合學習成就表現及認知負荷 ... 140 4.5.2 學習成就表現及認知負荷相關性統整 ... 143 5 5 5 5、、、、結論與建議結論與建議結論與建議結論與建議 ... 146146146146 5.1 研究結論 ... 146 5.2 檢討與建議 ... 147 5.2.1 對於教學之建議 ... 147

(9)

5.2.2 對於未來研究之建議 ... 148 參考文獻參考文獻參考文獻參考文獻 ... 150150150150 英文文獻 ... 150 中文文獻 ... 152 附錄一附錄一附錄一附錄一：：：實驗教材：實驗教材實驗教材實驗教材 ... ... 153153153153 附錄二附錄二附錄二附錄二：：：前測題目：前測題目前測題目前測題目 ... ... 158158158158 附錄三附錄三附錄三附錄三：：：後測題目：後測題目後測題目後測題目 ... ... 159159159159 附錄四附錄四附錄四附錄四：：：：認知負荷問卷認知負荷問卷認知負荷問卷認知負荷問卷 ... 160160160160

(10)

表

次

表 1 教學實驗總流程表教學實驗總流程表 ... 29 教學實驗總流程表教學實驗總流程表表 2 分組教材設計內容摘要表分組教材設計內容摘要表 ... 29 分組教材設計內容摘要表分組教材設計內容摘要表表 3 受試學生上學期三次定期評量總成績平均及標準差摘要表受試學生上學期三次定期評量總成績平均及標準差摘要表 ... 32 受試學生上學期三次定期評量總成績平均及標準差摘要表受試學生上學期三次定期評量總成績平均及標準差摘要表表 4 受試學生上學期三次定期評量總成績變異數同質性檢定受試學生上學期三次定期評量總成績變異數同質性檢定 ... 32 受試學生上學期三次定期評量總成績變異數同質性檢定受試學生上學期三次定期評量總成績變異數同質性檢定表 5 受試學生上學期三次定期評量總成績變異數分析摘要表受試學生上學期三次定期評量總成績變異數分析摘要表 ... 32 受試學生上學期三次定期評量總成績變異數分析摘要表受試學生上學期三次定期評量總成績變異數分析摘要表表 6 受試學生前測成績平均及標準差摘要表受試學生前測成績平均及標準差摘要表 ... 33 受試學生前測成績平均及標準差摘要表受試學生前測成績平均及標準差摘要表表 7 受試學生前測成績變異數同質性檢定受試學生前測成績變異數同質性檢定 ... 33 受試學生前測成績變異數同質性檢定受試學生前測成績變異數同質性檢定表 8 受試學生前測成績變異數分析摘要表受試學生前測成績變異數分析摘要表 ... 33 受試學生前測成績變異數分析摘要表受試學生前測成績變異數分析摘要表表 9 未學過之受試學生定期評量總未學過之受試學生定期評量總成績平均及標準差摘要表未學過之受試學生定期評量總未學過之受試學生定期評量總成績平均及標準差摘要表成績平均及標準差摘要表 ... 34 成績平均及標準差摘要表表 10 未學過之受試學生定期評量總成績變異數同質性檢定未學過之受試學生定期評量總成績變異數同質性檢定 ... 34 未學過之受試學生定期評量總成績變異數同質性檢定未學過之受試學生定期評量總成績變異數同質性檢定表 11 未學過之受試學生定期評量總成績變異數分析摘要表未學過之受試學生定期評量總成績變異數分析摘要表 ... 35 未學過之受試學生定期評量總成績變異數分析摘要表未學過之受試學生定期評量總成績變異數分析摘要表表 12 未學過之受試學生前測成績平均及標準差摘要表未學過之受試學生前測成績平均及標準差摘要表 ... 35 未學過之受試學生前測成績平均及標準差摘要表未學過之受試學生前測成績平均及標準差摘要表表 13 未學過之受試學生前測成績變異數同質性檢定未學過之受試學生前測成績變異數同質性檢定 ... 35 未學過之受試學生前測成績變異數同質性檢定未學過之受試學生前測成績變異數同質性檢定表 14 未學過之受試學生前測成績變異數分析摘要表未學過之受試學生前測成績變異數分析摘要表 ... 36 未學過之受試學生前測成績變異數分析摘要表未學過之受試學生前測成績變異數分析摘要表表 15 已學過之受試學生定期評量總成績平均及標準差摘要表已學過之受試學生定期評量總成績平均及標準差摘要表 ... 36 已學過之受試學生定期評量總成績平均及標準差摘要表已學過之受試學生定期評量總成績平均及標準差摘要表表 16 已學過之受試學生定期評量總成績變異數同質性檢定已學過之受試學生定期評量總成績變異數同質性檢定 ... 37 已學過之受試學生定期評量總成績變異數同質性檢定已學過之受試學生定期評量總成績變異數同質性檢定表 17 已學過之受試學生定期評量總成績變異數分析摘要表已學過之受試學生定期評量總成績變異數分析摘要表 ... 37 已學過之受試學生定期評量總成績變異數分析摘要表已學過之受試學生定期評量總成績變異數分析摘要表表 18 已學過之受試學生前測成績平均及標準差摘要表已學過之受試學生前測成績平均及標準差摘要表 ... 37 已學過之受試學生前測成績平均及標準差摘要表已學過之受試學生前測成績平均及標準差摘要表表 19 已學過之受試學生前測成績變異數同質性檢定已學過之受試學生前測成績變異數同質性檢定 ... 38 已學過之受試學生前測成績變異數同質性檢定已學過之受試學生前測成績變異數同質性檢定表 20 已學過之受試學生前測成績變異數分析摘要表已學過之受試學生前測成績變異數分析摘要表 ... 38 已學過之受試學生前測成績變異數分析摘要表已學過之受試學生前測成績變異數分析摘要表表 21 低學習成就之受試學生上學期定期評量總成績平均及標準差摘要表低學習成就之受試學生上學期定期評量總成績平均及標準差摘要表 ... 39 低學習成就之受試學生上學期定期評量總成績平均及標準差摘要表低學習成就之受試學生上學期定期評量總成績平均及標準差摘要表表 22 低學習成就之受試學生定期評量總成績變異數同質性檢定低學習成就之受試學生定期評量總成績變異數同質性檢定 ... 39 低學習成就之受試學生定期評量總成績變異數同質性檢定低學習成就之受試學生定期評量總成績變異數同質性檢定表 23 低學習成就之受試學生上學期定期評量總成績變異數分析摘要表低學習成就之受試學生上學期定期評量總成績變異數分析摘要表 ... 39 低學習成就之受試學生上學期定期評量總成績變異數分析摘要表低學習成就之受試學生上學期定期評量總成績變異數分析摘要表表 24 低學習成就之受試學生前測成績平均及標準差摘要表低學習成就之受試學生前測成績平均及標準差摘要表 ... 40 低學習成就之受試學生前測成績平均及標準差摘要表低學習成就之受試學生前測成績平均及標準差摘要表表 25 低學習成就之受試學生前測成績變異數同質性檢定低學習成就之受試學生前測成績變異數同質性檢定 ... 40 低學習成就之受試學生前測成績變異數同質性檢定低學習成就之受試學生前測成績變異數同質性檢定表 26 低學低學習成就之受試學生前測成績變異數分析摘要表低學低學習成就之受試學生前測成績變異數分析摘要表習成就之受試學生前測成績變異數分析摘要表 ... 41 習成就之受試學生前測成績變異數分析摘要表表 27 中學習成就之受試學生上學期定期評量總成績平均及標準差摘要表中學習成就之受試學生上學期定期評量總成績平均及標準差摘要表 ... 41 中學習成就之受試學生上學期定期評量總成績平均及標準差摘要表中學習成就之受試學生上學期定期評量總成績平均及標準差摘要表表 28 中學習成就之受試學生定期評量總成績變異數同質性檢定中學習成就之受試學生定期評量總成績變異數同質性檢定 ... 41 中學習成就之受試學生定期評量總成績變異數同質性檢定中學習成就之受試學生定期評量總成績變異數同質性檢定表 29 中學習成就之受試學生上學期定期評量總成績變異數分析摘要表中學習成就之受試學生上學期定期評量總成績變異數分析摘要表 ... 42 中學習成就之受試學生上學期定期評量總成績變異數分析摘要表中學習成就之受試學生上學期定期評量總成績變異數分析摘要表

(11)

表 30 中學中學習成就之受試學生前測成績平均及標準差摘要表中學中學習成就之受試學生前測成績平均及標準差摘要表習成就之受試學生前測成績平均及標準差摘要表 ... 42 習成就之受試學生前測成績平均及標準差摘要表表 31 中學習成就之受試學生前測成績變異數同質性檢定中學習成就之受試學生前測成績變異數同質性檢定 ... 42 中學習成就之受試學生前測成績變異數同質性檢定中學習成就之受試學生前測成績變異數同質性檢定表 32 中學習成就之受試學生前測成績變異數分析摘要表中學習成就之受試學生前測成績變異數分析摘要表 ... 43 中學習成就之受試學生前測成績變異數分析摘要表中學習成就之受試學生前測成績變異數分析摘要表表 33 高學習成就之受試學生上學期定期評量總成績平均及標準差摘要表高學習成就之受試學生上學期定期評量總成績平均及標準差摘要表 ... 43 高學習成就之受試學生上學期定期評量總成績平均及標準差摘要表高學習成就之受試學生上學期定期評量總成績平均及標準差摘要表表 34 高學習成就之受試學生高學習成就之受試學生定期評量總成績變異數同質性檢定高學習成就之受試學生高學習成就之受試學生定期評量總成績變異數同質性檢定定期評量總成績變異數同質性檢定 ... 43 定期評量總成績變異數同質性檢定表 35 高學習成就之受試學生上學期定期評量總成績變異數分析摘要表高學習成就之受試學生上學期定期評量總成績變異數分析摘要表 ... 44 高學習成就之受試學生上學期定期評量總成績變異數分析摘要表高學習成就之受試學生上學期定期評量總成績變異數分析摘要表表 36 高學習成就之受試學生前測成績平均及標準差摘要表高學習成就之受試學生前測成績平均及標準差摘要表 ... 44 高學習成就之受試學生前測成績平均及標準差摘要表高學習成就之受試學生前測成績平均及標準差摘要表表 37 高學習成就之受試學生前測成績變異數同質性檢定高學習成就之受試學生前測成績變異數同質性檢定 ... 45 高學習成就之受試學生前測成績變異數同質性檢定高學習成就之受試學生前測成績變異數同質性檢定表 38 高學習成就之受試學生前測成績變異高學習成就之受試學生前測成績變異數分析摘要表高學習成就之受試學生前測成績變異高學習成就之受試學生前測成績變異數分析摘要表數分析摘要表 ... 45 數分析摘要表表 39 實驗組實驗組 1實驗組實驗組111 教材原始頁和修正頁一覽表教材原始頁和修正頁一覽表教材原始頁和修正頁一覽表 ... 47 教材原始頁和修正頁一覽表表 40 實驗組實驗組 3實驗組實驗組333 教材原始頁和修正頁一覽表教材原始頁和修正頁一覽表教材原始頁和修正頁一覽表 ... 50 教材原始頁和修正頁一覽表表 41 試題之試題之可靠性統計量試題之試題之可靠性統計量可靠性統計量 ... 54 可靠性統計量表 42 學習成就測驗卷各題之難度學習成就測驗卷各題之難度 ... 55 學習成就測驗卷各題之難度學習成就測驗卷各題之難度表 43 學習成就測驗卷學習成就測驗卷中各題之鑑別度學習成就測驗卷學習成就測驗卷中各題之鑑別度中各題之鑑別度 ... 55 中各題之鑑別度表 44 認知負荷量表題目及說明認知負荷量表題目及說明 ... 56 認知負荷量表題目及說明認知負荷量表題目及說明表 45 相關係數的強度大小與意義相關係數的強度大小與意義 ... 62 相關係數的強度大小與意義相關係數的強度大小與意義表 46 全體受測學生後測成績平均及標準差摘要表全體受測學生後測成績平均及標準差摘要表 ... 64 全體受測學生後測成績平均及標準差摘要表全體受測學生後測成績平均及標準差摘要表表 47 全體全體受測學生後測成績變異數同質性檢定全體全體受測學生後測成績變異數同質性檢定受測學生後測成績變異數同質性檢定 ... 64 受測學生後測成績變異數同質性檢定表 48 全體全體受測學生後測成績變異數分析摘要表全體全體受測學生後測成績變異數分析摘要表受測學生後測成績變異數分析摘要表 ... 64 受測學生後測成績變異數分析摘要表表 49 全體受測學生後測成績多重比較表全體受測學生後測成績多重比較表-全體受測學生後測成績多重比較表全體受測學生後測成績多重比較表--- GGGGAMESAMESAMESAMES--H--HHHOWELLOWELLOWELLOWELL法法法法 ... 65

表 50 各組中未先學過之學生後測成績平均及標準差摘要表各組中未先學過之學生後測成績平均及標準差摘要表 ... 66 各組中未先學過之學生後測成績平均及標準差摘要表各組中未先學過之學生後測成績平均及標準差摘要表表 51 各組中未先學過之學生後測成績變異數同質性檢定各組中未先學過之學生後測成績變異數同質性檢定 ... 67 各組中未先學過之學生後測成績變異數同質性檢定各組中未先學過之學生後測成績變異數同質性檢定表 52 各組中未先學過之學生各組中未先學過之學生後測成績變異數分析摘要表各組中未先學過之學生各組中未先學過之學生後測成績變異數分析摘要表後測成績變異數分析摘要表 ... 67 後測成績變異數分析摘要表表 53 各組中未先學過之學生後測成績多重比較表各組中未先學過之學生後測成績多重比較表-各組中未先學過之學生後測成績多重比較表各組中未先學過之學生後測成績多重比較表--G-GGGAMESAMESAMESAMES-H---HHHOWELLOWELLOWELLOWELL法法法法 ... 68

表 54 各組中已學過之學生後測成績各組中已學過之學生後測成績平均及標準差摘要表各組中已學過之學生後測成績各組中已學過之學生後測成績平均及標準差摘要表平均及標準差摘要表 ... 69 平均及標準差摘要表表 55 各組中已學過之學生後測成績變異數同質性檢定各組中已學過之學生後測成績變異數同質性檢定 ... 70 各組中已學過之學生後測成績變異數同質性檢定各組中已學過之學生後測成績變異數同質性檢定表 56 各組中已學過之學生後測成績變異數各組中已學過之學生後測成績變異數分析摘要表各組中已學過之學生後測成績變異數各組中已學過之學生後測成績變異數分析摘要表分析摘要表 ... 70 分析摘要表表 57 各組各組低數學學習成就各組各組低數學學習成就低數學學習成就學生後測成績低數學學習成就學生後測成績學生後測成績平均及標準差摘要表學生後測成績平均及標準差摘要表平均及標準差摘要表 ... 71 平均及標準差摘要表表 58 各組各組低數學學習成就各組各組低數學學習成就低數學學習成就學生後測成績變異數同質性檢定低數學學習成就學生後測成績變異數同質性檢定學生後測成績變異數同質性檢定 ... 72 學生後測成績變異數同質性檢定表 59 各組各組低數學學習成就各組各組低數學學習成就低數學學習成就學生後測成績變異數分析摘要表低數學學習成就學生後測成績變異數分析摘要表學生後測成績變異數分析摘要表 ... 72 學生後測成績變異數分析摘要表表 60 各組低數學學習成就各組各組各組低數學學習成就低數學學習成就學生低數學學習成就學生學生後測成績多重比較表學生後測成績多重比較表後測成績多重比較表-後測成績多重比較表--T-TTTUKEY UKEY UKEY UKEY HSHSDHSHSDD 法D法法法 ... 72

(12)

表 61 各組中各組中數學學習成就各組中各組中數學學習成就數學學習成就學生後測成績數學學習成就學生後測成績學生後測成績平均及標準差摘要表學生後測成績平均及標準差摘要表平均及標準差摘要表 ... 74 平均及標準差摘要表表 62 各組中各組中數學學習成就各組中各組中數學學習成就數學學習成就學生後測成績變異數同質性檢定數學學習成就學生後測成績變異數同質性檢定學生後測成績變異數同質性檢定 ... 75 學生後測成績變異數同質性檢定表 63 各組中各組中數學學習成就各組中各組中數學學習成就數學學習成就學生後測成績變異數分析摘要表數學學習成就學生後測成績變異數分析摘要表學生後測成績變異數分析摘要表 ... 75 學生後測成績變異數分析摘要表表 64 各組中各組各組各組中中數學學習成就中數學學習成就數學學習成就學生數學學習成就學生學生後測成績多重比較表學生後測成績多重比較表後測成績多重比較表-後測成績多重比較表-T--TTTUKEY UKEY UKEY UKEY HSDHSD 法HSDHSD法法法 ... 76

表 65 各組高各組高數學學習成就各組高各組高數學學習成就數學學習成就學生後測成績數學學習成就學生後測成績學生後測成績平均及標準差摘要表學生後測成績平均及標準差摘要表平均及標準差摘要表 ... 78 平均及標準差摘要表表 66 各組高各組高數學學習成就各組高各組高數學學習成就數學學習成就學生後測成績變異數同質性檢定數學學習成就學生後測成績變異數同質性檢定學生後測成績變異數同質性檢定 ... 78 學生後測成績變異數同質性檢定表 67 各組高各組高數學學習成就各組高各組高數學學習成就數學學習成就學生後測成績變異數分析摘要表數學學習成就學生後測成績變異數分析摘要表學生後測成績變異數分析摘要表 ... 78 學生後測成績變異數分析摘要表表 68 整體受測學生認知負荷量平均數及標準差摘要表整體受測學生認知負荷量平均數及標準差摘要表 ... 80 整體受測學生認知負荷量平均數及標準差摘要表整體受測學生認知負荷量平均數及標準差摘要表表 69 整體受測學生認知負荷量變異數同質性檢定整體受測學生認知負荷量變異數同質性檢定 ... 82 整體受測學生認知負荷量變異數同質性檢定整體受測學生認知負荷量變異數同質性檢定表 70 整體受測學生認知負荷量整體受測學生認知負荷量變異數分析摘要表整體受測學生認知負荷量整體受測學生認知負荷量變異數分析摘要表變異數分析摘要表 ... 83 變異數分析摘要表表 71 整體受測學生認知負荷量多重比較表整體受測學生認知負荷量多重比較表-整體受測學生認知負荷量多重比較表整體受測學生認知負荷量多重比較表--- TTTTUKEY UKEY UKEY UKEY HSDHSDHSDHSD 法法法法 ... 84

表 72 未先學過之學生認知負荷量平均數及標準差摘要表未先學過之學生認知負荷量平均數及標準差摘要表 ... 90 未先學過之學生認知負荷量平均數及標準差摘要表未先學過之學生認知負荷量平均數及標準差摘要表表 73 未學過之學生認知負荷量變異數同質性檢定未學過之學生認知負荷量變異數同質性檢定 ... 92 未學過之學生認知負荷量變異數同質性檢定未學過之學生認知負荷量變異數同質性檢定表 74 未先學過之學生認知負荷量未先學過之學生認知負荷量變異數分析摘要表未先學過之學生認知負荷量未先學過之學生認知負荷量變異數分析摘要表變異數分析摘要表 ... 93 變異數分析摘要表表 75 未先學過之學生未先學過之學生認知負荷量多重比較表未先學過之學生未先學過之學生認知負荷量多重比較表認知負荷量多重比較表-認知負荷量多重比較表--T-TTTUKEY UKEY UKEY UKEY HSDHSD 法HSDHSD法法法 ... 94

表 76 未先學過之學生未先學過之學生認知負荷量多重比較表未先學過之學生未先學過之學生認知負荷量多重比較表認知負荷量多重比較表-認知負荷量多重比較表--G-GGGAMESAMESAMESAMES--H--HHHOWELLOWELLOWELLOWELL法法法法 ... 96

表 77 已先學過之學生認知負荷量平均數及標準差摘要表已先學過之學生認知負荷量平均數及標準差摘要表 ... 98 已先學過之學生認知負荷量平均數及標準差摘要表已先學過之學生認知負荷量平均數及標準差摘要表表 78 已先學過之學生認知負荷量變異數同質性檢定已先學過之學生認知負荷量變異數同質性檢定 ... 100 已先學過之學生認知負荷量變異數同質性檢定已先學過之學生認知負荷量變異數同質性檢定表 79 已先學過之學生認知負荷量變異數分析摘要表已先學過之學生認知負荷量變異數分析摘要表 ... 101 已先學過之學生認知負荷量變異數分析摘要表已先學過之學生認知負荷量變異數分析摘要表表 80 已先學過之學生已先學過之學生認知負荷量多重比較表已先學過之學生已先學過之學生認知負荷量多重比較表認知負荷量多重比較表-認知負荷量多重比較表--T-TTTUKEY UKEY UKEY UKEY HSDHSD 法HSDHSD法法法 ... 102

表 81 各組各組各組各組低數學學習成低數學學習成低數學學習成低數學學習成就就就就學生認知負荷量平均數及標準差摘要表學生認知負荷量平均數及標準差摘要表學生認知負荷量平均數及標準差摘要表學生認知負荷量平均數及標準差摘要表 ... 105 表 82 各組低數學學習成就各組低數學學習成就學生認知負荷量變異數同質性檢定各組低數學學習成就各組低數學學習成就學生認知負荷量變異數同質性檢定學生認知負荷量變異數同質性檢定 ... 107 學生認知負荷量變異數同質性檢定表 83 各組低數學學習成就各組低數學學習成就學生認知負荷量變異數分析摘要表各組低數學學習成就各組低數學學習成就學生認知負荷量變異數分析摘要表學生認知負荷量變異數分析摘要表 ... 108 學生認知負荷量變異數分析摘要表表 84 各組低數學學習成就各組低數學學習成就學生各組低數學學習成就各組低數學學習成就學生學生認知負荷量多重比較表學生認知負荷量多重比較表認知負荷量多重比較表-認知負荷量多重比較表---TTTTUKEY UKEY UKEY UKEY HSDHSD 法HSDHSD法法法 ... 109

表 85 各組各組低數學學習成就各組各組低數學學習成就低數學學習成就學生低數學學習成就學生認知負荷量多重比較表學生學生認知負荷量多重比較表認知負荷量多重比較表-認知負荷量多重比較表---GGGGAMESAMESAMESAMES--H--HHHOWELLOWELLOWELLOWELL法法法法 ... 110

表 86 各組中數學學習成就各組中數學學習成就學生認知負荷量平均數及標準差摘要表各組中數學學習成就各組中數學學習成就學生認知負荷量平均數及標準差摘要表學生認知負荷量平均數及標準差摘要表 ... 112 學生認知負荷量平均數及標準差摘要表表 87 各組中數學學習成就各組中數學學習成就學生認知負荷量變異數同質性檢定各組中數學學習成就各組中數學學習成就學生認知負荷量變異數同質性檢定學生認知負荷量變異數同質性檢定 ... 114 學生認知負荷量變異數同質性檢定表 88 各組中數學學習成就各組中數學學習成就學生認知負荷量變異數分析摘要表各組中數學學習成就各組中數學學習成就學生認知負荷量變異數分析摘要表學生認知負荷量變異數分析摘要表 ... 115 學生認知負荷量變異數分析摘要表表 89 各組中數學學習成就各組中數學學習成就學生各組中數學學習成就各組中數學學習成就學生學生認知負荷量多重比較表學生認知負荷量多重比較表認知負荷量多重比較表-認知負荷量多重比較表---TTTTUKEY UKEY UKEY UKEY HSDHSD 法HSDHSD法法法 ... 116

表 90 各組高數學學習成就各組高數學學習成就學生認知負荷量平均數及標準差摘要表各組高數學學習成就各組高數學學習成就學生認知負荷量平均數及標準差摘要表學生認知負荷量平均數及標準差摘要表 ... 118 學生認知負荷量平均數及標準差摘要表表 91 各組高數學學習成就各組高數學學習成就學生認知負荷量變異數同質性檢定各組高數學學習成就各組高數學學習成就學生認知負荷量變異數同質性檢定學生認知負荷量變異數同質性檢定 ... 120 學生認知負荷量變異數同質性檢定

(13)

表 92 各組高數學學習成就各組高數學學習成就學生認知負荷量變異數分析摘要表各組高數學學習成就各組高數學學習成就學生認知負荷量變異數分析摘要表學生認知負荷量變異數分析摘要表 ... 121 學生認知負荷量變異數分析摘要表表 93 各組高數學學習成就各組高數學學習成就學生認知負荷量各組高數學學習成就各組高數學學習成就學生認知負荷量學生認知負荷量多重比較表學生認知負荷量多重比較表多重比較表-多重比較表---TTTTUKEY UKEY UKEY UKEY HSDHSD 法HSDHSD法法法 ... 123

表 94 串流式教材組後測成績與認知負荷各題項的相關矩陣表串流式教材組後測成績與認知負荷各題項的相關矩陣表 ... 126 串流式教材組後測成績與認知負荷各題項的相關矩陣表串流式教材組後測成績與認知負荷各題項的相關矩陣表表 95 代數教材設計原則組後測成績與認知負荷各題項的相關矩陣表代數教材設計原則組後測成績與認知負荷各題項的相關矩陣表 ... 128 代數教材設計原則組後測成績與認知負荷各題項的相關矩陣表代數教材設計原則組後測成績與認知負荷各題項的相關矩陣表表 96 動態圖像表徵組後測成績與認知負荷各題項的相關矩陣表動態圖像表徵組後測成績與認知負荷各題項的相關矩陣表 ... 130 動態圖像表徵組後測成績與認知負荷各題項的相關矩陣表動態圖像表徵組後測成績與認知負荷各題項的相關矩陣表表 97 代數教材設計原則輔以動態圖像表徵組後測成績與認知負荷各題項的相關矩陣表代數教材設計原則輔以動態圖像表徵組後測成績與認知負荷各題項的相關矩陣表代數教材設計原則輔以動態圖像表徵組後測成績與認知負荷各題項的相關矩陣表代數教材設計原則輔以動態圖像表徵組後測成績與認知負荷各題項的相關矩陣表 ... 132 表 98 整體學生學習效率與投入分數數值整體學生學習效率與投入分數數值 ... 135 整體學生學習效率與投入分數數值整體學生學習效率與投入分數數值表 99 未學過及已學過學生學習效率與投入分數數值未學過及已學過學生學習效率與投入分數數值 ... 137 未學過及已學過學生學習效率與投入分數數值未學過及已學過學生學習效率與投入分數數值表 100 不同學習成就學生學習效率與投入分數數值不同學習成就學生學習效率與投入分數數值 ... 138 不同學習成就學生學習效率與投入分數數值不同學習成就學生學習效率與投入分數數值表 101 階段學習成就及認知負荷研究結果摘要表階段學習成就及認知負荷研究結果摘要表 ... 140 階段學習成就及認知負荷研究結果摘要表階段學習成就及認知負荷研究結果摘要表表 102 學習成就表現及認知負荷相關性分析表學習成就表現及認知負荷相關性分析表 ... 143 學習成就表現及認知負荷相關性分析表學習成就表現及認知負荷相關性分析表

(14)

圖

次

圖 1 多媒體學習認知模型 ... 9 圖 2 實驗組 3 教材，符合多媒體原則 ... 11 圖 3 實驗組 3 教材，符合空間接近原則 ... 11 圖 4 對照組教材，未符合分割原則 ... 13 圖 5 實驗組 3 教材，符合分割原則 ... 13 圖 6 實驗組 3 教材，符合信號原則 ... 14 圖 7 對照組教材，未具教學內容結構化 ... 15 圖 8 實驗組 1 教材，教學內容結構化 ... 15 圖 9 實驗組 3 教材，教學內容結構化 ... 16 圖 10 實驗組 3 教材，建立訊息關聯 ... 17 圖 11 研究實施步驟流程圖 ... 27 圖 12 變異數分析流程圖 ... 58 圖 13 學習效率圖 ... 59 圖 14 教學投入分數圖 ... 60 圖 15 學習效率與學習投入分數圖 ... 61 圖 16 學習效率與投入分數圖（整體） ... 136 圖 17 學習效率與投入分數圖（未學過與已學過學生） ... 137 圖 18 學習效率與投入分數圖（不同學習成就學生） ... 139

(15)

1、

、

、緒論

緒論

本章共分五節，主要說明本研究之研究動機與背景、研究目的、研究問題、研究範圍與研究限制。

1.1 研究動機

研究動機

有一句話是這麼說的：「自然為科學之父，數學為科學之母」。數學是自然科學與社會科學的共同基礎，聯合國教科文組織也將數學列為終身學習的基礎。透過數學的訓練，可以培養一個人具備敏捷的思考能力，並且擁有縝密的邏輯推理能力，當遇到問題時，往往能迅速冷靜判斷、當機立斷，採行最佳的策略以解決問題。然而，如此重要的一門知識，卻讓許多國中生感到十分頭痛，因此也間接成為補習街中最熱門的科目。探究其原因，往往是因為教材內容複雜，學生無法理解教師授課內容，導致數學學習成就低落，進而影響其學習興趣並失去自信，於是數學變成學生壓力的來源，缺乏正向的學習態度，最終形成惡性循環，數學學習成就日益低落，數學便成了令學生望之卻步的一門科目。邱俊仁 (200 3)調查高雄地區國一學生的數學焦慮感，發現數學焦慮對學生的學習成就與學習態度確實有負面的影響，特別是低成就而且有數學焦慮的學生，他們經常在學習時遭遇困難，有很大的挫折感，一旦知道有數學科的考試就會顯得很緊張，不僅排斥上課，甚至想要放棄數學。研究者身為國中教師，「希望能在這群孩子最需要的時候，適時伸出援手，拉他一把」是當初選擇教師這個職業作為志業的原因，然而同時身為數學教師的我，也總是以「讓孩子能在快樂中有效學習數學」作為教學的座右銘，因此希望能夠透過此研究，營造一個低壓力的學習情境，並設計一套使學生更易於理解的教材，讓國中生在學習數學時能感到輕鬆愉快，避免落入數學學習不利的惡性循環之中。社會變遷迅速，雖然時下許多教師都正朝著網路教學之路邁進，然而，研究者認為傳統教學法亦不可拋棄，傳統教學法讓師生能夠面對面做直接的溝通，教師能在第一時間掌握學生的學習狀況，並加以調整教學方式及步調。因此，研究者認為要達到「讓孩子能在快樂中有效學習數學」之理念，必須以傳統教學方式為精神，輔以資訊科技融入教學，改善教材設計，

(16)

提升學生學習興趣、降低學習壓力，同時也降低教師準備教材之難度。一堂成功的課除須包含教師生動的口語表達、肢體語言表達、良好的教室管理外，一套優良的教材更是其中不可或缺的元素。數學文字題的特點是用語文的型態來敘述數學情境問題，且常以日常生活事件為題材，因此比一般的計算涉及更多的認知歷程 (張景媛 , 1994)。在許多研究中發現，能否成功解決文字題，語意結構關係的理解是一個重要因素，許多學生解文字題失敗的原因，乃因沒能仔細思考題目的意義，看到數字就急著要直接進行運算 (古明峰 , 1997)，然而造成學生沒能仔細思考題目的原因除了該題語意較複雜外，也可能是因為教材編排方式不佳所致，因此本研究希望透過實驗設計，了解運用不同表徵模式設計之教材授課對於學生解文字題之幫助，建造一個使教師、學生、教材三者可以互相溝通的環境，製作一套能使學生專注且享受於學習的教材，以降低學生之認知負荷量，進而促進有效解題。根據葉子榕 (20 10)之研究，將代數教材設計原則結合動態圖像表徵呈現運用在教學設計上，對需進行補救教學的學生授課其學習成效表現顯著優於將代數教材設計原則運用於教學設計上。然而該研究僅針對低學業成就之學生進行實驗，而現今教育環境為常態編班，各個班級中的學生程度差異頗大，因此本研究將以常態編班下的學生為樣本進行施測，以了解將不同表徵模式之教材運用於常態編班下之影響；另，葉子榕 (2010)之研究除了對照組為「串流式教學」組外，僅將實驗分為「代數教材設計原則組」及「代數教材設計原則結合動態圖像表徵」組，然而本研究為確實了解「代數教材設計原則結合動態圖像表徵組」之學習成效表現較佳之主要因素為「代數教材設計」或「動態圖像表徵」，故本研究將加入「未具代數教材設計原則之動態圖像表徵」一組來了解真正影響學習成效之主要原因。此外，依據葉子榕 (2010)之建議，將後測試題由 5 題增加為 10 題，以提升施測結果的精確度。有鑑於以上種種因素，本研究將針對七年級「二元一次方程式聯立方程式文字題列式」之單元為教材內容，以激發式動態呈現方式，設計一套具備良好溝通性之教材，以有效協助教師引導學生進行學習，期能達成「在快樂中有效學習數學」之目標。

(17)

1.2 研究目的

研究目的

基於上述研究動機，本研究擬達成以下目的： (一 )分別探討以「串流式教材」、「代數教材設計原則」、「動態圖像表徵」及「代數教材設計原則輔以動態圖像表徵」所設計之教材運用於常態編班教學下，對學生的學習成就表現之影響。 (二 )分別探討以「串流式教材」、「代數教材設計原則」、「動態圖像表徵」及「代數教材設計原則輔以動態圖像表徵」所設計之教材運用於常態編班教學下，對學生的認知負荷之影響。 (三 )分別探討以「串流式教材」、「代數教材設計原則」、「動態圖像表徵」及「代數教材設計原則輔以動態圖像表徵」所設計之教材運用於常態編班教學下，學生的學習成就表現與認知負荷之間是否存在相關。 (四 )分別探討以「串流式教材」、「代數教材設計原則」、「動態圖像表徵」及「代數教材設計原則輔以動態圖像表徵」所設計之教材運用於先備知識高之學習者，是否會產生專業知識反轉效應。

1.3 研究

研究

研究問題

問題

根據上述研究目的，本研究要探討的問題如下：分別將「串流式教材」、「代數教材設計原則」、「動態圖像表徵」及「代數教材設計原則輔以動態圖像表徵」運用在常態編班之教材設計上，並以適性指標引導學生進行學習， 1 -1 對於整體學生的學習成就表現是否有影響？ 1 -2 對於未學過與已學過學生其學習成就表現是否有影響？ 1 -3 對於不同數學學習成就學生其學習成就表現是否有影響？ 2 -1 對於整體學生的認知負荷是否有影響？ 2 -2 對於未學過與已學過學生其認知負荷是否有影響？ 2 -3 對於不同數學學習成就學生其認知負荷是否有影響？ 3 -1「串流式教材組」之學生其學習成就與認知負荷量之間是否存在相關？ 3 -2 「代數教材設計原則組」之學生其學習成就與認知負荷量之間是否存在相關？ 3-3「動態圖像表徵組」之學生其學習成就與認知負荷量之間是否存在相關？ 3 -4 「代數教材設計原則輔以動態圖像表徵組」之學生其學習成就與認知

(18)

負荷量之間是否存在相關？ 4 -1 對於高數學學習成就與先學過學生是否會產生專業知識反轉效應？

1.4 研究範圍

研究範圍

(一 )本研究所發展的教材內容以九年一貫七年級數學領域中「二元一次聯立方程式應用問題」的單元為主題（康軒版，民國 100 年 2 月再版二刷，國民中學數學教科書第三冊）。 (二 )本研究以新竹市某常態編班之國中其七年級四個班為研究對象。

1.5 研究限制

研究限制

(一 )主題限制：本研究僅針對「二元一次聯立方程式的文字題列式」討論，因此對於不同的代數主題仍需設計不同的實驗與教材加以印證，無法類推。 (二 )母群體限制：本研究對象為新竹市某常態編班之國中其七年級四個班之學生，因此研究結果無法推論至全國國民中學的學生。 (三 )受試人員限制：由於部分受試樣本並非研究者任教之班級，因此對於研究者的教學模式、口語速度等均較不熟悉，雖然研究者已於正式實驗前至該些班級代課三節，但仍有可能會影響到施測結果。 (四 )施測時間限制樣本班級的教學與施測時間點稍不相同，稍微影響學生學習和受測的心態，可能會間接影響施測結果。

(19)

2、

、

、文獻探討

文獻探討

本章共分五節，主要對二元一次聯立方程式的文字題、多媒體學習理論、代數教材設計原則、多元表徵及認知負荷理論進行文獻探討。

2.1 二元一次聯

二元一次聯

二元一次聯立方程式的文字題

二元一次聯

立方程式的文字題

本節將針對二元一次聯立方程式的文字題其迷思概念、常見錯誤形式及解題歷程進行說明。

2.1.1 迷思概念

迷思概念

迷思概念指的是在教學的過程中，學生對於某一概念，因某種因素而產生的錯誤想法。可能造成迷思概念的原因如下 (林進財 , 1999)： (一 )編碼的問題：迷思概念可能是學習者在編碼的過程中，未循著正常的方式加以合適地編碼，導致學習能力受到限制。 (二 )學習信念的問題：學習信念是學生在學習歷程中，對於歷程中所有相關因素及變項所持有且信以為真的觀念，若是學習信念有偏差，那麼學生的迷思概念將產生。 (三 )經驗因素：形成迷思概念的原因可能來自於個體實際經驗的建構，這些經驗大都是屬於直覺推理而得，當個體進行錯誤的推理時，迷思概念便會產生。

2.1.2 二元一次聯立方程式文字題列式常見之錯誤形式

二元一次聯立方程式文字題列式常見之錯誤形式

(一 )學生看題目時，常忽略題目中關於「時間」的描述 (張景媛 , 199 4)。例如本研究之學習成就測驗第 6 題中，「九年前，父親的年齡是兒子的 5 倍」，學生列式時常常忘記九年前父親與兒子的年齡皆需「 -9」。 (二 )學生對於代名詞的用法不清楚 (張景媛 , 199 4)。例如本研究學習成就測驗第 9 題，「師父對徒弟說：『我在你這個年齡時，你只有 13 歲，等你到我這個年齡時，我已經 91 歲了。』」，學生常因為分不清楚題目中的「你」、「我」指的是誰，而無法列出正確式子。 (三 )國中學生在解文字題時，無法充分了解某些關鍵詞的意義，如「倍增」 (羅榮福 , 200 3)。

(20)

例如本研究學習成就測驗第 2 題中，「小哈的捐款比美美的三倍多 20 元」，學生因為對於倍增的概念不清楚，列式時常常不清楚究竟是小哈的捐款或美美的捐款該「_{×3」；又如本研究學習成就測驗第 7 題中，「把} 個位數字與十位數字對調後，所得的新數比原數的 2 倍多 18」，學生常因為無法理解「把個位數字與十位數字對調」之意義，且不會用代數符號來表示新數與原數之數值，當然也就無法列出正確的關係式；另外如本研究學習成就測驗第 8 題中，「男生的平均體重為 66 公斤」，學生對於「平均」此一關鍵詞觀念不清時，便無法正確列出關係式。 (四 )有些學生對某些關鍵詞的意義有直接反應，例如「每人分 1 0 個，則剩下 6 個」，敘述中有「分」這個字就以為要使用除法 (謝和秀 ,2000)。例如本研究學習成就測驗第 3 題中，「有一周長為 7 6 公分的長方形， ……，設長為 x 公分，寬為 y 公分， …」，學生在列式時常會直接反應為「 x+y=76」而忽略了周長之意義應為長與寬之和的兩倍，即「 2(x+ y)=76」。 (五 )學生認為題目中有數字的句子才是要運算的，沒有數字的句子就是無用的句子 (張景媛 , 1994)。 (六 )學生以為題目中所有的已知條件都會用到，因此想盡辦法要將所有的已知條件都列入式子中 (林清山 , 1990; 張景媛 , 1994)。 (七 )學生對於「關係句」的轉譯很困難 (林清山 , 1 990; 張景媛 , 199 4)。如本研究學習成就測驗第 9 題中，「師父對徒弟說：『我在你這個年齡時，你只有 13 歲，等你到我這個年齡時，我已經 91 歲了』」，學生對於敘述句中的師徒關係轉譯有困難，也就是無法正確理解題意，因此無法正確列出關係式。 (八 )學生面對較長的數學文字題時，常不知重點所在，不知從何處著手，所以會立即放棄思考問題 (戴文賓 , 1998)。如本研究學習成就測驗第 5 題中，「姊姊與妹妹各有數顆金莎巧克力，已知妹妹給姊姊 8 顆後，姊姊的顆數是妹妹的 2 倍，若姊姊給妹妹 8 顆後，兩人的顆數就一樣多，設姊姊原有 x 顆，妹妹原有 y 顆，請依題意列出 x 和 y 的關係式」，學生因為看到題目中之關係句十分冗長，不知道該從何處著手，便認定此題困難而放棄思考。 (九 )學生在看題意時，看了後一句就已忘了前一句，他們無法同時記住許多

(21)

條件，以致無餘力思考彼此間的關係 (張景媛 , 1994)，這也是本研究極力希望藉由教材之改良以解決之問題。

2.1.3 二元一次方程式

二元一次方程式

二元一次方程式解題歷程

解題歷程

P ol ya(195 7)在「怎樣解題」 (How to Solve It )一書中，將解題歷程分為四

個階段： (一 )了解問題：找出未知數、已知數及已知條件。 (二 )擬定計畫：找出已知數和未知數之間的關係。 (三 )執行計畫：檢查每一個步驟，把解題計畫付諸實現。 (四 )回顧解答：檢查所得的答案。本研究僅討論「列式」之部份，故以下僅對 Pol ya(1 95 7)在「怎樣解題」 (H ow to S olv e It)前兩項教學策略進行研究： 1.了解問題：教師教學時，可以透過以下幾種方式引導學生了解問題。 (1 )請學生將問題重述一次，透過請學生將題意重述一次，可協助確保學生已從文字敘述中初步了解題意。 (2 )請學生找出問題中的未知數、已知數及已知的條件，以確定學生能分析題意。 (3 )若是遇到需要圖形輔助的題目，請學生畫圖並在圖形上標示出未知數與已知數，以幫助學生將冗長的文字敘述融合於圖像中，解題時學生便不需一直回顧原始的文字題。 2.擬定計畫：教師教學時可以就下列方式引導學生擬定解題策略。 (1 )請學生把問題當中的主要關聯部份找出來，逐一地考慮這些部分。例如本研究學習成就測驗第 10 題中，「哥哥原來月薪為 a 元，弟弟原來月薪為 b 元，……，哥哥加薪 3%，姊姊加薪 7%，兩人共加薪 5895 元」，教師可以引導學生找出關聯部分「兩人共加薪 5895 元」，再引導學生說出哥哥增加的薪水為「 0.03a」元、姊姊增加的薪水為「 0.07b」，最後將兩者合併列出關係式。 (2 )有時文字敘述中的慣用語或專有名稱無法從字面上的意義去了解，此時便需重組一下條件的順序，並且運用不同的組合方式來考慮它們。例如本研究學習成就測驗第 8 題中，「男生有 a 人、女生有 b 人，已知男生比女生多 3 人，男生的平均體重為 66 公斤、女生的平均體重

(22)

為 55 公斤，若全班的平均體重為 61 公斤， ……」，學生常常無法從字面上理解「平均」之意涵，而出現「 6 6+5 5=61 」這種離譜的錯誤列式，因此教師應該導引學生了解「平均」與「整體」之關係，進而使學生正確列出「66a+55b=61(a+b)」。 (3 )因為題目冗長會造成學生看了一句就忘了前一句之情形，因此教師可以引導學生將各個部分拆開，寫出相對應的數學符號，進而列出相對應的代數式。例如本研究學習成就測驗第 5 題中，「妹妹給姊姊 8 顆後，姊姊的顆數是妹妹的 2 倍， ……」，此時可逐步引導學生「姊姊原有 x 顆、妹妹原有 y 顆，妹妹給姊姊 8 顆後，姊姊與妹妹分別有幾顆？」，並請學生寫下來。

2.2 多媒體學習理論

多媒體學習理論

多媒體工具的進展隨著科技的發展不斷創新，而真正影響學習成效的因素除了在於這些媒體所顯示的內容外，也包括了呈現內容之方式。創作多媒體學習內容時，創作者需要從使用者的角度考慮所呈現的訊息其適當性，亦即考量「人機介面」的設計，創作者必須考量人類的感官對於處理訊息的限制來設計數位教材呈現方式，因此本節將針對多媒體學習理論及教學設計原則進行介紹。

2.2.1 多

多

多媒體學習的定義

媒體學習的定義

多媒體學習 (Multi medi a Learni n g)指的是利用「文字 (Word )」與「圖像 (Pictu re)」來呈現教材內容的方式進行學習 (M a yer, 200 1)。其中「文字」包

括印刷文字與口述文字，不論是印刷在紙張上或是呈現在螢幕上的字幕皆可歸類為印刷文字，而旁白、演講者說出來的話等則為口述文字。「圖像」則包括靜態的與動態的，靜態的例如：圖畫、照片、地圖、圖表等，而動態的例如：動畫或影片等。

2.2.2 訊息處理的過程

訊息處理的過程

Ma yer(20 09 )認為當人類接收到多媒體訊息時，會進行以下三種認知處理

(23)

過程，如圖 1： (一 )選取 (S el ect )：當學習者接觸到文字或圖像等多媒體訊息時，會先由耳朵與眼睛等感官收錄後形成視覺與聽覺表徵，接著自動選取對其有意義的文字或圖像，將其儲存在工作記憶區中。 (二 )組織 (Organize)：接著，學習者在工作記憶區中將選取後的文字與圖像加以組織成一個連貫的、有整體性的模型，分別為語文模型 (Verbal Model)和圖像模型

(Picto rial Mo del)。 (三 )整合 ( Int egrate)：最後，學習者在工作記憶區中將語文模型及圖像模型加以配對，建立兩者之聯結，並與長期記憶中既有的相關知識加以融合，形成外在關聯，即為多媒體學習的認知過程。圖 1 多媒體學習認知模型資料來源資料來源資料來源

資料來源：修改自 Multimedia Learning (2nd ed.)（ p.61） , by Mayer, R. E.,

2009 , New Yo rk: C ambri d ge Univ ersit y Press.

2.2.3 多媒體學習理論的三大基本假

多媒體學習理論的三大基本假

多媒體學習理論的三大基本假設

設

多媒體學習理論有三個基本假設，分別為雙通道假設 (Dual-channel

Assu mptio n)、有限容量假設 ( Limit ed -cap acit y Ass umpt ion )及主動處理假設 (A ctiv e-p ro cessi n g Assu mptio n)(M a yer, 2001 )。

(一 )雙通道假設 (Du al-ch ann el As sump tion )

根據 Paivio 所提出的雙碼理論（ Dual-coding Theory）， Mayer 認為人文字耳朵聲音語文模型圖像眼睛圖像圖像模型先備知識多媒體呈現感官記憶工作記憶長期記憶選取選取選取選取文字文字文字文字選取選取選取選取圖像圖像圖像圖像組織組織組織組織文字文字文字文字組織組織組織組織圖像圖像圖像圖像整合整合整合整合

(24)

類視覺及聽覺訊息的兩個通道是獨立分開的，當視覺訊息被呈現到眼睛時，該訊息會由視覺通道進入工作記憶區，如圖表、字幕等，當聽覺訊息被呈現到耳朵時，則會由聽覺通道進入工作記憶區，如演講、旁白等 (Mayer,

2001 )，相關資料如上圖 1 。

(二 )有限容量假設（ Lim ited -capacit y A ssu m ption ）

有限容量假設指的是人類的視覺通道與聽覺通道一次所能處理的訊息量是有限的。所以當大量的訊息湧入時，我們無法完全接收訊息，僅能將少部分的訊息保留於工作記憶中，這些訊息很可能是片段的。

(三 )主動處理假設（ A cti ve-p ro cessin g Assu m ption ）

主動處理假設認為當訊息出現時，學習者會主動進行認知處理，並將所接收到的訊息與既有經驗、知識和基模一併整合。

創造一個具有「最少化無關訊息」、「使用核心且必要訊息」及「培養學習者主動學習」的學習環境是對一個教學設計者的挑戰 (Clark & Mayer,

2008 )。因此教學者應該考量如何適當的切割訊息、呈現訊息，使學習者能

夠將注意力投注在重要訊息上以進行有意義的學習。

2.2.4 多媒體學習理論教學設計原則

多媒體學習理論教學設計原則

(一 )多媒體原則 (M ultim edi a P rin cip le)

教材設計採用文字與圖像並用的學習效果會比僅用文字呈現好，也就是當學習者進行學習時，以多媒體組合的形式呈現教材會優於以單一媒體的形式呈現之教材。因為當文字及圖片一起呈現時，能幫助學習者建構語文及圖像模型之間的關連，文字的接收是線性的，也就是學習者在接收文字訊息時必須是依序的、逐一的，而圖像的訊息則可以是整體的、非線性的接收，也就是學習者可以同時接收較大量的完整訊息。根據多媒體學習的認知理論，文字與圖像分別在兩個不同的知識表徵管道，因此圖像及文字一同出現時並不會造成通道壅塞。本研究之實驗組 1 及實驗組 3 皆運用多媒體原則來設計教材，呈現資料如圖 2。

(25)

圖 2 實驗組 3 教材，符合多媒體原則

(二 )空間接近原則 (Sp ati al C onti guit y Pri ncip le)：

當學習者利用電腦螢幕或紙本學習時，若相關文字與圖像在畫面中的相對位置較近，學生的學習成效會比相對位置較遠時還好。因為文字與圖像的相對位置接近時，學習者不須把認知資源耗費在資料的搜尋上，此時學習者可將多餘的認知資源投注於其他訊息的獲取上，進而提升教學成效。本研究之教材皆秉持空間接近原則設計，如圖 3。圖 3 實驗組 3 教材，符合空間接近原則

(三 )時間接近原則 (T emp oral C onti guit y Pri nciple)：

當學習者利用電腦螢幕或紙本學習時，相關的文字與圖像同時呈現比接續呈現的效果好。因為人類的短期記憶容量有限，若學習者在聽完一段話後才開始播放相對應的動畫，此時學習者較無法在工作記憶區內同時留住文字與圖像表徵，也就較難以建立兩者之關聯，學習成效因此而降低。本研究之教材設計亦符合時間接近原則。

多元表徵應用於二元一次聯立方程式文字題列式教學之研究

國立交通大學

理學院科技與數位學習學程

碩 士 論 文

多 元 表 徵 應 用 於 二 元 一 次 聯 立 方 程 式

文 字 題 列 式 教 學 之 研 究

A Study of an Instructional Design by Using Multiple

Representations to Translate Word Problems of Two

Variables into A System of Linear Equations

研 究 生

：

廖 真 瑜

指 導 教 授

：

陳 明 璋 博 士

多元表徵應用於二元一次聯立方程式文字題列式教學之研究

A Study of an Instructional Design by Using Multiple

Representations to Translate Word Problems of Two

Variables into A System of Linear Equations

研 究 生 ： 廖真瑜

Student ： Chen-Yu Liao

指導教授 ： 陳明璋

Advisor ： Ming-Jang Chen

國 立 交 通 大 學

理 學 院 科 技 與 數 位 學 習 學 程

碩 士 論 文

A Thesis

Submitted to Degree Program of E-Learning

College of Science

National Chiao Tung University

in partial Fulfillment of the Requirements

for the Degree of

Master

In

Degree Program of E-Learning

July 2011

Hsinchu, Taiwan, Republic of China

多元表徵應用於二元一次聯立方程式文字題列式教學之研究

學生：廖真瑜 指導教授：陳明璋 博士

國立交通大學理學院科技與數位學習學程

中文摘要

中文摘要

中文摘要

中文摘要

A Study of an Instructional Design by Using Multiple Representations

to Translate Word Problems of Two Variables into A System of

Linear Equations

Student：Chen-Yu Liao Advisor：Ming-Jang Chen

Degree Program of E-Learning

National Chiao Tung University

Abstract

誌

誌

誌

誌

謝

謝

謝

謝

目

目

目

目

次

次

次

次

表

表

表

表

次

次

次

次

圖

圖

圖

圖

次

碩士論文

多元表徵應用於二元一次聯立方程式

文字題列式教學之研究

研究生

廖真瑜

指導教授

陳明璋博士

研究生：廖真瑜

指導教授：陳明璋

國立交通大學

理學院科技與數位學習學程

碩士論文

學生：廖真瑜指導教授：陳明璋博士

、緒論

緒論

緒論

緒論

1.1 研究動機

研究動機

研究動機

研究動機

1.2 研究目的

研究目的

研究目的

研究目的

1.3 研究

研究

研究

研究問題

問題

問題

問題

1.4 研究範圍

研究範圍

研究範圍

研究範圍

1.5 研究限制

研究限制

研究限制

研究限制

、文獻探討

文獻探討

文獻探討

文獻探討

2.1 二元一次聯

二元一次聯

二元一次聯立方程式的文字題

二元一次聯

立方程式的文字題

立方程式的文字題

立方程式的文字題

2.1.1 迷思概念

迷思概念

迷思概念

迷思概念

2.1.2 二元一次聯立方程式文字題列式常見之錯誤形式

二元一次聯立方程式文字題列式常見之錯誤形式

二元一次聯立方程式文字題列式常見之錯誤形式

二元一次聯立方程式文字題列式常見之錯誤形式

2.1.3 二元一次方程式

二元一次方程式

二元一次方程式

二元一次方程式解題歷程

解題歷程

解題歷程

解題歷程