國立台中教育大學教育測驗統計研究所理學碩士論文
指導教授:陳桂霞 博士
「二元一次聯立方程式」補救教學
之個案研究
研究生:楊承修 撰
中華民國一百零一年六月
謝辭
時間很快,兩年的碩士生涯即將結束。這一路走來,學習到的東西很多,也 令我成長不少,過程當然辛苦,但真的很開心。 首先對於本研究可以順利完成,要感謝的最大功臣當然是指導教授陳桂霞老 師,因為本身不是一個細心的人,所以在撰寫論文的同時,好多東西都需要老師 不厭其煩的提醒與指正,本篇論文才可以順利完成,另外,當然也要感謝兩位口 試委員吳博雅老師與吳德邦老師,給予寶貴的意見,他們的專業知識,讓本論文 內容更加完備。 在念研究所這段時間,我也特別想感謝,我的爸爸,細心栽培我長大,畢業 典禮時特地從高雄到台中來,我的姐姐,在做論文時,若有不順遂我的脾氣很容 易暴躁,他總是用耐心來包容我。還有最後也要感謝我的女朋友,在我忙碌的時 候,幫我解決好多雜事跟家事,用愛、耐心,體諒來協助我完成。 最後想把本篇論文獻給所有愛我的人跟我愛的人。 楊承修 2012 年 7 月摘要
本研究利用數學科「二元一次聯立方程式」補救教學對三位七年級學生進行 診斷與補救教學,並從活動實施探討學習成效。本研究屬個案研究,對象為台中 市某補習班七年級學生三位於「二元一次聯立方程式」學習中有迷思概念學生, 樣本選取依據自編問卷前測篩選,做補救教學對象。資料蒐集於 2012 年一月至 四月期間,實施「二元一次聯立方程式」補救教學活動,並對參與觀察以及自編 前測、後測試卷以及相關文件之蒐集加以分析,嗣後獲得以下之結果: 一、在「認識、化簡二元一次方程式,完成且判斷二元一次方程式的解」之中, 「分配律」之概念為「化簡二元一次方程式」必備概念之一。分數題型細心 即可正確作答。若未知數前無係數,則該數字即為 1,以及缺項即為 0 之概 念,有助於研究對象完成「認識二元一次方程式」。 二、在「代入消去法」之中,透過「分配律運用」與「係數為負時乘進括號內需 變號」的過程中,並多做練習,有助於研究對象解答「代入消去法」之題型。 三、在「加減消去法」之中,透過「兩式相加減」消去其中某一未知數,進而使 用一元一次方程式之方法解出另一未知數,需特別注意正負號之加減與移項 後正負號之轉換。並多做練習,有助於研究對象解答「加減消去法」之題型。 以及透過「解特殊題型」與多做練習有助於學生完成不同題型。 四、在「解的探討」之中。透過「各項係數與常數項比例」,助於理解「解的數 量」。以及非所有題目皆單選題,可能複選,正確檢查各選項才能確實答題。 五、在「列式與應用」之中,透過「文字轉換為算式」,助於學習列式。詢問有 幾種答案組合之題型,應先列出算式後,將其中一未知數依題目限制或自然 限制逐一解出另一未知數。最後,題目之答案不一定為數字,但解法相似。 關鍵字:二元一次聯立方程式、補救教學、個案研究、迷思概念、代入消去 法、加減消去法Abstract
The purpose of this study was to develop the teaching activities of two-dimensional linear systems of equations, besides reporting the effect of the corrective instruction on three seventh graders.
This study was a case study. The three seventh graders in a country who had misconception in learning two-dimensional linear systems of equations were selected from the result of self-made pro-test. The researcher collected information by participant-observation, the pro-written tests, post-written tests and document analysis from January to April in 2012. After remedial instruction, results indicated as follows:
1. On the part of completing and determining the results of linear equations in two variables from knowing and reducing linear equations in two variables, the conception of partition coefficient is demanded in reducing linear equations in two variables. Prudential participants can correctly answser the questions including a fractional number. If participants know that there is no figure in front of unknown number and the coefficient is one, the participants will more understand first degree polynomial in two variables.
2. On the part of getting the answers of two-dimensional linear systems of equations elimination by substitution, it is helpful for participant to answer the questions of elimination by substitution through the application of partition coefficient and altering a positive sign to a negative sign when the coefficients is a negative sign. 3. On the part of getting the answers of ftwo-dimensional linear systems of equations
questions o f elimination by addition or subtraction by subtracting the polynomial each other to eliminate an unknown number and then getting the anwer.
4. On the part of discussing the result, it is useful for participants to realize the quantity of the result by a rate of coefficients and a constant term. But not all of the questions is one anwer maybe two or more, panticipants have to correctly check each term to get the right answers.
5. On the part of applications and writing of two-dimensional linear systems of equations, it is helpful to learn to write the polynomial by altering the characters to the figures, and the question types which ask participants to answer how many result combinations it has. participants have to according to the unknown number which the question provides to answer the other unknown number. The result of the question is not always a figure, but the method to answer the question is the same.
Keywords: two-dimensional linear systems of equations, remedial instruction, case study, misconception, elimination by substitution, elimination by addition or subtraction
目錄
謝辭 ... I 摘要 ... II Abstract ... IV 目錄 ... VI 表目錄 ... IX 圖目錄 ... X 第一章 緒論 ... 1 第一節 研究背景與動機 ... 1 第二節 研究目的 ... 2 第三節 名詞解釋 ... 3 第四節 研究範圍限制 ... 5 第五節 研究架構 ... 5 第二章 文獻探討 ... 7 第一節 二元一次聯立方程式 ... 7 第二節 「二元一次聯立方程式」文字題型錯誤 ... 14 第三節 補救教學 ... 18 第四節 個案研究法 ... 24第三章 研究設計 ... 31 第一節 研究方法與參與者 ... 31 第二節 二元一次聯立方程式補救教學活動之介紹 ... 35 第三節 資料的蒐集、整理與分析 ... 39 第四節 研究流程 ... 44 第四章 研究結果與討論 ... 47 第一節 補救教學前的評量結果及補救教學前的迷思概念 ... 47 第二節 補救教學活動施行的情況與結果發現 ... 58 第三節 補救教學後之評量結果與概念之改變情形 ... 93 第五章 結論與建議 ... 111 第一節 結論 ... 111 第二節 建議 ... 113 參考文獻 ... 127 中文部份 ... 117 外文部份 ... 119 附錄 ... 122 附錄一 補救教學活動教案 ... 122 附錄二 學習單 ... 125 附錄三 評量單 ... 131
附錄四 「二元一次聯立方程式」測驗一 ... 138 附錄五 「二元一次聯立方程式」測驗二 ... 140 附錄六 「二元一次聯立方程式(測驗一)」測驗卷題目之雙向細目表 ... 142 附錄七 「二元一次聯立方程式(測驗二)」測驗卷題目之雙向細目表 ... 143
表目錄
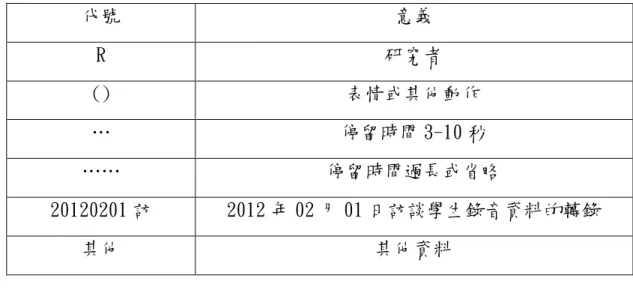
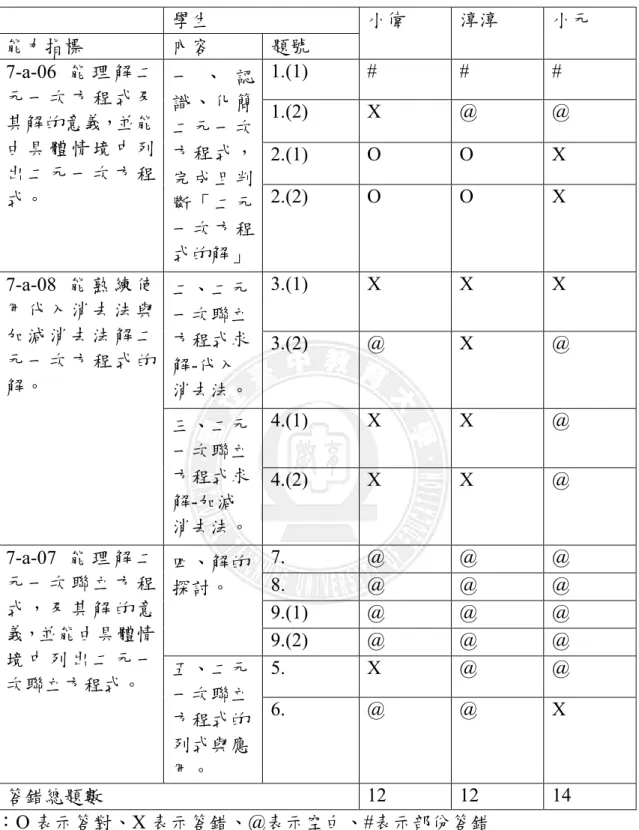
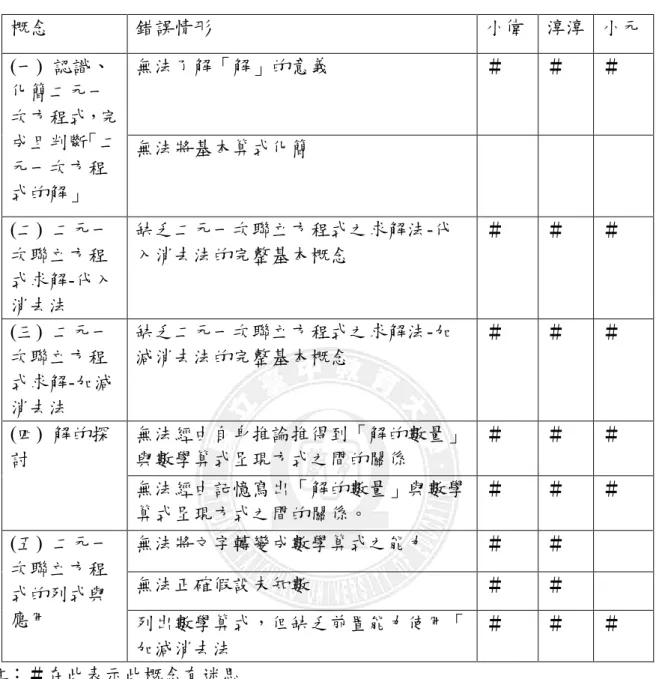
表 1 教科書一元一次方程式文字題型之列式分析 ... 17 表 2 三位研究對象在前測卷「二元一次聯立方程式(測驗一)」中的評量結果 34 表 3 資料標記說明表 ... 42 表 4 三位研究對象在前測「二元一次聯立方程式測驗卷(測驗一)」評量結果 48 表 5 研究對象在補救教學前「二元一次聯立方程式」之相關迷思概念 ... 57 表 6「二元一次聯立方程式」補救教學之活動實施過程發現 ... 92 表 7 三位研究對象在後測「二元一次聯立方程式測驗卷(測驗二)」評量結果 . 93 表 8 補救教學前後三位研究對象在「二元一次聯立方程式」答錯總題數之比較 ... 106圖目錄
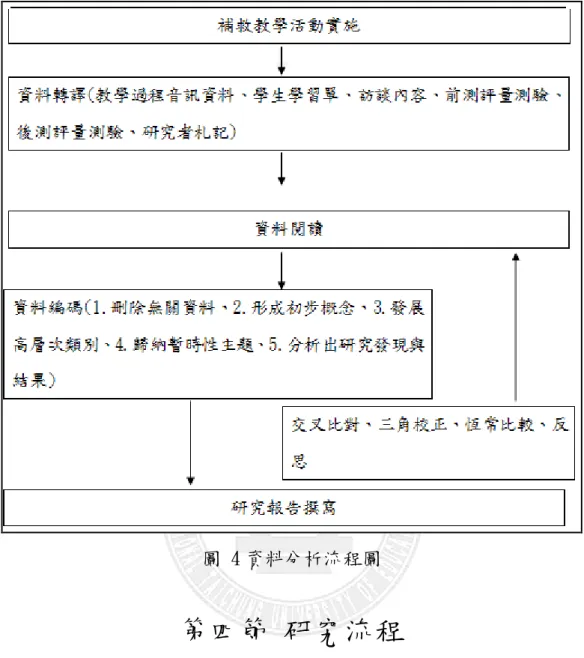
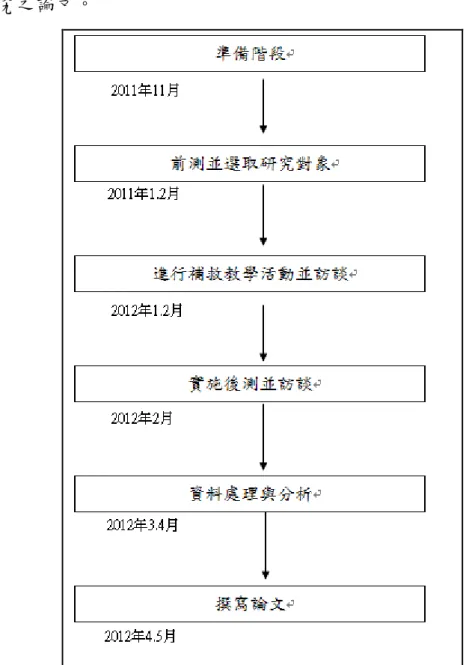
圖 1 二元一次聯立方程式教材內容分析圖 ... 9 圖 2 教材地位分析圖 ... 13 圖 3 補救教學活動流程圖 ... 37 圖 4 資料分析流程圖 ... 44 圖 5 研究流程圖 ... 46 圖 6 小元在前測中題 2.(1)之表現情形 ... 51 圖 7 小偉在前測中題 3 之表現情形 ... 52 圖 8 淳淳在前測中題 3 之表現情形 ... 53 圖 9 淳淳在前測中題 3 之表現情形 ... 54 圖 10 小元在前測中題 6 之表現情形 ... 57 圖 11 小偉於評量單一題 1.(2)的表現情形 ... 61 圖 12 小偉於評量單一題 3 的表現情形 ... 62 圖 13 小偉於評量單一題 2 的表現情形 ... 64 圖 14 小偉於評量單二題 1 的表現情形 ... 66 圖 15 小元於評量單二題 1 的表現情形 ... 67 圖 16 小偉於評量單二題 2 的表現情形 ... 68 圖 17 淳淳於評量單二題 3 的表現情形 ... 69 圖 18 小元於評量單二題 3 的表現情形 ... 70圖 19 小偉於評量單三題 1.(2)的表現情形 ... 72 圖 20 小偉於評量單三題 1.(4)的表現情形 ... 73 圖 21 小偉於評量單三題 1.(5)的表現情形 ... 74 圖 22 小偉於評量單三題 3.(1)的表現情形 ... 75 圖 23 小偉於評量單三題 2 的表現情形 ... 77 圖 24 淳淳於評量單三題 2 的表現情形 ... 77 圖 25 小元於評量單三題 2 的表現情形 ... 77 圖 26 小偉於評量單四題 2 的表現情形 ... 81 圖 27 淳淳於評量單四題 2 的表現情形 ... 81 圖 28 小偉於評量單四題 3 的表現情形 ... 83 圖 29 小元於評量單四題 3 的表現情形 ... 84 圖 30 淳淳於評量單 5 題 1.(2)的表現情形 ... 86 圖 31 小偉於評量單五題 2 的表現情形 ... 89 圖 32 淳淳於評量單五題 2 的表現情形 ... 89 圖 33 淳淳於評量單五題 5 的表現情形 ... 91 圖 34 小元於評量單五題 5 的表現情形 ... 91 圖 35 小偉於後測卷題 1.(2)的表現情形 ... 95 圖 36 小偉於後測卷題 3.(2)的表現情形 ... 96 圖 37 小偉於後測卷題 7 的表現情形 ... 97
圖 38 小偉於後測卷題 8 的表現情形 ... 99 圖 39 淳淳於後測卷題 8 的表現情形 ... 99 圖 40 小偉於後測卷題 9.(1)的表現情形 ... 101 圖 41 淳淳於後測卷題 9.(1)的表現情形 ... 102 圖 42 小偉於後測卷題 5 的表現情形 ... 104 圖 43 淳淳於後測卷題 5 的表現情形 ... 105
第一章 緒論
本章將對本研究中的研究動機與目的、名詞解釋、研究範圍與限制加以描 述。全章總共分為四節:第一節、研究背景與動機;第二節、研究目的;第三節、 名詞解釋;第四節、研究範圍限制。第一節 研究背景與動機
「因材施教」此理念早在春秋時代孔子早已提出,現今在教育改革呼聲中再 度被提及,與以往不同的是,現今教育改革的訴求是-「把每一位學生帶上來」。 而「因材施教」即依照學生之間程度的不同,教師實施適合於該位學生程度的教 學。研究者認為這句話涵蓋之內容包含資優教育到補救教學之所有層面;但是依 據教育改革訴求,「把每一位學生帶上來」是強調對於學習成效低落之學生施以 適當的教學,且研究者認為,每位學生都有公平的受教權利,不應該只是照顧成 績表現相對優異之學生,表現低落之學生相對於表現優異之學生反而需要更多的 關心與關注。故應給予學習成效低落之學生有再次學習的機會。 在「教育理念與地方教育實務」研討會會紀錄(1996)中,曾主張實施「補救 教學」:政府辦理國民教育,應該堅持它的普遍性與公平性特質。從學生走進學 校,劃入班級時,就應注意無論何種編班方式,都可能有其功效上的侷限。因此 在設計上,應盡力使每個學生都能得到最好的照顧。 這些論述顯示出:能建立一個完整的「補救教學系統」才能真正實踐「把每 一位學生帶上來」的教育改革理念之重要措施。自從教育部 1997 年起鼓勵國中 於學其中試辦「補救教學」,87 學年度起鼓勵國中於寒暑假辦理「潛能開發班」, 希望學校裡的補教教育可望改善學生的學業以及行為表現。但是在實施的實務現 況之中,許多實施補救教學的學校透露出遭遇到的困難,相關原因包含甚廣,例 如;學校行政人員、學校教師、學生家長、學生本人等各方面人員,以及學校教學與行政資源等。礙於這些困擾,使得補救教學變成了一項例行性的事務,但成 效卻未能確實的彰顯出來。為落實「把每一位學生帶上來」之理念,研究者參考 許多前人的補救教學相關經驗,擬訂適合學生的補救教學課程,進行補救教學活 動之研究。 除了現今教育行政當局的措施外,教育界的專家學者們則分別實驗各學科不 同型態的補救教學之方案(吳吉昌,2000)。這些補救教學的方案採用的課程或 是教學之設計各有特色,不同於教育當局所使用的型態,而其研究結果大多顯示 出其具有提高學生學習動機、降低學生數學焦慮、增強解題思考效能…等之成效。 研究者觀察七年級教材分析(教育部,2008),從國小升上七年級的學生, 除了透過數線的引導學習進而學習到正負數與正負數的加減、接著再以生活化例 題使用符號來代表未知數,也就是一元一次方程式之列式與計算解題,當然也有 因為螺旋式的課程分布,伴隨一些幾何圖形,幾何量變動的課程,接著即是一年 級下學期,學生首先遇到的即是解二元一次聯立方程式,接著進入直角坐標。而 由此看來,學生在面對代數方程式的解題過程處於剛開始熟悉的階段,隨即就進 入代數方程式與幾何圖形加以連結之部份,這對某些中低程度學生而言是相當吃 力的(游鯉謙,2003),研究者的教學經驗中亦是如此,故而研究者萌生於此單 元進行補救教學之念頭。而在此單元,主要是為了解決生活中的問題,此類問題 多數用文字題型及應用題方式呈現,然而文字題型的錯誤也是於此單元學生最容 易也較常發生錯誤,故在文獻探討中特別強調文字錯誤類型與迷思概念的探討。
第二節 研究目的
由上述動機可以發現學生能力發展與錯誤迷思對他們的學習影響很深,而數 學課程之相關能力的學習,在問題解決上是相當重要的,且經常是學生問題的所 在,問題解決的訓練在七年級的數學課程中便已經開始,此時與問題解決較為相 關課程級是應用題型之求解,這也是學習二元一次聯立方程式之主要原因。因此,研究者選定觀察內容為二元一次聯立方程式,並展開一系列的觀察,希望藉 此對學習成效低落之學生於學習二元一次聯立方程式過程之能力發展及其解題 的錯誤迷思徹底了解。 研究者於教育擔任第一線工作,本身從是補習班數學科授課教師,鑒於部份 學生從國小到國中階段,於「二元一次聯立方程式單元」經常出現某種程度上的 落差,而學生面對到成績突如其來的低落,亦會導致心情的低落,而部份學生因 此對數學科失去信心、失去興趣甚至最後產生厭惡感。 二元一次聯立方程式是代數的基礎,倘若學生於此單元的學習不良,可能造 成日後函數上學習的困難,研究探討相關之「方程式」文獻,多數集中於線型函 數主題上,反觀線型函數之先備知識-「一元一次方程式」之教學研究顯得不足, 因此,研究者才想要進行「二元一次聯立方程式」補救教學之研究,冀望研究結 果所得到結論,可提供數學教學工作者做為參考。故本研究希望透過研究所設計 之補救教學活動內容,採用補救教學方式,探討學生於本單元之改變情形。 故於此,研究者希望透過研究者本身所設計之補救教學活動,包含學習單、 評量單、測驗卷等,可以搜尋出國中二年級學生於「二元一次聯立方程式單元」 之概念迷思與學習上的困難,予以補救教學活動改善其概念迷思,且於探究補救 教學活動之後學生概念改變情況、成績提升結果與迷思概念的改善,前後測結果 之比較,希望可藉此提升往後的學生學習情況,也可供第一線教育工作者做為參 考。 因此,本研究之具體目的如下所列: 1. 探討研究對象於二元一次聯立方程式單元之學習困難。 2. 探討研究對象於研究者所設計的補救教學課程內容之學習表現。 3. 探究研究對象於補救教學活動之後的概念改變情形。
第三節 名詞解釋
一、二元一次聯立方程式 本研究所提及「二元一次聯立方程式」單元,僅在七年級之課程範圍內,其 中,「二元」是指兩個不同變數,「一次」是指此二變數之最高次方皆為一次。 凡是形如 y=ax+b 或 ax+by=c 之方程式之兩式,利用題目給定之兩式共同解出 兩個未知數,即稱為解二元一次聯立方程式,使用本單元所學習之兩種解法 「代入消去法」與「加減消去法」所解出答案,稱為二元一次聯立方程式。 二、補救教學 本研究補救教學主要為基於教學現場中,學生對於學習「二元一次聯立方程 式」相關概念所遭遇之困擾,進而設計「二元一次聯立方程式」補救教學活 動,共計 5 個活動,預計每一節課進行一活動,總計五堂課,每節課程為時 四十五分鐘。 三、個案研究(case study) 個案研究是進行社會科學研究之方法之一,其他方法還包括實驗調查法,調 查報告,歷史研究法、及檔案紀錄分析。 四、代入消去法 將兩個二元一次方程式其中一個未知數之形式代入另一個式子,將另一式轉 換為一元一次方程式解出該未知數,嗣後,再代回原式解出另一未知數,稱 為代入消去法。 五、加減消去法 將兩個二元一次方程式以兩式相加減之方式先消去其中一未知數,形成一元 一次方程式解出該未知數,嗣後,再代回原式解出另一未知數,稱為加減消 去法。
第四節 研究範圍限制
本研究的範圍與限制如下所述: 一、研究工具而言 本研究所使用研究工具包含主要概念為七年級的二元一次聯立方程式概 念,未能涵蓋所有的國中方程式概念,故只適合七年級學生的二元一次聯立方程 式概念教學亦或是補救教學之用與診斷學生的學習困難與迷思概念。 二、補救教學活動 本研究所設計的補救教學活動,教學內容主要是以七年級二元一次聯立方程 式之學習為主,並未涵蓋整個國中方程式知識。若想使用此教材進行補救教學 時,應針對實際教學情況加以做改善,以達成最好的教學效果。 三、研究對象 本研究的研究對象僅選取研究者所任教之補習班的班級中,施行前測後,於 該班選取出三位於此部份表現低落之學生,故研究結果不宜做過度推論。第五節 論文架構
由於本研究的最終目的是要透過研究者本身所設計之補救教學活動,包含學 習單、評量單、測驗卷等,可以搜尋出國中二年級學生於「二元一次聯立方程式 單元」之概念迷思與學習上的困難,且於補救教學活動之後學生概念改變情況、 成績提升結果與迷思概念的改善,因此必須診斷出學生的問題癥結點,並對這些 問題想辦法解決。最後則是根據這些事實與結果提出結論,歸納出對學生較好的 教法。因此,本文根據相關文獻,設計一套補救教學課程活動內容,包含前測卷 用以測驗出對此單元學習成效低落的學生群,學習單則是讓補救教學課程中,要 指導學生學會的內容,評量單部份為每一活動結束後,學生依舊存在的概念迷思 語學習困難,後測卷用以檢測學生對於整個補救教學活動過後概念之轉變情形。此外,本文亦以個案研究的方式,與個案學生進行訪談加以錄音,以原始呈現整 個補救教學過程。 第一章分別敘述研究背景與動機、研究目的、名詞解釋、研究範圍限制以及 論文架構;第二章開始為探討前人研究,探討內容包含二元一次聯立方程式、文 字題型錯誤、補救教學以及個案研究;第三章研究設計部份首先介紹研究方法與 研究參與者,其次則介紹研究者本身設計之補救教學活動,第三說明資料的蒐 集、整理與分析文章最後則為說明研究流程;第四章開始為研究者本身所研究之 呈現首先針對補救教學前測卷做探討,診斷參與補救教學之學生迷思概念所在, 其次探討補救教學活動之實施情況與結果發現,並以研究者與研究對象之訪談內 容與評量單同時呈現,最後施以後測並探究後測結果並比較補救教學前後,研究 對象概念改變之情形做比較;最後一章為結論與建議,分別敘述此次補救教學活 動之成效,與後人研究可注意之事項。並給予教育工作第一線工作者做為參考。
第二章 文獻探討
本章主要是針對此研究所需的知識做一探討分為四節做討論,第一節探討國 中目前數學課程中關於「二元一次聯立方程式」的教材及「二元一次聯立方程式」 相關概念研究,做為測驗一、測驗二與補救教學活動設計之依據;第二節探討國 中數學中,令多數學生頭痛之應用題型及文字題型之錯誤類型與迷思概念;第三 節探討補救教學之理念與相關研究,以說明此研究補救教學的內涵與實施歷程, 和進行補救教學應注意之原則;最後第四節探討個案研究之理念與相關研究,以 說明本研究個案研究的內涵與實施歷程,和進行個案研究應注意之原則。第一節 二元一次聯立方程式
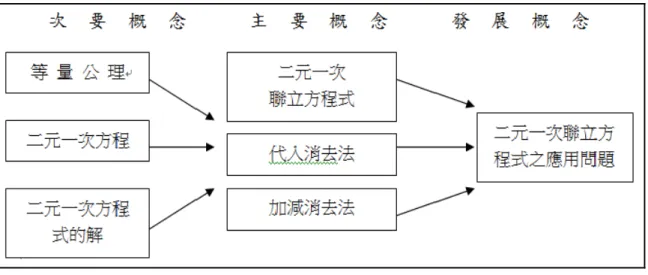
政府在九年一貫的課程中,曾經提及數學領域希望學生可以達到以下目標: 「掌握數、量、形的概念與關係,培養日常所需的數學素養,發展形成數學問題 與解決數學問題的能力,發展以數學做為明確表達、理性溝通工具的能力,培養 數學批判分析的能力,培養欣賞數學的能力。」然而方程式的學習在數學方面佔 有一席之地,主要是在培養解決問題。而方程式題型其中文字題型,即俗稱應用 題,文字題型解題過程與解決問題過程十分相近,都是針對問題,了解問題然後 做出判斷、做出假設、列出有效的解決方法(例如:列出方程式)、運算與求解、 最後對所求出的答案做出合理的解釋與判斷。國中課程中方程式領域即包含了, 一元一次方程式、二元一次方程式與一元二次方程式,這些單元是有其先後順序 的,因此學習二次方程式前的基礎必須先扎根於一次方程式,所以學生於一次方 程式的學習是很重要的。 本研究的「二元一次聯立方程式」單元是根據九年一貫課程綱要所列出的分 年能力指標,此單元概念內容指標(以下截自:國民中小學九年一貫課程綱要 2011學年度實施)-數學學習領域分年能力指標-資料來源:教育部國教司,2008): 7-a-01 能熟練符號的意義,及其代數運算。 7-a-02 能用符號算式記錄生活情境中的數學問題。 7-a-03 能理解一元一次方程式及其解的意義,並能由具體情境中列出一元一 次方程式。 7-a-04 能以等量公理解一元一次方程式,並做驗算。 7-a-05 能利用移項法則來解一元一次方程式,並做驗算。 7-a-06 能理解二元一次方程式及其解的意義,並能由具體情境中列出二元一 次方程式。 7-a-07 能理解二元一次聯立方程式,及其解的意義,並能由具體情境中列出 二元一次聯立方程式。 7-a-08 能熟練使用代入消去法與加減消去法解二元一次方程式的解。 7-a-14 能理解二元一次聯立方程式解的幾何意義。 上述乃是屬於九年一貫課程綱要中所述的五大主題與代數領域相關之分年 指標,內容包含:數與量數與量、幾何、統計與機率,代數、連結等。七年級的 課程已逐漸進入代數領域。因此,無論是現行的課程或者是九年一貫課程,代數 領域皆是相當重要的。 在學習二元一次聯立方程式之前,學生們在前面一元一次方程式單元會先學 習到等量公理,而二元一次聯立方程式單元在前半部份會先授予二元一次方程式 與二元一次方程式之解,接著再進入本單元核心二元一次聯立方程式,而此部份 主要有兩種解法,分別為代入消去法與加減消去法,待熟練此部份計算題後,最 後課題為應用問題,及文獻探討後會提及之文字題型,而此類題型主要是用於解 決生活中的問題。 以下呈現二元一次聯立方程式教材內容分析圖:
圖 1 二元一次聯立方程式教材內容分析圖 「代數 algebra」的解釋有二:1.藉由使用變數(variables)概括所有數來推廣算 數的初等數學來分,例如代數恆等式 x+y=y+x,其中的 x 與 y 可用來代表任何數。 2.特別指使用符號代表未知數以便由算數出等運算(elementary operations)求出他 的數值(E.Borowski, 1999)。 根據上述,代數學對於國中生來說是相當重要的。「符號」即是代數的焦點, 符號在小學時期,學生經常由較具體的符號(如○、□、…),國中時期經常使用 抽象符號(如 x、y)。以符號來代表生活中的數或量時,對於未知數與變數的情 形應提供足夠的經驗。除「符號」外,「方程式」即是代數的另一個焦點,方程 式定義如下:「方程式是判斷兩個表示式具有相同值的公式;他可以是恆等方程 式(identical equatiom,通常稱為恆等式,identity)對於任何變數值都成立;亦 可是條件方程式(conditional equation)對於變數之一定取值(即方程式的根,root) 才成立。例如:4x2 -9=(2x+3)(2x-3)是一個恆等式;而 2x2-3=15 則根是 x=3 或-3 之條件方程式」。在上述定義之中提及方程式的「根(解)」是不同表徵式當中的 一種共同關係,以式子而言,即滿足的數(E.Borowski, 1999)。更詳細來說,亦即 若稱一數為方程式之根(解),即這個根(解)代入此方程式之未知數後將會滿 足此方程式,使這方程式等號兩邊均相等。例如:以之一元一次方程式 3x+4=5x-8 的根(解)為 x=6,就是說將 x 以 6 代入,可以得到 3×6+4=5×6-8=22 滿足方程式。
在數學科目的教學之中,老師常常會提到「式子的解,就是代入方程式中會 滿足方程式」;在方程式之中,學生對等號的認識,並沒有等是兩邊等量(等號 的結構性),也沒有「還有」、「共有」、「得到或就是」之概念,經常純粹是由左 而右的順序(等號的程序性)的意義。然而「等號」即為「方程式」學習相當重 要之一環,又「方程式」是「代數」之核心,所以強化「不管情境或是敘述是何 程序,等號代表的都是兩邊等量」之概念是代數領能否進展相當重要之議題(南 一出版社,2010)。要使學生透過實際情境中「對於等量之物做相同之運算仍會 等量」的觀念,以便學習等量公理,利用等量公理來解決實際情境問題中所列出 之一元一次方程式,進而以兩個不同符號表示生活中的兩數,列出二元一次聯立 方程式並進行解題。 由上述課程內容指標,可以發現學生學習這些能力與概念時,必須有順序性 的學習與發展,而數學科與生活間的溝通是密切的,然而在學習的過程之中所產 生的迷思概念更為不容忽視,「早期發現早期治療」這句話用在數學科更是貼切, 若是發現得早即可及早做出防範和導正。但學者在研究中發現,多數七年級生尚 未達到形式運思的認知發展階段,且具體運思後期組與具體運思前期組的學生無 論在文字符號概念的理解或代數文字題的理解上,均出現極大的困難(袁媛, 1983)。因此,國中生於七年級上學期進行代數文字題的教學,是否應當時值得 進一步的研究。 研究者進行觀察時期,現今學校教育採用之數學教科書四大版本,包含:南 一版、康軒版、翰林版、部編版等。而在七年級學生數學教材中與本研究「二元 一次聯立方程式」相關課程的能力發展包含「以符號代表數」、「一元一次方程 式」、「解一元一次方程式」、「等量公理」、「二元一次方程式」、「二元一次方程式 的值」、「列二元一次方程式」、「解二元一次聯立方程式」、「二元一次聯立方程式 應用問題」等單元。以下分別介紹二元一次聯立方程式能力發展過程。 Rosnick (1982)曾經提及在每一科學及社會科學的領域中,符號化的過程所扮 演的角色是非常重要的。因為若能將生活中的語言和資料編輯的更有組織,並運
用較正確的符號表現出來,便可以有效地解決真實世界的許多問題(袁媛, 1983)。學習如何以符號代表數即為學習二元一次聯立方程式的首要概念,學生 必須學習的是不受到文字符號的影響,將文字符號看成數字來進行四則運算,於 南一版國中數學課本第一次中,表示「文字符號可以代表數」。現今世界大部份 國家皆以英文字母 x、y、z 等來表示未知數。郭汾派、林光賢、林福來(1989)國 中生從算數到代數的橋樑,即為使用文字符號來代表數,文字符號代表數更是數 學由抽象到形式的一個重要過程。文字符號代表數的學習在其他科學研究亦有重 大幫助。 Rosnick (1982) 稱 代 數 文 字 題 中 所 使 用 的 文 字 符 號 叫 做 「 形 容 的 數 字 (semantically laden letters)」。在台灣的數學科教育中,文字符號的出現於七年級上 學期第三章開始,學生們也是於此時開始接觸文字符號,對學生們來說這是一個 新的概念,想當然爾,不少學生為此感到恐懼,即使小學時期已學過「某數」之 概念,但是不分學生們無法接受文字符號,此時還只能接受「某數」之概念。因 此,無論學生或教師對於文字符號的學習與教學更應細心。例如:Collis (1975) 根據學生所理解的觀念,將學校課程中相關的文字符號概念細分為六個層次(文字 符號為「可算出的值(letter evaluated)」、「可忽略而不用的(letter ignored)」、「當作 物體(letter as object)」、「當作特定的未知數(letter as generalized number)」、「當作 變數(letter as variable)」)。他認為學生因為缺乏對文字符號的了解,所在解文字 符號之問題時就會發生困難,而文字符號對學生是否存在意義是學生解問題是否 覺得困難的重要因素(袁媛,1983)。 倘若學生對文字符號有部份程度上的了解後,學生就會試著將數學算式(含 文字符號)化簡,此動作將使算式更加簡單清楚;當學生能夠清楚了解算式中文 字符號的意義,進入下一主題「一元一次方程式」相關能力的學習。而所為方程 式即:含有等號的算式,例如:a=b;又如同日本數學家大村平說過「只限於特 定值的時候,才成立的等式,即稱為方程式。當被給予方程式時,找出該方程式 程式的特定值時,即稱為解方程式(李正宏譯,1990,第 36 頁)。一般而言,方
程式可以分為兩類,其一為恆等式,另一即稱做條件等式。所為恆等式:是一個 含有變數的方程式,且將任意數同時代入方程式等號兩邊的變數時皆會相等。例 如:0x=0,2(x-1)=2x-2,(x+y)2 =x2+2xy+y2。數學家萊布尼茲(Leibniz, 1646-1716) 是數學符號的偉大發明者之一。他定義符號「=」用來表式相等;符號「×」用來 代表乘。經常運用簡單的代數中「恆等式」之概念來解決問題。 代數之基本問題之一即為方程式理論,主要用來解決生活中的問題在距今約 四千年前,埃及人利用方程式的概念來解答一道數學問題:已知兩數的比是 2:1, 他們的平方和 400,求這兩數分別是多少?雖然當時不懂得使用未知數,但於解 題過程中已有此概念存在。巴比倫人也使用類似概念來解決數學問題。其中較典 型的問題:已知矩形的周長與面積,求這矩形的長與寬。解題方式是依據經驗, 逐步推算出來的。最後甚至發展出解一元二次方程式之公式解。 在西元三世紀,古希臘數學家吐蕃圖(Diophantus,古代希臘數學家,著有 「算數」、「論多邊形數」、「衍論」等名著)在方程式理論上有系統性的記錄著一 套縮寫符號,此時也開啟了代數學的發展。人們為紀念他的貢獻,在其墓誌銘上 刻著數學問題,留下了他的生平事蹟,其墓誌銘如下:『路過的人!這裡埋葬著 吐蕃圖。請計算下列數字,即可知道他一生經過多少寒暑:他一生的六分之一是 幸福的童年,十二分之一是無憂無慮的少年期,再過七分之一的年齡,他建立了 幸福的家庭。五年後兒子出生,不料兒子竟比他早四年逝世。年齡不過父親享年 之一半,晚年喪子老人真可憐,再悲痛中度過風燭殘年。請你計算,吐蕃圖活到 幾歲,才與死神見面?(袁小明,1998)』。 十七世紀笛卡兒(Descarter, 1596~1650)(法國偉大的哲學家、數學家與解析 幾何的創始人)曾經說過一些話:「一切問題都可以轉化為數學問題,一切數學 問題都可以轉化成代數問題,一切的代數問題都可以轉化成方程式,一切問題皆 會迎刃而解。」偉大的英國科學家牛頓(Newton, 1642~1727)曾經說過:「要解答一 個問題,如果裡面包含數量間的抽象關係,只要把題目從日常的語言譯成代數語 言就行了。」
而在「文字符號概念發展」之研究中,學者研究顯示學生主要在解決未知數 題型時主要出現了以下幾種類型錯誤:1. 加法合併問題,如:3x+6y=9xy;2.括 號問題,如:5(x+3),答案為 5x+3 或 x+15;3.誤認為符號不同及代表不同數,如: x+y=x+z 不一定成立;4. 辨識問題,如:學生習慣以 x、y 代表未知數,一但有 任何題目出現,就馬上設為 x、y,學生對文字符號的了解不夠深入;5.公式一般 化,意思即學生無法根據所學到的東西,找出一般通用的公式;6.注重答案,即 只求找出答案,不知為何用此種方法解題(郭汾派、林光賢、林福來,1989)。 於七年級上學期數學課程分別為「整數的運算」、「分數的運算」與「一元一 次方程式」,七年級下學期隨即進入「二元一次聯立方程式」、「平面直角坐標系」、 「比例」、「函數與圖形」與「一元一次不等式」等。由數學教材地位看來,二元 一次聯立方程式之前為代數的學習,經過二元一次聯立方程式的洗禮,漸漸出現 幾何。由方程式教材地位看來,二元一次聯立方程式之前為一元一次方程式,經 過二元一次聯立方程式後為一元一次不等式與一元二次方程式,處於一承先啟後 的位置,由此可見,二元一次方程式單元為代數與幾何的分水嶺,可想而知其教 材地位。其教材地位如下圖所示: 圖 2 教材地位分析圖 至於所謂「一元一次方程式」,意即一個方程式經過化簡之後,只含有一個 未知數,且最高次數為 1 次,即稱做「一元一次方程式」。如:6y=7,5x+6=3x+9。 學生認識了一元一次方程式,並了解它的意義,以及求解過程(過程包含「等量
公理」的認識與熟悉)之後,到此七年級上學期結束,經過寒假,七年級下學期 一即進入「二元一次聯立方程式」之單元。此單元通常用來解決生活中的問題, 當然學生們將會接觸到更多的應用問題,學生除了會列式、解方程式外,更需具 備判斷所求得之解是否符合現實環境之要求(如人數不為小數或分數),意即, 學生必須了解二元一次方程式解的含意。而求解過程中常見方法有二:一為代消 去法,另一為加減消去法。所謂「代入消去法」的基本原理是利用其中一個等式 之中的未知數,用另外一個未知數來表示它,再代入另外一個等式(此時方程式 即簡化成一元一次方程式),再把未知數解出。而「加減消去法」的原理是利用 兩個等式的可加減性,使他們其中一個未知數消去後求解。 學生有學不會的或是不了解的,甚至誤解之情況發生皆稱為產生錯誤迷思或 存在迷思概念。教師的存在即是從中協助加以輔導,幫助學生避免存在迷思概 念,迷思概念的存在對於學生發展一新能力時,通常會造成一極大傷害,此對學 生造成學習上的錯誤詮釋並將影響他以後的學習。
第二節 「二元一次聯立方程式」文字題型錯誤
在方程式的學習相關研究中,文字題行為當代數學教育探討的重要主題 (Lewis, 1989)。小學時期,文字題型即經常出現於數學課程當中,然而文字題型 比起一般計算題型或填充題型更加複雜,且經常以生活化的題材呈現並用語言去 描述數學問題(Cummins, 1991)。時代變遷,配合當代時事,文字題型相對變化多 端,如何將文字題行轉換為數學算式,對該年齡的學生而言相對困難;除將文字 題型轉換為數學算式外,符號運算規則與數學物件學習更成為學生認知歷程的負 擔。 學生遇到方程式文字題時,首要條件為了解問題敘述與情境,接著回憶或連 結至相關問題的基礎,然後試著建構出可以表徵此問題的模式,最後根據這個或 這些表徵推論出結果(唐淑華,1989)。多數學生之所以會對此一類問題感覺到困難,主因就在於剛開始時,如何將文字轉換成數學算式或方程式(Lewis & Mayer , 1987)。唐淑華(1989)的研究發現,數學理解能力與文字題型的各項解題能 力,均高度相關,這顯示數理理解能力較偏向語文能力層次。此外,也另有他人 研究顯示數理能力與閱讀能力或語文能力並沒有顯著相關(范金玉,1986)。
近年來有關方程式文字題型的研究大多注重「問題表徵」(problem representation)和「問題解決」(problem solution)(Hutchinson, 1993; Maccini & Hughes, 2000; Sebrechts, Enright, Bennett, & Martin, 1996, Maccini, Mulcahy, & Wilson, 2007)。方程式文字題型通常會於題目陳述時詳細呈現題目中的目標與限 制。但題目中仍有其他限制經常隱藏於問題的某些情境中,所以解此類題型的難 處之一在於如何發現這些隱藏的問題與限制,並將其組織成一大架構(Sebrechts et al., 1996)。學生遇到文字題型時,必須以自己的方式去詮釋或轉譯此問題的敘述, 進而用自己的方法或語言去表達出已知的事實。 學生們亦必須認識、了解專有名詞的意義,例如:單位(台尺;公尺)或等差 數列等類似的專有名詞,在問題轉換成算式過程中,找到足夠的線索亦成為另一 個困難的來源,例如已知條件與題目所要求的答案單位不同(時速與分速)。Lewis 和 Mayer (1987)的研究中顯示數學解題歷程中,將問題轉換為內在表徵(internal representation)的過程是造成學生解題最大困擾的重要因素,特別為包含關係語句 的方程式文字題,例如:「我是你的 3 倍與我多你 3 倍」此兩句話就有所差異。即 使是現代大學生,在轉換句子成為方程式方面,也出現不少的錯誤(Clement, Lochhead, & Monk, 1981)。例如:「學生人數是老師人數的 5 倍」經常出現的錯誤 為“5S=T”,研究者稱為“逆轉(reversal)的錯誤”。
Hinsley, Hayes, & Simon(1977)曾提及解決問題強的人會以問題分類做為解題 基礎的方式。他們也發現解決問題強的學生在得到問題敘述後可以分類出問題的 形式。這是一種專家知識的特徵之一,並且相當好用(Glaser, 1991)。Mayer (1982) 發現這類問題形式出現的頻率與學生正確回憶問題有正相關。相較成功與不成功 的解題者,成功解題者會以基本結構非表面特徵來分類這些問題(Silver, 1979)。
Muth (1991)研究發現,多數學生會將題目中所有資訊視為有效訊息,這成為他們 在問題整合上的困難。 於解題方面,當他們做解題及驗算答案時,多數的解題者傾向確認明確的解 題計畫,以觀察他們解題過程的成功。Lester (1985)的研究發現解題能力較差的 人習慣使用關鍵字來做為算式或運算符號,在將問題中出現的數字做運算。通常 他們在解題的時候,也以直覺來解題,認為只有一種解題方式,並不會想到有其 他解題方式(Briars, 1983)。 許多學者研究文字題型語句表達方式發現,影響學生理解題意的變數有三, 分別為:1.表達用語、用字為明示或暗示;2.未知數與已知數的關聯性;3.題目中 條件的排列順序(De Corte, Verschaffel, & De Win, 1985; Mestre, 1988, Orosco, Swanson, O'Connor, & Lussier, 2011)。De Corte 等學者(1985)的研究發現,題目說 明越清楚,學生答題越容易。故想解題目,必須先了解題目才能進行解題。Chaiklin (1989)認為方程式文字題會有四個歷程:讀懂題目、形成內在表徵、組織問題、 列出方程式。袁媛(1983)的研究則指出認知層次的差異,在文字題型解題能力上 有顯著差異;顯示出認知層次為影響學生解文字題型的重要因素。 王如敏(2003)研究國二學生在一元一次方程式的基本概念及應用問題的解題 情形與錯誤類型。結果發現在一元一次方程式的應用問題中,程度不同的學生在 學答題表現上有顯著差異;填充題型對於中間程度的學生幫助最大,因為其引導 的陳述方式有效提升學生的解題;多數學生在解題時沒辦法達到第一層次,由此 也可見多數學生在了解題意並把文字轉換為算式此一步驟已經出現很大的困 擾;而多數學生通常解題的方式也只有一個,若使用研究者設計之解題步驟與學 生解題之策略有所衝突時,學生經常會放棄作答。 林清山與張景媛(1994)研究中發現國中學生在解方程式應用題時,在問題轉 譯、問題整合、解題計畫及監控,和解題執行四方面容易發生錯誤概念。多數學 生在學習方程式時,並未有正確的「等價概念」(the concepts of equivalent
械化方式解題,但並未真正了解算是真正意義。 綜合上述,我們可以了解七年級學生剛開始接觸方程式之代數領域,學習文 字題型將產生許多不同的學習困難與錯誤類型,這些困難與錯誤多數發生在如何 將文字轉譯為算式或內在表徵,所以為有效提升學生於文字題型上之解題能力, 必須先教導學生如何讀懂題目,了解問題的敘述,才能對問題產生適合的策略來 解題。 現今代數課程從國小時期即利用符號,如:甲、乙、□……等開始建立起學 生對未知數的觀念,七年級時當學生熟練正負數與分數四則運算後,開始進入以 x、y、z……做為未知數的代數領域其中方程式單元是國中學生學習代數之課程 中最主要的課題之一,包含一元一次方程式、二元一次聯立方程式以及一元二次 方程式等單元。而研究者在進行本研究方程式補救教學,首先遇到的問題是要選 擇一元一次方程式單元,或是二元一次聯立方程式之單元。 研究者經過評估後,先是針對正式綱要所編排的教科書來做為分析,意即根 據教育部 2008 年公布之國民中小學九年一貫教學學習領域課程綱要之版本,挑 選出三個版本,分別為南一版、康軒版與翰林版之教科書。在正式綱要教科書排 版之中,七年級上學期首先學習一元一次方程式單元,一年級下學期則是學習二 元一次方程式、二元一次聯立方程式單元,根據研究者的經驗,當學生學習如何 以二元的方程式來解文字題時,學生普遍會反應,用聯立方程式之列式比起一元 一次方程式之列式容易得多。 研究者根據南一版、康軒版與翰林版三個版本之教科書之中一元一次方程式 單元之文字題型進行分析,發現:此三版本之教科書之一元一次方程式問題中皆 有六成以上的問題也可以用二元之方式來列式並解答,如表 1: 表 1 教科書一元一次方程式文字題型之列式分析 南一版 康軒版 翰林版 比例 62.5% 76.9% 85.7%
基於以上之分析結果,研究者決定以二元一次聯立方程式之單元來進行本研 究。
第三節 補救教學
此節將探討補救教學之相關研究,故此研究者分別依序討論補救教學之理 念、實施補救教學之歷程、補救教學課程類型、補救教學對象的界定、補救教學 之設計原則。壹、補救教學之理念
在現代教育改革中極力訴求的「因材施教」、「把每位學生帶上來」等觀念, 都顯示針對學生在學習方面跟不上原本班級進度者,透過補救教學幫助他二次學 習為目前教學實務中極為重要之任務,學生可能因為某個觀念無法理解或無法融 會貫通,進而影響之後的學習態度及信心,而在學校教師無法兼顧班上所有學生 的學習進度之情況下,此類學生即需要接受教師特別的幫助。然而補救教學 (remedial instruction)基本上是也一種診療教學的模式(clinical teaching,也稱臨床 教學模式),教師會在事先診斷學生之學習問題,選擇好準備接受補救教學的對 象後,進而進行一連串的補救教學活動(張新仁,2001; 陳長春,1992)。 即在教育改革時,應發展學習診斷工具,再配合適合的教師,規畫出適當的 課程與教材,使學生因觀念不清楚或學習經驗不足所造成之學習挫敗感能減至最 小,幫助他學習與成長。 補救教學的方式是為幫助學生釐清基本概念、發現問題所在及克服學習障 礙,並減少學習的挫折感與無力感,使其能改善原本的學習態度,進而增加其繼 續學習的信心,故此本研究為先診斷出必須實施補救教學之學生,分析其二元一 次方程式聯立方程式之問題點之後,再透過研究者本身設計補救教學課程實施以進行補救,以提升並強化學生在「二元一次方程式」的相關概念和能力,期望在 補救教學實行後,學生有能力跟上原本班級之教學進度,並能增加其學習信心, 日後亦能幫助學生在函數課程上的學習更上層樓。 所以,有效的補救教學取決於正確診斷,透過適當的題目測驗、教師的觀察 與評估,可以對學生的程度與迷思概念有進一步的了解,然後再決定補救教學之 方向,施行後,以學生之學習成果再判斷是否需調整教學方式,此類診斷-教學是 一個不斷循環的過程,直到學生可以達到學習目標(郭玉生,2000)。
貳、實施歷程
補救教學的歷程為「評量-教學-再評量」之循環,期望補救教學之實行後, 學生有能力跟上原本班級之教學進度,其歷程大致分為三階段(張新仁,2000)。 1.人員產生 補救教學的第一步工作在於篩選、診斷以選擇需接受補救教學的學生。 2.正式評量 評量的重點在於了解學生目前之學習成效,以學生無法正確解答之題目來評 估其可能之學習困難處,找出問題的癥結點以對症下藥,以幫助行補救教學。 評量的資料來源大致包含:學習困難報告、教室觀察紀錄,心理評量等項目。 依據各種評量的方式,可幫助教師隨時了解學生的學習情況,診斷出學習問 題點,並輔助補救教學能更快達成教學目標。 3.教學 補教教學也是一種診療教學模式,亦稱做臨床教學模式。其重點在於了解學 生的學習問題後,設計出一套適合學生的課程內容,並以有助於該生學習的 教學模式教習之。 根據以上補救教學之歷程,本研究補救教學前之評量主要是要了解學生在 「二元一次聯立方程式」該單元之學習困難,進而設計出一套符合學生需求之教學課程而進行補救教學,在進行補救教學之活動結束後,再實施評量,以評估是 否達成該階段之學習目標,因而本研究主要是依據「評量-教學-再評量」的歷程 進行研究。 因此,教師可以透過觀察習作、利用上台做答或採用隨堂測驗的方式,決定學生 的學習困難是否存在;其次藉由後續觀察、評估診斷出問題所在,並找出學習困 難的原因;最後擬訂補救教學之計劃。而補救教學之活動實施目的,主要希望學 生達到預期的學習目標,故需要定期檢討、評鑑、紀錄與追蹤,以了解其實施成 效。所以,有效的補救計畫來自於正確的診斷。
参、課程類型
單就課程內容而言,補救教學因教育理念、學習設備、教師素養與學生本身 的需要,而呈現出多樣化的類型。一般常用的教學課程內容設計有補償性、導生 性、適性、補充性、加強基礎性及學習策略等類型(杜正治, 1993)。而以下就 以本研究相關之類型加以說明: 1.導生式課程(tutorial program) 導生式課程主要在提供學生額外協助與解說,並對一般正規課程之教材再做 複習。除了實施小組教學或一對一等教學方式外,其餘皆與正式課程沒有差 異。故,導生式課程為正規課程的延伸。所以,由此課程實行補救教學的成 敗關鍵,在於正規教學教師與補救教學教師兩者之間的溝通與協調,並且一 起策劃出教學活動。導生式課程相當耗時,佔用教師大量精神與時間,所以 教師可以鼓勵學生同儕參加補救教學之活動,由同學互相指導學習。2.加強基礎課程(basic skills progarm)
加強基礎課程之重點,偏重於學生正規課程中並未習得之基本技巧。加強基 礎課程的基本假設認為:學習歷程為一種線性作用,因而七年級的學生無法受 益該年級之課程,除非該學生已經精通該年級以下的所有課程。如一位六年
級學生的作文能力還停留在四年級程度,則補救教學課程需要再強調四年級 之寫作技巧訓練。基於此觀點,在實施補救教學前,重要的課題不僅在於診 斷學生之學習困難,一樣重要的,必須清楚了解學生當時基本概念是否正確。 綜合上述,本研究補救教學之方向乃是由導生式課程與加強基礎課程設計結 合,就「加強基礎課程」設計之方向而言,本研究之目的在於在實施補救教學前, 診斷學生之學習困難及必須清楚了解學生的基本概念是否正確,且補救教學活動 偏重於正規課程中尚未習得之基本技巧。就「導生式課程設計」而言,本研究將 採用三位個案進行補救教學活動,並組成小組教學方式進行,除了可讓參加補救 教學之個案透過同儕間互相激勵學習,也可增強其學習動機;且在補救教學活動 中,對於研究者的引導概念已經理解的個案,研究者以鼓勵方式,使其對尚未理 解之個案說明解釋,此時研究者亦可檢驗補救教學之個案的理解程度為何。
肆、設計原則
張新仁(2001)指出補救教學的課程設計,首先須考量學習的原則:由易而 難、由簡至繁,從已學至未學,此來才能建立學生的自我信心與學習動機。其次, 課程內容必須緊密結合,莫讓學習者有銜接不上之感覺,同時學習目標需明確與 具體,才能掌握住學習的重點。此外,學習活動設計要考量到學生的理解能力、 學生接受之程度及足夠的學習動機。對中低學習成就學生來說,適合先釐清基本 概念,並簡化教材,且教學內容應具有趣味性與變化性。 杜正治(1993)認為一般補救教學課程之設計,必須考慮到下列項目: 1.分析基本能力 任何學科、任何單元學習要達成目標,需要一定程度的心智能力,內容包含 注意力、理解力、知覺力、想像力、記憶力與觀察力等。教師教學時不僅需 考慮到欲達成之學習目標,更須把學習主體放在學生身上,以學生程度為課 程設計之出發點。另外,學生先天上的個別差異,例如年級、程度、能力即先備知識,倘若相關能力不足的話也將造成學習上的困難,因此在設計補救 教學課程與教材時,需考量學生的相關能力與個別程度,進而配合教材教法, 如此才能達到事半功倍。 2.評量學科能力 在於進行補救教學之前,必須先針對學科的學習能力進行評量與測驗,以做 為課程設計之依據,而學科能力不單僅於該科目評量,如數學科之能力包含 基礎運算能力、邏輯能力、題目之閱讀能力,題型結構理解等,若是語文程 度不佳,而無法完整理解題意,必然影響學習成效。 3.評量學習動機 學習動機往往影響到學習成就,因此在進行補救教學之前,教師應先了解學 生學習動機之強弱。一方面可以考慮將學習動機強的成績低落學生為優先補 救對象,另一方面設法對學習動機弱之學生提供額外的加強,並引起其更強 烈之學習動機。 4.擬定課程目標 課程目標的擬定除了配合正規課程進度之外,亦取決於教學方法的選擇,其 也關係到補救教學的成效。而教師在擬定課程目標之時,須先了解學生之學 習能力,以及學習的客觀條件。課程目標的訂定,需根據學習對象、學習的 內容、教學方式、行為標準與評量的方式來訂立之。 5.選擇適合補救教學受教者能力的教材 有成效的補救教學課程設計,應該根據學生程度編設適合的教材,此包含訓 練有效的學習策略、簡化既有教科書內容、另行編選坊間教材、重新自行設 計教材。 至於成功的補救教學進行原則,Olivares (1993)主張如下:(1)徵求學生參加的 意願;(2)根據學生的學習程度教學;(3)適應學生的個別差異;(4)循序漸進, 小步驟進行;(5)提供回饋和安排增強;(6)使學習教材有意義化;(7)教材的份 量宜適中;(8)將學生安排為合作式小團體的學習;(9)提供充分而多樣化的練
習機會;(10)建立成功的經驗;(11)激勵學習動機;(12)建立良好的師生關係。 本研究之補救教學將依據前述之十二項原則做為二元一次聯立方程式之補救 教學之設計原則。 伍、對象的界定 現階段對於補救教學對象的界定為日常定期成績考查,即俗稱段考或月考, 學科成績不及格者(60 分以下),且學業表現與其他學生一定落差者,可稱 為該補救教學之學生(張新仁,2000)。補救教學的對象通常為智力正常,但 該科學習成就較低的學生,或該科學業成就表現低於其能力水準。可將此類 學生分為三類(張新仁,2000): (1)學生之實際學業表現明顯低於其應有的能力水準者。 (2)學生之實際學業表現明顯低於其班級平均水準者。 (3)學生學習成績不及格,且學業表現明顯低於其他許多人者。 就學業表現與行為表現來說明低學習成就學生之特徵(張新仁,2000): 1.學業表現部份,低學習成就學生之特色有:(1)於測驗表現上,呈現低的基本作 答技巧;(2)學業成績表現差;(3)在閱讀或數學的程度比一般學生低;(4)有學 業方面挫折;(5)經常藉口不交作業或遲交,或是像學生拷貝作業。 2.在日常行為表現部份,低學習成就學生之特徵有:(1)依賴性重,需要教師或家 長特別注意;(2)對於有興趣的科目或課程,有優異的理解力及記憶力,並有固 著的傾向;(3)不亦專心及努力工作;(4)學習態度不佳,缺乏動機、恆心;(5) 在自我或社會的控制適應部份有困難;(6)在學習部份,需要比其他同學花費更 多的時間;(7)不喜歡學校及家庭作業;(8)習慣性遲到及較低的出席率;(9)家 庭提供較少的支持。
第四節 個案研究法
個案研究法最早多用於醫學方面,應用在研究病例,後來陸續出現在心理 學、社會學以及工商管理學等各領域,在當代教育界的運用尤為廣泛,經常用於 教育和相關研究上,或者應用於兒童心理等領域,特別針對超常、特殊才能兒童、 學習落後或低度缺陷兒童等類型較特別之學習者的心理研究(葉重新,2011)。 而美國哈佛大學的法學院於 1870 年即創用個案研究法,用於訓練學生對法律的 個案原理。 實驗心理學家菲吉納於 1860 年針對個別的研究對象進行感官研究,並創立 新物法(psychopysical method)。在此之後,多位學者所涉及的研究中經常發現個 案研究法被運用的例子。例如:佛洛伊德(精神病學運用個案研究法的先驅)處 理精神病患致力於發現「一致的經驗模式」。在他細心探究下,能使病人回憶起 兒時所發生的事件,或是關於創傷性的意外事件,根據他的假設,這些事件可以 被用來解釋病人的生病行為。佛洛伊德曾經研究一位狼人(the wolf man),表題 為「來自嬰幼期神經症的生活史」(from the history of an infantile neurosis)撰寫 成書出版於 1918 年,此為他應用個案研究的典型範例,這項研究結果與他的假 設幾乎完全吻合,這也使得當時個案研究風靡一時,且被認為是有效處理事情的 方式。個案研究的分析在法律與醫學上,成為做基本的工具。在醫學上稱個案為病 例,而法律上稱為案例或判例。然而個案研究在社會學上的發展如下:
哈佛大學企業管理研究所於 1908 年創立,由 Edwin F Gay 擔任院長,Edwin F Gay 為一名經濟學家,認為企業管理應效法哈學大學法學院之教學方式,Edwin F Gay 稱為「問題方法」(problem method)。Wallace B. Donam 於 1920 年擔任 哈佛企業管理研究所主任。他令所屬教授從企業的活動中搜集資料,用來編制教 材,也鼓勵他們蒐集關於市場交易或是工商財務的個案。並吸收不拘傳統研究方 式的學者一同研究。其中一位參與者-Elton Mayo。領導了「霍桑實驗」(Hawthorn
studies)。「實地研究」屬於社會學方面,在人類行為的研究個案中收到效果。 在第二次世界大戰的中後期,哈佛大學教授,為了增進個案研究的教學,建立了 一個委員會。在 1937 年這個委員會致力於個案研究報告的寫作,在此個案研究 通常結構為 1.作者提出問題 2.考慮各種解決方案 3.採取解決方案之決定 4.總評 等,為一種標準程序。當時有超過一百個個案,但並沒有發揮太大效益。但它卻 影響到公共行政研究所,公共行政所的教授也開始蒐集研究生的報告關於個案研 究的資料。 美國的五所大學共同組織一個個案研究發展委員會於 1948 年,領導者為哈 佛大學教授,而此委員會獲得了卡內基(Carnegie Corporation)的經費支助。該 委員會的會員在 1951 年也拓展至其他大學,並將這個社團取名為「大學校際個 案教學組織」。大學校際個案組織在 1952 年發行一本個案彙編,主編者為 Harold Stein,從此之後個案由阿拉巴馬(Alabamea)大學出版組發行。最後 1957 年此 委員會從福特基金籌到一筆補助款,使這個個案研究計畫可以繼續,且拓展到其 他領域。經歷這麼多年的發展,個案研究法也逐漸被運用到各個領域。 一、定義 個案的定義為從許多相關的事時說明,找出問題,並尋找可以解決問題的方 案,所描述的事件必須是真實的,且至少有一個中心問題,做出客觀描述。「個 案」為一項事實或者一組事件,可提供一個以上的問題供人們思考,並嘗試去解 決它,因此可以將個案看成一個工具,提供人們引發思考判斷與正確行動。 個案於研究上可以指個人或是團體,包含家庭或學校等團體,但這些對象都 是具有代表性的,藉由選定的個案進行資料分析,期望最後可獲得結論。而從文 獻探討中,對於個案研究的定義可以整理如下:個案研究指對特別人或團體,蒐 集的資料之後,再對其問題的因果做深入的探究(葉重新,2001);之見,個案 研究可分個案為人、事、物所做的研究,或是對一個組織單位所做的研究。組織 於此包含學校、家庭、醫院等團體(陳李綢,1996);個案研究為一種系統性針 對個人或團體的行為、發展、概念等做深入研究分析(陳品玲,1996);無論實
驗法、調查法、歷史法、個案研究法或檔案分析法(archival analysis)都可運用 於運用於探索性、描述性或解釋性的研究上,而判斷標準為「研究問題的性質」、 「研究者對研究現象可掌控的程度」、及「研究現象是同時期或非同時期的事物」 (contemporary events)來進行研究方法之選擇。當研究者對於同時期的研究社會 現象提出如:為什麼、如何等研究問題,並對研究現象只有部份或沒有控制性時, 多數採用個案研究法;若是對於同時期的社會現象提出是誰、何處、是什麼等問 題時,則多採用調查法(Yin, 1994)。 個案研究是在自然環境下研究,且蒐集資料方式有多種,但重點在於觀察, 於研究模式中的自變數與應變數以及研究方式尚未確定,因此可被歸屬為探索性 研究(Alavi &Carlson, 1992);在教育百科辭典中,提及個案研究法是對人、事進 行深入研究的方法,且探究的人事可能具備某種特質,也可能不具備任何特質; 個案研究是經由多方資料來重組一段過去或正發的事,包含直接直接觀察、系統 的訪談、政府與私人收藏的檔案資料(Leonard-Barton, 1990);個案研究法是研究 單一環境中可能發生各種變化的研究策略,於本質上屬於探索性研究(Eisenhardt, 1989) 根據葉重新(2001)研究表示,因為個案研究為決定導致個人或團體狀態或 行為的因素之間的關係,因此,研究對象需做深入的研究,多方蒐集關於個案的 資料,並了解個案發展及現況,進而研究分析以確定問題癥結,提出建議,重點 在個案發展分析,一般研究者以具代表性的團體為對象,經過深入分析樣本資 料,期望從中得到結論,以推論至所屬母體。 個案研究於教育領域的意涵,指針對個人的特性或特殊行為做深入研究,此 過程需要透過各種方式蒐集資料並整合分析,以了解其形成原因,進而相關的應 應策略,以改善現況也增進個人適應性。換句話說,教育方面個案研究主要探討 人的行為偏差或特殊問題,其望了解問題或行為形成的癥結,以歸納出因應或解 決之道。 總結,個案研究主要針對單一或團體進行研究,借由多方資料與多重比較分
析,以期找出有規律的結果,是一種邏輯性導向思考過程,以求解決問題之道。 二、採行目的 個案研究的採行目的為深入檢視個案中不同的特性,研究人員經過長期觀察 蒐集資料或是訪談,與經驗法不同的是,研究者所需要的相關資料並非全部來自 主觀參與者手中,而是部份由客觀觀察中取得,故被認定為較客觀的方式。在教 育方面,個案研究法採行目的整理如下:1.經由資料蒐集與分析,深入了解個案 所要探究的問題,並找出解決方案;2.招集相關人員透過溝通以達成共識,針對 問題進行調整與配合;3.經由招開會議,教師互相分享經驗增進專業技能。目的 不僅為探究問題癥結點,並期望得到具體因應對策,並將問題解決方案行動。 個案研究可區分為探索性個案研究、描述性個案研究以及解釋性個案研究, 分述如下(葉重新,2001); 探索性個案研究的形式如:是什麼?例如:什麼方法能使學生成績提升?; 描述性個案研究的形式如:誰?何處?例如:誰會考班上第一名?;解釋性個案 研究的形式如:如何?為什麼?例如:如何提升學生成績?。 除上述三種方法,1994 年 Yin 提出 1.根據個案數量,可區分為單一個案 (single-case)與多重個案(multi-case)的個案研究;2.根據欲探討事件數量,可 區分為單一事件(single-incident)與多重事件(multi-incident)的個案研究等類 型。1998 年 Creswell 提出以研究過程中扮演的角色來區分該個案研究類型,若研 究者有興趣的是個案本身,最後結果呈現出個案全貌,則稱本質性個案研究 (intrinsic case study);
若以研究者感興趣的議題區分,個案僅提供做為輔佐案例,重點在議題非個 案,則稱工具性個案研究(instrumental case study),意即個案只是輔佐工具。綜 合上述,進行個案研究目的:1.找出事因,提出解決之道 2.深入研究議題,結論 出發現,以後續行動為依據 3.尋求個案潛在能力,幫助個案發展 4.當研究對象為 團體時,診斷管理上缺失,提出改進方案。
個案研究法設計邏輯包含:1.個案研究是在真實背景下,研究的現象尤其是 背景與現象界線不清時;2.個案研究的探究,於處理技術上特殊情境,研究者關 心的變數比資料多,所以非常需要多方證據來源,異質的資料則需在三角檢定法 下收斂並達成相同結論,個案研究是一種週延而完整的策略,並非一種蒐集資料 或設計特徵。就本質而言,特徵整理,葉重新(2001)認為 1.注重個體研究 2. 以多種方式蒐集資料 3.注重分析 4.注重診斷 5.需符合科學原理;白錦門(1994) 認為,1.其為質性研究,不易以數字表達,只能用文字描述 2.需詳盡且深入 3. 需正確描寫 4.非正式手續,意即個案研究可不拘時地,但需隨時注意;陳萬淇 (1985)認為,符合以下五種性質,包含探討性:研究者需對個案現有資料分析, 蒐集相關事實,且須分辨事實間的關係,診斷性:研究者需有良好判斷力,可行 性:提出解決之道後,需確認這些方法可行,比較性:針對各方案評估利弊,確 定性:確定方案以執行。 肆、實施的流程 實施流程包含三步驟:1.確定研究對象 2.調查且蒐集資料 3.個案分析與研究 進而撰寫報告,諸多學者為協助研究者進行個案研究時,有明確研究步驟,提供 相關步驟供參考:Yin(1994)提出,先確定研究問題性質,再蒐集相關資料、 分析資料,最後撰寫報告;廖榮利(1992)提出,先選擇一個社會現象為研究個 案,再蒐集跟此現象相關的資料,詳細分析、描寫發展過程與內在、外在各種因 素間的關係,最後與其他類似個案做比較分析,並將研究結果歸納整理而下一概 括論斷或定出某種原理法則;Eisenhardt(1989)指出,七步驟分別為定義研究問 題、選擇研究個案、利用各工具與資料、進入現場、資料分析、提出假說、文獻 比較與結論。 伍、資料來源 個案研究特性之一,即為個案研究蒐集資料的多樣化與資料型態呈現多元 性,是故個案研究來原可包含 1.文件:文件內容包含信件、備忘錄、公報、或會 議議程等,又如行政文件中,進度報告、提案、簡報等皆能成為個案研究者的資
訊 2.檔案紀錄:內容通常以電腦資料為主,包含服務紀錄(如服務客戶數目)、 組織紀錄(如某時期預算)、地圖、相關產品列表甚至是人口普查記錄 3.訪談: 訪談為個案研究最基本但卻是最重要的訊息。訪談方式包含開放式、焦點式以及 延伸自正式的問卷調查 4.直接觀察:如實地拜訪個案場所,此種觀察包含正是與 非正式,正式是指觀察計畫將成為個案研究計畫之一部份,非正式是指直接觀察 於實地拜訪過程中進行。5.參與觀察:經常被用於文化不同的人類學研究當中, 意可用於生活中的小群體。6.實體人造物:此為最後一種證據來源,內容包含技 術、工具、儀器甚至藝術作品。 六、報告撰寫 個案研究可不拘時地,亦沒有一定的樣式可循,甚至可以不需文字撰寫來完 成報告,即使如此,個案研究提供的資料仍受重視,樣式隨個案研究者需要而可 變化。個案研究關注人士相較於其他研究人數多,關注人士包含同領域之同僚、 決策者、領導者,及非專業個案研究的其他專業人員、學生論文評審委員、研究 經費贊助者。然而如上述,個案研究甚至可不需文字來完成,亦可以口頭報告方 式、一些表格或影片來呈現。但大多數個案研究還是以文字方式呈現,但進行報 告時,仍須慎重選擇適當且有效之方式。