國小四年級學童小數概念的概念階層分群與補救教學效益探討

國 立 臺 中 教 育 大 學 數 學 教 育 學 系 在 職 進 修

教 學 碩 士 學 位 班 碩 士 學 位 論 文

指 導 教 授 ：

林 原 宏 教 授

易 正 明 教 授

國小四年級學童小數概念的概念

階層分群與補救教學效益探討

研 究 生 ： 王 佩 芬 撰

中 華 民 國 九 十 八 年 六 月

謝 誌

三年來奔波於教職與研究所之間，在論文順利完成之際，這三年來的點點滴 滴浮現心頭，心頭充滿了無限的感謝。 感謝易正明教授與林原宏教授在這三年來的指導，儘管兩位教授相當忙碌， 但對論文的指導仍是十分嚴謹，對學生全心全意的付出，著實令我佩服。感謝老 師不斷的引導，使我更瞭解自己的研究，也才能撰寫出更完整的論文，感謝老師 如此用心指導論文，讓我著實成長了不少。 感謝口試委員朱延平教授、陳玉樹教授、陳錦杏教授在百忙之中仍抽空審閱 我的論文，並且在口試當天提供許多寶貴的意見，令我獲益匪淺，使得本論文更 加完備。也感謝系上多位教授在三年來在各方面的指導，不論是數學教育上的知 識或是論文研究的方法，都更加的充實了。 感謝陪我一路走來的同窗好友玫栞、惠雯、雅琦，讓我在學習的路上倍感溫 馨，除了同伴彼此之間的加油打氣，還不時給予論文上的建議，回想起來真是感 激備至。另外，還要感謝樹義國小的伙伴們在各方面的協助，讓我順利進修。也 感謝易臻老師與班上的小朋友們協助我完成問卷的施測，你們的協助是讓我完成 這本論文的最大動力，謹在此表達最深的謝意。 最後，感謝我最愛的家人，有你們的陪伴才有今日的我。 謹誌 民國九十八年六月

摘要

本研究旨在瞭解學童在小數概念的學習情況，再運用概念詮釋結構模式 (CAISM) 之方法，探討國小四年級在小數概念的知識結構，同時利用模糊集群 分析方法，將學童分群，以探討各群在小數概念的知識結構特性。研究者以五 年級為研究對象，共計 33 人。研究工具採用自編的「國小四年級小數概念試 題」。本研究主要發現如下： 一、由概念階層結構圖之概念間的上下位關係可瞭解到學童較易精熟與較不易精 熟的概念為何，從概念間的指向可得知較不易精熟的概念其下位概念有哪 些，可提供教學者進行補救教學的參考資訊。 二、低精熟組的學童，因為小學基本概念不精熟，較易猜測答案，所以其概念結 構圖較紊亂，概念 1 (小數意義的理解) 常不是位於最下層，而且概念間的指 向關係較異常，常不符合邏輯。 三、答對題數相同但反應組型不同的學童，除了精熟度有所不同之外，其小數概 念階層結構也不盡相同。對於低精熟組的學童而言，其概念結構圖大致相同， 但對中精熟組的學童而言，其概念結構圖差異頗大。由概念階層結構圖中判 斷出某個概念的異常情況，可提供補救教學的一個方針。 四、在進行補救教學前的概念結構圖不太符合邏輯性，分析其答案，發現學童答 錯的原因有可能是看錯選項、不瞭解題意或對概念的不熟悉而隨意猜測答 案，但仍然會造成相對應的概念精熟度下降，或使概念落在概念結構圖的不 同層次。所以在補救教學前的概念結構圖才會較不符合小數的邏輯性，但經 過補救教學後，概念結構圖較能符合邏輯性。 關鍵字：概念詮釋結構模式、模糊集群、小數、知識結構

II

Abstract

The purpose of this research is to explore the decimal concepts for pupils, and to apply the concept advanced interpretive structural modeling (CAISM) to investigate the knowledge structure about these decimal concepts. Meanwhile, the researcher employs the fuzzy cluster analysis to discuss the knowledge structural properties for each cluster. The sample includes 33 fifth graders. The research tool is self-designed test. The main results of this study are follows:

1. From the conceptual relations of CAISM graphs, the researcher realizes what kind of concepts the pupils can easily master them. According to the linkage of concepts, the researcher can obtain the non-master concept of pupils and references of the remedial instruction.

2. Because the low-proficient pupils easily guess in the tests, the CAISM graphs of the low-master pupils are not regular. Concept one (The realization of decimal meaning) is at the lowest layer, and the linkage of concepts is abnormal and does not fit in with the logic frequently.

3. Pupils who have the same total score with different response pattern own different masters and structures. For the low-master pupils, the CAISM graph is almost the same. However, for the mid-master pupils, the CAISM graph is quite different. The researcher can judge by the abnormal situation of the concept from the CAISM graph, and obtain the problem of the concepts.

4. Although the CAISM graph did not fit in with the decimal logic before the remedial instruction, it can fit in with the logic after the remedial instruction.

Keywords: concept advanced interpretive structural modeling, fuzzy cluster, decimal, knowledge structure

目 錄

第一章 緒論... 1

第一節 研究動機... 1 第二節 研究目的... 4 第三節 名詞釋義... 5

第二章 文獻探討 ... 7

第一節 小數知識... 7 第二節 小數迷思概念... 9 第三節 概念詮釋結構模式... 11 第四節 模糊集群分析... 15 第五節 認知診斷方法... 17

第三章 研究方法 ... 25

第一節 研究流程... 25 第二節 研究樣本... 27 第三節 研究工具... 27 第四節 資料分析... 32

第四章 結果結果與討論 ... 35

第一節 同一群學童之概念詮釋結構圖比較... 35 第二節 不同群學童之概念詮釋結構圖比較... 45 第三節 答對題數相同但反應組型不同之概念詮釋結構圖比較... 48 第四節 補救教學前後之概念詮釋結構圖差異... 55

第五章 結論與建議 ... 85

第一節 結論... 85

IV 第三節 建議... 88

參考文獻... 91

附錄一 小數概念預試試題 A 卷 ... 101

附錄二 小數概念預試試題B卷... 106

附錄三 小數概念試題 A 卷 ... 111

附錄四 小數概念試題 B 卷... 114

附錄五 受試者反應矩陣 ... 117

附錄六 試題屬性矩陣 ... 119

附錄七 不同精熟組學童之模糊關係矩陣 ... 120

附錄八 不同精熟組學童之模糊關係矩陣 ... 123

附錄九 低中精熟組學童之模糊關係矩陣 ... 125

附錄十 補救教學前低中精熟組學童之模糊關係矩陣 ... 127

附錄十一 補救教學後低中精熟組學童之模糊關係矩陣 ... 130

附錄十二 補救教學教案 ... 133

附錄十三 19 號學童補救教學逐字 ... 146

表目錄

表 2-2-1 小數迷思概念表... 9 表 3-3-1 試題概念表... 28 表 3-3-2 試題屬性矩陣... 28 表 3-3-3 預試試題難度... 30 表 3-3-4 預試鑑別度... 31 表 3-3-5 正式施測試題分析表... 32 表 4-1-1 學童的精熟度矩陣... 37 表 4-1-2 不同群數的分割係數與分割亂度... 37 表 4-1-3 各群學童的精熟度... 38 表 4-1-4 不同精熟度學童之答題情況... 39 表 4-1-5 不同精熟組學童之二元關係矩陣... 39 表 4-1-6 九年一貫暫行綱要之小數能力指標... 41 表 4-1-7 小數概念發展順序... 41 表 4-2-1 不同精熟組學童之答題情況... 45 表 4-2-2 不同精熟組學童之二元關係矩陣... 46 表 4-3-1 答對題數相同但反應組型不同的學童其答題情況... 49 表 4-3-2 答對題數相同但反應組型不同的學童其二元關係矩陣... 49 表 4-4-1 補救教學前之答題情況... 55 表 4-4-2 補救教學前之二元關係矩陣... 56 表 4-4-3 補救教學前後之答題情形... 65 表 4-4-4 補救教學後之二元關係矩陣... 65

VI

圖目錄

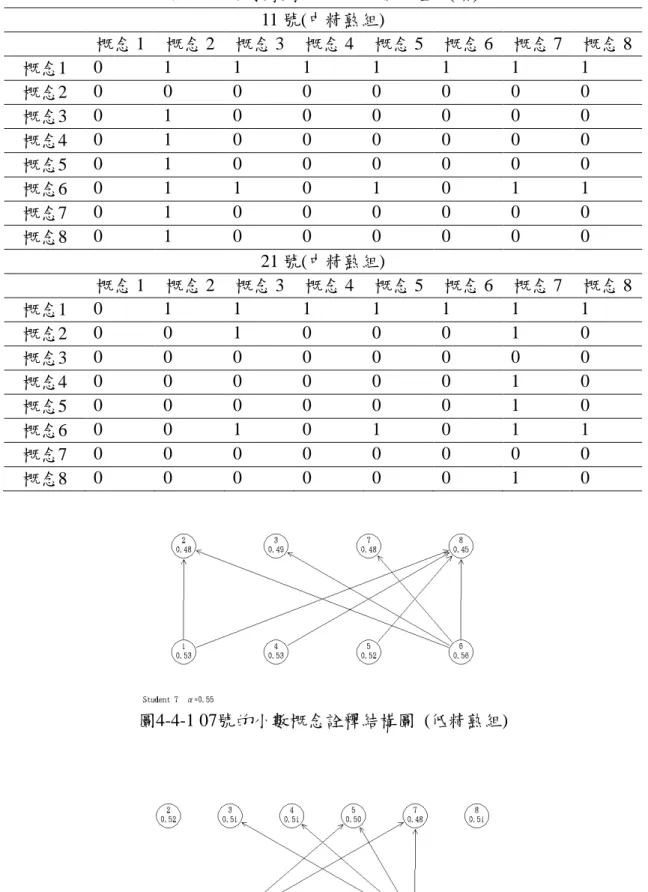
圖 3-1-1 研究流程圖... 26 圖 4-1-1 低精熟組學童的概念詮釋結構圖………..42 圖 4-1-2 中精熟組學童的概念詮釋結構圖... 43 圖 4-1-3 高精熟組學童的概念詮釋結構圖... 43 圖 4-2-1 27 號的概念詮釋結構圖 (低精熟組) ... 46 圖 4-2-2 03 號的概念詮釋結構圖 (中精熟組) ... 47 圖 4-2-3 20 號的概念詮釋結構圖 (高精熟組) ... 47 圖 4-3-1 01 號的概念詮釋結構圖 (低精熟組) ... 50 圖 4-3-2 06 號的概念詮釋結構圖 (低精熟組) ... 51 圖 4-3-3 03 號的概念詮釋結構圖 (中精熟組) ... 51 圖 4-3-4 15 號的概念詮釋結構圖 (中精熟組) ... 51 圖 4-4-1 07 號的概念詮釋結構圖 (低精熟組) ... 57 圖 4-4-2 19 號的概念詮釋結構圖 (低精熟組) ... 57 圖 4-4-3 30 號的概念詮釋結構圖 (低精熟組) ... 58 圖 4-4-4 18 號的概念詮釋結構圖 (中精熟組) ... 58 圖 4-4-5 11 號的概念詮釋結構圖 (中精熟組) ... 58 圖 4-4-6 21 號的概念詮釋結構圖 (中精熟組) ... 58 圖 4-4-7 07 號在補救教學前後的概念詮釋結構圖... 67 圖 4-4-8 07 號在補救教學前後的精熟度比較圖... 67 圖 4-4-9 19 號在補救教學前後的概念詮釋結構圖... 71 圖 4-4-10 19 號在補救教學前後的精熟度比較圖... 71 圖 4-4-11 30 號在補救教學前後的概念詮釋結構圖... 74 圖 4-4-12 30 號在補救教學前後的精熟度比較圖... 74 圖 4-4-13 18 號在補救教學前後的概念詮釋結構圖... 77

圖 4-4-14 18 號在補救教學前後的精熟度比較圖... 78

圖 4-4-15 11 號在補救教學前後的概念詮釋結構圖... 80

圖 4-4-16 11 號在補救教學前後的精熟度比較圖... 80

圖 4-4-17 21 號在補救教學前後的概念詮釋結構圖... 82

第一章 緒論

教師傳授知識，評量是檢驗教學效果的過程，教師應透過評量的方式來改 善自己的教學 (教育部，2003) ，但傳統的紙筆測驗只能提供對或錯的訊息， 無法清楚呈現學童不懂到什麼程度 (黃可欣，2006) ，學童的迷思概念只能由 教學經驗豐富的教師來發覺，否則很難判斷出來。因此本研究利用概念詮釋結 構模式(concept advanced interpretive structural modeling, CAISM) 與模糊集群分 析(fuzzy cluster analysis) 來探討國小四年級學童在小數概念上的表現，希望可 以藉由 CAISM 診斷出學童的迷思概念，並分析出概念間的上下位階關係，讓 教師能直接教授學童的迷思概念，提升學童的學習成效。本章將說明研究動機、 研究目的和名詞釋義。

第一節 研究動機

近年來，隨著資訊科技的創新、發展，知識隨手可得，也隨時被淘汰、更新。 今日，知識本身不再具有高價值，也因此各國教育上一個很重要的改變，就是從 強調知識的吸收，到愈來愈重視關鍵能力的培養 (楊素芬，2006) 。大多數的研 究者認為知識是儲存於大腦的網路中，概念之間彼此有階層關係，因此分析概念 結構對於教學就相當重要 (Bart & Orton, 1991) 。小朋友在接受這麼多訊息的同 時，有效的學習就顯現得十分重要，進一步來看，有效的教學才能達到有效的學 習，如何協助老師教學精緻化是未來教育的重要方向。在小學的課堂上，大多是 運用評量測驗卷來檢測學生學習的情形，但往往都運用所得的分數來探討小朋友 學習的成效，對於改正迷思概念並無助益。在心理計量領域，類似概念階層結構 之分析方法很多，例如：概念構圖 (concept mapping)、次序理論 (ordering theory, 簡稱OT)、詮釋結構模式 (interpretive structural modeling, 簡稱ISM) 、徑路搜尋 法(pathfinder)、試題關聯結構 (item relational structure, 簡稱IRS ) 、規則空間

(rulespace) 、知識空間 (knowledge space) 等。知識空間、徑路搜尋法、規則空 間都提供較少的試題概念及階層 (Lin, Hung & Yu, 2007) ，其他的方法的主要是 想從元素或試題間關係的資料中，找出上下從屬關係，來說明受試者的概念屬 性。而元素關係的系統化分析，運用ISM是一個相當重要又有效的方法 (林原 宏，2005) 。ISM方法是由Warfield (1976) 根據元素之間的關係矩陣，所提出一 種將元素階層化表示的方法。它原是被運用在社會系統工學 (social system engineering) 中彙整訊息的建模方法。數年後，Warfield (1982) 進而提出了ISM 在社會學、人類學、心理學及哲學等其他領域的應用。不過ISM分析法中的元素 關係只限於二元關係，並且只能得到整體受試者的概念詮釋結構圖，使其在應用 上大受限制。運用CAISM，突破了二元的限制，可以就學童的測驗資料提供個 人化的概念階層結構訊息，並可以數值和圖形結構呈現個人化概念階層結構 (Lin, Hung & Huang, 2006) ，以圖形化的方式來呈現各個概念間的關連性，讓讀 者瞭解概念間的上下位階關係，且可針對每位學童提供個人化的訊息，讓讀者瞭 解每位學童的迷思概念，且不因施測人數與他人作答情形而受影響，本研究針對 小樣本來進行研究，不同於以往研究中都是以大樣本來進行。

近年來，已經有許多研究者運用CAISM針對不同領域加以研究 (林原宏、陳 紹銘、黃國榮，2006；戴筱玲、洪文良、林原宏，2009；呂秀茹、洪文良、林原 宏，2009；Upadhyay, Gaur, Agrawal & Arora, 2007) ，可瞭解個別學生學習的概 念階層順序。但本研究不只是分析學童的試題概念屬性階層結構特徵，也不只是 瞭解概念間的上下位階關係，還更探討學童所的呈現的試題概念屬性階層結構特 徵是否與教師的預期有所差異，並且就精熟度不同的學童進行補救教學，瞭解學 童的迷思概念後，進行複本測驗，再分析一次學童的試題概念屬性階層結構特徵 是否有所改變，探討學童的迷思概念是否有所澄清，達到個別化診斷的目的，所 以本研究兼顧了質性與量性的特色。 在教學現場中，教師若能有效率的進行適性化教學，對於學童的學習會有很

童的補救教學，教師更能有效率的提升學童的學習成效。集群分析是根據資料變 數的相似度，客觀的加以分群，使同一群內有高度的均一性，不同群之間有明顯 的異質性 (林邦傑，1981) 。分群的方法很多，本研究採用模糊集群分析方法， 就是把模糊理論的隸屬度觀點融入集群分析 (Yang & Wu, 2006) ，就是為了透過 模糊邏輯的概念，有效完成集群分析，使研究者更容易判斷分群結果，來進行下 一步分析。 人類很早就有分數的概念，當一個不滿一個單位量的量，需要被原單位量予 以測量並加以描述 (數值化) 時，就產生了分數的問題，並發展出分數的數概 念；但是人類很晚才有小數的概念，當人們想將印度─阿拉伯記數系統由整數推 廣至分數情境時，才產生小數的問題，並發展出小數的數概念。小數與分數及整 數都有關係，以小數「0.35」為例，它和分數 100 35 的意義相同，都是等分割後的 結果；它的記法也和整數的記法相同，都滿足左邊位置的位值，都是相鄰右邊位 置位值 10 倍的位值概念，例如個位的位值是十分位位值的十倍，十分位的位值 是百分位位值的十倍。小數的出現，代表印度－阿拉伯記數系統，由整數範圍擴 展到了分數 (引自周筱亭、黃敏晃，2001) ，因此「小數」在數的發展過程中扮 演了一個重要的角色，在現今高度文明的社會，數學知識與數學能力，已逐漸成 為日常生活及職場裡應具備的基本能力 (教育部，2003) ，我國的國民中小學九 年一貫課程綱要將數學內容分成數與量、幾何、代數、統計與機率、連結等五大 主題，其中「數與量」在國民教育的數學課程中具有最重要的地位，其主要概念 的形成及演算能力的培養均奠基於國小階段，國小數與量的範圍較大，因此分為 「整數」、「量與實測」、「有理數」和「估算」等子題，而當中的「有理數」 是小學的核心課程之一，也是小學數學教育中，最有挑戰性的教學主題，「小數」 更是有理數的一大分支，不但承接了整數的學習，更與分數有密切的關係 (教育 部，2003) ，因此「小數」在整個國小課程中著實重要。 小數的主題相當重要，一方面是小數在生活中運用相當多，生活中數據的呈

現，亦是由小數進行使用，例如：時間 (1.5小時) 、報章雜誌所報導的統計數字 (1.28億人) 、測量容量時 (5.12公升、0.25毫公升) 、測量距離時 (7.6公里、3.26

公尺)……，所以「小數」在國小課程中日益受到重視；另一方面根據一些數學

教育的研究結果顯示，發現小朋友在學習小數時，常會發生迷思概念，造成學習 上的困難 (劉曼麗，1999，2001，2002b；陳文利，2001；Glasgow, Ragan, Fields, Reys & Wasman, 2000; Irwin, 2001) 。劉曼麗 (2005) 指出當學生學習小數時，對 於無法掌握的問題，往往將其所知的整數知識或分數知識過度類推，而產生迷思 概念。小數的學習是否穩固，會影響日後在數學概念上的學習，因此透過此研究 來加以診斷並進行補救教學，來提升小朋友在學習小數單元的成效，是有其必要 性的。 總而言之，本研究想以國小四年級教材的小數概念為研究內容，並以 CAISM 與模糊集群分析為理論基礎，來進行教學後的診斷，探討學童在小數概念的階層 結構特徵，接著進行補救教學，來幫助學生改變迷思概念後，再進行複本測驗， 並檢視對學童的迷思概念是否有所改變。

第二節 研究目的

一、根據模糊集群分析，針對概念詮釋結構模式的分析結果加以分群，探討各群 學童的圖形特徵與彼此間的關連性。 二、根據分群的結果，探討不同群(精熟度不同)的學童其圖形特徵與彼此間的關 連性。 三、探討總分相同，但反應組型不同的學童，其概念詮釋結構圖間的異同。 四、隨機選取精熟度不同的學童進行補救教學後，探討概念詮釋結構圖前後的差 異。

第三節 名詞釋義

一、小數 參與本研究的學童使用南一版四年級的數學教材，為了配合教材，所以本研 究中的小數是指一、二、三位的純小數與帶小數為研究範圍。例如：0.25 為二位 純小數，5.276 為三位帶小數；並且只限於有理數的範圍內，對於循環小數與無 理數則不包含在內。 二、小數概念 國小數學課程關於小數的教材內容可分為「小數的數概念」和「小數的運算」 兩大部分 (周筱亭、黃敏晃，2001) ，四年級學童在「小數的運算」此部分尚未 學習完，所以小數的運算不在本研究的範圍中。參考劉曼麗 (2002a) 對於「小 數概念」的分類，並且根據南一版四年級的數學教材的內容，因此本研究所指的 小數概念主要包括：1.小數意義的理解。2.小數的位值與位名。3.小數的化聚。 4.小數的十進位結構。5.小數與數線對應關係。6.比較小數大小。7.小數的稠密性。 8.小數與分數的轉換。

三、概念詮釋結構模式 (concept advanced interpretive structural model, 簡稱 CAISM)

此分析法是由 Lin, Hung and Huang (2006) 所提出，CAISM 的分析目的，是 根據受試者的測驗資料，提供個人化的概念階層結構訊息。此模式根據概念向量 比對 (concept vector matching) 和模糊理論 (fuzzy theory) 等計算方法，並利用 詮 釋 結 構 模 式 (interpretive structural modeling, ISM) 的 階 層 結 構 運 算 法 則 (Warfield, 1976, 1982 ) 可 以 數 值 和 圖 形 結 構 呈 現 個 人 化 概 念 階 層 結 構 (individualized concept hierarchy structure)。

四、模糊集群分析 (fuzzy cluster analysis)

把集群分析和模糊理論兩者的概念結合起來，即為模糊集群分析 (fuzzy cluster analysis) (Yang & Wu, 2006) ，透過模糊邏輯的概念，來完成集群分析。

在模糊集群分析中，隸屬度是決定元素之間距離的重要因素 (劉湘川、許天維、 林原宏，1998；Kaufman & Rousseeuw, 1990) 。根據模糊理論所進行的集群分析 方法很多，本研究使用目標函數法，把各概念精熟度相似的學童分在同一群。

第二章 文獻探討

第一節 小數知識

當一個不滿一個單位量的量，需要被原單位量予以測量並加以數值化描述 時，就產生了分數，並發展出分數的數概念；當人們想將印度─阿拉伯記數系統 由整數推廣至分數情境時，才產生了小數，並發展出小數的數概念 (周筱亭、黃 敏晃，2001) 。小數可視為不帶分母的十進位分數，以小數數字「2.34」為例， 可以記成「2.34＝2+ 10 3 + 100 4 」，因此，有人將小數稱為十進分數，小數的出現， 代表印度－阿拉伯記數系統，由整數範圍擴展到了分數。 小數與分數及整數都有關係，以小數「0.35」為例，它和分數 100 35 的意義相 同，都是等分割後的結果；它的記法也和整數的記法相同，都滿足左邊位置的位 值，都是相鄰右邊位置位值10倍的位值概念，例如個位的位值是十分位位值的十 倍，十分位的位值是百分位位值的十倍。 因為先發展出分數，再透過小數將分數推廣至印度─阿拉伯記數系統，所以 國小教材先引入整數及分數的教材，等到學童能掌握分數的意義及整數記法的位 值概念後，可朝兩個方向來學習小數：第一：因為分數與小數皆由等分割及合成 活動製作而成，所以透過分數概念引入小數的記法，例如：小數 0.1 是分數 10 1 的 另一種記法，小數 0.01 是分數 100 1 的另一種記法，0.38 是 38 個單位小數「0.01」 合成的結果；第二是由印─阿記數系統的位值概念來瞭解小數，例如：0.38 是記 錄 3 個「0.1」和 8 個「0.01」的合成結果，再幫助學童類比整數，發現小數的記 法和整數的記法相同，都滿足位值概念。 小數、整數、分數三者之間的關連如此密切，因此許多研究分析比較三者間 的異同 (Resnick, Nesher, Leonard, Magone, Omanson & Peled, 1989; Hiebert,

1992) ，整理如下：(1)小數與整數的異同:整數位名是從個位開始，順序是從右 到左 (個位，十位，百位，...) ，但讀整數的順序卻從左到右 (...，百位，十位， 個位) ；相對地，小數位名是從十分位開始，順序是從左到右 (十分位，百分位，...) 而讀小數的順序也是從左到右 (十分位，百分位，...) 。(2)小數與分數的異同： 純小數與真分數兩者都是表示0與1之間的一個值，當整體被分割成越多等分而每 一分的數值就越小，在0與1之間有無限多個分數也有無限多個小數。在分數的符 號表徵中，分母可顯示一個單位被等分成多少等分，分子顯示佔多少等分，整體 被分成任何等分，都能用分數表示；但在小數的符號中，一個單位被等分成多少 等分是隱含在位數中，佔多少等分是由小數點後的部份顯示，整體被分成10的冪 次方等分，才能以小數表示。 記數系統是數概念的一種表徵系統，它是人類文化上的產物，在印度─阿拉 伯十進位記數系統中，小數的記數系統是整數記數系統的延伸，因此仿整數記數 系統記數的方式，仍然採用 0～9 等 10 個數碼，配合位值概念，來記錄小數。在 整數記數系統中，各個相鄰位值間滿足 10 倍的等比例關係，以數字「1111」為 例，十位的 1 是個位的 1 的 10 倍 (個位的 1 是十位的 1 的 10 1 倍) ，百位的 1 是 十位的 1 的 10 倍 (十位的 1 是百位的 1 的 10 1 倍) ，千位的 1 是百位的 1 的 10 倍 (百位的 1 是千位的 1 的 10 1 倍) 。因此，當我們將印度─阿拉伯記數系統由整數 推廣至小數時，小數部份也必須滿足左邊位置的位值是相鄰右邊位置位值十倍的 等比例關係，也就是說，個位的 1 要是十分位的 1 的 10 倍 (十分位的 1 是個位 的 1 的 10 1 倍) ，十分位的 1 要是百分位的 1 的 10 倍 (百分位的 1 是十分位的 1 的 10 1 倍) 。當我們將整數計數系統推廣至小數時，小數部份十分位位置的位值 必須是個位位置位值的 10 1 倍，也就是說，十分位是記錄有幾個 10 1 的位置，因此 1

須是十分位位置位值的 10 1 倍，也就是說，百分位位置的位值必須是個位位置位 值的 100 1 倍，因此，引入單位小數 0.01 時，0.01 必須等於 100 1 (個 1) 。透過上 述方式將印度─阿拉伯記數系統推廣至小數時，小數也可以用十進表示法來溝通 位值概念，例如小數數字「30.078」表示 3 個十、0 個一、0 個 0.1 (十分之一) 、 7 個 0.01 (百分之一) 和 8 個 0.001 (千分之一) 的總和，也可以使用十進表示法 「30.078＝3×10＋0×1＋0×0.1＋7×0.01＋8×0.001」來記錄小數。也就是說，小數 的記法和整數的記法都滿足逢十進一的位值概念。

第二節 小數迷思概念

從文獻中發現，國內外的學童在學習小數時都會有很多的迷思概念，針對本 研究所探討的概念，整理出小數迷思概念表 2-2-1 如下。 表 2-2-1 小數迷思概念表 小數概念 迷思概念 文獻 1.小數意義的理解 ◎認為a.b 個就是a 個及將單 位量分成b 份取其中的一 份。 ◎在連續量的情境中，將小數 點左邊的數視為大單位的 個數，右邊的數視為小單位 的個數。 ◎將單位小數的內容物個數 皆視為1。 劉曼麗 (2003) 劉曼麗 (2003) 劉曼麗 (2002a) ；梁惠珍 (2003)

表 2-2-1 小數迷思概念表 (續) 2. 小 數 的 位 值 與 位 名 ◎認為a.b 個就是a 個及將單 位量分成b 份取其中的一 份。 ◎受到整數位名、位值的影 響，將整數的位名、位值套 用在小數上。 劉曼麗 (2003) 劉曼麗 (2002b) 3.小數的化聚 ◎受到0的影響而將個數放在 小數點後。 ◎直接移動小數點來決定化 聚 結 果 ， 如 ： 0.8 是 8 個 0.01、35 個0.1 是0.35 劉曼麗 (2002b) 陳文利 (2001)； 郭孟儒 (2002)； 劉曼麗 (2001, 2002b) 4.小數的十進結構 ◎在序數小數時，如遇進位便 容易出錯，例如：認為0.9 後為0.10。 Frobisher, Monaghan, Orton, Orton, Roper & Therlfall (2002) 6.比較小數大小 ◎整數法則：學童認為小數點 後數字越多，其值越大；小 數點後數字越少，其值越 小。 ◎分數法則：學童認為小數點 後數字越多，被分割成的部 分就越小，所以其值越小。 ◎完全忽視小數點的存在 劉曼麗 (1999, 2003) 艾如昀 (1994) ；Resnick, et al. (1989) Irit (2003) ；Roberta (2003) ；Hiebert & Wearne (1986)

7.小數的稠密性 ◎認為兩個小數之間並無任

何數的存在。

表 2-2-1 小數迷思概念表 (續) 8. 小 數 與 分 數 的 轉 換 ◎直接把分子當成整數部分 而 把 分 母 當 成 小 數 部 分 ( a b =a.b) ◎直接把分母當成整數部分 而 把 分 子 當 成 小 數 部 分 ( a b =b.a) ◎不管分母的數字，就直接把 分 子 拿 來 當 成 小 數 部 分 ( a b =0.b) 艾如昀 (1994) ；劉曼麗 (1999, 2003) ；Hiebert & Wearne (1986)

第三節 概念詮釋結構模式

Warfield (1976, 1982) 所 提 出 的 詮 釋 結 構 模 式 (interpretive structural modeling, ISM) 原本應用於社會系統工學，但Lin, Hung and Huang (2006) 擴展詮 釋結構模式，並根據察覺模糊邏輯模式 (fuzzy logic model of perception, FLMP) 和概念向量比對 (concept vector matching) ，以模糊截矩陣 (alpha cut) 之 ISM 演算，即可以數值和圖形結構呈現個人化概念階層結構 (individualized concept hierarchy structure)，而且試題不受二元計分所限制。其分析方式如下 (引自Lin, Hung & Huang, 2006) ：

假設某測驗有二元計分的M個試題，此測驗共測量A個概念，而受試者共 有 N 位。X(x_nm)_N_M為受試者反應矩陣，xnm 1表示受試者 n 答對試題 m ；反 之 x_nm 0 表 示 受 試 者 n 答 錯 試 題 m 。 Y(y_ma)_MA 為 試 題 屬 性 矩 陣 (item-attribute matrix)，y_ma 1表示試題 m 測量概念屬性 a ；反之y_ma 0表示試 題 m 沒有測量概念屬性 a 。A個概念構成 A 2 個典型概念向量 (ideal concept vector) ，此向量以

z

_i



(

z

_ia

)

_1A表示，且I  。每個典型概念向量係表示某種2A

典型受試者之概念向量。若z_ia 1，表示該典型概念向量具備概念 a ；反之，若 0



ia

z ，表示該典型概念向量尚未具備概念 a。每個典型概念向量z_i在M 個試題

構成典型反應向量 (ideal response vector) ，此向量以r_i 

 

r_{im 1M}表示。每個典型

反應向量係表示在該典型概念向量下，對應於試題屬性矩陣Y(y_ma)_MA所獲得

的反應矩陣。若r_im 1表示典型概念向量z_i能答對試題 m ；反之，r_im 0表示典 型概念向量z 答錯試題 m ，此_i I個向量構成矩陣R )(r_{im IM}。受試者的反應矩 陣為X(x_nm)_NM與典型反應向量r_i (r_im)_1M的標準化近似值矩陣 (standardized closeness matrix) 以SC(sc_ni)_NI表示。其中sc_ni表示受試者 n 的試題反應向量 (item response vector) (x_n1, x_n2,,x_nM)，與典型反應向量



r_i r_i1,r_i2,,r_iM



之近 似值 (closeness) 。接著進行 AMC、AFC、AFISM 三種演算步驟如下：

一、AMC (Algorithm for Mater of Concepts)

1. 針對已知的受試者反應矩陣X和試題屬性矩陣Y，計算典型反應向量r_i ，由於典型概念向量為z_i (z_ia)_1A，定義典型反應向量r_i (r_im)_1M的計算如下：        else , 0 , , 2 , 1 , ) )( ( , 1 z y y a A rim ia ma ma  (1) 2. 就每位受試者n ，計算其試題反應向量與典型反應向量r_i的近似值矩陣 I N ni c _  )( C 和標準化近似值(standardized closeness)矩陣SC(sc_ni)_NI如下： M r x c M m im nm ni



  1 ) ( ) (  (2) 其中       im nm im nm im nm r x r x r x , 0 , 1 ) ( ) (  (3)

(crisp recognition) ，則令標準化近似值sc_ni：       else c K sc_ni ni , 0 1 , / 1 (4) (2)若根據cni值，若cni 1 i1,2,,I，則表示存在模糊辨識(fuzzy recognition)， 令標準化近似值sc_ni 如下：



  I i ni ni ni c c sc 1 ₍₅₎ 由以上二式可知 0sc_ni 1 且



  I i ni sc 1 1 。 二、ASC (Algorithm for Subordination of Concepts)

1. 令 D(d_na)_NA 表 示 受 試 者 n 在 概 念 a 的 精 熟 程 度 ， 所 以 可 定 義 ) )( ( ) ( SC Z Dd_{na NA}  ，計算如下：



 I i ia ni na sc z d 1 ) )( ( (6)

2. 按照 Luce (1959) 的選擇規則 (choice rule) 理論和相對適合度準則 (relative goodness rule ， RGR) ， 以 及 察 覺 的 模 糊 邏 輯 模 式 (fuzzy logic model of perception, FLMP) 之觀點，對受試者n 而言，其概念 a 為概念 'a 的先備概念

( 即 合 概 念 a 指 向 概 念 'a 的 機 率 ) 之 從 屬 關 係 機 率 (subordination relation

                else d d d d d d d and d d and d p na na na na na na na na na na aa , ) )( 1 ( ) 1 )( ( ) 1 )( ( 0 0 , 0 1 1 , 1 ' ' ' ' ' ' (7) 三、AFISM (Algorithm for Fuzzy ISM)

1.對於每個受試者n 而言，其所有兩兩概念之間的從屬關係機率構成模糊關係矩

陣 (fuzzy relation matrix) F_n(p_aa')_AA。利用截集 (-cut) ，選定值且 1

0 運算後，可獲得二元關係矩陣 (binary relation matrix) 的相鄰矩陣 (adjacent matrix) 。亦即： A A aa n p F ( ') _   且          ' ' ' , 0 , 1 aa aa aa p p p ， 其中 01 (8) 將上述步驟由截集運算所得的二元關係矩陣進行 ISM 分析，即可獲得個 人化的概念詮釋結構圖。

CAISM在教學上的運用也很多：Lin, Hung and Yu (2007) 運用CAISM來分析 國小六年級465位學童等量公理概念的學習。Yih, Lin and Hung (2007) 運用 CAISM對25位大學生進行線性代數學習的認知診斷。Yih and Lin (2007) 運用 CAISM分析27位大學學生在MATLAB的學習情形。黃雅琦、林原宏與易正明 (2008) 透過電腦化數感診斷測驗及CAISM分析法來分析國小六年級學童在分數 及小數的數感發展知識結構。莊惠雯、林原宏與易正明 (2008) 運用CAISM分析 法與自編整數加減文字題來探討國小一年級學童在加減法文字題的概念結構。吳 玫栞、林原宏與易正明 (2008) 運用自編四邊形測驗與CAISM分析法探討國小六 年級學童的四邊形概念結構。王佩芬、林原宏與易正明 (2008) 運用CAISM分析 法與自編除法試題來探討國小四年級學童的除法概念結構。詹家明、林原宏 (2008) 運用CAISM分析法來探討國小五年級學童的在數與量分年細目的概念結 構。李青芷、林原宏 (2008) 運用CAISM分析法來探討在職進修教師的基礎統計

通班學生的面積概念結構。戴筱玲、洪文良與林原宏 (2009) 應用CAISM分析法 分析國小六年級學童速率概念知識結構並以SCM演算法進行分群，探討各群受 試者知識結構圖之特徵及異同。呂秀茹、洪文良與林原宏 (2009) 運用CAISM與 SCM分析法來分析國小五年級學童的時間化聚計算之概念結構。以上研究結果 均能有效圖繪並分析受試者的知識結構，並發現不同之受試者，其知識結構圖在 連結指向及階層上皆有明顯差異，提供課程編修、教學診斷及補救教學參考之用。

第四節 模糊集群分析

Zadeh (1965) 提出模糊集合理論，使元素和集合的關係不再是傳統的二分 法，不再是全有或全無，而是以隸屬度表示之。隸屬度為介於

 

0,1 之間的連續函 數，用明確的數字，描述元素屬於模糊集合的程度。集群分析與傳統方法不同之 處，在於傳統分類法的分類準則是事先決定的，而群集分析是按照自然類別 (nature grouping) ，將分佈於某一計量空間的點予以分類 (黃俊英，1995) ，其 目的是希望集群內元素同質性高，而集群間的元素異質性高 (林邦傑，1981) 。 結合這兩個概念，即為模糊集群分析 (Kaufman & Rousseeuw, 1990) 。在模糊集 群中，隸屬度為決定元素之間距離的重要因素，模糊集群的方法有很多，本研究 選目標函數法，說明如下 (Bezdek, 1981)。 令有N位分析個體，以n1,2,3,...,N 表示，每位受試者有M 個變項，以 M m1,2,3,..., 表示，資料矩陣呈現如公式1：(引自林原宏，2005)

 

x

nm N M

X



_{ (1)} 假設根據模糊分割方法，可以將整個受試者分成C個模糊集群(C ≥ 2 )，令 模糊隸屬度為U，表示樣本點n隸屬於集群C的隸屬度，個體隸屬度矩陣為公式2：

 

u

cn C N

U



_ (2) 令矩陣V為各類別之中心，如公式3：

 

v

cm C M

V



_{ (3)} 先定義一個目標函數，並求該函數的最小值，本研究採應用最廣的目標函數 (objective function) 如公式4、公式5：

 

_

   

  N n C c q cn q U V u d c n J 1 1 2 , , (4)

  

_



  M m cm nm v x n c d 1 2 2 , (5) q為大於或等於1的實數，由公式6可知q值影響隸屬度，q值越大分割越模糊，q 值越小則分割越明確 (Zimmermann, 1991) 。經驗上q值取

 

1.25,5 較佳。以最小 平方法 (least square method) 的準則，並以Lagrange’smultipliers方法，求Jq

 

U,V

的極小值，得u 、_cn v 的關係式如公式6、公式7。cm















                                C l q M m lm nm q M m cm nm cn v x v x u 1 1 1 1 2 1 1 1 2 1 1 (6)

  

 





   _N n q cn N n nm q cn cm u x u v 1 1 (7) 決定起始值和收斂標準後，經過疊代法疊代至u 、_cn v 收斂，得到的隸屬度_cm 矩陣U和類別中心矩陣V即為所求，但目標函數得到的極小值可能是局部極小 值，因此可考慮不同的起始值來估計參數。 以上是在知道類別數為C的情況進行，本研究則根據「分割係數」、「分割 亂度」這兩個指標決定類別數，兩個指標呈現如公式8、公式9。 (Bezdek, 1981) (一)分割係數 (partition coefficient)

 

_

 

   N n C c cn u N C U F 1 1 2 1 ; (8) 此數值的範圍是 1 F

 

U;C 1 C 。 (二)分割亂度 (partition entropy) 分割係數H

 

U;C 定義為：

 

_

 

      N n C c cn cn cn u u u N C U H 1 1 0 , ln 1 ; (9) 此數值的範圍是0H

  

U;C lnC 。在實際應用時，分割係數越大，分割亂度 越小，表所選的類別數較佳 (Bezdek, 1981) 。

模糊理論在各類學科中皆廣泛應用，Huang, Desarbo and Takane (2007) 利用 廣義結構化元素分析作為一種以元素為基礎的方法，來同時評估應答者在相異群 中的模糊分類。所提出的方法可以延伸加強其資料解析能力及其應用的範圍，由 幾個算例可知此法透過資料轉換可有效地處理離散變數。陳敏彥、林原宏 (2007) 利用模糊集群分析的目標函數法來做分群，並以 S-P 表與多元計分次序理論來分 析各群之知識結構特徵，來進行國小學童數學認知診斷之分析。黃馨瑩、林原宏、 莊曜遠 (2007) 利用模糊集群分析的目標函數法來取代傳統的統計分類方法，將 學生進行分群，並以 S-P 表與多元計分次序理論來分析各群之知識結構特徵，進 行國小學童容量概念之分析，發現模糊集群分群方式可將學童有效分群，且各分 群學童的不同學習特性，以提供補救教學或充實教學的參考及依據。

第五節 認知診斷方法

評量的目的除了瞭解學童的學習情況之外，也要能同時提供學童迷思概念的 診斷，才能讓教學者針對診斷結果進行適性化的補救教學。有許多學者主張，評 量的實施應以認知心理學對學習歷程的研究結果，作為編製測驗的理論依據，這 種結合評量與認知心理學理論的方式，就是認知診斷 (cognitively diagnostic) (涂 金堂，2003) 。認知診斷結合認知與心理計量兩大領域，認知領域把知識視為網

路結構，主要是在描述知識的一般本質，把個別差異當成干擾雜訊；心理計量領 域把知識視為多向度結構，主要是在精確描述個體的知識結構，瞭解個別差異與 需求 (游森期、余民寧，2006) 。以下簡介規則空間 (rule space) 、學生與試題 分析表 (Student-Problem Chart, S-P Chart) 、徑路搜尋 (pathfinder) 、概念構圖 (concept mapping) 、詮釋結構模式 (Interpretive Structural Modeling, ISM) 、次序 理論 (ordering theory) 、試題關連結構 (item realational structure, IRS) 這七種認 知診斷方法，並與概念詮釋結構模式加以分析比較。

壹、規則空間 (rule space)

Tatsuoka (1983) 運用試題評量得知學童的試題反應組型 (item response pattern) ，進而瞭解學童的潛在知識狀態 (latent knowledge state) ，以得知學童 的學習歷程與學習結果，獲得學童的潛在知識狀態後才能進一步瞭解學童的知識 結構，由知識結構圖中可瞭解哪些概念具有良好的連結關係，哪些概念尚未學 會，哪些概念間的連結不夠，需要再加強概念間的連結，也可分辨出獲得相同分 數的學童其概念精熟差異，因此，教師可從規則空間 (rule space) 的診斷結果得 知學童哪些部分需要再加強，進而對學童進行補救教學。 Tatsuoka (1995) 以參加學術性向測驗 (SAT) 的 2000 名學生為研究對象， 運用規則空間的方法，來探討學生在數學測驗的得分其所代表的知識狀態 (knowledge state) 。能提供學童其學習歷程的正確診斷是規則空間的最大優點， 但仍無法普遍成為教學現場的評量方式，原因如下：規則空間是以試題反應理論 (IRT) 為理論基礎，因此包含了較複雜的數學公式，教師會因為不熟悉此理論中 的公式，而不採用此種評量方式。除此之外，運用規則空間所編製的評量試題必 須根據心理學的研究結果，所以才能透過工作分析讓試題包含特定的認知屬性， 但目前心理學未對數學領域的所有單元建立完整的研究結果，若由教師自行編製

「Tatsuoka 的研究僅限於結構良好 (well-structured) 的問題領域，至於結構不良 的問題，規則空間是否仍能提供有用的訊息，則有待日後的證實。」 (引自余民 寧，1995) 。

貳、學生與試題分析表(Student-Problem Chart, S-P Chart)

佐 藤 隆 博 (Takahiro Sato) 在 1970 年 代 提 出 學 生 與 試 題 分 析 表 (Student-Problem Chart, S-P Chart) ，藉由分析學生答題的原始資料所獲得的統計 數值，即可得知試題與學童的得分組型，這是一種圖形化的方法，這種分析測驗 資料的方法，適用於小樣本資料的分析，也很適合用於形成性評量的資料分析， 這是一種不對母群體特性設定任何假設值的統計推論方法—無母數統計方法 (nonparametric method) 。而且能藉由提供差異係數 (disparity index) 、同質性係 數 (homogeneity index) 、試題注意係數 (item caution index) 、學生注意係數 (student caution index) 來分析學生在測驗試題上的「作答反應組型」，以分析反 應組型是否為異常，目的在獲得每位學生的學習診斷資料，來提供教師實施有效 的學習輔導。根據 S-P 表分析的結果，也可以用來診斷試題功能，以試題的注意 係數當橫軸，答對試題人數百分比當縱軸，根據每個試題的這兩項數據，將每道 試題標示在座標圖裡，這個座標圖即是試題診斷分析圖，可用來幫助診斷試題的 好壞 (余民寧，2002) 。 運用 S-P 表的研究相當多：游森期、余民寧 (2006) 運用數學科認知診斷成 就測驗為施測工具，針對 286 位國小學生施測，並進行知識結構診斷評量程式與 六大指數及 S-P 表分析。結果發現知識結構診斷評量程式所計算的六種指標，對 於效標分數具有預測力，且 S-P 表分析與路徑搜尋網路分析兩種認知診斷取向的 分析結果 具有一 致性 。李志宏 、林原 宏 (2008) 結合 模糊集 群 分析 (fuzzy clustering) 、S-P 表及多元計分次序理論，針對五年級學生做幾何的認知施測。 研究結果發現分成兩群最佳，且此兩群學生的概念階層結構圖迥異，概念順序也

不甚相同。

參、徑路搜尋(pathfinder)

Goldsmith, Johnson and Acton (1991) 運用Schvaneveldt (1990) 所研發的徑路 搜尋軟體 (pathfinder) 是採用相似性評定法，根據受試者在一組概念上，透過判 斷各概念配對間的相似性、相關性或心理距離所對應的接近性矩陣 (proximity matrix) ，將所獲得的概念相近性矩陣轉換成知識結構圖，透過比較專家與生手 的結構圖可獲得以下三種數值：1.圖形的理論距離指數 (graphical theoretical distance, GTD) ，用來表示兩個知識結構圖各個概念節點之間的距離 (以相距節 點的數目多少來計算) ；2.相似性指數或稱C指數 (closeness index, PFC) ，就是 用 集 合 理 論 (set theory) 計 算 兩 個 知 識 結 構 圖 各 節 點 共 有 的 鄰 近 節 點 (neighborhood) 的相似程度；3.接近性指數(proximity index, PRX)，是用評定量尺 法所獲得的概念間接近性資料矩陣 (proximity data matrix) 求得的相關係數。這 三個指數的值域均介於0與1之間，值愈小表示受試者與參照結構愈不相似，反之 則表示愈相似。徑路搜尋能比較不同知識網路結構的類似程度，但是在診斷錯誤 概念獲得認知診斷的訊息上有限，而且近似矩陣的評定方法沒有客觀的標準，但 卻是決定知識網路結構的關鍵之處 (余民寧，2002) 。

Laura, Rebecca and Roger (2000) 利用路徑搜尋法檢視內嵌在事件知識結構 中時間線索的特點，研究結果指出時間維度愈顯著，則孩童的活動力愈高且適用 於事件比較上，即使在說明中沒有被提到。反之，時間維度愈不顯著，則孩童的 活動力愈低且只適用於特定的事件。為了瞭解個別差異，許多研究運用徑路搜尋 進行專家與生手的比較。Nash, Bravaco and Simonson (2006) 利用徑路搜尋網路 量尺化算則來評估個人知識結構的呈現方式，以及評估在進行工作坊的前後其電 腦科學中知識的轉變，結果發現這群高中教師在進行完工作坊後的知識結構網路

似。黃美盼 (2007) 以徑路搜尋測量加減法文字題的知識結構，結果發現高能力 值組知識結構圖與標準參照知識結構圖較為相似，中低能力值組知識結構圖與標 準參照知識結構圖較不相似。

肆、概念構圖 (concept mapping)

概念構圖是一種教育工具，可使用它來具體化學習者的認知結構，來清楚瞭 解學習者的已知。Novak and Gowin (1984) 認為概念構圖是一種動詞，是一種教 學活動的過程，也就是給予學習者一組概念，讓學習者用適當的連接詞 (lable) 將這些概念連接起來，作為一個概念圖，教師可由此診斷出學童的知識結構 (knowledge structure) 與迷思概念 (misconcept) ，所以概念構圖不僅是一種教學 策略，也可作為一種評量工具。傳統選擇題測驗常無法測得學習者完整的知識狀 態 (Frederiksen & White, 1990) ，而概念構圖需要學生自己架構概念，並且由回 憶中辨認概念間的關連性，強調學習者將所具備的知識以具有結構性、組織性、 完整性的方式表達出來，可針對知識的組織與結構情形來瞭解學習狀態 (宋德 忠、林世華、陳淑芬、張國恩，1998)。

宋德忠等人 (1998) 指出概念構圖可以敏感的分辨教學方式 、考試方式、與 智力水準不同所造成的差異，但Herl, Baker and Niemi (1996) 認為，有不少以概 念構圖作為評量工具，但缺點就是缺乏適當的專家模型，和較好的計分法則，使 生手與專家結果之比較上太過僵化。

概念構圖在各方面的運用相當多：Komis, Ergazaki and Zogza (2007) 比較電

腦輔助動態模式與以‘紙與筆’概念構圖技巧在14歲學生合作活動的不同，研究結

果顯示在案例中四個主要的模式活動 (分析、合成、測驗說明、技術與認知支持) 透過模式運作定義模式流程的步驟，而特定的質化差異可以確實地被辨識。Kong and Kwok (2005) 設計一種認知工具來符合學習者理解新的程序知識，此工具主 要是用在傳達分數等效性的概念及計算分數的能力。再者，研究的結果指出此模

式能提供學習者在學習加法及減法分數上更有效的程序。

伍、詮釋結構模式 (Interpretive Structural Modeling, ISM)

Warfield (1976, 1982) 提出詮釋結構模式 (Interpretive Structural Modeling, ISM) 原本發展於社會系統工學，這個方法也可應用於概念層次結構分析探討。 日本學者佐藤隆博 (1987) 提出很多ISM分析法在教育領域裡課程與學習的應用 實例，把教學者腦中抽象的要素轉為具體化的關連構造階層圖，並透過學習者概 念元素彼此間的關係，獲得整體的概念結構圖 (林原宏、陳紹銘、黃國榮， 2006) 。ISM分析法是要將學習者腦中思考的概念單位結構，用具體的圖形或數 量表示出，建立整體概念元素間的關係，也就是經由部分元素間的關係，整合起 來形成所有元素整體的關係，也可由此看出元素的高低層次和順序關係 (許天 維、林原宏，1994) 。 ISM分析法在教學上的運用也很多：蔡秉燁 (2004) 運用ISM分析方法，針 對高中數學補救教材，設計結構化教材，發現圖像式階層結構教材內容，使教學 者能確切掌握教材呈現的順序，來提升補救教學的效果。鄭麗娜 (2004) 在九年 一貫課程社會領域地理概念研究上，應用ISM分析法，畫出地理概念階層圖，藉 此規劃地理概念學習的最佳路徑與群組概念。

陸、次序理論 (ordering theory)

次序理論是應用於心理計量 (psychometrics) 的一個另類分析取向，能夠呈 現試題間的次序性關係或研究問題的次序，以利編排試題，但僅以線性次序 (linear ordering) 的關係進行分析，所以會有以下兩個問題：(1)一組題目中的線 性順序只能顯示出最精簡的題目關係，一旦題目數增加，就愈難獲得複製力 (reproductability) 。(2)一些邏輯與統計的的分析結果指出並不是所有的次序都是

序的方法，將次序理論 (ordering theory) 應用在教育工學上 (Airasian & Bart, 1973; Bart, 1976) 。從心理計量的相關研究中可以發現，次序理論的分析可以呈 現試題階層 (item hierarchy) ，且其主要應用於衡量兩個試題之間先備條件 (precondition) 之次序關係。因為次序理論能有次序、有結構的呈現事物的特點， 因此被不少實證性研究採用，且以數學學習心理學的角度來看，學生的認知不但 有階段性還有結構性。

在Bart and Krus (1973) 提出次序理論的測量模式後，之後的相關研究主要是 探討J. Piaget認知理論發展中的發展階段的次序性 (林原宏、游森期，2006)。例 如：Jansson (1986) 以次序理論分析J. Piaget形式運思的16種邏輯推理的發展先後 順序之階層結構。余民寧、陳嘉成 (1998) 將次序理論應用於評量技術的開發， 來瞭解學童學習困難和診斷學習缺陷。

柒、試題關連結構 (item relational structure, IRS)

Takeya在1980年代根據Bart and Krus (1973) 的次序理論 (ordering theory) 提出另一種計算試題次序性係數 (ordering coefficient) 的方法，就是試題關連結 構理論 (item relational structure, IRS) ，Takeya (1980, 1991) 所提出的試題關連 結構，就是以二元計分 (dichotomous) 試題，根據其列聯表資料，來計算其前置 關係 (precondition) 或是順序性關係，因此IRS是根據施測結果，並按照試題通 過率和反應順序，來繪製出試題關連結構圖 (Lin, Bart & Huang, 2006) 。

運用試題關連結構的研究也相當多：楊秀倩、陳進春、許天維 (2006) 應用 試題關聯結構分析法來對國小高年級資賦優異學童進行施測，繪製具有上、下位 概念的結構關係，結果發現五、六年級資優學生梯形面積測量概念的聯聯結構圖 都分成二個分支係和一個獨立系列，且梯形面積測量概念的學習成效頗具穩定 性，較不受時間間隔的影響。沈佩怡 (2007) 運用試題關聯結構分析法，針對國 小四年級學生進行小數概念的施測與分析，研究結果發現小數的化聚概念是先由

單位化小數合成概念開始，經由「十分位不含零、不進位之單位化小數」、「十分 位含零、不進位之單位化小數」、「十分位不含零、進位之單位化小數」、「十分位 含零、進位之單位化小數」的歷程，漸次發展至單位化小數分解概念，待單位化 的小數化聚概念成熟，學童才能往上發展非單位化的小數化聚概念。 本研究所採用的認知診斷方法是概念詮釋結構模式，不但可顯現概念間的上 下位階層關係，還有概念間的從屬關係，更可得知每個概念的精熟度，綜觀各個 認知診斷方法，概念詮釋結構模式集合了各個認知診斷法的優點，更能精準的瞭 解學童的學習情況。

第三章 研究方法

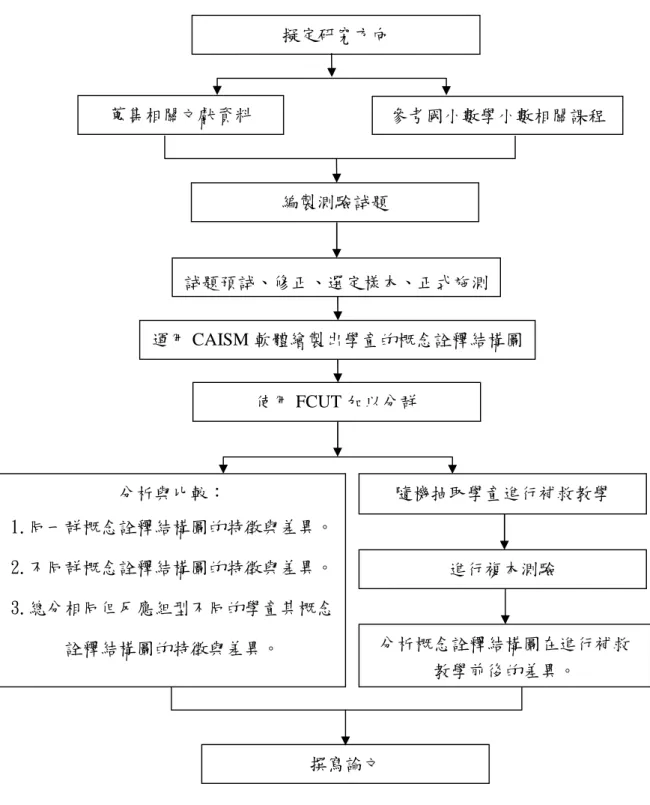
本研究以自編測驗對剛升上五年級學童進行施測，以獲得所需資料，本章將 說明本研究之研究流程、研究樣本和研究工具。

第一節 研究流程

本研究確定研究主題後，開始蒐集相關文獻：國小數學小數教材、小數相關 文獻、CAISM、模糊集群分析、認知診斷，同時開始編製預試試卷，經過專家 檢測試卷內容，並於上學期開學請幾位五年級學童進行預試後，進行試題編修， 確定正式施測試卷內容後，立即施測，施測結束後回收試卷進行整理及分析，接 著抽取幾名學童進行補救教學，再進行複本測驗，最後分析學童的概念結構圖在 進行補救教學前後的差異。本研究之流程圖如圖 3-1-1 所示。

圖 3-1-1 研究流程圖 擬定研究方向 蒐集相關文獻資料 編製測驗試題 試題預試、修正、選定樣本、正式施測 參考國小數學小數相關課程 使用 FCUT 加以分群 隨機抽取學童進行補救教學 運用 CAISM 軟體繪製出學童的概念詮釋結構圖 進行複本測驗 撰寫論文 分析與比較： 1.同一群概念詮釋結構圖的特徵與差異。 2.不同群概念詮釋結構圖的特徵與差異。 3.總分相同但反應組型不同的學童其概念 詮釋結構圖的特徵與差異。 分析概念詮釋結構圖在進行補救 教學前後的差異。

第二節 研究樣本

本研究以臺中市南區樹義國小五年某班 33 名學童為研究對象，這 33 名學童 四年級使用依據九年一貫暫行綱要所編的南一版數學教材，於 97 學年度上學期 一開學施測自編小數概念 A 卷後(如附錄三)，加以分析資料，並分群，隨機從各 群中抽取三位學童進行補救教學，補救教學後再施測自編小數概念 B 卷(如附錄 四)。

第三節 研究工具

本研究所使用的工具如下：自編小數概念測驗題，以及分析資料與繪圖的 SPSS12.0、EXCEL、CAISM軟體、FCUT軟體。分別說明如下：

壹、研究工具的編製

一、自編小數概念測驗題 本研究所使用的自編小數概念測驗題是參考劉曼麗 (2002a) 對於「小數概 念」的分類，並且根據南一版四年級的數學教材的內容與文獻中所提及的小數迷 思概念來編製試題，因此本研究所指的小數概念主要包括：1.小數意義的理解。 2.小數的位值與位名。3.小數的化聚。4.小數的十進結構。5.小數與數線對應關係。 6.比較小數大小。7.小數的稠密性。8.小數與分數的轉換。 二、試題屬性矩陣 本研究的自編小數概念測驗題題數為16題(如附錄三)，學童為研究者任教之 臺中市南區樹義國小五年級某班學童共33名，此測驗共測量8個概念，試題概念 表如表3-3-1所示。試題屬性矩陣如表3-3-2所示，該表中，1代表該題有測量到該 概念；0代表該題沒有測量到該概念，利用CAISM 軟體分析學童的個人化概念 階層結構。

表3-3-1試題概念表 編號 試題概念 1 小數意義的理解 2 小數的位值與位名 3 小數的化聚 4 小數的十進位結構 5 小數與數線對應關係 6 比較小數大小 7 小數的稠密性 8 小數與分數的轉換 表3-3-2 試題屬性矩陣 概念 1 2 3 4 5 6 7 8 題 號 1 1 0 0 0 0 0 0 1 2 0 1 0 0 0 0 0 0 3 1 0 1 1 0 0 0 0 4 1 0 1 1 0 0 0 0 5 1 1 0 0 1 0 0 0 6 1 0 0 0 0 1 0 0 7 1 0 0 0 0 1 0 0 8 1 0 0 0 0 0 0 1 9 1 0 1 1 0 0 0 0 10 1 1 0 0 1 0 0 1 11 1 0 0 1 0 0 0 0 12 1 0 0 0 0 1 0 0 13 1 0 0 1 0 0 0 0 14 1 0 0 0 1 1 0 0 15 1 0 0 0 0 0 1 0 16 1 0 0 0 0 0 0 1

貳、預試試題品質分析

一、信度 本研究預試A卷 (如附錄一) 之Cronbach 值為.82。B卷 (如附錄二) 之 Cronbach為.87，刪除試題並不會提高其信度。 二、效度 (一)內容效度 依據表3-3-2試題屬性矩陣，可檢查到測驗的題目的確有所要測驗的概念， 故本測驗試題具有內容效度。 (二)專家效度 本研究所使用之自編小數概念試題，經過兩位教授以及四位任職五年以上之 現職國小教師檢閱，故本測驗試題具有專家效度。 三、難度與鑑別度分析 本研究之試卷難度以高分組 (前25%) 的通過率加低分組 (後25%) 的通過 率之平均來表示，如表3-3-3所示：本研究預試之A卷各題難度介於.40~.90之間， B卷難度介於.40~.73之間。A卷之試卷平均難度為.56，對五年級學童而言整份試 卷難易適中，其中難度大於.70的題目只有一題，對五年級學童而言，唯有這一 題較容易。B卷之試卷平均難度為.53，其中難度大於.70的題目也只有一題，因 此，對五年級學童而言，也唯有這一題較容易。

表3-3-3 預試試題難度 題號 A 卷 B 卷 題號 A 卷 B 卷 1 .49 .40 11 .53 .50 2 .62 .57 12 .66 .60 3 .59 .40 13 .30 .33 4 .48 .60 14 .49 .67 5 .52 .40 15 .67 .57 6 .59 .50 16 .90 .73 7 .63 .57 17 .59 .63 8 .66 .57 18 .59 .53 9 .40 .47 19 .48 .57 10 .46 .50 20 .49 .43 本研究之試題鑑別度分析，先求出高分組及低分組的答對率，以P 及_H P 表_L 示，以 D 表示鑑別度，則D  。除此之外，也用獨立樣本t檢定的方式，P_H P_L 考驗高分組及低分組在各題得分的平均數的差異情形，來表示其鑑別度。如表 3-3-4所示，A卷鑑別度在 .27~.93之間，但A卷中第2、9、13、16題之獨立樣本t 檢定未達顯著水準，顯示此四題鑑別度偏低，其餘試題鑑別度良好。B卷鑑別度 在 .40~.93之間，且各題之獨立樣本t檢定皆達顯著水準，顯示B卷的試題鑑別度 良好。因此決定A、B卷皆刪除第2、9、13、16題，所以正式施測之題本變為16 題。

表3-3-4 預試鑑別度 題號 A 卷 B 卷 D 值 t 值 D 值 t 值 1 .71 5.18*** .67 4.91*** 2 .30 1.68 .87 9.54*** 3 .66 4.66*** .67 4.90*** 4 .57 3.53** .53 3.43** 5 .65 4.30*** .67 4.91*** 6 .66 4.66*** .87 9.19*** 7 .73 6.21*** .73 5.82*** 8 .52 3.45** .60 4.03*** 9 .27 1.47 .80 7.10*** 10 .78 6.47*** .73 5.71*** 11 .93 13.00*** .87 9.19*** 12 .52 3.45** .80 7.48*** 13 .33 1.93 .40 2.48* 14 .86 8.46*** .53 3.63** 15 .67 5.30*** .60 4.03*** 16 .20 1.87 .53 4.00** 17 .66 4.66*** .60 4.21*** 18 .66 4.66*** .93 14.00*** 19 .43 2.40* .73 5.82*** 20 .86 8.46*** .60 4.01*** *p＜.05 **p＜.01 ***p＜.001

參、正式施測測驗及試題

一、信度 本研究正式施測A卷 (如附錄三) 之Cronbach 值為.84，顯示本工具具有良 好的信度。 二、難度與鑑別度分析 本試卷各題的難度在.48~.91，平均難度為.65，顯示試卷無太困難的題目。 運用獨立樣本 t 檢定的方式，考驗高分組及低分組在各題得分的平均數的差異情 形，如表 3-3-5 所示，第 2、4、15 題之獨立樣本 t 檢定未達顯著水準，而第 1、

6 題的高分組平均通過率是 1，低分組平均通過率是 0，所以無法顯現獨立樣本 t 檢定。除此之外，分析各題與總分之間的相關，如表 3-3-5 所示，得知相關係數 之鑑別度介於.31~.82 之間，只有第 15 題未達顯著性，但考慮到第 15 題所測驗 到的概念七在別題無法測驗到，所以第十五題有其存在的必要性，因此不刪除此 題。 表 3-3-5 正式施測試題分析表 題號 難度 P t 值 相關係數 1 .64 .68*** 2 .52 1.64 .35* 3 .58 3.87** .52** 4 .91 2.12 .54** 5 .73 6.00** .63*** 6 .73 .82*** 7 .64 6.00** .63*** 8 .45 2.45* .43* 9 .76 2.83* .52** 10 .48 3.54** .48** 11 .79 2.83* .56** 12 .88 2.83* .63*** 13 .52 2.45* .42* 14 .79 3.87** .60*** 15 .48 1.73 .31 16 .48 6.00** .65*** *p＜.05 **p＜.01 ***p＜.001

肆、分析軟體

本研究使用之電腦軟體包括： ㄧ、利用 SPSS 12.0 來進行筆試題目資料的分析統計。 二、利用 CAISM 軟體來繪製個人化的概念階層結構圖。 三、利用 FCUT 軟體根據精熟度矩陣將學童分群。

第四節 資料分析

本研究主要透過國小四年級小數概念試題，探討學童知識結構的特徵，並 分析比較在進行補救教學前後知識結構圖的異同。在資料處理上，使用Lin et al. (2006) 所 發 展 的 概 念 詮 釋 結 構 工 具 (concept advanced interpretive structural model, 簡稱CAISM)、SPSS 12.0 for Windows 統計套裝軟體，其中的資料分析項 目及順序如下： 一、試題性質與解題表現之分析 (一)分析試題之難易度、鑑別度及測驗之信度。 (二)分析解題結果之概念全對通過率，呈現出學童的解題能力。 二、描繪學童小數概念知識結構圖 利用概念詮釋結構模式理論的電腦軟體程式 CAISM，輸入學童反應矩陣 M N nm x  ( ) X (x_nm 1表示學童 n 答對試題 m；x_nm 0表示學童 n 答錯試題 m )與試 題屬性矩陣 (item-attribute matrix) Y(y_ma)_M_A (yma 1表示試題 m 測量概念 屬 性 a ； y_ma 0 表 示 試 題 m 沒 有 測 量 概 念 屬 性 a ) ， 求 出 精 熟 度 矩 陣 A N na d  ( ) D ，以得知學童 n 在概念 a 的精熟程度，除此之外也可獲得對於每個學 童而言，在兩兩概念間的從屬關係機率所構成的模糊關係矩陣(fuzzy relation matrix) F_n(p_aa')_AA，可得知概念間的從屬機率大小。接著利用截集(-cut)， 選定值且01運算後，可獲得二元關係矩陣(binary relation matrix)的相鄰 矩陣(adjacent matrix)。亦即： A A aa n p F( _') _ 且          ' ' ' , 0 , 1 aa aa aa p p p ， 其中 01 將上述步驟的截集運算所得的二元關係矩陣進行 ISM 分析，即可獲得每位學 童的知識結構圖。 三、以模糊集群分析進行分群

使用模糊集群分析軟體FCUT，在FCUT軟體讀取各學童的精熟度矩陣 A N na d  ( ) D 後，研究者可依照軟體所輸出的分割係數 (partition coefficient) 和 分割亂度 (partition entropy) 之值，依據分割係數愈大，分割亂度愈小的原則， 找出最適合的群數並得知每個學童所隸屬之群組。 四、學童小數概念結構圖形分析 經上述分析流程，可繪製出不同能力值的學童之個人化概念詮釋結構圖，將 概念詮釋結構圖分析之重點說明下： (一)根據概念詮釋結構模式，針對小數的概念詮釋結構圖進行一般的描述性分 析，例如：分析學童概念詮釋結構圖的分層級數、最上層級及最下層級之概 念、層級間概念之特殊的階層關係等特點。 (二)比較同一群的學童、不同群的學童其概念詮釋結構圖的概念階層位置與連結 關係之異同。 (三) 比較答對題數相同但反應組型不同之學童，其概念詮釋結構圖概念階層位 置與連結關係之異同。 五、補救教學 在各群中，分別隨機抽取三位學童進行補救教學，補救教學的步驟如下： (一)在進行補救教學前先分析學童答錯的題目包含哪些概念，進行補救教學一開 始先測驗這些概念，驗證這些概念是否是學童較不精熟的。 (二)列出學童較不精熟的概念後，再按照 4-1-7 的小數概念發展順序與附錄十二 各概念的教案進行補救教學。每位學童的補救教學節數以一節課為原則， 但因各個學童需補救的概念數不同，且學童的學習時間不同，所以不同學 童的補救教學時間也會有所增刪。 (三)進行完補救教學後，立即進行複本測驗，繪製出概念詮釋結構圖後，比較學 童在進行補救教學前後的概念詮釋結構圖的概念階層位置與連結關係之異

第四章 研究結果與討論

本章主要在呈現研究結果的分析與討論，根據本研究目的，共分為四節。第 一節是不同精熟組的三群中，同一群的學童其小數概念詮釋結構圖之比較，第二 節是不同精熟組的三群中，不同群的學童其小數概念詮釋結構圖之比較，第三節 是不同精熟組的三群中答對題數相同但反應組型不同的學童，其小數概念詮釋結 構圖之比較，第四節是不同精熟組的兩群中，在進行補救教學前後之小數概念詮 釋結構圖的差異。

第一節 同一群學童之概念詮釋結構圖比較

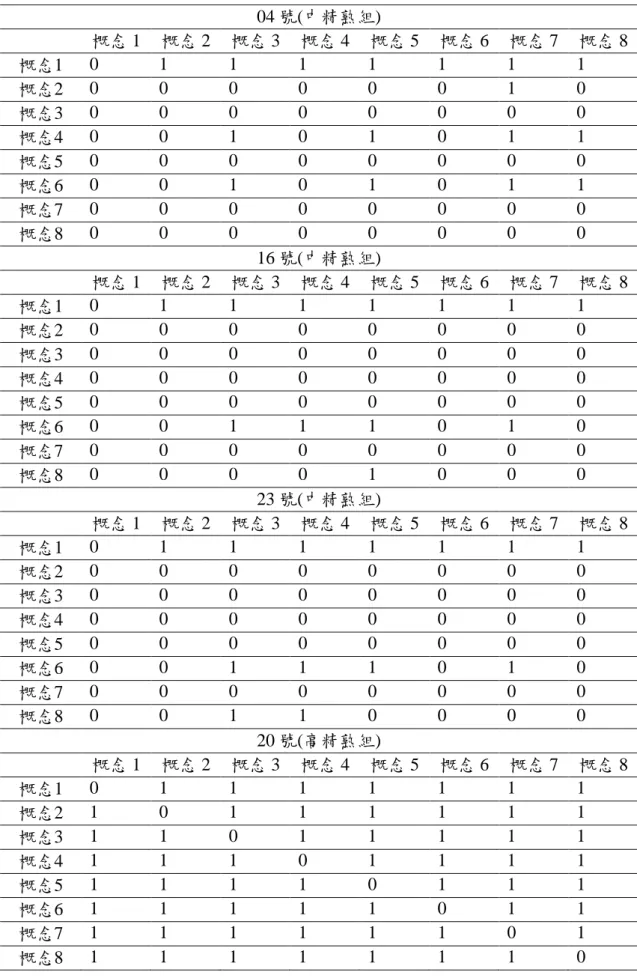
為了瞭解不同精熟度的學童其個別化概念差異，運用Lin et al. (2006) 所設計 的概念詮釋結構模式分析軟體CAISM，輸入受試者反應矩陣 (如附錄五) 與試題 屬性矩陣 (item-attribute matrix) (如附錄六) ，即可獲得各學童在八個概念中的的 精熟度矩陣 (master concept matrix) D(d_na)_N_A，如表4-1-1，對於每個受試者 n 而言，也可獲得所有兩兩概念之間的從屬關係機率構成模糊關係矩陣 (fuzzy relation matrix) F_n(p_aa')_AA，而所有學童的模糊關係矩陣，利用α截集 (α-cut) ，

選定α值且01運算後，即可獲得二元關係矩陣 (binary relation matrix) 的相 鄰矩陣 (adjacent matrix) 。

運用林原宏 (2003) 所設計的模糊集群分析軟體FCUT，在FCUT軟體中讀取 各學童的精熟度矩陣 (master concept matrix) D(d_na)_N_A後，如表4-1-1，調整 所要的群數，即可得到各群在各個概念的精熟度、分割係數 (partition coefficient) 和分割亂度 (partition entropy) 之值，如表4-1-2，因為分割係數要愈大愈好，分 割亂度要愈小愈好，所以決定將學童分成三群。見表4-1-3可得知這三群中，第 一群 (低精熟組) 有17位，每個概念的精熟度大約是.5左右，第二群 (中精熟組)

有15位，第一個概念較精熟大約是.7左右，其他的概念精熟度大約是.5左右，第 三群 (高精熟組) 只有一位，每個概念的精熟度都是1，顯示各個概念都很精熟。 在低、中、高精熟組三群中各自隨機抽取三位學童，低精熟度中的01號、06 號、22號，中精熟度中的04號、16號、23號，高精熟度只有20號一位，所以選取 20號，並以這七名學童各自比較同一群學童的概念詮釋結構圖之異同。此七名學 童的答題情況如表4-1-4所示，其模糊關係矩陣見附錄七，並以α = .55進行截矩陣 後，其二元關係矩陣如表4-1-5所示，根據這七名學童的二元關係矩陣，繪製其 概念詮釋結構圖，如圖4-1-1至4-1-3所示。 Wadsworth (1978) 根據J. Piaget的理論與主張，提出數學學習應採取的三項 原則：1.兒童只有透過對物體的自發性行動，才能建構數學的概念。2.兒童要瞭 解所使用的符號意義後，才能瞭解數學表象的歷程。3.兒童要瞭解數學概念，才 可以鼓勵他處理以象徵、符號表示的數目概念。根據Wadsworth所提出的三點與 九年一貫數學領域暫行綱要中有關小數的能力指標，如表4-1-6，可得知國小階 段在所有小數概念的學習順序，與本研究的八個小數概念比對後，可得知這八個 概念的概念發展順序如表4-1-7所示，概念1 (小數意義的理解) 包含在N-1-8的能 力指標中，是最先學習的概念，所以應位於概念階層結構圖的最下層，概念5 (小 數與數線的對應關係) 、概念7 (小數的稠密性) 包含在N-2-19的能力指標中，是 四年級學童最晚學習的概念，所以應位於概念階層結構圖的最上層，而概念2、 概念3、概念4、概念6、概念8包含在N-1-8與N-2-7中，所以應位於概念階層結構 圖的中間層。接下來會分別探討同一群的學童其概念詮釋結構圖的異同與其數學 意涵。