高中大學生對數學證明的學習狀況之研究

全文

(1)國立屏東教育大學應用數學系碩士班碩士論文 Department of Applied Mathematics National Pingtung University of Education Master’s Thesis. 高中大學生對數學證明的學習狀況之研究 A study of the learning mathematical proofs for high school and college students. 指導教授：詹勳國博士 Advisor: Dr. Hsungrow Chan 研究生：謝怡真 Student: Yi-Jen Shieh. 中. 華. 民國. 一. 百零. January, 2013. 二. 年一. 月.

(2)

(3) 謝. 誌. 本碩士論文研究能順利完成，首先感謝本系所的老師們給予指導與提攜。特別感謝詹勳國主任以豐富專業的學識並用心督促與指導，使我獲益量多。還有蔡典龍老師在統計資料分析上給予協助與指正，及吳進通老師與外校傅俊結老師，鉅細靡遺地找出論文中的缺失，使本研究更完整。為撰寫論文，訪談屏東女中與屏東高中的專業數學教師們，替我修訂與填寫問卷，感謝他們的熱心協助使此論文進行流暢且完善。再者，感謝所有幫助與陪伴我完成論文的同學、學弟妹與朋友的協助，因為有他們才能以愉悅的心情完成此論文。最後，感謝我最重要的家人，尤其是父母一路的栽培與鼓勵，也因為有他們的支持，才能順利取得碩士的學位文憑。謝謝你們的陪伴，擁有你們我很幸福，我永遠愛你們!. 怡真謹致於國立屏東教育大學應用數學系碩士班中華民國一百零二年一月.

(4) 高中大學生對數學證明的學習狀況之研究摘. 要. 本研究旨在探討高中大學生與高中教師對數學「證明題」的學習狀況及看法。首先完成自編問卷，內容包括數學證明的難易、相關知識與學習瞭解程度及所遇困難。接著進行問卷施測，對象為屏東縣一所國立大學學生 383 位與兩所國立高級中學學生 364 位，再從中選取訪談對象實施半結構式訪談。最後分析資料，研究結果如下：一、. 雖然高中教師強調證明的重要性，但還是有三分之一的學生主動跳過證明題。因為誤解升學考試不考，所以學生不會準備證明題。. 二、. 近乎一半的高中生學習證明時能瞭解證明的過程，但事後卻無法自行推演出證明。高中教師認為因為學生的先備知識不足，造成學生常有無從下筆的狀況。. 三、. 三分之一的高中生主動跳過數學證明，同時大多數學生沒信心回答證明題。高中教師認為部分原因是國中缺乏培養證明能力。. 四、. 近三分之一的大學生認為數乙不該出現證明題，超過一半的高中生認為數乙不該有證明題，並有一半的高中與大學生都認為應該明確的規定不考證明題。近一半的大學生無信心且完全沒有作答 100 年數乙考科的證明題，也有三分之一的學生對出現證明題感到驚訝。. 關鍵詞：關鍵詞：證明、證明、邏輯、邏輯、證明題. i.

(5) A study of the learning mathematical proofs for high school and college students ABSTRACT This study aimed to investigate the situation of learning mathematical proofs of high school and college students and the views of high school mathematics teachers. At first, we completed the self-questionnaire and then conducted the questionnaire. There were 384 college students and 364 high school students took the questionnaires. We selected 12 students to do the interview by the semi-structured method. Finally, we analyzed the data and got the results as follows: Firstly, although high school teachers emphasized the importance of proofs in class, one-third of students ignored learning the proofs. Because they misunderstood which the entrance exam would not have the proof problem, they did not study the proofs. Secondly, almost one half of high school students could understand the proof in class, but afterwards they were unable to deduce the proof. High school teachers considered that the students lacked the prior knowledge about proof. Thirdly, one-third of high school students skipped the mathematical proofs when learning. Most students did not have confidences to answer the proof problems. Partial high school teachers considered that the junior high school students did not learn well about proof. At last, one-third of college students agreed that the entrance exam shouldn’t have proof problems. More than one half of high school students agreed that the entrance exam shouldn’t have proof problem. One half of college students had no confidence to answer the proof of questions when they took the entrance exam. One third of the students were surprised when they realized there was a proof problem in the entrance exam. Keywords: proof, logic, and proof problem. ii.

(6) 目. 次. 摘. 要 ......................................................................................................... i. 目. 次 ........................................................................................................ I. 表. 次 ...................................................................................................... IV. 圖. 次 .................................................................................................... VII. 第一章緒論 .......................................................................................... 1 第一節研究背景與動機 ................................................................. 1 第二節研究目的 ............................................................................. 3 第三節名詞解釋 ............................................................................. 6. 第二章文獻探討 ................................................................................. 13 第一節證明的基本概念 ............................................................... 13 第二節數學教育對證明的要求 .................................................... 25 第三節數乙考科之證明考古題 .................................................... 31 第四節證明範例 ........................................................................... 36. I.

(7) 第三章研究方法 ................................................................................. 43 第一節研究架構 ........................................................................... 43 第二節研究對象 ........................................................................... 44 第三節研究工具 ........................................................................... 44 第四節研究流程 ........................................................................... 47. 第四章研究結果與討論 ..................................................................... 51 第一節問卷 A1 分析 .................................................................... 51 第二節問卷 A2 分析 .................................................................... 84 第三節問卷 B 分析 .................................................................... 113 第四節問卷 C 分析 .................................................................... 133. 第五章結論與建議 ........................................................................... 139 第一節結論 ................................................................................ 139 第二節建議 ................................................................................ 141. II.

(8) 參考文獻 ................................................................................................ 145 一、中文部份 .................................................................................. 145 二、英文部份 .................................................................................. 148. 附錄 ........................................................................................................ 151 附錄一證明學習狀況之問卷 A1 .................................................... 151 附錄二證明學習狀況之問卷 A2 .................................................... 153 附錄三證明學習狀況之問卷 B ...................................................... 155 附錄四證明學習狀況之問卷 C ...................................................... 156 附錄五雙向關聯表 ......................................................................... 157. III.

(9) 表. 次. 表 2-1-1. 證明的必要性 .................................................................... 14. 表 2-1-2. 證明的必備條件 ................................................................ 15. 表 2-1-3. 否定真偽表 ....................................................................... 17. 表 2-1-4. u ∧ v 真值表 ....................................................................... 17. 表 2-1-5. p ∨ q 真值表 ...................................................................... 17. 表 2-1-6. P ⇒ Q 真值表 .................................................................... 18. 表 2-1-7. P ⇔ Q 真偽表 ................................................................... 19. 表 2-2-1. 能力指標分析 ................................................................... 25. 表 2-2-2. 分年細目分析 ................................................................... 25. 表 2-2-3. 高中證明基礎 ................................................................... 29. 表 2-3-1. 100 年數乙考科題目與解答分析表 .................................. 32. 表 2-3-2. 96 年數乙考科題目與解答分析表 .................................... 33. 表 2-3-3. 93 年數乙考科題目與解答分析表 .................................... 34. 表 2-3-4. 91 年數乙考科題目與解答分析表 .................................... 35. 表 4-1-1. A1 問卷第二部份各題表現情形 ....................................... 52. 表 4-1-2. A1 問卷第三部份各題表現情形 ....................................... 54. 表 4-1-3. A1 問卷第二部份各題同質與平均數檢定 ........................ 56. 表 4-1-4. A1 問卷第三部份各題同質與平均數檢定 ........................ 58. 表 4-1-5. A1 問卷第二部份各題與變項之卡方檢定 ........................ 61. 表 4-1-6. A1 問卷第二部份之第一題分佈情形 ............................... 63. 表 4-1-7. A1 問卷第二部份之第二題分佈情形 ............................... 64. 表 4-1-8. A1 問卷第二部份之第四題分佈情形 ............................... 65. 表 4-1-9. A1 問卷第二部份之第五題分佈情形 ............................... 66. IV.

(10) 表 4-1-10. A1 問卷第二部份之第六題分佈情形 ............................. 67. 表 4-1-11. A1 問卷第二部份之第七題分佈情形 ............................. 68. 表 4-1-12. A1 問卷第二部份之第九題分佈情形 ............................. 69. 表 4-1-13. A1 問卷第二部份之第十題分佈情形 ............................. 70. 表 4-1-14. A1 問卷第三部份各題與變項之卡方檢定 ...................... 71. 表 4-1-15. A1 問卷第三部份之第一題分佈情形 ............................. 73. 表 4-1-16. A1 問卷第三部份之第三題分佈情形 ............................. 75. 表 4-1-17. A1 問卷第三部份之第四題分佈情形 ............................. 76. 表 4-1-18. A1 問卷第三部份之第五題分佈情形 ............................. 78. 表 4-1-19. A1 問卷第三部份之第六題分佈情形 ............................. 80. 表 4-1-20. A1 問卷第三部份之第七題分佈情形 ............................. 81. 表 4-1-21. A1 問卷第三部份之第八題分佈情形 ............................. 82. 表 4-2-1. A2 問卷第二部份各題表現情形 ..................................... 85. 表 4-2-2. A2 問卷第三部份各題表現情形 ..................................... 86. 表 4-2-3. A2 問卷第二部份各題同質與平均數檢定 ...................... 88. 表 4-2-4. A2 問卷第三部份各題同質與平均數檢定 ...................... 91. 表 4-2-5. A2 問卷第二部份各題與變項之卡方檢定 ...................... 93. 表 4-2-6. A2 問卷第二部份之第二題分佈情形 ............................. 95. 表 4-2-7. A2 問卷第二部份之第三題分佈情形 ............................. 96. 表 4-2-8. A2 問卷第二部份之第四題分佈情形 ............................. 97. 表 4-2-9. A2 問卷第二部份之第五題分佈情形 ............................. 99. 表 4-2-10. A2 問卷第二部份之第六題分佈情形 ........................... 100. 表 4-2-11. A2 問卷第二部份之第七題分佈情形 ........................... 101. 表 4-2-12. A2 問卷第二部份之第十題分佈情形 ........................... 102. 表 4-2-13. A2 問卷第三部份各題與變項之卡方檢定 .................... 103. 表 4-2-14. A2 問卷第三部份之第一題分佈情形 ........................... 105. 表 4-2-15. A2 問卷第三部份之第二題分佈情形 ........................... 106. V.

(11) 表 4-2-16. A2 問卷第三部份之第三題分佈情形 ........................... 107. 表 4-2-17. A2 問卷第三部份之第四題分佈情形 ........................... 108. 表 4-2-18. A2 問卷第三部份之第五題分佈情形 ........................... 109. 表 4-2-19. A2 問卷第三部份之第六題分佈情形 ........................... 110. 表 4-2-20. A2 問卷第三部份之第七題分佈情形 ........................... 111. 表 4-2-21. A2 問卷第三部份之第八題分佈情形 ........................... 112. 表 4-3-1. 問卷 B 第一題高中學生答題比較表 ............................ 124. 表 4-3-2. 問卷 B 第二題高中學生答題比較表 ............................ 126. 表 4-3-3. 問卷 B 第三題高中學生答題比較表 ............................ 129. 表 4-3-4. 問卷 B 第四題高中學生答題比較表 ............................ 132. 表 4-3-5. 問卷 B 第一題大學生答題比較表 ................................ 115. 表 4-3-6. 問卷 B 第二題大學生答題比較表 ................................ 117. 表 4-3-7. 問卷 B 第三題大學生答題比較表 ................................ 120. 表 4-3-8. 問卷 B 第四題大學生答題比較表 ................................ 122. 表 4-4-1. 問卷 C 第一題高中教師觀點比較表 ............................ 134. 表 4-4-2. 問卷 C 第二題高中教師觀點比較表 ............................ 136. 表 4-4-3. 問卷 C 第三題高中教師觀點比較表 ............................ 138. VI.

(12) 圖. 次. 圖 1-3-1. 畢氏定理證明圖(一) ........................................................... 9. 圖 1-3-2. 畢氏定理證明圖(二) ......................................................... 10. 圖 1-3-3. 畢氏定理證明圖(三) ......................................................... 10. 圖 2-1-1. 綜合法例圖 ....................................................................... 21. 圖 2-1-2. 倒推法例圖 ....................................................................... 21. 圖 2-1-3. 數學證明分析圖 ............................................................... 24. 圖 2-2-1. 九年一貫例圖 ................................................................... 26. 圖 2-4-1. 棋盤圖 ............................................................................... 37. 圖 2-4-2. 凸面體修剪流程圖 ............................................................ 38. 圖 2-4-3. 三角形排列圖 ................................................................... 41. 圖 2-4-4. 四角形排列圖 ................................................................... 41. 圖 2-4-5. 六角形排列圖 ................................................................... 42. 圖 3-4-1. 研究流程圖 ....................................................................... 50. 圖 4-3-1. S3 作答圖 ........................................................................ 127. 圖 4-3-2. S4 作答圖 ........................................................................ 128. 圖 4-3-3. S5 作答圖 ........................................................................ 128. 圖 4-3-4. S6 作答圖 ........................................................................ 128. 圖 4-3-5. S7 作答圖 ........................................................................ 118. 圖 4-3-6. S9 作答圖 ........................................................................ 118. 圖 4-3-7. S11 作答圖 ...................................................................... 119. 圖 4-3-8. S12 作答圖 ...................................................................... 119. VII.

(13) VII.

(14) 第一章. 緒論. 本研究之主題為探討學生及教師對證明學習狀況及看法，本章分三節說明，第一節闡述「研究背景與動機」、第二節說明「研究目的」、第三節提出「名詞解釋」。. 第一節. 研究背景與動機. 2011 年大學指定科目考試中的數乙考科非選擇題考了一題證明題，在教育界引發不小的討論，該年 7 月 2 日聯合晚報記者連線報導：「大學指定科目考試第二天，社會組考科登場，上午第一節考數學乙，不少考生反映去年的題目簡單，今年題目難易度明顯調整，比去年難一點。而且統計、機率的題目偏多，計算不繁複，鑑別度也比去年高；但是今天出現「轉移矩陣」的證明題，不少考生直言看到題目很傻眼，考前根本沒準備，只能硬著頭皮寫，是整份考卷最難的一題，這題應該會死很多人。」其餘各大報也以「驚訝」與「傻眼」等字來形容這次大學指定科目考試數乙考科出現「證明題」的第一反應。但以九年一貫以及高中課程綱要當中皆有提到證明的重要性，以及證明的邏輯推導能力，所以要求數學證明的能力是必要的。數學是不是就等於證明，那可不一定。但唯一能確定的是，證明能促進我們的邏輯思考，可以培養和訓練人們的推理能力，並按照正確思維形式和規律去進行理性思維，提高人們的思維能力。Gibilisco (2005) 曾說：「數學證明已成為許多學生學習數學領域之外的一個有趣課程，純粹是為了使他們的邏輯推理和分析更完整。」任何一個數學命題的成立都需要證明，證明的意義在於提供有關命題成立的論述，因此至少要做. 1.

(15) 到以嚴謹的推理確認從已知到結論的邏輯脈絡。(張海潮，2007) 一般數學命題的對與錯就是要看是不是可以提出證明，若未能找到其證明，那只能說是猜想。例如有名的「費馬最後定理：對任意正整數 n ≥ 3 ， x n + y n = z n 方程式沒有正整數解。」當時，這只能說是猜想，但. 是經過四百多年後到西元 1995 年，美國普林斯頓大學威爾斯教授才提出完整的證明，使得猜想成為證明。本研究選「數學證明」為研究題材，主要希望能藉此研究得知學生對學習證明題的瞭解狀況，包括對證明的喜好程度、感覺難易、對證明的定理過程的瞭解，以及所遇困難為何。希望研究結果能提供編寫教材者、教師以及學生們在證明上一的些建議，也讓學生在學習證明時有更佳的學習效果。雖然「證明題」一直是學生害怕的數學內容，但卻不能動搖其在數學中的重要地位。數學是一門學科，建立在引理和定理的證明上(Martin Aigner，2004)。L. Wittgenstein (1956)曾說：「數學是各式各樣的證明技巧。」2009 年有一本書討論小學到大學有關證明的教學與學習「Teaching and Learning Proof Across the Grades」，在編輯群(Stylianou, Blanton and Knuth, 2009) 的序言中提到 "If problem solving is the "heart of mathematics,"1 then proof is itssoul."意思是說如果解題是數學的心，則證明就是數學的靈魂。就如同 Beck and Geoghegan(2010)說：「數學的核心方法是公理、定理與證明。」由此可知，「證明」是數學的核心與精神，更顯得「證明」對數學的重要。「數學是產生必要的結論科學」(B.Peirce，1881)，這句話也間接的告訴我們，數學與證明似乎是一樣重要的。就像在自然科學當中，在數學中我們也會有檢驗與實驗的情況發生，去猜測推想一個定理，但不管實驗檢驗多支持這個猜想，但終究無法成立，因為實驗無法取代證明，似乎也告訴我們為什麼要去作證明這件事，因為就算數學家已經驗證實驗過許多個情形，但除非能給出一個明確的證明，否則誰也不能保證，. 2.

(16) 下一個驗證的結果不會是錯的。例如，對自然數 n 而言， f (n) = n 2 − n + 41 是不是質數？ n = 1， f (1) = 41； n = 2 ， f (2) = 43 ； n = 3 ， f (3) = 47 …… ，一直到 n = 40 ， f (n) 都是質數。但 f (41) = 41 × 41 ，不是一個質數。. 第二節. 研究目的. 九年一貫課程數學科綱要的分年能力指標『 8-s-17 ：學生能將幾何推理步驟所依據的性質用填空格方式做答。』這個指標的目的在於提供學生日後有用的核心幾何知識，並提供豐富的背景，以便於展示數學推理證明的過程與能力，而更強調推理能力的培養正是國中數學教育的重點之一。其實從小學的四則運算開始，學生即已進行有意識的推理活動。例如 3 + 2 = 2 + 3 ，在進行運算之後，知道等號的兩邊都是 5 。因為加法的運算符合交換律，所以學生能理解交換律於計算是正確的。而「普通高級中學數學科課程綱要」也強調認識定理的敍述與證明，並介紹命題、充分條件、必要條件、充要條件、反證法。Roberts 曾強調定理證明的課程的重要性，他認為幫助學生培養必要的技能寫清楚，正確，簡潔的證明是很重要的。Sultan 在 2010 年所寫的書當中也有提到，中學教師必須具備的條件之一就是包括數學推理與證明。Brumbaug 也建議可採用多種方法與活動來促進學生思考進而理解學習證明。數學證明還是有它的地位。證明是數學的基礎，因此，它是必不可少的 (VanSpronsen ， 2008)。就數學內容結構而言，正如近代著名數學家 Wely 說過：「邏輯是數學家為保持思想強健而遵守的衛生規則。」就學. 風而言，正如另一位著名數學家 Weil 說過：「嚴謹之於數學家，猶如道德之於人。」( 數學 = 證明 ?， 1992) Netz 在《 Ludic proof 》曾說：「數學家是創造性的作家，如同小說家一樣，利用圖、象徵、隱喻、雙關語和驚喜的元素，成為一個好故事讀起來就像一個很好的數學證明。」. 3.

(17) 數學證明還有另一個重要的功用，即是增加理解。Bourbaki 學派在一篇題為《The Architecture of Mathematics》(1950)的文章裡說了一段話：「每個數學工作者都知道，單是驗證了一個數學證明的逐步邏輯推導，卻沒有試圖洞察獲致這一連串推導的背後意念，那並不算理解了那個數學證明。」Lakatos(1976)也曾說過：「我的數學知識更加豐富，是因為嘗試連續去改善過程，也就是證明邏輯。」但 Stylianou, Blanton and Knuth (2009)也曾提到，學生對於證明的學習表現困難有許多原因，許多論文討論的很多。一是「傳統教學並沒有創造學生個人意義與說明的能力」，其二是「學生認知證明活動是一項額外的工作，而不是深度思考數學的工具」，另外「證明活動並不是發現的過程」。 Gfeller 在 2004 年所作的研究報告當中，發現了只有三分之一的學生能列出他們在做幾何證明時所遇到的性質或定理。我們從這些角度，反省國內有關「證明」教與學，似乎也有相同的問題，從小一到小六，並沒有正式的證明相關教學與評量，國中開始有幾何證明的課程，但忽略了學生的心路歷程，彷彿時間到了，學生就應該會，教學活動並沒有特別連接到「個人有意義」的概念，小學至國中也沒有特別的「數學說明」或「說明數學」的活動。國中大部分學生與部分老師都厭煩這額外的作業或訓練，反正「正式考試」只有選擇題。雖然考大學證明是寫在文件上必備的項目與能力之一，但是幾乎集體忽略這個重要的「數學思考與發現工具」，教學更是乏善可成，甚至已準備考試有名的「補習班」也沒有多所著墨。而學生在學習證明的情況及感受各有不同，因此本研究希望藉由學生填寫問卷，瞭解學生學習證明的狀況、對證明的瞭解程度以及遇到困難，研究結果可供教師教導證明時教學活動設計的參考，編寫教材者的教材安排以及使學生更有效率的學習證明。本研究主要的研究目的如下：. 4.

(18) 一、高中大學生學習數學證明題的狀況為何？. 二、高中大學生對證明題的理解的情形為何？. 三、高中大學生對證明題的喜惡與信心為何？. 四、高中大學生對指定科目考試數乙考科證明題的感想與答題狀況為何？. 5.

(19) 第三節. 名詞解釋. 本研究所涉及的相關重要名詞釋義如下：. 一、證明. 根據 Takeuti, Gaisi (1987)與 Pohlers, Wolfram (1989)可知，證明可說是一種根據已知真實的判斷來確定某一判斷的真實性的思維形式。 Franklin and Daoud (1996)認為證明在數學上來說一種介紹簡單且沒有多餘贅字的方法來解釋數學的核心技術。《辭海》指出，證明是在一個特定的公理系統中，根據一定的規則或標準，由公理和定理推導出某些命題的過程。比起證據，數學證明一般依靠演繹推理，而不是依靠自然歸納和經驗性的理據，這樣推導出來的命題也叫做該系統中的定理。 R.L.Wilder 曾說：「我們不要忘記，所謂證明，不只在不同的文化有不同的含義，就連在不同的時代也有不同的含義」(1968)。. 二、幾何. 依據《數學百科全書》，幾何一詞源於《幾何原本》的翻譯。《幾何原本》是世界數學史上影響最為久遠，最大的一部數學教課書。徐光啟和利瑪竇《幾何原本》中譯本的一個偉大貢獻是確定了研究圖形的這一學科中文名稱為「幾何」，並確定了幾何學中一些基本術語的譯名。「幾何」的原文是「geometria」(英文 geometry)，徐光啟和利瑪竇在翻譯時，取「geo」的音為「幾何」，而「幾何」二字中文原意又有「衡量大小」的意思。. 6.

(20) 三、九年一貫課程綱要. 根據國民教育司中的《97 年國民中小學九年一貫課程綱要(100 學年度實施)》，九年一貫課程為台灣教育改革主要政策之一，亦為該改革中最重要一環。以中華民國政府教育部為主導的該教育改革政策，乃指將臺灣境內國民小學與國民中學兩學校層級課程中的科目與內容，以教科書為主軸來做九年一貫的銜接，其目的在於學生能獲得連續且統合的學習與知識。九年一貫課程包含人與自己、人與社會、人與自然三個面向，整合所有國語、鄉土語言、英語、數學、社會、自然與生活科技、藝術與人文、健康與體育、綜合活動等學習領域，並依學生能力為指標，成為教育目標的依據。其中數學科教學目的在於數學的學習注重循序累進的邏輯結構，因此，過去國內外數學教材的演進，皆遵循此邏輯結構，以確保數學教育的穩定性。再者，數學是較能進行國際性評比的學習領域，教學的成效亦有較客觀的標準，因此，數學教育成效的評估應有其客觀基礎。. 四、普通高級中學課程綱要. 依據中等教育司中的《普通高級中學課程綱要(97 年版，99 學年度高一新生適用)》所提到，普通高級中學教育，除延續國民教育階段之目的外，並以提昇普通教育素質，增進身心健康，養成術德兼修、五育並重之現代公民為目的。為實現本階段教育目的，須從生活素養、生涯發展及生命價值三層面輔導學生達成下列目標：. 7.

(21) ㈠、提昇人文、社會與科技的知能。㈡、加強邏輯思考、判斷、審美及創造的能力。㈢、增進團隊合作與民主法治的精神及責任心。㈣、強化自我學習的能力及終身學習的態度。㈤、增強自我了解及生涯發展的能力。㈥、深植尊重生命與全球永續發展的觀念。. 其中普通高級中學必修科目「數學」課程綱要除了主要為延續國民教育階段之目的外，並以提昇普通教育素質、增進身心健康、養成術德兼修和五育並重之現代公民為目的。其中「數學」課程欲達成之目標如下：㈠、引導學生瞭解數學的內容，意義及方法。㈡、培養學生以數學思考問題，分析問題，解決問題的能力。㈢、提供學生在實際生活和學習相關學科方面所需的數學知能。㈣、培養學生欣賞數學內涵中以簡馭繁的精神和結構嚴謹完美特. 質。. 五、畢氏定理. 又可稱畢達哥拉斯定理或勾股定理。據說畢達哥拉斯證明了這個定理後，即斬了百頭牛作慶祝，因此又稱「百牛定理」。在中國，《周髀算經》記載了畢氏定理的特例，相傳是在商代由商高發現，故又有稱之為商高定理。在法國和比利時稱為驢橋定理，而埃及稱為埃及三角形。此 8.

(22) 定理證明方式目前發現約有四百多種，像是二十世紀早期，Elisha Scott Loomis 教授，發表了《畢氏定理》，書中就蒐集了其中三百六十七則證明的方式。以下是參考《數學教室 A to Z》整理出其中兩種證明方法。【證明方法 1】必要條件為「邊-角-邊」(SAS)全等判別格式，以及三角形三個角度的和，等於兩個直角三角形的角度和，也就是等於 180° 。 b. a. E. b a. D. A b. a c. C. a. 圖 1-3-1. B. b. 畢氏定理證明圖 (一 ). 設 ∆ABC 為直角三角形，如圖 1-3-1。大正方形每邊都有一個直角三角形，這幾個三角形的直角邊長都等於 a 和 b ，根據「邊 - 角 -邊」 (SAS) 判定彼此全等。因此，四個三角形就所有角度都完全相同，其斜邊也全都相等，即 BD = DE = EA = AB = c ，因此可知四邊形 BDEA 是個正方形。接著考慮 ∠ABD ，由於 CF. 是條直線，所以. 180° = ∠CBA + ∠ABD + ∠DBF = 90° + ∠ABD ，因此 ∠ABD = 90° 。. 另外，內側圖形的角亦為直角，同理可證，其餘三個角也為直角，且此面積為 c × c = c2 。外側正方形的邊長為 a + b 的大正方形，面積為 (a + b) 2 = a 2 + 2ab + b 2 。圖 1-3-1 之面積可分解成四個全等直角三角形，. 還有一個歪斜的內側正方形。. 9.

(23) 1 其面積可由下求得： 4 × (∆ABC )面積 + BDEA面積 = 4( ab) + c 2 = 2ab + c 2 。 2. 最後得到 a 2 + 2ab + b 2 = 2ab + c 2 ，兩邊各減去 2ab ，可得 a 2 + b 2 = c 2 。. 【證明方法 2 】 E A. b2. b1. h. C D. 圖 1-3-2. 畢氏定理證明圖 (二 ). 在圖 1-3-2 梯形面積，可畫出 CE 對角線，把梯形分成兩個等高的三角形。再將兩個等高的三角形相加後可推得梯形面積公式，現在將圖形轉向並重新標示如下圖 1-3-3 ： E A. b. c c. C. a. 圖 1-3-3. B. D. 畢氏定理證明圖 (三 ). 在圖 1-3-3 之直角三角形 ABC 中，直角位於點 C ，兩股長分別為 a 和 b，斜邊長為 c。從 B 作 AB 得垂線 BE，且 BE = c，並由 E 向下作垂線 ED ，. 且 D 為垂線底端與 CB 向右延伸的交點，最後作 AE 線。因為 ∠CBA + ∠CAB = 90° ，可知 ∠DBE = 180° − ∠ABE − ∠CBA = 180° − 90° − ∠CBA = 90° − ∠CBA = ∠CAB 。. 10.

(24) 既然 ∠DBE = ∠CAB 且 ∠BDE = 90° ，則推得 ∠BED = ∠ABC 。因此根據 ASA 全等判定，∆BED ≅ ∆ABC，其中 BE = AB，BD = AC = b 且 DE = BC = a 。由於四邊形 ACDE 中， BD 和 DE 兩對邊平行，因此這是個梯形，且與 CD 垂直。根據梯形面積公式，可得知梯形 ACDE 的面積 = ∆ACB + ∆ABE + ∆BDE =. 1 1 1 1 ab + c 2 + ab = ab + c 2 2 2 2 2. 1 1 (b + a )(b + a ) = ab + c 2 2 2 1 2 1 (b + 2ab + a 2 ) = ab + c 2 2 2. 最後等式兩邊皆乘 2 ，求得 b 2 + 2ab + a 2 = 2ab + c 2 ，則 a 2 + b 2 = c 2 。. 11.

(25) 12.

(26) 第二章. 文獻探討. 本章分為四節，第一小節「證明的基本概念」、第二節「數學教育對證明的要求」、第三節「數乙考科之證明考古題」和第四節「證明範例」，由相關文獻中進行探討。. 第一節. 證明的基本概念. 根據《維基百科》，數學的證明是在一個特定的公理系統中，根據一定的規則或標準，由公理和定理推導出某些命題的過程，而數學證明建立在邏輯之上，但通常會包含一些自然語言，因此並無固定的形式。西方學者公認證明始於公元前六世紀，當時希臘數學家與哲學家證明了幾條幾何定理，到了公元前四世紀，Euclid of Alexandria(歐基里德) 寫成了《幾何原本》，而奠定了證明的模式。公元前五世紀 Plato 在《理想國》說：「你一定曉得，研究幾何、算術或類似科學，是以奇數、偶數、圖形、三種角及一類東西作為基礎。這是他們研究的出發點，他們不認為有需要對這些再加任何的說明，這是開始的原理。」所以我們可知一開始證明研究的基礎。 Euclid of Alexandria(歐基里德)的《幾何原本》在每條定理證明完畢都寫上 “ 這是要證明的 ” ，後來變成拉丁文的 Quod Erat Demonstrandum(Q.E.D.)。Q.E.D.這三個字母，宣示了定理的真實性從此建立，代表數學真理與數學之美的同義詞，亦同於我們在證明結束後所寫的「故得證」。在我國古代也有邏輯推演的蹤跡，並且與其他古代國家數學文化相比毫不遜色，只是沒有繼續與數學結合發展下去。例如《墨經》中就有. 13.

(27) 不少的邏輯推演的篇章，像是《經上篇》有說：“彼，不兩可兩不可也。” 也就是說命題的正反，不能同時都正確，也不能同時都不正確，也就是數學邏輯中的排中律與無矛盾律。《九章算術》是我國古代數學的珍貴文獻，劉徽作註，在序言中有提到他領悟其中的奧祕就是推理，利用邏輯推理與直觀推理，即能得到簡潔清晰又嚴密完整的證明。 Cupillari 在 2012 所寫的《The Nuts and Bolts of Proofs》也提到說明必要的定理去證明是相當重要的細節。而另外《幾何學中的證明》(1999) 書中有歸納出以下數學證明的必要性：表 2-1-1. 證明的必要性. 1. 有少數幾個不加證明而承認的命題，這就是公理。其餘命題，也就是定理，都是以公理為基礎，經一系列演繹推理而證得的。 2. 需要證明是因為有人類思維的基本規律，及充足理由律。按照這一規律，要求我們的每一判斷都是正確的，都是建立在嚴格的論據之上。 3. 正確的證明只能藉助公理及以前證過的定理作出，絕不能只憑“明顯”。 4. 需要證明還因為要確立的是所證命題的普遍性質，即它在一切的特殊情況下都可應用。 5. 藉助證明，幾何學已整理成系統的科學知識的完整體系，在體系內，空間形式的各種不同關係都被揭示出來了。並且也提到學生在證明時，學生經常犯的錯誤為在引述直接定理時，卻正在用著其逆定理。另一錯誤是在證明過程中引用了尚未證明過的命題，以及學生有時在證明中用到了正要證明的命題。因此歸納出以下證明所必備的條件：. 14.

(28) 表 2-1-2. 證明的必備條件. 1. 證明必須建立在公理和前面證過的定理的基礎上。. 2. 證明中的全部推斷都必須是正確的。 3. 我們必須牢記證明的目的，那就是要判斷被證明題的真確性，不能代之以其他的命題。所以當我們證明一個幾何命題時，首先應當搞清楚要證明的命題的基本結論，應當由定理的原文中準確地找出已知條件以及證明所需的條件。證明的作用是以一些基本概念和基本公設為基礎，使用合乎邏輯的推理去決定判斷是否正確。在《Proofs and Fundamentals》(Bloch，2011) 書中強調邏輯是在證明前所需具備的。我們在求學過程中遇過無數的證明，對證明並不覺得陌生。以下的文獻內容主要來自教育部審定(高審字第 0582 號)普通高級中學『數學 2』(龍騰文化 2010)的附錄，以及詹勳國教授的上課內容。將「數學證明」的內容，分為以下的「邏輯」與「數學方法」來進行探討。. 一、邏輯. 邏輯的字根源起於希臘語邏各斯（希臘語：λόγος），最初的意思有詞語、思想、概念、論點、推理之意，而後發展為英文中的邏輯（英語： logic）。邏輯本身是指是推論和證明的思想過程，而邏輯學是研究「有效推論和證明的原則與標準」的一門學科。因此當處理複雜的事物，有許多方法與能力可以培養，而最簡便的方法就是學習邏輯，(張家龍， 2004)、(孫名福等，1997)、(林正弘，1988)、(何秀煌(譯)，1968) 數學證明與邏輯之間的關係可從《數學證明》書中得知，作者提到. 15.

(29) 數學證明所應遵守的一般邏輯規則是可以在一個證明的任何地方引入一個前提，或是如果一個證明中有一些先引入的前提，這些前提可以邏輯地推出一個命題，那麼就可以在這一證明中引入這個命題，抑或能從一個命題和一個前提集合推導出命題，那麼就可以從這個前提集合本身推導出命題。 Horgan 說：「證明就是可從一系列公理中的一套合乎邏輯的步驟先開始著手。」從希臘人身上，我們才找得到最早採嚴謹邏輯證明的命題。 (蔡承志(譯)，2009)除了說明邏輯對於證明的重要性，我們亦可得知，瞭解數學證明，其命題也是非常重要的。作為一個形式科學，邏輯透過對推論的形式系統與自然語言中的論證等來研究並分類命題與論證的結構。邏輯可包含「敘述」、「否定」及「複合敘述」，其說明如下：㈠、敘述：凡是能分辨真偽的句子。. 為真(True)以「T」表示，為偽(False)以「F」表示。例子： X + 7 = 20 是不是敘述？我們可知“不是”，其原因為不能分辨其真偽。例子： 5 > 7 是不是敘述？答案為“是”，因為我們知道 7 比 5 大，因此可判斷此命題為偽，所以這個句子是敘述。㈡、否定：相反敘述的句子。. 一般而言，令 P 為敘述， ~ P ( 非 P ) 為否定。此題型必須釐清的概念為量的否定，重點是「全部的否定是部分，部分的否定是全部」。例子：「 A 集合中至少有一個元素大於 1 」的否定敘述，為「 A 集合中沒有一個元素大於 1 。」例子：「此次期中考本班每人都及格」的否定敘述，為「此次期中考本班至少有一人不及格」。. 16.

(30) 敘述的真偽表如下：表 2-1-3. 否定真偽表. P. ~ P (非 P ). Ｔ. Ｆ. Ｆ. Ｔ. ㈢、複合敘述：可分為「且」與「或」、命題與複合命題三種方式. 來討論。 1. 「且」： p 且 q ( p ∧ q 、 “and”) 。. 例子：令 u 代表能提起重物 30kg，令 v 代表通過郵務筆試， u ∧ v 就代表能考上郵差。其真值表如下：表 2-1-4. u ∧ v 真值表. u. v. u ∧ v (考郵差 ). Ｔ. Ｔ. Ｔ. Ｔ. Ｆ. Ｆ. Ｆ. Ｔ. Ｆ. Ｆ. Ｆ. Ｆ. 2. 「或」： p 或 q ( p ∨ q 、 “or”) 。. 例子：令 p 代表大學畢業的學生，令 q 代表同等學歷，而 p ∨ q 代表能考研究所。其真值表如下：表 2-1-5. p ∨ q 真值表. p. q. p ∨ q (考研究所 ). Ｔ. Ｔ. Ｔ. Ｔ. Ｆ. Ｆ. Ｆ. Ｔ. Ｔ. 17.

(31) Ｆ. Ｆ. Ｔ. ㈣、連續推理. 1. 命題：若 P 則 Q 。( P(前提)  Q (結論) 、 P implies Q 、. Q whenever P 、 Q provided P ) 例子：若 ABC 為正三角形，則∠ A  60 。 (1). P  Q 為真. P 稱為 Q 的充分條件(sufficient condition)。 Q 稱為 P 的必要條件(necessary condition)。 (2). 錯誤命題 ( P  Q )不一定成立，若 P 成立，卻存在不符合 Q 。例子：若四邊形的對邊等長，則四邊形為長方形。 (3). 定理，必須正確的命題，而「正確」依賴「證明」。例子： P  Q 表 2-1-6. P  Q 真值表. P. Q. PQ. Ｔ. Ｔ. Ｔ. Ｔ. Ｆ. Ｆ. Ｆ. Ｔ. Ｔ. Ｆ. Ｆ. Ｔ. 2. 複合命題： P  Q 且 Q  P 、 P 若且唯若 Q 、 P  Q 、 P if and only if Q 、 P iff Q 。. 18.

(32) 例子： P ⇔ Q 表 2-1-7. P ⇔ Q 真偽表. P. Q. P⇒Q. Q⇒P. P⇔Q. Ｔ. Ｔ. Ｔ. Ｔ. Ｔ. Ｔ. Ｆ. Ｆ. Ｔ. Ｆ. Ｆ. Ｔ. Ｔ. Ｆ. Ｆ. Ｆ. Ｆ. Ｔ. Ｔ. Ｔ. 以上「敘述」、「否定」、「複合敘述」與「連續推理」四者，皆為數學證明的基本語言、架構與規則，所有的數學證明都要按照這些規則有系統的呈現。. 二、數學方法. 數學的定義包含有名詞的定義、符號的定義、性質的定義。數學的定理是「正確的命題( P ⇒ Q )」，其中的 P 代表前提或假設，稱為 assume、 suppose、assumption、hypothesis、given…。定理又稱為 theorem、theory、 lemma（引理）、proposition、property、corollary（系、推論）。一般來說證明方法可先略分為「自然歸納法」與「演繹法」。㈠、自然歸納法. 又稱數學歸納法，是數學證明的方法之一，通常被用於證明某個給定命題在整個自然數範圍內成立。根據《數學百科全書》的定義為：「一個與自然數有關的敘述 P ( x) ，如果能證明 P (1) 為真，且如果對任何一個自然數 n 當 P(n) 也為真，則可推得 P(n + 1) 為真。」《數學辭典》對數學歸納法的定義是：「數學證明與自然數 n 有關命題的一種方法，屬於完全歸納法。其中必需包括驗證當 n 取第一個自然. 19.

(33) 數時，必須為真；以及當 n 取某一個自然數 k 時為真，以此為條件，可以推論出 n 取自然數 k+1 時這個推論也會為真。以上此兩條件缺一不可。」歸納證明推理是一種使我們對命題增強信念的途徑，也是構思猜想證明的一條路徑。㈡、演繹法（連續命題）又可分「直接證」與「間接證」. 1. 直接證：可細分為以下四種方法。 (1). 分析法是指從已知條件直接分析。例子：證明多項式 P (x) 被一次式 x   所除，餘式為 P ( ) 。【證明】：設 P ( x)  a 0  a1 x  a 2 x 2  ...  a n x n ，已知 P (x) 被一次式 x   所除，則 P ( )  a 0  a1  a 2 2  ...  a n n 。因此，. P ( x)  P( )  (a0  a1 x  a 2 x 2  ...  a n x n )  (a 0  a1  a 2 2  ...  a n n )  a1 ( x   )  a 2 ( x 2   2 )  ...  a n ( x n   n )  ( x   )[a1  a 2 ( x   )  ...  a n ( x n 1  x n  2  ...   n 1 )]. 表示 P ( x)  P ( ) 可以被 x   所除，故 P (x) 被一次式 x   所除，餘式為 P ( ) ，故得證。. (2). 列舉法亦可稱為窮舉法，就是將所有的選項皆檢查一遍。例子：證明 x 2  x 。【證明】： x  R 可分成非負 ( x  0 ) 、負 ( x  0 ) 若 x  0 則 x2  x  x ；若 x  0 則 x2  x  x 。. Thus ， x 2  x for x  R 。. 20.

(34) (3). 綜合法畢氏定理一般可以使用幾何計算面積的方法證明 ( 直接證 )，亦可使用代數的方法，也就是綜合法。例子：欲證明 a 2  b 2  c 2 ，其中 a  BC 、 b  AC 且 c  AB 。. C 1 2 3 4 D. A. 圖 2-1-1. B. 綜合法例圖. 【證明】：因為 DBC 相似 DCA ， 2. 2. 所以 AD  AB  AC ， BD  BA  BC ， 2. 2. 2. 因此 b 2  a 2  AC  BC  AB( AD  BD)  AB  c 2 ，故得證。. (4). 倒推法例子：抓拈 ( 致勝策略 )「組合」。其中規則為：(1)20 個石子 (2) 每次必需拿 1-3 顆 (3) 拿到最後一顆勝，請問致勝策略。【證明】：控制 - 後拿的人，拿 1~3 顆但與前一人顆數總和要是. 4 的倍數。. ○○○○ ∣ ○○○○ ∣ ○○○○ ∣ ○○○○ ∣ ○○○ ○勝圖 2-1-2 倒推法例圖. 21.

(35) 2. 間接證：可細分為兩種方法。 (1). 反證法也可稱為矛盾法或歸謬法。先把結論否定，再導出與事實不符的結果，其中假設相反命題三段論為： (1) 矛盾 (2) 因此 (3) 正確命題。例子：證明 2 是無理數。【證明】：假設 2 . p 是有理數，其中 p 、 q 是互質的整數。 q. p2 兩邊同時平方可得 2  2 ，即 p 2  2q 2 ，因為是 2 的倍數，即 q 可知 p 2 為偶數，因此 p 也為偶數。假設 p  2k ，其中 k 是整數，則 p 2  4k 2  2q 2 ，得 q 2  2k 2 ，也為 2 的倍數，因此 q 2 也是偶數，故 q 也是偶數。由以上可得知 p 、 q 為偶數，其皆有公因數 2 ，與一開始的假設矛盾，因此 2 不是有理數，故得證。. (2). 同一法 ( 同義法 ) 利用邏輯等價 (p  q)  (~ q ~ p) 的證明。例子： 157 是否為質數。【證明】： 157  13 ，檢查 2 、 3 、 5 、 7 、 11 都不能整除 157 ，因此 157 為質數。命題：若小於或等於 n 之質數都不是 n 之因數，則 n 必為質數。變型命題：若滿足 p 2  n 之所有質數 p 不為 n 之因數，則 n 必為質數。. 22.

(36) 改寫命題 ( ~ Q ⇒~ P ，同義 P ⇒ Q ) ：若 n 不是質數，則滿足 p 2 ≤ n 之質數至少有一個為 n 之因數。再變型命題：若 n 為合成數，則 n 必有一質數 p 不為 n 之因數，則 n 必有一質數使得 p 2 ≤ n 。【證明】： n 是合成數，則存在因數 d 使得 1 < d < n 。 n=d×. n n ，則為 n 之正因數， d d. 令 p 為 n 之最小質因數，則 p ≤. n 且 p≤d， d. 故得證， p 2 ≤ n 。. 由本節內容可知，數學證明內容可從邏輯與數學證明兩部份來看。其中邏輯可包含「敘述」、「否定」、「複合敘述」及「連續推理」；數學證明的方法可分為「自然歸納法」與「演繹法」。茲整理如下圖：. 23.

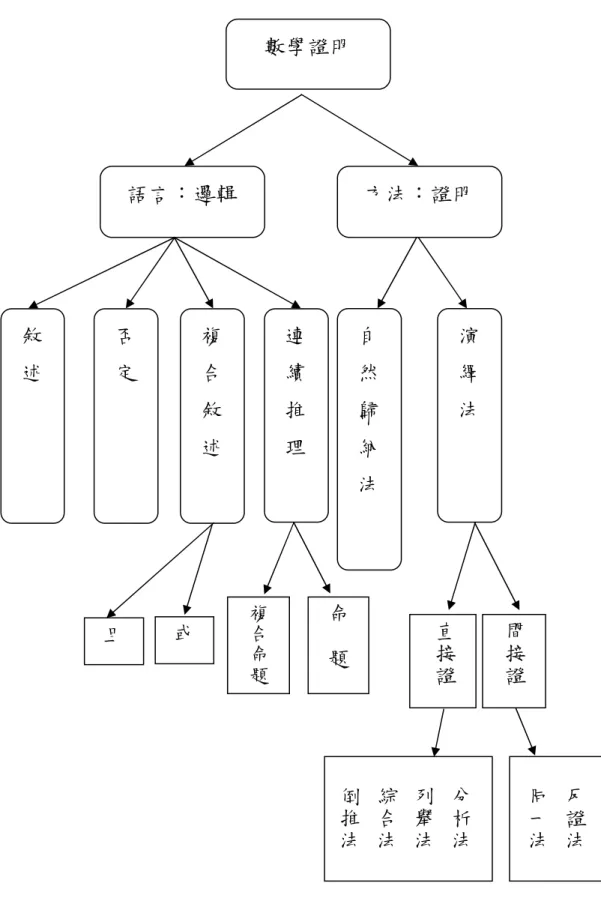
(37) 數學證明. 語言：邏輯. 方法：證明. 敘. 否. 複. 連. 自. 演. 述. 定. 合. 續. 然. 繹. 敘. 推. 歸. 法. 述. 理. 納法. 間接證. 題. 反證法. 同一法. 分析法. 列舉法. 綜合法. 倒推法. 24. 直接證. 命. 複合命題. 或. 且. 圖 2-1-3 數學證明分析圖.

(38) 第二節. 數學教育對證明的要求. 本節分可分兩個部分，說明教育部對「證明」的教學要求，第一部分將探討「九年一貫課程綱要數學學習領域對證明的要求」，第二部分是「高中課程綱要數學學習領域對證明的要求」。以下的內容主要根據《九年一貫課程綱要》以及《高中課程綱要》加以詳細說明。. 一、九年一貫課程綱要數學學習領域對證明的要求. 有關國民中小學的數學內容，是由《九年一貫課程綱要》所訂定。其中有關「證明」的能力指標與分年細目如下：表 2-2-1 能力指標分析能力指標. 內容. S-4-19. 能針對問題，利用幾何或代數性質做簡單證明。. A-4-20. 能針對問題，利用幾何或代數性質做簡單證明。. 表 2-2-2 分年細目分析分年細目內容. 對應能力指標. 能針對幾何推理中的步驟，寫出所依據的幾 8-s-17. 9-s-12. S-4-19. 何性質。. S-4-19. 能認識證明的意義。. A-4-20 在《九年一貫課程綱要》中，其分年細目並不要求學生能對幾何問題的證明做完全的推理及說明。僅要求學生能在幾何推理的教學中，能寫出有些步驟所依據的是什麼定理。. 25.

(39) 例子： ABCD 是一平行四邊形，試說明 AB = CD ， AD = BC ，寫出所要用的性質。【證明】：連接 B 與 D ，因為 AD // BC ，所以 ∠ABD = ∠CBD (平行線內錯角相等 )，因為 BD = BD (共用邊 )、 AB // CD ，所以 ∠ABD = ∠BDC ( 平行線內錯角相等 )，因此 ∆ABD ≅ ∆BCD (ASA 全等性質 )，所以 AD = BC ，且 AB = CD 。由以上可知數學證明是由已知條件或已經確定是正確的性質來推導出結論，因此學生在學習時，應將每一步驟所根據的理由切確地表達出來。在《九年一貫課程綱要》當中，證明並不侷限於幾何推理，也可以包括代數或數與量的推理。其教學目的僅要讓學生初步認識證明的意義，因此推理的步驟也以二、三個步驟為限。例子： AB 與 CD 為圓 O 之平行兩弦，試證明 AC弧長 = BD弧長。. 圖 2-2-1. 九年一貫例圖. 【證明】：連接 AD，因為 AB 與 CD 平行 ( 已知 )，所以 ∠ADC = ∠BAD (內錯角相等 ) 。因此 AC弧長 = BD弧長 (等角對等弧 ) 。例子：若 a、b、c 為三個正整數，且滿足 a 2 + b 2 = c 2 ，試證明 c − b 可以整除 a 2 。【證明】：由 a 2 + b 2 = c 2 ( 已知 ) ，得 a 2 = c 2 − b 2 = (c − b)(c + b) ( 平方差公式 ) ， a 2 ÷ (c − b) = c + b ，所以 c − b 可以整除 a 2 。幾何形體的理解包含察覺、操作、構造、推理證明等諸多面向。在. 26.

(40) 國中幾何教學的目標，首要在於提供學生日後有用的核心幾何知識，其次是提供豐富的背景，可以展示數學推理證明的過程與威力，而推理能力的培養正是國中數學教育的重點之一。因此在小學的時候不論是計算或是解答應用問題乃至於利用驗算來檢查答案的合理性都是推理學習的一部分。國中的幾何學習，由直觀、歸納轉入幾何推理與證明。幾何教學起初仍然以學生的幾何直覺經驗為前導，但開始強調幾何觀念的明確定義，及幾何相關量的計算，甚至到代數演算。學生同時應開始學習閱讀幾何性質的嚴格推理，最後，再學習自己動手寫出較短的證明。這對於日後數學邏輯推理能力及以抽象為主的高中數學學習皆很重要。不過，在《九年一貫課程綱要》有提到兩個問題，是因為傳統教學上幾何和證明綁得太緊的現象而產生的。第一個問題是「以為學習幾何等於學習歐氏幾何證明」。但在學習國中幾何當中，只是提供展示證明過程的背景，幾何學仍然有本身的核心觀念，超越於形式的證明之上。如果過份注重瑣碎形式證明的結果，甚至以為證明就是國中幾何的全部，反而無法完成國中幾何的教學目標。第二個問題是「不表示在國中其他數學教學時，就可以忽略嚴謹性」。因為幾何的確提供了豐富的背景，來展示證明的過程，但這事實上，推理能力的培養，應貫徹在國中的整個數學教學中。如果學生在完成解題之後，嘗試說明每一個步驟的合理性，這個說明的過程，就是證明。小學與國中學習不同之處原因有二，一是「由非形式化的推理逐漸提升至形式化的推理」。由於國中生較小學生年長，在語言及文字的呈現和對解題過程的反思都較成熟，因此應該學習如何將推理的步驟具體寫出，加強解題時的分析和溝通能力。原因二是「理解推理在幾何學習中扮演著提綱挈領的角色」。小學生在操作四則運算時，每一個步驟的合理性經常是透過算則或是經驗法則達成的定律。例如： a + b = b = a ，但是對於幾何圖形所擁有的性質，開始學習時並不明顯，或是必須依賴特定. 27.

(41) 的圖形，或是必須依賴操作的結果。例如：三角形三內角和等於 180° 這件事，就並不是那麼顯而易見的。再例如：等腰三角形兩底角相等，在呈現時，必須依賴一個特定的圖形，而非畫出所有的圖形，因此在建立定律的過程需要透過逐步的推理以建立一個普遍成立的陳述。又如畢氏定理，至少必須透過面積關係才能確認，並非經驗法則可以涵蓋。但是就整體的學習而言，觀察、判斷、嘗試做出結論仍然是在推理之前重要的過程。推理並非盲目的邏輯推演，推理代表的是對現象合理的終極分析。因此在學習推理的時候應把握最基本的概念和定律。從定性和定量兩個基本的方向，開始進行學習。其中定性的部分，包括對稱、全等、相似形；定量的部分包括面積公式，畢氏定理和相似形比例關係。掌握學習時什麼是最基本的，或者說在學習中，能夠分辨主體和輔體的區別，正是幾何推理對其他學科學習的重要貢獻。其中《九年一貫課程綱要》更特別提醒教師，推理能力的培養、證明的教學並不等於要求學生寫出冗長證明。國中以幾何直覺經驗為前導，使用主體或觀念的明確定義，探索幾何現象並以推理驗證是教學的重點。推理證明教學重點在於，學生應能領略證明如何使我們跳脫侷限經驗、延伸並確保思考正確性的好處，學習閱讀並反覆思考推理的過程，進而能夠養成自己言之有物的習慣，能夠辨認論證過程中容易犯的錯誤，最後再嘗試練習寫出較短的證明。. 二、高中課程綱要數學學習領域對證明的要求. 《高中課程綱要》中的推理能力方面，主要是能認識證明，並進行推論。其中必須認識定理的敍述與證明，介紹命題、充分條件、必要條件、充要條件、反證法。在「數」的學習中，要循序漸進地引領學生學習以文字替代具體數字的形式操作，包括展開、分解與化簡，以與國中的經驗連結，並作為. 28.

(42) 學習的基礎。例如：循環小數為有理數的證明，但僅需初步介紹。並讓學生發現數列的規律性，歸納成公式，並用數學歸納法加以證明。在高中課程綱要當中，也明確列出幾項學生必須學會的證明，其內容整理如下：表 2-2-3 高中證明基礎 1.最小平方法的證明。 2.透過因式定理證明插值多項式的唯一性。 3.正 n 次方根的存在唯一性的證明。(有理根判定法、勘根定理) 4.證明虛根成對定理。(實係數多項式的代數基本定理、虛根成對定理) 5.由生活中的實例說明機率函數要滿足的基本條件，並證明機率函數的基本性質。 6.透過直角三角形的面積公式及畢氏定理推得正弦、餘弦定理的證明。 7.差角公式的證明。 8.證明簡單平面幾何的性質。(如三角形兩邊中點連線定理) 9.平行四邊形相關定理的證明。 10.證明循環小數是有理數。 11. 2 為無理數的證明。以下是依據表 2-2-3 例舉兩個證明的範例，並參考普通高級中學『數學 1 』翰林 (2009)、普通高級中學『數學 2 』，普通高級中學『數學 1 』與普通高級中學『數學 2 』，整理如下：. 29.

(43) 4.證明虛根成對定理設 f ( x) = a n x n + a n −1 x n −1 + ... + a1 x + a 0 是實係數 n ( n ≥ 2 ) 次多項式，且. α = a + bi ( a 、 b 是實數， b ≠ 0 )是方程式 f ( x) = 0 的根，則 α = a − bi 也是方程式的根。【證明】由於 f (α ) = a n α n + a n −1 α n−1 + ... + a1 α + a 0 = a nα n + a n −1α n −1 + ... + a1α + a 0 = a nα n + a n −1α n −1 + ... + a1α + a 0 = f (α ) 若 f (α ) = 0 ，則 f (α ) = 0 = 0 ，得出 f (α ) = 0 。故 α 是方程式 f ( x) = 0 的根。. 6. 證明正弦定理 ∆ABC 的三內角是 ∠A 、 ∠B 、 ∠C ，三邊是 a = BC 、 b = CA 、 c = AB ，外. 接圓半徑是 R ，則. a b c = = = 2R 。 sin A sin B sin C. 【證明】設 ∆ABC 的外接圓圓心是 O ，當 A 是直角時，外接圓圓心 O 是邊 BC 的中點，當 ∠A 不是直角時，外接圓圓心不在邊 BC 上，作 O 到邊 BC. 的垂線，設垂足是 D ， θ 是直角三角形 BOD 的銳角 ∠BOD 。 (1) 當 ∠A 是銳角時，則 θ =. 1 ∠BOC = ∠A ， 2. 而有 a = BC = 2 BD = 2 R sin θ = 2 R sin A ，得出. (2) 當 ∠A 是直角時，則 sin A = 1 ，而有. 30. a = 2R 。 sin A. a 2R = = 2R 。 sin A 1.

(44) (3) 當 ∠A 是鈍角時，延長 O ， C 連線交圓於另一點 E ，則 θ =. 而有 θ =. 1 ∠BOC ， 2. 1 弧 BC 的圓心角 = ∠BEC = 180° − ∠A ， 2. 這時 a = BC = 2 BD = 2 R sin θ = 2 R sin(180° − A) = 2 R sin A ，同樣得出. a = 2R 。 sin A. 由以上內容可知，我國數學教育之證明能力的要求是從國小就開始的培養的，國中須開始學會二到三個證明的的條件定理，也不需過於冗長，強調在於，學生應能瞭解證明如何使我們跳脫侷限經驗、延伸並確保思考正確性的好處。到高中就會開始要求認識命題及證明的方法，並會幾項簡單的證明，因此可看出我國數學科教育對證明能力的要求及重視。. 第三節. 數乙考科之證明考古題. 本小節主要是列出歷屆之證明題，從 91 學年度開始正式由大學聯合招生考試轉為大學指定科目考試，因此將蒐集 91 學年度至 100 學年度大學指定科目考試數乙考科之考題。其題目來自大學入學考試中心的歷屆試題，並參考國字第 0990001359 號普通高級中學『數學 3 』與國字第 0990003762 號普通高級中學『數學 4 』、高審字第 0490 號普通高級中學. 『數學 1 』、高審字第 0582 號普通高級中學『數學 2 』、高審字第 0646 號普通高級中學『數學 3 』、高審字第 0687 號普通高級中學『數學 4 』的定義，解答與證明如下：. 31.

(45) 表 2-3-1 100 年數乙考科題目與解答分析表 100 學年度大學指學年度大學指定科目考試數乙考科大學指定科目考試數乙考科 a b  為二階實係數方陣，(1)當 A 為轉移矩陣時，是敘述實題目：設 A =  c d  數 a 、 b 、 c 、 d 須滿足的條件。(6 分) (2)試證：當 A 為轉移矩陣時， A 2 也是轉移矩陣(式中 A 2 代表 A 與 A 的乘積)。(6 分) 【證明】：這題設計的想法是考驗學生對轉移矩陣的基本認識，以及對證明的能力。轉移矩陣的定義：對正整數 n ≥ 2 ， n 階方陣 P = [ pij ]n×n 若滿足條件，第一是 pij ≥ 0 ， i ≥ 1， j ≤ n ；第二是 p1 j + p2 j + ... + pnj = 1 ， 1 ≤ j ≤ n ，及每一行元素和都. 是 1；則稱 p 是一轉移矩陣，對正整數 m ， p m 是 m 步的轉移矩陣。所以第一小題由以上定義，因此得知其條件為 0 ≤ a ≤ 1 ， 0 ≤ b ≤ 1 ， 0 ≤ c ≤ 1 ， 0 ≤ d ≤ 1且 a + c = 1 ， b + d = 1。. 第二小題解法是採用直接證的分析法，從已知條件去分析證明。因 b   a  ，其中 0 ≤ a ≤ 1 ， 0 ≤ b ≤ 1 。即可此當 A 為轉移矩陣時，設 A =  1 − a 1 − b . b   a  推得 A =  1 − a 1 − b  2. b   a 2 + b − ab  a    =  2 1 − a 1 − b   − a + 1 − b + ab. ab + b − b 2.  ，所以 − ab + 1 − b + b 2 . ( a 2 + b − ab ) + (− a 2 + 1 − b + ab ) = 1 且 ( ab + b − b 2 ) + (− ab + 1 − b + b 2 ) = 1 。又. 因為 0 ≤ a ≤ 1 ，所以 a 2 + b − ab = a 2 + b(1 − a ) ≥ 0。因為 0 ≤ a ≤ 1， 0 ≤ b ≤ 1，. 32.

(46) 得 a 2 + b − ab − 1 = a 2 − 1 + b − ab = (a + 1)(a − 1) + b(1 − a ) = (a − 1)(a + 1 − b) ≤ 0 ，故 a 2 + b − ab ≤ 1 ，同理 0 ≤ ab + b − b 2 ≤ 1 ，故得證， A 2 也是轉移矩陣。. 表 2-3-2. 96 年數乙考科題目與解答分析表. 96 學年度大學指學年度大學指定科目考試數乙考科大學指定科目考試數乙考科題目：設 r 、 s 為整數，已知整係數多項式 x 3 + rs + s 的因式分解是 x 3 + rs + s = ( x + a ) 2 ( x + b) ，其中 a、 b 為相異實數，求證 a、 b 都是有理數。 (13 分 ). 【證明】：. x 3 + rs + s = ( x + a ) 2 ( x + b) = ( x + 2ax + a 2 )( x + b) = x 3 + (2a + b) x 2 + (a 2 + 2ab) x + a 2b. 2a + b = 0..................(1)  比較其係數，得 a 2 + 2ab = r..............(2)  2 a b = s......................(3). 由 (1) 可得 b = −2a 再代入 (2) ⇒ a 2 + 2a (−2a ) = r ⇒ − 3a 2 = r......(4) 由 b = −2a 再代入 (3) ⇒ a 2 (−2a ) = s ⇒ − 2a 3 = s......(5) 當 a = 0 時， b = 0 (不合，因為 a ≠ b )。當 a ≠ 0 時，. (5) − 2a 3 s 2a s 3s ⇒ = ⇒ = ⇒a= 2 (4) − 3a r a r 2r. 33.

(47) 因為 r 、 s 為整數，所以 a =. 又 b = −2 a = −. 3s 為有理數。 2r. 3s 亦為有理數，故 a 、 b 都是有理數得證。 r. 表 2-3-3 93 年數乙考科題目與解答分析表 93 學年度大學指學年度大學指定科目考試數乙考科大學指定科目考試數乙考科題目：設 k 為一正整數，令 N = 10k + 5 。 1.求 N 2 除以 100 的商與餘數(以符號 k 表之)。(6 分) 2.證明 N 2 的百位數字是偶數。(5 分) 【證明】：1.因為 N = 10k + 5 ，所以 N 2 = (10k + 5) 2 = 100k 2 + 100k + 25 = 100(k 2 + k ) + 25 。因此除以 100 的商為 k 2 + k ，餘數為 25 。 2. N 2 的百位數字為偶數，因此 k 2 + k 是 2 的位數，若且唯若可得 k 2 + k = 2n ，其中 n ∈ Ν 。由以上可得： (1) k = 2a ，其中 a ∈ Ν ， ( 2 a ) 2 + ( 2 a ) = 4 a 2 + 2 a = 2( 2 a 2 + a ) 。 (2) k = 2a − 1 ，其中 a ∈ Ν ， (2a − 1) 2 + (2a − 1) = 4a 2 − 2a + 1 + 2a − 1 = 2(2a 2 ) 。. 34.

(48) 故 N 2 的百位數字是偶數的得證。. 表 2-3-4 91 年數乙考科題目與解答分析表 91 學年度大學指學年度大學指定科目考試數乙考科大學指定科目考試數乙考科題目：設數列 a n 的第 n 項 an 為： an =. 1 + 8n − 7 ( n ≥ 1) 2. 1. 依序列出 a2 、 a3 、 a4 、 a5 、 a6 、 a7 的值。 (6 分 ) 2. 設 k 為一正整數，試說明 k 2 − k 必為偶數。 (4 分 ) 3. 設 k 為一正整數，試證明在數列 a n 中，可以找到一個項 am 使 a m = k 。 (6 分 ). 【證明】： 1. 因為 an =. 得. a2 =. 1 + 8n − 7 ( n ≥ 1 )，所以 n 由 2 到 7 分別代入， 2. 1+ 8× 2 − 7 =2 2. a3 =. 、. 1 + 8 × 3 − 7 1 + 17 = 2 2. a4 =. 1+ 8× 4 − 7 =3 2. 、. a5 =. 1 + 8 × 5 − 7 1 + 33 = 2 2. a6 =. 1 + 8 × 6 − 7 1 + 41 = 、 2 2. a7 =. 1+ 8× 7 − 7 = 4。 2. 、. 、. 2. 因為 k 2 − k 可因式分解成 k (k − 1) ，而任連續兩整數相成必為偶數。 3. 要使 a m = k ，因此 a m =. 1 + 8m − 7 =k。 2. 整理可得 8m − 7 = 4k 2 − 4k + 1 ⇒ 8m = 4k 2 + 4k + 8 = 4k (k − 1) + 8 。. 35.

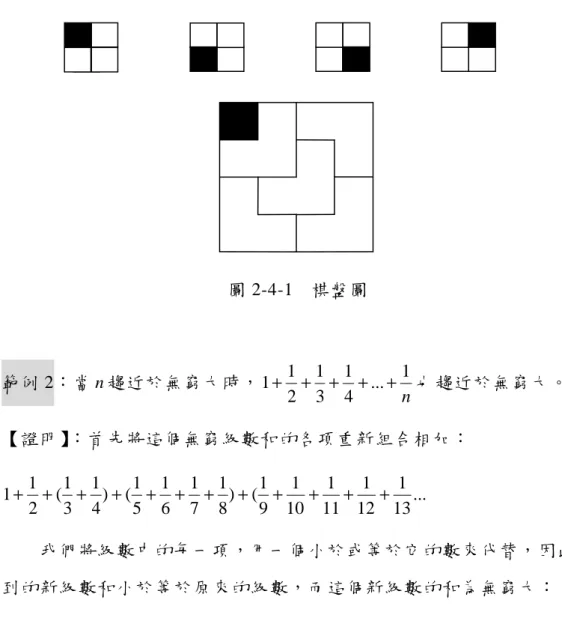
(49) 又已知 k (k − 1) 為偶數，可設為 k (k − 1) = 2t ，所以 8m = 4 × 2t + 8 ，可得 m = t + 1 ，故得證。. 由以上整理觀察出，大學指定科目考試數乙考科會考證明題且配分都在十分以上，並非因為是數乙考科就完全不考。且也可以藉由這些考古題得知，證明題考題都是經由一層一層的推演引導學生作答，會給一些先備條件與知識或例題，讓同學可以循這些規則與想法證明推導出題目要的結果。. 第四節. 證明範例. 數學證明要縝密且引用有據，形式上應簡潔清晰，這些數學證明的背後都藏著許多數學之美。這一節主要在蒐集一些證明精簡漂亮與經典的數學證明的題目，所以茲將呈現眾多解法中的一種，來作為此範例的證明。並參考《E-Z Geometry》(Leff , Lawrence，2009)、《數學證明》(蕭文強，2007)與《妙不可言的數學證明》(Burkard Polster，2006)整理歸納如下：範例 1：任一個 2 n ×2 n 的棋盤走一格後，必能用由三格所形成的 L 形所覆蓋。【證明】：利用數學歸納法，因為 2 n ×2 n 的棋盤走一格後成為 L 形，因此 n = 2 時定理成立(如下圖 2-4-1)。假設定理對 n 成立，考慮 2 n +1 ×2 n +1 的情. 形。我們將這個棋盤分為四份，然後走中心的三格，於是得到四個 2 n ×2 n 棋盤，而且每個棋盤上都移走了一格。根據假設，這四個部分均可以用 L 形覆蓋，於是得到 2 n +1 ×2 n +1 的一種 L 形的覆蓋方式，故得證。. 36.

(50) 圖 2-4-1. 範例 2：當 n 趨近於無窮大時， 1 +. 棋盤圖. 1 1 1 1 + + + ... + 也趨近於無窮大。 2 3 4 n. 【證明】：首先將這個無窮級數和的各項重新組合相加： 1+. 1 1 1 1 1 1 1 1 1 1 1 1 + ( + ) + ( + + + ) + ( + + + + ... 2 3 4 5 6 7 8 9 10 11 12 13. 我們將級數中的每一項，用一個小於或等於它的數來代替，因此得到的新級數和小於等於原來的級數，而這個新級數的和為無窮大： 1+. 1 1 1 1 1 1 1 1 1 1 1 1 + ( + ) + ( + + + ) + ( + + + + + ... 2 4 4 8 8 8 8 16 16 16 16 16. =1 +. 1 1 + 2 2. +. 1 2. 1 2. +. +….. 因為我們用一個比原來小於或等於它的數來代替，因此原本級數和也是無窮大，故得證。. 範例 3 ：在所有數當中，質數的個數是無窮的。【證明】：依據歸謬法。假設質數的個數有限，可以將它們全部乘起來，得到一個很大的數為 n ，其中 n = 2 × 3 × 5 × 7 × 11 × ...。因為 n + 1 比 n 的所有因數都要大，因此它不會是質數，那麼 n 的某個因數必為 n + 1 的因數，. 37.

(51) 於是， n + 1 − n = 1 也會含有這個因數，因此矛盾，所以一開始的假設是錯誤的，故得證，在所有數當中必有無限多個質數。. 範例 4：歐拉公式，凸面體的頂點數( V )+面數( F )-邊數( E ) = 2。【證明】：將頂點與邊的關係畫成網絡圖，其頂點數、面數及邊數與原立體相同。如果加上一條對角線，得到的值仍與 V + F − E 之值一樣，於是繼續加上對角線，直到得到的圖形是完全由三角形所組成的。最後，由圖形的外延開始，把三角形一個一個的修剪掉(如下圖)，最後只剩下一個三角形，此三角形有 3 個頂點、2 個面及 3 條邊。其中每一過程的 V + F − E 之值皆沒改變，因此 V + F − E = 3 + 2 − 3 = 2 。. ……….. 圖 2-4-2 凸面體修剪流程圖. 38.

(52) 範例 5：φ = 1 +. 1. 此連分數的第 n 階為 f n +1 f n ，這裡 f n 為第 n. 1. 1+ 1+. 1 1+. 1 1+. 1 .... 個費布納西數。. 【證明】：用數學歸納法證明。令第 n 階連分數為 g n 。第一階連分數 g1 就是. f 2 f1 = 1 1 = 1. ，. 假. 設. 第. n. g n +1 = 1 + 1 g n = 1 + f n f n +1 = ( f n +1 + f n ) f n+1. 階. g n = f n +1 f n. ，. 於. 是. 。根據費布納西數的定義. f n +1 + f n = f n+ 2 ，所以 g n +1 = f n + 2 f n +1 。. 範例 6 ：若一奇數可以寫成 n = 4k + 3 ，則該數不能寫成兩完全平方數之和，比方說 a 2 + b 2 。【證明】：因為 a 和 b 均有可能為奇或偶數，所以分別進行討論。狀況 1：如果 a 和 b 均為奇數，則 a 2 和 b 2 也均為奇數。所求 a 2 + b 2 亦為偶數，不能寫成奇數 n = 4k + 3 。狀況 2：如果 a 和 b 均為偶數，則 a 2 和 b 2 也均為偶數。所求 a 2 + b 2 亦為偶數，不能寫成奇數 n = 4k + 3 。狀況 3：假設 a 為偶數，也就是說為 2 的倍數，可表示成 a = 2 p ，其中 p 為某全數。假設 b 為奇數，可表示成 b = 2q + 1，其中 q 為某全數。 a 2 + b 2 = (2 p ) 2 + (2q + 1) 2. 因此可推得，. = 4 p 2 + (4q 2 + 4q + 1) 也就是 4 的倍數加 1 。 = 4( p 2 + q 2 + q ) + 1. 由以上三種情況可知，一奇數可以寫成 n = 4k + 3 ，則該數不能寫成兩完全平方數之和，故得證。. 39.

(53) 範例 7：從 1 開始連續累加奇整數，所得總和為完全平方數。【證明】：設 S 為 1 從到 2n − 1 連續累加奇數所得總和，即 S = 1 + 3 + 5 + 7 + ... + (2n − 1) 。把 1 從到 2n 的所有數累加，減去所有偶數的和，結果是 S 。則. S = [1 + 2 + 3 + 4 + ... + (2n − 1) + 2n] − [2 + 4 + 6 + 8 + ... + 2n] = [1 + 2 + 3 + 4 + ... + (2n − 1) + 2n] − 2[1 + 2 + 3 + 4 + ... + n] 1 1 S = 2n(2n + 1) − 2[ n(n + 1)] 2 2 S = n(2n + 1) − n(n + 1) = 2n 2 + n − n 2 − n = n 2. 所以，從 1 開始連續累加奇整數，所得總和為完全平方數，故得證。. 範例 8 ：以全等證多邊形圍繞共頂點排列，只有三種排法不帶「孔隙」。【證明】：先判定不等邊數 (含 3 、 4 邊，或為 n 邊 ) 正多邊形所含各角的角度大小。假設此圖為正 n 多邊形 ( n ≥ 3 ) ，每個角的大小都為 θ 。由中心點 O 向各頂點畫線，把正 n 多邊形分割成 n 個全等的三角形。因為所有頂點都在 O 點交會，因此所有三角形的頂點剛好環繞 O 點一圈，也就是 360° 。其中，三角形中 2n 個底角，各角的角度都為 θ 2 ，所以，多邊形. 中所有三角形的總角度數為 360° + 2n(θ 2) = 360° + nθ 。 360° + nθ = n × 180°. 因此每一個角度 θ 為. nθ = n × 180° − 360°. θ=. 。. n × 180° − 360° 360° = 180° − n n. 因為要不帶「孔隙」，所以我們令 k 為頂點銜接的全等證多邊形 ( k ≥ 3 )。 360° = k × (180° −. 於是可由剛剛上面得到的角度得. 1 1 1 = k( − ) 2 n. 40. 360° ) n. 。.

(54) 1 1 1 1 3 3 3 3 1 但因為 k ≥ 3，又得 1 = k ( − ) ≥ 3( − ) = − ，所以 ≥ − 1 = 。 2 n 2 n 2 n n 2 2. 交叉相乘得 3 × 2 ≥ n ×1 ， k ≤ 6 。則以下分別討論：情況 1：若 n = 3 ，則多邊形的每個角皆為 60° 的三角形。因此每個頂點為 360° 60° = 6 個等邊三角形的頂點銜接，而且不會留下孔隙，又. 稱蜂巢形排法。 ( 如下圖 ). 圖 2-4-3 三角形排列圖. 情況 2：若 n = 4 ，則多邊形的每個角皆為 90° 的四角形。因此每個頂點為 360° 90° = 4 個等邊四角形的頂點銜接，也不會產生孔隙。 (如下. 圖). 圖 2-4-4. 四角形排列圖. 情況 3 ：若 n = 5 ，則多邊形的每個角皆為 108° 的五角形。因此每個頂點為 360° 108° = 10 3 ，因此正五邊形無法填滿整個圓周，此情況不符。. 41.

(55) 情況 4：若 n = 6 ，則多邊形的每個角皆為 120° 的六角形。因此每個頂點為 360° 120° = 3 個等邊六角形的頂點銜接，亦不會有孔隙。( 如下圖). 圖 2-4-5 六角形排列圖. 42.

(56) 第三章. 研究方法. 本研究的目的為探究高中學生對證明的瞭解狀況，包括證明的定理、相關內容、過程步驟以及所遇到困難為何，也對大學參加指定科目考試數乙考科的學生，分析他們的感想與答題狀況。本章共分為四節，為『研究架構』、『研究對象』、『研究工具』和『研究流程』等部分闡述。. 第一節. 研究架構. 綜合第二章文獻探討的結果及研究目的，本研究方法分成兩個部分。第一部分為量的分析研究，蒐集大學生以及高中學生分別實施問卷 A1 與問卷 A2 之問卷調查，並統計分析。問卷 A1 是針對大學生，可分為三個主題，第一是「基本資料」，第二是「高中生學習證明的狀況」，第三是「參加大學指定科目考試數乙考科試題的意見感想」；問卷 A2 是針對高中生，亦可分為三個主題，第一是「基本資料」，第二是「高中生學習證明的狀況」，第三是「未來若參加大學指定科目考試數乙考科試題的想法」。兩份問卷中的每一主題均設計若干小題，每題皆請學生勾選出適合的選項。第二部分為質的分析研究，挑選成績較理想、中等與落後的學生各兩名，共六名不同程度的學生，進行問卷 B 之問卷調查，內容包括對數學證明的瞭解與應用，與進行證明的解題。並且也對國立高級中學的教師進行問卷 C 的調查，內容包括教師教授數學證明的狀況以及學生學習的情形。此 B、C 問卷皆進行筆答與半結構式訪談，而訪談過程中全程錄音，事後再由研究者將錄音檔轉為文字檔，以便進行質的分析研究。. 43.

(57) 第二節. 研究對象. 本研究的對象可分為兩部分。第一部份為大學生，是採自本研究者就讀的學校，該校是位於屏東縣的國立大學。第二部分為高級中學的學生，分別是以該縣的國立高級中學與國立女子高級中學。前者每年招收約兩千多人，全校 57 班，每年級有 19 班，其中包含了數理班、體育班與美術班。而後者每年招收 13 班普通班、1 班數理資優班及語文班，全是女生，另招一班音樂班，男女兼收。屏東地區與中、北部地區比較起來，人口較為稀少。但此國立大學為屏東縣優秀傑出的學校，而其餘高中兩校皆為男女生在屏東縣的第一志願。依此國立大學採取不同系所的學生，共 383 人進行 A1 問卷實施。另外兩所國立高級中學皆採常態形編班，因此分別隨機抽取各三班，共六班 364 人實施問卷 A2 問卷調查，以上皆為量的分析。另外在各兩所國立高級中學與國立大學各抽取程度較好、中等與較差的學生各 6 名共 12 人，進行問卷 B 之筆答與訪談；以及各三位老師，共 6 名，進行問卷 C 之訪談，進行質的研究分析。. 第三節. 研究工具. 本研究使用的研究工具有四種，其分述如下：. 一、問卷 A1 (詳見附錄一). 本問卷為自編問卷，是參考文獻與請教指導教授編定初稿，內容主要是探究大學生對證明的瞭解狀況，包括證明的定理、相關內容、過程步驟以及所遇到困難為何，也對大學參加指定科目考試數乙考科的學生，分析他們的感想與答題狀況。完成初稿後，再請 30 位大學生進行預. 44.