五年級學童分數加減概念個別化認知診斷與補救教學

(1)

國立臺中教育大學數學教育學系碩士班碩士論文

指導教授：易正明教授

五年級學童分數加減概念

個別化認知診斷與補救教學

研究生：李彩瑞撰

中華民國一 ○ ○ 年六月

(2)

摘要

本研究以國小五年級學童為研究對象，應用多元計分概念詮釋結構模式(Polytomous Concept Advanced Interpretive Structural Modeling, PCAISM) 與模糊集群分析(fuzzy clustering) ，依其測驗結果繪製學童之分數加減概念詮釋結構圖，分析其分數加減概念的階層結構，並在分群後挑選各群的學童進行訪談及補救教學，以了解其概念結構，糾正學童錯誤概念。本研究之發現為： (一) 運用概念詮釋結構圖可進行個別化的教學診斷，以作為補救教學之參考依據。 (二) 透過模糊集群分群有助於教學者進行分組補救教學。 (三) 進行補救教學後，受試者之概念結構與概念精熟度皆有所差異。 (四) 低精熟度學童對分數加減意義並不熟悉，教學時應加強因數倍數與分數的連結，並多舉生活中的實例，來強化學童對分數加減實質意義的理解。本研究之結果與發現，可提供教學者有關國小學生分數加減概念教學之參考，以及未來進一步研究之建議。關鍵字：分數加減、補救教學、模糊集群、概念詮釋結構模式

(3)

Abstract

This study focuses on the learning behaviors of the fifth-grade students by using

Polytomous Conceptadvanced Interpretive Structural Modeling (PCAISM) and fuzzy

clustering analysis method. According to the student’s math test results, we draw the

concept advanced interpretive structural figures of addition and subtraction on

fraction numbers, to analyze the concept stratum structure of addition and subtraction

on fraction. After clustering, we choose some students in each group and interview

with them. The recovery teaching is involved in the study in order to realize the

concept stratum structure and then collect the wrong concept of the students.

The interesting findings of the study are as follows.

(1) Use the Polytomous Conceptadvanced Interpretive Structural figure to analyze

the character of individual student’s fraction conception structure, and then

further take it as the reference of recovery teaching.

(2) It is helpful for teachers to use the fuzzy clustering method for separating

students into different groups.

(3) After recovery teaching, the individual student’s conception structure and the

conception familiarity are improved.

(4) The students with poor conception familiarity are not familiar with the meanings

of addition and subtraction on fraction. Therefore, the teachers should give more

examples in the real world life to students for strengthening the understanding of

the real meanings of addition and subtraction on fraction.

The results and findings in this study, we provide some suggestions to the teachers

who are interested in the concept teaching of addition and subtraction on fraction, and

some comments to the researchers who are interested in further study on this topic.

(4)

第一章緒論...1 第一節研究動機 ...1 第二節研究目的 ...3 第三節名詞釋義 ...3 第二章文獻探討...7 第一節分數相關概念...7 第二節概念詮釋結構模式 ...13 第三節認知診斷方法與補救教學 ...18 第三章研究方法...25 第一節研究流程 ...25 第二節研究樣本 ...26 第三節研究工具 ...28 第四節資料分析 ...38 (二)分析解題結果之概念全對通過率，呈現出學童的解題能力。 ...38 第四章研究結果與討論 ...42 第一節高低分群組及利用 f-cut 分群後各組 POT 圖比較 ...42 第二節同精熟群組學童之概念詮釋結構圖比較 ...49 第三節不同精熟群組學童概念詮釋結構圖之比較 ...53 第四節各分群受試者進行訪談及補救教學之表現情形 ...55 第五節補救教學前後的概念詮釋結構圖之差異 ...67 第五章結論與建議 ...77 第一節結論 ...77 第二節研究限制 ...80 第三節建議 ...80 參考文獻 ...83 附錄一分數新舊綱要對照表 ...93 附錄二分數加減概念預試試題...97 附錄三分數加減概念正式施測卷... 104 附錄四分數加減概念後測卷 ... 111 附錄五受試者反應矩陣 ... 116

(5)

附錄六試題屬性矩陣 ... 122

附錄七學童補救教學逐字稿（S04）... 123

附錄八學童補救教學逐字稿（S06）... 127

附錄九學童補救教學逐字稿（S15）... 128

(6)

表次

表 2-1-1 分數意義相關研究...9 表 2-1-1 分數意義相關研究(續) ...10 表 2-1-2 國小階段分數的意義整理表 ...12 表 2-1-3 國小階段分數的意義整理表(續)...13 表 2-2-1 試題屬性矩陣和受試者反應矩陣舉例...16 表 3-2-1 預試樣本人數分配表...27 表 3-2-2 研究樣本人數分配表...28 表 3-3-1 以九年一貫課程綱要為參照基準的分數概念對照表...29 表 3-3-1 以九年一貫課程綱要為參照基準的分數概念對照表(續) ...30 表 3-3-2 分數概念內容及說明...30 表 3-3-3 分數試題的概念屬性矩陣 ...31 表 3-3-4 預試信度分析表...32 表 3-3-5 試題與分年細目對應表 ...33 表 3-3-6 預試工具之難度...34 表 3-3-7 預試工具之鑑別度、相關及 t 檢定...35 表 3-3-8 分數試題的概念屬性矩陣 ...37 表 4-1-1 受試者在不同分群數所得之分割係數及分割亂度 ...45 表 4-4-1 高精熟組中不同受試者之答題情形...56 表 4-4-2 高精熟組中不同受試者之精熟度矩陣...56 表 4-4-3 分數加減試題的概念屬性矩陣及受試者 S04 答錯題號註記表 ..57 表 4-4-4 分數加減試題的概念屬性矩陣及受試者 S06 答錯題號註記表 ..60 表 4-4-5 低精熟組中不同受試者之答題情形...62 表 4-4-6 低精熟組中不同受試者之精熟度矩陣...62 表 4-4-7 分數加減試題的概念屬性矩陣及受試者 S15 答錯題號註記表 ..63 表 4-4-8 分數加減試題的概念屬性矩陣及受試者 S20 答錯題號註記表 ..66

(7)

圖次

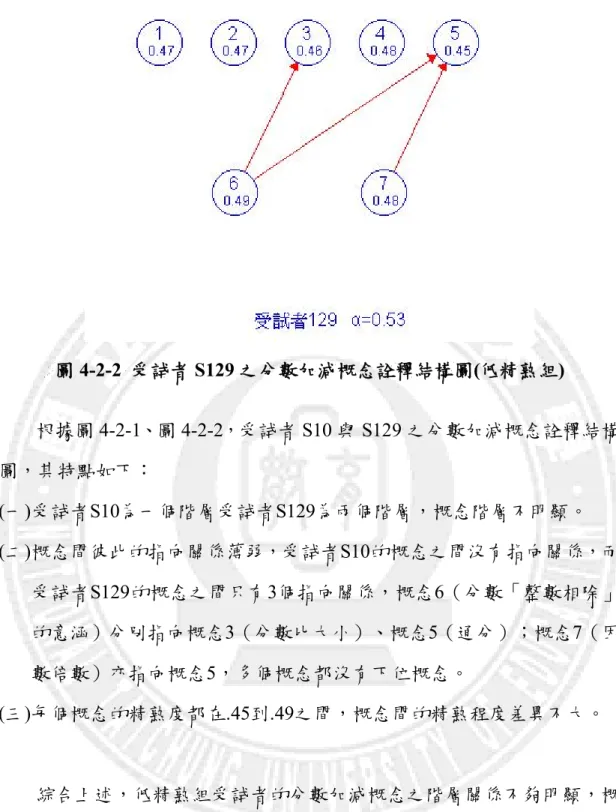
圖 2-2-1 多元計分概念詮釋結構模式的演算法(蔡孟憲、林原宏,2010) ...15 圖 2-2-2 兩位受試者的概念詮釋結構圖舉例...17 圖 3-1-1 研究流程圖 ...26 圖 3-4-1 概念詮釋結構圖圖例...40 圖 4-1-1 高分組的次序結構圖及概念答對率圖表 ...43 圖 4-1-2 低分組的次序結構圖及概念答對率圖表 ...44 圖 4-1-3 高精熟組的次序結構圖及概念答對率圖表 ...46 圖 4-1-4 低精熟組的次序結構圖及概念答對率圖表 ...47 圖 4-1-5 學童分數加減概念的思考路徑 ...48 圖 4-2-1 受試者 S10 之分數加減概念詮釋結構圖(低精熟組)...49 圖 4-2-2 受試者 S129 之分數加減概念詮釋結構圖(低精熟組)...50 圖 4-2-3 受試者 S04 之分數加減概念詮釋結構圖(高精熟組)...51 圖 4-2-4 受試者 S41 之分數加減概念詮釋結構圖(高精熟組)...51 圖 4-2-5 受試者 S148 之分數加減概念詮釋結構圖(滿分) ...53 圖 4-3-1 各精熟群組學童之分數加減概念詮釋結構圖 ...54 圖 4-4-1 受試者 S04 之分數加減概念詮釋結構圖...57 圖 4-4-2 受試者 S06 之分數加減概念詮釋結構圖...60 圖 4-4-3 受試者 S15 之分數加減概念詮釋結構圖...63 圖 4-4-4 受試者 S20 之分數加減概念詮釋結構圖...65 圖 4-5-1 受試者 S04 補救教學前後之分數加減概念詮釋結構圖...69 圖 4-5-2 受試者 S06 補救教學前後之分數加減概念詮釋結構圖...70 圖 4-5-3 受試者 S15 補救教學前後之分數加減概念詮釋結構圖...72 圖 4-5-4 受試者 S20 補救教學前後之分數加減概念詮釋結構圖...74 圖 4-5-5 受試者 S20 訪談後補救教學時作答情形...74 圖 4-5-6 受試者 S20 補救教學後作答情形 ...74

(8)

第一章緒論

本研究以國小五年級學童為研究對象，應用多元計分概念詮釋結構模式(Polytomous Concept Advanced Interpretive Structural Modeling, PCAISM) 與模糊集群分析(fuzzyclustering) ，依其測驗結果繪製學童之分數加減概念詮釋結構圖，分析其分數加減概念的階層結構，並在分群後挑選各群的學童進行訪談及補救教學，以了解其概念結構，糾正學童錯誤概念。本章共分三節，第一節研究動機，第二節研究目的，第三節名詞釋義，茲分述如下。

第一節研究動機

五年級數學被普遍認為是學童最吃力的階段，也往往在五年級產生成績的分歧，使越來越多學童放棄數學的學習，但另一方面高分組的學童會越感興趣，進而往更艱難的題目鑽研（宋在煥、金忠靜、孫靜華,2008）。有教學者認為這是因為學童到了五年級開始應用一到四年級所學，而首次面對的因數、倍數概念，在通分及分數加減運算中扮演重要的角色，究竟在這些難懂的概念中，學同是如何將觀念組織起來，又會在何處產生迷思概念，值得研究探討。在數學教育現場，有部分學童無法和同儕在同一個出發點進行學習，因為之前的迷思概念尚未解決，此時若針對迷思概念進行補救教學，即提

(9)

供學童學習的鷹架(Vygotsky，1978)，協助兒童達到盡可能的水平(張春興， 1994，2007)。此外教學強調的亦不只是教師如何教才能達到良好的教學效果，還要了解學童的錯誤概念，及如何使用策略來修正學童經驗中已有的錯誤概念(林彥宏，2002)，因此，了解學童未精熟的概念，作為教學的參考，是身為教學者應具備的能力。台灣普遍存在城鄉差距的問題。李家同(2010)更指出台灣的教育差距已呈 M 型化：偏遠的弱勢學童無法得到和都市學童一樣多的教學資源，學業明顯落後。若教學者懂得善用分析工具，了解學童概念階層結構所提供的訊息，進而應用在教學上，相信能有效率的提升偏鄉弱勢學童的學習。教學評量結果可以提供回饋訊息給老師，幫助老師在教學過程中瞭解學童的起點行為、作為改進教學的參考、確保教學目標的達成、評定學童的學習成果(余民寧，1998) 。但檢視目前的教育體系仍廣泛的運用傳統紙筆測驗作為學童學習評量的工具，多半僅著重在總結性的評量，提供答對或答錯的訊息，無法清楚呈現學童不懂到什麼程度(黃可欣，2006)，且只以ㄧ個總分來表徵學童的學習情形，很少注意學童在學習過程中的表現情形，甚至更少去瞭解學童在學習過程中的知識表徵模式(余民寧、林曉芳、蔡佳燕，2001)，此法較難分析受試者個人的試題概念屬性階層結構。每個學童的學習進度不一，但學童的迷思概念往往只能由教學經驗豐富的教師來發覺，否則難以判斷(王佩芬、易正明、林原宏，2008)，學習者的知識結構如能以具體的圖示方式呈現，明確的標示出各概念間的上下位階層、關係，讓教師了解學童的個別學習狀況，立即釐清、補足缺失，對教學將有所助益。由林原宏、洪文良、黃國榮(2006)所發展的概念詮釋結構模式(concept advanced interpretive structural modeling, CAISM)是一套適用於小樣本、個人化的概念分析工具，個人化的概念屬性階層結構在學童解題過程、策略和個別學習的輔導上，有極為重要的價值。

綜合上述各點，本研究將應用林原宏等人(2006)所發展的概念詮釋結構模式，針對國小五年級學童的分數加減概念進行探討，根據個別受試者

(10)

的概念階層結構圖，分析受試者的迷思概念，進而實施補救教學，並比教補救教學前後概念結構圖的變化，作為日後教學的參考。

第二節研究目的

本研究採用自編「分數加減概念試題」來探討國小五年級學童的分數概念和進行分數加減運算的表現，以數值和圖形呈現學童之個人化概念階層結構，再透過模糊集群分析進行分群，隨機抽取各群的學童針對其迷思概念進行補救教學，其後進行後測，探討各群學童進行補救教學後，概念詮釋結構圖前後的變化情形。本研究之研究目的如下：一、利用模糊分群及次序理論，探討國小五年級學童對分數加減概念之精熟度和上下位概念間的關係，並比較不同分群方法所呈現之結果。二、依據概念詮釋結構模式，針對國小五年級學童的分數加減概念進行描述性分析。三、利用模糊集群分析，將概念詮釋結構模式的結果進行分群，探討同一群的學童其概念詮釋結構圖的圖形特徵與彼此間的關連性。四、選取精熟度不同的學童進行訪談及補救教學後，探討其概念詮釋結構圖前後的變化情形。

第三節名詞釋義

此節針對本研究所涉及的特定名詞說明及定義如下：一、國小五年級學童本研究之國小五年級學童，係指接受九年一貫正式綱要課程，於九十

(11)

二、分數概念

依據教育部(2003) 所公佈之九年一貫數學領域分數概念相關能力指標，參考各版本三到六年級數學教材中之分數單元相關課程和相關研究(林碧珍，1990;彭海燕，1998;楊瑞智，2000;詹婉華，2003, 2004;Corwin,Russel, & Tierney, 1990; Behr,Harel,Post & Lesh, 1992) ，及文獻中所提及之兒童在分數概念的學習困難(楊壬孝，1989; 林福來、黃敏晃、呂玉琴，1996;詹婉華、呂玉琴，2004 ;Hunting, 1986) ，來進行研究試題之編製。本研究所指的分數加減概念主要包括：1.同分母分數的加減及整數倍運算與比較。2. 異分母分數的加減運算與比較。3.分數比大小 4.等值分數 5.通分 6.分數「整數相除」的意涵。7.因數倍數。三、概念詮釋結構模式 CAISM 是根據受試者的測驗資料，提供個人化的概念階層結構訊息。 Lin, Hung, & Huang (2006) 根據概念向量比對(concept vector matching)和模糊理論(fuzzy theory) 的計算方法，得到受試者概念間之關係矩陣，利用詮釋結構模式(ISM) 的階層結構運算法則(Warfield, 1976, 1982) ，提出概念詮釋結構模式 (concept advanced interpretive structural modeling, CAISM)，依據受試者的測驗資料，提供個人化的概念階層結構訊息，將個人化概念階層結構(individualized concept hierarchy structure) 以數值和圖形來呈現，透過概念精熟度、概念階層及概念指向關係，有助於了解學習者學習狀況，亦可提供教學者依照個別差異改進教學設計。

四、模糊集群

結合模糊理論和集群分析這兩個概念，即為模糊集群分析(fuzzy cluster analysis) (Kaufman & Rousseeuw, 1990)，將相似程度高的元素歸為同一個集群，希望集群內元素同質性高，而集群間的元素異質性高(林邦傑， 1981；林清山，1985) ，其中隸屬度是決定元素間距離的重要因素，根據

(12)

模糊理論所進行的集群分析方法很多，本研究使用目標函數法，把各概念精熟度相似的學童分在同一群。

(13)

(14)

第二章文獻探討

本章主要根據本研究中相關理論進行探討，各節內容分別為：第一節分數相關概念，第二節概念詮釋結構模式，第三節認知診斷方法與補救教學。

第一節分數相關概念

一、分數的意義 (一) 字源義分數一詞來自拉丁文「fangere」，具有打破、斷裂的意思，因此分數也曾被人稱為「破碎數」(張美玲)。分數的英文是“fraction”，具有小部分、片段、破碎的意義，但通常是指將全部分解為部份的意思(張平東，1995)。 (二) 概念義及學術義分數的概念起源於「分」，用於解決不滿一個單位量的量的數值問題(周筱亭、黃敏晃，2001)，在不同的情境有不同的意義，故具有豐富的意義(呂玉琴，1995)。人們為了描述不滿一個單位量的零頭部分的數值問題，將原單位量等分割形成單位分量，再把幾個單位分量合成一個量，用幾分之幾來描述它的數值，這幾分之幾就是所謂的分數(南一書局，2010)。九年一貫分數的定義：能化為 q p的形式，且 p、q 皆為整數，其中 p0，

(15)

稱為分數；p 稱為分母，q 稱為分子；若 0＜q ＜ p 時， q p 稱為真分數；否則， q p 稱為假分數；形如 ₃ 1 2 的分數，則稱為帶分數。並說明小學的有理數教學，必須釐清、練習並連結有理數的四種意涵： a.平分的意涵 b.測量的意涵 c.比例的意涵 d.部分/全體的意涵最後歸結成日後數學學習中，有理數最核心的意涵─「除的意涵」。(教育部，2008) Freudenthal (1983) 主張分數的起源是「分割」一物件的活動記錄與結果，分數可以表現真實現象的分割情況。Hunting (1986) 對於分數的最初概念是以一個連續物品細分(如蘋果、蛋糕、派)。Russell (1903) 將分數 m/n 定義為當 an = bm 時存在於 a 與 b 之間的關係；這個定義使我們能證 明，在 m 與 n 皆不為 0 的情況下，m/n 是一對一的關係(劉秋木，1996)。 國內外有許多學者都主張分數具有多重的意義 (林碧珍，1990；彭海燕，1998；楊壬孝，1989；楊瑞智，2000；Behr, Lesh, Post, & Silver, 1983; Behr, Harel, Post, & Lesh, 1992; Dickson, Brown, & Gibson, 1984; Kieren, 1976, 1980, 1988; Nesher, 1985; Ohlsson, 1988)，各家說法如下表所示：

(16)

表 2-1-1 分數意義相關研究

提出學者年份提出分數意義

Behr, Lesh,

Post & Silver 1983

分數有：分數測量(fraction measures)、比(ratio)、平均(含速率、密度) (rate)、商(quotient)、線性座標(linear coordinate)、小數(decimals)、運算元(operator) 七種不同的意義。 Dickson, Brown & Gibson 1984 分數的意義有：整個區域的子區域(sub-area of whole region)、子集合與全體集合間的比較(a comparison between a subset of discrete objects and the whole set)、位於兩個整數間數線上的一點(a point in number line which line at intermediate point between two whole numbers)、兩數相除所得的商(the result of a division operation)、二組集合或二個度量的大小比較的方法(a way of comparing the sizes of two sets of the objects or two measurements)。 Nesher 1985 認為分數有五種詮釋：部份－整體(part-whole)、商(quotient)、比(ratio)、運算元(operator)、機率(probability)。 Kieren 1988 分數概念的五種建構：部份－整體(part-whole)、比 (ratio)、商(quotient)、測量(measures)、運算元(operator) Ohlsson 1988 將分數分為四種建構及十一種涵義：

1. 商的函數 (the quotient function) ：包含等分除 (partitioning)、包含除(extracting)、縮小(shrinking)、引出(educing)。

2.有理數(rational number)：包含分數(fractions)與測量 (measures)。

3.二元向量(a binary vector)：包含比(ratio)、內涵量 (intensive quantities)、比例(proportion)、平均(含速率、密度) (rate)。

4.合成函數。

Behr, & Post 1983

分數為：

1.「部分/全部」的概念。

2. 比率：強調兩個數量的關係。

3. 比值：用一個量值來代表兩個數量的關係。 4. 商：兩數相除的結果。

(17)

分數的意義是多重的，唯周筱亭、黃敏晃主張為了學童理解及教學成效，分數的意義用一個就好：把一個或多個基準單位量（例如一盒糖果、一塊蛋糕、一條繩子等等）透過等分割活動成為 n 等份，而再合成其 m 份，命名為 n 分之 m，記為m n，即為分數的原始意義。(周筱亭、黃敏晃，2001)。 表 2-1-1 分數意義相關研究(續) 楊壬孝 1988 在國小學童分數概念發展的研究中提出，分數的四種意義是：一個全體之相等的部份、一個集合等分組後的幾組、數線上的一個數值、兩數相除的結果。林碧珍 1990 則將分數的意義分成五類：全部區域的部份區域(以連續量為主，如：長度、面積、容積)–部份/全體模式、集合中的部分集合–子集合/集合模式、數線上的一個數值–數線模式、兩個整數相除的結果–商模式、二個集合或二個度量相比的結果–比值模式。 Corwin,Russel, & Tierney 1990 以有理數來定義分數，即「p/q，p、qZ，q≠ 0」。彭海燕 1998 分數的意義分為：部分/全體、子集/集合、數線上的一點、兩數相除的結果、比值。楊瑞智 2000 就其分析的結果提出分數有十種涵義： 1.部份／全部(連續量)。 2.子集合／集合(離散量)。 3.乘法運算元。 4.等值分數。 5.整數除法的結果。 6.分數是一個數／數線上的一點。 7.平均(含速率、密度)。 8.當量。 9.比例中的比／比例尺／比值／比較量÷基準量。 10.機率等。詹婉華 2003 將分數概念分為「等分」、「簡單分數」、「單位量」、「等值分數」等四個子概念。

(18)

二、國小階段分數教材教育部並沒有將全部的分數意義納入國小階段的數學教材中，但是對於分數的解釋仍有所著墨： (一) 數學科教學研究(國立編譯館，1981)提出分數的兩個由來：第一個由來：將物件等分為若干分後，取其幾分的結果第二個由來：表示實測的結果以及兩數除法的商和兩數的比值 (二) 國小數學科教學指引(教育部國立編譯館，2000)又細分為六個角度： 1. 部分與全體的比較 2. 除法的活動 3. 算子：分成若干等分，取其中幾部分 4. 小數的另一種記法 5. 比的意義 6. 測量：不滿一個單位量的量 (三) 九年一貫數學領域課程綱要(教育部，2003)又做了另一番詮釋，包含： 1. 平分 2. 測量 3. 比例 4. 比率 5. 比值 6. 部分/全體 (四) 教育部修改了 92 年綱要後，發部 97 年課程綱要(教育部，2008)，研究者將分數修改的部分整理如附錄一。

(19)

綜合上述，將國小階段分數意義歸納為表 2-1-2(改自李彥典，2008)： 表 2-1-2 國小階段分數的意義整理表 意義解說引入階段等分在具體情境中，進行分裝、平分的活動。第一階段 (2 年級) 部份／全體在「整體 1(單位量)」的問題情境中強調「平分」的意義，將一個整體等分後，以分數來表示 N 個子分割單位的部分量和整體量之間關係。第一階段 (3 年級) 分數加減在具體情境中，初步認識分數加減，並解決同異分母分數的比較與加減問題。第二、三階段 (3~5 年級) 真分數、假分數、帶分數認識真分數、假分數、帶分數，熟練假分數、帶分數的互換。第二階段 (4 年級) 等值分數在存在一個整體中，等值分數用來表示不論在連續量或離散量情境中，兩個量的「部分－整體」相對關係不變。第二、三階段 (4~5 年級) 分數是一個數／數線上的一點將簡單的整數數線，延伸至分數數線，分數的意義擴展為數線上的一個點。位於數線上這個點的分數數值所表示的是當原點與單位長確定之後，這個點與原點和單位長與原點形成的相對關係。第二、三階段 (4~5 年級) 整數除法的結果當兩數相除無法用整數除盡時，其相除的結果用分數來表示，例如 3÷9=3/9 第二階段 (4 年級)

(20)

表 2-1-3 國小階段分數的意義整理表(續) 平均(含速率) 用分數來表示兩種度量單位以其中一種為基準量相比較的結果，例如：速率是長度和時間比較的結果。第三階段 (6 年級) 比例中的比／比例尺／比值／比較量÷基準量當兩個集合或兩個度量相比的結果、比例尺的表示及比值用 p/q 來表示時，分數的意義是兩量比較的結果。第三階段 (6 年級) 綜觀上列整理發現，小學數學教材最先引入的分數意義是「等分」以及「部分全體」兩種意義。國小分數概念的理解對未來數學學習具有重大的影響，不過在國小階段分數已代表多重意義，學童在理解分數概念時有諸多學習上的困難 (呂玉琴，1991)。

第二節概念詮釋結構模式

Warfield (1976, 1982) 所提出的詮釋結構模式(interpretive structural modeling, ISM)原本僅限於分析二元關係的資料矩陣，就一個集合內元素之間的關係矩陣，根據離散數學和圖形理論，呈現出元素間的階層圖形和先後順序關係，原本應用於社會系統工學，經日本學者佐籐隆博將之應用在教育上(林原宏，2005a；林原宏、陳進春、許天維，2005)，之後Lin, Hung & Huang (2006) 擴展詮釋結構模式，並根據概念向量比對(concept vector matching) 和模糊理論 (fuzzy theory) 等計算方法，並利用詮釋結構模式 (interpretive structural modeling, ISM)的階層結構運算法則，可以數值和圖形結構呈現個人化概念階層結構 (individualized concept hierarchy structure)。

(21)

多元計分概念詮釋結構模式是以林原宏等人(2006)所提出的概念詮釋結構模式(concept advanced interpretive structural modeling, CAISM)為基礎，針對其計分法進行擴展與改良，使其適用於多元或混合的計分測驗資料，增進概念詮釋結構模式理論之應用範疇Lin et al.(2006)。

一、多元計分概念詮釋結構模式之演算方式如下(Lin,Hung & Huang, 2006)：輸入受試者反應矩陣為X(x_nm)_N__M( x_nm 1表示受試者n答對試題 m；x_nm 0表示受試者n答錯試題m)與試題屬性矩陣Y(y_ma)_M__A(y_ma 1 表示試題m測量概念屬性a；y_ma 0表示試題m沒有測量概念屬性a)，接著求出精熟度矩陣D(d_na)_N__A 得到受試者n在概念a的精熟程度，除此之外也可獲得對於每個學童而言，在兩兩概念間的從屬關係機率所構成的模糊關係矩陣(fuzzy relationmatrix) F_n(p_aa_')_A__A得之概念的從屬關係。再利用  截集( -cut)，選定 值且0 1運算後，可獲得二元關係矩陣(binary relation matrix)的相鄰矩陣(adjacent matrix)。亦即：

A A aa n p F ( _') _ 且          ' ' ' , 0 , 1 aa aa aa p p p ，其中 0 1 將上述步驟所得的 截集運算所得的二元關係矩陣進行ISM分析，即可獲得學童的知識結構圖。

(22)

受試者反應矩陣 X 試題屬性矩陣 Y 典型概念矩陣 Z 模糊關係矩陣 F_n(p_aa_')_A__A 精熟度表現矩陣 D 標準化近似矩陣 SC 近似值矩陣 C _ni 進行詮釋結構模式分析，將可得受試者個人化概念結構圖 CAISM 相鄰矩陣  n F 典型反應矩陣 R 正規化得分矩陣 SX 蔡孟憲、林原宏(2010)將PCAISM的演算整理為流程圖，如圖2-2-1所示： 圖 2-2-1 多元計分概念詮釋結構模式的演算法(蔡孟憲、林原宏,2010)

(23)

二、實例說明李彩瑞、林原宏與易正明(2010)針對雲林縣某校三年級學童全班共5 名進行除法概念分析：「除法概念試題」共 20 題，欲測量 8 個概念，受試者 5 人，其受試者反應矩陣X和試題屬性矩陣Y如表 2-2-1 所示。 表 2-2-1 試題屬性矩陣和受試者反應矩陣舉例 受試者反應矩陣 X 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 0 0 0 1 0 1 1 0 1 0 1 0 1 1 1 0 1 1 1 1 0 1 3 1 1 1 1 0 1 1 1 1 1 1 1 1 0 0 0 1 0 1 1 1 0 0 1 0 0 1 0 1 1 1 0 0 0 1 0 1 1 1 0 0 1 1 0 1 0 0 試題屬性矩陣 Y 0 0 0 0 0 1 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 1 0 0 1 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 1 0 0 1 0 0 0 1 0 0 1 0 0 0 0 1 0 0 0 0 0 0 1 1 0 1 1 0 0 1 0 1 0 0 1 0 0 1 0 1 0 0 0 0 1 1 0 0 0 0 0 0 0 1 0 0 0 0 1 0 0 1 0 1 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0

(24)

在表 2-2-1 中受試者 4 和受試者 5 在測驗中得分皆為 9 分，但由圖 2-2-2 可以清楚的看到兩人的概念詮釋結構圖完全不同：受試者 4 概念間的關聯性明顯比受試者 5 多，而兩人概念 6 的精熟度不同，所以受試者 4 的概念 6 可當作補救的基礎，受試者 5 卻需要加強概念 6；兩人在概念 1、4 的精熟度也有明顯差距，顯示傳統總分相同，但其認知結構並不會相同。受試者 4 受試者 5 圖 2-2-2 兩位受試者的概念詮釋結構圖舉例 三、 CAISM 在教學上的運用

Lin, Hung & Yu (2007) 運用CAISM來分析國小六年級學童等量公理概念的學習。Yih, Lin & Hung (2007) 運用CAISM對大學生進行線性代數學習的認知診斷。Yih & Lin (2007) 運用CAISM分析大學學生在MATLAB 的學習情形。黃雅琦、林原宏與易正明(2008) 透過電腦化數感診斷測驗及 CAISM分析法來分析國小六年級學童在分數及小數的數感發展知識結構。莊惠雯、林原宏與易正明(2008) 運用CAISM分析法與自編整數加減文字題來探討國小一年級學童在加減法文字題的概念結構。吳玫栞、林原宏與易正明(2008) 運用自編四邊形測驗與CAISM分析法探討國小六年級學童的四邊形概念結構。王佩芬、林原宏與易正明(2008) 運用CAISM分析法

(25)

與自編除法試題來探討國小四年級學童的除法概念結構。詹家明、林原宏 (2008) 運用CAISM分析法來探討國小五年級學童的在數與量分年細目的概念結構。李青芷、林原宏(2008) 運用CAISM分析法來探討在職進修教師的基礎統計知識結構。鄭佩郡(2008) 應用CAISM分析法分析國小六年級資賦優異學童與普通班學童的面積概念結構。戴筱玲、洪文良與林原宏(2009) 應用CAISM分析法分析國小六年級學童速率概念知識結構並以SCM演算法進行分群，探討各群受試者知識結構圖之特徵及異同。呂秀茹、洪文良與林原宏(2009) 運用CAISM與SCM分析法來分析國小五年級學童的時間化聚計算之概念結構。蔡孟憲、林原宏(2010)運用CAISM對大學生進行微積分學習的認知診斷。李彩瑞、林原宏與易正明(2010)應用CAISM分析法分析國小三年級除法概念知識結構並提出補救教學策略。賴盈州、林原宏 (2010) 應用CAISM分析法分析國中七年級學童比與比例式概念知識結構並以S-P表進行分群，探討各群受試者知識結構圖之特徵及異同。黃婷鈺、易正明(2011)運用CAISM分析法與自編未知數基本運算測驗來探討國小五年級學童對未知數基本運算的學習概念結構。以上研究結果均能有效圖繪並分析受試者的知識結構，並發現不同之受試者，其知識結構圖在連結指向及階層上皆有明顯差異，提供課程編修、教學診斷及補救教學參考之用。

第三節認知診斷方法與補救教學

評量的目的除了瞭解學童的學習情況之外，也要能同時提供學童迷思概念的診斷，才能讓教學者針對診斷結果進行適性化的補救教學。有許多學者主張，評量的實施應以認知心理學對學習歷程的研究結果，作為編製測驗的理論依據，這種結合評量與認知心理學理論的方式，就是認知診斷 (cognitively diagnostic) (涂金堂，2003) 。認知診斷結合認知與心理計量兩大領域，認知領域把知識視為網路結構，主要是在描述知識的一般本質，

(26)

把個別差異當成干擾雜訊；心理計量領域把知識視為多向度結構，主要是在精確描述個體的知識結構，瞭解個別差異與需求(游森期、余民寧， 2006) 。在資深教學者的教學經驗中發現，大部分的學童在進行分數加減運算時，只學會程序性知識，無法瞭解概念性知識，因此無法將概念應用到生活情境中，因此教學時應從概念性知識著手，待學童理解後再自行抽取出程序性知識(呂玉琴、李源順、劉曼麗、吳毓瑩，2009)。認知診斷含蓋範圍廣泛，以下簡介概念構圖(concept mapping) 、詮釋結構模式 (Interpretive Structural Modeling, ISM) 、次序理論 (ordering theory) 、試題關連結構(item realational structure, IRS) 這四種認知診斷方法，並與概念詮釋結構模式加以分析比較。另一方面有許多研究著重在教學者協助學童理解概念的理論與方法，以下分別簡介鷹架理論、診斷教學法。

一、概念構圖(concept mapping)

概念構圖是一種教育工具，可使用它來具體化學習者的認知結構，來清楚瞭解學習者的已知。Novak & Gowin (1984) 認為概念構圖是一種動詞，是一種教學活動的過程，也就是給予學習者一組概念，讓學習者用適當的連接詞(lable)將這些概念連接起來，作為一個概念圖，教師可由此診斷出學童的知識結構(knowledge structure) 與迷思概念(misconcept) ，所以概念構圖不僅是一種教學策略，也可作為一種評量工具。傳統選擇題測驗常無法測得學習者完整的知識狀態(Frederiksen & White, 1990) ，而概念構圖需要學童自己架構概念，並且由回憶中辨認概念間的關連性，強調學習者將所具備的知識以具有結構性、組織性、完整性的方式表達出來，可針

(27)

恩，1998)。宋德忠等人(1998) 指出概念構圖可以敏感的分辨教學方式、考試方式、與智力水準不同所造成的差異，但Herl, Baker & Niemi (1996) 認為，有不少以概念構圖作為評量工具，但缺點就是缺乏適當的專家模型，和較好的計分法則，使生手與專家結果之比較上太過僵化。

概念構圖在各方面的運用相當多：Komis, Ergazaki & Zogza (2007) 比較電腦輔助動態模式與以‘紙與筆’概念構圖技巧在14歲學童合作活動的不同，研究結果顯示在案例中四個主要的模式活動(分析、合成、測驗說明、技術與認知支持)透過模式運作定義模式流程的步驟，而特定的質化差異可以確實地被辨識。Kong & Kwok (2005) 設計一種認知工具來符合學習者理解新的程序知識，此工具主要是用在傳達分數等效性的概念及計算分數的能力。再者，研究的結果指出此模式能提供學習者在學習加法及減法分數上更有效的程序。

二、詮釋結構模式(Interpretive Structural Modeling, ISM)

Warfield (1976, 1982) 提出詮釋結構模式 (Interpretive Structural Modeling,ISM) 原本發展於社會系統工學，這個方法也可應用於概念層次結構分析探討。日本學者佐藤隆博(1987) 提出很多ISM分析法在教育領域裡課程與學習的應用實例，把教學者腦中抽象的要素轉為具體化的關連構造階層圖，並透過學習者概念元素彼此間的關係，獲得整體的概念結構圖 (林原宏、陳紹銘、黃國榮，2006) 。ISM分析法是要將學習者腦中思考的概念單位結構，用具體的圖形或數量表示出，建立整體概念元素間的關係，也就是經由部分元素間的關係，整合起來形成所有元素整體的關係，也可由此看出元素的高低層次和順序關係(許天維、林原宏，1994) 。 ISM分析法在教學上的運用也很多：蔡秉燁(2004) 運用ISM分析方法，針對高中數學補救教材，設計結構化教材，發現圖像式階層結構教材內容，使教學者能確切掌握教材呈現的順序，來提升補救教學的效果。鄭

(28)

麗娜(2004) 在九年一貫課程社會領域地理概念研究上，應用ISM分析法，畫出地理概念階層圖，藉此規劃地理概念學習的最佳路徑與群組概念。三、次序理論(ordering theory) 次序理論是應用於心理計量(psychometrics) 的一個另類分析取向，能夠呈現試題間的次序性關係或研究問題的次序，以利編排試題，但僅以線性次序(linear ordering) 的關係進行分析，所以會有以下兩個問題：(1)一組題目中的線性順序只能顯示出最精簡的題目關係，一旦題目數增加，就愈難獲得複製力(reproductability) 。(2)一些邏輯與統計的的分析結果指出並不是所有的次序都是線性的。因此Airasian & Bart在1973年提出一個可分析線性與非線性次序的方法，將次序理論(ordering theory) 應用在教育工學上 (Airasian & Bart,1973; Bart, 1976) 。從心理計量的相關研究中可以發現，次序理論的分析可以呈現試題階層(item hierarchy) ，且其主要應用於衡量兩個試題之間先備條件(precondition) 之次序關係。

因為次序理論能有次序、有結構的呈現事物的特點，因此被不少實證性研究採用，且以數學學習心理學的角度來看，學童的認知不但有階段性還有結構性。在Bart & Krus (1973) 提出次序理論的測量模式後，之後的相關研究主要是探討J. Piaget認知理論發展中的發展階段的次序性(林原宏、游森期，2006)。例如：Jansson (1986) 以次序理論分析J. Piaget形式運思的 16種邏輯推理的發展先後順序之階層結構。余民寧、陳嘉成(1998) 將次序理論應用於評量技術的開發，來瞭解學童學習困難和診斷學習缺陷。

Airasian & Bart (1973) 所提出的次序理論僅限於二元計分，但在教育實務上的測驗大多採用多元計分，無法進行資料分析，Lin, Bart & Huang (2006) 將次序理論推廣為適用於多元計分模式的多元計分次序理論 (Polytomous Ordering Theory, POT ) ，以及加權式多元計分次序理論

(29)

元計分次序理論，可呈現出兩兩元素間的次序性與階層性(林原宏，2010)。

四、試題關連結構(item relational structure, IRS)

Takeya 在 1980 年代根據 Bart & Krus (1973) 的次序理論 (ordering theory)提出另一種計算試題次序性係數(ordering coefficient) 的方法，就是試題關連結構理論(item relational structure, IRS) ，Takeya (1980, 1991) 所提出的試題關連結構，就是以二元計分(dichotomous) 試題，根據其列聯表資料，來計算其前置關係(precondition) 或是次序性關係，因此IRS是根據施測結果，並按照試題通過率和反應順序，來繪製出試題關連結構圖(Lin, Bart & Huang, 2006) 。

運用試題關連結構的研究也相當多：楊秀倩、陳進春、許天維(2006) 應用試題關聯結構分析法來對國小高年級資賦優異學童進行施測，繪製具有上、下位概念的結構關係，結果發現五、六年級資優學童梯形面積測量概念的聯聯結構圖都分成二個分支係和一個獨立系列，且梯形面積測量概念的學習成效頗具穩定性，較不受時間間隔的影響。沈佩怡(2007) 運用試題關聯結構分析法，針對國小四年級學童進行小數概念的施測與分析，研究結果發現小數的化聚概念是先由單位化小數合成概念開始，經由「十分位不含零、不進位之單位化小數」、「十分位含零、不進位之單位化小數」、「十分位不含零、進位之單位化小數」、「十分位含零、進位之單位化小數」的歷程，漸次發展至單位化小數分解概念，待單位化的小數化聚概念成熟，學童才能往上發展非單位化的小數化聚概念。本研究所採用的認知診斷方法是概念詮釋結構模式，不但可顯現概念間的上下位階層關係，還有概念間的從屬關係，更可得知每個概念的精熟度，綜觀各個認知診斷方法，概念詮釋結構模式集合了各個認知診斷法的優點，更能精準的瞭解學童的學習情況。

(30)

五、鷹架理論(Instructional Scaffolding)

Vygotsky(1978)認為每個學童都有自己的潛能，也就是「可能發展區」 (ZPD, Zone of Proximal Development)，學童可藉由外來的協助助或指引，去完成他本來不會的問題。而接受協助所能提升的能力則是因人而異。這種在學童學習的過程中給予的協助或教學便是外在給予的鷹架(張春興， 2007)。近期鷹架理論的相關研究有：黃智瑛(2007)在研究中提到數學的學習應給予鷹架作為支持，奠定學童下一階段的數學學習能力；郭輝龍(2009) 利用互動式虛擬儀器測量學童的 ZPD 來驗證數位教學系統之效能。六、診斷教學法診斷教學法(Bell, 1992)使用教學策略，使學童主動查覺本身錯誤，造成認知不平衡，進而產生認知調整的學習需求。其特性如下： (一) 問題與學童學習經驗連結且須涵蓋迷思概念。 (二) 設計之問題活動要能引起有迷思概念學童的認知衝突。 (三) 針對需補救的迷思概念徹底討論，並給予學童正確性的回饋，使其整合出新的知識結構。 (四) 利用進一步的問題鞏固學童的概念。 (五) 問題有彈性，使不同初始能力的學童有挑戰機會。林福來、黃敏晃與呂玉琴(1996)針對學童分數解題行為提出符合診斷教學的假設發現： (一) 同年齡層學童常犯同樣的錯誤。 (二) 有些錯誤解題策略在學童心中根深蒂固，容易一再犯錯。 (三) 學童接觸他所擁有的資訊無法解決的情境時，能發展合理的解題策略，但往往過於簡化。

(31)

學童的認知衝突，經過討論釐清謬誤，重新建構正確的概念，將可利用診斷教學進行及時的補救教學，使教與學更有效率。

(32)

第三章研究方法

本研究以自編分數概念及其加減運算試題，對五年級學童進行施測，獲得所需資料，本章將說明本研究之研究流程、研究樣本、研究工具和資料分析方法。

第一節研究流程

研究者在確立研究主題與目的後，開始蒐集、閱讀相關文獻以及國小數學分數課程，同時進行試卷的編製，經過專家檢測試卷內容，於上學期開學之初，請六年級學童進行預試，利用 SPSS 軟體分析之後進行試題的編修，確定正式施測試卷內容。確定正式施測試卷內容後，便對五年級學童進行施測，回收試卷後即進行資料整理與分析，研究者利用概念詮釋結構模式的結果對不同能力的學童進行訪談及補救教學，再檢討成效，分析學童的概念詮釋結構圖在進行補救教學前後差異的比較。依據本研究的目的，提出研究流程，如圖 3-1-1 所示。

(33)

圖 3-1-1 研究流程圖

第二節研究樣本

研究主要的目的是在探討國小五年級學童分數概念的概念詮釋結構模式，研究係採立意取樣，對國小五、六年級學童進行複本測驗，以下分述預試樣本及正式施測樣本。修正題目內容研究結論與建議文獻探討參考國小分數課程確定研究目的與主題編製試題正式施測資料彙整分析與比較概念結構圖訪談、補救教學比較補救教學前後概念結構圖進行預試資料分析與整理

(34)

ㄧ、預試樣本本研究之預試對象為雲林縣完整學習國小五年級分數概念的國小六年級學童，在取得班級導師同意後共選取 11 校 14 班之六年級學童進行施測，共得有效樣本 281 位。預試樣本分配如表 3-2-1。 表 3-2-1 預試樣本人數分配表 縣市鄉鎮班別男生女生合計(名) A-1 18 13 31 A-2 19 14 33 A-3 18 12 30 B-1 8 2 10 C-1 11 9 20 北港 D-1 12 8 20 元長 E-1 14 6 20 F-1 7 6 13 G-1 10 10 20 水林 G-2 9 10 19 H-1 11 9 20 I-1 8 7 15 口湖 J-1 9 9 18 雲林縣台西 K-1 7 5 12 合計 161 120 281 二、正式施測樣本本研究旨在分析與繪製個人化概念詮釋結構圖，故以立意取樣方式，在完成預試分析與刪除、修正試題後，於學童學習分數加減法後進行施測。研究樣本為包含研究者任教班級之國小五年級學童共 195 名。

(35)

施測之樣本分配如表 3-2-2：縣市鄉鎮班別版本男生女生合計(名) A-1 南一 12 16 28 A-2 南一 19 14 33 A-3 南一 20 12 32 A-4 南一 19 13 32 C-1 康軒 7 9 16 北港 D-1 部編 8 6 14 元長 E-1 康軒 3 2 5 水林 F-1 南一 10 10 20 雲林縣台西 K-1 部編 5 10 15 合計 103 92 195

第三節研究工具

本研究所使用的工具包括自編分數概念及其加減運算之測驗，以及相關的統計、分析資料、概念繪圖軟體等。茲說明如下： 壹、研究工具的編製 使用依據九年一貫正式綱要所編的南一版數學教材，於 99 學年度上學期施測「自編分數概念及其加減運算測驗」(如附錄三)後，加以分析資料，之後對受試者進行訪談及補救教學，並立即確認各概念的精熟度。一、自編試題內容本研究探討國小五年級學童對分數概念及其加減運算之表現情形，測驗工具的擬定，是依據教育部(2008)所公佈之九年一貫數學領域各年級分 表 3-2-2 研究樣本人數分配表

(36)

數相關分年細目，並參考各版本之五年級數學課本分析出分數相關概念如下表：分年細目指標內容 3-n-11 能在具體情境中，初步認識分數，並解決同分母分數的比較與加減問題。 N-2-09 能在具體情境中，初步認識分數。 N-2-10 能認識真分數、假分數與帶分數，做同分母分數的比較、加減與整數倍計算，並解決生活中的問題。 4-n-07 能理解分數之「整數相除」的意涵。 N-2-11 能理解分數之「整數相除」的意涵。 4-n-08 能認識真分數、假分數與帶分數，熟練假分數與帶分數的互換，並進行同分母分數的比較、加、減與整數倍的計算。 N-2-10 能認識真分數、假分數與帶分數，做同分母分數的比較、加減與整數倍計算，並解決生活中的問題。 4-n-09 能認識等值分數，進行簡單異分母分數的比較，並用來做簡單分數與小數的互換。 N-2-12 能認識等值分數，並做簡單的應用。 N-2-16 能在數線上標記小數，並透過等值分數，標記簡單的分數。 4-n-10 能將簡單分數標記在數線上。 N-2-16 能在數線上標記小數，並透過等值分數，標記簡單的分數。 5-n-04 能理解因數和倍數。 N-3-03 能理解因數、倍數、公因數與公倍數。 5-n-05 能認識兩數的公因數、公倍數、最大公因數與最小公倍數。 N-3-03 能理解因數、倍數、公因數與公倍數。 5-n-06 能用約分、擴分處理等值分數的換算。 N-3-06 能理解等值分數、約分、擴分的意義。 5-n-07 能用通分做簡單異分母分數的比較與加減。 N-3-07 能理解通分的意義，並用來解決異分母分數的比較與加減問題。 5-n-08 能理解分數乘法的意義，並熟練其計算，解決生活中的問題。 N-3-09 理解分數(含小數)乘法的意義及計算方法，並解決生活中的問題。 5-n-09 能理解除數為整數的分數除法的意義，並解決生活中的問題。 N-3-10 能理解分數(含小數)除法的意義及計算方法，並解決生活中的問題。 6-n-03 能認識兩數互質的意義，並將分數約成最簡分數。 N-3-05 能認識最大公因數、最小公倍數與兩數互質的意義，並用來將分數化成最簡分數。 6-n-04 能理解分數除法的意義及熟練其計算，並解決生活中的問題。 N-3-10 能理解分數(含小數)除法的意義及計算方法，並解決生活中的問題。 表 3-3-1 以九年一貫課程綱要為參照基準的分數概念對照表

(37)

分年細目指標內容 6-n-05 能在具體情境中，解決分數的兩步驟問題，並能併式計算。 N-3-02 能熟練整數四則混合運算，並解決生活中的三步驟問題。 A-3-01 能在具體情境中，理解乘法對加法的分配律與其他乘除混合計算之性質，並運用於簡化計算。 6-a-02 能將分數單步驟的具體情境問題列成含有未知數符號的算式，並求解及驗算。 A-3-04 能用含未知數符號的算式表徵具體情境之單步驟問題，並解釋算式與情境的關係。 A-3-05 能解決用未知數列式之單步驟問題。依據表3-3-1 之分數概念對照表和文獻中所提及之概念分類進行本研究試題之編製，將試題分成7 個概念屬性，如表3-3-2 所示：概念內容概念類別 1.同分母分數的加減及整數倍運算與比較。程序性知識 2.異分母分數的加減運算與比較。程序性知識 3.分數比大小程序性知識 4.等值分數概念性知識 5.通分程序性知識 6.分數「整數相除」的意涵。概念性知識 7.因數倍數。概念性知識二、試題屬性矩陣本研究自編的分數概念及其加減運算試題之題數為26題，共測7個概念。試題屬性矩陣如表3-3-3所示，表中「1」代表該題有測量到該概念；「0」代表該題沒有測量到該概念。 表 3-3-1 以九年一貫課程綱要為參照基準的分數概念對照表(續) 表 3-3-2 分數概念內容及說明

(38)

概念 1. 2. 3. 4. 5. 6. 7. 試題同分母分數的加減及整數倍運算與比較異分母分數的加減運算與比較分數比大小等值分數通分分數「整數相除」的意涵因數倍數 na1 0 0 0 1 1 0 0 na2 1 0 1 0 0 1 0 na3 0 1 1 1 1 0 0 na4 0 1 1 1 0 1 0 nb1 0 0 0 0 0 0 1 nb2 0 0 0 0 0 0 1 nb3 0 0 0 0 0 0 1 nb4 1 0 1 0 0 1 0 nb5 0 0 0 0 0 1 0 nb6 1 0 0 0 0 0 0 nb7 1 0 0 0 0 0 0 nb8 0 0 1 0 0 0 0 nb9 1 0 0 0 0 0 0 nb10 1 0 0 0 0 1 0 nb11 0 1 1 0 1 0 0 nb12 0 1 1 0 1 0 0 nb13 0 0 1 0 0 0 0 nb14 1 0 1 0 0 0 0 nb15 0 1 1 0 0 1 0 nb16 0 1 1 0 0 0 0 nb17 0 1 0 0 1 0 0 nb18 0 1 1 0 1 0 0 nb19 0 0 0 0 0 1 0 nb20 0 1 0 0 1 0 0 nb21 0 1 0 0 1 1 0 nb22 0 1 0 0 1 0 0 表 3-3-3 分數試題的概念屬性矩陣

(39)

三、試題計分方式本試卷含兩部分，第一部分為4 題填充題，答案數共22格，第二部分為22 題單選題。每格答案正確給1 分、答錯給0 分，試卷共計42 分。 貳、預試試題品質分析 一、信度本研究預試卷(如附錄二) 之Cronbach α值為.952，如表3-3-4所示，預試試題Cronbach α值並沒有因為刪除某試題而變得非常高。題號項目刪除時的 Cronbach's Alpha 值題號項目刪除時的 Cronbach's Alpha 值 na1.1 .950 nb1 .950 na1.2 .950 nb2 .950 na1.3 .950 nb3 .950 na1.4 .950 nb4 .951 na2.1 .950 nb5 .952 na2.2 .950 nb6 .951 na2.3 .950 nb7 .950 na2.4 .950 nb8 .950 na3.1 .952 nb9 .950 na3.2 .950 nb10 .955 na3.3 .951 nb11 .949 na3.4 .952 nb12 .950 na3.5 .953 nb13 .950 na3.6 .955 nb14 .951 na4.1 .952 nb15 .951 na4.2 .953 nb16 .951 na4.3 .955 nb17 .951 na4.4 .952 nb18 .951 na4.5 .951 nb19 .951 na4.6 .950 nb20 .951 nb21 .954 nb22 .951 表 3-3-4 預試信度分析表

(40)

二、效度 (一)內容效度研究者依據九年一貫數學課程綱要及其分年細目編製試題，逐一檢查試題能測到其所要測量的概念，故本研究之測驗試題具有內容效度。試題與分年細目之對應如表3-3-5。分數部分的分年細目對照指標對應題目能在具體情境中，初步認識分數，並解決同分母分數的比較 a4、b14 3-n-11 與加減問題。 N-2-09 N-2-10 b6 4-n-07 能理解分數之「整數相除」的意涵。 N-2-11 b5、b19、 b15、b21 能認識真分數、假分數與帶分數，熟練假分數與帶分數的互換，並進行同分母分數的比較、 b4、b8、b13 加、減 b7 4-n-08 與整數倍的計算。 N-2-10 b9、b10 4-n-09 能認識等值分數，進行簡單異分母分數的比較，並用來做簡單分數與小數的互換。 N-2-12 N-2-16 a3、a4 4-n-10 能將簡單分數標記在數線上。 N-2-16 a2、a18 5-n-04 能理解因數和倍數。 N-3-03 b1 5-n-05 能認識兩數的公因數、公倍數、最大公因數與最小公倍數。 N-3-03 b2、b3 5-n-06 能用約分、擴分處理等值分數的換算。 N-3-06 a1、b15 能用通分做簡單異分母分數的比較 b11、b12、 b15、b16 5-n-07 與加減。 N-3-07 b17、b20、 b21、b22 表 3-3-5 試題與分年細目對應表

(41)

(二)專家審題本研究所使用之自編分數概念及其加減運算試題，經過一位教授以及五位任教於國小高年級的教師審閱、提供意見，研究者整合各專家意見加以修正，使得本測驗試題能使學童表現出欲測量的概念。 (三)建構效度由於建構效度是測量工具的重要指標，而建構效度的分析對測驗分數的正確性及欲測量概念的解釋深具意義，有鑑於此，研究者在本研究中以因素分析方法，檢驗分數概念及其加減運算試題之建構效度。效度分析 KMO值可達0.874，顯示刪題後的內容效度佳，構念效度含七個共同因素，能解釋的共同變異量為59.126％。三、難度及鑑別度本研究之試卷難度以高分組(前27%) 的通過率加低分組(後27%) 的通過率之平均來表示，如表3-3-6所示：本研究預試卷各題難度介於.36~.85 之間，平均難度為.58，對五年級學童而言整份試卷難度適中。題號難度題號難度題號難度 na1.1 .493 na4.1 .831 nb9 .539 na1.2 .513 na4.2 .649 nb10 .837 na1.3 .493 na4.3 .674 nb11 .519 na1.4 .513 na4.4 .740 nb12 .526 na2.1 .649 na4.5 .466 nb13 .584 na2.2 .656 na4.6 .649 nb14 .669 na2.3 .649 nb1 .558 nb15 .427 na2.4 .649 nb2 .571 nb16 .545 na3.1 .538 nb3 .617 nb17 .617 na3.2 .597 nb4 .584 nb18 .466 na3.3 .675 nb5 .355 nb19 .499 na3.4 .629 nb6 .512 nb20 .630 na3.5 .681 nb7 .500 nb21 .367 na3.6 .850 nb8 .597 nb22 .381 表 3-3-6 預試工具之難度

(42)

本研究之試題鑑別度分析，先求出高分組及低分組的答對率，以PH 及 PL表示，以D表示鑑別度，則D =PH －PL 。除此之外，也用皮爾森 （Pearson）相關分析各題得分和總分之間的相關情形，以及獨立樣本t檢定檢視高低分群組是否有顯著差異共三種方法來作為鑑別度優劣之參考，如表3-3-7所示。一般認為試題鑑別度應在0.2以上，高於0.4則為優良試題(Ebel & Frisbie, 1991)，預試卷之鑑別度有五題未達0.4，其餘試題鑑別度皆高於 0.4屬優良試題，而總分和各題的相關以及t檢定也有部分未達顯著，因此需要修改或刪除試題。題號 D=PH-PL Pearson _相關 t 檢定題號 D=PH-PL Pearson 相關 t 檢定 na1.1 .961 .75*** 42.62*** nb1 .857 .76*** 21.03*** na1.2 .869 .72*** 21.64*** nb2 .805 .70*** 17.21*** na1.3 .935 .76*** 32.32*** nb3 .766 .77*** 15.78*** na1.4 .948 .80*** 36.74*** nb4 .727 .60*** 13.43*** na2.1 .701 .78*** 13.36*** nb5 .606 .47*** 10.03*** na2.2 .688 .78*** 12.96*** nb6 .713 .60*** 12.48*** na2.3 .701 .78*** 13.36*** nb7 .869 .70*** 21.61*** na2.4 .701 .78*** 13.36*** nb8 .779 .72*** 16.11*** na3.1 .634 .49*** 10.14*** nb9 .870 .71*** 21.97*** na3.2 .753 .73*** 14.75*** nb10 .116 .00n.s. 1.95n.s. na3.3 .623 .67*** 10.99*** nb11 .961 .84*** 43.30*** na3.4 .531 .43*** 8.10*** nb12 .922 .81*** 29.57*** na3.5 .479 .31*** 7.39*** nb13 .831 .79*** 19.34*** na3.6 .037 .05n.s. 0.64n.s. nb14 .636 .61*** 11.30*** na4.1 .338 .46*** 6.22*** nb15 .751 .59*** 14.29*** na4.2 .518 .36*** 7.96*** nb16 .726 .63*** 13.10*** na4.3 .153 .04n.s. 2.03* nb17 .740 .64*** 14.46*** na4.4 .467 .44*** 7.75*** nb18 .699 .53*** 12.05*** na4.5 .725 .59*** 12.99*** nb19 .791 .59*** 15.88*** na4.6 .701 .72*** 13.36*** nb20 .662 .57*** 11.59*** nb21 .188 .10 n.s. 2.44* nb22 .737 .60*** 14.27*** 表 3-3-7 預試工具之鑑別度、相關及 t 檢定

(43)

四、修改或刪除試題由表 3-3-7 可發現本測驗中部分試題鑑別度在 0.2 以下，其相關係數和 t 檢定亦未達顯著，因此再次檢視 na3.6、na4.3、nb10、nb21 四題。考慮 na4.3 之 t 檢定達顯著，取概數後亦有 0.2 的鑑別度，且此題能測出學童對分數基本單位的迷思，因此保留此題；而 nb21 之 t 檢定亦達顯著且鑑別度之概數也有達到 0.2，且能測驗出學童對題意的迷思，亦給予保留；na2.1 到 na2.4 雖為良好試題，但考慮受試者做答時間以及 nb17 亦能測出 na2 欲測量的數線概念，因此予以刪除。五、編製正式測驗將前測試題重新排版，並將注意事項加以註記，且將 na3 題目中「不是的打×」標示為粗體。

(44)

綜合上述，刪除 na2、na3.6、nb10題，本研究之正式施測試題變為24 題。正式施測試題之概念屬性矩陣如表3-3-8所示：概念 1. 2. 3. 4. 5. 6. 7. 試題同分母分數的加減及整數倍運算與比較異分母分數的加減運算與比較分數比大小等值分數通分分數「整數相除」的意涵因數倍數 na1 0 0 0 1 1 0 0 na2 0 1 1 1 1 0 0 na3 0 1 1 1 0 1 0 nb1 0 0 0 0 0 0 1 nb2 0 0 0 0 0 0 1 nb3 0 0 0 0 0 0 1 nb4 1 0 1 0 0 1 0 nb5 0 0 0 0 0 1 0 nb6 1 0 0 0 0 0 0 nb7 1 0 0 0 0 0 0 nb8 0 0 1 0 0 0 0 nb9 1 0 0 0 0 0 0 nb10 0 1 1 0 1 0 0 nb11 0 1 1 0 1 0 0 nb12 0 0 1 0 0 0 0 nb13 1 0 1 0 0 0 0 nb14 0 1 1 0 0 1 0 nb15 0 1 1 0 0 0 0 nb16 0 1 0 0 1 0 0 nb17 0 1 1 0 1 0 0 nb18 0 0 0 0 0 1 0 nb19 0 1 0 0 1 0 0 nb20 0 1 0 0 1 1 0 nb21 0 1 0 0 1 0 0 表 3-3-8 分數試題的概念屬性矩陣

(45)

参、資料分析及繪圖軟體 本研究使用之電腦軟體包括：ㄧ、利用Excel 軟體進行原始資料的輸入與整理。二、利用SPSS 12.0 中文版軟體來進行筆試題目資料的分析統計。三、應用 PCAISM 軟體繪製學童之概念詮釋結構圖。

第四節資料分析

本研究主要透過國小五年級分數概念及其加減運算試題，探討學童知識結構的特徵，並分析比較在進行補救教學前後知識結構圖的異同。在資料處理上，使用Lin et al.(2006)所發展的概念詮釋結構工具(Polytomous concept advanced interpretive structural modeling, 簡稱PCAISM)、SPSS 12.0 for Windows統計套裝軟體，其中的資料分析項目及順序如下：一、試題性質與解題表現之分析 (一)分析試題之難易度、鑑別度及測驗之信度。 (二)分析解題結果之概念全對通過率，呈現出學童的解題能力。二、透過次序理論分析概念的先後順序性及階層性分別利用傳統分群及模糊分群(林原宏，2003,2005b)繪製代表學童的次序結構圖，分別檢視兩種分群方法所繪製的POT圖合者較能代表群中心，作為補救教學的參考依據三、描繪學童分數概念及其加減運算知識結構圖利用Excel建立受試者反應矩陣（如表3-4-1）以及分數加減概念試題屬性矩陣（如表3-4-2）：

(46)

表 3-4-1 分數加減概念受試者反應矩陣（擷取部分） #195 24; (5 6 6 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2) [0 2 3 1 1 1 1 0 1 1 1 1 1 1 1 1 0 1 0 0 0 0 1 1 4 5 5 1 1 1 1 0 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 4 0 1 1 0 0 1 1 1 0 1 1 1 1 1 1 1 0 0 1 0 0 2 3 3 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 0 0 1 0 0 0 0 2 1 1 0 0 0 0 0 0 0 0 1 1 0 1 0 1 0 0 1 1 0 4 4 5 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 表3-4-2 分數加減概念試題屬性矩陣 #24 7; [0 0 0 1 1 0 0 0 1 1 1 1 0 0 0 1 1 1 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 1 0 1 0 0 1 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 1 0 0 0 0 0 0 0 1 1 1 1 0 0 0 1 1 0 1 0 0 0 0 1 1 0 0 0 1 0 1 0 0 0 0 0 1 1 0 0 1 0 0 1 1 0 0 0 0 0 1 0 0 1 0 0 0 1 1 0 1 0 0 0 0 0 0 0 1 0 0 1 0 0 1 0 0 0 1 0 0 1 1 0

(47)

將受試者反應矩陣與試題屬性矩陣上傳到「認知診斷之測驗分析即時服務系統」選擇「PCAISM」進行分析，即可繪出每位受試者的分數加減概念詮釋結構圖，亦可得到每位受試者在七個概念中的精熟度矩陣。以  _{=.53 進行截矩陣後，根據學童的二元關係矩陣，繪製其概念詮釋結構圖。} 結構圖的判讀如圖 3-4-1： 圖 3-4-1 概念詮釋結構圖圖例 圖中之圓圈內上方的數字分代表概念 1 至概念 7；圓圈內下方的小數則代表受試者在該概念之精熟度，精熟度介於 0 和 1 之間，數值愈高代表受試者在該概念愈精熟；所輸入的 _{值不同，系統繪製出的關連指向也會} 不同。四、學童分數概念結構圖形分析經上述分析流程，可繪製出不同能力值的學童之個人化概念詮釋結構圖，將概念詮釋結構圖分析之重點說明如下： (一)根據概念詮釋結構模式，針對分數的概念詮釋結構圖進行一般的描述性分析，例如：分析學童概念詮釋結構圖的分層級數、最上層級及最下層級之概念、層級間概念之特殊的階層關係等特點。 (二)比較同一群的學童、不同群的學童其概念詮釋結構圖的概念階層位置與連結關係之異同。

(48)

(三)比較答對題數相同但反應組型不同之學童，其概念詮釋結構圖概念階層位置與連結關係之異同。五、補救教學在各群中，分別隨機抽取兩位學童進行訪談及補救教學，步驟如下： (一)在進行訪談前先分析學童答錯的題目包含哪些概念，再進一步於訪談時了解學童答題時的想法，釐清學童所犯的迷思謬誤，並測驗這些概念，驗證這些概念是否是學童較不精熟的。 (二)列出學童較不精熟的概念後，再按照由圖4-1-3所分析的分數概念發展順序與診斷教學法進行補救教學。每位學童的補救教學節數以一節課為原則，但因各個學童需補救的概念數不同，且學童的學習時間不同，所以不同學童的補救教學時間也會有所增刪。 (三)進行完補救教學後，立即進行測驗確認概念的精熟度，繪製出概念詮釋結構圖後，並再次進行訪談比較學童在進行補救教學前後的概念詮釋結構圖的概念階層位置與連結關係之異同。

(49)

第四章研究結果與討論

本章主要在呈現研究結果的分析與討論，根據本研究目的，共分為四節。第一節是高低分群組(27%)及利用 f-cut 分群後不同組別 POT 圖之比較，第二節是不同精熟組中，同一群的學童其分數的加減之概念詮釋結構圖之比較，第三節是不同精熟組中，不同群的學童其分數的加減之概念詮釋結構圖之比較，第四節是分析各群受試者在進行補救教學之表現情形，第五節是比較各群受試者在進行補救教學前後分數加減之概念詮釋結構圖的差異。

第一節高低分群組及利用 f-cut 分群後各組 POT 圖比較

為了確認選取之補救教學對象知識結構可解釋該群組，研究者在利用 CAISM 分析受試者概念結構之前，先採用廣義多元計分的次序理論 (林原宏，2005b)分析群特徵，希望能借此找出最具代表性的受試者進行訪談及補救教學。

(50)

ㄧ、高分組、低分組之 POT 圖：

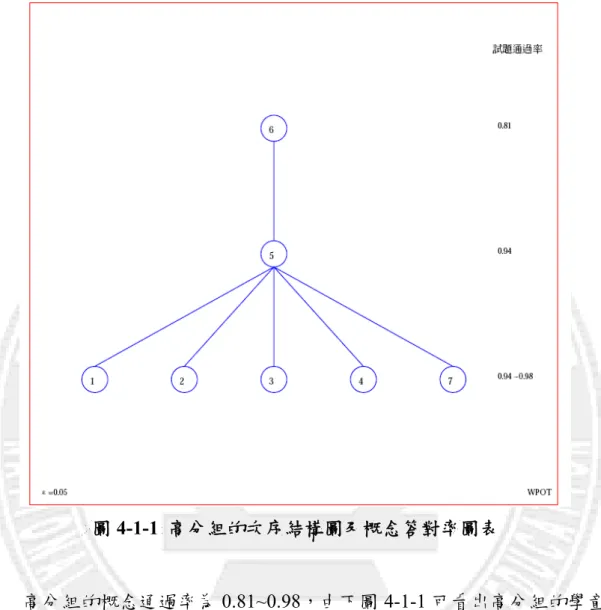
圖 4-1-1 高分組的次序結構圖及概念答對率圖表

高分組的概念通過率為 0.81~0.98，由下圖 4-1-1 可看出高分組的學童乃先精熟各概念後再去發展概念 5（通分），最後才精熟概念 6（分數「整數相除」的意涵）。

(51)

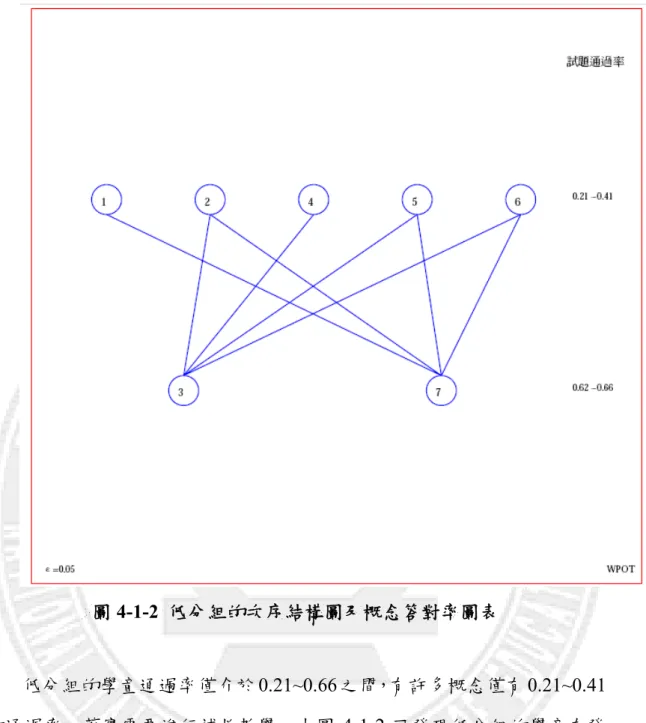
圖 4-1-2 低分組的次序結構圖及概念答對率圖表 低分組的學童通過率僅介於 0.21~0.66 之間，有許多概念僅有 0.21~0.41 的通過率，著實需要進行補救教學，由圖 4-1-2 可發現低分組的學童在發展分數概念時是以概念 3（分數比大小）及概念 7（因數倍數）為基礎去學習概念 2（異分母分數的加減運算與比較）、概念 5（通分）、概念 6（分數「整數相除」的意涵），也分別發展概念 1（同分母分數的加減及整數倍運算與比較）和概念 4（等值分數）。研究者發現： (一) 無論高低分組的下位概念皆有概念 3（分數比大小）及概念 7（因數倍數）。

(52)

(二) 高分組的下位概念尚有概念 1（同分母分數的加減及整數倍運算與比較）、概念 2（異分母分數的加減運算與比較）、概念 4（等值分數）對高分組而言，概念 6（分數「整數相除」的意涵）是不易理解的概念性知識。 (三) 高分組學童在概念 1（同分母分數的加減及整數倍運算與比較）、概念 2（異分母分數的加減運算與比較）、概念 4（等值分數）的表現非常好，通過率皆高於.94，對低分組的學童卻是精熟度低的概念。研究者回顧「自編分數概念及其加減運算測驗」發現概念 1、概念 2 的題目多屬文字敘述題，雖為操作性知識但需要有解題策略才能完成；概念 4（等值分數）雖非文字題，但擴分約分的程序較繁雜。綜合上述，高低分組（27％）的 POT 圖顯示學童學習分數的加減時之思考路徑皆以操作性知識為下位概念，但低分組學童無法完程過於繁複的操作性試題，原因尚待訪談學童以獲取最直接的資料；概念 6（分數「整數相除」的意涵）在小學四年級時就應學習，但對全部的學童而言皆難以理解。二、f-cut 分群後不同組別之 POT 圖：研究者將受試者分數七概念的得分輸入 f-cut 程式裡進行模糊集群分析，依序調整分群數量，即可得到各群在各個概念的精熟度、分割係數 (partition coefficient)和分割亂度(partition entropy)之值如表 4-1-1。

群數 2 3 4 5 分割係數 (partition coefficient) .81 .69 .55 .49 分割亂度 (partition entropy) .31 .54 .79 .96 表 4-1-1 受試者在不同分群數所得之分割係數及分割亂度

(53)

從表 4-1-1 中，研究者發現將受試者分成二群時，分割係數為.72 是最大值；分割亂度為.44 是最小值，因此判定最佳分群數為兩群。將學童分為高精熟組及低精熟組其 POT 圖分別如下所示： 圖 4-1-3 高精熟組的次序結構圖及概念答對率圖表 由圖 4-1-3 可看出高精熟組的學童分數加減概念的發展同樣是先精熟概念 3（分數比大小）及概念 7（因數倍數）且通過率很高，在 0.94 和 0.96 之間，可見教學者在這兩個基礎概念的的教學皆有達成效，之後循序發展，而概念 6（分數「整數相除」的意涵）仍舊是較不易理解的部分。

(54)

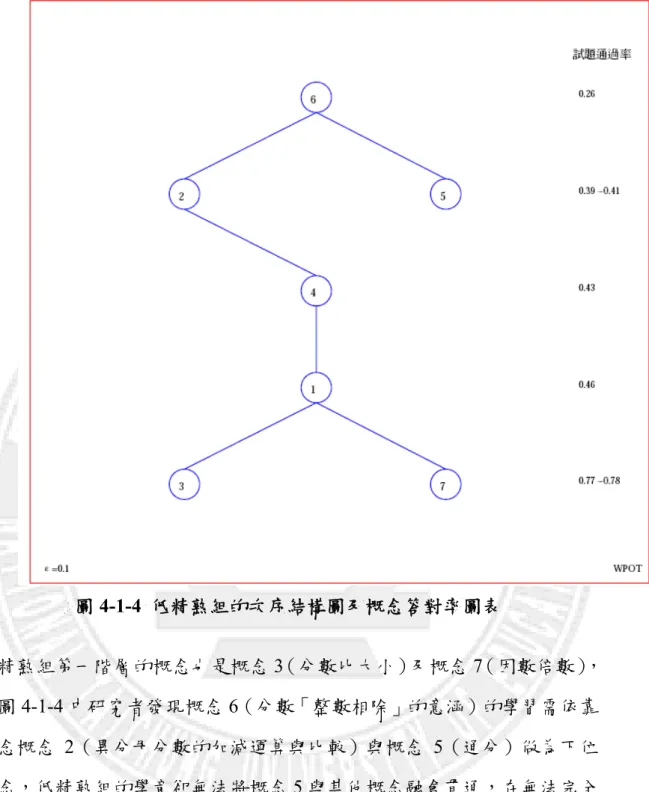
圖 4-1-4 低精熟組的次序結構圖及概念答對率圖表 低精熟組第一階層的概念也是概念 3（分數比大小）及概念 7（因數倍數），從圖 4-1-4 中研究者發現概念 6（分數「整數相除」的意涵）的學習需依靠概念概念 2（異分母分數的加減運算與比較）與概念 5（通分）做為下位概念，低精熟組的學童卻無法將概念 5 與其他概念融會貫通，在無法完全理解概念 2 及概念 5 的情況下，可以看到概念 6 的通過率僅 0.26。研究者發現： (一) 高低精熟組第一階層的概念皆為概念 3（分數比大小）、概念 7（因數倍數），通過率皆高於.77。 (二) 高精熟組的第二階概念是概念 4（等值分數），且概念 4 是概念 1

(55)

（同分母分數的加減及整數倍運算與比較）的下位概念；低精熟組卻恰巧相反，概念 1 是概念 4 的下位概念，有可能是因為概念 4 的題型屬於題組，高精熟組的學童懂得應用所學概念，低精熟組學童卻認為是需要繁複計算過程的大題組，自認為沒有能力填答因此放棄。 (三) 概念 6（分數「整數相除」的意涵）在 f-cut 的分群方法中還是最難理解的概念，此點發現與高低分組的 POT 圖相符。在比較不同分群方法所呈現的結果之後，利用傳統分群方法進行高低分組（27％）絕對分群和以模糊理論進行高低精熟組模糊分群的 POT 圖並不相同，除了絕對分群能分析出最基礎概念與最不易理解概的念外，模糊分群還能讓我們清楚看到學童學習分數加減概念的思考路徑如圖 4-1-5 所示： 圖 4-1-5 學童分數加減概念的思考路徑 分數比大小 （概念 3） 因數倍數 （概念 7） 等值分數 （概念 4） 同分母分數的加減及 整數倍運算與比較 （概念 1） 異分母分數的加 減運算與比較 （概念 2） 通分 （概念 5） 分數「整數相除」的意涵 _{（概念 6）}