國小六年級學童梯形面積之解題策略探討解題策略探討

(1)

國立臺中教育大學數學教育學系

在職進修教學碩士班碩士論文

指導教授：許天維博士

國小六年級學童梯形面積之

解題策略探討

研究生：陳福正撰

中華民國九十六年六月

(2)

國小六年級學童梯形面積之解題策略探討

摘要

本研究之目的在於建立符合認知心理學邏輯性的梯形專家結構，並藉由試題關聯結構分析法，瞭解國小六年級學生在梯形面積上解題策略的概念結構，比較專家與學生在梯形面積上解題策略的概念結構的差異性。本研究以彰化縣某國小一班六年級學童為研究對象，施測後，以IRSP電腦程式及試題關聯結構法，來進行測驗結果的分析及探討，期能從中獲得此班學童在梯形面積之解題策略的程序學習過程。根據結構圖所呈現的結果，比較前人的研究，獲得以下新發現：

一、梯形面積概念

1. 直線測量面積概念中側放梯形是正放梯形的上位概念，但若是以點數面積的方式，則側放梯形和正放梯形兩者等價。 2. 學生即使求出梯形分割後的各元件，不會相加來求得面積，而是另外使用面積公式，可見學生對於面積公式過於依賴。 3. 多重分割線(複合圖形)是一條分割線(複合圖形)的上位概念，而沒有分割線(複合圖形)是有分割線(複合圖形)的上位概念。 4. 面積的計算，都存在高的干擾，使得答對率相差20%左右。

二、梯形解題策略

1. 以點數方式求得梯形面積：學生在點數梯形面積的技巧是沒有問題的，尤其是低成就的學生，表現得比梯形面積公式還要好，但應用性不高。 2. 以梯形面積公式求得梯形面積：學生最常用的解題策略，梯形解題應用

(3)

是梯形面積公式的上位概念，但是難度差異大，必須有其他概念幫助連結，否則學生無法由梯形面積公式中連結到梯形的解題應用。 3. 將梯形分割成兩個三角形再拼湊成梯形面積：學生的概念結構和專家結構最相似，學生容易系統性的學習。 4. 將梯形分割成三角形與平行四邊形再拼湊成梯形面積：梯形的解題應用是分割後平行四邊形面積的上位概念，和分割後的三角形面積、平行四邊形再度組合後的梯形面積無關聯，若選此種解題策略當作梯形面積教學，學生未必能進行梯形面積的應用。 5. 拼湊成平行四邊形再分割出梯形面積：學生雖然可以輕易從中得知梯形面積公式的由來，但是卻很難應用至其他的面積應用題。三、學生的梯形解題策略應用：若能學會圖形的分割、拼湊等技巧，對於面積公式的掌握會更加穩定。重要的是對於面積的解題能力大為增加，尤其是以三角形為主的解題策略，難度較低，而應用範圍大。綜合以上結果，並根據此結果提出若干建議，以作為教學者及未來研究之參考。 關鍵詞：IRSP 試題關聯結構分析法梯形面積概念梯形解題策略

(4)

A Research Of Trapezoid Area Solving Strategy For

Sixth-grade Students

Abstract

The purpose of this research is to build a Trapezoid professional organization in accordance with cognitive psychological logic and to understand sixth-grade students’ concept structure in Trapezoid area solving strategy by the Item Relational Structure Analysis (IRS), thereby comparing the difference of concept structure in Trapezoid area solving strategy between the professionals and students.

The subjects of this research are the six-grade students of one class in an elementary school in Changhwa County. The result is analyzed and studied by using IRSP computer program and the Item Relational Structure Analysis (IRS)

for the purpose to acquire the learning process those students experience in Trapezoid area solving strategy. Based on the results presented by structure graph and compared with previous studies, new findings are as below:

一、The Trapezoid area concept

1. For measuring area, in the concept of straight line method, side positioned Trapezoid is the upper Ontology of front positioned Trapezoid, while in the way ofthe point number method, side positioned Trapezoid and front positioned Trapezoid equal.

2. Even rough all elements are acquired by dividing the Trapezoid, the students do not add them but use Trapezoid formula in order to get the result of area, which shows students’ over-reliance on the formula.

(5)

single cutting line whereas non-cutting line is the upper Ontology of cutting line.

4. Any calculation of the area is involved with high disturbance so that the difference of accuracy rate is about 20%.

二、The Trapezoid area solving strategy

1. By point number method:

There is no problem for students in solving Trapezoid area by using point number method. The performance is even better than that by using formula skill, especially for those low-level students. However, this method is not applied to very much.

2. By the Trapezoid area formula.

This is the common strategy that students use in solving area.

However, Trapezoid solving strategy application, the upper Ontology of Trapezoid area formula, varies in difficulty and needs to connect to other concepts; otherwise, students is not able to further apply the formula to the Trapezoid solving strategy.

3. By divide the Trapezoid into two triangles

The concept structures between students and professionals are most similar. In this way, students can learn systematically.

4. By divide the Trapezoid into triangle and parallelogram

The Trapezoid solving strategy application, the upper Ontology of the parallelogram, is irrelevant to the Trapezoid area into which the triangle area and parallelogram area combined. If this solving strategy is chosen by teachers to be used in teaching solving Trapezoid area, students may not

(6)

be able to conduct the Trapezoid area application.

5. By combine to parallelogram and then divide into Trapezoid area

In this way, students can easily understand the origin of the Trapezoid area formula but difficultly apply it to solving other areas.

三、Students’ Trapezoid area solving strategy application

The skills of graph division and combination can stabilize students in dealing with area formulas. Most importantly, it largely enhances the area solving strategies, especially those of triangle-based which are in low complexity but wide in application.

Integrate above results and present several suggestions accordingly for the reference of instructors and future researches.

Key word: IRSP, Item Relational Structure Analysis (IRS), the Trapezoid concept, and the Trapezoid area solving strategy.

(7)

目錄

目錄...I 圖目錄...II 表目錄...III 第一章緒論...1 第一節研究動機 ... 1 第二節研究目的與待答問題 ... 3 第三節名詞釋義 ... 3 第四節研究範圍與限制 ... 4 第二章文獻探討...5 第一節兒童面積概念發展 ... 5 第二節國小梯形面積概念 ... 12 第三節九年一貫課程數學領域「數與量」主題 ... 15 第四節九年一貫課程數學領域「幾何」主題 ... 19 第五節 2001 年版Bloom認知領域教育目標分類理論之相關研究 ... 24 第六節試題關聯結構分析法 ... 28 第三章研究方法...37 第一節研究架構 ... 37 第二節研究對象 ... 38 第三節研究工具 ... 39 第四節研究流程 ... 52 第五節資料處理 ... 53 第四章研究結果與分析...54 第一節受測學生梯形面積概念的學習情形 ... 54 第二節繪製不同的解題策略的試題與概念結構圖 ... 72 第三節學生解題策略結構圖與專家結構圖的比較 ... 81 第五章結論與建議...90 第一節結論 ... 90 第二節建議 ... 93 參考文獻...94 附錄一...99 附錄二...105 附錄三...106

(8)

圖目錄

圖 2- 1 點數單位面積圖... 7 圖2- 2 疊置法的面積測量概念實驗圖... 8 圖2- 3 單位測量法的面積測量概念實驗圖... 9 圖2- 4 平行四邊形分割、拼湊成長方形圖... 10 圖2- 5 面積合成圖...11 圖2- 6 點數示範圖... 12 圖2- 7 梯形面積的合成與分割法... 13 圖2- 8 Bloom 教育目標分類系統新舊版本對照圖... 24 圖2- 9 試題關聯結構圖範例... 32 圖3- 1 研究架構圖... 37 圖3- 2 梯形面積教材架構圖... 40 圖3- 3 梯形面積概念圖... 41 圖3- 4 研究流程圖... 52 圖4- 1 試題關聯結構圖簡化(一) ... 73 圖4- 2 試題關聯結構圖簡化(二) ... 73 圖4- 3 試題關聯結構圖簡化(三) ... 74 圖4- 4 第一種解題策略的試題關聯結構圖... 75 圖4- 5 第一種解題策略的概念關聯結構圖... 76 圖4- 6 第二種解題策略的試題關聯結構圖... 76 圖4- 7 第二種解題策略的概念關聯結構圖... 77 圖4- 8 第三種解題策略的試題關聯結構圖... 77 圖4- 9 第三種解題策略的概念關聯結構圖... 78 圖4- 10 第四種解題策略的試題關聯結構圖... 78 圖4- 11 第四種解題策略的概念關聯結構圖 ... 79 圖4- 12 第五種解題策略的試題關聯結構圖... 79 圖4- 13 第五種解題策略的概念關聯結構圖... 80 圖4- 14 第一種解題策略的專家和學生結構比較圖... 81 圖4- 15 第二種解題策略的專家和學生結構比較圖... 83 圖4- 16 第三種解題策略的專家和學生結構比較圖... 84 圖4- 17 第四種解題策略的專家和學生結構比較圖... 85 圖4- 18 第五種解題策略的專家和學生結構比較圖... 87 圖4- 19 學生梯形解題策略概念結構圖... 88

(9)

表目錄

表 2- 1 梯形各部位的通過率 ... 14 表 2- 2 九年一貫「數與量」主題中有關面積概念之分年細目 ... 17 表 2- 3 九年一貫「幾何」主題中有關面積概念之分年細目 ... 21 表 2- 4 數學領域第三階段知識向度百分比 ... 27 表 2- 5 數學領域第三階段認知歷程百分比 ... 27 表 2- 6 A、B兩組學生各試題的得分情況 ... 29 表 2- 7 機率的四分割表 ... 33 表3- 1 依據知識向度命題的梯形面積雙向細目表... 42 表3- 2 測驗之Cronbach’s α信度分析 ... 45 表3- 3 試題之難易度及鑑別度... 47 表3- 4 試題關聯順序性係數一覽表... 49 表3- 5 順序性係數之 0-1 矩陣表 ... 51 表4-1 各概念點的代表試題及標準... 70 表4-2 試題順序關係 0-1 矩陣表舉例 ... 72

(10)

第一章緒論

本研究利用測驗理論而編製試題，來了解國小六年級學生的梯形面積知識結構，並藉由試題關聯結構分析法（簡稱 IRS），來分析探究梯形面積在不同解題策略的概念結構圖是否符合專家知識結構圖，從中獲得學生解題策略形成的發展順序及概念學習不清楚之處，以提供教師改善教學。

第一節研究動機

面積雖然是學生日常生活中常接觸到也是最實用的經驗教材，照理說學生應該很容易學習，但事實不然，從許多研究均證實學生對於面積概念的混淆，公式的不正確使用（高敬文，1989；周武男，1988）。學生在解答面積問題時，所呈現之面積概念薄弱，對面積的認知，不過是一連串的公式，對於公式之由來並不了解其中的意義，套用公式時也未必清楚，而只針對題目上之資訊套用公式（陳鉪逸，1996）。面積的教學是透過一連串圖形的操作、點數、分割等才逐步形成面積的概念，為達到有效率的原則才有面積公式的引入，此時的面積公式不是只靠記憶而是透過了解，不只知道不同形狀的面積公式，而且能說出每個面積公式的意義及推算過程，如此的面積公式才能有效應用以增進解題能力（譚寧君，1995）。面積教材在國小數學課程中雖然是屬於「量與實測」領域，但是面積是封閉曲線「形」底下「量」的感覺，牽涉幾何的「形」到「量」的認知過程。盧銘法 (1996)指出，幾何的學習涉及數學教材中的數、量、形三個領域，學生對於幾何教材的學習仍然感到相當困難。而圖形的操作、點數、分割，必須深入理解，如此對於每一個面積公式才能深入理解意義及推算過程，進而增進解題、邏輯推理能力。面積公式在九年一貫暫行綱要課程中，是在第三階段的數與量單元中，到了

(11)

九年一貫正式綱要時，是放在新課程第二階段的幾何單元中。92 正綱：s-2-08 能運用分割重組，理解梯形的面積公式(同 n-2-19)，將圖形變換成可操作圖形，重點在以「某個可操作圖形」，透過圖形變換，將幾何問題轉換成「可解問題」。暫綱中的目標是面積量的「面積公式」，分割重組只是一種「形成公式的手段」，新綱中的目標則是幾何學的「解題策略」，分割重組是一種「幾何方法」，而面積公式則是應用這種方法的「一個例子」，正式綱要所注重的，就是學生帶著走的能力。也因此面積公式是解題的其中一種方法，面積公式的理解當然也只是這一種方式的理解，但並非是面積概念的全部，因此要發展各種圖形的面積解題策略，而規律圖形中，就屬梯形的解題策略最多元化。而在圖形面積的整合概念中，梯形是一般形狀，三角形可視為上底為 0 的梯形，而長方形，平行四邊形則可視為上下底等長的梯形，圖形面積的概念，若能瞭解一般圖形（梯形）面積的概念，就能瞭解特殊圖形（長方形、平行四邊形、三角形）的面積概念。基於上述原因，因此選定「梯形面積」為主題，再以梯形面積的知識結構來命題，而且以選擇題為主，希望建立一個簡單方便的工具，並且能做迅速的分析。然後根據學生作答情形探討普通班學生的梯形概念結構，與分析學生梯形面積的解題策略。這次測驗的對象只有一個班級學生數的大小，使用的方法是試題關聯結構分析法，如此可以獲得學生學習概念能力方面所呈現之形成性的結構圖，此種結構圖可與教師依教材的特性所建構的學習結構圖做比較，亦可與依教科書編者所製的教材地位分析圖做比較，比較結果對於改善教學方法與指導教材設計，都將有莫大的幫助（許天維，1995）。一個班級學生經過教學後其概念能力結構的變化，是教學上非常重要的課題（許天維，1996）。因此，這次的研究是利用試題關聯結構分析法來分析、探究學生梯形面積的概念架構，除了能了解學生的概念內涵，更能藉由此班級結構圖，了解教師的教學方式是否能適合學生完全的了解這些概念，建立這些概念。

(12)

第二節研究目的與待答問題

基於以上認知心理的動機，本研究的具體目的有下列幾項：一、建立符合認知心理學邏輯性的梯形專家結構。二、應用試題關聯結構分析法，瞭解國小六年級學生在梯形面積上解題策略的概念結構。三、應用試題關聯結構分析法，比較專家與學生在梯形面積上解題策略的概念結構的差異性。

第三節名詞釋義

本研究之主要目的為探究受測學生梯形面積之概念架構。茲將所提及的相關名詞做釋義如下：一、梯形恰有一雙對邊互相平行的四邊形稱為梯形。梯形之平行二邊中之短者為上底，長者為下底，二底間之垂直距離為梯形之高。其不平行二邊之中點，以直線連結之，等於其兩底之和之半。梯形之面積，即高與兩底和之積之半。二、面積（一）貓頭鷹數學辭典 1a.指包圍在指定邊界之內或幾何圖形之內的二維表面。 b.指這種表面的整體或部分的度量或大小。 2.指立體或其部分表面的度量或大小，尤其是指閉合曲線所包圍的表面。（二）幼獅數學大辭典係二維曲面，或其上之一區域，或平面上區域之大小的測度。即以一種假定單位之面，表示任何表面所容之積。量度面積單位通常為一正方，其一邊之長即

(13)

為量直線之單位。

三、試題關聯結構分析法

在 1980 年代，日本學者竹谷誠教授提出以試題測驗結果，按題目反應所得的順序關係製成有向性的箭頭圖形，來分析試題的特性，此種方法稱之為試題關聯結構分析法（Item relational structure analysis），簡稱IRS分析法。

第四節研究範圍與限制

本研究以國民小學六年級學生為研究對象，藉由試題關聯結構分析法（IRS），探究一個班級學生在梯形面積的概念架構，並解析學生在梯形面積的解題策略。茲將研究範圍與限制之說明就研究內容、研究對象及研究方法，分述如下：

一、就研究內容而言

本研究之測驗其主要內容為國民小學數學科六年級的「梯形面積」教材，不過重點在於了解學生梯形面積的解題策略，對於估測概念、面積單位的轉換不予探討，因此所編之題目較無法涵蓋整個面積概念。

二、就研究對象而言

本研究主要是在利用試題關聯結構法之分析，探究受測學生在梯形面積的概念架構，且本研究受限於研究時間、人力與經費等客觀因素，係以彰化縣某國民小學六年級一個班級的學生為研究對象，樣本維持原來班級建制進行研究；對於所產生的推論結果，不能做普遍性的類推。

三、就研究方法而言

本研究方法只能視為一種「驗證測試」，推論的結果只能運用於相同的情境，不能過度解釋（over generalized），對於其他不同的情境，應有其不同的研究方法。

(14)

第二章文獻探討

本研究的主要目的是應用試題關聯結構分析法，分析國小六年級學生梯形面積的概念結構，為了讓梯形面積公式的相關探討做完整的呈現，因而需要文獻佐證。在文獻的探討上，從心理學上來了解兒童面積概念發展；從課程上來探討九年一貫「數與量」、「幾何」兩大主題；從教學角度上來深入國小梯形面積教材的教學；再以 2001 年版 Bloom 認知領域教育目標分類理論來當作出題的根據；最後再以試題關聯結構做本研究的分析法來分析。

第一節兒童面積概念發展

本節內容主要是針對面積的定義及面積概念發展進行探討，分述如下：

壹、面積的意義

所謂「面積」，指的是某一封閉二維區域的大小，就是對某一特定區域被數個單位量的覆蓋程度，亦即被覆蓋面的大小（譚寧君，1995a）。此時的覆蓋活動，包含了兩個條件，即﹙1﹚面積是有周界的，故覆蓋物不能超過給定的邊界。﹙2﹚ 面積是從一維到二維掃描的結果，故覆蓋物不能重疊。

貳、面積概念的發展

譚寧君（1998b）在高年級面積教材分析中曾提及面積概念發展是漸進的，是從操作的經驗中察覺的，而非從背誦中了解。根據國民中小學九年一貫課程綱要數學學習領域目標分類，面積是屬於「量與實測」的教材領域，一般面積概念包括有面積保留概念、面積測量概念及面積估測概念。茲分別敘述如下：

一、面積的保留概念

(15)

次的經驗累積才逐步形成（譚寧君，1998b）。Piaget et al.（1960）認為面積保留是指兒童認知物件經過某種轉換後（如位置、形狀改變），其面積仍然保持不變的能力。面積保留概念又可包含二個子概念，分別敘述如下：（一）基本面積保留概念任何封閉範圍內面積的大小，不因位置改變而有不同，也就是說圖形的面積不會因為移動、轉動或分割而改變其面積大小。另外，若圖形本身是合成圖形，例如一個正方形是由二個三角形的面積組合而成，將其中一個三角形移動到另一側，形成一個大三角形，則此大三角形與原來正方形的形狀不同，但是面積還是相等，這就是等積異形的概念，此概念的形成有助於瞭解數學的重要屬性－不變性（譚寧君，1995b）。（二）互補面積保留概念互補面積保留是指在面積相等的二個面上，減去形狀不同但面積相同的兩塊小平面後，其所剩下的面積仍然相等，亦即等量減等量結果相等。互補面積保留為一逆向的邏輯思考，在兒童已經具備基本面積保留概念後，教學者才能提及此互補關係。 Piaget 曾針對此概念設計一草地內馬鈴薯園的實驗，以檢驗兒童何時開始具備互補面積保留概念。結果發現七歲以下的兒童無任何面積保留概念，七至八歲僅具備基本面積保留，八歲以上的兒童才逐步形成互補面積保留（譚寧君， 1995b）。

二、面積的測量概念

面積測量則是從個別物件，如利用課本和作業簿來描述桌面的大小，到個別單位，如用相同的十張報紙來描述黑板的大小，進而至普遍單位的使用，如用平方公分的方格板來記數，最後才察覺面積公式之由來。譚寧君（1998b）在高年級面積教材分析中提及面積概念有三種如下：（一）基本面積概念

(16)

在給定的平方單位格內，點數單位面積的個數，此表示在給定的平方單位格內點數單位面積的個數，如圖2-1，甲圖表示面積佔了2個平方單位，乙圖佔了4個平方單位，甲圖與乙圖可透過視覺直接點數，故較容易。但當面積非整數格時，即形成面積的補償作用。如圖丙中，合起來是2平方單位，此補償作用的關係是建立在面積的保留概念上。圖 2- 1 點數單位面積圖（二）單位面積概念此時面積的測量是透過各個不同單位量的覆蓋或拼湊而成。例如，一個長邊8 公分，寬邊4公分的長方形，可以由不同單位量加以描述面積的大小，如用邊長1 公分的正方形加以覆蓋，則長方形可用32個□蓋滿，即表示長方形的面積是32個平方單位；如用底和高各1公分的直角三角形，則長方形要用64個⊿蓋滿，此時雖為同一長方形，但由於單位量的不同（一為□，一為⊿），故其單位數亦有不同（一為32個□，一為64個⊿）。（譚寧君，1998b） Piaget等（1960）曾設計疊置法與單位測量法來研究兒童的單位面積概念，現將其研究略述如下： 1.疊置法（measurement by super-position）：主試者出示一直角三角形，和一個不規則的圖形（如圖2-2），然後給兒童一些比較小的測量紙卡，包括正方形，直角三角形和長方形，這些紙卡的數量正好可以疊置於直角三角形或不規則的圖形上，而且兩個小正方形紙卡是等於一個小長方形紙卡；而一個小正方形紙卡等於兩個小直角三角形。主試者讓兒童嘗試疊置這些測量紙卡於直角三角形與不規則圖上，

(17)

詢問兩圖形是否一樣大。主試者也可以教兒童如何疊置，但不暗示答案。這個實驗需要兩個重要的概念：（1）測量紙卡的合併運用，亦即兩個次級單位可以合併為一個單位。（2）一個圖形若被某些測量紙卡蓋滿，而另一個圖形也能用同樣的這些紙卡蓋滿，則兩圖形大小相等，亦即數學上的相等關係的遞移性（A＝B，B＝C，則A＝C）。這實驗的結果發現：七歲半到八歲以上已能正確回答，他們會使用測量紙卡，且具備遞移概念。圖 2- 2 疊置法的面積測量概念實驗圖 2.單位測量法（measurement by unit iteration）：

這個方法是只給兒童一個剪好的測量紙卡做為測量單位，以重複測量方式去比較不同圖形的面積是否相等的題目。Piaget等人設計下列Ａ、Ｂ、Ｃ、Ｄ、Ｅ五個不同形狀的圖形（如圖2-3），另外給兒童一個小正方形紙卡（大小與虛線所示正方形相同），各圖形出示給兒童時是空白，沒有畫線。主試者拿出一枝鉛筆要兒童用小正方形紙卡在Ａ、Ｂ、Ｃ圖形上描畫，量量看三個圖是否相等。然後給兒童一個長方形紙卡（為兩個正方形紙卡的和），一個直角三角形紙卡（為正方形紙卡的一半），連同原來的正方形紙卡，共三種測量紙卡，要兒童使用，亦可用鉛筆描畫，比較Ｄ、Ｅ兩個圖形是否相等。結果發現：七歲半到八歲以上的兒童已能正確且明白基本測量單位的關係。

(18)

圖 2- 3 單位測量法的面積測量概念實驗圖（三）直線測量面積概念

直線測量法（straight line measuring）與前述基本面積概念透過點數測量，單位面積概念透過覆蓋、拼湊、比較與分割等活動以進行測量是完全不同的，直線測量已包括單位在數學上的相乘關係，此屬於較抽象的推理層次，基本面積與單位面積則只是在單位數的累加與單位量的比較，但一般所謂的面積公式如長方形面積等於長乘以寬，三角形面積等於底乘以高除以二則屬於此範疇。（譚寧君， 1995a） Piaget等人（1960）以面積加倍的概念探討方式，來研究兒童使用直線測量，以測量出面積的概念。其設計是主試者出示一條三公分的線段，請兒童先畫出兩倍長的線段。然後給他一支尺與一根細線，及一個三公分見方的正方形，要兒童畫出原正方形兩倍大的正方形（不是長方形），其結果發現十一歲或十二歲左右的兒童開始了解「乘長度」來確定面積的問題，他知道先求原正方形面積 3×3＝9，再求兩倍的面積是 9×2＝18，而 4×4＝16 所以新的正方形每邊長度會比四略大一些，這已進入形式運思期的認知作用。譚寧君（1995b）的研究中提出直線測量面積概念包含4個部份：面積公式、面積作圖、單位量的轉換、面積的包含關係，分別敘述如下： 1.面積公式：兒童藉由了解長1公分、寬1公分的正方形面積為1平方公分，知道長4 公分、寬2公分的長方形面積，一排有4個1平方公分的正方形，共有2排，即有4×2＝8，8個1平方公分，而得到長方形的面積公式為長×寬。平行四邊形面積可透過分割、拼湊等活動合成一個長方形（如圖2-4），平行四邊形

(19)

長方形的面積＝長×寬＝底×高。圖 2- 4 平行四邊形分割、拼湊成長方形圖其他如三角形、梯形、圓形的面積都透過分割、拼湊等活動而發現了一般通式，即所謂的面積公式。面積的公式乃透過推演的過程而不是只靠記憶，如此兒童才能掌握各公式間的關連性。 2.面積作圖：請兒童在釘板上圍出8平方公分的圖形，或在方格上作圖，如畫出面積為12平方公分的平行四邊形、梯形、三角形……等，兒童可透過點數的經驗而圍出一封閉的區域並符合條件的圖形，用實作的方式來檢驗兒童的面積概念。 3.單位量的轉換：面積概念的重點之一即在單位量的掌握，在單位面積概念中單位量的轉換是透過實作逐漸形成的，以圖像呈現給定單位量的關係，進行單位量的化聚，直線測量面積概念中單位量的轉換是使用二維的測量公式，如長 30公分、寬20公分的長方形，要用邊長5公分的正方形去覆蓋需要多少個， 30÷5＝6 長的這一邊每排可以排6個正方形，20÷5＝4 共可以排4排，所以共需要6×4＝24，24個正方形才能覆蓋滿長方形。 4.面積的包含關係：在計算面積時，可透過分割後形成獨立的封閉區域，分別算出面積後再組合（如圖2-5Ａ），若是某一封閉區域為二個封閉區域所交集形成的（如圖2-5Ｂ），則學生需先瞭解集合的包含關係，再透過面積測量公式方能解題。此圖灰色部分為二個四分之一圓所交集而成的，其面積等於二個四分

(20)

圖 2- 5 面積合成圖

三、面積的估測概念

估測概念是目前數學教育內涵中不可或缺的概念發展，其是從保留概念的形成到測量概念的建立逐步發展，其包含估量與估算。James（1982）提出：「估量是用以前所形成的標準進行比較，形成標準必須靠經驗。」Hall（1984）認為：「估測是一種可以訓練的猜測活動，它能在未知數量前，進行估量的活動。當我們進行估量時，我們以心中既定的標準來進行估量。」由此可知，建立一系列的經驗對於估測來說是相當重要的。面積估測概念注重量感的培養，先利用目測或手測（自然的工具），以感覺的方式進行估測，如猜猜一張圖畫紙有多大？估測活動之後，再利用工具檢驗，此種先猜後檢驗的活動，既能引起學生參與的興趣，又能培養估測的能力。估測可以讓兒童檢驗計算的結果是否正確，Hiebert（1981）指出學生遇到需要利用特殊策略找出面積時，都必須預估面積的大小。Hilderth（1983）研究發現五、七年級的學生估測長度與面積的策略有：1.使用分割的線索：使用問題中有用的訊息將長度或面積分割。2.單位的累計：以單位進行累計。3.先前的經驗：問題中相關有用的訊息。4.比較：將待測物與其他物件做比較。5.分塊：將長度等分成小段，再以單位比較該小段。6.夾擠：給定一個最小的可能區間。7.長×寬：使用長度估測策略，再以面積公式計算出。8.重整：將圖形重整以便獲得更容易估測的區域，如將等腰三角形，分割重組為長方形。莊維展（2001）探討五年級學生在面積、長度、容量與重量的估量能力時發現：面積的估量表現在此四種量的表現較差。在晤談中發現在估量上所使用策略包括不知道、猜測（憑經驗或憑感覺）、普遍單位值接比較、個別單位比較、分解與重組以及數學公式策略等。

(21)

第二節國小梯形面積概念

長方形、平行四邊形、三角形乃至梯形的面積問題均為邏輯的推理關係，而非獨立存在，任何梯形均可分割成三角形與平行四邊形，故若如前述關係能充分瞭解，並能解決各類三角形等的面積問題，梯形面積問題當能處理：

壹、點數活動

在有格子的圖形上，讓學生從整數格的點數到非整數格的點，使學生經驗到分割、拼湊、分解、合成等經驗。如圖 2-5 中的甲圖整數格有 5 格，半格有 2 個等於 1 格，共有 6 個平方單位。乙圖整數格有 6 格，半格的有 8 個等於 4 格，共有 10 個平方單位。丙圖整數格有 5 格，半格有 6 個等於 3 格，共有 9 個平方單位。甲圖乙圖丙圖圖 2- 6 點數示範圖

貳、分割活動

將梯形分割成學習過的長方形、三角形與平行四邊形，透過此操作活動，讓學生再度經驗面積的可分割性，且根據其屬性有不同的合成與分割法。如下列各種分割方法均可解決梯形面積問題。

(22)

(1) (3) (4) (6) a a b

h

a b

h

b ₍₂₎ a b

h

a a b a b

h

a b

h

a b (5) 圖 2- 7 梯形面積的合成與分割法圖 2-7 中(1)—(6)有不同的處理方式，即表示不同的成熟度，如圖(1)將梯形分割成兩個三角形，可利用三角形面積公式解決問題；圖(2)或透過兩個全等梯形可以拼成平行四邊形的經驗，察覺梯形面積為平行四邊形面積的一半，且高相等、底邊恰為梯形兩底的和；圖(3)、(4)將梯形分割成一個三角形或兩個三角形和一個平行四邊形或長方形，再利用三角形面積及平行四邊形或長方形的求法解決問題；圖(5)—(6)則必須透過全等概念換算而知。(譚寧君，1998a)

參、上底、下底與高的命名及畫法活動

梯形有一雙平行的對邊，這一雙平行的對邊不等長，故將不等長的兩底邊分

(23)

線叫做高，梯形只有一組相對的高。陳鉪逸(1996)的研究中，學生對於釘板上正放梯形及側放梯形上底、下底和高的實測能力，其通過率如表 2-1。王選發(2002)的研究中，學生在正放梯形、側放梯形及斜放梯形的畫高表現，平均答對率都在八成以上，表現相當不錯。但出現一迷思概念，誤解「高」一定要畫在鉛直線上；或「高」的概念不清楚而誤以為梯形的對角線或指定邊的鄰邊為「高」。表 2- 1 梯形各部位的通過率通過率梯形的上底梯形的下底梯形的高正放梯形 75.00 76.66 76.25 側放梯形 68.88 75.06 75.30

肆、建構梯形面積公式意義的活動

康軒數學課本第十一冊(2006)在建構梯形面積公式意義的活動，提供了兒童可能建構的過程，有以下三種： (一)一個梯形可分割成兩個三角形，面積等於兩個三角形的面積和，梯形面積 =上底×高÷2+下底×高÷2=(上底+下底)×高÷2 (二)一個梯形可以分割後然後拼成長方形，長方形的長=上底+下底，長方形的寬=高的一半，梯形面積=長方形的面積=(上底+下底)×高÷2 (三)二個全等梯形可拼湊成一個平行四邊形，平行四邊形的底邊恰為梯形的上底與下底的和，故梯形面積為平行四邊形的一半，矛成(上底+下底)×高÷ 的面積公式。兒童在以上(一)、(二)、(三)具體操作的過程中，發現梯形面積公式為(上底 +下底)×高÷2。

(24)

第三節九年一貫課程數學領域「數與量」主題

面積公式在九年一貫暫行綱要課程中，是在第三階段的「數與量」單元中，到了九年一貫正式綱要時，是放在新課程第二階段的「幾何」單元中，因此首先就「數與量」的主題進行深入研究。

壹、「數與量」主題有關面積學習之歷程

量與實測為「數與量」主題中之子題，也是國小數學的核心課程之一，教學中的量包含長度、重量、容量、時間、角度、面積、體積等生活中常用的七種量。其中長度、容量、角度、面積、體積屬於幾何（視覺）量，處理上可以依賴學生的幾何經驗，比較容易。時間以外六種量的學習，大致上要經歷下列四個階段：初步概念與直接比較；間接比較與個別單位；常用單位的約定；常用單位的換算。一、初步概念與直接比較：首先，透過感官直接感覺該量，再對兩同類量作直接比較，最後是量的複製，這是下個階段的前置經驗。另外，也包括利用測量工具之刻度直接描述一量。量的複製包括：整體複製（例：給定一條繩子，比對著端點完整地剪下和所給定的繩子一樣長的繩子）、合成複製（例：用幾根木條頭尾相接拼出黑板的長；用一些硬幣平衡天平另一端放置之重物）與等量合成複製（例如：用等長木條頭尾相接拼出黑板的長；用相同的硬幣平衡天平另一端放置之重物）。二、間接比較與個別單位：對無法直接比較的兩同類量，能透過媒介量，分別作直接比較，並利用比較結果，做出兩量之比較(涉及量的保留概念與量的遞移律) 能作間接比較，便能使用個別單位作測量。量的保留概念由Piaget提出，他從實驗結果知道，未擁有某類量之保留概念的兒童，對此類量不能進行間接比較。但教師可透過恰當的教學與溝通，運過Piaget「同一性」、「互逆性」與「互補性」三原則，主動誘發學生早日發展保留概念。

(25)

三、常用單位的約定：認識某類量之常用單位，並能運用此單位，作量的比較、加、減、乘、除。四、常用單位的換算：在測量時，首先能用大小單位的複名數來描述測量結果。然後再學習使用單位換算的約定，來進行換算。例：1200 公尺＝1 公里 200 公尺＝1.2 公里。

貳、「數與量」主題之能力指標

一、九年一貫「數與量」主題中有關面積概念之各階段能力指標

在「數與量」主題所公佈的四個階段中，每一階段都各有其對應的能力指標，能力指標以三碼編排，其中第一碼表示主題，Ｎ表示「數與量」；第二碼表示階段，分別以 1,2,3 表示第一、二、三階段；第三碼則是能力指標的流水號，表示該細項下指標的序號。茲將九年一貫「數與量」主題中有關面積概念之各階段能力指標分列如下： (一)第一階段（1~3 年級）： N-1-9 能透過感官活動感覺一個量，並能對兩個同類量作直接比較，進而對一個量作複製活動(量：長度、容量、重量、角度、面積、體積)。 N-1-10 能使用生活中常用的測量工具(刻度尺的方式，即不涉及其結構)，以一階普遍單位描述一個量(量：長度、容量、重量、角度、面積、體積；普遍單位：米、厘米、分公升、千克、克、度、平方厘米、立方厘米)。 (一)第二階段（4~5 年級） N-2-9 能在保留概念形成後，進行兩個同類量的間接比較(利用完整複製) 及個別單位的比較(利用等量合成的複製)(量：長度、容量、重量、角度、面積、體積)。 N-2-10 能認識各種量的普遍單位，應用在生活中的實測和估測活動，並培

(26)

養出量感(普遍單位：千米、毫米、公升、毫公升、時、分、秒)。 N-2-13 能以個別單位的方式(利用等物合成複製後)描述面積、體積，並能用乘法簡化長方形面積、長方體體積之點算。 (三)第三階段（6~7 年級） N-3-9 能理解同類量中不同單位間的關係，並作化聚活動(可以有分數、小數)。 N-3-10 認識生活中使用的大的測量單位，如：千公斤(公噸)、千公升(公秉)、百平方米(公畝)、千平方米(公頃)。 N-3-11 能以分割後，重新拼湊組合的方式(幾何部份要配合)，將平行四邊形、三角形和梯形，變形成長方形而計算其面積，形成面積之計算公式。

二、九年一貫「數與量」主題有關面積概念之分年細目

此外，九年一貫 92 版與之前 87 版最大的不同在於 92 版有對各年級作出「分年細目」來補強以四個階段來分能力指標所造成的細膩度的不足與年級銜接時容易有部分能力指標的遺漏，以利教師對能力指標有更明確的掌握。分年細目以三碼編排，其中第一碼表示年級，分別以 1，2，…，9 表示一至九年級；第二碼表示主題，小寫字母 n 表示「數與量」主題、小寫字母 s 表示「幾何」主題；第三碼則是分年細目的流水號，表示該細項下分年細目的序號。茲將九年一貫「數與量」主題中有關面積概念之分年細目分列於下表。（如表 2-2）表 2- 2 九年一貫「數與量」主題中有關面積概念之分年細目年級分年細目對應指標二年級 2-n-17 能認識面積，並作直接比較。（同 2-s-05） N-1-14 S-1-03

(27)

續(表 2- 2) 年級分年細目對應指標三年級 3-n-18 能利用間接比較或以個別單位實測的方法比較不同面積的大小，並認識面積單位「平方分分」。（同 3-s-05） N-1-15 N-1-16 四年級 4-n-15 能認識面積單位「平方公尺」，及「平方公分」、「平方公尺」間的關係，並作相關計算。 4-n-16 能理解長方形和正方形的面積公式與周長公式。（同 4-s-09） N-2-15 N-2-17 S-2-07 五年級 5-n-15 能認識面積單位「公畝」、「公頃」、「平方公里」及其關係，並作相關計算。 5-n-16 能運用分割重組，理解三角形、平行四邊形與梯形的面積公式。（同 5-s-05） N-2-15 N-2-16 N-2-19 S-2-08 六年級 6-n-11*能以適當的正方形單位，對曲線圍成的平面區域估算其面積。（同 6-s-03*） N-3-15 S-3-03 從九年一貫數學領域暫綱與正綱的能力指標來看，面積的教學由第三階段六年級，提前到第二階段五年級來實施，顯示為人垢病的教材簡易的情形，已極力修正。

(28)

第四節九年一貫課程數學領域「幾何」主題

「幾何」主題在九年一貫修正後的綱要中，最大的改變在於平面幾何圖形性質的推理與證明、培養抽象思考及推理能力，因此面積的教學關係到整個「幾何」主題的基礎與應用。

壹、「幾何」主題有關面積教學之歷程

依據教育部（2003）依各階段的能力成長分四個階段來實施「幾何」的教學。幾何課程可概分為四階段：一、階段一（一年級到三年級）：較強調幾何形體的認識、探索與操作，學生對幾何形體中的幾何要素，也許能指認，但尚不清楚其結構意義。二、階段二（四年級到五年級）：由於數與量的發展逐漸成熟，學生開始結合「數」與「形」兩大主題，學習運用幾何形體的構成要素（如角、邊、面）及其數量性質（如角度、邊長、面積）。三、階段三（六年級到七年級）：透過形體的分割、拼合、截補、變形及變換等操作，來了解形體的性質與幾何量的計算及非形式化推理。透過方位描述及立體模型的展開與組合以培養空間能力及視覺推理。四、階段四（八年級到九年級）：開始由具體操作情境進入推理幾何情境中，最終目標是學會推理幾何證明，學習內容採漸進式安排，由基本幾何概念進入較深入的幾何推理領域中，學習方式最開始可由填充式推理幾何，慢慢養成完整能力，讓學生有能力及信心，快樂地學習幾何學領域的知識。教材內含有認識生活中的平面圖形，如三角形、四邊形、多邊形、圓形；認識點、線、角、符號及幾何相關名詞；使用基本性質描述某一類形體；能以最少性質對幾何圖形下定義、並熟練定義的相關操作；體會邏輯概念：包含關係、敘述及逆敘述推理幾何；求角度問題、長度問題、面積（表面積）問題、體積問

(29)

題；推理證明、尺規作圖、全等性質、相似性質、平行性質的應用、圓的相關性質。所以縱觀整個國小一至六年級面積學習的編排，從低年級開始幾何形體的認識、探索與操作概念；中年級再接著建立結合「數」與「形」兩大主題，學習運用幾何形體的構成要素（如角、邊、面）及其數量性質（如角度、邊長、面積）；再到高年級開始透過形體的分割、拼合、截補、變形及變換等操作，來了解形體的性質與幾何量的計算及非形式化推理，有著一系列的學習順序。而本研究著重於梯形面積概念的主題上，希冀能瞭解兒童關於九年一貫課程數學學習領域面積概念其知識結構的發展。透過此結構圖所呈現的訊息，以期對國小學童在梯形面積概念的學習及教師教學上有所助益。

貳、「幾何」主題之能力指標

一、九年一貫「幾何」主題中有關面積概念之各階段能力指標

茲將九年一貫「幾何」主題中有關面積概念之各階段能力指標分列於下 (一)第一階段（1~3 年級）： S-1-1 能由物體的外觀，辨認、描述與分類簡單幾何形體。 S-1-2 能描繪或仿製簡單幾何形體。 S-1-4 能認識平面圖形的內部、外部及其周界。 S-1-5 能透過操作，將簡單圖形分割重組成另一已知簡單圖形。 S-1-7 能認識生活周遭中水平、鉛直、平行與垂直的現象。 (二)第二階段（4~5 年級） S-2-1 能運用簡單幾何形體的組成要素，作不同形體的分類。 S-2-2 能理解垂直與平行的意義。

(30)

S-2-3 能透過操作，認識簡單平面圖形的性質。 S-2-4 能認識平面圖形全等的意義。 S-2-7 能理解長方形面積、周長與長方體體積的公式。（N-2-17） S-2-8 能運用分割重組，理解三角形、平行四邊形與梯形的面積公式。（N-2-19） (三)第三階段（6~7 年級） S-3-1 能利用幾何形體的性質解決簡單的幾何問題。 S-3-2 能認識平面圖形放大、縮小對長度、角度與面積的影響，並認識比例尺。 S-3-3 能以適當的正方形單位，對曲線圍成的平面區域估算其面積。（N-3-15）

二、九年一貫「幾何」主題有關面積概念之分年細目

再將九年一貫「幾何」主題中有關面積概念之分年細目分列於下表。（如表 2-3）表 2-3 九年一貫「幾何」主題中有關面積概念之分年細目年級分年細目對應指標一年級 1-s-02 能辨認、描述與分類簡單平面圖形與立體形體。 1-s-03 能描繪或仿製簡單平面圖形。 1-s-04 能依給定圖示，將簡單形體作平面舖設與立體堆疊。 S-1-01 S-1-02 S-1-02 S-1-05 二年級 2-s-02 能認識生活周遭中水平、鉛直、平行與垂直的現象。 2-s-05 能認識面積，並作直接比較。（同 2-n-17） S-1-07 N-1-14 S-1-03

(31)

續(表 2-3) 年級分年細目對應指標 2-s-06 能由邊長關係，認識簡單平面圖形與立體形體。 N-1-16 S-1-01 三年級 3-s-01 能認識平面圖形的內部、外部與其周界。 3-s-02 能認識周長，並實測周長。 3-s-05 能利用間接比較或以個別單位實測的方法比較不同面積的大小，並認識面積單位「平方公分」。（同 3-s-18） 3-s-06 能透過操作，將簡單圖形分割重組成另一已知簡單圖形。 S-1-04 N-1-16 S-1-04 N-1-15 N-1-16 S-1-05 四年級 4-s-01 能運用「角」與「邊」等構成要素，辨認簡單平面圖形。 4-s-02 能透過操作，認識基本三角形與四邊形的簡單性質。 4-s-03 能認識平面圖形全等的意義。 4-s-06 能理解平面上直角、垂直與平行的意義。 4-s-07 能由直角、垂直與平行的概念，認識簡單平面圖形。 4-s-08 能利用三角板畫出直角與兩平行線段，並用來描繪平面圖形。 4-s-09 能理解長方形和正方形的面積公式與周長公式。（同 4-s-16） S-2-01 S-2-03 S-2-04 S-2-02 S-2-02 S-2-03 S-2-02 S-2-03 N-2-17 S-2-07

(32)

續(表 2-3) 五年級 5-s-05 能運用分割重組，理解三角形、平行四邊形與梯形的面積公式。（同 5-s-16） N-2-19 S-2-08 六年級 6-s-01 能利用幾何形體的性質解決簡單的幾何問題。 6-s-02 能認識平面圖形放大、縮小對長度、角度與面積的影響，並認識比例尺。 6-s-03 能以適當的正方形單位，對曲線圍成的平面區域估算其面積。（同 6-s-11） S-3-01 S-3-02 N-3-15 S-3-03 和「數與量」主題相同，面積的教學由第三階段六年級，提前到第二階段五年級來實施。比較二個不同時期的教材綱要編排順序，可知其共通點就是都有注意到學童面積概念的發展，提供學童多樣化的操作經驗，進而探索形體的性質與關係，掌握由具體到抽象的順序，並重視課程的連貫性。

(33)

第五節

2001 年版 Bloom 認知領域教育目標分類理論之相關研究

本節主要探討Bloom認知領域教育目標分類理論，茲將其理論敘述如下：西元 1956 年經由 Bloom 等三十多人的努力，認知領域教育目標分類手冊（Taxonomy of Educational objective,Handbook1:Cognitive Domain）問世，並將認知領域教育目標分為知識（Knowledge）、理解（Comprehension）、應用（Application）、分析（Analysis）、綜合（Synthesis）、評鑑（Evaluation）六個主要類目；歷經多年使用後，在西元2001年出刊修定版（revised edition）（Anderson & Krathwohl, 2001)，修訂版將教育目標分類分成知識向度(knowledge dimension)和認知歷程向度(cognitive process dimension)兩部分(Anderson et al. , 2001)，前者為協助教師區分教什麼，後者在促進學生保留和遷移所習得的知識，見圖2-8 (譯自Anderson et al(2001)，p268) 。事實知識(Factual Knowledge) 修訂版(Anderson et al. ,2001) 概念知識(Conceptual Knowledge) 程序知識(Procedual Knowledge) 後設認知(Metacognitive Knowledge) 知識(Knowledge) 記憶( Remember) 理解(Comprehension) 了解(Understand) 應用(Application) 應用(Apply) 分析(Analysis) 分析(Analyze) 綜合(Synthesis) 評鑑(Evaluate) 評鑑(Evaluation) 創作(Create) 圖 2- 8 Bloom 教育目標分類系統新舊版本對照圖認知歷程向度知識向度舊版 (Bloom,1956)

(34)

一、2001 年版 Bloom 認知領域教育目標分類之理論分析

(一)知識向度之理論介紹

就知識向度而言，修訂版將知識分成事實知識(factual knowledge)、概念知識(concept knowledge)、程序性知識(procedure knowledge)、及後設認知知識 (metacognition knowledge)。事實知識與概念知識是指有關「什麼」的知識，主要的差異在於前者指學生學習科目後和解決問題時的應備知識，而後者則視為獨立和特定的元素；程序性知識是有關「如何」的知識，指對一系列或連串的步驟為一個程序；後設認知知識則包括對認知的知識，以及對認知歷程的控制 (control)、監控(monitoring)和調整(regulation)，包括適用所有工作的一般策略、使用策略情境、策略有效程度和自我知識等方面。以下將逐一說明： A 事實知識(Factual Knowledge)：指學生應了解的術語，或是特定細節和元素的知識。 B 概念知識(Conceptual Knowledge)：指分類和類別的知識、原理和通則的知識、或理論／模式／結構的知識。 C 程序知識(Procedural Knowledge)：指特定學科的技能和演算知識、特定學科的技術和方法知識，以及運用規準的知識。 D 後設認知知識(Metacognitive Knowledge)：指用於學習、思考和問題解決的策略知識，可跨領域應用的策略知識；也是學生了解可以運用後設認知的知識，意即「何時」與「為何」能適當運用策略的知識；更是自我的知識。 (二)認知歷程向度之理論介紹在認知歷程向度部分，修訂版分為較低層次的記憶 (remember) 、了解 (understand)、應用(apply)和分析(analyze)，以及較高層次的評鑑(evaluate) 與創造(crearte)，其中記憶和學習保留具密切關聯，而另五種則與學習遷移有關。以下將逐一說明： 1 記憶(Remember)：是從長期記憶中提取相關知識，找出與呈現資訊一致或

(35)

近似的知識。。 2 了解(Understand)：從教學訊息(在課堂中、在書本中或電腦螢幕上的口語、書面與圖形訊息)中創造意義(make sense)；建立所學新知識與舊經驗的連結。 3 應用(Apply)：牽涉使用程序(步驟)來執行作業或解決問題。與程序知識緊密連結。一項作業是指學生已經知道採用哪些程序的任務，所以是一種偏例行作業取向的任務。一項問題是事先不知道採用哪些程序的任務，所以是一種偏解決問題取向的任務。 4 分析(Analyze)：能區辨出有關的與無關的或是重要的與不重要的部分；能注意有關的或是重要的資訊；寫出或指出在所提供材料中最重要或最有關聯的部分；認出溝通情境中的各元素，能認出這些元素是如何統整在一起，更能對所呈現的資訊片段，建立系統與和諧的關聯。 5 評鑑(Evaluate)：檢查一組運作或是產品的內部矛盾與邏輯謬誤，根據外在規準與標準作評論。 6 創造(Create)：涉及將各個元素組裝在一起，形成一個完整且具功能的整體。創作的目標是要學生能透過在心智上重組元素或重組局部，使成一個過去鮮少出現的組型或結構。

二、九年一貫數學能力指標與修訂版 Bloom 認知領域教育目標分類之

對照分析（鄭蕙如、林世華，2001）：

本研究主題為梯形面積，對象為六年級學生，屬於「數與量」、「幾何」第三階段的範圍，因此根據這兩大領域分別做知識向度、認知歷程的分析。（一）各領域的知識向度分析知識向度分為事實知識、概念知識、程序知識、後設認知知識，根據這「數與量」、「幾何」這兩大領域分別求取各知識向度百分比，以進行比較，整理成

(36)

表2-4：表2- 4 數學領域第三階段知識向度百分比事實知識概念知識程序知識後設認知知識數與量 13 58 29 0 幾何 0 100 0 0 就知識向度而言，可以看到歸屬於事實知識的指標偏少，指標主要著重於概念知識及程序知識，第三階段則較強調概念知識。就教學現場來看，小學階段計算應是學習重要的一環，而隨著年齡的增長，對於數學概念也應具更深的了解；而在此領域中，缺乏後設認知知識的指標。（二）各領域的認知歷程分析認知歷程程分：記憶了解、應用、分析、評鑑、創造，本研究依主題、對象，分別求取認知歷程的百分比，以進行比較，整理成表2-5：表2- 5 數學領域第三階段認知歷程百分比記憶了解應用分析評鑑創造數與量 10 50 40 0 0 0 幾何 0 57 43 0 0 0 就數與量領域的認知歷程而言，年齡較小時所具備的能力以記憶為主。當年齡逐漸增長時，會呈現了解與應用的能力；就幾何領域的認知歷程而言，較重視了解與應用，而這兩大領域皆沒有分析、評鑑、創造等歷程。由以上兩個向度的分析，本研究工具的出題方向在知識向度方面，該著重在概念知識、程序知識，在認知歷程方面則著重在了解、應用。

(37)

第六節試題關聯結構分析法

在實施教學活動後，接著就必須了解班上學生之概念能力在結構上的變化，因此需要方法考證。在1980 年代，日本學者竹谷誠提出以測驗試題的結果，按題目彼此間反應所得的順序關係，製成具有指向性的圖形結構，來分析試題的特性，此種方法稱之為試題關聯結構分析法（Item relational structure analysis），簡稱IRS 分析法；有了此種方法，學習情況與教學成果的分析終於獲得解決（引自許天維，1995）。

一、試題關聯結構法的構想由來

美國學者Airasian P.W.與Bart W.M.於1973 年首先揭開「次序理論」

（Ordering theory）在教育工學的功用，（Airasian & Bart, 1973）。1977 年日本學者竹谷誠參加美國威斯康辛大學的研討會，因Baker F.B.的介紹，在返回日本後，便致力於改良「次序理論」的缺點，於1979 年發明「試題關聯結構分析法」，又於1980年完成試題關聯結構分析法的理論，並在教育現瑒實驗使用，前後有七、八年之久，證明是一個有效的分析工具。

二、試題關聯結構法理論

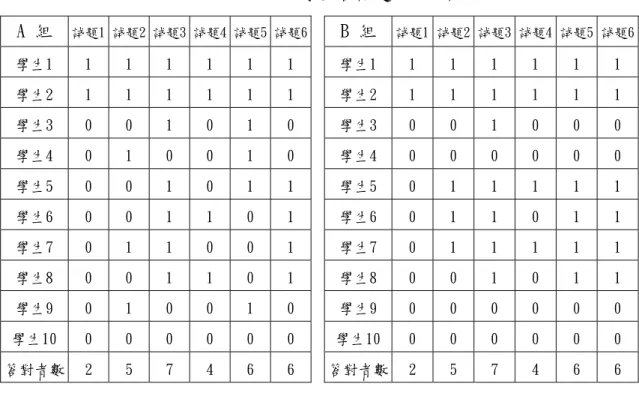
在此，略用篇幅詳細說明理論上直觀的意義，假設有A、B 兩組學生各有十位，均參加試題共為六題的同一種測驗，若假設答對者得一分，答錯者得零分，其得分情況如表2-6所示：

(38)

表 2- 6 A、B 兩組學生各試題的得分情況 A 組試題1 試題2 試題3 試題4 試題5 試題6 B 組試題1 試題2 試題3 試題4 試題5 試題6 學生1 1 1 1 1 1 1 學生1 1 1 1 1 1 1 學生2 1 1 1 1 1 1 學生2 1 1 1 1 1 1 學生3 0 0 1 0 1 0 學生3 0 0 1 0 0 0 學生4 0 1 0 0 1 0 學生4 0 0 0 0 0 0 學生5 0 0 1 0 1 1 學生5 0 1 1 1 1 1 學生6 0 0 1 1 0 1 學生6 0 1 1 0 1 1 學生7 0 1 1 0 0 1 學生7 0 1 1 1 1 1 學生8 0 0 1 1 0 1 學生8 0 0 1 0 1 1 學生9 0 1 0 0 1 0 學生9 0 0 0 0 0 0 學生10 0 0 0 0 0 0 學生10 0 0 0 0 0 0 答對者數 2 5 7 4 6 6 答對者數 2 5 7 4 6 6 由表可知兩組測驗後，各組各試題之答對者人數均相同，為方便起見，可以改成下表： A 組試題 B 組試題 1 2 3 4 5 6 1 2 3 4 5 6 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 2 1 1 1 1 1 1 3 0 1 0 0 1 0 3 0 0 1 0 0 0 4 0 1 0 0 1 0 4 0 0 0 0 0 0 5 0 1 1 1 1 1 5 0 1 1 1 1 1 6 0 0 1 0 0 1 6 0 1 1 0 1 1 7 0 0 1 1 0 1 7 0 1 1 1 1 1 8 0 0 1 0 0 1 8 0 0 1 0 1 1 9 0 0 1 0 0 0 9 0 0 0 0 0 0 學生 10 0 0 0 0 1 0 學生 10 0 0 0 0 0 0 答對者數 2 5 7 4 6 6 答對者數 2 5 7 4 6 6 其次，依照每位學生試題所得的總分高低，由上而下排序可得下表：

(39)

A 組試題 B 組試題 1 2 3 4 5 6 1 2 3 4 5 6 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 2 1 1 1 1 1 1 5 0 1 1 1 1 1 5 0 1 1 1 1 1 7 0 0 1 1 0 1 7 0 1 1 1 1 1 6 0 0 1 0 0 1 6 0 1 1 0 1 1 8 0 0 1 0 0 1 8 0 0 1 0 1 1 3 0 1 0 0 1 0 3 0 0 1 0 0 0 4 0 1 0 0 1 0 4 0 0 0 0 0 0 9 0 0 1 0 0 0 9 0 0 0 0 0 0 學生 10 0 0 0 0 1 0 高分低分學生 10 0 0 0 0 0 0 高分低分答對者數 2 5 7 4 6 6 答對者數 2 5 7 4 6 6 接著，以學生在各試題答對人數的多寡順序，由左而右排列，可得佐藤S-P表（佐藤隆博，1982）如下表： A 組試題 B 組試題 3 6 5 2 4 1 3 5 6 2 4 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 2 1 1 1 1 1 1 5 1 1 1 1 1 0 5 1 1 1 1 1 0 7 1 1 0 0 1 0 7 1 1 1 1 1 0 6 1 1 0 0 0 0 6 1 1 1 1 0 0 8 1 1 0 0 0 0 8 1 1 1 0 0 0 3 0 0 1 1 0 0 3 1 0 0 0 0 0 4 0 0 1 1 0 0 4 0 0 0 0 0 0 9 1 0 0 0 0 0 9 0 0 0 0 0 0 學生 10 0 0 1 0 0 0 學生 10 0 0 0 0 0 0 答對者數 7 6 6 5 4 2 答對者數 7 6 6 5 4 2 多少多少由上表可知兩組學生的總分順序及答對者人數的試題次序都相同；亦即二組

(40)

下列方法細加分析，就會有顯著的不同。 A 組中，答對試題1 的學生是1 號及2 號，他們亦同時答對了試題4 ，亦即答對試題1 的學生亦答對試題4 ，此時就有試題4 到試題1 的箭頭，記作4 →1；同理，答對試題4的學生是1 號、2 號、5 號及7號，他們亦同時答對了試題3、6，所以分別有3→4、6→4；另一方面，答對試題1的學生是1號及2號，他們亦同時答對了試題2，答對試題2的學生是1號、2號、3號、4號及5號，他們亦同時答對了試題5，所以分別有2→1、5→2；此外，答對試題4的學生有7號，但是沒答對試題2，故沒有試題2到試題4的指向箭頭，其餘均依此類推。同法，在B 組中，答對試題1的學生是1號及2號亦答對了試題4，亦即答對試題1的學生亦答對試題4，此時就有試題4到試題1的箭頭，記作4→1；答對試題4的學生是1號、2號、5號及7號亦答對了試題2，所以有2→4；答對試題2的學生是1號、 2號、5號、6號及7號分別答對了試題5、6，所以分別有5→2、6→2；答對試題5、 6的學生有1號、2號、5號、6號、7號及8號亦答對了試題3，故有3→5、3→6；其餘均依此類推。從以上分析，如果定義答對率為受試答對人數所有受試人數試題答對率＝則以答對率為縱座標，可將所有相關的指向箭頭標示出來，成為完整的試題關聯結構圖，如圖2-9所示：

(41)

A 組 B 組 0.2 0.3 0.4 0.5 0.6 0.7 0.2 0.3 0.4 0.5 0.6 0.7 答對率答對率 1 4 6 3 2 5 3 5 6 2 4 1 圖2- 9 試題關聯結構圖範例在此值得注意的是上面兩個試題關聯結構圖截然不同，儘管兩個試題其答對率雖然相同，然而兩組學生的理解結構卻不相同。左圖顯示A 組有兩個系列存在，即試題1、2、5 的系列以及試題1、4、5、6 系列，而右圖顯示B 組的試題形成一個單純的一元化系列。故試題關聯結構圖可看出在S-P表所觀察不到的各試題間的順序關係，可作有方向性的圖性判讀。

三、試題關聯結構順序性係數

以上所述只為闡明試題關聯結構分析法而設計的特殊實例，現在以數理推導理論來製造指向，為達到此目的，首先考慮令：Ｘ＝（ｘij）N×n i＝1,2,…,N； j＝ 1,2,…,n. 其中ｘij＝1 表第ｉ個學生答對試題Ij，ｘij＝0 表第ｉ個學生答錯試題Ij。又設： P（Ij）表試題Ij答對人數的機率。

(42)

P（Ik）表試題Ik答對人數的機率。 P（ I j）表試題Ij答錯人數的機率。 P（ I k）表試題Ik答錯人數的機率。 P（Ij，Ik）表試題Ij與試題Ik均答對的同時機率。 P（ I j，Ik）表試題Ij答錯且試題Ik答對的同時機率。 P（Ij， I k）表試題Ij答對且試題Ik答對的同時機率。 P（ I j， I k）表試題Ij與試題Ik均答錯的同時機率。則可知下面機率的四分割表（表2-7）：表 2- 7 機率的四分割表試題 Ik 對(1) 錯(0) 合計試題對(1) P（Ij，Ik） P（Ij，I k） P（Ij） Ij 錯(0) P（ I j，Ik） P（ Ij，Ik） P（ Ij）合計 P（Ik） P（ I k） 1 試題關聯結構順序性係數r* jk 表示法如下：（引自許天維，1995） r* jk＝1－P（ I j，Ik）/ [P（ I j）P（Ik）] 順序性係數r* jk代表試題ｊ指向試題ｋ的順序性程度，也就是說試題ｊ為下位

概念（lower concept），試題ｋ為上位概念（upper concept）的程度。順序性係數是一個數值，而竹谷誠（1991）以0.5 為閥值（threshold），由電腦模擬產生。若順序性係數大於閥值，則表示試題ｊ與試題ｋ有順序關係，反之則無。另

(43)

值為0.6。一般閥值介於0.4 到0.6 之間。

四、試題關聯結構法的功能

經過研究的結果，試題關聯結構分析法有下列五種功能：（一）教學設計：在單元教學活動前，教師可以將欲進行的課程內容的先前經驗概念，作一知識結構分析後，再依結構所對應的知識概念分別出題，並加以施測，所得的結果以「試題關聯結構分析法」進行分析，可以考驗出先前經驗概念不足之處，從而想像出未來指導時的困難所在，以為進行設計教學歷程的參考。（二）形成性評量（formative evaluation）：在單元教學活動後，欲知班上學習結果，可以利用知識結構分析出題，編製形成性評量，再加以施測，所得的結果以「試題關聯結構分析法」進行分析，就可以知道學生學習後的知識結構，以便對學生不清楚之處，加強補救教學。（三）認知學習構造：形成性評量的反應結果，亦可利用佐藤S-P 表獲得注意係數，從而偵測出異質性的學生，此類學生所畫出結構圖與班上的結構圖可以互為比較，即可知道此類學生異質的原因，從而加強輔導教學。（四）概念形成過程：對縱貫研究（longitudinal study）而言，學生概念的形成過程有層次之分，例如山田完對教師進行評定學生設有四層次，即操作經驗層次、知覺內化層次、言語抽象層次、因果論理層次，如果以此四層次來評定各年級班上學生的形成過程，並建立各年級的結構圖，即可知學生的概念形成過程的發展。對橫斷研究而言，亦可知班上學生的概念形成過程的分布。（五）課程教材構造：

(44)

由母群體隨機抽出樣本進行考驗後，透過「試題關聯結構分析法」進行構圖，可得一般學生的學習構造，對教科書編者而言，是貴重的資料，而且對於分析典範教師的學習指導構造圖的特質，都有很大的作用。

其次，值得提醒注意的是，此種「試題關聯結構圖」與「詮釋結構圖」（Interpretative structural modeling, 簡稱ISM）不能混為一談，因為詮釋結構圖沒有透過成就測驗或是形成性評量，而是使用經過設計的兩兩關係概念問卷來找出受試者概念間的指向，或是藉由受試者自行建構的兩兩關係概念指向，再運用圖形理論來統合所有被製造出來的指向，並加以畫出構圖，這是一種屬於知識結構分析的特殊方法。但由於國小學生對知識架構不夠成熟，使用此法通常無法獲得真正可靠的結果，所以此種方法僅適宜分析專家（expert）或是知識較為成熟的受試者的知識結構。事實上，上述「詮釋結構分析法」與「試題關聯結構分析法」，不但可解決日本教育學者坂元昂的授業改造技法一書中，所注重的教材構造分析與學習結構圖的編製，亦可解決美國著名的教育學者Scandura, J.M.所倡導的結構式學習理論（Structural learning theory, 簡稱SLT）的不足之處，（湯維玲，1994）。因為結構式學習理論，必須尋找理想化教師（idealized teacher），藉其專業能力，對教材內容的結構，進行有系統的分析。理想化教師依據教材的問題型式著手，並將知識化約成一套由領域（domain）、範圍（range）和運作（operation）三部份所組成的「規則」（rule），再以此「規則」為基礎，細分成許多原子要素，然後確認學習者已知或未精熟（nonmastery）之處，理想教師便從學習者失敗的路徑（path）要素，開始執行教學設計與活動。此時，在教學過程中可用「詮釋結構分析法」形成「規則」的結構路徑，而「確認學習者已知或未精熟的路徑」可用「試題關聯結構分析法」，來補足理想教師分析上實務的困難。根據Scandura 的研究，以結構分析的方式，處理幾何作圖問題、計算技巧、代數證明、小學數學課程以及Piaget 保留概念問題等，都有極豐碩的實證性研究成果，（Scandura

(45)

& Scandura，1980）。

綜上所述，本研究中所編之梯形面積試題主要是為了得知一個班級學生的知識概念結構，因此是為形成性評量，透過評量結果所建立的結構圖，可以用來瞭解學生知識結構不穩固的地方，而據以實施補救教學或改進教學設計，以更符合學生知識結構的發展。

(46)

第三章研究方法

本研究目的主要在探討國小六年級學生在梯形面積概念的試題關聯結構圖所呈現的訊息。透過文獻探討，提出研究架構、研究對象、研究工具、研究流程及資料處理等五節加以說明本研究的方法和程序。

第一節研究架構

本研究依據研究目的與文獻資料，提出以下之研究架構，如圖3-1 所示。圖 3- 1 研究架構圖編製梯形面積概念試題進行預試Ｂｌｏｏｍ雙向細目表梯形面積概念圖及各解題策略的子概圖國小梯形教材架構圖國民小學一～六年級數學領域教科書國民小學一～六年級數學領域教師手冊閱讀梯形相關文獻正式施測試題學生答題概念分析並選取概念點以IRS分析各解題策略的概念結構圖學生與專家概念結構的比較試題檢核表與專家質的核信效度分 N N Y Y 究結論研

(47)

第二節研究對象

本研究正式施測時，選取彰化縣某仁類位於小鎮的國民小學為對象，該校有 17 班，亦因時間、教師協調及行政溝通等各方面因素，故立意選取六年級一個班級學生共24 個人為施測對象，該班男生 15 人、女生 9 人。家長多是上班族，較無睱照顧小孩，故學生放學大多是參加安親班或任其自我學習，有少數幾位的家長是公教人員，有能力而且也親自指導，所以學生素質差異相當大。為減少環境、情境等其它因素之影響，使學生能在最熟悉的環境下施測，故施測地點在該班教室。施測前，先說明測驗的目的與作答的方式，學生作答時間為 40 分鐘（詳如附錄一）。

(48)

第三節研究工具

本研究之主要研究工具為「國小六年級學生拼湊梯形面積概念測驗」，以及相關的統計軟體等，茲說明如下：

壹、國小六年級學生梯形面積概念測驗的編製過程

一、編製梯形教材架構圖

本試題的編製是由研究者參考現行國民小學六年級數學領域梯形教材以及教師手冊內容，編製梯形教材架構圖，如圖3-2。

二、建立梯形面積概念結構圖

然後，參酌梯形概念的相關研究文獻，配合學生的認知發展，依據研究目的— 探討梯形面積的解題策略來選擇所需要的概念，架構出梯形面積概念圖，如圖 3-3，在此不探討梯形的性質、面積的估測、面積單位的換算，甚至是解題策略之一的分割並重組成長方形，因為涉及國中全等概念，基於學習程序，也予以刪除，縮小研究範圍，以求深入。

三、編製梯形面積概念試題

再依據此概念圖編製梯形面積概念之試題(如附錄一)。

(49)

由圖形的外觀辨認出梯形梯形面積的解題策略認識梯形各部位名稱透過實測察覺梯形的性質面積單位的認識與換算（化聚）保留概念與遞移律點數單位面積梯形面積的解題應用梯形面積公式化長方形面積公式 (2)將梯形分割成兩個三角形，再求梯形面積 (3)分割並重組成長方形，再求梯形面積 (1)利用兩個全等梯形拼湊成平行四邊形，再求梯形面積平行四邊形面積公式三角形面積公式 (4)將梯形分割成三角形和平行四邊形，再求梯形面積圖 3- 2 梯形面積教材架構圖

(50)

兩個不同三角形拼湊成梯形面積 20 三角形和平行四邊形拼湊成梯形面積 14.23 由平行四邊形面積求出梯形的面積 17 梯形解題應用(多重分割線) 27 梯形解題應用(一條分割線)24.25. 26 梯形的上下底 7 梯形的高 6 梯形面積公式計算 8、9 平行四邊形面積的計算 1 將梯形分割成兩個已知底和高的三角形並求得面積 15、18、19 將兩個全等的梯形組合成平行四邊形 14、16 將梯形分割成三角形和平行四邊形，並求得三角形面積 22 點數正放梯形面積 10 點數側放梯形面積 11 點數斜放梯形面積 12 點數複合面積 13 面積保留概念 3、 4、 5 將梯形分割成三角形和平行四邊形，並求得平行四邊形面積21 三角形面積的計算 2 圖 3- 3 梯形面積概念圖